EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A90 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A90
Number of page(s) 15
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201321423
Published online 06 September 2013

© ESO, 2013

1. Introduction

The formation of new low-mass stars begins with the gravitational collapse of a cold dense core inside a molecular cloud which then heats up in its centre as the pressure and density increase from the compression, a problem which entails many physical processes (hydrodynamics, radiative transfer, magnetic fields, etc.) over a very large range of spatial scales (Larson 1969; Stahler et al. 1980; Masunaga et al. 1998). The collapsing material is initially optically thin to the thermal emission from the cold gas and dust grains and all the energy gained from compressional heating is transported away by the escaping radiation, which causes the cloud to collapse isothermally in the initial stages of the formation of a protostar. When the optical depth of the cloud reaches unity, the radiation is absorbed by the system which starts heating up, taking the core collapse through its adiabatic phase. The strong compression forms an accretion shock at the border of the adiabatic core (also known as Larson’s first core). The first core continues to accrete the surrounding material, grows in mass but still contracts further thanks to the gravity which overcomes the thermal support as well as radiative losses. With contraction comes a rise in gas temperature, and as it reaches 2000 K the hydrogen molecules begin to dissociate. This leads the system into its second phase of collapse because of the endothermic nature of the dissociation process. The second collapse ends when most or all of the H2 molecules have been split and a second much more dense and compact hydrostatic core is formed at the centre; Larson’s second core is born (Larson 1969; Masunaga & Inutsuka 2000, hereafter MI00; Stamatellos et al. 2007, hereafter SWBG07; Tomida et al. 2013, hereafter Tea13).

Numerical studies of the first and second collapse are very demanding, they require the solutions to the full radiation hydrodynamics (RHD) system of equations, and three-dimensional RHD simulations have only just recently become possible with modern computers. One-dimensional studies including the most complex physics are still leading in terms of understanding and discovering the physical processes at work. In particular, including frequency dependent radiative transfer is essential to properly take into account the strong variations of the interstellar gas and dust opacities as a function of frequency (see for example Ossenkopf & Henning 1994; Li & Draine 2001; Draine 2003a; Semenov et al. 2003; Ferguson et al. 2005). Three-dimensional full frequency-dependent radiative transfer is still out of reach of current computer architectures and only rare attempts with simplified methods have been made in the context of star formation (see e.g. Kuiper et al. 2011). In this paper, we continue the recent one-dimensional simulations of the first collapse of Vaytet et al. (2012, hereafter Paper I) by following the evolution of the system through the second phase of the collapse up to the formation of the second Larson core. This involves the inclusion of a sophisticated equation of state (EOS) to reproduce the effects of the H2 dissociation, which cannot be achieved using the more common ideal gas EOS. A new set of frequency-dependent opacities was also developed since the one used in Paper I was only valid for temperatures below ~2000 K.

We first describe the numerical method, EOS, and opacities used in the simulations. The frequency dependence is implemented through the multigroup method in which the frequency domain is divided into a finite number of bins or groups, and the opacities are averaged within each group (Vaytet et al. 2011). The thermal evolution of the system is then described and radial profiles are presented. Simulations of the collapse of clouds with different initial masses were performed and the properties of the first and second cores are listed.

2. The multigroup RHD collapse simulations

2.1. Numerical method and initial conditions

The code used to solve the multigroup RHD equations was an updated version of the one-dimensional fully implicit Lagrangian code used in Paper I. Most of the code remained unchanged, but a new EOS and opacity database were added (see Sect. 2.2), as well as a parallelisation scheme using OpenMP. The grid comprises 2000 cells logarithmically spaced in the radial direction.

The initial setup for the dense core collapse was identical to Paper I. A uniform density sphere of mass M0 = 1  M⊙, temperature T0 = 10 K (cs0 = 0.187  km   s-1), and radius R0 = 104 AU collapses under its own gravity. The ratio of thermal to gravitational energy in the cold gas cloud is 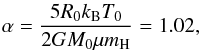(1)where G is the gravitational constant, kB the Boltzmann constant, μ the mean molecular weight, and mH the mass of the hydrogen atom. The cloud’s free-fall time is tff ~ 0.177 Myr1. The radiation temperature is in equilibrium with the gas temperature (the energy of a black body with T = 10 K is divided among the frequency groups according to the Planck distribution) and the radiative flux is set to zero everywhere. The boundary conditions are reflexive at the centre of the grid (r = 0) and have imposed values equal to the initial conditions at the outer edge of the sphere.

2.2. Gas equation of state

We used the gas equation of state (EOS) of Saumon et al. (1995, hereafter SCvH95 which models the thermal properties of a gas containing the species H2, H, H+, He, He+, and He2 + (the He mass concentration was 0.27). We extended their original EOS table to low temperatures (below 125 K) and densities (below 10-6  g   cm-3) by computing the partition function for H, He, and H2 (taking into account the correct rotational excitation levels for H2). The Debye-Hückel interaction term and the Hummer & Mihalas (1988) excluded volume interaction are both included in the computation of the chemical equilibrium, and the zero point of energy is chosen as the ground state of the H2 molecule. The calculation is trivial but rather tedious and, for the sake of conciseness, is not explicited further.

Figure 1 displays μ and the effective ratio of specific heats (γeff) obtained from the resulting table as a function of temperature for five different gas densities. The table recovers the transition around 85 K (see Sears & Salinger 1975, p. 378) from a monatomic γeff = 5/3 at low temperatures (when the H2 rotational levels are frozen) to a diatomic gas with γeff = 7/5. Because of the Boltzmannian nature of the energy distribution, rotational levels start to get excited as early as 30 K, and the transition from a monatomic to a diatomic γeff operates smoothly as the temperature increases. This realistic EOS table also enables us to properly model the second phase of the collapse which begins with the dissociation of H2 around T ~ 2000 K (also visible in Fig. 1; we note that the dissociation temperature varies somewhat with the gas density).

thumbnail Fig. 1

SCvH95 EOS and its extension to low densities: μ(a) and γeff(b) as a function of temperature for five different densities (see colour key in each panel).

2.3. Interstellar dust and gas opacities

For our multigroup simulations, we require temperature and density-dependent monochromatic opacities for the interstellar gas. A complete set of monochromatic opacities, covering the range 10-19  g   cm-3 < ρ < 102  g   cm-3 and 5  K < T < 107  K does not exist in the literature and we had to piece together several different tables. We used three different opacity sets, one for interstellar dust, one for molecular gas, and one for atomic gas; this is illustrated in Fig. 2.

At low temperatures (below 1500 K), the opacities of the interstellar material are dominated by the one percent in mass of dust grains present in the medium. For this temperature region, we used (as in Paper I) the monochromatic opacities from Semenov et al. (2003)2 who provide dust opacities for various types of grains in five different temperature ranges (we assume that the dust opacities are independent of gas density and that the dust is in thermal equilibrium with the gas; see e.g. Galli et al. 2002). We used the spectral opacities for homogeneous spherical dust grains and normal iron content in the silicates (Fe/(Fe + Mg) = 0.3). At the high frequency end (ν > 3 × 1015 Hz), we have completed the set with high-energy dust opacities from Draine (2003b), giving a total of 583 frequency bins between 3 × 109 and 3 × 1018 Hz. The opacities at those high frequencies are not very important since the dust is only present at low gas temperatures (below 1500 K) and there will be virtually no radiative energy in that part of the spectrum. The Draine opacities were only included so that the UV and X-ray frequency groups had a non-zero opacity in the cold parts of the simulation. The dust κ(ρ,T,ν) data set is pictured in Fig. 2 (red circles).

For temperatures between ~1500−3200 K, the dust grains are rapidly destroyed and molecular gas opacities prevail (see Ferguson et al. 2005). We have used a set of monochromatic opacities for the range 10-17  g   cm-3 < ρ < 10-5  g   cm-3 and 1500  K < T < 3200  K for an interstellar gas with solar abundances comprising ~26 000 frequency bins between 6 × 1011 and 3 × 1017 Hz that were calculated based on the computations discussed in Ferguson et al. (2005). This is shown in Fig. 2 (green crosses).

Finally, at temperatures above ~3200 K there are no more molecules and the atomic opacities take over. In the range 10-20  g   cm-3 < ρ < 106  g   cm-3 and 103.5  K < T < 108  K, we have used a set of monochromatic OP opacities with 10 000 frequency bins in the range 0.1 < hν/kBT < 20 (Badnell et al. 2005). The atomic gas opacities are represented in Fig. 2 by blue squares.

thumbnail Fig. 2

Spectral opacities κ(ρ,T,ν). Each data point represents a set of spectral opacities for a given density and temperature. The table has been compiled from three different opacity collections. At low temperatures (below 1500 K), the dust opacities are from Semenov et al. (2003) and are completed by the dust grains opacities of Draine (2003b) at the high frequency end (red circles). For temperatures between 1500 and 3200 K, the opacities for molecular gas based on the Ferguson et al. (2005) calculations are used (green crosses). Finally, for temperatures above 3200 K, the atomic gas opacities are from the OP project (Badnell et al. 2005, blue squares). Two coloured areas, grey and yellow, show the approximate range of densities and temperatures typically reached during the first and second stages of the collapse of a cloud core, respectively.

thumbnail Fig. 3

The three steps in the construction of the regular opacity table. (a) Group average opacities are computed for each spectral point in the (ρ,T) table. (b) A Delaunay triangulation is computed in the (ρ,T) plane using each table point as a triangle vertex. Each triangle from the Delaunay triangulation represents a plane in the (ρ,T,κg) space. (c) We then overlay a fine rectanglar grid of opacity points which are computed from their coordinates in the opacity planes (see text for more details).

thumbnail Fig. 4

Grey Rosseland mean opacity as a function of temperature and density. The steep trench (dark blue) along the density dimension around T ~ 1500 K corresponds to the destruction of dust grains, while the high peak (in red) represents the region where the dominant atomic gas opacities become very high.

Our resulting raw table covers the entire evolutionary track of a two-stage cloud collapse, as opposed to the one used by Tea13 which is incomplete, especially towards the high temperatures and densities reached during the second collapse, where they used simple extrapolations as opposed to real opacities (see their Appendix B).

In our multigroup method, we need to compute Planck (κP) and Rosseland (κR) mean opacities as a function of density and temperature for each frequency group. We describe below the three-step process we employ to efficiently compute the group mean opacities κPg and κRg (see Fig. 3).

  • (a)

    κPg and κRg are computed for each spectral point in the (ρ,T) table (Fig. 2) once at the beginning of the simulation.

  • (b)

    Since the points in the table are not all regularly spaced in ρ and T, a Delaunay triangulation is computed in the (ρ,T) plane using each table point as a triangle vertex.

  • (c)

    Each triangle from the Delaunay triangulation represents a plane in the (ρ,T,κg) space. We are now able to overlay a fine rectanglar grid of opacity points which are computed from their coordinates in the opacity planes (triangles).

This fine rectangular mean opacity grid allows for fast index finding and efficient bicubic interpolation during the rest of the simulation. The edges of the table, outside of all the triangles, were filled by simply using the outermost value of the closest triangle, giving more or less a flat opacity surface. This was only included for consistency as these extreme values of (ρ,T) were never reached in the simulations. The fine regular mesh of Rosseland mean opacities averaged over the entire frequency range (in the case of a single frequency group) is shown in Fig. 4. We note the presence of the sharp opacity gap in the region log   (T) ~ 3.2 corresponding to the destruction of the dust grains. We also see that there is an opacity peak for log (T) ~ 4−5 at high densities.

3. Results

Grey (run 1) and multigroup (run 2) simulations of the collapse of a dense core were performed (see Table 1). In the grey run, the radiative quantities were integrated over the entire frequency range (0 to 1019 Hz) while for the multigroup run, 20 frequency groups were used; the decomposition of the frequency domain is illustrated in Fig. 5. The simulations were run until the central density reached ρc = 6 × 10-2  g   cm-3.

Table 1

Initial conditions for the different simulations.

thumbnail Fig. 5

Decomposition of the frequency domain using 20 groups, presented over the monochromatic dust opacities. The first and last groups are used to make sure no energy is omitted at the low and high ends of the spectrum, respectively. The other groups offer an almost log-regular splitting of frequencies in the range 2.0 × 1011−3 × 1016 Hz. The group numbers are indicated just above the opacity curve. The presented spectral opacities are for typical initial conditions of ρ = 10-18  g   cm-3 and T = 10 K.

3.1. The two phases of the 1 M⊙ cloud collapse

Figure 6 shows the thermal evolution at the centre of the cloud core for the grey (black) and the multigroup (red) simulations alongside results from other studies. The protostellar collapse occurs as follows:

  • The cloud core first contracts under its own gravity and, as thecloud is optically thin, all the compression heating is radiatedaway; the cloud collapses isothermally.

  • As the density inside the core increases, the optical depth eventually surpasses unity and the cloud begins to retain the heat from compression. This is the formation of the first core (M ~ 2 × 10-2  M⊙, R ~ 10 AU) and the core subsequently contracts adiabatically.

  • In the adiabatic phase, the temperatures are high enough for the rotational degrees of freedom of H2 to be excited, and the effective adiabatic index γeff is that of a diatomic gas (=7/5). The first core continues to contract and accrete infalling material.

  • When the temperature inside the first core reaches ~2000 K, the molecules of H2 begin to dissociate. This endothermic process constitutes an important energy sink which initiates the second phase of the collapse. During this phase, γeff is usually approximated to about 1.1 (see MI00), although our results suggests that it is in fact somewhat higher.

  • Finally, once all the H2 has been dissociated, the second collapse ends, the adiabatic regime is restored, and the second core is formed (M ~ 10-3  M⊙, R ~ 3 × 10-3  AU ≃ 0.62  R⊙).

The thermal evolutions of the grey and multigroup simulations are very similar to each other. Small differences are visible at the time of first hydrostatic core formation, with the multigroup simulation developing a core slightly earlier. The time of first core formation corresponds to the time when the collapsing envelope becomes optically thick and the radiation can no longer escape from inside the system. If the opacities are different in the grey and multigroup cases, one would expect the first cores to form at different times; in this particular situation, it appears that the overal absorption of photons is more efficient in the multigroup case since the core becomes adiabatic earlier.

The results are also in good agreement with the works of MI00, Whitehouse & Bate (2006), SWBG07, and Tea13. The centre of the core in the Tea13 simulation during the first adiabatic contraction is hotter than our results (and the other studies mentioned). This appears to be due to the use of a different EOS; in our simulation γeff starts to drop below 5/3 earlier than in the EOS used by Tea13 (20 K compared to 100 K for Tea13; see Fig. 1b and Fig. 1 in Tea13). This is also illustrated by the orange curve in Fig. 6 which represents the thermal evolution of a simulation we ran with exactly the same setup as run 1 but using an ideal gas EOS with a fixed γ = 5/3 instead of the SCvH95 EOS. We can clearly see that for densities below 10-10  g   cm-3, the Tea13 behaves very much like an ideal gas with γ = 5/3. The EOS used by Whitehouse & Bate (2006) seems to operate in a very similar manner, while the simulations of MI00 and SWBG07 follow our thermal track much more closely.

One of the main differences between the various EOS used by the different studies is the treatment of the different spin isomers of the H2 molecule in the low-to-moderate temperature regime. At the time of formation of the first core (and for a while later), the gas is composed entirely of neutral H2 and He, with H2 being the dominant species. The H2 molecules come in two forms corresponding to the two different spin configurations called para- (singlet state) and ortho- (triplet state) hydrogen. The SCvH95 EOS takes into account the symmetry of the nuclei wave-functions explicitly and makes no assumptions about the population ratios of the two species, which inherently implies thermodynamic equilibrium. However, the transition to ortho-para equilibrium is known to be a lengthy process, unless a magnetic catalyst (e.g. iron) is present in the medium, so that at low temperatures (T ≲ 300 K) the population distribution of the two H2 monomers is not the equilibrium value. Observations indeed suggest that the real abundance ratio in molecular clouds and star forming regions is far from the thermal equilibrium value (see Pagani et al. 2011; and Dislaire et al. 2012, for two recent examples), even though large discrepancies (due to observational difficulties) between the studies remain. For this reason, SWBG07 and Tea13 have made the assumption that the ortho:para abundance ratio remains frozen at its initial value of 3:1 (which reflects the statistical weight of each variety according to their spin degeneracies), as ortho- and para-hydrogen form on the surface of dust grains. Using a fixed rather than an equilibrium ratio can potentially have a significant impact on the early thermal evolution of the collapsing body (i.e. when temperatures remain below the spin equilibrium temperature of ~170 K). On the other hand, Flower & Watt (1984) have shown that under typical molecular cloud conditions (n ~ 100−1000  cm-3) the time when ortho:para equilibrium is reached is of the order of 1 Myr. This is of course five to ten times larger than the free-fall time of the core we are modelling, but this core is formed as a result of turbulence in the molecular cloud which spawns over-densities that eventually become gravitationally unstable. The collapse will begin long after the formation of the molecular cloud which has a typical lifetime of ~10 Myr and it is thus very possible that at the onset of the collapse, ortho:para equilibrium has already been reached. In summary, it is not clear which ortho:para strategy (fixed ratio or equilibrium) is the most representative of the initial conditions of star formation.

thumbnail Fig. 6

Thermal evolution at the centre of the collapsing cloud: the central temperature as a function of the central density for the grey (solid black) and multigroup (solid red) simulations. The different phases of the protostellar collapse are labelled. The results from MI00 (dashed green), Whitehouse & Bate (2006) (dashed purple), SWBG07 (dashed cyan), and Tea13 (dashed blue) are also plotted for comparison. The orange solid line is a grey simulation using an ideal gas EOS.

Different treatments of H2 molecules will not affect the optically thin parts of the system where the gas temperature is controlled by the radiation field (and the value of γeff does not matter), but could explain why the simulation of Tea13 produces a first core which is hotter than our own for the same densities. A hotter first core can in turn have an effect on the properties of the second core, since the H2 dissociation temperature is reached earlier (in terms of central density) and the second phase of the collapse will thus also end earlier (the amount of H2 which has to be dissociated remains the same). Consequently, the initial protostellar seed formed at the end of the second collapse will have a lower density and its radius will probably be larger. As it turns out, Tea13 have found a second core which is also slightly more massive than us (a factor of ~2.5), yielding a much (~10 times) larger body (see the properties of the second core formed in our simulations in Sect. 3.2).

It is, however, not possible to determine if the ortho/para H2 treatment is the main contributor to the differences in thermal evolutions. The only robust method would be to compute a new EOS table using the SCvH95 code, forcing the ortho:para ratio to remain fixed at 3:1, but this procedure is rather complex and beyond the scope of this paper. Nevertherless, we can speculate by looking more closely at the other studies. Indeed, SWBG07 have used the same assumption as Tea13 but their thermal evolution mirrors our curve. In contrast, the thermal evolution of the Whitehouse & Bate (2006) study, which makes use of an equilibrium model from Black & Bodenheimer (1975) that is very similar to our own, tends to follow the Tea13 path. If the ortho:para ratio was the dominant factor, one would expect it to be the other way round (SWBG07 ≃ Tea13; Whitehouse & Bate 2006 ≃ this work), which leads us to believe that the abundances of the H2 flavours cannot alone be responsible for the discrepancies between the studies.

Finally, we also note that even though they use the same EOS, the results of MI00 show a second core forming later than in our calculations; this is most probably due to a difference in opacities used.

The inset in Fig. 6 shows a bounce in the thermal evolution. There is a time during the simulation when the core becomes thermally supported, stops contracting, and begins to inflate. The density and gas temperature inside the adiabatic body decrease and the first core radius increases until the thermal pressure is no longer high enough to prevent contraction. The collapse then resumes and this time the infalling gas has enough momentum to drive the collapse past this point, to a state where gravity once again becomes dominant, enabling further contraction. This bounce was not seen by MI00 and Tea13, but it is visible (with a smaller amplitude) in Fig. 7 of SWBG07 (it is, however, not visible in our approximate reproduction of the SWBG07 data). A bounce is also visible in a very similar test in Fig. 14 of SWBG07 but it is not mentioned or discussed in the text.

thumbnail Fig. 7

Thermal evolution for the grey (dashed) and multigroup (solid) simulations.

Figure 7 shows snapshots of the state of the gas in the system at six different epochs for the grey (dashed) and multigroup (solid) simulations. The thermal evolution of the central fluid element from Fig. 6 is also plotted for reference (black). At early times (ρc ≤ 10-10  g   cm-3), all the gas in the grid follows approximately the same thermal evolution as the centre of the core. At later times, shock heating and absorption of radiation coming from the hot centre enable the outer layers of the system to have much higher temperatures than the central point. We note here again that differences between the grey and multigroup simulations are small. A displacement in the position of the first core accretion shock away from the centre is also visible on this plot; this is discussed in Sect. 3.5.

3.2. Radial profiles

thumbnail Fig. 8

Radial profiles of various properties during the collapse of a 1  M⊙ dense clump at a core central density ρc = 6 × 10-2  g   cm-3, for the grey models (black dashed lines) and multigroup models (coloured lines). For the multigroup run, the gas and total radiative quantities (summed over all groups) are plotted in magenta, while the other colours represent the individual groups (the colour-coding is the same as in Fig. 5); see legend in (b). From top left to bottom right: (a) density, (b) gas temperature (magenta and black) and radiation temperature (other colours), (c) velocity, (d) entropy, (e) optical depth, (f) luminosity, (g) Rosseland average opacity, and (h) radiative flux.

Table 2

Summary of the first and second core properties when ρc = 6 × 10-2  g   cm-3 for the different simulations.

Figure 8 shows the radial profiles of the density, temperature, velocity, entropy, optical depth, luminosity, opacity, and radiative flux for the grey (black dashed line) and multigroup simulations (colours) for a central density ρc = 6 × 10-2  g   cm-3. The first and second core borders are visible at ~30 AU and 3 × 10-3 AU, respectively, and can be seen very clearly in the density (a) and velocity (c) panels. The temperature plot (b) reveals that the first core accretion shock is supercritical (pre- and post-shock temperatures are equal, see discussion in Commerçon et al. 2011), while the shock at the second core border is subcritical (the simulations of Tea13 also show this). Table 2 lists the main properties of the first and second cores; these are the core radius (R) and mass (M), the mass accretion rate at the core border (Ṁ), the accretion luminosity (Lacc), the total radiated luminosity (Lrad), the temperature at the first core border (Tfc) and at the centre of the second core (Tc), the entropy at the centre of the system (Sc), the accretion shock Mach number, the first core lifetime (tfc) and the time in the simulation when the central density has reached 6 × 10-2  g   cm-3. Further details on the derivation of these quantities can be found in Paper I.

Compared to the first collapse simulations in Paper I, the first core has now grown both in size and mass, from 7 to about 30 AU and from 2 × 10-2  M⊙ to ~4    ×    10-2  M⊙. We also notice that the temperatures at the first core border is half the value reported in Paper I, probably because of its increased size and the use of a slightly different EOS. The first core lifetime tfc is defined as the time elapsed between the formation of the first core (chosen as the time when ρc > 3 × 10-10  g   cm-3) and the beginning of the second collapse (when the central temperature exceeds 2000 K). The subsequent formation of the second core, after which the spectral properties of the collapsing system change dramatically (e.g. MI00), is almost instantaneous (see Sects. 3.3 and 3.5). Our simulation yields a lifetime of ~1000 years, which is a relatively short time for a chance to observe a first core in its formation stage. This value is, of course, a lower limit because no support from rotation is present in our spherically symmetric model.

The second core is very compact, measuring only 3 × 10-3 AU in size for a mass of 10-3  M⊙. The accretion luminosity 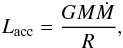(2)where M is the mass contained within the radius R and Ṁ is the mass accretion rate, is an estimate of the luminosity at the accretion shock assuming that all the infalling kinetic energy is transformed into radiation. At the second core border, Lacc greatly outweighs the total radiative luminosity (by about 12 orders of magnitude) which, together with the fact that the shock is subcritical, shows that all the accretion energy is transfered to the second core, none of it is radiatied away; the accretion shock is almost completely adiabatic. This strongly differs from what happens at the first core border where the vast majority of accretion energy is transformed into radiation (see Paper I). We note that the situation could be different in 3D simulations where a significant fraction of the accretion energy may be transported away by outflows. We also remark that the mass accretion rates at the second core border are colossal (0.2  M⊙/yr); the mass of the second core grows very rapidly.

Stahler et al. (1980) predicted that whether the second core accretion shock would be sub- or supercritical would depend on the magnitude of a dimensionless parameter κρR, computed just ahead of the shock (R is the shock radius). For κρR ≪ 1 the shock would be subcritical whereas in the case of κρR ≫ 1 the shock would be supercritical. This parameter does not make any sense to us because what determines whether a shock is in the sub- or supercritical regime is the optical depth of the gas downstream and, more importantly, upstream of the shock (see Drake 2006, pages 296+ for a discussion). Here, κρR is only a simple estimate of the optical thickness of the gas downstream of the shock (assuming ρ and κ to be constants inside the core), and the upstream condition is ignored altogether. In addition, if we consider their subcritical scenario, they estimate that about 3/4 of the accreted energy is transfered to the core; as mentioned above we find it to be ~1.

There are two peaks in radiative flux; the first one around 0.3 AU originates from the region where the opacity has fallen sharply thanks to the destruction of dust grains when the temperature exceeds 1500 K (see gaps in Figs. 8g and 4). This represents the dust border (see e.g. Stahler et al. 1980), but only the radiative flux is strongly affected at that location; the hydrodynamical quantities seem relatively insensitive to the presence of this border, except for a small kink visible in the temperature profile. The second burst in radiative flux occurs at the second core border where the sharp jump in gas and radiative temperature provoke a rise in radiative flux. The high optical depth at that radius means that the flux is very rapidly absorbed and the flux burst only appears as a sharp spike in the profiles.

Surprisingly, the grey and multigroup simulations yield very similar results. The curves overlap in most places; only the core borders are at slighty different locations and the multigroup gas temperature is above its grey counterpart between 20 and 1000 AU. Differences of ~10−20% in the sizes and masses of the first and second cores are reported in Table 2, which are significant from a theoretical point of view but are in no way detectable through obervations. The second collapse is a very short and violent and dynamic event in the lifetime of protostars, and the details of the radiation transport may not have time to affect the system dynamics significantly. However, multi-frequency radiative transfer could have a greater effect on the long-term evolution of the protostar. One can estimate the characteristic timescale of the second core by integrating the total energy inside the core and computing how long it will take for the core to radiate all of its energy with the current luminosity at the core border, that is 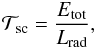(3)where 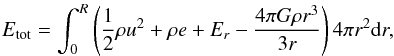(4)where u is the gas velocity, e the specific internal energy, and Er the radiative energy. The characteristic timescales are listed in the last column of the second core sub-table in Table 2. We can see that even though differences in core mass, radius, and luminosity between grey and multigroup simulations are small, they can lead to considerable variations in characteristic timescales. The subsequent evolution of the protostar is of course very complex, with continued accretion and the ignition of thermonuclear reactions, and we are obviously not making any strong claims with our simple estimate, but merely suggesting that multi-frequency effects might be more significant in the long run than is visible here.

3.3. The second core formation

thumbnail Fig. 9

Radial profiles of the (a) gas density, (b) normalised entropy SN (see text), (c) temperature, (d) species concentrations, (e) mean molecular weight μ, and (f) effective ratio of specific heats γeff. In all panels, the dotted line describes the first core profiles while the dashed and solid lines represent the quantities just before and after the formation of the second core, respectively.

Figure 9 illustrates what happens at the time of second core formation; the different panels show the radial profiles of the gas density (a), normalised entropy SN (b), temperature (c), species mass concentrations (d), mean molecular weight μ (e), and effective ratio of specific heats γeff (f). The normalised entropy SN is defined as the entropy per free particle multiplied by ρ/mH which is simply 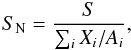(5)where i is summed over all the species, X is the species mass concentration, and A their atomic number. The dotted line describes the first core profiles while the dashed and solid curves represent the state of the system just before and after the formation of the second core, respectively.

The first core profiles in panels (d) and (e) show that it is constituted entirely of H2 and neutral He with a constant mean molecular weight of 2.31. The dashed lines represent the profiles of the system when the second collapse is already well underway but the second core has not yet materialised. Between radii of 0.5 and 104 AU, the hydrogen and helium concentrations, as well as the mean molecular weight, remain constant. Below 0.5 AU, the dissociation of H2 starts to take place as the gas temperature exceeds 2000 K, and the fraction of atomic hydrogen increases, which consequently causes μ to decrease. The molecular and atomic hydrogen concentrations exhibit symmetric profiles, as a rise in one is compensated by a fall in the other. They both reach a plateau below 5 × 10-3 AU, as is the case for the gas density, temperature, and pressure.

The formation of the second core is very abrupt; the time between the two outputs (dashed and solid) is approximately two days. The second core is formed as the dissociation of H2 begins to shut down. In the centre, as most the H2 is destroyed, the energy sink provided by the dissociation no longer operates, and this starts to prevent further collapse. As the outer infalling material smashes into the gas at the centre which is no longer collapsing, a strong hydrodynamical shock is created at the border. The temperature and density of the accreted material increase sharply as they flow through the shock. We can see that downstream from the shock, almost all the H2 has been dissociated, a third of the atomic H has been ionised, and there is also a very small amount of He that gets ionised because of the high gas temperature.

The entropy of the gas at the centre of the system Sc listed in Table 2 is identical for the first and second cores, i.e. the first core sets the properties of the system. However, the normalised entropy SN in Fig. 9b shows that the entropy per free particle decreases significantly between the first and second cores as a result of the dissociation of H2 that increases the number of particles. A further decrease is seen between the dashed and solid profiles because of the additional dissociation taking place inside the second core.

Figure 9f shows the effective ratio of specific heats γeff = p/e + 1 where p is the gas pressure and e the gas internal gas energy. It shows that the initial cloud starts out as a monatomic ideal gas (γeff = 5/3) and transitions to a diatomic gas (γeff ≃ 7/5) as the temperature exceeds 20 K where the rotational degrees of freedom of the H2 molecules begin to be excited. Inside the first core (between 0.5 and 20 AU), the gas is akin to a diatomic adiabatic polytrope (γeff ≃ 7/5). Then, during the second collapse, the effective γeff drops as low as 1.2 amid a phase transition from H2 to H. Finally, inside the newly formed second core, the gas becomes essentially mono-atomic, and we expect γeff to return to 5/3. However, there is ~5% of H2 remaining inside the core and a small amount of dissociation is still operating, which lowers γeff. In addition, at such high temperatures and densities, correlation effects start to become noticeable that also alter the value of γeff (see Saumon & Chabrier 1992).

3.4. Varying the initial parameters

To check the universality/robustness of the results above, we also performed simulations of the collapse of a 0.1 M⊙ and a 10 M⊙ cloud using 1 and 20 frequency groups. The initial setups were identical to that of Paper I in that the thermal to gravitational energy ratio was kept constant (see Table 2 for details). The results are shown in Fig. 10 (panels a to f), along with the previous results from the 1 M⊙ case.

thumbnail Fig. 10

Comparison of the radial profiles of collapse simulations at a central density of ρc = 6 × 10-2  g   cm-3 using various initial parameters (see Table 2 for details). The different panels display the following as a function of radius: (a) and (g) density, (b) and (h) gas temperature, (c) and (i) entropy, (d) and (j) radiative luminosity, and (e) and (k) enclosed mass. Panels (f) and (l) display the thermal evolution at the centre of the grid. Panels (e) and (k) show the colour legend.

As in Paper I, the results are strikingly similar to the 1 M⊙ case, for both 0.1 M⊙ and a 10 M⊙ clouds. The properties of the first and second cores for the new cloud masses are listed in Table 2, which emphasizes this point even more. The masses, temperatures, and sizes of both cores seem invariant of the initial cloud mass, with the second core showing the highest convergence between models. Second core radii differ by less than 3% while the masses exhibit variations of only 2%. The sizes and masses of the second cores also agree fairly well with the analytical estimates of Baraffe et al. (2012). All the simulations begin with the same gravitational to thermal energy ratio, and it is thus not very surprising to see such a tight concordance of results. We also add that in all cases, differences between grey and multigroup simulations remain very small (for the sake of clarity this is not shown in the figures).

thumbnail Fig. 11

Evolution of the first core for runs 2, 4, 6, 7, 8, 9, and 10 (see colour legend in top-left panel). (a) Core radius as a function of time. (b) Core radius as a function of central density. The dashed line represents the Masunaga et al. (1998) estimate. (c) Central density as a function of time. (d) First core mass as a function of time. (e) Mass accretion rate at the core border as a function of time. (f) Central temperature as a function of time. t0 represents the time when ρc ≥ 10-10  g   cm-3, taken as the time of first core formation; t0 is listed for each run next to the colour key in panel (a). In all panels, the circles mark the onset of the second collapse and the bold lines trace the transition region when the central density and temperature increase more slowly than during the rest of the simulation (see text).

Four additional simulations were run, this time changing the initial gravitational to thermal energy ratio and the temperature of the parent gas cloud (see Table 2 for details). Runs 7 and 8 were performed with a parent cloud half and double the size, respectively (the gas in run 8 was colder so that the cloud would collapse). The initial temperature of the gas in runs 9 and 10 was 5 and 20 K, respectively (the size of the cloud in run 10 was halved to overcome the stronger thermal support provided by the hotter gas). The radial profiles are displayed in Fig. 10 (panels g to l).

The different simulations yield similar results, and the sizes and masses (listed in Table 2) of the second cores further confirm their insensitivity and ignorance of the initial conditions. The size of the first core varies from 6 AU for runs 7 and 10 to about 20−30 AU for the other runs; 6 AU is the size the first core has at its time of formation (see Paper I) and we explore the origin of the expansion of the first core in the next section.

3.5. The evolution of the first core

As mentioned in Sects. 3.1 and 3.4, the first core border is not stationary throughout the simulations, and this is also illustrated by the temporal evolutions plotted in Fig. 11. The timeframe shown begins when the central density reaches 10-10  g   cm-3 (taken as t0). At early times (t < 200 yr), all the simulations show one or several bounces (panels a, c, and f) during which the first core is momentarily thermally supported and oscillates between thermal and gravitational pressure3. This was already visible in Fig. 6, and Tea13 also observed similar bounces. Figure 11b shows the evolution of the core radius as a function of the central density, which again presents oscillations in the lower left corner.

In the case of run 2 (black), after a small period of time during which it remains approximately constant (125  yr < t < 225  yr), the first core radius enters a phase of steady increase. Panel (e) shows that the core has an almost constant accretion rate during that phase and is continuously growing in mass, while panel (c) reveals that the central density, for most of the core’s lifetime (300  yr < t < 950  yr), does not increase as strongly as it did at earlier times; this transition period has been highlighted in bold in the figure. A more massive core with the same density can only be larger, which explains the increase in core border radius. A second possible contribution to the inflation of the first core comes from the radiation from the hot centre of the core which heats the gas in the outer layers (see Fig. 7), causing it to expand. This increase in size was also found by Schönke & Tscharnuter (2011), but is in disagreement with the analytical analysis of Masunaga et al. (1998) who predicted that the first core radius would decrease in time (see dashed line in panel b). We believe that the origin of the discrepancy lies in the assumption of Masunaga et al. that the first core is isentropic, which is not strictly the case, as seen in Fig. 8d. Radiative transfer is capable of re-distributing entropy outwards, which invalidates their assumption. It is a shame that MI00 do not show the results they obtained for the first core radius evolution when running new simulations with the same EOS (SCvH95) as we have used in this work, which would have allowed us to conduct a better comparison.

All runs but two, namely 7 and 10, follow a similar evolution pattern, with a lengthy transition phase of slowly increasing central density and temperature. As for runs 7 and 10, the behaviour is markedly different; the core radius remains approximately constant during the entire core lifetime. The parent cloud in these two runs is half the size of that of run 2 and is therefore more unstable (much smaller free-fall time; see Table 1), i.e. it collapses faster (in simple terms, dividing the radius of the parent cloud by its free-fall time gives a dimensional estimate of the infall velocity which scales with r−1/2 for a given cloud mass). The higher infall velocity yields a larger mass accretion rate at the core border (see panel d). The increased effects of gravity on a core fast becoming more massive boost the rate of contraction and in the process enhance heating at the centre. The 2000 K mark is reached earlier (see green and orange curves in panel f) and the second collapse begins before the first core has had time to grow (no transition period is visible in the time profiles). In addition, radiative heating of the outer layers of the core is again present in runs 7 and 10, but it seems incapable of driving the core expansion against the strong ram pressure applied by the infalling matter at the core border. Finally, even though the results for core radius as a function of central density are very different from the run 2 results, they are still not in agreement with the Masunaga et al. (1998) analytical estimate (see panel b). The free-fall time (or by extension the initial cloud density) appears to be the dominant factor in setting the subsequent size of the first core.

Figure 11 also shows again how sudden the second collapse phase is, with the central density shooting up almost instantaneously (on the plotted timescale) in panel (a).

3.6. Impact of the mass of Larson’s second core for early protostar evolution

Baraffe et al. (2009) and Baraffe & Chabrier (2010) showed that episodic accretion on a newborn protostar provides a plausible explanation for the observed luminosity spread in young stellar clusters and star forming regions without invoking any age spread and can also explain unexpectedly high depletion levels of lithium that have been observed in some young objects. This scenario was questioned by Hosokawa et al. (2011) who argued that the scenario could not hold in the lower (Teff ≲ 3500 K) part of the Hertzsprung-Russell diagram. The issue has been addressed in detail in Baraffe et al. (2012), where the authors have shown that the only reason why Hosokawa et al. (2011) could not reproduce the observed luminosity spread in the aforementioned domain stems from their assumed value for the second Larson core mass (i.e. the protostar initial mass), namely 10  Mjup, a value more representative of the first Larson core (see Paper I, for example). Using smaller values, in particular 1  Mjup or so, Baraffe et al. (2012) adequately reproduced the observed spread within the very same episodic accretion scenario. Baraffe et al. (2012) thus confirmed a unified picture for early evolution of accreting protostars and concluded that the controversy raised by Hosokawa et al. (2011) should be closed, except if it was shown unambiguously that the initial protostar/BD mass could not be smaller than 10  Mjup. The present calculations, pointing to a universality of the second core mass of about 1  Mjup thus agree with the analytical estimate of Baraffe et al. (2012) and confirm their conclusions.

4. Conclusions

We have performed multigroup RHD simulations of the gravitational collapse of a 1 M⊙ cold dense cloud core up to the formation of the second Larson core, reaching a central density of ρc = 6 × 10-2  g   cm-3. Twenty groups were used to sample the opacities in the frequency domain and the results were compared to a grey simulation. Only small differences were found between the two runs, with no major structural or evolutionary changes. The main properties of the resulting first and second cores formed in the centre of the grid such as their mass and size exhibited differences of ~10−20%, which is substantial from a theoretical standpoint, but appears relatively insignificant/undetectable in observational studies (note that the gas entropy inside the cores was almost identical in the two simulations).

Nevertherless, we found that following its formation, the first core continues to accrete envelope material, steadily growing in mass and size. By the time the second core is formed, its radius has increased by a factor of 5 to 6 (a result in disagreement with the prediction of Masunaga et al. 1998). The accretion shock at the first core border remains supercritical throughout the simulations, with the vast majority of the accretion energy being lost at the border in the form of radiation. The accretion shock at the second core border was, however, found to be subcritical, with very little energy converted to radiation; the second core appears to absorb all the energy from the infalling material. In addition, contrary to the predictions of Stahler et al. (1980) and the calculations of Schönke & Tscharnuter (2011), the dust destruction front located between the first and second core borders has only a very minimal effect on the hydrodynamic properties of the pre-stellar system (this was also reported in Tea13). Additionally, we found that once the first core is formed, less than ~1000 years go by before the second core is formed.

We also performed simulations of the collapse of a 0.1 and 10 M⊙ parent cloud, in order to confirm the robustness of the results stated above. The properties of the first and second cores (apart from the first core lifetimes) were found to be quasi-independent the initial mass of the cloud for the same thermal to gravitational energy ratio; the second cores formed in our simulations all have a radius of 3 × 10-3 AU, a mass of ~10-3  M⊙, and an entropy at the centre of ~109  erg  K-1  g-1. Finally, further simulations varying the size and temperature of the parent cloud yielded virtually equivalent results, endorsing a fairly universal mass and size of the second core.

The grey approximation for radiative transfer appears to perform well in one-dimensional simulations of protostellar collapse. It reproduces accurately the multi-frequency results, most probably because of the high optical thickness of the majority of the protostar-envelope system. However, this multigroup method was developed primarily for 3D simulations where full spectral radiative transfer is too heavy for current computational architectures. We still expect to see differences between grey and multigroup methods in 3D due to different optical depths along different directions, parallel or perpendicular to the protostellar disk. In addition, a simple estimate of the characteristic timescale of the second core suggests that the effects of using multigroup radiative transfer may be more important in the long-term evolution of the protostar.

1

In Paper I we had α = 0.98 for the same set of initial conditions because of a mean particle weight of 2.375 that corresponds to a gas of solar abundances, while in our new EOS only H and He are considered and the mean particle weight is 2.31 for a He concentration of 0.27.

3

A drop in central density or temperature coincides with an increase in core radius, as expected for a gas sphere (almost) in hydrostatic equilibrium.

Acknowledgments

The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013 Grant Agreement no. 247060). BC greatfully acknowledges support from the ANR Retour Postdoc programme (ANR-11-PDOC-0031). Finally, the authors would like to thank the referee for very useful comments that have lead to a more thorough analysis of our results which has in turn vastly improved the overall robustness of this work.

References

  1. Badnell, N. R., Bautista, M. A., Butler, K., et al. 2005, MNRAS, 360, 458 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baraffe, I., & Chabrier, G. 2010, A&A, 521, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Baraffe, I., Chabrier, G., & Gallardo, J. 2009, ApJ, 702, L27 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baraffe, I., Vorobyov, E., & Chabrier, G. 2012, ApJ, 756, 118 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bate, M. R. 2009, MNRAS, 397, 232 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bate, M. R. 2011, MNRAS, 417, 2036 [NASA ADS] [CrossRef] [Google Scholar]
  7. Black, D. C., & Bodenheimer, P. 1975, ApJ, 199, 619 [NASA ADS] [CrossRef] [Google Scholar]
  8. Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., & Teyssier, R. 2010, A&A, 510, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Commerçon, B., Audit, E., Chabrier, G., & Chièze, J.-P. 2011, A&A, 530, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Dislaire, V., Hily-Blant, P., Faure, A., et al. 2012, A&A, 537, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Draine, B. T. 2003a, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
  12. Draine, B. T. 2003b, ApJ, 598, 1026 [NASA ADS] [CrossRef] [Google Scholar]
  13. Drake, R. P. 2006, in High Energy Density Physics: Foundations, Inertial Fusion, and Experimental Astrophysics (Berlin: Springer), Chap. 7.4 [Google Scholar]
  14. Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
  15. Flower, D. R., & Watt, G. D. 1984, MNRAS, 209, 25 [NASA ADS] [Google Scholar]
  16. Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Hosokawa, T., Offner, S. S. R., & Krumholz, M. R. 2011, ApJ, 738, 140 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hummer, D. G., & Mihalas, D. 1988, ApJ, 331, 794 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kuiper, R., Klahr, H., Beuther, H., & Henning, T. 2011, ApJ, 732, 20 [NASA ADS] [CrossRef] [Google Scholar]
  20. Larson, R. B., 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
  21. Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
  22. Masunaga, H., & Inutsuka, S.-I. 2000, ApJ, 531, 350 [NASA ADS] [CrossRef] [Google Scholar]
  23. Masunaga, H., Miyama, S. M., & Inutsuka, S.-I. 1998, ApJ, 495, 346 [Google Scholar]
  24. Offner, S. S. R., Klein, R. I., McKee, C. F., & Krumholz, M. R. 2009, ApJ, 703, 131 [NASA ADS] [CrossRef] [Google Scholar]
  25. Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
  26. Pagani, L., Roueff, E., & Lesaffre, P. 2011, ApJ, 739, L35 [NASA ADS] [CrossRef] [Google Scholar]
  27. Saumon, D., & Chabrier, G. 1992, Phys. Rev. A, 46, 2084 [Google Scholar]
  28. Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
  29. Schönke, J., & Tscharnuter, W. M. 2011, A&A, 526, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Sears, F. W., & Salinger, G. L. 1975, Thermodynamics, kinetic theory, and statistical thermodynamics (Addison-Wesley Pub. Co) [Google Scholar]
  31. Semenov, D., Henning, T., Helling, C., Ilgner, M., & Sedlmayr, E. 2003, A&A, 410, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Stahler, S. W., Shu, F. H., & Taam, R. E. 1980, ApJ, 241, 637 [NASA ADS] [CrossRef] [Google Scholar]
  33. Stamatellos, D., Whitworth, A. P., Bisbas, T., & Goodwin, S. 2007, A&A, 475, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Tomida, K., Tomisaka, K., Matsumoto, T., et al. 2013, ApJ, 763, 6 [NASA ADS] [CrossRef] [Google Scholar]
  35. Vaytet, N. M. H., Audit, E., Dubroca, B., & Delahaye, F. 2011, JQSRT, 112, 1323 [NASA ADS] [CrossRef] [Google Scholar]
  36. Vaytet, N., Audit, E., Chabrier, G., Commerçon, B., & Masson, J. 2012, A&A, 543, A60 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Whitehouse, S. C., & Bate, M. R. 2006, MNRAS, 367, 32 [NASA ADS] [CrossRef] [Google Scholar]
  38. Winkler, K.-H. A., & Newman, M. J. 1980, ApJ, 236, 201 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Initial conditions for the different simulations.

In the text
Table 2

Summary of the first and second core properties when ρc = 6 × 10-2  g   cm-3 for the different simulations.

In the text

All Figures

thumbnail Fig. 1

SCvH95 EOS and its extension to low densities: μ(a) and γeff(b) as a function of temperature for five different densities (see colour key in each panel).
In the text
thumbnail Fig. 2

Spectral opacities κ(ρ,T,ν). Each data point represents a set of spectral opacities for a given density and temperature. The table has been compiled from three different opacity collections. At low temperatures (below 1500 K), the dust opacities are from Semenov et al. (2003) and are completed by the dust grains opacities of Draine (2003b) at the high frequency end (red circles). For temperatures between 1500 and 3200 K, the opacities for molecular gas based on the Ferguson et al. (2005) calculations are used (green crosses). Finally, for temperatures above 3200 K, the atomic gas opacities are from the OP project (Badnell et al. 2005, blue squares). Two coloured areas, grey and yellow, show the approximate range of densities and temperatures typically reached during the first and second stages of the collapse of a cloud core, respectively.
In the text
thumbnail Fig. 3

The three steps in the construction of the regular opacity table. (a) Group average opacities are computed for each spectral point in the (ρ,T) table. (b) A Delaunay triangulation is computed in the (ρ,T) plane using each table point as a triangle vertex. Each triangle from the Delaunay triangulation represents a plane in the (ρ,T,κg) space. (c) We then overlay a fine rectanglar grid of opacity points which are computed from their coordinates in the opacity planes (see text for more details).
In the text
thumbnail Fig. 4

Grey Rosseland mean opacity as a function of temperature and density. The steep trench (dark blue) along the density dimension around T ~ 1500 K corresponds to the destruction of dust grains, while the high peak (in red) represents the region where the dominant atomic gas opacities become very high.
In the text
thumbnail Fig. 5

Decomposition of the frequency domain using 20 groups, presented over the monochromatic dust opacities. The first and last groups are used to make sure no energy is omitted at the low and high ends of the spectrum, respectively. The other groups offer an almost log-regular splitting of frequencies in the range 2.0 × 1011−3 × 1016 Hz. The group numbers are indicated just above the opacity curve. The presented spectral opacities are for typical initial conditions of ρ = 10-18  g   cm-3 and T = 10 K.
In the text
thumbnail Fig. 6

Thermal evolution at the centre of the collapsing cloud: the central temperature as a function of the central density for the grey (solid black) and multigroup (solid red) simulations. The different phases of the protostellar collapse are labelled. The results from MI00 (dashed green), Whitehouse & Bate (2006) (dashed purple), SWBG07 (dashed cyan), and Tea13 (dashed blue) are also plotted for comparison. The orange solid line is a grey simulation using an ideal gas EOS.
In the text
thumbnail Fig. 7

Thermal evolution for the grey (dashed) and multigroup (solid) simulations.
In the text
thumbnail Fig. 8

Radial profiles of various properties during the collapse of a 1  M⊙ dense clump at a core central density ρc = 6 × 10-2  g   cm-3, for the grey models (black dashed lines) and multigroup models (coloured lines). For the multigroup run, the gas and total radiative quantities (summed over all groups) are plotted in magenta, while the other colours represent the individual groups (the colour-coding is the same as in Fig. 5); see legend in (b). From top left to bottom right: (a) density, (b) gas temperature (magenta and black) and radiation temperature (other colours), (c) velocity, (d) entropy, (e) optical depth, (f) luminosity, (g) Rosseland average opacity, and (h) radiative flux.
In the text
thumbnail Fig. 9

Radial profiles of the (a) gas density, (b) normalised entropy SN (see text), (c) temperature, (d) species concentrations, (e) mean molecular weight μ, and (f) effective ratio of specific heats γeff. In all panels, the dotted line describes the first core profiles while the dashed and solid lines represent the quantities just before and after the formation of the second core, respectively.
In the text
thumbnail Fig. 10

Comparison of the radial profiles of collapse simulations at a central density of ρc = 6 × 10-2  g   cm-3 using various initial parameters (see Table 2 for details). The different panels display the following as a function of radius: (a) and (g) density, (b) and (h) gas temperature, (c) and (i) entropy, (d) and (j) radiative luminosity, and (e) and (k) enclosed mass. Panels (f) and (l) display the thermal evolution at the centre of the grid. Panels (e) and (k) show the colour legend.
In the text
thumbnail Fig. 11

Evolution of the first core for runs 2, 4, 6, 7, 8, 9, and 10 (see colour legend in top-left panel). (a) Core radius as a function of time. (b) Core radius as a function of central density. The dashed line represents the Masunaga et al. (1998) estimate. (c) Central density as a function of time. (d) First core mass as a function of time. (e) Mass accretion rate at the core border as a function of time. (f) Central temperature as a function of time. t0 represents the time when ρc ≥ 10-10  g   cm-3, taken as the time of first core formation; t0 is listed for each run next to the colour key in panel (a). In all panels, the circles mark the onset of the second collapse and the bold lines trace the transition region when the central density and temperature increase more slowly than during the rest of the simulation (see text).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.