| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321304 | |
| Published online | 26 August 2013 | |
Terrestrial planets in high-mass disks without gas giants
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata and Instituto de Astrofísica de La Plata, CCT La Plata-CONICET-UNLP, Paseo del Bosque S/N, 1900 La Plata, Argentina
e-mail: gdeelia@fcaglp.unlp.edu.ar
Received: 15 February 2013
Accepted: 24 May 2013
Context. Observational and theoretical studies suggest that planetary systems consisting only of rocky planets are probably the most common in the Universe.
Aims. We study the potential habitability of planets formed in high-mass disks without gas giants around solar-type stars. These systems are interesting because they are likely to harbor super-Earths or Neptune-mass planets on wide orbits, which one should be able to detect with the microlensing technique.
Methods. First, a semi-analytical model was used to define the mass of the protoplanetary disks that produce Earth-like planets, super-Earths, or mini-Neptunes, but not gas giants. Using mean values for the parameters that describe a disk and its evolution, we infer that disks with masses lower than 0.15 M⊙ are unable to form gas giants. Then, that semi-analytical model was used to describe the evolution of embryos and planetesimals during the gaseous phase for a given disk. Thus, initial conditions were obtained to perform N-body simulations of planetary accretion. We studied disks of 0.1, 0.125, and 0.15 M⊙.
Results. All our simulations form massive planets on wide orbits. For a 0.1 M⊙ disk, 2–3 super-Earths of 2.8 to 5.9 M⊕ are formed between 2 and 5 AU. For disks of 0.125 and 0.15 M⊙, our simulations produce a 10–17.1 M⊕ planet between 1.6 and 2.7 AU, and other super-Earths are formed in outer regions. Moreover, six planets survive in the habitable zone (HZ). These planets have masses from 1.9 to 4.7 M⊕ and significant water contents ranging from 560 to 7482 Earth oceans, where one Earth ocean represents the amount of water on Earth’s surface, which equals 2.8 × 10-4M⊕. Of the six planets formed in the HZ, three are water worlds with 39%–44% water by mass. These planets start the simulations beyond the snow line, which explains their high water abundances. In general terms, the smaller the mass of the planets observed on wide orbits, the higher the possibility to find water worlds in the HZ. In fact, massive planets can act as a dynamical barrier that prevents the inward diffusion of water-rich embryos located beyond the snow line.
Conclusions. Systems without gas giants that harbor super-Earths or Neptune-mass planets on wide orbits around solar-type stars are of astrobiological interest. These systems are likely to harbor super-Earths in the HZ with significant water contents, which missions such as Kepler and Darwin should be able to find.
Key words: protoplanetary disks / astrobiology / methods: numerical
© ESO, 2013
1. Introduction
The number of confirmed planets discovered to date outside the solar system amounts to 6941, of which more than 70% are gas giants with masses higher than that of Saturn. However, it is worth noting that most techniques of planet detection that have allowed discovering the majority of the observed exoplanets present a bias toward shorter orbital periods and higher planet masses. Thus, the current sample of known exoplanets is not representative of the great diversity of planetary systems in the Universe.
During the past years, several observational works (Cumming et al. 2008; Mayor et al. 2012) have studied the occurrence rate of planetary systems around solar-type stars. Cumming et al. (2008) analyzed eight years of precise radial velocity measurements from the Keck planet search and suggested that 17%–19% of the solar-type stars have giant planets with masses M > 100 M⊕ within 20 AU. Moreover, using the results of an eight-year survey carried out at the La Silla Observatory with the HARPS spectrograph, Mayor et al. (2012) recently inferred that about 14% of the solar-type stars have planets with masses M > 50 M⊕ within 5 AU. Several theoretical works (Mordasini et al. 2009; Miguel et al. 2011) have also studied the great diversity of planetary system architectures. In particular, Mordasini et al. (2009) used a core-accretion model to synthesize populations of extrasolar planets orbiting solar-type stars. Their results indicate that the occurrence rate of planets with masses M > 100 M⊕ is 14.3%, which is consistent with the rate obtained by Cumming et al. (2008). On the other hand, Miguel et al. (2011) developed a semi-analytical model for computing the formation of planetary systems and predicted that those with only small rocky planets represent the vast majority. According to these observational and theoretical works, the planetary systems consisting only of rocky planets would seem to be the most common in the Universe.
Here, we present results of N-body simulations aimed at studying the process of terrestrial planet formation and volatile delivery in protoplanetary disks without gas-giant planets. Particularly, we are interested in high-mass disks that do not form gas giants. These scenarios are of special interest because the resulting systems are likely to harbor super-Earths or Neptune-mass planets around the snow line, which should be detectable by the gravitational microlensing technique (Gaudi 2012). The main goal of the present work is to study the potential habitability of the terrestrial planets formed in such systems. Basically, our research is aimed at answering the following questions: if super-Earths or Neptune-mass planets were found on wide orbits in systems without gas giants around solar-type stars, would it be interesting to study the terrestrial planets of such systems in detail? Are the planetary systems studied here targets of astrobiological interest?
In general terms, the most important condition required for a planet to be habitable is the permanent presence of liquid water on its surface. The circumstellar region inside which a planet can retain liquid water on its surface is known as the habitable zone (HZ). However, a planet found in the HZ is not necessary habitable. In fact, the maintenance of habitable conditions on a planet requires to satisfy other conditions, some of them are related to the existence of organic material, suitable atmospheric properties, magnetic field, plate tectonics that replenish the atmosphere of CO2, among others. From a theoretical point of view, it is difficult to determine which planets could be able to harbor life. Given the information obtained from our N-body simulations, we require potentially habitable planets to form in the HZ and have a significant water content. These will be the criteria adopted throughout the present paper to distinguish potentially habitable planets in our N-body simulations.
This paper is therefore structured as follows. The properties of the protoplanetary disks used in our study are presented in Sect. 2. In Sect. 3, we discuss the semi-analytical model that allows us to describe the evolution of the system in the gas phase. Then, we outline our choice of initial conditions for the N-body simulations in Sect. 4, while we describe the main characteristics of the N-body code used by us in Sect. 5. In Sect. 6, we show our results and carry out a detailed analysis of all simulations. Finally, we discuss these results and present our conclusions in Sect. 7.
2. Properties of the protoplanetary disk
One relevant parameter that determines the distribution of material in a protoplanetary disk is the surface density. The surface density profile adopted in our model of protoplanetary disks is based on the evolution of a thin Keplerian disk subject to the gravity of a point-mass central star M⋆ (Lynden-Bell & Pringle 1974; Hartmann et al. 1998). Thus, the gas-surface density profile Σg(R) is given by 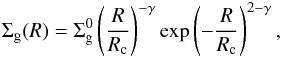 (1)where
(1)where 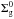 is the normalization constant, Rc the characteristic radius, and γ the exponent that defines the surface density gradient2. Integrating Eq. (1) over the total disk area,
is the normalization constant, Rc the characteristic radius, and γ the exponent that defines the surface density gradient2. Integrating Eq. (1) over the total disk area, 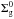 is written in terms of the total disk mass Md by
is written in terms of the total disk mass Md by 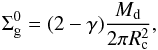 (2)for γ ≠ 2.
(2)for γ ≠ 2.
In the same way, the solid-surface density profile Σs(R) is given by 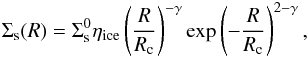 (3)where ηice is the parameter that represents an increase in the amount of solid material due to the condensation of water beyond the snow line. According to Hayashi (1981), ηice adopts values of 0.25 and 1 inside and outside the snow line, respectively, which is located at 2.7 AU.
(3)where ηice is the parameter that represents an increase in the amount of solid material due to the condensation of water beyond the snow line. According to Hayashi (1981), ηice adopts values of 0.25 and 1 inside and outside the snow line, respectively, which is located at 2.7 AU.
The relation between the gas and solid surface densities is linked with the star metallicity [Fe/H] by ![\begin{eqnarray} \left(\frac{\Sigma_{\text{s}}^{0}}{\Sigma_{\text{g}}^{0}}\right)_{\star} = \left(\frac{\Sigma_{\text{s}}^{0}}{\Sigma_{\text{g}}^{0}}\right)_{\odot}10^{[\text{Fe}/\text{H}]} = z_{0}10^{[\text{Fe}/\text{H}]}, \label{e4} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21304-13/aa21304-13-eq21.png) (4)where z0 is the primordial abundance of heavy elements in the Sun and has a value of 0.0149 (Lodders 2003).
(4)where z0 is the primordial abundance of heavy elements in the Sun and has a value of 0.0149 (Lodders 2003).
We assumed that the protoplanetary disk presents a radial compositional gradient. Following Raymond et al. (2004, 2006), we adopted an initial distribution of water content that is based on data for primitive meteorites from Abe et al. (2000). According to these works, bodies inside 2 AU and beyond 2.5 AU present a water content of 0.001% and 5% by mass, respectively, while between 2 and 2.5 AU they contain 0.1% water by mass. Given that the solid-surface density has a jump past the snow line, we assume that bodies beyond 2.7 AU contain 50% water by mass. This distribution is similar to that used by Mandell et al. (2007), who studied the formation of Earth-like planets during and after giant-planet migration. Thus, the water content by mass W(R) assumed in our protoplanetary disk as a function of the radial distance R is given by 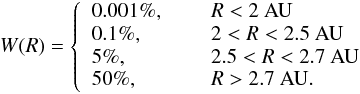 This water distribution is assigned to each body in our simulations based on its starting location. It is worth emphasizing that the water contents used here are based on data for our own solar system. While it is unclear whether the initial water distribution of our solar system is representative of the great diversity of protoplanetary disks in the Universe, we adopted it to analyze the water contents of the resulting terrestrial planets and their potential habitability.
This water distribution is assigned to each body in our simulations based on its starting location. It is worth emphasizing that the water contents used here are based on data for our own solar system. While it is unclear whether the initial water distribution of our solar system is representative of the great diversity of protoplanetary disks in the Universe, we adopted it to analyze the water contents of the resulting terrestrial planets and their potential habitability.
Several parameters, such as M⋆, [Fe/H], γ, Rc, and Md, must be quantified to specify the scenario of our simulations. On the one hand, our simulations assume a central star of 1 M⊙ and solar metallicity (namely, [Fe/H] = 0). On the other hand, γ and Rc are assumed to be 0.9 and 39 AU, respectively, which are the median values obtained by Andrews et al. (2010) from the analysis of 17 protoplanetary disks in the 1 Myr-old Ophiuchus star-forming region.
To define the mass Md of the protoplanetary disks used in our simulations, it is necessary to study in detail the evolution of the systems during the gas phase. We recall that we aim to analyze the evolution of planetary systems in disks that lead to the formation of Earth-like planets, super-Earths, or mini-Neptunes, but not gas giants. To specify which type of protoplanetary disks can lead to these scenarios, we make use of a semi-analytical model that is able to analyze the evolution of a planetary system in the gaseous phase. As we will see in Sects. 3 and 4, this model allows us to define the mass Md of the protoplanetary disks as well as the initial conditions for the distribution of embryos and planetesimals that need to be used in the N-body simulations.
3. Semi-analytical model for the protoplanetary disk: description
Here, we describe the semi-analytical model used for analyzing the evolution of the protoplanetary disk during the gaseous phase. This model is based on the works of Brunini & Benvenuto (2008) and Guilera et al. (2010) with the inclusion of some minor improvements. We considered an axisymmetric protoplanetary disk characterized by a gaseous and solid component. The gaseous component is represented by a 1D grid corresponding to the radial coordinate. The solid component (a planetesimal disk) is represented by a 2D grid: one dimension represents the radial coordinate and the other one is reserved for the different planetesimal sizes. While some quantities are only functions of the radial coordinate (R) such as the gas-surface density Σg(R), or the temperature profile T(R), other quantities are functions of the planetesimal sizes, for example, the planetesimal surface densities Σp(R,rp), the planetesimal inclinations and eccentricities i(R,rp) and e(R,rp), respectively, and the planetesimal migration velocities vmig(R,rp), where rp represents the planetesimal radius.
We used logarithmic equally spaced bins for the radial grid, in which the radial step is given by ΔR = log (Rout/Rin)/(N − 1), where Rout (Rin) represents the outer (inner) radii of the disk and N is the number of bins (we usually used a dense grid between 5000 and 10 000 bins).
Kokubo & Ida (2000) showed that in the oligarchic regime large planetesimals follow a power-size distribution dn/dm ∝ m− α, with α between 2 and 3. More recently, Ormel et al. (2010) showed that the transition between the runaway and oligarchic regime is characterized by a planetesimal power size distribution dn/dm ∝ m-2.5. Therefore, to account for a planetesimal size distribution we introduced an initial power law for the mass distribution given by dn/dm ∝ m-2.5 3. We considered that the different radii are logarithmic equally spaced, so the j species is given by 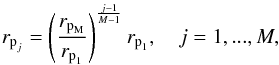 (5)
(5)
where rpM and rp1 are the maximum and minimum radii of the size distribution, respectively, and M is the number of size bins considered. If mpj is the mass between mpj − 1/2 and mpj + 1/2, so ![\begin{eqnarray} m_{\text{p}_j} & = & \int_{m_{\text{p}_{j-1/2}}}^{m_{\text{p}_{j+1/2}}}~mn(m)~{\rm d}m \\ & = & \frac{\textrm{C}m_{\text{p}_1}^{2-\alpha}}{2-\alpha} \left[ \Delta^{\frac{3(j-1/2)(2-\alpha)}{M-1}} - \Delta^{\frac{3(j-3/2)(2-\alpha)}{M-1}} \right], \end{eqnarray}](/articles/aa/full_html/2013/09/aa21304-13/aa21304-13-eq48.png) where we used that mpj = Δ3(j − 1)/(M − 1)mp1 with Δ = rpM/rp1. In the same way, the total mass is given by
where we used that mpj = Δ3(j − 1)/(M − 1)mp1 with Δ = rpM/rp1. In the same way, the total mass is given by ![\begin{eqnarray} m_\text{T} & = & \int_{m_{\text{p}_{1-1/2}}}^{m_{\text{p}_{M+1/2}}}~mn(m)~{\rm d}m, \\ & = & \frac{\textrm{C}m_{\text{p}_1}^{2-\alpha}}{2-\alpha} \left[ \Delta^{\frac{3(M-1/2)(2-\alpha)}{M-1}} - \Delta^{\frac{3(2-\alpha)}{2(M-1)}} \right]. \end{eqnarray}](/articles/aa/full_html/2013/09/aa21304-13/aa21304-13-eq51.png) Then, the amount of mass relative to the total mass provided by the j species is given by
Then, the amount of mass relative to the total mass provided by the j species is given by ![\begin{eqnarray} p_j & = & \frac{m_{\text{p}_j}}{m_\text{T}}, \\ & = & \left[ \frac{\Delta^{\frac{3(j-1/2)(2-\alpha)}{M-1}} - \Delta^{\frac{3(j-3/2)(2-\alpha)}{M-1}}}{\Delta^{\frac{3(M-1/2)(2-\alpha)}{M-1}} - \Delta^{\frac{3(2-\alpha)}{2(M-1)}}} \right]\cdot \end{eqnarray}](/articles/aa/full_html/2013/09/aa21304-13/aa21304-13-eq52.png) In a numerical treatment, the amount of mass corresponding to the planetesimals of radius rpj is given by multiplying pj and the total mass of solids of the disk. In this way, we can obtain the planetesimal surface density corresponding to the planetesimals of radius rpj (Σp(R,rpj)). Then, we treat each planetesimal size independently. With this approach we can use only a planetesimal size (in this case p = 1) or a discrete number (M) of bins to approximate the continuous planetesimal size distribution.
In a numerical treatment, the amount of mass corresponding to the planetesimals of radius rpj is given by multiplying pj and the total mass of solids of the disk. In this way, we can obtain the planetesimal surface density corresponding to the planetesimals of radius rpj (Σp(R,rpj)). Then, we treat each planetesimal size independently. With this approach we can use only a planetesimal size (in this case p = 1) or a discrete number (M) of bins to approximate the continuous planetesimal size distribution.
3.1. Evolution of planetesimal eccentricities, inclinations, and velocity migrations
Following Chambers (2006), we considered that the evolution of the eccentricities and inclinations of the planetesimals are governed by two main processes: the gravitational excitations caused by the embryos immersed in the disk, and the damping due to the gas drag.
The stirring rates of the eccentricity and inclination due to a planetary embryo can be modeled by (Ohtsuki et al. 2002) 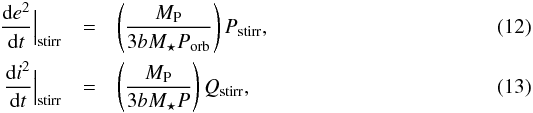 where \begin{lxirformule}$M_\text{P}$\end{lxirformule} is the mass of the planetary embryo, b the full width of the feeding zone of the planetary embryo in terms of its Hill radius (usually b ~ 10), and Porb the orbital period of the planetary embryo. Finally, Pstirr and Qstirr are functions of the planetesimal eccentricities and inclinations (for more details see Chambers 2006). However, it is worth noting that this is a local approach (specifically, this approach is valid in a neighborhood of the planetary embryo). The gravitational excitations decrease with increasing distance between the planetary embryo and the planetesimals. Hasegawa & Nakazawa (1990) showed that when the distance from the planetary embryo is larger than about four times its Hill radius, the excitation over the planetesimals decays significantly. Therefore, we need to restrict this effect to the neighborhood of the planetary embryo. Using the EVORB code (Fernández et al. 2002), we fit a a modulation function to reproduce the excitation over the quadratic mean value of the eccentricity of a planetesimal. We found this excitation to be well reproduced by
where \begin{lxirformule}$M_\text{P}$\end{lxirformule} is the mass of the planetary embryo, b the full width of the feeding zone of the planetary embryo in terms of its Hill radius (usually b ~ 10), and Porb the orbital period of the planetary embryo. Finally, Pstirr and Qstirr are functions of the planetesimal eccentricities and inclinations (for more details see Chambers 2006). However, it is worth noting that this is a local approach (specifically, this approach is valid in a neighborhood of the planetary embryo). The gravitational excitations decrease with increasing distance between the planetary embryo and the planetesimals. Hasegawa & Nakazawa (1990) showed that when the distance from the planetary embryo is larger than about four times its Hill radius, the excitation over the planetesimals decays significantly. Therefore, we need to restrict this effect to the neighborhood of the planetary embryo. Using the EVORB code (Fernández et al. 2002), we fit a a modulation function to reproduce the excitation over the quadratic mean value of the eccentricity of a planetesimal. We found this excitation to be well reproduced by 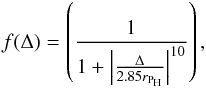 (14)where Δ = R − RP represents the distance from the planetary embryo (RP is the planetary embryo position), rPH the planetary embryo Hill radius, and f(Δ) guarantees that the eccentricity and inclination profiles of the planetesimals are smooth enough along the entire disk and that the planetary excitation on planetesimals is restricted to the embryo neighborhood.
(14)where Δ = R − RP represents the distance from the planetary embryo (RP is the planetary embryo position), rPH the planetary embryo Hill radius, and f(Δ) guarantees that the eccentricity and inclination profiles of the planetesimals are smooth enough along the entire disk and that the planetary excitation on planetesimals is restricted to the embryo neighborhood.
On the other hand, the eccentricities and inclinations of the planetesimals are damping by the gaseous component of the protoplanetary disk. The drag force acting on a planetesimal depends on its relative velocity with respect to the gas, 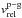 , and on the ratio between its radius rp and the molecular mean free path λ. Adopting a gaseous disk mainly composed of molecular hydrogen (H2), λ is given by (Adachi 1976)
, and on the ratio between its radius rp and the molecular mean free path λ. Adopting a gaseous disk mainly composed of molecular hydrogen (H2), λ is given by (Adachi 1976) 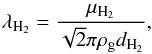 (15)where μH2 and dH2 are the molecular weight and molecular diameter of the molecular hydrogen, respectively, and ρg is the volumetric gas density.
(15)where μH2 and dH2 are the molecular weight and molecular diameter of the molecular hydrogen, respectively, and ρg is the volumetric gas density.
Following Rafikov (2004) and Chambers (2008), we considered three different regimes:
-
Epstein regime (rp < λH2);
-
Stokes regime (rp > λH2 and Re < Retrans); and
-
Quadratic regime (rp > λH2 and Re > Retrans);
where 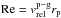 /ν is the Reynolds number and Retrans = 20 is the transition between Stokes and quadratic regimes (Rafikov 2004). The viscosity ν represents the molecular viscosity ν = λH2cs/3, where cs is the local speed of sound.
/ν is the Reynolds number and Retrans = 20 is the transition between Stokes and quadratic regimes (Rafikov 2004). The viscosity ν represents the molecular viscosity ν = λH2cs/3, where cs is the local speed of sound.
The three drag regimes can be characterized in terms of the stopping time, which are given by (Chambers 2008)  where ρp is the planetesimal density. The relative velocity between planetesimals and gas is given by
where ρp is the planetesimal density. The relative velocity between planetesimals and gas is given by ![\begin{eqnarray} v_{\text{rel}}^{\text{p}-\text{g}}(R,r_\text{p})= v_\text{k}(R) * \left[ \eta^2(R) + \frac{5}{8}e^2(R,r_\text{p}) + \frac{1}{2}i^2(R,r_\text{p}) \right]^{1/2}, \end{eqnarray}](/articles/aa/full_html/2013/09/aa21304-13/aa21304-13-eq86.png) (19)where vk is the Keplerian velocity, η = (vk − vg)/vk is the ratio of the gas velocity to the Keplerian velocity, and where we explicitly note the radial and size planetesimal dependencies.
(19)where vk is the Keplerian velocity, η = (vk − vg)/vk is the ratio of the gas velocity to the Keplerian velocity, and where we explicitly note the radial and size planetesimal dependencies.
The damping rates of the eccentricities and inclinations for each regime are given by (Rafikov 2004; Chambers 2008) 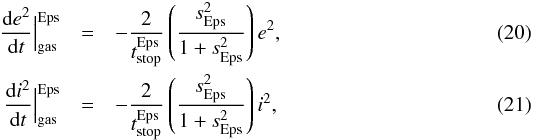 where
where 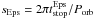 ,
, 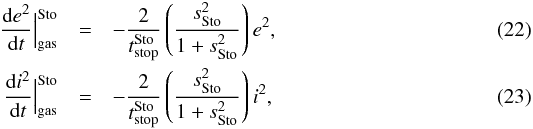 with
with 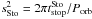 , and
, and  Finally, the evolution of the eccentricities and inclinations are given solving the coupled equations by a semi-implicit numerical method
Finally, the evolution of the eccentricities and inclinations are given solving the coupled equations by a semi-implicit numerical method  The gas drag also causes an inward planetary orbit migration. Then, the planetesimal migration velocities are given by
The gas drag also causes an inward planetary orbit migration. Then, the planetesimal migration velocities are given by ![\begin{eqnarray} v_{\text{mig}}= \left\{ \begin{array}{cc} - \frac{2a\eta}{t_{\text{stop}}^{\text{Eps}}}\left(\frac{s^2_{\text{Eps}}}{1+s^2_{\text{Eps}}}\right) & \textrm{Epstein regime} \\[3.5mm] - \frac{2a\eta}{t_{\text{stop}}^{\text{Sto}}}\left(\frac{s^2_{\text{Sto}}}{1+s^2_{\text{Sto}}}\right) & \textrm{Stokes regime} \\[3.5mm] - \frac{2a\eta}{t_{\text{stop}}^{\text{Qua}}} & \textrm{quadratic regime}. \end{array} \right. \end{eqnarray}](/articles/aa/full_html/2013/09/aa21304-13/aa21304-13-eq95.png) (28)
(28)
3.2. Oligarchic accretion regime
We considered that the embryos grow in the oligarchic regime. Considering the particle in a box approximation, the planetesimal accretion rate of the j species is given by (Inaba et al. 2001) 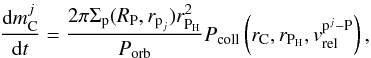 (29)where mC is the embryo mass and Pcoll is the collision probability between the planetesimal j species and the embryo (see Guilera et al. 2010 for the explicit expression of Pcoll). This last quantity is a function of the embryo core radius (rC), the embryo Hill radius, and the relative velocity between the planetesimal j species and the embryo, which is given by
(29)where mC is the embryo mass and Pcoll is the collision probability between the planetesimal j species and the embryo (see Guilera et al. 2010 for the explicit expression of Pcoll). This last quantity is a function of the embryo core radius (rC), the embryo Hill radius, and the relative velocity between the planetesimal j species and the embryo, which is given by 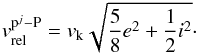 (30)If we take into account that the embryo has a non-negligible gaseous envelope, we have to incorporate the enhancement of the embryo’s effective capture radius. Following Inaba & Ikoma (2003), we used a rapid estimation for the radius of the planetesimal captured as a function of the embryo enhanced radius
(30)If we take into account that the embryo has a non-negligible gaseous envelope, we have to incorporate the enhancement of the embryo’s effective capture radius. Following Inaba & Ikoma (2003), we used a rapid estimation for the radius of the planetesimal captured as a function of the embryo enhanced radius 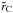
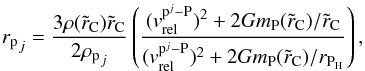 (31)where
(31)where 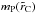 and
and 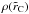 are the total mass of the embryo and the density of the embryo’s envelope contained within
are the total mass of the embryo and the density of the embryo’s envelope contained within 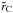 , respectively. Inaba & Ikoma (2003) proposed replacing
, respectively. Inaba & Ikoma (2003) proposed replacing 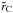 for rC in the expressions of collision probability, so
for rC in the expressions of collision probability, so 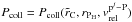 . The equations governing the evolution of the gaseous envelope are those of classic stellar evolution theory (transport and structure equations). These equations are solved coupled self-consistently to the planetesimal accretion rate, employing a standard finite difference method (Henyey), and the detailed constitutive physics is described in Fortier et al. (2007, 2009) and Guilera et al. (2010).
. The equations governing the evolution of the gaseous envelope are those of classic stellar evolution theory (transport and structure equations). These equations are solved coupled self-consistently to the planetesimal accretion rate, employing a standard finite difference method (Henyey), and the detailed constitutive physics is described in Fortier et al. (2007, 2009) and Guilera et al. (2010).
The embryo’s feeding zone is often defined as the ring around itself where planetesimals can be accreted. We defined the width of the feeding zone as about four times (at both sides of the embryo) the embryo’s Hill radius. So, we integrate Eq. (29) over the radial grid 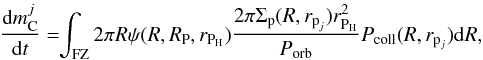 (32)where ψ(R,RP,rPH) is a normalization function which satisfies
(32)where ψ(R,RP,rPH) is a normalization function which satisfies 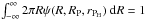 . In contrast with our previous work, we chose that
. In contrast with our previous work, we chose that 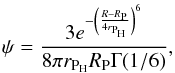 (33)where Γ is the gamma function. With this new choice of ψ,
(33)where Γ is the gamma function. With this new choice of ψ, 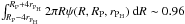 , so that the tail of the function has a negligible contribution in Eq. (32) and continues be smooth for a numerical treatment. We employed a Simpson rule to integrate Eq. (32), where for each embryo there are at least ten radial bins between RP − 4rPH and RP + 4rPH. Finally, the total planetesimal accretion rate is given by
, so that the tail of the function has a negligible contribution in Eq. (32) and continues be smooth for a numerical treatment. We employed a Simpson rule to integrate Eq. (32), where for each embryo there are at least ten radial bins between RP − 4rPH and RP + 4rPH. Finally, the total planetesimal accretion rate is given by 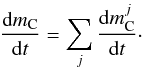 (34)
(34)
3.3. Evolution of surface densities
The solid distribution along the disk is affected by the inward migration of the planetesimals. Thommes et al. (2003), Chambers (2006), and Guilera et al. (2010, 2011) showed that this effect has important consequences on the timescale of planetesimal accretion and in the planetesimal surface density evolution, especially for small bodies (rp ≲ 1 km).
As a consequence of the conservation of mass, the planetesimal surface density obeys a continuity equation. Moreover, because we neglected the planetesimal-planetesimal interaction, we can consider each planetesimal size independently, so ![\begin{eqnarray} \frac{\partial \Sigma_\text{p}(R,r_{\text{p}_j})}{\partial t} - \frac{1}{R} \frac{\partial}{\partial R} \Big[ Rv_{\text{mig}}(R,r_{\text{p}_j})\Sigma_\text{p}(R,r_{\text{p}_j}) \Big] = \mathcal{F}(R,r_{\text{p}_j}), \label{eq:evol_Sp} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21304-13/aa21304-13-eq117.png) (35)with rpj = r1,...,rM. ℱ(R,rpj) represents the sink term due to the accretion onto the embryos, and it is given by
(35)with rpj = r1,...,rM. ℱ(R,rpj) represents the sink term due to the accretion onto the embryos, and it is given by 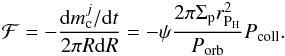 (36)Equation (35) was numerically solved using a fully implicit method in finite differences.
(36)Equation (35) was numerically solved using a fully implicit method in finite differences.
For simplicity, we considered that the gaseous component dissipated exponentially 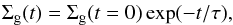 (37)where τ is a characteristic timescale. Following Mamajek (2009), who showed that the cumulative distribution of disk lifetimes decays exponentially with a timescale of ~2.5 Myr, we fit τ = 2.5 Myr. Alexander et al. (2006) and Armitage (2010) showed that after a few Myr of viscous evolution, the disk is completely dissipated on a timescale of ~105 yr, when photoevaporation is included. Thus, we calculated our simulation from t = 0 to t = 2.5 Myr, when we considered that the protoplanetary disk is completely dissipated.
(37)where τ is a characteristic timescale. Following Mamajek (2009), who showed that the cumulative distribution of disk lifetimes decays exponentially with a timescale of ~2.5 Myr, we fit τ = 2.5 Myr. Alexander et al. (2006) and Armitage (2010) showed that after a few Myr of viscous evolution, the disk is completely dissipated on a timescale of ~105 yr, when photoevaporation is included. Thus, we calculated our simulation from t = 0 to t = 2.5 Myr, when we considered that the protoplanetary disk is completely dissipated.
4. Semi-analytical model for the protoplanetary disk: application
Here, we use the semi-analytical model presented in the last section to determine the mass of the protoplanetary disks of our simulations as well as the distribution of embryos and planetesimals to be used as the initial condition of our N-body simulations.
4.1. Mass of the protoplanetary disk
The mass of the protoplanetary disk is one of the free parameters that completely defines the disk. We aim to determine disk masses that lead to the formation of Earth-like planets, super-Earths, or mini-Neptunes, but not gaseous giant planets.
The standard model of giant planet formation (Mizuno 1980; Pollack et al. 1996) proposes that planetary growth takes place in two main stages. First, the formation of a massive core by accretion of planetesimals. When the core is massive enough (≳10 M⊕), it is capable of gravitationally binding the surrounding gas, and the gas accretion becomes more effective. When the mass of the envelope approximately reaches the mass of the core, gas accretion is triggered and starts the often described gaseous runaway accretion.
To determine the mass of the disk to be used in our simulations, we calculated the in situ formation of an embryo with a gaseous envelope using the semi-analytical model described in Sect. 3. We aim to determine if such an embryo is able to achieve the critical mass to become a giant planet. The growth of the embryo depends primarily on its distance from the central star. This distance regulates two important factors in the embryo growth. The first one is the value of the planetesimal surface density, i.e., the amount of material that the embryo can accrete; the second one is the width of the feeding zone. These two combined factors maximize around the snow line. Brunini & Benvenuto (2008) showed that the most massive embryos in a protoplanetary disk are formed nearly at the snow line. From this, we calculated the formation of a planet at about the snow line for different disk masses.
Results for the formation of a planet at 3 AU for different disk masses.
 |
Fig. 1 Total mass of the planets as a function of the distance from the central star at the end of the gas phase for a 0.15 M⊙ disk. The plot represents the simultaneous formation of several embryos separated by 0.5 AU between 1 AU and 8 AU. The most massive planet is located immediately beyond the snow line at 3 AU. The red point size represents in scale the total mass, while the black point size represents the core mass in the same scale. The adopted scale size is 1.25m, where m is the mass. Except for embryos located immediately beyond the snow line, the embryo core mass practically is the embryo total mass. A color version of this figure is available in the electronic version of the journal. |
The location of the embryo is ~3 AU and the initial mass of the core is ~5 × 10-3 M⊕ with an envelope of ~10-13M⊕. We assumed only one species of planetesimals with a classical size of 10 km of radius and a density of 1.5 g cm-3. The role of the size of planetesimals in oligarchic growth is extensively discussed in the recent work of Fortier et al. (2013). To avoid introducing a new free parameter, we decided to choose a classical planetesimal size. Table 1 summarizes our results. We see that for disk masses between 0.05 M⊙ and 0.15 M⊙, only Earth-like planets, super-Earths, and mini-Neptunes are formed4. At this location the most massive planet of the disk is expected. To corroborate this, we analyzed the simultaneous in situ formation for embryos separated by 0.5 AU between 1 AU and 8 AU for the most massive disk. In Fig. 1, we can see that the most massive planet is located at 3 AU, and also that the only planets with a non-negligible envelope are situated immediately beyond the snow line (the red and black points represent the total mass and the core mass in scale, respectively).
It is important to remark that we are not taking into account planetesimal fragmentation. Inaba et al. (2003), Kobayashi et al. (2011), and Ormel & Kobayashi (2012) suggested that a significant amount of mass can be lost through planetesimal fragmentation. Guilera et al. (2013, in prep.) found that collisions between initial planetesimals of 10 km of radius can drastically reduce the mean value of the surface density of solids in the embryo-feeding zone, so that the final mass achieved by an embryo is lower than when planetesimal fragmentation is not considered.
It is worth remarking that we did not include type I migration in our model (Ward 1997). In fact, we did not account for the orbital decay of embryos and planet-sized bodies through tidal interaction with the gaseous disk. The main reason for neglecting this effect is that many quantitative aspects of the type I migration are still uncertain.
According to the analysis in this section, protoplanetary disks with masses lower than 0.15 M⊙ are unable to form gas giant planets. Given the high computational cost of N-body simulations, we decided to study only protoplanetary disks of 0.1, 0.125, and 0.15 M⊙. In the following, we describe the distribution of planetary embryos and planetesimals for each of these disks at the end of the gaseous phase. These distributions represent the initial conditions that are to be used in the N-body simulations, that describe the evolution of the planetary system in the post-gas phase.
4.2. Distribution of embryos and planetesimals
After defining the mass of the protoplanetary disk, we used the semi-analytical model described in Sect. 3 to calculate the formation of several embryos between 0.5 AU and 5 AU. The embryos were separated by 10 mutual Hill radii and the mass of each embryo corresponded to the transition between runaway and oligarchic growth following the criteria derived by Ida & Makino (1993). According to these authors, this mass is given by 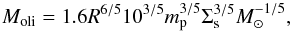 (38)where R is the distance from the central star, mp the planetesimal mass, Σs the solid-surface density, and M⊙ the mass of the star. Embryos grow by accretion of planetesimals and also by collisions between them. We considered that when the distance between two embryos becomes smaller than 3.5 mutual Hill radii, they merge into one object. We assumed perfect inelastic collisions. It is important to remark that for mergers between embryos we neglected the presence of embryo gaseous envelopes. Thus, we underestimated the planetesimal accretion rates, but this is compensated for by the mergers. Table 2 summarizes the results for the total mass contained in embryos and planetesimals between 0.5 AU and 5 AU for each disk under consideration at the end of the gaseous phase.
(38)where R is the distance from the central star, mp the planetesimal mass, Σs the solid-surface density, and M⊙ the mass of the star. Embryos grow by accretion of planetesimals and also by collisions between them. We considered that when the distance between two embryos becomes smaller than 3.5 mutual Hill radii, they merge into one object. We assumed perfect inelastic collisions. It is important to remark that for mergers between embryos we neglected the presence of embryo gaseous envelopes. Thus, we underestimated the planetesimal accretion rates, but this is compensated for by the mergers. Table 2 summarizes the results for the total mass contained in embryos and planetesimals between 0.5 AU and 5 AU for each disk under consideration at the end of the gaseous phase.
Distribution of solid material between 0.5 AU and 5 AU for disks of 0.1, 0.125, and 0.15 M⊙ at the end of the gaseous phase.
 |
Fig. 2 Distribution of embryos and planetesimals for disks of 0.1, 0.125, and 0.15 M⊙. The top panels represent the mass distributions of planetary embryos as a function of the distance from the central star, while the bottom panels show the surface density profiles of planetesimals for each disk under consideration. |
Figure 2 shows the results of our semi-analytical model for the distribution of embryos and planetesimals for disks of 0.1, 0.125, and 0.15 M⊙ at the end of the gas phase. In particular, the top panels represent the mass distributions of planetary embryos as a function of the distance from the central star, while the bottom panels show the surface density profiles of planetesimals. These distributions represent the initial condition to be used in our N-body simulations, which analyze the evolution of the system in the post-gas phase for each disk under consideration. The main characteristics of our N-body code are discussed in the next section.
5. N-body simulations: characterization, parameters, and initial conditions
The N-body code used to carry out our study was developed by Chambers (1999) and is known as MERCURY. In particular, we used the hybrid integrator, which uses a second-order mixed variable symplectic algorithm to treat the interaction between objects with separations greater than 3 Hill radii, and a Burlisch-Stoer method for resolving closer encounters. We integrated each simulation for at least 200 Myr, which is a good choice as an upper limit for the formation timescale of the terrestrial planets of our solar system (Touboul et al. 2007; Dauphas & Pourmand 2011). To develop the integration, we used a time step of six days, which is shorter than 1/20th of the orbital period of the innermost body in the simulation. Moreover, to avoid any numerical error for small-perihelion orbits, we used a non-realistic size for the Sun’s radius of 0.1 AU.
The MERCURY code evolves the orbits of planetary embryos and planetesimals and allows collisions to occur. To reduce the CPU time, our model assumed that embryos interact gravitationally with all other bodies of the simulation, but planetesimals are not self-interacting (see Raymond et al. 2006 for a detailed discussion of this problem). Moreover, collisions were treated as inelastic mergers, conserving mass and water content.
To use the MERCURY code, it is necessary to specify physical and orbital parameters for the planetary embryos and planetesimals. For disks of 0.1, 0.125, and 0.15 M⊙, the system contains 46, 44, and 37 planetary embryos between 0.5 AU and 5 AU, respectively. The individual masses and semimajor axes associated to the embryos for each protoplanetary disk are given in the top panels of Fig. 2. As we can see, for a 0.1 M⊙ disk, the embryos have masses between 0.04 M⊕ and 2.6 M⊕. For a 0.125 M⊙ disk, the embryo mass ranges between 0.05 M⊕ and 5 M⊕. Finally, for a 0.15 M⊙ disk, the embryo masses are between 0.07 M⊕ and 9 M⊕. For any disk, we assumed physical densities of 3 g cm-3 for all planetary embryos. For the orbital parameters, eccentricities and inclinations lower than 0.02 and 0.5°, respectively, were randomly assigned to the embryos. Finally, the longitude of ascending node Ω, the argument of pericenter ω, and the mean anomaly M were randomly chosen between 0° and 360°.
For each of the three disks under consideration, we included 1000 planetesimals. For disks of 0.1, 0.125, and 0.15 M⊙, we assigned individual masses for planetesimals of 0.0135, 0.0142, and 0.0127 M⊕, respectively, according to Table 2. Moreover, we assumed physical densities of 1.5 g cm-3 for all planetesimals of the system. For the orbital parameters, the semimajor axes of the planetesimals were generated using the acceptance-rejection method developed by John von Neumann. This technique indicates that if a number a is selected randomly from the domain of a function f, and another number f∗ is given at random from the range of this function, the condition f∗ ≤ f(a) will generate a distribution for a whose density is f(a)da. For each of the three disks under consideration, the f function is represented by the surface density profile of planetesimals, each of which is shown in the bottom panel of Fig. 2. Thus, the a values obtained from these functions will be accepted as possible initial conditions for the semimajor axes of the planetesimals associated to the three disks of our study. Just like for embryos, eccentricities and inclinations lower than 0.02 and 0.5°, respectively, were randomly assigned to planetesimals. Moreover, the longitude of ascending node Ω, the argument of pericenter ω, and the mean anomaly M were randomly chosen between 0° and 360°.
Given the stochastic nature of the accretion process, we carried out three different numerical simulations for each protoplanetary disk of 0.1, 0.125, and 0.15 M⊙. Energy is conserved better than 1 part in 103 in all cases.
In the following section, we describe in detail the results obtained for a disk of 0.125 M⊙. Then, we analyze the dependence of our results on the mass of the protoplanetary disk, discussing the simulations developed using disks of 0.1 M⊙ and 0.15 M⊙.
 |
Fig. 3 Evolution in time of the S1 simulation, which uses a protoplanetary disk of 0.125 M⊙. The planetary embryos are plotted as red circles, the planetesimals as small black points. The solid black curves denoted by q = 0.8 AU and Q = 1.5 AU represent curves of constant perihelion and aphelion, respectively. The sky-blue zone indicates the HZ. Only one planet survives in the HZ after 200 Myr of evolution. This planet is a super-Earth located at 0.93 AU with a mass of 3.16 M⊕ and a water content of 9.1% by mass, which is equal to 1027 Earth oceans. A color version of this figure is available in the electronic version of the journal. |
6. Results
Here, we present N-body simulations for the formation of terrestrial planets without gas giants for a protoplanetary disk of 0.125 M⊙. As we mentioned in the last section, we carried out three simulations for that disk, which are referred to as S1, S2, and S3. Then, we discuss the dependence of our results on the mass of protoplanetary disk.
The main goal of our research is to study the potential habitability of the terrestrial planets formed in such systems. Specifically, we are interested in planets formed in the HZ with a significant water content. For a solar-type star, the HZ of the system is defined to lie between 0.8 AU and 1.5 AU (Kasting et al. 1993, Selsis et al. 2007). However, it is worth noting that a planet on an eccentric orbit with a semimajor axis between 0.8 AU and 1.5 AU may spend much time outside the HZ. Thus, the planet would likely be too cold or warm to host liquid water on its surface in different parts of its orbit. To avoid this, we considered that a planet is in the HZ of the system and so can hold permanent liquid water on its surface if it has a perihelion q ≥ 0.8 AU and an aphelion Q ≤ 1.5 AU.
6.1. Simulations with 0.125 M⊙ disks
Figure 3 shows six snapshots in time on the semimajor axis-eccentricity plane of the evolution of the S1 simulation. In general terms, the overall progression of this simulation can be described as follows. From the beginning, the planetary embryos are quickly excited by their own mutual gravitational perturbations. At the same time, the planetesimals significantly increase their eccentricities due to perturbations from embryos. In fact, planetesimals are not self-interacting bodies, and owing to this, they feel the gravitational presence of the planetary embryos, but not each other’s presence. In time, the eccentricities of embryos and planetesimals increase until their orbits cross and accretion collisions occur. Thus, planetary embryos grow by accretion of other embryos and planetesimals and the total number of bodies decreases. The region between 0.5 AU and 5 AU is almost entirely clear of planetesimals within hundreds of Myr. By the end of the simulation, only a few planets remain inside 5 AU. Between them, it is possible to distinguish three very interesting planets: 1) the innermost planet of system; 2) the planet in the HZ; and 3) the most massive planet of the system. Table 3 shows the general characteristics of these three distinctive planets resulting from the S1, S2, and S3 simulations. The main similarities and differences obtained in these simulations for the planets are discussed in this section.
General characteristics of the most distinctive planets formed in the S1, S2, and S3 simulations using a disk of 0.125 M⊕.
 |
Fig. 4 Evolution of eccentricities a) and inclinations b) as a function of time for the innermost planet (black curve) and the most massive planet (red curve) of the system shown in Fig. 3. The effects of the dynamical friction are clearly visible for the most massive planet, which evolves beyond 2 AU, where the protoplanetary disk contains originally ~14 M⊕ in planetesimals. In contrast, the innermost planet of the system never felt the dynamical friction effects during 200 Myr, which can be seen in the significantly high values of its eccentricities and inclinations. A color version of this figure is available in the electronic version of the journal. |
From the beginning of the simulation, the dynamical friction is a significant phenomenon. This dissipative force dampens the eccentricities and inclinations of large bodies such as planetary embryos embedded in a swarm of smaller bodies represented by planetesimals. Figure 3 shows significant differences of the eccentricities of the planetary embryos within and without ~2 AU during the whole simulation. For comparison, Fig. 4 shows the evolution of the eccentricities and inclinations for the innermost planet and the most massive planet of the system, which evolve in regions of the protoplanetary disk within and without ~2 AU, respectively. The innermost planet reaches the highest values for the eccentricity and inclination of 0.42 and 19.3°, respectively, while the most massive planet of the system evolves with eccentricities and inclinations always lower than 0.13 and 3.5°, respectively. These significant differences in the behavior of the eccentricities and inclinations of these planets reveal that the dynamical friction effects are very different along the protoplanetary disk. In fact, the dynamical friction plays an important role for planetary embryos located beyond 2 AU, where the protoplanetary disk contains ~14 M⊕ in planetesimals at the beginning of the simulation. The dynamical evolution of the protoplanetary disk inside ~2 AU is very different. According to the results of our semi-analytical model, the planetary embryos of the inner disk accrete the entire solid material of their feeding zones during the gaseous phase. Owing to that, no planetesimals remain to provide dynamical friction from the beginning of the N-body simulation, whose time zero represents the epoch at which the gas has disappeared. The accretion seed5 of the innermost planet of the system shown in Fig. 3 started the simulation at 0.98 AU and therefore never felt the dynamical friction effects during 200 Myr. Table 3 shows that the planets resulting from the S2 and S3 simulations present orbital parameters consistent with their analogs of the S1 simulation. The different simulations show similar results for the dynamical friction effects during the evolutionary history of the resulting planets.
 |
Fig. 5 Fraction of planetary embryos (solid curve) and planetesimals (dashed curve) removed from the S1 simulation as a function of time for a 0.125 M⊙ disk. The number of planetary embryos and planetesimals surviving in the system after 200 Myr is 20.5% and 21.1% of the original number, respectively. |
Figure 5 shows the fraction of planetary embryos and planetesimals removed from the S1 simulation as a function of time. According to this, the percentage of planetary embryos and planetesimals on stable orbits at the end of our simulation is 20.5% and 21.1% of the original number, respectively. However, the main removal mechanisms are different in each case. For the planetary embryos, 70.4% are removed via collisions with other embryos and only 9.1% of them are ejected from the system. Of the planetesimals, 17.5% are removed via collisions with the resulting planets, while only 7.1% are removed via collisions with the central body. The most important removal mechanism of planetesimals is ejection by planetary embryos associated to the outer disk. In fact, 54.3% of planetesimals are removed via ejections. Considering that the planetesimal population originally contained ~14 M⊕, our simulation suggests that more than 7 M⊕ of small bodies are ejected from the system during 200 Myr. Again, 21.1% of the initial number of planetesimals remain in the planetary system at the end of the simulation. Figure 6 shows that this population of remnant planetesimals forms a scattered disk of small bodies, which extends from 5 AU to 50 AU and contains a total mass of ~3 M⊕. The evolution of this small-body population is beyond the scope of this work. However, we suggest that it would be very interesting to analyze the collisional evolution of this minor planet population. From this, it would be possible to compute the production rate of dust and then to infer if the planetary systems under study efficiently produce debris disks, which should be detected at micrometric wavelengths. It is worth noting that the S2 and S3 simulations show similar results as the S1 simulation for the final fates of planetary embryos and planetesimals.
 |
Fig. 6 Distribution of planetary embryos (red circles) and planetesimals (black dots) after 200 Myr of evolution for a 0.125 M⊙ disk. The population of remnant planetesimals forms a scattered disk that extends from 5 AU to 50 AU and contains ~3 M⊕ of material. A color version of this figure is available in the electronic version of the journal. |
Figure 3 shows that only one planet survives in the HZ of the system resulting from the S1 simulation after 200 Myr. This planet is a super-Earth with a mass of 3.16 M⊕ at 0.93 AU. Figure 7 shows the evolution of mass of this super-Earth as a function of time. According to this, the growth of this planet is a result of a smooth accumulation of a large number of planetesimals and punctuated accretion events from a small number of planetary embryos. From this point of view, the planetesimals do not play an important role since they only represent 15% of the final mass of the planet. Figure 7 also allows us to see that the last giant impact6 on that super-Earth occurred 25.6 Myr into the simulation. By that time, the planet had ~90% of its final mass. This last giant impact was produced by a planetary embryo of 0.1 M⊕ (the mass of Mars). An impact event like this that occurred on Earth is thought to be responsible for the formation of the Moon (Benz et al. 1986; Canup & Asphaug 2001). However, the timescale specified for the planet in the HZ of our simulation is shorter than that associated to the Earth. In fact, Touboul et al. (2007) analyzed tungsten (W) isotope data for lunar metals and constrained the age of the Moon and Earth to 62 Myr after the formation of the solar system.
Myr after the formation of the solar system.
 |
Fig. 7 Mass of the planet in the HZ obtained from the S1 simulation as a function of time. |
A topic of significant interest to analyze is the final content of water of the planet that survives in the HZ. An embryo of 1.42 M⊕ located at 2.6 AU at the beginning of the S1 simulation served as the accretion seed for the potentially habitable planet. This object migrated inward due to gravitational interactions with planetesimals and other embryos, ending in the HZ. Given its starting position in the protoplanetary disk, the accretion seed presented an initial water content of 5%, which equals 0.071 M⊕. However, the super-Earth of 3.16 M⊕ that survives in the HZ ends up with 9.1% water by mass after 200 Myr of evolution, which represents 0.286 M⊕. It is worth noting that the accretion seeds of all embryos hit by the potentially habitable planet started the simulation inside 1 AU. Thus, giant impacts are responsible for almost 75% of the final mass of that planet, but do not provide large amounts of water. In contrast, most planetesimals (91%) accreted by that planet started the simulation beyond the snow line so that they are water-rich small bodies. From this point of view, the planetesimals play a significant role because they provide 75% of the final water content of the planet that survives in the HZ. The Earth’s water content is not well known because the mass of water in the present-day mantle is uncertain. On the one hand, the amount of water on Earth’s surface is 2.8 × 10-4 M⊕, which will be referred to as one Earth ocean. On the other hand, the mass of water contained in the mantle has been estimated to be between 0.8 and 8 × 10-4 M⊕ (Lécuyer et al. 1998). Recently, Marty (2012) suggested that the current water content in Earth’s mantle is ~ 2 × 10-3 M⊕. From these studies, the current Earth might have a water content of about 0.1%–0.2% by mass. It is worth noting that Earth may have had a greater amount of water in its early stages, and subsequently has lost it during core formation and impacts. As we have already said in Sect. 5, our N-body simulations treat collisions as inelastic mergers conserving mass and water content. In fact, we do not account for water loss during impacts so that the water contents of the resulting planets are upper limits. Regardless, our study suggests that the planet of the HZ resulting from the S1 simulation is a water-rich body. In fact, that planet of 3.16 M⊕ finally has 9.1% water by mass, which represents 1027 Earth oceans.
Table 3 allows us to compare the main characteristics of the planets located at the HZ for the S1, S2, and S3 simulations. From this, it is evident that the final water content of the planet that survives in the HZ for the S3 simulation is consistent with that obtained for the potentially habitable planet of the S1 simulation. This similarity concerning the water content arises because the accretion seed for the planet located at the HZ was an embryo within the snow line for both simulations. Moreover, for the S3 simulation, the planetesimals only represent 11% of the final mass of the potentially habitable planet, while they provide 54% of its final water content. This result agrees well with that obtained from the S1 simulation. The differences for the final values of the mass and the formation timescale for the planets located at the HZ of the S1 and S3 simulations can probably be attributed to the stochastic nature of the accretion process.
According to the Table 3, the planet in the HZ that results from the S2 simulation is very interesting because it is a water world. In fact, this particular planet is a super-Earth with a mass of 4.74 M⊕ and a final water content of 44.2% (2.1 M⊕ of water = 7482 Earth oceans). It is necessary to analyze the accretion history of that planet to understand the highly important value of its final water content. Unlike the S1 and S3 simulations, a super-embryo of 3.68 M⊕ located beyond the snow line at 2.87 AU acted as the accretion seed for the planet of the HZ in the S2 simulation. In this case, the planetesimals did not play an important role because they only represent 12% of the final mass of the potentially habitable planet, and besides they only provide 12% of its final water content.
 |
Fig. 8 Evolution of mass a) and the semimajor axis b) of the most massive planets formed in the S1, S2, and S3 simulations as a function of time. A color version of this figure is available in the electronic version of the journal. |
Our simulations suggest that the final water content of the planet in the HZ strongly depends on the accretion history of the most massive planet of the system. Figures 8a, and b show the evolution of mass and semimajor axis of the most massive planets formed in the S1, S2, and S3 simulations as a function of time, respectively. For the S1 and S3 simulations, the accretion seed of the most massive planet abruptly increases its mass at 5.7 and 1.5 × 105 yr, respectively, which leads to the early formation of a super-embryo of ~9 M⊕ in each of these systems. For each simulations, this super-embryo significantly migrates inward due to gravitational interactions with planetesimals and other embryos, ending up at ~2 AU after 200 Myr. It is worth noting that the early formation and subsequent migration of these super-embryos act as a dynamical barrier that prevents the inward diffusion of water-rich embryos that are originally located beyond the snow line. In fact, Figures 9a–c show the evolution of the semimajor axis of the five planetary embryos starting beyond the snow line for the S1, S2, and S3 simulations, respectively. For the S1 and S3 simulations, the only such embryo that survives inside the snow line is the accretion seed of the most massive planet of the system. Of the four remaining embryos, two collide with the most massive planet of the system in both simulations, while two others end up beyond 4 AU. According to this, the early formation of a massive planet in the system prevents water-rich embryos originally located beyond the snow line from ending up in the HZ.
 |
Fig. 9 Evolution in time of the semimajor axis of the planetary embryos originally located beyond the snow line for the S1 a); S2 b); and S3 c) simulations. For the S1 and S3 simulations, only the accretion seed of the most massive planet (black curve) of the system survives within the snow line at ~2 AU. For the S2 simulation, two planetary embryos migrate inside 2 AU, one of which ends up in the HZ with a water content of 44.2% by mass. A color version of this figure is available in the electronic version of the journal. |
The dynamical behavior observed in the S2 simulation presents some differences. In this case, the most massive planet of system grows more slowly than those associated to the S1 and S3 simulations. In fact, Fig. 8a shows that the accretion seed of the most massive planet abruptly increases its mass up to 8.4 M⊕ on a timescale of 2.2 Myr. At this time, that super-embryo starts to migrate inward from 4 AU, ending up at 2.5 AU after 200 Myr (see Fig. 8b). Figure 9b shows that some water-rich embryos originally located beyond the snow line efficiently migrate inside 2 AU. Unlike the S1 and S3 simulations, one such embryo ends up in the HZ of the system, leading to the formation of a very interesting water world.
Table 3 shows that the most massive planets of the S1, S2, and S3 simulations end up with 13.4, 10, and 12.7 M⊕, respectively. Such planets are super-Earths composed of almost equal parts ice and rock. It is worth noting that these planets have negligible gaseous envelopes. In fact, the time zero of each N-body simulation represents the epoch at which the gas has disappeared and the accretion seeds of the most massive planets of our simulations have ~5 M⊕ and gaseous envelopes of just ~0.1 M⊕, which represents the ~2% of the total mass (see Table 1). These planets are like mini-Neptunes composed of ice and rock. In fact, the theoretical estimations of the envelope masses for Neptune and Uranus give values between 0.5–3.2 M⊕, and 0.5–4.2 M⊕, respectively (Podolak et al. 2000, Guillot 2005). These values represent the ~3%–20% of the total mass for Neptune, and ~3.5%–30% of the total mass for Uranus. Moreover, it is probable that these objects have lost a significant amount of their envelopes through embryo collisions during the dynamical evolution. The most massive planets of our simulations are objects of significant interest because they are super-Earths located beyond the HZ with very high contents of ice water. With these characteristics, the planets could harbor life in their subsurfaces. However, it is worth noting that such a biosphere would be unable to modify the environment in an observable way, and therefore it would be difficult to find signs of life.
 |
Fig. 10 Mass of the innermost planet obtained from the S1 simulation as a function of time. |
The innermost planet of the resulting system of the S1 simulation (Fig. 3) resides around 0.48 AU and has a mass of 0.97 M⊕. This object seems to be a good Venus-analog although somewhat more massive (0.97 M⊕ vs. 0.815 M⊕) and located farther inward (0.48 AU vs. 0.72 AU) than Venus. The accretion seed of this planet was an embryo of 0.13 M⊕ located at 0.98 AU at the beginning of the simulation. Figure 10 shows the mass of the innermost planet of the simulation as a function of time. At the beginning, the planetary growth is due to a small number of giant impacts produced by other embryos. The timescale for the last giant impact is 6.7 Myr, with which the planet acquires 87% of its final mass. After this time, the planet reaches its total mass by a smooth accumulation of planetesimals. As for orbital parameters, the innermost planet of the system represented in Fig. 3 shows final values for the eccentricity and inclination of 0.11 and 6.9°, respectively. These values prove the absence of the dynamical friction effects during the evolution of this planet. The results shown in Table 3 suggest that the innermost planets resulting from our simulations seem to have the most eccentric and inclined orbits of the system. This result is consistent with the orbital parameters of Mercury, which shows the highest values of eccentricity and inclination of the planets of our solar system, with eMercury = 0.2 and iMercury7°. According to Table 3, the orbital and physical characteristics associated to the innermost planets resulting from the S1, S2 and S3 simulations are similar. Although there are some relevant differences for the final values of mass and the formation timescale, they can probably be attributed to the stochastic nature of the accretion process.
 |
Fig. 11 Snapshots in time of the evolution of a simulation that uses a protoplanetary disk of 0.1 M⊙. The planetary embryos and planetesimals are plotted as red circles and small black points, respectively. The solid black curves denoted by q = 0.8 AU and Q = 1.5 AU are curves of constant perihelion and aphelion, respectively. The sky-blue zone represents the HZ. After 200 Myr, three super-Earths of about 4 M⊕ are formed between 1 AU and 3.5 AU. All of them started the simulation beyond the snow line and are therefore water-rich bodies. In particular, one of them survives in the HZ. This planet is a real water world with a mass of 4.2 M⊕ and a water content of 39.3% by mass, which is equal to 5895 Earth oceans. A color version of this figure is available in the electronic version of the journal. |
6.2. Dependence on the disk mass
To analyze the dependence of our results on the mass of the protoplanetary disk, we performed another six N-body simulations assuming disks of 0.1 M⊙ and 0.15 M⊙. Figures 11 and 12 show the time evolution of two simulations using protoplanetary disks of 0.1 M⊙ and 0.15 M⊙, respectively. While the overall progression of these simulations is very similar to that described for a disk of 0.125 M⊙, there are some significant differences in the masses, water contents, and dynamical characteristics of the resulting planets.
 |
Fig. 12 Evolution in time of a simulation using a protoplanetary disk of 0.15 M⊙. The planetary embryos are represented as red circles, the planetesimals as small black points. The solid black curves denoted by q = 0.8 AU and Q = 1.5 AU are curves of constant perihelion and aphelion, respectively. The HZ is represented by the sky-blue region. After 200 Myr, two massive planets with masses of 9.7 and 8.8 M⊕ are formed in 2.7 and 5.5 AU, respectively. Moreover, a super-Earth of 5.9 M⊕ is located at 1.91 AU. The accretion seed of this planet started the simulation beyond the snow line. Finally, a planet survives in the HZ with a mass of 4.5 M⊕ and a water content of 4.5% by mass, which equals 723 Earth oceans. A color version of this figure is available in the electronic version of the journal. |
For a 0.1 M⊙ disk, our simulations do not form planets more massive than 6 M⊕. In fact, the resulting planetary systems show 2–3 super-Earths with masses ranging from 2.8 M⊕ to 5.9 M⊕ and semimajor axes between 2 AU and 5 AU. The absence of Neptune-mass planets allows water-rich embryos originally located beyond the snow line to efficiently migrate toward the inner regions of the disk through gravitational interactions with planetesimals and other embryos. This dynamical behavior can be seen by analyzing the characteristics of the planets that survive in the HZ. Our simulations produced two planets in the HZ with masses of 3.7 M⊕ and 4.2 M⊕ and very high water contents of 43.7% and 39.3% by mass, respectively. These percentages represent ~5800–5900 Earth oceans. These water worlds started the simulation beyond the snow line, which explains their high water abundance. Our simulations suggest that these planetary systems are very likely harboring real water worlds in the HZ.
For a 0.15 M⊙ disk, a planet of ~9 M⊕ is present around the snow line from the beginning of the simulations. In general terms, this planet acts as a dynamical barrier that prevents the efficient inward diffusion of water-rich embryos that are originally located beyond the snow line. In our three simulations, only one planetary embryo starting past the snow line migrates inward, ending up in 1.91 AU with a mass of 5.9 M⊕. On the other hand, our simulations produce one planet in the HZ with a mass of 4.5 M⊕ and a water content of 4.5% by mass, which equals 723 Earth oceans. Our simulations suggest that these planetary systems are likely to harbor potentially habitable planets with significant water contents. However, they seem to be unable to form water worlds in the HZ.
7. Discussion and conclusions
We studied the main aspects of planet formation in systems without gas giants around solar-type stars. First of all, we used a semi-analytical model to determine the correct mass of protoplanetary disks able to form Earth-like planets, super-Earths, and mini-Neptunes, but not gas giants. We found that protoplanetary disks with masses lower than 0.15 M⊙ are incapable of producing gas-giant planets. Therefore, we focused on protoplanetary disks of 0.1, 0.125, and 0.15 M⊙. After defining the mass range of disks, we used the same semi-analytical model to describe the evolution of each protoplanetary disk during the gaseous phase, which lasts for 2.5 Myr. For each disk, the semi-analytical model allowed us to determine the distributions of planetary embryos and planetesimals at the end of the gas phase, which were used as initial conditions for the N-body simulations. We performed a total of nine N-body simulations to study the planetary formation process in disks of 0.1, 0.125, and 0.15 M⊙. These simulations produced a wide variety of planets with different masses, water contents, and dynamical characteristics.
A common characteristic of our simulations is that all of them formed massive planets on wide orbits. For a disk of 0.1 M⊙, our simulations produced 2–3 planets with masses ranging from 2.8 M⊕ to 5.9 M⊕ between 2 AU and 5 AU. For disks of 0.125 M⊙ and 0.15 M⊙, our runs consistently formed a 10–17.1 M⊕ planet between 1.6 AU and 2.7 AU, and in addition other super-Earths were produced in outer regions.
The gravitational microlensing technique is currently sensitive to some of the most massive planets formed in our simulations, and therefore will probably play a significant role in the detection of planetary systems similar to those obtained in our work. Microlensing detects planets through the instantaneous gravitational perturbation of the light rays of a source star by the planet. Moreover, when it is detected together with the microlensing event caused by its host star, the planet typically perturbs rays of light passing close to the angular Einstein ring radius of the host lens, which is given by 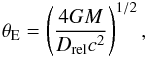 (39)where G is the gravitational constant, M the mass of the (host) lens, c the speed of light, and
(39)where G is the gravitational constant, M the mass of the (host) lens, c the speed of light, and 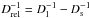 , with Dl and Ds the distances to the lens and source, respectively. For typical source and lens distances, this corresponds to a physical distance at the location of the lens of rE ≡ θEDl ≃ (2 − 4) AU(M/M⊙)1/2 (Gaudi 2012). Thus, unlike other techniques such as the transit method or radial velocities, the microlensing technique is sensitive to planets on wide orbits.
, with Dl and Ds the distances to the lens and source, respectively. For typical source and lens distances, this corresponds to a physical distance at the location of the lens of rE ≡ θEDl ≃ (2 − 4) AU(M/M⊙)1/2 (Gaudi 2012). Thus, unlike other techniques such as the transit method or radial velocities, the microlensing technique is sensitive to planets on wide orbits.
Currently, the main microlensing surveys for exoplanets are the Optical Gravitational Lensing Experiment (OGLE; Udalski 2003) and the Microlensing Observations in Astrophysics (MOA; Sako et al. 2008). To date, microlensing has detected a total number of 18 planets, which are distributed on a plane semimajor axis-mass as in Fig. 13. By analyzing this sample, we suggest that only three planets may be similar to the most massive planets formed in our simulations, which are OGLE-05-390L b, OGLE-05-169L b, and MOA-2009-BLG-266L b. OGLE-05-390L b is a very low mass planet with only 5.5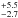 M⊕ which orbits a low-mass M dwarf of 0.22
M⊕ which orbits a low-mass M dwarf of 0.22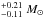 with a semimajor axis of 2.6
with a semimajor axis of 2.6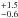 AU (Beaulieu et al. 2006). OGLE-05-169L b is a planet of ~13 M⊕ orbiting a low-mass star of 0.49
AU (Beaulieu et al. 2006). OGLE-05-169L b is a planet of ~13 M⊕ orbiting a low-mass star of 0.49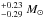 (if it is a main-sequence star) with a semimajor axis of ~2.7 AU (Gould et al. 2006). Finally, MOA-2009-BLG-266L b is a planet with 10.4 ± 1.7 M⊕ orbiting a star of 0.56 ± 0.09 M⊙ with a semimajor axis of 3.2
(if it is a main-sequence star) with a semimajor axis of ~2.7 AU (Gould et al. 2006). Finally, MOA-2009-BLG-266L b is a planet with 10.4 ± 1.7 M⊕ orbiting a star of 0.56 ± 0.09 M⊙ with a semimajor axis of 3.2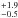 AU (Muraki et al. 2011). This planet represents a detection of interest since its mass and that of its host star are known with good precision. It is worth noting that OGLE-05-390L b, OGLE-05-169L b, and MOA-2009-BLG-266L b orbit low-mass stars, and therefore a comparison with the planets formed in our simulations should be made carefully.
AU (Muraki et al. 2011). This planet represents a detection of interest since its mass and that of its host star are known with good precision. It is worth noting that OGLE-05-390L b, OGLE-05-169L b, and MOA-2009-BLG-266L b orbit low-mass stars, and therefore a comparison with the planets formed in our simulations should be made carefully.
In addition to the current microlensing surveys, the Korean Microlensing Telescope Network (KMTNet; Poteet et al. 2012) and the Wide-Field InfraRed Survey Telescope (WFIRST; Green et al. 2011) will play a significant role in the search of exoplanets via microlensing, improving the sensitivity to lower-mass planets and increasing the planet detection rate. KMTNet is a ground-based project with plans to build three identical 1.6-m telescopes that will be located at South Africa, South America, and Australia to start operating in 2015. WFIRST is a space-based microlensing survey that could, in principle, be sensitive to all planets with mass ≳0.1 M⊕ and separations ≳0.5 AU, including free-floating planets. This mission could be ready for launch in 2020. According to this, we think that 3–17 M⊕ planets with a semimajor axis of 1.6–5 AU around Sun-like stars in systems without gas giants should be detectable via microlensing within this decade.
Of the planets resulting from our simulations, those formed in the HZ of the system are of special interest. A total number of six planets formed in the HZ with masses from 1.9 M⊕ to 4.7 M⊕ and with water contents ranging from 560 to 7482 Earth oceans. In particular, three of these planets are water worlds with 39%–44% water by mass. Although these water contents are upper limits, we conclude that all potentially habitable planets formed in our simulations are water-rich bodies.
The NASA Kepler spacecraft should be capable of detecting planets analogous to those formed in the HZ of our simulations. The Kepler mission has the primary goal of discovering transiting Earth-mass planets with a ≲ 1 AU around F- to K-type stars (Koch et al. 2010). Today, a total of 105 candidates in the Kepler data have been confirmed as planets. Moreover, there are 2740 Kepler candidates that require additional follow-up observations and analysis to be confirmed as planets. Figure 14 shows the distribution of confirmed Kepler planets and Kepler candidates on a plane semimajor axis-planetary radius. The current data indicate that 13% of Kepler candidates are planets with 0.8–1.25 times the size of Earth, while 30% are super-Earths with sizes of 1.25–2 Earth radii. The potentially habitable planets formed in our simulations have sizes ranging from 1.5 to 2.05 Earth radii, assuming physical densities of 3 g cm-3. Of the 2740 Kepler candidates, only one is similar to the habitable planets of our simulations. This candidate, referred to as KOI7 87.01, has a size of 2.1 Earth radii and orbits around a star similar to our Sun with a semimajor axis of 0.805 AU. Of the confirmed Kepler planets, Kepler-22b would seem to be a good analog to those planets formed in the HZ of our simulations. Kepler-22b has a size of 2.38 Earth radii and orbits around a solar-mass star with a semimajor axis of 0.849 AU. However, there is no strong evidence to confirm that Kepler-22b is a rocky planet (Borucki et al. 2012). Figure 14 shows that the Kepler mission has not yet discovered planets like those formed in the HZ of our simulations. It is worth noting that since February 2012, the number of Kepler candidates has increased by 20%. The most significant increases are observed in the number of Earth-size and super Earth-size candidates discovered, which grew by 43% and 21%, respectively. From this, we think that rocky planets with sizes of 1.5–2 Earth radii orbiting in the HZ of Sun-like stars will probably be very soon discovered by the Kepler mission.
 |
Fig. 13 Distribution of the 18 exoplanets detected via microlensing. The blue zone represents the region occupied by the massive planets on wide orbits formed in our simulations. Data extracted from http://exoplanets.org/. A color version of this figure is available in the electronic version of the journal. |
According to our analysis, the planets formed in the HZ of our simulations are very interesting because of their high water contents. Thus, if 3–17 M⊕ planets were found via microlensing on wide orbits around Sun-like stars in absence of gas giants, the planets in the HZ of these systems should be targets of special astrobiological interest. From this point of view, the main contribution of our work is that it allows us to determine significant targets of study for missions such as Kepler and Darwin. We just need to await observational evidence for a better understanding of the mechanisms involved in the processes of planet formation.
 |
Fig. 14 Distribution of confirmed Kepler planets and Kepler candidates. The blue zone represents the region occupied by the potentially habitable planets of our simulations. Data extracted from http://kepler.nasa.gov/. A color version of this figure is available in the electronic version of the journal. |
It is worth noting that Eq. (1) is an analytic solution to a simplified model for a viscous disk with a particular viscosity law. Real disks are not guaranteed to follow this profile.
For the most massive disk of our simulations (M = 0.15 M⊙), the planetesimal surface density at 3 AU is 5.42 g cm-2. It is worth noting that the numerical code of Guilera et al. (2010) needs a solid-surface density higher than 15 g cm-2 for an embryo to reach the critical mass to become a giant planet in less 2.5 My.
Following Raymond et al. (2009), we define a planet’s accretion seed as the larger body in each of its collisions.
Acknowledgments
We thank Pablo Javier Santamaría for helping us to improve the manuscript.
References
- Abe, Y., Ohtani, E., Okuchi, T., Righter, K., & Drake, M. 2000, Origin of the earth and moon, eds. R. M. Canup, & K. Righter (Tucson: University of Arizona Press), 413 [Google Scholar]
- Adachi, I., Hayashi, C., & Nakazawa, K. 1976, Prog. Theor. Phys., 56, 1756 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R. D., Clarke, C. J., & Pringle, J. E. 2006, MNRAS, 369, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, Chunhua, & Dullemond, C. P. 2010, ApJ, 723, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2010, Astrophysics of Planet Formation (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Beaulieu, J. P., Bennett, D. P., Fouqué, P., et al. 2006, Nature 439, 437 [Google Scholar]
- Benz, W., Slattery, W. L., & Cameron, A. G. W. 1986, Icarus, 66, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D. G., Batalha, N., et al. 2012, ApJ, 745, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Brunini, A., & Benvenuto, O. G. 2008, Icarus, 194, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Canup, R. M., & Asphaug, E. 2001, Nature 412, 708 [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chambers, J. E. 2006, Icarus, 180, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 2008, Icarus, 198, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
- Dauphas, N., & Pourmand, A. 2011, Nature, 473, 489 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fernández, J. A., Gallardo, T., & Brunini, A. 2002, Icarus, 159, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Fortier, A., Benvenuto, O. G., & Brunini, A. 2007, A&A, 473, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortier, A., Benvenuto, O. G., & Brunini, A. 2009, A&A, 500, 1249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortier, A., Alibert, Y., Carron, F., Benz, W., & Dittkrist, K.-M. 2013, A&A, 549, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaudi, B. S. 2012, ARA&A, 50, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., Udalski, A., An, D., et al. 2006, ApJ, 644, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Green J., Schechter P., Baltay C., et al. 2011, Wide-Field InfraRed Survey Telescope (WFIRST) interim report. Des. Ref. Mission Interim Rep., Sci. Def. Team [arXiv:1108.1374] [Google Scholar]
- Guilera, O. M., Brunini, A., & Benvenuto, O. G. 2010, A&A, 521, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilera, O. M., Fortier, A., Brunini, A., & Benvenuto, O. G. 2011, A&A, 532, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T. 2005, Ann. Rev. Earth Planet. Sci., 33, 493 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Hartmann, L, Calvet, N., Gullbring, E., & D’Alessio, P. 1998, AJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, M., & Nakazawa, K. 1990, A&A, 227, 619 [NASA ADS] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ida, S., & Makino, J. 1993, Icarus, 106, 210 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Inaba, S., Tanaka, H., Nakazawa, K., Wetherill, G. W., & Kokubo, E. 2001, Icarus, 149, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Inaba, S., & Ikoma, M. 2003, A&A, 410, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inaba, S., Wetherill, G. W., & Ikoma, M. 2003, Icarus, 166, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kobayashi, H., Tanaka, H., & Krivov, A. V. 2011, ApJ, 738, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 2000, Icarus, 143, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Lécuyer, C., Gillet, P., & Robert, F. 1998, Chem. Geol., 145, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E. 2009, Exoplanets and Disks: Their Formation and Diversity, AIP Conf. Proc., 1158, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Mandell, A. M., Raymond, S. N., & Sigurdsson, S. 2007, ApJ, 660, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Marty B. 2012, Earth Planet. Sci. Lett., 313/314, 55 [Google Scholar]
- Mayor, M, Marmier, M., Lovis, C., et al. 2012, A&A, submitted [Google Scholar]
- Miguel, Y., Guilera, O. M., & Brunini, A. 2010, MNRAS, 417, 314 [Google Scholar]
- Mizuno, H. 1980, Prog. Theor. Phys., 64, 544 [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muraki, Y., Han, C., Bennett, D. P., et al. 2011, ApJ, 741, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Ohtsuki, K., Stewart, G. R., & Ida, S. 2002, Icarus, 155, 436 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ormel, C. W., & Kobayashi, H. 2012, ApJ, 747, id. 115 [Google Scholar]
- Ormel, C. W., Dullemond, C. P., & Spaans, M. 2010, ApJ, 714, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Podolak, M., Podolak, J. I., & Marley, M. S. 2000, Planet. Space Sci., 48, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Poteet, W. M., Cauthen, H. K., Kappler, N., et al. 2012, Ground-based and Airborne Telescopes IV., Proc. SPIE, 8444, 84445 [CrossRef] [Google Scholar]
- Rafikov, R. R. 2004, AJ, 128, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2004, Icarus, 168, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2006, Icarus, 183, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., O’Brien, D. P., Morbidelli, A., & Kaib, N. A. 2009, Icarus, 203, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Sako, T., Sekiguchi, T., Sasaki, M., et al. 2008, Exp. Astron, 22, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Selsis, F., Kasting, J. F., Levrard, B., et al. 2007, A&A, 476, 1373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 2003, Icarus, 161, 431 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Touboul, M., Kleine, T., Bourdon, B., Palme, H., & Wieler, R. 2007, Nature, 450, 1206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Udalski, A. 2003, Acta Astron., 53, 291 [NASA ADS] [Google Scholar]
- Ward, W. R. 1997, Icarus, 126, 261 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Distribution of solid material between 0.5 AU and 5 AU for disks of 0.1, 0.125, and 0.15 M⊙ at the end of the gaseous phase.
General characteristics of the most distinctive planets formed in the S1, S2, and S3 simulations using a disk of 0.125 M⊕.
All Figures
 |
Fig. 1 Total mass of the planets as a function of the distance from the central star at the end of the gas phase for a 0.15 M⊙ disk. The plot represents the simultaneous formation of several embryos separated by 0.5 AU between 1 AU and 8 AU. The most massive planet is located immediately beyond the snow line at 3 AU. The red point size represents in scale the total mass, while the black point size represents the core mass in the same scale. The adopted scale size is 1.25m, where m is the mass. Except for embryos located immediately beyond the snow line, the embryo core mass practically is the embryo total mass. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
 |
Fig. 2 Distribution of embryos and planetesimals for disks of 0.1, 0.125, and 0.15 M⊙. The top panels represent the mass distributions of planetary embryos as a function of the distance from the central star, while the bottom panels show the surface density profiles of planetesimals for each disk under consideration. |
| In the text | |
 |
Fig. 3 Evolution in time of the S1 simulation, which uses a protoplanetary disk of 0.125 M⊙. The planetary embryos are plotted as red circles, the planetesimals as small black points. The solid black curves denoted by q = 0.8 AU and Q = 1.5 AU represent curves of constant perihelion and aphelion, respectively. The sky-blue zone indicates the HZ. Only one planet survives in the HZ after 200 Myr of evolution. This planet is a super-Earth located at 0.93 AU with a mass of 3.16 M⊕ and a water content of 9.1% by mass, which is equal to 1027 Earth oceans. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
 |
Fig. 4 Evolution of eccentricities a) and inclinations b) as a function of time for the innermost planet (black curve) and the most massive planet (red curve) of the system shown in Fig. 3. The effects of the dynamical friction are clearly visible for the most massive planet, which evolves beyond 2 AU, where the protoplanetary disk contains originally ~14 M⊕ in planetesimals. In contrast, the innermost planet of the system never felt the dynamical friction effects during 200 Myr, which can be seen in the significantly high values of its eccentricities and inclinations. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
 |
Fig. 5 Fraction of planetary embryos (solid curve) and planetesimals (dashed curve) removed from the S1 simulation as a function of time for a 0.125 M⊙ disk. The number of planetary embryos and planetesimals surviving in the system after 200 Myr is 20.5% and 21.1% of the original number, respectively. |
| In the text | |
 |
Fig. 6 Distribution of planetary embryos (red circles) and planetesimals (black dots) after 200 Myr of evolution for a 0.125 M⊙ disk. The population of remnant planetesimals forms a scattered disk that extends from 5 AU to 50 AU and contains ~3 M⊕ of material. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
 |
Fig. 7 Mass of the planet in the HZ obtained from the S1 simulation as a function of time. |
| In the text | |
 |
Fig. 8 Evolution of mass a) and the semimajor axis b) of the most massive planets formed in the S1, S2, and S3 simulations as a function of time. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
 |
Fig. 9 Evolution in time of the semimajor axis of the planetary embryos originally located beyond the snow line for the S1 a); S2 b); and S3 c) simulations. For the S1 and S3 simulations, only the accretion seed of the most massive planet (black curve) of the system survives within the snow line at ~2 AU. For the S2 simulation, two planetary embryos migrate inside 2 AU, one of which ends up in the HZ with a water content of 44.2% by mass. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
 |
Fig. 10 Mass of the innermost planet obtained from the S1 simulation as a function of time. |
| In the text | |
 |
Fig. 11 Snapshots in time of the evolution of a simulation that uses a protoplanetary disk of 0.1 M⊙. The planetary embryos and planetesimals are plotted as red circles and small black points, respectively. The solid black curves denoted by q = 0.8 AU and Q = 1.5 AU are curves of constant perihelion and aphelion, respectively. The sky-blue zone represents the HZ. After 200 Myr, three super-Earths of about 4 M⊕ are formed between 1 AU and 3.5 AU. All of them started the simulation beyond the snow line and are therefore water-rich bodies. In particular, one of them survives in the HZ. This planet is a real water world with a mass of 4.2 M⊕ and a water content of 39.3% by mass, which is equal to 5895 Earth oceans. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
 |
Fig. 12 Evolution in time of a simulation using a protoplanetary disk of 0.15 M⊙. The planetary embryos are represented as red circles, the planetesimals as small black points. The solid black curves denoted by q = 0.8 AU and Q = 1.5 AU are curves of constant perihelion and aphelion, respectively. The HZ is represented by the sky-blue region. After 200 Myr, two massive planets with masses of 9.7 and 8.8 M⊕ are formed in 2.7 and 5.5 AU, respectively. Moreover, a super-Earth of 5.9 M⊕ is located at 1.91 AU. The accretion seed of this planet started the simulation beyond the snow line. Finally, a planet survives in the HZ with a mass of 4.5 M⊕ and a water content of 4.5% by mass, which equals 723 Earth oceans. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
 |
Fig. 13 Distribution of the 18 exoplanets detected via microlensing. The blue zone represents the region occupied by the massive planets on wide orbits formed in our simulations. Data extracted from http://exoplanets.org/. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
 |
Fig. 14 Distribution of confirmed Kepler planets and Kepler candidates. The blue zone represents the region occupied by the potentially habitable planets of our simulations. Data extracted from http://kepler.nasa.gov/. A color version of this figure is available in the electronic version of the journal. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


