EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A106 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A106
Number of page(s) 12
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201321127
Published online 11 September 2013

© ESO, 2013

1. Introduction

The initial mass function (IMF), the evolution, the final fates, and the yields of metal-free and metal-poor stars are keys to understanding the chemical evolution of the primitive Universe.

The primordial IMF plays a central role in determining the different stellar contributions to the chemical enrichment processes in early galaxies. In particular, asymptotic giant branch (AGB) stars have a potential importance in the enhancement of carbon in observed metal-poor stars in the Galactic halo because they can contribute to formation of carbon-enhanced metal-poor (CEMP) stars through binary mass transfer and/or AGB winds. The primordial IMF has been studied through numerical simulations of the collapse of gas clouds, whose composition is that expected from Big-Bang nucleosynthesis (Bromm & Loeb 2003; Nakamura & Umemura 2001), and through the comparison of the results of population synthesis models with observations (Suda et al. 2012, 2013; Izzard et al. 2009; Komiya et al. 2007). The IMFs preferred by different authors, even when using analogous approaches to the problem, differ widely. For instance, Bromm & Loeb (2003) conclude that the primordial IMF has to be biased towards very high masses (≳100 M⊙), whereas the work by Nakamura & Umemura (2001) suggests there is a bimodal primordial IMF, peaking both at about 1 M⊙ and at about 10 M⊙. Izzard et al. (2009) conclude that a low-mass-dominated IMF is needed, whereas Suda et al. (2013) show the necessity of taking a primitive IMF biased towards higher masses into account. All these results, even when contradictory, provide context and information on the problem of the IMF of the early Universe and the evolution and yields of the oldest stars in the Universe.

From the point of view of stellar evolution, a huge amount of work has been devoted to the study of primordial to extremely metal-poor (EMP) stars. According to Beers & Christlieb (2005), these are stars with [Fe/H]  <  − 3. Earlier work on these stars has been done by D’Antona (1982), Fujimoto et al. (1990), Cassisi et al. (1997), Chieffi et al. (2001), Siess et al. (2002), Marigo et al. (2001), Suda & Fujimoto (2010), Gil-Pons et al. (2005, 2007), Lau et al. (2007, 2009), Campbell & Lattanzio (2008), Stancliffe (2010), and Lugaro et al. (2012). These authors mostly studied the low- and intermediate-mass ranges, whereas Heger et al. (2000), Heger & Woosley (2002), Limongi & Chieffi (2005), Meynet et al. (2006), and Hirschi et al. (2008) extended evolutionary calculations to the high-mass range. Still, important uncertainties in the input physics remain an enormous problem, even to the point where we cannot confidently predict the final fates (and consequently the yields) of stars of metallicity Z ≲ 10-3 yet (Heger et al. 2003).

The main sources of uncertainties are the mass-loss rates due to stellar winds and the chemical and energy transport processes. These uncertainties hamper determination of the evolution of the core and envelope masses and, therefore, our knowledge of the final fates of intermediate-mass primitive stars as a function of initial mass, either as white dwarfs or as supernovae of different types. In the cases of stars of solar or moderately low metallicity, observations can help us constrain the problem of the wind mass-loss rates and, up to a certain point, the chemical and energy transport in stellar interiors. On the other hand, most (if not all) of the primordial stars died long ago, and even though the number of observed very metal-poor stars is increasing thanks to large studies, such as the Hamburg/ESO (Wisotzki et al. 2000; Christlieb et al. 2001) survey, HK (Beers et al. 1992) survey, and SEGUE(SDSS) (Yanny et al. 2009), it is still difficult to get a fully coherent picture of the evolution between primordial and extremely low metallicities.

Chemical evolution models of the Galaxy (Kobayashi et al. 2006; Cescutti et al. 2006; Chiappini et al. 2005) are also useful for understanding the early Universe, since they provide information on which proposed stellar objects should be retained or discarded, such as SNI1/2. They can also be used for probing the primitive IMF (Suda et al. 2013).

Stellar models show that the physical properties of primordial to EMP stars, namely their higher overall compactness and smoother entropy profiles near the active burning shells compared to models of metal-rich stars (Fujimoto et al. 2000), cause peculiar nucleosynthetic and mixing behaviours. For instance Fujimoto et al. (1990, 2000) and, more recently, Suda et al. (2004) and Campbell & Lattanzio (2008) showed that the convective instabilities due to helium-core and shell flashes in low mass and low metallicity stars can extend to hydrogen-rich regions and cause hydrogen flashes which then enable the transport of carbon to the stellar surface. Chieffi et al. (2001) described carbon ingestion, a similar process occurring during thermal pulses of more massive thermally-pulsing asymptotic giant-branch, TP-AGB stars (MZAMS ≲ 5 M⊙).

In this work we compute and analyse the evolution of stars having a metallicity of Z = 10-5 in a mass range between 4 and 9 M⊙. We follow the stellar evolution from the main sequence until the late stages of their TP-(S)AGB1 phase and study in detail whether these objects show unusual mixing events like the cases mentioned above. Our results represent progress with respect to former works on stellar evolution at this metallicity and mass range. Instead of evolving only the early stages of the TP-(S)AGB phase and then extrapolating the mass loss and core growth to the end of the star’s life (Gil-Pons et al. 2008), we now complete the computation of the stellar sequences almost until the end of the TP-(S)AGB. The calculations only halt when an Fe-opacity-induced instability of the type described in Lau et al. (2012) is encountered. This way we expect to get a better approach to the problem of the final fates and CNO yields of the studied objects.

The present work is organised as follows. The second section is dedicated to a brief description of the evolutionary code and the particular input physics that are relevant to this work. The third section covers the evolution prior to the TP-(S)AGB, with special attention to the corrosive second dredge-up and dredge-out phenomena. The fourth section analyses the evolution along the TP-(S)AGB. The fifth section deals with the yields and the final fates of our model stars. In the last section we draw the main conclusions that can be derived form our work.

Table 1

Relevant times, structure and composition values that characterise the evolution prior to the TP-(S)AGB.

2. A brief description of MONSTAR and the input physics

For this work we use MONSTAR, the Monash University Stellar Structure code (see e.g. Frost & Lattanzio 1996; Campbell & Lattanzio 2008, and references therein). The code allows one to compute the evolution of low and intermediate-mass stars from the pre-main sequence until the last stages of the TP-(S)AGB phase. It has been used to compute stellar evolution models of metallicity ranging from solar and Magellanic Cloud values (Karakas & Lattanzio 2007; Doherty et al. 2010), to primordial (Z = 0) and Ultra-Metal-Poor ([Fe/H]  <  − 4), as defined by Beers & Christlieb (2005), and EMP (Campbell & Lattanzio 2008).

We treat convective boundaries using the Schwarzschild criterion in combination with the search for convective neutrality method, as in Wood (1981) and Frost & Lattanzio (1996). The computation of the dredge-out phenomenon requires the use of time-dependent mixing and, for the stars that undergo this process, we used the diffusion equation to approximate this mixing, as described in Campbell & Lattanzio (2008).

MONSTAR considers only the isotopes that are relevant for the structural evolution (H, 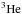, , 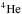, , 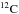, 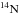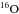and all other species are included in Zother). The nuclear reaction rates are from Caughlan & Fowler (1988). The 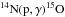rate is updated from the REACLIB value (Runkle et al. 2005). The computational aspects of the carbon-burning process are explained in Doherty et al. (2010). The stellar evolution results from MONSTAR are usually fed into a post-processing nucleosynthetic code, MONSOON, based on Cannon (1993) and adapted and extended at Monash University (Lattanzio et al. 1996; Lugaro et al. 2004). The current models experience a large number of thermal pulses (from a few hundred to more than a thousand). The number of time steps required to complete the evolution (around 10 million) and, to a lesser extent, the very high temporal and spatial resolution required, makes the task of computing the full nucleosynthesis for these models extraordinarily demanding. Therefore in this paper we report only the structural evolution and the yields of some key elements and leave a further nucleosynthetic study for a future work. The initial composition for our model stars is X(H) = 0.752, X(He) = 0.248, X(12C) = 1.8 × 10-6, X(14N) = 5.6 × 10-7 and X(16O) = 5.1 × 10-6, that is, the scaled-solar composition from Grevesse & Noels (1993), corresponding to [Fe/H] = –3.2.

thumbnail Fig. 1

HR diagram of the Z = 10-5 models for masses between 4 and 9  M⊙.

MONSTAR uses OPAL opacities (Iglesias & Rogers 1996) for the interior, and molecular opacities that consider the variations of carbon and nitrogen abundances at the surface (Lederer & Aringer 2009; Marigo & Aringer 2009). One may expect this last update to be relevant for the computation of Z = 10-5 TP-(S)AGB models. The reason is that stars of this metallicity experience a very deep second dredge-up during the early (S)AGB phase that increases the abundance of carbon at the surface drastically. It has been shown that these characteristic surface abundances in higher metallicity stars cause a decrease in surface temperature, an increase in the upper envelope opacity and, consequently, an increase in surface radius and luminosity; see e.g. Marigo (2002); Cristallo et al. (2007); Ventura & Marigo (2010); Ventura et al. (2012). Under these circumstances the mass loss rates increase, the duration of the TP-(S)AGB is shortened, and the total yields vary.

We used the prescription of Vassiliadis & Wood (1993) to compute the mass loss rates during the early and TP-(S)AGB phase. It must be noted at this point that there are many uncertainties about these rates because there are no observational data to compare to at the metallicity we are considering. It is usually understood that the most metal-poor stars (from primordial metallicity up to Z such that the envelope CNO catalysts after the SDU are too low to allow efficient H-shell burning) tend to be more compact and less luminous during the AGB (Fujimoto et al. 1984), thus their mass loss rates are lower. In general for low metallicity stars of different initial masses and evolutionary stages, some authors simply apply standard mass-loss rate formulae and assume these laws also apply at this metallicity (Karakas & Lattanzio 2007; Siess 2010). Other authors use the so-called Z-scaling, that is, they multiply the results given by the standard wind prescriptions by a certain power of the metallicity Z, usually (Z/Z⊙)1/2 (Eldridge & Vink 2006), or (Z/Z⊙)3/2 (Vink et al. 2001). We actually find, as we explain in the next section, that the second dredge-up episode in intermediate-mass Z = 10-5 stars leads to surface CNO abundances near-solar values and that stellar radii are around 800 R⊙, also similar to those of solar metallicity SAGB stars. Thus we use the same prescriptions that are applied to solar metallicity stars, with no modifications.

3. Evolution before the TP-(S)AGB phase

The early evolution of intermediate-mass models with metallicity Z ≲ 10-3 is characterised by both core H- and He-burning occurring in the blue part of the HR diagram (Girardi et al. 1996; Chieffi et al. 2001). We can see this feature in Fig. 1, which shows helium ignition occurs in the blue, soon after hydrogen exhaustion. The loop in the HR diagram is caused by this ignition of He and it interrupts the usual evolution to the red giant branch.

In Table 1 we report the initial masses of the computed Z = 10-5 stars, the core H- and core He-burning lifetimes (tCHB and tCHeB, respectively), the masses of the hydrogen-exhausted cores after core H-burning (MHe), the masses of the helium-exhausted cores after core He-burning (MCO), and the central carbon and oxygen abundances at the end of CHeB. We also indicate which models ignite central carbon.

Table 2 presents the surface abundances of important species for our models at different times. Specifically we give the C, N and O mass fractions after the end of the SDU or dredge-out (DO), whichever occurs for the given mass, followed by the (number) ratios C/O and N/O. We then give the same information at the time when carbon surface abundance reaches its maximum, which occurs during early phases of the TP-SAGB phase for models of initial mass ≲6 M⊙ and during the SDU or DO for the higher mass models. Finally we give the same values after the 20th thermal pulse (TP) and for the last calculated model. The 20th pulse is a representative early pulse. For all our models the 20th pulse occurs after the occurrence of the local maximum in carbon surface abundance and its corresponding abundances (by comparison with those at the end of the SDU/DO) reflect that both the TDU and HBB are operative from the first pulses. The high abundances seen in the 8 and 9 M⊙ are a consequence of the corrosive second dredge-up episode that we explain in the next subsection. Such surface CNO enrichment in primordial stars has been reported by other authors, e.g. Chieffi et al. (2001); Siess et al. (2002); Gil-Pons et al. (2007); Lau et al. (2009) and Suda & Fujimoto (2010).

Table 2

CNO surface composition values and quotients at selected times along the evolution of our model stars.

thumbnail Fig. 2

Upper panel: evolution of surface abundances of carbon, nitrogen and oxygen during the second dredge-up episode (SDU) and the first thermal pulses of the TP-AGB phase for the 4 M⊙ model. Lower panel: evolution of the advance of the base of the convective envelope (grey shading) during the same interval of time. The light grey and the black dashed lines represent the location of the H-burning shell (HBS) and the He-burning shell (HeBS) respectively. The vertical line marks the beginning of the TP-AGB phase at the onset of the first thermal pulse.

thumbnail Fig. 3

Upper panel: evolution of surface abundances of carbon, nitrogen and oxygen during the corrosive second dredge-up episode and the first thermal pulses of the TP-SAGB phase for the 8 M⊙ model. Lower panel: evolution of the advance of the base of the convective envelope (grey shading) during the same interval of time. The lines have the same meaning as in Fig. 2. Letters a, b, c and d refer to the times for the corresponding panels of Fig. 4.

thumbnail Fig. 4

Abundance profiles of carbon, nitrogen and oxygen showing the progress of the corrosive second dredge-up episode for the 8  M⊙ star, at the times labeled in Fig. 3. The shaded region represents the convective envelope.

thumbnail Fig. 5

Upper panel: evolution of surface abundances of carbon, nitrogen and oxygen during carbon burning and the dredge-out episode (DO). Lower panel: evolution of the advance of the base of the convective envelope during carbon-burning and the DO episode. Both panels are for the 9 M⊙ star. The lines have the same meaning as in Fig. 2.

thumbnail Fig. 6

Mass of intershell convective zones versus pulse number for our models.

3.1. The corrosive second dredge-up episode

Once helium is exhausted in the core, the model stars begin ascending the second2 giant branch – the AGB. At this phase the models undergo the second dredge-up episode (SDU)3.

Models with core masses ≲1.1 M⊙ after the SDU are unable to burn carbon and evolve along the TP-AGB phase (Nomoto 1984, 1987; Siess 2007). Models with core masses ≳1.1 M⊙ after the SDU go on to ignite carbon and, as we see in the following sections, either enter the TP-SAGB phase to become white dwarfs or electron-capture SNe (hereafter EC-SNe), or evolve directly to core-collapse supernovae. The lower initial mass limit for C-burning at Z = 10-5 is about 7.0 M⊙, but this value changes for different metallicities and input physics (Gil-Pons et al. 2003; Siess 2007; Gil-Pons & Doherty 2010).

For those models that ignite carbon, the SDU episode occurs either before (for initial masses up to 7.5–8 M⊙) or after carbon burning (for initial masses above 8 M⊙). Standard SDU is characterised by the advance inwards of the convective envelope towards regions that have been processed by the CN(O) cycle, and therefore it manifests itself as an increase in N surface abundances and a decrease in C and O surface abundances (see Fig. 2).

The SDU has an interesting peculiarity in the case of EMP stars of masses ≳8  M⊙ (see Fig. 3). In these stars the convective envelope reaches beyond regions processed by H burning and it is able to penetrate to regions where He burning has been active, as seen in Fig. 4. Therefore the SDU is able to transport not only the products of CNO nucleosynthesis, but also the products of He burning. This was also reported by Suda & Fujimoto (2010). Due to this phenomenon the effective Z (dominated now by C+N+O) increases by several orders of magnitude (see Table 2). We call this process the corrosive SDU episode (Doherty et al., in prep.). It is also interesting to see in Fig. 3 that, just after the corrosive SDU but before the TP-SAGB begins, the surface abundance of nitrogen increases, while the carbon abundance and, to a lesser extent, oxygen abundance, decrease. This is caused by the early onset of hot-bottom-burning (HBB).

3.2. The dredge-out episode

It is well known that at the upper mass range of SAGB stars there is a complex interplay of overlapping convective zones. It has been common to refer to “dredge-out” in the case where the outer convective region (rich in hydrogen) makes contact with the inner He-burning convective region at the end of carbon burning (Ritossa et al. 1999; Siess 2007; Gil-Pons & Doherty 2010). This results in a proton ingestion episode (PIE), as described by e.g. Campbell & Lattanzio (2008) in the context of lower mass stars.

The high CNO surface abundances seen in our 9 M⊙ model are a result of such behaviour, as shown in Fig. 5. In this model we see convection due to C burning in a shell in the inner part of the star (M ~ 0.4  M⊙). Pockets of convective He burning arise, notably at time ~26.5837 Myr and mass ~1.4–2 M⊙. Immediately after this there is a rapid advance of the hydrogen-rich envelope downward. Crucially this convective zone joins with the He burning convective region below, causing a rapid ingestion of protons into regions of very high temperature so that a hydrogen flash (with LH as high as 1010  L⊙) occurs. In time scales of months intense H- and He-burning occurs at very high rates (C burning continues at inner regions), and the products of the CNO-cycle and the 3α reactions are mixed to the surface.

4. Evolution during the TP-(S)AGB phase

Following the SDU or DO episodes, the stars proceed to the TP-(S)AGB. From Table 2 we see that either due to corrosive SDU or to the DO process, the envelopes of our 8 and 9 M⊙ stars are sufficiently enriched in CNO isotopes that their total surface metallicities at the beginning of the TP-SAGB phase are all higher than 10-3. Stars of 4 and 5 M⊙ experience early and very deep third dredge-up (TDU), combined with strong hot bottom burning, which leads to a similar result. After the first 10 thermal pulses the surface abundances of carbon, Xsurf(C), are higher than 10-4, and keep increasing until they reach a local maximum at the 12th and the 13th pulses for the 4 and 5 M⊙ models respectively. HBB is responsible for an increase in surface nitrogen abundance to values Xsurf(N) > 10-3 at their 20th thermal pulses, as shown in Table 2. The 6 and 7 M⊙ models experience more moderate SDU and early TDU episodes. Thus their total surface metallicities at their 20th pulses are comparatively low. Nevertheless the combination of TDU and HBB eventually increases their Xsurf(N) to values higher than 10-3 at the 30th and the 60th pulses, respectively. Considering that the corresponding models undergo 372 and 607 thermal pulses, we can say that these stars also host envelopes enriched in C, N and O during most of their TP-(S)AGB. Therefore the hydrogen-burning shells (HBS) in our models burn efficiently via CNO-cycling in a very similar way to that of higher metallicity stars and the structural characteristics of the envelopes are also very similar to those of stars of higher metallicity.

Our calculations halt when an envelope instability of the type studied by Lau et al. (2012), Petrovic et al. (2006) or Wagenhuber & Weiss (1994) is encountered. The code can not converge because of the lack of a hydrostatic solution which occurs due to the region just above the hydrogen shell exceeding the Eddington luminosity. When this occurs the models still have envelopes ranging from 0.25 M⊙ for the 4 M⊙ model, and up to 1.5 M⊙ for the 9 M⊙ model. As a result of this instability some considerable uncertainty is introduced into the predictions for the final fates of the stars as well as the yields, as we discuss in the following sections.

These massive (S)AGB stars begin their thermally pulsing evolution with relatively large cores, and hence small interpulse periods, which decrease further during the evolution. For the 4 M⊙ model the interpulse decreases from about 10 000 years to 3000 years in 200 thermal pulses, while the 8 and 9 M⊙ models have, respectively, periods of only about 200 years and 40 years between pulses, which number over 1000 before the end of the calculations. Similarly, the intershell convective region is exceptionally thin in SAGB stars, extending only about 0.0002 M⊙ in the 8 M⊙ model, for example, although it increases to about 0.004 for masses as low as 4 M⊙, as shown in Fig. 6.

thumbnail Fig. 7

Upper left panel: evolution of the luminosity associated with hydrogen and helium burning for the 9M⊙ model star, during pulses 125 and 126. Lower left panel: evolution of convective regions during the same pulses. Right panels represent the same as left panels for the case of pulses 1125 and 1126.

The temperature in the intershell convective region is very high, being about 360 million degrees for all masses. This is sufficiently high for a strong activation of the 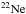neutron source and hence substantial s-processing is expected. The details of this neutron capture nucleosynthesis will be the subject of a later paper. For now we note that the thin intershell means that only small amounts of material are dredged up to the surface following each pulse, even though the dredge-up parameter λ may be quite large (near 1 for initial masses M ≲ 6 M⊙, decreasing to about 0.5 for the 8 M⊙ model and 0.05 for 9 M⊙ model). The surface of the star will be nevertheless enriched in s-process elements, which is expected to be noticeable because of the very small initial reservoir of such species present in models with such low metallicity.

The evolution during the TP-SAGB phase of the 9 M⊙ model is shown in Fig. 7. On the left we show two consecutive early pulses, numbers 125 and 126, while the right hand panel shows two consecutive pulses much later in the evolution, being thermal pulse numbers 1125 and 1126. We can see the expected increase in the peak luminosity of the He shell in later pulses, but we also note a new behaviour. The hydrogen burning luminosity, which in low mass stars drops to essentially zero during dredge-up, here remains reasonably high. It does decrease with later pulses, as seen in the diagram, but surprisingly the shell is not extinguished during the brief dredge-up phase itself. This plays a role in terminating the dredge-up earlier than would be expected normally for massive (S)AGB stars, keeping λ as low as 0.05 compared to values near unity for stars at the lower end of our mass range (e.g. 4 M⊙). A similar behaviour has been described by Chieffi et al. (2001) and by Herwig (2004), who named it Hot-TDU. We note in passing that Fig. 7 highlights the need for high resolution in both space and time. The duration of each convective shell associated with helium flashes is as short as a few months and its extent is typically a few 10-5  M⊙.

thumbnail Fig. 8

Evolution of surface abundances versus time for the 4, 6, 8 and 9 M⊙ models.

The main nucleosynthesis process acting in these stars is hot bottom burning with temperatures at the base of the convective envelope above 140 million degrees. These temperatures are enough for efficient CNO cycling as well as the activation of the Ne-Na and Mg-Al reactions.

The evolution of surface abundances of carbon, nitrogen and oxygen along the TP-(S)AGB for the 4, 6, 8 and 9 M⊙ models is show in Fig. 8. We note that, either due to the corrosive SDU or to the TDU, the number ratio C/O remains higher than one during most of the TP-(S)AGB phase of the stars considered, despite the very strong HBB. Table 3 shows some relevant results from the evolutionary calculations along the TP-(S)AGB of our models.

Table 3

Relevant results from the evolutionary calculations that characterise the TP-(S)AGB of our models.

Table 4

Total ejected envelope masses and hydrogen, helium, carbon, nitrogen and oxygen yields from our model stars.

5. Yields and final fates of single intermediate-mass Z = 10-5 stars.

We computed the yields of hydrogen, helium, carbon, nitrogen and oxygen, according to the expression: 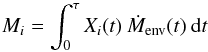(1)where Mi is the ejected mass of element i, Xi(t) is the mass fraction of that element at a certain time t, Menv(t) is the envelope mass at t and τ is the time at the end of our calculations.

Because non-negligible envelope masses remain at the end of calculations, the total yields we present are computed in two different ways. First we assume that, immediately after the Lau et al. (2012) instability is reached, the envelope mass is lost on dynamical time scales. Thus the remnant yield of element i at this time is 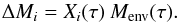(2)As a second option we assume that the stars are able to recover after the Lau et al. (2012) instability and proceed along further thermal pulses that mimic the characteristics (duration, average mass loss rates) of the last computed thermal pulse. This is the spirit of the synthetic approach used by Karakas & Lattanzio (2007) and references therein, which uses the dredge-up parameter of the last computed model to calculate the variations of the envelope composition. Because in our most massive models hot-bottom burning is still moderately active, we considered the combined effect of composition variations due to TDU and HBB simply by getting the envelope mass fraction variation of each element between the last two thermal pulses and then iterating until the envelope mass is zero. We proceeded as follows.

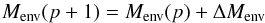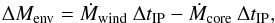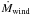The envelope mass at pulse p + 1 is computed as (3)where (4) and 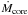are the mass loss rate due to stellar winds and the core growth rate respectively, and ΔtIP is the time between two consecutive thermal pulses. Because 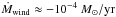and 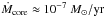in our models, the variation of the envelope mass is dominated by the effect of the winds.

The yield of element i at pulse p + 1 is 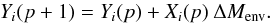(5)The envelope mass fraction variation is obtained using the masses of element i at the envelope for two consecutive pulses, Mi(p − 1) and Mi(p): 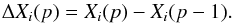(6)Thus the envelope mass fraction of i at the thermal pulse p + 1 is 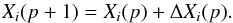(7)The numbers of additional thermal pulses we obtain are: 2 for the 4 M⊙, 6 for the 5 M⊙, 13 for the 6 M⊙, 21 for the 7 M⊙, 46 for the 8 M⊙ and 576 for the 9 M⊙ model.

thumbnail Fig. 9

[C/N] (upper panel) and [C/O] (lower panel) versus metallicity. Black symbols correspond to the yields of our computed models. The cases in which dilution has been taken into account are represented in grey. They should be located at the same [Fe/H] as the non-diluted yields, but we displaced them –0.1 dex for the sake of clarity. For comparison, observational data of EMP (black solid circles) and CEMP (red open circles) from the SAGA database are represented in both panels.

Our yield results are presented in Table 4. In the mass range studied the dominance of nitrogen shows the relevance of hot-bottom burning during most of the TP-(S)AGB evolution. The occurrence of corrosive second dredge-up, dredge-out and third dredge-up episodes also cause relatively high carbon yields (higher than the oxygen yields for all our models except the 9 M⊙ case). For most elements the differences in the final yields using the two approaches described above is very small, although we can see that the 6, 7 and 8 M⊙ cases present C yields which are 11%, 24% and 22% higher when the synthetic treatment is used. Also O yields are higher, but their increase is less important. These higher C and O yields are the result of the TDU process, which is active during our last computed pulses. The effect of the synthetic pulse treatment on the 9 M⊙ model is different, as TDU is very mild (λ = 0.05). Instead, HBB acting along 562 additional synthetic pulses causes an increase of 15% in N from ON cycling. It should be recalled that the synthetic approach we have described is a simplification. HBB tends to become milder (or extinct) as the envelope mass and the temperature at its base decrease at the last stages of the TP-(S)AGB phase. TDU, on the other hand, remains active (and increasingly efficient) at these last stages, so we might be underestimating the effects of TDU and overestimating the effects of HBB.

The lower part of Table 4 presents the same yields (with the assumption that the instability ends the evolution) using the notation [A/B]  = Log10(NA/NB)∗ − Log10(NA/NB)⊙. In this expression (NA/NB)∗ refers to our final number fractions and (NA/NB)⊙ refers to solar number fractions.

Most of the matter ejected by our model stars is expected to contribute to the enrichment of the ISM. The importance of such a contribution depends on the nature of the primordial Galactic IMF which, as we mentioned in the Introduction, is still an open question. A fraction of stars in the mass range studied here would have been primary components of wide binaries and therefore part of the matter ejected through their stellar winds may have been accreted by their low mass companions, polluting their surfaces. This is the standard scenario for the formation of CEMP stars, proposed by Suda et al. (2004) and Lucatello et al. (2005), and supported by their observational data, which are consistent with all CEMP-s stars belonging to binary systems.

We considered the scenario where our TP-(S)AGB model stars might have been polluters of currently observed CEMP stars. Given the facts that observed CEMP stars have masses <1 M⊙ and that we are considering intermediate-mass stars in the high mass range, the mass quotient, q, between primary and secondary component masses, would have been ≥4. High q values in close binaries that experience mass transfer due to Roche lobe overflow are associated with orbital instability, the occurrence of common envelopes and, eventually, with the merger of the components. However mergers can be avoided if the interacting binary is wide enough to avoid Roche lobe overflow. In this scenario mass transfer via stellar winds could pollute the companion. Keeping this idea in mind, we compared our yields to observational data from the SAGA database Suda et al. (2008), simply to check if our results fit within the ranges given by observations. Our results for the abundance quotients [C/N] and [C/O] are presented in Fig. 9. The [C/O] ratios in our yields show reasonable agreement with the CEMP observations at this metallicity. However the [C/N] ratios are too low compared to most of the CEMP values.

thumbnail Fig. 10

Masses of degenerate cores versus initial mass, at the end of the second dredge-up or dredge-out episode and at the end of our full computations for our model stars.

We also present in Fig. 9 the computed yields under the effect of dilution in the secondary component’s envelope. We estimated the effects of dilution by calculating what would happen if 1% of the material ejected from a primary star were accreted and homogeneously mixed in the 0.3 M⊙ convective envelope of a 0.8 M⊙ secondary giant star. This percentage of accretion is consistent with the value obtained using the Bondi-Hoyle approximation (Bondi & Hoyle 1944), as in Hurley et al. (2002), with a wind velocity of 10 km s-1 characteristic of the stellar radii of our TP-(S)AGB stars, and the parameter αw = 3/2.

The approximation of mixing into a 0.3 M⊙ envelope is reasonable in the case of giant secondary stars, whereas in the case of dwarfs a more realistic approach to the problem should consider the structure of the accreting star and an appropriate treatment of the mixing mechanisms in their thin convective envelopes (Stancliffe et al. 2007). We find our dilution estimates do not significantly alter the result of our comparisons with the CEMP observations (Fig. 9).

As mentioned above we have not yet computed nucleosynthesis with an extended network and therefore we cannot compare s-process yields to observations. But given the high temperatures reached at the intershell convective regions and the values of the dredge-up parameter for most of our models (see Sect. 4), we can expect the presence of s-process elements in the real counterparts of our model stars. This is also consistent with the high fraction (about 80%) of s-enriched CEMP stars (Aoki et al. 2007).

thumbnail Fig. 11

Variation of mass-loss rates, envelope mass and core mass versus time along the TP-AGB phase of the 4 M⊙ star. The thick black lines correspond to the results of our full calculations and thereafter values represented in thin lines correspond to extrapolations. Black lines correspond to VW mass-loss rates and grey lines correspond to the case VW/10 (see full text for details). The insert in the top panel highlights the evolution of the mass-loss rates at the end of our full computations. The Chandrasekhar mass, mCh, is shown for reference in the lower panel.

The final fates of TP-(S)AGB stars is the result of a competition between core growth and mass loss rates which, as we commented in Sect. 2, are particularly uncertain at very low metallicities. In Fig. 10 we show the core masses after the SDU or DO episodes and at the end of the computed TP-(S)AGB versus the initial masses of our models. It can be seen that the cores of our model stars do not reach the Chandrasekhar mass and therefore these objects are able to avoid becoming either SNe I1/2 in the case of stars hosting CO cores (Arnett 1969), or electron-capture supernovae (Nomoto 1984) in the case of stars hosting ONe cores.

thumbnail Fig. 12

Variation of mass-loss rates, envelope mass and core mass versus time along the TP-SAGB phase of the 9 M⊙ star. The lines have the same meaning as in Fig. 11.

It has recently been proposed by Wood (2011) that stars of very low metallicities may not experience strong enough pulsations that could lift envelope matter to the photosphere and, by cooling, form grains. It is radiation pressure onto these grains that drives stellar winds, so their absence might switch-off or decrease substantially such winds. Mass loss rates are critical for the final fates of our model stars, so in this section we briefly explore this uncertainty. As a test we consider how the final fates of our models would change if the VW93 prescription is overestimating the mass loss rates by one order of magnitude. In this case we did not follow the complete evolution but, instead, we divided the VW93 rates obtained along our full calculations by a factor 10, starting at the beginning of the TP-(S)AGB phase. Then we integrated these mass loss rates in time to obtain the corresponding envelope masses. As one may expect the final envelope masses we get in this way are still very high (more than 90% of the original values). We use Bulirsch and Stoer algorithm (Stoer & Bulirsch 1980) to extrapolate the mass loss rate values beyond those that we can obtain directly. Once more these values can be integrated to obtain the evolution of the envelope masses until the time when the envelope has been completely ejected. We assumed that the core growth rates are the same as the ones we find when using VW93. Our results for the 4 and the 9 M⊙ cases are show in in Figs. 11 and 12, respectively. As we can see, for both cases, the decrease of one order of magnitude in the standard rates is enough to recover the possibility of the occurrence of supernovae. If the initial mass is less than about 7 M⊙, our model stars would develop degenerate CO cores and explode as SNI1/2, whereas if their initial mass is between 7 M⊙ and 9 M⊙, they would develop ONe cores and undergo an electron-capture supernova. Hence we can not confidently say that Z = 10-5 stars avoid the possibility of ending their lives as SNI1/2. It is also interesting to see that the extrapolations for the 9 M⊙ standard VW93 case show that the time for the core to reach mCh and the time necessary to complete the envelope ejection are very similar. Therefore our 9 M⊙ case is very close to the limit for the formation of EC-SNe at the end of its TP-SAGB phase. For a comparison, the minimum initial mass for our models to reach mCh near the end of core carbon burning is ~9.3 M⊙. The summary of our results for different initial masses and wind rate prescriptions is shown in Fig. 13.

thumbnail Fig. 13

Mass limits at Z = 10-5 for the formation of carbon-oxygen and oxygen-neon white dwarfs, supernovae type I1/2 (for stars whose CO core reach mCh), electron-capture supernovae (for stars whose ONe cores reach mCh) and supernovae type II. These mass limits are represented for the cases in which Vassiliadis & Wood (1993) are used (full calculations), and for the cases in which this rates are decreased one order of magnitude.

6. Summary

The evolution of model stars of metallicity Z = 10-5 and masses between 4 and 9 M⊙ has been followed from the main sequence until the Fe-opacity peak instability described in Lau et al. (2012) halts the calculations. The very large increase in metal abundances in the envelope caused by the dredge-out and corrosive second dredge-up episodes gives rise to rather cool and extended stellar envelopes during the early and TP-(S)AGB phases. This causes mass loss rate values comparable to those of moderate-metallicity objects, when keeping the prescription by Vassiliadis & Wood (1993) to characterise stellar winds.

Our stars between 4 and 8 M⊙ experience the combined effects of TDU and HBB along their TP-(S)AGB evolution. The TDU parameter λ is near 0.9 for our lowest mass models and decreases to 0.5 and 0.05 (practically negligible) for our 8 and 9 M⊙ models, respectively. TDU is responsible for a steady increase in C surface abundances in models between 4 and 8 M⊙ and, even though we did not follow neutron-capture in this work, is also expected to enrich in s-process elements the surfaces of these stars. All our models experience a very strong HBB which results in significant surface enrichment in N.

Given the uncertainty in the outcome of our model stars once the Fe-peak instability is reached, we computed two sets of stellar yields based on two different assumptions. In the first case we assumed that the models can not recover after the instability and that the remnant envelopes are lost on dynamical time scales. In the second case (synthetic treatment) we assumed that the models recover after the instability and proceed further along the TP-(S)AGB phase. We showed that the second treatment has negligible effects on the lowest mass models, but it gives C yields which are 11%, 24% and 22% higher for the 6, 7 and 8 M⊙ models respectively. This is a consequence of the TDU remaining operative during the last thermal pulses. The 9 M⊙ model, in which TDU is negligible but HBB is very important, yields 15% more N when the synthetic treatment is used.

We also considered the uncertainties that surround mass loss at the studied metallicity range. In particular we explored the possibility that we might be overestimating mass-loss rates; see, for instance, Wood (2011). We artificially evolved our model stars along the TP-(S)AGB considering mass-loss rates between the standard values and down to one order of magnitude below. This decrease is enough to prevent the fast ejection of the stellar envelope and, therefore, to allow the formation of SNI1/2 in the case of stars of initial mass up to 7 M⊙, or electron-capture SNe in the case of stars of initial masses between 7 and 9 M⊙. Stars above this mass would end up their lives as core-collapse supernovae.

It must be kept in mind that a reduction in mass loss rates due to stellar winds is not the only reason why very low metallicity intermediate mass stars might end their lives as SNeI1/2. As reported by Lau et al. (2008), who computed primordial intermediate-mass stars, these objects might have a peculiar behaviour in the midst of their TP-(S)AGB. Their thermal pulses gradually become weaker and eventually stop (while the model star keeps numerically stable) when their envelopes still contain a few solar masses. From this point on, the stellar cores keep growing up to the Chandrasekhar mass and the model stars are expected to end their lives as SNeI1/2. In Lau et al. (2008) scenario thermal pulses cease because He-burning becomes stable due to the high temperatures reached in the region where it is active. Such high temperatures are favoured by the existence of a relatively massive degenerate core (1.1 M⊙) and specially by the low envelope CNO mass fraction (about 10-6, which allows very hot H-burning) and by the lack of occurrence of TDU (this process would cool the intershell region). In our Z = 10-5 models TDU is very efficient for initial masses up to 7 M⊙, so these stars seem likely to avoid the Lau et al. (2008) scenario, even if lower mass-loss rates allowed a longer TP-(S)AGB phase. On the other hand, our more massive models do not experience such efficient TDU episodes and might eventually develop stable He-shell burning in spite of their high envelope CNO mass fractions. Either way, this phenomenon has not been fully explored and, even though it does not seem likely to occur, we cannot confirm or discard its occurrence in our model stars.

Most of the matter ejected by our stars is expected to enrich the ISM, but a small fraction might be accreted by companion stars of wide binaries. We compared our results to observations of EMP and CEMP stars from the SAGA database in order to see if our yields fit in the observed ranges. Our [C/O] yields are consistent with these observations, however the [C/N] yield values are too low compared to most of the observations of CEMP stars.

It would be interesting to obtain a wider set of yields with a postprocessing nucleosynthesis code in order to perform further comparisons with observational data in the near future. Still, the huge number of thermal pulses to follow and the strict spatial and temporal resolution required makes this task enormously demanding.

1

We use this acronym to denote both AGB and Super-AGB stars.

2

This is actually the first and only ascension of the giant branch for these low-metallcity stars since they avoid the RGB. We retain the terminology for continuity with higher metallicity stars.

3

Similarly this is actually the first dredge-up episode for low-metallicity stars but again we retain the terminology.

Acknowledgments

This work was supported by Jordi Ortiz Domenech and the Monash Centre for Astrophysics (MoCA). PGP would also like to thank the MoCA group for their kind hospitality and for the stimulating research atmosphere they provide. SWC acknowledges support from the Australian Research Council’s Discovery Projects funding scheme (project DP1095368) and a Monash Early Career Researcher grant (2012).

References

  1. Aoki, W., Beers, T. C., Christlieb, N., et al. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arnett, W. D. 1969, Ap&SS, 5, 180 [NASA ADS] [CrossRef] [Google Scholar]
  3. Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
  4. Beers, T. C., Preston, G. W., & Shectman, S. A. 1992, AJ, 103, 1987 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bromm, V., & Loeb, A. 2003, Nature, 425, 812 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
  7. Campbell, S. W., & Lattanzio, J. C. 2008, A&A, 490, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cannon, R. C. 1993, MNRAS, 263, 817 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cassisi, S., Castellani, M., & Castellani, V. 1997, A&A, 317, 108 [NASA ADS] [Google Scholar]
  10. Caughlan, G. R., & Fowler, W. A. 1988, Atom. Data Nucl. Data Tables, 40, 283 [Google Scholar]
  11. Cescutti, G., François, P., Matteucci, F., Cayrel, R., & Spite, M. 2006, A&A, 448, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Chiappini, C., Matteucci, F., & Ballero, S. K. 2005, A&A, 437, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Chieffi, A., Domínguez, I., Limongi, M., & Straniero, O. 2001, ApJ, 554, 1159 [NASA ADS] [CrossRef] [Google Scholar]
  14. Christlieb, N., Wisotzki, L., Reimers, D., et al. 2001, A&A, 366, 898 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Cristallo, S., Straniero, O., Lederer, M. T., & Aringer, B. 2007, ApJ, 667, 489 [NASA ADS] [CrossRef] [Google Scholar]
  16. D’Antona, F. 1982, A&A, 115, L1 [NASA ADS] [Google Scholar]
  17. Doherty, C. L., Siess, L., Lattanzio, J. C., & Gil-Pons, P. 2010, MNRAS, 401, 1453 [NASA ADS] [CrossRef] [Google Scholar]
  18. Eldridge, J. J., & Vink, J. S. 2006, A&A, 452, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Frost, C. A., & Lattanzio, J. C. 1996, ApJ, 473, 383 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fujimoto, M. Y., Iben, Jr., I., Chieffi, A., & Tornambe, A. 1984, ApJ, 287, 749 [NASA ADS] [CrossRef] [Google Scholar]
  21. FFujimoto, M. Y., Iben, Jr., I., & Hollowell, D. 1990, ApJ, 349, 580 [NASA ADS] [CrossRef] [Google Scholar]
  22. Fujimoto, M. Y., Ikeda, Y., & Iben, Jr., I. 2000, ApJ, 529, L25 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  23. Gil-Pons, P., & Doherty, C. L. 2010, Mem. Soc. Astron. Italiana, 81, 974 [NASA ADS] [Google Scholar]
  24. Gil-Pons, P., García-Berro, E., José, J., Hernanz, M., & Truran, J. W. 2003, A&A, 407, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Gil-Pons, P., Suda, T., Fujimoto, M. Y., & García-Berro, E. 2005, A&A, 433, 1037 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Gil-Pons, P., Gutiérrez, J., & García-Berro, E. 2007, A&A, 464, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Gil-Pons, P., Gutierrez, J., & Garcia-Berro, E. 2008, in First Stars III, eds. B. W. O’Shea, & A. Heger, AIP Conf. Ser., 990, 241 [Google Scholar]
  28. Girardi, L., Bressan, A., Chiosi, C., Bertelli, G., & Nasi, E. 1996, A&AS, 117, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, Symp. in Honour of Hubert Reeves’ 60th birthday: Origin and evolution of the elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse (Cambridge University Press), 15 [Google Scholar]
  30. Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
  31. Heger, A., Woosley, S. E., & Waters, R. 2000, in The First Stars, Proc. MPA/ESO Workshop Held at Garching, Germany, 4–6 August 1999, ESO Astrophysics Symp., eds. A. Weiss, T. G. Abel, & V. Hill, 121 [Google Scholar]
  32. Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
  33. Herwig, F. 2004, ApJ, 605, 425 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hirschi, R., Chiappini, C., Meynet, G., Maeder, A., & Ekström, S. 2008, in IAU Symp., 250, eds. F. Bresolin, P. A. Crowther, & J. Puls, 217 [Google Scholar]
  35. Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
  36. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  37. Izzard, R. G., Glebbeek, E., Stancliffe, R. J., & Pols, O. R. 2009, A&A, 508, 1359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Karakas, A., & Lattanzio, J. C. 2007, PASA, 24, 103 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  40. Komiya, Y., Suda, T., Minaguchi, H., et al. 2007, ApJ, 658, 367 [NASA ADS] [CrossRef] [Google Scholar]
  41. Lattanzio, J., Frost, C., Cannon, R., & Wood, P. R. 1996, Mem. Soc. Astron. Italiana, 67, 729 [Google Scholar]
  42. Lau, H. H. B., Stancliffe, R. J., & Tout, C. A. 2007, MNRAS, 378, 563 [NASA ADS] [CrossRef] [Google Scholar]
  43. Lau, H. H. B., Stancliffe, R. J., & Tout, C. A. 2008, MNRAS, 385, 301 [NASA ADS] [CrossRef] [Google Scholar]
  44. Lau, H. H. B., Stancliffe, R. J., & Tout, C. A. 2009, MNRAS, 396, 1046 [NASA ADS] [CrossRef] [Google Scholar]
  45. Lau, H. H. B., Gil-Pons, P., Doherty, C., & Lattanzio, J. 2012, A&A, 542, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Lederer, M. T., & Aringer, B. 2009, A&A, 494, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Limongi, M., & Chieffi, A. 2005, in 1604: Supernovae as Cosmological Lighthouses, eds. M. Turatto, S. Benetti, L. Zampieri, & W. Shea, ASP Conf. Ser., 342, 122 [Google Scholar]
  48. Lucatello, S., Tsangarides, S., Beers, T. C., et al. 2005, ApJ, 625, 825 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lugaro, M., Ugalde, C., Karakas, A. I., et al. 2004, ApJ, 615, 934 [NASA ADS] [CrossRef] [Google Scholar]
  50. Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 747, 2 [NASA ADS] [CrossRef] [Google Scholar]
  51. Marigo, P. 2002, A&A, 387, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Marigo, P., & Aringer, B. 2009, A&A, 508, 1539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Marigo, P., Girardi, L., Chiosi, C., & Wood, P. R. 2001, A&A, 371, 152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Nakamura, F., & Umemura, M. 2001, ApJ, 548, 19 [NASA ADS] [CrossRef] [Google Scholar]
  56. Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
  57. Nomoto, K. 1987, ApJ, 322, 206 [NASA ADS] [CrossRef] [Google Scholar]
  58. Petrovic, J., Pols, O., & Langer, N. 2006, A&A, 450, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Ritossa, C., García-Berro, E., & Iben, Jr., I. 1999, ApJ, 515, 381 [NASA ADS] [CrossRef] [Google Scholar]
  60. Runkle, R. C., Champagne, A. E., Angulo, C., et al. 2005, Phys. Rev. Lett., 94, 082503 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  61. Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Siess, L. 2010, A&A, 512, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Siess, L., Livio, M., & Lattanzio, J. 2002, ApJ, 570, 329 [NASA ADS] [CrossRef] [Google Scholar]
  64. Stancliffe, R. J. 2010, MNRAS, 403, 505 [NASA ADS] [CrossRef] [Google Scholar]
  65. Stancliffe, R. J., Glebbeek, E., Izzard, R. G., & Pols, O. R. 2007, A&A, 464, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Stoer, J., & Bulirsch, R. 1980, Introduction to Numerical Analysis (New York: Springer-Verlag) [Google Scholar]
  67. Suda, T., & Fujimoto, M. Y. 2010, MNRAS, 405, 177 [NASA ADS] [Google Scholar]
  68. Suda, T., Aikawa, M., Machida, M. N., Fujimoto, M. Y., & Iben, Jr., I. 2004, ApJ, 611, 476 [NASA ADS] [CrossRef] [Google Scholar]
  69. Suda, T., Katsuta, Y., Yamada, S., et al. 2008, PASJ, 60, 1159 [NASA ADS] [Google Scholar]
  70. Suda, T., Komiya, Y., Yamada, S., et al. 2012, in First Stars IV, from Hayashi to the future, AIP Conf. Proc., 1480, 421 [NASA ADS] [CrossRef] [Google Scholar]
  71. Suda, T., Komiya, Y., Yamada, S., et al. 2013, MNRAS, 432, L46 [NASA ADS] [CrossRef] [Google Scholar]
  72. Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
  73. Ventura, P., & Marigo, P. 2010, MNRAS, 408, 2476 [NASA ADS] [CrossRef] [Google Scholar]
  74. Ventura, P., Criscienzo, M. D., Schneider, R., et al. 2012, MNRAS, 424, 2345 [NASA ADS] [CrossRef] [Google Scholar]
  75. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Wagenhuber, J., & Weiss, A. 1994, A&A, 290, 807 [NASA ADS] [Google Scholar]
  77. Wisotzki, L., Christlieb, N., Bade, N., et al. 2000, A&A, 358, 77 [NASA ADS] [Google Scholar]
  78. Wood, P. R. 1981, ApJ, 248, 311 [NASA ADS] [CrossRef] [Google Scholar]
  79. Wood, P. R. 2011, in ASP Conf. Ser. 451, eds. S. Qain, K. Leung, L. Zhu, & S. Kwok, 87 [Google Scholar]
  80. Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Relevant times, structure and composition values that characterise the evolution prior to the TP-(S)AGB.

In the text
Table 2

CNO surface composition values and quotients at selected times along the evolution of our model stars.

In the text
Table 3

Relevant results from the evolutionary calculations that characterise the TP-(S)AGB of our models.

In the text
Table 4

Total ejected envelope masses and hydrogen, helium, carbon, nitrogen and oxygen yields from our model stars.

In the text

All Figures

thumbnail Fig. 1

HR diagram of the Z = 10-5 models for masses between 4 and 9  M⊙.
In the text
thumbnail Fig. 2

Upper panel: evolution of surface abundances of carbon, nitrogen and oxygen during the second dredge-up episode (SDU) and the first thermal pulses of the TP-AGB phase for the 4 M⊙ model. Lower panel: evolution of the advance of the base of the convective envelope (grey shading) during the same interval of time. The light grey and the black dashed lines represent the location of the H-burning shell (HBS) and the He-burning shell (HeBS) respectively. The vertical line marks the beginning of the TP-AGB phase at the onset of the first thermal pulse.
In the text
thumbnail Fig. 3

Upper panel: evolution of surface abundances of carbon, nitrogen and oxygen during the corrosive second dredge-up episode and the first thermal pulses of the TP-SAGB phase for the 8 M⊙ model. Lower panel: evolution of the advance of the base of the convective envelope (grey shading) during the same interval of time. The lines have the same meaning as in Fig. 2. Letters a, b, c and d refer to the times for the corresponding panels of Fig. 4.
In the text
thumbnail Fig. 4

Abundance profiles of carbon, nitrogen and oxygen showing the progress of the corrosive second dredge-up episode for the 8  M⊙ star, at the times labeled in Fig. 3. The shaded region represents the convective envelope.
In the text
thumbnail Fig. 5

Upper panel: evolution of surface abundances of carbon, nitrogen and oxygen during carbon burning and the dredge-out episode (DO). Lower panel: evolution of the advance of the base of the convective envelope during carbon-burning and the DO episode. Both panels are for the 9 M⊙ star. The lines have the same meaning as in Fig. 2.

In the text
thumbnail Fig. 6

Mass of intershell convective zones versus pulse number for our models.
In the text
thumbnail Fig. 7

Upper left panel: evolution of the luminosity associated with hydrogen and helium burning for the 9M⊙ model star, during pulses 125 and 126. Lower left panel: evolution of convective regions during the same pulses. Right panels represent the same as left panels for the case of pulses 1125 and 1126.
In the text
thumbnail Fig. 8

Evolution of surface abundances versus time for the 4, 6, 8 and 9 M⊙ models.

In the text
thumbnail Fig. 9

[C/N] (upper panel) and [C/O] (lower panel) versus metallicity. Black symbols correspond to the yields of our computed models. The cases in which dilution has been taken into account are represented in grey. They should be located at the same [Fe/H] as the non-diluted yields, but we displaced them –0.1 dex for the sake of clarity. For comparison, observational data of EMP (black solid circles) and CEMP (red open circles) from the SAGA database are represented in both panels.
In the text
thumbnail Fig. 10

Masses of degenerate cores versus initial mass, at the end of the second dredge-up or dredge-out episode and at the end of our full computations for our model stars.
In the text
thumbnail Fig. 11

Variation of mass-loss rates, envelope mass and core mass versus time along the TP-AGB phase of the 4 M⊙ star. The thick black lines correspond to the results of our full calculations and thereafter values represented in thin lines correspond to extrapolations. Black lines correspond to VW mass-loss rates and grey lines correspond to the case VW/10 (see full text for details). The insert in the top panel highlights the evolution of the mass-loss rates at the end of our full computations. The Chandrasekhar mass, mCh, is shown for reference in the lower panel.
In the text
thumbnail Fig. 12

Variation of mass-loss rates, envelope mass and core mass versus time along the TP-SAGB phase of the 9 M⊙ star. The lines have the same meaning as in Fig. 11.
In the text
thumbnail Fig. 13

Mass limits at Z = 10-5 for the formation of carbon-oxygen and oxygen-neon white dwarfs, supernovae type I1/2 (for stars whose CO core reach mCh), electron-capture supernovae (for stars whose ONe cores reach mCh) and supernovae type II. These mass limits are represented for the cases in which Vassiliadis & Wood (1993) are used (full calculations), and for the cases in which this rates are decreased one order of magnitude.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.