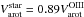| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 60 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220515 | |
| Published online | 20 September 2013 | |
The DiskMass Survey
VI. Gas and stellar kinematics in spiral galaxies from PPak integral-field spectroscopy⋆,⋆⋆
1 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: verheyen@astro.rug.nl; westfall@astro.rug.nl
2 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: martinsson@strw.leidenuniv.nl
3 Department of Astronomy, University of Wisconsin, 475 N. Charter St., Madison, WI 53706, USA
e-mail: mab@astro.wisc.edu; andrew@astro.wisc.edu
4 NRC Herzberg Institute of Astrophysics, 5071 West Saanich Road, Victoria, British Columbia, V9E 2E7, Canada
e-mail: david.andersen@nrc-cnrc.gc.ca
5 National Optical Astronomy Observatory, 950 North Cherry Ave., Tucson, AZ 85719, USA
e-mail: swaters@noao.edu
Received: 7 October 2012
Accepted: 9 May 2013
We present ionized-gas ([Oiii]λ5007 Å) and stellar kinematics (velocities and velocity dispersions) for 30 nearly face-on spiral galaxies out to as many as three K-band disk scale lengths (hR). These data have been derived from PPak integral-field-unit spectroscopy from 4980−5370 Å observed at a mean resolution of λ/Δλ = 7700 (σinst = 17 km s-1). These data are a fundamental product of our survey and will be used in companion papers to, e.g., derive the detailed (baryonic+dark) mass budget of each galaxy in our sample. Our presentation provides a comprehensive description of the observing strategy and data reduction, including a robust measurement and removal of shift, scale, and rotation effects in the data due to instrumental flexure. Using an in-plane coordinate system determined by fitting circular-speed curves to our velocity fields, we derive azimuthally averaged rotation curves and line-of-sight velocity dispersion (σLOS) and luminosity profiles for both the stars and [Oiii]-emitting gas. Along with a clear presentation of the data, we demonstrate: (1) The [Oiii] and stellar rotation curves exhibit a clear signature of asymmetric drift with a rotation difference that is 11% of the maximum rotation speed of the galaxy disk, comparable to measurements in the solar neighborhood in the Milky Way. (2) The e-folding length of the stellar velocity dispersion (hσ) is 2hR on average, as expected for a disk with a constant scale height and mass-to-light ratio, with a scatter that is notably smaller for massive, high-surface-brightness disks in the most luminous galaxies. (3) At radii larger than 1.5hR, σLOS tends to decline slower than the best-fitting exponential function, which may be due to an increase in the disk mass-to-light ratio, disk flaring, or disk heating by the dark-matter halo. (4) A strong correlation exists between the central vertical stellar velocity dispersion of the disks (σz,0) and their circular rotational speed at 2.2hR (V2.2hROiii), with a zero point indicating that galaxy disks are submaximal. Moreover, weak but consistent correlations exist between σz,0/V2.2hROiii and global galaxy properties such that disks with a fainter central surface brightness in bluer and less luminous galaxies of later morphological types are kinematically colder with respect to their rotational velocities.
Key words: techniques: imaging spectroscopy / galaxies: spiral / galaxies: structure / galaxies: kinematics and dynamics / galaxies: fundamental parameters
Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC).
Table 2 and Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Kinematic measurements of disk galaxies have been used for decades in the study of the distribution of dark matter. In fact, although “missing mass” was first reported in clusters of galaxies (Zwicky 1933), the ongoing quest of finding and explaining dark matter only began in earnest when it became clear that the rotation curves of spiral galaxies remain constant (“flat”) out to the largest measured radius, which can be well beyond the optical disk when using Hi data (early observations include Roberts 1966; Rogstad & Shostak 1972; Bosma 1978, 1981a,b; Rubin et al. 1980). Within the framework of Newtonian gravity, these observations cannot be explained by the implied mass distribution of the visible stars and gas alone, requiring that a significant dark component be present as well.
Although the existence of dark-matter halos is firmly established (again within the context of Newtonian dynamics), a robust measure of the density profile of these halos and the relative amounts of dark and luminous matter in real galaxies is highly uncertain. This is primarily caused by the uncertainty in the mass associated with the visible stars, or the stellar mass-to-light ratio (Υ∗). Even when a parameterized density distribution is assumed for the dark-matter halo (such as the two-parameter pseudo-isothermal sphere (e.g. Ostriker & Caldwell 1979) or NFW halo (Navarro et al. 1997), one cannot unambiguously decompose the mass contributions to the observed rotation curve without determining Υ∗. For a wide range of Υ∗, equally acceptable decompositions can be constructed with a corresponding wide range of dark-matter-density profiles (e.g. van Albada et al. 1985; Verheijen 1997; Dutton et al. 2005); while this is true in general, a poignant illustration of this fact is provided by Bershady et al. (2010a, hereafter Paper I using Hi data for NGC 3198.
This “disk-halo degeneracy” is most commonly circumvented by adopting the so-called “maximum-disk hypothesis” (van Albada & Sancisi 1986), which assumes that the visible baryons contribute maximally to the gravitational potential regardless of the corresponding Υ∗. The maximum-disk hypothesis is equivalent to minimizing the amount of dark matter needed to explain the observed rotation curve. When invoking the presence of a dark-matter halo to explain the outer parts of observed rotation curves, application of the maximum-disk hypothesis results in the baryonic disk contributing 85 ± 10% to the rotational velocity at 2.2 disk scale lengths (hR) in order to avoid a hollow halo (Sackett 1997). Although ad hoc, the maximum-disk hypothesis can explain the shapes of the inner rotation curves very well. This has provided empirical evidence that the dynamical mass distribution of disk galaxies follows the light distribution in the central regions (e.g. Sancisi 2004; Noordermeer et al. 2007; Swaters et al. 2011; Fraternali et al. 2011); however, such results only provide circumstantial evidence in validating the maximum-disk hypothesis. A robust validation of the maximum-disk hypothesis requires one to break the disk-halo degeneracy, thereby deriving meaningful density profiles of the dark-matter halos from rotation curve decompositions. To do so, one must obtain independent measures of Υ∗.
Although a flourishing industry exists for deriving stellar masses by matching photometric measurements to the predictions of stellar population synthesis (SPS) models (e.g. Bell & de Jong 2001; Kauffmann et al. 2003; Zibetti et al. 2009), these models are hampered by significant uncertainties in the stellar initial mass function, the star-formation history, the effect of late phases of stellar evolution, and the chemical-enrichment history of a galaxy. Alternatively, stellar dynamics can be used to determine the dynamical mass surface density of galaxy disks (Σdyn), which provides Υ∗ when combined with other data that quantifies the gas mass (e.g., Westfall et al. 2011b, hereafter Paper IV). For the Milky Way, the vertical density distribution and motions of stars in the solar neighborhood (e.g. Kuijken & Gilmore 1991) can be used to determine the restoring force to the Galactic mid-plane and, thus, the Galactic Σdyn. The essence of this concept can be extended to external galaxies as well (e.g. van der Kruit & Freeman 1984), and this idea is at the heart of the DiskMass Survey (DMS; Paper I).
Although many surveys exist that include spiral galaxies, few have measured stellar kinematics in the low-surface-brightness outer regions of their disks. The main reason for this has been the observational difficulties of obtaining data with the high signal-to-noise ratio (S/N) and high spectral resolution needed to measure stellar velocity dispersions in galaxy disks, which are typically ~20 km s-1 in the outer part. Previous studies (e.g., van der Kruit & Freeman 1986; Bottema 1993; Kregel et al. 2005) have used long-slit spectroscopy to measure the stellar velocity dispersions in disks; however, these observations only reached out to 1−2hR and suffered from large uncertainties in the vertical density distribution, significant projection effects due to high inclination, and rather low S/N of the acquired spectra. Nevertheless, these studies concluded that the disks of the galaxies in their samples only contribute ~60 ± 15% to their total rotation velocity, significantly less than the value found by applying the maximum-disk hypothesis.
With the advent of integral-field-unit (IFU) spectroscopy, the study of galaxy kinematics has taken a significant leap forward. Instead of only observing along one-dimensional long-slits, it has now become possible to obtain spectra with two-dimensional coverage on the sky. This allows the construction of three-dimensional data cubes with a spectrum at every position on the sky, a capability achieved in radio astronomy for decades, although by the use of different techniques. Additionally, IFU spectroscopy has the potential to boost the S/N of the data by averaging spectra from adjacent positions in the galaxy disks.
The DMS employs the two custom-built IFUs SparsePak (Bershady et al. 2004, 2005) and PPak (Verheijen et al. 2004; Kelz et al. 2006), both with a field-of-view in excess of one arcminute, a spectral resolution of λ/Δλ = 8000 − 12 000, and light-collecting fibers (spaxels) that are 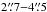 in diameter. The main goal of the survey is to determine Σdyn in ~40 disk galaxies thereby breaking the disk-halo degeneracy and directly constraining Υ∗ and the density profiles of their dark-matter halos. Our strategy includes measuring the gas and stellar kinematics in the galaxy disks, particular the vertical stellar velocity dispersion (σz), which provides a direct estimate of Σdyn (Paper I) when assuming a reasonable vertical mass distribution.
in diameter. The main goal of the survey is to determine Σdyn in ~40 disk galaxies thereby breaking the disk-halo degeneracy and directly constraining Υ∗ and the density profiles of their dark-matter halos. Our strategy includes measuring the gas and stellar kinematics in the galaxy disks, particular the vertical stellar velocity dispersion (σz), which provides a direct estimate of Σdyn (Paper I) when assuming a reasonable vertical mass distribution.
Existing surveys employing IFU spectroscopy are unsuitable for these analyses. For instance, Ganda et al. (2006) used SAURON on the 4.2 m WHT telescope at La Palma to obtain IFU spectroscopy of the inner regions of 18 late-type galaxies. Due to its limited field-of-view (33″ × 41″), spectral resolution (λ/Δλ = 1200 or 250 km s-1), and surface-brightness sensitivity (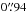 spaxels collecting relatively little light), stellar kinematic observations with SAURON were limited to the inner, high surface-brightness regions of galaxies (Rmax < 1hR for 14 out of 18 galaxies) where often a bulge or bar dominates the light. Other spectroscopic surveys including disk galaxies, such as the PINGS survey (Rosales-Ortega et al. 2010) or the CALIFA survey (Sánchez et al. 2012), also lack the high spectral resolution needed in order to measure velocity dispersions in the outskirts of galaxy disks.
spaxels collecting relatively little light), stellar kinematic observations with SAURON were limited to the inner, high surface-brightness regions of galaxies (Rmax < 1hR for 14 out of 18 galaxies) where often a bulge or bar dominates the light. Other spectroscopic surveys including disk galaxies, such as the PINGS survey (Rosales-Ortega et al. 2010) or the CALIFA survey (Sánchez et al. 2012), also lack the high spectral resolution needed in order to measure velocity dispersions in the outskirts of galaxy disks.
Here, we present gas and stellar kinematic data obtained for thirty nearly face-on spiral galaxies using the PMAS fiber package (PPak). We describe, in detail, the observational strategy, data reduction and analysis methods. Some preliminary results regarding the stellar and gas kinematics are presented as well. Ultimately, these PPak data will allow us to determine Σdyn out to as far as 3hR, to break the disk-halo degeneracy, to calibrate the mass scale of SPS models, and to determine the dark-matter distribution in spiral galaxies with unprecedented accuracy.
We start with a description of our galaxy sample in Sect. 2, followed by a description of our re-analysis of near-infrared 2MASS images in Sect. 3. Sections 4 and 5 provide brief overviews of the instrumental setup and observational strategy, respectively. Due to our original reduction methodology, and because of the importance of these data in future papers, Sect. 6 describes the data reduction in great detail; additional detail is provided by Martinsson (2011). Section 7 describes our derivation of the line-of-sight kinematics of the stars and gas, while the derivation of σz, the core data product of the DMS project, is presented in Sect. 8. Finally, Sect. 9 summarizes this paper. Throughout this paper, we adopt H0 = 73 km s-1 Mpc-1 for the Hubble parameter.
2. The PPak sample
The sample selection and observational strategy of the DMS has been described in detail in Paper I. In short, we selected a parent sample of 1661 galaxies from the Uppsala General Catalogue of Galaxies (UGC; Nilson 1973) that adhere to the following criteria: (a) a blue-band diameter of to appropriately match the field-of-view of our custom-built IFUs; (b) a blue-band minor-to-major axis ratio of 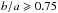 to ensure a nearly face-on orientation; (c) a Galactic extinction below
to ensure a nearly face-on orientation; (c) a Galactic extinction below 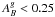 mag; and (d) a numerical Hubble type of
mag; and (d) a numerical Hubble type of 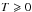 to select disk-dominated systems. We culled this sample of galaxies with dominant bars, significant asymmetries, large bulges, possibly interacting companions, and overcrowding of nearby bright stars via visual inspection of optical images and luminosity profiles resulting in 231 galaxies in our “Phase-A” sample. We measured Hα velocity fields for 146 galaxies in the Phase-A sample using SparsePak, which we call the Hα sample. Of these 146, we selected 40 galaxies for follow-up stellar-absorption-line spectroscopy; this “Phase-B” sample excludes galaxies in the Hα sample that are too face-on, kinematically lopsided, or significantly warped, and those that exhibited strong streaming motions. The 30 galaxies in the Phase-B sample observed using PPak are presented in this paper, which we refer to as the PPak sample. The distributions of galaxy properties in the PPak and Phase-A samples agree well, with similar color and surface-brightness ranges. However, the PPak sample lacks the least luminous galaxies and the few early-type galaxies (E & S0) present in the Phase-A sample. The PPak sample also has a higher fraction of Sc galaxies. See Paper I (especially Figs. 10−14 and Table 3) for a more detailed comparison between the different samples.
to select disk-dominated systems. We culled this sample of galaxies with dominant bars, significant asymmetries, large bulges, possibly interacting companions, and overcrowding of nearby bright stars via visual inspection of optical images and luminosity profiles resulting in 231 galaxies in our “Phase-A” sample. We measured Hα velocity fields for 146 galaxies in the Phase-A sample using SparsePak, which we call the Hα sample. Of these 146, we selected 40 galaxies for follow-up stellar-absorption-line spectroscopy; this “Phase-B” sample excludes galaxies in the Hα sample that are too face-on, kinematically lopsided, or significantly warped, and those that exhibited strong streaming motions. The 30 galaxies in the Phase-B sample observed using PPak are presented in this paper, which we refer to as the PPak sample. The distributions of galaxy properties in the PPak and Phase-A samples agree well, with similar color and surface-brightness ranges. However, the PPak sample lacks the least luminous galaxies and the few early-type galaxies (E & S0) present in the Phase-A sample. The PPak sample also has a higher fraction of Sc galaxies. See Paper I (especially Figs. 10−14 and Table 3) for a more detailed comparison between the different samples.
Table 1 lists salient properties of the galaxies in this sample. In summary, the PPak sample contains galaxies that range in Hubble type from Sa to Im (22 of them are Sc or later), in absolute K-band magnitude (MK) from − 25.4 to − 21.0, in B − K color from 2.7 to 4.2, and in central disk K-band surface brightness (μ0,K) from 15.8 to 19.7 mag arcsec-2.
3. Near-Infrared photometry
We retrieved the broadband J, H, and Ks (hereafter K) imaging data for each galaxy from the public 2MASS archive1. Where available, SDSS images were also retrieved from their respective archives because these are used for source identification (see below). Source Extractor (Bertin & Arnouts 1996) catalogs were constructed for all images to identify neighbouring sources to be masked when producing the primary galaxy photometry. This masking is important both to ensure an accurate sky-level determination and to inhibit foreground and background source contamination in the target photometry apertures, since the targets are relatively large and we need to reach low surface-brightness levels.
The so-called “Kron” apertures calculated by Source Extractor are of adequate size for masking the majority of sources, which all are nearly stellar. This aperture is defined to have a radius 2.5 times the first moment of the light profile, r1 (Kron 1980, who used 2r1 to define a total aperture magnitude), and it has been shown that such schemes undercount the total source flux by 10−25% for extended sources depending on the shape of the light profile (Bershady et al. 1994). This appears to be particularly the case for brighter sources with Source Extractor, likely because of the isophotal limits used for determining r12. Empirically, we found that defining a masking aperture of 5r1(1.625 − 0.03125minst), where minst is the instrumental magnitude such that 1 DN corresponds to 28.368 mag, resulted in a conservatively large mask at bright magnitudes (including the primary source) without masking overly large regions of the image from faint sources in all bands.
Additionally, Source Extractor has difficulty identifying the target galaxies because of their relatively large size compared to the point-spread-function (PSF), creating many smaller sources out of non-axisymmetric substructure rather than finding a single source for all galactic emission. For these reasons we hand-edited the J-band and (when available) SDSS r-band catalogs, since these images were generally the deepest, to increase the size of the contaminant sources, and to remove galactic features erroneously identified as separate sources. Some of the latter were difficult to identify with confidence; for these sources we also consulted color mosaics of SDSS data (when available) and when still in doubt chose to mask out the source. We also took this opportunity to identify any additional sources not found by Source Extractor within 5r1 of the primary source.
An important aspect of the source masking is to force the masking apertures to be identical in all bands. This ensures that the multi-aperture photometry samples identical regions of the galaxy at all wavelengths in the case where masked sources are within the target-source apertures. To accomplish this, source catalogs from all bands were merged together to create one master catalog. To avoid contamination near the galaxy, all sources within 7.5r1 were copied to the master catalog verbatim from the cleaned catalog. For all other positions, sources were matched across all images, with a distance threshold for matching of 0.5 times the semi-major axis of the ellipses (or the closest match in the case of multiple matches), which we found resulted in accurate matches without significant levels of false positives. For all matched sources, the source with the largest aperture was then chosen for the master catalog. This minimized contamination from the faint wings of foreground stars and background galaxies.
After blanking all contaminant sources in the master catalog, and determining the sky between 3.5r1 and 6.5r1 away from the primary galaxy, we computed an initial surface-brightness profile of the galaxy using apertures with constant ellipticity and position angle set to the isophotal value derived from Source Extractor. Next, we fit this profile between 1.25r1 and 2.5r1 with an exponential function, and extrapolated this fit to 7.5r1. The extrapolated profile is then subtracted from the image to ensure that any low-level galaxy flux outside of the masking region is not subtracted in the subsequent surface fits that are used to correct the sky foreground.
We fit and subtract the sky foreground separately in each passband using the source masks and the iterative method described in Paper IV and by Schechtman-Rook & Hess (2012). At each iteration the order of the fit is increased, up to order 9; the surface-brightness profile of the galaxy was recomputed, re-fit, and re-subtracted for each iteration. The need for such a rigorous effort is due both to the desire to obtain very high precision photometry and the large-scale background fluctuations present in some of the 2MASS images. Figure 1 shows how well this correction works for one of the worst cases. While this surface-fitting method is generally stable, we chose the fit order that minimized the standard deviation of the pixels in the image as the “best” fit (typically orders between 5 and 9), and use photometry from that order in our analysis. The final surface photometry was defined in elliptical apertures with constant ellipticity and position angles defined from the kinematic analysis.
Properties of the galaxies in the PPak sample.
 |
Fig. 1 Illustration of our surface-fitting and source-blanking algorithms. Left panel: H-band 2MASS image of UGC 4555. The galaxy itself is toward the bottom of the frame; black ellipses mark radii of 2.5, 3.5, and 6.5r1. Second panel: same image but with neighboring sources blanked and the estimated galaxy profile subtracted. Third panel: 9th-order surface fit using our iterative scheme, which was chosen to be the “best” fit to the image. Right panel: residual image after surface subtraction. All images have the same dynamic range of 3DN, where 1DN corresponds to 20.7 mag arcsec-2. They have been smoothed by a Gaussian with a FWHM of 9 pixels (1″/pix) to enhance low-signal structure. |
To improve the S/N of the images, the J-, H- and K-band images were combined into a single JHK image, assuming that color gradients between these passbands can be neglected; for 21 nearby S0 to Sbc galaxies, Peletier & Balcells (1997) found an average J − K color gradient of − 0.01 (with a variance of 0.12) mag per K-band disk scale length. A JHK curve-of-growth was determined for each galaxy within concentric elliptical apertures with constant position angle and ellipticity as a function of radius, and with a logarithmic radial sampling. The apertures were centered on the morphological centers of the galaxies (Sect. 6.11), with position angles that correspond to the kinematic position angles and ellipticities that reflect the inclinations as suggested by the inverted Tully-Fisher relation (see Sect. 7.2 for more details).
Based on the curves-of-growth, for each galaxy the radial range was determined in which the residual sky foreground and its uncertainty were calculated. The radial range was typically between 6hR − 11hR. From this, the radial JHK surface-brightness profiles were derived. These JHK profiles were re-scaled to the K-band surface-brightness profiles to provide a pseudo-K-band surface-brightness profile for each galaxy that extends much further in radius than the K-band-only profile. The normalization was calculated using the photometric data within half the radius outside which the sky level was determined. These pseudo-K-band surface-brightness profiles are presented in Appendix D (hereafter the Atlas).
For each galaxy, a representative photometric scale length (hR) and central surface brightness (μ0,K) of the disk was determined by fitting a straight line to the pseudo-K-band luminosity profile in an iterative manner. Starting with a radial range of 10″ − 50″, a straight line was fit from which follows an initial estimate of hR. Subsequently, the radial fitting range was adjusted to 1hR − 4hR to avoid the inner region where a bulge or bar may dominate (Kormendy & Kennicutt 2004; Erwin 2005) and the outer region where the exponential disk may be (anti-) truncated (Kregel & van der Kruit 2004; Pohlen & Trujillo 2006). The fit was repeated to yield a new value of hR, which defined a new fitting range 1hR − 4hR. This procedure was repeated until convergence was achieved. The corresponding values of μ0,K and hR of the final fit are listed in Table 1, and this fit is indicated in the Atlas with a dotted line overlaid on the luminosity profile. This line is drawn as solid over the converged fitting range 1hR − 4hR.
The total extrapolated K-band magnitude is calculated by first integrating the observed luminosity profile to the radius where the K-band surface brightness plus its error falls below 25 mag/arcsec2, yielding an aperture magnitude maper,K. Outside that radius, the luminosity profile is extended with a modeled exponential decline that follows the scale length of the outer disk, which can be steeper or shallower than the representative scale length hR depending on the radial structure of the luminosity profile. The extended model profile is then integrated analytically from the aperture radius to infinity to yield mext,K. From this follows the total extrapolated K-band magnitude as the proper sum of maper,K and mext,K. These total extrapolated K-band magnitudes are also listed in Table 1.
Finally, we performed bulge-disk decompositions using the one-dimensional surface-brightness profiles. For this purpose, the disk of a galaxy is modeled with one or more exponential segments to properly subtract the inner disk, e.g. in the case of a type-II profile. The modeled (multi-)exponential disk is subtracted and the excess light in the inner region is modeled iteratively with a general Sérsic profile that was convolved with a Gaussian to accommodate seeing effects. These convolved bulge models are also shown underneath the inner luminosity profiles provided in the Atlas. We produce bulge-to-disk ratios by integrating the bulge model and comparing it to the total remaining luminosity that is assumed to be from the disk component, i.e., B/D = B/(mK − B) where B is the luminosity of the bulge, not the B-band magnitude. A proper, two-dimensional structural analysis of each galaxy based on our deep 2.1 m imaging will be presented in a forthcoming paper. These provisional B/D measurements derived from the 2MASS photometry are listed in Table 1.
Both the disk and the bulge have small Galactic extinction (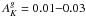 mag; Table 1) and k-corrections (κK = 0.01 − 0.10 mag; Table 5). For the disk surface brightness, we also correct the line-of-sight measurements to be the surface brightness as seen face-on by calculating
mag; Table 1) and k-corrections (κK = 0.01 − 0.10 mag; Table 5). For the disk surface brightness, we also correct the line-of-sight measurements to be the surface brightness as seen face-on by calculating ![\begin{equation} \mu_{K,\rm disk}^{i} = \mu_{K,\rm disk} - 2.5 C_{K} \log\left[\cos\left(\itf\right)\right], \label{eq:deproj_mu} \end{equation}](/articles/aa/full_html/2013/09/aa20515-12/aa20515-12-eq75.png) (1)where the coefficient CK = 1, assuming a transparent system with no internal dust extinction. The face-on correction ranges from 0.01 − 0.38 mag, depending on the inclination (iTF; see Sect. 7.2.3) of the disk, with an average and standard deviation of 0.14 ± 0.09 mag. The central surface brightness with applied corrections for each galaxy can be found in Table 1. The modeled bulge and resulting disk surface brightness can be seen in the Atlas. For later analysis, we define the “bulge radius”, Rbulge, to be the radius where μK,bulge − μK = 2.5 mag, i.e. where the light from the bulge contributes 10% to the total light. These radii can also be found in Table 1.
(1)where the coefficient CK = 1, assuming a transparent system with no internal dust extinction. The face-on correction ranges from 0.01 − 0.38 mag, depending on the inclination (iTF; see Sect. 7.2.3) of the disk, with an average and standard deviation of 0.14 ± 0.09 mag. The central surface brightness with applied corrections for each galaxy can be found in Table 1. The modeled bulge and resulting disk surface brightness can be seen in the Atlas. For later analysis, we define the “bulge radius”, Rbulge, to be the radius where μK,bulge − μK = 2.5 mag, i.e. where the light from the bulge contributes 10% to the total light. These radii can also be found in Table 1.
4. PPak instrumental setup
In this section, we provide a brief overview of the custom-built PPak fiber bundle and the detailed setup used for our observations of the PPak sample. We provide a new astrometric table for the PPak fibers based on the post fabrication of the fiber bundle (as opposed to the nominal positions provided by Kelz et al. 2006). We also discuss our analysis of the spectrum of the dome flood lamps, which we have used for the wavelength calibration of our science spectra.
4.1. The PPak fiber bundle
Galaxies in the PPak sample were observed using PPak, which is a bundle of 382 optical fibers that has been permanently integrated as an add-on module in the pre-existing PMAS spectrograph at the 3.5-m telescope at Calar Alto in southern Spain. Figure 2 shows a direct image of the back-illuminated PPak fiber-bundle in the focal plane, located behind a f/3.3 focal reducer lens. The main fiber cluster consists of 331 science fibers, each with a core diameter of 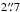 , packed in a regular hexagonal grid with a diagonal field-of-view of 64″ × 74″ and a filling factor of 60%. Thirty-six fibers, identical to the science fibers, are distributed over 6 mini-IFU’s located on the circumference of a circle with a radius of 72″ relative to the main IFU head; these fibers nominally sample the night sky and are used for sky subtraction of the science spectra. The 367 active fibers are surrounded by short inactive fibers (dark in Fig. 2) for protection during polishing and for a uniform stress-load on the active fibers. The remaining 15 fibers are arranged in a similar mini-IFU configuration to receive light at the same focal ratio from the integrating sphere of a separate calibration unit. During the science exposures, the 15 calibration fibers can be illuminated with a controllable mixture of light from several arc lamps and a halogen lamp. The spots of the emission lines in the calibration spectra are used to keep track of the flexure in the Cassegrain-mounted PMAS spectrograph, as well as the effective spectral resolution of a particular science exposure. All 331+36+15 fibers are uniformly distributed along a pseudo-slit in the spectrograph such that science, sky and calibration spectra are recorded simultaneously in all areas of the detector. A more detailed description of the PMAS spectrograph and PPak fiber bundle is provided by Roth et al. (2005) and Kelz et al. (2006).
, packed in a regular hexagonal grid with a diagonal field-of-view of 64″ × 74″ and a filling factor of 60%. Thirty-six fibers, identical to the science fibers, are distributed over 6 mini-IFU’s located on the circumference of a circle with a radius of 72″ relative to the main IFU head; these fibers nominally sample the night sky and are used for sky subtraction of the science spectra. The 367 active fibers are surrounded by short inactive fibers (dark in Fig. 2) for protection during polishing and for a uniform stress-load on the active fibers. The remaining 15 fibers are arranged in a similar mini-IFU configuration to receive light at the same focal ratio from the integrating sphere of a separate calibration unit. During the science exposures, the 15 calibration fibers can be illuminated with a controllable mixture of light from several arc lamps and a halogen lamp. The spots of the emission lines in the calibration spectra are used to keep track of the flexure in the Cassegrain-mounted PMAS spectrograph, as well as the effective spectral resolution of a particular science exposure. All 331+36+15 fibers are uniformly distributed along a pseudo-slit in the spectrograph such that science, sky and calibration spectra are recorded simultaneously in all areas of the detector. A more detailed description of the PMAS spectrograph and PPak fiber bundle is provided by Roth et al. (2005) and Kelz et al. (2006).
 |
Fig. 2 Left: photograph of the focal plane layout of PPak. The 331 science fibers and 36 sky fibers are back-illuminated. Right: the PPak fiber-footprint overlaid on top of a direct image of UGC 463. |
4.1.1. PPak fiber positions
We have produced a post-fabrication astrometric fiber-position table of the PPak IFU. We converted the high-contrast direct image of PPak in Fig. 2 to FITS format and calculated the relative positions of all 331 science fibers and 36 sky fibers using Source Extractor. The scale of the image (in pixels/arcsec) was calculated from the values given by Kelz et al. (2006). As can be seen in Fig. 2, the hexagonal grid of fibers is not perfectly regular. In particular, there is some appreciable curvature in the most northern fiber rows. The characterization of such fabrication artifacts are important to the fidelity of our reconstructed-continuum and kinematic maps (see the Atlas). The derived PPak fiber-position table can be found in Appendix C.
4.2. Spectrograph settings
All observations were taken with the J1200 grating, which has a blaze angle of and a blaze wavelength of 1200 Å in first order. By mounting the grating such that the grating normal is pointing toward the camera (“backward”), one can increase the spectral resolution by a factor of two due to the significant anamorphic demagnification. We observed the second order of the grating by properly setting the grating angle and using a stacked combination of Schott’s GG395 and BG40 glass filters. Although meeting our spectral resolution requirements (Paper I), this configuration results in a geometric light loss of ~15% because the grating is overfilled by the collimated beam.
Each fiber provides a spectrum covering approximately 430 Å dispersed along rows of the CCD, as seen in Fig. 4. We often refer to the spectral and spatial (cross-dispersion) dimensions in the discussion of our PPak spectroscopy using the variables X and Y, respectively. Due to the different entrance angles of each fiber along the pseudo-slit, not all spectra cover exactly the same spectral region: the spectra near the edges of the slit are shifted ~27 Å with respect to a spectrum near the center of the slit (Fig. 4). For each observation, the extracted spectral range common to all spectra is typically 4975–5375 Å.
We minimized the effects of read-noise via on-chip binning of the CCD detector. We binned by two pixels in the spatial (cross-dispersion) direction, but performed no binning in the spectral direction. The full-width at half maximum (FWHM) of the PSF is ~3 binned pixels in the cross-dispersion direction; ~5 pixels separate peaks of the PSF for adjacent fibers. With this setup, spatially adjacent spectra contributed less than 1% scattered light to any single aperture when defining an extraction aperture width of one FWHM centered on the peak of the spatial PSF (Sect. 6.6). In the spectral direction, the FWHM of the resolution element is 0.66 Å and the linear dispersion is ~0.21 Å/pixel (or ~12 km s-1 per pixel at 5150 Å).
Nominally, our spectrograph setup provides resolutions of λ/Δλ ≈ 7900 at a central wavelength of λc = 5200 Å (Kelz et al. 2006). However, in practice the resolution was often worse due to the combination of a less-than-perfect spectrograph focus, flexure effects during the one-hour exposures, and/or the somewhat curved surface of the CCD detector; we find that 97% and 87% of our observations have resolutions of λ/Δλ > 6000 and λ/Δλ > 7000, respectively (Sect. 6.9).
4.3. The dome flood lamps
The 15 calibration fibers collect light from the internal calibration lamps of the PMAS spectrograph, but the (331) science and (36) sky fibers cannot. Thus, wavelength calibration of the science and sky fibers nominally requires interpolation based on the calibration fibers (e.g. Rosales-Ortega et al. 2010), which can limit the accuracy of the calibration. Fortunately, the inside of the dome can be illuminated by six bright flood lamps that are attached to a walkway spanning the dome high above the telescope. In the spectral region of our interest, the spectrum of these flood lamps contains many more emission lines than the internal Thorium-Argon (ThAr) lamps, as shown in Fig. 3. Therefore, we devised an observing strategy that takes advantage of these spectra to increase the fidelity of our wavelength calibration. We describe the wavelength calibration of the flood-lamp spectrum below, and we describe its typical use in the wavelength calibration of our science and sky spectra in Sect. 6.
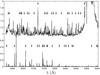 |
Fig. 3 Spectrum of the dome flood lamps (top) and the ThAr calibration lamp (bottom); the latter has been used to wavelength calibrate the former. The flux units are arbitrary and offset for illustration purposes. The arrows mark the emission lines in the ThAr-lamp spectrum that were used to calibrate the flood-lamp spectrum (bottom), and the emission lines in the flood-lamp spectrum that were used to wavelength calibrate our science spectra (top). |
4.3.1. Calibration of the flood-lamp spectrum
For use in wavelength calibration of our science spectra, we first calibrated the wavelengths of the flood-lamp emission lines; the wavelengths of these lines were not provided by the manufacturer. To do so, we partly dismantled the calibration unit that feeds the 15 calibration fibers of PPak such that they could be illuminated by either the flood lamps via an external mirror or the normal calibration lamps. Sets of five exposures each were taken of the internal ThAr lamp, the internal halogen lamps, and the external flood lamps, respectively. Only the 15 calibration fibers were illuminated; the science and sky fibers were kept dark. The telescope altitude and azimuth were fixed during these observations to prevent flexure shifts.
The five images in each set were combined to increase S/N and reject cosmic-ray detections. Using the IRAF task dohydra in the HYDRA package, we used the halogen image to trace and extract the 15 spectra from both the ThAr lamp and flood lamps. The wavelength scale of the flood-lamp spectra were calibrated by the ThAr spectra by fitting a first-order cubic-spline function to the 21−23 isolated Argon lines in each ThAr spectrum. None of the Thorium lines could be unambiguously identified from our library of known Thorium emission lines. The root-mean-square (RMS) scatter of the wavelength calibration ranges from 0.009 Å to 0.015 Å.
Twenty-five isolated emission lines across the observed spectral range of the flood-lamp spectrum were selected and their central wavelengths were determined for each calibration fiber by fitting a single Gaussian to each line. These measurements made for the uppermost calibration-fiber aperture deviated significantly from those of the corresponding emission lines in the other 14 apertures; this aperture is typically affected by the non-uniform focus of the spectrograph across the detector, which results in platykurtic line profiles (flatter than a nominal Gaussian) in the upper part of the frame3. After excluding the measurements from the uppermost calibration-fiber aperture, we calculated the average wavelength of each emission line in the calibrated flood-lamp spectrum and find a standard deviation of less than 0.01 Å. The error in these mean line centroids propagates in a systematic way to the calibration of our science spectra; however, no relative error is incurred among the calibrated science spectra.
Having calibrated the wavelength scale of the flood-lamp spectrum, we have found that many of the lines seem to come from Dysprosium and possibly also from Thorium by comparing the line centroids to literature line lists (e.g. in the online atomic-line database provided by the National Institute of Standards and Technology [NIST]4). Unfortunately, most of the lines in the flood-lamp spectrum are blended such that the measured centroids cannot be unambiguously correlated to the literature reference values. Instead, we choose to adopt the values found from our ThAr calibration, which should have errors smaller than 0.01 Å.
5. Observational strategy
Our primary objective is to observe stellar absorption lines at the highest spectral resolution achievable with PPak in the low-surface-brightness regions (R ≲ 3hR) of stellar disks. Therefore, we need to pay particular attention to the quality of the calibration of the science exposures while minimizing the amount of calibration overhead during the precious allocated dark time. To some extent, this notion has driven the design of the PPak IFU with its 15 calibration fibers, and the observing and calibration strategy described in this section has been devised to take advantage of these calibration fibers. In the end, our observations span eight dark-night observing runs between November 2004 and February 2008 with an overall success rate of ~55%; the success rate is mainly due to adverse weather at Calar Alto.
5.1. Calibration observations
For calibration images (taken at the beginning of the evening and the end of the morning of an observing night), the telescope was parked at a declination of δ = + 10° and an hour angle of − 2 h. This is the general direction in which most of the science observations have been taken. By parking the telescope for several minutes before beginning observations, we minimize flexure changes and, thereby, ensure that all calibration spectra were recorded at the same location on the detector. Moreover, this effort minimizes the differential flexure between the calibration images and the science images. Morning calibrations are taken in reverse order to those taken in the evening (as described below) to maximize on-sky observing.
Our evening calibration sequence typically consisted of ten bias frames, followed by five exposures each of the flood lamp, the continuum dome flat, and the twilight sky flat. Flood-lamp exposures were typically 30 s. We allowed several minutes between turning on the flood lamps and beginning the sequence of exposures to minimize spectral variability in the flood-lamp spectra due to temperature and pressure variations. Simultaneous ThAr-lamp spectra via the calibration fibers were taken during the flood-lamp exposures, which provided spots on the detector that were used to correct for flexure differences between the calibration and science observations. Continuum dome-lamp exposures were typically 20 s. These data are used to flat-field and trace the spectra in the science frames, as well as the other calibration frames. During dome-lamp exposures, the calibration fibers were illuminated by the halogen lamp to allow for robust tracing of the ThAr spectra. Sky-flat exposures ranged from 1−360 s, depending on the sky brightness. The sky-flat data are used to correct for variations in the fiber-to-fiber throughput. Occasionally, a series of hour-long dark-frame exposures were taken as well. Figure 2.3 from Martinsson (2011) provides examples of unprocessed bias, flood-lamp, dome-flat, and sky-flat images.
5.2. Galaxy observations
Our galaxy observations are read-noise limited: the S/N in the spectrum of the dark night sky is limited by the read-noise of the detector, and the galaxy surface-brightness levels at R ≲ 3hR are typically well below the surface brightness of the dark night sky. Therefore, we need to maximize the integration time for each science exposure. In practice, we are limited by the density of cosmic-ray hits in a single exposure. We have chosen an integration time of 3600 seconds for each science exposure, with the number of exposures per galaxy depending on the surface brightness of the galaxy, the transparency of the atmosphere and the darkness of the night sky. The number of exposures per galaxy is presented in Tables 3 and 4. Figure 4 shows an example exposure of a target galaxy.
Properties of the 41 combined galaxy exposures.
Galaxies with multiple pointings.
 |
Fig. 4 Examples of unprocessed PPak science exposures. Top: the result of drifting a template star through the central row of 21 fibers while the 15 calibration fibers are illuminated with the internal ThAr lamp. Spectra of the template star are recorded all over the detector. Bottom: a representative one-hour exposure of the galaxy UGC 4368. Again, the 15 calibration fibers are illuminated with the internal ThAr lamp. The curvature of the imaged pseudo-slit is clearly visible. |
Since the PMAS spectrograph is mounted at the Cassegrain focus of the telescope, its internal structure is subject to a changing gravity vector while the telescope is moving during the night. This induces flexure between the various components of the instrument due to a limited stiffness of the spectrograph structure. Such flexure may result in a deteriorating focus during the night, a changing location of the spectra on the detector, and a smearing of the spectra on the detector during the one-hour long exposure. As part of the pilot and feasibility study for the DMS with the PPak module, extensive flexure tests were performed by pointing the telescope at different positions in hour angle and declination, taking short arc-lamp exposures at each position to track shifts of the emission-line spots on the detector. The results are presented by Roth et al. (2005), showing that the shifts are relatively small for negative hour angles, i.e. on rising objects (see their Fig. 21). However, since the shift of only one spot was considered, the test did not characterize any changes in the plate scale or its rotation. We present our measurements and corrections for all such flexure distortions in Sect. 6.4. To minimize the detrimental effects of flexure during and in between our science exposures, we decided to observe only rising targets east of the meridian.
Simultaneously with our science exposures, the 15 calibration fibers were illuminated independently by the internal ThAr lamp. Typically, the shutter of the internal lamp was opened 5 × 8 s, interspersed regularly throughout each hour-long integration, producing emission-line spots in all areas of the detector. This procedure allowed us to trace any image shifts due to the flexure (Sect. 6.4) and to calculate the effective resolution of every science exposure as a function of wavelength and aperture number (Sect. 6.9).
A particularly salient feature of the PMAS spectrograph and its built-in guide CCD is its capability to save and reload the exact position of a guide star with an accuracy of 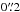 , the scale of a single pixel. This allowed for an accurate reproduction of the PPak pointing for each galaxy. However, since several telescope maintenance operations occurred over the course of our observing campaign, including a removal of the PPak unit on 16 November 2006 and a dismount of the Acquisition and Guide (A&G) camera on 24 April 2006, the relative offset between the guide camera and the PPak IFU was not consistent between runs before and after these dates. Thus, although our reacquisition strategy was successful for a given run, shifts in the PPak pointing between two runs could be larger than one fiber diameter. This has some consequences for our ability to co-add multiple exposures of a single galaxy taken over more than one run (Sect. 6.8).
, the scale of a single pixel. This allowed for an accurate reproduction of the PPak pointing for each galaxy. However, since several telescope maintenance operations occurred over the course of our observing campaign, including a removal of the PPak unit on 16 November 2006 and a dismount of the Acquisition and Guide (A&G) camera on 24 April 2006, the relative offset between the guide camera and the PPak IFU was not consistent between runs before and after these dates. Thus, although our reacquisition strategy was successful for a given run, shifts in the PPak pointing between two runs could be larger than one fiber diameter. This has some consequences for our ability to co-add multiple exposures of a single galaxy taken over more than one run (Sect. 6.8).
Finally, the operating system of the PMAS spectrograph allows for each exposure of the guide star, typically 15−120 s long, to be archived. For each galaxy exposure the series of guide-star exposures can be combined to yield an average guide-star image from which the effective seeing for that particular exposure can be determined (Sect. 6.10). The measured seeing will be used in future papers to correct the data for the effects of beam smearing caused by the relatively large on-sky fiber diameter.
5.3. Observations of template stars
During nautical and astronomical twilight, we observed 69 stars with a wide range in spectral type, luminosity class and metallicity. The stellar spectra, obtained with the same instrumental setup as the science exposures, are used as spectral templates in our cross-correlation approach for measuring the stellar kinematics of the galaxies (Westfall et al. 2011a, hereafter Paper III). A list of the observed template stars can be found in Table 2. For the analysis in this paper we have used the single stellar spectrum of the K1 III star HD162555 as a template (highlighted in Table 2).
To improve both the S/N and efficiency of our template-star observations, we observed the stars by drifting them from east to west over the central row of fibers. The drift speed depended on the apparent magnitude of the star, resulting in effective integration times per fiber that varied from 3−27 s. In this way, 21 fibers could be illuminated in a single drift scan, yielding at least 21 spectra that were later combined into a single template spectrum with a very high S/N as tabulated in Table 2. Figure 4 shows an example exposure of a template star.
6. Data reduction
This paper describes an extensive data set collected during eight different observing runs over a period of more than three years. We have made substantial efforts to ensure that the reduction and analysis of these data have been carried out in a robust, consistent, and homogeneous manner. Due to the need for high-precision kinematic measurements, we have been extra careful to minimize the errors in the wavelength calibration.
The first basic reduction steps have been done in a standard way by subtracting the bias and dark currents from all calibration and science images, and subsequently dividing the resulting images by a flat-field image to correct for pixel-to-pixel sensitivity variations. The distortions due to differential flexure have been robustly determined, using the ThAr spots in the calibration fibers as described in Sect. 6.4. Subsequently, the high S/N calibration images have been reprojected to match the shift, rotation and plate scale of each individual science exposure. Using the hydra package in IRAF5, the galaxy spectra have been extracted using dome-flat spectra to define the extraction apertures, sky-flat spectra to correct for fiber-to-fiber throughput variations, and calibrated spectra from the flood lamps to wavelength calibrate the science spectra. The quality of the wavelength calibrations has been inspected extensively (Sect. 6.6). Finally, we have subtracted the simultaneously recorded sky spectra (Sect. 6.7) and combined the exposures for each galaxy (Sect. 6.8) using various programs from the GIPSY software package (van der Hulst et al. 1992; Vogelaar & Terlouw 2001).
For subsequent analysis, it is important to determine the effective instrumental spectral resolution in the extracted galaxy and template-star spectra. This can vary significantly between different apertures, at different wavelengths, and in different images. Therefore, we have measured the spectral resolution of each science exposure by fitting Gaussian profiles to the Argon lines in the simultaneously recorded and extracted ThAr spectra from the 15 calibration fibers. These measurements are then interpolated in both spatial and spectral directions for every aperture and wavelength channel (Sect. 6.9).
Below follows a more detailed description of these reduction steps.
6.1. Bias and dark-current subtraction
An overscan region is provided by the CCD controller, but we have not applied a traditional overscan correction; charge from the exposed part of the detector, especially in the areas exposed to light from bright science fibers, often spills over into the overscan region. Therefore, we simply subtracted a master-bias image constructed from at least 14 individual bias read-outs. There is significant spatial structure in the bias with an increase in the bias level of 7 ADU from the bottom to the top of the bias frames (see Fig. 2.3 from Martinsson 2011). Depending on the temporal stability of the shape of the bias pattern, master-bias images were constructed for each night, for a series of consecutive nights, or for an entire observing run. Maximizing the number of individual bias read-outs combined in the master-bias minimizes the contribution of the master-bias correction to the total error budget of the extracted science spectra.
During each of 12 nights on 6 different runs, up to 5 dark exposures of 3600 s each were collected. After subtracting the associated master-bias images, the statistical properties of the dark current, like its mean and RMS noise, vary across the detector and among dark images from different observing runs (Martinsson 2011). However, the statistical variations within and among the dark-current images is sufficiently small. Therefore, we do not subtract these noisy dark images from the science images but simply subtract a representative dark current of 3.0 ADU/h from all images.
6.2. Pixel-to-pixel map and bad-pixel correction
Due to flexure, the location of the science spectra on the detector changes slightly during the night such that the sensitivities sampled by our calibration frames will not exactly correspond to those sampled by the science frames. To correct for this, we have created a normalized pixel-to-pixel sensitivity map using unfocused and focused dome-flat frames over several different runs, which homogenizes the illumination of the CCD frame. To each row in this combined dome-flat image we have fit a high-order (20) cubic-spline function in the dispersion direction and have divided each row by this smooth function to obtain a pixel-to-pixel sensitivity map normalized to unity (see Fig. 2.6 from Martinsson 2011). The smooth variations in this normalized map are typically much smaller than one percent, with the exception of a few small areas where sensitivities drop to a few percent lower than the mean and one elliptical “dark spot” of ~100 × 50 pixels that is half as sensitive at its center as compared to the rest of the frame (Martinsson 2011). This dark spot typically affects 5–10 fibers in a ~20 Å wide window in the red (near λ ~ 5350 Å). We also identified defunct pixels and pixel columns using the master-bias frames from both November 2004 and January 2007. The values of these bad pixels in each image were replaced by a linear interpolation of their neighboring pixels.
6.3. Combining calibration spectra
Dome-flat, sky-flat, and flood-lamp images were combined to increase their S/N and to remove cosmic rays, typically using four or five images for each set of exposures. To both successfully reject cosmic rays and produce high S/N images, the emission lines in these data must have a relatively stable flux; if not, the statistical rejection scheme would have inadvertently modified the shape, and thus the centroid, of the emission lines in the combined image thereby degrading, e.g., the wavelength calibration. This motivated our decision to allow ample time for the temperature and pressure in the lamps to settle. In addition, we checked the emission-line stability of, specifically, the flood-lamp spectra among a particular set by considering difference images. If any of the images were different from the majority, they were excluded in the combined image. Often the first image in a series was affected and rejected, indicating that our nominal settling time was insufficient for yielding a stable flood-lamp temperature and pressure. The sky-flat and dome-flat images were also carefully checked to ensure their statistical similarity and co-location of their spectra before combining them.
6.4. Flexure corrections
Shifts in the location of the spectra on the detector due to flexure in the PMAS spectrograph have been presented by Roth et al. (2005). However, we also detect non-negligible scale and rotation effects that can vary between the calibration and science frames, not previously investigated by Roth et al. (2005). Since the dome-flat images are used to trace the spectra on the science frames, and the flood-lamp images are used to wavelength calibrate the science spectra, it is important to establish a robust method of measuring flexure in the spectrograph and correct for its effects on our data.
The shift, rotation and scale differences were found by using several strong ThAr emission lines in the 15 calibration spectra that are simultaneously observed during the science and flood-lamp observations. As can be seen in Fig. 5, these emission lines create spots distributed over the entire CCD frame; 60 of these spots have been used to calculate the pixel-coordinate transformation matrix used to correct for flexure. By fitting two-dimensional Gaussian profiles to these 60 spots, their positions in every flood lamp and science frame were measured to an accuracy of 0.05 pixels or better. Using these 60 positions, the mean shift, rotation and scale differences between the flood-lamp and science frames could then be calculated with very high accuracy.
 |
Fig. 5 Central part of a raw image from a one-hour science exposure with inverted color map, illustrating how the emission lines in the ThAr spectra create spots all over the detector. These spots are used to track the effective spectral resolution and flexure in the Cassegrain-mounted spectrograph. |
We find that the shifts between the calibration and associated science frames, due to the difference in telescope pointing between the observations, are generally smaller than one pixel in both the X (spectral) and Y (spatial) directions; however, 30% of the frames have shifts of 1.0−3.6 pixels in X and/or Y, and 10% of the frames are shifted more than one pixel in both directions. Figure 6 demonstrates the scale and rotation effects between an example calibration frame and its associated science frame. Over all data, we find that the scale differences are always less than 0.05%, and less than 0.01% in more than 50% of the images, resulting in shifts of, respectively, 0.5 and 0.1 pixels at the edge of the detector.
 |
Fig. 6 Measured shifts in the locations of 60 ThAr spots from a flood-lamp exposure and from one of the science frames taken during the same night, illustrating a severe case of flexure. The shifts are indicated by arrows, calculated after the mean shift (ΔX = 0.21 and ΔY = 0.46 pixels) has been subtracted; the arrows have been magnified 1000 times for illustration purposes. The change in scale is clearly visible. |
After determining the coordinate transformation matrix, the calibration frames were shifted, scaled and rotated with respect to every science frame. By performing the transformations on the calibration frames, the interpolation algorithms only affect the high S/N frames, leaving the individual low S/N science frames unaltered.
We assess the accuracy of our flexure corrections by determining the positions of the ThAr lines in the reprojected flood-lamp frames using the method described above. The remaining differences between the centroids of the ThAr spots in the science frames and in the reprojected flood-lamp frames are on average 0.023 ± 0.017 pixels, with an extreme case at 0.16 pixels. Comparing the distribution of uncertainties to the non-corrected values (see Figs. 2.8 and 2.10 from Martinsson 2011), it is clear that the remaining deviations are much smaller than the original offsets and generally negligible. For frames with large uncertainties in the reprojection matrix, however, additional checks were made before further processing of the reprojected calibration frames. In particular, the precision of the wavelength calibration was assessed. Overall, the uncertainty in the wavelength calibration caused by these shifts is less than 0.04 and 0.16 spectral pixels (0.5 km s-1 and 1.9 km s-1 at 5150 Å) for 90% and 100% of our data.
6.5. Error spectra
We have calculated error spectra for our science observations as necessary for our approach to measuring stellar kinematics (see Sect. 7.1 and Paper III). We briefly describe the procedure used to generate these error spectra here; a more detailed description can be found in Appendix B from Westfall (2009).
Using the gain, η (e− /ADU), and read-noise, ϵRN (e−), of the detector, we calculate the noise in each pixel of the raw image as 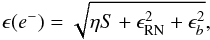 (2)where S (ADU) is the total signal and ϵb (e−) is the added noise due to subtraction of the master-bias images. We neglect the noise that is added when correcting for the pixel-to-pixel sensitivity variation (Sect. 6.2). We produced error spectra by processing the two-dimensional error image in a way that complements the processing of our science data, accounting for the appropriate propagation of the errors at every step. In particular, the spectral extraction, spectral resampling, and sky subtraction are all properly accounted for in the final error spectra.
(2)where S (ADU) is the total signal and ϵb (e−) is the added noise due to subtraction of the master-bias images. We neglect the noise that is added when correcting for the pixel-to-pixel sensitivity variation (Sect. 6.2). We produced error spectra by processing the two-dimensional error image in a way that complements the processing of our science data, accounting for the appropriate propagation of the errors at every step. In particular, the spectral extraction, spectral resampling, and sky subtraction are all properly accounted for in the final error spectra.
6.6. Extraction and wavelength calibration of science spectra
We have extracted and wavelength calibrated the science spectra using the HYDRA package in IRAF. For calibration, we selected the set of calibration data (taken during the evening or morning) that are the most complete (i.e., containing dome-flat, sky-flat, and flood-lamp images), have the smallest flexure correction, and provide the most robust wavelength calibration.
Flexure solutions were calculated and applied to the dome-flat images for each science and wavelength-calibration frame, and these corrected dome-flat images were used to define the extraction aperture for each spectrum. We used a fifth-order cubic-spline function to trace the spatial centroid of the PSF, and we set the extraction width to the FWHM of the PSF near the central wavelength of the spectrum. This extraction width limits the scattered light between spatially adjacent apertures to less than 1%, as determined by considering the PSF of bright stellar apertures adjacent to dark sky apertures in our template-star observations (see Bershady et al. 2005, for a detailed discussion of optimal extraction apertures). Dome-flat spectra were also used to correct for spectral vignetting of the science spectra (Figs. 2.3 from Martinsson 2011), whereas our sky-flat spectra were used to correct for fiber-to-fiber throughput variations.
Wavelength solutions for each science spectrum were found by fitting a first-order cubic-spline function to the pixel coordinates of the wavelength-calibrated emission lines in the extracted flood-lamp spectra. Low-quality wavelength solutions occurred for spectra near the top edge of the PPak pseudo-slit for some frames (notably those taken on 2−3 November 2005 and 14−15 October 2006). This was due to a poor focus of the spectrograph that resulted in strongly platykurtic (sometimes doubly peaked) emission lines, particularly toward the blue part of the spectrum for high aperture numbers. For the affected spectra, we found a high RMS scatter in our wavelength calibration; we also flagged and omitted these spectra when combining the galaxy spectra from multiple runs (Sect. 6.8). After wavelength calibration, all science spectra are resampled to a common (linear and log-linear) wavelength scale for subsequent analysis; all spectra contain 2048 pixels and have a wavelength range from 4980−5369 Å (0.19 Å per pixel for the linear wavelength scale).
We have performed several inspections of the wavelength-calibrated flood-lamp and galaxy spectra to quantify and assess any adverse effects that our flexure solutions may have had on the quality of the wavelength calibration. First, we have determined the RMS difference between the measured and tabulated wavelengths of the 18−23 flood-lamp emission lines as a measure of the relative precision of the wavelength calibration. The typical RMS difference is ~0.01 Å or ~5% of a spectral pixel; only 1.2% of all calibrated spectra have a wavelength-calibration RMS above 0.03 Å (~2 km s-1). An image with the RMS values for all observations is provided in Fig. 2.11 from Martinsson (2011).
Second, we inspected the accuracy of the wavelength-calibration zero-point using sky lines in the galaxy spectra. Unfortunately, only the Ni line at 5197.9 Å, near the center of the observed spectral range, was strong enough for reliable centroid measurements. When possible, we measured centroids for strong Ni lines (exceeding three times the RMS in the continuum level) in 10 galaxy spectra spread equally along the pseudo-slit, which was possible for 39 science exposures from all but one observing run. Figure 7 compares these measurements with the tabulated value of Ni provided by NIST.
 |
Fig. 7 Measured wavelength of the Ni sky-line at 5197.9 Å as a function of fiber number. The thin, grey lines connect measurements from 10 spectra in individual science exposures. Crosses show the averages of these measurements, and the thick, black lines indicate the standard deviation from the mean. The dash-dotted line depicts the tabulated value of Ni in air, as given by NIST. |
Figure 7 demonstrates that the error in our wavelength calibration is lowest for spectra near the middle of the pseudo-slit, increasing toward both low and high aperture numbers. However, the spread in Ni centroids toward the edges of the pseudo-slit is also effected by the error in the centroid measurements due to a decrease in the line S/N according to the vignetting function. At the center of the pseudo-slit, we find a marginal systematic shift of ~0.022 Å (~0.12 spectral pixels or ~1.3 km s-1) toward the red, most likely introduced by the wavelength calibration of the flood-lamp spectrum using the internal ThAr lamp. We note that temperature and/or pressure changes during calibration may have contributed to this effect: an emission line may shift by 0.02 Å if the ambient temperature of the air changes by 4 degrees. Although not true of all frames, the Ni line generally shifts toward the red going from the bottom to the top of the pseudo-slit, which may be due to a minute systematic residual in the reprojection matrix from the flexure solutions (Sect. 6.4). In any event, the scatter and the trend is at the level of 1−2 km s-1 and will have no astrophysical implications when analyzing the galaxy spectra.
6.7. Sky subtraction
The 36 dedicated sky fibers have been used to subtract the sky from our target spectra for each science frame. Given the change in spectral resolution across the pseudo-slit, we do not subtract an average sky spectrum from our target spectra. Instead, we fit a second-order polynomial along the spatial direction at every (wavelength-calibrated) spectral pixel. Pixels in the sky spectra that are affected by cosmic rays, or entire sky spectra that are contaminated by nearby sources (e.g., stars), were rejected during this fit. We then subtract the sky from the target spectra by interpolating the sky flux between sky apertures as determined by this fit. Our error spectra account for noise in this sky subtraction by adding (in quadrature) the RMS difference in the fit to errors calculated prior to sky subtraction; the sky-subtraction error is typically 20% of the noise in the outer, read-noise dominated galaxy spectra before sky subtraction.
Sky subtraction of our template-star observations is generally more difficult than for our galaxy spectra because the stellar spectra contaminate adjacent spectra, including the sky spectra. Therefore, we include any spectrum free of stellar emission in the sky subtraction procedure, regardless of its designation as a sky or science fiber.
6.8. Combining science spectra
As explained in Sect. 5, we expect some galaxies observed during several observing runs to have pointings that are not common to all exposures. In Table 3, we group science exposures that have a common pointing and provide some relevant information regarding the observations. In particular, this table provides the number of one-hour exposures taken for each galaxy at a particular pointing. This section details how we have combined these exposures, typically 3−8 per galaxy, to increase S/N and eliminate the effects of cosmic rays.
We mask the cosmic rays by identifying statistically aberrant pixels in each exposure. We do this by subtracting the median of each group of exposures from each exposure in the group. Subsequently, we ran an iterative sigma-clipping algorithm to create a cosmic-ray mask for each exposure. This works satisfactorily despite the small flexure shifts between the exposures within a group and the varying intensity of the sky during a long series of exposures. For galaxies with only one or two exposures, cosmic-ray masks were created manually. Masked pixels have been given a zero weight when averaging the images together. UGC 6903 is the only galaxy in our sample with a single exposure; the masked pixels in this case were replaced by a linear interpolation in the spectral dimension using neighboring, uncontaminated pixels.
Extracted spectra from individual frames within a group of exposures have been combined on a fiber-by-fiber basis. For the central fibers (fibers 148−183; all within 11″ from the central fiber 164) the spectra were weighted by the square of their mean S/N, times the mean spectral resolution of the spectrum. That is, the weight (wi) of fiber i is 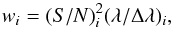 (3)where (λ/Δλ)i is the mean spectral resolution of the spectrum. The noise in fibers at larger distances from the center with fainter continuum levels is dominated by the read-noise, and thus similar for all spectra. Nevertheless, a varying transparency of the atmosphere motivates assigning different weights to the different exposures. Therefore, we use the average S/N of all recorded spectra as relative weights in Eq. (3). Spectra with large errors on the wavelength calibration, i.e., with a large rms in the fit (Sect. 6.6), are completely masked in the weighted average. The error in each weighted-average spectrum is calculated by propagating the errors on the individual spectra.
(3)where (λ/Δλ)i is the mean spectral resolution of the spectrum. The noise in fibers at larger distances from the center with fainter continuum levels is dominated by the read-noise, and thus similar for all spectra. Nevertheless, a varying transparency of the atmosphere motivates assigning different weights to the different exposures. Therefore, we use the average S/N of all recorded spectra as relative weights in Eq. (3). Spectra with large errors on the wavelength calibration, i.e., with a large rms in the fit (Sect. 6.6), are completely masked in the weighted average. The error in each weighted-average spectrum is calculated by propagating the errors on the individual spectra.
Weighted-average spectra for galaxies with multiple exposure groups (8 of 30 galaxies; see Table 4) could not simply be combined on a fiber-by-fiber basis because the pointing differences would result in an unacceptable effective on-sky beam smearing. These spectra were instead combined at a later stage, after the difference in the pointing had been determined (see Sect. 6.8.1).
Possible wavelength shifts between different exposures of the same galaxy, e.g., due to significantly different flexure corrections or wavelength calibrations, have been estimated by considering spectral shifts of the Ni sky line (Sect. 6.6). Only negligible wavelength shifts were detected. Note that possibly larger wavelength shifts may exist between the spectra from different apertures in the same exposure than between spectra from the same aperture in different exposures. However, line broadening due to slight wavelength shifts between the spectra from different exposures is always much smaller than the instrumental resolution, and therefore ignored.
6.8.1. Merging galaxy spectra from different pointing centers
Eight of our galaxies were observed during multiple runs. For these galaxies, we combined the spectra from exposures with identical pointings, determined the continuum levels in the combined spectra, and reconstructed the continuum image as described in Sect. 6.11; this produced a reconstructed continuum image for each exposure set. Subsequently, we determined the pointing offsets between the 2−4 reconstructed continuum images within an exposure set (Sect. 6.11) and these offsets are listed in Table 3.
With the pointing offsets known, we determined sets of fibers to combine that were within 1.5 fiber radii of one another. If the pointing offsets were small enough, this procedure simply led to a larger beam profile for the 331 science fibers. However, in many cases the offsets were enough that some fibers near the edge of the field-of-view were not combined with any other fiber.
The groups of “spatially overlapping” fibers were combined using a weighted average as described above when using Eq. (3). Note that the final number of merged spectra may exceed the number of fibers in the PPak IFU if the pointing offsets are sufficiently large. Because consecutive observations of a galaxy may have been acquired after several months had passed, the spectra to be combined were shifted to zero heliocentric velocity in order to avoid broadening of the spectral lines due to differences in apparent recession velocity. For each merged spectrum, we calculated the new effective spectral resolution and effective seeing. The effective sky position of each fiber is taken to be the weighted fiber position, where the weight for each fiber is wi from Eq. (3) divided by the square of the error in the pointing position. The effective fiber diameter for each merged spectrum is taken to be the sum of the nominal fiber diameter and the quadrature difference between the weighted standard deviation in the fiber position and the propagated error in the position in each dimension. These attributes of the merged spectra can be found in Table 4. The combined and merged individual spectra are displayed in greyscale in the upper-right panel of the accompanying Atlas, where the spectra have been reordered based on the aperture distance to the center. The [Oiii] emission lines are clearly visible, as well as many stellar absorption lines. With a favorable north-south orientation of the kinematic major axis, the rotation of the stellar disk can be clearly discerned by an offset in wavelength of the absorption lines. This effect is particularly visible for UGC 4036 and UGC 6918.
6.8.2. Combining template-star spectra
For our observed template-star frames (Sect. 5.3), we combined all extracted spectra with S/N > 20 and λ/Δλ > 5500; each spectrum was weighted according to 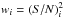 . As provided in Table 2, our observational strategy has resulted in template-star spectra with S/N > 300 and λ/Δλ > 6500 (σinst ≈ 20 km s-1); the effective spectral resolution in each combined spectrum is calculated using Eq. (4).
. As provided in Table 2, our observational strategy has resulted in template-star spectra with S/N > 300 and λ/Δλ > 6500 (σinst ≈ 20 km s-1); the effective spectral resolution in each combined spectrum is calculated using Eq. (4).
6.9. The instrumental spectral resolution
Accurate stellar-velocity-dispersion measurements require a detailed matching of the instrumental dispersions (σinst) in the galaxy and template spectra, or for corrections to be made to the raw kinematic measurements (as we do here). In either case, one requires measurements of σinst for both spectra. For our PPak observations, this has been achieved using the 15 ThAr spectra from the simultaneously illuminated calibration fibers in the science frames. These ThAr spectra were extracted in an identical manner as the science spectra and wavelength calibrated using the argon lines (see Fig. 3). Due to the strong curvature of the imaged slit on the detector (see, e.g., Fig. 4), the algorithm used by dohydra to automatically shift the calibration to adjacent spectra failed, requiring an initial manual shifting of the spectra to be done before running dohydra.
 |
Fig. 8 Distribution of the average instrumental spectral resolution in all science exposures. The average resolution is λ/Δλ = 7680 ± 640 (σinst ≈ 16.6 ± 1.4 km s-1), which is somewhat lower than the most common resolution λ/Δλ ≈ 7800 due to the tail in the distribution toward low λ/Δλ. |
The intrinsic widths of the argon lines are much smaller than the instrumental resolution (σAr ≈ 1 km s-1 ≪ σinst); therefore, we measured σinst by fitting a Gaussian function to the Ar emission profiles. We then fit low-order-polynomial surfaces to these measurements to provide interpolated σinst values at every pixel of every extracted spectrum. Based on these surface fits, we have calculated the average spectral resolution for every galaxy spectrum extracted from all science frames; a histogram of these values is shown in Fig. 8. The tail of low-resolution values is primarily due to spectra obtained from high aperture numbers in exposures taken during only a few nights. On the whole, 97% and 87% of all spectra have resolutions of λ/Δλ > 6000 (σinst ≈ 21 km s-1) and λ/Δλ > 7000 (σinst ≈ 18 km s-1), respectively. The average instrumental dispersion for all spectra, σinst ≈ 16.6 ± 1.4 km s-1, is slightly better than reported by Bershady et al. (2010b, hereafter Paper II.
For each galaxy, the spectral-resolution maps from each exposure were combined to calculate the effective resolution of the combined galaxy spectra. Each measurement of σinst is assumed to describe a Gaussian instrumental profile, such that σinst of the combined data is the second moment of a weighted sum of Gaussian profiles with no offset in their centroid; i.e., we calculated  (4)where wi is the same weight as used in Eq. (3) (Westfall 2009). Figure 9 shows the average instrumental dispersion in all combined images. In the center of the detector σinst is typically 15−17 km s-1 and increases toward high aperture numbers and shorter (bluer) wavelengths. Except for the very highest aperture numbers in some of the frames, the instrumental dispersion is always less than 20 km s-1. The average spectral resolution in each of the 41 combined images is presented in Table 3.
(4)where wi is the same weight as used in Eq. (3) (Westfall 2009). Figure 9 shows the average instrumental dispersion in all combined images. In the center of the detector σinst is typically 15−17 km s-1 and increases toward high aperture numbers and shorter (bluer) wavelengths. Except for the very highest aperture numbers in some of the frames, the instrumental dispersion is always less than 20 km s-1. The average spectral resolution in each of the 41 combined images is presented in Table 3.
 |
Fig. 9 Average instrumental dispersion (σinst) as a function of wavelength and aperture number. |
The uncertainty in σinst is primarily due to the error in the Gaussian fit to the argon lines. We estimate this uncertainty on the basis of the RMS about the polynomial fit to the measured values, yielding one error value per spectrum. Errors from single exposures are typically around 0.3 km s-1 (0.4−1.0 km s-1 for the 30 highest aperture numbers where poor focus is a particular problem during the nights mentioned earlier), assuming independent and random measurement errors on the line fits. The errors on the instrumental dispersion for the weighted-average spectra (δσcomb) are calculated by propagating the errors from the individual spectra following  (5)where ϵi is the error in a single spectrum and
(5)where ϵi is the error in a single spectrum and 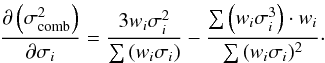 (6)The typical formal error on σinst in the combined images is 0.1−0.2 km s-1.
(6)The typical formal error on σinst in the combined images is 0.1−0.2 km s-1.
6.10. Seeing
On-sky seeing measurements are useful for our interpretation of, and correction for, beam smearing of our data. Therefore, we calculated the effective seeing for every science exposure using guide-star images recorded by the A&G camera during our science observations. These images are 50 × 50 pixels ( pixels) and have exposure times of 15−120 s. Each guide-star image was “bias-subtracted” by subtracting the average value of the upper six pixels in every column from all pixels in the same column. This was done to correct for differences of up to 30 ADU seen between neighbouring columns in the images, and was especially important for seeing measurements of faint guide stars that could have peak fluxes of less than 50 ADU above the bias level. We combined all guide-star images taken throughout each science exposure (typically 100 or more) to produce a high-fidelity image of the on-sky PSF.
pixels) and have exposure times of 15−120 s. Each guide-star image was “bias-subtracted” by subtracting the average value of the upper six pixels in every column from all pixels in the same column. This was done to correct for differences of up to 30 ADU seen between neighbouring columns in the images, and was especially important for seeing measurements of faint guide stars that could have peak fluxes of less than 50 ADU above the bias level. We combined all guide-star images taken throughout each science exposure (typically 100 or more) to produce a high-fidelity image of the on-sky PSF.
The IRAF task psfmeasure was then used to measure the FWHM of the stellar PSF; here, we define the effective seeing to be the FWHM of the Moffat profile fitted to the average image of the guide star. Our seeing measurements range from  to
to  with an average and standard deviation of
with an average and standard deviation of 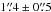 . The effective seeing values in the combined science exposures, calculated in the same way as the instrumental spectral dispersion (Eq. (4)), are presented in Table 3.
. The effective seeing values in the combined science exposures, calculated in the same way as the instrumental spectral dispersion (Eq. (4)), are presented in Table 3.
6.11. Coordinate registration
Reconstructed continuum images from the PPak spectra were registered against blue plates from the second Palomar Observatory Sky Survey (POSS-II) to accurately determine the telescope pointing. The PPak continuum images were constructed by inserting sigma-clipped, mean continuum values for each spectrum into a blank map at the relative locations of the corresponding fibers (Sect. 4.1.1); a 3σ-clip level excludes the [Oiii] and sky emission lines from the calculation of the mean continuum flux. Interstitial pixels in this map were filled by convolving the discrete continuum measurements with a Gaussian kernel having a FWHM that is 1.5 times the fiber diameter. The Atlas provides both the direct (POSS-II) and reconstructed continuum images demonstrating that the detailed morphologies are easily visible in the PPak data. The pointing center of the PPak data is determined by matching the pixel coordinates of two-dimensional Gaussian functions fitted to the central parts of both the reconstructed (PPak) and direct (POSS-II) continuum images using gaufit2d in GIPSY6. In this way, we have effectively attached a World Coordinate System (WCS) to the PPak continuum images with an estimated accuracy of better than 1″.
With a WCS attached, we can use the two-dimensional PPak images to identify the locations of the morphological centers of the galaxies, which we define to coincide with the peak flux in the inner regions. For galaxies that have been imaged by the Sloan Digital Sky Survey7 (SDSS), we have adopted the coordinates as reported by NED8. The correspondence between our fitted centers and the SDSS coordinates is excellent: we find an RMS difference of 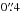 and an extreme case of
and an extreme case of 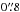 . The coordinates reported by NED for galaxies without SDSS imaging are mostly derived from 2MASS, where the agreement is often worse. By comparing with the centers provided by NED to the central peak in the maps, we find that our Gaussian-fitted centers provided a better estimate for the morphological center, and we adopt our own center measurements for galaxies without SDSS imaging. The coordinates of the adopted morphological centers of the galaxies can be found in Table 1.
. The coordinates reported by NED for galaxies without SDSS imaging are mostly derived from 2MASS, where the agreement is often worse. By comparing with the centers provided by NED to the central peak in the maps, we find that our Gaussian-fitted centers provided a better estimate for the morphological center, and we adopt our own center measurements for galaxies without SDSS imaging. The coordinates of the adopted morphological centers of the galaxies can be found in Table 1.
6.12. [OIII] intensity maps
We have constructed two-dimensional maps of the relative [Oiii] intensities using the same mapping algorithm as described in Sect. 6.11. The [Oiii] intensities are calculated by integrating over a 20 Å region surrounding the [Oiii] line after subtracting a baseline continuum flux. The continuum is set to be a straight line connecting the average flux in 20 Å wide spectral regions with centers separated by 20 Å on either side of the [Oiii] line. The resulting [Oiii] intensity maps are presented in the Atlas. We find that the [Oiii]-emitting gas is patchier than the stellar continuum light, characterized by small regions of strong emission. In general, these regions seem to be aligned with the spiral arms (e.g. UGC 7244 and UGC 9965) and likely coincide with star-formation complexes.
7. Kinematics of the stars and gas
Using our properly reduced spectra, we measure the line-of-sight recession velocity and velocity dispersion of both the stars and the [Oiii] gas within each fiber aperture. We have used these data to produce the two-dimensional velocity fields and velocity-dispersion maps presented in the Atlas. We also determine the orientation parameters of the galaxy disks, including their dynamical centers, heliocentric systemic velocities, position angles and inclinations. These orientation parameters allow us to derive the gas and stellar rotation speed and velocity-dispersion as a function of radius. As such, these measurements are fundamental to many of the overall goals of our survey, such as the calculation of asymmetric drift, estimation of the shape of the stellar velocity ellipsoid, and determination of the dynamical disk mass surface densities.
7.1. Extracting stellar and gas kinematics
The stellar kinematics in our target galaxies were derived using DC3, a program implementing the refined cross-correlation technique described fully in Paper III. For our PPak spectra, this means that our stellar kinematics (velocity, V, and velocity dispersion, σLOS) are largely determined by comparing the Mg and Fe absorption features present in both the galaxy and template-star spectra. Although we have observed many template stars (Sect. 5.3), the stellar kinematics presented herein are based on the K1 III template star HD162555 (log g = 2.49; [Fe/H] = −0.15). In general, one should use a mix of stellar template spectra appropriately matching the stellar populations represented within each fiber aperture; however, this exercise is deferred to a future paper. An analysis of the anticipated effects of template mismatch is presented in Paper II (Sect. 3.4) and concludes that the median random error on the derived velocity dispersion due to template mismatch is of order 4%.
Stellar velocity measurements are corrected to the heliocentric reference frame and for the velocity of the template star. Famaey et al. (2005) report a heliocentric velocity of − 14.84 ± 0.20 km s-1 for HD162555. By fitting Gaussian profiles to the centroids of three MgIb and three Fe absorption lines, we measure a less blue-shifted heliocentric velocity of − 13.09 ± 0.80 km s-1. The difference of + 1.75 ± 0.82 km s-1 is similar to the measured redshift of the Ni sky line as discussed in Sect. 6.6. For the remainder of this paper, we will ignore this small apparent systematic offset in velocity because it is irrelevant to our rotation-curve and velocity-dispersion measurements. We correct our stellar velocity-dispersion measurements for instrumental broadening (Sect. 6.9) following the procedure outlined in the Appendix of Paper III; see also Paper IV.
The kinematics of the ionized gas in our target galaxies is derived by fitting the [Oiii]λ5007 Å emission-line profile using software developed by Andersen et al. (2006, 2008). We fit both single- and double-Gaussian profiles to each line within a 20 Å window centered at the redshifted wavelength of the emission line. Emission-line profiles are considered more aptly fit by a double-Gaussian function when the reduced chi-square decreases by more than 10% compared to that found for the single Gaussian function. In 14% of the fits, a double-Gaussian fit to the [Oiii] line was preferred. For each fitted line, the fitting procedure returns measures of the velocity and velocity dispersion, and their associated errors as determined by a formal covariance-matrix analysis. In case of a double-Gaussian fit, the individual Gaussian profile with the largest flux was taken to represent the recession velocity and velocity dispersion of the ionized gas. The radial velocities of the [Oiii] line have also been corrected to the heliocentric reference frame. We determine the velocity dispersion of the ionized gas by subtracting σinst in quadrature from the velocity dispersion of the fitted line profile.
For illustration purposes, the heliocentric gas and stellar recession velocities and velocity dispersions as measured in each spectrum are placed in a two-dimensional map at the locations of the centers of the corresponding fibers. Similar to the reconstructed continuum images, the pixels in between the fiber locations have been filled by interpolation with a Gaussian convolution function with a FWHM of 1.5 fiber diameter (see Appendix A of Paper IV for details on the interpolation scheme). This yielded the two-dimensional velocity fields and velocity-dispersion maps as presented in the Atlas. We stress that the analysis of the kinematic data is not based on these interpolated maps but rather on the individual measurements from each fiber combined with the location of that fiber in the plane of the sky. The right-most panels of the Atlas show the S/N for each fiber footprint in which the stellar or gas velocity dispersion has been measured.
7.2. Orientation of the galaxy disks
To derive rotation curves and velocity-dispersion profiles for both dynamical tracers (gas and stars), we first determine the location of the dynamical center (x0,y0), the systemic velocity (Vsys), the position angle (φ0), and the inclination (i) of each galaxy using a step-wise approach. Our procedure assumes these geometric parameters are independent of radius; i.e., we assume that the gas and stellar ensemble rotate on circular, concentric, co-planar orbits around a common dynamical center. Additionally, to minimize the degrees of freedom when fitting the orientation of the rotating disks, we use a hyperbolic-tangent (tanh) parameterization of the shape of the rotation curve because it mimics a monotonically rising rotation curve with a near-linear rise in the inner regions and a smooth turn-over at a scale radius (rs) into a flat part with an asymptotic maximum rotation speed (Varot); i.e., 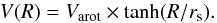 (7)At radius R = rs the rotation speed has reached V(rs) = 0.76Varot. It should be noted, however, that this parameterization cannot accommodate rotation curves that are declining over a certain radial range (e.g. UGC 4458) or rotation curves that show significant structure (e.g. UGC 4555).
(7)At radius R = rs the rotation speed has reached V(rs) = 0.76Varot. It should be noted, however, that this parameterization cannot accommodate rotation curves that are declining over a certain radial range (e.g. UGC 4458) or rotation curves that show significant structure (e.g. UGC 4555).
In this way, we model the projected, two-dimensional velocity field of a rotating galaxy disk using seven parameters: x0, y0, Vsys, φ0, i, Varot, and rs. In principle, all seven parameters can be fit simultaneously to the full two-dimensional velocity field using a program developed by Andersen (2001) and Andersen & Bershady (2003). In practice, there is significant covariance between i and Varot for galaxies seen nearly face-on, and the dynamical center is poorly defined for a velocity field in which the solid-body part of the rotation curve extends to a large radius (large rs) such that the inner isovelocity contours of the velocity field are nearly parallel. To ameliorate these issues, we have adopted a few additional assumptions as motivated in the following subsections.
7.2.1. Dynamical center
We first determine the dynamical center of the rotating disk by simultaneously fitting all seven velocity-field parameters. The left panel of Fig. 10 demonstrates that we find no significant systematic offset between the dynamical and morphological centers (Sect. 6.11) for either tracer. The offsets can be largely explained by the measurement uncertainties on the locations of the dynamical centers. The distribution of offsets is similar for the dynamical centers derived from the stellar and the gas velocity fields although the largest outliers tend to come from the gas kinematics. The right panel of Fig. 10 shows the differences between the dynamical centers from the stellar and the gas kinematics. Again, no systematic offset or trend is detected and the width of the distribution is similar to that in the left panel.
Although Fig. 10 shows that the dynamical centers lie within half a fiber diameter from the morphological centers, which have a precision of 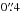 (Sect. 6.11), there are still many galaxies with significantly deviating dynamical centers. We believe this to be an artifact of the velocity-field modeling procedure, not a true reflection of the difference between the morphological and dynamical centers. Hereafter, therefore, we have chosen to affix the dynamical centers to the more accurately determined morphological centers for all galaxies in our modeling of the velocity-field. The underlying assumption is that the dynamical and morphological centers are co-located astrophysically.
(Sect. 6.11), there are still many galaxies with significantly deviating dynamical centers. We believe this to be an artifact of the velocity-field modeling procedure, not a true reflection of the difference between the morphological and dynamical centers. Hereafter, therefore, we have chosen to affix the dynamical centers to the more accurately determined morphological centers for all galaxies in our modeling of the velocity-field. The underlying assumption is that the dynamical and morphological centers are co-located astrophysically.
 |
Fig. 10 Left: offsets between the morphological centers of the galaxies as determined from direct images, and the dynamical centers as determined from the two-dimensional velocity fields. Open and solid symbols correspond to the dynamical centers derived for the [Oiii] and stellar velocity fields, respectively. Right: offsets between the dynamical centers as derived for the [Oiii] and stellar velocity fields. |
7.2.2. Systemic velocity and position angle
As the next step in our multi-stage fitting process, we have determined the systemic velocities (Vsys) and kinematic position angles (φ0); these parameters are determined independently for the gas and stellar velocity fields. In addition to forcing the coincidence of the dynamical and morphological centers, we also fix other velocity-field parameters that are largely independent of Vsys and φ0; this strategy does not affect the accuracy of our Vsys and φ0 measurements, even if the fixed parameters are only approximations (Begeman 1989). Therefore, while fitting Vsys and φ0, we have fixed i, Varotsini and rs (see Eq. (7)) in the following way.
For each galaxy, the projected asymptotic maximum rotation speed (Varotsini) was kept fixed to (Vmax − Vmin)/2, where Vmax and Vmin are, respectively, the maximum and minimum observed recession velocities after rejecting the 10% highest and lowest values. These rejection percentiles were verified by inspecting the outliers in preliminary made projected position-velocity diagrams. The inclination of the galaxy disk was kept fixed to the value calculated by inverting the Tully-Fisher (TF) relation (Tully & Fisher 1977) using our fixed Varotsini and the total absolute K-band magnitude (MK); see Sect. 7.2.3 for further details. Finally, for the fitting of Vsys and φ0, we fix rs = 0.42hR, where hR is the K-band photometric radial scale length of the exponential light distribution (Table 1). The factor 0.42 follows from fitting a tanh function to the model rotation curve of an exponential disk with scale length hR that was forced to remain flat beyond 2.15hR, where the model rotation curve of the exponential disk reaches its maximum.
 |
Fig. 11 Differences between velocity-field model parameters for the stars and [Oiii]-emitting gas. The parameters compared are the systemic velocities (top left), position angles (top right), projected rotation velocity (bottom left) and rotation scale (bottom right). The systematic offset between the projected rotation speeds of the stars and gas is expected given the significant asymmetric drift of the stars. The average asymmetric drift, |
Provided with our independent fits using the two different tracers, we compare the best-fitting velocity-field parameters for the gas and the stars in Fig. 11. The upper-left panel shows  versus the average value of Vsys for each galaxy. The weighted mean in ΔVsys is − 2.06 ± 0.20 km s-1 (0.2 pixels), indicated by the dashed line, such that the systemic velocity of the ionized gas is slightly (but significantly) blue-shifted with respect to that of the stars. In Sects. 6.6 and 7.1, we reported small systematic offsets in the wavelength calibration that is consistent for, respectively, the Ni sky line and the template star. The insignificant difference of ~0.5 km s-1 between these shifts is, however, too small to explain the observed ΔVsys. This shift may, in fact, be physical: the moderate blue-shift of the [Oiii] emission line relative to the stars may reflect our biased view of ionized-gas expansion in star-forming regions, where we preferentially see the near side due to extinction within these regions. However, regardless of its physical and/or instrumental origin, this slight difference is largely irrelevant to our measurements of the rotation curves. Therefore, we bring the systemic velocities of the stars and the gas on par by subtracting the observed average systematic offset of 2.1 km s-1 from all Vsys measurements of the stars. Velocity-field models fitted hereafter adopt the weighted average of Vsys from the two kinematic tracers for each galaxy, after correcting for the offset of the stellar data. These adopted average values of Vsys can be found in Table 5.
versus the average value of Vsys for each galaxy. The weighted mean in ΔVsys is − 2.06 ± 0.20 km s-1 (0.2 pixels), indicated by the dashed line, such that the systemic velocity of the ionized gas is slightly (but significantly) blue-shifted with respect to that of the stars. In Sects. 6.6 and 7.1, we reported small systematic offsets in the wavelength calibration that is consistent for, respectively, the Ni sky line and the template star. The insignificant difference of ~0.5 km s-1 between these shifts is, however, too small to explain the observed ΔVsys. This shift may, in fact, be physical: the moderate blue-shift of the [Oiii] emission line relative to the stars may reflect our biased view of ionized-gas expansion in star-forming regions, where we preferentially see the near side due to extinction within these regions. However, regardless of its physical and/or instrumental origin, this slight difference is largely irrelevant to our measurements of the rotation curves. Therefore, we bring the systemic velocities of the stars and the gas on par by subtracting the observed average systematic offset of 2.1 km s-1 from all Vsys measurements of the stars. Velocity-field models fitted hereafter adopt the weighted average of Vsys from the two kinematic tracers for each galaxy, after correcting for the offset of the stellar data. These adopted average values of Vsys can be found in Table 5.
The upper-right panel of Fig. 11 presents  for each galaxy. Overall, the position angles agree very well, with a weighted mean difference of as indicated by the dashed line. We find Δφ0 to be significant for a few galaxies, which is a result of velocity-field asymmetries combined with a patchy distribution of the [Oiii] emission. The errors in
for each galaxy. Overall, the position angles agree very well, with a weighted mean difference of as indicated by the dashed line. We find Δφ0 to be significant for a few galaxies, which is a result of velocity-field asymmetries combined with a patchy distribution of the [Oiii] emission. The errors in  are typically larger than those in
are typically larger than those in 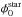 . Velocity-field models fitted hereafter adopt the error-weighted average of the gas and stellar φ0, provided in Table 5.
. Velocity-field models fitted hereafter adopt the error-weighted average of the gas and stellar φ0, provided in Table 5.
7.2.3. Inclination
Due to the nearly face-on orientation of the galaxies in our sample, inclinations derived by kinematic modeling of the velocity fields can result in large uncertainties (Andersen 2001; Martinsson 2011). To the contrary, inclinations inferred from the TF relation (iTF) are generally more precise in this inclination regime given (1) the well-defined Varotsini of our gas tracers ([Oiii], Hα, and Hi); (2) the availability of well-measured MK; and (3) the small observed scatter in the MK-Vflat TF relation. Given these considerations, we adopt i = iTF for our analysis of the PPak data in this paper.
Verheijen (2001) determined the TF relation for a sample of 21 spiral galaxies in Ursa Major using deep K-band photometric images and the detailed shapes of Hi rotation curves derived from 21 cm aperture synthesis imaging. The latter allowed for an accurate measurement of the amplitude of the flat part of the extended rotation curves. The total observed scatter in the MK − Vflat relation was 0.26 mag. The estimated depth of the Ursa Major sample contributes 0.17 mag to this total observed scatter, and the remaining quadrature difference of 0.20 mag can be attributed to the measurement errors. Here, we adopt the inverse TF relation 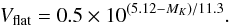 (8)Our determination of mK (Sect. 3) follows the same procedure as used by Verheijen (2001), as appropriate for our use of Eq. (8). We then calculate MK by applying the same corrections for extinction and the distance modulus as listed in Table 2 of Paper I, and with k-corrections applied according to Bershady (1995). Errors on Vflat include an adopted intrinsic scatter in the TF relation of 0.2 mag, the photometric error on mK, and a distance error proportional to the recession velocity increased by 150 km s-1 to account for uncertainties in the peculiar motions of the galaxies. The estimated values of Vflat and its error are listed in Table 5.
(8)Our determination of mK (Sect. 3) follows the same procedure as used by Verheijen (2001), as appropriate for our use of Eq. (8). We then calculate MK by applying the same corrections for extinction and the distance modulus as listed in Table 2 of Paper I, and with k-corrections applied according to Bershady (1995). Errors on Vflat include an adopted intrinsic scatter in the TF relation of 0.2 mag, the photometric error on mK, and a distance error proportional to the recession velocity increased by 150 km s-1 to account for uncertainties in the peculiar motions of the galaxies. The estimated values of Vflat and its error are listed in Table 5.
Parameterization of the orientation and kinematics of the galaxy disks.
We use the TF-predicted Vflat and our measurements of Varotsini to calculate the inclination and its error. Our measurements of Varotsini take advantage of the multiple gas tracers provided by our full dataset ([Oiii], Hα, Hi; see forthcoming papers for a presentation of the latter two tracers), but do not consider the stars such that we avoid the effects of asymmetric drift. Moreover, these measurements are made using the position-velocity data for all three gas tracers, not the parameterized values returned by our velocity-field models. The observed Varotsini determined by a weighted average of data from our three tracers and the resulting iTF are provided in Table 5.
The galaxies in the PPak sample are on average one magnitude brighter than the galaxies in the Ursa Major sample, but otherwise span a similar range of MK magnitudes with a similar scatter. The overlap of 3.5 mag in MK is sufficient to limit any systematic offset between the two samples. Furthermore, the morphological mix of galaxies in the samples is quite similar, although the Ursa Major sample contains somewhat more bar-dominated systems and low-surface-brightness galaxies. However, there is no statistically significant offset in the K-band TF-relation between low- and high-surface-brightness galaxies, or barred and non-barred galaxies (e.g. Courteau et al. 2003). For the TF-relation in Verheijen (2001), a distance to Ursa Major of 18.6 Mpc (Tully & Pierce 2000) was used. Based on recent results (Sorce et al. 2013), a distance of 18.0 ± 0.9 Mpc seems more appropriate. Although the distance uncertainty for Ursa Major may result in a ~0.5 systematic error on iTF for the PPak galaxies, this is negligible and inconsequential to the results presented in this paper.
systematic error on iTF for the PPak galaxies, this is negligible and inconsequential to the results presented in this paper.
It should be noted that we may refine the inclination estimates in forthcoming papers using improved kinematic models, improved photometric measurements, and/or an improved statistical treatment of the joint probability distributions for the various inclination measurements. However, these improved values are not expected to alter the results presented here.
7.3. Rotation curves and velocity-dispersion profiles
Below, we use the orientation parameters and systemic velocities determined in the previous section to calculate the rotation curves and the line-of-sight velocity-dispersion profiles, for both the gas and stars, of the galaxy disks.
7.3.1. Parameterized rotation curves
We derive Varot and rs for both the gas and stellar kinematics in each galaxy by fitting our kinematic model to their measured velocity fields while keeping the geometric parameters and systemic velocities fixed; the results are presented in the bottom row of Fig. 11. The bottom-left panel shows that, in general, the derived asymptotic rotation speed of the stars is less than that of the ionized gas. This is in accordance with the expectation that the asymmetric drift (AD) of the stars is significantly larger than that of the ionized gas. We find that 27 of the 30 galaxies show a ≥1σ signature of AD. When deprojected to the in-plane rotation, for all 30 galaxies we find − 5 ≤ km s-1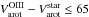 km s-1, which is between − 2% and 31% of the maximum gas rotation speed (
km s-1, which is between − 2% and 31% of the maximum gas rotation speed (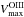 ). The average AD is 11 ± 8% of
). The average AD is 11 ± 8% of 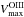 , which is similar to other measurements of local disk galaxies (e.g. Ciardullo et al. 2004; Herrmann & Ciardullo 2009) and comparable to measurements in the solar neighborhood of the Milky Way (e.g. Ratnatunga & Upgren 1997; Olling & Dehnen 2003). A more detailed investigation of AD, with an analysis of the data itself instead of the parameterized maximum rotation speed, is deferred to a forthcoming paper.
, which is similar to other measurements of local disk galaxies (e.g. Ciardullo et al. 2004; Herrmann & Ciardullo 2009) and comparable to measurements in the solar neighborhood of the Milky Way (e.g. Ratnatunga & Upgren 1997; Olling & Dehnen 2003). A more detailed investigation of AD, with an analysis of the data itself instead of the parameterized maximum rotation speed, is deferred to a forthcoming paper.
The bottom-right panel of Fig. 11 shows a significant scatter in the correlation between the best-fitting rs for the gas and stellar rotation curves. Contrary to nominal expectations based on AD, the scale lengths of the gas rotation curves are generally larger than those of the stellar rotation curves. However, we suspect that this is an artefact of the kinematic model in combination with the relatively poor sampling of the gas velocity field by the [Oiii] emitting gas near the dynamical center where the rotation curve rises most steeply. Considering the formal errors from the fits, it is noteworthy that the measurements with the smallest errors tend to indicate that 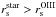 as would be expected for AD. In general, the errors correlate with the ratio
as would be expected for AD. In general, the errors correlate with the ratio 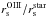 , a strong indication for a measurement bias. Therefore, we assign little astrophysical meaning to any relation between
, a strong indication for a measurement bias. Therefore, we assign little astrophysical meaning to any relation between 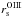 and
and 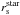 in Fig. 11.
in Fig. 11.
Velocity fields based on our kinematic model are presented in the Atlas. These maps project the rotation velocity of the model for each fiber to the sky plane following the derived disk orientation and use an interpolation scheme identical to that described for the observations (Sect. 7.1). The irregular sampling of the velocity field and the finite size of the Gaussian kernel introduce asymmetries into the interpolated model velocity fields despite its intrinsic axisymmetry. We have chosen this approach in an attempt to match irregularities in the observed velocity field that may be introduced by these same effects, as is particularly relevant to the residual maps shown in the Atlas. The residual maps help to identify large scale, non-circular or streaming motions in the stellar and gas disks. The particularly notable residuals in the gas velocity field of UGC 4458 are primarily due to the inability of our kinematic model to reproduce a declining rotation curve. This shortcoming motivates the non-parametric modeling of the rotation curve pursued in the next section.
7.3.2. Kinematics from constrained tilted-ring fits
The parameterization of the rotation curves in Eq. (7) helps to stabilize the kinematic modeling, but this functional form is merely an approximation to the actual shape of the rotation curve. Therefore, we have also derived non-parametric descriptions of the rotation curves by fitting tilted rings to the two-dimensional kinematic data.
All rings are forced to have the same orientation, following the parameters determined in Sect. 7.2. Within the range 2.5″ ≤ R ≤ 37.5″ (where R is defined in the plane of the galaxy), rings are defined by a continuous set of annuli with widths of 5″, yielding seven equally spaced rings. Individual fiber measurements are considered within a ring if the fiber center falls within the ring annulus. Assuming circular rotation and a marginal rotation-speed gradient within the ring, the line-of-sight velocity as a function of azimuthal position within each ring is a cosine function whose amplitude is the projected rotation speed of the ring (Vrotsini). Thus, by plotting these amplitudes as a function of radius, we create a non-parametric projected rotation curve for each tracer for each galaxy at seven discrete radii.
Within the same seven annuli, we calculate the error-weighted mean of the individual σLOS measurements for both the stars and the gas, excluding measurements with errors in excess of 8 km s-1. We also determine the effective radius of each annulus by calculating the weighted mean of each radius where the weights are determined by the error in the velocity dispersion.
The azimuthally averaged Vrotsini and σLOS profiles are presented in the Atlas. The seven radial points per profile are projected onto position-velocity diagrams of measurements for individual spectra, separate for each tracer. In the Atlas, the radial profiles from both tracers are also overplotted to facilitate a qualitative comparison. In general, the non-parametric rotation curves from the tilted-ring fits agree reasonably well with the fitted tanh model; however, there are notable exceptions such as UGC 4458.
Exponential fits to the σLOS and σz radial profiles.
 |
Fig. 12 Velocity-dispersion profiles (top: σLOS, bottom: σz) for all galaxies. The plotted data are the seven azimuthally averaged values from Sect. 7.3.2 normalized by the fitted central velocity dispersion for each galaxy. The radius of each datum is scaled by half of the e-folding length of the exponential fit to its associated galaxy. Data likely affected by bulge kinematics, as well as all data from UGC 4458 and UGC 8196, are marked with smaller symbols (and no errors); these data have been excluded from the calculation of the scatter given near the top of each panel. The exponential model is plotted as a thick grey line with five times the scatter about this line shown as dashed lines. Points above the upper dashed line are plotted in Fig. 13. The models have not been fit directly to the data shown, but to the individual fiber measurements for every galaxy separately (see the Atlas). |
8. The vertical stellar velocity dispersion
8.1. Exponential fits to σLOS
It is reasonable to expect that the velocity-dispersion profile of disk galaxies closely follows an exponential in radius: 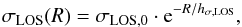 (9)where hσ,LOS is the radial scale length of the velocity dispersion. This expectation follows from the following set of assumptions: (1) stars act as trace particles of the disk mass distribution at all radii; (2) the scale height (hz), disk mass-to-light ratio, and axial ratios of the stellar velocity ellipsoid (SVE) are all constant across the entire disk; and (3) the surface-brightness profile is exponential in radius. If these assumptions hold, one should find hσ,LOS = 2hR (e.g. van der Kruit & Searle 1981); see Sect. 8.3.
(9)where hσ,LOS is the radial scale length of the velocity dispersion. This expectation follows from the following set of assumptions: (1) stars act as trace particles of the disk mass distribution at all radii; (2) the scale height (hz), disk mass-to-light ratio, and axial ratios of the stellar velocity ellipsoid (SVE) are all constant across the entire disk; and (3) the surface-brightness profile is exponential in radius. If these assumptions hold, one should find hσ,LOS = 2hR (e.g. van der Kruit & Searle 1981); see Sect. 8.3.
Thus, we have fit an exponential function to the radial distribution of the individual σLOS measurements, incorporating the error in each measurement. In this fit, we exclude σLOS measurements with errors that exceed 8 km s-1 and those at R ≤ Rbulge; for some galaxies, like UGC 7917, we also exclude regions that are likely affected by a bar. The fitted parameters (σLOS,0 and hσ,LOS) are tabulated in Table 6. Using the results from these fits, the top panel in Fig. 12 provides σLOS/σLOS,0 versus 2R/hσ,LOS for all galaxies, where the plotted σLOS measurements are the azimuthally averaged values derived in Sect. 7.3.2. Azimuthally averaged σLOS measurements from designated bulge regions are represented by smaller symbols without errors, and the solid line corresponds to the fitted exponential function. Excluding the smaller symbols, the error-weighted scatter around the exponential fit is 3.0%.
Several previous studies have reported a decrease in the observed stellar velocity dispersion toward the centers of disk galaxies (Bottema 1993; Emsellem et al. 2001; Márquez et al. 2003; Shapiro et al. 2003; Ganda et al. 2006). It has been argued that these “dips” are caused by a small, kinematically cold, central and young stellar disk of high surface brightness that dominates the luminosity-weighted kinematic measurements, outshining the hotter bulge component. Indeed, some of these studies focused on barred galaxies, Seyfert galaxies, or galaxies with a significant bulge where one might expect to find such products of centrally concentrated, recent star formation. However, for edge-on galaxies, Kregel & van der Kruit (2005) have shown that σLOS drops naturally toward the center as a result of the sampling of the stellar kinematics along the sight line. Moreover, disk-dominated galaxies may exhibit central dips in σLOS by strictly adhering to the asymmetric-drift equation or having a disk with a roughly constant stability (Westfall 2009). The galaxies in our PPak sample are all close to face-on and were selected to, largely, avoid prominent bars, bulges or nuclear activities. In addition, the galaxies also suffer from beam smearing in their most inner regions. It may therefore not be surprising that central dips in σLOS are not easily detected in our galaxies.
8.2. Deriving σz from σLOS
A fundamental goal of the DMS is to calculate dynamical mass surface densities of the disks (Σdyn) for which the relevant kinematic measurement is not σLOS but the vertical component (σz) of the SVE. We, therefore, deproject σLOS to σz following Paper II (Eq. (4)): ![\begin{equation} \sigz^2 = \frac{\slos^2}{\cos^2 i}\ \left[ 1 + \frac{\tan^2 i}{\alpha^2}\left(\sin^2\theta + \beta^2\cos^2\theta\right)\right]^{-1}, \label{eq:slos2sz} \end{equation}](/articles/aa/full_html/2013/09/aa20515-12/aa20515-12-eq229.png) (10)where α = σz/σR and β = σθ/σR describe the triaxial shape of the SVE, i is the inclination of the disk, and θ is the azimuthal angle in the plane of the disk relative to the major axis. As demonstrated for UGC 463 in Paper IV, we can derive α and β using the combination of our gas and stellar kinematic data, assuming that the epicycle approximation and the asymmetric-drift equation hold. Similar analyses for the PPak sample and the remainder of the DiskMass Phase-B sample is ongoing. Here, we follow Paper II and adopt α = 0.6 ± 0.15 and β = 0.7 ± 0.04 for all galaxies.
(10)where α = σz/σR and β = σθ/σR describe the triaxial shape of the SVE, i is the inclination of the disk, and θ is the azimuthal angle in the plane of the disk relative to the major axis. As demonstrated for UGC 463 in Paper IV, we can derive α and β using the combination of our gas and stellar kinematic data, assuming that the epicycle approximation and the asymmetric-drift equation hold. Similar analyses for the PPak sample and the remainder of the DiskMass Phase-B sample is ongoing. Here, we follow Paper II and adopt α = 0.6 ± 0.15 and β = 0.7 ± 0.04 for all galaxies.
The conversion of σLOS to σz is applied to every individual σLOS measurement. Analogous to our fits to σLOS (Sect. 8.1), we fit an exponential function to these σz measurements, yielding hσ,z and σz,0 (Table 6). Due to the complexity in the error propagation, we do not average the individual σz measurement. Instead, the radially-binned σz measurements are calculated from the error-weighted azimuthal averages of σLOS derived in Sect. 7.3.2. The results for the radial profiles of σz are shown in the bottom panel of Fig. 12. Qualitatively, the behavior of σz matches σLOS, but the weighted RMS scatter is reduced slightly to 2.4%, indicating the merit of considering the SVE shape.
 |
Fig. 13 Measurements of σLOS that significantly deviates from the exponential decline. The grey band indicates the range in σinst; the σLOS measurements presented in this figure have not been corrected for the instrumental broadening to emphasize that these measurements are well above the instrumental resolution limit. One measurement from UGC 8196 at ~ 58 km s-1 is not plotted. |
Figure 12 shows that σz (as well as σLOS) decreases more slowly than the fitted exponential function beyond a radius of R ≈ 1.5(hσ,z/2) ≈ 1.5hR for several galaxies. The data at these radii are from lower surface-brightness regions of the disk where errors in σz result in a minor influence on the results of the exponential fit compared to the higher surface brightness inner regions. It is interesting to question whether or not this difference between the inner and outer scale length of σz, or “kinematic flaring” of the disk, is astrophysical in origin. In Fig. 13, we plot the σLOS data from Fig. 12 that lie five times the weighted scatter above the exponential fit; 15 galaxies have at least one σLOS measurement outside of 1.3hR that satisfies this criterion. The range of σinst is also shown to demonstrate that most of the measured σLOS values are significantly larger than the instrumental dispersion, indicating that this “kinematic flaring” is likely real. A similar observation was made by Herrmann & Ciardullo (2009): Using observations of planetary nebulae in five nearby spiral galaxies, they find that σz falls exponentially out to ~3hR, then stops declining and becomes flat with radius. This effect appears to occur at smaller radii for our galaxy sample. Although a full discussion of this “kinematic flaring” is beyond the scope of our paper, three example astrophysical scenarios that could lead to this observation are (1) an increase in the disk mass-to-light ratio; (2) an increase of the disk scale height (a flared disk); or (3) disk heating due to a massive dark-matter halo.
8.3. Photometric and dispersion scale lengths
Using the parallel-plane approximation for a galaxy disk, van der Kruit (1988) has shown that the mass surface density follows  . If mass traces light and if the mass-to-light ratio of the disk is constant, we expect Σdyn ∝ μ such that
. If mass traces light and if the mass-to-light ratio of the disk is constant, we expect Σdyn ∝ μ such that  . Thus, for an exponential surface-brightness distribution with scale length hR, we expect σz to have an exponential distribution with a scale length of hσ,z ≡ 2hR. We test this expectation using our direct measurements of hσ,z and the K-band measurements of hR (Sect. 3) by plotting the ratio of these two quantities versus other salient galaxy properties in Fig. 14. As can be seen from the scatter, hσ,z/2hR varies by up to a factor of 2.5, which is substantially larger than expected given the formal fitting errors. A weighted-average of all measurements yields log (hσ,z/2hR) = 0.069 ± 0.092 dex, indicating that there is no significant systematic deviation from the expectation that hσ,z ≡ 2hR. However, there is no correlation between those galaxies having hσ,z > 2hR and those that exhibit the “kinematic flaring” discussed in the previous section. Disks that deviate from hσ,z ≡ 2hR may have a radially varying mass-to-light ratio, a radially varying scale height, and/or a change in the vertical distribution of mass with radius.
. Thus, for an exponential surface-brightness distribution with scale length hR, we expect σz to have an exponential distribution with a scale length of hσ,z ≡ 2hR. We test this expectation using our direct measurements of hσ,z and the K-band measurements of hR (Sect. 3) by plotting the ratio of these two quantities versus other salient galaxy properties in Fig. 14. As can be seen from the scatter, hσ,z/2hR varies by up to a factor of 2.5, which is substantially larger than expected given the formal fitting errors. A weighted-average of all measurements yields log (hσ,z/2hR) = 0.069 ± 0.092 dex, indicating that there is no significant systematic deviation from the expectation that hσ,z ≡ 2hR. However, there is no correlation between those galaxies having hσ,z > 2hR and those that exhibit the “kinematic flaring” discussed in the previous section. Disks that deviate from hσ,z ≡ 2hR may have a radially varying mass-to-light ratio, a radially varying scale height, and/or a change in the vertical distribution of mass with radius.
Of all the abscissae in Fig. 14, hσ,z/2hR appears to be most strongly correlated with hR. We find that small disks yield σz values that decline more slowly with radius than expected on the basis of the light distribution, whereas σz in larger disks declines more quickly. We also find that the scatter in hσ,z/2hR appears to decrease for disks with higher σz,0, K-band central surface brightness μ0,K, MK, and B/D (Sect. 3). In conclusion, our theoretical expectation that hσ,z = 2hR seems to hold best for stellar disks with a high central velocity dispersion, high central surface brightness, in the brightest galaxies with a significant bulge component.
 |
Fig. 14 Ratio of the exponential scale length of σz (hσ,z) and twice the photometric scale length (2hR) as a function of several global properties of the galaxies. This ratio is expected to be 1 (log [hσ,z/2hR] = 0) for an isolated exponential stellar disk. |
8.4. σz,0 versus Vmax
As discussed in Sect. 1, a key science objective of the DMS is to break the disk-halo degeneracy in rotation-curve mass decompositions (van Albada & Sancisi 1986). Using only our measurements of σz,0 of the stellar disk and Vmax of the galaxy (based on our tanh fits to the [Oiii] gas from Sect. 7.3.1), we can take a first step toward doing so by estimating the disk contribution to the rotational velocity, without engaging in a full rotation curve decomposition analysis: for a radially exponential disk with a certain oblateness (q), vertical density distribution (k) and central vertical velocity dispersion of the disk stars (σz,0), its dynamical mass can be calculated analytically (Bottema 1993). From this follows the gravitational potential that governs the corresponding maximum rotational velocity 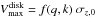 that occurs at a radius near 2.2hR (Casertano 1983, Paper II). Thus, we can define the maximality of the disk (
that occurs at a radius near 2.2hR (Casertano 1983, Paper II). Thus, we can define the maximality of the disk ( ) as the fractional contribution of the stellar+gas disk to the total rotational velocity of the galaxy at the radius where the rotation curve of the disk peaks: i.e.,
) as the fractional contribution of the stellar+gas disk to the total rotational velocity of the galaxy at the radius where the rotation curve of the disk peaks: i.e., 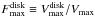 . Measurements of
. Measurements of  made in this way for the PPak sample have been presented by Bershady et al. (2011, hereafter Paper V, who also provide the functional form of f(q,k). Consequently, we limit ourselves here to investigating the relation between the observables σz,0 and the circular rotation speed of the [Oiii] gas at 2.2hR (
made in this way for the PPak sample have been presented by Bershady et al. (2011, hereafter Paper V, who also provide the functional form of f(q,k). Consequently, we limit ourselves here to investigating the relation between the observables σz,0 and the circular rotation speed of the [Oiii] gas at 2.2hR (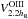 ).
).
 |
Fig. 15 Relation between the central stellar velocity dispersion (σLOS,0 to the left and σz,0 to the right) and the circular speed of the disks at 2.2hR. The black solid line in each panel indicates the error-weighted fit, and the black dashed lines are the error-weighted RMS scatter in the ratio. The grey lines show the relation determined by Bottema (1993). |
Figure 15 shows 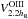 versus σLOS,0 and σz,0 for all galaxies in the PPak sample; as with Fig. 12, both σLOS and σz are plotted to demonstrate the merit of considering the shape of the SVE, even though the galaxies in our sample are nearly face on. Compared to the relation using σLOS,0, the relation between
versus σLOS,0 and σz,0 for all galaxies in the PPak sample; as with Fig. 12, both σLOS and σz are plotted to demonstrate the merit of considering the shape of the SVE, even though the galaxies in our sample are nearly face on. Compared to the relation using σLOS,0, the relation between 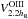 and σz,0 has a shallower slope, as expected, and the scatter in the correlation decreases. The slope is also significantly shallower than what was found by Bottema (1993). The fitted slope, f(q,k), indicates that nearly all of the galaxy disks in our sample are significantly submaximal, as discussed in Paper V.
and σz,0 has a shallower slope, as expected, and the scatter in the correlation decreases. The slope is also significantly shallower than what was found by Bottema (1993). The fitted slope, f(q,k), indicates that nearly all of the galaxy disks in our sample are significantly submaximal, as discussed in Paper V.
 |
Fig. 16
|
Figure 16 shows the ratio 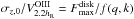 versus various global properties of the galaxies. Weak correlations between
versus various global properties of the galaxies. Weak correlations between 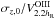 and
and  , MK, B − K, and morphological type can be discerned. Although weak, these correlations are all consistent in terms of galaxy properties along the Hubble sequence; later-type, fainter and bluer galaxies of lower surface brightness generally have kinematically colder disks for a fixed rotation velocity. It should be noted that these global properties along the Hubble sequence also correlate along the TF relation; brighter galaxies have a larger
, MK, B − K, and morphological type can be discerned. Although weak, these correlations are all consistent in terms of galaxy properties along the Hubble sequence; later-type, fainter and bluer galaxies of lower surface brightness generally have kinematically colder disks for a fixed rotation velocity. It should be noted that these global properties along the Hubble sequence also correlate along the TF relation; brighter galaxies have a larger 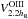 . Therefore, a significant covariance between MK and
. Therefore, a significant covariance between MK and 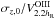 would result in trends that are opposite to those observed.
would result in trends that are opposite to those observed.
9. Summary and conclusions
We have presented gas and stellar kinematics obtained for 30 nearly face-on spiral galaxies from an extensive observing campaign with PPak, a custom-built fiber-based IFU module for the Cassegrain-mounted PMAS spectrograph on the 3.5m telescope at Calar Alto. To measure the velocity dispersions of the stars in the outer low-surface-brightness (μB ≈ 25 mag/arcsec2) regions of the disks of spiral galaxies, multiple hour-long exposures per galaxy were carried out at the highest spectral resolution (λ/Δλ = 7680 ± 640, on average) achievable with PMAS, covering a wavelength range of 4980−5369 Å. During dusk and dawn, a total of 69 spectra of bright stars were taken with the same spectrograph setting for use as template spectra in our measurements of the stellar kinematics. The design of PPak in combination with the chosen observing strategy allowed for zero calibration overheads during the precious dark nights.
We describe, in detail, the great care that was taken in our data reduction procedure, as required to overcome the adverse effects of flexure and optical aberrations in the instrument and ensure the highest possible quality of the final data products. The description of our data reduction procedure includes spectral calibration of the external flood lamps, correction for shifts and a changing plate scale on the detector due to flexure, pixel-to-pixel and fiber-to-fiber flat-fielding, sky subtraction by interpolation along the slit to account for optical aberrations in the spectrograph, and mapping the spectral resolution that changes significantly across the detector. After extraction and wavelength calibration, spectra from the same fiber but from different exposures were combined, weighting each spectrum by its S/N and effective spectral resolution. Observations of eight galaxies taken in multiple observing runs were combined in groups of spatially overlapping fibers, taking into account the differences in heliocentric velocities and in pointings of the instrument.
The kinematics of the ionized gas were obtained by fitting Gaussian functions to the [Oiii]λ5007 Å emission line, provided the line was sufficiently bright, yielding recession velocities and velocity dispersions of the [Oiii] gas at each fiber position. The stellar kinematics were measured using a robust cross-correlation technique (DC3; Paper III) based on a single K1 III template spectrum as a reference for all galaxies, yielding recession velocities and velocity dispersions of the stars at each fiber position. For illustration purposes, two-dimensional maps of the stellar continuum and [Oiii] line intensity were reconstructed for each galaxy, as well as the velocity fields and velocity dispersion maps for both the stars and the [Oiii] gas. The reconstructed continuum images were used to register a coordinate system to the PPak fiber positions.
The measured recession velocities of the gas and stars in combination with the fiber positions were used to derive the orientation of the galaxy disks. Dynamical centers were assumed to coincide with the morphological centers and an axisymmetric kinematic model with a hyperbolic-tangent prescription for the shape of the rotation curve was fitted to the velocity fields. A systematic blueshift in the global recession velocities of the [Oiii] gas with respect to the stars of − 2.1 km s-1 was detected and preliminarily ascribed to the expansion of star-forming regions from which the [Oiii] emission originates. However, the offset is small, and it should be noted that a systematic uncertainty of the same order exists between the gas and stellar velocities due to an uncertainty in the heliocentric velocity of the used template star. No systematic offset is detected between the kinematic position angles of the rotating gas and stellar disks. The Tully-Fisher relation (Verheijen 2001) was invoked to determine the inclination of the galaxy disks. Given the dynamical centers, systemic velocities and orientations of the galaxy disks, the radial dependence of the rotational velocity and velocity dispersion of the gas and stars was determined.
The asymptotic maximum velocities of the fitted parameterized rotation curves of the gas and stars clearly indicate the presence of asymmetric drift in the stellar disks for nearly all galaxies in the sense that 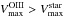 . Using parameterized asymptotic rotation speeds from our tanh-fit modeling we find this asymmetric drift to be on average 11 ± 8% of
. Using parameterized asymptotic rotation speeds from our tanh-fit modeling we find this asymmetric drift to be on average 11 ± 8% of 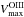 . However, several galaxies have large uncertainties and a more detailed analysis using the actual data points instead of modeled rotation curves will be presented in a forthcoming paper.
. However, several galaxies have large uncertainties and a more detailed analysis using the actual data points instead of modeled rotation curves will be presented in a forthcoming paper.
The observed line-of-sight velocity dispersions (σLOS) of the stars were corrected for an adopted shape of the stellar velocity ellipsoid (α = 0.6, β = 0.7), assumed to be the same within and among galaxies, yielding the vertical velocity dispersions (σz) of the stars which have been measured out to 2−3 photometric disk scale lengths (hR). The radial decline of the stellar velocity dispersion has been fitted with an exponential decrease, yielding central velocity dispersions and dispersion scale lengths for both σLOS and σz. For several galaxies, the stellar velocity dispersion declines more slowly than exponential beyond ~1.5hR, with 15 galaxies having at least one σz value measured outside of 1.3hR that is larger than five times the RMS above the exponential fit. The origin of this kinematic flaring is unclear, but may be related to an increase in the disk mass-to-light ratio, an increase of the disk scale height (a flared disk), or disk heating due to a massive dark-matter halo.
For the ensemble of 30 galaxies, the weighted-average ratio of the dispersion scale lengths and two times the photometric scale length (hσ,z/2hR) is consistent with the theoretically expected value of unity, but with a variance of 0.09 dex; larger than can be explained on the basis of the measurement errors. More massive disks with a higher central surface brightness show less scatter in this ratio and adhere closer to the theoretical expectation. A weak trend with hR seems to suggest that hσ,z > 2hR in galaxies with hR < 4 kpc and hσ,z < 2hR in galaxies with hR > 4 kpc.
The relation between the central stellar velocity dispersion of the disk and the rotational velocity at R = 2.2hR becomes tighter when σz is used instead of σLOS, indicating the merit of considering the shape of the stellar velocity ellipsoid. The ratio 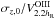 seems to show trends with the disk central surface brightness, absolute K-band magnitude, B − K color and morphological types that are weak but consistent with the global properties along the Hubble sequence; when compared to their rotational velocities, later-type spiral galaxies have stellar disks that are kinematically colder than earlier-type galaxies.
seems to show trends with the disk central surface brightness, absolute K-band magnitude, B − K color and morphological types that are weak but consistent with the global properties along the Hubble sequence; when compared to their rotational velocities, later-type spiral galaxies have stellar disks that are kinematically colder than earlier-type galaxies.
The main purpose of this paper has been to present the kinematic data of the gas and stars as obtained with the custom-built PPak IFU for 30 galaxies in the DiskMass Survey, and to present a first exploration of the kinematics. Any further analysis of these data is deferred to forthcoming papers.
Online material
Properties of the spectral template stars observed with PPak.
Appendix A: Notes on individual galaxies
IC 43. High quality kinematics. Significant bulge with second highest bulge-to-disk ratio (B/D = 0.32). Gas rotation curve rises quite sharply. A small bar and significant spiral structure are visible morphologically but exhibit little kinematic influence.
NGC 234. High quality kinematics. PPak and SparsePak data studied in detail in Paper IV. Strong, three-arm spiral structure with minor streaming motions. Some [Oiii] spots are clearly associated with star formation in the south-west arm.
NGC 575, IC 1710. Strongly barred galaxy. Bright field star within the PPak field-of-view. A Type-II break exists in μK(R) at roughly 1hR (approximately the same as the bar length). Very patchy [Oiii] emission. Stellar rotation curve shows interesting structure within 1hR.
Very patchy [Oiii] emission, some of which is associated with the visible spiral arms. “Ringing” present in μK(R) associated with the azimuthal coherence of the tightly wound spiral arms. “Kinematic flaring” starts just beyond 1hR. Host to Type Ia SN 1999dk (Modjaz & Li 1999).
IC 193. High quality kinematics. Sc galaxy, rather typical of our sample, apart from the high inclination (iTF = 39°). Rather weak [Oiii] emission. A dip in the [Oiii] rotation curve occurs at ~1hR without a morphological counterpart.
IC 208. Poor [Oiii] data. A Type II break in μK(R) occurs at ~1hR with a corresponding dip in the [Oiii] rotation curve; any dynamical association between these features is unknown. “Kinematic flaring” begins at about 2hR.
Unique among our sample: It has the lowest luminosity, MK = −21.0, one magnitude fainter than the second least luminous galaxy (UGC 3701). Two Type II breaks exist in μK(R) (at ~23″ and ~60″), but no indication of a bulge component; inner break is caused by the spiral arms. Appears to have a rather large bar, as well. Data within 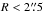 (indicated with a dotted vertical line in the Atlas) are excluded in the analysis of σLOS and σz, to avoid beam-smearing affects particularly strong in the center. Rather constant σLOS with radius such that hσ,z/2hR = 2.5, an extreme value among our sample with only UGC 3701 having a larger ratio.
(indicated with a dotted vertical line in the Atlas) are excluded in the analysis of σLOS and σz, to avoid beam-smearing affects particularly strong in the center. Rather constant σLOS with radius such that hσ,z/2hR = 2.5, an extreme value among our sample with only UGC 3701 having a larger ratio.
NGC 927, Mrk 593. Barred galaxy with a rather weak Type II break in μK(R) at ~1hR. Classified as a Starburst Nucleus Galaxy (SBNG), but its nucleus has an ambiguous activity classification between H 2 and LINER (Contini et al. 1998). Strong [Oiii] emission near the galaxy center and associated with the spiral arms.
Since the bulge/disk fitting routine resulted in a non-existing bulge, the excess light in the central region is interpreted as an inner disk. As with UGC 1862, σLOS and σz data within 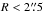 are excluded from our analysis. Strong [Oiii] emission associated with the spiral arms. [Oiii] velocity dispersions are roughly the same as σLOS.
are excluded from our analysis. Strong [Oiii] emission associated with the spiral arms. [Oiii] velocity dispersions are roughly the same as σLOS.
NGC 1642. Very close to face on with iTF = 14°. Nicely defined spiral structure but slightly lopsided. [Oiii] rotation curve rises more steeply than the stellar rotation curve then declines to approximately the same value at ~1hR. The μK profile breaks to a more extended disk (larger scale length) at R ~ 16″.
Second lowest surface brightness disk in our sample. Rather constant σLOS resulting in hσ,z/2hR = 2.9, an extreme value for our sample (see also UGC 1862). Some ringing in the μK profile due to the spiral arms. Rotation curves rise slowly.
Classified as Im by RC3 with low surface brightness. Bright field star just to the west of the nucleus. Stellar and [Oiii] rotation curves dip at ~1hR where the “kinematic flaring” begins. Rather low value of hσ,z/2hR = 0.6 measured.
NGC 2441. Host of Type Ia SN 1995E (Molaro et al. 1995; Quinn et al. 2006). Observations are dominated by ring-like structure, likely due to weak bar. Isovelocity twisting exists in the stellar velocity field. Streaming motions likely affect both the stellar and [Oiii] rotation curves. Very strong [Oiii] emission at the center likely indicates an active nucleus.
High-quality kinematics. Well-defined three-arm spiral structure. Type II break in μK(R) at R ~ 20″ accompanied by a drop in the [Oiii] velocity dispersion. Bright field star toward the north-east.
NGC 2532. Two close companions ~4′ to the north connected by an Hi bridge (Martinsson 2011). Interaction has likely produced the bright arm toward the east and the lopsidedness of the galaxy. High star-formation rate with very bright [Oiii] emission associated with visible star-formation regions. Stellar and [Oiii] rotation curves have dramatically different shapes; the [Oiii] gas is likely effected by streaming motions.
NGC 2575. Highest inclination in the sample (iTF = 45°) with two bright field stars within the PPak field-of-view. High-quality stellar kinematics. Two Type II breaks in μK(R), one at R ~ 16″ and the other at R ~ 30″.
Low-inclination galaxy (iTF = 13.8°) with a small apparent size and scale length (hR = 10″). Stellar kinematic data have limited radial extent, and the stellar rotation curve declines dramatically at R > 1.5hR, likely erroneously.
NGC 2599, Mrk 389. Earliest morphological type in our sample (Sa), with the largest bulge-to-disk ratio (B/D = 0.72). Some spiral structure visible at large radii, but very smooth morphology otherwise. Hi rotation curve declines from 350 km s-1 to 250 km s-1 (Martinsson 2011); [Oiii] rotation curve not well fit by a tanh model yielding large error on rs,OIII. Bulge dominates all stellar kinematic data; however, we fit an exponential to σLOS beyond R = 27″ (the dotted line in the Atlas). We find an outlying value of hσ,z/2hR = 0.4. [Oiii] velocity dispersion declines smoothly over all radii.
NGC 2649. Strong spiral structure affects μK(R). Bright field star visible to the north. High-quality stellar kinematic data. Weak [Oiii] emission in the center (resulting in aberrant isovelocity contours); very bright emission associated with the arms at larger radii. Rather extreme value of hσ,z/2hR = 1.8.
The most distant galaxy in the sample (Vsys = 12830 km s-1; D = 178 Mpc). Stellar kinematics limited to R < 15″; [Oiii] emission is rather extended. Type II break in μK(R) at R ~ 15″. Fourth highest bulge-to-disk ratio with B/D = 0.16.
Barred galaxy with rather low surface brightness. Poorest quality kinematic data in our sample (only one 3600s observation). Stellar-continuum S/N map shows that only fibers in the bar and spiral-arm regions have S/N > 1. Strong dip in μK(R) at R ~ 20″. Rather low value of hσ/2hR ~ 0.5. Stars rotate faster than the [Oiii] gas, violating asymmetric drift equation. Latter two comments should consider the quality of the data.
NGC 3982. High-surface-brightness member of the Ursa Major cluster. Very high-quality kinematic data. Host of Type Ia SN 1998aq (Hurst et al. 1998; Saha et al. 2001). Classified as a Seyfert 1.9 (Véron-Cetty & Véron 2006). Very strong [Oiii] emission associated with the nucleus and with the spiral arm to the south. Warped and lopsided extension to the Hi gas (Martinsson 2011); PPak kinematics are regular. Included in DMS pilot sample as presented in early publications (Verheijen et al. 2004; Bershady et al. 2005; Westfall 2009). Type II break in μK(R) at R ~ 1hR; σLOS transitions to a shallower slope at this radius. Large value of hσ,z/2hR = 1.6.
NGC 4195. As with UGC 3091, this barred galaxy has been modeled assuming no bulge; inner excess in μK(R) (R ≤ 8″) interpreted as inner disk. As with UGC 1862, we exclude 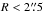 from our analysis of σLOS (vertical dotted line in Atlas). Stellar kinematic measurements only reach R ~ 20″. Rather high value of hσ,z/2hR = 1.7.
from our analysis of σLOS (vertical dotted line in Atlas). Stellar kinematic measurements only reach R ~ 20″. Rather high value of hσ,z/2hR = 1.7.
NGC 4662. Weakest [Oiii] emission in our sample, particularly within R < 10″. High-quality stellar kinematics. Excluded σLOS data at R < 1hR (vertical dotted line in the Atlas) to remove bar-associated regions. Type II break in μK(R) at R ~ 25″. Fifth highest bulge-to-disk ratio, with B/D = 0.14.
NGC 4977. Early-type spiral (SAb). Third highest bulge-to-disk ratio with B/D = 0.24. Low-surface-brightness, extended disk with strong spiral structure not probed by our kinematics. Rather complex μK(R), transitions to a shallower slope at R ~ 10″, which may be an extent of the bulge not accounted for in our bulge-disk decomposition. Data within R < 15″ is excluded from our analysis of σLOS. Central velocity dispersion errors are large due to the few data points used in the fit. Weak [Oiii] emission in the disk yields a poor rotation curve. Strong [Oiii] emission in the center suggests an active nucleus.
Well-defined spiral structure affecting μK(R). High inclination (iTF = 40°) and high-quality rotation curves for both the gas and stars. Measurements of σLOS limited to R < 25″, whereas [Oiii] dispersions are largely beyond that radius. The [Oiii] emission associated with some bright star-forming regions.
High-quality [Oiii] data with many star-forming regions producing large EW [Oiii] emission. Stellar data has a limited radial extent. Weak morphological bar does not affect the kinematics. Shallower slope in μK(R) beyond ~1hR. Low value of hσ,z/2hR = 0.5.
IC 1132. Very nearly face-on (iTF = 12°) with strong spiral structure visible in μK(R). Bulgeless galaxy; as with UGC 1862, we exclude data within 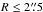 in the analysis of σLOS (vertical dotted line in Atlas). Many [Oiii]-emitting star-formation regions associated with the spiral arms.
in the analysis of σLOS (vertical dotted line in Atlas). Many [Oiii]-emitting star-formation regions associated with the spiral arms.
NGC 6691. Barred galaxy. Lowest inclination in the sample (iTF = 5.8°), yielding a very low-amplitude projected rotation curves. Type II break in μK(R) at ~1hR that matches a flattening of the σLOS profile. Strong [Oiii] emission near the galaxy center that may indicate an active nucleus.
NGC 7495. Stellar and [Oiii] rotation curves dip at ~1hR that may match a slight rise in μK(R), indicating streaming motion along a spiral arm. Type II break in μK(R) at R ~ 25″. Bright star-forming knots in the extended parts of the disk.
Appendix B: Atlas of Galaxy kinematics
This Atlas presents a collection of the relevant photometric and kinematic data obtained for the 30 galaxies in the PPak sample, one galaxy per page. For each galaxy, the top half of the page displays two-dimensional images, whereas the bottom half shows the derived radial profiles and contains tables with relevant parameters.
Appendix B.1: Images
The two-dimensional images are organized in three rows: The left-most panel in the first row shows the optical image of the galaxy extracted from blue POSS-II plates, illustrating its morphology and giving an impression of its surface brightness. SDSS multicolor images are provided in Paper I. The elongated panel to the right of the first row shows the extracted, wavelength-calibrated, sky-subtracted and combined(+merged) galaxy spectra organized along pixel rows. Most images consist of 331 spectra (331 rows); however, five galaxies have more than 331 spectra due to spatial offsets between the different combined pointings (see Sect. 6.8.1 and Table 4). The spectra have been reordered in radial distance from the galaxy center. Toward the blue (left) spectral regions in this panel, the [Oiii]λ5007 Å emission line (position indicated above the panel) is readily visible, as well as the [Oiii]λ4961 Å line for most galaxies with recession velocities larger than 1500 km s-1. For distant galaxies (e.g., UGC 1908), the Hβ line has also been redshifted into the observed spectral range. Toward the red (right) spectral regions, various stellar absorption lines are visible including the MgIb triplet (position indicated above the panel) and several Fe lines.
In the following two rows, we provide images based on information extracted from the PPak fibers reconstructed in two dimensions. The second row provides information based on the stellar continuum, while the third row is for the [Oiii]λ5007 Å emission line. Each map is 90′′ on a side, centered on the galaxy, and the small white cross inside a slightly larger black cross indicates the morphological center of the galaxy. From left to right, the panels provide:
-
1.
Reconstructed intensity maps of the stellar continuum (second row) and the total flux in the [Oiii]λ5007 Å emission line (third row). The procedure used to create these images, including the interpolation scheme used to fill interstitial regions is discussed in Sect. 6.11. The FWHM of the Gaussian kernel used to smooth the image (1.5 fiber diameter or ~
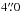 ) is shown as a hatched circle in the lower-right corner of the panel. These reconstructed continuum maps reproduce, in detail, the morphologies of the galaxies as seen in the POSS II images provided in the first row. The [Oiii] intensity maps are much patchier, concentrated toward the spiral arms, and have holes in areas where no [Oiii] emission was detected.
) is shown as a hatched circle in the lower-right corner of the panel. These reconstructed continuum maps reproduce, in detail, the morphologies of the galaxies as seen in the POSS II images provided in the first row. The [Oiii] intensity maps are much patchier, concentrated toward the spiral arms, and have holes in areas where no [Oiii] emission was detected. -
2.
Observed velocity fields with data points weighted by their errors and smoothed with a Gaussian kernel with FWHM of ~
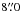 . The method used to generate these maps is the same as described in Appendix A of Paper IV. Isovelocity contours are plotted to highlight the structure in each velocity field; the contour levels are given in the table at the bottom right of each page. The thick black contour indicates the systemic velocity while the thin black and white contours show the receding and approaching sides of the disk, respectively.
. The method used to generate these maps is the same as described in Appendix A of Paper IV. Isovelocity contours are plotted to highlight the structure in each velocity field; the contour levels are given in the table at the bottom right of each page. The thick black contour indicates the systemic velocity while the thin black and white contours show the receding and approaching sides of the disk, respectively. -
3.
Model velocity fields based on the fitted tanh-model for the rotation-curve shape as described in Sect. 7.2. Although the model provides a velocity for all fibers, only those fibers with measured velocities are included. These model velocities are smoothed in exactly the same way as the observational data, except that all data have the same weight. As discussed in Sect. 7.3.1, non-axisymmetric features in the model velocity fields are the result of irregular sampling due to missing fibers without observed data and the interpolation scheme. Consequently, deviations from axisymmetry occur mainly at the edges of the field-of-view for the stellar data and, for the same reason, near the galaxy centers for the [Oiii] velocity fields. The isovelocity contour levels are the same for the model and observed velocity fields.
-
4.
Residual velocity fields calculated simply as the observed minus the modeled velocity fields. The contour levels are listed in the table, where black contours indicate positive residuals and white contours negative residuals.
-
5.
Line-of-sight velocity dispersion maps, also interpolated and smoothed using a Gaussian kernel with a FWHM of ~8″, where the data points with errors on σLOS exceeding 8 km s-1 have been rejected and the remaining data is weighted by the errors. Contours are drawn in steps of 8 km s-1; the lowest contour (thick line) is at 16 km s-1, which is similar to the instrumental spectral dispersion.
-
6.
Signal-to-noise maps that use no interpolation to fill interstitial regions; any point lying within a fiber aperture is given the value of the S/N of the spectrum from that fiber. In the second row, the plotted values are the average S/N in the spectral continuum; for the third row, they are the ratio of the [Oiii] intensity to its error. No values are plotted for spectra that had measurements with S/N < 1.
Appendix B.2: Radial profiles
The bottom half of each page presents various quantities measured for each galaxy as a function of in-plane radius. These radii are determined using the geometric projection parameters derived in Sect. 7.2.
Above the tables to the right, we provide the K-band surface-brightness profile discussed in Sect. 3. The dotted line indicates the result from the iterative fit of an exponential disk; the line is solid within the converged radial fitting range of 1–4hR, where 1hR is indicated by an arrow. The corresponding photometric scale lengths and central surface brightness are considered as representative for the disk. The curved solid line in the inner region represents the best-fitting bulge profile, a Gaussian smoothed Sérsic profile as described in Sect. 3. The dashed vertical line indicates the radius at which the bulge contributes 10% to the azimuthally-averaged surface brightness (Rbulge).
To the left, we provide four groups of two panels. Clockwise, starting from the upper left, these groups provide:
-
1.
Continuum and [Oiii] intensities: the greypoints show the intensities in individual spectra, while the blackpoints show the weighted-average data in radial bins. The verticaldashed line marks Rbulge. The scatter in the grey points at a certain radius indicates the azimuthal surface-brightness fluctuations at that radius. The very high [Oiii] intensities at the centers of some galaxies indicate the presence of an active galactic nucleus (see, e.g., UGC 1908, UGC 4036 and UGC 6918).
-
2.
Position–velocity diagrams of the stellar and [Oiii] gas recession velocities for data within ±45° of the kinematic major axis; the line-of-sight velocities have been corrected for the in-plane azimuth to match the line-of-sight velocities along the major axis. The solid and dashed curves indicate the hyperbolic-tangent function fitted to the shape of the rotation curve for the stars and [Oiii] gas, respectively; see Sect. 7.3.1. The black points indicate the velocities as derived from the tilted-ring fitting (Sect. 7.3.2). Both the parameterized rotation curve and the tilted-ring fits are based on data from both the approaching and receding sides of the galaxy. Thus, the derived rotation curves are symmetric around R = 0, even though the data may show kinematic asymmetries.
-
3.
Line-of-sight velocity dispersions (σLOS) of the stars and [Oiii] gas. Grey error bars correspond to individual measurements while black filled (stars) and open ([Oiii]) circles represent weighted-averages in radial bins (Sect. 7.3.2). The vertical dashed line indicates Rbulge. The black solid line represents the exponential fit to σLOS of the stars described in Sect. 8.1; this fit excluded σLOS measurements with errors larger than 8 km s-1 (also excluded from the Figure) and data within Rbulge.
-
4.
Projected rotation curves and velocity-dispersion profiles for both the stars (solid points) and [Oiii] gas (open circles) in the same panel. The solid lines indicate the best-fitting parameterized models for the stars; the best-fitting model rotation curve for the [Oiii] gas is shown as a dashed line. These curves are the same as those provided in the second and third panel groups.
Appendix B.3: Tables
In the lower right corner of each Atlas page, we provide two tables. The upper table lists the parameters of the derived orientation and kinematics of the galaxy, including the coordinates (α and δ; Sect. 7.2.1) of the morphological center, the systemic velocity and position angle of the receding side of the kinematic major axis (Vsys and φ0; Sect. 7.2.2), the Tully-Fisher-based inclination of the galaxy disk (iTF; Sect. 7.2.3), the asymptotic rotational velocity and the scale radius of the fitted parameterized rotation curve (stellar: Varot,star and rs,star; [Oiii] gas: Varot,OIII and rs,OIII); Sect. 7.3), and the fitted central line-of-sight velocity
dispersion and dispersion scale length of the stellar disk (σ0, ∗ and hσ∗; Sect. 8.1). The optical radial scale length (hR) and the radius (Rbulge) at which the bulge contributes 10% to the surface brightness is tabulated in the bottom. The second table provides the contour levels and intervals for the observed, modeled and residual velocity fields, as well as the velocity-dispersion maps.
Appendix C: The PPak fiber position table
On-sky positions (in arcsec) of the 331 science fibers (1−331) and 36 sky fibers (501−536), relative to the central fiber #164.
Appendix D: The Atlas
Analysis of optical (UBVRI) and near-infrared (JHK) images obtained from the 2.1 m telescope at Kitt Peak (Paper I) are ongoing.
This is also the case for some of the science frames as discussed in Sect. 6.6.
Acknowledgments
We wish to thank the referee for useful comments and suggestions. The staff at Calar Alto are thanked for their dedication and help during our observations. M.A.W.V. and T.P.K.M. acknowledge financial support provided by NOVA, the Netherlands Research School for Astronomy, and travel support from the Leids Kerkhoven-Bosscha Fonds. Support for this work has also been provided by the National Science Foundation (NSF) via grants AST-0307417 and AST-0607516 (M.A.B., K.B.W., and A.S.-R.), OISE-0754437 (K.B.W.), and AST-1009491 (M.A.B. and A.S.-R.). K.B.W. is also supported by grant 614.000.807 from the Netherlands Organisation for Scientific Research (NWO). R.A.S. and M.A.B. acknowledge support from NASA/Spitzer grant GO-30894. This work has taken advantage of the online NED9, SDSS10 DSS11 and 2MASS12 databases and data archives.
References
- Andersen, D. R. 2001, Ph.D. Thesis, The Pennsylvania State University [Google Scholar]
- Andersen, D. R., & Bershady, M. A. 2003, ApJ, 599, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Andersen, D. R., Bershady, M. A., Sparke, L. S., et al. 2006, ApJS, 166, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Andersen, D. R., Walcher, C. J., Böker, T., et al. 2008, ApJ, 688, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Begeman, K. G. 1989, A&A, 223, 47 [NASA ADS] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Bershady, M. A. 1995, AJ, 109, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Bershady, M. A., Hereld, M., Kron, R. G., et al. 1994, AJ, 108, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Bershady, M. A., Andersen, D. R., Harker, J., Ramsey, L. W., & Verheijen, M. A. W. 2004, PASP, 116, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Bershady, M. A., Andersen, D. R., Verheijen, M. A. W., et al. 2005, ApJS, 156, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Bershady, M. A., Verheijen, M. A. W., Swaters, R. A., et al. 2010a, ApJ, 716, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Bershady, M. A., Verheijen, M. A. W., Westfall, K. B., et al. 2010b, ApJ, 716, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Bershady, M. A., Martinsson, T. P. K., Verheijen, M. A. W., et al. 2011, ApJ, 739, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosma, A. 1978, Ph.D. Thesis, Groningen Univ. [Google Scholar]
- Bosma, A. 1981a, AJ, 86, 1791 [NASA ADS] [CrossRef] [Google Scholar]
- Bosma, A. 1981b, AJ, 86, 1825 [NASA ADS] [CrossRef] [Google Scholar]
- Bottema, R. 1993, A&A, 275, 16 [NASA ADS] [Google Scholar]
- Casertano, S. 1983, MNRAS, 203, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Cenarro, A. J., Peletier, R. F., Sánchez-Blázquez, P., et al. 2007, MNRAS, 374, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Durrell, P. R., Laychak, M. B., et al. 2004, ApJ, 614, 167 [Google Scholar]
- Contini, T., Considere, S., & Davoust, E. 1998, A&AS, 130, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Courteau, S., Andersen, D. R., Bershady, M. A., MacArthur, L. A., & Rix, H.-W. 2003, ApJ, 594, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., Courteau, S., de Jong, R., & Carignan, C. 2005, ApJ, 619, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Greusard, D., Combes, F., et al. 2001, A&A, 368, 52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erwin, P. 2005, MNRAS, 364, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., Jorissen, A., Luri, X., et al. 2005, A&A, 430, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraternali, F., Sancisi, R., & Kamphuis, P. 2011, A&A, 531, 64 [Google Scholar]
- Ganda, K., Falcón-Barroso, J., Peletier, R. F., et al. 2006, MNRAS, 367, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Herrmann, K. A., & Ciardullo, R. 2009, ApJ, 705, 1686 [NASA ADS] [CrossRef] [Google Scholar]
- Hurst, G. M., Armstrong, M., & Arbour, R. 1998, IAU Circ., 6875, 1 [NASA ADS] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kelz, A., Verheijen, M. A. W., Roth, M. M., et al. 2006, PASP, 118, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kregel, M., & van der Kruit, P. C. 2004, MNRAS, 355, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kregel, M., & van der Kruit, P. C. 2005, MNRAS, 358, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Kregel, M., van der Kruit, P. C., & Freeman, K. C. 2005, MNRAS, 358, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Kron, R. G. 1980, ApJS, 43, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., & Gilmore, G. 1991, ApJ, 367, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Heiter, U. 2007, AJ, 133, 2464 [NASA ADS] [CrossRef] [Google Scholar]
- Márquez, I., Masegosa, J., Durret, F., et al. 2003, A&A, 409, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinsson, T. P. K. 2011, Ph.D. Thesis, Univ. of Groningen [Google Scholar]
- Massarotti, A., Latham, D. W., Stefanik, R. P., & Fogel, J. 2008, AJ, 135, 209 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A. 1990, ApJS, 74, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., & Li, W. D. 1999, IAU Circ., 7237, 1 [NASA ADS] [Google Scholar]
- Molaro, P., Gabrielcic, A., Boehm, C., & Tessicini, G. 1995, IAU Circ., 6137, 1 [NASA ADS] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Nilson, P. 1973, Uppsala general catalogue of galaxies (Uppsala: Astronomiska Obs.) [Google Scholar]
- Noordermeer, E., van der Hulst, J. M., Sancisi, R., Swaters, R. S., & van Albada, T. S. 2007, MNRAS, 376, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P., & Dehnen, W. 2003, ApJ, 599, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. P., & Caldwell, J. A. R. 1979, in The Large-Scale Characteristics of the Galaxy, ed. W. B. Burton, IAU Symp., 84, 441 [NASA ADS] [Google Scholar]
- Peletier, R. F., & Balcells, M. 1997, New A, 1, 349 [Google Scholar]
- Pohlen, M., & Trujillo, I. 2006, A&A, 454, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quinn, J. L., Garnavich, P. M., Li, W., et al. 2006, ApJ, 652, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, S. V., Sellgren, K., Carr, J. S., et al. 2000, ApJ, 537, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Ratnatunga, K. U., & Upgren, A. R. 1997, ApJ, 476, 811 [Google Scholar]
- Roberts, M. S. 1966, ApJ, 144, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Rogstad, D. H., & Shostak, G. S. 1972, ApJ, 176, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Rosales-Ortega, F. F., Kennicutt, R. C., Sánchez, S. F., et al. 2010, MNRAS, 405, 735 [NASA ADS] [Google Scholar]
- Roth, M. M., Kelz, A., Fechner, T., et al. 2005, PASP, 117, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, V. C., Ford, W. K. J., & Thonnard, N. 1980, ApJ, 238, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Sackett, P. D. 1997, ApJ, 483, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, A., Sandage, A., Tammann, G. A., et al. 2001, ApJ, 562, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sancisi, R. 2004, in Dark Matter in Galaxies, eds. S. Ryder, D. Pisano, M. Walker, & K. Freeman, IAU Symp., 220, 233 [Google Scholar]
- Schechtman-Rook, A., & Hess, K. M. 2012, ApJ, 750, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, K. L., Gerssen, J., & van der Marel, R. P. 2003, AJ, 126, 2707 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., Courtois, H. M., Tully, R. B., et al. 2013, ApJ, 765, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Bienaymé, O., Mishenina, T. V., & Kovtyukh, V. V. 2008, A&A, 480, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swaters, R. A., Sancisi, R., van Albada, T. S., & van der Hulst, J. M. 2011, ApJ, 729, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Tully, R. B., & Pierce, M. J. 2000, ApJ, 533, 744 [NASA ADS] [CrossRef] [Google Scholar]
- van Albada, T. S., & Sancisi, R. 1986, Roy. Soc. London Philosoph. Trans. Ser. A, 320, 447 [Google Scholar]
- van Albada, T. S., Bahcall, J. N., Begeman, K., & Sancisi, R. 1985, ApJ, 295, 305 [NASA ADS] [CrossRef] [Google Scholar]
- van der Hulst, J. M., Terlouw, J. P., Begeman, K. G., Zwitser, W., & Roelfsema, P. R. 1992, in Astronomical Data Analysis Software and Systems I, eds. D. M. Worrall, C. Biemesderfer, & J. Barnes, ASP Conf. Ser., 25, 131 [Google Scholar]
- van der Kruit, P. C. 1988, A&A, 192, 117 [NASA ADS] [Google Scholar]
- van der Kruit, P. C., & Freeman, K. C. 1984, ApJ, 278, 81 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C., & Freeman, K. C. 1986, ApJ, 303, 556 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C., & Searle, L. 1981, A&A, 95, 105 [NASA ADS] [Google Scholar]
- Verheijen, M. A. W. 1997, Ph.D. Thesis, Univ. Groningen, The Netherlands [Google Scholar]
- Verheijen, M. A. W. 2001, ApJ, 563, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Verheijen, M. A. W., Bershady, M. A., Andersen, D. R., et al. 2004, Astron. Nachr., 325, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty, M.-P., & Véron, P. 2006, A&A, 455, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogelaar, M. G. R., & Terlouw, J. P. 2001, in Astronomical Data Analysis Software and Systems X, eds. F. R. Harnden Jr., F. A. Primini, & H. E. Payne, ASP Conf. Ser., 238, 358 [Google Scholar]
- Westfall, K. B. 2009, Ph.D. Thesis, Univ. of Wisconsin-Madison [Google Scholar]
- Westfall, K. B., Bershady, M. A., & Verheijen, M. A. W. 2011a, ApJS, 193, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Westfall, K. B., Bershady, M. A., Verheijen, M. A. W., et al. 2011b, ApJ, 742, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Zibetti, S., Charlot, S., & Rix, H. 2009, MNRAS, 400, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1933, Helvetica Physica Acta, 6, 110 [Google Scholar]
All Tables
On-sky positions (in arcsec) of the 331 science fibers (1−331) and 36 sky fibers (501−536), relative to the central fiber #164.
All Figures
 |
Fig. 1 Illustration of our surface-fitting and source-blanking algorithms. Left panel: H-band 2MASS image of UGC 4555. The galaxy itself is toward the bottom of the frame; black ellipses mark radii of 2.5, 3.5, and 6.5r1. Second panel: same image but with neighboring sources blanked and the estimated galaxy profile subtracted. Third panel: 9th-order surface fit using our iterative scheme, which was chosen to be the “best” fit to the image. Right panel: residual image after surface subtraction. All images have the same dynamic range of 3DN, where 1DN corresponds to 20.7 mag arcsec-2. They have been smoothed by a Gaussian with a FWHM of 9 pixels (1″/pix) to enhance low-signal structure. |
| In the text | |
 |
Fig. 2 Left: photograph of the focal plane layout of PPak. The 331 science fibers and 36 sky fibers are back-illuminated. Right: the PPak fiber-footprint overlaid on top of a direct image of UGC 463. |
| In the text | |
 |
Fig. 3 Spectrum of the dome flood lamps (top) and the ThAr calibration lamp (bottom); the latter has been used to wavelength calibrate the former. The flux units are arbitrary and offset for illustration purposes. The arrows mark the emission lines in the ThAr-lamp spectrum that were used to calibrate the flood-lamp spectrum (bottom), and the emission lines in the flood-lamp spectrum that were used to wavelength calibrate our science spectra (top). |
| In the text | |
 |
Fig. 4 Examples of unprocessed PPak science exposures. Top: the result of drifting a template star through the central row of 21 fibers while the 15 calibration fibers are illuminated with the internal ThAr lamp. Spectra of the template star are recorded all over the detector. Bottom: a representative one-hour exposure of the galaxy UGC 4368. Again, the 15 calibration fibers are illuminated with the internal ThAr lamp. The curvature of the imaged pseudo-slit is clearly visible. |
| In the text | |
 |
Fig. 5 Central part of a raw image from a one-hour science exposure with inverted color map, illustrating how the emission lines in the ThAr spectra create spots all over the detector. These spots are used to track the effective spectral resolution and flexure in the Cassegrain-mounted spectrograph. |
| In the text | |
 |
Fig. 6 Measured shifts in the locations of 60 ThAr spots from a flood-lamp exposure and from one of the science frames taken during the same night, illustrating a severe case of flexure. The shifts are indicated by arrows, calculated after the mean shift (ΔX = 0.21 and ΔY = 0.46 pixels) has been subtracted; the arrows have been magnified 1000 times for illustration purposes. The change in scale is clearly visible. |
| In the text | |
 |
Fig. 7 Measured wavelength of the Ni sky-line at 5197.9 Å as a function of fiber number. The thin, grey lines connect measurements from 10 spectra in individual science exposures. Crosses show the averages of these measurements, and the thick, black lines indicate the standard deviation from the mean. The dash-dotted line depicts the tabulated value of Ni in air, as given by NIST. |
| In the text | |
 |
Fig. 8 Distribution of the average instrumental spectral resolution in all science exposures. The average resolution is λ/Δλ = 7680 ± 640 (σinst ≈ 16.6 ± 1.4 km s-1), which is somewhat lower than the most common resolution λ/Δλ ≈ 7800 due to the tail in the distribution toward low λ/Δλ. |
| In the text | |
 |
Fig. 9 Average instrumental dispersion (σinst) as a function of wavelength and aperture number. |
| In the text | |
 |
Fig. 10 Left: offsets between the morphological centers of the galaxies as determined from direct images, and the dynamical centers as determined from the two-dimensional velocity fields. Open and solid symbols correspond to the dynamical centers derived for the [Oiii] and stellar velocity fields, respectively. Right: offsets between the dynamical centers as derived for the [Oiii] and stellar velocity fields. |
| In the text | |
 |
Fig. 11 Differences between velocity-field model parameters for the stars and [Oiii]-emitting gas. The parameters compared are the systemic velocities (top left), position angles (top right), projected rotation velocity (bottom left) and rotation scale (bottom right). The systematic offset between the projected rotation speeds of the stars and gas is expected given the significant asymmetric drift of the stars. The average asymmetric drift, |
| In the text | |
 |
Fig. 12 Velocity-dispersion profiles (top: σLOS, bottom: σz) for all galaxies. The plotted data are the seven azimuthally averaged values from Sect. 7.3.2 normalized by the fitted central velocity dispersion for each galaxy. The radius of each datum is scaled by half of the e-folding length of the exponential fit to its associated galaxy. Data likely affected by bulge kinematics, as well as all data from UGC 4458 and UGC 8196, are marked with smaller symbols (and no errors); these data have been excluded from the calculation of the scatter given near the top of each panel. The exponential model is plotted as a thick grey line with five times the scatter about this line shown as dashed lines. Points above the upper dashed line are plotted in Fig. 13. The models have not been fit directly to the data shown, but to the individual fiber measurements for every galaxy separately (see the Atlas). |
| In the text | |
 |
Fig. 13 Measurements of σLOS that significantly deviates from the exponential decline. The grey band indicates the range in σinst; the σLOS measurements presented in this figure have not been corrected for the instrumental broadening to emphasize that these measurements are well above the instrumental resolution limit. One measurement from UGC 8196 at ~ 58 km s-1 is not plotted. |
| In the text | |
 |
Fig. 14 Ratio of the exponential scale length of σz (hσ,z) and twice the photometric scale length (2hR) as a function of several global properties of the galaxies. This ratio is expected to be 1 (log [hσ,z/2hR] = 0) for an isolated exponential stellar disk. |
| In the text | |
 |
Fig. 15 Relation between the central stellar velocity dispersion (σLOS,0 to the left and σz,0 to the right) and the circular speed of the disks at 2.2hR. The black solid line in each panel indicates the error-weighted fit, and the black dashed lines are the error-weighted RMS scatter in the ratio. The grey lines show the relation determined by Bottema (1993). |
| In the text | |
 |
Fig. 16
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.