| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321924 | |
| Published online | 07 August 2013 | |
Near-infrared imaging polarimetry of HD 142527⋆,⋆⋆
1
Departamento de Fisica y Astronomía Universidad de Valparaíso,
Valparaíso,
Chile
e-mail:
hector.canovas@dfa.uv.cl
2 UMI-FCA, (UMI 3386) CNRS/INSU France
3
Atacama Large Millimeter/Submillimeter Array, Joint ALMA
Observatory, Alonso de Córdova
3107, Vitacura 763-0355, Santiago, Chile
4
National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, Virginia, 22903-2475, USA
5
Instituto de Astrofísica, Pontificia Universidad Católica de
Chile, Av. Vicuña Mackenna 4860,
7820436 Macul, Santiago, Chile
6
Departamento de Astronomía, Universidad de Chile,
Casilla 36-D, Santiago, Chile
7
Science and Technology Research Institute, University of
Hertfordshire, College
Lane, Hatfield
AL10 9AB,
UK
8
UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et
d’Astrophysique de Grenoble (IPAG), UMR 5274, 38041
Grenoble,
France
9
Millenium Nucleus “Protoplanetary Disks in ALMA Early Science”,
Universidad de Chile, Casilla
36-D, Santiago,
Chile
Received:
21
May
2013
Accepted:
26
June
2013
Context. HD 142527 is a pre-transition disk with strong evidence for ongoing planet formation. Recent observations show a disrupted disk with spiral arms, a dust-depleted inner cavity and the possible presence of gas streams driving gas from the outer disk toward the central star.
Aims. We aim to derive the morphology of the disk and the distribution and properties of the dust at its surface.
Methods. We have obtained polarized differential images of HD 142527 at H and Ks bands with NaCo at the VLT. Combining these images with classical PSF-subtraction, we are able to derive the polarization degree of this disk.
Results. At H band the polarization degree of the disk varies between 10% and 25%. This result cannot be reproduced by dust distributions containing highly porous material. The polarization is better matched by distributions of compact particles, with maximum sizes at least up to a few microns, in agreement with previous observations. We also observe two regions of low emission (nulls) in total and in polarized intensity. In particular, one of these nulls is at roughly the same position as the maximum of the horse-shoe shape observed in submillimeter continuum emission ALMA band-7 (345 GHz) observations. We discuss the possible link between these two features.
Key words: protoplanetary disks / stars: variables: T Tauri, Herbig Ae/Be / techniques: polarimetric
Reduced NaCo/VLT images (as FITS files) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/556/A123
© ESO, 2013
1. Introduction
Transition disks are a particular type of protoplanetary disks. Their identifying characteristic is a decrement of near-, mid-infrared flux when compared to the median of the classical T Tauri stars (CTTs) in the Taurus cloud (e.g. Williams & Cieza 2011, and references therein). This observational feature is explained by a drop in the optical depth (τν). This drop can be caused by a decrement in opacity or by a drop of dust density (i.e., a gap/cavity). Binarity, planet formation, dust growth and photoevaporation are the proposed mechanisms to explain these “optical depth” holes (e.g. Dodson-Robinson & Salyk 2011; Dullemond & Dominik 2004; Owen et al. 2012). Each one of them can be identified by measuring observables such as accretion rates, spectral energy distribution (SED) shapes or disk masses (Najita et al. 2007; Cieza et al. 2012; Romero et al. 2012). Recent studies combining observations at different wavelengths have tried to identify the dominant mechanism in a sample of transition disks (among others, Andrews et al. 2011; Mathews et al. 2012; Isella et al. 2012; Hashimoto et al. 2012; Cieza et al. 2012; Casassus et al. 2013). In any case, it is evident that transition disks represent a very important phase in the evolution of the protoplanetary disk, and that understanding them is fundamental for explaining planet formation.
In this paper we focus on HD 142527, a remarkable transitional disk around a Herbig Ae star. This disk features an inner disk, a dust-depleted gap and an outer disk, which places it in the category of pre-transition disks (Espaillat et al. 2007). Verhoeff et al. (2011) found that the inner disk can be fitted assuming a radius of ≤30 AUs, the gap extends up to ≈130 AUs, and that the scale height at the inner wall of the outer disk must be extremely high (≈60 AUs). HD 142527 has been imaged at near-infrared (NIR) by Fukagawa et al. (2006), Casassus et al. (2012) and Rameau et al. (2012), showing several spiral features on the innermost parts of the outer disk. The disk is believed to be inclined by ≈20°, as suggested by mid-infrared (MIR) and NIR observations, and to be rotating in clock-wise direction, as suggested by the orientation of its spiral features. More recently, Casassus et al. (2013) confirmed the horse-shoe shape of the continuum emission in this system that was first noted by Ohashi (2008), and found two possible dense gas streams transporting material from the outer disk toward the central star. These gas streams are predicted by current models of giant-planet formation (Dodson-Robinson & Salyk 2011), so they could be a direct signpost of planet formation. Biller et al. (2012) discussed a possible close-in binary companion, although its existence needs confirmation.
We present polarized differential imaging (PDI) observations of HD 142527 at H and Ks bands obtained with the NaCo instrument at the Very Large Telescope (VLT). By means of polarimetry, it is easy to remove most of the (unpolarized) stellar light to obtain an image of the circumstellar environments in scattered light. Currently, PDI is becoming a standard technique to directly image protoplanetary disks, as proven by the increasing amount of systems observed with polarimeters at 8-m-class telescopes (among others Quanz et al. 2013; Mayama et al. 2012; Tanii et al. 2012; Hashimoto et al. 2012; Kusakabe et al. 2012). In most of these studies, only the polarized intensity (PI) image of the disk is presented. Although PI images directly show the disk’s surface in scattered light, the information contained in these images is limited and cannot be used to constrain the properties of the dust-scattering particles, unless PI images at different wavelengths are combined. This is because PI is the product of two quantities: the total intensity and the polarization degree. A classical example of the degeneracies left when analyzing polarized intensity images alone is the discussion about the “hole” detected in polarized intensity in AB Aurigae (see Oppenheimer et al. 2008; Perrin et al. 2009). Using the polarization degree, it is possible to break some of these degeneracies and to put constraints on the size, composition and/or shape of the dust particles if enough wavelength coverage is available (Dong et al. 2012; Min et al. 2012; Murakawa 2010). In this work we combine PDI with classical point spread function (PSF) subtraction to derive the polarization degree in HD 142527. The observations and data reduction are described in Sects. 2 and 3, respectively. Our results are presented in Sect. 4. The discussion and final conclusions are given in Sects. 5 and 6, respectively.
2. Observations
The observations were performed in service mode during July and August 2012 with NaCo (Lenzen et al. 2003; Rousset et al. 2003) at the VLT/UT 4. NaCo is a very flexible instrument that combines an adaptive optics (AO)-system with a NIR camera. We used NaCo in its polarimetric mode. In this setup, a half-wave plate (HWP) rotates the polarization plane of the light by φ = 2 × θ, where θ is the angle measured east of north. A Wollaston prism1 placed after the HWP separates the incoming light into two orthogonally polarized beams, which are projected on different regions of the camera. The images generated by these two beams are hereafter named as Io (for the ordinary beam), and Ie (for the extra-ordinary beam). Each frame recorded by the camera contains these two simultaneous images with orthogonal polarization states. The separation between the two images is fixed to 3.3′′ in the y-direction of the detector and remains constant during the whole observing run. A field mask prevents beam-overlapping. The pixel size of the camera was set to 0.027′′/px, the readout mode to Double_RdRstRd and detector mode to HighDynamic. The north-south direction on the sky coincides with the vertical axis on the detector and with the zero position of the fast axis of the HWP (i.e., θ = 0°).
2.1. Data acquisition
Description of HD 142527 and HD 161743.
Observing log of the observations.
HD 142527 and the comparison star HD 161743 were observed in H and Ks bands. A brief description of both objects is given in Table 1. Four datasets taken with the HWP rotated by θ = 0°, 22.5°, 45° and 67.5° were recorded during each observation. In what follows, “dataset” always refers to images recorded under the same HWP position angle. An observing log is given in Table 2. HD 142527 was observed using exposure times of 0.4, 1, and 5 s in the H band and 0.4 and 4 s in the Ks band. Three subsets of images per dataset (Ditpos) recorded at different regions on the detector were obtained to minimize the effect of bad pixels on the final images. The comparison star HD 161743 was observed in H band with exposure times of 3, 10, and 15 s and in Ks band with exposure times of 10 and 15 s. Only one subset of images per HWP angle was recorded in these measurements. All images except the 0.4 s H-band observations of HD 142527 were overexposed on the central star. The saturated region reaches a maximum size of radius rsat ≈ 0.32′′ in the 5 s H-band images.
Together with the science observations a set of dark frames with the same exposure times as the science images were acquired. Dome and sky flats were taken with and without polarization optics, respectively. Different exposure times ranging from 0.2 to 30 s were used during the flat acquisition.
3. Data analysis
Polarized light can be described by means of the Stokes parameters I,
Q, U and V. Stokes I
represents the total intensity. Stokes Q and U describe
linearly polarized light, while Stokes V describes circularly polarized
light. In this work we focus on measuring linearly polarized light, so we do not consider
the Stokes V parameter. The polarized intensity
(PI) is described by 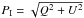 ,
while the degree of polarization (P) is computed as
P = PI/I.
The polarization angle (Pθ), which indicates
the plane of vibration of the electric field associated with the light, is computed as
,
while the degree of polarization (P) is computed as
P = PI/I.
The polarization angle (Pθ), which indicates
the plane of vibration of the electric field associated with the light, is computed as
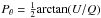 .
.
There is no standard pipeline to reduce polarimetric NaCo data. We used our own routines written in IDL. In the following subsections we describe our data-processing method.
3.1. Basic reduction
The individual dark frames were median-combined to generate a set of master darks for each exposure time. Master flats were produced in the same way from the individual sky flats (taken without the polarization optics). The different master flats were visually inspected to discard those affected by light gradients and artifacts. Each science image was master-dark-subtracted and divided by the normalized master flat. The effect of hot and bad pixels was reduced by sigma-clipping and median-combining the different subsets of images. The performance of the AO-system was stable during the whole run, and no images were discarded due to poor Strehl ratios. Furthermore, given the discrete amount of images obtained per dataset (see Table 2) we used all observations to increase the signal-to-noise ratio (S/N) of the final images.
Image alignment is a critical problem in polarimetric imaging (e.g., Apai et al. 2004; Canovas et al. 2011), and must be performed with sub-pixel accuracy. We performed several tests combining different aligning procedures (shift-and-add, cross-correlation with different templates) to find the combination that produced the best alignment. We concluded that separately aligning each dataset by means of a cross-correlation algorithm (accuracy of 1/5 of a pixel) provided the best results for our images. The aligning procedure works as follows. First, all images are centered with a classical shift-and-add method to generate a template. Second, the Io of each frame is centered with respect to this template by means of a cross-correlation. This process is repeated to center the Ie using the Io image as a reference. This process is applied in the same way to each pair of Io and Ie images.
The sky background was computed as the median of two different sky regions (0.29′′ × 0.29′′ each), and then subtracted from the individual Io and Ie images. These sky regions are located at 4′′ away from the star to ensure that the contribution from the stellar PSF is negligible.
3.2. Polarimetry
Once the images were aligned and sky-subtracted, they were combined to extract the Stokes parameters I, Q and U. There are two standard approaches to do this in imaging polarimetry: the “difference” and “ratio” methods (see among others, Keller 1996; Kuhn et al. 2001; Hinkley et al. 2009; Quanz et al. 2011; Canovas et al. 2011, 2012). The difference method is less sensitive to PSF variations and more sensitive to flat-field variations, while the ratio method behaves in the opposite way (for a detailed discussion on the topic see Canovas et al. 2011). Both methods were tested in our analysis, concluding that the difference-method delivers results with a higher S/N. In what follows we describe how the polarized light was extracted from the aligned images by means of the difference method.
The individual Stokes Q images were produced from each pair of
Io and Ie images taken with the
HWP rotated at θ = 0°,45° (i.e.,
the polarization plane is rotated by
φ = 2 × θ = 0°,90°):
 Similarly,
the individual Stokes U images were obtained from
Similarly,
the individual Stokes U images were obtained from 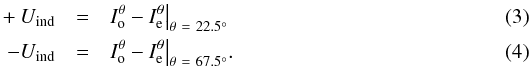 Each
+ Q/−Q and
+ U/−U image was corrected for
instrumental polarization. Individual intensity images at each HWP position
(Iθ) were generated by adding the
Io and Ie images:
Each
+ Q/−Q and
+ U/−U image was corrected for
instrumental polarization. Individual intensity images at each HWP position
(Iθ) were generated by adding the
Io and Ie images: 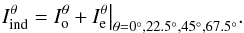 (5)
(5)
3.2.1. Instrumental polarization
Average polarization degree within ringIP at H band.
The instrumental polarization (IP) is usually corrected for (in imaging polarimetry) by subtracting the polarized light measured at the position of the central star. This is equivalent to assuming that the central resolution element is unpolarized. This method, previously used by several authors (e.g. Perrin et al. 2008; Quanz et al. 2011, 2013; Canovas et al. 2011, 2012), efficiently removes any polarized signal produced by the telescope + instrument system as well as the interstellar polarization, but it may also remove the contribution to the polarized light from the inner disk in HD 142527. On the other hand, the central star of HD 142527 saturates in almost all our observations inside the inner rsat ≤ 0.32′′ from the star. Because of this, we chose to compute the IP in a ring (ringIP) of inner radius ri = 0.35′′ and outer radius of ro = 0.5′′, centered on the star. This ring falls inside the huge, dust-depleted gap of HD 142527 (Rameau et al. 2012; Casassus et al. 2012, 2013). The average polarization inside ringIP was computed and subtracted from each individual + Q/−Q and + U/−U image. The average values of the polarization inside ringIP for the H-band observations are shown in Table 3. The IP is extremely sensitive to the telescope orientation, as reflected by our results. The interstellar polarization can be estimated as PInt ≤ 3Av (see Draine 2003, and references therein), where Av is the total extinction. Using the Av = 0.6 derived by Verhoeff et al. (2011), we obtained a highest interstellar polarization of PInt = 1.8%. On the other hand, the instrumental polarization of NaCo can reach a highest value of 4% (Witzel et al. 2011). Therefore we conclude that inside the gap where we estimate IP, the contribution from PInt and the instrumental polarization dominates over any polarization signal produced by dust scattering (see Table 3, all values are below 2.3%).
 |
Fig. 1 Processed images of HD 142527 (top row) and HD 161743 (bottom row) in H band. From left to right: intensity image (I) in logarithmic scale, Stokes Q, U and PI images in linear scale. For comparison purposes, HD 161743 has been scaled by an arbitrary factor. Units are given in counts. The area corresponding to the saturated pixels (rsat ≤ 0.32′′) in HD 142527 has been masked out in all images. The polarized images of HD 142527 show a complex structure, while the comparison star only shows remnant noise. In all images north is up and east is left. This applies to all the figures in this paper. |
3.2.2. Final images
The individual (IP-corrected) + Q images were centered with a
cross-correlation algorithm using the first + Q image of the dataset as
the centering-template. Once aligned, they were median-combined to produce a final
+ Q image. This process was repeated with the individual
− Q, + U, − U and
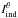 images. An
intensity image per dataset (Iθ) was
created by median-combining the
images. An
intensity image per dataset (Iθ) was
created by median-combining the 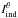 . The final Stokes
Q and U images were generated from the
median-combined images as
. The final Stokes
Q and U images were generated from the
median-combined images as  The
polarized intensity (PI) and the polarization angle
(PΘ) were computed from these images:
The
polarized intensity (PI) and the polarization angle
(PΘ) were computed from these images:  Witzel et al. (2011) detected an offset of
13.2° in the HWP of NaCo that is included in our calculations of
PΘ. The final intensity image (I) was
produced by averaging the Iθ images
generated for each dataset:
Witzel et al. (2011) detected an offset of
13.2° in the HWP of NaCo that is included in our calculations of
PΘ. The final intensity image (I) was
produced by averaging the Iθ images
generated for each dataset: 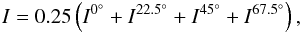 (10)where
the superscript indicates the θ angle. Finally, the images are
normalized to 1 s exposure time. The I, Q,
U and PI images of HD 142527 (5 s
exposure time) and HD 161743 (5 s exposure time) at H band are shown in
Fig. 1.
(10)where
the superscript indicates the θ angle. Finally, the images are
normalized to 1 s exposure time. The I, Q,
U and PI images of HD 142527 (5 s
exposure time) and HD 161743 (5 s exposure time) at H band are shown in
Fig. 1.
We note that Quanz et al. (2013) (see also Schmid et al. 2006) used the radial Stokes parameters Qr and Ur to produce a polarized intensity image with reduced levels of noise (we refer to that paper for a detailed explanation of these coefficients). As noted by these authors, this approach is valid when the disk is nearly face-on. We reduced our images with the method described by Quanz et al. (2013) (and Avenhaus et al. 2013, in preparation), concluding that the use of Qr and Ur indeed delivers significantly lower levels of noise in the centermost regions of the images. However, at larger distances from the image center (r ≥ 0.4′′), the differences between the two methods are within the error bars. Given that we do not consider the centermost regions (r ≤ 0.3′′) of the images in this work (due to the saturation of our images), and that the inclination of HD 142527 is best fit by ≈20°, we preferred to use the “classical” polarized intensity as described in Eq. (8) of this paper.
3.3. PSF-subtraction
An important part of the information contained in the polarized light is encoded in the degree of polarization (P = PI/I). This quantity directly traces the size and properties of the dust particles that scatter the light, polarizing it (e.g. Volten et al. 2007; Min et al. 2012). However, the I image derived in the previous subsection contains the contribution of the star + disk. Therefore, it is necessary to obtain an intensity image of the disk (Idisk) alone to derive the degree of polarization (P) of the disk. To that end, we used the observations of the comparison star HD 161743 (I images) to perform PSF-subtraction to the HD 142527 I images. In what follows, we describe our PSF-subtraction process.
Before starting the process we checked for the presence of ghosts and gradients by subtracting from each image an azimuthally averaged version of itself. We did this with both the HD 142527 and the comparison star. This way we identified several static ghosts (i.e., ghosts that remain at fixed positions over the detector) that could be mistakenly identified as bright clumps on the disk of HD 142527. This is especially important in our Ks-band observations, where we found at least twice as many ghosts/artifacts as in our H-band images. Most of these artifacts were unpolarized, since they do not appear in the corresponding PI images. We also conclude that the images with longer exposure times are strongly affected by spatial gradients. This can be explained by the lower performance of the AO when observing at longer exposure times. Because of this, we removed the images taken with the longer exposure times from the analysis.
The scaling coefficient α(r) used to flux-scale the HD 161743 images was computed as the ratio between HD 142527 and HD 161743 at a given position. α(r) was computed at radii ranging from r = 0.37′′ from the central star (outside of the saturated area) to r = 0.67′′ (before the outer disk’s emission becomes significant). The final scaling coefficient (αf) was computed as the average of the different α(r). The standard deviation of this coefficient is more than one order of magnitude lower than its value, indicating that the radial profiles of HD 142527 and HD 161743 are very similar within the [0.37′′−0.67′′] region from the central star. However, we note that the radial profiles of both stars at larger distances from the center (r ≥ 1.5′′) are fairly different, making a uniform PSF-subtraction over the whole field of view impossible (see also Rameau et al. 2012, who noticed the same when performing PSF-subtraction for this target at L band). After flux-scaling the comparison PSFs, they were aligned and subtracted from the HD 142527 images. We did not rotate the HD 161743 (as is usually done to match the spider’s pattern in the two images) to minimize the effect of the static artifacts (see Fig. 2). Owing to the uncertainties of the entire process, we consider our results as lower limits of the flux of the disk. We used the sky regions of the PSF-subtracted image to give an estimation of the upper limit of the disk’s emission. Computing the mean in eight different sky regions over the image (using boxes of 5 × 5 pixels), we obtained a value of ≈7 counts for the background. We therefore used this value as a 1σ estimation. We constructed the upper limit to the brightness of the disk as three times this quantity.
 |
Fig. 2 Idisk images at H band. Left: without rotating the flux-scaled HD 161743 image. Right: rotating the HD 161743 image to match the spider’s pattern (indicated by dashed-lines) in the HD 142527 image. The innermost (r ≤ 0.67′′) regions are masked out to remove artifacts. The white arrows point to previously identified ghosts, which are enhanced when rotating the PSF to correct for the spiders. Bar units are given in counts. The bright path to the east, immediately above the dotted spider line, is an artifact of the PSF-subtraction process. |
4. Results
The images taken with the shortest exposure time (0.4 s) at H and Ks band were excluded from this analysis due to their poor S/Ns. Because of this, we focused our analysis on the 1s images at H band and the 4 s images at Ks band. Figure 3 shows the PI (top row) and Idisk (bottom row) images at H (left column) and Ks band (right column). The two PI images are plotted with the same color scale, as is done with the Idisk images in the bottom row. All the bright clumps in the Idisk image at Ks band are caused by instrumental, unpolarized artifacts.
 |
Fig. 3 PI (top row) and Idisk (bottom row) images at H (left column) and Ks band (right column) of HD 142527. Masked area in the PI images cover the saturate region, while in the PSF-subtracted images cover the artifact-dominated regions. The PI are plotted with the same scale to enhance differences/similarities. The same is done with the Idisk images. The bright patch in the Idisk image at north-east direction in Ks band is an artifact due to the PSF-subtraction (as it is the bright path on the east direction in the Idisk image at H band, see also the caption in Fig. 2). Color bar units are given in counts. |
The overall disk structure recovered from the PSF-subtracted images matches previous images at Ks band (Fukagawa et al. 2006; Casassus et al. 2012) and L band (Rameau et al. 2012) well. The polarized signal inside the gap is within 3σPI of the sky background. We estimated σPI of the background by computing the median of the standard deviation in four sky regions (5 × 5 px each) of the PI image. There is a marginal detection of the spiral feature (PA ≈ 260°) labeled as “2” in Fig. 2 by Casassus et al. (2012). Both the PSF-subtracted and the PI images at H and Ks bands show two nulls or gaps at position angles of PA: [340° to 10°] (northern null) and PA: [130° to 165°] (southern null). Inside the cavity, the best detection limit for a point source in the intensity image is ΔmH = 5.5 mag at 0.6′′ from the central star. In polarized intensity, the best 3σ limit is 13.5 mags/arcsec2 at the same position. With these limits we do not detect the HCO+ streamers claimed by Casassus et al. (2013) and cannot verify the putative companion claimed by Biller et al. (2012).
4.1. Brightness asymmetries and color of the PI images
The eastern side of the disk is more extended than the western side in the PI images at both H and Ks bands. The eastern side is also brighter at H band, while both sides have a similar peak brightness at Ks band, as shown in Fig. 3. Furthermore, the disk shows strong asymmetries along its inner rim. To further test this asymmetry we generated radial cuts on the PI images at different orientations instead of computing the radial brightness distribution along the major or minor axis of the disk, as is usually done. The results are shown in Fig. 4. The H- and Ks-band results are represented by black stars and red diamonds, respectively. The two images are very similar only along the vertical direction (0° plot), which is the major axis of the disk (Casassus et al. 2012). The other plots clearly show that the disk’s asymmetries between the east and west sides in PI are more accentuated in the H than in the Ks band.
 |
Fig. 4 PI radial cuts: H- and Ks-band cuts are plotted in black asterisks and red diamonds, respectively. Innermost regions have been masked out due to their significantly higher noise. Each point represents the mean value of the PI image at a given distance from the center, within a squared piece of 3 × 3 px (0.08′′ × 0.08′′). The error bars are the standard deviation inside each piece. The number at the upper-right corner in each plot indicates the PA (measured east of north) of the cut. The plot at 0° shows a cut from north (top) to south (bottom). In the other plots, the radial cuts start from the eastern side (left-side) of the images to the western side (right-side) of the images. |
We show the polarized-color of the disk in Fig. 5. This image was smoothed with a Gaussian filter of 4-px kernel to reduce the noise and focus on the large-scale structures. In that figure, we outline the position of the disk as seen in polarized intensity at H band (see Fig. 3, top left) with black contours. We see that at the position of the two nulls the polarized color is redder than in the rest of the disk. In particular, there is a difference of ≈0.5 mag between the northern and the southern null, with the southern null the redder.
 |
Fig. 5 PI color. Inner regions have been masked out to remove artifacts. The black contours outline the position of the disk seen in polarized intensity at H band (Fig. 3, top left). The image has been smoothed with a 4-px Gaussian kernel. The two nulls have more neutral colors. |
4.2. Spiral features
We used different edge-filter operators over the PI images to bring out morphological features of the disk such as spiral features. In Fig. 6 we show the result of applying a Sobel filter (or operator, see Gonzalez & Woods 2002) to the PI image at H band (with the inner regions of the image masked out to remove artifacts). This filter highlights regions of the image with strong gradients. High values of the gradient magnitude correspond to places with a rapid change in the image values and vice versa. To reduce the effects of noise, the total polarized intensity image was convolved with a two-dimensional Gaussian kernel with σ = 1 pixel before applying the Sobel operator. Both H and Ks band clearly show the spiral features labeled “2” in Fig. 2 of Casassus et al. (2012) (see also Rameau et al. 2012), as well as a faint, tentative spiral feature that matches the one labeled “3” in that figure. We also clearly detect a new spiral feature on the east side at a position angle of PA ≈ 60° (see Fig. 6). These spiral features are also visible when using different edge-detection filters, so we conclude that the new spiral on the eastern side is real and no artifact.
 |
Fig. 6 PI images at H band after applying a Sobel filter to highlight the regions of the image with edges. The three arrows indicate spiral arms on the disk. For comparison, we used the same notation as in Casassus et al. (2012) (see also Rameau et al. 2012) to label the spiral arms. The spiral arm labeled “2” perfectly matches its equivalent in Casassus et al. (2012). The spiral arm labeled “3” is barely visible in our images. The spiral arm on the east side is detected for the first time. Color bar is in arbitrary units. |
4.3. Polarization degree and azimuthal variations
As explained in Sect. 3.3, our Idisk image provided us with a lower limit of the real intensity of the disk, although we can use the sky regions to estimate the upper limits. This translates into lower and upper limits to the true polarization degree of the disk. We used a two pixel-thick ellipsoid divided into 36 10°-sectors to compute the azimuthal variation of the I, Q and U images. We computed the average values of these quantities inside each sector, from which we derived the associated PI and P, as explained in Sect. 3. For the ellipsoid, we used the same parameters as those derived by Casassus et al. (2012) to fit the disk of HD 142527. The azimuthal profiles are plotted in Figs. 7 and 8. In all the plots, each point represents the mean value of the plotted image over the corresponding sector. The data points that are at the position of the telescope’s spiders were removed from the P plots, since those points were severely affected by noise. The error bars represent the standard deviation inside each sector divided by the total amount of images used to produce the final images. We show the P plot at Ks band for completeness, but it is too contaminated by the instrumental artifacts to be useful to derive any physical parameters, and we focused on the P image at H band. The (black) stars and the (red) triangles represent the upper and lower limits of P, respectively. On average, the east side of the disk has a higher polarization degree (P ≲ 19.0%) than the west side (P ≲ 15.8%). The polarization angle (Pθ) is shown in Fig. 9. To obtain Pθ we first binned the Stokes Q and U images using a binning size of 5 px. We then computed the average I, Q and U inside each bin and derived the corresponding PI, P and Pθ. Only regions of the image where PI ≥ 3σPI, where σPI is the noise of the PI image, were considered to compute Pθ. The length of the vectors is proportional to the average of the local (upper limit of) P. The centrosymmetric pattern indicates that the central star is the source of the scattered light in our images.
 |
Fig. 7 Azimuthal (angles computed east of north) variation of the Stokes Q (top row) and U (bottom row) images for the H- (left column) and Ks-band (right column) measurements. |
 |
Fig. 8 Azimuthal (angles computed east of north) variation of the PI (top row) and P (bottom row) images, for the H (left column) and Ks bands (right column). The position of the telescope’s spiders is indicated by the dashed lines. In the P plot at H band, the stars and the triangles represent the lower and upper limits of P (see text for a detailed explanation). The P image at Ks band is too contaminated by artifacts (see Fig. 3, right-bottom plot). |
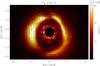 |
Fig. 9 Polarization angle (Pθ) indicated by the green vectors, plotted over the PI image. The length of the vectors is proportional to the local polarization degree (P). The vectors are plotted in regions of the image where the polarized intensity PI is higher than three times the standard deviation (σPI) of the sky background (see text). |
5. Discussion
5.1. Orientation and surface brightness of the disk
From MIR imaging, previous studies have inferred that the disk around HD 142527 is inclined by ≈20°, with the western side being the near side (Fujiwara et al. 2006; Verhoeff et al. 2011). Our observations agree well with this orientation. On the eastern side, the inner disk wall is directly exposed to the observer and the larger (apparent) radial extension of the disk is a natural consequence of the large vertical extent of the disk inner wall in that configuration. The large vertical extent has been suggested to explain the very bright mid- and far-infrared excess emission (Verhoeff et al. 2011).
Previous studies have estimated the NIR surface brightness of the disk along cuts at PA = 47 and 60 degrees, i.e., more or less along the north-east to south-west direction (Fukagawa et al. 2006; Rameau et al. 2012). Because the disk is elliptical and not centered, these radial surface brightness profiles peak at different radii, closer to the center in the NE direction, and farther out to the SW. Our data show the same behavior. To extract the azimuthal SB profile in the H band, we fitted ellipses to the disk along the ridge of maximum brightness. The peak surface brightness is similar on both sides of the disk in H band. The Ks-band intensity map is too noisy to extract a reliable azimuthal profile.
5.2. Polarization: comparison with other disks
Maps of the polarized intensity exist for several disks, but to our knowledge there are just four protoplanetary disks with spatially resolved maps of the polarization degree: GG Tau (Silber et al. 2000), AB Aurigae (Perrin et al. 2009), and the edge-on disk PDS 144N (Perrin et al. 2006), all observed with the Hubble Space Telescope, and UX Tau A (Tanii et al. 2012), observed with the subaru telescope. PDS 144N is the only edge-on disk in this sample. Therefore, we focused on the other three disks. In GG Tau and AB Aur the reported polarization levels oscillate between a minimum of ≈20% and a maximum of ≈50%, at 2 μm for AB Aur and 1 μm for GG Tau. UX Tau A shows a wider range of polarization levels, with P varying between ≈1.6% and ≈66%. For all three disks as well as for HD 142527, the polarization level (P) is higher on the back side of the disk, farther away from the observer, where backscattering is occurring (assuming that the eastern side is the back side for HD 142527, see Sect. 5.1).
Several factors affect the highest polarization observed. The inclination of the disk and its flaring (i.e., opening angle) as well as the dust properties are expected to have a strong effect. HD 142527 is seen with an inclination of about 20°. This is slightly more pole-on than the other three. The disk of AB Aur is tilted in the range 22° < i < 35°, for GG Tau the inclination of the circumbinary ring is ≈37°, and the inclination derived for UX Tau A is 46°. If we assume that the four disks have similar opening angles (i.e., flaring), then HD 142527 is the one where scattering should on average be closest to 90deg. As a consequence of this, HD 142527 should show fewer differences between the front and back side because the scattering angles are also limited to a more narrow range.
The range of variation of the observed polarization is indeed narrow, from ≈10% to ≈25%, as expected for a system seen near pole-on. The azimuthal profiles of the Stokes Q and U parameters are presented in Fig. 7 and the azimuthal profiles of the polarization levels (and polarized intensities) are shown in Fig. 8. Interestingly, however, the polarization levels in the disk of HD 142527 are also the ones with the lowest observed maximum (and average), although scattering at angles close to 90 degrees, as is the case here, are usually favorable to produce high polarizations. It is tempting to attribute this behavior, the low polarization levels, to the dust properties.
Other protoplanetary disks for which the H-band integrated polarization degree is known are TW Hya (Hales et al. 2006), HD 100546 (Quanz et al. 2011), and SR 21 (Follette et al. 2013). In all these disks, the average P does not exceed 40% at H band.
 |
Fig. 10 Polarizability as a function of scattering angles for different mixtures of dust. The polarizability is the ratio of the -S12 over S11 elements of the Mueller matrix. In all cases, dust mixtures have power-law size distributions with amin = 0.03 μm and a slope of − 3.5. Six cases with increasing values of amax are considered. The red curves show the polarizability for Mathis & Whiffen (1989) grains (a mix of astrosilicates and amorphous carbon and 80% porosity). The dotted green curves are for pure astronomical silicates with 80% porosity (Draine 2003). The blue dashed curves are for compact astronomical silicates without porosity (Draine 2003). The black curve is for a mixture of compact no porosity grains made of 100% amorphous carbon. All models with porosity have a high polarizability near 90 degrees scattering angles. Models with compact particles show lower maximum polarizations. |
5.3. Dust properties
The dust in the disk of HD 142527 is made of a mixture of particles with different sizes and composition (Verhoeff et al. 2011). At H and Ks bands the dust opacity is high and the measured scattered light probes the disk surface, high above the disk mid-plane. A mixture of dust containing only small particles in the Rayleigh regime, i.e., with radii much smaller than the wavelength, produces isotropic scattering and very high levels of polarization. The observed azimuthal variations of the brightness (the phase function) is compatible with nearly isotropic scattering (peak brightnesses are equal on the back and front side). However, the observed polarization levels are significantly too low (see Fig. 10, top left panel). At the surface of the disk, a mixture of dust containing only small grains can probably be ruled out.
Previous measurements at NIR and MIR were used to report particle sizes on the order of a micrometer or more (Fukagawa et al. 2006; Fujiwara et al. 2006). The strong emission associated with hot silicate particles (van Boekel et al. 2004) is well fitted by mixtures dominated by dust grains with sizes of ≈1.5 μm at the rim and at the surface, where the emission is coming from. These particles are not in the Rayleigh regime at H and Ks bands and are compatible with the observed polarization presented here.
Assuming furthermore that the size distribution follows a power-law (e.g., with a slope of –3.5 as in previous studies), calculations also show that mixtures of particles with significant porosity (50% or more) produce very high polarizations in all cases, with P = 50% or more for scattering angles near 90 degrees (see Fig. 10). Mixtures with grains with high porosities are very likely incompatible with the data as well. This statement is valid whether the mixture is of pure silicate or contains amorphous carbon as well.
Distribution of compact particles with a maximum size is of about 1.0 micron or more but without porosity naturally produce low levels of polarizations, in agreement with what is observed in HD 142527. The shape of the particles may also affect the polarization levels. We have neglected the effect of shape in our study.
5.4. Intensity nulls
There are two remarkable features in the disk that can be found due north and south-south-east. At these two positions the polarized intensity shows a deep minimum, but does not go to zero (see Figs. 3 and 9). These two “nulls” are also detectable in the intensity images (see Figs. 2 and 3). The polarization levels also show a marginally significant decrease at the position of the nulls, but these variations are probably part of a larger azimuthal variation pattern where the front (back) face of the disk exhibits a lower (higher) polarization.
These nulls in HD 142527 were previously observed in scattered-light intensity by Casassus et al. (2012) at K and L bands and by Rameau et al. (2012) at L band. They are also visible in the Q band (i.e., in thermal emission at 19 microns) in the VISIR image presented by Verhoeff et al. (2011).
A similar “gap” in the map of polarized intensity in the disk of AB Aur was observed by Oppenheimer et al. (2008) However, Perrin et al. (2009) subsequently showed that this feature in AB Aur is not caused by a decrease in local density. They showed instead that it is caused by a local variation of the polarization in the back side of that disk rather than a true decrease of the surface brightness level. In HD 142527, contrary to AB Aur, two nulls are detected instead of one and they are located along the major axis of the disk and not on the back side. Because the nulls are also visible in intensity images, both in scattered light and in thermal emission, the evidence is strong that they are tracing density and/or structural features in the disk.
The origin of these nulls is not known in detail. They may be the result of surface features in the disk, such as local enhancements of the scale height that may change the illumination pattern. In this case the nulls would trace more shadowed areas, that are colder (less thermal emission) and scatter less light. It is worth noting that the two nulls are located between spiral features identified in Casassus et al. (2012), which may also correspond with local changes in the density, scale height, or at least position of the optically thick surface of the disk. In their Fig. 2, the northern null (feature No. 1 in green) is located between spiral features Nos. 1 and 4 (shown in red). The southeastern null (No. 2 in green) is located between spiral features Nos. 1 and 2 (in red again). These spiral features could be linked to deformations on the surface of the disk, producing the observed nulls.
Another possibility can be derived from the more recent high-resolution submillimeter images of HD 142527 that became available with ALMA. In the northern direction, a very conspicuous surface brightness enhancement is visible in the form of a horse-shoe or banana-like feature. The observed feature is described in detail in Casassus et al. (2013). Retrospectively, the feature could also be seen in previous SMA data, but with a lower contrast (Ohashi 2008). Horseshoe-like features at mm-wavelengths have been previously observed in the transition disks LkHa 330, SR 21N and HD 135344B by Brown et al. (2009), and very recently in IRS 48 by van der Marel et al. (2013), and they now seem to be a common feature of transition disks when observed with ALMA. They have been tentatively interpreted in terms of dust trapping (e.g., Menard et al., in prep., Casassus et al. 2013; Birnstiel et al. 2013; Ataiee et al. 2013; van der Marel et al. 2013) either by a high-pressure vortex created by a Rossby wave instability or by resonances with a planet located in the disk gap. For HD 142527, the highest intensity observed in the horseshoe is nearly azimuthally coincident with the northern null. It is tempting to relate the two features. The enhanced dust density and/or abundance of large grains in the vortex (the horseshoe) may lead to less scattered light from the surface because, if transported close to the surface, grains much larger than the wavelength are less efficient scatterers and polarize differently than small grains. Similarly, the higher dust density in the vortex may lead to a lower local dust temperature, resulting in less thermal emission at 20 microns (Q band). At the same time, more dust, in particular larger dust more prone to be trapped by the gas high-pressure, would naturally produce the increase in submillimeter emission, as observed in the ALMA images. The other null, located SSE, is more difficult to interpret in that context. These suggestions will be tested in more detail in a forthcoming paper.
A third possibility, obvious and very popular these days, is that the nulls are the traces of hidden and bigger bodies that are currently evacuating the disk material around them, e.g., planets in the runaway accreting phase. This possibility seems difficult to reconcile with all the observations however, in particular the difference in submillimeter properties between the two nulls.
6. Summary and conclusions
We presented H- and Ks-imaging polarimetry of HD 142527. We used our polarized intensity (PI) images to morphologically describe the disk. The presence of two nulls or regions with lower PI at the north (top null) and south-east (bottom null) is clearly detected. Our results confirm previous observations of this system, showing a heavily dust-depleted inner gap extending up to 130 AU. We did not detect the continuum counterpart of the HCO+ streamers claimed by Casassus et al. (2013), but our sensitivity to faint extended features was limited inside the gap. We detected a new spiral feature on the east side of the disk by applying an edge-detection filter to our polarized intensity images. We obtained a direct image of the disk at H band by applying classical PSF-subtraction. This image also shows the two nulls, which rules out geometrical scattering effects as a possible explanation for them. We combined the PI and the PSF-subtracted images to place upper and lower limits to the polarization degree in this disk, which was found to vary between 10% and 25%. In both cases, the eastern side of the disk shows a higher polarization degree than the western side.
HD 142527 shows a lower polarization degree and lower azimuthal variations than the protoplanetary disks GG Tau, AB Aurigae, and UX Tau A. The modest azimuthal variation of the polarization degree is expected when the disk is seen nearly pole-on, which agrees with previous results that suggested an inclination of ≈20 degrees for HD 142527. Furthermore, the low polarization degree indicates that the distribution of dust particles on the disk’s surface must extend at least to micron sizes or more. Comparison with different grain populations suggests that the dust grains on the surface of the disk are not very porous, pointing toward compact grains. We also compared our images with ALMA band-7 continuum observations of the same disk. These images show that mm-sized dust follows a horse-shoe shape, with its highest emission placed at roughly the same azimuthal position as the northern null observed on our images. We have suggested possible explanations for the nulls, such as Rossby wave instabilities or local enhancements of the scale height of the disk. It is also tentative to link these nulls with the formation of planetesimals, although more evidence is needed to support this hypothesis.
A Wollaston prism separates the light by means of birefringence. The component of the light that vibrates parallel to the optical axis of the prism is affected by the extraordinary refraction index, ne, while the perpendicular component of the light is affected by the ordinary refraction index, no.
Acknowledgments
We are grateful to the ESO staff, and Julien Girard in particular, for their help during the observations. This research was funded by Millenium Science Initiative, Chilean Ministry of Economy, Nucleus P10-022-F. A.J. also acknowledges support from Fondecyt project 1130857. We acknowledge funding from the European Commission’s 7th Framework Program contract PERG06-GA-2009-256513 and from Agence Nationale pour la Recherche (ANR) of France under contract ANR-2010-JCJC-0504-01.
References
- Andrews, S. M., Rosenfeld, K. A., Wilner, D. J., & Bremer, M. 2011, ApJ, 742, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Apai, D., Pascucci, I., Brandner, W., et al. 2004, A&A, 415, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ataiee, S., Pinilla, P., Zsom, A., et al. 2013, A&A, 553, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biller, B., Lacour, S., Juhász, A., et al. 2012, ApJ, 753, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Pinilla, P. 2013, A&A, 550, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Canovas, H., Rodenhuis, M., Jeffers, S. V., Min, M., & Keller, C. U. 2011, A&A, 531, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canovas, H., Min, M., Jeffers, S. V., Rodenhuis, M., & Keller, C. U. 2012, A&A, 543, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casassus, S., Perez, M. S., Jordán, A., et al. 2012, ApJ, 754, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., van der Plas, G., Perez, S. M., et al. 2013, Nature, 493, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L. A., Schreiber, M. R., Romero, G. A., et al. 2012, ApJ, 750, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246 [Google Scholar]
- Dodson-Robinson, S. E., & Salyk, C. 2011, ApJ, 738, 131 [CrossRef] [Google Scholar]
- Dong, R., Rafikov, R., Zhu, Z., et al. 2012, ApJ, 750, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espaillat, C., Calvet, N., D’Alessio, P., et al. 2007, ApJ, 670, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Follette, K. B., Tamura, M., Hashimoto, J., et al. 2013, ApJ, 767, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fujiwara, H., Honda, M., Kataza, H., et al. 2006, ApJ, 644, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Fukagawa, M., Tamura, M., Itoh, Y., et al. 2006, ApJ, 636, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, R. C., & Woods, R. E. 2002, Digital image processing, 2nd edn. (Prentice Hall) [Google Scholar]
- Hales, A. S., Gledhill, T. M., Barlow, M. J., & Lowe, K. T. E. 2006, MNRAS, 365, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, J., Dong, R., Kudo, T., et al. 2012, ApJ, 758, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkley, S., Oppenheimer, B. R., Soummer, R., et al. 2009, ApJ, 701, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Houk, N. 1982, Michigan Catalogue of Two-dimensional Spectral Types for the HD stars, (Ann Arbor, MI: Department of Astronomy, Univ. Michigan), 3 [Google Scholar]
- Isella, A., Pérez, L. M., & Carpenter, J. M. 2012, ApJ, 747, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, C. U. 1996, Sol. Phys., 164, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, J. R., Potter, D., & Parise, B. 2001, ApJ, 553, L189 [NASA ADS] [CrossRef] [Google Scholar]
- Kusakabe, N., Grady, C. A., Sitko, M. L., et al. 2012, ApJ, 753, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 944 [Google Scholar]
- Mathews, G. S., Williams, J. P., & Ménard, F. 2012, ApJ, 753, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., & Whiffen, G. 1989, ApJ, 341, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Mayama, S., Hashimoto, J., Muto, T., et al. 2012, ApJ, 760, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Canovas, H., Mulders, G. D., & Keller, C. U. 2012, A&A, 537, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murakawa, K. 2010, A&A, 518, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Najita, J. R., Strom, S. E., & Muzerolle, J. 2007, MNRAS, 378, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Ohashi, N. 2008, Ap&SS, 313, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, B. R., Brenner, D., Hinkley, S., et al. 2008, ApJ, 679, 1574 [Google Scholar]
- Owen, J. E., Clarke, C. J., & Ercolano, B. 2012, MNRAS, 422, 1880 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Duchêne, G., Kalas, P., & Graham, J. R. 2006, ApJ, 645, 1272 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Graham, J. R., & Lloyd, J. P. 2008, PASP, 120, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Schneider, G., Duchene, G., et al. 2009, ApJ, 707, L132 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Schmid, H. M., Geissler, K., et al. 2011, ApJ, 738, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Avenhaus, H., Buenzli, E., et al. 2013, ApJ, 766, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2012, A&A, 546, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero, G. A., Schreiber, M. R., Cieza, L. A., et al. 2012, ApJ, 749, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, in SPIE Conf. Ser. 4839, eds. P. L. Wizinowich, & D. Bonaccini, 140 [Google Scholar]
- Schmid, H. M., Joos, F., & Tschan, D. 2006, A&A, 452, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silber, J., Gledhill, T., Duchêne, G., & Ménard, F. 2000, ApJ, 536, L89 [Google Scholar]
- Tanii, R., Itoh, Y., Kudo, T., et al. 2012, PASJ, 64, 124 [NASA ADS] [Google Scholar]
- van Boekel, R., Min, M., Leinert, C., et al. 2004, Nature, 432, 479 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Boekel, R., Min, M., Waters, L. B. F. M., et al. 2005, A&A, 437, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Verhoeff, A. P., Min, M., Pantin, E., et al. 2011, A&A, 528, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volten, H., Muñoz, O., Hovenier, J. W., et al. 2007, A&A, 470, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Witzel, G., Eckart, A., Buchholz, R. M., et al. 2011, A&A, 525, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Processed images of HD 142527 (top row) and HD 161743 (bottom row) in H band. From left to right: intensity image (I) in logarithmic scale, Stokes Q, U and PI images in linear scale. For comparison purposes, HD 161743 has been scaled by an arbitrary factor. Units are given in counts. The area corresponding to the saturated pixels (rsat ≤ 0.32′′) in HD 142527 has been masked out in all images. The polarized images of HD 142527 show a complex structure, while the comparison star only shows remnant noise. In all images north is up and east is left. This applies to all the figures in this paper. |
| In the text | |
 |
Fig. 2 Idisk images at H band. Left: without rotating the flux-scaled HD 161743 image. Right: rotating the HD 161743 image to match the spider’s pattern (indicated by dashed-lines) in the HD 142527 image. The innermost (r ≤ 0.67′′) regions are masked out to remove artifacts. The white arrows point to previously identified ghosts, which are enhanced when rotating the PSF to correct for the spiders. Bar units are given in counts. The bright path to the east, immediately above the dotted spider line, is an artifact of the PSF-subtraction process. |
| In the text | |
 |
Fig. 3 PI (top row) and Idisk (bottom row) images at H (left column) and Ks band (right column) of HD 142527. Masked area in the PI images cover the saturate region, while in the PSF-subtracted images cover the artifact-dominated regions. The PI are plotted with the same scale to enhance differences/similarities. The same is done with the Idisk images. The bright patch in the Idisk image at north-east direction in Ks band is an artifact due to the PSF-subtraction (as it is the bright path on the east direction in the Idisk image at H band, see also the caption in Fig. 2). Color bar units are given in counts. |
| In the text | |
 |
Fig. 4 PI radial cuts: H- and Ks-band cuts are plotted in black asterisks and red diamonds, respectively. Innermost regions have been masked out due to their significantly higher noise. Each point represents the mean value of the PI image at a given distance from the center, within a squared piece of 3 × 3 px (0.08′′ × 0.08′′). The error bars are the standard deviation inside each piece. The number at the upper-right corner in each plot indicates the PA (measured east of north) of the cut. The plot at 0° shows a cut from north (top) to south (bottom). In the other plots, the radial cuts start from the eastern side (left-side) of the images to the western side (right-side) of the images. |
| In the text | |
 |
Fig. 5 PI color. Inner regions have been masked out to remove artifacts. The black contours outline the position of the disk seen in polarized intensity at H band (Fig. 3, top left). The image has been smoothed with a 4-px Gaussian kernel. The two nulls have more neutral colors. |
| In the text | |
 |
Fig. 6 PI images at H band after applying a Sobel filter to highlight the regions of the image with edges. The three arrows indicate spiral arms on the disk. For comparison, we used the same notation as in Casassus et al. (2012) (see also Rameau et al. 2012) to label the spiral arms. The spiral arm labeled “2” perfectly matches its equivalent in Casassus et al. (2012). The spiral arm labeled “3” is barely visible in our images. The spiral arm on the east side is detected for the first time. Color bar is in arbitrary units. |
| In the text | |
 |
Fig. 7 Azimuthal (angles computed east of north) variation of the Stokes Q (top row) and U (bottom row) images for the H- (left column) and Ks-band (right column) measurements. |
| In the text | |
 |
Fig. 8 Azimuthal (angles computed east of north) variation of the PI (top row) and P (bottom row) images, for the H (left column) and Ks bands (right column). The position of the telescope’s spiders is indicated by the dashed lines. In the P plot at H band, the stars and the triangles represent the lower and upper limits of P (see text for a detailed explanation). The P image at Ks band is too contaminated by artifacts (see Fig. 3, right-bottom plot). |
| In the text | |
 |
Fig. 9 Polarization angle (Pθ) indicated by the green vectors, plotted over the PI image. The length of the vectors is proportional to the local polarization degree (P). The vectors are plotted in regions of the image where the polarized intensity PI is higher than three times the standard deviation (σPI) of the sky background (see text). |
| In the text | |
 |
Fig. 10 Polarizability as a function of scattering angles for different mixtures of dust. The polarizability is the ratio of the -S12 over S11 elements of the Mueller matrix. In all cases, dust mixtures have power-law size distributions with amin = 0.03 μm and a slope of − 3.5. Six cases with increasing values of amax are considered. The red curves show the polarizability for Mathis & Whiffen (1989) grains (a mix of astrosilicates and amorphous carbon and 80% porosity). The dotted green curves are for pure astronomical silicates with 80% porosity (Draine 2003). The blue dashed curves are for compact astronomical silicates without porosity (Draine 2003). The black curve is for a mixture of compact no porosity grains made of 100% amorphous carbon. All models with porosity have a high polarizability near 90 degrees scattering angles. Models with compact particles show lower maximum polarizations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


