| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321229 | |
| Published online | 20 June 2013 | |
Recurrent coronal jets induced by repetitively accumulated electric currents⋆
1 School of Astronomy and Space Science, Nanjing University, 210093 Nanjing, PR China
e-mail: guoyang@nju.edu.cn
2 Key Laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, 210093 Nanjing, PR China
3 LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
4 Departamento de Física, Universidad de Los Andes, A.A. 4976, Bogotá, Colombia
5 W. W. Hansen Experimental Physics Laboratory, Stanford University, Stanford, CA 94305, USA
Received: 3 February 2013
Accepted: 3 May 2013
Context. Jets of plasma are frequently observed in the solar corona. A self-similar recurrent behavior is observed in a fraction of them.
Aims. Jets are thought to be a consequence of magnetic reconnection; however, the physics involved is not fully understood. Therefore, we study some jet observations with unprecedented temporal and spatial resolutions.
Methods. The extreme-ultraviolet (EUV) jets were observed by the Atmospheric Imaging Assembly on board the Solar Dynamics Observatory (SDO). The Helioseismic and Magnetic Imager (HMI) on board SDO measured the vector magnetic field, from which we derive the magnetic flux evolution, the photospheric velocity field, and the vertical electric current evolution. The magnetic configuration before the jets is derived by the nonlinear force-free field extrapolation.
Results. Three EUV jets recurred in about one hour on 17 September 2010 in the following magnetic polarity of active region 11106. We derive that the jets are above a pair of parasitic magnetic bipoles that are continuously driven by photospheric diverging flows. The interaction drove the buildup of electric currents, which we observed as elongated patterns at the photospheric level. For the first time, the high temporal cadence of the HMI allows the evolution of such small currents to be followed. In the jet region, we found that the integrated absolute current peaks repetitively in phase with the 171 Å flux evolution. The current buildup and its decay are both fast, about ten minutes each, and the current maximum precedes the 171 Å also by about ten minutes. Then, the HMI temporal cadence is marginally fast enough to detect such changes.
Conclusions. The photospheric current pattern of the jets is found to be associated with the quasi-separatrix layers deduced from the magnetic extrapolation. From previous theoretical results, the observed diverging flows are expected to continuously build such currents. We conclude that the magnetic reconnection occurs periodically, in the current layer created between the emerging bipoles and the large-scale active region field. The periodic magnetic reconnection induced the observed recurrent coronal jets and the decrease of the vertical electric current magnitude.
Key words: magnetic fields / Sun: corona / Sun: surface magnetism / Sun: UV radiation
Two movies are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Solar jets are observed at many wavelengths, such as Hα, ultraviolet (UV), extreme-ultraviolet (EUV), and X-rays (Schmieder et al. 1988; Shibata et al. 1992a; Canfield et al. 1996; Chae et al. 1999; Uddin et al. 2012). They are called surges in cold spectral lines (e.g., Hα) and jets at other wavelengths, which indicates that both cold plasma (e.g., Srivastava & Murawski 2011; Kayshap et al. 2013) and hot plasma are accelerated in the jet phenomenon. Magnetic reconnection is widely accepted as the central physical mechanism. There are different magnetic reconnection models for coronal jets according to photospheric flow patterns and coronal magnetic topologies, for instance, the emerging flux model (Heyvaerts et al. 1977; Shibata et al. 1992b; Gontikakis et al. 2009; Archontis et al. 2010), the converging flux model (Priest et al. 1994), the quasi-separatrix layer (QSL) model (Mandrini et al. 1996), and the null-point and fan-separatrix model (Moreno-Insertis et al. 2008; Török et al. 2009; Pariat et al. 2009, 2010). To drive the magnetic reconnection in their simulations, Moreno-Insertis et al. (2008) and Török et al. (2009) use emerging flux, while Pariat et al. (2009, 2010) use horizontal photospheric twisting motion. While some of the aforementioned models focus on solar flares and coronal bright points, there has also been discussion of the associated jet phenomenon.
 |
Fig. 1 a)–c) SDO/AIA EUV composite images. Each EUV image consists of three channels (red, blue, and green) in the 304 Å, 171 Å, and 211 Å channels, whose characteristic temperature corresponds to 0.05 MK, 0.6 MK, and 2 MK, respectively. The larger solid box marks the jet region where the 171 Å fluxes are integrated. The smaller solid box on the clock indicates the position and field of view of the EUV image on the solar disk. The dashed box indicates the region where the background flux for the 171 Å band is computed. d) SDO/HMI line-of-sight magnetic field. The black/white color represents the negative/positive polarity. The solid box marks the region of the footpoints of the jets, where the line-of-sight magnetic field flux is integrated. The dotted box marks the field of view for the analysis of the vector magnetic field. |
The Hα surges and EUV/X-ray jets emanating from the same region tend to appear recurrently (Schmieder et al. 1995; Asai et al. 2001; Chifor et al. 2008; Wang & Liu 2012; Zhang et al. 2012). The period ranges from tens of minutes to several hours. It is still not clear which physical mechanism accounts for the quasi-periodicity. Pariat et al. (2010) proposed a null-point and fan-separatrix model driven by a photospheric twisting motion. As a consequence of the continuous driving by photospheric motions, this model produces recurrent jets, which explains the quasi-periodicity. Zhang et al. (2012) proposed another possible mechanism, whereby the null-point reconnection responsible for the quasi-periodicity is modulated by trapped slow-mode waves along the spine field lines, and the slow-mode wave has been reported in, for example, Cirtain et al. (2007). Both models consider magnetic topologies with null points. But can those events whose magnetic topologies are QSLs or bald patches be explained? Moreover, the photospheric motion is believed to be the driver of these recurrent jets. Can we find any indicator of the quasi-periodicity from the photosphere, such as from the magnetic flux evolution, the velocity field, or the electric current evolution?
In this paper, we present three recurrent coronal jets that were observed on 17 September 2010 by the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on board the Solar Dynamics Observatory (SDO). To find a clue on the magnetic reconnection model and the physical mechanism accounting for the quasi-periodicity, we study the EUV flux, the magnetic flux, the velocity field, and the vertical electric current evolutions. The vector magnetic fields are observed by the Helioseismic and Magnetic Imager (HMI; Scherrer et al. 2012; Schou et al. 2012b) on board SDO. Section 2 presents the data analysis and results. Discussion and conclusion are given in Sect. 3.
2. Data analysis and results
2.1. Jets observed in EUV
The SDO/AIA provides high cadence of 12 s, high spatial resolution of 1.5′′ (the pixel sampling is 0.6′′ per pixel), and high signal-to-noise observations nearly simultaneously in seven EUV lines, two UV continuums, and one white-light band. Figure 1 displays three composite EUV images showing that three coronal jets recurred on the border of active region (AR) 11106. All the EUV images have been aligned with “aia_prep.pro” in the Solar SoftWare (SSW). A line-of-sight magnetic field observed by SDO/HMI is displayed in Fig. 1d as an example, which shows that some parasitic positive polarities distribute in the main negative polarities. The SDO/HMI has a spatial resolution of 1′′ (the spatial sampling is 0.5′′ per pixel) and a cadence of 45 s for the line-of-sight magnetic field. It has also been aligned with the EUV images with “aia_prep.pro”.
We computed the EUV flux in the 171 Å band to give a quantitative representation of the evolution of the recurrent jets. The 171 Å flux was computed within a rectangle containing the full jet region as shown by the larger solid box (130′′ × 80′′) in Figs 1a–c. We selected two time ranges to compute the 171 Å flux evolution, that is, a context range from 00:00 to 10:00 UT and a smaller analysis range centered on the analyzed jets from 03:00 to 05:00 UT. Due to the limitation of computation resources, the temporal resolution for the context range is two minutes and 12 s for the analysis range. The 171 Å flux evolutions for the two time ranges are plotted in Figs. 2a, b, respectively. The data gap between 06:31 to 07:13 UT is due to the SDO eclipse by the Earth. We normalized the 171 Å flux to its background level, which was computed in a quiet region as shown in the dashed box of Figs. 1a–c. The 171 Å background flux shows a flat curve (Fig. 2a). Therefore, the variations in the 171 Å flux curve in the jet region are mainly due to the jets themselves and not to the background.
 |
Fig. 2 SDO/AIA 171 Å averaged and normalized flux and SDO/HMI line-of-sight magnetic flux. a) Blue stars indicate the 171 Å flux in the jet region divided by the number of pixels in the box (larger solid box as shown in Figs. 1a–c) normalized to the background flux, which is computed in the dashed box shown in Fig. 1. Plus signs represent the averaged background flux per pixel. The temporal resolution is about 2 min. The two vertical lines mark the time range for 171 Å flux as shown in the bottom panel. b) The temporal resolution for the 171 Å flux is about 12 s. The three vertical lines mark the peak times of the 171 Å flux. Dash-dotted, dotted, and solid lines indicate positive, unsigned negative, and total unsigned line-of-sight magnetic flux, respectively. |
Figure 2a shows many fluctuations or peaks in the 171 Å flux curve during the context range, which indicates that there are many brightening points or jets during this time range in the selected region. However, the peaks during the analysis range are more distinct than the others. Therefore, we selected this time range for a detailed analysis. The 171 Å flux curve in Fig. 2b has three main peaks at 03:17 UT, 03:57 UT, and 04:22 UT, respectively. There are some smaller peaks before the jet at 03:57 UT. Using the 171 Å movie (attached to Fig. 7), we find that this jet consists of successive ejections during a short period. The other two events are relatively simple, with only one ejection in each event.
2.2. Line-of-sight magnetic flux evolution
 |
Fig. 3 a) SDO/AIA 171 Å image overlaid by the line-of-sight magnetic field observed at the same time as that of the 171 Å image. Gray/black lines mark the contour levels of the positive/negative polarities. The contour levels of Bz are –1200, –900, –600, 300, and 600 G. b) Map of photospheric transverse velocities derived from LCT analysis with the HMI magnetograms, employing a FWHM correlation window of 5′′ during the time interval 02:25–02:50 UT. Arrows represent velocities and the background is the line-of-sight magnetogram with positive (white) and negative (black) polarities. Black/white arrows are located on positive/negative polarities. North/south is up/down, west/east is towards right/left. The magnetic polarities involved in the jets are identified with annotations (p1 and p2 for parasitic positive, n1 and n2 for parasitic negative, N0 and N1 for the main following negative polarities). The circle highlights the region of interest where the diverging flows are found. A movie showing the evolution of the line-of-sight magnetic field from 02:00 to 06:00 UT is available online. |
Figure 2b displays the unsigned line-of-sight magnetic flux evolution. The line-of-sight magnetic flux is integrated in a small rectangle containing mainly the footpoints of the jets with a size of 48′′ × 28′′ as shown by the solid box in Fig. 1d. The box size for the 171 Å flux computation is larger than that for the magnetic flux because, on one hand, jets are events occupying areas in the corona that are more extended than the triggering magnetic field region in the photosphere below. On the other hand, the parasitic polarities involved with the jets are surrounded by main polarities of the active region, which would bias the computation of the line-of-sight magnetic flux if the box is too large. The positive magnetic flux increases from 02:00 to 03:00 UT and evolves almost steadily from 03:00 to 05:00 UT (Fig. 2b, dash-dotted curve). The negative flux curve is dominated by the main negative polarity of the active region, and some of the flux is close to the border of the selected region (Fig. 1d). Then, due to convective motions of the photospheric plasma, magnetic flux might be displaced and is no longer captured by the selected area. For this reason, the unsigned negative flux evolution (Fig. 2b, dotted curve) is not necessarily related to the jetting events. It evolves steadily from 02:00 to 03:00 UT and decreases during the recurrent jets from 03:00 to 05:00 UT. Comparing the magnetic flux evolution with the 171 Å flux evolution, we do not find a clear relationship between them. The unsigned magnetic flux in the negative polarity either decreases (for the jets at 03:17 and 04:22 UT) or increases (for the jet at 03:57 UT) before a jet. There is also no significant evolution of the positive magnetic flux related to the jets. This result is coherent with a progressive storage of magnetic energy in the corona, which reaches a critical point and releases part of the free magnetic energy without affecting the magnetic flux crossing the photosphere.
Figure 3a shows that the footpoints of the EUV jets are located where parasitic polarities appear. As shown in Fig. 1d, AR 11106 consists of a leading positive and a following negative polarity, which has two strong concentrated polarities N0 and N1. The parasitic polarities noted as p1, p2, n1, and n2 in Fig. 3b are present in the following negative polarity of AR 11106. The positive parasitic polarities p1 and p2 separate westward from the eastern negative polarity (n1 and n2). Polarities n1 and n2 have almost merged with the following main polarity N1 of AR 11106, while p2 is pushed against another part of the following main polarity (N0). The evolution of these polarities can be seen in the movie of the line-of-sight magnetic field attached to Fig. 3 (available online).
We further studied the transverse flows of photospheric magnetic features with local correlation tracking techniques (LCT; November & Simon 1988). By using a Gaussian tracking window of full width at half maximum (FWHM) of 5′′, we computed the proper motions of magnetic elements over the SDO/HMI sequence of magnetograms. The window size of 5′′ is appropriate because it is large enough to contain the coherent structures that are to be correlated, but not too large so that as much as possible of the spatial resolution can be kept and computation time can be limited to feasible values. The time series used for this analysis starts at 02:00 UT on 17 September 2010 and is composed of 137 images with a cadence of 45 s. Images are grouped in 25 min series for the LCT analysis. Prior to applying LCT, the sequence of images is aligned to eliminate possible jitter and rotation of the observed target within the field of view. Since the differential rotation is of minor influence here due to the small field of view, we did not remove this effect. Taking the first image as reference, the second image is aligned to it by correlating them. Then, the third image is aligned with the second one with the same method. The process is repeated until all the 137 images are aligned with each other. We find that the maximum shift is up to 21 pixels in the east-west direction and less than one pixel in the north-south direction. The absolute values of the transverse velocities should be taken with caution because the LCT technique in general produces some systematic errors in the determination of proper motions (November & Simon 1988). While the LCT method may underestimate 20%–30% of the velocities in extreme cases (Molowny-Horas 1994), it usually generates reliable flow patterns (November & Simon 1988; Vargas Domínguez et al. 2008).
The results confirm the emergence pattern seen in the magnetic field movie. There is indeed a diverging flow with the polarities p1 and p2 moving mostly westward and their negative counterparts, n1 and n2, moving mostly eastward (this diverging flow pattern is on average inclined by about 20° on the east-west direction), while the bipoles n1-p1 and n2-p2 are mostly east-west oriented at that time.
 |
Fig. 4 a) SDO/HMI vertical component of the magnetic field (Bz). The projection effect is removed. b) SDO/HMI vector magnetic field with the 180° ambiguity removed. c)–g) Distribution of the vertical electric current density jz averaged over 12 min at different times and observed by SDO/HMI. The middle time of the observations is indicated at the top of each panel. Gray/black lines mark the contour levels of the positive/negative polarities. The contour levels of Bz are –1200, –900, –600, 300, and 600 G. The color bar of jz is shown on the right side. h) Distribution of jz observed by THEMIS/MTR centered at 09:42 UT. The scan duration is about 16 min in this field of view. The contour levels of Bz are –882, –661, –440, 110, and 220 G, which are at the same percentage of their minimum (for the negative contours) and maximum (for the positive contours) values as that in Fig. 4g. |
2.3. Vector magnetic field
We further analyzed the vector magnetic fields observed by SDO/HMI, which records six filtergrams at each of six wavelengths every 135 s. The filtergrams at each wavelength correspond to six polarization states, that is, I ± S, where S = Q,U, and V, where the notations I,Q,U, and V represent the four Stokes parameters. In order to increase the signal-to-noise ratio and remove the p-mode signals, all the filtergrams are averaged over 12 min. More precisely, the average uses a cosine-apodized boxcar with an FWHM of 720 s. The tapered temporal window is actually 1215 s. The Stokes parameters, I, Q, U, and V, are computed from the filtergrams at each of the six wavelengths. The vector magnetic field and other thermodynamical parameters are fitted by the inversion code of Very Fast Inversion of the Stokes Vector (VFISV; Borrero et al. 2011). The 180° ambiguity for the transverse components of the vector magnetic field has been resolved by the improved version of the minimum energy method (Metcalf 1994; Metcalf et al. 2006; Leka et al. 2009). We analyzed all the 11 vector magnetic fields between 03:00 to 05:00 UT. The selected field of view for the analysis is x ∈ [ − 300′′,190′′] and y ∈ [ − 560′′, − 315′′].
To study the electric current well after the recurrent jets and to compare with other observations, we analyzed two more vector magnetic fields, one observed by SDO/HMI at 09:36 UT and the other one by the Télescope Héliographique pour l’Étude du Magnétisme et des Instabilités Solaires/Multi-Raies (THEMIS/MTR; López Ariste et al. 2000; Bommier et al. 2007). The THEMIS/MTR is a spectro-polarimeter with higher polarimetry accuracy but lower cadence than that of SDO/HMI. It is free from systematic instrumental polarization (López Ariste et al. 2000), while the polarimetric accuracy of SDO/HMI is about 0.4% (Schou et al. 2012a). The THEMIS/MTR scanned the solar surface from east to west to cover the field of view 161′′ × 104′′ in the time range of 09:34–10:38 UT. The scan step size along the east–west direction is about 0.8′′, the pixel sampling along the north–south direction is about 0.2′′. We aligned the magnetic field observed by THEMIS/MTR with that by SDO/HMI using a common feature identification method. First, a line-of-sight SDO/HMI magnetic field at the middle time (10:06 UT) of the THEMIS/MTR observation is interpolated to the THEMIS/MTR spatial resolution. Then, we selected some common features on both line-of-sight magnetic fields and recorded their coordinates. Finally, the offsets of the THEMIS/MTR data referred to the SDO/HMI data were computed with the coordinates recorded in the previous step.
Since the centers of the field of views for the regions of interest are not close to the center of the solar disk, the projection effect must be removed. We removed this effect with the method proposed by Gary & Hagyard (1990), which converts the line-of-sight (Bζ) and transverse components (Bξ and Bη) to the heliographic components (Bx,By, and Bz), and we projected those fields from the image plane to the plane tangent to the solar surface at the center of the field of view. This coordinate transformation is applied in the field of views given above, while a smaller region is cut and displayed in Figs. 4a,b as an example.
2.4. Electric current evolution
Using the vector magnetic field, we computed the vertical electric current density with Ampère’s law, 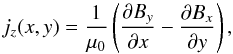 (1)where μ0 = 4π × 10-3 G m A-1. The vertical electric current densities are computed for all the analyzed vector magnetic fields. Some selected jz distributions before, close to the three peaks of, and after the recurrent jets are plotted in Figs. 4c–h. The jz distributions close to the jet peaks have very similar patterns, as shown in Figs. 4c–f. However, the magnetic field at 09:36 UT well after the jets has much lower electric current density (Fig. 4g) than do those in the jets’ duration (Figs. 4c–f). The jz distribution computed by the vector magnetic field observed by THEMIS/MTR as shown in Fig. 4h also shows very low electric currents. The difference between Figs. 4g, h is caused by the different spatial and temporal resolutions and spectro-polarimetric accuracies of SDO/HMI and THEMIS/MTR. Besides the above reasons, they are instruments of two different types, where THEMIS/MTR is a spectrograph and SDO/HMI is a filtergraph. THEMIS/MTR records the Stokes line profiles along a slit at one exposure but needs to scan perpendicularly to the slit to cover a required field of view. In contrast, SDO/HMI records an image at a wavelength point at one exposure but needs to scan along the wavelength to get the Stokes line profiles.
(1)where μ0 = 4π × 10-3 G m A-1. The vertical electric current densities are computed for all the analyzed vector magnetic fields. Some selected jz distributions before, close to the three peaks of, and after the recurrent jets are plotted in Figs. 4c–h. The jz distributions close to the jet peaks have very similar patterns, as shown in Figs. 4c–f. However, the magnetic field at 09:36 UT well after the jets has much lower electric current density (Fig. 4g) than do those in the jets’ duration (Figs. 4c–f). The jz distribution computed by the vector magnetic field observed by THEMIS/MTR as shown in Fig. 4h also shows very low electric currents. The difference between Figs. 4g, h is caused by the different spatial and temporal resolutions and spectro-polarimetric accuracies of SDO/HMI and THEMIS/MTR. Besides the above reasons, they are instruments of two different types, where THEMIS/MTR is a spectrograph and SDO/HMI is a filtergraph. THEMIS/MTR records the Stokes line profiles along a slit at one exposure but needs to scan perpendicularly to the slit to cover a required field of view. In contrast, SDO/HMI records an image at a wavelength point at one exposure but needs to scan along the wavelength to get the Stokes line profiles.
Next, we integrated | jz | in the field of view as shown in Figs. 4a–h for those regions where | jz | is above the noise level 0.02 A m-2 estimated by the formula (1/μ0)(δBT/Δx) (Gary & Démoulin 1995), where δBT ~ 100 G is the assumed transverse field error, and Δx = 0.5′′ is the grid size. The fields of view in Figs. 4a–h are selected to be similar to the one used to compute the line-of-sight magnetic flux (Figs. 1d and 2b). But they are not identical, since the projection effect has been corrected to compute the vertical electric currents. Figure 5a displays the evolution of the integrated vertical electric current, Iz, where an obvious quasi-periodicity can be found. This recurrent evolution is present on the background of a stationary current pattern, whose average electric current is (2.51 ± 0.06) × 1012 A. The current pattern is stationary since the vertical current density distribution does not change too much during the jets as shown in Figs. 4c–f. The fluctuation of Iz around the background (defined as 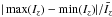 , where
, where 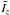 denotes the average of Iz) is limited within 8%, which is above the errors of Iz (around 2%). The integrated electric currents, Iz, for the magnetic fields observed by SDO/HMI at 09:36 UT (Fig. 4g) and by THEMIS/MTR at 09:42 UT (Fig. 4h) are around (1.88 ± 0.05) × 1012 A and (0.43 ± 0.04) × 1012 A, respectively. Therefore, the currents significantly decrease later on.
denotes the average of Iz) is limited within 8%, which is above the errors of Iz (around 2%). The integrated electric currents, Iz, for the magnetic fields observed by SDO/HMI at 09:36 UT (Fig. 4g) and by THEMIS/MTR at 09:42 UT (Fig. 4h) are around (1.88 ± 0.05) × 1012 A and (0.43 ± 0.04) × 1012 A, respectively. Therefore, the currents significantly decrease later on.
The errors for the integrated Iz as shown in Fig. 5a are estimated by a Monte-Carlo method. The basic assumption is that the errors for Iz are normally distributed in the whole field of view of Fig. 4 and three times the standard deviation of the errors is 0.02 A m-2. We added those errors to Iz and integrated their absolute values with the criteria described in the previous paragraph. After repeating 50 times for each observation time, the errors are estimated as the standard deviation of the 50 integrated Iz.
Figure 5 also shows the integrated vertical electric currents overlaid on the 171 Å flux. The integrated vertical current is derived from the deprojected heliographic vector maps, while the 171 Å flux is computed in the image plane (plane of the sky). The deprojection allows us to derive the vertical current density, which has a more physical meaning than the line-of-sight one before deprojection. Since the EUV jets are coronal events and the electric current is on the photosphere, the field of view for computing the vertical electric current does not need to be the same as that for the 171 Å flux. We find that the peaks on the Iz curve have a good coincidence with those on the 171 Å flux. They both repeat three times. However, the magnitudes of the peaks on the Iz curve have large differences, which can be explained by the lower temporal cadence of SDO/HMI vector magnetic field observations (12 min). Therefore, sample points on the Iz curve are randomly distributed compared to the 171 Å flux peak time (Fig. 5a).
To mimic a higher temporal resolution of the Iz evolution, we combine the observations at the three peaks with one assumption. We assumed that the vertical electric current accumulation and decrease processes are similar for all three recurrent jets, which are homologous from EUV observations, that is, we assume that the peak magnitude of the Iz curve and the evolution timing relative to the 171 Å flux are almost the same. Then, we shifted the Iz curve around t1 = 03:17 and t3 = 04:22 UT to the time t2 = 03:57 UT, as shown in Fig. 5b. From the combined Iz curve in Fig. 5b, we find that the vertical electric current increases first and then decreases in a jet process.
The combined Iz curve in Fig. 5b also shows two additional features. First, the Iz curve peak is earlier than the 171 Å flux peak. Second, the vertical electric current seems to increase faster than it decreases. However, we remind the limited temporal cadence of SDO/HMI, so both results will need to be checked with other observations.
 |
Fig. 5 a) Evolutions of the 171 Å flux (normalized as in Fig. 2) and the unsigned vertical electric current Iz, which is integrated in the field of view as shown in Fig. 4. Blue stars mark the normalized 171 Å flux and red diamonds mark the unsigned vertical electric current Iz. b) The electric current evolution curves at the first and third peaks have been shifted to the second peak, and the total profile is shown with a continuous line. The shifted time differences are t2 − t1 and t3 − t2 for the two curves (denoted by dashed and dash-dotted lines), respectively. We note that the vertical axes for both the 171 Å flux and Iz do not start from zero. |
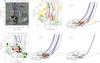 |
Fig. 6 a) Magnetic field lines computed from the NLFFF model. Different colors indicate different field line systems. The background is the vertical magnetic field Bz shown with gray levels. White/black color represents positive/negative magnetic polarity. The box marks the field of view shown in panels b)–f). b), c) Orange ribbons represent the QSL sections on the photosphere. Only the QSLs with the squashing degree Q ≥ 1014 are plotted. Gray/black contours are the same as that in Fig. 4c. d), e) Magnetic field lines overlaid on the photospheric distribution of the vertical electric current density jz as shown in Fig. 4c. The current jz is computed with the non-preprocessed vector magnetic field. f) Similar to panels d) and e), but only some sample field lines with magnetic dips are shown. |
2.5. Magnetic configuration before the recurrent jets
The magnetic configuration is one part of the information necessary for discriminating different magnetic reconnection models. For this reason, we study the three-dimensional magnetic field with the nonlinear force-free field (NLFFF) extrapolation of the coronal field from the vector magnetic field as the boundary condition. The optimization method is selected for the NLFFF extrapolation (Wheatland et al. 2000; Wiegelmann 2004). The bottom boundary is provided by the SDO/HMI vector magnetic field at 03:00 UT, so just before the studied jets. The projection effect was corrected as described in Sect. 2.2. Since the photospheric vector magnetic field does not satisfy the force-free condition, we applied the preprocessing method to remove the net magnetic force and torque on the bottom boundary (Wiegelmann et al. 2006). A requirement for the preprocessing is that the magnetic field at the bottom boundary needs to be isolated and flux balanced. Therefore, we selected a field of view as shown by the dotted box in Fig. 1d to enclose the major magnetic flux of AR 11106. Since removing the projection effect changes the geometry of the field of view, we cut off the edges where the data are incomplete to get a rectangle box, which is resolved by 932 × 486 grid points with Δx = Δy ≈ 0.5′′. To measure the flux balance quantitatively, we define the flux balance parameter as 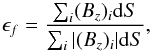 (2)where the pixel index i runs all over the field of view and dS is the area of one pixel. The flux balance parameter ϵf is about 0.03 for the magnetic field in this field of view, which is a tolerably small imbalance.
(2)where the pixel index i runs all over the field of view and dS is the area of one pixel. The flux balance parameter ϵf is about 0.03 for the magnetic field in this field of view, which is a tolerably small imbalance.
The boundary field of view for the NLFFF extrapolation is shown in Fig. 6a. There are two reasons why we use this small field of view. First, the region of interest where the jets originate is small. It is acceptable if we put it in the center. Secondly, the spatial sampling of SDO/HMI is high (0.5′′). Thus, in the selected field of view (about 100′′ × 100′′) and the height range, the computation box includes 200 × 200 × 200 grid points, which are reasonable sizes for the computation. However, DeRosa et al. (2009) pointed out that it is critical for the vector magnetic field to cover areas as large as possible for successful NLFFF modeling. To fulfill this requirement in the limited field of view, we prepared the boundary and initial conditions for the higher resolution NLFFF extrapolation as follows. First, we computed a lower resolution NLFFF with the vector magnetic field in the field of view used above for the preprocessing, as shown by the dotted box in Fig. 1d. Due to the limitation of computation resources, the lower resolution NLFFF is computed in a box of 466 × 243 × 201 grid points with Δx = Δy = Δz ≈ 1.0′′. Then, we cut out a sub-volume in the field of view as shown in Fig. 6a with a height of 100′′ and interpolate the NLFFF to the spatial resolution of Δx = Δy = Δz ≈ 0.5′′. The interpolated NLFFF is used as the initial, lateral, and top boundary conditions for the higher resolution NLFFF extrapolation. The bottom boundary is provided by the aforementioned preprocessed vector magnetic field in the field of view as shown in Fig. 6a, which is cut from the larger flux-balanced area. We used a buffer zone with 25 grid points in the NLFFF optimization method to decrease the effect of these boundaries. The weighting function decreases from 1 to 0 with a cosine profile in the buffer zone. Finally, we refer to Wheatland et al. (2000) and Wiegelmann (2004) for more detailed descriptions of the extrapolation method.
We adopted two metrics to test if the NLFFF has reached the force-free and divergence-free state. The force-free metric is defined as the current-weighted average of sinθ (Wheatland et al. 2000): 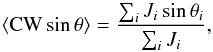 (3)where
(3)where 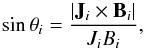 (4)θ represents the angle between the current density J and the magnetic field B, and B = | B |, J = | J |. The summation is done in the sub-domain of 77 × 75 × 35 grid points, whose projection is shown as the solid box in Fig. 6a. Only the grid points where J ≥ 0.02 A m-2 (the noise level in Sect. 2.4) are considered in computing sinθ. For a perfectly force-free magnetic field, the force-free metric should be zero, that is, the current density J and the magnetic field B are parallel to each other. The divergence-free metric is defined as the unsigned average of the fractional flux unbalance, ⟨ | fi | ⟩, where
(4)θ represents the angle between the current density J and the magnetic field B, and B = | B |, J = | J |. The summation is done in the sub-domain of 77 × 75 × 35 grid points, whose projection is shown as the solid box in Fig. 6a. Only the grid points where J ≥ 0.02 A m-2 (the noise level in Sect. 2.4) are considered in computing sinθ. For a perfectly force-free magnetic field, the force-free metric should be zero, that is, the current density J and the magnetic field B are parallel to each other. The divergence-free metric is defined as the unsigned average of the fractional flux unbalance, ⟨ | fi | ⟩, where 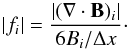 (5)While the divergence-free metric is computed in the same domain as that for the force-free metric, the difference is that all the grid points of the sub-domain are considered. This metric should be zero in a truly divergence-free field.
(5)While the divergence-free metric is computed in the same domain as that for the force-free metric, the difference is that all the grid points of the sub-domain are considered. This metric should be zero in a truly divergence-free field.
The force-free and divergence-free metrics for the NLFFF model are 0.19 and 3.0 × 10-3, respectively. The corresponding angle for the force-free metric, which is defined as arcsin ⟨ CWsinθ ⟩, is 11.0°. Metcalf et al. (2008) compared various NLFFF algorithms using simulated chromospheric and photospheric vector fields. The force-free metric 0.19 that we derive here is slightly better than that of 0.26 using the preprocessed and smoothed photospheric boundary with the optimization code of Wiegelmann (2004). However, it is larger and therefore worse than the force-free metric 0.11 using the chromospheric boundary. The divergence-free metric 3.0 × 10-3 is larger (and worse) than both the metrics using the chromospheric and preprocessed and smoothed photospheric boundaries with the optimization method as listed in Table 5 of Metcalf et al. (2008). This is because they adopted simulated vector magnetic fields as boundary conditions, which are smoother than the observational boundaries that we use in this paper.
 |
Fig. 7 a) SDO/AIA 171 Å image. The box marks the region where the 171 Å fluxes are computed. b) SDO/AIA 171 Å flux normalized to the background level, which is defined as the flux in the quiet Sun region (see Sect. 2.1 for more details). The vertical dashed line marks the time of the 171 Å image in panel a). A movie showing the evolution of this figure from 03:00 to 05:00 UT is available online. |
Some selected magnetic field lines in the NLFFF model are plotted in Fig. 6. The overall magnetic configuration in Fig. 6a shows different connectivities with small closed field lines linking the small diverging bipole (represented by the red lines connecting positive polarities p1 and p2 to negative ones n1 and n2) and long field lines (represented by the blue lines anchored in polarities N0 and N1). We find no magnetic null point in between these two set of field lines, thus no separatrix. Rather, a continuous but drastic change of magnetic connectivity, a QSL, is separating both types of connectivities. We computed the squashing degree Q as defined in Titov et al. (2002) to locate the position of the QSLs. Figures 6b and 6c show the QSL sections on the bottom boundary. The closed (red) and long (blue) field lines are clearly separated by QSLs between them.
We also overlaid the magnetic field lines on the photospheric distribution of the vertical electric current density jz, as shown in Figs. 6d,e. The footpoints of the field lines close to the QSL are rooted on the regions where jz is large. This result is coherent with previous findings, where concentrated electric currents have been found at the border of the QSLs in flare configurations (see Démoulin et al. 1997,and references therein). For a thin QSL, a moderate difference of magnetic stress across the QSL creates strong electric current. Then, a current layer is easily built up at a QSL. For the first time, the high temporal cadence and magnetic sensitivity of SDO/HMI allows such current layer evolution for such small events as the studied jets to be diagnosed.
Due to the existence of the parasitic positive magnetic polarities, some blue field lines are bent down from higher altitudes to lower altitudes. Magnetic dips and bald patches are present where the magnetic field lines are bent down, as shown in Fig. 6f. We refer to the following theoretical or observational papers for detailed definition and analysis of magnetic dips and bald patches, such as Titov et al. (1993), Bungey et al. (1996), Mandrini et al. (2002), and Démoulin (2005). However, it is not clear if the bald patches played any role in the magnetic reconnection of the studied jets, which asks for further studies.
3. Discussion and conclusion
In summary, we find that three EUV jets observed by SDO/AIA from 03:00 to 05:00 UT on 17 September 2010 recurred in the same region close to the border of AR 11106. The time differences between the three successive 171 Å peaks are 40 min and 25 min. On the border of the following negative polarity, parasitic positive polarities (polarities p1 and p2 in Fig. 3) are present close to the footpoints of the EUV jets. They are parts of a magnetic bipole that is growing in size, as shown by the diverging flow pattern. The line-of-sight magnetic flux evolution does not have a clear relationship with the 171 Å flux evolution. However, the high time cadence of SDO/HMI (12 min for the vector magnetic field) allows us to follow the photospheric current evolution. We integrated the absolute vertical electric current density found in the region of the jets. The peaks of this total current have a good temporal coincidence with the peaks of the 171 Å flux.
The aforementioned features can only be partly explained by the emerging flux model (Shibata et al. 1992b) and the converging flux model (Priest et al. 1994) since the newly emerged magnetic flux is consistent with the former model and the bald patch configuration is consistent with the latter one. But both models are two dimensional with magnetic reconnection in separatrices (as implied by their dimensionality), while the magnetic connectivity is not necessarily discontinuous in the three-dimensional space. The above models can be generalized as a three-dimensional configuration with a magnetic null point (e.g., Moreno-Insertis et al. 2008; Török et al. 2009; Pariat et al. 2009, 2010). However, in the present study, no null point is found in the corona with the NLFFF extrapolation. Rather, continuous changes of connectivity are present with drastic changes at some locations. Indeed, the computed coronal configuration has a QSL separating a small-scale evolving double bipole (polarities p1–n1 and p2–n2 in Fig. 3) from the large-scale AR magnetic field, a configuration comparable to those found previously, for example, in an X-ray bright point (Mandrini et al. 1996).
The temporal evolution of the photospheric magnetic field (see the movie attached to Fig. 3) and the velocities deduced by LCT both indicate divergent flows in the small parasitic bipoles. These flows would force the closed field lines of the small parasitic bipole to grow in size and interact with the overlying large-scale field lines (Fig. 6). This kind of evolving magnetic configuration is known to build up a narrow current layer in the QSL, as conjectured analytically (Démoulin et al. 1996) and found in numerical simulations, even for relatively small displacements (Aulanier et al. 2005; Effenberger et al. 2011). The main reason is that the magnetic stresses of very distant regions, which have been generated by photospheric flows, are brought close to one another, typically over the QSL thickness. This current layer becomes thinner and stronger with time. When the currents reach the dissipative scale, there is a breakdown of ideal MHD in the QSLs, magnetic reconnection occurs, and part of the magnetic energy is released (Aulanier et al. 2006). In the configuration studied above, this process would create some lower lying field lines with less shear and some higher field lines, along which hot collimated plasma is ejected into the higher corona.
The quasi-periodicity and homology of the coronal jets requires two conditions. First, the magnetic energy is injected into the corona uninterruptedly in almost the same region, and secondly, it releases intermittently. The first condition is satisfied by the observed diverging photospheric motions, which inject free magnetic energy in the coronal field without changing the photospheric magnetic field distribution too much. The second condition requires the current layer to become thin enough recurrently in order to reconnect and rapidly release part of the plasma trapped in the low-lying loops (of the diverging bipole). The observed periodic buildup and decrease of the photospheric currents, in phase with the EUV jets (Fig. 5), is an evidence that this second condition is met. Indeed, only a small fraction of the current is dissipated, an indication that the reconnection stops rapidly when the current layer weakens. Then, the next buildup of current starts from a non-potential configuration. This allows a relatively fast buildup of a new thin current layer and may explain the small time interval between the jets (40 and 25 min). The photospheric flows displace the magnetic polarities by only about 300–480 km during the successive jets, where we use v = 0.2 km s-1 estimated by the LCT velocity data as the average velocity in the encircled region of Fig. 3.
What is still surprising is that the buildup and decay times of the currents are comparable (Fig. 5). Usually, the buildup time is thought to be much longer than the decay time for many solar activities, such as flares and coronal mass ejections. A reason for the comparable time scale could be the limited time cadence of SDO/HMI, which includes the constrain of a large enough signal-to-noise ratio, so that this kind of study needs a higher cadence and better polarimetric accuracy to get a more precise temporal evolution of the currents. We mimic a higher temporal cadence by supposing that the evolution processes are the same and then combine the current measurements of the three jets using the EUV flux maximum as a time reference. With these limits, we find a current maximum near the beginning of the EUV flux rise, about ten minutes before the EUV flux maximum. This indicates that the free magnetic energy starts to decrease as soon as there is an evidence of reconnection.
In conclusion, we find evidence indicating that the studied recurrent coronal jets are caused by magnetic reconnection in the QSL, which is present between a diverging bipole and the main AR magnetic field. Magnetic energy is injected by the continuous diverging motions observed at the photospheric level. We assume that this process has built a thin current layer whose photospheric cross section is deduced from the vector magnetograms. The current evolution is found in phase with the EUV flux with a current maximum present before the jets followed by a relaxation to lower value. However, this evolution of the current intensity is limited to around 8% of the average background. We note that only the vertical component of electric currents is derived on the photosphere. If the NLFFF assumption is valid, the coronal currents are directly related to the photospheric currents since α = μ0jz/Bz and α is constant along a field line. Therefore, we conclude that the magnetic system always stays close to the resistive instability of the current layer. The jets do not change the photospheric vertical current distribution too much, and only a moderate photospheric evolution is needed to restart a new jet.
All together, we interpret these observations as the consequence of the continuous photospheric driving of the coronal field. A thin current layer is built in the QSL, where the magnetic field reconnects when the electric currents are strong enough and stops reconnecting soon afterward. The magnetic reconnection dissipates only a small part of the electric currents. The above phenomena repeat in time and drive the recurrent jets into the large-scale field as the confined plasma in the closed loops is accelerated after reconnection.
Online material
Movie to Figure 3 Access here
Movie to Figure 7 Access here
Acknowledgments
We thank the anonymous referee very much for his/her constructive comments that improve this paper. Data are courtesy of SDO and the HMI and AIA science teams. THEMIS is a French telescope operated by CNRS on the island of Tenerife in the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias. We thank the THEMIS team for the observations. Y.G. and M.D.D. were supported by the National Natural Science Foundation of China (NSFC) under the grant numbers 11203014, 10933003, 10878002, and the grant from the 973 project 2011CB811402. B.S. thanks the team of the flux emergence workshop lead by K. Galsgaard and F. Zuccarello for fruitful discussions in Bern at ISSI.
References
- Archontis, V., Tsinganos, K., & Gontikakis, C. 2010, A&A, 512, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asai, A., Ishii, T. T., & Kurokawa, H. 2001, ApJ, 555, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Aulanier, G., Pariat, E., & Démoulin, P. 2005, A&A, 444, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aulanier, G., Pariat, E., Démoulin, P., & Devore, C. R. 2006, Sol. Phys., 238, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Bommier, V., Landi Degl’Innocenti, E., Landolfi, M., & Molodij, G. 2007, A&A, 464, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Tomczyk, S., Kubo, M., et al. 2011, Sol. Phys., 273, 267 [Google Scholar]
- Bungey, T. N., Titov, V. S., & Priest, E. R. 1996, A&A, 308, 233 [NASA ADS] [Google Scholar]
- Canfield, R. C., Reardon, K. P., Leka, K. D., et al. 1996, ApJ, 464, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Qiu, J., Wang, H., & Goode, P. R. 1999, ApJ, 513, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Chifor, C., Isobe, H., Mason, H. E., et al. 2008, A&A, 491, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cirtain, J. W., Golub, L., Lundquist, L., et al. 2007, Science, 318, 1580 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Démoulin, P. 2005, in Chromospheric and Coronal Magnetic Fields, eds. D. E. Innes, A. Lagg, & S. A. Solanki, ESA SP, 596, 22 [Google Scholar]
- Démoulin, P., Hénoux, J. C., Priest, E. R., & Mandrini, C. H. 1996, A&A, 308, 643 [NASA ADS] [Google Scholar]
- Démoulin, P., Bagalá, L. G., Mandrini, C. H., Henoux, J. C., & Rovira, M. G. 1997, A&A, 325, 305 [NASA ADS] [Google Scholar]
- DeRosa, M. L., Schrijver, C. J., Barnes, G., et al. 2009, ApJ, 696, 1780 [Google Scholar]
- Effenberger, F., Thust, K., Arnold, L., Grauer, R., & Dreher, J. 2011, Phys. Plasmas, 18, 032902 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, G. A., & Démoulin, P. 1995, ApJ, 445, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, G. A., & Hagyard, M. J. 1990, Sol. Phys., 126, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Gontikakis, C., Archontis, V., & Tsinganos, K. 2009, A&A, 506, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyvaerts, J., Priest, E. R., & Rust, D. M. 1977, ApJ, 216, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Kayshap, P., Srivastava, A. K., & Murawski, K. 2013, ApJ, 763, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Leka, K. D., Barnes, G., Crouch, A. D., et al. 2009, Sol. Phys., 260, 83 [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- López Ariste, A., Rayrole, J., & Semel, M. 2000, A&AS, 142, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandrini, C. H., Démoulin, P., van Driel-Gesztelyi, L., et al. 1996, Sol. Phys., 168, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Mandrini, C. H., Démoulin, P., Schmieder, B., Deng, Y. Y., & Rudawy, P. 2002, A&A, 391, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metcalf, T. R. 1994, Sol. Phys., 155, 235 [Google Scholar]
- Metcalf, T. R., Leka, K. D., Barnes, G., et al. 2006, Sol. Phys., 237, 267 [Google Scholar]
- Metcalf, T. R., De Rosa, M. L., Schrijver, C. J., et al. 2008, Sol. Phys., 247, 269 [Google Scholar]
- Molowny-Horas, R. 1994, Ph.D. Thesis, Univ. Oslo [Google Scholar]
- Moreno-Insertis, F., Galsgaard, K., & Ugarte-Urra, I. 2008, ApJ, 673, L211 [Google Scholar]
- November, L. J., & Simon, G. W. 1988, ApJ, 333, 427 [Google Scholar]
- Pariat, E., Antiochos, S. K., & DeVore, C. R. 2009, ApJ, 691, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Pariat, E., Antiochos, S. K., & DeVore, C. R. 2010, ApJ, 714, 1762 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., Parnell, C. E., & Martin, S. F. 1994, ApJ, 427, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schmieder, B., Mein, P., Simnett, G. M., & Tandberg-Hanssen, E. 1988, A&A, 201, 327 [NASA ADS] [Google Scholar]
- Schmieder, B., Shibata, K., van Driel-Gesztelyi, L., & Freeland, S. 1995, Sol. Phys., 156, 245 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Schou, J., Borrero, J. M., Norton, A. A., et al. 2012a, Sol. Phys., 275, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012b, Sol. Phys., 275, 229 [Google Scholar]
- Shibata, K., Ishido, Y., Acton, L. W., et al. 1992a, PASJ, 44, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, K., Nozawa, S., & Matsumoto, R. 1992b, PASJ, 44, 265 [NASA ADS] [Google Scholar]
- Srivastava, A. K., & Murawski, K. 2011, A&A, 534, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titov, V. S., Priest, E. R., & Demoulin, P. 1993, A&A, 276, 564 [NASA ADS] [Google Scholar]
- Titov, V. S., Hornig, G., & Démoulin, P. 2002, J. Geophys. Res. (Space Phys.), 107, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Török, T., Aulanier, G., Schmieder, B., Reeves, K. K., & Golub, L. 2009, ApJ, 704, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Uddin, W., Schmieder, B., Chandra, R., et al. 2012, ApJ, 752, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Vargas Domínguez, S., Rouppe van der Voort, L., Bonet, J. A., et al. 2008, ApJ, 679, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., & Liu, C. 2012, ApJ, 760, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Wheatland, M. S., Sturrock, P. A., & Roumeliotis, G. 2000, ApJ, 540, 1150 [Google Scholar]
- Wiegelmann, T. 2004, Sol. Phys., 219, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., Inhester, B., & Sakurai, T. 2006, Sol. Phys., 233, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q. M., Chen, P. F., Guo, Y., Fang, C., & Ding, M. D. 2012, ApJ, 746, 19 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 a)–c) SDO/AIA EUV composite images. Each EUV image consists of three channels (red, blue, and green) in the 304 Å, 171 Å, and 211 Å channels, whose characteristic temperature corresponds to 0.05 MK, 0.6 MK, and 2 MK, respectively. The larger solid box marks the jet region where the 171 Å fluxes are integrated. The smaller solid box on the clock indicates the position and field of view of the EUV image on the solar disk. The dashed box indicates the region where the background flux for the 171 Å band is computed. d) SDO/HMI line-of-sight magnetic field. The black/white color represents the negative/positive polarity. The solid box marks the region of the footpoints of the jets, where the line-of-sight magnetic field flux is integrated. The dotted box marks the field of view for the analysis of the vector magnetic field. |
| In the text | |
 |
Fig. 2 SDO/AIA 171 Å averaged and normalized flux and SDO/HMI line-of-sight magnetic flux. a) Blue stars indicate the 171 Å flux in the jet region divided by the number of pixels in the box (larger solid box as shown in Figs. 1a–c) normalized to the background flux, which is computed in the dashed box shown in Fig. 1. Plus signs represent the averaged background flux per pixel. The temporal resolution is about 2 min. The two vertical lines mark the time range for 171 Å flux as shown in the bottom panel. b) The temporal resolution for the 171 Å flux is about 12 s. The three vertical lines mark the peak times of the 171 Å flux. Dash-dotted, dotted, and solid lines indicate positive, unsigned negative, and total unsigned line-of-sight magnetic flux, respectively. |
| In the text | |
 |
Fig. 3 a) SDO/AIA 171 Å image overlaid by the line-of-sight magnetic field observed at the same time as that of the 171 Å image. Gray/black lines mark the contour levels of the positive/negative polarities. The contour levels of Bz are –1200, –900, –600, 300, and 600 G. b) Map of photospheric transverse velocities derived from LCT analysis with the HMI magnetograms, employing a FWHM correlation window of 5′′ during the time interval 02:25–02:50 UT. Arrows represent velocities and the background is the line-of-sight magnetogram with positive (white) and negative (black) polarities. Black/white arrows are located on positive/negative polarities. North/south is up/down, west/east is towards right/left. The magnetic polarities involved in the jets are identified with annotations (p1 and p2 for parasitic positive, n1 and n2 for parasitic negative, N0 and N1 for the main following negative polarities). The circle highlights the region of interest where the diverging flows are found. A movie showing the evolution of the line-of-sight magnetic field from 02:00 to 06:00 UT is available online. |
| In the text | |
 |
Fig. 4 a) SDO/HMI vertical component of the magnetic field (Bz). The projection effect is removed. b) SDO/HMI vector magnetic field with the 180° ambiguity removed. c)–g) Distribution of the vertical electric current density jz averaged over 12 min at different times and observed by SDO/HMI. The middle time of the observations is indicated at the top of each panel. Gray/black lines mark the contour levels of the positive/negative polarities. The contour levels of Bz are –1200, –900, –600, 300, and 600 G. The color bar of jz is shown on the right side. h) Distribution of jz observed by THEMIS/MTR centered at 09:42 UT. The scan duration is about 16 min in this field of view. The contour levels of Bz are –882, –661, –440, 110, and 220 G, which are at the same percentage of their minimum (for the negative contours) and maximum (for the positive contours) values as that in Fig. 4g. |
| In the text | |
 |
Fig. 5 a) Evolutions of the 171 Å flux (normalized as in Fig. 2) and the unsigned vertical electric current Iz, which is integrated in the field of view as shown in Fig. 4. Blue stars mark the normalized 171 Å flux and red diamonds mark the unsigned vertical electric current Iz. b) The electric current evolution curves at the first and third peaks have been shifted to the second peak, and the total profile is shown with a continuous line. The shifted time differences are t2 − t1 and t3 − t2 for the two curves (denoted by dashed and dash-dotted lines), respectively. We note that the vertical axes for both the 171 Å flux and Iz do not start from zero. |
| In the text | |
 |
Fig. 6 a) Magnetic field lines computed from the NLFFF model. Different colors indicate different field line systems. The background is the vertical magnetic field Bz shown with gray levels. White/black color represents positive/negative magnetic polarity. The box marks the field of view shown in panels b)–f). b), c) Orange ribbons represent the QSL sections on the photosphere. Only the QSLs with the squashing degree Q ≥ 1014 are plotted. Gray/black contours are the same as that in Fig. 4c. d), e) Magnetic field lines overlaid on the photospheric distribution of the vertical electric current density jz as shown in Fig. 4c. The current jz is computed with the non-preprocessed vector magnetic field. f) Similar to panels d) and e), but only some sample field lines with magnetic dips are shown. |
| In the text | |
 |
Fig. 7 a) SDO/AIA 171 Å image. The box marks the region where the 171 Å fluxes are computed. b) SDO/AIA 171 Å flux normalized to the background level, which is defined as the flux in the quiet Sun region (see Sect. 2.1 for more details). The vertical dashed line marks the time of the 171 Å image in panel a). A movie showing the evolution of this figure from 03:00 to 05:00 UT is available online. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


