| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201220722 | |
| Published online | 24 June 2013 | |
The extended ROSAT-ESO flux limited X-ray galaxy cluster survey (REFLEX II) II. Construction and properties of the survey⋆,⋆⋆
1
Max − Planck − Institut für extraterrestrische Physik,
85748
Garching,
Germany
e-mail: hxb@mpe.mpg.de
2
Astrophysics Research Institute, Liverpool John Moores
University, Twelve Quays House,
Egerton Wharf, Birkenhead, CH41
1LD, UK
3
INAF − Osservatorio Astronomico di Brera-Merate, via Bianchi
46, 23807
Merate,
Italy
4
Max − Planck − Institut für Physik, Föhringer Ring 6, 80805
München,
Germany
5
Deutsches Zentrum für Luft-und Raumfahrt,
Oberpfaffenhofen, 82234
Weling,
Germany
Received: 12 November 2012
Accepted: 22 April 2013
Context. Galaxy clusters provide unique laboratories to study astrophysical processes on large scales and are important probes for cosmology. X-ray observations are currently the best means of detecting and characterizing galaxy clusters. Therefore X-ray surveys for galaxy clusters are one of the best ways to obtain a statistical census of the galaxy cluster population.
Aims. In this paper we describe the construction of the REFLEX II galaxy cluster survey based on the southern part of the ROSAT All-Sky Survey. REFLEX II extends the REFLEX I survey by a factor of about two down to a flux limit of 1.8 × 10-12 erg s cm (0.1−2.4 keV).
Methods. We describe the determination of the X-ray parameters, the process of X-ray source identification, and the construction of the survey selection function.
Results. The REFLEX II cluster sample comprises currently 915 objects. A standard selection function is derived for a lower source count limit of 20 photons in addition to the flux limit. The median redshift of the sample is z = 0.102. Internal consistency checks and the comparison to several other galaxy cluster surveys imply that REFLEX II is better than 90% complete with a contamination less than 10%.
Conclusions. With this publication we give a comprehensive statistical description of the REFLEX II survey and provide all the complementary information necessary for a proper modeling of the survey for astrophysical and cosmological applications.
Key words: galaxies: clusters: general / large-scale structure of Universe / X-rays: galaxies: clusters
Full Tables 2 and 3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/555/A30
© ESO, 2013
1. Introduction
Galaxy clusters are important astrophysical laboratories and cosmological probes (e.g. Sarazin 1986; Voit 2005; Borgani 2006; Vikhlinin et al. 2009; Allen et al. 2011; Böhringer 2011). While the latter references are based on X-ray observations of galaxy clusters, a lot of recent progress has also been made by optical cluster surveys (e.g. Rozo et al. 2010) and millimeter wave surveys using the Sunyaev-Zel’dovich effect (Reichardt et al. 2012; Benson et al. 2012; Marriage et al. 2011; Sehgal et al. 2011; Planck Collaboration 2011). However, the currently most detailed view on the structure and the properties of clusters comes from X-ray observations. An X-ray survey is also the best means of efficiently detecting galaxy clusters as gravitationally bound and well evolved objects. X-ray observations thus provide statistically well defined, approximately mass selected cluster samples, since (i) X-ray luminosity is tightly correlated to mass (e.g. Pratt et al. 2009); (ii) bright X-ray emission is only observed for evolved clusters with deep gravitational potentials; (iii) the X-ray emission is highly peaked and projection effects are minimized; and (iv) for all these reasons the survey selection function can be accurately modeled.
The X-ray emission originates in the several 10 Million degree plasma trapped in the cluster’s gravitational potential well. In hydrostatic equilibrium, which is well approximated in most clusters that are not just in a stage of collision and merging, the intracluster density is tracing the equipotential surfaces. The observed X-ray luminosity is proportional to the square of the plasma density with usually a very weak temperature dependence in the X-ray energy band used by X-ray telescopes. The X-ray image provides, therefore, very important information on the mass distribution in the cluster and on its structure, even though we can see only one projection of the volume X-ray emission of the cluster (e.g. Böhringer et al. 2010). Systematic searches for galaxy clusters in X-rays are thus the currently most established prerequisite for comprehensive astrophysical studies, as well as for cosmological model testing.
The ROSAT All-Sky Survey (RASS, Trümper 1993), is the only existing full sky survey conducted with an imaging X-ray telescope, providing a sky atlas in which one can search systematically for clusters in the nearby Universe. So far the largest, high-quality sample of X-ray selected galaxy clusters is provided by the REFLEX Cluster Survey (Böhringer et al. 2001, 2004) based on the southern extragalatic sky of RASS at declination ≤ 2.5 degree. The quality of the sample has been demonstrated by showing that it can provide reliable measures of the large-scale structure (Collins et al. 2000; Schuecker et al. 2001a; Kerscher et al. 2001), yielding cosmological parameters (Schuecker et al. 2003a,b; 2011) in good agreement within the measurement uncertainties with the subsequently published WMAP results (Komatsu et al. 2011). The REFLEX data have also been used to study the galaxy velocity dispersion − X-ray luminosity relation (Ortiz-Gil et al. 2004), the statistics of Minkowski functionals in the cluster distribution (Kerscher et al. 2001), and to select statistically well defined subsamples like the HIFLUGCS (Reiprich & Böhringer 2002) and REXCESS (Böhringer et al. 2007). The latter is particularly important as a representative sample of X-ray surveys to establish X-ray scaling relations (Croston et al. 2008; Pratt et al. 2009, 2010; Arnaud et al. 2010) and the statistics of the morphological distribution of galaxy clusters in X-rays (Böhringer et al. 2010). We also constructed a catalog of superclusters from the latest version of the REFLEX catalog comprising 164 superclusters including close pairs of clusters (Chon et al. 2013).
Other galaxy cluster surveys based on the RASS comprise XBACs (X-ray-brightest Abell-type clusters; Ebeling et al. 1996), BCS (ROSAT Brightest Cluster Sample) and eBCS survey (Ebeling et al. 1997, 1998), RBS (RASS1 Bright Sample; De Grandi et al. 1999), NORAS (Northern ROSAT ALL-SKY Survey Cluster Sample; Böhringer et al. 2000), the SGP survey (South Galactic Pole cluster survey; Cruddace et al. 2002), MACS (Most Massive Galaxy Clusters; Ebeling et al. 2000) and the CIZA survey (Clusters in the Zone of Avoidance; Ebeling et al. 2002; Kocevski et al. 2007). The RBS and SGP surveys were part of the early efforts to create the REFLEX survey.
In this paper we describe the extension of the REFLEX survey from the previous flux limit of 3 × 10-12 erg s cm in the 0.1−2.4 keV band to 1.8 × 10-12 erg s cm. The number of clusters increases from 447 to 915 with this extension. We have already used this cluster sample to assess the power spectrum of the galaxy cluster distribution (Balaguera-Antolinez et al. 2010) with the interesting finding that the bias behavior of clusters in two-point statistics is exactly what is predicted by the theoretical statistical models. While this study was conducted when about 5% of the galaxy cluster redshifts were still missing, we have now almost completed the spectroscopic follow-up observations in two observing campaigns in 2010 and 2011 (Chon & Böhringer 2012) which leaves only 7 galaxy clusters without redshift information. This small number of missing redshifts will not significantly affect the statistics of the survey described in the present paper and in some first cosmological applications. Our plan for the publication of the full cluster catalog in the near future will be based on the completion of the redshift measurements. In the following we will use the term REFLEX II for the extended cluster survey and REFLEX I for the previous cluster survey.
The paper is organized as follows. In Sect. 2 we provide an overview on the global properties of the survey. Section 3 describes the determination of the X-ray parameters of the clusters and Sect. 4 provides an overview on the source identification process, the selection of cluster candidates and the description of the follow-up observations. In Sect. 5 we describe the construction of the survey selection function and in Sect. 6 we derive various statistical properties of the REFLEX II survey. In Sect. 7 we compare our cluster detections to several other cluster surveys. Section 8 provides a discussion of the results and of the completeness and contamination of the REFLEX II cluster sample. Section 9 comprises the summary and conclusions.
For the derivation of distance dependent parameters we use a geometrically flat Λ-cosmological model with Ωm = 0.3 and h70 = H0/70 km s Mpc-1 = 1. All uncertainties without further specifications refer to 1σ confidence limits.
2. Survey properties
Regions of the sky at the LMC and SMC excised from the Survey.
Like REFLEX I, the extended survey covers the southern sky outside the band of the Milky Way (|bII| ≥ 20 deg) with regions around the Magellanic clouds excised as defined in Table 1. The total survey area after this excision amounts to 4.24 steradian (or 13 924 deg2) which corresponds to 33.75% of the sky. Different from REFLEX I, we use the refined RASS product RASS III (Voges et al. 1999) in which several small attitude errors were corrected and to which about 5−10% survey exposure was added, which had been vetoed for RASS II mostly due to attitude problems and for which a better attitude solution could be derived for RASS III. The improvement of the survey exposure from RASS II to RASS III is illustrated in Fig. 1. This improvement allows us among other things to recover also some clusters above the REFLEX I flux limit, which had too few counts to be detected in REFLEX I.
 |
Fig. 1 Comparison of the exposure time distribution of the previous RASS II survey product used for REFLEX I (thin line) and the improved survey analysis product RASS III (Voges et al. 1999) which is used for REFLEX II. The increased total exposure coverage is mostly filling some gaps in the survey. |
The cluster candidate X-ray sources were selected from a reprocessed source list of RASS III. The input source list for the reprocessing was taken from an intermediate stage source detection analysis for the production of the public RASS source catalog (W. Voges, priv. comm.) with a total of 157 492 detections for the entire sky and 105 968 detections at |bII| ≥ 20 deg. The latter source list was reanalysed with the growth curve analysis (GCA) method (further described in Sect. 3) to ensure that the flux of extended sources is well captured, since it is known that the standard analysis tuned for point sources tends to underestimate the flux of extended X-ray emission (Böhringer et al. 2000). The results of the GCA processing were used to construct an extragalactic source list of 5933 sources with nominal flux1 ≥ 1.8 × 10-12 erg s cm. For this source list double detections of the same extended source were already removed. Since with the GCA method a stable plateau of the cumulative source count rate is not always found, depending on the background properties or on source confusion, we also included a list of sources with plateau flags 4 or 5 (indicating a non-stable plateau − for more details see Böhringer et al. 2000) comprising another 1606 objects with fluxes ≥ 10-12 erg s cm. For all these sources the cause of the non-stable plateau was inspected and an appropriate correction (with a better background determination from a well chosen comparison region) was applied individually. From both source lists 4050 sources fall within the REFLEX survey region. To make sure that we are not missing any X-ray source listed in the public RASS III source catalog2, which was produced at a different survey analysis stage than the extended preliminary list used above, we also cross-correlated our intermediate source list with this public data set and found 410 further sources above the flux limit to inspect. These sources do not necessarily represent sources missed in the earlier source list, since we use a recentering algorithm in GCA and the GCA source positions do not directly correspond to the detection positions of the input catalog sources3. We find indeed a large number of double detections of very extended sources in this additional source list. With this excercise we found only 8 previously not included clusters. Since this comprises less than 1% of the total sample we do not expect any particular effect on the source detection statistics from this additional screening. Thus in total 4460 X-ray sources have been inspected in detail for the construction of the REFLEX II cluster candidate list. The further selection process of the candidates is described in Sect. 4.
3. Determination of X-ray parameters
The X-ray count rates, fluxes, and luminosities of the REFLEX clusters are determined from the count rate measurements provided by the GCA obtained in the energy band defined byROSAT PSPC channels 52 to 201 (approximately 0.5 to 2 keV) where the signal to noise is highest. While we use the 0.5 to 2 keV band for the detection, we quote all the fluxes and luminosities in the ROSAT band, 0.1 to 2.4 keV. The conversion factor between both bands is almost constant over a wide temperature range. The GCA method is explained in more detail in Böhringer et al. (2000, 2001) and we discuss only the relevant features of the technique here. The observed count rate is determined in two alternative ways. In one approach an outer radius of significant X-ray emission, rsig, is determined from the point where the increase in the 1σ error is larger than the increase of the source signal. The integrated count rate is then taken at this radius. In the second approach a horizontal level is fitted to the outer region of the growth curve (at r ≥ rsig). The value of this plateau is then adopted as the observed count rate. We use the second approach as the standard method but use also the first method as a check, and a way to estimate systematic uncertainties in the count rate. Specifically the error in the count rate is obtained from the square root of the quadratic addition of the Poisson statistical error of the count rate inside rsig and the difference of the count rate determined by the two methods. There is no statistical justification of this error calculation, but it was adopted purely as a practical measure of the combined uncertainty. The Poisson statistical error of the count rate within rsig also contains the uncertainty of the subtracted background count rate, which is a minor contribution due to the fact that the region from which the background surface brightness is estimated is much larger than the source region. For all further work we use the plateau count rates. The radius at which the plateau is reached by the cumulative count rate curve is documented as the detection aperture radius, rout.
Not in all cases we obtain a flat plateau, which can be due to contaminating sources, very large source extent, or structure in the background. These cases, which comprise up to 10% of all sources, are automatically flagged and the reason for the distortion is carefully inspected and corrections are performed individually. A conservatively estimated uncertainty is assigned to the source count rate in this process.
To determine the cluster X-ray flux we convert the measured count rate into an unabsorbed “nominal” X-ray flux for the ROSAT band (0.1 to 2.4 keV), Fn, by assuming a thermal plasma spectrum for a temperature of 5 keV, a metallicity of 0.3 of the solar value (Anders & Grevesse 1989), a redshift of zero, and an interstellar hydrogen column density given for the line-of-sight in the compilation by Dickey & Lockman (1990), as provided within EXSAS (Zimmermann et al. 1994). The value of Fn is used to make the flux cut independent of any redshift information (since the redshift is not available for all objects at the start of the survey). With the redshift value at hand, the unabsorbed X-ray flux, Fx, is re-determined with an improved spectral model, where the temperature is now estimated (iteratively) from the preliminarily derived X-ray luminosity and the luminosity-temperature relation 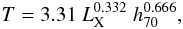 (1)where T is in keV and LX is measured in the 0.1−2.4 keV energy band inside r500 4 in units of 1044 erg s. This relation is obtained from the LX − T relation by Pratt et al. (2009). Motivated by the results of Reichert et al. (2011), we assume that the LX − T relation has no redshift dependence.
(1)where T is in keV and LX is measured in the 0.1−2.4 keV energy band inside r500 4 in units of 1044 erg s. This relation is obtained from the LX − T relation by Pratt et al. (2009). Motivated by the results of Reichert et al. (2011), we assume that the LX − T relation has no redshift dependence.
 |
Fig. 2 Comparison of the radius of the detection aperture, rout, and the fiducial cluster radius, r500, in physical units. For less massive objects the surface brightness is lower and they are detected out to smaller scaled radii, while the objects with the largest detection apertures are very luminous clusters in particular those at high redshift where the PSF smearing increases the emission region additionally. |
The estimated temperature of the cluster is now taken into account by folding the appropriate redshifted thermal spectrum with the instrument response and the interstellar absorption, leading to a revised flux, Fx of the source (this correction is less than 5% for sources with an X-ray luminosity above 4 × 1043 erg s). To obtain the cluster rest-frame luminosity from the flux, Fx we use the usual conversion with the cosmological luminosity distance and further scale the luminosity by the ratio of the luminosity integrated in the observed (redshifted) and rest frame 0.1−2.4 keV band. The latter is equivalent to the K-correction of optical astronomy.
The X-ray luminosities calculated and quoted in the following (if not specified otherwise) are for the rest frame 0.1 to 2.4 keV energy band. We aim for a determination of the X-ray luminosity inside r500. This is an improvement over the treatment in the REFLEX I publication, when precise scaling relation were not available and we used a rather ad hoc scaling law. The correction requires two considerations. We have to estimate the cluster masses from LX to get r500 and further have to take into account, that the flux measurement is performed with a limited angular resolution where the flux is spread outside the r500 aperture due to the point spread function (PSF) of the survey. The half power radius of the RASS PSF is almost 1.5 arcmin, and thus this large PSF cannot be neglected.
r500 is determined from the cluster mass (M500) which is estimated from the M500 − LX,500 relation. We use a relation that is a compromise of the results of the studies by Pratt et al. (2009), Vikhlinin et al. (2009), and Reichert et al. (2011): 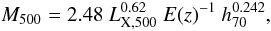 (2)and
(2)and 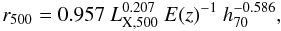 (3)where M is in units of 1014 M⊙, r500 in units of Mpc, and LX is measured in the 0.1−2.4 keV band in units of 1044 erg s.
(3)where M is in units of 1014 M⊙, r500 in units of Mpc, and LX is measured in the 0.1−2.4 keV band in units of 1044 erg s.
In Fig. 2 we compare r500 with the detection aperture radius (both in units of Mpc). For ~57% of the clusters the detection radius is smaller than r500 and we have to correct for the missing flux. The largest corrections are needed for the clusters with small r500, which are the low mass and low X-ray luminosity clusters. The low mass systems have a lower surface brightness within the self-similar model of cluster structure (e.g. Croston et al. 2008) and thus their emission is not traced as far out as for massive clusters. The largest aperture radii come from the most massive clusters at higher redshifts where also the PSF smearing has an effect and from some irregular, diffuse or double clusters. For these clusters the flux will be corrected down by a few percent.
 |
Fig. 3 Cumulative flux profiles for a point source with the average RASS PSF (dotted line), a β-model profile with a core radius of 1 arcmin (dashed line), and the same β-model profile convolved with the PSF (solid line). The profiles are normalized to unity at infinity. The observed flux fraction is read off from the solid line at rout and the expected flux fraction at r500 is marked as f500. The ratio of the two values gives the correction factor for the missing flux. |
To perform the missing flux correction we have to adopt a generic model for the surface brightness profile of the cluster. As in our previous studies and many other studies in the literature we assume that clusters can be described with good enough approximation in a self-similar fashion by a β-model (Cavaliere & Fusco-Femiano 1976) with a β-value of 2/3. The observed cluster is then assumed to have a model surface brightness profile folded with the PSF. Figure 3 compares the cumulative flux profiles of a cluster with a core radius of 1 arcmin, with and without folding with the PSF. The curves are normalized by the flux integrated to infinity. The recipe for correcting for the missing flux in this case is then straightforward. The integrated flux at r500, FX,500, is determined from the observed flux, Fobs, and the fractions, fobs, which can be read off from the PSF convolved curve at the detection aperture radius (rout) and f500 the fraction read off from the unconvolved curve at r500. We then have 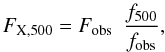 (4)and the missing flux fraction is
(4)and the missing flux fraction is 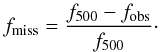 (5)To implement this correction we have to know the core radius of the cluster. An inspection of the self-similar intracluster electron density profile of the clusters in the REXCESS sample (Croston et al. 2008) shows that the logarithmic slope of the density profile has a value of one (that is at the core radius for β = 2/3) at about 0.15 to 0.2 × r500, which implies r500 ~ 5−7 × rc. The log-mean value of r500/rc determined for the clusters in the HIFLUGCS sample (Reiprich & Böhringer 2002) is about 9.5. We therefore adopted a value of r500/rc = 7 but also explore values of 5 and 10. For the further calculations we have then tabulated the values of the curves shown in Fig. 3 for the full range of relevant core radii.
(5)To implement this correction we have to know the core radius of the cluster. An inspection of the self-similar intracluster electron density profile of the clusters in the REXCESS sample (Croston et al. 2008) shows that the logarithmic slope of the density profile has a value of one (that is at the core radius for β = 2/3) at about 0.15 to 0.2 × r500, which implies r500 ~ 5−7 × rc. The log-mean value of r500/rc determined for the clusters in the HIFLUGCS sample (Reiprich & Böhringer 2002) is about 9.5. We therefore adopted a value of r500/rc = 7 but also explore values of 5 and 10. For the further calculations we have then tabulated the values of the curves shown in Fig. 3 for the full range of relevant core radii.
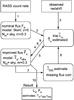 |
Fig. 4 Scheme of the iterative flux and luminosity correction taking the temperature estimate, the K-correction and the missing flux correction into account. In the first part the nominal flux, Fn, is calculated by assuming a temperature of 5 keV and a redshift of zero. In the second part, in the loop comprising steps 4, 5, 6, an improved flux and luminosity is calculated taking the estimated temperature and measured redshift into account. In the third part comprising steps 7, 8, 9 the missing flux is taken into account and once more a better temperature estimate is included in the new flux and luminosity calculation. |
Note that different conventions have been used for the missing flux correction. Ebeling et al. (1996, 1998) and De Grandi et al. (1999) for example extrapolate their flux corrections to infinity. For the assumptions used here, with r500 = 5,7,10 × rc the fraction of the flux inside r500 compared to infinity for a β-model with slope 2/3 is 80%, 84%, and 90%, respectively. The agreement between the results of, for example, Ebeling et al. (1998) and Böhringer et al. (2000) indicates, however, a bias smaller than this difference. We attribute this to the fact that our GCA method is capturing slightly more of the cluster flux than the other methods.
The two corrections, the first for the proper spectrum determined by temperature and redshift and the second for the missing flux, have to be performed iteratively, since the LX − T and LX − r500 relations are defined for the corrected values. Figure 4 shows how this iterative calculation is performed in practice. In the loop of steps 4, 5, and 6 the cluster parameters are stepwise improved taking the estimated temperature and measured redshift into account. A second loop with steps 7, 8, and 9 then includes the missing flux correction simultaneously iterating over the LX − T and LX − r500 relations. In both loops the convergence is so rapid, that two to three iterations are sufficient.
We use the REFLEX II results in the following to illustrate the relevance of the missing flux correction. We see in Fig. 2 already that our detection aperture captures most or all of the X-ray flux, FX,500, for the majority of the clusters and thus we expect the missing flux correction to be small, except for the systems with the lowest X-ray luminosities. The resulting missing flux fraction that has to be corrected for is shown in Fig. 5. We found that one of the clearest and strongest dependencies of the missing flux parameter, fmiss, is on the X-ray luminosity. More X-ray luminous and more massive galaxy clusters have brighter X-ray surface brightness profiles and will therefore be traced out to larger radii by the GCA method. This is by far the most important effect that shows up in Fig. 5. For clusters with luminosities above 1043 erg s, the mean correction is smaller than 2%. The mean becomes even slightly negative for clusters with LX > 1044 erg s. This figure also shows a fitted function of the mean of the correction in the following form: 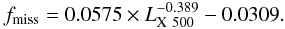 (6)The most challenging objects for the flux correction are small nearby groups with low surface brightnesses. For the smallest objects the formal corrections can be 30−60%. We should be careful, however, since we are using scaling relations mainly calibrated for galaxy clusters and the scaling and thus the corrections for these very low X-ray luminosities marking the boundary of isolated giant ellitpicals and groups is uncertain.
(6)The most challenging objects for the flux correction are small nearby groups with low surface brightnesses. For the smallest objects the formal corrections can be 30−60%. We should be careful, however, since we are using scaling relations mainly calibrated for galaxy clusters and the scaling and thus the corrections for these very low X-ray luminosities marking the boundary of isolated giant ellitpicals and groups is uncertain.
 |
Fig. 5 Estimated missing flux as a function of X-ray luminosity for the clusters in the REFLEX II sample. The horizontal bars show the mean values in 8 X-ray luminosity bins. The dashed line shows the best fitted power law function with linear offset as given in Eq. (6). |
Thus for the bulk of the REFLEX II clusters the corrections are small and the adoption of the simple β-model for the description of all cluster profiles, irrespective of their true structure, will not introduce a large error in the overall result. An inspection of the results changing the r500 − core radius relation to a ratio of 5 or 10 introduces an additional uncertainty of the order of 5%. Since this additional uncertainty is smaller than the overall flux uncertainty, we do not include this uncertainty in the quoted flux error.
Count rate to flux conversion factors for different temperatures (for Z = 0.3 solar, z = 0) as a function of column density.
K-correction table for different temperatures and redshifts.
A comparison of the cluster fluxes determined from the RASS with those of deeper observations from e.g. the XMM-Newton or Chandra observatories could in principle provide important tests for the accuracy of the flux determination method. Our literature survey in Reichert et al. (2011, Fig. C.1) shows, however, that the flux determination from XMM-Newton observations of the same cluster by different authors typically varies by factors of about 1.5, larger than our flux uncertainties. A sensible comparison of REFLEX II fluxes with deeper observations therefore requires a thorough and comprehensive new analysis of a large data set which is out of the scope of the present paper.
Another important parameter, that has to be quantified for the modeling of the cluster survey for future applications, is the error in the flux and luminosity determination. As explained above, the major source of uncertainty in the flux (for most of the sources) is the Poisson statistics of the source photons. Thus in studying the dependence of the flux error on various parameters, it comes as no surprise, that one of the clearest dependencies found is that on the number of source photons detected. Using the number of source photons for the modeling of the survey would imply the involvement of instrument specific operations to convert from physical units into detected counts. Therefore, in looking for a very similar, but more physical parameter that can be used as a substitute for the photon number, we use the product of flux and exposure and find that the correlation with the flux error is indeed similarly good. This relation is shown in Fig. 6 where also a fit to this relation is presented. The fit is indeed very close to a square root function, demonstrating that the Poisson-noise is the driving force for the error. The error function shown can be expressed as: 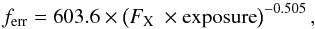 (7)where FX is given in units of 10-12 erg s cm.
(7)where FX is given in units of 10-12 erg s cm.
The overall mean uncertainty is 20.6%, significantly larger than for REFLEX I due to the lower flux limit. Most of the data that appear in Fig. 6 as points up-scattered from the statistical line include those cases where sources have been deblended and new uncertainties including the deblending uncertainty have been calculated case by case.
 |
Fig. 6 Uncertainty of the flux determination as a function of the product of flux and exposure time (a quantity close to the number of detected source photons). The horizontal bars show the mean values of the uncertainty in 8 bins of flux × exposure. The dashed line shows the best power law fit given in Eq. (7), which is close to a square root dependence on the number of photons, as expected for Poisson statistical errors. |
To allow the reader to easily reproduce our present results in connection with the REFLEX II catalog to be published we provide here all the conversion tables used in the flux and luminosity determination described above. The tables are the same as used for REFLEX I. The printed version only shows the first few lines of these tables, which are given in full size in the electronic version. Table 2 provides the count rate to unabsorbed flux conversion for different temperatures and interstellar column densities, while Table 3 shows the conversion factors as a function of temperature and redshift. The conversion table for the unabsorbed flux in the 0.1 to 2.4 keV to the flux in the 0.5−2 keV band (which is now most often used in the literature to quote fluxes and luminosities of galaxy clusters) as well as the conversion to bolometric flux can be found in the REFLEX I catalog paper (Böhringer et al. 2004)5. To distinguish the REFLEX cluster sources with their properties and sky positions as determined with the described GCA method from the X-ray sources in the RASS catalog, we designate the REFLEX clusters with the name RXCJ+coordinate, as was done for the REFLEX I catalog.
Two further important parameters delivered by the GCA method which help to characterize the X-ray sources are the spectral hardness ratio and the source extent. The hardness ratio, HR, is defined as 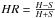 where H is the hard and S the soft band source count rate (both determined for the same outer aperture radius). The hard and soft bands are defined to comprise the ROSAT PSPC energy channels from 10 to 40 and from 52 to 201, which correspond roughly to the energy bands 0.1−0.4 keV and 0.5 to 2.0 keV, respectively. The hardness ratio expected for galaxy clusters with temperatures above 2 keV depends mostly on the interstellar hydrogen column density. Since this parameter is known we can approximately calculate the expected hardness ratio and use this parameter as one criterion in the identification.
where H is the hard and S the soft band source count rate (both determined for the same outer aperture radius). The hard and soft bands are defined to comprise the ROSAT PSPC energy channels from 10 to 40 and from 52 to 201, which correspond roughly to the energy bands 0.1−0.4 keV and 0.5 to 2.0 keV, respectively. The hardness ratio expected for galaxy clusters with temperatures above 2 keV depends mostly on the interstellar hydrogen column density. Since this parameter is known we can approximately calculate the expected hardness ratio and use this parameter as one criterion in the identification.
The source extent is another important piece of information for identification purposes, since the majority of the extended sources are expected to be clusters of galaxies. This is assessed in two ways. In the first analysis a β-model profile (Cavaliere & Fusco-Femiano 1976) convolved with the averaged survey PSF is fitted to the differential count rate profile (using a fixed value of β of 2/3) yielding a core radius, rc, and a fitted total count rate. Secondly, a Kolmogorov-Smirnov (KS) test is used to estimate the probability that the source is consistent with a point source. The source is flagged to be extended when the KS probability is less than 0.01. Tests with X-ray sources which have been identified with stars or AGN show a false classification rate as extended sources of typically less than 5%. We make mostly use of the KS test results for the source identification.
4. Source identification and selection of the cluster candidates
Further selection of cluster candidates from the flux limited list of X-ray sources was based on the experience acquired with REFLEX I. We cannot rely on the detection of an extent of the X-ray emission for this selection, since a fraction of the clusters at higher redshifts will not be resolved in the survey with its broad PSF of ~1.5 arcmin. We therefore have to consider all X-ray sources. The construction of REFLEX I was partly based on a statistical characterization of the X-ray sources through the possible coincidences with galaxy over-densities in the COSMOS Survey of the Royal Observatory Edinbourgh6. The depth of this photographic survey is not sufficient to make a unique decision, however, in particular for the most distant clusters in the sample. Therefore already for the identification of the possible cluster candidates in REFLEX I we had to rely on the combination of all other available information.
The main sources of information considered here for the selection are: the detailed X-ray properties determined from the RASS, the large number of identifications of X-ray sources obtained from NED7, and digital sky images obtained from DSS8. An important aspect of the inspection of DSS images included their combination with X-ray surface brightness overlays.
 |
Fig. 7 Hardness ratio parameter distribution of various groups of X-ray source classes: galaxy clusters, AGN, stars, and unidentified objects. The hardness ratio parameter shown is the deviation in units of sigma of the observed hardness ratio value from the expectation for a 5 keV cluster at z = 0 with given interstellar absorption in the line-of-sight. |
The way we make use of the X-ray spectral and source extent information in the selection process is explained in the following. To calculate the expected hardness ratio of a cluster, we use the same model assumptions as for the nominal flux: a temperature of 5 keV, a metallicity of 0.3 solar and redshift z = 0. The interstellar absorption used is the one for the sky position of the cluster. We compare the expected HR values to the observed ones with their estimated errors and determine the deviation of the two results in terms of the sigma errors. Figure 7 compares the hardness ratio deviations for different X-ray source types. Cluster sources pile up on the high end of the hardness ratio and the most important discrimination is that toward softer sources. A conservative value to mark an X-ray source to be too soft for a cluster is therefore taken as a value of less than −3σ. We see in Figs. 7 and 8 a few cluster sources below this threshold. They are on one hand very bright nearby clusters where the very good photon statistics causes a deviation from the simple fiducial model. There is no doubt about their identification as clusters, however. Another fraction of these sources are those which are contaminated by soft point sources which have been deblended as well as possible (we did not re-estimate the hardness ratio after deblening since this would be more uncertain than a simple flux deblending).
We can see from Fig. 7 that most of the stars are softer than clusters, while for the AGN only a fraction of the X-ray counterparts can be ruled out as too soft. Also for the sample of unidentified sources only a smaller fraction can easily be ruled out from being clusters based on their hardness ratio parameter.
For the source extent evaluation we use the KS probability parameter with a value of less than 0.01 of being a point source to characterize highly likely extended sources. Tests with samples of known point sources (e.g. AGN) show that the probability of these sources being characterized as extended is less than 5%. Several factors, like an uneven survey PSF, influence of background noise, and slight attitude shifts in those orbits that contribute to the photon counts of the source can contribute to produce an artificial extent which is not accounted for in the KS test. This explains why the fraction of false extents is larger than predicted by the KS test. Nevertheless, the fact that a cut at 1% results in a contamination of clearly less than 5% is a very reassuring result that the spatial characterization of the X-ray sources works very well.
 |
Fig. 8 Comparison of the distribution of the hardness ratio and source extent parameters of X-ray sources identified as clusters (blue dots), and tentatively classified AGN (red squares) in the upper panel and stars (red dots) as well as unidentified sources (blue squares) in the lower panel. |
Figure 8 shows the combined distribution of the hardness ratio and extent parameter for X-ray sources identified as galaxy clusters, tentatively identified with stars and AGN, and unidentified sources. A large fraction of the clusters occupy the upper right corner of extended, hard sources which is less frequented by the other sources. Thus the majority of the REFLEX II cluster sources are quite readily identified, in particular as most of these clusters show up as optical galaxy concentrations in DSS sky images. However, 31% of the cluster sources have a point source probability larger than 0.01 and are classified as pointlike in our conservative scheme. Therefore the large effort of inspecting all the sources has to be conducted to arrive at the desired high sample completeness.
Figure 9 gives an overview on the cluster candidate selection strategy. For X-ray sources already clearly identified in the literature we adopt this classification if we have no doubt about it after an inspection of the observational information. To conservatively rule out further X-ray sources from being a cluster we typically use at least two negative criteria: (i) the source is too soft and is consistent with being a point source; (ii) the source is a point source and coincident with a bright star, known galactic X-ray source, or AGN; (iii) the source is flagged as extended and coincident with a nearby galaxy, galactic HII region, or supernova remnant; (iv) the source is flagged as extended but best explained by multiple sources with a hardness ratio or other properties inconsistent with being a cluster. For a number of point sources with spectral properties not inconsistent with a cluster we are left with no classification. In case there is any weak indication of some faint galaxies at the X-ray center or for completely blank fields we have taken deeper images as part of our observation runs. Inspecting more than 40 such borderline cases that had not been flagged as promising candidates we did not find a cluster. Since most promising fields have been targeted, we are convinced that we have reached a high completeness in our cluster identification of the flux limited source list. On the positive selection side we could be more generous to include weak cluster candidates since with the follow-up spectroscopic identification, which is described below, the false clusters are revealed.
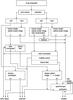 |
Fig. 9 Scheme of the galaxy cluster selection process from the list of X-ray sources. The list starts at the top with the classification of the sources by means of the X-ray parameters for source extent and hardness ratio. For the further identification this information is combined with information from NED, the literature and available sky images. |
 |
Fig. 10 Sensitivity map of RASS III in the area of the REFLEX II survey. Five levels of increasing grey scale have been used for the coding the sensitivity levels given in units of the number of photons detected at the flux limit: >60 , 30−60 , 20−30, 15−20, and <15, respectively. The coordinate system is equatorial for the epoch J2000. |
In some cases we found that the clusters were contaminated by point sources. In this case we did the best effort to deblend the point source from the cluster emission and added the estimated uncertainty of the deblending procedure to the flux error. Specifically, in addition to the visual inspection we used the procedure described in Böhringer et al. (2000) testing for irregularities in the statistics of photon counts in annuli sectors of the source to flag potential off-center contaminating sources. While this method also provides a first estimate of the possible contaminating flux, it does not provide a distinction between cluster substructure and source contamination. After a further test to decide if the contaminating source is most likely a point source or not, we decided to deblend the clearly pointlike sources while accepting the flux of non-pointlike sources as substructure. In special cases the contamination by a non-cluster source becomes evident from the difference between the hardness ratio of the contaminating source and the cluster emission. Figure 3 in Chon & Böhringer (2012) gives a nice example for such infrequent cases. In another class of X-ray sources we could either see a galaxy grouping or cluster at the X-ray position or we found information on the previous identification of a group or cluster, but it was obvious that the X-ray emission is dominated most likely by an AGN and the possible cluster emission is below the flux threshold of the survey. In these cases we identified the source as AGN in a cluster and we will provide information on such sources with the publication of the cluster catalog, as we have done in the catalog publication for REFLEX I (Böhringer et al. 2004).
In total we arrive very roughly at the following tentative classification for the non-cluster sources: 46% stars, 30% AGN, 3% galaxies and galactic sources, 21% unidentified sources. It shows that at this flux level a large number of sources can be readily identified with high probability and the number of unidentified sources is a small, but far from a negligible fraction.
The spectroscopic confirmation and redshift measurement by follow-up observations has been described in detail for REFLEX I in Guzzo et al. (2009) and more information on the REFLEX II follow-up is given in Chon & Böhringer (2012). In summary almost all the dedicated follow-up observations for REFLEX II have been carried out at the 3.6 m and NTT telescopes at La Silla between 2000 and 2011 using the EFOSC instruments. In most cases multi-slit spectroscopy was used providing spectra for typically about 7 cluster members. To increase the efficiency of the observing runs long slit observations with two or three targets per slit were performed in particular for nearby clusters where the inclusion of a clear cluster BCG helped to get a unique redshift. The typical galaxy redshift accuracy reached in the follow-up observations is 50−60 km s.
The complete identification process provided a catalog of currently 915 galaxy clusters. This sample does not include a predefined lower limit on the total source photon number.
5. Survey selection function
For the analysis and modeling of the REFLEX II cluster data we need to know the survey selection function. In a first step we calculate the nominal flux limit for each position in the REFLEX II survey area (in the same way as was done for REFLEX I in Böhringer et al. 2004). For this we use the exposure time of RASS III and the interstellar column density taken from Dikey & Lockmann (1990). Using the same count rate to flux conversion calculation as for the determination of the nominal flux above, that is assuming a temperature of 5 keV, a redshift of zero, and a metallicity of 0.3 solar, we calculate the flux corresponding to one source photon for the given RASS III exposure time. We call this the sensitivity map of the survey and show it in Fig. 10. In the figure this map is show in the form of number of detectable photons for the nominal flux limit. Large stripes of low sensitivity are due to low exposure areas, that result from times when the detectors on ROSAT were switched off during the high particle flux in the South Atlantic Anomaly region. Compared to the corresponding map for REFLEX I in Böhringer et al. (2004) several of the smaller low sensitivity regions disappeared, due to the more comprehensive attitude solution of the RASS III survey product. The sensitivity map is defined on a 1 deg2 sky pixel grid. This is good enough for our purpose, since the exposure variations are not large over these angular scales, given that the ROSAT PSPC camera has a 2 degree diameter field-of-view.
 |
Fig. 11 Effective sky coverage of the REFLEX II sample. The thick line gives the effective sky area for the nominal flux limit of 1.8 × 10-12 erg s cm and a minimum number of 20 photons per source (as used e.g. for the correction of the log N − log S-curve shown in Fig. 15. For further details see text). |
To calculate the nominal flux limit for the survey as a function of sky position, we have to impose a limit for the minimum number of counts for the acceptable detection of an X-ray source. This value may not be fixed, but different values can be used for different applications depending on the need of accuracy versus large number of objects. For example, in the modeling of REFLEX I a 30 photon limit was for used to determine the X-ray luminosity function, while for the determination of the density fluctuation power spectrum we preferred to maximize the number of data points in space and used a limit of 20 source photons. Going deeper in flux with REFLEX II, the preferred number will be a count limit of 20 source photons. The motivation for this choice will be given below.
Figure 11 shows the resulting cumulative sky area covered by the survey as a function of the nominal flux limit for three different detection count limits, 15, 20 and 30 counts. In addition to this variable count limits we have the fixed flux cut at 1.8 × 10-12 erg s cm, shown as a vertical line in the Figure, which is taken as the minimum flux limit in all cases. We note that for the three cases, 86.1%, 77.6%, and 43.8% of the sky area are covered by the minimum flux limit, respectively, and only the smaller remaining parts have a higher limiting flux.
Note that the effective sky coverage function is based on the assumption of a 100% detection efficiency above the flux limit. This is justified, since our flux limit is well above the detection limit which has a soft boundary between 1 and 5 × 10-13 erg s cm (see Voges et al. 1999, e.g. Fig. 6). Even though this detection limit mostly represents the bulk of the sources which are pointlike, our flux limit is still high enough to also provide a nearly unit detection probability for the peaked extended sources of clusters of galaxies. No flux errors have been folded into this function. The error folding is performed in our modeling at a subsequent stage.
 |
Fig. 12 Redshift distribution of the clusters in the REFLEX II (solid line) compared to the REFLEX I sample (dashed line). The most distant cluster at z = 0.537 is not represented in the plot. |
 |
Fig. 13 X-ray luminosity limit for the cluster X-ray source detection as a function of redshift. The solid line shows the median for the survey area while the dashed line shows the values for the 10% area with the lowest sensitivity. If we would plot other percentiles from 30 to 90%, they would hardly be distinguishable from the median line. |
For the determination of the X-ray luminosity function and other cosmological statistics like the power spectrum (Balaguera-Antolinez et al. 2010), we need to know the selection of the clusters according to their true luminosity. We calculate this in the form of the limiting luminosity that will be detected in the survey as a function of sky position and redshift. We call this multi-dimensional function the luminosity selection mask of the REFLEX II survey. This mask was for example used to construct mock samples from cosmological N-body simulations in the study of the REFLEX II power spectrum (Balaguera-Antolinez et al. 2010).
The selection mask is determined in the following way. For each sky pixel of 1 deg2 size we calculate from the nominal limiting flux for a given redshift the limiting luminosity (first for 5 keV and unredshifted spectrum) while iterating over the correction for the estimated temperature and redshifted spectrum. We also correct in this iterative procedure for the missing flux according to Eq. (6). The mask is tabulated for 160 redshifts out to z = 0.8 and for 13 951 sky pixels. The mask will be published together with the REFLEX II cluster catalog.
Figure 13 provides a statistical summary of the mask by showing the lower limit to the X-ray luminosity for a detection as a function of redshift for the median sensitivity of the sky and for the 10% region with the lowest sensitivity. Similar curves for other percentiles comprising the area of ≤ 70% of the best exposure in the sky are practically indistinguishable from the median line.
From the mask we can also calculate the effective survey volume of REFLEX II as a function of X-ray luminosity, which is the basic statistic on which for example the construction of the luminosity function depends. This statistic is shown in Fig. 14 for the fiducial ΛCDM cosmological model defined in the introduction. The calculations were limited to redshifts up to z = 0.8 with the results given by the solid line, and further calculations with redshift limits of z = 0.3 and z = 0.22 are also shown by dashed lines in the figure. For a luminosity of LX = 5 × 1044 erg s, which is not far from L ⋆ of the X-ray luminosity function, we reach a survey volume of ~2.5 pc3. The redshift limit of z = 0.3 approximately correspond to this limiting luminosity (as seen in Fig. 13).
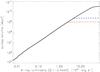 |
Fig. 14 Effective survey volume probed by REFLEX II as a function of X-ray luminosity. The solid curve shows the estimated survey volume for a redshift limit of z = 0.8, while the dashed lines are determined for a redshift limit of z = 0.3 (blue, dashed) and z = 0.22 (red, dashed-dotted), respectively. |
 |
Fig. 15 Log N − log S distribution of the REFLEX II clusters. The solid step function shows the log N − log S-function for the observed flux, FX, and the dashed function the flux corrected to an aperture of r500. The solid line shows a power law function convolved with a flux dependent flux error and fitted to the data by means of a maximum likelihood method. The underlying power law function has a slope of 1.36( ± 0.07). |
 |
Fig. 16 LX and redshift distribution of the REFLEX II clusters. The clusters identified by those listed by Abell (1958) and Abell et al. (1989) are shown with filled dots, the non-Abell clusters by open symbols. |
 |
Fig. 17 Surface density of REFLEX II clusters in the sky as a function of the interstellar hydrogen column density, nH. The dashed line shows the distribution of nH-values in the REFLEX region for comparison. The dotted line shows the mean value of 0.068 degree. Note that the regions with a flux limit smaller than the nominal flux limit have been scaled to a smaller effective area as explained in the text. The last bin contains all regions with nH > 1021 cm. |
6. Statistical properties of the cluster sample
The cluster number counts per unit sky area as a function of limiting flux, the so-called log N − log S distribution, for the REFLEX II cluster sample for 861 clusters detected with more than 20 counts is shown in Fig. 15. The source density is calculated with a sky area normalization derived from the nominal flux, Fn, and the sensitivity map shown in Fig. 10. The flux values are the corrected observed flux, FX (solid line), and the flux corrected for missing flux (dashed line). The best slope for the observed Log N − log S function is about −1.39 (see also Fig. A.1 in the Appendix).
To account for selection biases in the presence of flux errors in the determination of the log N − log S function we model the underlying function as a power law. We convolve this function with the flux error and fit the resulting function to the data by means of a maximum likelihood method (e.g. Murdoch et al. 1973). We use two models for the flux error. In the first approach we assume a constant error of 20% and in the second model we use an error that is decreasing with increasing flux according to 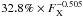 which is motivated by Eq. (7) for a mean exposure time of about 360 s. In the constant error model we determine a function slope of 1.405( ± 0.075) and in the variable error model we find a shallower slope of 1.36( ± 0.07). The uncertainty in the normalization is about 7−8%. Among the two models applied we consider the one with variable flux error as the more precise description.
which is motivated by Eq. (7) for a mean exposure time of about 360 s. In the constant error model we determine a function slope of 1.405( ± 0.075) and in the variable error model we find a shallower slope of 1.36( ± 0.07). The uncertainty in the normalization is about 7−8%. Among the two models applied we consider the one with variable flux error as the more precise description.
The cluster distribution in luminosity redshift space is shown in Fig. 16. 97 clusters have redshifts above z = 0.25. In the figure we marked clusters listed in the Abell catalogs (Abell 1958; Abell et al. 1989). In total 421 of the REFLEX II clusters are from Abell’s sample. There are only 18 Abell clusters above redshift 0.25 and 4 above z = 0.3. The median redshift of the REFLEX II is z = 0.102.
In Fig. 17 we show the cluster surface density in the sky as a function of interstellar hydrogen column density, nH. For this calculation we normalized the number of galaxy clusters in each bin by the sky area with this nH range. For all sky regions, where the local flux limit is smaller than the nominal flux limit, we apply a correction factor determined from the log N − log S function as 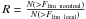 . We devide all sky regions where R is not unity by R and use this “effective” sky area for the normalization. We note in Fig. 17 that there is no variation of the detection efficiency as a function of interstellar absorption. An exception is the last bin, in which all regions with nH-values above 1021 cm are collected. Only in this bin do we observe a small deficit.
. We devide all sky regions where R is not unity by R and use this “effective” sky area for the normalization. We note in Fig. 17 that there is no variation of the detection efficiency as a function of interstellar absorption. An exception is the last bin, in which all regions with nH-values above 1021 cm are collected. Only in this bin do we observe a small deficit.
7. Comparison to other cluster surveys
In this section we compare our cluster detections to some previous cluster surveys in order to check the completeness of our catalog. We include here four major surveys, the published cluster detections of the Planck microwave satellite (Planck Collaboration 2011), which detects clusters through the hot intracluster plasma via the Sunyaev-Zel’dovich effect, the MACS survey (Ebeling et al. 2000) based on the RASS, the 400d Survey (Burenin et al. 2007), which is based on ROSAT pointed observations, and the cluster sample from the South Pole Telescope Sunyaev-Zel’dovich effect survey published by Reichardt et al. (2012). We also check the consistency with the SGP cluster sample of Cruddace et al. (2002).
While 83 of the clusters in the catalog of the early data release (Planck Collaboration 2011) coincide with clusters in the REFLEX II catalog, nine Planck clusters in the REFLEX II area have not been indentified in our cluster selection process. PLCK277.8-51.7 is below the REFLEX II flux limit, three (PLCK345.4-39.3, PLCK287.0-32.9, PLCK 262.7-40.9) fall into very low exposure regions and have no significant detections in the RASS, one with intermediate exposure, PLCK292.5-22.0, has only 11 photons. The remaining four clusters that should be included in the REFLEX II catalog, PLCK206.0-39.5, PLCK239.3-26.0, PLCK308.3-20.2, and PLCK283.2-22.9 have redshifts in the range 0.39 to 0.44 (with one redshift unknown) and were missed by the limited depth of our optical identification. Four other southern clusters, PLCK288.6-37.7, PLCK271.2-31.0, PLCK286.6-31.3, and PLCK304.8-41.4 fall into the regions of the Magellanic clouds that have been cut out from our survey.
 |
Fig. 18 Angular distance between the Planck and REFLEX II detections of 83 clusters overlapping in the two catalogs. 78% of the clusters are found with a detection offset smaller than 2 arcmin. |
We also studied the positional coincidence of the Planck and REFLEX II detections. The result is shown in Fig. 18. Of the total number of 83 overlapping clusters 78% are found within a matching radius of 2 arcmin. This is not too surprising, even though the positional uncertainty for the Planck detections is about 5 arcmin, as X-ray information was also used in the validation and compilation of the clusters detected by Planck.
Comparing our results to the published catalogs of the brightest (Ebeling et al. 2010) and the most distant MACS clusters with z > 0.5 (Ebeling et al. 2007) we find that only two clusters RXC J0159.8-0849 (z = 0.406) and RXC J0547.0-3904 (z = 0.319) have not been included into our sample prior to the publication of the MACS data, because we had no clear sign of a cluster in optical images and we had not performed follow-up observations yet. But they had been marked as unidentified objects that could possibly be clusters and are now included in the REFLEX II sample. All other 22 clusters in the REFLEX area of the bright sample, and the 2 clusters of the distant sample, RXC J0454.1-0300 and RXC J2214.9-1359 with fluxes above our survey limit have been detected in REFLEX II.
Comparing to the cluster catalog constructed from ROSAT pointed observations by Burenin et al. (2007) we find that 101 clusters fall into the REFLEX area. Only one cluster that should most probably be in REFLEX II has been missed since the X-ray flux of this X-ray source is by far dominated by a star and the X-ray emission cannot be deblended with the angular resolution of the RASS. This cluster, RXC J1501.3-0830, has not been included in the present catalog.
We have also compared the galaxy cluster X-ray sources of our catalog with the south Galactic pole (SGP) X-ray cluster sample by Cruddace et al. (2002) which resulted from a precursor project of REFLEX. We find that our catalog recovers, as expected, all the sources in the SGP sample above the flux limit. There are five clusters in the SGP catalog listed with a higher flux than the flux limit used by us: RXC J0012.9-0853, RXC J0108.5-4020, RXC J0213.9-0253, RXC J0251.7-4109, RXC J2346.7-1028. These sources have been found in our detailed analysis of the X-ray emission to contain contamination from a second, in most cases significantly softer X-ray source. These sources fall after deblending of the second source below the flux limit of REFLEX II and have been excluded from our sample. Another cluster source, RXC J2214.4-1701, has an AGN in the center of the cluster and is consistent with a point source. We have therefore also removed this object from the REFLEX II catalog.
The final comparison is with the galaxy cluster catalog from the 720 deg2 area survey by the South Pole Telescope in the millimeter regime detecting the clusters through the Sunyaev-Zel’dovich effect (Reichardt et al. 2012). Of the 224 galaxy clusters in the catalog 13 are in the REFLEX II sky and flux limit. 12 are contained in the catalog and one, RXC J2332.3-5358, is at the flux boundary and has a redshift of z = 0.4020. As the flux is just 2% above the flux limit in our recent analysis, we include the cluster in our sample. Again we find that no cluster with a redshift below z = 0.35 has been missed by our compilation.
8. Discussion
 |
Fig. 19 Number of clusters expected in bins of photon number as calculated from the best fit log N − log S power law function (blue solid line) compared to the observed galaxy clusters sorted into bins of detected number of photons. |
Performing an X-ray survey of galaxy clusters constitutes a special challenge as the source identification process is more complex than for most other surveys. First, the counterpart of an X-ray source in the optical is not a single object coinciding with the source center, but a collection of galaxies which have to be proven to be close in redshift space. Second, it has to be shown that the X-ray emission of the detected source originates from the intracluster medium of the cluster and not from another X-ray source in the line-of-sight of a cluster or an AGN in the cluster. In this case it crucially helps to detect the X-ray emission of the source as extended. This is in our case true for 69% of the REFLEX II clusters, but we cannot rely on this property for the remaining fraction of REFLEX II catalog objects. Last, for providing proper X-ray parameters and to justify the inclusion of a cluster in the flux-limited catalog we have to make sure that the X-ray emission is not substantially contaminated by another X-ray source (in particular from an AGN in the cluster). This makes the X-ray source identification, as sketched in Fig. 7 very complex. For the current catalog we can give a very high probability that most of the cluster sources have a correct cluster identification. But improving the catalog is to some degree a continuing effort. We therefore keep a detailed record on any uncertainties of the identification process and use various sources of new information (as for example deeper pointed observations) to improve the quality of the REFLEX II sample.
An important quality criterion of a survey is its completeness within the given selection parameters. There is no obvious way to test the completeness of our catalog in an independent way. But we can perform a number of internal consistency checks and we can compare to other cluster surveys that cover part of the survey parameter space of REFLEX to see which objects might have been missed.
A first obvious check is to look for any deficiency of galaxy clusters as a function of X-ray flux. The source identification becomes more difficult with decreasing flux, not only because there are in general fewer photons for the detection and the further characterization of the X-ray source, but also other means of identification like the inspection of optical images becomes notably more difficult on average at lower fluxes. Therefore we expect that these deficiencies would show up most significantly at the lowest fluxes. The good fit of a straight power law line to the log N − log S distribution shown in Fig. 15 already indicates that there is no severe deficiency.
To quantify this fact we use the fit of a power law to the number count function in Fig. A.1 to test for deviations at the low luminosity end and find a small deficit of 45 ± 29 clusters. Restricting the fit to a higher flux range of FX ≥ 3 × 10-12 erg s cm results in a slightly steeper slope of −1.44 yielding a formal deficit of 110 ± 30 clusters. This does not take into account, however, that the log N − log S distribution is not expected to be a straight power law but is expected to bend toward a shallower slope. Thus this estimate is a pessimistic upper limit. A more correct calculation can be performed when the X-ray luminosity function and its evolution has been determined.
In a second test we inspect the photon number count distribution shown in Fig. 19. To determine this distribution we use the best fit to the log N − log S function to predict the expected number of clusters for each sky pixel with given detection sensitivity with photon counts in ten bins of photon number. The bin boundaries for the ten bins are 5, 10, 20, 30, 40, 50, 60, 70, 100, 150, infinity. In Fig. 19 we compare this predictions with the actually observed photon number distribution. The two distributions agree quite well. Inspecting the low photon count region we find lower numbers for the observations than for the prediction: 95 clusters in the bin 20−30 photons for a predicted number of 110 ± 10 counts, 50 instead of 68.5 counts in the bin 10−20 photons, and 5 instead of 14.4 in the bin 5 to 10 photons. There is no deficit in the next three higher bins. Therefore the possible missing number of clusters in the lowest three bins is about 43. For the cluster selection with a minimum number of 20 photons the 1σ upper limit of the deficit is 25 clusters.
For the last test we use the NH distribution in Fig. 17 which shows no significant density variation with interstellar absorption, except for the last bin. The deficit in the last bin amounts to about 21 clusters which is a small fraction of the total sample.
The comparison with other catalogs leads to the following implications. In the comparison with the Planck detections where 4 out of 87 clusters were not found in the REFLEX II catalog, we conclude that 6.4% have been missed. These missing clusters all have high redshifts >0.3, a distance range for which we do not claim a high completeness. Comparing to MACS we find 2/24 cluster missing which yields a deficit of 8.3%. Again this concerns mostly the high redshift clusters. The comparison with the 400 degree survey yields 1/101 missing which is a fraction of ~1%.
In summary none of the tests have shown a serious deficit larger than 10%. We expect a larger fractional deficit at high redshifts (z ≥ 0.35), where it gets more difficult to identify all clusters without much more follow-up observations. Our best guess for the total number of missing clusters is thus of the order of about 50.
For the test of the possible fraction of clusters severely contaminated by AGN X-ray emission we refer the reader primarily to the inspection of the hardness ratio distribution as shown for REFLEX I (Böhringer et al. 2004) where we concluded that the contamination should not be larger than about 6%. A similar exercise with the current catalog gives contamination fractions not much larger. Therefore we conclude that the clusters where contamination by AGN may have been overlooked is not larger than 10% and our best guess for the number of clusters with contamination problems is also of the order of about 50.
9. Summary and conclusion
The REFLEX II sample with 915 galaxy clusters together with the northern NORAS II sample of RASS detected clusters constitutes the largest statistically well defined sample of X-ray luminous galaxy clusters to date and will probably remain so until the exploitation of the eROSITA All-Sky X-ray Survey (Predehl et al. 2011) becomes effective. The sample will therefore be important for astrophysical as well as cosmological studies. For these investigations the statistical properties of the survey and the survey selection process has to be well known. We have therefore made a large effort to construct a detailed three-dimensional survey selection function providing the luminosity selection limit as a function of the sky position and redshift. This provides a basis not only for the construction of simple zero order distribution functions like the X-ray luminosity function but also that of higher order functions like the N-point correlation functions, the power spectrum or e.g. Minkowski functionals.
The survey selection function is not the only ingredient for the modeling of the survey in cosmological applications. A precise characterization of the measurement errors is equally important. Here it is the uncertainty of the measured photon counts which is practically proportional to the error of the measurement of the source flux and X-ray luminosity. As an improvement over REFLEX I where we have used a mean flux error for the modeling, we have made an effort to derive a more detailed description of the flux uncertainty. Through a careful study of the dependence of the flux error on various cluster parameters, we have found that the most important parameter dependence of the flux error can be modeled as a function of flux × exposure as described in Sect. 3.
We have shown in Sect. 8 that the best estimate for the completeness of the REFLEX II catalog is of the order of 95% while we expect a contamination level of about 5%. Therefore it is not surprising that with this good quality of the catalog we can obtain a good, uncontaminated measure of the power spectrum of the spatial distribution of the clusters (Balaguera-Antolinez et al. 2010).
To estimate how many clusters are still waiting to be detected in the REFLEX area of the RASS among the more than 100 000 X-ray sources in total, we can use the same type of calculation as used for the photon number distribution shown in Fig. 17. We estimate the total number of clusters expected to have more than six counts without any flux limit. With the low X-ray background of the RASS, a detection of six photons has still a high probability to be real. The result for the total number of these clusters in the REFLEX region is about 9100. Thus we have only detected a small fraction of all clusters in the RASS so far. We have, however, reached some quality limit. Pursuing cluster detection to lower fluxes would increase the mean flux error to values higher than 20% and also the cluster identification is getting notecibly more difficult.
The RASS source catalogs can be found at http://www.xray.mpe.mpg.de/rosat/survey/rass-bsc/ and http://www.xray.mpe.mpg.de/rosat/survey/rass-fsc/
The conversion tables are also available at http://www.mpe.mpg.de/~hxb/REFLEX/
The COSMOS Survey is the results of digital scans of photographic plates taken at the UK Schmidt telescope in Australia, see http://www-wfau.roe.ac.uk/sss/
Acknowledgments
We like to thank the ROSAT team at MPE for the support with the data and advice in the reduction of the RASS and the staff at ESO La Silla for the technical support during the numerous observing runs conducted for the REFLEX project since 1992. Special thanks goes to Peter Schuecker, who was a very essential part of our team and who died unexpectedly in 2006. H.B. and G.C. acknowledge support from the DfG Transregio Program TR33, the Munich Excellence Cluster “Structure and Evolution of the Universe”, and under grant no. 50 R 1004 by the DLR.
References
- Abell, G. O. 1958, ApJS, 3, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Abell, G. O., Corwin, H. G., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 157 [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, 92 [Google Scholar]
- Balaguera-Antolinez, A., Sanchez, A., Böhringer, H., et al. 2010, MNRAS, 413, 386 [Google Scholar]
- Benson, B. A., de Haan, T., Dudley, J. P., et al. 2013, ApJ, 763, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H. 2011, AIP Conf. Proc., 1381, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2001, A&A, 369, 826 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Collins, C. A., Guzzo, L., et al. 2002, ApJ, 566, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Pratt, G. W., Arnaud, M., et al. 2010, A&A, 514, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Dolag, K., & Chon, G. 2012, A&A, 539, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borgani, S., & Guzzo, L. 2001, Nature, 409, 39 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burenin, R. A., Vikhlinin, A., Hornstrup, A., et al. 2007, ApJS, 172, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- Chon, G., & Böhringer, H. 2012, A&A, 538, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chon, G., Böhringer, H., & Nowak, N. 2013, MNRAS, 429, 3272 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, C. A., Guzzo, L., Böhringer, H., et al. 2000, MNRAS, 319, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Pratt, G. W., Böhringer, H., et al. 2008, A&A, 487, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cruddace, R., Voges, W., Böhringer, H., et al. 2002, ApJS, 140, 239 [NASA ADS] [CrossRef] [Google Scholar]
- de Grandi, S., Böhringer, H., Guzzo, L., et al. 1999, ApJ, 514, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Dikey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ebeling, H., Voges, W., Böhringer, H., et al. 1996, MNRAS, 281, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Fabian, A. C., et al. 1997, ApJ, 479, 101 [Google Scholar]
- Ebeling, H., Edge, A. C., Böhringer, H., et al. 1998, MNRAS, 301, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Allen, S. W., et al. 2000, MNRAS, 318, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., & Henry, J. P. 2001, ApJ, 553, 668 [Google Scholar]
- Ebeling, H., Mullis, C. R., & Tully, R. B. 2002, ApJ, 580, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Barrett, E., Donovan, D., et al. 2007, ApJ, 661, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Mantz, A. B., et al. 2010, MNRAS, 407, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Schuecker, P., Böhringer, H., et al. 2009, A&A, 499, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerscher, M., Mecke, K., Schuecker, P., et al. 2001, A&A, 377, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kocevski, D. D., Ebeling, H., Mullis, C. R., et al. 2007, ApJ, 662, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Marriage, T. B., Acquaviva, V., Ade, P. A. R., et al. 2011, ApJ, 737, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Murdoch, H. S., Crawford, D. F., Jauncey, D. L. 1973, ApJ, 183, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz-Gil, A., Guzzo, L., Schuecker, P., et al. 2004, MNRAS, 348, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P., Andritschke, R., Becker, W., et al. 2011, SPIE, 8145, 247 [NASA ADS] [Google Scholar]
- Reichardt, C. L., Stadler, B., Bleem, C. E., et al. 2013, ApJ, 763, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Reichert, A., Böhringer, H., Fassbender, R., et al. 2011, A&A, 535, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Wechsler, R. A., Rykoff, E. S., et al. 2010, ApJ, 708, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Schuecker, P., Böhringer, H., Guzzo, L., et al. 2001a, A&A, 368, 86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuecker, P., Böhringer, H., Reiprich, T. H., et al. 2001b, A&A, 378, 408 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuecker, P., Guzzo, L., Collins, C. A., et al. 2002, MNRAS, 335, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuecker, P., Böhringer, H., Collins, C. A. et al. 2003a, A&A, 398, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuecker, P., Caldwell, R. R., Böhringer, H., et al. 2003b, A&A, 402, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sehgal, N., Trac, H., Acquaviva, V., et al. 2011, ApJ, 732, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, R., Evrard, A. E., Böhringer, H., et al. 2006, ApJ, 648, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Trümper, J. 1993, Science, 260, 1769 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zimmermann, H. U., Becker, W., Belloni, T., et al. 1994, EXSAS User’s Guide, MPE Report No. 257 [Google Scholar]
Appendix A: Log N – Log S distribution for the nominal flux
The nominal flux defined and used for the construction of the REFLEX II cluster sample is directly related to the observed number counts and only depends on the interstellar hydrogen absorption column density, nH. It is therefore a purly observational quantity analogous to an optical magnitude corrected for extinction. Therefore the log N − log S distribution for the nominal flux is an important statistic for the characterization of the REFLEX II survey and it has been used in Sects. 5 and 8 for various calculations. Therefore we show this function in Fig. A.1.
 |
Fig. A.1 Cumulative number counts of the REFLEX II clusters as a function of limiting flux per steradian for the nominal flux, Fn. To characterize this function analytically we fitted a power-law function to the data, as shown in the figure, obtaining a value for the slope of 1.385( ± 0.075). |
All Tables
Count rate to flux conversion factors for different temperatures (for Z = 0.3 solar, z = 0) as a function of column density.
All Figures
 |
Fig. 1 Comparison of the exposure time distribution of the previous RASS II survey product used for REFLEX I (thin line) and the improved survey analysis product RASS III (Voges et al. 1999) which is used for REFLEX II. The increased total exposure coverage is mostly filling some gaps in the survey. |
| In the text | |
 |
Fig. 2 Comparison of the radius of the detection aperture, rout, and the fiducial cluster radius, r500, in physical units. For less massive objects the surface brightness is lower and they are detected out to smaller scaled radii, while the objects with the largest detection apertures are very luminous clusters in particular those at high redshift where the PSF smearing increases the emission region additionally. |
| In the text | |
 |
Fig. 3 Cumulative flux profiles for a point source with the average RASS PSF (dotted line), a β-model profile with a core radius of 1 arcmin (dashed line), and the same β-model profile convolved with the PSF (solid line). The profiles are normalized to unity at infinity. The observed flux fraction is read off from the solid line at rout and the expected flux fraction at r500 is marked as f500. The ratio of the two values gives the correction factor for the missing flux. |
| In the text | |
 |
Fig. 4 Scheme of the iterative flux and luminosity correction taking the temperature estimate, the K-correction and the missing flux correction into account. In the first part the nominal flux, Fn, is calculated by assuming a temperature of 5 keV and a redshift of zero. In the second part, in the loop comprising steps 4, 5, 6, an improved flux and luminosity is calculated taking the estimated temperature and measured redshift into account. In the third part comprising steps 7, 8, 9 the missing flux is taken into account and once more a better temperature estimate is included in the new flux and luminosity calculation. |
| In the text | |
 |
Fig. 5 Estimated missing flux as a function of X-ray luminosity for the clusters in the REFLEX II sample. The horizontal bars show the mean values in 8 X-ray luminosity bins. The dashed line shows the best fitted power law function with linear offset as given in Eq. (6). |
| In the text | |
 |
Fig. 6 Uncertainty of the flux determination as a function of the product of flux and exposure time (a quantity close to the number of detected source photons). The horizontal bars show the mean values of the uncertainty in 8 bins of flux × exposure. The dashed line shows the best power law fit given in Eq. (7), which is close to a square root dependence on the number of photons, as expected for Poisson statistical errors. |
| In the text | |
 |
Fig. 7 Hardness ratio parameter distribution of various groups of X-ray source classes: galaxy clusters, AGN, stars, and unidentified objects. The hardness ratio parameter shown is the deviation in units of sigma of the observed hardness ratio value from the expectation for a 5 keV cluster at z = 0 with given interstellar absorption in the line-of-sight. |
| In the text | |
 |
Fig. 8 Comparison of the distribution of the hardness ratio and source extent parameters of X-ray sources identified as clusters (blue dots), and tentatively classified AGN (red squares) in the upper panel and stars (red dots) as well as unidentified sources (blue squares) in the lower panel. |
| In the text | |
 |
Fig. 9 Scheme of the galaxy cluster selection process from the list of X-ray sources. The list starts at the top with the classification of the sources by means of the X-ray parameters for source extent and hardness ratio. For the further identification this information is combined with information from NED, the literature and available sky images. |
| In the text | |
 |
Fig. 10 Sensitivity map of RASS III in the area of the REFLEX II survey. Five levels of increasing grey scale have been used for the coding the sensitivity levels given in units of the number of photons detected at the flux limit: >60 , 30−60 , 20−30, 15−20, and <15, respectively. The coordinate system is equatorial for the epoch J2000. |
| In the text | |
 |
Fig. 11 Effective sky coverage of the REFLEX II sample. The thick line gives the effective sky area for the nominal flux limit of 1.8 × 10-12 erg s cm and a minimum number of 20 photons per source (as used e.g. for the correction of the log N − log S-curve shown in Fig. 15. For further details see text). |
| In the text | |
 |
Fig. 12 Redshift distribution of the clusters in the REFLEX II (solid line) compared to the REFLEX I sample (dashed line). The most distant cluster at z = 0.537 is not represented in the plot. |
| In the text | |
 |
Fig. 13 X-ray luminosity limit for the cluster X-ray source detection as a function of redshift. The solid line shows the median for the survey area while the dashed line shows the values for the 10% area with the lowest sensitivity. If we would plot other percentiles from 30 to 90%, they would hardly be distinguishable from the median line. |
| In the text | |
 |
Fig. 14 Effective survey volume probed by REFLEX II as a function of X-ray luminosity. The solid curve shows the estimated survey volume for a redshift limit of z = 0.8, while the dashed lines are determined for a redshift limit of z = 0.3 (blue, dashed) and z = 0.22 (red, dashed-dotted), respectively. |
| In the text | |
 |
Fig. 15 Log N − log S distribution of the REFLEX II clusters. The solid step function shows the log N − log S-function for the observed flux, FX, and the dashed function the flux corrected to an aperture of r500. The solid line shows a power law function convolved with a flux dependent flux error and fitted to the data by means of a maximum likelihood method. The underlying power law function has a slope of 1.36( ± 0.07). |
| In the text | |
 |
Fig. 16 LX and redshift distribution of the REFLEX II clusters. The clusters identified by those listed by Abell (1958) and Abell et al. (1989) are shown with filled dots, the non-Abell clusters by open symbols. |
| In the text | |
 |
Fig. 17 Surface density of REFLEX II clusters in the sky as a function of the interstellar hydrogen column density, nH. The dashed line shows the distribution of nH-values in the REFLEX region for comparison. The dotted line shows the mean value of 0.068 degree. Note that the regions with a flux limit smaller than the nominal flux limit have been scaled to a smaller effective area as explained in the text. The last bin contains all regions with nH > 1021 cm. |
| In the text | |
 |
Fig. 18 Angular distance between the Planck and REFLEX II detections of 83 clusters overlapping in the two catalogs. 78% of the clusters are found with a detection offset smaller than 2 arcmin. |
| In the text | |
 |
Fig. 19 Number of clusters expected in bins of photon number as calculated from the best fit log N − log S power law function (blue solid line) compared to the observed galaxy clusters sorted into bins of detected number of photons. |
| In the text | |
 |
Fig. A.1 Cumulative number counts of the REFLEX II clusters as a function of limiting flux per steradian for the nominal flux, Fn. To characterize this function analytically we fitted a power-law function to the data, as shown in the figure, obtaining a value for the slope of 1.385( ± 0.075). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


