A survey of young, nearby, and dusty stars conducted to understand the formation of wide-orbit giant planets

J. Rameau; G. Chauvin; A.-M. Lagrange; H. Klahr; M. Bonnefoy; C. Mordasini; M. Bonavita; S. Desidera; C. Dumas; J. H. Girard

doi:10.1051/0004-6361/201220984

Free Access

Issue		A&A Volume 553, May 2013


Article Number		A60
Number of page(s)		19
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/201220984
Published online		03 May 2013

A&A 553, A60 (2013)

VLT/NaCo adaptive optics thermal and angular differential imaging^⋆

J. Rameau¹, G. Chauvin¹, A.-M. Lagrange¹, H. Klahr², M. Bonnefoy², C. Mordasini², M. Bonavita³, S. Desidera⁴, C. Dumas⁵ and J. H. Girard⁵

¹ UJF – Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
e-mail: julien.rameau@obs.ujf-grenoble.fr
² Max Planck Institute für Astronomy, Königsthul 17, 69117 Heidelberg, Germany
³ Department of Astronomy and Astrophysics, University of Toronto, 50 St. George Street, Toronto, Ontario, M5S 3H4, Canada
⁴ INAF – Osservatorio Astronomico di Padova, Vicolo dell’ Osservatorio 5, 35122 Padova, Italy
⁵ European Southern Observatory, Alonso de Cordova 3107, Vitacura, Santiago, Chile

Received: 21 December 2012
Accepted: 21 February 2013

Abstract

Context. Over the past decade, direct imaging has confirmed the existence of substellar companions on wide orbits from their parent stars. To understand the formation and evolution mechanisms of these companions, their individual as well as the full population properties must be characterized.

Aims. We aim at detecting giant planet and/or brown dwarf companions around young, nearby, and dusty stars. Our goal is also to provide statistics on the population of giant planets at wide-orbits and discuss planet formation models.

Methods. We report the results of a deep survey of 59 stars, members of young stellar associations. The observations were conducted with the ground-based adaptive optics system VLT/NaCo at L′-band (3.8 μm). We used angular differential imaging to reach the best detection performances down to the planetary mass regime. A statistical analysis of about 60% of the young and southern A-F stars closer than 65 pc allowed us to derive the fraction of giant planets on wide orbits. We used gravitational instability models and planet population synthesis models following the core-accretion scenario to discuss the occurrence of these companions.

Results. We resolve and characterize new visual binaries and do not detect any new substellar companion. The survey’s median detection performance reaches contrasts of 10 mag at 0.5″ and 11.5 mag at 1.0″. We find the occurrence of planets to be between 10.8 and 24.8% at 68% confidence level assuming a uniform distribution of planets in the interval [1,13] M_J and [1,1000] AU. Considering the predictions of planetary formation models, we set important constraints on the occurrence of massive planets and brown dwarf companions that would have formed by gravitational instability. We show that this mechanism favors the formation of rather massive clumps (M_clump > 30 M_J) at wide (a > 40 AU) orbits, which may evolve dynamically and/or fragment. For the population of close-in giant planets that would have formed by core accretion (without considering any planet – planet scattering), our survey marginally explores physical separations (≤20 AU) and cannot constrain this population. We will have to wait for the next generation of planet finders to start exploring that population, and even for the extremely large telescopes for a more complete overlap with other planet-hunting techniques.

Key words: instrumentation: adaptive optics / stars: early-type / methods: statistical / planetary systems

^⋆

Based on observations collected at the European Organization for Astronomical Research in the Southern Hemisphere, Chile, ESO: runs 084.C-0396A, 085.C-0675A, 085.C-0277B, 087.C-0292A, 087.C-0450B, 088.C-0085A, 089.C-0149A.

© ESO, 2013

1. Introduction

Most of the giant planets have been discovered so far through to indirect techniques (radial velocity (RV) and transit) at short orbits (≤5 AU). Almost 20 years of systematic search led to numerous surveys around solar-type, lower/higher mass (Endl et al. 2006; Bonfils et al. 2013; Lagrange et al. 2009a), or even evolved stars (Johnson 2007; Lovis & Mayor 2007). The sample of detected and characterized planets thus becomes large enough to perform a reliable statistical analysis of the population and test planetary formation theories. In that sense, the planet occurrence frequency has been determined for giant and telluric planets. Mayor et al. (2011) found that 50% of solar-type stars harbor at least one planet of any mass and with a period of up to 100 days. This occurrence decreases to 14% when giant planets larger than 0.3 M_J are considered and varies if we consider giant planets around lower/higher mass stars (Cumming et al. 2008; Johnson et al. 2010; and Mayor et al. 2011) (see Table 1). These rates thus confirm that planet formation is not rare.

Table 1

Frequency of giant planets reported by various surveys around the full spectral type range.

Observational evidence of close-in planets favors formation by the core-accretion mechanism (CA, e.g. Pollack et al. 1996). Sousa et al. (2011) showed that the presence of close-in giant planets is correlated with the metallicity of their host stars. If the planets orbit within 3 AU, then this correlation is also related to their host-star mass (Lovis & Mayor 2007; Johnson et al. 2010; Bowler et al. 2010). Another correlation has been found between the content in heavy elements of the planets and the metallicity of their parent star (e.g. Guillot et al. 2006; Miller & Fortney 2011). These are hints that CA is operating in short orbits. According to this scenario, the first steps of the growth of giant gaseous planets are identical to those of rocky planets. The dust settling toward the mid plane of the protoplanetary disk leads to the formation of increasingly larger aggregates through coagulation up to meter-sized planetesimals. These cores grow through collisions with other bodies until they reach a critical mass of 10 M_⊕ (Mizuno 1980). When their gravitational potentials are high enough, they trigger runaway gas accretion and become giant planets. However, this scenario requires a high surface density of solids on the disk to provide enough material to form the planet core and a large amount of gas. Large gaseous planets are not expected to form in situ below the ice line. Lin et al. (1996); Alibert et al. (2004); Mordasini et al. (2009) refined the model with inward migration to explain the large amount of giant planets that orbit very close to their parent stars.

At wider (≥30 AU) orbits, the situation is very different since this core accretion mechanism has difficulties to form giant planets (Boley et al. 2009; Dodson-Robinson et al. 2009). The timescales for forming massive cores become longer than the gas dispersal timescales and the disk surface density is too low. Additional outward migration mechanisms must be invoked (corotation torque in radiative disks, Kley & Nelson 2012; or planet-planet scattering, Crida et al. 2009). Alternatively, cloud fragmentation can form objects down to planetary mass regime (Whitworth et al. 2007) and is a good alternative to explain the existence of very wide orbit substellar companions. Finally, disk fragmentation, also called gravitational instability (GI, Cameron 1978; Stamatellos & Whitworth 2009) remains an attractive mechanism for the formation of massive giant planets beyond 10 to 20 AU. According to this scenario, a protoplanetary disk becomes unstable if it is cool enough which leads to the excitation of global instability modes, i.e., spiral arms. Due to their self-gravity, these arms can break up into clumps of gas and dust, which are the precursors for giant planets.

Understanding how efficient these different mechanisms are as a function of the stellar mass, the semi-major axis, and the disk properties are the key points to fully understand the formation of giant planets. Understanding how giant planets form and interact with their environment is crucial because they will ultimately shape the planetary system’s architecture and drive the telluric planet’s formation and the possible existence of conditions favorable to life.

Fig. 1

Graphical summaries of the main properties of the target stars. Top row: left: histogram of distances with 10 pc bin. Right: histogram of ages of known members of considered moving groups (AB Dor – 70 Myr, β Pictoris – 12 Myr, Tuc/Hor & Col – 30 Myr, Her/Lyr – 200 Myr, Argus – 40 Myr, and Upper Cen/Lup – 5/10 Myr) and additional stars with 10 Myr bin. Central row: left: histogram of K-band magnitude with 0.5 mag bin. Right: histogram of apparent proper motions with 25 mas/yr bin. Bottom row: histogram of spectral types.

Open with DEXTER

Massive dusty disks around young stars, such as HR 8799 and β Pictoris, may be a good indicator recently formed exoplanetary systems (Rhee et al. 2007). Observations at several wavelengths revealed asymmetry structures, sometimes ring-like, or even warps, which could arise from gravitational perturbations imposed by one or more giant planets (e.g. Mouillet et al. 1997; Augereau et al. 2001; Kalas et al. 2005). Thanks to the improvement of direct imaging (DI) technique with ground-based adaptive optics systems (AO) or space telescopes, a few planetary mass objects and low-mass brown dwarfs have been detected since the first detection by Chauvin et al. (2004). Moreover, these were breakthrough discoveries of giant planets between 8 and 68 AU around young, nearby, and dusty early-type stars (Kalas et al. 2008; Lagrange et al. 2009b; Marois et al. 2008, 2010; Carson et al. 2013). Direct imaging is the only viable technique to probe for planets at large separations, but detecting planets need to overcome the difficulties caused by to the angular proximity and the high contrast involved.

Nevertheless, numerous large DI surveys to detect giant planet companions have reported null-detections (Masciadri et al. 2005; Biller et al. 2007; Lafrenière et al. 2007; Ehrenreich et al. 2010; Chauvin et al. 2010; Janson et al. 2011; Delorme et al. 2012), but this allowed set upper limits to the occurrence of giant planets. Table 1 reports the statistical results of several DI surveys as a function of the sample, separation and mass ranges, and planet distribution. All surveysbefore that of Vigan et al. (2012) derived upper limits to the occurrence of giant planets, usually more massive than 1−3 M_J, between a few to hundreds of AU. These surveys found that less than 10−20% of any star harbor at least one giant planet if the distribution is flat or similar to the RV one, taking into account all assumptions beyond these results. Janson et al. (2011, 2012) also included in the planet distribution limitations giant planets formed via GI. They showed that the occurrence of planets might be higher for high-mass stars than for solar-type stars, but GI is still a rare formation channel. On the other hand, Vigan et al. (2012) took into account two planetary system detections among a volume-limited set of 42 A-type stars to derive lower limits for the first time. Apparently, the frequency of Jovian and massive giant planets is higher than 5.9% around A-F stars. However, all these surveys suggest a decreasing distribution of planets with increasing separations, which counterbalances the RV trend.

In this paper we report the results of a deep direct imaging survey of 59 young, nearby, and dusty stars aimed at detecting giant planets on wide orbits, conducted between 2009 and 2012. The selection of the target sample and the observations are detailed in Sect. 2. In Sect. 3, we describe the data reduction and analysis to derive the relative astrometry and photometry of companion candidates, and the detection limits in terms of contrast. Section 4 is dedicated to the main results of the survey, including the discovery of new visual binaries, the characterization of known substellar companions, and the detection performances. Finally, we present in Sect. 5 the statistical analysis over two special samples: A-F type stars and A-F dusty stars, from which we constrain the planet frequency based on different formation mechanisms or planet population hypotheses.

2. Target sample and observations

2.1. Target selection

The target stars were selected to optimize our chance of planet detection according to:

Distance: with a given angular resolution limited by the telescope’s diffraction limit, the star’s proximity enables one to access closer physical separations and fainter giant planets when background-limited. We therefore limited the volume of our sample to stars closer than 150 pc, even closer than 100 pc for 94% of them (see Fig. 1, top left panel).
Observability and magnitude: stars were selected 1) according to their declination (δ ≤ 25 deg) so that they were observable from the southern hemisphere; 2) their K-band brightness (K ≲ 7 mag) to ensure optimal AO corrections; 3) if they were single to avoid degradation of the AO performances and 4) if they were never observed in deep imaging (see Sect. 2).
Age: evolutionary models (Baraffe et al. 2003; Marley et al. 2007) predict that giant planets are intrinsically more luminous at young ages and become fainter with time. Therefore, for a given detection threshold, observing younger stars is sensitive to lower mass planets. Our sample selection is based on recent publications on associations (AB Dor, β Pic, Her/Lyr, Argus, Tuc/Hor, Columba, and Upper Cen/Lupus) from Zuckerman et al. (2011), Torres et al. (2008) and Rhee et al. (2007). Indeed, stars belonging to these moving groups share common kinematic properties and ages. These parameters are measured from spectroscopy, astrometry, and photometry (optical and X-rays). Sixty-four percent of the selected stars belong to young and nearby moving groups. Eighty-eight percent of the targets are younger than 200 Myr and 62% are even younger than 70 Myr (see Fig. 1, top right panel).
Spectral type: recently imaged giant planets have been detected around the intermediate-mass HR 8799, Fomalhaut, and β Pictoris stars with separations from 8 to 110 AU. More massive stars imply more massive disks, which potentially allows the formation of more massive planets. We therefore biased 79% of our sample toward spectral types A and F (see Fig. 1, bottom panel).
Dust: dusty debris disks around pre- and main-sequence stars might be signposts for the existence of planetesimals and exoplanets (see a review in Krivov 2010). Seventy-six percent of our sample are stars with high infrared excess at 24 and/or 70 μm (IRAS, ISO, and Spitzer/MIPS), which is indicative of cold dust emission. The remaining stars have no excess reported in the literature.

The name, coordinates, galactic latitude (b), proper motions (μ), spectral type (SpT), distance (d), K magnitude, and age of the target stars are listed in Table 2 together with the reference for the age determination and the moving group they belong to, if they do¹. Figure 1 summarizes the main properties of the target stars. Briefly, the sample consists of 59 B- to M-type stars whose the median star would be an F-type at distance of 40 pc with an age of 30 Myr, a K-magnitude of 5.5, and an apparent proper motion of 85 mas/yr.

Table 2

Sample of young, nearby, and dusty stars observed during our VLT/NaCo thermal and angular differential imaging survey.

Table 3

Additional young, nearby and southern A-F stars for the statistical analysis.

To analyze an homogeneous and volume-limited sample, we performed the statistical study on stars that have 1) d ≤ 65 pc; 2) age ≤ 100 Myr; 3) Dec ≤ 25 deg; and 4) spectral type = A or F. We assembled set of 68 young, nearby, and southern A-F stars from the literature. Thirty-three stars in our survey fulfill these criteria (flagged with a ⋆ symbol in Table 2), i.e., 48% limit of completeness. To increase this rate, we added four stars observed with VLT/NaCo from a previous survey (Vigan et al. 2012)² (see Table 3), which led to reach a representative rate of 56%. We refer to this star sample as the A-F sample.

Moreover, we also aim at constraining the formation mechanism and rate of giant planets around β Pictoris analogs. A subset of stars was extracted from the A-F homogeneous sample by considering an IR excess at 24 and/or 70 μm (from the same references as for our survey plus Mizusawa et al. 2012; Rebull et al. 2008; Hillenbrand et al. 2008; and Su et al. 2006). Among the full set of 68 stars, 39 are dusty. Our survey plus one star from Vigan et al. (2012), i.e., 28 stars, reaches a completeness level of 72%. We refer to this sample as the A-F dusty sample. Table 4 summarizes all different samples.

2.2. Observing strategy

The survey was conducted between 2009 and 2012 with the NAOS adaptive optics instrument (Rousset et al. 2003) combined with the CONICA near-infrared camera (Lenzen et al. 2003). NaCo is mounted at a Nasmyth focus of one of the 8.2 m ESO Very Large Telescopes. It provides diffraction-limited images on a 1024 × 1024 pixel Aladdin 3 InSb array. Data were acquired using the L27 camera, which provides a spatial sampling of ≃27.1 mas/pixel and a field of view (FoV) of 28″ × 28″. To maximize our chance of detection, we used thermal-infrared imaging with the broadband L′ filter (λ_c = 3.8 μm, Δλ = 0.62 μm) which is best-suited to detect young and warm massive planets with a peak of emission around 3−4 μm.

NaCo was used in pupil-tracking mode to reduce instrumental speckles that limit the detection performances at inner angles, typically between 0.1″ and 2.0″. This mode provides a FoV rotation to use angular differential imaging (ADI, Marois et al. 2006). The pupil stabilization is a key element for the second-generation instruments GPI and VLT/SPHERE. NaCo suffered from a drift of the star with time (few pixels/hours depending on the elevation) associated to the pupil-tracking mode until October 2011 (Girard et al. 2012). Higher performance was obtained after the drift was corrected. To optimize the image selection and data post-processing, we recorded short individual exposures coupled to the windowing mode of 512 × 514 pixels (reduced FoV of ≈14″ × 14″). The use of the dithering pattern combined with the cube mode also ensured accurate sky- and instrumental- background removal. The detector integration time (DIT) was set to 0.2 s to limit the background contribution to the science images.

Each observing sequence lasted around 90 min, including telescope pointing and overheads. It started with a sequence of short unsaturated exposures at five dither positions with the neutral density filter ND_long (transmission of 1.17%). This allowed estimating of the stellar point spread function (PSF) and served as photometric calibrator. Then, saturated science images were acquired with a four-dithering pattern every two DIT × NDIT exposures with NDIT = 100 stored into a datacube was repeated over more than 100 times to provide sufficient FoV rotation for a given star. The PSF core was saturating the detector across a ≃5 pixel-wide area. Twilight flat-fields were also acquired. For some target stars, second epoch data on NaCo were acquired with the same observing strategy. Finally, the θ₁ Ori C field was observed as astrometric calibrator for each observing run. The same set of stars originally observed with HST by McCaughrean & Stauffer (1994) (TYC058, 057, 054, 034 an 026) was imaged with the same set-up (L′ with the L27 camera). The mean platescale and true north orientation were measured and are reported in Table 5.

2.3. Observing conditions

Observations in periods 84 and 85 were performed in visitor mode because the pupil stabilization mode was not offered in service mode. Observations in periods 87, 88, and 89 were then completed in service mode to benefit from the best atmospheric conditions. A summary of the observing conditions is reported in Fig. 2 showing histograms of explored parallactic angle ranges, airmass, and the atmospheric conditions: seeing and coherence time τ₀. NAOS corrects the atmospheric turbulences for bright stars when τ₀ remains longer than 2 ms (63% of the observations). When τ₀ decreases, the image quality and precision for astrometric and photometric measurements are degraded. The observations were conducted under good conditions, however since the median seeing is 0.9″, the median τ₀ is 3.2 ms and the median airmass was 1.15. Finally, 72% of the stars were observed with a parallactic angle exploration larger than 20 deg.

3. Data reduction and analysis

3.1. Unsaturated images

The unsaturated dithered exposures of each star were processed with the Eclipse software developed by Devillar (1997): bad-pixel removal, sky-subtraction constructed as the median of the images followed by flat-fielding were applied to the data; the final PSF image was then obtained by shifting and median-combining the images.

3.2. Saturated angular differential images

The ADI saturated dithered datacubes were reduced with the dedicated pipeline developed at the Institut de Planétologie et d’Astrophysique de Grenoble (IPAG). This pipeline has been intensively used and gave probing results: Lagrange et al. (2010, 2012), Bonnefoy et al. (2011), Chauvin et al. (2012), Delorme et al. (2012), and Rameau et al. (2012). We describe the main steps in the following.

Table 4

Sample definitions.

Table 5

Mean platescale and true north orientation measured on the θ₁ Ori C field with the NaCo and L′/L27 set-up.

Fig. 2

Graphical summaries of the observation log of the target young, nearby dusty stars observed with VLT/NaCo between 2009 and 2012. Top left: histogram of median seeing (image quality seen by the active optics sensor) with 0.2″ bin. The DIMM seeing has been overplotted with dashed columns. Top right: histogram of median τ₀ with 0.5 ms bin as calculated by NAOS. Bottom left: histogram of median airmass with 0.1 bin. Bottom right: histogram of explored parallactic angles with 10 deg bin.

Open with DEXTER

We obtained twilight flats which allowed us to achieve the best flat-fielding and bad-pixel identification. We used the Eclipse software to extract these calibrations frames. The raw data were then divided by the flat-field and removed for the bad and hot pixels through interpolating the closest neighbor pixels. Sky estimation was performed by taking the median of the 400 s closest-in-time dithered exposures within a cube and then subtracted to each frame. Low quality frames were removed from the cubes following a selection based on cube statistics such as the flux maximum, the total flux, and the encircled energy in each frame in an annulus outside the saturated pixels. Poor-quality frames due to degraded atmospheric conditions were rejected (typically less than 10% of the complete observing sequence, see Girard et al. 2010 for the cube advantages). The good-quality frames were recentered to a common central position using the Eclipse software for the shift and Moffat-profile fitting (Moffat 1969) on the PSF wings to register the central star position. We obtained good-quality cleaned and recentered images within a single master cube associated with their parallactic angle values. A visual inspection was made to check the quality of the final frames.

Subsequent steps were the estimation and subtraction of the stellar halo for each image, followed by derotation and stacking of the residuals. The most critical step is estimating the stellar halo that drives the level of the residuals. We applied different ADI algorithms to optimize the detection performances and to identify associated biases. Since the quasi-static speckles limit the performances on the inner part of the FoV, we performed the ADI reduction onto reduced frames, typically 200 × 200 pixels. We recall here the difference between the four ADI procedures:

in classic ADI (cADI, Marois et al. 2006), the stellar halo is estimated as the median of all individual reduced images and then subtracted to each frame. The residuals are then median-combined after the derotation;
in smart ADI (sADI, Lagrange et al. 2010), the PSF-reference for one image is estimated as the median of the n closest-in-time frames for which the FoV has rotated more than α × FWHM at a given separation. Each PSF-reference is then subtracted from each frame and the residuals are mean-stacked after the derotation; we chose a PSF-depth of n = 10 frames for the PSF-building, which satisfies a separation criterion of α = 1FWHM at a radius of 1.3″;
the radial ADI (rADI, Marois et al. 2006) procedure is an extension of the sADI where the n frames with a given rotation used for the stellar halo building are selected according to each separation. The PSF-depth and the α coefficient were chosen as for sADI (n = 10 and α = 1FWHM). The radial extent of the PSF-building zone is Δr = 1.4 FWHM below 1.6″ and 3 FWHM beyond;
in the LOCI approach (Lafrenière et al. 2007), the PSF-reference is estimated for each frame and each location within this frame. Linear combinations of all data are computed to minimize the residuals into an optimization zone, which is much bigger than the subtraction zone to avoid the self-removal of point-like sources. We considered here a radial extent of the subtraction zone Δr = 0.9 FWHM below 1.6″ and 3 beyond; a radial-to-azimuthal width ratio was set to g = 1; a standard surface of the optimization zone was N_A = 300 PSF cores; the separation criterion of N_δ = 1 FWHM.

All target stars were processed in a homogeneous way using similar sets of parameters. It appears that when the PSF remained very stable during a sequence (i.e. τ₀ ≥ 4 ms), advanced ADI techniques do not strongly enhance the performance.

ADI algorithms are not the best-performing tools for background-limited regions because the PSF-subtraction process adds noise. We therefore processed the data within the full window (i.e. 512 × 514 pixels with the dithering pattern) with what we called the non-ADI (nADI) procedure. It consists of 1) computing an azimuthal average of each frame within a one-pixel-wide annulus; 2) circularizing the estimated radial profile; 3) subtracting the given profile to each frame; and 4) derotating and mean-stacking the residuals. nADI by-products can help to distinguish some ADI artifacts from real features as well.

We inspected the five residual maps for each star to look for candidate companions (CC).

3.3. Relative photometry and astrometry

Depending on the separation and the flux of the detected CC, different techniques were used to retrieve the relative photometry and astrometry with their uncertainties:

for bright visual binaries, we used the deconvolution algorithm of Veran & Rigaut (1998);
for CCs detected in background-limited regions (in nADI final images), the relative photometry and astrometry were obtained using a 2D Moffat fitting and classical aperture photometry (Chauvin et al. 2010). The main limitation of this technique remains the background subtraction which affects the residual level;
for speckle-limit objects, fake planets were injected following the approach of Bonnefoy et al. (2011) and Chauvin et al. (2012) with the scaled PSF-reference at the separation of the CC but at different position angles. The injections were made into the cleaned mastercubes, which were processed with the same setup. We then measured the position and the flux of the fake planets, which minimized the difference with the real CC. The related uncertainties associated with this method were also estimated using the various sets of fake planets injected at different position angles.

In both algorithms, the main error for the relative astrometry is the actual center position of the saturated PSF (up to 0.5 pixel). Other sources of errors come from the Moffat fitting, the self-subtraction, the residual noise, or the PSF shape. More details are provided in the dedicated analysis on CC astrometry uncertainties using VLT/NaCo ADI data (Chauvin et al. 2012). We investigated the status (background source or comoving object) of a CC observed at several epochs (follow-up or archive) by determining its probability to be a stationary background object, assuming no orbital motion. This approach is the same as in Chauvin et al. (2005) and compares the relative positions in α and δ of the parent-star between the two epochs from the expected evolution of the positions of a background object, given the proper and parallactic motions and associated error bars.

3.4. Detection limits

The detection performances reached by our survey were estimated by computing 2D detection limit maps for each target star at 5σ in terms of L′ contrast with respect to the primary. For each set of residual maps for each target, we computed the pixel-to-pixel noise within a sliding box of 1.5 × 1.5 FWHM. The second step was to estimate the flux loss due to self-subtraction by the ADI processing. We created free-noise-cubes with bright fake planets (100 ADU) at three positions, 0, 120, and 240 deg, each 20 pixels from the star, with the same FoV rotation as real datacubes for each star and then processed the ADI algorithms with the same parameters. For LOCI, we injected the fake planets in the cleaned and recentered datacubes before applying the reduction. Then we compared the injected flux with that retrieved from the final fake-planet images with aperture photometry. This allowed us to derive the actual attenuation for all separations from the central star by interpolating between the points. Finally, the 5σ detection limits were derived by taking the flux loss and the transmission of the neutral-density filter into account, which were normalized by the unsaturated PSF flux. 2D contrast maps were therefore available for each star with each reduction technique.

To compare the detection performances between the stars, we built 1D contrast curves. We azimuthally averaged the noise map within one-pixel annuli of increasing radius, followed by flux-loss correction and unsaturated PSF flux scaling. This approach tends to degrade the performances at close-in separations due to asymmetric speckle and spider residuals on NaCo data, or even the presence of bright binary component. To retrieve the detection performances within the entire FoV, we created composite maps of ADI-processed and nADI-processed ones. Indeed, beyond 2″ from the central star, where the limitations are due to photon and read-out noises, nADI remains the best adapted reduction technique. It has been shown that the limiting long-lived (from few minutes to hours) quasi-static speckles are well correlated for long-time exposures (Marois et al. 2006), which lead to a non-Gaussian speckle noise in the residual image. Therefore, the definition and the estimation of σ to provide a detection threshold in the region limited by the quasi-static speckle noise might not be appropriate and overestimated. However, we achieved the Gaussian noise distribution in the background noise regime, the 5σ detection threshold corresponds to the expected confidence level. Moreover, the conversion from contrast to mass detection limits is much more affected by the uncertainties on the age of the target stars and the use of evolutionary models than by uncertainties on the detection threshold.

4. Results

Our survey aims at detecting close-in young and warm giant planets, even those that interact with circumstellar disks in the case of stars with IR excess. Four stars in the sample have been identified as hosting substellar companions in previous surveys. The redetection of these companions allowed us to validate our observing strategy and data reduction and might give additional data points for orbital monitoring. We also imaged a transitional disk at an unprecedented resolution at 3.8 μm for the first time around HD 142527 (HIP 78092), which was presented in a dedicated paper (Rameau et al. 2012). However, we did not detect any new substellar companions in this study.

In this section, we describe the properties of the newly resolved visual binaries, we review the observed and characterized properties of known substellar companions and of the candidates identified as background sources. We then report the detection performances of this survey in terms of planetary masses explored. Finally, we briefly summarize the results on some previously resolved disks, especially of HD 142527, in the context of a deep search for giant planets in its close environment.

4.1. Binaries

Despite the rejection of known binaries with 1. − 2.″ separation, eight visual multiple systems were resolved (Fig. 3). Their relative position and magnitude are reported in Table 6. Four pairs are very close-in, with separations below 0.4″, whereas the remaining ones lie in the range 4 − 7″. Only HIP 38160 has been observed at a second epoch and was confirmed as a comoving pair. HIP 88399 B and HIP 117452 B and C were known from the literature, and HIP 59315 B might indeed be bound to its host-star according to archive data.

	Fig. 3 Resolved visual binaries with the VLT/NaCo in ADI-L′ imaging mode. HIP 9685, HIP 53524, and HIP 93580 have not been confirmed as double systems from second-epoch observations or archived data. North is up, east to the left. Counts are displayed in linear scale but differently for each panel.
Open with DEXTER

HIP 9685 – HIP 9685 is referenced to a Δ μ astrometric binary (Makarov & Kaplan 2005) and was associated to a ROSAT source by Haakonsen & Rutledge (2009). In this work, we report the detection of a close-in binary candidate companion at a projected separation of 14 AU if we adopt a distance of 47.7 pc. In the 2MASS images in JHK taken in october 1999, a point source is visible toward the northeast direction, at a separation of around 12″ and a position angle of ≃15 deg. From the two relative positions, it is apparent that the 12″-CC in the 2MASS images is not compatible with a background star at the position of our 0.3″-CC. It is also very unlikely that the 2MASS 12″-CC has traveled in projection from 540 AU to 14 AU in ten years. Instead, the astrometric acceleration suggests that our NaCo 0.3″-CC is bound and is responsible for the astrometric signature. Because the 2MASS PSF is symmetric, our 0.3″-CC may have been at a much smaller separation in 1999 since the orbital motion is significant, which does not contradict the proposed status. If this is true, we derive a mass of 0.8 M_⊙for our 0.3″-CC from the measured M_L′ = 4.1 mag using the isochrones from Siess et al. (2000), assuming a solar metallicity, and an age of 30 Myr. This is in the regime of a K6 star.

Table 6

Relative astrometry and photometry of the new visual binaries resolved with the VLT/NaCo L′ and ADI imaging mode.

HIP 38160 – A companion with a magnitude of L′ = 7.84 is detected at two different epochs (November 2009 and December 2010) 4.8 AU away (0.141″) from HIP 38160 at 35 pc. The companion shows a common proper motion with the central star between the two epochs. The 2MASS JHK images taken in 2000 also reveal an asymetric PSF, which additionally confirms the bound status of this companion. According to the Siess et al. (2000) isochrones for pre- and main-sequence stars, this companion probably has 0.6 − 0.7 M_⊙, assuming an age of 200 Myr and solar-metallicity. Hence, HIP 38160 B could be a late-K or ealy-M star. HIP 38160 was already cataloged as an astrometric binary (Makarov & Kaplan 2005) and as a double-star system in the Catalog of Component of Double or Multiple stars (CCDM, Dommanget & Nys 2002). However, with a separation of 23.3 arcsec, this additional candidate turns to be only a visual companion (WDS, Mason et al. 2001).

HIP 53524 – This star lies at a very low Galactic latitude (b ≤ 10 deg). It is therefore very likely that the candidate companion, located at a large separation from the central-star (≥4″), is a background star. Indeed, from HST/NICMOS archive data taken in 2007, we measured the relative position of the clearly seen CC. Even excluding the systematics between the two instruments, the CC appears to be a background object.

HIP 59315 – The star HIP 59315 is not cataloged as being part of a multiple physical system. However, it lies at relative low Galactic latitude (b = 13 deg), but only one point source has been detected with VLT/NaCo in ADI and L′ imaging in 2010. Chauvin et al. (2010) observed this star with VLT/NaCo in H band in coronographic mode and have identified an additional background source more than 5.5 ″ away with a PA around 100 deg. If our 0.36″-CC is a background contaminant, it would lie in April 2004 at a separation of 1.35 ″ and a position angle of 254 deg so that it would have been detected on NaCo H images. The other possibility is that our 0.36″-CC is indeed bound to HIP 59315 and was occulted by the mask. Therefore, it is likely that it is indeed bound to the star. This would imply a projected separation of 14 AU and an absolute magnitude M_L′ = 8.2 at 37.8 pc for the companion. The mass derived from the COND model (Baraffe et al. 2003) assuming an age of 100 Myr is 0.1 M_⊙, consistent with a late-M dwarf.

HIP 88399 – This star is referenced as a double star in SIMBAD with an M2 star companion (HIP 88399 B) at 6.35″ from the 2MASS survey. Given the separation in our observation and the L′ magnitude, the CC is indeed the M-dwarf companion, lying at 310 AU from the primary.

HIP 93580 – The star is a 70 Myr old A4V star at 55.19 pc and b = −68.6 deg. A point source 3.9 mag fainter than the primary is detected at a projected separation of 13.24 AU. Neither archive nor second-epoch observations could infer the status of this CC. Comparison to the Siess et al. (2000) isochrones at 70 Myr with a solar metallicity would place this object as an early M-type dwarf, with a mass of 0.5 M_⊙.

HIP 117452 – Already known as a triple system (De Rosa et al. 2011) from observations made in 2009, the two companions are detected from our data in july, 2012. The brightest companion lies at ≈160 AU in projection from the primary while the third component is at a separation of 11 AU from HIP 117452 B. The large error bars on the astrometry in De Rosa et al. (2011) make it difficult to infer any orbital motion of the two companions in two years.

We also have two spectroscopic binaries (HIP 101800 and HIP 25486) in our survey. Pourbaix et al. (2004) give a period of about 11 d, an eccentricity of 0.23, and a velocity amplitude of the primary of K₁ = 26 km s^-1 for HIP 101800. For HIP 25486, Holmberg et al. (2007) reported a standard deviation for the RV signal of 4.4 km s^-1, an SB2 nature with an estimated mass ratio of 0.715. However, we did not detect any source with a contrast from 5 mag at 100 mas up to 12 mag farther out than 1.5″ around both stars. The two companions are probably too close to their primary to be resolved, or may even lie behind them.

Table 7

Relative astrometry and photometry of the known substellar companions observed with the VLT/NaCo L′ and ADI imaging mode.

4.2. Substellar companions

Four targets in the sample – HR 7329, AB Pictoris, β Pictoris, and HR 8799 – have been previously reported to host a brown dwarf and/or planet companions (Lowrance et al. 2000; Chauvin et al. 2005; Lagrange et al. 2010; and Marois et al. 2008, 2010). Only one identified substellar CC to HIP 79881 has also been stated as background object. We review below the latest results about these companions since their initial confirmation. Table 7 lists their relative astrometry and photometry from our observations (see Fig. 4).

	Fig. 4 Known substellar companions of HR 7329, AB Pic (top left and right), and β Pictoris and HR 8799 (bottom left and right) observed with the VLT/NaCo in ADI-L′ modes. North is up, east to the left, the count scale is linear. We were not able to retrieve HR 8799 e with a good signal-to-noise ratio due to the low parallactic angle amplitude (20.9 deg).
Open with DEXTER

HIP 79881 – Clearly seen in July 2010 observations in L′, the 11.6 mag-contrast CC to HIP 79881 (separation of 4.528 ± 0.008″ and a position angle of 175.54 ± 0.8 deg) has also been resolved in Keck/NIRC2 images in 2003 and 2005. The relative positions of the CC monitored for 7 years clearly showed that it is a background object.

HIP 95261 / HR 7329 – HR 7329 b was discovered by Lowrance et al. (2000) with the Hubble Space Telescope/NICMOS. It is separated from its host star, a member of the β Pic. moving group, which harbors a debris disk (Smith et al. 2009) of 4.17 ± 0.09″ (≃200 AU at 48 pc) at a position angle of 167.4 ± 0.7 deg. The age and the known distance of the star together with HST/STIS spectra and photometry from H to L′ bands are consistent to infer that HR 7329 B is a young M7-8 brown dwarf with a mass between 20 and 50 M_J. Neuhäuser et al. (2011) conducted a 11 yr follow-up study to confirm the status of the companion and to try to constrain the orbital properties. Owing to the very weak orbital motion, they concluded that HR 7329 B lies near the apastron of a very inclined – but not edge-one – and eccentric orbit. Our observations are consistent with these results and exclude additional companions down to 4 M_J beyond 40 AU.

HIP 30034 / AB Pic – This member of the Columba association hosts a companion at the planet-to-brown-dwarf boundary of 13 ± 2 M_J, discovered by Chauvin et al. (2005). Located at 5.4 ± 0.07″ and 175.2 ± 0.7 deg, AB Pic b has a mass of 13−14 M_J deduced from evolutionary models and JHK photometries. Subsequently, Bonnefoy et al. (2010) and recently Bonnefoy et al. (2013) conducted observations with the integral field spectrograph VLT/SINFONI to extract medium-resolution (R_λ = 1500−2000) spectra across a range of 1.1−2.5 μm. They derived a spectral type of L0-L1, an effective temperature of ≃1700 − 1800 K, and a surface gravity of log (g) ≃ 4.5 dex from a comparison with synthetic spectra. The relative astrometry and photometry we measured from our observations are similar to these results. More investigations are mandatory to derive similar conclusions as for HR 7329. Due to our highest spatial resolution and sensitivity, surely planets more massive than 3 M_J with a semi-major axis greater than 80 AU can be excluded.

HIP 27321/β Pictoris – β Pic b (Lagrange et al. 2010) remains up to now the most promising case of an imaged planet probably formed by core accretion. Recent results by Chauvin et al. (2012), including measurements from this survey, refined the orbital parameters with a semi-major axis of 8 − 9 AU and an eccentricity lower than e ≤ 0.17. In addition, Lagrange et al. (2012a) could accurately show that the planet is located in the second-warped component of the debris disk surrounding the star, which confirms previous studies (Mouillet et al. 1997; Augereau et al. 2001) that suggested that the planet plays a key role in the morphology of the disk. More recently, Lagrange et al. (2012b) directly constrained the mass of the planet through eight years of high-precision RV data, offering thus a rare perspective for the calibration of mass-luminosity relation of young massive giant planets. Finally, Bonnefoy et al. (2013) built for the first time the infrared spectral energy distribution of the planet. They derived temperature (1600 − 1800 K), log g(3.5−4.5), and luminosity (log (L/L_⊙) = −3.87 ± 0.08) for β Pic b from the set of new and previously published photometric measurements. They also derives its mass (6−15.5 M_J) by combining predictions from the latest evolutionary models (“warm-start”, “hot-start”) and dynamical constraints.

HIP 114189 / HR 8799 – HR 8799 is a well-known λ Boo, γ Dor star, surrounded by a debris disk (Patience et al. 2011) and belonging to the 30 Myr-old Columba association (Zuckerman et al. 2011). It hosts four planetary-mass companions between 14 and 68 AU (Marois et al. 2008, 2010), which makes this multiple-planet system the first imaged so far. Spectra and photometry studies (e.g. Bowler et al. 2010; Janson et al. 2010) inferred that the planets lie between 5 and 7 M_J. Soummer et al. (2011) monitored the motion of the planets b, c, and d thanks to the HST/NICMOS archive data giving a ten yr amplitude to constrain the orbits of these planets. Invoking mean-motion resonances and other assumptions for the outer planets, these authors derived the inclination of the system to be ~28 deg. Esposito et al. (2012) also considered the planet e for the dynamical analysis of the system. They showed that the coplanar and circular system cannot be dynamically stable with the adopted planet masses, but can be consistent when they are about 2 M_J lighter. In our images, HR 8799 b, c, and d are clearly detected. The measured contrasts between the host star and each planet are very similar to the previously reported ones. No new orbital motion for planets b, c, and d is found from our observations compared to the latest reported astrometric measurements at the end of 2010. Finally, the e component could not be retrieved with a high signal-to-noise ratio due to the short amplitude of parallactic angle excursion (20.9 deg).

Fig. 5

Survey detection limits in L′-band contrast between the central star and any point source vs. the angular separation at the 5σ level using the VLT/NaCo in ADI mode. Solid lines are representative of median performances, whereas the bottom dashed lines are for the best performance reached by our survey. cADI (red) and LOCI (blue) are very similar, whereas sADI (orange) and rADI (aqua) remain slightly above the LOCI and cADI curves. The LOCI curves stop at 0.15 ″ because of the central exclusion area.

Open with DEXTER

Fig. 6

Mean detection probability map of our survey as a function of the mass and semi-major axis (left) and probability curves for different mass bin as function of the semi-major axis (right). The mean is obtained over all targets of the survey. The detectability of the simulated planets was compared with the detection maps from LOCI and nADI algorithms and using the COND03 (Baraffe et al. 2003) evolutionary models.

Open with DEXTER

4.3. Detection performances

Typical contrasts reached by our survey using ADI algorithms and nADI algorithms are presented in Fig. 5. For cADI/sADI/rADI or LOCI, the performances are very similar, except within the exclusion area of LOCI. The median azimuthally averaged L′ contrast vs. the angular separation is plotted together with the best curves. The typical range of detection performances at all separations beyond 0.5″ is about 2 mag with a median contrast of 10 mag at 0.5″, 11.5 mag at 1″, and slightly below 12 mag at 2″. Our best performances even reach very deep contrast, up to 13.5″ at 0.5″ around HIP 118121.

The detection limits (2D-maps and 1D-curves) were converted into absolute L′ magnitudes using the target properties and to predicted masses using the COND03 (Baraffe et al. 2003) evolutionary models for the NaCo passbands.

The overall sensitivity of our survey can be estimated using Monte-Carlo simulations. We used an optimized version of the MESS code (Bonavita et al. 2012) to generate large populations of planets with random physical and orbital parameters and checked their detectability by comparing with the deep-detection limits of our survey. We performed simulations with a uniform grid of mass and semi-major axis in the interval [1,20] M_J and [1,1000] AU with a sampling of 0.5 M_J and 2 AU. For each point in the grid, 10⁴ orbits were generated. These orbits are randomly oriented in space from uniform distributions in sin(i), ω, Ω, e ≤ 0.8, and T_p³. The on-sky projected position (separation and position angle) at the time of the observation was then computed for each orbit. Using 2D information, one can take into account projection effects and constrain the semi-major instead of the projected separation of the companion. We ran these simulations for each target to compute a completeness map with no a priori information on the companion population and therefore considering a uniform distribution in mass and semi-major axis. In this case, the mean detection probability map of the survey is derived by averaging the 59 individual maps. The result is illustrated in Fig. 6 with contour lines as a function of sma and masses. The decreasing detection probability for very large semi-major axis reflects the fact that such a companion could be observed within the FoV only for a fraction of their orbits given favorable parameters. The sensitivity peak of our survey occurs at semi-major axes between 40 and 300 AU, with the highest sensitivity around 100 AU. Our survey’s completness peaks at 94%, 80%, and 58% for 10 M_J and 5 M_J at 100 AU, and 3 M_J at 220 AU, respectively. The overall survey sensitivity at 1 M_J is very low, with a maximum of 15% at 141 AU.

4.4. Giant planets around resolved disks

Among the targets of our sample, HD 142527 is the youngest. It has been identified by Acke & van den Ancker (2004) as member of the very young (≃5 Myr) Upper Centaurus-Lupus association. HD 142527 was selected to take advantage of the capability offered by VLT/NaCo in thermal and angular differential imaging to resolve its circumstellar environment for the first time at the sub-arcsecond level. Indeed, Fukagawa et al. (2006) detected a complex transitional disk in the NIR with a huge gap of up to 100 AU. Our observations reported by Rameau et al. (2012) confirm some of the previously described structures but reveal important asymmetries such as several spiral arms and a non-circular large disk cavity down to at least 30 AU. The achieved detection performances enable us to exclude the presence of brown dwarfs and massive giant planets beyond 50 AU. In addition, two sources were detected in the FoV of NaCo. The relative astrometry of each CC was compared to that extracted from archived observations and to the track of the relative position of stationary background object. Both were identified as background sources. Finally, the candidate substellar companion of 0.2 M_⊙ at 13 AU recently reported by Biller et al. (2012) may be responsible for the structured features within the disk. These structures might also be created by type-II migration or by planetary formation through GI. More investigations of the environment of HD 142527 might be able set constraints on planetary formation and disk evolution.

In our sample, we also have included some stars surrounded by debris disks that have been resolved in previous observations (49 Cet, HD 10647, HD 15115, Zeta Lep, 30 Mon, HD 181296, HD 181327, HD 181869, HD 191089, and AU Mic). Because the observation and reduction processes having been designed to search for point sources, we do not report results about disk properties. However, we investigated the presence of giant planets and plot in the Fig. 7 the detection limits for these stars in terms of mass vs. projected separation. These limits could help to constrain some disk properties that can be created by gravitational perturbation of giant planets. The detection sensitivity around AU Mic reaches the sub-Jovian mass regime at very few AU from the star because AU Mic is a very nearby M dwarf. On the other hand, the detection limits around HD 181869 are poor because of bad quality data. We recall that these limits are azimuthally averaged therefore they might be affected by the presence of the disk.

Fig. 7

Detection limits of giant planets with Jupiter mass vs. the projected distance from the central star for stars with known debris disks. The detections are expressed at the 5σ level, using VLT/NaCo in ADI mode, after LOCI (close-in region) and nADI (background-limited region) processing. The COND03 (Baraffe et al. 2003) mass–luminosity relationship is used to convert from L′ contrast to Jupiter mass. For AU Mic, the model does not reach below 0.5 M_J, therefore we cut the curve when it reached this limit.

Open with DEXTER

5. Giant planet properties, occurrence, and formation mechanisms

The frequency of giant planets f can be derived using known planets and detection limits in case of a null-detection. For an arbitrary giant planet population, one can compute within the mass and semi-major axis ranges probed by the survey. Numerous deep-imaging surveys did not report the detection of at least one substellar or planetary mass companion. The authors (e.g. Kasper et al. 2007; Lafrenière et al. 2007; Nielsen & Close 2010; and Chauvin et al. 2010) nevertheless performed statistical analyses with MC simulations to fully exploit the potential of their data and provided upper limits to the frequency of planets. Vigan et al. (2012) took into account the planets already identified (β Pic, HR 8799) to derive also lower limits to this frequency.

In this section, we derive the rate of wide-orbit giant planets following the statistical approach used in previous works (Carson et al. 2006; Lafrenière et al. 2007; and Vigan et al. 2012) that is described in the appendix. Similarly to Bonavita et al. (2012), we take into account the binary status of some stars to exclude semi-major axis values for orbits that would be unstable. The whole section relies on the two previously defined subsamples: 37 A-F stars and 29 A-F dusty stars (Table 4). First, the frequency of wide-orbit planets is derived assuming a uniform distribution. We then use and discuss the extrapolation of RV statistics to wide-orbits in the light of DI planets. Planet formation is finally considered, GI and CA, to estimate the impact on the observed occurrence of giant planets.

Fig. 8

A-F sample probability density of the fraction f of stars hosting at least one giant planet at wide orbit, taking into account the detections ({ d_j }) of the two planetary systems β Pictoris and HR 8799 and a linear-flat prior. The interval considered is [1,1000] AU and [1,13] M_J. The confidence interval at 68% confident level, labeled CL, (blue) and at 95% CL (dark blue) are overplotted on the distribution. A uniform planet population has been generated with random orbital parameters.

Open with DEXTER

5.1. Occurrence of giant planets from a uniform distribution

Assuming a uniform distribution of planets on a grid [1,1000] AU and [1,13] M_J, we used MC simulations to measure the detection probability p_j around each star given the detection sensitivity, as in Sect. 4.3. The probability density function was then derived using Eqs. (A.1) and (A.2), assuming a flat prior. Finally, the confidence interval of the true f was computed using Eq. (A.4).

First, we focus on the relevant A-F statistical sample (see Table 1). In this sample, two stars harbor at least one giant planet, β Pictoris and HR 8799. Since these two stars match our selection criteria, they were originally included in our sample, even if the giant planets were discovered by other observations. We thus take, in our analysis, at least two planetary detections (since our observations confirmed their status). Figure 8 shows the posterior distribution as a function of f in the interval [1,1000] AU and [1,13] M_J. The observed rate of giant giant planets at wide orbit leads f to be 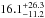% with a confidence level (CL) of 95%. At 68% CL, this rate becomes 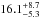%. If one considers the sample of 29 A-F dusty stars, i.e., with the same planet detections, the giant planet occurrence is 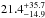% at 95% CL or 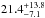% at 68% CL. Due to our poor sensitivity to close-in and/or low mass planets, these values are relatively high. If we restrain the interval of interest to [5,320] AU and [3,14] M_J as in Vigan et al. (2012), the A-F sample has an occurrence of giant planets of 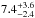% at 68% CL, which matches the results obtained by the authors.

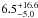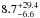With the same approach we derived the frequency of brown dwarfs. Taking into account the detection of HR 7329 b in the A-F sample, f is % and % in the A-F dusty sample in the interval [1,1000] AU and [14,75] M_J at 95% CL. The confidence interval is smaller compared to the statistical results for giant planets due to our high sensitivity to brown dwarfs.

Finally, the full survey of 59 young, nearby, and B- to M-type stars can also give some constraints on the occurrence of planets within a broad sample of stars. Since the companions to AB Pic, HR 7329, HR 8799, and β Pictoris were previously detected out of our observations, we considered here a null-detection within 55 stars of our survey. Using Eq. (A.6), an upper limit to the frequency of giant planets can be derived with our detection limits and MC simulations. This yields that fewer than 25% among our 55 stars harbor a giant planet in the range [40,600] AU and [5,13] M_J at 95% CL. This upper limit sharply increases toward smaller mass planets and also for a wider semi-major range due to our poor sensitivity. We also recall that this sample is statistically less relevant than the previous ones since it is more heterogenous in terms of stellar mass, distance, and spectral type.

5.2. Giant planet population derived from extrapolated radial velocity results

Radial velocity results provided many statistical results on the giant planet properties but also on the distribution of the population with respect to the mass and/or semi-major axis. However, such results are intrinsically limited so far to close-in planets (typically 3 − 5 AU). Numerous publications presented statistical analyses on giant planets detected by deep imaging using an extrapolation of the RV frequencies and distributions to planets on larger orbits (Lafrenière et al. 2007; Kasper et al. 2007; Nielsen & Close 2010; and Vigan et al. 2012). We briefly present in the following sections the results of our sample based on the same approach, considering the detections around β Pic and HR 8799.

5.2.1. Extrapolation of the radial velocity planets distribution

We assumed that the mass and semi-major axis distributions follow the simple parametric laws of index α and β: d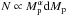 with α = −1.31 and dN ∝ a^βda with β = −0.61⁴ (Cumming et al. 2008). Here, we blindly extrapolated the distribution to larger semi-major axes while it is formally valid only for planets with semi-major axes below ≃3 AU.

For this calculation, we populated a grid of mass and semi-major axis in the intervals [1,13] and [1,1000] (M_J and AU) to the Cumming et al. (2008) power-laws and ran MC simulations to derive the probability density distribution as in Sect. 5. If the giant planet population on wide orbits follows the RV power-laws, their frequency range according to our study is 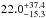% at 95% CL or 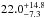% at 68% CL in the A-F sample. This rate becomes 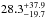% at 95% CL or 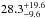% at 68% CL in the A-F dusty sample.

However, there are intrinsic limitations on this study and the results, even though close-in values such as those reported from an uniform distribution, have to be taken with care. This distribution fits the statistic for solar-type stars up to a few AU (derived from RV surveys) and was arbitrarily extrapolated to large separations. There is no evidence either that the few planets detected so far at large orbit separations have similar properties and distributions.

Fig. 9

Contours showing the confidence level at which we can reject a planet distribution following a mass power law dN ∝ M^αdM and a semi-major axis law dN ∝ a^βda at a given semi-major axis cutoff. Top: semi-major axis cutoff vs. semi-major axis power law index β for α = −1.5. Bottom: semi-major axis cutoff vs. semi-major axis power law index β for α = 1.1, i.e., with more massive planets. The upper cutoff for the Cumming et al. (2008)β index of − 0.61 is overplotted (dotted line). These figures use the LOCI and nADI detection limits and COND03 (Baraffe et al. 2003) for the mass–luminosity relationship.

Open with DEXTER

5.2.2. Constraining the parametric laws for the giant planet distribution

This likelihood approach answers the question about the consistency of a given giant planet population with our observing results. Answering this question requires one first, to know all giant planet population parameters, and second, to know the fraction of stars with giant planets according to this given distribution. For each star, we can then derive the number of expected detections given the detection sensitivity and compare this with our observations. Such a comparison allows us to constrain a given distribution of wide-orbit giant planets. Likewise, a giant planet population in which 95% of the predicted planets would have led to detections can be considered as strongly inconsistent with our survey. Finally, this study is based on the strong assumption that we know the frequency of giant planets in the range our survey is sensitive to.

In the following, we use a population of planets given by power laws similar to those from Cumming et al. (2008) and also add an additional parameter, a_cutoff, the semi-major axis beyond which there are no planets. Our intervals of interest for the simulation are [1,1000] AU and [1,13] M_J, normalized with f = 10.5% over the range [0.3,10] M_J, [2,2000] days in period from Cumming et al. (2008). f_norm is thus set with the ratio of the integrated power laws for a pair (α, β) over [1,13] M_J and [1,1000] AU and the same over the RV ranges.

We explored a grid of α, β, and a_cutoff with a sampling of 0.2 for the power law indices and 20 AU for the cutoff to derive the expected number of planets for each combination of parameters over the A-F sample (similar results are obtained with the A-F dusty sample). We illustrate the confidence level at which we can reject each model in Fig. 9 as a function of β and a_cutoff for the A-F sample for two values of α: − 1.5 and 1.1, values corresponding to the extrema of our grid and thus showing the trend of the rejections. All results (ours and previous publications) are consistent with a decreasing number of giant planets (β ≤ − 0.61) while their mass increases. Considering the Cumming et al. (2008) distributions, a semi-major axis cutoff around 45−65 AU at 95% CL is found.

We recall that mixing power-laws derived from RV and giant planets with possibly different formation processes and evolutions have to be considered with caution.

Fig. 10

Left: mean detection probability map of the A-F sample as function of the mass and semi-major axis of the substellar companion. A uniform grid distribution has been used to generate the population, but the formation limits derived from the gravitational instability models excludes for each star the planets that do not fulfill both criteria. The detection maps from LOCI and nADI algorithms were used with COND03 (Baraffe et al. 2003) evolutionary models to convert from contrast to mass. Contour lines are regular from 0.5 to 0.9 plus one at 0.1. Right: corresponding estimate of the upper limit, with a confidence level of 95%, on the fraction of stars from the A-F sample that harbor at least one object companion in the same semi-major axis range. The curves for 25 M_J, 18 M_J, 13 M_J, and 10 M_J have been plotted since lower mass planets are not allowed to form via the disk instability mechanism.

Open with DEXTER

5.3. Giant planet formation by gravitational instability

Gravitational instability is a competitive scenario to form giant planets, especially at large separations. This process becomes more efficient within massive disks, i.e., around massive stars. Since our statistical sample contains A-F and/or dusty stars, i.e., massive stars, we were strongly tempted to test the predictions of GI models with our observing results. We hence adopted the same approach as Janson et al. (2011). We refer to Gammie (2001) for a detailed description. The 1D current model of disk instability provides formation criteria, which, if fulfilled, create an allowed formation space in the mass–sma diagram. The first one is the well-known Toomre parameter (Toomre 1981), which has to be low enough to allow local gravitational instability in a Keplerian accretion disk:

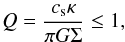where Q is the Toomre parameter, c_s the sound speed, κ the epicyclic frequency and Σ the gas surface density. The Toomre parameter is fulfilled at larger radii only when the local mass is high enough. Therefore, fulfilling the Toomre criterion leads to a given value Σ that can be converted in mass and thus states a lower limit in the mass–sma diagram:

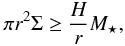where H = c_s/Ω is the disk scale height. The other parameter that drives the instability is the cooling time, τ_c which, if higher than a few local Keplerian timescales Ω^-1, i.e., at small separation, stabilizes the disk through turbulent dissipation (Gammie 2001; Rafikov & Goldreich 2005). It thus provides an upper boundary in the mass-sma diagram:

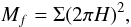where 2πH is the wavelength of the most unstable mode. Such boundaries, which are global and exclude long-term evolution, assume planets formed in-situ with masses of the disk fragments.

Fig. 11

Disk instability model predictions for β Pictoris. The lower solid curve corresponds to the Toomre criterion which excludes the formation of planets below it. The upper dashed curve corresponds to the cooling criteria which only allows disk fragmentation below it. The allowed formation space is in between. The 1D average detection limit curve has been overplotted (blue solid line) but with a projected separation. The location of β Pictoris b has been overplotted on the graph with the new error bars from Bonnefoy et al. (2013).

Open with DEXTER

The model computes both boundary curves for each star in the sample, taking into account the stellar mass, luminosity, and metallicity, the later being extracted from Ammons et al. (2006) or set to the solar one when the information was not available, and luminosities derived from the isochrones of Siess et al. (2000) using their absolute K magnitude, spectral-type age, and metallicity. The model is very sensitive to the stellar luminosity since strong illumination favors the disk to be gravitationally stable (Kenyon & Hartmann 1987). Figure 11 shows one example for β Pictoris. The Toomre and cooling criteria are fulfilled around 40 AU for very massive planets (≥3 M_J), and this trend rapidly increases with the separation, thus leading to the brown dwarf and stellar regimes. Considering a lower mass star would led to push the boundaries inward.

We then ran MC simulations in a uniform grid of mass and semi-major axes in the interval [1,100] and [1,1000] (M_J AU) as in Sect. 5. Points of the grid beyond the allowed range for each star were removed according to the formation limits. We recall that these predictions are not normalized because we lack of the physical and statistical properties of protoplanetary disks in which GI starts. The mean detection probability over the A-F sample is plotted in Fig. 10, left panel. Only high-mass planets and brown dwarfs fulfill the formation criteria, and almost all are detectable.

β Pictoris b and HR 8799 b, c, and d are too light and too close to their stars, so they do not fulfill both GI boundary conditions (M ≤ 10 M_J below 70 AU). Therefore, we cannot use these detections to derive the rate of giant planets according to the GI mechanism. We instead estimated the upper limit on f, f_max using Eq. (A.6). We derived and plot f_max (Fig. 10, right panel) for the A-F sample only for the mass regime allowed by this approach, which span over very few tens of AU. The curves are offset from one another because higher mass object can be formed in-situ at a larger distance from the central star. It came out that less than 20% (≤23% for the A-F dusty sample) stars harbor at least a 13 M_J planet between 40 and 60 AU and less than 25% (≤27%) a 10 M_J in the range [32,45] AU.

On the other hand, first Fig. 10, left panel, shows our high sensitivity to brown dwarfs on wide orbits, and second, HR 7329, belonging to the A-F dusty sample and to the A-F one, hosts a detected brown dwarf companion for which the formation is allowed according to our GI model. We can therefore estimate the rate of formed objects as in Sect. 5. Since GI can form planetary-to-brown-dwarf mass objects, we explored the full range [1,75] and [1,1000] (M_J and AU). We found that f equals 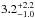% for the A-F sample and 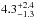% for the A-F dusty one at 68% CL if formed by this mechanism.

These GI boundaries prevent the formation of low-mass and close-in giant planets but would increase the presence of brown dwarf and low-mass star companions. Since high-mass stars would facilitate the GI mechanism by harboring massive disks, one would expect to find a higher occurrence of low-mass stars or substellar companions rather than planets and a continuous distribution of the wide-orbit giant planets detected so far and higher mass objects (Kratter et al. 2010).

This approach is a first step toward understanding planet formation by GI, and the analysis can be improved by taking into account the following steps. First, Meru & Bate (2011) showed that using proper 3D global radiative transfer codes and hydrodynamical simulations, the closer-in disk region might become unstable, a phenomenon that was prevented by assuming a general simple cooling time law. Kratter & Murray-Clay (2011) refined the definition of Q and the cooling time, which made GI possible at smaller separations. Second, the probability of clump formation toward planets was assumed to be one, but long-lived clumps require careful consideration of their disk dynamics (Durisen et al. 2007). Then, clump evolution (e.g. Galvagni et al. 2012) and fragmentation might lead to the formation of lower mass planets. HR 8799 seems a good test-case for this hypothesis. Indeed, the three outer planets orbit the star too far away to have formed via core accretion. Gravitational instability naturally is the alternative scenario. However, each planet, with its mass and separation, does not fulfill the Toomre and cooling time criteria of our models. Considering all three together, even four mass planets (≃30 M_J) onto a single disk fragment at a mean separation satisfy our boundaries. One might speculate that this clump would have broken after the collapse leading to an individual evolution of the planets. Finally, long-term clump evolution was also not taken into account in our study. A self-graviting clump will still accrete a large amount of gas. Even if the disk fragments into an initially planetary mass clump, this fragment will accrete gas, become more massive, and thus might exceed the deuterium-burning limit mass (Boss 2011). However, such a formation takes about 10⁵ yr, gas accretion is expected to be turned off by disk dissipation by strong UV irradiation of the surrounding high mass stars in the host-star forming region (Durisen et al. 2007) so that one might expect light clump growth to stop before it becomes too massive.

5.4. Giant planet formation by core-accretion

We now investigate the planet formation and evolutionary model of Mordasini et al. (2012), which predicts the final state of planets following the core-accretion scenario normalized by the frequency of observed disks. The synthetic population is calculated assuming a 2 M_⊙ central star, a mean disk lifetime of 4 Myr, gap formation that does not reduce gas accretion⁵, and considering one embryo per disk simulation (hence no outward migration of resonant pairs or scattering). A comparison with RV data shows that this simulation produces too massive and too close-in giant planets, but this synthetic population can be considerered as a rough approximation (see also Alibert et al. 2011). We then tested the predicted expected population at wide orbits with this approach so with direct imaging results. We ran the MC simulations with planets extracted from this synthetic population. 10⁴ random orbits were generated for each planet and the projected position on the sky was computed as before.

In Fig. 12, we show the extracted planet population (already normalized) as well as the detection probability at 20%, 60%, and 80% for the A-F sample. Synthetic population and the results of our survey are compatible. Indeed, we are marginally sensitive to the farthest predicted giant planets (the predicted fraction with detectable planets is around 0.06%), consequently, we cannot reject their existence. Notwithstanding, CA is expected to become inefficient forming planets at separations larger than some tens of AU. Moreover, the domain probed by our detection sensitivity, i.e., beyond 40 AU, well matched the region where CA is inoperable as seen in Fig. 12. The 5−20 AU gap between deep-imaging surveys and those from radial velocity will be at least partly filled in thanks to the forthcoming extreme adaptive-optic instruments VLT/SPHERE (Beuzit et al. 2008) and Gemini/GPI (Macintosh et al. 2008) because of excellent detection limits and lower inner working angles. Using the same MC simulations, we computed the mean detection probability curves (Fig. 12)⁶. We show that the improved capabilities of SPHERE will indeed allow to decrease this gap by detecting a few Jupiter-like planets down to 5 AU. However, its overall sensibility (in mass and separation) will not allow one to entirely probe the predicted giant planet population (the predicted fraction with detectable planets is around 0.6%). Another complementary way to fill this gap is to use both RV and direct imaging on selected young targets, as demonstrated in Lagrange et al. (2012c).

Fig. 12

Synthetic planetary population predicted assuming the core-accretion scenario similar as in Mordasini et al. (2012) for the case of 2 M_J central stars. The 20%, 60%, and 80% detection probability curves (red) are overplotted on the planet population, revealing the poor sensitivity of our survey for this type of formed planets. The SPHERE/IFS performances (dashed) have also been plotted assuming the contrast curves from Mesa et al. (2011). The short high-sensivity window is due to the small FoV of the IFS (1.77″), which can be overcome with the larger IRDIS FoV.

Open with DEXTER

6. Concluding remarks

We have reported the observations and analysis of a survey of 59 stars with VLT/NaCo at L′-band (3.8 μm) with the goal of detecting and characterizing giant planets on wide orbits. The selected sample favored young, i.e., ≤70 Myr, nearby, ≤100 pc, dusty, and early-type stars to maximize the range of mass and separation across which the observations are sensitive. The optimized observation strategy with the angular differential imaging in thermal-band and a dedicated data reduction using various algorithms allowed us to reach a contrast between the central star and an off-axis point source of 12 mag at 0.3″, 13.5 mag at 0.5″ up to 14 mag farther away in the best case. Despite the good sensivity of our survey, we did not detect any new giant planet. New visual binaries were resolved, HIP 38160 was confirmed as a comoving pair, and HIP 79881 and HIP 53524 were confirmed as background objects. We also reported the observations of a perfect laboraty-case for disk evolution with the subarcsecond resolved disk surrounding HD 142527 (dedicated publication in Rameau et al. 2012).

We used Monte-Carlo simulations to estimate the sensitivity of the survey performance in terms of planetary mass and semi-major axis. The best detection probability matches the range 40−300 AU, with maxima at 93% for a 10 M_J planet and 58% for a 3 M_J planet. Brown dwarfs would have been detected with more than 70% probability within the same semi-major axis range.

Table 8

Confidence interval of the giant planet frequency of with a confidence level of 68% reported in this work around young, nearby and dusty A-F stars assuming different planet populations, the detections of β Pictoris b, and the system around HR 8799 for planets, and the detection of HR 7329 b as brown dwarf.

A dedicated statistical analysis was carried out to understand and constrain the formation mechanism of giant planets. From literature and archive data, we focused on two volume-limited samples, representatives of almost 60% to more than 70% of the full set of stars that are younger than 100 Myr, closer than 65 pc, to the south (Dec ≤ 25 deg), A-or F-type, and with/without infrared excess at 24 and/or 70 μm. We computed the frequency of giant planets at wide orbits, in the interval [1,13] and [1,1000] (M_J and AU), summarized in Table 8:

in the A-F and A-F dusty samples, two giant planetary systems have been detected so far: β Pictoris and HR 8799, yielding a wide-orbit giant planet occurrence between 4.9% and 42.4% for the A-F sample and between 6.5% and 56.9% for the A-F dusty sample at 95% CL, assuming a uniform distribution. These results are consistent with the upper limit found in the literature and also with the rate of planets around the volume-limited sample of 42 A-type stars by Vigan et al. (2012) (see results in Table 1);
if the population of giant planets on wide orbits follows the distribution of those detected by RV below 5 AU from Cumming et al. (2008), the 95% confidence interval for f is 6.7−59.5% for the A-F sample, and 8.6−66.2% for the A-F dusty sample. We recall that this assumption is probably incorrect because it implicitly assumes that wide-orbit giant planets have similar origins and properties as close-in ones around Sun-like stars;
planets formed via gravitational instability within protoplanetary disks are expected to be massive and to orbit far away from their host stars if they remain in situ. We considered such planets to form and remain in situ where such an instability could occur. Since β Pic b and HR 8799 b,c, and d are not allowed to form via GI according to our model, we only computed upper limits to the giant planet frequency. We found that fewer than 25% of stars could form and retain a 10−13 M_J between 30−60 AU in the A-F sample (so as for the A-F dusty sample). Closer in, disk instabilities are quickly prevented so that no planet can be formed, whereas the disk fragmentation rapidly leads to brown dwarfs and stellar regimes farther away.

These results may corroborate the correlation between the presence of debris disk and giant planets since the rates tend to be slightly higher in the A-F dusty sample than in the A-F sample. The results also point toward a similar occurrence of giant planets on wide (from AO imaging) and close (from RV measurement) separations. They suggest a break-up of the positive correlation between the separation, the mass, and the distribution derived from close-in CA planets and the population of wide-orbit giant planets. This is consistent with a decreasing distribution with larger semi-major axis. All previous surveys reported this bimodal behavior of the distribution, which would be a signpost of different modes of gas giant formation (Boley et al. 2009). Upcoming extreme AO surveys will probe the transition region between the two regimes and reveal whether it is continuous, i.e., the same formation process or, not (Kratter et al. 2010).

Since our survey is very sensitive to high mass objects (i.e. ≥10 M_J), we were able to derive the rate of brown dwarfs as 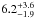% in the A-F sample and 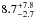% in the A-F dusty, at 68% CL in the interval [14,75] and [1,1000] (M_J AU) assuming a uniform distribution, which is consistent with results in the literature. From the GI formation boundaries, these rates become 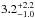% in the A-F sample and 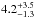% in the A-F dusty one.

We finally recall that all detection limit estimations were based on mass-luminosity relations that are still debated. Moreover, they strongly relied on age estimates that are much less accurate for early-type stars that they do not belong to a moving group. The long-term dynamical evolution of planetary systems (migration in e.g. Papaloizou et al. 2007; scattering Crida et al. 2009; Raymond et al. 2012) also plays a key role, and the giant planet distribution at a given age could be different from the one at formation stages.

We attempted to derive the age in a homogeneous way. If the star belongs to a moving group, the age of that group was adopted for this star. If the star does not belong to a known association, we ensured that the age was determined in similar way as for the membership identification, i.e.,the Galactic space motions UVW, the Li λ6708 Å line equivalent width, or the X-ray emission.

These additional stars werealso observed using ADI techniques but with the Ks filter on VLT/NaCo.

They correspond to the inclination, the argument of the periastron with respect to the line of nodes, the longitude of the ascending node, the eccentricity, and the time of passage at periastron.

⁴

While they derived the distribution for mass and period in logarithmic bins using α as the index for P, we used the mass and semi-major axis distribution with linear bins using α referring to a.

⁵

This question is still debated since gap formation might lead to a reduction (e.g. Lubow et al. 1999), but this might be counterbalanced by the effects of eccentric instability (Kley & Dirksen 2006).

⁶

Only a small semi-major axis range is covered by the curves since we considered only the IFS, instrument which has a small FoV (1.77″). Larger FoV will be provided by the IRDIS focal instrument.

Acknowledgments

The authors are grateful to the anonymous referee for useful advice and comments that improved the readability of this publication. J.R. thanks the ESO staff for conducting the observations and A. Vigan for fruitful discussion about MC simulations and for providing his published detection limits. This research has made use of the SIMBAD database and the VizieR catalogue access tool, operated at CDS, Strasbourg, France. The original description of the VizieR service was published in A&AS 143, 23. This work makes also use of EURO-VO TOPCAT software. The EURO-VO has been funded by the European Commission through contracts RI031675 (DCA) and 011892 (VO-TECH) under the 6th Framework Programme and contracts 212104 (AIDA) and 261541 (VO-ICE) under the 7th Framework Programme. We also use data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. J.R., G.C., and A.M.L. acknowledge financial support from the French National Research Agency (ANR) through project grant ANR10-BLANC0504-01. S.D. acknowldeges partial support from PRIN INAF 2010 “Planetary systems at young ages”.

References

Acke, B., & van den Ancker, M. E. 2004, A&A, 426, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Alibert, Y., Mordasini, C., & Benz, W. 2004, A&A, 417, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Alibert, Y., Mordasini, C., & Benz, W. 2011, A&A, 526, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Allard, F., & Homeier, D. 2012, EAS Publ. Ser., 57, 3 [CrossRef] [EDP Sciences] [Google Scholar]
Ammons, S. M., Robinson, S. E., Strader, J., et al. 2006, ApJ, 638, 1004 [NASA ADS] [CrossRef] [Google Scholar]
Augereau, J. C., Nelson, R. P., Lagrange, A. M., Papaloizou, J. C. B., & Mouillet, D. 2001, A&A, 370, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
Biller, B. A., Close, L. M., Masciadri, E., et al. 2007, ApJS, 173, 143 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Biller, B., Lacour, S., Juhász, A., et al. 2012, ApJ, 753, L38 [NASA ADS] [CrossRef] [Google Scholar]
Boley, A. C., Lake, G., Read, J., & Teyssier, R. 2009, ApJ, 706, L192 [NASA ADS] [CrossRef] [Google Scholar]
Bonavita, M., Chauvin, G., Desidera, S., et al. 2012, A&A, 537, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bonnefoy, M., Chauvin, G., Rojo, P., et al. 2010, A&A, 512, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bonnefoy, M., Lagrange, A.-M., Boccaletti, A., et al. 2011, A&A, 528, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bonnefoy, M., Boccaletti, A., Lagrange, A.-M., et al. 2013, A&A, in press, DOI: 10.1051/0004-6361/201220838 [Google Scholar]
Boss, A. P. 2011, ApJ, 731, 74 [NASA ADS] [CrossRef] [Google Scholar]
Bowler, B. P., Liu, M. C., Dupuy, T. J., & Cushing, M. C. 2010, ApJ, 723, 850 [NASA ADS] [CrossRef] [Google Scholar]
Burrows, A., Sudarsky, D., & Lunine, J. I. 2003, ApJ, 596, 587 [NASA ADS] [CrossRef] [Google Scholar]
Cameron, A. G. W. 1978, Moon and Planets, 18, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Carson, J. C., Eikenberry, S. S., Smith, J. J., & Cordes, J. M. 2006, AJ, 132, 1146 [NASA ADS] [CrossRef] [Google Scholar]
Carson, J., Thalmann, C., Janson, M., et al. 2013, ApJ, 763, L32 [NASA ADS] [CrossRef] [Google Scholar]
Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2004, A&A, 425, L29 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
Chauvin, G., Lagrange, A.-M., Zuckerman, B., et al. 2005, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Chauvin, G., Lagrange, A.-M., Bonavita, M., et al. 2010, A&A, 509, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Chauvin, G., Lagrange, A.-M., Beust, H., et al. 2012, A&A, 542, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Crepp, J. R., & Johnson, J. A. 2011, ApJ, 733, 126 [NASA ADS] [CrossRef] [Google Scholar]
Crida, A., Masset, F., & Morbidelli, A. 2009, ApJ, 705, L148 [NASA ADS] [CrossRef] [Google Scholar]
Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog II/246 [Google Scholar]
De Rosa, R. J., Bulger, J., Patience, J., et al. 2011, MNRAS, 415, 854 [NASA ADS] [CrossRef] [Google Scholar]
Delorme, P., Lagrange, A. M., Chauvin, G., et al. 2012, A&A, 539, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Devillar, N. 1997, The Messenger, 87 [Google Scholar]
Dodson-Robinson, S. E., Veras, D., Ford, E. B., & Beichman, C. A. 2009, ApJ, 707, 79 [NASA ADS] [CrossRef] [Google Scholar]
Dommanget, J., & Nys, O. 2002, VizieR Online Data Catalog I/274 [Google Scholar]
Durisen, R. H., Boss, A. P., Mayer, L., et al. 2007, Protostars and Planets V, 607 [Google Scholar]
Ehrenreich, D., Lagrange, A.-M., Montagnier, G., et al. 2010, A&A, 523, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Endl, M., Cochran, W. D., Kürster, M., et al. 2006, ApJ, 649, 436 [Google Scholar]
Esposito, S., Mesa, D., Skemer, A., et al. 2012, ApJ, 753, 14 [NASA ADS] [CrossRef] [Google Scholar]
Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
Fukagawa, M., Tamura, M., Itoh, Y., et al. 2006, ApJ, 636, L153 [NASA ADS] [CrossRef] [Google Scholar]
Galvagni, M., Hayfield, T., Boley, A., et al. 2012, MNRAS, 427, 1725 [NASA ADS] [CrossRef] [Google Scholar]
Gammie, C. F. 2001, ApJ, 553, 174 [NASA ADS] [CrossRef] [Google Scholar]
Girard, J. H. V., Kasper, M., Quanz, S. P., et al. 2010, in SPIE Conf. Ser., 7736 [Google Scholar]
Girard, J. H. V., O’Neal, J., Mawet, D., et al. 2012, in SPIE Conf. Ser., 8447 [Google Scholar]
Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Haakonsen, C. B., & Rutledge, R. E. 2009, ApJS, 184, 138 [NASA ADS] [CrossRef] [Google Scholar]
Hillenbrand, L. A., Carpenter, J. M., Kim, J. S., et al. 2008, ApJ, 677, 630 [NASA ADS] [CrossRef] [Google Scholar]
Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
Janson, M., Bergfors, C., Goto, M., Brandner, W., & Lafrenière, D. 2010, ApJ, 710, L35 [NASA ADS] [CrossRef] [Google Scholar]
Janson, M., Bonavita, M., Klahr, H., et al. 2011, ApJ, 736, 89 [NASA ADS] [CrossRef] [Google Scholar]
Janson, M., Bonavita, M., Klahr, H., & Lafrenière, D. 2012, ApJ, 745, 4 [NASA ADS] [CrossRef] [Google Scholar]
Johnson, J. A. 2007, in Meeting Abstracts, BAAS, 39, 1002 [NASA ADS] [Google Scholar]
Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
Kains, N., Wyatt, M. C., & Greaves, J. S. 2011, MNRAS, 414, 2486 [NASA ADS] [CrossRef] [Google Scholar]
Kalas, P., Graham, J. R., & Clampin, M. 2005, Nature, 435, 1067 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Kasper, M., Apai, D., Janson, M., & Brandner, W. 2007, A&A, 472, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 682, 1264 [NASA ADS] [CrossRef] [Google Scholar]
Kenyon, S. J., & Hartmann, L. 1987, ApJ, 323, 714 [NASA ADS] [CrossRef] [Google Scholar]
Kley, W., & Dirksen, G. 2006, A&A, 447, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
Kratter, K. M., & Murray-Clay, R. A. 2011, ApJ, 740, 1 [NASA ADS] [CrossRef] [Google Scholar]
Kratter, K. M., Murray-Clay, R. A., & Youdin, A. N. 2010, ApJ, 710, 1375 [NASA ADS] [CrossRef] [Google Scholar]
Krivov, A. V. 2010, Res. Astron. Astrophys., 10, 383 [NASA ADS] [CrossRef] [Google Scholar]
Lafrenière, D., Marois, C., Doyon, R., Nadeau, D., & Artigau, É. 2007, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
Lagrange, A.-M., Desort, M., Galland, F., Udry, S., & Mayor, M. 2009a, A&A, 495, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lagrange, A.-M., Gratadour, D., Chauvin, G., et al. 2009b, A&A, 493, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Lagrange, A.-M., Boccaletti, A., Milli, J., et al. 2012a, A&A, 542, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lagrange, A.-M., De Bondt, K., Meunier, N., et al. 2012b, A&A, 542, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lagrange, A.-M., Meunier, N., Chauvin, G., et al. 2012c, A&A, submitted [Google Scholar]
Lenzen, R., Hartung, M., Brandner, W., et al. 2003, in SPIE Conf. Ser., 4841, 944 [Google Scholar]
Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606 [NASA ADS] [CrossRef] [Google Scholar]
López-Santiago, J., Montes, D., Crespo-Chacón, I., & Fernández-Figueroa, M. J. 2006, ApJ, 643, 1160 [NASA ADS] [CrossRef] [Google Scholar]
Lovis, C., & Mayor, M. 2007, A&A, 472, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lowrance, P. J., Schneider, G., Kirkpatrick, J. D., et al. 2000, ApJ, 541, 390 [NASA ADS] [CrossRef] [Google Scholar]
Lubow, S. H., Seibert, M., & Artymowicz, P. 1999, ApJ, 526, 1001 [NASA ADS] [CrossRef] [Google Scholar]
Macintosh, B. A., Graham, J. R., Palmer, D. W., et al. 2008, in SPIE Conf. Ser., 7015 [Google Scholar]
Makarov, V. V., & Kaplan, G. H. 2005, AJ, 129, 2420 [NASA ADS] [CrossRef] [Google Scholar]
Marley, M. S., Fortney, J. J., Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2007, ApJ, 655, 541 [NASA ADS] [CrossRef] [Google Scholar]
Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [NASA ADS] [CrossRef] [Google Scholar]
Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Masciadri, E., Mundt, R., Henning, T., Alvarez, C., & Barrado y Navascués, D. 2005, ApJ, 625, 1004 [NASA ADS] [CrossRef] [Google Scholar]
Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [NASA ADS] [CrossRef] [Google Scholar]
Mayor, M., Marmier, M., Lovis, C., et al. 2011 [arXiv:1109.2497] [Google Scholar]
McCaughrean, M. J., & Stauffer, J. R. 1994, AJ, 108, 1382 [NASA ADS] [CrossRef] [Google Scholar]
Meru, F., & Bate, M. R. 2011, in IAU Symp. 276, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 438 [Google Scholar]
Mesa, D., Gratton, R., Berton, A., et al. 2011, A&A, 529, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Miller, N., & Fortney, J. J. 2011, ApJ, 736, L29 [NASA ADS] [CrossRef] [Google Scholar]
Mizuno, H. 1980, Prog. Theor. Phys., 64, 544 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Mizusawa, T. F., Rebull, L. M., Stauffer, J. R., et al. 2012, AJ, 144, 135 [NASA ADS] [CrossRef] [Google Scholar]
Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
Morales, F. Y., Rieke, G. H., Werner, M. W., et al. 2011, ApJ, 730, L29 [NASA ADS] [CrossRef] [Google Scholar]
Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mordasini, C., Alibert, Y., Benz, W., Klahr, H., & Henning, T. 2012, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mouillet, D., Larwood, J. D., Papaloizou, J. C. B., & Lagrange, A. M. 1997, MNRAS, 292, 896 [NASA ADS] [CrossRef] [Google Scholar]
Nakajima, T., & Morino, J.-I. 2012, AJ, 143, 2 [NASA ADS] [CrossRef] [Google Scholar]
Neuhäuser, R., Ginski, C., Schmidt, T. O. B., & Mugrauer, M. 2011, MNRAS, 416, 1430 [NASA ADS] [CrossRef] [Google Scholar]
Nielsen, E. L., & Close, L. M. 2010, ApJ, 717, 878 [NASA ADS] [CrossRef] [Google Scholar]
Papaloizou, J. C. B., Nelson, R. P., Kley, W., Masset, F. S., & Artymowicz, P. 2007, Protostars and Planets V, 655 [Google Scholar]
Patience, J., Bulger, J., King, R. R., et al. 2011, A&A, 531, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pecaut, M., & Mamajek, E. 2010, in BAAS, 42, 215, 455.30 [Google Scholar]
Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rafikov, R. R., & Goldreich, P. 2005, ApJ, 631, 488 [NASA ADS] [CrossRef] [Google Scholar]
Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2012, A&A [Google Scholar]
Raymond, S. N., Armitage, P. J., Moro-Martín, A., et al. 2012, A&A, 541, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rebull, L. M., Stapelfeldt, K. R., Werner, M. W., et al. 2008, ApJ, 681, 1484 [NASA ADS] [CrossRef] [Google Scholar]
Rhee, J. H., Song, I., Zuckerman, B., & McElwain, M. 2007, ApJ, 660, 1556 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Roccatagliata, V., Henning, T., Wolf, S., et al. 2009, A&A, 497, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rousset, G., Lacombe, F., Puget, P., et al. 2003, in SPIE Conf. Ser., 4839, 140 [Google Scholar]
Schlieder, J. E., Lépine, S., & Simon, M. 2012, AJ, 143, 80 [NASA ADS] [CrossRef] [Google Scholar]
Seager, S., & Rogers, L. A. 2011, in BAAS Am. Astron. Soc. Meet. Abstracts #218, 211.08 [Google Scholar]
Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
Smith, R., Churcher, L. J., Wyatt, M. C., Moerchen, M. M., & Telesco, C. M. 2009, A&A, 493, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Song, I., Caillault, J.-P., Barrado y Navascués, D., & Stauffer, J. R. 2001, ApJ, 546, 352 [NASA ADS] [CrossRef] [Google Scholar]
Soummer, R., Brendan Hagan, J., Pueyo, L., et al. 2011, ApJ, 741, 55 [NASA ADS] [CrossRef] [Google Scholar]
Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Stamatellos, D., & Whitworth, A. P. 2009, MNRAS, 392, 413 [NASA ADS] [CrossRef] [Google Scholar]
Su, K. Y. L., Rieke, G. H., Stansberry, J. A., et al. 2006, ApJ, 653, 675 [NASA ADS] [CrossRef] [Google Scholar]
Toomre, A. 1981, in Structure and Evolution of Normal Galaxies, eds. J. A. Fall, & D. Lynden-Bell, 111 [Google Scholar]
Torres, C. A. O., Quast, G. R., Melo, C. H. F., & Sterzik, M. F. 2008, in Young Nearby Loose Associations, ed. B. Reipurth, 757 [Google Scholar]
Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Veran, J.-P., & Rigaut, F. J. 1998, in SPIE Conf. Ser. 3353, eds. D. Bonaccini, & R. K. Tyson, 426 [Google Scholar]
Vigan, A., Patience, J., Marois, C., et al. 2012, A&A, 544, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Whitworth, A., Bate, M. R., Nordlund, Å., Reipurth, B., & Zinnecker, H. 2007, Protostars and Planets V, 459 [Google Scholar]
Zuckerman, B., Song, I., Bessell, M. S., & Webb, R. A. 2001, ApJ, 562, L87 [NASA ADS] [CrossRef] [Google Scholar]
Zuckerman, B., Song, I., & Bessell, M. S. 2004, ApJ, 613, L65 [NASA ADS] [CrossRef] [Google Scholar]
Zuckerman, B., Bessell, M. S., Song, I., & Kim, S. 2006, ApJ, 649, L115 [NASA ADS] [CrossRef] [Google Scholar]
Zuckerman, B., Rhee, J. H., Song, I., & Bessell, M. S. 2011, ApJ, 732, 61 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Statistical formalism

Our likelihood analysis approach follows the work by Carson et al. (2006), Lafrenière et al. (2007), and Vigan et al. (2012). We here recall the steps.

The principle of detecting a planet around a star is a Bernoulli event. We denote with p_j the probability of detecting a giant planet around a star j if it is indeed there. This probability depends on the distance, the luminosity, and the age of the star, on the projected position, the luminosity of a planet, and also on the instrumental performances. We also note the fraction of stars f that harbor at least one planet in the interval [m_min,m_max] and [a_min,a_max]. We assume f to be constant around the star sample. For a given j star, the probability of detecting a giant planet companion is fp_j. Given the observational results of a survey, one can let d_j represent the detection efficiency such that d_j = 1 if a planet has been detected around the star j, and 0 otherwise. Therefore, the likelihood function of the data for a set of N star will be the product of each Bernoulli event since there are independent, so that: 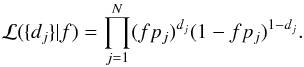(A.1)Then, we can apply the Bayes rule, which links the likelihood function of the data ({ d_j }) given the model f ℒ( { d_j } | f) to the probability density of the model given the data, or posterior distribution P(f | { d_j }). We obtain: 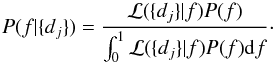(A.2)The Bayes rule also relies on the assumption on the initial probability of the model, or prior distribution P(f), which can be the most controversial part. One can use the posterior distribution from previous studies or construct priors by considering no previous knowledge on f so that P(f) = 1, excluding any bias on f. The later is our assumption for a direct comparison between surveys.

As for any estimation of a random variable, here f, the confidence interval [f_min,f_max] in which the true f can be determined with the equation, considering a confidence level CL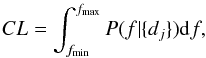(A.3)which can be split into implicit equations on f_min and f_max: 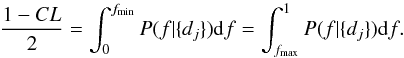(A.4)For a null detection, Poisson statistics dictates the probability of detecting a giant planet around a given star such that the likelihood Eq. (A.1) becomes 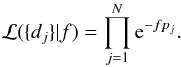(A.5)A null detection sets f_min = 0 and the Eq. (A.3) becomes an explicit equation for f_max given CL: 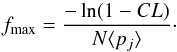(A.6)

All Tables

Table 1

Frequency of giant planets reported by various surveys around the full spectral type range.

In the text

Table 2

Sample of young, nearby, and dusty stars observed during our VLT/NaCo thermal and angular differential imaging survey.

In the text

Table 3

Additional young, nearby and southern A-F stars for the statistical analysis.

Sample definitions.

Mean platescale and true north orientation measured on the θ₁ Ori C field with the NaCo and L′/L27 set-up.

In the text

Table 6

Relative astrometry and photometry of the new visual binaries resolved with the VLT/NaCo L′ and ADI imaging mode.

In the text

Table 7

Relative astrometry and photometry of the known substellar companions observed with the VLT/NaCo L′ and ADI imaging mode.

In the text

Table 8

In the text

All Figures

	Fig. 1 Graphical summaries of the main properties of the target stars. Top row: left: histogram of distances with 10 pc bin. Right: histogram of ages of known members of considered moving groups (AB Dor – 70 Myr, β Pictoris – 12 Myr, Tuc/Hor & Col – 30 Myr, Her/Lyr – 200 Myr, Argus – 40 Myr, and Upper Cen/Lup – 5/10 Myr) and additional stars with 10 Myr bin. Central row: left: histogram of K-band magnitude with 0.5 mag bin. Right: histogram of apparent proper motions with 25 mas/yr bin. Bottom row: histogram of spectral types.
Open with DEXTER
In the text

	Fig. 2 Graphical summaries of the observation log of the target young, nearby dusty stars observed with VLT/NaCo between 2009 and 2012. Top left: histogram of median seeing (image quality seen by the active optics sensor) with 0.2″ bin. The DIMM seeing has been overplotted with dashed columns. Top right: histogram of median τ₀ with 0.5 ms bin as calculated by NAOS. Bottom left: histogram of median airmass with 0.1 bin. Bottom right: histogram of explored parallactic angles with 10 deg bin.
Open with DEXTER
In the text

	Fig. 3 Resolved visual binaries with the VLT/NaCo in ADI-L′ imaging mode. HIP 9685, HIP 53524, and HIP 93580 have not been confirmed as double systems from second-epoch observations or archived data. North is up, east to the left. Counts are displayed in linear scale but differently for each panel.
Open with DEXTER
In the text

	Fig. 4 Known substellar companions of HR 7329, AB Pic (top left and right), and β Pictoris and HR 8799 (bottom left and right) observed with the VLT/NaCo in ADI-L′ modes. North is up, east to the left, the count scale is linear. We were not able to retrieve HR 8799 e with a good signal-to-noise ratio due to the low parallactic angle amplitude (20.9 deg).
Open with DEXTER
In the text

	Fig. 5 Survey detection limits in L′-band contrast between the central star and any point source vs. the angular separation at the 5σ level using the VLT/NaCo in ADI mode. Solid lines are representative of median performances, whereas the bottom dashed lines are for the best performance reached by our survey. cADI (red) and LOCI (blue) are very similar, whereas sADI (orange) and rADI (aqua) remain slightly above the LOCI and cADI curves. The LOCI curves stop at 0.15 ″ because of the central exclusion area.
Open with DEXTER
In the text

	Fig. 6 Mean detection probability map of our survey as a function of the mass and semi-major axis (left) and probability curves for different mass bin as function of the semi-major axis (right). The mean is obtained over all targets of the survey. The detectability of the simulated planets was compared with the detection maps from LOCI and nADI algorithms and using the COND03 (Baraffe et al. 2003) evolutionary models.
Open with DEXTER
In the text

	Fig. 7 Detection limits of giant planets with Jupiter mass vs. the projected distance from the central star for stars with known debris disks. The detections are expressed at the 5σ level, using VLT/NaCo in ADI mode, after LOCI (close-in region) and nADI (background-limited region) processing. The COND03 (Baraffe et al. 2003) mass–luminosity relationship is used to convert from L′ contrast to Jupiter mass. For AU Mic, the model does not reach below 0.5 M_J, therefore we cut the curve when it reached this limit.
Open with DEXTER
In the text

	Fig. 8 A-F sample probability density of the fraction f of stars hosting at least one giant planet at wide orbit, taking into account the detections ({ d_j }) of the two planetary systems β Pictoris and HR 8799 and a linear-flat prior. The interval considered is [1,1000] AU and [1,13] M_J. The confidence interval at 68% confident level, labeled CL, (blue) and at 95% CL (dark blue) are overplotted on the distribution. A uniform planet population has been generated with random orbital parameters.
Open with DEXTER
In the text

	Fig. 9 Contours showing the confidence level at which we can reject a planet distribution following a mass power law dN ∝ M^αdM and a semi-major axis law dN ∝ a^βda at a given semi-major axis cutoff. Top: semi-major axis cutoff vs. semi-major axis power law index β for α = −1.5. Bottom: semi-major axis cutoff vs. semi-major axis power law index β for α = 1.1, i.e., with more massive planets. The upper cutoff for the Cumming et al. (2008)β index of − 0.61 is overplotted (dotted line). These figures use the LOCI and nADI detection limits and COND03 (Baraffe et al. 2003) for the mass–luminosity relationship.
Open with DEXTER
In the text

	Fig. 10 Left: mean detection probability map of the A-F sample as function of the mass and semi-major axis of the substellar companion. A uniform grid distribution has been used to generate the population, but the formation limits derived from the gravitational instability models excludes for each star the planets that do not fulfill both criteria. The detection maps from LOCI and nADI algorithms were used with COND03 (Baraffe et al. 2003) evolutionary models to convert from contrast to mass. Contour lines are regular from 0.5 to 0.9 plus one at 0.1. Right: corresponding estimate of the upper limit, with a confidence level of 95%, on the fraction of stars from the A-F sample that harbor at least one object companion in the same semi-major axis range. The curves for 25 M_J, 18 M_J, 13 M_J, and 10 M_J have been plotted since lower mass planets are not allowed to form via the disk instability mechanism.
Open with DEXTER
In the text

	Fig. 11 Disk instability model predictions for β Pictoris. The lower solid curve corresponds to the Toomre criterion which excludes the formation of planets below it. The upper dashed curve corresponds to the cooling criteria which only allows disk fragmentation below it. The allowed formation space is in between. The 1D average detection limit curve has been overplotted (blue solid line) but with a projected separation. The location of β Pictoris b has been overplotted on the graph with the new error bars from Bonnefoy et al. (2013).
Open with DEXTER
In the text

	Fig. 12 Synthetic planetary population predicted assuming the core-accretion scenario similar as in Mordasini et al. (2012) for the case of 2 M_J central stars. The 20%, 60%, and 80% detection probability curves (red) are overplotted on the planet population, revealing the poor sensitivity of our survey for this type of formed planets. The SPHERE/IFS performances (dashed) have also been plotted assuming the contrast curves from Mesa et al. (2011). The short high-sensivity window is due to the small FoV of the IFS (1.77″), which can be overcome with the larger IRDIS FoV.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.