EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 553 (May 2013) A&A, 553 (2013) A28 Full HTML
Free Access
Issue
A&A
Volume 553, May 2013
Article Number A28
Number of page(s) 12
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201219939
Published online 25 April 2013

© ESO, 2013

1. Introduction

V479 And was identified as a cataclysmic variable (CV) by Szkody et al. (2005) in the Sloan Digital Survey (SDSS J001856.93+3454) because it shows narrow Balmer emission lines, He i, and strong He ii. The two-hour follow-up observations were not sufficient to detect any significant radial velocity variations to reveal an orbital period. Szkody et al. (2005) also performed polarimetry and found no linear polarization within those two hours. Similarly, Dillon et al. (2008) found no orbital period of this system from four nights of photometric observations. González et al. (2010) conducted an extensive spectroscopic campaign in 2008-09 to pin down the orbital period. A 14.52 ± 0.53 h period was found by cross-correlating absorption features in the spectra of the object, with a K4 V standard-star template. Calculations of the orbital period, derived from the emission line radial velocity measurements (fitted with a single Gaussian), did not match the orbital period determined from the absorption lines. Therefore, the authors assumed that the object might be an asynchronous polar. In this paper we present new extensive optical, IR, UV, and X-ray data and a comprehensive study of this object.

Table 1

Log of time-resolved observations.

2. Observations

2.1. Spectroscopy

Time-resolved spectroscopy of V479 And  was performed with the 2.1 m telescope at the Observatorio Astronómico Nacional1 at San Pedro Mártir, Baja California, México (OAN SPM) in 2008 and 2009 with the Boller & Chivens spectrograph, using a 600 grooves mm-1 grating and a 24 μm 1024 × 1024 pixel SITe CCD with a spectral resolution of 4.1 Å. In 2010 we made two additional runs, using the 1200 grating with a 15 μm 2048 × 2048 pixel Thomson CCD, with a spectral resolution of 1.8 Å. The wavelength calibration was made with an arc lamp taken every tenth exposure, and spectrograph flexion with azimuth was also corrected by using night-sky lines. The spectra of the object were flux-calibrated using spectrophotometric standard stars observed during the same night. The instrument cannot automatically rotate the slit to the corresponding parallactic angle, and for simplicity we routinely used an E-W slit orientation. In addition, the slit width was kept narrow (180 μm = 2 arcsec) for better resolution. These two factors make a correct flux calibration difficult, although this is usually not a problem in radial velocity (RV) studies. However, on the night of September 07, 2010 we observed the object and several late spectral type standards using a wide 450 μm slit to ensure better flux calibration. The standard long-slit reduction of the data was made using IRAF2 procedures after applying basic CCD preliminary procedures. Only cleaning cosmic rays, which are abundant on 1200 s exposures, was made with the external task lacos (van Dokkum 2001). The log of spectroscopic observations is given in Table 1.

We also used the SDSS spectrum of the object from DR8. The original spectrum of V479 And was obtained on December 10, 2003, but the new reduction was made with an improved calibration using the software version v5-3-12 of February, 2008. The SDSS spectrum covers a wider range of wavelengths than our own spectra and provides a reliable flux calibration. A list of the main emission lines and their measurements are presented in Table 2.

2.2. Photometry and photopolarimetry

Time-resolved I and J bands near-IR photometry and V-band linear polarimetry were obtained using the 1.5 m and the 0.84 m telescopes, respectively, at the OAN SPM. The first was obtained using the direct CCD image mode with the RUCA and CAMILA instruments1, while the latter was obtained with the POLIMA1, using four polarization positions (0, 45, 90, and 135 degrees). Two polarimetric standards, one of which has zero polarization, were observed together with the object for calibration purposes. The log of photometric observations is also given in Table 1. The data were reduced with IRAF and a pipeline software for POLIMA3. The images were corrected for bias and flat-fields before aperture photometry. Flux calibration was performed using standard stars from the lists of Landolt (1992) and van der Bliek et al. (1996), observed in the same nights. The errors in optical V and I bands are estimated to be less than 0.05 magnitudes. We had problems with the telescope during the IR J-band observations, and thus only a rough  ± 0.3 mag estimate of brightness is available.

2.3. UV and X-ray observations

V479 And was observed with Swift as a target of opportunity (ToO target ID: 31872) for 31 h on November 26 and 27, 2010 with a total on-source exposure time of 26.7 ks. We used two of the three instruments on board, of the Swift gamma-ray burst explorer (see Gehrels et al. 2004): the X-ray Telescope (XRT; e.g. Burrows et al. 2005) and the Ultraviolet/Optical Telescope (UVOT; e.g. Roming et al. 2005). Standard data processing was made later at the Swift Science Data Centre in 2010 December. The results presented in this paper are based on data collected when the XRT was operating in the PC mode, in which full imaging and spectroscopic resolutions are retained, but timing resolution is limited to 2.5 s.

Simultaneous UV images in the UVW1 and UVM2 filters, centered at 2600 and 2246 Å, respectively, were obtained with the UVOT. One entire binary orbital cycle was covered. Eleven images were collected with the UVW1 filter and eight with the UVM2 filter. We used standard aperture photometry to measure fluxes on calibrated images, which were supplied after pipeline reduction of the UVOT data.

Table 2

Measurements of the main emission lines.

3. System composition

3.1. Spectroscopic orbital period

The spectroscopic orbital periods of close binaries are better determined from the radial velocity variation of the absorption lines of the stellar components when available than from the lines originating in the accretion disk. In the case of V479 And we were able to use the absorption line complex around the λλ 5050−5850 Å region by a cross-correlating with a template spectrum of the corresponding class. The absorption features around 5200 Å are the strongest and are very similar to late-G or early-K stars. We used the IRAF xcsao procedure for the cross-correlation. The regions that contained an emission line or were affected by a sky line falling into our selected range were excluded from the analysis. The results presented here are based on a cross-correlation with the spectrum of HD 099491, a K0 IV star (Edwards 1976). We also used templates of spectral types, varying from G8 to K2, with luminosity types V and IV, which do not show notable differences between measured velocities. Standard spectra of late stars observed simultaneously with the object show similar results.

The radial velocities of all spectra taken in 2008 to 2010 were measured. The velocities for 2008 and 2009 match those reported in González et al. (2010), where a K4 V template was used. The RV were first analyzed for periods using CLEAN (Schwarz 1978), a discrete Fourier transform method, which convolves the power spectrum with the spectral window to eliminate alias frequencies originating from uneven data distribution. We also conducted a Scargle-Lomb (Scargle 1982) test on the data, which is a least-squares spectral analysis similar to the Fourier one, but which mitigates the long-periodic noise in the long gapped records. The results of both period analyses are shown on Fig. 1. The Scargle-Lomb produces two equal peaks at frequencies 1.6803 and 1.6832 day-1, while CLEAN gives a clear preference to the latter frequency, which we used hereafter as the orbital period of the system, although the other period gives a similar RV curve and similar scatter of points to the fitted sinusoidal curve. This period is within the errors of the value reported by González et al. (2010). The ephemerides, according to the combined 2008–2010 data, are 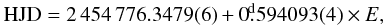where HJD0 at E = 0 refers to the inferior conjunction of the secondary star.

thumbnail Fig. 1

Power spectrum of the radial velocities of the secondary star. Peaks around 0.7 and 2.7 day-1 are one-day aliases of the orbital period at 1.68325 day-1. The aliases are strong because the orbital period is long and only part of a cycle is observed nightly. In the inset box of the figure the CLEANed power spectrum peak is shown, marking the precise period of the system.

3.2. Orbital parameters of the binary components

The orbital parameters of the secondary star can be found from a sinusoidal fit of the form 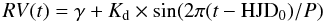to the RV curve. A least-squares fit yields Kd = 59 km s-1 and γ = −73 km s-1, where P and HJD0 have been taken from the calculated ephemeris. Figure 2 shows the velocities folded with these parameters together with the sinusoidal fit (Table 3).

Table 3

Radial velocity fit parameters.

thumbnail Fig. 2

Radial velocities of the absorption line complex determined by cross-correlating the object with a standard K0 star template and folded with the orbital period. The red line is the best-fit sinusoid to the measurements.

The emission lines of this object are very intense and single-peaked. The average FWHM of Balmer lines is 500–600 km s-1, which is quite narrow for an ordinary CV. González et al. (2010) measured the radial velocities of these lines by fitting a single Gaussian to the line profiles. This resulted in a scatter of points, with no clear periodic nature. The same results were achieved by cross-correlating the emission lines with a synthetic line constructed with a Gaussian profile of 5 Å width. The scattered measurements were incorrectly interpreted by González et al. (2010). The new, higher resolution spectra obtained in 2010 show that the lines do not have a Gaussian profile. The base of the lines is wider for a Gaussian, and there might be a contribution from a broader, but less intense component. An example of a Hβ line profile is shown in Fig. 3 with a single Gaussian fitted to the peak of the line. To measure the wings of the emission lines, a double-Gaussian method was proposed by Schneider & Young (1980). We followed here a prescription developed by Shafter (1983). Best results for the set of 2010 spectra were achieved with Gaussian widths of 5.3 Å and a separation of 16–17 Å (≈ 1000 km s-1). These solutions show an orbital modulation with the same period as that obtained from the secondary star and are, as expected, in counter phase with the absorption lines. The semi-amplitudes and systemic velocities obtained for H i and He ii λ4686 Å, with the orbital period and zero phase fixed, are also summarized in Table 3.

thumbnail Fig. 3

Typical Hβ line profile from a spectrum obtained in 2010 with a 2.1 FWHM spectral resolution. A single-Gaussian profile with 5.0 Å FWHM is over-plotted on the line to demonstrate that the base of the line deviates from a Gaussian.

We remeasured the He ii λ4686 Å line also with a single-Lorentzian fit. Unlike a single-Gaussian fit, this takes into account the wings of the line. The orbital solution is similar to that obtained with the double-Gaussian fitting, but with a lower semi-amplitude of the radial velocities. To ensure that the RV variability in the wings of the emission lines was not influenced by the absorption features from the donor, we repeated the analysis after subtracting a standard K0 V spectrum, observed at the same time and with the same instrument setup, scaled to a flux and Doppler-shifted to a velocity corresponding to a contributing companion star. In the two lower panels of Fig. 4 we show the measured RVs for Hβ (bottom) and He ii λ 4686 Å (middle) folded with the orbital period and phase obtained from the analysis of absorption lines. Corresponding fits are also shown as sinusoidal curves. The filled square symbols mark the RVs measured with the double-Gaussian method, while the open squares are measurements with the single-Lorentzian fits to He ii λ4686 Å. The uppermost panel shows the distribution of the line widths of the Lorentzian fits. We note that in this fit, the profile of emission lines becomes twice as narrow at about orbital phase φorb = 0.1−0.2, as can be seen in the top panel of Fig. 4.

thumbnail Fig. 4

Emission line measurements of V479 And from 2010 higher resolution spectra. The radial velocities of Hβ and He ii measured by a double-Gaussian method are marked by solid black squares in the bottom and middle panel. The horizontal bars attached to each point indicate the duration of individual exposures. The radial velocity curves obtained as sinusoidal fits to these points are overplotted. In the middle panel measurements of He ii line by single-Lorentzian fits are marked by open squares. The upper panel shows measurements of the width of the Lorentzian profiles fitted to the He ii line.

thumbnail Fig. 5

Spectra of V479 And (black) and standard stars. In the right upper panel we show the observed spectrum of the object along with a K0 IV star (red, dotted), scaled to reflect the real contribution of the secondary star to the total flux. The continuous red line over the K0 star is a high-order polynomial fit to the spectrum excluding strong absorption features. In the lower right panel, the residual (V479 And minus K0 IV) is plotted. It is well-described by a power law plotted by the dashed (blue) line. This power law is summed with the fit to the secondary star spectrum and plotted over the object in the upper panel to illustrate coincidences of the troughs in the continuum. In the left panels zoomed portions of the spectra are displayed in the λλ 4220−4340 Å (bottom) and λλ 5100−5300 Å (top) intervals. The thick black line in the left panels corresponds to the SPM spectrum, while the dotted line shows the SDSS spectrum. Two standard stars are plotted in colors, G0 V in blue, and K0 IV in red. The standard star spectra are scaled to overlap with the object in each spectral interval separately. The SPM spectra in the left panels are combined after correction for the secondary star orbital motion to increase the signal-to-noise ratio.

It is not clear where the wings of the emission lines originate. Comparing the relative intensity of the Balmer lines from Table 2 with those computed by Williams (1980) shows that the Balmer decrement of V479 And is much flatter than expected from the accretion disk of a CV, even with a very high 10-9 M⊙/year mass–transfer rate. The strong He ii line is not commonly observed in an ordinary accretion disk. Moreover, He ii spots in the disk or elsewhere in the binary would not have similar widths and orbital phases as the Balmer lines, which are normally produced by the entire disk. In polars, the emission lines often contain a narrow component, which at times can be intense and dominate the line profile, but this component is formed in a stream of matter and usually produces a high radial velocity component (HVC) (e.g. Schmidt et al. 1983; Schwope et al. 1997; Tovmassian et al. 1999). A ballistic stream, or a coupling region should produce a dominant high-velocity contribution, and it will not be exactly shifted 0.5 to the phase of the absorption lines. At the radius of magnetosphere, which prevents the formation of a disk, the speed in a ballistic stream will reach hundreds of km s-1, and even in a low-inclination system its radial velocity will easily surpass the orbital velocity of either stellar component.

Because we do not detect high radial velocities in V479 And, but rather see low radial velocities exactly in counter phase to the absorption lines, we conclude that the emission lines originate somewhere in the vicinity of the accreting star, but probably do not arise from the usual components in a standard Roche-lobe-filling/stream-mass-transfer CV model. To summarize, we consider the orbital velocity of the accreting component in this binary system to be within the range of semi-amplitudes measured by He ii and Hβ lines.

3.3. The spectral classification of the secondary star

The right panel of Fig. 5 shows portions of V479 And spectrum together with two late-type stars. The starts of G0 to K2 spectral types with no peculiarities and the highest signal-to-noise ratio were selected from ELODIE archive (Baranne et al. 1996) to compare them with the object. The spectra were degraded to a spectral resolution corresponding to our observations. In the left panel, we show two spectral intervals: λ 4220−4340 Å (bottom) and λ 5100−5300 Å (top) in which a number of absorption features belonging to a late-type star show up in the spectra of V479 And. The complex of Fe II + Mg I features around λ 5173  Å and Fe I + Ca I around λ 5270  Å and others in the λ 5000−5800  Å range indicate the wide range of spectral types from G0 to K4. But additional lines in a more contaminated λ 4200−4340  Å region, particularly Ca I (4226), Cr I (4254, 4290), and Fe I (4271) allow one to seek a balanced solution between individual line depths and the spectral energy distribution. To successfully fit absorption lines in both selected regions, the contribution from the continuum of the secondary star should be adequately taken into account. In the left panels the standard spectra are arbitrarily scaled to overlap with the absorption features of the object, i.e., the continuum of each comparison star is adjusted to the observed continuum in each region separately. G-K type stars have numerous absorption lines that form troughs of different depth and width in their spectra. Their locations move with the change of the overall shape of the continuum depending on the temperature. We delineated these features by fitting a high-order polynomial to the spectra of the comparison stars (excluding strong absorption lines) in a strictly homogeneous way. In the right upper panel of Fig. 5 we show an example of a standard spectrum of a K0 IV star and the fit to it. Obviously, the troughs in the continuum of a late-type star are visible also in the spectrum of the object. The depth of the feature around 5200 Å and the slope of the continuum between the Hγ and Hδ lines in the observed spectrum can be best reproduced by summing of G8−K0 IV and a power law, although it is very difficult to evaluate the agreement quantitatively. Employing other spectral types will require more complex contribution than that of a simple power law from the rest of the system.

thumbnail Fig. 6

M2–M1 diagram for V479 And. The solution probably lies between thick diagonal lines corresponding to q = 0.54 and 0.7 as measured by RV amplitude ratio of He ii and Hβ emission lines to the absorption. Dashed curves denote the orbital inclination of the system. The shaded area corresponds to the mass range of a K0 star from ZAMS to luminosity class IV.

The lower right panel shows the residual spectra after subtracting the K0 IV star. The overplotted dashed line represents a power law accounting for difference in the continuum of the observed object and a donor star. Subtracting a standard earlier than G8 or later than K2 produces an odd continuum, different than a smooth power law expected from accretion-powered radiation. This shows that the secondary contributes about 45% of the flux to the total luminosity of the object at 5000 Å.

3.4. Masses and radii

Obtaining mass and radius limits of the binary components may help us to understand the dynamics of the accretion region. We can determine 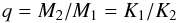from Table 2. We obtain q = 0.54 if we take the semi-amplitude of the primary star from the Hβ line and q = 0.71 if the determination from the He ii λ4686 Å is correct. The solution is somewhere in between since these these two values largely overlap if errors are taken into account. The M2 − M1 diagram is presented in Fig. 6. Diagonal lines denote different mass ratios q, with upper and lower limits corresponding to values determined from Hβ and He ii marked by thicker lines. Since the semi-amplitude depends on the inclination angle, the different inclination curves of the system are plotted. The vertical line shows the Chandrasekhar mass limit and divides the white dwarf and neutron star regimes. The shaded area marks the mass range of a K0 star from ZAMS to luminosity class IV, limited at the bottom by a 0.79 M⊙ main-sequence K0 star and at the top by a 1.23 M⊙, K0 IV star (Torres et al. 2010); at the left it is limited by a 0.6 M⊙ white dwarf mass (corresponding to the peak in the oxygen-carbon white dwarf mass distribution). Note that our upper q crosses the Chandrasekhar mass limit at about M2 ≈ 1.03 M⊙. Therefore, it is probable that the accretor in this system is a massive white dwarf or even a neutron star. The possible presence of a massive white dwarf in this system is an intriguing feature. Several exceptionally long-period systems appear to have massive white dwarfs, e.g. RU Peg with Porb ~ 9 h; (Friend et al. 1990), and EY Cyg with Porb ~ 11 h; (Echevarría et al. 2007). A disproportionally large portion of CVs with high-mass white dwarfs are also magnetic which, as Vennes (1999) pointed out, can be the result of their peculiar formation. Finally, we can point out from Fig. 6 that the possible solutions show that we are dealing with a very low inclination system.

The secondary star in V479 And cannot be a zero-age main-sequence K star since for an orbital period of 14.26 h the star would be far from filling its Roche lobe. More likely the companion is an evolved star. To assess its luminosity class we can calculate the Roche lobe size of the companion for mass ratio values 0.54 ≤ q ≤ 0.7 and a range of primary masses 1.1–1.4 M⊙. These values are shown in Fig. 7 with the short, thick black line. The crosses mark very precise mass and radius determinations for detached spectroscopic binaries and the filled squares those for well-known interferometric binaries (Torres et al. 2010). Subgiant stars are singled out; open black squares correspond to detached binaries, and solid black squares to interferometric binaries. The broken thin black line is the mass-radius relation for main-sequence donor stars of CVs with orbital periods <6 h (Knigge 2006). It is evident from Fig. 7 that V479 And is certainly off the zero-age main sequence, although it is still far from reaching the K subgiant region. The mean mass and radius values of V479 And, obtained form the Roche lobe constraints discussed above, are M2 = 0.79 M⊙ and R2 = 1.29 R⊙. We can compare these values with some of the closely similar spectroscopic binaries. For example, a comparison with HS Aur B, a K0V star with M = 0.88 M⊙ and R = 0.87 R⊙ that is close to the zero-age main sequence with a large surface gravity log g = 4.5 (cgs), shows that its radius is much smaller than that of V479 And.

thumbnail Fig. 7

Md/Rd relation for low-mass stars. Crosses are parameters of normal stars measured in detached binaries, while solid red squares are measurements obtained from interferometry. A few subgiants from the sample are marked individually. The possible location of V479 And is marked by a thick black line. The thin, broken black line corresponds to main-sequence donors in CVs with shorter orbital periods.

thumbnail Fig. 8

Light curves of V479 And in V and I bands as indicated on the panels and obtained at four different epochs are folded with the orbital period. The integer numbers at the X-axes above each panel correspond to the orbital cycle in which the data plotted with filled squares were taken, the decimals correspond to the orbital phases. The data from immediately previous and following orbital cycles are marked with different symbols. The magnitudes at the Y-axes are calibrated using secondary standards in the field of the object.

If we look at the subgiants AI Phe A, a K0IV with M = 1.23 M⊙ and R = 2.93 R⊙, and V432 Aur, an F9IV star with M = 1.20 M⊙ and R = 2.43 R⊙, both with low surface gravity values log g = 3.59 (cgs) and log g = 3.75 (cgs), respectively (both plotted in the Fig. 7), we observe that they have radii nearly a factor of three larger than V479 And. Finally, we look at two intermediate surface gravity stars that have masses and radii comparable to V479 And, the G5 V stars V568 Lyr A and RW Lac A, both of which appear well off the zero-age main sequence, but have radii 1.2−1.4 R⊙ that are comparable to V479 And. We must be very cautious in accessing the donor star parameters because intermediate to low-mass stellar evolution models have been highly criticized for being unable to predict the radii and effective temperatures of detached eclipsing binary stars. Recent models that incorporate magnetic fields help improve the situation (Feiden & Chaboyer 2012), and we are convinced that the donor star in V479 And  is magnetically active (see the following sections).

3.5. Distance estimates

We can derive rough distance estimates to the system. A firm lower limit on the distance would be 3.0 ± 0.2 kpc, taken from the distance module and assuming the donor is a main-sequence star with a flux Fλ ≈ 1.8 × 10-16  erg cm-2 s-1 Å-1 at 5500 Å and an interstellar extinction of E(B − V) = 0.056 in the direction of V479 And. But the donor star is certainly not a zero-age main-sequence star. We have shown in the previous section that the Roche lobe size of V479 And is probably about 1.3 R⊙. This would imply a distance to the object of about 4 kpc. This places the object in the halo of the Galaxy, at 1.8 kpc above the Galactic plane.

3.6. Photometric variability and polarimetry

The limited photometric coverage in the V and I bands shows variability up to 0.5 mag. There is no clear evidence of an orbital modulation, i.e., the pattern of variability does not repeat from cycle to cycle. In Fig. 8 the light curves of the object are presented, folded with the orbital period determined from spectroscopy. The V and I magnitudes were obtained by observations of Landolt (1992) stars and defining secondary standards in the field of the object. In each panel, in addition to the orbital phase marked at the bottom, the X-axis at the top of panels indicate the mean Eth cycle given by the ephemerides (Sect. 3.1). More than one orbital cycle has been observed at each observational run, thus the symbols refer to different orbital cycles around the mean. In the V-band, during cycle 1217, a variability appears that resembles a double-humped light curve, typical of close binaries with irradiated secondaries. But during the previous cycle 1167, the light curve is fairly flat. Similarly, in the I-band, the light curve around cycle 1175 is practically flat, while at the earlier cycle 1128 there is a strong, irregular variability. This behavior is similar to that obtained from the optical photometry by Dillon et al. (2008); this authors reported irregular variations of light, but no clear orbital modulation. The infrared J data, obtained in SPM, are very noisy and cover only a fraction of the binary orbit. Our average flux estimate J = 16.25(25) is significantly different from the 2MASS magnitude J = 15.77(8), H = 15.22(10), K = 15.29(16). Evidently, the IR flux is also variable.

We detected no linear polarization in the V band above a 2% threshold. Szkody et al. (2005) also failed to detect any polarization, although their orbital phase coverage is not complete. While a polarization detection is a good indicator of magnetic activity, linear polarization is not always observed in magnetic systems such as polars.

In the X-ray, we found a variability with a systematic pattern. Two orbital periods where covered with Swift, during which the light curve shows two pulse-like events. With only two orbital cycles and the limited time-resolution given by the Swift orbits, it is not possible to determine the period. Nevertheless, folding the X-ray light curve with the orbital period determined from the spectroscopy shows a single-hump curve in which the pulses of both cycles overlap. The X-ray light curve is presented in Fig. 9 (bottom panel). The data are folded according to the spectroscopic ephemerides. The UV magnitudes obtained in parallel with the X-ray data with the UVOT detector show a similar behavior, confirming that the X-ray pulses are not accidental spikes. The UV data taken in two different bands in each cycle are shown in the same figure (upper panel). The light curve in filter UVW1 clearly shows a trend similar to that of the X-ray data and is modulated with the orbital period. However, the phase of the peak in the near-UV trails the X-ray pulse by ~0.1 orbital phase. In the UVM2 filter the data corresponding to the peak in UVW1 are missing.

3.7. X-ray spectrum

The X-ray spectrum from the 26.7 ks of Swfit XRT observations accumulated from a 9.8′′ radius circle around the source contains only ~380 photons. Thus, it was meaningless to perform an in-depth spectral analysis. Most of these photons arrived during the “peak phase”, which corresponds to the orbital phases from roughly 0.12 to 0.30 (see Fig. 9). The peak phase has a much softer spectrum than the non-peak phase and varied component, suggesting a compact eclipsed emission with a lower temperature than the non-eclipsed diffuse gas component. A much higher signal-to-noise, phase-resolved spectroscopy with XMM-Newton and/or Suzaku would be very useful for understanding this object.

thumbnail Fig. 9

X-ray and UV light curves folded with the orbital period and ephemerides determined from the spectroscopy. The two orbital periods were observed by Swift. The X-ray flux peaks briefly at around orbital phase 0.2, while there seems to be a deep minimum at the phase between phases 0.5 and 0.7. The UV light curve in two filters (UVW1 blue squares and UVM2 red triangles) presented in the upper panel shows a behavior similar to that in the X-ray, except that the maximum peak is shifted relative to X-rays by 0.2 orbital phases and reaches maximum at 0.4.

thumbnail Fig. 10

Spectral energy distribution of V479 And from UV to IR (right to left). The two black squares are the GALEX FUV and NUV measurements, triangles are Swift UVOT UVM2 & UVW1 filters followed by black circles corresponding to the SDSS ugriz bands and our own BVRIJ measurements marked with open pentagons. Finally, the three open black squares are 2MASS JHK measurements. The large vertical error bars are not measurements errors, but show the extent of variability detected in the corresponding filter during long-term monitoring. The filled blue pentagons are interstellar-extinction-corrected data using E(B − V) = 0.056 and the blue dashed line corresponds to SDSS spectrum after de-reddening. The continuous red and dashed blue lines are simultaneous black body fits to the observations with 5200 and 19 000 K, respectively. The cool black body corresponds to the presence of a donor star in the binary system and is also represented by K0 IV or G8 IV spectra of standard stars. The black continuous line is the sum of the K0 IV spectrum and a 19 000 K black body, which appears to fit most of the observed data well.

3.8. Spectral energy distribution

The spectral energy distribution (SED) of V479 And from the IR to the UV range is shown in Fig. 10. Different black symbols mark photometric measurements from different instruments as indicated in the figure caption. Since the source is clearly variable, observations taken at different times do not necessarily match. The extent of the variability is shown by the bars placed on the data corresponding to the UVW1 & UVM2, g and J bands, where relatively long continuous observations are available. Therefore these large bars are not measurement errors.

On top of the black symbols, the blue pentagons correspond to the data after a de-reddening of E(B − V) = 0.056. Also shown in blue is the de-reddened SDSS optical spectrum. In Sect. 3.3 we have shown that the secondary star is a late-G/ early-K star. The red line in Fig. 10 corresponds to a contribution of K0 IV star and the cyan line to a G8 subgiant, as was determined in Sect. 3.3. Although we have argued that the secondary star has a much smaller radius than a sub-giant, their SED should not differ substantially from our object. For simplicity, the contribution of the secondary can be fitted alternatively by a ~5000 K black body (smooth continuous red line). Apparently, the secondary alone with 40–45% input around 5000 Å cannot account for the whole IR flux, even if some of the disparity between the optical and the IR data is caused by the variability of the object. Moreover, there is a strong unaccounted UV radiation. In theory, the UV excess can be fitted with a second black body with a temperature of ~19 000 K (blue dashed line). The sum of a K0 star and a 19 000 K black body is drawn by a black line. However, the origin of the UV radiation source is not obvious. When the energy budget is considered, it appears that the hot component must have a radius only ten times smaller than the cool component to produce sufficient flux to be represented by the blue dash line in Fig. 10. This is certainly inconsistent with the size of the WD primary. Thus, the UV excess needs a different explanation than a black body coming from a stellar component. A radiation from an accretion disk can also be excluded, because usually there are much higher temperatures in the inner parts of the disk, and the corresponding SED at these frequencies is a flat power law. Fortunately, a SED like this has been observed and successfully interpreted before. Szkody et al. (2006), using GALEX observations, discovered that the UV flux from the polar EF Eri is much higher than the underlying 9500 K white dwarf might produce, and that it is highly modulated with the orbital period. Subsequently, Campbell et al. (2008) reported IR observations of the same object with SpeX on the IRTF and showed that its near-IR SED is dominated by cyclotron emission and that the cyclotron emission can satisfactory explain the UV flux as well. To do this, the white dwarf must have a complex multi-pole structure with a variety of field strengths instead of a simple centered dipole with only two components. Beuermann et al. (2007) showed that such complex multi-pole structures exist in more than one object. For EF Eri, in addition to low-strength pole components, they inferred a quite large B ≈ 100 MG field strength. Campbell et al. (2008) used a B = 115 MG value to successfully fit the observed UV flux and its variability. We believe that similarly, the IR and UV-excess observed in V479 And is caused by a cyclotron emission from a highly magnetic white dwarf with a complex field structure and a range of strengths that generates cyclotron lines on both sides of the optical domain.

4. Classification of V479 And

We to summarize what we were able to learn about V479 And so far. The object is a binary with a 14.3 h orbital period. One of the stellar components is a late-G–early-K evolved star. The strong emission lines suggest that it is an interacting binary with a matter transfer from the visible star to an accreting compact and undetected component. The highly ionized plasma emits not only in hydrogen and neutral helium lines, but also in He ii, which is comparable in strength to the intense Hβ. The radial velocity amplitude and the orbital phasing of the wings of the H and He lines advocate that there is hot plasma closely associated with the accreting stellar component. In a classical interacting close binary system the matter transferred from the donor star to the more massive companion forms an accretion disk, which is the source of emission lines and a hot continuum. However, an accretion disk hardly ever produces such a strong He ii line, and even if it does, the emission normally comes from a smaller area with a hot spot. If there is such a spot, the emission lines obtain a narrow component that varies with a different phase than the rest of the disk and is detected as an S-wave within the broader emission lines formed in the bulk of the disk. It is also remarkable that the cores of the emission lines are symmetrical, narrow and probably devoid of radial velocity variability. These facts coupled with the flatness of Balmer decrement speak in favor of more diffuse and static gas than which can be found in an accretion disk. The form of the SED in the UV also does not correspond to that of an accretion disk. Therefore, we conclude that the accretion in this object probably occurs not via a disk.

The alternative is magnetically governed accretion onto the surface of a highly magnetized white dwarf. We propose a polar scenario to explain the modulated X-ray light curve of the object. It also helps to understand the UV and IR excess in terms of cyclotron emission from a strongly magnetic white dwarf. Accordingly, the magnetic nature of this binary system is deduced from the above mentioned variability and the strong high-ionization lines of He ii in the optical spectrum. The discovery of V1309 Ori (RX 0515.41+0104.6) at an eight hour orbital period (Garnavich et al. 1994), twice as long as the nearest known long-period polar, caused confusion, because to maintain the synchronization of the white dwarf at a separation corresponding to an eight hour period, the magnetic field must be extremely strong or the accretion rate low, which was not observed (Shafter et al. 1995; Beuermann et al. 1996). To resolve the paradox, Frank et al. (1995) suggested that the secondary star in V1309 Ori, which was identified as an early-M dwarf, might be slightly evolved, possess a strong magnetic field and stellar wind, which would ensure the necessary accretion rate and synchronization by dipole-dipole locking of two magnetic components. For V1309 Ori it is difficult to produce an evolved secondary, because the nuclear evolution of an M0–M1 star would take 1011 years to expand sufficiently. For V479 And the orbital period is almost twice as long that of V1309 Ori, but the secondary is more massive and the probability that it is evolved is much higher.

thumbnail Fig. 11

Requirements for synchronizing the white dwarf spin as a function of the magnetic field of the white dwarf and the mass transfer rate from the donor. The white dwarf spins synchronously if B exceeds the limit shown by the dash-dotted line. Above the solid line the accretion disk is absent since the pressure of the equatorial magnetic field exceeds the free-fall ram pressure of the accretion stream. The shaded area corresponds to the mass accretion rates determined for V479 And from X-ray luminosity. Isolines of equal velocity calculated for the treading region, i.e., the highest velocity reached by the stream of matter from the donor star to the treading radius where the magnetosphere of white dwarf captures matter and diverts it to the white dwarf surface are shown by dashes. This is the radial velocity of the emission line components that are expected to be emitted if the stream and, particularly, the coupling region are ionized.

We have no measurement of the magnetic field, but we can assume that the magnetic field strength is sufficient to prevent formation of the disk and to synchronize rotation of the white dwarf with the orbital period. We consider the place of V479 And in the Ṁ– B plane (Fig. 11). We relied on the prescriptions provided by Warner (1996), where a modest magnetic moment of the donor star (on the order of 100 G) was also taken into account, to calculate the corresponding relations. The solid line corresponds to the radius of the magnetosphere at which the formation of an accretion disk is prevented (Eq. (31) in Warner 1996). It appears that the condition for synchronization requires significantly weaker fields, marked by the dash-dot line (Ch. 4 in Warner 1996, and references therein). With dashed lines we also show the velocity of particles in the ballistic stream when it reaches the coupling region where it is captured by the magnetosphere and channeled onto the white dwarf. Assuming that the X-ray luminosity is generated by the accretion on the magnetic pole, we can estimate the lower limit of the accretion rate (Ṁ ≈ 1016.4 g s-1). At log  Ṁ > 16.4 a B > 80 MG magnetic field is necessary to prevent formation of a disk and at the same time to synchronize the spin of white dwarf. Such a magnetic field will also generate cyclotron lines in the UV. At such a radius the ballistic stream has a significant velocity, and if the matter there is ionized, we should see the corresponding velocities in the emission line profiles.

A standard polar scenario assumes mass transfer via a stream of matter leaving the L1 point and falling ballistically toward the more massive magnetic white dwarf. The stream of matter that reaches the magnetosphere of the white dwarf is captured at the so-called treading region and is channeled to the magnetic pole via magnetic lines. In the absence of accretion disk, emission lines of polars originate mostly in the stream (in ballistic and/or magnetic part) and sometimes from the irradiated face of the donor star. As a result, emission lines in polars usually appear to be multi-component, asymmetric, some with large velocity amplitudes, all modulated with the orbital period with distinct phases. We see none of this in V479 And. If the emission lines originated in the stream, the wings of the emission lines would be asymmetric and the double-Gaussian procedure would not convolve in most of the orbital phases. Thus, we assume that mass transfer in this system occurs not through the stream, but rather via stellar wind from a donor star caught in an evolutionary expansion. We further speculate that the bulk of the emission lines is radiated by the ionized wind matter, which is captured by the gravitational and magnetic fields of the WD and ultimately channeled onto the magnetic pole of the WD. This channeled part has an intrinsic velocity that broadens the line and is more significant in the wings of the lines. For the same reason this emission line component becomes narrower when the observer’s line of sight is aligned with the streamed matter, i.e., near the phase when the magnetic pole shines toward the observer and the X-ray flux intensity reaches maximum, as can be seen by comparing Figs. 4 and 9.

In a way, this object is similar to the small group of systems that were called low accretion rate polars (LARP) when they were first discovered (Reimers et al. 1999; Reimers & Hagen 2000), which were recently renamed pre-polars (Schmidt et al. 2005). Vogel et al. (2011) argued that the magnetic WD in these CVs captures matter from the weak wind (10-13 M⊙ yr-1) of pre-main sequence red dwarfs. Others believe there is a stream departing from L1 (Tovmassian & Zharikov 2007; Kafka et al. 2010). In V479 And  however, the mass accretion rate is at least 103 times higher than in pre-polars that contain M-type donors and 100 times higher than the wind of a main-sequence mid-G star can provide. Nuclear evolution of the donor to the terminal age main-sequence will not increase mass loss rate by the wind to such a degree. In a close binary with coupled magnetic fields the wind-loss process can be different from non-magnetic systems, but the angular momentum loss rate differs from the “standard” one that is usually applied in CV studies by a factor of several only (e.g., Cohen et al. 2012). There are no specific models to describe the situation with V479 And  and our observations do not provide sufficient information to unambiguously identify the mode of mass transfer. It might be possible that the donor star fills its Roche lobe, but we are not able to see the stream because of the orientation of the flow, lack of ionization of the high-velocity component, or maybe because the interacting magnetic fields prevent ballistic trajectory.

Despite the possible difference in evolution, in the absence of any more realistic models, we illustrate the possible origin of V479 And with the model for a non-magnetic system in which the donor is filling its Roche lobe and losing mass via L1. We speculate that whatever angular momentum loss mechanism brought the donor star into contact, the dominant factor that determines evolution of the system after Roche lobe overflow (RLOF) by the donor is the evolutionary state of the latter at the instant of overflow. Then, if the time scale of angular momentum loss by the system is not drastically different from the time scale of that process in the “standard” scenarios applied in the studies of non-magnetic CVs, as concluded by Cohen et al. (2012), we may expect that the subsequent evolution will be close to the path presented below. We also expect that in the RLOF mode of mass transfer the magnetic nature of the white dwarf would not alter the evolutionary scenario developed for non-magnetic systems.

thumbnail Fig. 12

Spectral types and effective temperatures of the donors of CVs (black dots) and LMXB (green triangles) plotted vs. their orbital periods (an update of the Beuermann et al. 1998 list). CVs with remarkably long periods are marked individually. V479 And is shown by a solid blue square. The black dot-dashed line marks the bifurcation period. The red line corresponds to the periods of semi-detached systems with main-sequence donors and 0.7 M⊙ accretors. The evolutionary track of the system with initial masses of donor and accretor equal to 1 M⊙ is plotted with the blue line. Dotted parts of the line correspond to a detached state, solid parts of the line to the semi-detached state, while the dash-dotted part corresponds to the semi-detached state in which the mass transfer rate is below 10-10 M⊙ yr-1 and the system may hardly be observed. (i) effective temperatures of CVs below about 4500 K (later than K5) are considered as unreliable and (ii) evolutionary models with gray atmosphere boundary conditions overestimate the Teff of low-mass stars (Chabrier & Baraffe 1997).

In Fig. 12 we present an orbital period – spectral type of the donor – effective temperature diagram for CVs. The thick red line connecting dots for different mass stars shows this relation based on Eq.  (2.87) from Warner (1995), which assumes that the secondaries follow the empirical mass-radius relation for main-sequence stars; the calibration of spectral types and effective temperatures is based on empirical data from Knigge (2006) and Malkov (2007). Systems with low-mass donors mostly remain close to the red line since the donors are not nuclearly evolved. Their deviation from this line is discussed in detail by Knigge et al. (2011). The donors with initial mass 0.95 ≲ M2/M⊙ ≲ 1.3 may exhaust a significant fraction of the hydrogen in their cores prior to RLOF. Then, depending on the central hydrogen abundance of the donor (Xc), upon RLOF, newborn CV might evolve to shorter or longer orbital periods (Tutukov et al. 1985, 1987), i.e., “converge” or to “diverge” (in the terms coined by Pylyser & Savonije 1988). For every mass combination of components in a pre-CV there is a certain critical value of the orbital period at RLOF that divides binaries into converging and diverging ones (“bifurcation period”, Pb). Bifurcation periods calculated for systems with 0.6 M⊙ accretors and (0.95–1.3) M⊙ donors are shown in Fig. 12 with a dash-dotted line. Systems in which RLOF occurs at periods only slightly shorter than Pb (corresponding to Xc ≲ 0.1) evolve into ultracompact binaries with Porb ≲  80 min, while the systems with only slightly longer periods at RLOF (initial masses of He-cores  ≲0.01 M⊙) meander close to Pb before evolving to long Porb. These systems may spend ≳100 Myr at periods ~1 day, i.e., still in the CV-range.

We show in Fig. 12 the track of a system with initial masses of donor and accretor 1 M⊙, computed assuming that angular momentum loss follows the Knigge et al. (2011) semi-empirical law (Yungelson et al., in prep.)4. In the semi-detached stage, the mass of the accretor was kept constant, since expected mass-exchange rate is low and it is assumed that all matter transferred to the donor is, furthermore, lost from the system due to hydrogen-burning shell explosions that reduce specific angular momentum of the accretor. The initial (post-common-envelope) period of the system is 2.5 days. The track crosses the position of V479 And. The donor fills its Roche lobe at Porb ≈ 0.68 day, when hydrogen just became exhausted in its center (Xc ≈ 10-12). At the position of V479 And, which is reached in  ≈ 80 Myr after RLOF, the mass of the donor is close to 0.8 M⊙, complying with the estimates of the donor mass of V479 And, and the mass-loss rate is 1.7 × 10-9 M⊙ yr-1. In the course of the preceding evolution Ṁ was close to this value; in our evolutionary picture this implies that V479 And may be a former nova. The accretion efficiency of the stream matter in non-magnetic CV is estimated to be 20–30 per cent (Zhilkin et al. 2012). Then, using expression LX ≈ (1/3)GMaṀa/Ra for the X-ray luminosity of CVs in the (0.2–10)KeV range and Ra = 109 cm, we obtain LX ≃ 1033 erg s-1, in agreement with observations. The mass transfer rate drops below 10-10 M⊙ yr-1 shortly after orbital period turnaround toward longer periods when the system, probably, will become hardly detectable (at least, if it is non-magnetic)5. It exists as a CV for ≈ 2.7 Gyr. The final state of the system is a detached pair of white dwarfs.

5. Conclusions

We presented multi-wavelength observations of the close binary system V479 And. The orbital period of the system is 0.5941 days based on the radial velocity variability of the absorption lines emanating from the late-G/early-K donor star. The radial velocity of the emission lines, the X-ray and UV radiation were all modulated with the period corresponding to the orbital one. We argued that the compact binary contains a highly magnetic accreting white dwarf with a spin period synchronized to the orbital period, which produces X-rays and cyclotron emission. The latter is not detected directly but was invoked to explain the variable IR and UV excess radiation. This makes V479 And the polar with the longest known orbital period. However, several key questions remain unresolved. The magnetic field does not manifest itself directly and we only suspect that it has a complex multipole structure with low and high field strengths. We are also not sure how the mass transfer proceeds. Roche-lobe overflow is required for the mass-transfer rate ~10-9 M⊙ yr-1, which may sustain an X-ray luminosity of ~1033 erg s-1, as estimated based on the shortest distance that assumes a main-sequence donor-star. Meanwhile, we do not have any observational evidence of the stream common for CVs. But we presented firm evidence that the donor star has to be significantly evolved and larger than a normal main-sequence star of corresponding spectral type. This provokes speculation that maybe the magnetic fields of the compact star and evolved donor are coupled (which is also required to keep the rotation of the white dwarf synchrone with the orbital period at such a long period/separation) and the mass transfer proceeds quite differently. The models presented by Cohen et al. (2012), while being far from realistic, indicate that the white dwarf magnetic field results in a significant distortion of the companion field in ways that differ according to dipole alignments, white dwarf field strength, and orbital separation. It was shown that strong magnetic fields of the white dwarf could inhibit the donor wind outflow, reducing open field regions and instead capturing the stellar wind from the donor and reducing the magnetic braking relative to single stars. Whether this might provide a sufficient mass accretion rate to fuel the observed X-ray luminosity is still doubtful. However, if that happens and the systemic angular momentum loss time scale is strongly different from the one according to the Knigge et al. (2011) law, the evolutionary scenario for V479 And may be different from the one presented in Sect. 4. If the donor star fills its Roche lobe and transfers matter in the manner as other CVs, we can expect the system to evolve into a wide pair of white dwarfs. We emphasize that other paths of evolution, if existent, are very intriguing, considering the fact that V479 And contains quite heavy white dwarf already close to the Chandrasekhar limit.

Further studies are required to clarify the nature of this object and validate speculations implied in this paper. A new time resolved UV and IR observations are vitally important to confirm the presence of cyclotron lines and affirm claims of magnetic nature of the accretion in this interesting binary system.

2

IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation.

4

For computations, an appropriately modified version of P.P. Eggleton code (Eggleton 1971; Pols et al. 1995; Eggleton 2006, priv. comm.), was used.

5

In this respect, it will be similar to the post-period-minimum ordinary CVs.

Acknowledgments

D.G.B. is grateful to CONACyT for providing the financing for his doctoral studies and to the organizers of the IAU Symposium 281 for a travel grant to attend the conference. G.T. and S.Z. acknowledge PAPIIT grants IN-109209/IN-103912 and CONACyT grants 34521-E; 151858 for resources provided for this research. J.E. has been supported by the PAPIIT grant IN122409. L.R.Y. is indebted to P.P. Eggleton for providing a copy of his evolutionary code. L.R.Y. is supported by RFBR grant 10-02-00231 and the Program of the Presidium of Russian academy of sciences P-21.

References

  1. Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Beuermann, K., Burwitz, V., Reinsch, K., Schwope, A. D., & Thomas, H.-C. 1996, in Roentgenstrahlung from the Universe, eds. H. U. Zimmermann, J. Trümper, & H. Yorke, 107 [Google Scholar]
  3. Beuermann, K., Baraffe, I., Kolb, U., & Weichhold, M. 1998, A&A, 339, 518 [NASA ADS] [Google Scholar]
  4. Beuermann, K., Euchner, F., Reinsch, K., Jordan, S., & Gänsicke, B. T. 2007, A&A, 463, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
  6. Campbell, R. K., Harrison, T. E., Schwope, A. D., & Howell, S. B. 2008, ApJ, 672, 531 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] [Google Scholar]
  8. Cohen, O., Drake, J. J., & Kashyap, V. L. 2012, ApJ, 746, L3 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dillon, M., Gänsicke, B. T., Aungwerojwit, A., et al. 2008, MNRAS, 386, 1568 [NASA ADS] [CrossRef] [Google Scholar]
  10. Echevarría, J., Michel, R., Costero, R., & Zharikov, S. 2007, A&A, 462, 1069 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Edwards, T. W. 1976, AJ, 81, 245 [NASA ADS] [CrossRef] [Google Scholar]
  12. Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
  13. Feiden, G. A., & Chaboyer, B. 2012, ApJ, 761, 30 [NASA ADS] [CrossRef] [Google Scholar]
  14. Frank, J., Lasota, J.-P., & Chanmugam, G. 1995, ApJ, 453, 446 [NASA ADS] [CrossRef] [Google Scholar]
  15. Friend, M. T., Martin, J. S., Connon-Smith, R., & Jones, D. H. P. 1990, MNRAS, 246, 654 [NASA ADS] [Google Scholar]
  16. Garnavich, P. M., Szkody, P., Robb, R. M., Zurek, D. R., & Hoard, D. W. 1994, ApJ, 435, L141 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
  18. González, D., Tovmassian, G., Zharikov, S., Aviles, A., & Echevarria, J. 2010 [arXiv:1009.5803] [Google Scholar]
  19. Kafka, S., Tappert, C., & Honeycutt, R. K. 2010, MNRAS, 403, 755 [NASA ADS] [CrossRef] [Google Scholar]
  20. Knigge, C. 2006, MNRAS, 373, 484 [NASA ADS] [CrossRef] [Google Scholar]
  21. Knigge, C., Baraffe, I., & Patterson, J. 2011, ApJS, 194, 28 [NASA ADS] [CrossRef] [Google Scholar]
  22. Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
  23. Malkov, O. Y. 2007, MNRAS, 382, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  24. Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
  25. Pylyser, E., & Savonije, G. J. 1988, A&A, 191, 57 [NASA ADS] [Google Scholar]
  26. Reimers, D., & Hagen, H.-J. 2000, A&A, 358, L45 [NASA ADS] [Google Scholar]
  27. Reimers, D., Hagen, H.-J., & Hopp, U. 1999, A&A, 343, 157 [NASA ADS] [Google Scholar]
  28. Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
  29. Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
  30. Schmidt, G. D., Stockman, H. S., & Grandi, S. A. 1983, ApJ, 271, 735 [NASA ADS] [CrossRef] [Google Scholar]
  31. Schmidt, G. D., Szkody, P., Vanlandingham, K. M., et al. 2005, ApJ, 630, 1037 [NASA ADS] [CrossRef] [Google Scholar]
  32. Schneider, D. P., & Young, P. 1980, ApJ, 238, 946 [NASA ADS] [CrossRef] [Google Scholar]
  33. Schwarz, U. J. 1978, A&A, 65, 345 [NASA ADS] [Google Scholar]
  34. Schwope, A. D., Mantel, K.-H., & Horne, K. 1997, A&A, 319, 894 [NASA ADS] [Google Scholar]
  35. Shafter, A. W. 1983, ApJ, 267, 222 [NASA ADS] [CrossRef] [Google Scholar]
  36. Shafter, A. W., Reinsch, K., Beuermann, K., et al. 1995, ApJ, 443, 319 [NASA ADS] [CrossRef] [Google Scholar]
  37. Szkody, P., Henden, A., Fraser, O. J., et al. 2005, AJ, 129, 2386 [NASA ADS] [CrossRef] [Google Scholar]
  38. Szkody, P., Harrison, T. E., Plotkin, R. M., et al. 2006, ApJ, 646, L147 [NASA ADS] [CrossRef] [Google Scholar]
  39. Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
  40. Tovmassian, G. H., & Zharikov, S. V. 2007, A&A, 468, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Tovmassian, G. H., Szkody, P., Greiner, J., et al. 1999, in Annapolis Workshop on Magnetic Cataclysmic Variables, eds. C. Hellier, & K. Mukai, ASP Conf. Ser., 157, 133 [Google Scholar]
  42. Tutukov, A. V., Fedorova, A. V., Ergma, E. V., & Yungelson, L. R. 1985, Sov. Astron. Lett., 11, 52 [NASA ADS] [Google Scholar]
  43. Tutukov, A. V., Fedorova, A. V., Ergma, E. V., & Yungelson, L. R. 1987, Sov. Astron. Lett., 13, 328 [Google Scholar]
  44. van der Bliek, N. S., Manfroid, J., & Bouchet, P. 1996, A&AS, 119, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
  46. Vennes, S. 1999, ApJ, 525, 995 [NASA ADS] [CrossRef] [Google Scholar]
  47. Vogel, J., Schwope, A. D., & Schwarz, R. 2011, A&A, 530, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Warner, B. 1995, Cambridge Astrophys. Ser., 28 [Google Scholar]
  49. Warner, B. 1996, Ap&SS, 241, 263 [Google Scholar]
  50. Williams, R. E. 1980, ApJ, 235, 939 [NASA ADS] [CrossRef] [Google Scholar]
  51. Zhilkin, A. G., Bisikalo, D. V., & Boyarchuk, A. A. 2012, Physics Uspekhi, 55, 115 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Log of time-resolved observations.

In the text
Table 2

Measurements of the main emission lines.

In the text
Table 3

Radial velocity fit parameters.

In the text

All Figures

thumbnail Fig. 1

Power spectrum of the radial velocities of the secondary star. Peaks around 0.7 and 2.7 day-1 are one-day aliases of the orbital period at 1.68325 day-1. The aliases are strong because the orbital period is long and only part of a cycle is observed nightly. In the inset box of the figure the CLEANed power spectrum peak is shown, marking the precise period of the system.

In the text
thumbnail Fig. 2

Radial velocities of the absorption line complex determined by cross-correlating the object with a standard K0 star template and folded with the orbital period. The red line is the best-fit sinusoid to the measurements.
In the text
thumbnail Fig. 3

Typical Hβ line profile from a spectrum obtained in 2010 with a 2.1 FWHM spectral resolution. A single-Gaussian profile with 5.0 Å FWHM is over-plotted on the line to demonstrate that the base of the line deviates from a Gaussian.
In the text
thumbnail Fig. 4

Emission line measurements of V479 And from 2010 higher resolution spectra. The radial velocities of Hβ and He ii measured by a double-Gaussian method are marked by solid black squares in the bottom and middle panel. The horizontal bars attached to each point indicate the duration of individual exposures. The radial velocity curves obtained as sinusoidal fits to these points are overplotted. In the middle panel measurements of He ii line by single-Lorentzian fits are marked by open squares. The upper panel shows measurements of the width of the Lorentzian profiles fitted to the He ii line.
In the text
thumbnail Fig. 5

Spectra of V479 And (black) and standard stars. In the right upper panel we show the observed spectrum of the object along with a K0 IV star (red, dotted), scaled to reflect the real contribution of the secondary star to the total flux. The continuous red line over the K0 star is a high-order polynomial fit to the spectrum excluding strong absorption features. In the lower right panel, the residual (V479 And minus K0 IV) is plotted. It is well-described by a power law plotted by the dashed (blue) line. This power law is summed with the fit to the secondary star spectrum and plotted over the object in the upper panel to illustrate coincidences of the troughs in the continuum. In the left panels zoomed portions of the spectra are displayed in the λλ 4220−4340 Å (bottom) and λλ 5100−5300 Å (top) intervals. The thick black line in the left panels corresponds to the SPM spectrum, while the dotted line shows the SDSS spectrum. Two standard stars are plotted in colors, G0 V in blue, and K0 IV in red. The standard star spectra are scaled to overlap with the object in each spectral interval separately. The SPM spectra in the left panels are combined after correction for the secondary star orbital motion to increase the signal-to-noise ratio.

In the text
thumbnail Fig. 6

M2–M1 diagram for V479 And. The solution probably lies between thick diagonal lines corresponding to q = 0.54 and 0.7 as measured by RV amplitude ratio of He ii and Hβ emission lines to the absorption. Dashed curves denote the orbital inclination of the system. The shaded area corresponds to the mass range of a K0 star from ZAMS to luminosity class IV.
In the text
thumbnail Fig. 7

Md/Rd relation for low-mass stars. Crosses are parameters of normal stars measured in detached binaries, while solid red squares are measurements obtained from interferometry. A few subgiants from the sample are marked individually. The possible location of V479 And is marked by a thick black line. The thin, broken black line corresponds to main-sequence donors in CVs with shorter orbital periods.

In the text
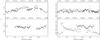thumbnail Fig. 8

Light curves of V479 And in V and I bands as indicated on the panels and obtained at four different epochs are folded with the orbital period. The integer numbers at the X-axes above each panel correspond to the orbital cycle in which the data plotted with filled squares were taken, the decimals correspond to the orbital phases. The data from immediately previous and following orbital cycles are marked with different symbols. The magnitudes at the Y-axes are calibrated using secondary standards in the field of the object.

In the text
thumbnail Fig. 9

X-ray and UV light curves folded with the orbital period and ephemerides determined from the spectroscopy. The two orbital periods were observed by Swift. The X-ray flux peaks briefly at around orbital phase 0.2, while there seems to be a deep minimum at the phase between phases 0.5 and 0.7. The UV light curve in two filters (UVW1 blue squares and UVM2 red triangles) presented in the upper panel shows a behavior similar to that in the X-ray, except that the maximum peak is shifted relative to X-rays by 0.2 orbital phases and reaches maximum at 0.4.

In the text
thumbnail Fig. 10

Spectral energy distribution of V479 And from UV to IR (right to left). The two black squares are the GALEX FUV and NUV measurements, triangles are Swift UVOT UVM2 & UVW1 filters followed by black circles corresponding to the SDSS ugriz bands and our own BVRIJ measurements marked with open pentagons. Finally, the three open black squares are 2MASS JHK measurements. The large vertical error bars are not measurements errors, but show the extent of variability detected in the corresponding filter during long-term monitoring. The filled blue pentagons are interstellar-extinction-corrected data using E(B − V) = 0.056 and the blue dashed line corresponds to SDSS spectrum after de-reddening. The continuous red and dashed blue lines are simultaneous black body fits to the observations with 5200 and 19 000 K, respectively. The cool black body corresponds to the presence of a donor star in the binary system and is also represented by K0 IV or G8 IV spectra of standard stars. The black continuous line is the sum of the K0 IV spectrum and a 19 000 K black body, which appears to fit most of the observed data well.
In the text
thumbnail Fig. 11

Requirements for synchronizing the white dwarf spin as a function of the magnetic field of the white dwarf and the mass transfer rate from the donor. The white dwarf spins synchronously if B exceeds the limit shown by the dash-dotted line. Above the solid line the accretion disk is absent since the pressure of the equatorial magnetic field exceeds the free-fall ram pressure of the accretion stream. The shaded area corresponds to the mass accretion rates determined for V479 And from X-ray luminosity. Isolines of equal velocity calculated for the treading region, i.e., the highest velocity reached by the stream of matter from the donor star to the treading radius where the magnetosphere of white dwarf captures matter and diverts it to the white dwarf surface are shown by dashes. This is the radial velocity of the emission line components that are expected to be emitted if the stream and, particularly, the coupling region are ionized.

In the text
thumbnail Fig. 12

Spectral types and effective temperatures of the donors of CVs (black dots) and LMXB (green triangles) plotted vs. their orbital periods (an update of the Beuermann et al. 1998 list). CVs with remarkably long periods are marked individually. V479 And is shown by a solid blue square. The black dot-dashed line marks the bifurcation period. The red line corresponds to the periods of semi-detached systems with main-sequence donors and 0.7 M⊙ accretors. The evolutionary track of the system with initial masses of donor and accretor equal to 1 M⊙ is plotted with the blue line. Dotted parts of the line correspond to a detached state, solid parts of the line to the semi-detached state, while the dash-dotted part corresponds to the semi-detached state in which the mass transfer rate is below 10-10 M⊙ yr-1 and the system may hardly be observed. (i) effective temperatures of CVs below about 4500 K (later than K5) are considered as unreliable and (ii) evolutionary models with gray atmosphere boundary conditions overestimate the Teff of low-mass stars (Chabrier & Baraffe 1997).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.