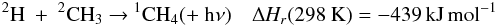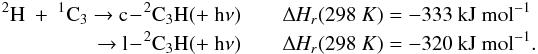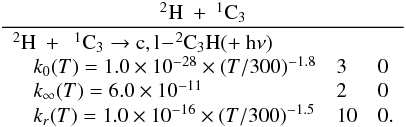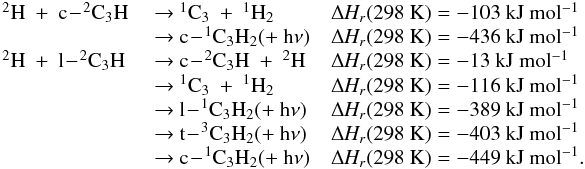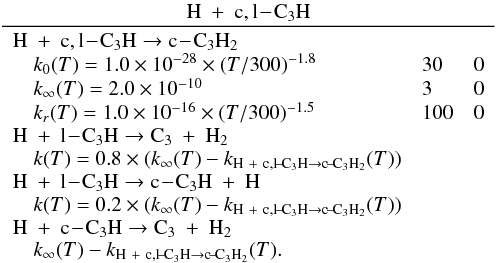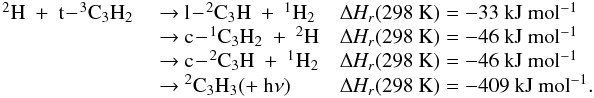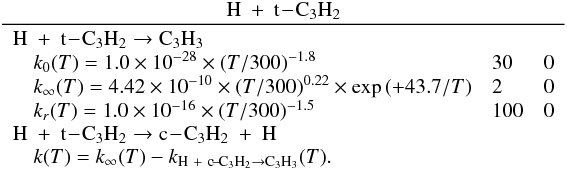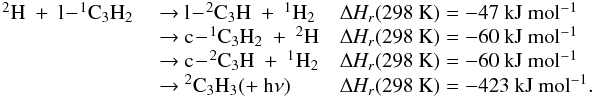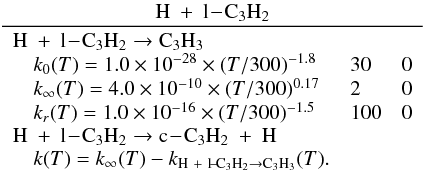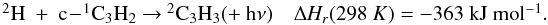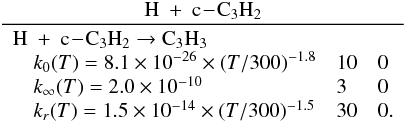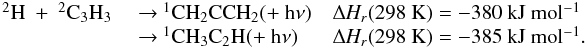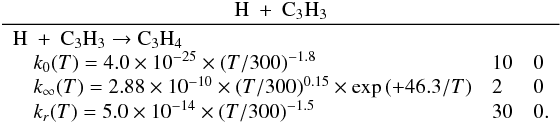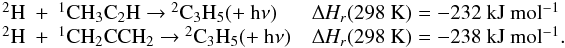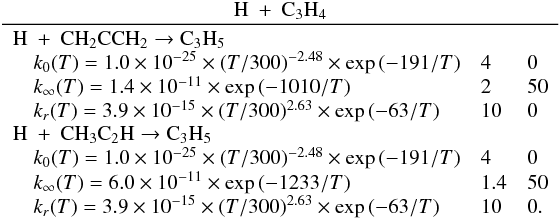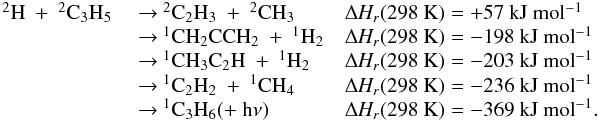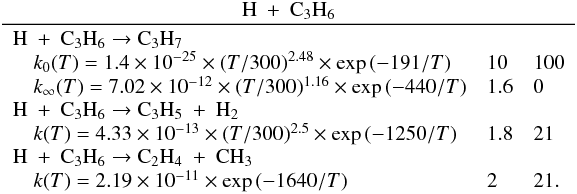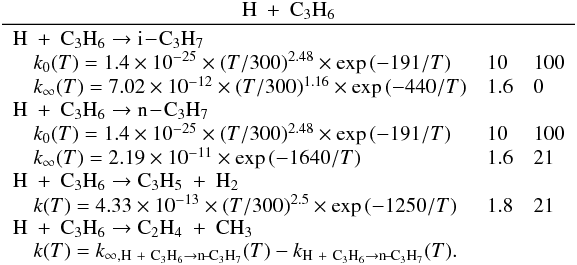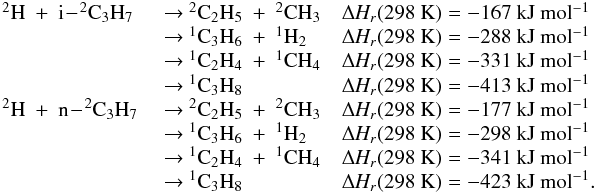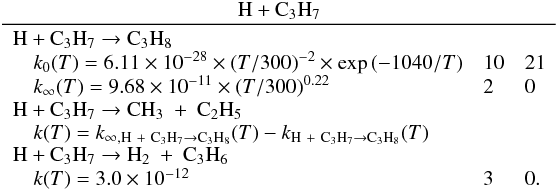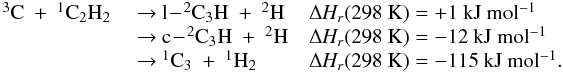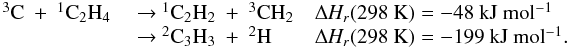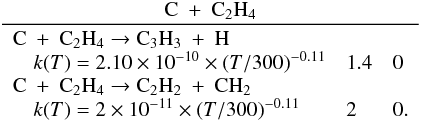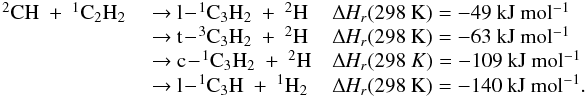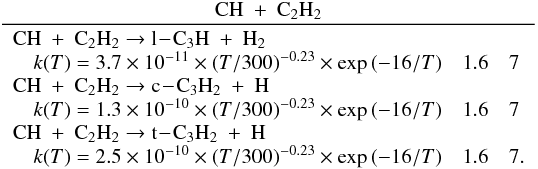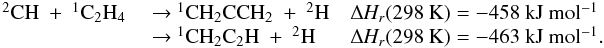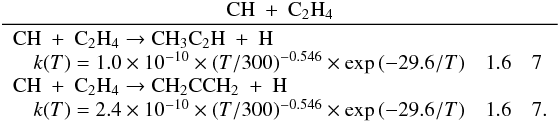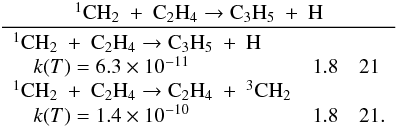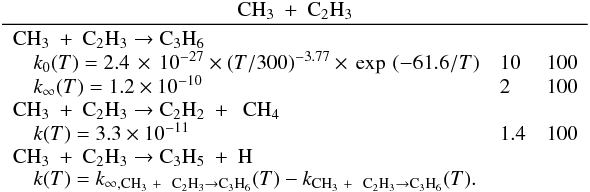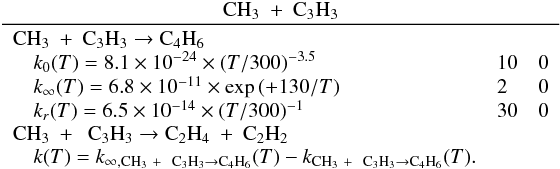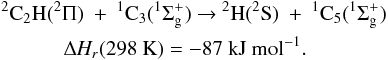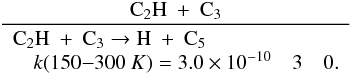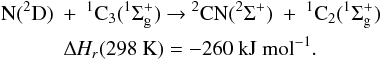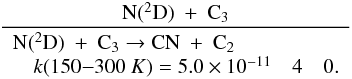| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 21 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220686 | |
| Published online | 16 April 2013 | |
Photochemistry of C3Hp hydrocarbons in Titan’s stratosphere revisited
1
Université de Bordeaux, Laboratoire d’Astrophysique de Bordeaux, UMR
5804, 33270
Floirac, France
e-mail: hebrard@obs.u-bordeaux1.fr
2
CNRS, Laboratoire d’Astrophysique de Bordeaux, UMR
5804, 33270
Floirac,
France
3
Université de Bordeaux, Institut des Sciences Moléculaires, UMR
5255, 33400
Talence,
France
4
CNRS, Institut des Sciences Moléculaires, UMR 5255,
33400
Talence,
France
Received:
1
November
2012
Accepted:
22
January
2013
The description of C3 hydrocarbon chemistry in current photochemical models of Titan’s atmosphere is found to be far from complete. We have carefully investigated the photochemistry involving C3Hp compounds in the atmosphere of Titan (considering both photolysis and neutral reactions), which considerably impacts the abundances of many other hydrocarbon species (including C2 compounds). Model results indicate that three species (C3, c-C3H2 and C3H3) could be abundant enough to be present in the Cassini/INMS data. Because the error bars on predicted C3-hydrocarbon abundances are considerably larger than those of the observational data, new experimental and theoretical studies targeting the measurement of low-temperature reaction rate constants and product branching ratios are required to reduce current model uncertainties. In particular, we highlight 30 “key reactions”, the uncertainty factors of which should be lowered to improve the quality of photochemical models involving C3Hp molecules.
Key words: planets and satellites: individual: Titan / planets and satellites: atmospheres / planets and satellites: composition / astrochemistry
© ESO, 2013
1. Introduction
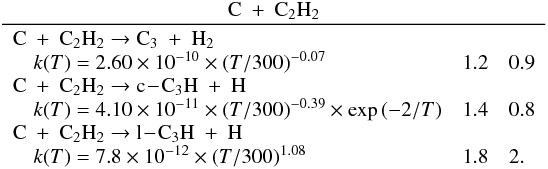
The latest results obtained by the Cassini-Huygens mission confirmed that the dissociation and ionization of methane of CH4 and nitrogen N2 in the high stratosphere of Titan initiates a complex photochemistry of hydrocarbons and nitrogen compounds through molecule-molecule and ion-molecule reactions, which leads to the production of CnHp hydrocarbons (up to n = 6 at least; the heaviest hydrocarbon clearly detected is benzene, see for instance Brown et al. 2009, for a comprehensive review of our current knowledge about Titan). The modeling of such an atmospheric system is limited by the lack of kinetic and photolytic data at low temperature (T ∈ [100,150] K) especially for heavy hydrocarbons. Hébrard et al. (2007) pointed out that a great deal of information regarding the larger species (n > 3) is missing from current photochemical models. In particular, only a small fraction of all possible reactions producing or involving C3-compounds is included in current photochemical models, from which we conclude that several important processes could be missing. To correctly understand how the C3-, C4- and C6-hydrocarbons previously detected in the atmosphere of Titan (CH3C2H, C3H6, C3H8, C4H2 and C6H6) are produced, it is necessary to complete the chemical scheme for lighter species (i.e., C2- and C3-compounds). In a recent study, Hébrard et al. (2012) updated the chemical scheme of C2-hydrocarbons to provide a solid basis for the study of HCN and HNC neutral productions. In this previous model, we modified various rate constants and branching ratios for reactions involving C and CH. These changes did not play a major role in the chemistry of HCN/HNC but strongly affected C and C3Hp concentrations. One of the main changes concerned the C + C2H2 reaction, which was predicted to lead to the formation of the C3H2 adduct (as in all photochemical models of giant planets’ and Titan’s atmospheres where this reaction is present, Lebonnois et al. 2001; Wilson & Atreya 2004; Moses et al. 2005; Lavvas et al. 2008) but in fact leads to the formation of C3 + H2 and C3H + H (see Appendix C). Moreover, Zhang et al. (2010) highlighted the fact that atomic carbon C is likely to be more abundant in Titan’s upper atmosphere than previously predicted. Carbon atoms are indeed efficiently produced by both the H + CH (van Harrevelt et al. 2002) and the N + CN (Daranlot et al. 2012) reactions, whereas they are only very slowly consumed by their reaction with N2 (Husain & Kirsch 1971) and do not react at all with CH4 (Husain & Kirsch 1971; Kim et al. 2003). As a result, the C + C2H2 (along with C + C2H4) reaction is an efficient source of C3Hp species, such as C3, a very stable bi-carbene molecule found to be abundant in various interstellar media (Oka et al. 2003; Mookerjea et al. 2010) and in comets (Huggins 1881; Rousselot et al. 2001), but absent from any current models of Titan’s atmosphere. In the present study, we continue our systematic approach to improve the neutral chemical scheme of Titan’s atmosphere, focusing specifically on C3-hydrocarbons. This work is also important for the modeling of ion-molecule reactions involving C3Hp species in the ionosphere of Titan, and vice versa. Abundances of neutral species (and their uncertainties) and ion species are indeed strongly coupled (Carrasco et al. 2007). The Ion and Neutral Mass Spectrometer (INMS) instrument onboard Cassini moreover revealed a few neutrals with densities that pure neutral photochemical chemistry could not easily reproduce. This is for example the case for benzene C6H6, which has been detected in abundance with the INMS instrument, the production of which is now assumed to involve ion chemistry, and notably dissociative recombinations (Westlake et al. 2012; Plessis et al. 2012).
Another important question clearly points out the need for a careful study of C3-hydrocarbons chemistry. From an uncertainty propagation study and a global sensitivity analysis point of view, Hébrard et al. (2009) found that C3H2 is a key compound in the photochemistry of Titan (i.e., several reactions involving C3H2 are responsible for large uncertainties in the abundances of major compounds). It is therefore crucially important to update and complete the chemical scheme related to this compound. Peng et al. (2010) showed a linear increase of the uncertainty factor of species abundance with increasing molecular mass for the three major hydrocarbon families (alkanes, alkenes and alkynes) and a nonlinear uncertainty growth pattern with increasing mass for Cn and CnH2 species. Consequently, it is necessary to lower the uncertainties on the current chemical scheme of C2- and C3-hydrocarbons to improve the precision of model results for heavy hydrocarbons. This requires us to first evaluate the uncertainties on the computed abundances of C3-compounds and then to identify the key reactions responsible for the largest of them (following the methodology of Hébrard et al. 2009).
The photochemical model used in the present study is derived from the model of Hébrard et al. (2012): details about the model are given in that paper. Our methodology to improve the chemical scheme for C3-compounds is presented in Sect. 2. The abundances of C3-hydrocarbons are presented in Sect. 3. In particular, we show the main differences between the present and our previous model (Hébrard et al. 2012) and we present the main reactions that are responsible for the production and loss of the major C3-hydrocarbons (for the nominal model only). In Sects. 4 and 5 we perform an uncertainty propagation study and a global sensitivity analysis to determine the key reactions responsible for the model result uncertainties for C3-compounds. This new list of key reactions is discussed in detail in Appendix C.
2. Chemical scheme
2.1. Chemical reactions
Many important photochemical processes involving C3Hp species in Titan’s atmosphere are found to retain the C3 carbon backbone whilst changing the corresponding number of H atoms. For example, photodissociations such as the C3H6 + hν → C3H5 + H reaction lead to lower saturation levels, while the opposite is true for termolecular reactions such as the C3H5 + H + M → C3H6 + M reaction. There are only a few reactions producing C3Hp molecules from smaller carbon containing species. These include bimolecular reactions: C + C2H2, C + C2H4, CH + C2H2, CH + C2H4, CH + C2H6, 1CH2 + C2H2, 1CH2 + C2H4, CH3 + C2H and termolecular reactions CH3 + C2H3 + M and CH3 + C2H5 + M. The bimolecular reactions dominate at high altitude (above 800 km) and the termolecular reactions dominate at low altitude and higher pressures. In terms of total production flux, the CH3 + C2H3 + M and CH3 + C2H5 + M termolecular reactions are the most efficient.
In the present work, several rate constants have been updated and some reactions have been added. Our new chemical scheme, derived from the chemical scheme presented in Hébrard et al. (2006, 2009, 2012), includes 143 compounds and 944 reactions (102 photodissociation processes, 2 dissociation processes of N2 by cosmic rays, 737 bimolecular reactions and 103 termolecular reactions). A major change in this update is the introduction of radiative association reactions, following the work of Vuitton et al. (2012). The complete list of reactions is available upon request and can be downloaded from the KIDA database (Wakelam et al. 2012). In the following sections, we explain how we evaluated some unknown rate constants and how we assigned their uncertainty factors in the chemical scheme we propose.
2.2. Photolysis processes
To better describe the photochemistry of the C3Hp species, we reviewed the parameters important for their photolysis (cross sections, quantum yields and dissociation limits). The photoabsorption cross sections were calculated from formula (3) of van Hemert & van Dishoeck (2008). We also updated the photolysis parameters for C2H2 and HC3N. Table 1 presents the photodissociation limits corresponding to the exit channel exothermicities for barrierless dissociations or to the exit Transition State (TS) energies when the values are known. These values correspond to the product appearance only if photodissociation arises from the unimolecular decay of a molecule in an excited vibrational level of the electronic ground state formed by a non-radiative transition from the electronically excited state. Experimental branching ratio determinations are very scarce. Uncertainties on these branching ratios are therefore very large, particularly below 200 nm where many exit channels are possible. We discuss of the quantum yields and dissociation limits in Appendix A for all species presented in Table 1 along with the absorption cross sections for selected important species.
New or modified photodissociation processes included in the model (update of Hébrard et al. 2012).
2.3. Methodology for the chemical review
The reactions and rate constants were updated following the same procedure used to complete the photochemistry of HCN and HNC (Hébrard et al. 2012). First, a systematic literature search was performed (particularly for the reactions of C, CH and 1CH2 reactions with C2H2 and C2H4). When no information was found, we performed density functional theory (DFT) calculations at the M06-2X/cc-pVTZ level using the Gaussian09 software package (Frisch et al. 2009) to evaluate the presence and the values of any energetic barriers to the entrance valley for the important reactions (in terms of production and/or loss rate). For some critical reactions or when DFT results were ambiguous, we also performed MRCI+Q/cc-pVTZ calculations using the Molpro software package (Werner et al. 2010). When no energetic barrier was found present, the value of the considered rate constant was estimated using long-range forces, mainly through dispersion interactions (Stoecklin & Clary 1992; Georgievskii & Klippenstein 2005) and by taking into account the electronic degeneracy, γel. We investigated certain association reactions that play a major role in Titan’s atmosphere but are not well characterized, particularly in the low-pressure region. We present in Appendix B a semi-empirical model (called “kassociation − ρ”), based on the calculations of Vuitton et al. (2012) and also on various experimental rate constants, which has allowed us to estimate values of the low-pressure limiting rate constant for associations reactions, k0, as a function of the vibrational density of states of the adduct, ρ(E0). We also applied this model to some radiative association processes addressed by Vuitton et al. (2012) as well as in earlier calculations.
Many of the reactions involved in the atmosphere of Titan are of the type atom/radical + radical or atom/radical + unsaturated compound. For these processes, there is often competition between the formation of bimolecular products and adduct stabilization. Adduct stabilization A + B → C designates the conjugation of the termolecular reaction A + B + M → C + M and the radiative association A + B → C + hν. When bimolecular product formation occurs through a distinct mechanism, we can easily separate the bimolecular channel from the adduct formation channel. For example, for H atom abstraction in the reactions of H and CH3 with some hydrocarbon radicals, there is either a direct pathway or an adduct formation pathway followed by an elimination. However, the TSs for this latter type of system leading from the adduct to H2 or CH4 products are generally located above the energy of the separated reagents, as is the case for the H + C2H5 → C2H4 + H2 (Irle & Morokuma 2000) and the CH3 + C2H5→ CH4 + C2H4 reactions (Zhu et al. 2004). For the H + C2H3 reaction, the TSs leading to H2 and C2H2 are below the entrance level (Chang et al. 1998) but an experimental study by Monks et al. (1995) strongly indicated that H2 + C2H2 formation occurs mainly through a direct mechanism. Therefore we considered here that H-atom abstraction is always a direct channel, clearly separated from the other bimolecular product channels that arise from adduct formation. When bimolecular product formation occurs through the same first step as adduct formation, i.e., through addition, we cannot separate bimolecular product formation from adduct stabilization. A good example is the H + C2H5 → C2H6/CH3 + CH3 reaction. Here, bimolecular product formation competes with adduct stabilization and with redissociation to the reagents. The main effect of the existence of an exit bimolecular channel from the adduct is to reduce the fraction of adduct stabilization at low pressure, which leads to a lower value for the low-pressure limiting rate constant k0. For small systems (CHp, C2Hp) with an open bimolecular exit channel from the adduct, adduct stabilization is negligible when compared with bimolecular reaction for pressures below 0.1−1 Torr (corresponding to altitudes greater than ~200 km in Titan’s atmosphere). In most cases we can therefore neglect adduct stabilization. For large systems or when the bimolecular exit TSs are located close to the entrance level, adduct stabilization cannot be ignored. To deal with such systems we must consider a multiple-well treatment using the master equation for each system, which is beyond the scope of this study. Instead, we used experimental values for the termolecular reaction rate constant (when these were available in the literature) or we estimated them using our semi-empirical “kassociation − ρ” model, dividing k0 (and kr) values by factors between 10 and 1000, depending on the size of the system and the position of the exit TS to take into account the effect of the open bimolecular exit channel. When the radiative association was estimated to be very weak (<10-16 cm3 molecule-1 s-1), it was neglected. When there is a competition between adduct stabilization and bimolecular product formation, we considered that the total rate constant was a constant leading to kbimolecular = k∞ − kadduct (see Appendix B). This competitive behaviour is always considered at the outset, but can be neglected for most reactions. Exceptions include the H + C2H5, H + C3H, H + l,t-C3H2 and H + C3H7 reactions (for which the k0 values are low) and the H + C3H6, H + C4H3, CH3 + C2H3 and CH3 + C3H3 reactions (for which the k0 values are high). This competitive behavior is neglected for all other investigated reactions as our results are relevant only for altitudes above 200 km. However, many association reactions may play a more important role at altitudes lower than 200 km, for example the C2H + alkenes reactions (Woon & Park 2009). Details on how rate constants and uncertainty factors were calculated are given in Appendix B.
 |
Fig. 1 Comparison between the previous model of Hébrard et al. (2012) (blue solid line) with the present work (red solid line) for four representative compounds: acetylene C2H2, ethane C2H6, diacetylene C4H2 and benzene C6H6. 5th and 15th 20-quantiles (red long-dashed lines) and 1st and 19th 20-quantiles (red short-dashed lines) for the abundances distributions of the present model are also given. |
2.4. Importance of isomers
In reconsidering the chemical network for C3 hydrocarbon species, we have found it necessary to introduce several isomers of species already present in the chemical scheme for two main reasons. Firstly, if the various isomers are present at sufficiently high densities, they might be distinguished by observations. Secondly, the different isomers may also have different chemical reactivity than the other species present in the model and introducing them might open some new chemical pathways that were absent from the previous model. As a result, some reactions with new isomers could also be key reactions because they could prove to be a significant source of uncertainties in the current photochemical model. In the present study, we have introduced the isomers of two compounds: C3H and C3H2. We did not consider the isomers of the other C3-compounds for several reasons. One isomer of C3H3 is considerably more stable than the others. For C3H7, we considered only one isomer because n-C3H7 and i-C3H7 have been shown to have similar reactivities (Tsang 1988). Nevertheless, reactions involving these isomers as reactants are likely to have different products, so it will be necessary to differentiate between these isomers when studying heavier hydrocarbons (Cn-compounds, n > 3). It is also important to note that the reactivity of N(4S) with the various isomers introduced can give different products. Future studies of the inclusion of nitrogen in complex organic compounds for Titan’s atmosphere should therefore pay particular attention to these reactions.
3. Photochemical model results
First, we stress the limitations of our model. Microphysics of particles in Titan’s lower stratosphere and troposphere as well as the attenuation of solar photons by aerosols and the impact of cosmic rays in the lower atmosphere are not taken in account in our model (except for the dissociation of N2). As a consequence, the results presented here for altitudes below approximately 200 km are not fully relevant. It is also important to note that including aerosols in the model would introduce additional uncertainties in the calculations of the actinic flux and of condensation processes. The propagation of these uncertainties is not treated in the present model. Due to the absence of coupling with ions in the upper atmosphere, the total production and loss of some neutral compounds is only poorly constrained above 800 km (Plessis et al. 2012). The aim of the present work is to improve the neutral photochemistry of Titan’s atmosphere (which will serve as a basis for future modeling studies including ion-molecule reactions), not to constrain some physical parameters (like the eddy diffusion coefficient). The incident solar flux at every level in the atmosphere was calculated as a function of the diurnally averaged unattenuated solar flux at the top of the atmosphere for a medium solar activity (normalized from Thuillier et al. 2004).
3.1. Comparison with the previous model of Hébrard et al. (2012)
To illustrate how the model results have been affected by the improvement of the chemical scheme for C3-compounds, we compare our results with the recent model of Hébrard et al. (2012) (quoted as “previous model” in the following). We first checked to what extent the update of the chemical scheme for C3Hp compounds affected the abundances of nitrogen compounds, C2-hydrocarbons and Cn-hydrocarbons (n > 3). For nitrogen compounds, the difference between the previous and the present model results are small and always within the error bars of the model, whatever the altitude. For hydrocarbons, the situation depends on the compounds (see Fig. 1). For some compounds, the difference is noticeable but still lies within the error bars of the model (like C2H6 and C4H10). For other compounds the difference is outside the error bars of the model (like C2H2 and C6H6) and can reach several orders of magnitude (like C4H2 and C4H6).
 |
Fig. 2 Comparison of the previous model of Hébrard et al. (2012) (blue solid lines) with the present work (red solid lines) for the carbon trimer C3, 2-cyclopropyn-1-yl c-C3H and 2-propynylidyne l-C3H, cyclopropenylidene c-C3H2, propadienylidene l-C3H2 and propynylidene t-C3H2, propargyl radical C3H3 and allyl radical C3H5. |
 |
Fig. 3 Comparison of the previous model of Hébrard et al. (2012) (blue solid lines) with the present work (red solid lines) for methylacetylene CH3C2H and allene CH2CCH2, propene C3H6, propyl radical C3H7 and propane C3H8. |
More evidently, the present update has a noticeable effect on the abundances of many C3-compounds, mainly C3, C3H, C3H2, C3H3, C3H4 and C3H6. Comparisons between the previous and the present models are presented in Figs. 2 and 3. For the other C3-compounds the differences are less pronounced between the two models and are within the error bars of the model (see also Figs. 4−7).
3.2. Main production and loss processes
In the following, the main processes that contribute to the production or the loss of a given compound are given at the steady state for the nominal set of rate constants (unperturbed by the Monte-Carlo procedure explained in Sect. 4). Values in parentheses give the relative importance in percentage terms of the total production or loss rates. The emphasis is placed on compounds that show pronounced differences between the previous and the present model. Owing to the uncertainty factors attached to all reactions and all abundances, the relative importance of each reaction to the total production and loss rates might be very different in the Monte-Carlo runs than in the nominal one.
 |
Fig. 4 Abundance profiles of the carbon trimer C3 and cyclopropenylidene c-C3H2 obtained after 900 runs. Thick black solid line: initial profile. Black dotted line: median profile obtained from the uncertainty propagation study. Black dashed-dotted lines: 5th and 15th 20-quantiles of the distribution. Black long-dashed lines: 1st and 19th 20-quantiles of the distribution. |
 |
Fig. 5 Abundance profiles of the propargyl radical C3H3 and propene C3H6 obtained after 900 runs. Thick black solid line: initial profile. Black dotted line: median profile obtained from the uncertainty propagation study. Black dashed-dotted lines: 5th and 15th 20-quantiles of the distribution. Black long-dashed lines: 1st and 19th 20-quantiles of the distribution. The red open triangle refers to Cassini/INMS observations from Magee et al. (2009). |
 |
Fig. 6 Abundance profiles of methylacetylene CH3C2H and allene CH2CCH2 obtained after 900 runs. Black solid line: initial profile. Black dotted line: median profile obtained from the uncertainty propagation study. Black dashed-dotted lines: 5th and 15th 20-quantiles of the distribution. Black long-dashed lines: 1st and 19th 20-quantiles of the distribution. The blue open diamond refers to ISO observations from Coustenis et al. (2003), the red open triangle to Cassini/INMS observations from Magee et al. (2009), the green crossed squares to Cassini/INMS observations from Cui et al. (2009), the orange squares to the corrected Cassini/INMS observations from Cui et al. (2009), the pink crosses to the Cassini/CIRS observations at 3.5˚N from Vinatier et al. (2010). |
 |
Fig. 7 Abundance profiles of propane C3H8 obtained after 900 runs. Black solid line: initial profile. Black dotted line: median profile obtained from the uncertainty propagation study. Black dashed-dotted lines: 5th and 15th 20-quantiles of the distribution. Black long-dashed lines: 1st and 19th 20-quantiles of the distribution. The blue open diamond refers to ISO observations from Coustenis et al. (2003), the red open triangle to Cassini/INMS observations from Magee et al. (2009), the green crossed squares to Cassini/INMS observations from Cui et al. (2009), the orange square to the corrected Cassini/INMS observations from Cui et al. (2009), the pink crosses to Cassini/CIRS observations at 3.5˚N from Vinatier et al. (2010). |
3.2.1. Carbon trimer C3
C3 was
introduced in the previous model, but was described by only a limited network of
reactions. As shown in Fig. 2, the present update
of the earlier reaction scheme has a dramatic effect on the abundance of
C3 in the lower
atmosphere and C3
is now the most abundant C3Hp species above 700 km. The main
source for C3 at
high altitudes is the C + C2H2 reaction, whereas at lower altitudes, the H +
l-C3H and,
especially, the H + c-C3H processes take over gradually. The main processes
responsible for the loss of C3 in the lower atmosphere are the termolecular reactions,
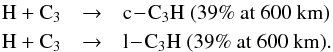 These associations were not present in the
previous model. The photolysis of C3 leading to the formation of C2 and C represents 18% of the
total loss at 600 km.
These associations were not present in the
previous model. The photolysis of C3 leading to the formation of C2 and C represents 18% of the
total loss at 600 km.
3.2.2. 2-cyclopropyn-1-yl c-C3H and 2-propynylidyne l-C3H
Cyclic C3H
(c-C3H) and
linear C3H
(l-C3H) are
predicted to have similar abundances (within a factor 2) but their relatively low
densities throughout the atmosphere, as a result of their high reactivity with atomic
hydrogen H, probably prevent a differentiation in their putative detection. Their
profiles differ noticeably from C3H profile (which was considered as a single species in
the previous model) below 700 km, where several important reactions for C3H were missing. For instance,
at 600 km, the main processes responsible for their production are
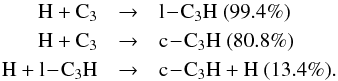 None of these reactions were present in our
previous model. We found that both C3H isomers have a similar reactivity with the other
species present in the model. We also note (see Sect. 5) that two reactions involving l-C3H are key reactions for the production of the carbon
trimer C3.
None of these reactions were present in our
previous model. We found that both C3H isomers have a similar reactivity with the other
species present in the model. We also note (see Sect. 5) that two reactions involving l-C3H are key reactions for the production of the carbon
trimer C3.
3.2.3. Cyclopropenylidene c-C3H2
Cyclic C3H2 (c-C3H2) is by far the most abundant C3H2 isomer. Nevertheless, the
importance of the propadienylidene l-C3H2 and propynylidene t-C3H2 isomers lies in their
different reactivity with many compounds. As an example, N(4S) is supposed to react only
with t-C3H2 to produce HC3N. Also, the three isomers react differently with
CH3 to produce
C2H3, which is involved in many subsequent reactions. Figure
2 clearly shows that c-C3H2 is even more abundant in the
present work than total C3H2 in the previous model (which was considered as a single
species previously). Many reactions participate in the production of c-C3H2 in the upper atmosphere of
Titan (above 800 km, which corresponds to the altitude where the total production rate
of c-C3H2 is at its maximum), including
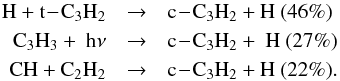 This production is counterbalanced by the
photolysis of c-C3H2, which represents 93% of its total loss around 1000 km.
None of these reactions were present in our previous model.
This production is counterbalanced by the
photolysis of c-C3H2, which represents 93% of its total loss around 1000 km.
None of these reactions were present in our previous model.
3.2.4. Propargyl radical C3H3
C3H3 is much more abundant in the upper atmosphere in the
present model than in the previous one. However, the main reactions that contribute to
the total production rate are similar in the two models. For instance, at 1000 km, these
are: 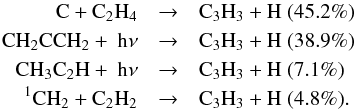 The increase in the abundance of
C3H3 comes from a nonlinear competition between reactions
involving atomic hydrogen H (H + c-C3H2, H + C3H3) and C3H4 isomers photodissociation.
The increase in the abundance of
C3H3 comes from a nonlinear competition between reactions
involving atomic hydrogen H (H + c-C3H2, H + C3H3) and C3H4 isomers photodissociation.
3.2.5. Propene C3H6
C3H6 is found to be much more abundant in the present model
compared to the previous one. At 1000 km, the main reactions that contribute to the
production of this molecure are 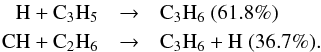 The rate constant of the first addition
reaction has been updated since the previous model to include radiative association.
Whilst termolecular reaction is negligible at this altitude, radiative association is
seen to be important even if the rate is predicted to be relatively slow.
The rate constant of the first addition
reaction has been updated since the previous model to include radiative association.
Whilst termolecular reaction is negligible at this altitude, radiative association is
seen to be important even if the rate is predicted to be relatively slow.
Key reactions responsible for the uncertainties on major C3Hp compounds at an altitude of 1300, 1000, 600, and 200 km.
4. Uncertainty propagation study
4.1. Method
The methodology used to study the propagation of uncertainties in the model is described in Hébrard et al. (2007, 2009). In this study, we performed 900 Monte-Carlo runs to obtain statistically significant results. The integration time for each run was set to 1012 s for simplicity and to limit the computation time. This time is sufficient to reach a steady state for each run. The uncertainty factor was set to 1.2 for all photodissociation rates for simplicity (see Peng et al. (2012) for a valuable discussion about uncertainties on photodissociation rates). A detailed investigation of all sources of uncertainties in these photodissociations rates (arising mainly from uncertainties in absorption cross sections and quantum yields) is beyond the scope of the present paper but should be performed in the future to improve the present model.
4.2. Results
Abundance distribution types depend on the compound and can vary with altitudes: distributions are not always normal or log-normal for a given altitude. In this case, quantiles are useful measures to represent the distributions. Consequently, Figs. 4−6 display both the 5th and 15th 20-quantiles and the 1st and 19th 20-quantiles, which represent the intervals containing respectively 50% and 90% of the abundance profiles for several important species in Titan’s atmosphere.
The main conclusion of these results is that although the agreement in terms of abundance is good, the current accuracy of photochemical models is quite poor for C3Hp compounds (compared to uncertainties on observations when available), especially below 800 km. Theoretical and experimental studies are clearly required to improve the situation. We see in the next section that global sensitivity analysis can pinpoint the key reactions that are responsible for these large uncertainties.
Observational data are presented to give an idea of the agreement between our photochemical model (using a mean eddy diffusion coefficient K(z), Hörst et al. 2008) and available observations for C3-compounds. We did not try to better constrain K(z) because of the current limitations of our model and uncertainties on the model results.
Key reactions responsible to uncertainties on major C3Hp compounds at an altitude of 1300, 1000, 600, and 200 km.
5. Global sensitivity analysis: determination of key reactions
The technique we used to determine the key reactions is based on the computation of Rank Correlation Coefficients (RCCs) between reaction rate constants and mole fractions at different altitudes. It has been previously used and described in Carrasco et al. (2007), Dobrijevic et al. (2008) and Hébrard et al. (2009). The greater the absolute value of the RCC, the more significant the contribution of a given reaction rate to the uncertainty on the mole fraction of a given species. Consequently, all reactions with a high RCC absolute value should be targeted to improve the accuracy of the model. The power of this technique to improve photochemical models has already been demonstrated for Titan by Hébrard et al. (2009) and for Neptune by Dobrijevic et al. (2010).
Tables 2 and 3 give RCCs for the main C3-species. The RCC threshold has been arbitrarily set to 0.2. This choice gives for each compound a reasonable set of reactions allowing us to pinpoint only the most significant ones. Thirty key reactions were identified for four representative altitudes. We see that association reactions in general are predicted to be significant in all parts of the atmosphere. The termolecular reaction H + C2H2 → C2H3 in particular is a key reaction for all but one of the C3-compounds, listed in Tables 2 and 3. Comments on some of these reactions are given in Appendix C.
The reaction N(2D) + HCN → CH + N2 is also a main key reaction for HCN (see Hébrard et al. 2012). A discussion about the reaction H + CH → C + H2 can be found as a datasheet in the KIDA database (Wakelam et al. 2012). Details about these two reactions are therefore not repeated here.
6. Conclusion
We have performed a systematic study of all potentially important processes that produce or consume C3Hp compounds. This extensive review has led us to make recommendations for a large number of reaction rates and therefore to improve significantly the chemical schemes published so far for Titan’s atmosphere. Several photolysis processes were updated and the rate constants and branching ratios for many bimolecular reactions between neutral species were updated/reinvestigated. A new semi-empirical model based on previous calculations and various experimental data was implemented to allow us to predict the rates of the most important termolecular reactions and radiative associations for Titan’s atmosphere. Our update of the chemical network relating to C3Hp substantially modified the overall chemical scheme of Titan’s atmosphere. We showed that several important reactions were indeed missing from our previous model (Hébrard et al. 2012) and also from other current photochemical models. This improvement of the C3Hp chemistry has noticeable effects on the abundances of C2- and Cn-compounds (n > 3), which are more or less pronounced, depending on the compound. For some species the differences brought about by the update stay within the error bars of the previous model (such as for C2H6), whereas for other compounds the differences lead to predicted abundances outside the error bars of the previous model (such as for C2H2, C2H4, C6H6). In some cases, the update has resulted in a change in predicted abundance of several orders of magnitude (for example, C4H2 is over two orders of magnitude less abundant at low altitudes in the updated model). We showed in particular that a careful update of the chemical scheme for a given family of compounds can have a drastic effect (or no effect at all) for other seemingly unrelated compounds. It is therefore important to complete the chemical scheme as far as possible before creating a reduced scheme that can be able to correctly predict the abundance of all the atmospheric constituents.
We found that many of the main processes involving the C3Hp species in Titan’s atmosphere recycle C3Hp species (which essentially changes the degree of saturation of the C3 backbone), either through photodissociations or through reactions with H atoms. There are only a few reactions that produce C3Hp species: bimolecular reactions such as C + C2H2, C + C2H4, CH + C2H2, CH + C2H4, CH + C2H6, 1CH2 + C2H2, 1CH2 + C2H4 and CH3 + C2H3 and association reactions like CH3 + C2H3 and CH3 + C2H5.
We found that some C3-molecules such as the carbon trimer C3, the cyclopropenylidene radical c-C3H2 and the propargyl radical C3H3 present predicted abundances high enough to be potentially present in the Cassini/INMS data and should therefore be considered in models that aim to interpret these spectra.
The present work confirms previous studies Hébrard et al. (2007, 2009, 2012) that demonstrated that the uncertainties in the results of current photochemical models of Titan’s atmosphere could be very important and that the theoretical/experimental determination of rate constants and branching ratios at low temperature is crucial to better constrain in fine some physical parameters.
Among all the new processes introduced in the present chemical scheme, some are important reactions for the production and loss of C3-compounds and/or are also identified as key reactions (reactions for which the uncertainty factors need to be lowered to improve the predictivity of photochemical models) by uncertainty propagation and global sensitivity analysis. We showed in this study only the most significant key reactions for C3-compounds. The complete list of all main key reactions for Titan’s atmosphere (concerning all species for which observational data are available) will be available from the KIDA database.
Our model does not take into account ionic chemistry, which is known to have a noticeable
impact on the abundances of neutral species (see Plessis et
al. 2012). As a consequence, it is important to keep in mind that the abundances of
some compounds presented in our study might be significantly affected by the coupling of our
neutral chemical scheme with a ionospheric model. This is the case in particular for
C3. Considering the
Proton Affinity of C3
(767 kJ mol-1, Hunter & Lias 1998) and because exothermic proton
transfer reactions generally do not present a barrier, C3 will react with the most abundant
ions in Titan’s ionosphere (HCNH+, CH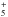 , C2H
, C2H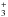 , C2H
, C2H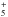 ), which will lead to C3H+ formation. Ionic chemistry is
likely to be a strong sink for C3 because C3H+ loss will be dominated by its reaction with
CH4 (Raksit & Bohme 1983).
), which will lead to C3H+ formation. Ionic chemistry is
likely to be a strong sink for C3 because C3H+ loss will be dominated by its reaction with
CH4 (Raksit & Bohme 1983).
The next step of the present study should be the improvement of C4Hp chemistry (photolysis and neutral reactions). Considering the results we present here, we may expect that such an update of the chemical scheme could have a significant impact on the abundances of many compounds (even lighter ones).
This study might also help us to better understand the complexification of organic compounds in Titan’s atmosphere.
Acknowledgments
E.H. acknowledges support from the European Research Council (ERC Starting Grant 209622: E3ARTHs).
References
- Adachi, H., & Basco, N. 1981, Int. J. Chem. Kinet., 13, 367 [CrossRef] [Google Scholar]
- Aguilera-Iparraguirre, J., Daniel Boese, A., Klopper, W., & Ruscic, B. 2008, Chem. Phys., 346, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksandrov, E., Arutyunov, V., Dubrovina, I., & Kozlov, S. 1980, Kinet. Catal. Engl. Trans., 21, 1323 [Google Scholar]
- Atkinson, D. B., & Hudgens, J. W. 1999, J. Phys. Chem. A, 103, 4242 [CrossRef] [Google Scholar]
- Baulch, D., Cobos, C., Cox, R., et al. 1992, J. Phys. Chem. Ref. Data, 21, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Baulch, D., Cobos, C., Cox, R., et al. 1994, J. Phys. Chem. Ref. Data, 23, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Baulch, D. L., Bowman, C. T., Cobos, C. J., et al. 2005, J. Phys. Chem. Ref. Data, 34, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeat, A., & Loison, J.-C. 2001, Phys. Chem. Chem. Phys., 3, 2038 [CrossRef] [Google Scholar]
- Berman, M., Fleming, J., Harvey, A., & Lin, M. 1982, Chem. Phys., 73, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Borrell, P., Cervenka, A., & Turner, J. W. 1971, J. Chem. Soc. B, 2293 [Google Scholar]
- Boullart, W., Devriendt, T., Borms, R., & Peeters, J. 1996, J. Phys. Chem., 100, 998 [CrossRef] [Google Scholar]
- Brouard, M., Macpherson, M. T., & Pilling, M. J. 1989, J. Phys. Chem., 93, 4047 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, R., Lebreton, J.-P., & Waite, H. 2009, Titan from Cassini-Huygens (New York: Springer) [Google Scholar]
- Butler, J., Fleming, J., Goss, L., & Lin, M. 1981, Chem. Phys., 56, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Camilleri, P., Marshall, R., & Purnell, J. 1974, J. Chem. Soc., Faraday Trans. 1, 70, 1434 [CrossRef] [Google Scholar]
- Canosa, A., Sims, I., Travers, D., Smith, I., & Rowe, B. 1997, A&A, 323, 644 [NASA ADS] [Google Scholar]
- Canosa-Mas, C. E., Frey, H. M., & Walsh, R. 1985, J. Chem. Soc., Faraday Trans. 2: Mol. Chem. Phys., 81, 283 [CrossRef] [Google Scholar]
- Carrasco, N., Hébrard, E., Banaszkiewicz, M., Dobrijevic, M., & Pernot, P. 2007, Icarus, 192, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Castiglioni, L., Bach, A., & Chen, P. 2006, Phys. Chem. Chem. Phys., 8, 2591 [CrossRef] [Google Scholar]
- Chang, K. W., & Graham, W. R. M. 1982, J. Chem. Phys., 77, 4300 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, A. H. H., Mebel, A. M., Yang, X. M., Lin, S. H., & Lee, Y. T. 1998, Chem. Phys. Lett., 287, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Chastaing, D., James, P., Sims, I., & Smith, I. 1998, Faraday Discuss., 109, 169 [Google Scholar]
- Chastaing, D., James, P., Sims, I., & Smith, I. 1999, Phys. Chem. Chem. Phys., 1, 2247 [Google Scholar]
- Chastaing, D., Picard, S. D. L., Sims, I. R., & Smith, I. W. M. 2001, A&A, 365, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, F., Judge, D., & Wu, C. 2000, Chem. Phys., 260, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C., Braams, B., Lee, D. Y., et al. 2011, J. Phys. Chem. A, 115, 6797 [CrossRef] [Google Scholar]
- Clarke, D. W., & Ferris, J. P. 1995, Icarus, 115, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Cody, R. J., Payne, W. A., Thorn, R. P., et al. 2002, J. Phys. Chem. A, 106, 6060 [CrossRef] [Google Scholar]
- Cody, R. J., Romani, P. N., Nesbitt, F. L., et al. 2003, J. Geophys. Res., 108, 5119 [Google Scholar]
- Costes, M., Halvick, P., Hickson, K. M., Daugey, N., & Naulin, C. 2009, ApJ, 703, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Coustenis, A., Salama, A., Schulz, B., et al. 2003, Icarus, 161, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, J., Yelle, R., Vuitton, V., et al. 2009, Icarus, 200, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Daranlot, J., Hincelin, U., Bergeat, A., et al. 2012, Proc. Natl. Acad. Sci. U. S. A., 109, 10233 [Google Scholar]
- Davis, S. G., Law, C. K., & Wang, H. 1999a, Comb. Flame, 119, 375 [CrossRef] [Google Scholar]
- Davis, S. G., Law, C. K., & Wang, H. 1999b, J. Phys. Chem. A, 103, 5889 [CrossRef] [Google Scholar]
- Deyerl, H.-J., Fischer, I., & Chen, P. 1999, J. Chem. Phys., 111, 3441 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrijevic, M., Carrasco, N., Hébrard, E., & Pernot, P. 2008, Planet. Space Sci., 56, 1630 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrijevic, M., Cavalié, T., Hébrard, E., et al. 2010, Planet. Space Sci., 58, 1555 [NASA ADS] [CrossRef] [Google Scholar]
- Dubnikova, F., & Lifshitz, A. 1998, J. Phys. Chem. A, 102, 3299 [CrossRef] [Google Scholar]
- Eisfeld, W. 2006, J. Phys. Chem. A, 110, 3903 [CrossRef] [Google Scholar]
- Fahr, A., & Nayak, A. 2000, Int. J. Chem. Kinet., 32, 118 [CrossRef] [Google Scholar]
- Fahr, A., Laufer, A., & Tardy, D. 1999, J. Phys. Chem. A, 103, 8433 [CrossRef] [Google Scholar]
- Faravelli, T., Goldaniga, A., Zappella, L., et al. 2000, Proc. Combust. Inst., 2601 [Google Scholar]
- Fernandes, R., Luther, K., & Troe, J. 2006, J. Phys. Chem. A, 110, 4442 [CrossRef] [Google Scholar]
- Forst, W. 1991, J. Phys. Chem., 95, 3612 [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2009, Gaussian 09 Revision A.1, Gaussian Inc. Wallingford CT [Google Scholar]
- Galland, N., Caralp, F., Hannachi, Y., Bergeat, A., & Loison, J.-C. 2003, J. Phys. Chem. A, 107, 5419 [CrossRef] [Google Scholar]
- Gannon, K., Blitz, M., Liang, C.-H., et al. 2010a, Faraday Discuss., 147, 1 [CrossRef] [Google Scholar]
- Gannon, K. L., Blitz, M. A., Liang, C. H., et al. 2010b, J. Phys. Chem. A, 114, 9413 [CrossRef] [Google Scholar]
- Georgievskii, Y., & Klippenstein, S. J. 2005, J. Chem. Phys., 122, 194103 [NASA ADS] [CrossRef] [Google Scholar]
- Gingerich, K. A., Finkbeiner, H. C., & Schmude, R. W. 1994, J. Am. Chem. Soc., 116, 3884 [CrossRef] [Google Scholar]
- Goncher, S. J., Moore, D. T., Sveum, N. E., & Neumark, D. M. 2008, J. Chem. Phys., 128, 114303 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, S., Mulac, W., & Nangia, P. 1971, J. Phys. Chem., 75, 2087 [NASA ADS] [CrossRef] [Google Scholar]
- Gosavi, R. K., Safarik, I., & Strausz, O. P. 1985, Can. J. Chem., 63, 1689 [CrossRef] [Google Scholar]
- Goulay, F., Trevitt, A. J., Meloni, G., et al. 2009, J. Am. Chem. Soc., 131, 993 [CrossRef] [Google Scholar]
- Groß, C., Noller, B., & Fischer, I. 2008, Phys. Chem. Chem. Phys., 10, 5196 [CrossRef] [Google Scholar]
- Guadagnini, R., Schatz, G. C., & Walch, S. P. 1998, J. Phys. Chem. A, 102, 5857 [CrossRef] [Google Scholar]
- Haider, N., & Husain, D. 1993a, J. Chem. Soc., Faraday Trans., 89, 7 [Google Scholar]
- Haider, N., & Husain, D. 1993b, J. Photochem. Photobiol. A – Chem., 70, 119 [CrossRef] [Google Scholar]
- Halpern, J. A., Miller, G. E., Okabe, H., & Nottingham, W. 1988, J. Photochem. Photobiol. A – Chem., 42, 63 [Google Scholar]
- Hanning-Lee, M. A., & Pilling, M. J. 1992, Int. J. Chem. Kinet., 24, 271 [CrossRef] [Google Scholar]
- Harding, L. B., Georgievskii, Y., & Klippenstein, S. J. 2005, J. Phys. Chem. A, 109, 4646 [CrossRef] [Google Scholar]
- Harding, L., Klippenstein, S., & Georgievskii, Y. 2007, J. Phys. Chem. A, 111, 3789 [CrossRef] [Google Scholar]
- Harich, S., Lee, Y. T., & Yang, X. 2000a, Phys. Chem. Chem. Phys., 2, 1187 [CrossRef] [Google Scholar]
- Harich, S., Lin, J. J., Lee, Y. T., & Yang, X. 2000b, J. Chem. Phys., 112, 6656 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, E., Dobrijevic, M., Bénilan, Y., & Raulin, F. 2006, J. Photochem. Photobiol. C – Photochem. Rev., 7, 211 [Google Scholar]
- Hébrard, E., Dobrijevic, M., Bénilan, Y., & Raulin, F. 2007, Planet. Space Sci., 55, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, E., Dobrijevic, M., Pernot, P., et al. 2009, J. Phys. Chem. A, 113, 11227 [CrossRef] [PubMed] [Google Scholar]
- Hébrard, E., Dobrijevic, M., Loison, J. C., Bergeat, A., & Hickson, K. M. 2012, A&A, 541, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E. 1982, Chem. Phys., 65, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., Roueff, E., & Talbi, D. 2010, Mol. Phys., 108, 2171 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, G. H., Lin, M. S., Wang, Y. L., & Chang, T. W. 1998, J. Chem. Phys., 109, 5868 [NASA ADS] [CrossRef] [Google Scholar]
- Holbrook, K. A., Pilling, M. J., & Roberston, S. H. 1996, Unimolecular reactions, 2nd edn. (Chichester: John Wiley & Sons Ltd.) [Google Scholar]
- Hörst, S. M., Vuitton, V., & Yelle, R. V. 2008, J. Geophys. Res. – Planet., 113, 10006 [Google Scholar]
- Huggins, W. 1881, Proc. R. Soc. Lond., 33, 1 [CrossRef] [Google Scholar]
- Hunter, E. P. L., & Lias, S. G. 1998, J. Phys. Chem. Ref. Data, 27, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Husain, D., & Kirsch, L. 1971, Trans. Faraday Soc., 67, 2025 [CrossRef] [Google Scholar]
- Irle, S., & Morokuma, K. 2000, J. Chem. Phys., 113, 6139 [NASA ADS] [CrossRef] [Google Scholar]
- Jodkowski, J. T., Ratajczak, E., Fagerstrom, K., et al. 1995, Chem. Phys. Lett., 240, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, E. W. 1993, J. Phys. Chem., 97, 11681 [CrossRef] [Google Scholar]
- Kim, G.-S., Nguyen, T., Mebel, A., Lin, S., & Nguyen, M. 2003, J. Phys. Chem. A, 107, 1788 [CrossRef] [Google Scholar]
- Knyazev, V. D., & Slagle, I. R. 2001, J. Phys. Chem. A, 105, 3196 [CrossRef] [Google Scholar]
- Kovàcs, T., Blitz, M. A., & Seakins, P. W. 2010, J. Phys. Chem. A, 114, 4735 [CrossRef] [Google Scholar]
- Läuter, A., Lee, K., Jung, K., et al. 2002, Chem. Phys. Lett., 358, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Lavvas, P. P., Coustenis, A., & Vardavas, I. M. 2008, Planet. Space Sci., 56, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Le, T. N., Lee, H., Mebel, A. M., & Kaiser, R. I. 2001, J. Phys. Chem. A, 105, 1847 [CrossRef] [Google Scholar]
- Lebonnois, S., Toublanc, D., Hourdin, F., & Rannou, P. 2001, Icarus, 152, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S.-H., Lee, Y.-Y., Lee, Y. T., & Yang, X. 2003, J. Chem. Phys., 119, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J.-C., & Bergeat, A. 2009, Phys. Chem. Chem. Phys., 11, 655 [CrossRef] [Google Scholar]
- Luo, C., Du, W.-N., Duan, X.-M., & Li, Z.-S. 2008, ApJ, 687, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Magee, B. A., Waite, J. H., Mandt, K. E., et al. 2009, Planet. Space Sci., 57, 1895 [NASA ADS] [CrossRef] [Google Scholar]
- Maksyutenko, P., Zhang, F., Gu, X., & Kaiser, R. I. 2010, Phys. Chem. Chem. Phys., 13, 240 [CrossRef] [Google Scholar]
- Martin, J. M. L., & Taylor, P. R. 1995, J. Chem. Phys., 102, 8270 [NASA ADS] [CrossRef] [Google Scholar]
- Matsugi, A., Suma, K., & Miyoshi, A. 2011, J. Phys. Chem. A, 115, 7610 [CrossRef] [Google Scholar]
- McKee, K., Blitz, M. A., Hughes, K. J., et al. 2003, J. Phys. Chem., 107, 5710 [Google Scholar]
- Mebel, A. M., & Kaiser, R. I. 2002, Chem. Phys. Lett., 360, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Mebel, A. M., Jackson, W. M., Chang, A. H. H., & Lin, S. H. 1998, J. Am. Chem. Soc., 120, 5751 [CrossRef] [Google Scholar]
- Mebel, A. M., Kislov, V. V., & Hayashi, M. 2007, J. Chem. Phys., 126, 204310 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. A., & Klippenstein, S. J. 2003, J. Phys. Chem. A, 107, 2680 [CrossRef] [Google Scholar]
- Miller, J. A., Senosiain, J. P., Klippenstein, S. J., & Georgievskii, Y. 2008, J. Phys. Chem. A, 112, 9429 [CrossRef] [Google Scholar]
- Minsek, D. W., & Chen, P. 1993, J. Phys. Chem., 97, 13375 [CrossRef] [Google Scholar]
- Monks, P. S., Nesbitt, F. L., Payne, W. A., et al. 1995, J. Phys. Chem., 99, 17151 [NASA ADS] [CrossRef] [Google Scholar]
- Monninger, G., Förderer, M., Gürtler, P., et al. 2002, J. Phys. Chem. A, 106, 5779 [CrossRef] [Google Scholar]
- Mookerjea, B., Giesen, T., Stutzki, J., et al. 2010, A&A, 521, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moses, J., Fouchet, T., Bézard, B., et al. 2005, J. Geophys. Res. - Planet., 110, E08001 [NASA ADS] [CrossRef] [Google Scholar]
- Nakashima, N., & Yoshihara, K. 1987, Laser Chemistry, 7, 177 [CrossRef] [Google Scholar]
- Nguyen, T. L., Mebel, A. M., & Kaiser, R. I. 2001a, J. Phys. Chem A., 105, 3284 [CrossRef] [Google Scholar]
- Nguyen, T. L., Mebel, A. M., Lin, S. H., & Kaiser, R. I. 2001b, J. Phys. Chem. A, 105, 11549 [CrossRef] [Google Scholar]
- Ni, C.-K., Huang, J. D., Chen, Y. T., Kung, A. H., & Jackson, W. M. 1999, J. Chem. Phys., 110, 3320 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T., Thorburn, J. A., McCall, B. J., et al. 2003, ApJ, 582, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Park, W. K., Park, J., Park, S. C., et al. 2006, J. Chem. Phys., 125, 081101 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Z., Dobrijevic, M., Hebrard, E., Carrasco, N., & Pernot, P. 2010, Faraday discussions, 147, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Z., Cailliez, F., Dobrijevic, M., & Pernot, P. 2012, Icarus, 218, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Plessis, S., Carrasco, N., Dobrijevic, M., & Pernot, P. 2012, Icarus [Google Scholar]
- Qu, Y., Su, K., Wang, X., et al. 2010, J. Comput. Chem., 31, 1421 [Google Scholar]
- Raksit, A. B., & Bohme, D. K. 1983, Int. J. Mass Spectrom. Ion Proc., 55, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Rousselot, P., Arpigny, C., Rauer, H., et al. 2001, A&A, 368, 689 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Satyapal, S., & Bersohn, R. 1991, J. Phys. Chem., 95, 8004 [CrossRef] [Google Scholar]
- Seakins, P., Robertson, S., Pilling, M., et al. 1993, J. Phys. Chem., 97 [Google Scholar]
- Seki, K., & Okabe, H. 1992, J. Phys. Chem., 96, 3345 [CrossRef] [Google Scholar]
- Seki, K., He, M., Liu, R., & Okabe, H. 1996, J. Phys. Chem., 100, 5349 [CrossRef] [Google Scholar]
- Selby, T. M., Meloni, G., Goulay, F., et al. 2008, J. Phys. Chem. A, 112, 9366 [CrossRef] [Google Scholar]
- Silva, R., Gichuhi, W. K., Kislov, V. V., et al. 2009, J. Phys. Chem. A, 113, 11182 [CrossRef] [Google Scholar]
- Sivaramakrishnan, R., Su, M. C., Michael, J. V., et al. 2011, J. Phys. Chem. A, 115, 3366 [CrossRef] [Google Scholar]
- Slagle, I. R., Gutman, D., Davies, J. W., & Pilling, M. J. 1988, J. Phys. Chem., 92, 2455 [CrossRef] [Google Scholar]
- Smith, I. W. M. 1989, Chem. Phys., 131, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. P. 2003, Chem. Phys. Lett., 376, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Stoecklin, T., & Clary, D. C. 1992, J. Phys. Chem., 96, 7346 [CrossRef] [Google Scholar]
- Stoliarov, S. I., Knyazev, V. D., & Slagle, I. R. 2000, J. Phys. Chem. A, 104, 9687 [CrossRef] [Google Scholar]
- Stranges, D., Stemmler, M., Yang, X., et al. 1998, J. Chem. Phys., 109, 5372 [NASA ADS] [CrossRef] [Google Scholar]
- Stranges, D., O’Keeffe, P., Scotti, G., Santo, R. D., & Houston, P. L. 2008, J. Chem. Phys., 128, 151101 [NASA ADS] [CrossRef] [Google Scholar]
- Szpunar, D. E., Morton, M. L., Butler, L. J., & Regan, P. M. 2002, J. Phys. Chem. B, 106, 8086 [CrossRef] [Google Scholar]
- Takayanagi, T. 2006, J. Phys. Chem. A, 110, 361 [CrossRef] [Google Scholar]
- Takahashi, J., & Yamashita, K. 1996, J. Chem. Phys., 104, 6613 [NASA ADS] [CrossRef] [Google Scholar]
- Teng, L., & Jones, W. E. 1972, J. Chem. Soc., Faraday Trans. 1: Phys. Chem. Cond. Phases, 68, 1267 [Google Scholar]
- Thiesemann, H., MacNamara, J., & Taatjes, C. 1997, J. Phys. Chem. A, 101, 1881 [CrossRef] [Google Scholar]
- Thiesemann, H., Clifford, E. P., Taatjes, C. A., & Klippenstein, S. J. 2001, J. Phys. Chem. A, 105, 5393 [CrossRef] [Google Scholar]
- Thorn, R. P., Payne, W. A., Chillier, X. D. F., et al. 2000, Int. J. Chem. Kin., 32, 304 [CrossRef] [Google Scholar]
- Thuillier, G., Floyd, L., Woods, T. D., et al. 2004, Adv. Space Res., 34, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Tonokura, K., & Koshi, M. 2000, J. Phys. Chem. A, 104, 8456 [CrossRef] [Google Scholar]
- Tsang, W. 1988, J. Phys. Chem. Ref. Data, 17, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Tsang, W. 1991, J. Phys. Chem. Ref. Data, 20, 221 [NASA ADS] [CrossRef] [Google Scholar]
- van Harrevelt, R., van Hemert, M. C., & Schatz, G. C. 2002, J. Chem. Phys., 116, 6002 [NASA ADS] [CrossRef] [Google Scholar]
- van Hemert, M., & van Dishoeck, E. 2008, Chem. Phys., 343, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Vazquez, J., Harding, M. E., Gauss, J., & Stanton, J. F. 2009, J. Phys. Chem. A, 113, 12447 [CrossRef] [Google Scholar]
- Vereecken, L., & Peeters, J. 1999, J. Phys. Chem. A, 103, 5523 [CrossRef] [Google Scholar]
- Vereecken, L., Pierloot, K., & Peeters, J. 1998, J. Chem. Phys., 108, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Vinatier, S., Bézard, B., Nixon, C. A., et al. 2010, Icarus, 205, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Vuitton, V., Yelle, R. V., Lavvas, P., & Klippenstein, S. J. 2012, ApJ, 744, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, H., & Zellner, R. 1972, Ber. Bunsenges. Phys. Chem., 667 [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJSS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Walch, S. P. 1995, J. Chem. Phys., 103, 7064 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Z.-X., & Huang, M.-B. 1998, Chem. Phys. Lett., 291, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Hou, H., Yoder, L. M., Muckerman, J. T., & Fockenberg, C. 2003, J. Phys. Chem. A, 107, 11414 [CrossRef] [Google Scholar]
- Werner, H.-J., Knowles, P. J., Knizia, G., et al. 2010, MOLPRO, version 2010.1, a package of ab initio programs, see http://www.molpro.net [Google Scholar]
- Westlake, J. H., Waite, Jr., J. H.,Mandt, K. E., et al. 2012, J. Geophys. Res. - Planet., 117, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Whitten, G. Z., & Rabinovitch, B. S. 1963, J. Chem. Phys., 38, 2466 [NASA ADS] [CrossRef] [Google Scholar]
- Whytock, D. A., Payne, W. A., & Stief, L. J. 1976, J. Chem. Phys., 65, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, E. H., & Atreya, S. K. 2004, J. Geophys. Res. - Planet., 109, E06002 [NASA ADS] [CrossRef] [Google Scholar]
- Woon, D. E., & Park, J.-Y. 2009, Icarus, 202, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X., Ajello, J. M., & Yung, Y. L. 2010, ApJ, 708, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, Y.-L., Laufer, A. H., Halpern, J. B., & Fahr, A. 2007, J. Phys. Chem. A, 111, 8330 [CrossRef] [Google Scholar]
- Zhu, R., Xu, Z., & Lin, M. 2004, J. Chem. Phys., 120, 6566 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Cross sections and quantum yield of several compounds
Appendix A.1: Photolysis of C2H2
C2H2 photodissociation was reconsidered using the latest measurements, which lead exclusively to the formation of C2H + H between 121.6 and 193 nm (Kovàcs et al. 2010; Läuter et al. 2002).
Appendix A.2: Photolysis of C3
C3(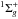 ) has two main transitions, the
) has two main transitions, the
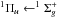 transition around 405 nm and the
transition around 405 nm and the
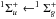 transition around 165 nm (Monninger et al. 2002; van Hemert & van Dishoeck 2008; Chang & Graham 1982). Because the dissociation limit is equal to 7.62 eV
(162.7 nm) (Baulch et al. 2005; Martin & Taylor 1995; Gingerich et al. 1994), only the
transition around 165 nm (Monninger et al. 2002; van Hemert & van Dishoeck 2008; Chang & Graham 1982). Because the dissociation limit is equal to 7.62 eV
(162.7 nm) (Baulch et al. 2005; Martin & Taylor 1995; Gingerich et al. 1994), only the
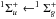 transition leads to photodissociation.
The photodissociation cross section was calculated using the oscillator strengths
calculated by van Hemert & van Dishoeck
(2008) with a constant width at half maximum Δλ = 20 nm and taking
into account the dissociation energy equal to 735.22 kJ mol-1.
transition leads to photodissociation.
The photodissociation cross section was calculated using the oscillator strengths
calculated by van Hemert & van Dishoeck
(2008) with a constant width at half maximum Δλ = 20 nm and taking
into account the dissociation energy equal to 735.22 kJ mol-1.
Branching ratios (in %) for C3H6 photolysis.
Branching ratios (in %) for HC3N photolysis.
 |
Fig. A.1 Photoabsorption cross sections for C3 along with the dissociation limits for the various channels considered. |
 |
Fig. A.2 Photoabsorption cross sections for c-C3H (top) and l-C3H (bottom) along with the dissociation limits for the various channels considered. |
 |
Fig. A.3 Photoabsorption cross sections for c-C3H2 (top), l-C3H2 (middle) and t-C3H2 (bottom) along with the dissociation limits for the various channels considered. |
 |
Fig. A.4 Photoabsorption cross sections for C3H3 along with the dissociation limits for the various channels considered. |
 |
Fig. A.5 Photoabsorption cross sections for C3H5 along with the dissociation limits for the various channels considered. |
 |
Fig. A.6 Photoabsorption cross sections for C3H7 along with the dissociation limits for the various channels considered. |
Appendix A.3: Photolysis of C3H and C3H2
c-C3H, l-C3H, c-C3H2, l-C3H2 and t-C3H2 photodissociation cross sections were calculated using the oscillator strengths calculated by van Hemert & van Dishoeck (2008) with a constant width at half maximum Δλ = 20 nm. These five radicals absorb in the UV and visible part of the spectrum where the solar flux is highest. Therefore the photodissociation will be dominated by these absorptions, which mainly lead to C-H bond rupture. The photodissociations of c-C3H and l-C3H are dominated by the visible and near-UV regions and should yield only C3 + H. The products of c-C3H2 and l-C3H2 photodissociation were derived from Mebel et al. (1998), Park et al. (2006) and Großet al. (2008) and were set to l-C3H + H (30%), c-C3H + H (30%), and C3 + H2 (40%). The C3 + H2 exit channel shows a notable exit barrier (Mebel et al. 1998; Park et al. 2006). The products of t-C3H2 photodissociation were also derived from Mebel et al. (1998) and Park et al. (2006) and were set to l-C3H + H (50%) and c-C3H + H (50%), although the spin-allowed 3C + C2H2 exit channel may not be negligible. The absorption cross sections of C3H and C3H2 are given in Figs. A.1, A.2 and A.3.
Appendix A.4: Photolysis of C3H3
The lowest energy electronic absorption spectrum of the C3H3 radical between 290 and 345 nm shows diffuse bands (Atkinson & Hudgens 1999; Eisfeld 2006; Matsugi et al. 2011), attributed to predissociation in the excited state. This leads to an upper limit of 360.1 kcal mol-1 for the bond dissociation energy, which corresponds to 346 nm and yields c-C3H2 + H. The second (strongest) absorption near 240 nm has been confirmed by Deyerl et al. (1999) by H-atom photofragment yield spectra. The main products after photodissociation at 248 nm are also C3H2 + H with a ratio H/H2 = (97.6/2.4) ± 1.2. We then assumed that C3H2 is the only product in the UV wavelength range. Identifying the different C3H2 isomers is more delicate. Deyerl et al. (1999) attributed the measured fragments to c-C3H2 + H, while an Rice−Ramsperger−Kassel−Marcus (RRKM) analysis (Nguyen et al. 2001b) found t-C3H2 + H to be the dominant channel. Goncher et al. (2008) have shown that some c-C3H2 is produced. To a first approximation, we estimated the products to be 50% c-C3H2 and 50% t-C3H2. The absorption cross section of C3H3 is given in Fig. A.4.
Appendix A.5: Photolysis of C3H4 isomers
The photoabsorption cross sections of CH3C2H and CH2CCH2 are well known (Ho et al. 1998; Chen et al. 2000). Photolysis studies of these molecules have been performed at 193 nm (Seki & Okabe 1992; Ni et al. 1999) and at 155 nm (Harich et al. 2000a,b). There are some differences. For the CH2CCH2 photolysis, the main production channels are H and C3H3 (70%) followed by CH2 + C2H2 (20%) with small yields of H2 + c-C3H2 (5%) and H2 + l-C3H2 (5%). For the CH3C2H photolysis, the main production channels are also H and C3H3 (80%) followed by CH3 + C2H (≈7%), CH2 + C2H2 (≈3%) and then H2 + c-C3H2 (5%) and H2 + l-C3H2 (5%). Photodissociation of CH3C2H at 193 nm mainly leads to CH3CC production and not to CH2CCH (Satyapal & Bersohn 1991; Seki & Okabe 1992).
Appendix A.6: Photolysis of C3H5
In Titan’s atmosphere, photodissociation of the allyl radical H2C=CH-•CH2 will be dominated by absorption near 403 nm (Tonokura & Koshi 2000; Matsugi et al. 2011) and by the strongest absorption in the 220−240 nm range (Selby et al. 2008; Nakashima & Yoshihara 1987). The absorption cross section of C3H5 is given in Fig. A.5. Photodissociation in the 403 nm band leads to H-atom loss only (Stranges et al. 1998), and mainly to CH2CCH2 + H formation (Castiglioni et al. 2006; Szpunar et al. 2002). At 248 nm the H atom loss channel has been found to be equal to 84% with the CH3 + C2H2 channel equal to 16% (corrected to 5% subsequently Stranges et al. 2008). The ratio of CH2CCH2 to CH3C2H formation in the 240−250 nm region may be estimated from Minsek & Chen (1993) and leads to a ratio between 2:1 and 3:1. RRKM calculations of the ground state dissociation (Stranges et al. 1998) favor CH3C2H formation and also lead to 31% of CH3 + C2H2 products at 351 nm in contrast to experimental results. Recent trajectory calculations (Chen et al. 2011) better agree with experimental results and mainly lead to CH2CCH2 + H formation. The recommended branching ratios for each absorption band are presented in Table 1.
 |
Fig. B.1 Low-pressure limiting and radiative association rate constants k0, kr as a function of the vibrational density of states of the adduct, ρ(E0). The stars are the experimental k0 values at 300 K, the open circles are the calculated k0 values at 300 K from Vuitton et al. (2012), the diamond is the calculated k0 value at 300 K performed for this study and the solid circles are the kr calculations at 150 K from Vuitton et al. (2012). Units on the left axis are in cm6 molecule-2 s-1 for k0 and cm3 molecule-1 s-1 for kr. Experimental data are taken from: H + NH2 (Gordon et al. 1971), H + CH3 (Brouard et al. 1989), CH3 + O2 (Fernandes et al. 2006), CH3 + NO (Kaiser 1993), CH3 + NH2 (Jodkowski et al. 1995), CH3 + CH3 (Slagle et al. 1988; Cody et al. 2002). The solid and dashed lines correspond to the general expression we derived for the low-pressure limiting rate constants k0 for H addition and CH3 addition, respectively. The dashed-dotted line corresponds to the general expression we derived for the radiative association rate constants kr. |
Appendix A.7: Photolysis of C3H6
The photofragmentation of propene (C3H6) is complex and wavelength-dependent. Considering the studies of Borrell et al. (1971) at 184 nm, of Lee et al. (2003) at 157 nm as well as the theoretical study of Qu et al. (2010), we considered the product yields to be those given in Table A.1.
Appendix A.8: Photolysis of C3H7
For the C3H7 photodissociation we considered only absorption in the 220−260 nm range from Adachi & Basco (1981), which leads to C3H6 + H (see Fig. A.6).
Appendix A.9: Photolysis of HC3N
HC3N photochemistry has been studied between 185 and 254 nm. The main channel seems to be HC3N∗∗ metastable product (Clarke & Ferris 1995; Seki et al. 1996; Halpern et al. 1988) with a quantum yield as high as 70% at 193 nm (Seki et al. 1996). The main bimolecular exit channel is H + C3N formation with a quantum yield of approximately 30% at 193 nm, whereas the C2H + CN exit channel is very minor (Seki et al. 1996). Recent experimental and ab-initio calculations (Silva et al. 2009) agree well with theoretical work from Luo et al. (2008) and lead to the branching ratios (for bimolecular products only) given in Table A.2. The possible minor production of C2 + HCN (less than 10%) as well as the production of metastable HC3N∗∗ were neglected in this study.
Appendix B: “kassociation − ρ” model to determine k0
Statistical theories allow us to calculate the temperature-dependent low-pressure
limiting rate constants k0(T) (Holbrook et al. 1996) but specific calculations are
required for each reaction. Vuitton et al. (2012)
performed a master-equation analysis to determine k0 for various
reactions and proposed a general formula (k0 = 8 × 10-30 × exp(4.7 × N),
where N is
the number of adduct carbon atoms) for saturated molecule formation (C2H6, C3H8, etc.). As stated by Vuitton et al. (2012), this relation, obtained from a
fit of their calculations, is valid only if the number of H atoms is equal or close to
2N + 2. For
unsaturated molecule formation, the rate constant is lower because of the reduced number
of vibrational modes. As many important reactions involve the formation of highly
unsaturated species, such as the C3 + H → C3H reaction, we propose a new semi-empirical model based in
part on a fit of the k0 calculations from Vuitton et al. (2012) and also on various experimental
data for barrierless addition as a function of a power of the vibrational density of
states of the adduct, ρ(E0), with
E0 corresponding to the exothermicity of
the addition. ρ(E0) was calculated
using the Whitten-Rabinovitch formula (Whitten &
Rabinovitch 1963; Holbrook et al. 1996):
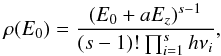 (B.1)where s is the number of
vibrators, E0 is the enthalpy of addition,
Ez is the zero-point
vibrational energy, and a is a semi-empirical parameter to account for the
level of quantization (a a value ranging between 0.80 and 0.95 is typical),
which varies as a function of molecular size and also as a function of the relative
E0/Ez
value (Holbrook et al. 1996). The vibrational
frequencies are calculated using Gaussian 2009 at the M06/aug-pVTZ level (see Fig. B.1).
(B.1)where s is the number of
vibrators, E0 is the enthalpy of addition,
Ez is the zero-point
vibrational energy, and a is a semi-empirical parameter to account for the
level of quantization (a a value ranging between 0.80 and 0.95 is typical),
which varies as a function of molecular size and also as a function of the relative
E0/Ez
value (Holbrook et al. 1996). The vibrational
frequencies are calculated using Gaussian 2009 at the M06/aug-pVTZ level (see Fig. B.1).
Radiative association rate constants, kr, are complex to calculate accurately (Herbst 1982). kr values are highly dependent on the size of the system, of the exothermicity of the addition process, and on the radiative emission rate constant, kIR. For high kr values, very long adduct lifetimes are required, close to the 1/kIR value (10-3 to 10-2 s), so that radiative associations are important only for large molecule formation. In a similar manner to the molecular association reactions, we performed a fit of the Vuitton et al. (2012) radiative association rate constants with the kr = kcapture × [kIR/(kdissociation + kIR)] expression, where kdissociation varies as a function of ρ(E0) considering similar IR emission probabilities for all adducts.
For a reaction between two chemical species A and B, the temperature dependences of k0 and kr can be approximated to T−(rA + rB + 1)/2, where r refers to the number of rotational degrees of freedom for a reactant: r = 2 for a linear species and r = 3 for a spherical top (Herbst et al. 2010). As a result and also taking into account the various experimental dependencies of H and CH3 association reactions with CH3, NO and O2 as well as the Vuitton et al. (2012) calculations, we used a T-1.8 dependence for H reactions and T-3.5 for CH3 reactions in the 100−300 K range. The temperature dependence for radiative association is more complex because the radiative rate constants saturate at kcapture if no stabilization by collision occurs.
Our “kassociation − ρ” semi-empirical model leads to
-
For H addition: k0 = 1.6 × 10-31 × (T/300)-1.8 × ρ0.9.
-
For CH3 addition: k0 = 4.0 × 10-33 × (T/300)-3.5 × ρ0.9.
-
For radiative association: kr = 1.0 × 10-18 × (T/300)-1.5 × ρ0.66 × kcapture/(1.0 × 10-18 × (T/300)-1.5 × ρ0.66 + kcapture).
To estimate the association rate constant it is difficult to use a unique formula for all
the cases because radiative association must compete with termolecular reaction. For the
C3Hp system, the radiative association
rate constants kr are in general
small with respect to kcapture. For barrierless reactions,
kcapture = k∞
and the overall kinetics are described by a modified Troe formula:
![\appendix \setcounter{section}{2} \begin{equation} k_\text{adduct} = \frac{\left( k_0[M]F + k_r \right)k_{\infty}}{k_0[M] + k_{\infty}} \end{equation}](/articles/aa/full_html/2013/04/aa20686-12/aa20686-12-eq131.png) (B.2)with
(B.2)with ![\hbox{$\log(F) = \frac{\log(F_{\rm c})}{1 + \left[ \frac{\log(k_0[M] + k_{\rm capture})}{N} \right]^2}$}](/articles/aa/full_html/2013/04/aa20686-12/aa20686-12-eq132.png) , Fc = 0.60 and
N = 1. When
the radiative association rate constants kr become comparable to
k∞, it may be more realistic for
intermediate pressure behavior to use
, Fc = 0.60 and
N = 1. When
the radiative association rate constants kr become comparable to
k∞, it may be more realistic for
intermediate pressure behavior to use ![\hbox{$k_\text{association} = \min(k_{\infty},k_r + \frac{k_0k_{\infty}[M]F}{k_0[M] + k_{\infty}})$}](/articles/aa/full_html/2013/04/aa20686-12/aa20686-12-eq136.png) , but the differences are however much
smaller than the uncertainties.
, but the differences are however much
smaller than the uncertainties.
Appendix C: Comments on selected reactions
These reactions were identified as the key reactions following our global sensitivity
analysis (see Sect. 5). For each reaction, we
recommend a value for its rate constant and its uncertainty factors along with a
justification for these recommendations. 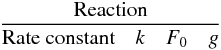 F0 is the uncertainty in the rate
constant k(T) at T = 300 K and
g is the
“uncertainty-extrapolating” coefficient defined for use with F0 to obtain the
rate constant uncertainty F(T) at different temperatures
following the expression adapted from KIDA (Wakelam et
al. 2012). k∞(T) and
kr(T)
are expressed in cm3 molecule-1 s-1 and k0(T) in
cm6 molecule-2 s-1.
F0 is the uncertainty in the rate
constant k(T) at T = 300 K and
g is the
“uncertainty-extrapolating” coefficient defined for use with F0 to obtain the
rate constant uncertainty F(T) at different temperatures
following the expression adapted from KIDA (Wakelam et
al. 2012). k∞(T) and
kr(T)
are expressed in cm3 molecule-1 s-1 and k0(T) in
cm6 molecule-2 s-1.
All following ΔHR were calculated
using  taken from Baulch et al. (2005) except for
taken from Baulch et al. (2005) except for
 (C3(X
(C3(X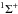 )) = 830 ± 10 kJ mol-1(Gingerich et al. 1994)
)) = 830 ± 10 kJ mol-1(Gingerich et al. 1994)
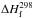 (c-C3H(X2B2)) = 715 ± 8 kJ mol-1(Costes et al. 2009)
(c-C3H(X2B2)) = 715 ± 8 kJ mol-1(Costes et al. 2009)
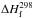 (l-C3H(X2A’)) = 728 ± 8 kJ mol-1(Costes et al. 2009)
(l-C3H(X2A’)) = 728 ± 8 kJ mol-1(Costes et al. 2009)
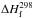 (c-C3H2(X1B1)) = 497 ± 4 kJ mol-1(Vazquez et al. 2009)
(c-C3H2(X1B1)) = 497 ± 4 kJ mol-1(Vazquez et al. 2009)
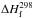 (t-C3H2(X3B)) = 543 ± 8 kJ mol-1(Aguilera-Iparraguirre et al. 2008)
(t-C3H2(X3B)) = 543 ± 8 kJ mol-1(Aguilera-Iparraguirre et al. 2008)
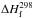 (l-C3H2(X1A1)) = 557 ± 4 kJ mol-1(Vazquez et al. 2009)
(l-C3H2(X1A1)) = 557 ± 4 kJ mol-1(Vazquez et al. 2009)
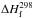 (C3H3(X2B1)) = 352 ± 4 kJ mol-1(Vazquez et al. 2009).
(C3H3(X2B1)) = 352 ± 4 kJ mol-1(Vazquez et al. 2009).
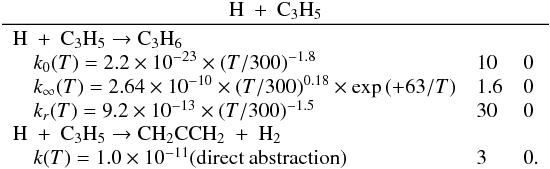
Appendix C.1: H + CH3
Brouard et al. (1989) have performed a detailed
experimental study of this reaction. Forst (1991)
performed RRKM calculations scaled to the experimental data in the 300−1000 K range, leading to the expressions
k0(T) = 2.63 × 10-28 × (T/300)-2.98 × exp−635/T
cm6
molecule-2
s-1 for He as
the bath gas with k∞(T) = 4.57 × 10-10 × (T/300)-0.20
cm3 molecule-1 s-1. The k0 expression seems reliable, but only
above 300 K. Baulch et al. (1994) proposed
k0(T) = 6.20 × 10-29 × (T/300)-1.80
cm6 molecule-2 s-1 with He as the bath gas in the 300−1000 K range and k∞(T) = 3.5 × 10-10
cm3 molecule-1 s-1. Smith
(2003) performed RRKM simulations in the 65−300 K range, leading to k0(T) = 5.1 × 10-29 × (T/300)-1.06 × exp(+ 17/T)
cm6 molecule-2 s-1 (Fc = 0.56) in He and k∞(T) = 3.5 × 10-10 × (T/300)-0.09 × exp(+ 12/T)
cm3 molecule-1 s-1. Vuitton et al.
(2012) have performed new calculations between 50 and 300 K. There is a
relatively good agreement between the calculations (Baulch et al. 1994; Smith 2003; Vuitton et al. 2012) and the experimental data
(Brouard et al. 1989), even if the results of
Vuitton et al. (2012) seem to be slightly
overestimated. However, is not possible to fit the entire temperature and pressure range
with only one expression, and the results of Vuitton et
al. (2012) are likely to be the more precise ones at low temperature and low
density. We recommend their values with k0 scaled to the available
experimental data at 300 K using the Troe expression in N2 with Fc = 0.60,
N = 1.
The radiative association rate constant given by Vuitton et al. (2012) at 150 K, kr(150 H) = 2.8 × 10-16
cm3 molecule-1 s-1, agrees relatively well with Smith (1989), who used a similar methodology, that led to a value of
7.0 × 10-16
cm3 molecule-1 s-1 without tunneling.

Appendix C.2: H + C3
There is no bimolecular exit channel for this reaction. Mebel & Kaiser (2002) performed ab initio calculations that showed no barrier at the CCSD(T)/6-311+G(3df,2p)//B3LYP/6-311G(d,p) level. Because this reaction is a very important sink for C3, we also performed DFT (M06-2X/aug-cc-pVTZ) calculations, which showed no barrier, and ab-initio calculations (MRCI+Q/aug-cc-pVTZ), that showed a very small barrier (1 kJ mol-1) for this reaction. Therefore we recommend a slightly lower value for k∞ than kcapture to take into account the possible presence of an activation barrier. (Mebel & Kaiser 2002) also showed that the isomerization barrier between both C3H isomers is considerably lower than the entrance valley. Therefore we considered to a first approximation an equal production of both isomers for termolecular reaction and also for radiative association. We estimated k0 and kr using our “kassociation − ρ” semi-empirical model. We also performed RRKM calculations in the same way for the two reactions H + C3 → C3H and the well-known H + CH3 → CH4, and obtained k0(H + C3) = 2.5 k0(H + CH3), in good agreement with our “kassociation − ρ” semi-empirical model.
With 50% of c-C3H and 50% of l-C3H production.
Appendix C.3: H + C3H
These reactions have been studied theoretically in great detail during studies of the 3C + C2H2 and 1C + C2H2 reactions (Mebel et al. 2007; Takayanagi 2006; Takahashi & Yamashita 1996; Park et al. 2006). They have no barrier on the singlet surface and on one of the triplet surfaces, which leads to various 1,3C3H2 isomers. The main exit channel leads to C3 + H2 formation on the singlet surface with a notable barrier on the exit channel located only −10 kJ mol-1 below the reactants. Recent calculations coupled with low-temperature experiments (Costes et al. 2009) indicate that the exit channel C(3P) + C2H2 might be thermoneutral or even slightly exothermic with respect to H + l-C3H. Nevertheless, once the cyclic 3C3H2 intermediate has been formed, both exit channels H + c-C3H and C + C2H2 can be reached without barrier; the former being lower in energy. As a result, the formation of C(3P) + C2H2 products is likely to be very low, whilst isomerization to H + c-C3H is also likely to be low with respect to C3 + H2 formation given the lower exit barriers. As shown experimentally (Costes et al. 2009; Bergeat & Loison 2001) and theoretically (Mebel et al. 2007), intersystem crossing is efficient enough to quickly convert 3C3H2 into 1C3H2. The electronic degeneracy factor is then high and the rate constant should be close to the capture rate constant. Taking into consideration the various uncertainties the global rate constant for H + c-C3H and H + l-C3H reactions is estimated to be equal to 2.0 × 10-10 cm3 molecule-1 s-1. Stabilization of the c-C3H2 adduct (we neglect the other l,t-C3H2 adducts) may play a non-negligible role at high pressure because the complex has a long lifetime (Park et al. 2006). Because there is one bimolecular exit channel, we considered that these association reactions had rates close to the H + C3 one, neglecting the possibility of radiative stabilization through electronic emission.
Appendix C.4: H + t-C3H2
The reaction 2H + t-3C3H2 can proceed through direct abstraction or through addition. Ab initio calculations (Nguyen et al. 2001a; Goulay et al. 2009; Harding et al. 2007; Vereecken et al. 1998) showed no barrier for addition, which leads to an excited C3H3∗∗ adduct. Subsequent evolution of C3H3∗∗ leads either to stabilization at high pressure or to H + c-C3H2. The l-C3H + H2 exit channel is thermodynamically accessible but involves a high exit barrier (40 kJ mol-1) above the exit level and close to the entrance channel. The stabilization cannot be neglected because the only exit channel (c-C3H2 + H) is not very exothermic and involves a complex rearrangement, which leads to a long C3H3 adduct lifetime. We neglected however the 2H + l-1C3H2 →2H + t-3C3H2 reaction as well as the C3H + H2 production from the adduct and also the direct C3H + H2 formation. The 2H + t-3C3H2 reagents correlate with doublet and quadruplet states but the products 2H + 1,c−C3H2 only correlate with doublet states. There is then a 2/6 = 1/3 electronic degeneracy factor for this reaction, but not for the 2H + l-1C3H2 reaction. Harding et al. (2007) performed variable reaction coordinate transition state theory calculations (VRC-TST) that led to a high value for kH + t − C3H2 → C3H3 = 4.42 × 10-10 × (T/298)0.22 × exp(+ 43.7/T) cm3 molecule-1 s-1. Because there is one bimolecular exit channel, we considered that the association reactions were similar to those of H + C3, neglecting the possibility of radiative stabilization through electronic emission.
Appendix C.5: H + l-C3H2
This reaction can also proceed through direct abstraction or addition. We neglected
direct C3H +
H2 production
from H atom abstraction. Ab initio calculations (Nguyen
et al. 2001a; Goulay et al. 2009; Vereecken et al. 1998) showed no barrier for
addition, which leads to 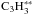 . The subsequent evolution of
. The subsequent evolution of
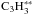 leads either to stabilization at high
pressure or to H + c-C3H2, neglecting the 2H + l-1C3H2 → 2H
+ t-3C3H2 reaction and the C3H + H2 production. The
2H +
l-1C3H2 reagents correlate with doublet states, as the
2H +
c-1C3H2 products do. As a result, there is no electronic
degeneracy factor for this reaction, which leads to a very high total rate constant.
However, the potential curve is likely to be less attractive than the potential energy
curve for the 2H
+ t-3C3H2 reaction, a reaction between two open shell radical
species. As a result, the variational TS (Georgievskii
& Klippenstein 2005) should occur at high energy, slowing down the
corresponding rate constant. Taking into account the higher electronic degeneracy factor
for l-C3H2, we recommend using the same value for both reactions,
with a global rate constant equal to 4.0 × 10-10 cm3 molecule-1 s-1. Because there is one
bimolecular exit channel we considered that the association reactions are similar to the
H + C3 ones,
neglecting the possibility of radiative stabilization through electronic emission.
leads either to stabilization at high
pressure or to H + c-C3H2, neglecting the 2H + l-1C3H2 → 2H
+ t-3C3H2 reaction and the C3H + H2 production. The
2H +
l-1C3H2 reagents correlate with doublet states, as the
2H +
c-1C3H2 products do. As a result, there is no electronic
degeneracy factor for this reaction, which leads to a very high total rate constant.
However, the potential curve is likely to be less attractive than the potential energy
curve for the 2H
+ t-3C3H2 reaction, a reaction between two open shell radical
species. As a result, the variational TS (Georgievskii
& Klippenstein 2005) should occur at high energy, slowing down the
corresponding rate constant. Taking into account the higher electronic degeneracy factor
for l-C3H2, we recommend using the same value for both reactions,
with a global rate constant equal to 4.0 × 10-10 cm3 molecule-1 s-1. Because there is one
bimolecular exit channel we considered that the association reactions are similar to the
H + C3 ones,
neglecting the possibility of radiative stabilization through electronic emission.
Appendix C.6: H + c-C3H2
The only exothermic reaction is association. There are several ab initio calculations (Nguyen et al. 2001a; Goulay et al. 2009; Vereecken et al. 1998) on the H + c-C3H2 reactions (related to unimolecular dissociation of the propargyl radical and the CH + C2H2 reaction). All calculations lead to the absence of a barrier, or a very small one (0.4 kJ mol-1), which will have a minor effect in the 150−200 K range and lead to relatively high value for addition rate constant in this temperature range, fixed at 2.0 × 10-10 cm3 molecule-1 s-1. We estimated k0 and kr using our “kassociation − ρ” semi-empirical model, neglecting the possibility of radiative stabilization through electronic emission.
Appendix C.7: H + C3H3
The only possible reaction is the association found to happen without a barrier with k∞(T) = 2.88 × 10-10 × (T/300)0.15 × exp(+ 46.30/T) cm3 molecule-1 s-1 (Harding et al. 2007; Miller & Klippenstein 2003). The high-pressure limit should be reached at relatively low pressures compared with the H + C3H5 reaction (Hanning-Lee & Pilling 1992) (no clear pressure-dependence between 98 and 400 Torr). Branching ratio calculations have been performed by Miller & Klippenstein (2003), leading to 25% of allene and 75% of methylacetylene, but the calculations have been performed only above 500 K and the rate was found to be pressure-dependent. We estimated k0 and kr using our “kassociation − ρ” semi-empirical model, neglecting the possibility of radiative stabilization through electronic emission.
We estimated the branching ratios to be 80% of CH3C2H and 20% of CH2CCH2 below 300 K.
Appendix C.8: H + C3H4
The rate constant values for the H + methylacetylene (CH3C2H) and H + allene (CH2CCH2) reactions were taken from various experimental measurements, particularly from Whytock et al. (1976) and Faravelli et al. (2000) for H + CH3C2H and from Wagner & Zellner (1972) and Aleksandrov et al. (1980) for H + CH2CCH2. We also used the recent theoretical work by Miller et al. (2008). The CH3 + C2H2 production channel is always very minor and was neglected. We also neglected H + CH2CCH2 → H + CH3C2H because it is a minor channel and CH3C2H reacts mainly with H atoms to produce the C3H5 radical. We recommend to use the experimental k∞(T) values and the calculated k0 and kr values (Vuitton et al. 2012) for the H + CH3C2H and H + CH2CCH2 reactions.
Appendix C.9: H + C3H5
There are three C3H5 isomers: H2C=CH-•CH2 (allyl), H3C-•C=CH2 and H3C-CH=•CH, the allyl being by far the most stable one and the only isomer considered here. There is one experimental determination of the rate constant for this reaction by Hanning-Lee & Pilling (1992). They measured the room temperature rate constants at four pressures in the range 98−400 Torr, which showed no clear pressure-dependence in this range with the mean rate constant equal to (2.8 ± 1.0) × 10-10 cm3 molecule-1 s-1. Calculations based on the Troe factorization method confirm that this reaction is near its high-pressure limit under their experimental conditions. Theoretical results (Qu et al. 2010; Zhao et al. 2007) clearly show that there are no bimolecular exit channels. These calculations agree well with Zhao et al. (2007) for the roaming channel (leading to C2H2 + CH4) with the TS calculated to be at +11 kJ mol-1 with respect to the reactant energies. The high-pressure rate constants have been determined theoretically (Harding et al. 2007), leading to a good agreement with experiments (Hanning-Lee & Pilling 1992). The C2H3 + CH3 exit channel is endothermic. Davis et al. (1999a) proposed a global kinetic mechanism for propene pyrolysis that does not fully agree with the ab initio calculations. There are no bimolecular exit channels, which leads to a high rate constant for the association reaction. We estimated k0 and kr using our “kassociation − ρ” semi-empirical model, neglecting the possibility of radiative stabilization through electronic emission.
Appendix C.10: H + C3H6
There have been various experimental measurements over a wide temperature range (Tsang 1991; Seakins et al. 1993). The H atom can add at two positions, which leads to i,n−2C4H7 formation (Galland et al. 2003). The n-2C3H7 isomer can evolve towards CH3 + C2H4, which is a pressure-dependent channel, but the bimolecular exit channels do not compete with i-C3H7 formation but only with n-C3H7 formation. In this study we considered only one C3H7 isomer. Because the main pathway of this reaction in the low-pressure limit of the addition is dominated by i-C3H7 production, the rate constant should be close to the low-pressure-limiting rate constant k0 of the H + C3H4 reaction (Vuitton et al. 2012).
Considering only one C3H7 isomer:
Considering i-C3H7 and n-C3H7 isomers:
Appendix C.11: H + C3H7
To a first approximation we considered only one C3H7 isomer. This system is very similar to that of H + C2H5 (Baulch et al. 2005). Direct H atom abstraction may happen without a barrier but is considered to be a minor channel compared with the H + C2H5 reaction (Camilleri et al. 1974). Therefore the rate constant is estimated to be equal to 3.0 × 10-12 cm3 molecule-1 s-1 and independent of temperature (Tsang 1991). There is very likely no barrier for the addition leading to propane. The various exit channels have been calculated by Zhu et al. (2004), showing a high barrier for the H2 + C3H6 exit channel but no barrier for the CH3 + C2H5 exit channel. New calculations (Sivaramakrishnan et al. 2011) show an accessible tight TS for CH4 + C2H4 formation (roaming channel). The various calculations led us to conclude that the main exit channel at low pressure is the formation of CH3 + C2H5. The total rate constants (excluding direct H atom abstraction) have been calculated by Harding et al. (2005), leading to k(H + C3H6)) = 9.68 × 10-11 × (T/300)0.22 cm3 molecule-1 s-1. Because there is one bimolecular exit channel without an exit barrier and with high exothermicity, the addition rate constant at low pressure will be low. The k0, value for the H + C3H7 → C3H8 reaction is taken from Teng & Jones (1972).
Appendix C.12: C + C2H2
A considerable amount of work has been performed on this reaction; see for example Costes et al. (2009) and the references therein. The carbon atom in its triplet electronic state can add either to a single carbon of the acetylene molecule to form triplet t-C3H2, or to the triple bond to produce triplet c-C3H2, both additions occurring without a barrier. The exit channels on the triplet surface lead to c-C3H + H and l-C3H + H. Because these channels are not very exothermic, the lifetime of the triplet adduct is long enough (Guadagnini et al. 1998; Mebel et al. 2007) to allow intersystem crossing to the singlet surface and then production of C3 + H2, which is the main exit channel below 300 K (85% between 150 and 200 K, Costes et al. 2009). As a result of this exit channel, the pressure dependence of the rate constants should be weak for P < 100 Torr (Guadagnini et al. 1998) and C3H2 stabilisation should not occur.
Appendix C.13: C + C2H4
The rate constant for this reaction has been measured in the 15−300 K range by various groups (Haider & Husain 1993a,b; Chastaing et al. 1999, 2001; Bergeat & Loison 2001). The recommended value is an average of the room temperature rate with the temperature dependence of the Chastaing et al. (2001) experiment. The H atom branching ratio has been determined at 300 K (Bergeat & Loison 2001) to be equal to 0.92 ± 0.04 and co-products and other branching ratios have been determined using ab initio calculations (Le et al. 2001). Adduct stabilization is negligible.
Appendix C.14: CH + C2H2
The reaction kinetics of CH with C2H2 has been widely studied (Butler et al. 1981; Berman et al. 1982; Canosa et al. 1997; Thiesemann et al. 1997) for temperatures ranging from 23 K (Canosa et al. 1997) to 710 K (Thiesemann et al. 1997). The experimental temperature dependence of the total rate constant is given by the expression 1.59 × 10-9 × T-0.233 × exp(−16/T) cm3 molecule-1 s-1 between 23 K and 295 K, suggesting that this reaction proceeds without a barrier. The absence of any pressure dependence for the rate constant shows that stabilization is not competitive with dissociation of the intermediates. There have been five experimental branching ratio determinations for the CH + C2H2 reaction (Boullart et al. 1996; McKee et al. 2003; Goulay et al. 2009; Loison & Bergeat 2009; Maksyutenko et al. 2010) in addition to various theoretical studies (Walch 1995; Vereecken et al. 1998; Vereecken & Peeters 1999; Guadagnini et al. 1998; Nguyen et al. 2001b; Mebel et al. 2007; Goulay et al. 2009). The ab-initio/RRKM calculations give scattered results on this system (Vereecken & Peeters 1999; Mebel et al. 2007; Goulay et al. 2009). A review of the various studies is given by Maksyutenko et al. (2010). There is a general agreement for a branching ratio of 91 ± 4% for H atom production and 9 ± 2% for H2 production. The co-product isomers of the H atom have been determined by Maksyutenko et al. (2010) in a single collision experiment but at relatively high collisional energy (16.8 kJ mol-1): 31 ± 5% of c-C3H2 + H and 60 ± 5% of t-C3H2/l-C3H2 + H and by Goulay et al. (2009): 90% of c-C3H2 + H in a slow-flow reactor at 4 Torr and 293 K. The apparent disagreement may be explained by H-atom-assisted isomerization of the nascent C3H2 product to the cyclic c-C3H2 isomer through l,t−C3H2 + H → C3H3 → c-C3H2 + H (Mebel et al. 2007; Goulay et al. 2009). Considering that the branching ratio does not depend on the collision energy, we can reasonably use the value of Maksyutenko et al. (2010). Given the scatter of the various RRKM calculations, we considered that only t-C3H2 is formed in the t-C3H2/l-C3H2 + H pathway.
Appendix C.15: CH + C2H4
The reaction kinetics of CH with C2H4 has been widely studied (Butler et al. 1981; Berman et al. 1982; Canosa et al. 1997; Thiesemann et al. 1997, 2001) for temperatures ranging from 23 K (Canosa et al. 1997) to 726 K (Thiesemann et al. 2001). There are three experimental branching ratio determinations for the CH + C2H4 reaction (McKee et al. 2003; Goulay et al. 2009; Loison & Bergeat 2009) and also theoretical studies (Gosavi et al. 1985; Wang & Huang 1998) as well as coupled ab initio/RRKM studies of this reaction (McKee et al. 2003) or studies on the evolution of the excited allyl radical C3H5 (Davis et al. 1999b; Stranges et al. 2008), which is thought to be the main reaction intermediate. The experimental temperature dependence of the global rate constant of the CH + C2H4 reaction, 7.74 × 10-9 × T-0.546 × exp(−29.6/T) cm3 molecule-1 s-1 between 23 K and 295 K, suggests that this reaction proceeds without a barrier. There is a good agreement with the various experimental results as well as with the ab initio/RRKM calculations, leading to 70 ± 8% of CH2CCH2 + H, 30 ± 8% of CH3C2H + H.
Appendix C.16: 1CH2 + C2H2
This reaction has been studied experimentally between 195 and 798 K by Gannon et al. (2010a,b). They measured the H atom branching ratio between 298 and 398 K and
calculated that adduct stabilization was negligible below 100 Torr. Because there are no
models to describe the H atom production increase between 195 K and 298 K and because
the rate constant is almost constant in the 195−300 K range, we recommend to use the 195
K value in the 150−200 K
range. 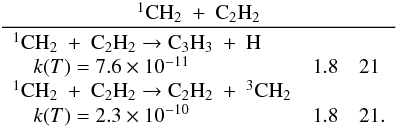
Appendix C.17: 1CH2 + C2H4
This reaction has been studied experimentally at low pressure (1 Torr) between 195 and 798 K by Gannon et al. (2010a,b). They measured the H atom branching ratio between 298 and 398 K but calculated neither adduct stabilization, nor the exit channels. An earlier experiment by Canosa-Mas et al. (1985) showed that cyclopropane formation is the main exit channel at 400 Torr. The first step of this reaction is likely to be cyclopropane formation resulting from the addition of 1CH2 to the double bond (with 427 kJ mol-1 in internal energy), so much more than the cyclopropane isomerization barrier toward propene equal to 276 ± 10 kJ mol-1 (Dubnikova & Lifshitz 1998) or propene formation resulting in 1CH2 insertion into one C-H bond (with 460 kJ mol-1 in internal energy). The bi-radical H2C•-CH2-•CH2 formation is either endothermic or is only a local minimum. Because the formation of allyl H2C = CH-•CH2 + H is exothermic (−91 kJ mol-1) without an exit barrier (Harding et al. 2007), this will be the main exit channel at low pressure, and adduct stabilization plays a role only at high pressure (Canosa-Mas et al. 1985). Because there are no models to describe the H atom production increase between 195 K and 298 K and the rate constant is almost constant in the 195−300 K range, we recommend to use the 195 K values in the 150−200 K range. We also neglected adduct stabilization.
Appendix C.18: CH3 + CH3
This reaction has been widely studied (Slagle et al. 1988; Cody et al. 2002, 2003). Wang et al. (2003) have fitted various experimental data between 202 and 900 K, leading to k0(T) = 1.14 × 10-25 × (T/300)-3.75 × exp(−494/T) cm6 molecule-2 s-1 and k∞(T) = 7.4 × 10-11 × (T/300)-0.69 × exp(−88/T) cm3 molecule-1 s-1. The k0 value at low temperature from the fit is not precise due to the lack of experimental data; the measured rate constants at 155 K are already approaching the high pressure limit. Smith (2003) performed RRKM simulations in the 65−300 K range, that led to k0(T) = 8.3 × 10-26 × (T/300)-4.28 × exp(−131/T) cm6 molecule-2 s-1 (Fc = 0.3) with H2 bath gas (k0(N2) = 0.7 × k0(H2)Smith 2003) and k∞(T) = 8.1 × 10-11 × (T/300)-0.262 × exp (−37/T) cm3 molecule-1 s-1. Vuitton et al. (2012) have performed new calculations between 50 and 300 K, but their results are slightly overestimated with regard to the available experimental data. However, it is not possible to fit the entire temperature and pressure range with only one expression, and the results of Vuitton et al. (2012) are likely to be the most precise at low temperature and low density. We recommend their values with k0 scaled to fit the experimental data (using Troe expression in N2 with Fc = 0.60, N = 1).
Appendix C.19: CH3 + C2H3
There is no barrier on the singlet surface, leading to the C3H6 adduct (Thorn et al. 2000; Qu et al. 2010), and this reaction has been studied experimentally by Fahr et al. (1999), Thorn et al. (2000) and Stoliarov et al. (2000) between 1 and 200 Torr. The H atom abstraction reaction by CH3 is likely to be a separate channel with a rate constant that has been measured on several previous occasions (Fahr et al. 1999; Stoliarov et al. 2000). The C3H6 adduct can lead to C3H5 + H formation, which means that adduct stabilization and bimolecular product formation compete. The results of Stoliarov et al. (2000) and Fahr et al. (1999) as a function of pressure lead to lower k0 values than k0,CH3 + CH3 → C2H6(T). We estimate k0,CH3 + C2H3 → C3H6(T) = 0.1 × k0,CH3 + CH3 → C2H6(T). The open-exit channels from the adduct also prevent efficient radiative association, therefore we neglected radiative association in this case.
Appendix C.20: CH3 + C2H5
We recommend the Vuitton et al. (2012) values scaled to the Troe formula with Fc = 0.60 and N = 1. We adopted the Baulch et al. (1992) value for the H atom abstraction channel by CH3.
Appendix C.21: CH3 + C3H3
The H atom abstraction channel by CH3 is very likely to have a barrier in the entrance valley, because the C-H bond strength in C3H3 is high. Adduct formation occurs without a barrier with k∞(T) = 6.8 × 10-11 × exp(+ 130/T) cm3 molecule-1 s-1 (Knyazev & Slagle 2001). Fahr & Nayak (2000) studied this reaction at room temperature at 50 Torr using laser photolysis of the precursors, GC/MS product analysis, and kinetic modelling. They identified the main products as approximately 60% of 1-butyne and 40% of 1,2-butadiene, which shows that at 50 Torr adduct stabilization is the main channel. Lee et al. (2003) found that the H2CC + C2H4 product channel is accessible through a TS localized 22 kJ mol-1 below the reactants, leading to these bimolecular products at low pressure. Lee et al. (2003) also found that the other bimolecular exit channels involve TSs located above the entrance level. We estimated k0 and kr using our “kassociation − ρ” semi-empirical model, k0 and kr being then divided by 100 to take into account the open bimolecular exit channel. The H2CC produced should isomerize quickly to C2H2.
Appendix C.22: C2H + C3
The C2H radical
is highly reactive, particularly with unsaturated hydrocarbons (Chastaing et al. 1998). There is therefore little doubt that the
C2H +
C3 → H +
C5 reaction has
no barrier in the entrance valley. In the Cs geometry; the reactants correlate with
2(A′ + A′′) ⊗ 1A′ = 2A′ + 2A′′ states and the products correlate with
2A′⊗ 1A′ = 2A′ states, i.e., there is an electronic
degeneracy factor of  . Applying classical capture theory
(Georgievskii & Klippenstein 2005) and
considering only the isotropic dispersion term for long-range interaction, the capture
rate constant is close to 6 × 10-10 cm3 molecule-1 s-1 at 300 K, leading to a rate constant value of
3 × 10-10
cm3 molecule-1 s-1 taking into account the electronic degeneracy. This
value is close to the rate constant of C2H + alkene reactions (Chastaing et al. 1998). Considering the small variation of the rate constant
for these reactions, we recommend a constant value in the 150−300 K range.
. Applying classical capture theory
(Georgievskii & Klippenstein 2005) and
considering only the isotropic dispersion term for long-range interaction, the capture
rate constant is close to 6 × 10-10 cm3 molecule-1 s-1 at 300 K, leading to a rate constant value of
3 × 10-10
cm3 molecule-1 s-1 taking into account the electronic degeneracy. This
value is close to the rate constant of C2H + alkene reactions (Chastaing et al. 1998). Considering the small variation of the rate constant
for these reactions, we recommend a constant value in the 150−300 K range.
Appendix C.23: N(2D) + C3
There are no measurements of this reaction, but we considered the N(2D) + C3 reaction to be slightly faster than the N(2D) + C2H2 reaction. N(2D) reactions with closed-shell molecules, for which only scattered information exists, are particularly important for modeling Titan’s atmosphere and need to be studied in more detail.
All Tables
New or modified photodissociation processes included in the model (update of Hébrard et al. 2012).
Key reactions responsible for the uncertainties on major C3Hp compounds at an altitude of 1300, 1000, 600, and 200 km.
Key reactions responsible to uncertainties on major C3Hp compounds at an altitude of 1300, 1000, 600, and 200 km.
All Figures
 |
Fig. 1 Comparison between the previous model of Hébrard et al. (2012) (blue solid line) with the present work (red solid line) for four representative compounds: acetylene C2H2, ethane C2H6, diacetylene C4H2 and benzene C6H6. 5th and 15th 20-quantiles (red long-dashed lines) and 1st and 19th 20-quantiles (red short-dashed lines) for the abundances distributions of the present model are also given. |
| In the text | |
 |
Fig. 2 Comparison of the previous model of Hébrard et al. (2012) (blue solid lines) with the present work (red solid lines) for the carbon trimer C3, 2-cyclopropyn-1-yl c-C3H and 2-propynylidyne l-C3H, cyclopropenylidene c-C3H2, propadienylidene l-C3H2 and propynylidene t-C3H2, propargyl radical C3H3 and allyl radical C3H5. |
| In the text | |
 |
Fig. 3 Comparison of the previous model of Hébrard et al. (2012) (blue solid lines) with the present work (red solid lines) for methylacetylene CH3C2H and allene CH2CCH2, propene C3H6, propyl radical C3H7 and propane C3H8. |
| In the text | |
 |
Fig. 4 Abundance profiles of the carbon trimer C3 and cyclopropenylidene c-C3H2 obtained after 900 runs. Thick black solid line: initial profile. Black dotted line: median profile obtained from the uncertainty propagation study. Black dashed-dotted lines: 5th and 15th 20-quantiles of the distribution. Black long-dashed lines: 1st and 19th 20-quantiles of the distribution. |
| In the text | |
 |
Fig. 5 Abundance profiles of the propargyl radical C3H3 and propene C3H6 obtained after 900 runs. Thick black solid line: initial profile. Black dotted line: median profile obtained from the uncertainty propagation study. Black dashed-dotted lines: 5th and 15th 20-quantiles of the distribution. Black long-dashed lines: 1st and 19th 20-quantiles of the distribution. The red open triangle refers to Cassini/INMS observations from Magee et al. (2009). |
| In the text | |
 |
Fig. 6 Abundance profiles of methylacetylene CH3C2H and allene CH2CCH2 obtained after 900 runs. Black solid line: initial profile. Black dotted line: median profile obtained from the uncertainty propagation study. Black dashed-dotted lines: 5th and 15th 20-quantiles of the distribution. Black long-dashed lines: 1st and 19th 20-quantiles of the distribution. The blue open diamond refers to ISO observations from Coustenis et al. (2003), the red open triangle to Cassini/INMS observations from Magee et al. (2009), the green crossed squares to Cassini/INMS observations from Cui et al. (2009), the orange squares to the corrected Cassini/INMS observations from Cui et al. (2009), the pink crosses to the Cassini/CIRS observations at 3.5˚N from Vinatier et al. (2010). |
| In the text | |
 |
Fig. 7 Abundance profiles of propane C3H8 obtained after 900 runs. Black solid line: initial profile. Black dotted line: median profile obtained from the uncertainty propagation study. Black dashed-dotted lines: 5th and 15th 20-quantiles of the distribution. Black long-dashed lines: 1st and 19th 20-quantiles of the distribution. The blue open diamond refers to ISO observations from Coustenis et al. (2003), the red open triangle to Cassini/INMS observations from Magee et al. (2009), the green crossed squares to Cassini/INMS observations from Cui et al. (2009), the orange square to the corrected Cassini/INMS observations from Cui et al. (2009), the pink crosses to Cassini/CIRS observations at 3.5˚N from Vinatier et al. (2010). |
| In the text | |
 |
Fig. A.1 Photoabsorption cross sections for C3 along with the dissociation limits for the various channels considered. |
| In the text | |
 |
Fig. A.2 Photoabsorption cross sections for c-C3H (top) and l-C3H (bottom) along with the dissociation limits for the various channels considered. |
| In the text | |
 |
Fig. A.3 Photoabsorption cross sections for c-C3H2 (top), l-C3H2 (middle) and t-C3H2 (bottom) along with the dissociation limits for the various channels considered. |
| In the text | |
 |
Fig. A.4 Photoabsorption cross sections for C3H3 along with the dissociation limits for the various channels considered. |
| In the text | |
 |
Fig. A.5 Photoabsorption cross sections for C3H5 along with the dissociation limits for the various channels considered. |
| In the text | |
 |
Fig. A.6 Photoabsorption cross sections for C3H7 along with the dissociation limits for the various channels considered. |
| In the text | |
 |
Fig. B.1 Low-pressure limiting and radiative association rate constants k0, kr as a function of the vibrational density of states of the adduct, ρ(E0). The stars are the experimental k0 values at 300 K, the open circles are the calculated k0 values at 300 K from Vuitton et al. (2012), the diamond is the calculated k0 value at 300 K performed for this study and the solid circles are the kr calculations at 150 K from Vuitton et al. (2012). Units on the left axis are in cm6 molecule-2 s-1 for k0 and cm3 molecule-1 s-1 for kr. Experimental data are taken from: H + NH2 (Gordon et al. 1971), H + CH3 (Brouard et al. 1989), CH3 + O2 (Fernandes et al. 2006), CH3 + NO (Kaiser 1993), CH3 + NH2 (Jodkowski et al. 1995), CH3 + CH3 (Slagle et al. 1988; Cody et al. 2002). The solid and dashed lines correspond to the general expression we derived for the low-pressure limiting rate constants k0 for H addition and CH3 addition, respectively. The dashed-dotted line corresponds to the general expression we derived for the radiative association rate constants kr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.