| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A169 | |
| Number of page(s) | 22 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202244447 | |
| Published online | 30 November 2022 | |
A photochemical model of Triton’s atmosphere paired with an uncertainty propagation study★
1
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N,
Allée Geoffroy Saint-Hilaire,
33615
Pessac, France
e-mail: benjamin.benne@u-bordeaux.fr
2
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris Diderot,
Sorbonne Paris Cité, 5 place Jules Janssen,
92195
Meudon, France
3
Institut des Sciences Moléculaires, CNRS, Univ. Bordeaux,
351 Cours de la Libération,
33400
Talence, France
Received:
7
July
2022
Accepted:
29
August
2022
Context. The largest satellite of Neptune, Triton, is a likely Kuiper Belt object captured by the planet. It has a tenuous nitrogen atmosphere, similar to that of Pluto, and it may be an ocean world. The Neptunian system has only been visited once: by Voyager 2 in 1989. Over the past few years, the demand for a new mission to the ice giants and their systems has risen. Thus, a theoretical basis upon which to prepare for such a mission is needed.
Aims. We aim to develop a photochemical model of Triton’s atmosphere with an up-to-date chemical scheme, as previous photochemical models date back to the post-flyby years. This purpose is to achieve a better understanding of the mechanisms governing Triton’s atmospheric chemistry and to highlight the critical parameters that have a significant impact on the atmospheric composition. We also study the model uncertainties to find what chemical studies are necessary to improve the modeling of Triton’s atmosphere.
Methods. We used a model of Titan’s atmosphere and tailored it to Triton’s conditions. We first used Titan’s chemical scheme before updating it to better model Triton’s atmospheric conditions. Once the nominal results were obtained, we studied the model uncertainties with a Monte Carlo procedure, considering the reaction rates as random variables. Finally, we performed global sensitivity analyses to identify the reactions responsible for model uncertainties.
Results. With the nominal results, we determined the composition of Triton’s atmosphere and studied the production and loss processes for the main atmospheric species. We highlighted key chemical reactions that are most important for the overall chemistry. We also identified some key parameters that have a significant impact on the results. The uncertainties are high for most of the main atmospheric species since the atmospheric temperature is very low. We identified key uncertainty reactions that have the greatest impact on the result uncertainties. These reactions must be studied as a priority in order to improve the significance of our results by finding ways of lowering these uncertainties.
Key words: planets and satellites: atmospheres / astrochemistry
Supplementary material related to this article is available at: https://doi.org/10.13140/RG.2.2.12820.99203
© B. Benne et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Triton is the largest satellite of Neptune, whose orbit is inclined and retrograde, suggesting that it is a former Kuiper Belt Object (KBO) that was captured by Neptune (McKinnon et al. 1995; Agnor & Hamilton 2006). This assumption has been reinforced by the similarities observed with Pluto. Triton was visited by Voyager 2 in August 1989, the only mission thus far to have studied the Neptunian system. The flyby allowed for the observation and characterization of the surface ices, composed of N2, CO2, H2O, CH4, and CO (Brown et al. 1995; Yelle et al. 1995), as well as the discovery of the presence of plumes of organic material and hazes (Herbert & Sandel 1991; Yelle et al. 1991, 1995; Krasnopolsky et al. 1992). A study of the atmosphere was performed by occultations and the measurement of its airglow (Broadfoot et al. 1989). It showed that the atmosphere is mainly composed of N2 and traces of CH4 were found near the surface. The presence of atomic nitrogen and atomic hydrogen was also deduced from these measurements. The surface pressure and temperature were determined using the radio data of Voyager (Tyler et al. 1989) and were found to be 16 ± 3µbar and 38 K, respectively. It is believed that the atmosphere is formed by sublimation of the surface ices and that it is at vapor pressure equilibrium with those ices (Yelle et al. 1995). Furthermore, CO was not detected during this mission but was observed from Earth (Lellouch et al. 2010). A dense ionosphere was also detected with a peak concentration of electrons of about 104 cm−3 (Tyler et al. 1989) and the thermospheric temperature was measured to be 95 ± 5 K (Broadfoot et al. 1989). A review of the data acquired on Triton during the mission can be found in Cruikshank et al. (1995).
The chemistry in the lower atmosphere is mainly triggered by the photolysis of CH4 by Lyman-α photons coming from solar irradiation and from the interplanetary medium (Strobel et al. 1990b; Herbert & Sandel 1991; Krasnopolsky et al. 1992, 1993; Krasnopolsky & Cruikshank 1995; Strobel & Summers 1995; Strobel & Zhu 2017). However, at higher altitudes, it is governed by the photolysis of N2 by solar EUV radiation (λ < 100 nm) and by its interaction with energetic electrons from Neptune’s magnetosphere (Strobel et al. 1990a; Krasnopolsky et al. 1993; Krasnopolsky & Cruikshank 1995; Strobel & Summers 1995; Strobel & Zhu 2017).
Aside from these findings, very little is known about Triton, as no mission has been sent to the Neptunian system since Voyager 2. This is why the demand for a new mission to the ice giants is currently rising among the community. In addition, Triton is thought to be an ocean world (such as Titan, Enceladus, Europa, and Ganymede) meaning that it may have a liquid ocean under its icy surface, heated by obliquity tides (Rymer et al. 2021; Fletcher et al. 2020). This makes it a high-priority target for studying the possibility of developing life in the outer worlds of the Solar System (Committee on the Planetary Science and Astrobiology Decadal Survey et al. 2022). Hence, a mission to the Neptunian system would allow for studies across a very large spectrum of disciplines. In order to prepare such a mission, it is important to develop photochemical models of Triton’s atmosphere, as this will give a theoretical basis for developing the instruments as well as to anticipate future in situ measurements.
Due to the scarcity of data available after the Voyager flyby, few articles about the photochemistry of Triton’s atmosphere have been published, which include: Majeed et al. (1990), Strobel et al. (1990b), Lyons et al. (1992), Krasnopolsky et al. (1993), Krasnopolsky & Cruikshank (1995), and Strobel & Summers (1995). Significant improvements to the modeling of the photochemistry of Titan’s atmosphere have been made thanks to the Cassini-Huygens data, particularly with regard to the determination of the chemical scheme. A lot of models of this atmosphere have been developed and refined, and they are now quite robust (e.g., Dobrijevic et al. 2016; Loison et al. 2019; Nuñez-Reyes et al. 2019a,b; Hickson et al. 2020; Vuitton et al. 2019). These models can be used as a starting point for the development of a new photochemical model of Triton’s atmosphere, since it is composed of N2 and CH4, which happen to be also the main constituents of Titan’s atmosphere. Recent 1D photochemical models use thousands of chemical reactions and consider hundreds of species, including neutral and ionic compounds. Using a more complete chemical scheme could change the vision and the understanding of the chemical mechanisms governing Triton’s atmosphere. It is also important to take into account ground-based observations such as those of Lellouch et al. (2010), who measured its abundance of CO.
As the temperature of Triton’s atmosphere is particularly low (<100 K at all altitudes), we expect to have large uncertainties with regard to the chemistry. Indeed, reaction rates are mostly measured or calculated at room temperature. Hence, their values may be wrong in Triton’s conditions, even if these rates are given with an uncertainty factor which accounts for errors within the experiments or the computations. This problem was presented in Hébrard et al. (2009). To consider the impact of these uncertainties on our results, we used a Monte Carlo procedure over all reaction rates, as done in Dobrijevic & Parisot (1998); Dobrijevic et al. (2003, 2010a); Hébrard et al. (2007), and subsequent works. Along with this study, we also performed global sensitivity analyses to determine which reactions had the strongest impact on chemical uncertainties, which we call key uncertainty reactions. The determination of these reactions indicate which reactions need to be measured as a priority thanks to new chemical studies.
The aim of the present work is to develop a new photochemical model of Triton’s atmosphere and determine the key uncertainty reactions that must be studied in priority to reduce the uncertainties on model results. Our atmospheric model is presented in Sect. 2, followed by our photochemical model in Sect. 3, our updated chemical scheme in Sect. 4, our results for the nominal chemistry with this updated scheme in Sect. 5, and our study of chemical uncertainties and the determination of key uncertainty reactions in Sect. 6. We give our conclusions in Sect. 7.
2 Atmospheric model
In this section, we present all the basic inputs of our model. These inputs are the temperature, pressure and density profiles, the altitude grid, the boundary conditions, the diffusion coefficients, and the atmospheric escape rates. All of these inputs are independent from the chemical scheme and from the photochemical parameters.
2.1 Atmospheric profiles and altitude grid
With the measurement of the surface temperature, the thermospheric temperature, Tth, was inferred by using the number density of N2 and assuming hydrostatic equilibrium, giving: Tth = 95 ± 5 K (Broadfoot et al. 1989); however, the complete temperature profile could not be determined and this has been the subject of several subsequent studies (see Yelle et al. 1991; Stevens et al. 1992; Krasnopolsky et al. 1993; Strobel & Zhu 2017).
Due to the presence of plumes (that were observed up to 8 km above the surface) and clouds, it is thought that the temperature gradient near the surface is negative, indicating the presence of a troposphere (Yelle et al. 1991, 1995). Energy is brought to the atmosphere by solar extreme ultraviolet (EUV) photons and by precipitating electrons from Neptune’s magnetosphere (Strobel et al. 1990a; Yelle et al. 1991; Stevens et al. 1992; Strobel & Summers 1995; Krasnopolsky & Cruikshank 1995; Strobel & Zhu 2017). Energy is then transferred through the atmosphere by conduction (Yelle et al. 1991, 1995; Strobel & Summers 1995). Magnetospheric electrons (ME) have not always been taken into account, with some models considering the Sun and the interplanetary radiation flux as the only energy sources, as in Lyons et al. (1992). However, Strobel et al. (1990a), Stevens et al. (1992), Krasnopolsky & Cruikshank (1995), and Strobel & Zhu (2017) showed that they are necessary in explaining the thermospheric temperature measured by Voyager. Another critical parameter is the abundance of CO because of its cooling capabilities (Stevens et al. 1992; Krasnopolsky et al. 1993; Strobel & Zhu 2017). As its abundance was not measured by Voyager, it was adjusted to fit the measured tangential N2 column densities (Stevens et al. 1992). Krasnopolsky et al. (1993) tried different values of the initial abundance of CO but were unable to constrain its value from thermal balance calculations. This abundance was measured as (2–18) × 10−4 by high-resolution spectroscopic observations in the 2.32−2.37 µm range, using the CRyogenic high-resolution InfraRed Echelle Spectrograph (CRIRES) at the Very Large Telescope (VLT; Lellouch et al. 2010) and is consistent with the upper limit inferred by Voyager data (i.e., <1% Broadfoot et al. 1989).
In a more recent paper, taking advantage of the similarities between Pluto and Triton, Strobel & Zhu (2017) adapted the thermal model of Pluto from Zhu et al. (2014) to Triton. The main differences between the two atmospheres are the mole fraction of CH4 (i.e., it is higher on Pluto) and the energy supply from magnetospheric electrons from Neptune’s magnetosphere. They used the abundance of CO determined in Lellouch et al. (2010) and studied three different models to see the impact of magnetospheric electrons on the thermal profile: two models without magnetospheric electrons and with different CH4 abundances and a third with magnetospheric electrons. Their conclusion was that magnetospheric heating is necessary to retrieve N2 tangential column number densities comparable to the measurements from Voyager 2.
In our model, we used data from their Triton-3 model, which considers precipitations of magnetospheric electrons, and we used the associated temperature and pressure profiles. It has to be noted that this thermal profile does not consider a troposphere as the temperature gradient is always positive, in contrast to the work of Krasnopolsky et al. (1993), Krasnopolsky & Cruikshank (1995), Yelle et al. (1991, 1995).
The maximum altitude for this model is 1026 km. The temperature varies between 37.8 and 90.3 K from the surface to the upper end of the atmosphere, the pressure between 16 and 2.8 × 10−8 µbar, and the number density is computed following the ideal gas law.
We sampled the altitude grid with H/5 steps, where H(z) = 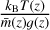 is the scale height of the atmosphere at altitude z (kB is the Boltzmann constant, while T,
is the scale height of the atmosphere at altitude z (kB is the Boltzmann constant, while T, 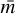 , and g are, respectively, the temperature, mean mass, and gravitational acceleration at altitude z). Using these criteria, our altitude levels are spaced by 2 km near the surface and by 21 km near the top of the atmosphere, giving a 96 level grid. Temperature and number density profiles are shown in Fig. 1, along with the altitude levels.
, and g are, respectively, the temperature, mean mass, and gravitational acceleration at altitude z). Using these criteria, our altitude levels are spaced by 2 km near the surface and by 21 km near the top of the atmosphere, giving a 96 level grid. Temperature and number density profiles are shown in Fig. 1, along with the altitude levels.
The electronic temperature profile is a parameter that is required to compute the reaction rates of dissociative recombination reactions. As it has never been measured, we considered that the electronic temperature is equal to the neutral temperature at all altitudes.
 |
Fig. 1 Initial profiles used in our model: (a) Initial abundance profiles of N2 (green solid line), CH4 (orange dash-dotted line), and CO (red dashed line). The CH4 abundance decreases exponentially with a scale height of 9 km. (b) Temperature (red dashed line) and number density (orange solid line) profiles from the Triton-3 case of Strobel & Zhu (2017) that are used as inputs in our model. The altitudinal grid is composed of 96 levels and the total number density is plotted with blue dots. |
2.2 Initial and boundary conditions
The initial abundance of a given species corresponds to the value taken at the beginning of the program, before the photochemical calculations. To maintain consistency with the use of the thermal, pressure, and number density profiles of Strobel & Zhu (2017), we also used their initial abundance of CO: y0(CO) = 6.0 × 10−4, which corresponds to the measurement made by Lellouch et al. (2010). The initial abundance of CO is constant throughout the atmosphere. The initial mole fraction of CH4 was taken equal to the 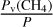 ratio at the surface, with Pv being the vapor pressure and P the total pressure. Based on the formula of Fray & Schmitt (2009), this corresponds to y0(CH4) = 0.89 × 10−4. Thus, the initial abundance is 40% lower than the value of Strobel & Zhu (2017), which is y0(CH4) = 1.5 × 10−4.
ratio at the surface, with Pv being the vapor pressure and P the total pressure. Based on the formula of Fray & Schmitt (2009), this corresponds to y0(CH4) = 0.89 × 10−4. Thus, the initial abundance is 40% lower than the value of Strobel & Zhu (2017), which is y0(CH4) = 1.5 × 10−4.
We chose to take an exponentially decreasing profile for CH4 as the initial condition, with a scale height of 9 km corresponding to Voyager’s observations (Strobel et al. 1990b). Then, at all altitudes, we simply filled the rest of the atmosphere with N2 by taking ![${y_{{{\rm{N}}_{\rm{2}}}}}\left( z \right) = 1 - \left[ {{y_{{\rm{C}}{{\rm{H}}_{\rm{4}}}}}\left( z \right) + {y_{{\rm{CO}}}}\left( z \right)} \right]$](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq4.png) . The initial profiles of these three compounds are plotted in Fig. 1.
. The initial profiles of these three compounds are plotted in Fig. 1.
Comparison of the different Kzz(z) used in previous Triton photochemical models since the flyby of Voyager 2 in 1989.
2.3 Eddy diffusion coefficient
The eddy diffusion coefficient Kzz is a critical parameter of the model. In previous works on the photochemistry of Triton’s atmosphere, this coefficient was adapted to match the CH4 profile measured by Voyager 2 (Strobel et al. 1990b; Herbert & Sandel 1991; Krasnopolsky & Cruikshank 1995). All the profiles inferred in these studies are different, as shown in Table 1 and Fig. 2.
We tested the different profiles from Table 1 and obtained the best agreement with observations using the profile from Herbert & Sandel (1991), which we then kept it for the rest of our study.
2.4 Molecular diffusion coefficient
The other main type of diffusion in planetary atmospheres is molecular diffusion. It is used to describe the diffusion of minor species in one or more major species. This type of diffusion occurs when the number density of the minor species deviates from its distribution at hydrostatic equilibrium. A coefficient is linked to this type of diffusion and we computed it with formulas (1) and (2) taken from Poling et al. (2001), as we considered molecular diffusion in the two main species of Triton’s atmosphere. In this case, one of the terms of (1) always depends on N2 as it is the most abundant species throughout the atmosphere, but the second main species varies with altitude. The latter is noted j2 in (1) describing the molecular diffusion coefficient of species i at altitude z:
where Di,j is the diffusion coefficient of the minor species, i, in a single major species, j, whose relative abundance is yj. Di,j is computed with:
where T is the temperature, P the pressure, Mi,j = µi,j × 2 with µi,j the reduced mass of species, i and j, and Σv is the diffusion volume.
 |
Fig. 2 Comparison between the eddy diffusion coefficients Kzz of Strobel et al. (1990b; black dotted line), Herbert & Sandel (1991; blue dashed line), and Krasnopolsky & Cruikshank (1995; red dash-dotted line). For the Strobel et al. (1990b) profile, we plotted Kzz = 6.0 × 103 cm2 s−1 and for the Herbert & Sandel (1991) profile |
2.5 Atmospheric escape
The atmospheric escape of neutral and ionized species is considered in many papers about Triton, such as Summers & Strobel (1991) or Krasnopolsky & Cruikshank (1995). It is thought that this mass load in Neptune’s magnetosphere could affect Neptune’s auroras (Broadfoot et al. 1989).
In our model, we simply consider Jeans thermal escape from the top of the atmosphere, which is at 1026 km. The flux is computed for each neutral species i following Eq. (3):
with 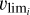 the escape velocity of species i at the top of the atmosphere, corresponding to the altitude zmax, ni its number density, mi its mass, and kB the Boltzmann constant. Then, T(zmax) is the neutral temperature at this altitude level and q is computed as follows, with RT the radius of Triton:
the escape velocity of species i at the top of the atmosphere, corresponding to the altitude zmax, ni its number density, mi its mass, and kB the Boltzmann constant. Then, T(zmax) is the neutral temperature at this altitude level and q is computed as follows, with RT the radius of Triton:
In contrast to the study of Krasnopolsky & Cruikshank (1995), we did not consider ion escape and we did not scale our electronic profile on this escape above 600 km.
Comparison between the initial and updated chemical schemes.
3 Photochemical model
3.1 Baseline chemical scheme
As our model is one-dimensional, we have the option of using a complex chemical scheme without the need for excessively long computation times. Capitalizing on the similarities between the major constituents of Triton’s and Titan’s atmospheres, we used the chemical scheme of Titan’s atmosphere presented in Dobrijevic et al. (2016) as a basis for our work. This chemical scheme was updated in Loison et al. (2019), Nuñez-Reyes et al. (2019a,b) and Hickson et al. (2020). The number of reactions and atmospheric species used in this scheme is presented in Table 2.
Although the initial composition of the atmospheres of Titan and Triton are quite similar, differences have to be noted as they could have an impact on the results. Firstly, CH4 is only a trace species on Triton, whereas its abundance on Titan reaches 20% at the top of the atmosphere. Thus, some reactions could be less important on Triton due to the absence of methane in the upper atmosphere. Conversely, some reactions that do not have a great impact on Titan could be crucial on Triton. Secondly, the temperature and pressure are much lower on Triton and this directly impacts the reaction rates and the condensation of some species, such as hydrocarbons. Thus, this initial scheme was modified after the first results were obtained, following the methodology presented in Sect. 4.
3.2 Generalities about calculations
Our photochemical model solves the continuity Eq. (5) for all the considered species i at all the altitude levels. At an altitude, z, it gives:
where ni is the number density of the species i, Pi is the chemical production term in cm−3 s−1 and Li the chemical loss term in s−1. 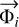 is the particle vertical flux computed by:
is the particle vertical flux computed by:
where Di is the molecular diffusion coefficient, Kzz is the eddy diffusion coefficient, yi the abundance, Hi is the scale height of species i, and H is the atmospheric scale height. Here, the thermal diffusion is neglected.
Equation (5) is integrated over time until steady state is reached, that is, when 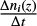 is below a given threshold. This ratio is computed at the end of each time step. In our case, the threshold was fixed at 10%, because such a variation was small in comparison to the uncertainties related to the model results caused by chemical uncertainties.
is below a given threshold. This ratio is computed at the end of each time step. In our case, the threshold was fixed at 10%, because such a variation was small in comparison to the uncertainties related to the model results caused by chemical uncertainties.
To compute the abundance profiles of all the considered atmospheric species, we took the following steps. At the start, we used an atmosphere only composed of N2, CH4, and CO and computed the chemical rates and the actinic flux. Then, we calculated chemical and transport terms to integrate the continuity equation and determine the abundance profiles of all the species. When convergence was reached, we computed again the chemical rates and the actinic flux with the newly obtained abundance profiles and ran the integration again. This pattern was repeated until the difference between the results of two successive steps was weak compared to the model uncertainties. In our case, three iterations were needed to reach steady state. In the following, we describe each parameter that is useful to compute all the terms of Eqs. (5) and (6).
3.3 Energy sources
3.3.1 Solar flux
Triton is 30 AU away from the Sun. Consequently, the solar flux it receives is 900 times lower than on Earth and so approximately 10 times lower than on Titan. Despite this, the ionosphere of Triton is denser than the one of Titan.
We used different sources of data for the solar flux, allowing us to consider different solar activity cases. For the low-activity case, we used a high-resolution composite spectrum built with data from Curdt et al. (2001, 2004) that has a resolution of 0.004 nm between 67 and 160 nm and from Thuillier et al. (2004). This spectrum is the same as the one used in Dobrijevic et al. (2016).
For medium and high solar activity, we used low-resolution spectra with a resolution of 1 nm. As the flyby of Triton in 1989 occurred at a maximum solar activity, we used the corresponding low-resolution file between 1 and 730 nm in our calculations.
3.3.2 Magnetospheric electrons
As the solar flux seemed too weak to explain the presence of a dense ionosphere, a second source of energy was hypothesized (Majeed et al. 1990). The most obvious candidate was the precipitation of energetic electrons from Neptune’s magnetosphere, as energetic electrons were observed with the Low-Energy Charged Particles (LECP) instrument aboard Voyager 2 (Krimigis et al. 1989).
These measurements were used in Strobel et al. (1990a) to calculate the production rates of 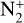 and N+ in Triton’s atmosphere. They show that without electron precipitation, the predicted electronic peak derived using only the solar flux does not correspond to the one observed by Voyager, as it is weaker and at a higher altitude. Adding magnetospheric electrons, they find a more reliable profile but at an altitude that is lower than expected. Thus, their ionization profile has to be moved up by two scale heights in order to find an electronic peak that fits with the observations (Summers & Strobel 1991). Finally, as the incident electronic flux used for the calculations was measured when Triton was close to Neptune’s magnetic equator, the ionization profile has to be adapted to represent mean orbital conditions, as done in Strobel et al. (1990a), Stevens et al. (1992), Krasnopolsky & Cruikshank (1995), and Strobel & Summers (1995).
and N+ in Triton’s atmosphere. They show that without electron precipitation, the predicted electronic peak derived using only the solar flux does not correspond to the one observed by Voyager, as it is weaker and at a higher altitude. Adding magnetospheric electrons, they find a more reliable profile but at an altitude that is lower than expected. Thus, their ionization profile has to be moved up by two scale heights in order to find an electronic peak that fits with the observations (Summers & Strobel 1991). Finally, as the incident electronic flux used for the calculations was measured when Triton was close to Neptune’s magnetic equator, the ionization profile has to be adapted to represent mean orbital conditions, as done in Strobel et al. (1990a), Stevens et al. (1992), Krasnopolsky & Cruikshank (1995), and Strobel & Summers (1995).
In our model, we need an electron production rate to compute the reaction rates of the ionizations and dissociations of N2 by magnetospheric electrons. Thus, we used the ionization profile of Strobel et al. (1990a), moved it up by two scale heights, and divided it by 6 in order to represent mean conditions, as done in Krasnopolsky & Cruikshank (1995).
The reaction rates k(ME,N2) for the interaction between magnetospheric electrons and N2 can then be computed with Eq. (7):
where prod(z) is the production rate of electrons at altitude z, br is the branching ratio of the reaction, and 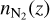 is the number density of N2 at the altitude z.
is the number density of N2 at the altitude z.
We considered three different reactions between magne-tospheric electrons and N2 for which branching ratios are respectively 0.8, 0.2 and 0.6 (Fox & Victor 1988):
3.3.3 Interplanetary flux
We also took into account the interplanetary radiation flux. As stated in Strobel et al. (1990b), at Triton’s distance from the Sun, this radiation is not negligible with a flux, F, at Lyman-a (121.6nm) of 340R (Broadfoot et al. 1989), 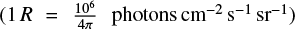 , equivalent to a flux of 8.5 × 107 photons cm−2 s−1, that may be compared to a 3.1 x 108 photons cm−2 s−1 solar flux at Lyman-α with a maximum solar activity. In addition, we considered two additional interplanetary radiation fluxes: one at Lyman-β (102.5 nm) with a ratio
, equivalent to a flux of 8.5 × 107 photons cm−2 s−1, that may be compared to a 3.1 x 108 photons cm−2 s−1 solar flux at Lyman-α with a maximum solar activity. In addition, we considered two additional interplanetary radiation fluxes: one at Lyman-β (102.5 nm) with a ratio 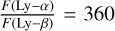 and one at the Helium line (58.4nm), with a ratio of
and one at the Helium line (58.4nm), with a ratio of 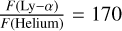 , as in Dobrijevic (1996).
, as in Dobrijevic (1996).
3.4 Condensation
As the temperature is very low in the lower atmosphere of Triton, condensation occurs for several species. This is consistent with observations of hazes in the lowest 30 km by Voyager 2. This haze is thought to be composed of hydrocarbons that are the products of CH4 photolysis (Strobel et al. 1990b; Herbert & Sandel 1991; Krasnopolsky et al. 1992). In our model, we use a simplified consideration of the condensation, by fixing the abundance of the condensing species at 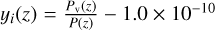 if the abundance of the considered species exceeds the
if the abundance of the considered species exceeds the 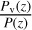 ratio.
ratio.
Our formulas to compute the vapor pressure Pv of the different species come from different sources, in particular, those of Lara et al. (1996), Fray & Schmitt (2009), the NIST database, and Haynes (2012). It must be noted that as the temperature near the surface of Triton is very low, small differences in the vapor pressure formulas in the temperature range where they are commonly measured could lead to significant differences in the final abundance profiles, as these abundances are restricted by the 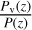 ratio.
ratio.
4 Update of the chemical scheme
As stated in Sect. 3.1, we expected some chemical differences to emerge between the Titan and Triton models, forcing us to modify the initial chemical scheme. To do so, we first performed a run under the assumed conditions of Triton’s atmosphere. A very important difference between the atmospheres of Triton and Titan arises from the absence of CH4 in the higher atmosphere of Triton, which impacts the overall chemistry. To complete our chemical network, we focused on the species that have become much more abundant in the atmosphere of Triton. This is particularly the case for some atomic species such as N(4S), N(2D), C, and C+, as noted previously by Krasnopolsky & Cruikshank (1995). The low abundance of CH4 in the upper atmosphere of Triton induces low abundances of hydrocarbons and hydrocarbon radicals (in particular CH3). As a result, association reactions with N2 become much more important, such as the C+ N2 → CNN reaction, which is the main loss reaction for atomic carbon in the new model. It is thus also necessary to include these new species (e.g., CNN) and to introduce their chemical network. The high abundance of atomic carbon associated with its low ionization energy makes charge transfer reactions efficient. This leads to a high abundance of ionized atomic carbon which becomes the main ion above 175 km; this comprises an important difference with regard to the atmosphere of Titan. Once the new reactions to be included in the network were identified, the rate constants and branching ratios were chosen mainly from literature searches (e.g., Husain & Kirsch 1971 for the new critical reaction C + N2 or Anicich 2003 for the C+ reactions). When no study existed on this aspect, we followed the same methodology as in our previous studies on Titan’s chemistry (Hébrard et al. 2012; Loison et al. 2015). As some reactions require the introduction of new species, we needed a few iterations to build the nominal chemical scheme. We also took care to compare our final network with that of Krasnopolsky & Cruikshank (1995), allowing us to identify several important differences (described later in this work). We also compared our results with data derived from the Voyager 2 observations presented in Broadfoot et al. (1989), Tyler et al. (1989) and Herbert & Sandel (1991) and with results from previous photochemical models such as Krasnopolsky & Cruikshank (1995) and Strobel & Summers (1995). This methodology is presented in Fig. 3.
After modifying the chemical scheme, we ended up with a nominal chemical scheme consisting of 220 atmospheric species and 1764 reactions, as described in Table 2. A file containing a list of all the atmospheric species and their masses is available as supplementary material.
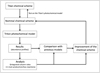 |
Fig. 3 Methodology used to adapt Titan’s chemical scheme to Triton. |
5 Nominal results with the updated chemical scheme
For the nominal model, we used the nominal values of the chemical reaction rates, meaning that we did not consider any uncertainty in their computation. In this way, we only had to run the program once. As described in Sect. 3, we proceeded with three steps before reaching steady abundance profiles. In the following, we present the abundance profiles of the main neutral species and of the main ions. We detail the main production and loss processes for each important species in order to better understand the main mechanisms of Triton’s atmospheric chemistry and why they are different to those found for Titan. Tables containing all these reactions and plots displaying their reaction rates depending on altitude are given in the supplementary material associated with this paper. We also aim to identify the parameters that have the greatest impact on the final abundance profiles and we compare our results with observations at the end of this section.
5.1 Neutral atmosphere
5.1.1 Main species
The most abundant neutral species are N2, N (N(4S) and N(2D)) as well as CH4, C, CO, H, H2, and O(3P). Their abundance profiles are given in Fig. 4. Here, N(4S) corresponds to the ground state of atomic nitrogen and N(2D) is its first excited state. We only consider O(3P) here since the abundance of O(1D) remains negligible.
We can observe that N2 remains the main atmospheric species present throughout the atmosphere. Near the surface, CO, CH4, and H2 are the most abundant trace species. The abundance of CH4 decreases quickly at higher altitude due to its photolysis by Lyman-α radiation. Above 50 km, we see a large increase in the abundances of atomic species N, C, O, and H, while N becomes the second-most abundant species and C the third.
In the following, we detail the main production and loss processes for each of these species in order to understand these evolutions (we note that the third body of all the three-body reactions is N2, thus, it is not indicated further in the rest of the paper). All the reactions used in this model and their integrated column rates are given as supplementary material.
N2. With N2 being the main species of Triton’s atmosphere, it is used as a reservoir in our model. Therefore, its abundance is not renormalized at each time step. It is destroyed by photodissociation, photoionization, and interactions with magnetospheric electrons. These reactions produce atomic nitrogen N(4S) and N(2D) as well as 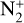 and N+ ions. The loss rate by photointeraction is of the order of one third of that by electrointeraction. This is consistent with the input energy flux, namely, the energy carried by magnetospheric electrons being higher than that of the solar flux. More details are given about this in Sect. 5.2.2. The interaction with magnetospheric electrons is the second most important loss process for N2, the first one being the three-body reaction with C giving CNN. N2 also reacts with CH, which is a product of methane photolysis, to produce HCNN, with a loss rate half that of the previous reaction. Photoionization and reactions with magnetospheric electrons reach their maximum rate in the ionosphere, at 390 and 345 km, respectively, while other loss reactions mainly occur below 200 km.
and N+ ions. The loss rate by photointeraction is of the order of one third of that by electrointeraction. This is consistent with the input energy flux, namely, the energy carried by magnetospheric electrons being higher than that of the solar flux. More details are given about this in Sect. 5.2.2. The interaction with magnetospheric electrons is the second most important loss process for N2, the first one being the three-body reaction with C giving CNN. N2 also reacts with CH, which is a product of methane photolysis, to produce HCNN, with a loss rate half that of the previous reaction. Photoionization and reactions with magnetospheric electrons reach their maximum rate in the ionosphere, at 390 and 345 km, respectively, while other loss reactions mainly occur below 200 km.
We note that N2 is mostly produced through the CNN cycle:
| N2 + C | → | CNN |
| CNN + N(4S) | → | N2 + CN |
| CN + N(4S) | → | N2 + C |
| net N(4S) + N(4S) | → | N2 |
and the peak rate of these reactions occurs at 121 km. The reaction between H and HCNN giving 1CH2 + N2 has an integrated production rate four times lower than the ones of the CNN cycle but it stands as the main production process below 50 km; this is logical, as the reaction producing HCNN reaches its maximum rate at 10 km. At altitudes higher than 250 km, dissociative recombination of N2H+ is the main source of N2.
CH4. Given that as its photolysis is a source of the CH, 3CH2,1CH2, and CH3 radicals, of H and H2, it is clear that CH4 is very important for Triton’s atmospheric chemistry. It also leads to the production of more complex hydrocarbons. Its chemistry is triggered by photodissociation and photoionization by Lyman-α radiation from the Sun and from the interstellar medium (ISM). Photodissociation reactions account for 71% of the total loss of CH4. This species also reacts with CH to produce C2H4. This reaction contributes for 29% of the total loss of CH4, explaining why C2H4 is the most abundant hydrocarbon in the lower atmosphere (cf. Sect. 5.1.2). These results are consistent with the description of Strobel et al. (1990b). All these reactions reach their maximum rate at 10 km, which corresponds to the altitude where the atmosphere becomes optically thick at the Lyman-α wavelength, as shown in Fig. 5.
Almost all CH4 production comes from the three-body reaction between CH3 and H, in agreement with Strobel et al. (1990b). This reaction accounts for 94.5% of the integrated production and peaks at 10 km, again at the photolysis maximum. At altitudes higher than 75 km, CH4 is produced by diverse ion-neutral reactions, the main one being 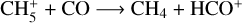 .
.
N(4S) and N(2D). Atomic nitrogen is the second most abundant species between 155 km and the top of the atmosphere. In our chemical scheme, we consider two distinct states of atomic nitrogen: the ground state N(4S) and the first excited state N(2D).
In particular, N(2D) is produced through reactions between N2 and magnetospheric electrons (32%), but also by photodissociation (12.5%) and photoionization (1%) of this species. However, the main production process is the dissociative recombination of 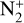 (54.5%). The production peaks of all these reactions are located around 350 km, except for the photodissociation of N2 giving N(4S) + N(2D) whose peak is at 71 km (the other channel producing 2N(2D) peaks at 378 km).
(54.5%). The production peaks of all these reactions are located around 350 km, except for the photodissociation of N2 giving N(4S) + N(2D) whose peak is at 71 km (the other channel producing 2N(2D) peaks at 378 km).
Then, N(2D) is quenched to ground state N(4S) through collisions with CO (75.5%), C (15%) and O(3P) (9.5%), whose loss rates are maximum at 334 km for the former reaction and 356 km for the others. These reactions account for 47.5, 9.5 and 6% of the integrated production of N(4S) respectively. This species is also produced by dissociative recombination of 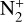 (11%) and dissociation of N2 by magnetospheric electrons (13%). Photodissociation of N2 accounts for 4.5%. The CN + O(3P) → N(4S) + CO reaction is the main production process of N(4S) around 120 km where the production rate of this reaction is maximum. It contributes for 2.3% of the integrated production of N(4S).
(11%) and dissociation of N2 by magnetospheric electrons (13%). Photodissociation of N2 accounts for 4.5%. The CN + O(3P) → N(4S) + CO reaction is the main production process of N(4S) around 120 km where the production rate of this reaction is maximum. It contributes for 2.3% of the integrated production of N(4S).
As stated in Krasnopolsky & Cruikshank (1995), the CNN cycle is an important loss process for atomic nitrogen. In our case, it contributes for 81.5% of the integrated loss of N(4S). Around 35 km, N(4S) also reacts with species from methane photolysis such as H, CH3 and 3CH2, producing NH, H2CN + H and HCN + H respectively. The rates of these reactions are at least one order of magnitude lower than those of the CNN cycle.
H2 and H. The direct photolysis of CH4 only accounts for 38.5% of the integrated production of H2 (considering the reactions producing H2 directly from CH4). Also, H2 is produced through other reactions involving products of CH4 photolysis, such as H, 3CH2, or CH3. The main one is H + 3CH2, which gives H2 + CH (51% of the integrated production). Consequently, H2 is mainly produced around 10 km, the altitude where the photolysis loss rate of CH4 is at its maximum.
Losses of H2 mainly occur at higher altitudes, through ion-neutral reactions, with 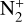 giving N2H+ + H (50% of the integrated loss, maximum loss rate at 303 km), with N+ producing NH+ + H (13%, maximum at 356 km), with CO+ which gives (HCO+ HOC+) + H (14%, maximum at 127 km), and with CH+ and
giving N2H+ + H (50% of the integrated loss, maximum loss rate at 303 km), with N+ producing NH+ + H (13%, maximum at 356 km), with CO+ which gives (HCO+ HOC+) + H (14%, maximum at 127 km), and with CH+ and 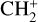 giving
giving 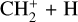 and
and 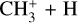 respectively (12% and 7%, maxima at 127 km). The reaction with N+ is the main loss process above 550 km.
respectively (12% and 7%, maxima at 127 km). The reaction with N+ is the main loss process above 550 km.
Atomic hydrogen is also produced directly by CH4 photolysis (43.5%) and through the reaction CH + CH4 → C2H4 + H (28%) near the methane photolysis peak. In the ionosphere, it is mainly produced through the 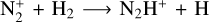 reaction and by the dissociative recombination of the latter ion (each reaction contributes for 3.5% of the integrated production of H).
reaction and by the dissociative recombination of the latter ion (each reaction contributes for 3.5% of the integrated production of H).
Atomic hydrogen is mainly lost through reactions with 3CH2 (56% of the integrated loss) and HCNN (28.5%) to produce CH + H2 and 1CH2 + N2, respectively. These reactions are important in the lower atmosphere as they involve products of methane photolysis (HCNN is produced by N2 + CH → HCNN whose production rate peaks at 10 km). Also, H is converted to H2 through the following cycle:
The three-body reaction H + H → H2 is an important loss process for H in Krasnopolsky & Cruikshank (1995), but this reaction is much less noticeable in our case, as it contributes only 0.025% on the integrated loss.
CO. Losses of CO mostly occur in the ionosphere, where it reacts with N+. This explains the decrease of its relative abundance observed in Fig. 4. It also photodissociates and photoionizes in the lower atmosphere, with maximum rates reached at 181 and 127 km, respectively. It has to be noted that in our model CO absorbs solar radiation up to 163 nm, but is only photoionized by radiation with λ < 89 nm and photodissociated by radiation with λ ∈ [89, 108[nm. Thus, CO absorbs radiation between 108 and 163 nm without being dissociated. This leads to an attenuation of the solar flux at these wavelengths, thus impacting the photolysis of hydrocarbons such as C2H2 (see Fig. 5). We should consider that CO molecules re-emit absorbed photons at these wavelengths in every direction, thus contributing to the photolysis of other species, but this is not done in our model.
CO is mainly produced through reactions of O(3P) with CNN and CN, which produce respectively N2 + CO and N(4S) + CO, with the latter having a slightly higher production rate.
C. We find a higher relative abundance of C throughout the atmosphere than was reported the findings of Krasnopolsky & Cruikshank (1995). The peak concentration is 5.2 × 107cm3 at 167 km, as compared with ~1.5 × 107cm3 at ~ 130 km in their study. This species is mainly produced through the reaction N(4S) + CN → N2 + C (68.5% of the integrated production of C), which is part of the CNN cycle converting atomic nitrogen into N2. But this production is counterbalanced by the N2 + C → CNN reaction whose integrated rate is 9% higher and contributes for 76% of the integrated loss of C, being therefore the main loss process. The rates of these reactions are maximum at 121 km. Various ionic reactions also produce C, such as the dissociative recombination of CO+ (8% of the integrated production), the radiative recombination of C+ (1.5%) or the ion-neutral reaction CO + N+ → C + NO+ (1%).
Apart from the reaction with N2, C is lost through various reactions with ions in the ionosphere, but these reactions are at least two orders of magnitude less significant than the former reaction.
O(3P). In our model, O(3P) is also an abundant species. As in Krasnopolsky & Cruikshank (1995), the peak concentration of O(3P) is about 108 cm−3. We recall that we do not consider O(1D) here because its abundance is negligible in comparison to O(3P). This species is mainly produced by dissociative recombination of the CO+ and NO+ ions (the latter contributing approximately eight times less than the former). These reactions are important in the ionosphere as their peak rate is reached at 345 km. At lower altitudes, O(3P) is produced through the reaction N(4S) + NO → O(3P) + N2, with an integrated rate one order of magnitude lower than for the dissociative recombinations.
In particular, O(3P) is mainly lost through reactions with CNN and CN as discussed above and whose maximum rates are reached at 121 km. Below this altitude, O(3P) reacts with various species such as CH3, NH, or H2CN, giving (H2CO + H, CO + H2 + H), NO + H, and (OH + HCN, HCNO + H), respectively; however, the integrated rates of these reactions are one order of magnitude lower than those of reactions with CN and CNN.
 |
Fig. 4 Relative abundances of the main neutral species in the atmosphere of Triton: (a) Relative abundance of N2 (green solid line), CH4 (orange solid line with circles), CO (red dashed line), H2 (blue dash-dotted line), and H (dark blue dotted line), (b) Relative abundances of N(4S), (black solid line), N(2D), (black dotted line), C (gray dash-dotted line), and O(3P), (cyan dashed line). We only give the O(3P) profile as the abundance of O(1D) is negligible. |
 |
Fig. 5 Altitude at which the optical thickness of the atmosphere is 1 depending on the wavelength of the incident radiation. The plot is cut at 200 nm as the atmosphere is not optically thick for all wavelengths above 160 nm, but the initial solar flux goes from 0 to 730 nm. |
 |
Fig. 6 Relative abundances of the main hydrocarbons and comparison with their vapor pressure ratio: (a) Relative abundances of the main hydrocarbons (orange solid line with circles for CH4, solid pink line for C2H2, purple dash-dotted line for C2H4 and brown dashed line for C2H6), and blue dotted line for HCN. (b) Relative abundances (solid lines) compared to the ratio of the vapor pressure, Pv, and the pressure, P, (dashed lines) depending on altitude for CH4, the main C2Hx, and HCN. When the curves of the Pv/P ratio and the abundance merge, this means that the species is condensing, as its abundance cannot be higher than this ratio. |
5.1.2 Hydrocarbons and HCN
The abundances of the main hydrocarbons and of HCN are presented in Fig. 6. In agreement with Krasnopolsky & Cruikshank (1995), the most abundant hydrocarbon in our model is C2H4. However, it is half as abundant in their model as compared to ours, with a peak concentration of 5.1 × 106 cm−3 at 47 km, whereas we have 2.0 × 107cm−3 at 36 km. We also find that C2H6 is more abundant than C2H2, as the peak concentration of the former is 1.9 × 106cm−3 at 36 km compared with 4.4 × 105 cm−3 at 56 km for the latter. In Krasnopolsky & Cruikshank (1995), these two species have approximately the same peak number density (1.3 × 106 cm−3 and 1.4 × 106 cm−3, respectively). These differences come from the different vapor pressure formula used in our model. In comparison, for the summer and winter hemispheres respectively, Strobel & Summers (1995) found (2.6–1.6) × 107 cm−3 at (17–30) km for C2H4 and (3.3 × 105−1.3 × 106) cm−3 at (100–104) km for C2H2. In addition, our HCN abundance is much lower, its peak number density being 1.8 × 102 cm−3 against 3 × 106 cm−3 for Krasnopolsky & Cruikshank (1995), while the peak concentration of HCN is nearly 107 cm−3 in Strobel & Summers (1995). This difference comes from the vapor pressure of HCN that is much lower than the ones of the studied hydrocarbons, as shown in the right-hand panel of Fig. 6, and which forces the number density of this species to drop below 275 km. As for neutral species, we discuss the main production and loss processes for these compounds in the following paragraphs.
C2H2. As the vapor pressure of C22H2 is lower than that of C2H4 and C2H6, it is the least abundant of the three C2Hx studied here. Its production relies almost exclusively on methane photolysis as it is produced at 53.5% through 3CH2 + 3CH2 → C2H2 + H2 and 39% through CH3 + HCNN → C2H2 + H2 + N2. The remaining production comes from C2H4 photolysis (4.5%). The two former reactions reach their peak production rate at 10 km, whereas C2H4 photolysis peaks at 36 km.
This hydrocarbon is mainly lost around 56 km, where it reacts with C to form C3 + H2 and c-C3H + H (37 and 59.5%), or is photodissociated, which gives C2H + H (2%). The C + C2H2 → I-C3H + H channel also exists, but its integrated rate is two orders of magnitude lower than that of the C-C3H channel. In particular, C2H2 condenses below 60 km, as the temperature falls when approaching the surface, as shown in Fig. 6. The integrated condensation rate of C2H2 is 1.1 × 107 cm−2 s−1, which corresponds to a mass condensation rate of 4.6 × 10−16 g cm−2 s−1. This value is one order of magnitude higher than the one of Krasnopolsky & Cruikshank (1995), which is 4 × 10−17 g cm−2 s−1. This difference comes from the use of a lower vapor pressure profile and a different chemical scheme, leading to a higher integrated production rate for this compound compared to Krasnopolsky & Cruikshank (1995).
C2H4. This is the most abundant C2Hx species. Strobel et al. (1990b) stated that C2H4 is produced through the reaction 3CH2 + 3CH2 → C2H4 and also through CH + CH4 → C2H4 + H. In our case, we effectively find that the latter is responsible for 84% of the integrated production but the former is not taken into account, as we consider 3CH2 + 3CH2 → C2H2 + H2. Instead, 15.5% of the production is due to the reaction 3CH2 + CH3 → C2H4 + H. The production rates of these reactions are maximum at 10 km, which is consistent with the fact that C2H4 derives from methane photolysis, which reaches its maximum at this altitude.
In particular, C2H4 is lost by photodissociation (22.5%), yielding C2H2, C2H3, H2, and H. It also reacts with C (9.5%) to produce C3H3 and H, but the main loss process is the three-body reaction with H giving C2H5 (60.5%). The photodissociation peak is located at 36 km, as the maximum rate of the three-body reaction, whereas the reaction with C peaks at 46 km. It condenses below 40 km (Fig. 6). The integrated condensation rate of C2H4 is 9.0 × 107 cm−2 s−1, which corresponds to a mass condensation rate of 4.2 × 10−15 g cm−2 s−1. Krasnopolsky & Cruikshank (1995) found a value of 4.3 × 10−15 g cm−2 s−1, which is very close to our result.
C2H6. This species is entirely produced by a three-body reaction between two CH3 (99.98%), with a maximum production rate at 10 km (again due to methane photolysis).
It is destroyed by photolysis (97.5%) and reaction with CN (2%) and condenses below 40km (Fig. 6). All these reactions reach their maximum loss rate at 36 km. The integrated condensation rate of C2H6 is 2.0 × 107cm−2s−1, which corresponds to a mass condensation rate of 1.0 × 10−15g cm−2 s−1. The value given in Krasnopolsky & Cruikshank (1995) is 8.9 × 10−16g cm−2 s−1, which is slightly lower than ours. The ratio between these two rates is nearly the same as the ratio of our integrated production rates, thus the difference comes from the chemical scheme.
HCN. While it is mostly produced through reactions involving H2CN (produced through the reaction N(4S) + CH3 → H2CN + H), which reacts with H and O(3P) to give respectively HCN + H2 (47% of the integrated production) and HCN + OH (6.5%), HCN is also produced through the following reactions involving N(4S):
The maximum rates of these reactions are reached between 31 and 51 km. The HCN molecule is lost in the ionosphere through reactions with N(2D) giving CH and N2 (19%) and with H+ giving HNC+ and H (80.5%). These reaction rates peak at 303 km and 293 km respectively. This species condenses below 280 km (Fig. 6), thus at a much higher altitude than the C2Hx species.
 |
Fig. 7 Relative abundances of the radicals that appeared in the key chemical reactions of the main neutral species (solid blue line for CH, orange dashed line for CH2, green solid line with circles for CH3. dash-dotted pink line for CN, and purple dotted line for CNN). The CH2 profile corresponds to 3CH2, as the relative abundance of 1CH2 is negligible. |
5.1.3 Radicals
As radicals were evoked during our study of key chemical reactions for the main neutral species, we give their relative abundances in Fig. 7. We know that 1CH2 is completely converted to 3CH2 through collisions with N2. Therefore, its abundance is negligible and we focus on 3CH2 in the following.
In agreement with what we discussed above, the production of CH3 and 3CH2 is maximum at 10 km as it depends on methane direct photolysis, this process contributing for respectively 97% and 8.5% of the integrated production of these species. The remaining production of 3CH2 comes from collisions between 1CH2 and N2 (91%). Also, 1CH2 can be produced by direct methane photolysis (54.5%) and through H + HCNN → 1CH2 + N2 (45%), thus dependent on H, which is also a photolysis product.
We know that CH3 mainly reacts with other CH3 radicals to produce C2H6 (55.5% of the integrated loss), but also with 3CH2 (19%) and N(4S) (13.5%), which yields C2H4 + H and H2CN + H respectively. The reaction between CH3 and 3CH2 accounts for 8.5% of the integrated loss of 3CH2. The latter compound reacts mainly with H to produce CH + H2 (80% of the integrated loss). It also reacts with other 3CH2 radicals to form C2H2 + H2 (7%). All these reactions reach their maximum rate at 10 km apart from the N(4S) + CH3 reaction whose maximum is at 31 km.
Then, CH is mainly produced through the 3CH2 + H → CH + H2 reaction (87%) and direct methane photolysis (12%). It is mainly lost through CH + CH4 → C2H4 + H (49.5%) and CH + N2 → HCNN (49%). All these reactions also reach their maximum rate at 10 km.
Furthermore, CN and CNN are mostly produced and lost through the CNN cycle that converts atomic nitrogen to N2, as seen above. Thus, CN is almost exclusively produced through the reaction N(4S) + CNN → CN + N2 (96%) and CNN through C + N2 → CNN (100%). Then, CN is mostly lost through N(4S) + CN → C + N2 (94%) and CNN through N(4S) + CNN → CN + N2 (92.5%). These reactions all reach their maximum rate at 121 km. In addition, CN and CNN react with O(3P) to yield CO + N(4S) and CO + N2, respectively, with these reactions accounting for 6% and 5% of the integrated loss.
5.1.4 Heavier Cx-compounds
The most abundant C3Hx species is C3 with a peak relative abundance of 1.4 × 10−7 at 103 km. It intervenes in a cycle converting atomic hydrogen into molecular hydrogen, which we discuss above. Reactions of this cycle account for 98.25% of the integrated production of C3 and 96.28% of its integrated loss. The integrated rates of the production reactions are slightly higher than the ones of the loss reactions. Apart from this cycle, C3 is produced through the reaction C + C2H2 → C3 + H2 and lost by photodissociation producing 3C2 + C.
Aside from this species, the other neutral C3-compounds are much less abundant. For example, the second most abundant is C3H3CN and the third is c-C3H2 – with respective peak relative abundances of 1.7 × 10−10 at 46 km and 2.5 × 10−11 at 181 km. C3H3CN is mostly produced through the reaction CN + CH3CCH → C3H3CN + H (11% of the integrated production) and H + CH2C3N → C3H3CN (79%). It is lost at 77.2% by photodissociation, producing CH2C3N + H and C3H3 + CN. It also reacts with 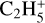 to produce CH3C3NH+ + C2H4 (15% of the integrated loss). Then, c-C3H2 is mainly produced through H + (c-C3H + I-C3H) → c-C3H2 (72%) and dissociative recombinations of
to produce CH3C3NH+ + C2H4 (15% of the integrated loss). Then, c-C3H2 is mainly produced through H + (c-C3H + I-C3H) → c-C3H2 (72%) and dissociative recombinations of 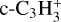 (5.9%),
(5.9%), 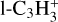 (3.7%) and
(3.7%) and 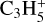 (9.2%); finally, c-C3H2 is almost exclusively lost through a three-body reaction with H producing C3H3 (97.7% of the integrated loss).
(9.2%); finally, c-C3H2 is almost exclusively lost through a three-body reaction with H producing C3H3 (97.7% of the integrated loss).
The most abundant C3Hx ion is 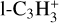 , with a peak relative abundance of 2.0 × 10−12 at 153 km. It is mainly produced through
, with a peak relative abundance of 2.0 × 10−12 at 153 km. It is mainly produced through 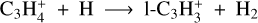 (12.7%). It is lost by dissociative recombination (91.5%) and reactions with C2H4 producing heavier ions
(12.7%). It is lost by dissociative recombination (91.5%) and reactions with C2H4 producing heavier ions 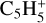 and
and 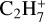 (3.5% of the integrated loss for each channel). The second-most abundant C3Hx ion is
(3.5% of the integrated loss for each channel). The second-most abundant C3Hx ion is 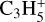 with a peak relative abundance of 7.9 × 10−13 at 109 km. It is produced through
with a peak relative abundance of 7.9 × 10−13 at 109 km. It is produced through 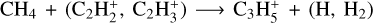 (10%, 83%) and
(10%, 83%) and 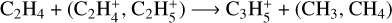 (5%, 1.5%). It is mainly lost by reacting with H (19%), which gives
(5%, 1.5%). It is mainly lost by reacting with H (19%), which gives 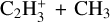 or by dissociative recombination (68%). It also reacts with C2H4 to produce
or by dissociative recombination (68%). It also reacts with C2H4 to produce 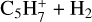 .
.
In total, eight neutral C3-compounds and eight 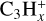 ions have a relative abundance higher than 10−15. In the same interval, we find seven neutral C4-compounds, the most abundant being nC4H8 with a peak abundance of 6.5 × 10−13. We also identify six heavier ions
ions have a relative abundance higher than 10−15. In the same interval, we find seven neutral C4-compounds, the most abundant being nC4H8 with a peak abundance of 6.5 × 10−13. We also identify six heavier ions 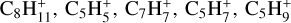 , and
, and 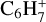 – with peak abundances ranging from 1.6 × 10−14 to 2.2 × 10−15 (species are given in order of decreasing abundance).
– with peak abundances ranging from 1.6 × 10−14 to 2.2 × 10−15 (species are given in order of decreasing abundance).
 |
Fig. 8 Relative abundances of the main ions of the atmosphere of Triton: (a) Most abundant ions that are the focus of this study – blue solid line with circles for C+, orange dashed line for N+, green dash-dotted line for N2+, purple dotted line for H+, thin brown solid line for CO+, thin dark blue dashed line for N2H+, and red solid line for electrons. (b) Most abundant ions below 175 km. |
5.2 Ionosphere
A dense ionosphere was observed by Voyager 2. Surprisingly, it was found to be denser than the one of Titan despite the larger and denser atmosphere of the latter. The peak of the electronic number density profile was found at (340–350) km with a peak concentration of (3.5 ± 1) × 104 cm−3 (Tyler et al. 1989; Krasnopolsky & Cruikshank 1995). In this section, we investigate the main ionization processes in Triton’s atmosphere and study the composition of its ionosphere.
5.2.1 Main ions
Using nominal chemical reaction rates, we find that the main ions of Triton’s ionosphere are C+, N+, H+, and 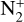 , as shown in Fig. 8. The electronic number density is maximum at 334 km, which is close to the interval (340–350) km given in Tyler et al. (1989). We can see that the electronic number density quickly increases above 175 km, where the concentration of C+ varies strongly. It nearly corresponds to the sharp ionospheric cutoff around 200 km observed in Voyager’s data and shown in Tyler et al. (1989). In Krasnopolsky & Cruikshank (1995), the main ions were C+ and N+, with H+ being only the sixth most abundant ion. Another difference is that in their model C+ and N+ abundances tend to converge after the electronic peak, but this behavior in less pronounced in our results.
, as shown in Fig. 8. The electronic number density is maximum at 334 km, which is close to the interval (340–350) km given in Tyler et al. (1989). We can see that the electronic number density quickly increases above 175 km, where the concentration of C+ varies strongly. It nearly corresponds to the sharp ionospheric cutoff around 200 km observed in Voyager’s data and shown in Tyler et al. (1989). In Krasnopolsky & Cruikshank (1995), the main ions were C+ and N+, with H+ being only the sixth most abundant ion. Another difference is that in their model C+ and N+ abundances tend to converge after the electronic peak, but this behavior in less pronounced in our results.
In panel b of Fig. 8, we present the most abundant ions below 175 km. We can observe that the higher mass ions reach their peak relative abundance at lower altitude than the lower mass ones, with 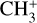 being the main ion between 175 and 125 km. Then
being the main ion between 175 and 125 km. Then 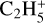 , NH2CO+, and HCO+ are most abundant between 125 and 60 km and finally
, NH2CO+, and HCO+ are most abundant between 125 and 60 km and finally 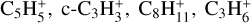 , and NH2CO+ dominate below 60 km. This is consistent with the fact that heavier species are abundant in the lower atmosphere only (e.g., hydrocarbons), whereas lighter species (e.g., atomic species as C, O, and N) are dominant at higher altitudes. However, the relative abundances of these heavy ions remain low in comparison to the lighter ions in the upper atmosphere. Therefore, we did not focus on the lower atmosphere ions in the remainder of our study.
, and NH2CO+ dominate below 60 km. This is consistent with the fact that heavier species are abundant in the lower atmosphere only (e.g., hydrocarbons), whereas lighter species (e.g., atomic species as C, O, and N) are dominant at higher altitudes. However, the relative abundances of these heavy ions remain low in comparison to the lighter ions in the upper atmosphere. Therefore, we did not focus on the lower atmosphere ions in the remainder of our study.
Photoionization reactions with the highest integrated column rates.
5.2.2 Photoionization and interaction with magnetospheric electrons
The photoionization reactions with the highest integrated column rates are listed in Table 3. These reactions contribute for 99.98% of the total photoionization integrated column rate. For the interaction with magnetospheric electrons, the main reactions and their integrated column rates are given in Table 4. Unsurprisingly, ionization of N2 dominates as it is the main atmospheric species. These reactions are sources of ions 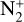 , N+ but also of atomic nitrogen. Dissociation of N2 by mag-netospheric electrons is also a source of the latter species. We note that the peak of these reactions is located slightly above the electronic peak, which is located at 334km.
, N+ but also of atomic nitrogen. Dissociation of N2 by mag-netospheric electrons is also a source of the latter species. We note that the peak of these reactions is located slightly above the electronic peak, which is located at 334km.
We can see that ionization by magnetospheric electrons is more important than photoionization. The ratio between the rates for photoionization and the rates for magnetospheric interaction is 3/8, which is comparable to the ratio of 0.5 given in Krasnopolsky & Cruikshank (1995).
Ionization and dissociation reactions by magnetospheric electrons (ME) and their integrated column rates.
5.2.3 Production and loss processes
We detail here the main production and loss processes for the main ions of the ionosphere of Triton.
C+. This is the most abundant ionospheric ion in Strobel & Summers (1995), and Krasnopolsky & Cruikshank (1995). Lyons et al. (1992) were the first to consider C+ as an abundant ion after using a charge exchange reaction between 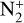 and C. In our model, this reaction is the main source of C+, accounting for 74.5% of the integrated production. This ion is also produced by two other charge exchange reactions between C and N+ or CO+, with respective contributions of 11 and 14.5%. The maximum production rate of the reaction between C and
and C. In our model, this reaction is the main source of C+, accounting for 74.5% of the integrated production. This ion is also produced by two other charge exchange reactions between C and N+ or CO+, with respective contributions of 11 and 14.5%. The maximum production rate of the reaction between C and 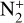 is located at 334 km, which corresponds to the electronic concentration peak. The production peak for charge exchange with N+ is located at 414 km and the one for charge exchange with CO+ at 313 km.
is located at 334 km, which corresponds to the electronic concentration peak. The production peak for charge exchange with N+ is located at 414 km and the one for charge exchange with CO+ at 313 km.
C+ is almost exclusively lost by radiative recombination (98%), whose maximum rate is at 334 km as well. In Krasnopolsky & Cruikshank (1995), the main chemical process for loss of C+ is by reacting with CH4, but in our case, this reaction has an integrated loss rate 104 times lower than the radiative recombination reaction mentioned before. This is due to the very low number density of CH4 at ionospheric altitudes. Moreover, we do not consider atmospheric escape for ions, which is the main loss process in Krasnopolsky & Cruikshank (1995). This may explain why we have a higher number density of C+.
N+ This is the second main ion of the ionosphere, as in Krasnopolsky & Cruikshank (1995). On the other hand, in Strobel & Summers (1995), N+ is the second main ion between 250 and 550 km and then becomes the most abundant ion. In our case, N+ was the main ion with the initial chemical scheme, but this changed with the updated one where the  C+ reaction was added, making C+ the main ion. In our updated chemical scheme, we also added reactions between N+ and CO, based on Anicich (2003). These reactions became important for N+, as they account for 87.5% of its integrated loss. Their loss rate is maximum at 345 km, where the ionization reactions of N2 giving N+ are maximum. Also, N+ reacts with H2 to produce NH+ + H. The loss rate of this reaction is maximum at 356 km and accounts for 11% of the integrated loss of N+.
C+ reaction was added, making C+ the main ion. In our updated chemical scheme, we also added reactions between N+ and CO, based on Anicich (2003). These reactions became important for N+, as they account for 87.5% of its integrated loss. Their loss rate is maximum at 345 km, where the ionization reactions of N2 giving N+ are maximum. Also, N+ reacts with H2 to produce NH+ + H. The loss rate of this reaction is maximum at 356 km and accounts for 11% of the integrated loss of N+.
The ionization of N2 by magnetospheric electrons contributes for 75% of the integrated production of N+. Photoionization contributes for 10% and charge exchange between 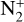 and atomic nitrogen for 15%. The first two reactions reach the production peak at 345 km, whereas the latter reaches it at 334 km.
and atomic nitrogen for 15%. The first two reactions reach the production peak at 345 km, whereas the latter reaches it at 334 km.
N2+. Even though N2 is the main atmospheric species and the ionization reactions giving 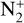 have a higher branching ratio compared to those giving N+, we see that
have a higher branching ratio compared to those giving N+, we see that 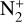 is only the third- or fourth-most abundant ion of Triton’s ionosphere, depending on altitude. It is produced by photoionization and electron impact ionization of N2 (respectively, 29 and 71% of the integrated production) but it quickly recombines with electrons to produce atomic nitrogen (82% of the integrated loss). It also reacts with H2 to produce N2H+ (10.5%) and with C, N(4S), and CO through charge-exchange reactions (7% in total). The loss rate for dissociative recombination is maximum at 356 km, whereas the one for charge exchange with C and N(4S) is at 334km (293 km for charge exchange with CO). For the reaction with H2, the maximum rate is reached at 303 km.
is only the third- or fourth-most abundant ion of Triton’s ionosphere, depending on altitude. It is produced by photoionization and electron impact ionization of N2 (respectively, 29 and 71% of the integrated production) but it quickly recombines with electrons to produce atomic nitrogen (82% of the integrated loss). It also reacts with H2 to produce N2H+ (10.5%) and with C, N(4S), and CO through charge-exchange reactions (7% in total). The loss rate for dissociative recombination is maximum at 356 km, whereas the one for charge exchange with C and N(4S) is at 334km (293 km for charge exchange with CO). For the reaction with H2, the maximum rate is reached at 303 km.
H+. This is mostly produced through a charge exchange reaction between CO+ and H, whose maximum rate is reached at 293 km and accounts for 96% of the integrated production. Photoionization of H contributes for 3% and is maximum at 146 km. It is lost by radiative recombination (29% of the integrated loss) around 345 km, but mostly by reacting with HCN and HNC to produce HNC+ + H (45.88%), whose rates are maximum at 293 and 264 km respectively. It also appears in charge exchange reactions with C and C3 (4.5 and 17%) and reacts with CH4 to produce 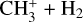 (2.5%).
(2.5%).
5.3 Key chemical reactions for the main species
We studied in the previous sections the main production and loss processes for the main species of Triton’s atmosphere. The reactions associated to these processes thus contribute significantly to the production or loss of these species. We call these reactions key chemical reactions. All these reactions are given as supplementary material. Table 5 displays the reactions that contribute significantly to the production or loss of several of the main atmospheric species. We can identify several groups of reactions in this table:
CH4 photolysis: unsurprisingly, we find that photolysis of CH4 is important, as stated in Strobel et al. (1990b), Krasnopolsky & Cruikshank (1995) and Strobel & Summers (1995). Its products also appear in other key chemical reactions. It triggers the chemistry in the lower atmosphere, the photolysis peak being located at 10 km. It is a source of H, H2 and radicals.
Photoionization of N2 and reactions with magnetospheric electrons: these reactions impact logically the number density of N2, 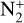 , N+, electrons, and atomic nitrogen. These products appear in numerous reactions shown in the table (as presented in the following points), thus, the former reactions are important for the atmospheric chemistry in general.
, N+, electrons, and atomic nitrogen. These products appear in numerous reactions shown in the table (as presented in the following points), thus, the former reactions are important for the atmospheric chemistry in general.
 dissociative recombinations: these reactions have a significant impact on the electronic and
dissociative recombinations: these reactions have a significant impact on the electronic and 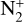 loss as these species recombine together quickly. This gives atomic nitrogen in the ground or first excited state.
loss as these species recombine together quickly. This gives atomic nitrogen in the ground or first excited state.
Atomic nitrogen: several reactions involve atomic nitrogen. We can in particular identify a cycle involving CNN that regenerates N2 from N(4S). N(2D) is quenched to ground state N(4S) through collisions with CO, O(3P), and C (the main channel being the one with CO).
5.4 Discussion
As the data available about Triton mostly come from Voyager 2, we have very few data points we could use to validate our results. As given in Krasnopolsky & Cruikshank (1995), we know that the number density of N2 at 575 km is (4 ± 0.4) × 108 cm−3 and that the concentration of atomic nitrogen at 400 km is (1 ± 0.25) × 108 cm−3 and (5 ± 2.5) × 108 cm−3 at 200 km. Our N2 profile is in agreement with the data as we find 3.7 × 108 cm−3 at 571 km and likewise for the atomic nitrogen data at 400 km, as we find 1.0 × 108 cm−3 at 402 km. However, our value at 200 km is slightly above the corresponding interval, as we have 9.6 and 8.8 × 108 cm−3 at 196 and 204km, respectively. At this level, we expect chemical uncertainties to be quite significant, possibly explaining the departure of our nominal value from the observed range. The peak concentration of atomic nitrogen is 2.0 × 109 cm−3 at 80 km, which is close to values from Krasnopolsky & Cruikshank (1995), and Strobel & Summers (1995), which are about ~1 × 109 cm−3 at ~115 km.
We also have the CH4 number density profiles near the surface for the two solar occultation points from Herbert & Sandel (1991). With the actual model and nominal reaction rates, we are nearly in agreement with these profiles, as shown in panel a of Fig. 9. The differences at low altitude are only due to our lower CH4 abundance at the surface coming from the use of the vapor pressure formula of Fray & Schmitt (2009). We also note that we were unable to match the data if we used a different Kzz profile or if we used a solar flux not corresponding to a maximum solar activity. Therefore, these two parameters seem to be critical for the modeling of Triton’s atmosphere. As Kzz impacts strongly our results, it could be important to better determine its profile as the one we use was inferred by using the CH4 number density near the surface only (Herbert & Sandel 1991).
The spectral resolution of the solar flux was found to have a non-negligible impact on the abundance profiles of CH4 as shown in the right-hand panel of Fig. 9. Following these observations, we may need a high resolution spectrum for high solar activity in order to obtain more representative results.
If we sum the mass condensation rates for the three C2Hx studied in this section, we find a total mass condensation rate of 5.7 × 10−15 g cm−2 s−1, which fits with the aerosol production rate interval of [4–8] × 10−15 g cm−2 s−1 given in Strobel & Summers (1995) for the winter and summer hemispheres, respectively.
For ions, we first examine if our electronic profile corresponds to the profiles presented in Tyler et al. (1989) and derived from Voyager data. These profiles are shown in Fig. 10. We can observe that our electronic peak is located at 334 km, which is slightly lower than the altitudinal range (340-350) km determined from Voyager measurements and given in Tyler et al. (1989). Also, our electronic peak concentration is 1.0 × 105 cm−3, which is higher than the interval of (3.5 ± 1) × 104 cm−3 given in Krasnopolsky & Cruikshank (1995). We show in Sect. 6 the impact of chemical uncertainties on the electronic profile. However, as we found that reactions with magnetospheric electrons had a large impact on the atmospheric chemistry, these results could change significantly if we took another electronic production profile. In addition, we modified the ionization profile from Strobel et al. (1990a) in a rather arbitrary way, following the manipulations made in Summers & Strobel (1991) and Krasnopolsky & Cruikshank (1995). Thus, changing these arbitrary values could also impact our results in a significant way. In order to model the interaction between magnetospheric electrons and Triton’s atmosphere better, we recommend using an electron transport code in further studies.
We also recall that we considered the electronic temperature to be equal to the neutral temperature in all the atmosphere because this parameter was not measured by Voyager. However, we observed that dissociative recombination reactions of 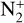 were among the most important key chemical reactions for the main species. As the rates of these reactions are computed using the electronic temperature, having a good estimation or measurements of this parameter seems mandatory in order to improve the confidence in our model.
were among the most important key chemical reactions for the main species. As the rates of these reactions are computed using the electronic temperature, having a good estimation or measurements of this parameter seems mandatory in order to improve the confidence in our model.
In the same way, recent occultation measurements presented in Oliveira et al. (2022) indicate that the thermal profile in the lower atmosphere could be quite different from the profile that we use here, with a strong positive gradient near the surface and the potential presence of a mesosphere. If correct, this could greatly impact the profiles of condensable species such as methane and hydrocarbons.
Key chemical reactions for the main atmospheric species.
 |
Fig. 9 Comparison of our CH4 profile with other datasets and impact of the resolution of the solar spectrum on our results: (a) CH4 number density profiles near the surface derived from Voyager 2 data and presented in Herbert & Sandel (1991; dark blue and orange), data points from Strobel & Zhu (2017; black dots) and result from our model using nominal reaction rates (red), i.e. without considering any uncertainty. (b) Comparison of the relative abundances of the main neutral species when using a high resolution solar spectrum (solid lines) versus a low resolution spectrum |
 |
Fig. 10 Number densities of the main ions in Triton’s atmosphere. The black triangles and dark blue circles represent the electronic profiles measured by Voyager 2 at the two occultations points (Tyler et al. 1989). |
6 Chemical uncertainties
As the temperature is very low on Triton, we expect to have large uncertainties on our abundance profiles. Indeed, chemical reaction rates are determined experimentally or theoretically but always with an uncertainty. It is expressed with two different factors: the temperature-dependent uncertainty factor Fi(T) and gi, a coefficient that is used to extrapolate Fi depending on temperature. The uncertainty factor is computed from Eq. (8), (see e.g., Sander et al. 2006; Hébrard et al. 2006, 2007, Hébrard et al. 2009):
where Fi(300 K) is the uncertainty factor at 300 K, which is commonly given with the reaction rates, as they are mainly measured around room temperature. This is why we expect uncertainties to be high: given that the temperature on Triton is below 100 K, we use rate formulas that are generally not known in these conditions and we extrapolate the associated uncertainty factors, about which we have a very limited knowledge. This generally leads to a greater uncertainty for most of the reaction rates that subsequently propagates into the model. Thus, it is necessary to examine how these uncertainties propagate during the calculations and their impact on the results and, thus, on the number density profiles of the different species.
To study the propagation of chemical uncertainties in our model, we used a Monte Carlo simulation. After the model was run with nominal reaction rates, that is, without considering any uncertainty (as done in the previous section), we compute again all the reaction rates using the uncertainty factors Fi and gi, considering each rate as a random variable, ki, with a log-normal distribution centered on the nominal rate,  ∙, and with a standard deviation, log Fi (Hébrard et al. 2007; Dobrijevic et al. 2008b). For two-body reactions, ki is obtained from Eq. (9):
∙, and with a standard deviation, log Fi (Hébrard et al. 2007; Dobrijevic et al. 2008b). For two-body reactions, ki is obtained from Eq. (9):
where ɛi is a random number with a normal distribution centered on zero and with a standard deviation of one. With this, we have a 68.3% probability to find ki in the interval ![$\left[ {{{{k_{{0_i}}}} \over {{F_i}}},{k_{{0_i}}} \times {F_i}} \right]$](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq77.png) . To avoid considering extreme values of ki, we only use values of ki computed with |ε| < 2.
. To avoid considering extreme values of ki, we only use values of ki computed with |ε| < 2.
For three-body reactions, the reaction rate is given by:
with [M] being the number density of the third body, k0 the reaction rate for low pressure conditions, k∞ the reaction rate for high pressure conditions, and kr the rate for recombination. Also, χ is the uncertainty factor of Troe which is computed with (for all three-body reactions except H + C2H2 and H + C4H2 that have their own formulas):
Thus, we have to compute an uncertainty factor for k0, k∞, and kr by using the formula in Eq. (8), with a F(300 K) and a g for each. Then, each ki is recalculated using Eq. (9).
For photodissociation, photoionization, and electron-impact dissociation and ionization, the corresponding reaction rates do not depend on temperature. In this case, we assume a constant uncertainty factor of Fi = 1.2 (which may be underestimated) for all these reactions. Reaction rates are then computed directly with Eq. (9).
For ion-neutral and dissociative recombination reactions, branching ratios are applied on reaction rates to express the probability that the reaction gives a specific set of products. These branching ratios are also measured or computed theoretically and thus have an associated uncertainty. To account for this, we also generated, for each run of the program, a new branching ratio, bri, randomly generated between ![$\left[ {{{b{r_{{0_i}}}} \over {{F_{b{r_i}}}}},b{r_{{0_i}}} \times {F_{b{r_i}}}} \right]$](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq80.png) using a Dirichlet uniform distribution (cf. Carrasco et al. 2007); here,
using a Dirichlet uniform distribution (cf. Carrasco et al. 2007); here, 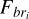 is the uncertainty factor for the considered branching ratio and
is the uncertainty factor for the considered branching ratio and 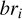 is the nominal branching ratio. The chemical reaction rate of each branch is then multiplied by
is the nominal branching ratio. The chemical reaction rate of each branch is then multiplied by 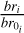 .
.
Mean abundances ӯi and associated uncertainty factors F(ӯi) for the main atmospheric species.
6.1 Results
We performed 250 iterations of the Monte Carlo procedure. In Fig. 11, we present the nominal mole fraction profiles of six species alongside the 250 profiles generated by the procedure. Histograms of mole fractions at the altitude where the associated uncertainty is maximum are also plotted. As the reaction rates have a log-normal distribution, we would expect to find normal distributions with reasonable standard deviations, as shown for H in Fig. 11. However, in Triton’s low temperature atmosphere, we find large uncertainties for the majority of the studied species, meaning high standard deviation values. In Table 6, we give the mean abundances and the standard deviation of these abundance distributions, expressed by an uncertainty factor F(ӯi) at the altitude where the uncertainty is maximum.
We see that very few species have a standard deviation lower than two at the level where their uncertainty is maximum, as it is only the case for N2, H2, CO, N+, and 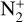 . The maximum uncertainty factor is obtained for O(3P) and gives a ratio between the high and the low value of the 1-σ interval of 1.4 × 103. We can observe that highly reactive species such as atomic nitrogen or CH4 also have high uncertainty factors. For the majority ofthe studied species, high uncertainties emerge at the altitude level where their mole fractions vary strongly. This can be seen for O(3P) in Fig. 11.
. The maximum uncertainty factor is obtained for O(3P) and gives a ratio between the high and the low value of the 1-σ interval of 1.4 × 103. We can observe that highly reactive species such as atomic nitrogen or CH4 also have high uncertainty factors. For the majority ofthe studied species, high uncertainties emerge at the altitude level where their mole fractions vary strongly. This can be seen for O(3P) in Fig. 11.
By plotting the histograms of the abundances of these species at the considered levels, we can highlight bimodalities in some of the distributions. This aspect was studied in Dobrijevic et al. (2008a) for Titan’s atmosphere. They are due to uncertainties on reaction rates and show that two distinct paths are explored by the model, which gives a bimodal distribution instead of the expected unimodal one as reaction rates follow a log-normal distribution. We call them epistemic bimodalities as they do not correspond to any real phenomenon but are artifacts arising from the large uncertainties of some reaction rates in Triton’s conditions (Dobrijevic et al. 2008a). As an example, in Fig. 11, the histogram of O(3P) shows a bimodality. To cancel out these effects, we have to find which reactions strongly impact the model uncertainties.
6.2 Identifying key uncertainty reactions
In order to have more significant results, we need to reduce the chemical uncertainties. To do this, we must identify the key uncertainty reactions. This kind of key reaction must not be confused with the key chemical reactions: the latter reactions are defined as the ones that have the most important influence on the chemical scheme, whereas key uncertainty reactions are defined as those that have the most important contribution to the overall uncertainty on species abundances.
Thus, we have to identify these key uncertainty reactions for each species in order to see if we can reduce the uncertainty over the abundance profiles by improving our knowledge about these reactions. Dobrijevic et al. (2010b) presented different methods to determine key uncertainty reactions. In our case, we performed global sensitivity analyses, as presented in the following.
6.2.1 Global sensitivity analysis
This type of analysis allows us to vary all the input factors at each run (in this case, the chemical reaction rates) and study the link between these input factors and the uncertainty on the outputs, which are the abundance profiles of the studied species obtained with the Monte Carlo procedure. It also allows us to conserve the non-linearity and coupling of the model, resulting from the use of a high number of species and reactions.
To do this, we use Rank Correlation Coefficients (RCCs). As shown in Carrasco et al. (2007); Hébrard et al. (2009); Dobrijevic et al. (2010a,b), these coefficients convert a nonlinear but monotonic relationship between the input factors and the outputs into a linear relationship. To do so, it replaces the values of the sampled inputs and outputs by their respective ranks (Helton et al. 2006). The outcome of this procedure is a coefficient between −1 and 1 for each input-output couple. If the coefficient is positive, it means that the two correlated parameters vary in the same way. Thus, in our case, each coefficient links a reaction to the uncertainty on the abundance profile of a particular species. Reactions with high RCCs (in absolute value) contribute strongly to the uncertainty on the abundance of this species and are therefore key uncertainty reactions.
We analyze RCCs in two different ways. First, we perform the analysis for each of the main species at the altitude where their uncertainty is maximum (one species at a time). Second, we choose some characteristic atmospheric levels and perform an analysis over all the species at a time. Coupling the results of these two studies allows us to determine the key uncertainty reactions of our model.
 |
Fig. 11 Abundance profiles and histograms of the logarithm of the abundance of H, O(3P), N(2D), CH4, C2H2, and C for 250 runs of the Monte-Carlo procedure. Histograms are plotted at the altitude where the uncertainty is maximum for each species (red dashed line). |
6.2.2 Results for the study for one species at a time
For this study, we chose to focus on reactions that have a RCC higher than 0.2 in absolute value.We ran this sensitivity analysis for the 18 main species at the altitude where their uncertainty is maximum, as given in Table 6. Reactions that were found for more than one of these species are given in Table A.1. We identified 35 reactions: 12 neutral-neutral reactions, 10 ion-neutral reactions, 4 dissociative recombinations, 3 photodissociations, 3 photoionizations, and 3 reactions with magnetospheric electrons.
We also identified which reactions gave high RCC absolute values, even if they do not necessarily appear for more than one species. These reactions are given in Table A.2, with the species associated to a high RCC value. One additional reaction appears in this table.
For the majority of these reactions, we always have a high value of Fi or gi and sometimes both. This confirms that for this study, high RCCs are often linked to a lack of knowledge about reaction rates.
Main key uncertainty reactions identified through sensitivity analyses.
6.2.3 Results for the study of all species at a given altitude
We also performed a sensitivity analysis at a given altitude level and for all the species of our model at the same time. In this case, we count the number of times that a reaction has a RCC higher than 0.2 (in absolute value) over the total number of species. For each level, we then rank the reactions that appear the most and therefore contribute the most to the overall uncertainty at this level. We chose to perform this test at seven different levels to sample diverse altitudes: 0, 86, 220, 334, 502, 758, and 1026 km. Reactions that appear for at least one quarter of the species of our chemical scheme at these levels are given in Table A.3.
We notice that the reaction N(2D) + CO → N(4S) + CO appears at each studied level. We also find that the main key uncertainty reactions are different depending on the considered altitude. In the lower atmosphere (0 and 86 km), neutral-neutral reactions are dominant. At 86 km, we highlight three different three-body reactions. At 220km, in the lower ionosphere, photolysis of CH4 and CO is important. At higher levels, de-excitation of N(2D) through collisions with CO and C are the main key uncertainty reactions. For levels higher than 500 km, the charge exchange between N+ and C giving N(4S) + C+ also contributes significantly.
We also performed a complementary study focusing on the main atmospheric species to avoid biases from species with negligible abundances. This study highlights key uncertainty reactions that we already found in the previous analyses, confirming their contribution to the overall uncertainty.
Finally, as we did for the study with one species at a time, we listed the reactions with high RCC values. These reactions are given in Table A.4 with the involved species at each of the seven levels studied here. Again, we find reactions that were previously highlighted but also some new ones, in general important for only one species at one or more levels, for example reactions between N+ and CO that are important for the uncertainty of N+. This also confirms that key uncertainty reactions depend on the studied altitude.
6.3 Discussion - Uncertainties and key uncertainty reactions
By computing the RCCs in various cases, we were able to identify reactions that were responsible for large uncertainties for a particular species or more globally at a given level. If we look at all the results presented in Appendix A, we see that some reactions are involved in all (or nearly all) the treated cases. These reactions are presented in Table 7.
We also find that many of the reactions that were identified through the sensitivity analyses appeared to be key chemical reactions for the main species of the atmosphere. Thus, it appears that is essential that we improve our knowledge of the kinetics of these reactions as they have the biggest influence on the number density profiles of the main species. Without this supplementary knowledge at low temperature, it seems difficult to obtain a clearer image of the composition of Triton’s atmosphere.
We also note that O(3P) appears as a reactant in key chemical reactions for some of the main species and also in key uncertainty reactions. At present, we have not considered any interplanetary dust flux. However, Moses & Poppe (2017) showed that the external flux of water in Neptune’s atmosphere is likely coming from interplanetary dust. If true, this flux should also impact Triton’s atmospheric chemistry, as stated in Poppe & Horányi (2018). Thus, it will be interesting to add this dust delivery and observe its impact on the number density profiles and also on chemical uncertainties.
In Sect. 5, we observed that the electronic number density profile was higher than expected when comparing to observations presented in Tyler et al. (1989). If we examine the electronic profiles of the 250 runs of the Monte Carlo procedure, we find that the mean number density at the electronic peak is 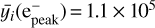 cm−3, with an uncertainty factor of 1.38 at 1-σ. Thus, the peak concentration of electrons found with our model is consistently higher than the measured value of (3.5 ± 1) × 104 cm−3 (Tyler et al. 1989; Krasnopolsky & Cruikshank 1995).
cm−3, with an uncertainty factor of 1.38 at 1-σ. Thus, the peak concentration of electrons found with our model is consistently higher than the measured value of (3.5 ± 1) × 104 cm−3 (Tyler et al. 1989; Krasnopolsky & Cruikshank 1995).
The altitude of the electronic peak also varies at each run. For 250 runs, we find 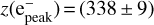 km, which matches the interval of (340–350) km given in Krasnopolsky & Cruikshank (1995). However, the electronic production, as well as the electronic density, depends mostly on N2 impact ionization by magnetospheric electrons; thus, it depends on how the interaction between Triton’s atmosphere and Neptune’s magnetosphere is modeled. In our case, we used the arbitrarily modified ionization profile from Strobel et al. (1990a). Thus, the results may be significantly affected when changing these arbitrary parameters. Moreover, the uncertainty factors of reactions involving magnetospheric electrons is constant and equal to 1.2. These uncertainties may be underestimated and thus the observed difference between Voyager’s data and our results may not be significant.
km, which matches the interval of (340–350) km given in Krasnopolsky & Cruikshank (1995). However, the electronic production, as well as the electronic density, depends mostly on N2 impact ionization by magnetospheric electrons; thus, it depends on how the interaction between Triton’s atmosphere and Neptune’s magnetosphere is modeled. In our case, we used the arbitrarily modified ionization profile from Strobel et al. (1990a). Thus, the results may be significantly affected when changing these arbitrary parameters. Moreover, the uncertainty factors of reactions involving magnetospheric electrons is constant and equal to 1.2. These uncertainties may be underestimated and thus the observed difference between Voyager’s data and our results may not be significant.
In Sect. 5, we failed to find a number density of atomic nitrogen that matches the value given in Krasnopolsky & Cruikshank (1995) at 200km, that is, (5 ± 2.5) × 108 cm−3, when using nominal reaction rates. With 250 runs, the number density of N is (11 ± 4) × 108 cm−3 at 196 km and (10 ± 4) × 108 cm−3 at 204 km. Thus, these intervals and the one of Krasnopolsky & Cruikshank (1995) overlap. As for electrons, the production of atomic nitrogen depends mostly on the interaction between magnetospheric electrons and N2 (directly or indirectly), reactions for which we consider a constant and probably underestimated uncertainty factor. Therefore, the small differences observed between our results and the measured data are not significant.
7 Discussion and conclusions
Our goal in this study is to create a 1D photochemical model of Triton’s atmosphere with an up-to-date chemical scheme in order to determine the atmospheric composition and the main parameters that have an impact on it. We also seek to highlight which studies are necessary to reduce uncertainties on model results.
To do this, we used an existing model of Titan’s atmosphere from Dobrijevic et al. (2016) and adapted it to Triton’s conditions. We used input data from Strobel & Zhu (2017) for our initial conditions (temperature and number density profiles, initial abundance of CO), along with the eddy diffusion profile of Herbert & Sandel (1991), and we took a solar flux corresponding to a maximum solar activity, added interplanetary radiation, and considered the interaction between Triton and Neptune’s magnetosphere through reactions between N2 and magnetospheric electrons. Considering the latter processes was crucial in order to find nominal results for CH4 and atomic nitrogen that would be in agreement with the Voyager data.
We also improved our chemical scheme by comparing the results with the Voyager data and previous articles about the photochemistry of Triton such as those by Krasnopolsky & Cruikshank (1995) or Strobel & Summers (1995). In doing so, we added nearly 40 atmospheric species and 500 reactions to our initial scheme, giving a total of 220 species and 1764 reactions.
With this updated model, we studied 18 species in particular which are the main neutral species (N2, N(4S), N(2D), CH4, CO, H2, H, C, O(3P)), hydrocarbons (C2H2, C2H4, C2H6), nitriles (HCN), and ions (C+, N+,  , H+, electrons), highlighting their main production and loss processes through the identification of key chemical reactions. Nitrogen chemistry is triggered by ionization and dissociation of N2 by solar radiation and magnetospheric electrons, while methane chemistry results from its photolysis by Lyman-α radiation from the Sun and the interstellar medium, creating radicals and hydrogen (atomic and molecular). These radicals then react to form hydrocarbons that condense due to the very low temperature in the lower atmosphere, the most abundant C2Hx being C2H4. Molecular hydrogen reacts mostly with ions, while H reacts mainly with HCNN or radicals. Atomic nitrogen produced in the N(2D) state is converted to ground state N(4S) through collisions with CO, C, and O(3P). N(4S) is then converted back to N2 through the CNN cycle. CO is depleted in the higher atmosphere by reacting with N+ ions and
, H+, electrons), highlighting their main production and loss processes through the identification of key chemical reactions. Nitrogen chemistry is triggered by ionization and dissociation of N2 by solar radiation and magnetospheric electrons, while methane chemistry results from its photolysis by Lyman-α radiation from the Sun and the interstellar medium, creating radicals and hydrogen (atomic and molecular). These radicals then react to form hydrocarbons that condense due to the very low temperature in the lower atmosphere, the most abundant C2Hx being C2H4. Molecular hydrogen reacts mostly with ions, while H reacts mainly with HCNN or radicals. Atomic nitrogen produced in the N(2D) state is converted to ground state N(4S) through collisions with CO, C, and O(3P). N(4S) is then converted back to N2 through the CNN cycle. CO is depleted in the higher atmosphere by reacting with N+ ions and  ions recombine rapidly with electrons producing atomic nitrogen.
ions recombine rapidly with electrons producing atomic nitrogen.
We find a dense ionosphere with a cutoff around 175 km, where the abundance of C+ increases strongly. This ion is the most abundant in the majority of the ionosphere and is produced by charge exchange reactions between  , CO+, N+, and C. The other abundant ions are N+, H+, and
, CO+, N+, and C. The other abundant ions are N+, H+, and 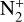 . Below 175 km, the main ions are heavier but their abundances are low. The electronic peak is located at 334 km, which is consistent with Voyager data presented in Tyler et al. (1989). Our number density profile is higher than the one given in the latter article, even considering chemical uncertainties. However, these results are very dependent on the modeling of the interaction between Triton’s atmosphere and Neptune’s magnetosphere.
. Below 175 km, the main ions are heavier but their abundances are low. The electronic peak is located at 334 km, which is consistent with Voyager data presented in Tyler et al. (1989). Our number density profile is higher than the one given in the latter article, even considering chemical uncertainties. However, these results are very dependent on the modeling of the interaction between Triton’s atmosphere and Neptune’s magnetosphere.
Using a Monte Carlo procedure over all the chemical reaction rates, we studied uncertainties on the abundance profiles. We performed 250 runs and found that for the majority of species, the uncertainty factors on these profiles are significant. This is due to our lack of knowledge about chemical reaction rates at the very low temperatures of Triton’s atmosphere. These uncertainties also lead to epistemic bimodalities in the abundance distributions of some species, at the level where the associated uncertainty is at a maximum. We determined the key uncertainty reactions responsible for the observed uncertainties and bimodalities. To do so, we performed global sensitivity analyses using rank correlation coefficients to determine correlations between the outputs (number density profiles) and the input factors (chemical reaction rates) of the model. We carried out this study for each of the 18 most abundant species at the level where the uncertainty on their abundance is maximum, but also for all the species of our model at different altitudes. We identified the main key uncertainty reactions for which we absolutely need to improve our knowledge if we want to improve the significance of the model results. Finally, we found that a great number of key uncertainty reactions also appeared as key chemical reactions for the main species, which confirms the call for new studies on these reactions.
Ultimately, the use of an up-to-date chemical scheme allows a much deeper comprehension of the composition and of the mechanisms governing the chemistry of Triton’s atmosphere in comparison to the work of Krasnopolsky & Cruikshank (1995) and Strobel & Summers (1995), while the study of the model uncertainty is the first of its kind for Triton’s atmosphere.
However, the current model of Triton’s atmosphere can be improved in many areas. As oxygenated species appeared in several key uncertainty reactions, we need to study how the interplanetary water flux could impact the results of our model. As the precipitation of magnetospheric electrons has a strong impact on the atmospheric chemistry, obtaining a better model that would really consider the temporal variation of the precipitation, depending on the position of Triton in Neptune’s complex magnetosphere, should improve the significance of the model results.
The chemical scheme can also be simplified in order to decrease the computation time (cf. Dobrijevic et al. 2011). This is not feasible before obtaining the uncertainties on model results as they give an objective criterion to verify if the results given by the reduced scheme are in agreement with the nominal model.
Acknowledgements
B.B., M.D. and T.C. acknowledge funding from CNES. B.B., M.D., T.C. and K.M.H. acknowledge funding from the “Programme National Planétologie” (PNP) of CNRS/INSU. K.M.H. acknowledges support from the French program “Physique et Chimie du Milieu Interstellaire” (PCMI) of the CNRS/INSU with the INC/INP co-funded by the CEA and CNES.
Appendix A Identification of key uncertainty reactions
Reactions with |RCC| > 0.2 for several of the main atmospheric species.
Reactions with |RCC| > 0.5 for the main atmospheric species.
Reactions with |RCC| > 0.2 for at least one quarter of the species considered in our chemical scheme (=55).
Reactions with |RCC| > 0.5 for at least one of the main atmospheric species at one of the seven considered altitude levels.
References
- Agnor, C. B., & Hamilton, D. P. 2006, Nature, 441, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Anicich, V. G. 2003, An index of the literature for bimolecular gas phase cationmolecule reaction kinetics - National Aeronautics and Space Administration, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California [Google Scholar]
- Broadfoot, A. L., Atreya, S. K., Bertaux, J. L., et al. 1989, Science, 246, 1459 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, R. H., Cruikshank, D. P., Veverka, J., Helfenstein, P., & Eluszkiewicz, J. 1995, Neptune and Triton (Tucson: Univ. Arizona Press), 991 [Google Scholar]
- Carrasco, N., Hébrard, E., Banaszkiewicz, M., Dobrijevic, M., & Pernot, P. 2007, Icarus, 192, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Committee on the Planetary Science and Astrobiology Decadal Survey, Space Studies Board, Division on Engineering and Physical Sciences, & National Academies of Sciences, Engineering, and Medicine. 2022, Origins, Worlds, and Life: A Decadal Strategy for Planetary Science and Astrobiology 2023-2032 (Washington, D.C.: National Academies Press), 26522 [Google Scholar]
- Cruikshank, D. P., Matthews, M. S., & Schumann, A. M. 1995, Neptune and Triton (Tucson: Univ. Arizona Press) [Google Scholar]
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curdt, W., Landi, E., & Feldman, U. 2004, A&A, 427, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobrijevic, M. 1996, These de doctorat, Bordeaux 1, France [Google Scholar]
- Dobrijevic, M., & Parisot, J. 1998, Planet. Space Sci., 46, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrijevic, M., Ollivier, J. L., Billebaud, F., Brillet, J., & Parisot, J. P. 2003, A&A, 398, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobrijevic, M., Carrasco, N., Hébrard, E., & Pernot, P. 2008a, Planet. Space Sci., 56, 1630 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrijevic, M., Claeys-Bruno, M., Sergent, M., & Phan-Tan-Luu, R. 2008b, Planet. Space Sci., 56, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrijevic, M., Cavalié, T., Hébrard, E., et al. 2010a, Planet. Space Sci., 58, 1555 [CrossRef] [Google Scholar]
- Dobrijevic, M., Hébrard, E., Plessis, S., et al. 2010b, Adv. Space Res., 45, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrijevic, M., Cavalié, T., & Billebaud, F. 2011, Icarus, 214, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrijevic, M., Loison, J., Hickson, K., & Gronoff, G. 2016, Icarus, 268, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Simon, A. A., Hofstadter, M. D., et al. 2020, Philosophical Transactions of the Royal Society A, 378, 2187 [Google Scholar]
- Fox, J., & Victor, G. 1988, Planet. Space Sci., 36, 329 [Google Scholar]
- Fray, N., & Schmitt, B. 2009, Planet. Space Sci., 57, 2053 [Google Scholar]
- Haynes, W. 2012, CRC Handbook of Chemistry and Physics, 93rd edn., 100 Key Points (Taylor & Francis) [Google Scholar]
- Hébrard, E., Dobrijevic, M., Bénilan, Y., & Raulin, F. 2006, J. Photochem. Photobiol. C: Photochem. Rev., 7, 211 [CrossRef] [Google Scholar]
- Hébrard, E., Dobrijevic, M., Bénilan, Y., & Raulin, F. 2007, Planet. Space Sci., 55, 1470 [CrossRef] [Google Scholar]
- Hébrard, E., Dobrijevic, M., Pernot, P., et al. 2009, J. Phys. Chem. A, 113, 11227 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, E., Dobrijevic, M., Loison, J. C., Bergeat, A., & Hickson, K. M. 2012, A&A, 541, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helton, J., Johnson, J., Sallaberry, C., & Storlie, C. 2006, Reliabil. Eng. Syst. Saf., 91, 1175 [CrossRef] [Google Scholar]
- Herbert, F., & Sandel, B. R. 1991, J. Geophys. Res., 96, 19 [NASA ADS] [Google Scholar]
- Hickson, K. M., Bray, C., Loison, J.-C., & Dobrijevic, M. 2020, Physical Chemistry Chemical Physics, 22, 14026 [NASA ADS] [CrossRef] [Google Scholar]
- Husain, D., & Kirsch, L. J. 1971, J. Chem. Soc. Faraday Trans., 67, 2025 [CrossRef] [Google Scholar]
- Krasnopolsky, V. A., & Cruikshank, D. P. 1995, J. Geophys. Res., 100, 21271 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnopolsky, V. A., Sandel, B. R., & Herbert, F. 1992, J. Geophys. Res., 97, 11695 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnopolsky, V. A., Sandel, B. R., Herbert, F., & Vervack, R. J. 1993, J. Geophys. Res., 98, 3065 [NASA ADS] [CrossRef] [Google Scholar]
- Krimigis, S. M., Armstrong, T. P., Axford, W. I., et al. 1989, Science, 246, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Lara, L. M., Lellouch, E., López-Moreno, J. J., & Rodrigo, R. 1996, J. Geophys. Res.: Planets, 101, 23261 [NASA ADS] [CrossRef] [Google Scholar]
- Lellouch, E., de Bergh, C., Sicardy, B., Ferron, S., & Käufl, H.-U. 2010, A&A, 512, A8 [Google Scholar]
- Loison, J., Hébrard, E., Dobrijevic, M., et al. 2015, Icarus, 247, 218 [CrossRef] [Google Scholar]
- Loison, J., Dobrijevic, M., & Hickson, K. 2019, Icarus, 329, 55 [CrossRef] [Google Scholar]
- Lyons, Yung, Y., & Allen, M. 1992, Science, 256, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Majeed, T., McConnell, J. C., Strobel, D. P., & Summers, M. E. 1990, Geophys. Res. Lett., 17, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- McKinnon, W. B., Lunine, J. I., & Banfield, D. 1995, Neptune and Triton (Tucson: Univ. Arizona Press), 807 [Google Scholar]
- Moses, J. I., & Poppe, A. R. 2017, Icarus, 297, 33 [Google Scholar]
- Nuñez-Reyes, D., Loison, J.-C., Hickson, K. M., & Dobrijevic, M. 2019a, Phys. Chem. Chem. Phys., 21, 6574 [CrossRef] [Google Scholar]
- Nuñez-Reyes, D., Loison, J.-C., Hickson, K. M., & Dobrijevic, M. 2019b, Phys. Chem. Chem. Phys., 21, 22230 [CrossRef] [Google Scholar]
- Oliveira, J. M., Sicardy, B., Gomes-Júnior, A. R., et al. 2022, A&A, 659, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poling, B. E., Prausnitz, J. M., & O’Connell, J.P. 2001, The Properties of Gases and Liquids, 5th edn. (Mc Graw Hill Education) [Google Scholar]
- Poppe, A. R., & Horányi, M. 2018, A&A, 617, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rymer, A. M., Runyon, K. D., Clyde, B., et al. 2021, Planet. Sci. J., 2, 184 [CrossRef] [Google Scholar]
- Sander, S., Rvishankara, A., Golden, D., et al. 2006, JPL Publication, 06-2, 1 [Google Scholar]
- Stevens, M. H., Strobel, D. F., Summers, M. E., & Yelle, R. V. 1992, Geophys. Res. Lett., 19, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Strobel, D. F., & Summers, M. E. 1995, Neptune and Triton (Tucson: Univ. Arizona Press), 1107 [Google Scholar]
- Strobel, D. F., & Zhu, X. 2017, Icarus, 291, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Strobel, D. F., Cheng, A. F., Summers, M. E., & Strickland, D. J. 1990a, Geophys. Res. Lett., 17, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Strobel, D. F., Simmers, M. E., Herbert, F., & Sandel, B. R. 1990b, Geophys. Res. Lett., 17, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Summers, M. E., & Strobel, D. F. 1991, Geophys. Res. Lett., 18, 4, 689 [NASA ADS] [Google Scholar]
- Thuillier, G., Floyd, L., Woods, T., et al. 2004, Adv. Space Res., 34, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Tyler, G. L., Sweetnam, D. N., Anderson, J. D., et al. 1989, Science, 246, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Vuitton, V., Yelle, R., Klippenstein, S., Hörst, S., & Lavvas, P. 2019, Icarus, 324, 120 [CrossRef] [Google Scholar]
- Yelle, R. V., Lunine, J. I., & Hunten, D. M. 1991, Icarus, 89, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Yelle, R. V., Lunine, J. I., Pollack, J. B., & Brown, R. H. 1995, Neptune and Triton (Tucson: Univ. Arizona Press), 1031 [Google Scholar]
- Zhu, X., Strobel, D. F., & Erwin, J. T. 2014, Icarus, 228, 301 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison of the different Kzz(z) used in previous Triton photochemical models since the flyby of Voyager 2 in 1989.
Ionization and dissociation reactions by magnetospheric electrons (ME) and their integrated column rates.
Mean abundances ӯi and associated uncertainty factors F(ӯi) for the main atmospheric species.
Reactions with |RCC| > 0.2 for at least one quarter of the species considered in our chemical scheme (=55).
Reactions with |RCC| > 0.5 for at least one of the main atmospheric species at one of the seven considered altitude levels.
All Figures
 |
Fig. 1 Initial profiles used in our model: (a) Initial abundance profiles of N2 (green solid line), CH4 (orange dash-dotted line), and CO (red dashed line). The CH4 abundance decreases exponentially with a scale height of 9 km. (b) Temperature (red dashed line) and number density (orange solid line) profiles from the Triton-3 case of Strobel & Zhu (2017) that are used as inputs in our model. The altitudinal grid is composed of 96 levels and the total number density is plotted with blue dots. |
| In the text | |
 |
Fig. 2 Comparison between the eddy diffusion coefficients Kzz of Strobel et al. (1990b; black dotted line), Herbert & Sandel (1991; blue dashed line), and Krasnopolsky & Cruikshank (1995; red dash-dotted line). For the Strobel et al. (1990b) profile, we plotted Kzz = 6.0 × 103 cm2 s−1 and for the Herbert & Sandel (1991) profile |
| In the text | |
 |
Fig. 3 Methodology used to adapt Titan’s chemical scheme to Triton. |
| In the text | |
 |
Fig. 4 Relative abundances of the main neutral species in the atmosphere of Triton: (a) Relative abundance of N2 (green solid line), CH4 (orange solid line with circles), CO (red dashed line), H2 (blue dash-dotted line), and H (dark blue dotted line), (b) Relative abundances of N(4S), (black solid line), N(2D), (black dotted line), C (gray dash-dotted line), and O(3P), (cyan dashed line). We only give the O(3P) profile as the abundance of O(1D) is negligible. |
| In the text | |
 |
Fig. 5 Altitude at which the optical thickness of the atmosphere is 1 depending on the wavelength of the incident radiation. The plot is cut at 200 nm as the atmosphere is not optically thick for all wavelengths above 160 nm, but the initial solar flux goes from 0 to 730 nm. |
| In the text | |
 |
Fig. 6 Relative abundances of the main hydrocarbons and comparison with their vapor pressure ratio: (a) Relative abundances of the main hydrocarbons (orange solid line with circles for CH4, solid pink line for C2H2, purple dash-dotted line for C2H4 and brown dashed line for C2H6), and blue dotted line for HCN. (b) Relative abundances (solid lines) compared to the ratio of the vapor pressure, Pv, and the pressure, P, (dashed lines) depending on altitude for CH4, the main C2Hx, and HCN. When the curves of the Pv/P ratio and the abundance merge, this means that the species is condensing, as its abundance cannot be higher than this ratio. |
| In the text | |
 |
Fig. 7 Relative abundances of the radicals that appeared in the key chemical reactions of the main neutral species (solid blue line for CH, orange dashed line for CH2, green solid line with circles for CH3. dash-dotted pink line for CN, and purple dotted line for CNN). The CH2 profile corresponds to 3CH2, as the relative abundance of 1CH2 is negligible. |
| In the text | |
 |
Fig. 8 Relative abundances of the main ions of the atmosphere of Triton: (a) Most abundant ions that are the focus of this study – blue solid line with circles for C+, orange dashed line for N+, green dash-dotted line for N2+, purple dotted line for H+, thin brown solid line for CO+, thin dark blue dashed line for N2H+, and red solid line for electrons. (b) Most abundant ions below 175 km. |
| In the text | |
 |
Fig. 9 Comparison of our CH4 profile with other datasets and impact of the resolution of the solar spectrum on our results: (a) CH4 number density profiles near the surface derived from Voyager 2 data and presented in Herbert & Sandel (1991; dark blue and orange), data points from Strobel & Zhu (2017; black dots) and result from our model using nominal reaction rates (red), i.e. without considering any uncertainty. (b) Comparison of the relative abundances of the main neutral species when using a high resolution solar spectrum (solid lines) versus a low resolution spectrum |
| In the text | |
 |
Fig. 10 Number densities of the main ions in Triton’s atmosphere. The black triangles and dark blue circles represent the electronic profiles measured by Voyager 2 at the two occultations points (Tyler et al. 1989). |
| In the text | |
 |
Fig. 11 Abundance profiles and histograms of the logarithm of the abundance of H, O(3P), N(2D), CH4, C2H2, and C for 250 runs of the Monte-Carlo procedure. Histograms are plotted at the altitude where the uncertainty is maximum for each species (red dashed line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



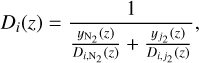
![${D_{i,j}}\left( z \right) = {{0.00143 \times T{{\left( z \right)}^{{1 \over 3}}}} \over {P\left( z \right)M_{i,j}^{{1 \over 2}}{{\left[ {\left( {{\sum _v}} \right)_i^{{1 \over 3}} + \left( {{\sum _v}} \right)_j^{{1 \over 3}}} \right]}^2}}},$](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq7.png)
![${K_{zz}} = 1.4 \times {10^3}{\left( {{{{{\left[ {{{\rm{N}}_2}} \right]}_0}} \over {\left[ {{{\rm{N}}_2}} \right]\left( z \right)}}} \right)^{0.5}}{\rm{c}}{{\rm{m}}^2}{\rm{ }}{{\rm{s}}^{ - 1}}$](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq139.png)
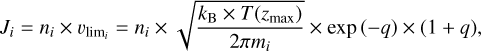
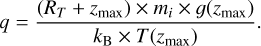
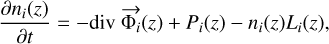
![$\matrix{{{{\rm{\Phi }}_i}\left( z \right) = } \hfill & { - {D_i}\left( z \right){n_i}\left( z \right)\left[ {{1 \over {{y_i}\left( z \right)}}{{\partial {y_i}\left( z \right)} \over {\partial z}} + {1 \over {{H_i}\left( z \right)}} - {1 \over {H\left( z \right)}}} \right]} \hfill \cr {} \hfill & { - {K_{zz}}\left( z \right){n_i}\left( z \right)\left[ {{1 \over {{y_i}\left( z \right)}}{{\partial {y_i}\left( z \right)} \over {\partial z}}} \right],} \hfill \cr} $](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq13.png)
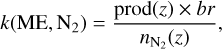
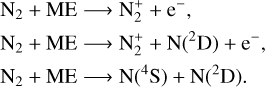
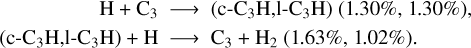
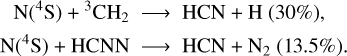
![${F_i}\left( T \right) = {F_i}\left( {300\,{\rm{K}}} \right) \times \exp \left\{ {{g_i}\left[ {{1 \over T} - {1 \over {300}}} \right]} \right\},$](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq74.png)
![$\log \left( {{k_i}} \right) = \log \left( {{k_{{0_i}}}} \right) + {\varepsilon _i}\log \left[ {{F_i}\left( T \right)} \right],$](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq76.png)
![${k_i}\left( z \right) = {{{k_0} \times \left[ M \right]\chi + {k_r}} \over {1 + {{{k_0}\left[ M \right]} \over {{k_\infty }}}}},$](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq78.png)
![$\chi = {{\log \left( {0.64} \right)} \over {1 + {{\left[ {\log \left( {{{{k_0}\left[ M \right]} \over {{k_\infty }}}} \right)} \right]}^2}}}.$](/articles/aa/full_html/2022/11/aa44447-22/aa44447-22-eq79.png)