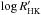| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201220512 | |
| Published online | 11 April 2013 | |
The place of the Sun among the Sun-like stars⋆,⋆⋆
1
Physikalisch-Meteorologishes Observatorium Davos, World Radiation Center,
7260
Davos Dorf,
Switzerland
e-mail:
alexander.shapiro@pmodwrc.ch
2
Institute for Atmospheric and Climate science ETH,
Zurich,
Switzerland
Received: 7 October 2012
Accepted: 14 February 2013
Context. Monitoring of the photometric and chromospheric HK emission data series of stars similar to the Sun in age and average activity level showed that there is an empirical correlation between the average stellar chromospheric activity level and the photometric variability. In general, more active stars show larger photometric variability. Interestingly, the measurements and reconstructions of the solar irradiance show that the Sun is significantly less variable than indicated by the empirical relationship.
Aims. We aim to identify possible reasons for the Sun to be currently outside of this relationship.
Methods. We employed different scenarios of solar HK emission and irradiance variability and compared them with available time series of Sun-like stars.
Results. We show that the position of the Sun on the diagram of photometric variability versus chromospheric activity changes with time. The present solar position is different from its temporal mean position as the satellite era of continuous solar irradiance measurements has accidentally coincided with a period of unusually high and stable solar activity. Our analysis suggests that although present solar variability is significantly smaller than indicated by the stellar data, the temporal mean solar variability might be in agreement with the stellar data. We propose that the continuation of the photometric program and its expansion to a larger stellar sample will ultimately allow us to constrain the historical solar variability.
Key words: stars: activity / stars: solar-type / stars: variables: general / Sun: activity / Sun: atmosphere
Appendices A and B are available in electronic form at http://www.aanda.org
All time series are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/552/A114
© ESO, 2013
1. Introduction
The comparison of the Sun with Sun-like stars helps to improve our understanding of both solar and stellar physics. One of its important applications is the study of the solar irradiance variability. The consecutive measurements of the solar irradiance have only been available for the last three decades. The photometric observations of the large number of Sun-like stars can help to extend the time coverage and constrain the historical variability of the solar irradiance.
The first monitoring of the photometric flux and chromospheric HK emission (which characterises the amount of non-thermal heating in the chromosphere and consequently activity, see Baliunas et al. 1995) of the stars similar to the Sun in age and average activity level revealed an empirical correlation between the stellar photometric variability and mean chromospheric activity level (Lockwood et al. 1992). The continuation of the program (see e.g. Lockwood et al. 1997, 2007; Radick et al. 1998) showed that the variability of a star with solar chromospheric activity level is expected to be about 0.1% in the Strömgren filters b and y (centred at 467 and 547 nm, respectively). At the same time the regression of the observed total solar irradiance (TSI) variability to the variability in Strömgren filters b and y yielded a somewhat smaller value of about 0.04% (Radick et al. 1998).
Several attempts were made to explain this disagreement. For example, Foukal (1994) proposed that the relatively low solar variability can be explained by the dependence of the faculae to starspot ratio on the magnetic activity. Later, Radick (1994) showed that this explanation is not consistent with the stellar data. Schatten (1993) suggested that the special position of the Earth-based observer who sees the Sun from its equatorial plane can reduce the variability of solar brightness. However, detailed calculations showed that the equatorial position of the observer leads to only a 30% (most probable value) decrease in the solar variability and does not affect the mean level of the chromospheric activity (Knaack et al. 2001). The out-of-ecliptic measurements of the Sun are needed to validate the model and accurately assess the effects from the hemispherical asymmetry of the density flux (Vieira et al. 2012).
A significant part of the disagreement can also be attributed to the selection effect in the stellar sample. For example, Hall et al. (2009), using another stellar sample, presented a different version of variability versus activity regression. It is based on the monitoring of 28 Sun-like stars over time periods ranging from 6 to 15 yr. The slopes of the Lockwood et al. (2007) and Hall et al. (2009) regressions are approximately the same, but the Hall et al. (2009) regression indicates about 0.1 dex less variability.
Recently Judge et al. (2012) proposed comparing the reconstructed time series of the solar irradiance with the photometry of Sun-like stars. In this paper we follow up on this idea. We re-evaluate the value of the solar variability in Strömgren b and y filters obtained by Radick et al. (1998) and show that the present location of the Sun on the variability versus activity diagram is anomalous.
The continuous measurements of solar irradiance have been available only since the beginning of satellite observations (i.e. since 1978). Meanwhile, the proxy data indicate that the Sun has been at a maximum plateau-state in its long-term evolution during the last 50 years (Lockwood et al. 1999; Solanki et al. 2004). Therefore, the amplitude of the 11-year activity cycle is expected to be relatively large, while the amplitude of the secular component, whose existence is actively speculated in the literature (cf. Lockwood 2011), is very small in the most recent past. At the same time cosmogenic isotope records indicate that during the last millennia the level of the long-term solar activity has been significantly variable (McCracken et al. 2004; Vonmoos et al. 2006). This implies that the amplitude of the 11-year cycle also has been changing in time and, additionally, that the Sun undergoes periods when the long-term photometric variations could be relatively strong. Therefore, the temporal mean of solar variability might be significantly different from the presently measured value. To investigate this possibility we locate the Sun on the variability versus chromospheric activity diagram, employing different scenarios of solar long-term variability.
2. Comparison of the stellar and present solar variability
Figure 1 presents the regression of the stellar variability versus chromospheric activity calculated with data from Lockwood et al. (2007). To calculate the regression line we only consider the stars which were deemed variable by Lockwood et al. (2007).
 |
Fig. 1 Photometric variability versus chromospheric activity. The blue stars indicate the stars with observed variability from Lockwood et al. (2007). Magenta triangles indicate lower limits for stars with unconfirmed variability set at about 0.5 below the regression line. The solid (5.892+1.810 |
One can see that even for the stars with the same chromospheric activity level there is some divergence in the photometric variabilities. The variability of the less variable stars with low magnetic activity would be very difficult to detect (e.g. two of the five stars with unconfirmed variability had 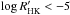 ). Therefore, the regression was made using only the stars with
). Therefore, the regression was made using only the stars with 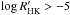 .
.
Originally the Lowell Observatory program contained 41 stars (Lockwood et al. 1997). Some of the stars with unconfirmed variability were later excluded from the program so the final set contained only 32 stars. Seven stars from the original dataset had 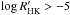 but unconfirmed variability. The inability to detect the variability of the star is either because its variability is indeed small or because the comparison stars are too variable. In the second case, the exclusion of the star is justified; however, in the former case the exclusion of such star from the analysis would affect the variability versus chromospheric activity dependency. To estimate the possible effect of such stars on the regression, we located the stars (magenta triangles in Fig. 1) with unconfirmed variability below the regression line on the distance equal to the maximum deviation of the stars with confirmed variability from the regression line. While the original regression indicates that the root mean square (rms) variability of a star with the solar chromospheric activity level should be about 0.001 mag, the new regression yields a value of 0.00072 mag. These two numbers can be considered as lower and upper limits of the variability of a star with solar chromospheric activity level, yielded from the present stellar sample.
but unconfirmed variability. The inability to detect the variability of the star is either because its variability is indeed small or because the comparison stars are too variable. In the second case, the exclusion of the star is justified; however, in the former case the exclusion of such star from the analysis would affect the variability versus chromospheric activity dependency. To estimate the possible effect of such stars on the regression, we located the stars (magenta triangles in Fig. 1) with unconfirmed variability below the regression line on the distance equal to the maximum deviation of the stars with confirmed variability from the regression line. While the original regression indicates that the root mean square (rms) variability of a star with the solar chromospheric activity level should be about 0.001 mag, the new regression yields a value of 0.00072 mag. These two numbers can be considered as lower and upper limits of the variability of a star with solar chromospheric activity level, yielded from the present stellar sample.
To take into account the new data of Hall et al. (2009) we also calculated two regressions: one using the Hall et al. (2009) data corrected for the variability of the comparison stars and another using the Hall et al. (2009) data combined with the Lockwood et al. (2007) data. All these different versions of the regression yield solar variability within the error bars, estimated above (0.00072–0.001 mag). In Fig. 1 we show the variabilities of four stars from the ELODIE top ten solar analogs (Soubiran & Triaud 2004) taken from Hall et al. (2009).
Establishing the present solar position in Fig. 1 is not a straightforward task as there are no long-term measurements of the spectral solar variability in the band filters. Radick et al. (1998) and Lockwood et al. (2007) assumed the total solar irradiance and photometric variabilities to be connected as if they were caused by a change in the solar effective temperature. This resulted in 0.00044 mag estimation of the rms of annual Strömgren (b + y)/2 values.
The modern physically-based reconstructions of the solar irradiance that attribute the solar variability on the 11-year time scale to the competition between the dark sunspots and bright active regions (e.g. Lean et al. 2005; Krivova et al. 2010; Shapiro et al. 2011), give smaller values of the present solar variability for the last 50 years: 0.00027, 0.00017, and 0.00017 mag respectively. We used the mean of these three numbers to locate the Sun in Fig. 1.
Let us note that if instead of using the annual averages of the solar irradiance we emulate the stellar observations and consider the seasonal averages then the calculated solar variability can be increased by the rotational cycle. We calculated the real seasonal means using the Lockwood et al. (2007) time series and estimated that the increase is generally smaller than 40%.
The measurements obtained by spectral irradiance monitor (SIM) on-board of the solar radiation and climate experiment (SORCE) satellite show yet another picture of solar variability over the last seven years (Harder et al. 2009). The rms of the annual (b + y)/2 values for 2004–2011 period is 0.00029 mag. The extrapolation of the SIM annual (b + y)/2 values to the entire solar cycle using the annual values of the sunspot number results in 0.0004 mag for the rms. (Fontenla, priv. comm.) suggested that a physics-based extrapolation of the SIM data could put the Sun even closer to the regression line from Fig. 1.
3. Comparison of the stellar and historical solar variability
Our main proposition is that the location of the Sun in Fig. 1 is not fixed in time. Therefore, instead of using present solar variability for the comparison with Sun-like stars, one should use the temporal mean of the variability over a time interval long enough to reveal the entire range of solar variability. Because of the high solar activity the amplitude of the 11-year cycle has been relatively large during the last 50 years. So, if the 11-year cycle is the only contributor to the solar irradiance variability then the temporal mean of solar photometric variability is lower than its present value (see calculations below). This would imply that the disagreement between the stellar and solar photometric variabilities is even more pronounced than presently thought. Instead, a secular component in the solar irradiance can significantly increase the temporal mean of the solar photometric variability.
The present consensus is that secular changes in solar irradiance are proportional to secular changes in solar activity proxies. However, there is no agreement on the scaling coefficient (Lean et al. 2005; Tapping et al. 2007; Krivova et al. 2010; Schrijver et al. 2011; Vieira et al. 2011; Shapiro et al. 2011; Thuillier et al. 2012; Judge et al. 2012). To illustrate the effect of the secular variations on the solar photometric variability in Fig. 2 we plot variations of annual (b + y)/2 values and magnitudes of rms20 (the rms20 value for the year X is the rms of (b + y)/2 values in the [X-9 yr, X+10 yr] dataset) for three recent spectral solar irradiance (SSI) reconstructions to the past. Most of the stars used in this study had been observed for approximately 20 years, so the rms20 value can be used for direct comparison of the Sun and stars. According to all three reconstructions the secular changes in the solar irradiance have been very small during the last 50 years. Therefore, during this period the solar variability (i.e. rms20 value) is roughly the same in all three reconstructions. At the same time, there were periods before 1950 when the long-term solar activity changed significantly (McCracken et al. 2004; Steinhilber et al. 2008) and the reconstructions with large and small secular components are dramatically different.
In order not to be limited by any particular reconstruction we introduce two parameters, V11 and VLT, which describe the 11-year and long-term variability, respectively. We define V11 as rms variability of solar annual Strömgren (b + y)/2 fluxes during cycles 21 and 22 (the 1976–1996 period) and VLT as relative change of Strömgren (b + y)/2 flux between 22/23 and the Maunder minima. In Appendix A we describe a simple model which allows us to calculate the solar variability over the millennia as a function of V11 and VLT parameters, using the cosmogenic isotope records (McCracken et al. 2004; Vonmoos et al. 2006). We show that while our approach does rely on the assumptions, they do not constrain its applicability, and by choosing corresponding VLT and V11 parameters we can roughly reproduce very different scenarios of the solar variability published in the recent literature.
 |
Fig. 2 Upper panel: annual (b + y)/2 values versus time according to the spectral solar irradiance (SSI) reconstructions to the past as calculated by Krivova et al. (2010) (red), Lean et al. (2005) (blue) and Shapiro et al. (2011) (magenta: thick and thin curves are original data and data with removed secular changes, respectively). Stars indicates the SIM/SORCE measurements. Lower panel: calculated for the 20 year time intervals rms20 values versus time. |
Let us note that V11 and VLT values cannot be directly compared because V11 corresponds to the rms variation during a 20-year interval, whereas VLT describes an absolute change over 300 years.
An example for a chosen pair of parameters is illustrated in Fig. B.2 (available as Online Material) for the time period from 400 BC to present.
The mean level of the solar chromospheric activity can also change with time. Currently there is no reason to suggest that it underwent significant changes in the past (Hall & Lockwood 2004; Judge & Saar 2007). Saar (2006) showed that the minimum chromospheric activity of stars with solar metallicity corresponds to 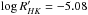 . We will now consider two extreme cases. The first one corresponds to the absence of a secular component in the mean solar chromospheric activity (which does not imply the absence of the secular component in the photometric variability). So changes of the solar activity index occur only because of the evolution of the solar activity cycle. The second case (hereafter, case of strong secular changes) corresponds to the assumption that the mean solar chromospheric activity can reach a minimum boundary value
. We will now consider two extreme cases. The first one corresponds to the absence of a secular component in the mean solar chromospheric activity (which does not imply the absence of the secular component in the photometric variability). So changes of the solar activity index occur only because of the evolution of the solar activity cycle. The second case (hereafter, case of strong secular changes) corresponds to the assumption that the mean solar chromospheric activity can reach a minimum boundary value 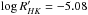 during the periods of zero modulation potential. In Appendix A we show how the mean solar chromospheric activity can be reconstructed to the past in both of these cases.
during the periods of zero modulation potential. In Appendix A we show how the mean solar chromospheric activity can be reconstructed to the past in both of these cases.
Figure 3 shows the trajectories of the Sun over last 9000 years in the photometric variability versus chromospheric activity diagram for a few different scenarios. The upper-left panel represents the scenario without secular variability. The VLT = 0.044% (upper-right panel) corresponds to the secular variability reported by Krivova et al. (2010). During the last thirty years the Sun was unusually active so its mean chromospheric activity over the last 9000 years is shifted towards lower values relative to the present position. The mean value of 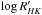 equals − 4.92 without the long-term trend in the chromospheric activity, while with strong long-term trend it equals − 4.96. The amplitude of the 11-year cycle in Strömgren (b + y)/2 averaged over the last 9000 years is approximately 40% smaller than its present amplitude, so if the photometric variability is not affected by a secular component then the “mean” Sun is located even lower than it is now. However, a secular component in the photometric variability shifts the “mean” Sun towards larger variabilities and in combination with a displacement towards lower chromospheric activities moves it to the regression line.
equals − 4.92 without the long-term trend in the chromospheric activity, while with strong long-term trend it equals − 4.96. The amplitude of the 11-year cycle in Strömgren (b + y)/2 averaged over the last 9000 years is approximately 40% smaller than its present amplitude, so if the photometric variability is not affected by a secular component then the “mean” Sun is located even lower than it is now. However, a secular component in the photometric variability shifts the “mean” Sun towards larger variabilities and in combination with a displacement towards lower chromospheric activities moves it to the regression line.
Let us note that our basic assumption implies that the variability of Sun-like stars is also time-dependent (see Appendix B). In combination with the inclination effect and measurement errors this can explain the scatter in the activity versus variability diagram, which most probably, is real.
 |
Fig. 3 The same as Fig. 1, but with trajectories of the Sun over the last 9000 years (orange dots) for different sets of the long-term variability VLT and the 11-year variability V11. The red square and cross symbols indicate the positions of the present and “mean” Sun. |
4. Discussion and conclusions
We have compared the available photometric records of Sun-like stars with a parameterized reconstruction of the solar irradiance over the last 9000 years. We assumed different scenarios of the solar secular variability and showed that if the solar irradiance is not affected by secular variations then there is a significant disagreement between the stellar variabilities and temporary mean variability of the Sun. Part of this disagreement can be explained by the selection effect in the stellar sample (Hall et al. 2009), relatively small number of stars, and short time span of the stellar observations.
At the same time, we show that the presence of a secular component in the solar irradiance can increase the temporal mean of solar variability. By assuming that the temporal mean Sun obeys the activity versus regression correlation, and employing the currently available datasets to constrain the V11 parameter, we try to estimate the magnitude of the secular component. The calculations are presented in Appendix B. While the currently available stellar data yield relatively large amplitude of the secular component, careful estimation of the involved uncertainties shows that a 0.17% decrease of the solar flux in the Strömgren (b + y)/2 filters during the Maunder minimum compared to the present value is within 95% confidence level. The trajectories of the Sun in the photometric variability versus chromospheric activity diagram which correspond to this amplitude of the secular component are shown in the middle panels of Fig. 3 (for two scenarios of the chromospheric activity variability). We note that the positions of the Sun-like stars on the variability versus activity diagram are also not necessarily fixed in time, and this can affect the variability versus activity regression. This is taken into account in Appendix B and therefore, while the VLT = 0.17% value is consistent with stellar data, the corresponding temporal mean position of the Sun is still below the regression line. The VLT = 0.17% value corresponds to 1.9–2.7 W/m2 TSI change (see Appendix B).
We note that this number is based solely on the empirical relationship between the stellar variability and activity and does not depend on mechanisms of stellar and solar variability. It is given by the present stellar sample and should be carefully re-evaluated when more stellar data become available and the low end of the activity sequence is studied. The continuation of the stellar photometric program will thus ultimately allow one to prove or disprove the existence of the secular variations of the solar irradiance.
Online material
Appendix A: Model description
The annual solar Strömgren (b + y)/2 flux values F(t) can be decomposed into the long-term FLT(t) and cyclic F11(t) components (see, e.g. Tapping et al. 2007) 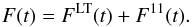 (A.1)While cyclic component F11(t) varies on the 11-year time scale and controls the activity cycle, the long-term component FLT(t) varies on secular time scales and leads to a changeable level of the flux during the solar activity minima.
(A.1)While cyclic component F11(t) varies on the 11-year time scale and controls the activity cycle, the long-term component FLT(t) varies on secular time scales and leads to a changeable level of the flux during the solar activity minima.
Most of the stars in the Lockwood et al. (2007) dataset are observed over an approximately 20-year period. Therefore, to compare stellar and solar variabilities we will introduce the rms20 value. For any given year t, it is the rms variability of the dataset which consists of twenty annual flux values (from year t−9, till year t + 10).
The total variability of the solar flux can be calculated as the geometrical sum of the long-term and cyclic variabilities 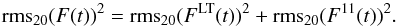 (A.2)We introduce parameter V11 as rms variability of the annual (b + y)/2 flux values for the 1976–1996 period (solar cycles 21 and 22). The Krivova et al. (2010), Shapiro et al. (2011), and Lean et al. (2005) reconstructions show the value of V11 parameter equals 0.00019 mag, 0.00018 mag, and 0.000032 mag, respectively.
(A.2)We introduce parameter V11 as rms variability of the annual (b + y)/2 flux values for the 1976–1996 period (solar cycles 21 and 22). The Krivova et al. (2010), Shapiro et al. (2011), and Lean et al. (2005) reconstructions show the value of V11 parameter equals 0.00019 mag, 0.00018 mag, and 0.000032 mag, respectively.
To calculate the cyclic component backwards in time, we assume that its amplitude is proportional to the long-term solar activity φ(t). The latter can be reconstructed over the millennia from the cosmogenic isotope data, which gives a 22-year running mean of the modulation potential (Steinhilber et al. 2008; Herbst et al. 2010). Thus, the cyclic rms variability for any given year t can be calculated as 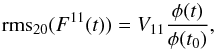 (A.3)where φ(t) is the modulation potential and φ(t0) is the mean value of the modulation potential for the 1976–1996 period. The modulation potential is deduced from the composite of the neutron monitor data (Usoskin et al. 2005) and 10Be data (McCracken et al. 2004; Vonmoos et al. 2006). It is normalised to the Castagnoli & Lal (1980) local interstellar spectra. The homogenisation procedure is discussed in Shapiro et al. (2011) and Thuillier et al. (2012). The average uncertainty of the modulation potential changes is ~80 MeV (Vonmoos et al. 2006) and does not have a significant contribution to the temporary mean of the solar variability.
(A.3)where φ(t) is the modulation potential and φ(t0) is the mean value of the modulation potential for the 1976–1996 period. The modulation potential is deduced from the composite of the neutron monitor data (Usoskin et al. 2005) and 10Be data (McCracken et al. 2004; Vonmoos et al. 2006). It is normalised to the Castagnoli & Lal (1980) local interstellar spectra. The homogenisation procedure is discussed in Shapiro et al. (2011) and Thuillier et al. (2012). The average uncertainty of the modulation potential changes is ~80 MeV (Vonmoos et al. 2006) and does not have a significant contribution to the temporary mean of the solar variability.
To calculate the rms20(FLT(t)) contribution we introduce parameter VLT as a relative change of FLT between the present and the Maunder minimum. The changes of the solar flux between three recent solar minima are within the uncertainties of the reconstructions and measurements of the solar irradiance (see review by Ermolli et al. 2012), so the FLT component can be approximated by a constant for the last solar cycles. Therefore, for simplicity we define VLT as the relative change of the (b + y)/2 flux between the 1996 and the Maunder minima.
We assume that the long-term changes of the solar irradiance are proportional to the changes of the solar activity φ(t) 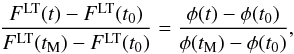 (A.4)where t0 refers to our reference period (1976–1996 average) and tM refers to the Maunder minimum.
(A.4)where t0 refers to our reference period (1976–1996 average) and tM refers to the Maunder minimum.
Substituting FLT(tM) − FLT(t0) = VLT FLT(t0), one can connect the relative changes of the solar flux and activity 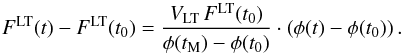 (A.5)Equation (A.5) links rms20(FLT(t)) and rms20(φ(t)) via the parameter VLT. In combination with Eqs. (A.2) and (A.3) it allows one to reconstruct the solar variability backwards in time as a function of V11 and VLT parameters.
(A.5)Equation (A.5) links rms20(FLT(t)) and rms20(φ(t)) via the parameter VLT. In combination with Eqs. (A.2) and (A.3) it allows one to reconstruct the solar variability backwards in time as a function of V11 and VLT parameters.
The approach, presented above is based on three assumptions:
-
1.
The amplitude of the activity cycle is proportional to thelong-term (i.e. cycle-averaged) solar activity.
-
2.
The long-term changes of the solar irradiance are proportional to the long-term changes of the solar activity.
-
3.
The long-term solar activity can be reconstructed from the cosmogenic isotope data.
Let us note that these assumption are either employed or fulfilled because of the physical reasons in most of the available reconstructions, independently from the proposed mechanism for the secular changes.
To estimate the accuracy of our approach we consider three different reconstructions of the solar irradiance to the past: Krivova et al. (2010) (VLT = 0.044%, V11 = 0.000019 mag), Shapiro et al. (2011) with removed long-term trend (VLT = 0%, V11 = 0.000018 mag), and the original Shapiro et al. (2011) reconstruction (VLT = 0.38%, V11 = 0.000018 mag). They yield 0.0001 mag, 0.00009 mag, and 0.00036 mag for the mean solar rms20 variability over the 1620–1995 period. The same values calculated with the set of Eqs. (A.2)–(A.5) are 0.00013 mag, 0.00012 mag, and 0.00035 mag. One can see that our approach slightly overestimates the first two numbers. The reason for this is that to allow a homogeneous reconstruction over the millennia we use the solar modulation potential to scale the cyclic variability (see Eq. (A.3)) instead of the sunspot number. The annual sunspot number is very close to zero during the Maunder minimum period, so the reconstructions predict the cessation of the cyclic variations (see Fig. 2). At the same time the modulation potential and consequently the cyclic variability in our approach did not go to zero during the Maunder minimum (McCracken et al. 2004). Such deviations are comparable to the uncertainties of the reconstructions and are not essential for our conclusions.
 |
Fig. B.1 Left panel: the dependency of the VLT parameter on the solar variability, retrieved from the stellar data. The shaded area indicates the uncertainty (2σ) due to the limited number of stars. The V11 parameter is set to 0.00044 mag. The dashed line corresponds to the expected mean solar variability rms20 = 0.00082. The projection onto VLT-axis yields the 95% interval for expected long-term variability of the Sun: 0.43% < VLT < 0.76%. Right panel: the same as the left panel, but the contour calculated with V11 = 0.0002 mag is added. The four dashed lines correspond to four values of expected mean solar variability rms20: 0.00097 mag (no chromospheric secular changes, regression with solid line from Fig. 1), 0.00082 mag (strong chromospheric secular changes, regression with solid line), 0.00065 mag (no chromospheric secular changes, regression with dashed line), 0.00053 mag (strong chromospheric secular changes, regression with dashed line). The projection onto the VLT-axis yields the interval 0.17% < VLT < 1.2%. |
 |
Fig. B.2 Upper panel: rms20 back to 400 BC, adopting VLT = 0.001 (lower curve) and VLT = 0.005 (upper curve). V11 is set to 0.0002 mag. Lower panel: modulation potential back to 400 BC. The interval in the upper-right corner denotes the satellite era of continuous solar irradiance measurements. |
The calculation of the Ca II H and K lines, which are used to determine the solar chromospheric activity, made even more complicated by the effect of the non-local thermodynamical equilibrium (Ermolli et al. 2010). So the mean solar chromospheric activity cannot be directly deduced from the available reconstructions of the solar irradiance over the millennia. Instead we will linearly scale it with the long-term solar activity 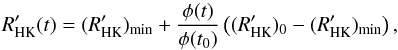 (A.6)where
(A.6)where 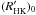 is the present value of the mean solar chromospheric activity (
is the present value of the mean solar chromospheric activity (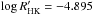 , see Lockwood et al. 2007) and
, see Lockwood et al. 2007) and 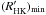 is the value of the mean chromospheric activity corresponding to φ = 0.
is the value of the mean chromospheric activity corresponding to φ = 0.
In Fig. 3 we consider two extreme scenarios (see Sect. 3), one without the secular component in the solar chromospheric activity, and another with a strong secular component. Without the secular component the changes of the mean solar chromospheric activity are only caused by the variable amplitude of the solar activity cycle and the 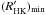 value corresponds to the present value of the solar activity at minimum conditions (
value corresponds to the present value of the solar activity at minimum conditions (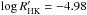 ; see Judge & Saar 2007). To describe the case of a strong secular component in the chromospheric activity we put the
; see Judge & Saar 2007). To describe the case of a strong secular component in the chromospheric activity we put the 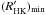 value equals to the boundary value from Saar (2006) (
value equals to the boundary value from Saar (2006) (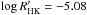 ).
).
Appendix B: Possible constraints on the historical solar variability
The amplitude of the secular solar photometric variability can be constrained by demanding the temporal mean solar variability be in agreement with the variability, indicated by the stellar data. The latter depends on the version of the variability versus activity regression and the scenario of the chromospheric activity behaviour. To investigatedifferent cases in Fig. B.1 we plot the long-term solar variability VLT as a function of the mean solar variability (rms20) given by the stellar data, for two values of the 11-year variability V11. The inclination effect was calculated according to Knaack et al. (2001).
Let us note, however, that the positions of the Sun-like stars in Fig. 3 are also not necessarily fixed in time. This can affect the coefficients of the regression line and accordingly the estimated variability of the Sun. For example it is possible that, by coincidence, most of the stars among the twenty-one used for our analysis represent the periods of the relatively low (or high) variability. This will lead to the shifted position of the regression line and consequently to the deviations in the Vlt parameter determined using this limited selection of stars.
If the behaviour of the stellar variabilities after the regression to the solar level of the chromospheric activity is identical to the solar variability, i.e. the solar and regressed stellar variabilities can be parameterised employing the approach described in Sect. 3 and Appendix A, then the resulting uncertainty can be found by performing the Monte Carlo simulation. To do this we considered a large number of sets consisting of 21 stars. Every star in these sets represents the Sun at some random twenty-year interval period (chosen from the full 9000-year dataset) and with a random angle between the stellar rotation axes and the direction to the observer. The rms20 variability of these stars is calculated, employing the approach described in Sect. 3 and Appendix A and the Knaack et al. (2001) dependency of the 11-year variability on the angle between the solar rotation axes and the direction to the observer. For every set we calculated the mean rms20 variability of the stars in the set, so for every pair of VLT and V11 parameters we have a distribution of mean rms20 variabilities. This allows us to calculate the range of VLT and V11 parameters which can lead to the present value of the linear coefficients of the activity versus variability regression line. In Fig. B.1 we mark the resulting 2σ uncertainty in VLT parameter with a shaded area.
The mean solar 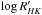 index in the case of the strong secular component in chromospheric activity is − 4.96 (see Fig. 3). Using the solid blue line in Fig. 1 one can find that this index corresponds to the 8.2 × 10-4 rms variability. This value is inserted in the left panel of Fig. B.1 and one can see that it yields VLT = (0.43%−0.76%).
index in the case of the strong secular component in chromospheric activity is − 4.96 (see Fig. 3). Using the solid blue line in Fig. 1 one can find that this index corresponds to the 8.2 × 10-4 rms variability. This value is inserted in the left panel of Fig. B.1 and one can see that it yields VLT = (0.43%−0.76%).
In the right panel of Fig. B.1 we also plotted the contour with V11 = 0.0002 mag and indicated four different values of the expected solar variability, corresponding to different treatments of the chromospheric secular changes and two regressions from Fig. 1. One can see that the minimum value of VLT equals 0.17%.
The parameter VLT characterises the long-term variability as it is observed in the Strömgren b and y filters. Its connection with the variability at another spectral domain (or TSI) depends on the mechanism of the secular changes. For example a VLT equal to 0.17% leads to a 2.7 W/m2 TSI change between the Maunder and the last solar minima, adopting the model of Shapiro et al. (2011), and to 1.9 W/m2, assuming that it is caused by the variations of the solar effective temperature.
Acknowledgments
The research leading to this paper was supported by the Swiss National Science Foundation under grant CRSI122-130642 (FUPSOL). We thank Phillip Judge for initiating this study and for the productive discussions, Natalie Krivova for the careful reading of the manuscript and the useful suggestions, and Wes Lockwood for providing the stellar data and helping us to understand them. The work has benefited from the COST Action ES1005 TOSCA (http://www.tosca-cost.eu).
References
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Castagnoli, G., & Lal, D. 1980, Radiocarbon, 22, 133 [Google Scholar]
- Ermolli, I., Criscuoli, S., Uitenbroek, H., et al. 2010, A&A, 523, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ermolli, I., Matthes, K., Dudok de Wit, T., et al. 2012, Atmosph. Chem. Phys. Discussions, 12, 24557 [Google Scholar]
- Foukal, P. 1994, Science, 264, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, J. C., & Lockwood, G. W. 2004, ApJ, 614, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, J. C., Henry, G. W., Lockwood, G. W., Skiff, B. A., & Saar, S. H. 2009, AJ, 138, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Harder, J. W., Fontenla, J. M., Pilewskie, P., Richard, E. C., & Woods, T. N. 2009, Geophys. Res. Lett., 36, 7801 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, K., Kopp, A., Heber, B., et al. 2010, J. Geophys. Res. (Space Phys.), 115, [Google Scholar]
- Judge, P. G., & Saar, S. H. 2007, ApJ, 663, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Judge, P., Lockwood, G. W., Radick, R. R., et al. 2012, A&A, 544, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knaack, R., Fligge, M., Solanki, S. K., & Unruh, Y. C. 2001, A&A, 376, 1080 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova, N. A., Vieira, L. E. A., & Solanki, S. K. 2010, J. Geophys. Res. (Space Phys.), 115, 12112 [Google Scholar]
- Lean, J., Rottman, G., Harder, J., & Kopp, G. 2005, Sol. Phys., 230, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, M. 2011, Nature Climate Change, 1, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Baliunas, S. L., & Radick, R. R. 1992, Nature, 360, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., & Radick, R. R. 1997, ApJ, 485, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, M., Stamper, R., & Wild, M. N. 1999, Nature, 399, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Henry, G. W., et al. 2007, ApJS, 171, 260 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, K. G., McDonald, F. B., Beer, J., Raisbeck, G., & Yiou, F. 2004, J. Geophys. Res. (Space Phys.), 109, 12103 [NASA ADS] [CrossRef] [Google Scholar]
- Radick, R. R. 1994, Science, 266, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Radick, R. R., Lockwood, G. W., Skiff, B. A., & Baliunas, S. L. 1998, ApJS, 118, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H. 2006, in BAAS 38, AAS/Solar Physics Division Meeting #37, 240 [Google Scholar]
- Schatten, K. H. 1993, J. Geophys. Res., 98, 18907 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Livingston, W. C., Woods, T. N., & Mewaldt, R. A. 2011, Geophys. Res. Lett., 38, 6701 [Google Scholar]
- Shapiro, A. I., Schmutz, W., Rozanov, E., et al. 2011, A&A, 529, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K., Usoskin, I. G., Kromer, B., Schüssler, M., & Beer, J. 2004, Nature, 431, 1084 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Soubiran, C., & Triaud, A. 2004, A&A, 418, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinhilber, F., Abreu, J. A., & Beer, J. 2008, Astrophys. Space Sci. Trans., 4, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tapping, K. F., Boteler, D., Charbonneau, P., et al. 2007, Sol. Phys., 246, 309 [Google Scholar]
- Thuillier, G., Deland, M., Shapiro, A., et al. 2012, Sol. Phys., 277, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I. G., Alanko-Huotari, K., Kovaltsov, G. A., & Mursula, K. 2005, J. Geophys. Res. (Space Phys.), 110, 12108 [Google Scholar]
- Vieira, L. E. A., Solanki, S. K., Krivova, N. A., & Usoskin, I. 2011, A&A, 531, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieira, L. E. A., Norton, A., Dudok de Wit, T., et al. 2012, Geophys. Res. Lett., 39, 16104 [Google Scholar]
- Vonmoos, M., Beer, J., & Muscheler, R. 2006, J. Geophys. Res. (Space Phys.), 111, 10105 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Photometric variability versus chromospheric activity. The blue stars indicate the stars with observed variability from Lockwood et al. (2007). Magenta triangles indicate lower limits for stars with unconfirmed variability set at about 0.5 below the regression line. The solid (5.892+1.810 |
| In the text | |
 |
Fig. 2 Upper panel: annual (b + y)/2 values versus time according to the spectral solar irradiance (SSI) reconstructions to the past as calculated by Krivova et al. (2010) (red), Lean et al. (2005) (blue) and Shapiro et al. (2011) (magenta: thick and thin curves are original data and data with removed secular changes, respectively). Stars indicates the SIM/SORCE measurements. Lower panel: calculated for the 20 year time intervals rms20 values versus time. |
| In the text | |
 |
Fig. 3 The same as Fig. 1, but with trajectories of the Sun over the last 9000 years (orange dots) for different sets of the long-term variability VLT and the 11-year variability V11. The red square and cross symbols indicate the positions of the present and “mean” Sun. |
| In the text | |
 |
Fig. B.1 Left panel: the dependency of the VLT parameter on the solar variability, retrieved from the stellar data. The shaded area indicates the uncertainty (2σ) due to the limited number of stars. The V11 parameter is set to 0.00044 mag. The dashed line corresponds to the expected mean solar variability rms20 = 0.00082. The projection onto VLT-axis yields the 95% interval for expected long-term variability of the Sun: 0.43% < VLT < 0.76%. Right panel: the same as the left panel, but the contour calculated with V11 = 0.0002 mag is added. The four dashed lines correspond to four values of expected mean solar variability rms20: 0.00097 mag (no chromospheric secular changes, regression with solid line from Fig. 1), 0.00082 mag (strong chromospheric secular changes, regression with solid line), 0.00065 mag (no chromospheric secular changes, regression with dashed line), 0.00053 mag (strong chromospheric secular changes, regression with dashed line). The projection onto the VLT-axis yields the interval 0.17% < VLT < 1.2%. |
| In the text | |
 |
Fig. B.2 Upper panel: rms20 back to 400 BC, adopting VLT = 0.001 (lower curve) and VLT = 0.005 (upper curve). V11 is set to 0.0002 mag. Lower panel: modulation potential back to 400 BC. The interval in the upper-right corner denotes the satellite era of continuous solar irradiance measurements. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.