| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201220437 | |
| Published online | 09 April 2013 | |
Radial velocity signatures of Zeeman broadening
1
Universität Göttingen, Institut für Astrophysik,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
e-mail:
Ansgar.Reiners@phys.uni-goettingen.de
2
Department of Physics and Astronomy, Uppsala
University, Box
516, 75120
Uppsala,
Sweden
Received: 25 September 2012
Accepted: 14 January 2013
Stellar activity signatures such as spots and plages can significantly limit the search for extrasolar planets. Current models of activity-induced radial velocity (RV) signals focus on the impact of temperature contrast in spots according to which they predict the signal to diminish toward longer wavelengths. The Zeeman effect on RV measurements counteracts this: the relative importance of the Zeeman effect on RV measurements should grow with wavelength because the Zeeman displacement itself grows with λ, and because a magnetic and cool spot contributes more to the total flux at longer wavelengths. In this paper, we model the impact of active regions on stellar RV measurements including both temperature contrast in spots and line broadening by the Zeeman effect. We calculate stellar line profiles using polarized radiative transfer models including atomic and molecular Zeeman splitting over large wavelength regions from 0.5 to 2.3 μm. Our results show that the amplitude of the RV signal caused by the Zeeman effect alone can be comparable to that caused by temperature contrast; a spot magnetic field of ~1000 G can produce a similar RV amplitude as a spot temperature contrast of ~1000 K. Furthermore, the RV signal caused by cool and magnetic spots increases with wavelength, in contrast to the expectation from temperature contrast alone. We also calculate the RV signal caused by variations in average magnetic field strength from one observation to the next, for example due to a magnetic cycle, but find it unlikely that this can significantly influence the search for extrasolar planets. As an example, we derive the RV amplitude of the active M dwarf AD Leo as a function of wavelength using data from the HARPS spectrograph. Across this limited wavelength range, the RV signal does not diminish at longer wavelengths but shows evidence for the opposite behavior, consistent with a strong influence of the Zeeman effect. We conclude that the RV signal of active stars does not vanish at longer wavelength but sensitively depends on the combination of spot temperature and magnetic field; in active low-mass stars, it is even likely to grow with wavelength.
Key words: line: profiles / techniques: radial velocities / stars: activity / starspots / stars: magnetic field
© ESO, 2013
1. Introduction
The precise determination of radial velocities (RV) and their temporal variations is a key data analysis method in stellar astrophysics. It is applied to detect extra-solar planets and to measure their projected mass, which requires high-precision RV data that reach about m s-1 and below (Mayor & Udry 2008; Udry et al. 2009). Radial velocities can also be used to determine the periodic motion of the stellar surface, enabling asteroseismology to reveal sensitive information on fundamental stellar parameters including a view into the interior of stars (Cunha et al. 2007; Bazot et al. 2011).
Measurement of RV time series allows the detection of the projected motion of a star or its surface from their spectral lines. For the detection of planets, the assumption is that the shape of a spectral lines does not vary with time so that its centroid position provides information about the projected velocity of the star. The relative RV shift between two epochs is measured either by searching for the best agreement between two spectra with RV as a free parameter, or by locating the centroid position in a cross-correlation profile calculated from the spectrum and some template. Both methods assume that the spectral line shape is identical. It is well known, however, that variations in the shape of stellar line profiles on timescales similar to planetary orbits can be caused by several mechanisms, e.g., by the transit of a planet (Rossiter 1924; McLaughlin 1924) or stellar activity. The latter poses a number of problems to stellar RV measurements: first, active stars are the typically fast rotators, implying wider line profiles, which reduces the achievable accuracy in a given RV measurement (e.g., Bouchy et al. 2001). Second, activity is believed to be caused by magnetic areas that can produce cool spots or hot plages, which are in general not symmetrically distributed over the star; this allows the reconstruction of surface maps in tomographic imaging studies (e.g., Vogt & Penrod 1983). Third, magnetic regions can suppress convective motion and alter the signature of stellar convective blueshifts (see Gray 2009; Meunier et al. 2010). Cool spots that co-rotate with the stellar surface are widely studied for the Sun, and much larger spots are known to exist on other stars (Berdyugina 2005; Strassmeier 2009). Line profile distortions caused by these features can lead to significant shifts of the line barycenter, introducing an offset to the real central line position (e.g., Saar et al. 1998). Useful information for the correction of stellar RV curves for activity signatures can be provided by activity indicators like the strength of chromospheric emission lines or absorption line bisectors (Santos et al. 2000). Several examples exist where periodicities in RV curves were interpreted as due to planetary companions but were later retracted since the reason for RV variability was found to be stellar activity. Additionally, differences in RV amplitude between optical and infrared bands have been detected in a few systems (e.g., Martín et al. 2006; Huélamo et al. 2008; Mahmud et al. 2011).
The effect of cool active regions on RV measurements due to temperature contrast alone has been investigated in detail by, e.g., Saar & Donahue (1997); Desort et al. (2007); Makarov et al. (2009); Lagrange et al. (2010); Reiners et al. (2010); Barnes et al. (2011). Magnetic flux tubes on the Sun are known to exist also in the so-called network and plage areas (e.g., Solanki & Stenflo 1984). These regions show high magnetic fields well above B = 1 kG, temperature contrasts of a few hundred K, and occupy a much larger part of the solar surface than cool spots do. Owing to their relatively low temperature contrast but high filling factor, plages are difficult to characterize on surfaces of stars other than the Sun. The impact of bright regions on RV measurements (together with the impact of inhibited convection) was investigated by Meunier et al. (2010) using solar 2D images as templates for the spatial distribution of bright and dark areas. In principle, the effect of bright areas on RV measurements is comparable to that of cool spots, but because the flux contrast is reversed, the RV signal has the opposite sign. RV distortions from adjacent bright and dark areas can therefore partially cancel out. The total contribution of plages to the variability of solar irradiance is larger than the contribution of cool spots (e.g., Fröhlich & Lean 1998), but the two cannot be distinguished in any other star so far. Therefore, plages and quiet stellar regions are often described by one single atmospheric component, which probably is somewhat hotter than the “quiet” atmosphere. Line profile distortions in stars other than the Sun are often described in a two-temperature model defining a cool spot component in active stars. The real effect is likely a result of combined spot and plage variability.
In general, co-rotating active regions can lead to spurious RV variations in phase with the stellar rotation period. The amplitude of the variation depends on the projected rotational velocity of the star, v sini, the fractional surface coverage of the spotted area, f, the temperature contrast between “quiet” star and active regions, and the wavelength used for observations. Since the (absolute) flux ratio between active regions and photosphere is lower at longer wavelengths (independent of whether the active region is cool or hot), it is expected that RV distortions caused by stellar activity are lower at infrared than at optical wavelengths. It has therefore been claimed that RV-based planet searches in very cool stars and brown dwarfs (these objects are typically very active) should be best conducted at infrared wavelengths rather than at optical (e.g., Martín et al. 2006).
The aim of this paper is to investigate the impact of magnetic fields on the spectral appearance of active stars. It is not only the temperature difference that affects stellar line profiles, but also the field itself that may introduce significant distortions through the Zeeman effect. The Zeeman effect counteracts the temperature contrast with more significant influence at longer wavelengths. Our aim is to model the RV signal of active regions including temperature and magnetic effects. After introducing our model techniques and demonstrating the general picture in a few toy model cases, we conclude that the Zeeman effects likely plays a very significant role in the determination of RVs in active stars.
2. Zeeman splitting in stellar spectra
Our picture of stellar surface properties is motivated by the appearance of the Sun, where rising magnetic flux tubes inhibit convection in active regions and produce both hot and cool surface regions. Strongest flux concentrations are observed in cool spots with typical temperatures several 100–1000 K below photospheric average and typical magnetic flux densities of several 100–1000 G (Solanki 2003).
The general framework of stellar active regions is consistent with observations from more active stars and stars of different spectral type (Strassmeier 2009). An important ingredient is that active regions differ from the quiet photosphere in temperature and magnetic properties; in particular, large starspots are believed to be cool and magnetic. Owing to our limited ability to measure localized magnetic fields in other stars, however, we lack good understanding of magnetic fields in stars other than the Sun. In particular, we have no empirical evidence of the relation between magnetic field and spot temperature in very active stars. Nevertheless, we may find it reasonable to assume that local magnetic field strengths in other stars are on the same order as in the Sun, and that large active regions can be similar to very large sunspots. Empirical results on average magnetic fields in very active low-mass stars are consistent with this picture, finding very strong average surface fields at the kilo-Gauss level in mid- and late-M dwarfs (e.g., Reiners & Basri 2007).
The appearance of a spectral line in the presence of a magnetic field is determined by the Zeeman effect: each energy level with a total angular momentum quantum number J splits into (2J + 1) states of energy with different magnetic quantum numbers M. In absence of a magnetic field, the transition energy is unique but it splits into three groups of transitions according to the change in the magnetic quantum number M invoked by the transition (ΔM = −1,0, + 1). The appearance of the spectral line also depends on the geometry of the field, but this effect is often neglected assuming an “homogeneous” distribution of field lines over the stellar surface. We refer to Reiners (2012) for a deeper discussion of magnetic field observations.
For the context of RV measurements, we are interested in the amplitude of spectral line deformations caused by magnetic fields. The two σ-groups with magnetic quantum numbers M = −1, + 1 are shifted with respect to the π-group (M = 0) by an amount that depends on the level’s quantum numbers, condensed in the Landé-factor g, and is proportional to the magnetic field B. In velocity units, the displacement can be equated as 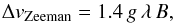 (1)with v in m s-1, λ in μm, and B in Gauss. The Landé-factor g is on the order of unity. Equation (1) has two important implications: 1) the typical displacement of Zeeman components in the presence of magnetic fields is on the order of 1 m s-1 G-1. For typical field strengths of solar active regions (100–1000 G), flux from active regions can therefore be displaced, through the Zeeman effect, by several hundred m s-1; 2) in velocity units, the displacement is proportional to wavelength, λ, of the spectral line under consideration. Thus, the displacement is larger for longer wavelengths, which is in contrast to the displacement from temperature contrast (see, e.g., Reiners et al. 2010). We note that RV signatures caused by temperature contrast always diminish with wavelength, independent of whether they are hotter or cooler than the rest of the star. The translation from the displacement of Zeeman components, ΔvZeeman, into a shift of the line profile barycenter, Δvvrad, is non-trivial and subject of this paper. The typical amplitude of ΔvZeeman together with typical field strengths on stars show that even if the net signal (Δvvrad) in a spectral line only would be a few percent of ΔvZeeman, this still would easily be in the range relevant for detecting planetary orbits through the RV method.
(1)with v in m s-1, λ in μm, and B in Gauss. The Landé-factor g is on the order of unity. Equation (1) has two important implications: 1) the typical displacement of Zeeman components in the presence of magnetic fields is on the order of 1 m s-1 G-1. For typical field strengths of solar active regions (100–1000 G), flux from active regions can therefore be displaced, through the Zeeman effect, by several hundred m s-1; 2) in velocity units, the displacement is proportional to wavelength, λ, of the spectral line under consideration. Thus, the displacement is larger for longer wavelengths, which is in contrast to the displacement from temperature contrast (see, e.g., Reiners et al. 2010). We note that RV signatures caused by temperature contrast always diminish with wavelength, independent of whether they are hotter or cooler than the rest of the star. The translation from the displacement of Zeeman components, ΔvZeeman, into a shift of the line profile barycenter, Δvvrad, is non-trivial and subject of this paper. The typical amplitude of ΔvZeeman together with typical field strengths on stars show that even if the net signal (Δvvrad) in a spectral line only would be a few percent of ΔvZeeman, this still would easily be in the range relevant for detecting planetary orbits through the RV method.
For the purpose of this paper, we are interested in the effect of Zeeman splitting on stellar RV curves. A constant average magnetic field may affect the overall shape of a line profile with respect to the non-magnetic case, but as long as this profile is not time-variable, it is not relevant for a RV analysis. On the other hand, any time-variability in the magnetic properties of stellar surfaces can have significant consequences for stellar RV curves. Variability can be caused either by localized magnetism on time-variable (projected) surface areas, like co-rotating spots, or by intrinsic time-variability of the magnetic field observed on the visible hemisphere (e.g., magnetic cycles). We will consider both types of line profile variability in the following.
3. Co-rotating magnetic spots
Spectral lines of rotating stars are broader than lines of non-rotating stars because of the Doppler effect: light emerging from the area of the star rotating toward us is shifter blue while light coming from the area moving away from us is shifted red. The net effect is a characteristic spectral line broadening that allows a precise measurement of the star’s projected rotational velocity, v sini (e.g., Gray 2005). If a certain area of a star is cooler, this area emits less flux than other regions. In absorption lines, this leads to a characteristic bump at the position in the line profile corresponding to the local velocity projected toward the observer. In a similar fashion, the flux emitted from co-rotating magnetic spots will alter the appearance of a Doppler-broadened line profile, and the shape of the overall profile will change when the star is observed at different rotational phases.
Stellar convective blueshift is another result of Doppler broadening in spectral lines. Due to the imbalance between rising hot plasma and cooler downflows, spectral lines are generally shifted blue in sun-like stars (e.g., Gray 2009). In magnetic areas, convective motion is suppressed, which can result in significant RV signatures. Meunier et al. (2010) have modeled this effect assuming that in active regions the average convective blueshift seen in all lines is attenuated by Δv = 190 m s-1 perpendicular to the solar surface. Meunier et al. (2010) found that in the Sun, the RV signature from convective blueshifts dominates the activity-induced stellar RV signal; with an amplitude of several m s-1, the convective RV signal is stronger than the signal caused by flux contrast by a factor of a few. In our study, we excluded the signal from convective blueshifts because we are concentrating on the additional effect of Zeeman splitting. Following Meunier et al. (2010), one can argue that the RV variations caused by blueshift can be separated from the effects of the line shape (flux contrast and Zeeman splitting).
 |
Fig. 1 Sketch of the effect of a magnetic spot on RV measurements. Top: rotating star with large spot, covering 5% of the visible surface if observed at disk center, seen at three phases. The star is rotating with the spot approaching in the left column, centered in the middle column, and rotating out of view in the right column. Second row: stellar line profile broadened by rotation but without spot flux, showing the impact of a dark star spot. Third row: flux emerging from spot only, assuming the same temperature as in the photosphere. Row four: sum of surrounding and the spot region. Row five: radial velocity determined from fitting a Gaussian profile to the spectral lines in row four. In rows three to five, black solid lines show the case without a magnetic field (and zero spot temperature contrast). Blue and red dashed lines show cases in which the spot area has B = 1 kG and 2 kG, respectively (λ = 1.2 μm and g = 1.0). |
3.1. Toy model
In the following, we calculate a line profile for an artificial star rotating at v sini = 2 km s-1 and simulate a line profile distortion caused by an artificial spot with the same temperature as the quiet photosphere. The distortion is only caused by Zeeman splitting of the line that emerges from the spot. In our examples, we calculate the rotational phases corresponding to a maximum displacement of the line center, i.e., we compute the semi-amplitude K of the apparent RV curve caused by a magnetic spot (see Fig. 8 of Reiners et al. 2010). The RV is then calculated from cross-correlating the undistorted template spectrum with the spectrum of the spotted star. The barycenter of the cross-correlation function is determined by fitting it with a Gaussian profile.
The top panel in Fig. 1 shows a sketch of rotating star at three rotational phases. The stellar surface shows a large magnetic spot that is rotating into view in the left column, is centered in the middle column, and is rotating out of view in the right column. The spot covers 5% of the visible surface at the center of the disk but it appears smaller if viewed closer to the limb. The second (from top) row of Fig. 1 shows a stellar line profile broadened by rotation with projected rotation velocity v sini = 2 km s-1 but without any flux coming from the spot region; the total flux is reduced by 5% in this (central) example. This shows the typical line profile when looking at the temperature effect only. The third row shows the flux emerging from the spotted area only, assuming it has the same temperature as the surrounding photosphere. In general, large sun- or starspots are believed to be cooler than the surrounding atmosphere, but we look at the case of identical temperatures first to isolate the impact of the Zeeman effect from the temperature contrast. Row four shows the sum of the surrounding region (star without spot) plus the spot region. In panels three and four, black solid lines show the case for no magnetic field. Here, the profile is just the undistorted spectral line. Dashed blue and red lines show cases in which the spot area harbors a magnetic field with an average field strength of 1 kG and 2 kG, respectively. A spectral line at λ = 1.2 μm and g = 1.0 is assumed. The spectral line emerging from the spot region is broader and shallower in the magnetic case. In row four, the effect of one co-rotating magnetic spot (again, without any temperature difference) on a spectral line is displayed. Clearly, the Zeeman effect significantly distorts the line profile and consequently shifts the apparent center of the line. Finally, in the bottom panel, we quantify this by showing the center of the spectral line as derived from a fit assuming a Gauss function. We note that the RV shift is a consequence of the non-axisymmetric field distribution, implying that polar spots or other axisymmetric configurations cannot introduce RV shifts through this mechanism (but see Sect. 4). We can compare Fig. 1 of this work to Fig. 8 in Reiners et al. (2010) to see that the line profile deformation induced by the Zeeman effect is similar to a deformation induced by cool spots. In particular, the RV signal from a magnetic spot through the Zeeman effect has the same sign as the signal from a cool spot due to flux contrast.
The amplitude of the apparent RV shift in our example is approximately 100 m s-1 for B = 2 kG, and approximately 25 m s-1 for B = 1 kG. It is worth noting that the projected rotational velocity chosen for this example, v sini = 2 km s-1, is similar to the solar rotation, which is considered rather slow compared to typical late-type stars. Nevertheless, the amplitude is significant for the precision required for the RV accuracy level needed for planet search. For more rapidly rotating stars the distortion scales with v sini (cf. Reiners et al. 2010). Because of the similarities between temperature and Zeman RV signatures, line profile diagnostics such as bisectors (Desort et al. 2007) can be useful tools to investigate activity-related reasons for velocity shifts in observed stellar spectra.
 |
Fig. 2 Toy model RV signal caused by the Zeeman effect from a co-rotating magnetic spot with zero temperature contrast. The signal is calculated for three different field strengths inside the spot (green: 100 G, black: 600 G, and red: 4000 G); for each case three different spot sizes are used (f = 1%,3%, and 10%). Gray dashed lines show an analytical approximation of the scaling using Eq. (2). The dotted line visualizes the 1 m s-1 limit. |
3.2. Dependence on wavelength and field strength
In Fig. 2 we show the RV amplitude due to the Zeeman effect calculated from one spectral line with g = 1.0 as a function of wavelength. The line distortion is induced by a magnetic spot with one out of three different values of magnetic field strength inside the spot (B = 100 G, 600 G, and 4000 G) and one out of three different spot filling factors (f = 1%,3%, and 10%). While little is known about the geometric concentration of small magnetic areas on cool stars, the total magnetic energy assumed in our examples is easily justified by observations of cool star magnetic fields (Reiners 2012); our example stars have average fields of Bf = 1–400 G (concentrated in one single spot) well in the range of average fields observed that can be as strong as several kG (Reiners et al. 2009).
In all cases, the apparent RV shift scales with spot size, and a higher field strength introduces a stronger RV shift. For relatively weak fields (B ≲ 1 kG), the signal also grows with wavelength, as can be expected since the Zeeman effect grows as well. The amplitude of the RV signal during stellar rotation due to the signature of the spot can be approximated by the scaling relation 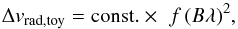 (2)with f the relative fraction of the spot area, B the magnetic field inside the spot, and λ the wavelength. The gray dashed lines in Fig. 2 illustrate the scaling of Eq. (2); the RV shift is proportional to the filling factor, and the dependence on B is identical to the one on λ, which is consistent with Eq. (1).
(2)with f the relative fraction of the spot area, B the magnetic field inside the spot, and λ the wavelength. The gray dashed lines in Fig. 2 illustrate the scaling of Eq. (2); the RV shift is proportional to the filling factor, and the dependence on B is identical to the one on λ, which is consistent with Eq. (1).
The amplitude of the RV shift is below 1 m s-1 as long as the field inside this one spot is on the order of B = 100 G. In this case, only relatively high spot coverage (10%) at long wavelengths (λ > 2 μm) can cause signals stronger than ~1 m s-1. For the Sun we know that field strengths inside a spot can easily be stronger than 100 G (but note that spots with strong fields are typically cool, which is not considered in this simple model). In our simulation, spots with field strengths of several hundred Gauss and filling factors of a few percent can introduce RV signals well above the m s-1 level. For example, the signal of a spot with f = 3% and B = 600 G causes a RV signal with an amplitude of Δvrad ≈ 1 m s-1 at λ = 500 nm. The signal grows with wavelength up to Δvrad ≈ 10 m s-1 at λ = 2200 nm.
The case of very strong magnetic fields (4000 G) inside the spot region shows a somewhat different behavior. While the RV shift in this case is stronger than in the other cases with weaker fields, it does not scale with wavelength and remains almost at a constant value between 10 and 100 m s-1 depending on the filling factor. We interpret this behavior as a saturation effect in the sense that the line profile distortion caused by a spot with B ≈ 4000 G does not distort a measurement of the line center much more than a spot with B ≈ 1000 G does. The reason for this is that Zeeman broadening already is so significant that the essential effect in the line profile is similar to a very cool spot in which the flux from the spot area is simply missing. For a field strength of B = 4000 G, the displacement of σ-components is vZeeman ~ 6 km s-1 (Eq. (1)), which means that flux from the spot area is essentially removed to the wings of the spectral line (note that the typical line width in Fig. 1 is ~10 km s-1). In other words, the RV signal does not grow any further as soon as the amplitude of Zeeman splitting from the spot area is comparable to the line width of the rotating star.
The conclusion from this exercise is that the Zeeman signal introduced by a magnetic spot that is not cooler than the rest of the star can be significant for RV surveys aiming at precisions on the order of a meter per second. The RV signature has the same sign as the signature of a cool (non-magnetic) spot. The Zeeman signal grows with wavelength for moderate values of B inside the spot. The effect of a (non-magnetic) cool spot can also be very significant on the m s-1 level, but it scales with opposite sign, i.e., it is strong at short wavelengths but diminishes toward long wavelengths. For a similar simulation using a toy model of (non-magnetic) cool spots, we refer to Reiners et al. (2010). In their Fig. 10, the authors show that in a cool star (T ~ 4000–6000 K), the effect of a f = 2% spot that is ΔT = 200 K cooler than the surrounding is on the order of 10 m s-1 at λ = 550 nm, and the amplitude is a factor of 3 smaller at λ = 1800 nm. Furthermore, they show that the RV amplitude is larger if temperature contrast is stronger (cooler spots in that example), but dependence on wavelength also becomes much weaker for stronger temperature contrast (see Reiners et al. 2010, for more details).
 |
Fig. 3 Example of apparent velocity shift in magnetically sensitive spectral lines. Black solid line: spectrum containing four lines of molecular FeH without magnetic fields in a T = 3700 K atmosphere; red dashed line: same spectral lines influenced by a magnetic field of B = 1000 G. Inset shows auto-correlation function of the field-free case (black solid line) and cross-correlation between field-free spectrum with magnetic case spectrum (red dashed line). |
4. Symmetric line broadening
In addition to the signature of co-rotating spots, the effect of a variable average magnetic field distributed over the entire star can also be very interesting. This could, for example, approximate the effect of a magnetic cycle in an active star, or it can be caused by stellar rotation since the average field visible at a given epoch can differ from the one seen in other snapshots while the field distribution is rather symmetric. However, in our model description of the atomic and molecular Zeeman effect the pattern of Zeeman splitting is always symmetric (see Sect. 5). Thus, for a geometrically symmetric field distribution and single lines, no RV shift can be introduced because the spectral line’s barycenter always remains constant. On the other hand, the symmetry of the appearance of several lines is broken as soon as line blending occurs. This can be seen in Fig. 3. Here, the difference between the two spectra is due to a change in the average field not restricted to a starspot. Because of line blending, the two spectra are now very different, and the barycenter of the merit-function (the cross-correlation function or the goodness-of-fit estimate) will be distorted, introducing a spurious line shift1. Deviations from the center of the non-distorted line may be significant on the m s-1 level, which is much less than 1/1000 of the line width.
Sign and amplitude of the RV shift depends on the sensitivity of the lines to the Zeeman effect but also on the amount of blending between different lines. Therefore, the apparent RV shift likely scatters between different wavelength bands and the net result is probably enhanced (random) jitter in the RV signal instead of a systematic RV offset like in the case of co-rotating spots. We calculate this effect and its limitations, predicting its amplitude in Sect. 6.3. To do so, we require accurate spectral line data and a realistic description of the Zeeman effect over wide ranges of the stellar spectrum. We describe the line data we use for our more sophisticated model in the next section.
 |
Fig. 4 Average Landé g factors for lines deeper than 2% of the continuum in the modeled spectra range (blue circles) together with rms scatter of all Landé g values considered in that region (error bars). The three panels show three different atmospheric temperatures as indicated in the figure. The low values at 2.3 μm are caused by the CO band. |
5. Model atmospheres and line data
For the detailed calculation of stellar spectral lines over large wavelength regions, we used the MARCS2 model atmospheres (Gustafsson et al. 2008) using three different models: Teff = 5750 K, log (g) = 4.5 (a solar-type star), Teff = 3700 K, log (g) = 5.0 (an early-M-type star of spectral type ~M1), and Teff = 2800 K, log (g) = 5.0 (~M6.5 star). For all models, solar abundances according to Asplund et al. (2005) were assumed. Our theoretical spectra were computed using the synmast code (Kochukhov 2007), which can treat atomic and molecular transitions in a magnetized medium.
Atomic line data were extracted from the VALD database (Piskunov et al. 1995; Kupka et al. 1999). The Landé g-factors were taken as provided by VALD or were computed using available term designations assuming the LS-coupling approximation.
The spectra of cool stars are dominated by molecular absorption. However, for most molecular lines the Zeeman effect is only poorly understood. The lack of laboratory measurements of Landé g-factors and the complex physics behind molecular line formation in plasmas with strong magnetic fields make it very challenging to accurately model spectra of these objects. For this work, we concentrate mostly on the effect of molecular FeH. We tested theoretically computed Zeeman patterns on observations of a number of M-dwarfs as described by Shulyak et al. (2010). FeH line data were taken from Dulick et al. (2003)3, and we used corrected line intensities and positions following Wende et al. (2010). We also included FeH lines in the range 1.0–1.7 μm using the same procedure for computing Landé g-factors as in Shulyak et al. (2010). In addition to FeH lines, we also included the line list of X1Σ+ CO transitions from Goorvitch (1994). The well-known 2.3 μm band of CO is often used for RV measurements because of its magnetic insensitivity (see, e.g. Bean et al. 2010).
We did not consider Zeeman splitting of molecular bands other than from FeH and CO. Thus, the present investigation is only an approximation of the effect of Zeeman splitting on RV signals; a complete model should include all molecular lines present in the stellar spectra. Nevertheless, FeH is the most important opacity source in near-infrared spectra of very cool stars, and we believe that the main effects from Zeeman splitting can be captured by our approach. Prominent molecular bands not included in our model are caused by, e.g., TiO, CH, OH, and MgH. Some of them are known to exhibit moderate or strong magnetic sensitivity, as discussed in Berdyugina & Solanki (2002). Since our main goal is to characterize the general behavior of RV signals by comparing different wavelength regions, and since a large part of the trends can be described neglecting detailed line list information (see Sect. 6), we see no reason why the addition of more molecular species would systematically change our results. Nevertheless, quantitative predictions about absolute RV distortions need to be interpreted with great care, bearing in mind the limits of our modeling approach. Including more magnetically sensitive lines will also result in stronger blending, hence implications from line blending presented in this work are probably lower limits.
Figure 4 shows a compilation of average Landé g-values used in our model spectra. For parts of 100 nm length, we calculated average Landé g-values taking into account all atomic and molecular lines stronger than 2% (neglecting line broadening due to surface motion and stellar rotation). The figure also visualizes the spectral regions we considered for our investigation, which are similar to the photometric bands V,I,Y,J,H, and K. Cooler stars show more molecular absorption than hotter stars do. This becomes apparent in the lower values of average Landé g-values since on average molecular lines have lower g.
6. Results
The mechanism causing an RV signal in an idealized spectral line through the Zeeman effect was demonstrated in Sect. 3. The amplitude of an RV signal occurring in a realistic spectrum will also depend on blending and the properties of lines contributing to RV information, foremost their Landé factors and central wavelength. The influence on RV measurements in real stars can therefore be expected to differ significantly from the results of our simple toy model. Furthermore, RV shifts from temperature contrast and from Zeeman splitting lead to amplitudes that are comparable in absolute values if calculated independently, but active regions on the Sun are magnetic and differ in temperature. In analogy to the solar case, we expect that the stronger magnetic fields on other stars are present in spots that are both cool and magnetic, but it is very difficult to assess realistic values for temperature and magnetic field contrasts. In the following, we first calculate the RV signature of a magnetic spot using not a single line, but synthetic spectra including several thousand atomic and molecular lines that are split because of the Zeeman effect. After that, we show a few example cases for magnetic, cool spots and the net RV signal from the two competing effects, and we calculate the RV signal of average magnetic field variations using synthetic model spectra.
6.1. Co-rotating magnetic spot
We calculated model spectra of rotating stars with magnetic spots as in our toy model above, but for the more realistic case we used spectra from our polarized radiative transfer code. As above, the cross-correlation function is calculated using the non-spotted (non-magnetic) star as a template and the star with a magnetic spot as our data set. For each case, we calculated the barycenter of the cross-correlation function in six wavelength areas of more than 100 nm each (see Fig. 4). Three stars of temperature T = 5750 K, T = 3700 K, and T = 2800 K are calculated, spot sizes of f = 1%,5%,10%, and 20%, and field strengths inside the spot of B = 100 G and 1000 G are used. The results are shown in Fig. 5.
 |
Fig. 5 Zeeman RV signature of co-rotating magnetic spots calculated from polarized radiative transfer over several wavelength bands. Stars and filled circles indicate the six wavelength bands where the RV signature was measured, a fit to the first five bands using a straight line is shown as a solid line for each case (the CO band is not included in the fit). Dashed lines show the scaling expected from our our toy model, i.e., a = 2 in Eq. (3). |
For our hottest example, the results from the synthetic model do not differ very much from the trends we found in our toy model using a single line with constant Landé g. In all cases, spots with magnetic fields of 1 kG introduce RV signals exceeding 1 m s-1 at all wavelengths. The scaling of Eq. (2) is a very good approximation to the situation seen in the case for T = 5700 K. In our cooler examples, however, the values we calculate from the synthetic atmosphere models show significantly less dependence on λ in the sense that the RV signal does not grow proportional to λ squared. Nevertheless, we can approximate the RV signal in all three examples using the formula 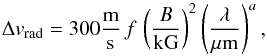 (3)with the relative fraction of the spot area, f, the magnetic field inside the spot, B, and the wavelength λ. The value of the constant results from the geometry of the surface and on the distribution of Landé factors across the wavelength range, but not on other free parameters. While a ≈ 2 in our hottest example (same value as in our toy model), we find a < 2 for cooler stars. The reason for this is clear from the distribution of Landé g-values shown in Fig. 4. While in the sun-like case (T = 5750 K) the typical Landé g-values are not a function of wavelength (the CO band being the only exception), Landé g-values are significantly lower at longer wavelengths in the cooler stars, partially compensating for the linear increase of the total Zeeman shift as a function of wavelength (see Eq. (1)). This is because at cooler temperatures, molecular lines become more and more important in relation to atomic lines, and (at least in our model) the molecular lines tend to have lower Landé g-values on average.
(3)with the relative fraction of the spot area, f, the magnetic field inside the spot, B, and the wavelength λ. The value of the constant results from the geometry of the surface and on the distribution of Landé factors across the wavelength range, but not on other free parameters. While a ≈ 2 in our hottest example (same value as in our toy model), we find a < 2 for cooler stars. The reason for this is clear from the distribution of Landé g-values shown in Fig. 4. While in the sun-like case (T = 5750 K) the typical Landé g-values are not a function of wavelength (the CO band being the only exception), Landé g-values are significantly lower at longer wavelengths in the cooler stars, partially compensating for the linear increase of the total Zeeman shift as a function of wavelength (see Eq. (1)). This is because at cooler temperatures, molecular lines become more and more important in relation to atomic lines, and (at least in our model) the molecular lines tend to have lower Landé g-values on average.
A central result of our simulation is that the RV signal because of a co-rotating spot of 1% the size of the projected stellar disk and a magnetic field strength of 1 kG has an amplitude of approximately 3 m s-1 if observed at λ = 1 μm. The amplitude scales linearly with filling factor and quadratically with both magnetic field strength and wavelength. In stars significantly cooler than the Sun, the scaling with wavelength is weaker than quadratic because the relevant spectral features are magnetically less sensitive.
 |
Fig. 6 Radial velocity amplitude due to co-rotating cool magnetic spots (f = 1%, B = 1000 G, v sini = 2 km s-1) using our synthetic atmosphere model for different star/spot temperatures. Black circles show the influence of temperature only (B = 0), red circles show the net effect including temperature contrast and Zeeman broadening in the spot. Blue crosses are average values and ranges for six wavelength bands. Green triangles show residuals between red and black circles, i.e., the effect caused by Zeeman broadening. Left panel shows a sun-like star with T = 5750 K, right panel shows an early M-type star with T = 3700 K. Top to bottom panels show different values of ΔT = Tstar − Tspot; top panel: ΔT = 200 K; middle panel: ΔT ≈ T/5; bottom panel: ΔT ≈ T/3. |
6.2. Cool and magnetic spot
In the preceeding sections and in Reiners et al. (2010), the effects of magnetic spots (at the same temperature as the photosphere) and of (non-magnetic) temperature spots were modeled independently. In reality, of course, spots are understood to be both magnetic and effectively cooler than the quiet photosphere. As a first approximation, we compared the two effects. We found that temperature and magnetic effects can cause RV signatures of comparable amplitude, but temperature effects are stronger at short wavelengths while magnetic influence is more significant at long wavelengths.
 |
Fig. 7 Radial velocity scatter caused by variable average magnetic field. Red circles show results from cross-correlation between spectra of a non-magnetic star and a star with an average magnetic field. Blue crosses and error bars show average and rms-scatter of individual chunks for six wavelength bands. Left panel: surface fraction f = 10% of the star is covered with magnetic field varying between 0 and 100 G; right panel: the entire star (f = 100%) shows magnetic field variability of 100 G. The small scatter at 2.3 μm is caused by the CO-band. Note the different scaling on the y-axis. |
The first-order approximation looking at each effect independently is probably not realistic because a low-temperature spot emits less flux than a hotter one, which will lead to a weaker influence of the Zeeman effect on the line profile and its dependence on wavelength. In order to consider the two effects in a consistent way, we calculated models of stars with spots that are both cool and magnetic, and we show the results of the RV amplitude in Fig. 6. In all cases, spot parameters are f = 1 % and B = 1000 G, the star is assumed to be rotating at v sini = 2 km s-1. We show results for a sun-like star with T = 5750 K and for a cooler (M-type) star with T = 3700 K; the T = 2800 K does not provide new information and we do not include it in this example. For spot temperatures, three cases are considered for each star: one with ΔT = Tstar − Tspot = 200 K (top panel), one with ΔT ≈ T/5 (middle panel), and a third with ΔT ≈ T/3 (bottom panel).
Our first result is that in all cases the net effect is a non-trivial combination of temperature contrast and magnetic Zeeman splitting. The two mechanisms work in the same direction; the total RV signal accounting for both effects is always stonger than the signal from one mechanism alone. The net effect reaches values up to the 10 m s-1 level. In our examples with the lowest spot/star temperature ratio (ΔT = 200 K), the RV signal monotonically grows with wavelength. In our intermediate cases of temperature contrast (ΔT ≈ T/5, center row), the net signal has a local minimum around 1 μm, it is dominated by temperature contrast effects at shorter wavelengths and by Zeeman splitting at longer wavelengths. In our examples with the highest temperature contrast (bottom panel), the wavelength dependence of the total RV signal is nearly constant with wavelength: in the sun-like star (bottom left), the RV signals from the temperature effect and from the Zeeman effect almost cancel; in the cooler star with the coolest spot (bottom right), the RV signal is always dominated by the temperature contrast. In the latter case, the spot contributes so little flux that the Zeeman signal is not significant even at the longest wavelengths used here. Interestingly, the signal from the temperature spot alone shows some scatter with wavelength that is not monotonic in λ and is produced by the temperature dependence of individual absorption lines that show different intensities inside and outside the spot region (cf. Reiners et al. 2010). For example, the CO lines in this case become deeper with lower temperature, which counteracts missing line absorption emerging from the spot area and leads to a reduced RV signal within the CO line region.
Even if the model we show in Fig. 6 includes radiative transfer of atomic and molecular spectral lines, and both the influence of temperature and Zeeman splitting, we are aware of the problem that our model is probably very different from any real star. Values of spot temperature and field strengths in our model are probably not unrealistic for some individual spots, but the real range in temperature and field strengths are largely unkown. Perhaps more important, active stars most probably are very different from a one-spot model and evolve in time. Therefore, we restrict ourselves to the examples shown in this section and do not attempt to make any more specific predictions on RV signals in active stars.
We conclude from our examples that in active stars, the influence of temperature contrast and the Zeeman effect can be of comparable amplitude, and that the details of spot distribution and their temperatures and magnetic fields determine amplitude and wavelength-scaling of the RV signature caused by activity. Thus, RV signals caused by active regions cannot be expected to vanish at infrared wavelengths. In contrast, in many stars the influence of starspots may be much more severe at longer wavelengths. The best way to discriminate between a planet and a starspot is therefore simultaneous measurement of RVs at many different wavelengths; even if the scaling of the RVs with wavelengths is difficult to predict, it is improbable that a signal caused by co-rotating active regions is independent of wavelength. Any wavelength-dependent signal will rule out companions as source, and the scaling with wavelengths will provide useful information on the nature of active regions.
6.3. Average field variations
Magnetic and cool spots on the surface of a rotating star introduce line profile variations as discussed above. Radial velocity signals caused by this effect are introduced by the deformation of all individual spectral lines and show the same period as the rotation of the star. Another effect caused by the Zeeman effect was introduced in Sect. 4 and is caused by systematic mismatch between large spectral regions observed at one time with respect to another observation. A possible reason for such a mismatch can be variation in the (average) magnetic field of a star, for example during a magnetic cycle. In a single line, average-field variability would not lead to a RV signal assuming symmetric Zeeman splitting (as always assumed here). In spectral regions containing many lines, however, an apparent shift may be introduced because lines are usually blended with others (see Fig. 3).
In Fig. 7, we show the results from cross-correlating a spectrum with no magnetic field with a spectrum of average field of Bf = 10 G (left panel) and Bf = 100 G (right panel). For field variations with respect to a non-zero field we expect similar results since Zeeman splitting is linear in B. The spectra are constructed assuming B = 100 G field strength in active regions homogeneously covering f = 10% (10 G case) and f =100% (100 G case) of the projected stellar disk. The examples represent the cases in which the average magnetic field varies by ΔB = 10 G and ΔB = 100 G, respectively. We show results from individual wavelength regions covering 10 nm each. In contrast to the cases with co-rotating spots, the RV shift does not follow a systematic pattern because the signal we measure here is a result of the random blending of broadened lines. On average, the signal is zero but variations in the field strength introduce scatter that depends on the properties of the field variations and wavelength. In Fig. 7, we show average values (blue crosses) and rms-scatter for wavelength bands containing several adjacent individual wavelength parts. As expected, we find that the average values of the RV shift is consistent with zero at all bands, but the rms grows with wavelength (an exception is again the CO band at 2.3 μm).
 |
Fig. 8 Zeeman-induced RV scatter for the case of variable average magnetic fields. Six cases are shown in which the fractional coverage of the field is between 1% and 100%. In that area, the field varies by 100 G. The scatter depends on wavelength and can be approximated by the dashed gray lines calculated from Eq. (4). |
In Fig. 8, the rms-values of the RV signal are displayed as a function of wavelength for the two models of Fig. 7 plus four more models with fractional coverage between f =1% and 100%. Note that the amplitude of rms scatter is given in cm s -1. We fit a power law to our results (gray dashed lines in Fig. 8) and find an approximation to the RV scatter introduced by variations in the average magnetic field:  (4)for ΔB = 100 G. This approximation is valid for all wavelength bands except the one containing the CO lines. For the ΔB = 10 G case, we find that while the effect is of course weaker than the one for ΔB = 100 G, there is no simple scaling relation that relates the cases of different ΔB. Nevertheless, we can conclude that additional scatter in RV measurements can be introduced by variable average magnetic fields. The uncertainty of a RV measurement at a given wavelength can be affected by field variability, but the amplitude of this effect is likely well below 1 m s-1 in realistic cases. Even stars with very strong magnetic fields are not believed to show variations in average field strength on the order of kilo-Gauss, and such stars would probably show very strong variability in chromospheric emission lines, too, which could help to identify such cases.
(4)for ΔB = 100 G. This approximation is valid for all wavelength bands except the one containing the CO lines. For the ΔB = 10 G case, we find that while the effect is of course weaker than the one for ΔB = 100 G, there is no simple scaling relation that relates the cases of different ΔB. Nevertheless, we can conclude that additional scatter in RV measurements can be introduced by variable average magnetic fields. The uncertainty of a RV measurement at a given wavelength can be affected by field variability, but the amplitude of this effect is likely well below 1 m s-1 in realistic cases. Even stars with very strong magnetic fields are not believed to show variations in average field strength on the order of kilo-Gauss, and such stars would probably show very strong variability in chromospheric emission lines, too, which could help to identify such cases.
7. An active star example: AD Leo
Our calculations predict that magnetically active stars may show wavelength-dependent RV variations with a stronger RV signal at longer wavelengths. For a first test of our results, we searched the HARPS-ESO archive for magnetically active stars with clear periodicities. A very clear and prominent example is AD Leo (Gl 388, Spectral Type M4.5Ve). HARPS observations on this star span a time baseline of 900 d and have a typical signal-to-noise ratio (S/N) of 50 at 600 nm. As reported by Bonfils et al. (2013), AD Leo shows a very strong periodic signal in the RVs at 2.22 d, which is consistent with the stellar rotation period found in the Zeeman Doppler imaging analysis by Morin et al. (2008). At the present time, 40 spectra are publicly available. We analyzed the data using the HARPS-TERRA software (Anglada-Escudé & Butler 2012). HARPS-TERRA derives RV measurements by least-squares matching each observation to a high S/N template generated by co-adding all available observations. It also allows one to obtain the Doppler measurement using a limited number of Echelle orders at a time, enabling the analysis of RV signals as a function of wavelength. To accumulate enough S/N to derive good quality RV measurements, we split the stellar spectrum into seven parts using 419, 450, 486, 528, 583, 631, and 665 nm as the central wavelength of each part. Except for the redder two parts, each part spans ten HARPS Echelle orders, that is: orders 10–19, 20–29, 30−39, 50−59, 60−66, and 68–71. The last two parts are chosen to avoid order 67 that contains Hα, which is highly variable in active stars. In all these parts, the 2.22 d period is clearly detected in the periodograms (Cumming 2004). The ten bluest echelle apertures (0–9) are not discussed here because the S/N is very low at the bluest orders (at the fifth echelle aperture it was typically below 5), and uncertainties associated to each individual RV were about 50 m s-1.
 |
Fig. 9 Upper panel: phase-folded RVs and fitted signals to the preferred Doppler period of 2.22704 d. The phase-folded fit to the BIS is also provided. For illustration purposes the BIS data have been shifted and multiplied by 10. Right panel: semi-amplitude K of the signal as a function of wavelength. The best fit to a linear model representing the wavelength dependence of K is given as a thick dashed line. The semi-amplitudes derived from the full spectrum (using CCF and HARPS-TERRA measurements) are also shown as solid brown circles. Note that both measurements provide incompatible results, which provides yet another test to assess the reality of a Doppler signal. |
In the upper panel of Fig. 9, we show our fit with period P = 2.22704 d to the RVs derived for each part. For simplicity, a sinusoid with the fixed period derived from the best fit to the RVs using the full spectrum (see top periodogram in Fig. 10) was adjusted to each part, so the only free parameters were amplitude and phase of the signal. In the lower panel of Fig. 9, we plot the derived semi-amplitudes as function of central wavelengths for each part. The uncertainties were derived using the bootstrap technique, i.e., computing the scatter of the amplitude as obtained by randomly selecting samples of the observations. The HARPS-data reduction software also provides a measure of the mean spectral line asymmetry, called the bisector span (BIS). This is a measure of the asymmetry of the cross-correlation function in RV space as obtained from cross-correlating the stellar spectrum to a binary mask (M2 binary mask, see Pepe et al. 2002). As demonstrated in several studies (e.g. Queloz et al. 2001), BIS often anti-correlates with spurious RV offsets if a cool spot is responsible for the apparent RV shifts. The BIS periodogram of AD Leo shows four peaks of similar power at 1.813, 1.950, 2.041, and 2.219 d (bottom panel in Fig. 10). These periods are all related through daily aliases (standard and sidereal day) and they likely correspond to the same physical periodicity. Since none of the BIS periods exhibits a false-alarm probability lower than 1%, the periods are subject to significant uncertainties; only an approximate match can be made when comparing the BIS measurements with those in the RV signals.
The photometric period (and, presumably, the rotation period of AD Leo) has been reported to be 2.23 d (Engle et al. 2009), favoring the period of 2.219 d as the most likely fundamental signal in the BIS. To see how it compares to the RV signal, we fixed the period of a sinusoid to the preferred RV period and adjusted the amplitude and phase of the BIS curve (see Fig. 9). Doing this we found that BIS appears to be anti-correlated with the RV curve, which is consistent with the expectations for a cool spot-induced signal. Note that, for visualization purposes, the BIS measurements in Fig. 9 were multiplied by a factor of 10 (and are offset). Also note that while the 2.22 d periodicity is clearly detected in the RVs, the F-ratios of the BIS candidate signals are 15 times lower and barely significant (see Fig. 10). We also looked at other activity indicators typically associated to spurious RV signals on M dwarfs (e.g., FWHM of the CCF or the S-index; see Lovis et al. 2011; Anglada-Escudé et al. 2012), but we did not find any further indication of a peak near 2.22 d.
 |
Fig. 10 Top: periodogram of the RVs obtained using the full spectral range of HARPS. Bottom: periodogram of the BIS. The 1% FAP threshold is illustrated as solid horizontal lines in both panels. The four peaks in the bottom panel are likely strong aliases of the same signal (2.22 days would be compatible with the photometric period of the star). Note that their average FAP is only 5%. |
Assuming that the Doppler signal is caused by cool spots (neglecting Zeeman broadening), one would expect its amplitude to become weaker at redder wavelengths. We obtained a weighted fit to our values of K shown in the bottom panel of Fig. 9 using a linear model of the form K [λ] = Aλ + b, where A is the slope and is measured in units of velocity per unit of wavelength (m s-1 μm-1). The obtained slope is 26.4 m s-1 μm-1, which is positive and different from 0 at a 5-σ level. Therefore, we conclude that the RV signal does not diminish toward longer wavelengths in the range covered by HARPS. Instead, the obtained wavelength dependence of the amplitude has a significantly positive slope with larger amplitudes K toward longer wavelengths. Our data do not extend into the infrared wavelength range, and we cannot reach any firm conclusion on the behavior of the RV signal wavelengths longer than 700 nm. Nevertheless, our example provides first evidence that the RV signal of an active star does not always diminish at longer wavelengths. Since RV signals from cool spots caused by temperature contrast alone are supposed to show a monotonic behavior across optical and infrared wavelength regions, we interpret this as evidence that another mechanism causes the positive slope of the RV curve. The results of this paper indicate that the Zeeman effect is the reason for this, and that the amplitude of this signal would be even larger at infrared wavelengths.
We note that the semi-amplitude derived from CCF measurements differs from the one derived from HARPS-TERRA RVs using the full spectrum; the result from CCF is K = 30.5 ± 1.0 m s-1, the result from HARPS-TERRA is K = 23.4 ± 0.9 m s-1. This indicates that the changes in the line shapes affect each method in a very different way, further indicating that the measured RV offsets are due to changes in the line profile shapes rather than real Keplerian signals. In conclusion, even in this example, in which we know the photometric period and see an anti-correlation between the RV with line asymmetries, the assumption that the RV signal is induced by the temperature contrast effects alone is likely to produce an incorrect interpretation of the data and can lead to the erroneous prediction that the spurious RV signal is suppressed at nIR wavelengths. This misconception would have serious consequences if one attempts to correct the RV curve for activity signals. Nevertheless, it is certainly true that Keplerian signals cannot be wavelength-dependent. If stellar activity on a timescale similar of a Doppler signal is suspected, only a comprehensive analysis of its wavelength dependence can shed light on its true physical origin.
8. Discussion
We have investigated the influence of magnetic activity on RV measurements in active stars. In contrast to earlier calculations, we included the Zeeman effect and calculated line barycenter shifts caused by spots that are cool and magnetic. Furthermore, we looked at the case of varying average magnetic fields that are not concentrated in co-rotating regions and may introduce signals not in phase with stellar rotation.
Our most important result is that co-rotating magnetic starspots can be expected to significantly distort stellar line profiles and RV measurements. Neglecting the cool temperature of the spots, the signal from the Zeeman effect alone easily exceeds the 1 m s-1 level even for very small active regions (f = 1%) and slow rotation (v sini = 2 km s-1) if the field inside the spot is comparable to sunspot fields (B ~ 1 kG). This signal has the same sign as the signal from a non-magnetic, cool spot, it grows with magnetic field as well as with wavelength, and is approximately four times stronger at λ = 1000 nm than at λ = 500 nm. Its amplitude saturates for very strong fields above approximately 1 kG. Comparable RV signals are also expected from the temperature contrast of cool spots alone (neglecting the Zeeman effect) as shown in earlier investigations, but they are strongest at short wavelengths. We note that the effect of Zeeman broadening on integrated (non-polarized) light is independent of magnetic polarity. Therefore, the RV signature does not depend on magnetic polarity, and in particular does not cancel out if magnetic areas consist of several spots with opposite polarity.
In contrast to the systematic fake RV signals from co-rotating spots, the RV signal caused by variable average (non-localized) fields is of statistical nature and only affects the noise floor of the measurements. The typical uncertainty of jitter induced by an average magnetic field that varies by 100 G is on the 10 cm s-1 level. No systematic signal is expected from variations in the mean magnetic field strength.
Including both temperature contrast and the Zeeman effect is necessary to understand RV signals in active stars. In case of strong contrast (very cool spots), the Zeeman effect is less important because the integrated spectrum contains less flux from the magnetic (spot) region. Nevertheless, since temperature contrast diminishes at long wavelengths and the influence of Zeeman broadening grows in the same direction, the RV signature of the Zeeman effect is significant in infrared observations of active stars. Thus, the RV signal of active stars does not vanish at long wavelengths, and infrared observations are not less affected by activity than observations at optical wavelengths. This may be particularly important for moderately active stars that could be populated by magnetic areas in a way similar to the Sun (Lagrange et al. 2010).
The magnetically insensitive CO lines in the K-band provide a notable exception. Their response to magnetic fields is so low that even strong fields do not substantially distort their line profiles. These CO lines can be very useful to disentangle RV variations caused by Keplerian orbits from magnetic activity. Unfortunately, the CO lines are contaminated by telluric lines, which introduces other problems when an accuracy on the m s-1 level is desired (Bean et al. 2010).
Radial velocity signatures caused by convective blueshift can also be significant in sun-like stars (Meunier et al. 2010). Their amplitude likely depends on line depth and therefore adds additional complexity to disentangling stellar activity from Keplerian signals.
It is very difficult to predict the dependence of the RV signal as a function of wavelength because it sensitively depends on the combination of spot temperatures and their magnetic field strengths. Both are poorly constrained by currently available data and simulations suggest that differences between solar and very cool star magnetic structures exist (Beeck et al. 2011). Simultaneous measurements of RV amplitude over large wavelength regions provides useful information for characterizing stellar activity, most importantly, starspot temperature and magnetic fields. In moderately active stars, the precision required for such a measurement is on the level of a few m s-1 for wavelength intervals of several hundred nm, which is a challenge for typical RV surveys. Simultaneous RV measurements at different wavelength bands are possible already in a few spectrographs and will become accessible over huge ranges with high-precision RV spectrographs operating at infrared wavelengths, as for example CARMENES (Quirrenbach et al. 2010) and SPIRou (Artigau et al. 2011). Data from these facilities will not only provide a reliable method to distinguish a Keplerian signal from magnetic activity, they will also allow a deep look into the magnetic and temperature structure of stellar surfaces.
The amplitude of this shift will in fact depend on the method used to locate the barycenter: fitting the dashed line in the inset in Fig. 3 will provide a different result than searching for the absolute maximum of that function.
Acknowledgments
A.R. acknowledges research funding from DFG grant RE 1664/9-1 and support by the European Research Council under the FP7 Starting Grant agreement number 279347, D.S. is supported by DFG research grant RE 1664/7-1, G.A.E. by the German Federal Ministry of Education and Research under 05A11MG3, and M.Z. by DFG research grant RE 1664/4-1. J.M. acknowledges funding as a Humboldt fellow. O.K. is supported by grants from the Knut and Alice Wallenberg Foundation and the Swedish Research Council.
References
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Arriagada, P., Vogt, S. S., et al. 2012, ApJ, 751, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Artigau, É., Donati, J.-F., & Delfosse, X. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 771 [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Barnes, J. R., Jeffers, S. V., & Jones, H. R. A. 2011, MNRAS, 412, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Bazot, M., Ireland, M. J., Huber, D., et al. 2011, A&A, 526, L4 [Google Scholar]
- Bean, J. L., Seifahrt, A., Hartman, H., et al. 2010, ApJ, 713, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Beeck, B., Schüssler, M., & Reiners, A. 2011, in ASP Conf. Ser. 448, eds. C. Johns-Krull, M. K. Browning, & A. A. West, 1071 [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Berdyugina, S. V., & Solanki, S. K. 2002, A&A, 385, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Pepe, F., & Queloz, D. 2001, A&A, 374, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cumming, A. 2004, MNRAS, 354, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, M. S., Aerts, C., Christensen-Dalsgaard, J., et al. 2007, A&ARv, 14, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Desort, M., Lagrange, A.-M., Galland, F., Udry, S., & Mayor, M. 2007, A&A, 473, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dulick, M., Bauschlicher, Jr., C. W.,Burrows, A., et al. 2003, ApJ, 594, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Engle, S. G., Guinan, E. F., & Mizusawa, T. 2009, in AIP Conf. Ser. 1135, eds. M. E. van Steenberg, G. Sonneborn, H. W. Moos, & W. P. Blair, 221 [Google Scholar]
- Fröhlich, C., & Lean, J. 1998, Geophys. Res. Lett., 25, 4377 [NASA ADS] [CrossRef] [Google Scholar]
- Goorvitch, D. 1994, ApJS, 95, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres [Google Scholar]
- Gray, D. F. 2009, ApJ, 697, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huélamo, N., Figueira, P., Bonfils, X., et al. 2008, A&A, 489, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kochukhov, O. P. 2007, in Physics of Magnetic Stars, eds. I. I. Romanyuk, D. O. Kudryavtsev, O. M. Neizvestnaya, & V. M. Shapoval, 109 [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Lagrange, A.-M., Desort, M., & Meunier, N. 2010, A&A, 512, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, A&A, submitted [arXiv:1111.5019] [Google Scholar]
- Mahmud, N. I., Crockett, C. J., Johns-Krull, C. M., et al. 2011, ApJ, 736, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V., Beichman, C. A., Catanzarite, J. H., et al. 2009, ApJ, 707, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, E. L., Guenther, E., Zapatero Osorio, M. R., Bouy, H., & Wainscoat, R. 2006, ApJ, 644, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Udry, S. 2008, Phys. Scripta T, 130, 014010 [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Meunier, N., Desort, M., & Lagrange, A.-M. 2010, A&A, 512, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2008, MNRAS, 390, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Mandel, H., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
- Reiners, A. 2012, Liv. Rev. Sol. Phys., 9, 1 [Google Scholar]
- Reiners, A., & Basri, G. 2007, ApJ, 656, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Basri, G., & Browning, M. 2009, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Bean, J. L., Huber, K. F., et al. 2010, ApJ, 710, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., Butler, R. P., & Marcy, G. W. 1998, ApJ, 498, L153 [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2000, A&A, 361, 265 [NASA ADS] [Google Scholar]
- Shulyak, D., Reiners, A., Wende, S., et al. 2010, A&A, 523, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Solanki, S. K., & Stenflo, J. O. 1984, A&A, 140, 185 [NASA ADS] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., Torres, G., Nordström, B., et al. 2009, Trans. Int. Astron. Union Ser. A, 27, 316 [Google Scholar]
- Vogt, S. S., Penrod, G. D. 1983, PASP, 95, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Wende, S., Reiners, A., Seifahrt, A., & Bernath, P. F. 2010, A&A, 523, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Sketch of the effect of a magnetic spot on RV measurements. Top: rotating star with large spot, covering 5% of the visible surface if observed at disk center, seen at three phases. The star is rotating with the spot approaching in the left column, centered in the middle column, and rotating out of view in the right column. Second row: stellar line profile broadened by rotation but without spot flux, showing the impact of a dark star spot. Third row: flux emerging from spot only, assuming the same temperature as in the photosphere. Row four: sum of surrounding and the spot region. Row five: radial velocity determined from fitting a Gaussian profile to the spectral lines in row four. In rows three to five, black solid lines show the case without a magnetic field (and zero spot temperature contrast). Blue and red dashed lines show cases in which the spot area has B = 1 kG and 2 kG, respectively (λ = 1.2 μm and g = 1.0). |
| In the text | |
 |
Fig. 2 Toy model RV signal caused by the Zeeman effect from a co-rotating magnetic spot with zero temperature contrast. The signal is calculated for three different field strengths inside the spot (green: 100 G, black: 600 G, and red: 4000 G); for each case three different spot sizes are used (f = 1%,3%, and 10%). Gray dashed lines show an analytical approximation of the scaling using Eq. (2). The dotted line visualizes the 1 m s-1 limit. |
| In the text | |
 |
Fig. 3 Example of apparent velocity shift in magnetically sensitive spectral lines. Black solid line: spectrum containing four lines of molecular FeH without magnetic fields in a T = 3700 K atmosphere; red dashed line: same spectral lines influenced by a magnetic field of B = 1000 G. Inset shows auto-correlation function of the field-free case (black solid line) and cross-correlation between field-free spectrum with magnetic case spectrum (red dashed line). |
| In the text | |
 |
Fig. 4 Average Landé g factors for lines deeper than 2% of the continuum in the modeled spectra range (blue circles) together with rms scatter of all Landé g values considered in that region (error bars). The three panels show three different atmospheric temperatures as indicated in the figure. The low values at 2.3 μm are caused by the CO band. |
| In the text | |
 |
Fig. 5 Zeeman RV signature of co-rotating magnetic spots calculated from polarized radiative transfer over several wavelength bands. Stars and filled circles indicate the six wavelength bands where the RV signature was measured, a fit to the first five bands using a straight line is shown as a solid line for each case (the CO band is not included in the fit). Dashed lines show the scaling expected from our our toy model, i.e., a = 2 in Eq. (3). |
| In the text | |
 |
Fig. 6 Radial velocity amplitude due to co-rotating cool magnetic spots (f = 1%, B = 1000 G, v sini = 2 km s-1) using our synthetic atmosphere model for different star/spot temperatures. Black circles show the influence of temperature only (B = 0), red circles show the net effect including temperature contrast and Zeeman broadening in the spot. Blue crosses are average values and ranges for six wavelength bands. Green triangles show residuals between red and black circles, i.e., the effect caused by Zeeman broadening. Left panel shows a sun-like star with T = 5750 K, right panel shows an early M-type star with T = 3700 K. Top to bottom panels show different values of ΔT = Tstar − Tspot; top panel: ΔT = 200 K; middle panel: ΔT ≈ T/5; bottom panel: ΔT ≈ T/3. |
| In the text | |
 |
Fig. 7 Radial velocity scatter caused by variable average magnetic field. Red circles show results from cross-correlation between spectra of a non-magnetic star and a star with an average magnetic field. Blue crosses and error bars show average and rms-scatter of individual chunks for six wavelength bands. Left panel: surface fraction f = 10% of the star is covered with magnetic field varying between 0 and 100 G; right panel: the entire star (f = 100%) shows magnetic field variability of 100 G. The small scatter at 2.3 μm is caused by the CO-band. Note the different scaling on the y-axis. |
| In the text | |
 |
Fig. 8 Zeeman-induced RV scatter for the case of variable average magnetic fields. Six cases are shown in which the fractional coverage of the field is between 1% and 100%. In that area, the field varies by 100 G. The scatter depends on wavelength and can be approximated by the dashed gray lines calculated from Eq. (4). |
| In the text | |
 |
Fig. 9 Upper panel: phase-folded RVs and fitted signals to the preferred Doppler period of 2.22704 d. The phase-folded fit to the BIS is also provided. For illustration purposes the BIS data have been shifted and multiplied by 10. Right panel: semi-amplitude K of the signal as a function of wavelength. The best fit to a linear model representing the wavelength dependence of K is given as a thick dashed line. The semi-amplitudes derived from the full spectrum (using CCF and HARPS-TERRA measurements) are also shown as solid brown circles. Note that both measurements provide incompatible results, which provides yet another test to assess the reality of a Doppler signal. |
| In the text | |
 |
Fig. 10 Top: periodogram of the RVs obtained using the full spectral range of HARPS. Bottom: periodogram of the BIS. The 1% FAP threshold is illustrated as solid horizontal lines in both panels. The four peaks in the bottom panel are likely strong aliases of the same signal (2.22 days would be compatible with the photometric period of the star). Note that their average FAP is only 5%. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


