| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 24 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201935315 | |
| Published online | 18 June 2019 | |
Magnetic fields in M dwarfs from the CARMENES survey
1
Max-Planck-Institute für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37075
Göttingen,
Germany
e-mail: shulyak@mps.mpg.de
2
Institut für Astrophysik, Göttingen Universität,
Friedrich-Hund-Platz 1,
37075
Göttingen,
Germany
3
Hamburger Sternwarte,
Gojenbergsweg 112,
21029
Hamburg,
Germany
4
Department of Geophysics, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University,
Tel Aviv
6997801,
Israel
5
Institut de Ciéncies de l’Espai (ICE, CSIC),
Campus UAB, c/ de Can Magrans s/n,
08193
Bellaterra,
Barcelona,
Spain
6
Institut d’Estudis Espacials de Catalunya (IEEC),
08034
Barcelona,
Spain
7
Landessternwarte, Zentrum für Astronomie der Universität Heidelberg,
Königstuhl 12,
69117
Heidelberg,
Germany
8
Instituto de Astrofisica de Andalucia (IAA-CSIC),
Glorieta de la Astronomia s/n,
18008
Granada,
Spain
9
Centro de Astrobiologia (CSIC-INTA), ESAC,
Camino Bajo del Castillo s/n,
28692
Villanueva de la Cañada,
Madrid,
Spain
10
Queen Mary University of London,
Mile End Road,
London
E1 4NS, UK
11
Departamento de Astrofisica, Universidad de La Laguna,
C/ Via Láctea s/n,
La Laguna,
Tenerife
38206, Spain
12
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778
Tautenburg,
Germany
13
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
14
Centro Astronómico Hispano-Alemán (CSIC-MPG), Observatorio Astronómico de Calar Alto,
Sierra de los Filabres,
04550
Gérgal,
Almeria, Spain
15
Instituto de Astrofísica de Canarias,
Vía Láctea, s/n E38205,
La Laguna,
Tenerife,
Spain
16
Departamento de Física de la Tierra y Astrofísica and IPARCOS-UCM (Instituto de Física de Partículas y del Cosmos de la UCM), Facultad de Ciencias Físicas, Universidad Complutense de Madrid,
28040
Madrid,
Spain
Received:
20
February
2019
Accepted:
14
April
2019
Context. M dwarfs are known to generate the strongest magnetic fields among main-sequence stars with convective envelopes, but we are still lacking a consistent picture of the link between the magnetic fields and underlying dynamo mechanisms, rotation, and activity.
Aims. In this work we aim to measure magnetic fields from the high-resolution near-infrared spectra taken with the CARMENES radial-velocity planet survey in a sample of 29 active M dwarfs and compare our results against stellar parameters.
Methods. We used the state-of-the-art radiative transfer code to measure total magnetic flux densities from the Zeeman broadening of spectral lines and filling factors.
Results. We detect strong kG magnetic fields in all our targets. In 16 stars the magnetic fields were measured for the first time. Our measurements are consistent with the magnetic field saturation in stars with rotation periods P < 4 d. The analysis of the magnetic filling factors reveal two different patterns of either very smooth distribution or a more patchy one, which can be connected to the dynamo state of the stars and/or stellar mass.
Conclusions. Our measurements extend the list of M dwarfs with strong surface magnetic fields. They also allow us to better constrain the interplay between the magnetic energy, stellar rotation, and underlying dynamo action. The high spectral resolution and observations at near-infrared wavelengths are the beneficial capabilities of the CARMENES instrument that allow us to address important questions about the stellar magnetism.
Key words: stars: low-mass / stars: magnetic field / stars: rotation / stars: atmospheres
© D. Shulyak et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
Magnetic fields are found in all types of stars throughout the Herzsprung–Russel diagram (Mathys et al. 2001). Among main-sequence stars with outer convective envelopes, M dwarfs are know to generate strong kG magnetic fields (Saar & Linsky 1985; Johns-Krull & Valenti 1996; Reiners & Basri 2007, 2010; Reiners et al. 2009). These fields are generated by convective dynamos that operate in stellar interiors and are powered by stellar rotation (Pallavicini et al. 1981; Pizzolato et al. 2003; Wright et al. 2011; Reiners et al. 2014). Dynamo-generated magnetic fields reach the surface of a star and initiate a number of phenomena that we call stellar activity: amongst others, stellar spots, plages, hot chromospheres, and coronae, which are observed indirectly via the analysis of, for example, emission lines, X-rays, photometric variability (e.g., Irwin et al. 2011; Newton et al. 2017) and radio emission (e.g., McLean et al. 2012).
Perhaps one of the most remarkable findings was establishing the so-called rotation-activity relation (Noyes et al. 1984; Kiraga & Stepien 2007; Reiners et al. 2014; Newton et al. 2017). A key feature of this relation is the existence of two distinct branches (or groups) of stars that show very different behavior of X-ray fluxes with stellar rotation. On the first branch the amount of X-ray flux decreases as rotation periods of stars increase as they spin down due to the magnetic braking. This is direct evidence that stellar rotation powers dynamo action in these stars. On the contrary, when the rotation period reaches a certain value of about four days (the exact value is actually a function of the stellar mass), the X-ray fluxes show no (or very marginal) dependence on rotation (Reiners et al. 2014). In this case, the stellar dynamo saturates and the amount of non-thermal energy released by a star reaches a certain limit. There might be several explanations for the observed phenomena, but it is generally believed that they are connected to the underlying dynamo (see discussion in Reiners et al. 2014).
Similar to the X-ray emission, Reiners et al. (2009) find the same two-branch behavior of magnetic flux densities with stellar rotation. In that paper, the value of the saturated magnetic field is not well constrained because of limitation of available analysis methods, but believed to be somewhere equal or slightly above 4 kG.
As analysis methods improved, it has become possible to measure magnetic fields in M dwarfs from a direct spectrum synthesis in atomic and molecular lines (Berdyugina & Solanki 2002; Afram et al. 2008; Shulyak et al. 2010, 2014). In their investigation Shulyak et al. (2017, Sh2017 hereafter) reported the detection of the magnetic fields well above the presumed saturated value in few M dwarf stars. The authors used rich spectropolarimetric observationsof a sample of stars obtained with ESPaDOnS (Canada-France-Hawaii Telescope) and NARVAL (Telescope Bernard Lyot) instruments and carried out magnetic field measurements from atomic titanium (Ti) and molecular iron hydride (FeH) lines. In particular, to date the strongest average magnetic field of about ⟨B⟩ ≈7 kG was reported for the fully convective star WX UMa, which questioned the concept of the magnetic field saturation. Furthermore, Sh2017 were able to measure magnetic fields in stars with large projected rotational velocities (υ sin i, where υ is the equatorial rotation velocity and i is the angle between the stellar rotation axis and the line of sight) from the effect of magnetic intensification of the well separated Ti lines located in the Z-band. Because many M dwarfs with short periods also have large υ sin i values, thesestars were previously excluded from the measurements of total magnetic fields thus biasing results toward stars with relatively small υ sin i values.
Combining their results of magnetic field strength measurements with the results from the polarimetric studies of global magnetic field geometries presented in Morin et al. (2010), Sh2017 find that the stars that generate strongest fields are also those with very simple, dipole-dominant magnetic field geometries, while stars with multipole-dominant global fields do not generate fields stronger than ≈ 4 kG. They also point out that from their limited sample (25 stars) it could be seen that the magnetic field in stars with dipole-dominated geometry does not show an obvious saturation effect. These findings provide the first observational evidence for the existence of two distinct dynamo states in M dwarfs that differ not only in the geometry of the large-scale magnetic field, which has been known since the extensive polarimetric campaign reported in Morin et al. (2010), but also in total magnetic energy generated. To explain the observed dichotomy of dipole- vs. multipole-dominant magnetic fields, an idea of bi-stable dynamo models is proposed and confirmed with dedicated simulations (Gastine et al. 2013). The finding of Sh2017 that the magnetic fields may not saturate in particular stars or that they saturate to a much larger values that previously thought needs to be confirmed through additional observations and theoretical models.
Motivated by our recent findings and availability of the new CARMENES instrument, in this work we have carried out the first magnetic field measurements from the high-resolution near-infrared spectroscopy in a subsample of stars with short rotation periods. Because CARMENES does not have the capacity to take polarimetry measurements, we performed measurements of the total magnetic flux density but we are not able to constrain dynamo states in our targets for which measurements of their fields are done for the first time. Therefore, our main goal is to constrain the relation between the magnetic field and stellar rotation and to mark targets with strong magnetic fields for future spectropolarimetric follow up campaigns.
2 Observations
The detailed description of the CARMENES instrument and the overview of the survey can be found in Quirrenbach et al. (2014); Alonso-Floriano et al. (2015); Reiners et al. (2018). CARMENES is the first high-resolution spectrograph that simultaneously covers the optical and near-infrared (NIR) wavelength range between 520 and 1710 nm. In two channels (VIS and NIR), the instrument provides data at a resolution higher than R = 80 000. In particular, the NIR channel covers the wavelength range 960–1000 nm that is essential for our analysis.
In this work we have concentrated on the subsample of 31 stars presented in Tal-Or et al. (2018) which we called the RV-loud sample. All these stars had at least 11 measurements over the last two years (2016–2017), projected rotational velocity of greater than two, and radial velocity scatter amplitude greater than ten (as measured from the visual arm of the instrument). Further details about RV-loud sample are summarized in Table 1 in Tal-Or et al. (2018). In this work we make use of the near-infrared arm of CARMENES because this is where our magnetically sensitive spectral features are located. The data reduction and wavelength calibration for the CARMENES spectra is done with the dedicated tool CARACAL (Caballero et al. 2016b), and the high-precision radial velocities are then computed using SERVAL package (Zechmeister et al. 2018). Additionally to radial velocities, SERVAL also produces a final co-added template spectrum of each star which is built from all available individual exposures. These templates represent a smoothed and oversampledversion of the stellar spectrum with rejected obvious outliers (cosmic rays, night sky emission lines, and others) and boosted signal-to-noise ratio (S/N). We also used these templates for some of our magnetic field measurements.
The NIR spectra from CARMENES are often affected by strong telluric absorption from atmospheric water. This is a challenge for our analysis because several of the Ti lines are at wavelengths close to telluric water lines. We rejected observations of Ti lines when contamination by telluric lines systematically affected our profile analysis.
In Table 1 we provide information on the number of individual exposures taken per star, number of used spectra after rejecting those with very low S/N and/or telluric removal artifacts, and the S/N of the finally co-added spectra that were used inthe analysis of the magnetic fields.
3 Methods
Our magnetic field measurements are based on the direct spectral synthesis of spectroscopic features subject to the photospheric magnetic fields. In order to predict observed line profiles we utilized the MAGNESYN spectrum synthesis code, which is the part of the LLMODELS stellar atmosphere package (Shulyak et al. 2004). The radiative transfer equation is solved in all four Stokes parameters for a given configuration of the magnetic field. Our approach to measure magnetic fields is mostly the same as in our early study of active M dwarfs presented in Sh2017.
There are two main problems that limit our analysis of cool star spectra. First, despite obvious improvements in molecular opacity, most of the spectra of M dwarfs are still far from being a satisfactory fit to the accuracy required by modern high-resolution spectrographs. Much of the background opacity is still missing, or not accurate enough. This becomes gradually worse in late-type M dwarfs where molecules dominate opacity in all spectral domains. Second, the line formation itself is not well understood because of uncertainties in model atmospheres and line broadening mechanisms. Therefore, it is very difficult to choose a proper set of spectral lines that would accurately separate effects of the magnetic field and atmospheric parameters (e.g., effective temperature, metallicity, rotation, etc.). Similar to Sh2017, we used lines of the FeH molecule at λλ 990–995 nm of the Wing–Ford F4 Δ − X4 Δ transitions, as well as Ti lines located at λλ960–980 nm. We chose FeH lines because they contain magnetically very sensitive and weakly sensitive lines, and the whole Wing–Ford band is virtually free from telluriccontamination. However, the fundamental problem with FeH lines is the absence of an accurate theory for the calculation of Landé g-factors (Asensio Ramos & Trujillo Bueno 2006; Berdyugina & Solanki 2002). Apart from a few examples (Harrison et al. 2008; Crozet et al. 2012, 2014), the laboratory measurements are not available for the lines that are most important for magnetic field analysis. On the other hand, the g-factors for Ti lines are accurately known and can be computed assuming standard Russell–Saunders coupling scheme. Unfortunately, these Ti lines do suffer from strong telluric contamination. In particular, the Ti I λ974.3 nm line is essential for disentangling magnetic broadening from the effects of metallicity and rotation because this line has zero magnetic sensitivity (i.e., effective g-factor geff = 0), but very often the profile of this line is severely distorted by a nearby telluric feature. A few more Ti lines are also affected by direct telluric hits. Therefore, it is essential to extract maximum information by using both FeH and Ti lines and cross checking consistency between the results. For that, we used semi-empirical Landé g-factors for FeH lines as described in Shulyak et al. (2010), and removed telluric contribution from Ti lines by direct modeling of telluric absorption with the MOLECFIT1 tool (Smette et al. 2015; Kausch et al. 2015).
Removing telluric features with MOLECFIT was done by fitting the atmospheric transmission model to the observed spectrum and adjusting mixing ratios of corresponding atmospheric gases, such as H2 O and CO2. The atmospheric temperature and pressure as a function of altitude for a given observing time were extracted from the Global Data Assimilation System (GDAS) database2. The other essential parameters such as, surface temperature and pressure, local humidity, and airmass, are taken from the fits files generated by the instrument software. Current version of MOLECFIT utilizes molecular line lists from the HITRAN database3. After the state of the Earth’s atmosphere has been defined, the code runs Levenberg-Marquardt χ2 -minimization algorithm to find best fit molecular number densities. The code can also fit polynomials of different orders for the normalization of the transmission spectrum. Once the best fit parameters have been found, the observed spectrum is divided by the predicted transmission model. This procedure was applied to each individual CARMENES exposure. The accuracy of the telluric removal depends strongly on the S/N of the data and atmospheric humidity. For instance, if telluric lines are deep then even small mismatch between model and observations in line cores may give rise to strong artifacts after spectra division. Therefore, the application of the same procedure to spectra obtained at different seasons and/or different observatories can lead to deviations the spectra corrected for atmospheric transmission.
In stars with large projected rotational velocities, the rotational broadening dominates the shape of line profiles, which means that narrow and dense FeH lines become strongly blended and it is difficult or even impossible to accurately constrain the strength of surface magnetic fields from FeH lines alone. To the contrary, Ti lines are well separated from each other and remain unblended even with largest υ sin i’s found in M dwarf stars. Strong telluric contamination is the only reason these lines were never used in magnetic field studies. However, if telluric contamination can be accurately removed, these lines become perfect probes of magnetic fields in fast rotating stars because one can use the effect of magnetic intensification to measure magnetic flux density. For instance, in the case of a saturated spectral line, its equivalent width will be proportional to the intensity of the magnetic field and the number of individual Zeeman components, so-called Zeeman pattern (Landi Degl’Innocenti & Landolfi 2004). Therefore, at large υ sin i the depths of individual spectral lines subject to strong magnetic field will depend on their Zeeman patterns. The lines of Ti in λλ 960–980 nm region all have very different Zeeman patterns and thus one can fit their depths to measure intensity of the magnetic field (provided that other stellar parameters are known). The obvious caveats in this analysis is that the magnetic intensification (to a certain degree) can be mimicked by other effects, such as, for example, metallicity or temperature effects: changing either of them will make lines look deeper or shallower, so that one can always satisfactorily fit a magnetically sensitive line with a non-magnetic model by adjusting atmospheric parameters. Therefore, using the magnetic insensitive Ti I λ974.3 nm line is the only way to break this degeneracy because it helps to constrain stellar parameters separately from the magnetic field. From the magnetic intensification we can only measure magnetic fields that are strong enough to noticeably affect the equivalent widths of spectroscopic lines. Nevertheless, this effect opened a way to measure magnetic fields in stars with extreme υ sin i values that was for many years believed impossible (Kochukhov & Lavail 2017; Sh2017).
Our approach is to measure magnetic flux density from unpolarized light (i.e., Stokes – I). This way we can capture the magnetic fields that are organized at both large and small scales. However, the geometry of the magnetic field remains unconstrained, meaning that we are blind to the sign of the field that we are looking at. To address this question one would need additional polarimetric observations with another instrument(s). Still, strong surface magnetic fields in stars with convective envelopes originate from spots and other active regions that differ in, for example, size or number, distorting profiles of spectral lines differently from a case where the magnetic field was homogeneously distributed over the stellar surface. This gives us a possibility to measure what we call the complexity of surface field by assuming a distribution of magnetic field components |B|i each covering a particular portion of the star represented by filling factor fi. The total magnetic field is then a simple sum ⟨B⟩ = ∑ |B|ifi. We used the Levenberg–Marquardt minimization algorithm to find best fit values of filling factors for a given combination of atmospheric parameters. We simultaneously processed rotational velocity, atmospheric abundance of a given element, continuum scaling factor for each spectral region that we fit, and 11 filling factors distributed between 0 and 20 kG as free parameters. The continuum scaling factors are needed to account for possible mismatch between observed and predicted spectra that may originate from, for example, artifacts left after flat fielding and/or order merging, missing molecular opacity, uncertainties in model atmospheres, amongst others. We note that because the stellar continuum cannot be accurately defined, especially in late type M dwarfs with strong absorption caused by numerous photospheric water lines in the vicinity of our Ti lines, we fit a low order polynomial to each CARMENES echelle order prior to merging them into single 1D spectrum. This spectrum is thus normalized to stellar pseudo-continuum, but small offsets could still be present and we account for them in our fitting approach with additional scaling factors.
Similar to Sh2017, we computed theoretical line profiles using MARCS model atmospheres (Gustafsson et al. 2008). The effective temperatures of our sample stars were computed from their spectral types employing dedicated calibrations (Kenyon & Hartmann 1995; Golimowski et al. 2004). We took spectral types from the CARMENCITA database (Alonso-Floriano et al. 2015; Caballero et al. 2016a). The other parameter – surface gravity log (g) – was calculated from the stellar radii and mass assuming R ∝ M0.9 relation which provides surface gravities close to those predicted by stellar evolution models (Dotter et al. 2008; Bressan et al. 2012). We did not use effective temperatures and surface gravities from Passegger et al. (2018) because they were not able to derive such parameters for the most active and fastest rotating CARMENES stars, which just comprise our sample.
The transition parameters of Ti lines were extracted from the Vienna Atomic Line Database (VALD; Ryabchikova et al. 2015), and for FeH lines we used molecular constants taken from Dulick et al. (2003)4. Transition probabilities for some of these lines were corrected according to Wende et al. (2010).
Also, similar to Sh2017, we treated pressure broadening by including contributions from hydrogen and helium only and ignore contribution from molecular hydrogen H2 because it grossly overestimates the observed widths of atomic lines especially at late spectral types (see, e.g., Pavlenko et al. 2007). Another source of line broadening is the velocity field caused by convective motions. However, as shown by 3D hydrodynamic simulations (Wende et al. 2009), the velocity fields in atmospheres of M dwarfs with temperatures Teff < 3500 K are well below 1 km s−1. This has a weak impact on line profiles, leaving the Zeeman effect and rotation to be the dominating broadening mechanisms. Therefore, we assumed zero micro- and macroturbulent velocities in all calculations.
The filling factors that we derive with our method sometimes show high-field magnetic components. A characteristic example is illustrated in Fig. 1, where we show the filling factors of J12156+526as derived from the Ti lines. Here we derive a very smooth distribution of filling factors between 0 and 10 kG, but then we also find two stand-alone magnetic field components at the tailed 18 and 20 kG, respectively.As mentioned in Sh2017, these components result from the code trying to fit details in observed line profiles originated from the poor data quality and/or bad understanding of background molecular absorption. The filling factors of these components are small, but they contribute a significant fraction to the final result: ignoring them drop the average magnetic field from 5.5 to 4.5 kG, respectively.We note that the magnetic components with strongest field appear always irregardless of the choice of the limiting magnetic field. In other words, it does not matter if one truncates the final magnetic component to, for instance, 15 kG instead of 20 kG because the 15 kG magnetic component will then simply appear to have a large filling factor etc. We also were not able to use too few magnetic field components because we would under-fit profiles of spectral lines. Because we have no physically motivated reason to believe that these high field components truly exist, we ignored them in our estimates of stellar magnetic fields.
While the initial guess for abundances and υ sin i does not have a strong impact on the final results, this is not always the case for filling factors. Again, we find that this is more often an issue for stars with poor data quality. Interestingly, even if filling factor distributions look different, the total magnetic field strength is usually not affected much (with a scatter on the order of a few hundred Gauss in our sample). The stars for which the initial guess of filling factors also affects the resulting field strength are those with υ sin i > 20 km s−1 and only when we derive fields from FeH lines. This is expected because strong blending of FeH lines and uncertainties in their transition and magnetic parameters act together contributing to the uncertainty of the results.
Summary of observations.
 |
Fig. 1 Example of magnetic filling factors of J12156+526 as derived from Ti I lines. Original distribution contains high field components (left panel), and ignoring them with subsequent re-scaling of the rest of filling factors drops the average magnetic field by 1 kG (right panel). |
Magnetic field measurements.
4 Results
Our present sample comprises of 29 active stars with short rotation periods ranging between 10 and 0.1 d. Among them, there are 16 objects without previous magnetic field measurements, and 5 objects with υ sin i > 30 km s−1. Two stars, J18356+329 and J19255+096, were excluded from the analysis because of poor data quality (see Table 1). We summarize our magnetic field measurements in Table 2 and describe them in detail below. In addition, we provide our model fits to individual spectral lines in Appendix A (Figs. A.1–A.29). We note that because filling factors are correlated parameters, it was not possible to estimate robust error bars on the values of the magnetic field strength and filling factors from our approach. Besides, the formal errors from the chi-square fit on the parameters are likely underestimating the true uncertainties because of additional sources of uncertainties such as, choice of the spectral lines, accuracy of the telluric correction. It appears very difficult to quantify all possible sources because we would need to run a lot more individual measurements for each star which is very computationally demanding. Therefore, similar to our previous works we put a conservative 1 kG error bars on measured magnetic fields in stars with υ sin i > 20 km s−1. For the rest of the sample we provide uncertainties on the derived magnetic fields as a difference between measurements from FeH and Ti lines, similar to Sh2017.
4.1 Magnetic fields of sample stars
In Fig. 2 we compare magnetic fields measured from Ti and FeH lines, respectively. In general, we obtain very consistent estimates of the magnetic fields from Ti and FeH lines in stars with good data quality and relatively small υ sin i values, such as, for example, J03473-019, J05365+113, J07446+035, J15218+209, and J22468+443 (see Table 2). Thus, despite of telluric removal problem and uncertainties in magnetic g-factors, both Ti andFeH lines can be successfully used for the magnetic field measurements.
At the same time, for stars J06000+027 and J18498-238 we obtain very different estimates even though the data for these stars look relatively good and their υ sin i values are relatively small, too (see Table 2). We note that in these stars we measure systematically higher υ sin i from Ti lines compared to FeH lines and hence lower values of magnetic fields, which can partly be due to the distortion of the magnetic insensitive Ti I λ974.3 nm line by telluric removal procedure. If we fixed υ sin i in these stars to the lower values (i.e., to the values derived from the fit to FeH lines) we always obtain estimates close to that derived from FeH lines. It is thus possible that inaccuracies in υ sin i values can explain the observed discrepancy in derived magnetic fields in these objects.
In three stars we find a deviation of more than 1 kG between measurements from Ti and FeH lines, and we marked them with their names in Fig. 2. The largest deviations of 2.4 kG is found in J17338+169. In this star the red wing of the Ti λ974.3 nm line is affected by telluric removal artifact (see Fig. A.19). Alternatively, we used different individual spectra to fit this line and obtained a weaker field of ⟨B⟩ = 6 kG with higher υ sin i = 39 km s−1 instead of ⟨B⟩ = 6.9 kG, but the large deviation between measurements from Ti and FeH still remained. In J01352-072 the fit to FeH spectrum is very inaccurate. In addition, we were only able to use half of the region covered by FeH lines. At the same time, our fit to Ti lines is much more accurate. In J18189+661 we could not accurately remove telluric feature from the Ti I 974.3 nm line that made this line look deeper. As a result, we measured an overestimated Ti abundance and hence a weaker magnetic field from Ti lines compared to that from FeH lines.
In stars with rotation velocities υ sin i > 20 km s−1 we often (but not always) measure weaker fields from FeH lines compared to Ti lines. The same effect was observed and explained in Sh2017 as being likely caused by strong line blending which leads to the degeneracy in fitting parameters (i.e., temperature, abundance, rotation). The results of these measurements depend strongly on data quality and set of FeH lines used for the analysis. Especially in fast rotating stars the result of our measurements from Ti lines must be preferred over values derived from FeH lines.
 |
Fig. 2 Comparison between the magnetic field measurements from Ti and FeH lines with υ sin i color coded. Dashed and dash-dotted lines represent 1 and 2 kG deviations from the central line, respectively. |
4.2 Comparison with previous measurements
Our sample contains 12 objects withpreviously measured magnetic fields, in nine of which we find a good agreement between literature values and our measurements. Stars for which our new measurements disagree with previous results are J01033+623, J15218+209, and J19169+051.
In J01033+623, Sh2017 measured a field of ⟨B⟩ = 6.1 kG from the ESPaDOnS data, while from CARMENES data we derive much weaker ⟨B⟩ = 4.8 kG. This is because now we derive more smooth distribution of filling factors with a reduced 12 kG component. If we exclude this component from our fit to ESPaDOnS data we get very close ⟨B⟩ = 5 kG average field, but then the fit to the data looks worse. The same discrepancy is found for FeH lines, and at this point it is difficult to decide which of the fit should be preferred.
In J15218+209 we find a 0.5 kG stronger field from CARMENES data both from Ti and FeH lines, but our FeH spectrum is very noisy. The difference in measured magnetic field from Ti lines could be explained by quite different, that is, we measure υ sin i = 3.9 km s−1 and υ sin i = 4.9 km s−1 from CARMENES and ESPaDOnS spectra, respectively. We find that the higher υ sin i measured from the ESPaDOnS data is likely due to the telluric removal artifact that affected the profile of the magnetic insensitive Ti I λ974.3 nm line which made it broader in ESPaDOnS data.
In J19169+051S we measure a stronger field of ⟨B⟩ = 2.2 kG compared to previous estimate of ⟨B⟩ = 1.3 kG from Reiners & Basri (2007). Our fit to Ti lines in this star was not very accurate because we could use only four lines and the observed line profiles were affected by surrounding strong molecular features prominent at these cool temperatures. On the other hand, FeH spectrum looks better and from them we derive still field of ⟨B⟩ = 2.4 kG. We note that Reiners & Basri (2007) measured field in J19169+051S indirectly, that is, without employing radiative transfer models, which could explain the difference in the magnetic fields between their and our measurements. On the other hand, our understanding of line formation in cool temperatures of late type M dwarfs is far from been satisfactorily understood. Uncertainties in, for example, molecular broadening can bias our results. This question needs to be addressed on a larger sample of stars.
4.3 Complexity of surface magnetic fields
We used magnetic filling factors in our attempts to measure magnetic fields because complex shapes of magnetically sensitive spectral lines in M dwarfs can not be represented by a single magnetic field component. In order to recover accurate distributions of filling factors data with very high S/N are required. Moreover, filling factors are sensitive to the available magnetic information (i.e., set of spectral lines) and atmospheric parameters (especially elemental abundance and rotation broadening). Therefore, the filling factors presented in this paper should be taken with caution, at least for fast rotating stars. The results are shown on Figs. 3 and 4 as derived from Ti lines.
Our filling factors seem to show two distinct patterns. We detect either very smooth distributions (e.g., J01033+623, J07446+035, J08298+267 – Fig. 4, J12156+526 – Fig. 3), or more patchy patterns with distinct dominant magnetic field components (e.g., J02088+494 – Fig. 3, J16555-083, J22012+283 – Fig. 4, J18022+642, J18189+661 – Fig. 3). In our sample there are four M dwarfs that, according to their spectral types (SpT < M3.5), should have partly convective envelopes (J03473-019, J05365+113, J15218+209, J22518+317), while the rest should be fully convective objects. However, we do not observe an obvious change in the complexity of the fields between these two groups. For instance, the distribution of filling factors in partly convective J03473-019 and J22518+317 (Fig. 3) can be compared to, for example, those of fully convective J19169+051S (Fig. 4) and J19511+464 (Fig. 3). The only noticable feature is that fully convective stars tend to have stronger average magnetic fields represented by magnetic components of stronger strength. For instance, in the hottest partly convective star J05365+113(Fig. 3) we derive a very weak magnetic field with only two magnetic components (0 and 2 kG, respectively).
In our sample, we find several objects with remarkably very similar properties of their magnetic fields. For the two stars with largest υ sin i values, J01352-072 (Fig. 3) and J04472+206 (Fig. 3), we recover the same average magnetic fields with identical filling factors. The only difference between these stars is that J04472+206 is one spectral type cooler. Next, we find a twin of J07446+035 (very well studied M dwarf YZ CMi, Fig. 4), which is J23548+385 (not studiedat all, Fig. 3). Both stars have very similar filling factors, average magnetic field, projected rotational velocities, but slightly different spectral types. In addition, another famous M dwarf J22468+443 (EV Lac) has filling factors similar to J07446+035 and J23548+385, although its average magnetic field is noticeably weaker.
We next looked for a connection between our filling factors and the geometry of large scale magnetic fields. In our sample, we have nine stars for which the geometry of their surface magnetic fields was previously derived from polarimetric measurements. In particular, Morin et al. (2010) showed that partly convective M dwarfs tend to have complex multipole fields with strong toroidal contribution, while stars that are fully convective generate dipole-dominant predominantly poloidal magnetic fields. Following this classification, in Fig. 4 we grouped M dwarfs in columns depending on whether the star has dipole-dominant magnetic field (left column) or more complex multipole-dominant field (right column). One can see that there is no obvious difference in filling factors between these two groups. A smooth distribution is found for dipole-dominant J01033+623 on one side, and multipole-dominant J08298+267 and J19169+051S on the other side. Likewise, J07446+035 and J22468+443 have almost identical filling factors but their magnetic field geometries were found to be very different. Nevertheless, there seems to be one common feature that is intrinsic to complex multipole fields as observed from filling factors, which is the appearance of strong zero-field components. This zero-field component is strongest in four out of five stars with multipole-donimant fields with an exception of J22468+443.
 |
Fig. 3 Distribution of filling factors as derived from Ti lines. The stars are sorted according to the S/N of their spectra (S/N decreases from left to the right and top to bottom). |
 |
Fig. 3 continued. |
4.4 Magnetic field and rotation
The detection of very strong magnetic fields in M dwarfs needs to be understood in terms of underlying dynamo processes. Because dynamos in these stars are powered by convective motions subject to stellar rotation, it is essential to compare our magnetic field measurements with rotation periods which we plot in Fig. 5. We also plot measurements from Sh2017 and other literature sources for stars that are not in our sample. We also include recent measurements of the magnetic field in the eclipsing binary system YY Gem (Kochukhov & Shulyak 2019). The rotation periods are from Díez Alonso et al. (2019) and Morin et al. (2010 and references therein).
The general pattern of increasing magnetic field strength as period decreases down to about P ≈ 4 d is evident from Fig. 5. When M dwarfs rotate faster, the regime becomes activity saturation in terms of X-ray fluxes (Noyes et al. 1984; Reiners et al. 2014). The magnetic field strength in this regime show large scatter with values between 2 and 7 kG. The magnetic field in GJ 3622 was measured in Sh2017 and its magnitude seems to be too weak as for the rotation period of P = 1.5 d. It is thus important to obtain new magnetic field measurements for this star in future studies.
From Fig. 5 it is difficult to see a well defined trend of the magnetic flux density increasing with rotation for periods below four days. We are currently lacking accurate magnetic field measurements in stars with ultra-short periods and our current results are consistent with the generally accepted conclusion that the magnetic flux density saturates in stars with saturated activity. More work needs to be done to fully address this effect.
5 Discussion
5.1 Magnetic filling factors
From our analysis of filling factors we find two distinct patterns in their distribution. The first pattern is a very smooth distribution of filling factors and the second looks more patchy and can not be approximated by a smooth function. It is difficult to find strict connections between patterns in our filling factors and other essential stellar parameters such as rotation or temperature. However, it is possible to draw some preliminary conclusions.
First, we find no clear difference in patterns of filling factors between fully and partially convective stars. However, we observe that fully convective stars tend to have stronger average magnetic fields represented by stronger magnetic components. This reflects the conclusion already drawn in previous investigations that fully convective stars generate on average stronger surface magnetic fields (Reiners & Basri 2007).
Second, there seems to be no pronounced difference in filling factors for stars that are known to have different geometries of their large scale fields. Our Fig. 4 suggests that stars with multipole-dominant fields seem to have stronger zero field magnetic component compared to stars with dipole-dominant fields. This is an interesting observation because it may tell us that these stars have different spot distributions and, perhaps, spot sizes on their surfaces compared to stars with dipole-dominant fields. For instance, spots that are present in a few small localized areas on a visible disk of the star while the rest of the photosphere is non-magnetic would result in strong zero field component. On the contrary, a large spot or groups of spots around magnetic poles that occupy considerablefraction of the stellar disk would have a reduced zero field component or even none if observed at small inclination. Recent analysis of stellar spots in a binary system Gl 65-AB seem to support this idea (Barnes et al. 2017). It would be thus interesting to combine polarimetric and photometric techniques to address this question in future.
Another remarkable finding is the detection of twins in our sample. In stars J01352-072 and J04472+206 we recover same average magnetic fields with identical filling factors. The other twins are J07446+035 and J23548+385. These stars have very close υ sin i’s, spectral types, average magnetic fields, and pattern of filling factors. Because J07446+035 has stable dipole-dominant magnetic field geometry (Morin et al. 2008) we predict that this should be the same for J23548+385. However, for J22468+443 with a multipole-dominant field, we also derive filling factors that look surprisingly similar to those of dipole-dominant J07446+035. A possible explanation would be just a coincidence because J22468+443 has complex variable magnetic field and it might just have happened that the star was observed when its surface field was simple. Because the spectra of J22468+443 has very high S/N, we looked for a possible seasonal magnetic field variation between spectra obtained in 2016 (June–December) and 2017 (January–October). For each year, we co-added individual spectra to build a high S/N template as described in Sect. 3. We find that line profiles of Ti did not show any significant changes, as can be seen from the top panel of Fig. 6 where we plot spectra obtained in 2016 and 2017 around three magnetic sensitive Ti lines. We also derive filling factors for these two data sets and found them to be very similar with only marginal change in the total magnetic field strength, as illustrated in the bottom panel of Fig. 6. We note that J22468+443 was observed to have very strong variability of the large scale component of its magnetic field with large areas of positive and negative fields located in the same hemisphere (see Fig. 4 in Morin et al. 2008). Such features have never been detected in stars with dipole-dominant fields (e.g., WX UMa, AD Leo, and Gl 51) and thus we still place J22468+443 in the group of stars with complex multipole fields. Additional spectropolarimetric measurements will surely help to address this question in more detail.
Next, with certain exceptions we can conclude that M dwarfs of spectral types around M7.0 and later tend to have smooth distributions of their filling factors with obviously dominant zero-field magnetic component like, for example, J08298+267 and J19169+051S, with an exception of J16555-083 which shows more patchy filling factors pattern (Fig. 4). If confirmed with future studies, this would imply that magnetic dynamo in stars at the very cool end of the M-type sequence fails to generate large spots and perhaps decays out because temperatures of this objects are too cool to support efficient dynamo action.
In stars with large υ sin i > 20 km s−1 we usually find smooth distribution of filling factors that peak at non-zero magnetic field component. This could mean that the stars have simple dipole-dominant magnetic fields, that is, consistent with what one would expect in fully convective objects with short rotation periods.
In this work we have not studied the rotational variability in individual line profiles which could be caused by variable magnetic field strength over the stellar surface. This variability could be seen in stars with largest υ sin i values due to a better spatial resolution provided by the Doppler broadened line profiles. The first evidence of such variability was reported in Kochukhov & Lavail (2017) for the B component of the binary system Gl 65. At the same time, no line profile variability was recently detected by Kochukhov & Shulyak (2019) in another fast rotating binary YY Gem, possibly implying that the variability is very weak due to a different distribution of small scale magnetic fields over the surface of these stars compared to the case of Gl 65 B. Unfortunately, the S/N of individual spectra for our stars is much lower than those used in both mentioned above studies and we could not detect any significant variability above the photon noise limit. This also implies that the total magnetic field strength remains very much stable over the time spawn of our observationsand does not bias our analysis. However, it is no doubt important to study line profile variability in future studies.
 |
Fig. 4 Distribution of filling factors as derived from Ti lines for stars with known geometry of their large-scale magnetic fields. Left column: dipole-dominant, right column: multipole-dominant. |
 |
Fig. 5 Average magnetic fields in stars from our sample as a function of rotation period. Measurements in stars with known dipole and multipole states are shown as solid upward- and downward-pointing triangles, respectively. Stars with unknown dynamo states are shown as solid blue circles. Our measurements from this work are shown with blue color and the literature values are shown with the red one. The symbol size scales with stellar mass (see legend on the plot). The horizontal dashed line marks the 4 kG threshold of saturated magnetic field assigned to stars with multipole dynamo regime. Similar to our previous works we include conservative 1 kG error bars onmeasured magnetic fields in stars with υ sin i > 20 km s−1. |
5.2 Magnetic field and rotation
Our new measurements add nine new objects to the set of stars having very strong fields above 4 kG and one object (J05365+113) to the subsample of stars with long rotation period and weak fields. From Fig. 5 one can still see a large scatter in magnetic fields for stars with periods shorter than 4 d and it remains inconclusive whether magnetic fields keep growing as periods decrease or do they saturate to some maximum magnetic field which could be defined by the stellar dynamo state, as suggested in Sh2017. Additional measurements are clearly needed. In particular, it is needed to analyze stars with ultra-short rotation periods P < 0.3 d.
Another important property of stellar magnetic fields is the geometry of their large scale components. The current understanding of stellar magnetism predicts complex multipole-dominant magnetic fields in partly convective M dwarfs and more simple, dipole-dominant fields in stars that are fully convective (Morin et al. 2010; Gastine et al. 2013). However, there are cases of a fast rotating fully convective object that generate complex mostly multipole fields (e.g., DX Cnc, GJ 1245 B, and Gl Vir). Rotation alone can not explain this observation because both types of geometries are found in stars that have similar spectral types and rotation periods. It is believed that dynamo in M dwarfs (at least when they are fully convective) become bi-stable and the choice of the dynamo state is somehow linked to the properties of the initial magnetic field that existed during the star formation (Gastine et al. 2013). Furthermore, when the rotation decreases (e.g., due to the magnetic braking), a fully convective star may change its dynamo state from a stable dipole-dominant to a variable complex magnetic field thereby developing magnetic cycles, that is, the magnetic field geometry will vary with time (Yadav et al. 2016).
From our CARMENES data we do not have information about the geometry of the magnetic fields in our stars, but from our measurements we find objects with very strong fields and fast rotation so we predict that they should have dipole-dominant fields. It is therefore essential to follow up these stars with spectropolarimetric observations. This would help to better constrain the connection between field intensity, geometry, and the rotation of the star.
There are many more potential applications of our findings, as magnetic fields play critical role in all stages of stellar and even planetary evolution. For instance, knowing magnetic properties of stars is one of the pieces in the puzzle called stellar activity and includes understanding connections between the magnetic fields, rotation braking, stellar spots, X-ray fluxes, and finally understanding the hazardous environment around planets orbiting these active stars (Vidotto et al. 2015; Garraffo et al. 2017). Very strong magnetic fields may even have a direct impact on the planetary structure by providing additional source of energy via the induction heating (Kislyakova et al. 2017, 2018). Especially M dwarfs with dipole dynamo states are interesting objects in this regard because they maintain stable large scale magnetic fields whose energy decay with a separation to the star much slower compared to stars with multipole-dominant fields. Ultra-fast rotating M dwarfs are very interesting and exotic objects in many ways.
From our analysis we find that in six stars with periods P < 0.3 d we find three of them missing a significant zero field component in their filling factor distributions. If confirmed with future studies and it will appear that all stars with ultra-short periods show little of the non-magnetic areas, this would imply that most of the stellar surface is covered with active regions – an effect which was proposed as one of the possible reason for activity saturation (Jeffries et al. 2011; Reiners et al. 2014). More accurate magnetic field measurements in late type M dwarfs, especially those with periods P < 0.3 d, are therefore essential to explore properties of stellar dynamos in this parameter range.
 |
Fig. 6 Mean CARMENES spectra (top panel) around three magnetic sensitive Ti lines obtained in 2016 (full black line) and 2017 (dashed red line) and corresponding filling factors derived from these data sets (bottom panel). |
6 Summary
In this workwe present the first magnetic field measurements from the high-resolution NIR spectroscopic observations taken with the CARMENES instrument. We specifically concentrated on the so-called RV-loud sample of 31 M dwarfs presented inTal-Or et al. (2018) because these stars are expected to have strong magnetic fields as indicated by analysis of their activity indicators. We employed the most advanced current radiative transfer model to measure average magnetic fields from the Zeeman broadening of atomic and molecular lines. Our main conclusions are summarized as follows:
-
We detect strong magnetic fields ⟨B⟩ > 1 kG in all ourtargets. In 16 of them the measurements were done for the first time. In 12 of them our data indicate a presence of very strong fields above 4 kG.
-
We observe 17 stars with short rotation periods P < 1 d and our new measurements are consistent with the effect of magnetic field saturation, however the magnetic field may as well still grow at least in stars with dipole dynamo states.
-
Our analysis of filling factors points toward the existence of particular features in their patterns that may help to distinguish between the stars that have different dynamo states and/or spot patterns.
-
We find two stars, J07446+035 and J23548+385, that are twins in terms of their average magnetic fields and distribution of filling factors. It would be interesting to compare the geometry of their global magnetic fields and test whether they are the same as well. This would be an important additional test for our analysis methods.
-
Our study adds 16 new objects to the list of stars with strong magnetic fields and short rotation periods. However, in order to fully characterize magnetic properties of stars and to put our findings in the context of bi-stable dynamos we lack information about the geometry of large scale magnetic fields and instruments with polarimetric capabilities are needed. Thus, the next logical step would be to follow up our targets with polarimetry and derive maps of their photospheric magnetic fields.
Acknowledgement
CARMENES is an instrument for the Centro Astronómico Hispano-Alemán de Calar Alto (CAHA, Almeria, Spain). CARMENES is funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Cientificas (CSIC), the European Union through FEDER/ERF FICTS-2011-02 funds, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofisica de Andalucia, Landessternwarte Königstuhl, Institut de Ciéncies de l’Espai, Insitut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofisica de Canarias, Hamburger Sternwarte, Centro de Astrobiologia and Centro Astronómico Hispano-Alemán), with additional contributions by the Spanish Ministry of Economy, the German Science Foundation through the Major Research Instrumentation Programme and DFG Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, and by the Junta de Andalucia. L.T.-O. acknowledges support from the Israel Science Foundation (grant No. 848/16). This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. We also acknowledge the use of electronic databases SIMBAD and NASA’s ADS.
Appendix A Model fit to the observed spectra in FeH and Ti lines
 |
Fig. A.1 Model fit to Ti and FeH lines in J01033+623. We show the comparison between observed and predicted spectra for a set of Ti (top panel) and FeH lines (bottom panel). Black circles – observations; red full line – best fit model spectrum; blue dashed line – spectrum computed assuming zero magnetic field. |
References
- Afram, N., Berdyugina, S. V., Fluri, D. M., Solanki, S. K., & Lagg, A. 2008, A&A, 482, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Floriano, F. J., Morales, J. C., Caballero, J. A., et al. 2015, A&A, 577, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asensio Ramos, A., & Trujillo Bueno, J. 2006, ApJ, 636, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. R., Jeffers, S. V., Haswell, C. A., et al. 2017, MNRAS, 471, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., & Solanki, S. K. 2002, A&A, 385, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, J. A., Cortés-Contreras, M., Alonso-Floriano, F. J., et al. 2016a, in 19th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (CS19), 148 [Google Scholar]
- Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016b, Proc. SPIE, 9910, 99100E [Google Scholar]
- Crozet, P., Tourasse, G., Ross, A., Paletou, F., & López Ariste, A. 2012, EAS Pub. Ser., 58, 63 [CrossRef] [Google Scholar]
- Crozet, P., Ross, A. J., Alleq, N., et al. 2014, in Magnetic Fields throughout Stellar Evolution, eds. P. Petit, M. Jardine, & H. C. Spruit, IAU Symp., 302, 164 [NASA ADS] [Google Scholar]
- Díez Alonso, E., Caballero, J. A., Montes, D., et al. 2019, A&A, 621, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Dulick, M., Bauschlicher, Jr. C. W., Burrows, A., et al. 2003, ApJ, 594, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Garraffo, C., Drake, J. J., Cohen, O., Alvarado-Gómez, J. D., & Moschou, S. P. 2017, ApJ, 843, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Gastine, T., Morin, J., Duarte, L., et al. 2013, A&A, 549, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Golimowski, D. A., Leggett, S. K., Marley, M. S., et al. 2004, AJ, 127, 3516 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, J. J., Brown, J. M., Chen, J., Steimle, T. C., & Sears, T. J. 2008, ApJ, 679, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Berta, Z. K., Burke, C. J., et al. 2011, ApJ, 727, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Jackson, R. J., Briggs, K. R., Evans, P. A., & Pye, J. P. 2011, MNRAS, 411, 2099 [NASA ADS] [CrossRef] [Google Scholar]
- Johns-Krull, C. M., & Valenti, J. A. 1996, ApJ, 459, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kiraga, M., & Stepien, K. 2007, Acta Astron., 57, 149 [NASA ADS] [Google Scholar]
- Kislyakova, K. G., Noack, L., Johnstone, C. P., et al. 2017, Nat. Astron., 1, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Kislyakova, K. G., Fossati, L., Johnstone, C. P., et al. 2018, ApJ, 858, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O., & Lavail, A. 2017, ApJ, 835, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O., & Shulyak, D. 2019, ApJ, 873, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines, Astrophys. Space Sci. Lib. (Dordrecht: Kluwer Academic Publishers), 307 [Google Scholar]
- Mathys, G., Solanki, S. K., & Wickramasinghe, D. T. 2001, in Magnetic Fields Across the Hertzsprung-Russell Diagram, ASP Conf. Ser., 248 [Google Scholar]
- McLean, M., Berger, E., & Reiners, A. 2012, ApJ, 746, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2008, MNRAS, 390, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2010, MNRAS, 407, 2269 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Newton, E. R., Irwin, J., Charbonneau, D., et al. 2017, ApJ, 834, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Pallavicini, R., Golub, L., Rosner, R., et al. 1981, ApJ, 248, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Passegger, V. M., Reiners, A., Jeffers, S. V., et al. 2018, A&A, 615, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlenko, Y. V., Zhukovska, S. V., & Volobuev, M. 2007, Astron. Rep., 51, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91471F [Google Scholar]
- Reiners, A., & Basri, G. 2007, ApJ, 656, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Basri, G. 2010, ApJ, 710, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Basri, G., & Browning, M. 2009, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Schüssler, M., & Passegger, V. M. 2014, ApJ, 794, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Zechmeister, M., Caballero, J. A., et al. 2018, A&A, 612, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr., 90, 054005 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Linsky, J. L. 1985, ApJ, 299, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz, C., & Weiss, W. W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shulyak, D., Reiners, A., Wende, S., et al. 2010, A&A, 523, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shulyak, D., Reiners, A., Seemann, U., Kochukhov, O., & Piskunov, N. 2014, A&A, 563, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shulyak, D., Reiners, A., Engeln, A., et al. 2017, Nat. Astron., 1, 0184 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tal-Or, L., Zechmeister, M., Reiners, A., et al. 2018, A&A, 614, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidotto, A. A., Fares, R., Jardine, M., Moutou, C., & Donati, J.-F. 2015, MNRAS, 449, 4117 [NASA ADS] [CrossRef] [Google Scholar]
- Wende, S., Reiners, A., & Ludwig, H.-G. 2009, A&A, 508, 1429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wende, S., Reiners, A., Seifahrt, A., & Bernath, P. F. 2010, A&A, 523, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K., Christensen, U. R., Wolk, S. J., & Poppenhaeger, K. 2016, ApJ, 833, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Example of magnetic filling factors of J12156+526 as derived from Ti I lines. Original distribution contains high field components (left panel), and ignoring them with subsequent re-scaling of the rest of filling factors drops the average magnetic field by 1 kG (right panel). |
| In the text | |
 |
Fig. 2 Comparison between the magnetic field measurements from Ti and FeH lines with υ sin i color coded. Dashed and dash-dotted lines represent 1 and 2 kG deviations from the central line, respectively. |
| In the text | |
 |
Fig. 3 Distribution of filling factors as derived from Ti lines. The stars are sorted according to the S/N of their spectra (S/N decreases from left to the right and top to bottom). |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 4 Distribution of filling factors as derived from Ti lines for stars with known geometry of their large-scale magnetic fields. Left column: dipole-dominant, right column: multipole-dominant. |
| In the text | |
 |
Fig. 5 Average magnetic fields in stars from our sample as a function of rotation period. Measurements in stars with known dipole and multipole states are shown as solid upward- and downward-pointing triangles, respectively. Stars with unknown dynamo states are shown as solid blue circles. Our measurements from this work are shown with blue color and the literature values are shown with the red one. The symbol size scales with stellar mass (see legend on the plot). The horizontal dashed line marks the 4 kG threshold of saturated magnetic field assigned to stars with multipole dynamo regime. Similar to our previous works we include conservative 1 kG error bars onmeasured magnetic fields in stars with υ sin i > 20 km s−1. |
| In the text | |
 |
Fig. 6 Mean CARMENES spectra (top panel) around three magnetic sensitive Ti lines obtained in 2016 (full black line) and 2017 (dashed red line) and corresponding filling factors derived from these data sets (bottom panel). |
| In the text | |
 |
Fig. A.1 Model fit to Ti and FeH lines in J01033+623. We show the comparison between observed and predicted spectra for a set of Ti (top panel) and FeH lines (bottom panel). Black circles – observations; red full line – best fit model spectrum; blue dashed line – spectrum computed assuming zero magnetic field. |
| In the text | |
 |
Fig. A.2 Same as in Fig. A.1 but for J01352-072. |
| In the text | |
 |
Fig. A.3 Same as in Fig. A.1 but for J02088+494. |
| In the text | |
 |
Fig. A.4 Same as in Fig. A.1 but for J03473-019. |
| In the text | |
 |
Fig. A.5 Same as in Fig. A.1 but for J04472+206. |
| In the text | |
 |
Fig. A.6 Same as in Fig. A.1 but for J05365+113. |
| In the text | |
 |
Fig. A.7 Same as in Fig. A.1 but for J06000+027. |
| In the text | |
 |
Fig. A.8 Same as in Fig. A.1 but for J07446+035. |
| In the text | |
 |
Fig. A.9 Same as in Fig. A.1 but for J08298+267. |
| In the text | |
 |
Fig. A.10 Same as in Fig. A.1 but for J09449-123. |
| In the text | |
 |
Fig. A.11 Same as in Fig. A.1 but for J12156+526. |
| In the text | |
 |
Fig. A.12 Same as in Fig. A.1 but for J12189+111. |
| In the text | |
 |
Fig. A.13 Same as in Fig. A.1 but for J14173+454. |
| In the text | |
 |
Fig. A.14 Same as in Fig. A.1 but for J15218+209. |
| In the text | |
 |
Fig. A.15 Same as in Fig. A.1 but for J15499+796. |
| In the text | |
 |
Fig. A.16 Same as in Fig. A.1 but for J16313+408. |
| In the text | |
 |
Fig. A.17 Same as in Fig. A.1 but for J16555-083. |
| In the text | |
 |
Fig. A.18 Same as in Fig. A.1 but for J16570-043. |
| In the text | |
 |
Fig. A.19 Same as in Fig. A.1 but for J17338+169. |
| In the text | |
 |
Fig. A.20 Same as in Fig. A.1 but for J18022+642. |
| In the text | |
 |
Fig. A.21 Same as in Fig. A.1 but for J18189+661. |
| In the text | |
 |
Fig. A.22 Same as in Fig. A.1 but for J18498-238. |
| In the text | |
 |
Fig. A.23 Same as in Fig. A.1 but for J19169+051S. |
| In the text | |
 |
Fig. A.24 Same as in Fig. A.1 but for J19511+464. |
| In the text | |
 |
Fig. A.25 Same as in Fig. A.1 but for J20093-012. |
| In the text | |
 |
Fig. A.26 Same as in Fig. A.1 but for J22012+283. |
| In the text | |
 |
Fig. A.27 Same as in Fig. A.1 but for J22468+443. |
| In the text | |
 |
Fig. A.28 Same as in Fig. A.1 but for J22518+317. |
| In the text | |
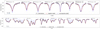 |
Fig. A.29 Same as in Fig. A.1 but for J23548+385. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


