| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220249 | |
| Published online | 15 March 2013 | |
A detailed study of the radio-FIR correlation in NGC 6946 with Herschel-PACS/SPIRE from KINGFISH⋆
1 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: taba@mpia.de
2 Observatories of the Carnegie Institution for Science, Pasadena, CA 91101, USA
3 Max-Planck Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
4 Department of Astronomy, University of Massachusetts, Amherst, MA 01003, USA
5 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
6 Infrared Processing and Analysis Center, MS 100-22, Pasadena, CA 91125, USA
7 Department of Physics & Astronomy, McMaster University, Hamilton, Ontario L8S 4M1, Canada
8 Princeton University Observatory, Peyton Hall, Princeton, NJ 08544-1001, USA
9 Department of Physics & Astronomy, University of Wyoming, Laramie, WY 82071, USA
10 Institut de RadioAstronomie Millimétrique, 38406 Grenoble, France
11 Steward Observatory, University of Arizona, 933 N. Cherry Ave., Tucson, AZ 85721, USA
12 Raytheon Company, 1151 E. Hermans Road, Tucson, AZ 85756, USA
13 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
14 Institut d’Astrophysique de Paris, Université Pierre et Marie Curie (UPMC), CNRS (UMR 7095), 75014 Paris, France
Received: 17 August 2012
Accepted: 22 January 2013
We derive the distribution of the synchrotron spectral index across NGC 6946 and investigate the correlation between the radio continuum (synchrotron) and far-infrared (FIR) emission using the KINGFISH Herschel-PACS and SPIRE data. The radio-FIR correlation is studied as a function of star formation rate, magnetic field strength, radiation field strength, and the total gas surface density. The synchrotron emission follows both star-forming regions and the so-called magnetic arms present in the inter-arm regions. The synchrotron spectral index is steepest along the magnetic arms (αn ~ 1), while it is flat in places of giant Hii regions and in the center of the galaxy (αn ~ 0.6−0.7). The map of αn provides observational evidence for aging and energy loss of cosmic ray electrons (CREs) propagating in the disk of the galaxy. Variations in the synchrotron-FIR correlation across the galaxy are shown to be a function of both star formation and magnetic field strength. We find that the synchrotron emission correlates better with cold rather than with warm dust emission, when the diffuse interstellar radiation field is the main heating source of dust. The synchrotron-FIR correlation suggests a coupling between the magnetic field and the gas density. NGC 6946 shows a power-law behavior between the total (turbulent) magnetic field strength B and the star formation rate surface density ΣSFR with an index of 0.14 (0.16) ± 0.01. This indicates an efficient production of the turbulent magnetic field with the increasing gas turbulence expected in actively star forming regions. Moreover, it is suggested that the B-ΣSFR power law index is similar for the turbulent and the total fields in normal galaxies. On the other hand, for galaxies interacting with the cluster environment this index is steeper for turbulent magnetic fields than it is for the total magnetic fields. The scale-by-scale analysis of the synchrotron-FIR correlation indicates that the ISM affects the propagation of old/diffused CREs, resulting in a diffusion coefficient of D0 = 4.6 × 1028 cm2 s-1 for 2.2 GeV CREs.
Key words: galaxies: individual: NGC 6946 / radio continuum: ISM / ISM: magnetic fields / infrared: ISM / galaxies: star formation
Maps as FITS files are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/552/A19
© ESO, 2013
1. Introduction
The correlation between the radio and far-infrared (FIR) emission of galaxies has been shown to be largely invariant over more than 4 orders of magnitude in luminosity (e.g. Yun et al. 2001) and out to a redshift of z ~ 3 (e.g. Sargent et al. 2010). This correlation is conventionally explained by the idea that the FIR and radio emission are both being driven by the energy input from massive stars, and thus star formation. However, this connection is complicated by the observation that the FIR emission consists of at least two components; one heated directly by massive stars (i.e. the “warm” dust component), and one heated by the diffuse interstellar radiation field or ISRF (i.e. the “cold” dust component; see e.g. Draine et al. 2007), which includes the emission from the old stellar population (e.g. Xu 1990; Bendo et al. 2010).
Similarly, the radio emission consists of two main components; the thermal, free-free emission and nonthermal synchrotron emission. A direct connection between the free-free emission (of thermal electrons in Hii regions) and young massive stars is expected (e.g. Osterbrock & Stockhausen 1960). Conversely, the connection between the synchrotron emission and massive stars is complicated by the convection and diffusion of cosmic ray electrons (CREs) from their place of birth (supernova remnants, SNRs) and by the magnetic fields that regulate the synchrotron emission in the interstellar medium (ISM).
Hence, warm dust emission/thermal radio emission can be directly associated with young stars and a correlation between warm dust and thermal radio emission is not surprizing. On the other hand, the connection between cold dust emission/nonthermal synchrotron emission and massive stars (and thus star formation) is less clear. A better correlation of the FIR with the thermal than the nonthermal radio emission has already been shown in the Large Magellanic Cloud, M 31, and M 33 (Hughes et al. 2006; Hoerneset al. 1998; Tabatabaei et al. 2007a). The CREs experience various energy losses while interacting with matter and magnetic fields in the ISM, causing the power law index of their energy distribution to vary. Significant variation of the nonthermal spectral index was found in M 33 with a flatter synchrotron spectrum in regions of massive star formation (SF) than in the inter-arm regions and the outer disk (Tabatabaei et al. 2007b).
The critical dependence of the synchrotron emission on both magnetic fields and CRE propagation could cause the nonlinearity in the synchrotron-FIR correlation seen globally for galaxy samples (e.g. Niklas 1997). Propagation of the CREs can also cause dissimilarities of the synchrotron and FIR morphologies particularly on small scales. For instance, Galactic SNRs do not seem to be well-correlated with the FIR emission (e.g. Cohen et al. 1984). Moreover, within a few 100 pc of the star-forming Orion nebula, no correlation exists (Boulanger & Perault 1988). In nearby galaxies, a lack of correlation on small scales has been shown via detailed multi-scale analysis using wavelet transformation (e.g. Hughes et al. 2006; Dumas et al. 2011). Murphy et al. (2006, 2008) showed that recent massive SF could reduce these dissimilarities due to generation of a new episode of CREs, assuming that the FIR emission is attributed to dust heating by the same stars.
Assuming that the massive SF is the source of both FIR and synchrotron emission, Helou & Bicay (1993) and Niklas & Beck (1997) considered a coupling between magnetic field strength and gas density as the reason for the tight radio-FIR correlation in spite of the sensitive dependence of the synchrotron emission on the magnetic field. A modified version of this model was suggested by Hoerneset al. (1998) to explain the correlation between the cold dust heated by the ISRF and the synchrotron emission, whose energy sources are independent. The scale at which the correlation breaks down provides an important constraint on these models, explaining the scale where static pressure equilibrium between the gas and CREs/magnetic fields holds.
Within nearby galaxies, variations in the radio-FIR correlation have been shown to exist by several authors (e.g. Gordon et al. 2004; Murphy et al. 2006, 2008; Dumas et al. 2011; Hughes et al. 2006) through a change in the q ratio (Helou et al. 1985, see Sect. 7.3 for definition) or in the fitted slope. Furthermore, the smallest scale at which the radio-FIR correlation holds is not the same from one galaxy to another (Hughes et al. 2006; Tabatabaei et al. 2007a; Dumas et al. 2011).
As the variations in the radio-FIR correlation are possibly due to a range of different conditions such as the star formation rate (SFR), magnetic fields, CRE propagation, radiation field and heating sources of dust, this correlation can be used as a tool to study the unknown interplay between the ISM components and SF. These are addressed in this paper through a detailed study of the radio-FIR correlation in NGC 6946.
NGC 6946 is one of the largest spiral galaxies on the sky at a distance of 6.8 Mpc (Karachentsev et al. 2000). Its low inclination (38°) makes it ideal for mapping various astrophysical properties across the galaxy (Table 1). NGC 6946 shows a multiple spiral structure with an exceptionally bright arm in the north-east of the galaxy. Having several bright giant Hii regions, this Sc (SABc) galaxy has active SF as well as strong magnetic fields as traced by linearly polarized observations (Beck & Hoernes 1996). The global SFR is ≃7.1 M⊙ yr-1 (as listed by Kennicutt et al. 2011,assuming a Kroupa IMF and a mass range of 0.1−100 M⊙). The dynamical mass of this galaxy is ≃1.9 × 1011 M⊙ (Crosthwaite & Turner 2007). This galaxy harbors a mild starburst nucleus (e.g. Ball et al. 1985) and there is no strong evidence for AGN activity (e.g. Tsai et al. 2006).
Frick et al. (2001) presented the wavelet analysis of the radio and mid-infrared (ISOCAM LW3) emission in NGC 6946. Here we study this correlation for dust emission at FIR wavelengths with Herschel-PACS and SPIRE from the KINGFISH project (Key Insights on Nearby Galaxies: a Far-Infrared Survey with Herschel, Kennicutt et al. 2011) and using various approaches.
The paper is organized as follows. The relevant data sets are described in Sect. 2. After deriving the maps of the free-free and synchrotron emissions (Sect. 3), we derive the distribution of the synchrotron spectral index in Sect. 4. We map the magnetic field strength in Sect. 5. The radio-FIR correlation is calculated using various approaches i.e. the q-method, classical pixel-by-pixel correlation, and as a function of spatial scale in Sect. 6. We further discuss the correlations versus magnetic fields, SFR, radiation field and gas density (Sect. 7). Finally, we summarize the results in Sect. 8.
General parameters adopted for NGC 6946.
Images of NGC 6946 used in this study.
2. Data
Table 2 summarizes the data used in this work. NGC 6946 was observed with the Herschel Space Observatory as part of the KINGFISH project (Kennicutt et al. 2011) and was described in detail in Dale et al. (2012) and Aniano et al. (2012). Observations with the PACS instrument (Poglitsch et al. 2010) were carried out at 70, 100, 160 μm in the Scan-Map mode. The PACS images were reduced by the Scanamorphos data reduction pipeline (Roussel et al. 2010; Roussel 2012), version 12.5. Scanamorphos version 12.5 includes the latest PACS calibration available and aims to preserve the low surface brightness diffuse emission. The 250 μm map was observed with the SPIRE instrument (Griffin et al. 2010) and reduced using the HIPE version spire-5.0.1894. The data were subtracted for the sky as detailed in Aniano et al. (2012).
The 70, 100, 160 and 250 μm images were convolved from their native PSFs to a Gaussian PSF with 18″ FWHM using the kernels from Aniano et al. (2011) and resampled to a common pixel size of 6″ (~170 pc).
The radio continuum (RC) data at 3.5 and 20 cm are presented in Beck (1991) and Beck (2007). At 3.5 cm, NGC 6946 was observed with the 100-m Effelsberg telescope of the MPIfR1. The 20 cm data were obtained from observations with the Very Large Array (VLA2) corrected for missing short spacings using the Effelsberg data at 20 cm. To trace the ordered magnetic field, the linearly polarized intensity data at 6 cm presented in Beck & Hoernes (1996) were used. The average degree of polarization is ≃30% for the entire galaxy.
To investigate the connection between the neutral gas and the magnetic field, we used the map of the total gas (HI + H2) mass surface density derived using the VLA HI-21 cm data (as part of the THINGS survey, Walter et al. 2008) and the IRAM 30-m CO(2–1) data from the HERACLES survey as detailed in Bigiel et al. (2008) and Leroy et al. (2009).
We used the Hα map of NGC 6946 observed with the KPNO 0.9 m in a 23′× 23′ field of view and with 0.69″ pixel-1 (resolution of 1.5″), subtracted for the continuum (Ferguson et al. 1998) and foreground stars. The contribution from the [NII] line emission was subtracted following Kennicutt et al. (2008). The Hα emission is corrected for attenuation by the Galactic cirrus using the extinction value given by Schlegel et al. (1998). The Hα map has a calibration uncertainty of ≃20%.
The radio and Hα maps were smoothed to 18″ resolution (using a Gaussian kernel). All the maps were normalized to the same grid, geometry, and size before comparison.
3. Thermal/nonthermal separation
Constraints on the origin and propagation of cosmic rays can be achieved by studying the variation in the spectral index of the synchrotron emission across external galaxies. To determine the variation in the nonthermal radio spectral index, we separate the thermal and nonthermal components using a thermal radio tracer (TRT) approach in which one of the hydrogen recombination lines is used as a template for the free-free emission (see e.g. Dickinson et al. 2003; Tabatabaei et al. 2007b). For NGC 6946, we use the Hα line emission which is the brightest recombination line data available. Both the free-free and the Hα emission are linearly proportional to the number of ionizing photons produced by massive stars, assuming that the Hα emitting medium is optically thick to ionizing Lyman photons (Osterbrock 1989; Rubin 1968, see also Sect. 3.2). However, the observed Hα emission may suffer from extinction by dust which will lead to an underestimate of the free-free emission. Hence, following Tabatabaei et al. (2007b) and Tabatabaei & Berkhuijsen (2010), we first investigate the dust content of NGC 6946 in an attempt to de-redden the observed Hα emission. Then we compare our de-reddening method with the one based on a combination of the total infrared (TIR) and Hα luminosity (Kennicutt et al. 2009).
3.1. De-reddening of the Hα emission
Following Draine & Li (2007), the interstellar dust heating has been modeled in NGC 6946 (Aniano et al. 2012) assuming a δ-function in radiation field intensity, U, coupled with a power-law distribution Umin < U < Umax, ![\begin{eqnarray} {\rm d}M_{\rm dust}/{\rm d}U &=& {M_{\rm dust} \Bigg[(1 - \gamma)\,\delta(U - U_{\rm min})} \nonumber\\ &&\,\,+ \gamma \,\frac{\alpha-1}{U^{1-\alpha}_{\rm min} - U^{1-\alpha}_{\rm max}}\,U^{-\alpha}\Bigg], \end{eqnarray}](/articles/aa/full_html/2013/04/aa20249-12/aa20249-12-eq36.png) (1)where U is normalized to the local Galactic interstellar radiation field, Mdust is the total dust mass, and (1 − γ) is the portion of the dust heated by the diffuse interstellar radiation field defined by U = Umin. The minimum and maximum interstellar radiation field intensities span 0.01 < Umin < 30 and 3 < log Umax < 8 (see Dale et al. 2001, 2012). Fitting this model to the dust SED covering the wavelength range between 3.5 μm and 250 μm, pixel-by-pixel, results in the 18″ maps (with 6″ pixels) of the dust mass surface density (σ), the distribution of the radiation fields (U), and the total infrared (TIR) luminosity emitted by the dust.
(1)where U is normalized to the local Galactic interstellar radiation field, Mdust is the total dust mass, and (1 − γ) is the portion of the dust heated by the diffuse interstellar radiation field defined by U = Umin. The minimum and maximum interstellar radiation field intensities span 0.01 < Umin < 30 and 3 < log Umax < 8 (see Dale et al. 2001, 2012). Fitting this model to the dust SED covering the wavelength range between 3.5 μm and 250 μm, pixel-by-pixel, results in the 18″ maps (with 6″ pixels) of the dust mass surface density (σ), the distribution of the radiation fields (U), and the total infrared (TIR) luminosity emitted by the dust.
The map of σ is equivalent to a map of the dust optical depth at Hα wavelengths given by τHα = σ κHα where κHα is the dust opacity. Taking into account both absorption and scattering, κHα = 2.187 × 104 cm2 g-1, assuming a Milky-Way value of the total/selective extinction ratio of Rv = 3.1 (Weingartner & Draine 2001). The distribution of τHα over the disk of NGC 6946 overlaid with contours of the Hα emission is shown in Fig. 1. We note that the dust mass from modeling the SED at 18′′ resolution may be overestimated by ~20% due to the lack of longer wavelength constraints (Aniano et al. 2012).
 |
Fig. 1 Left: dust optical depth at Hα wavelength τHα overlaid with contours of the Hα emission from NGC 6946. Contour levels are 1, 3, 6, 15, 30, 40 μerg s-1 cm-2 sr-1. The bar at the right shows the values of τHα. Right: radiation field U map (mass-weighted mean starlight heating intensity) of NGC 6946 in units of radiation field in solar neighborhood U⊙ (Aniano et al. 2012), indicated by the bar at the right of the image. The beam area is shown in the lower left corners. |
Regions with considerable dust opacity (τHα > 0.7) follow narrow dust lanes along the spiral arms (e.g. the narrow lane in the inner edge of the bright optical arm) and are found mainly in the inner disk. High opacity dust is found in the center of the galaxy with τHα ≃ 5. This corresponds to a silicate optical depth of τ9.7 ≃ 0.5 which agrees well with Smith et al. (2007). In the central ~60 pc which is much smaller than our resolution, much larger estimates of the extinction have been found using total gas masses (Schinnerer et al. 2006).
Figure 1 also shows that the Hii complexes are dustier in the inner disk (with τHα ≳ 1.4) than in the outer parts (with τHα ≲ 0.6) of NGC 6946. Across the galaxy, the mean value of τHα is 0.43 ± 0.04 (median of 0.34 ± 0.04). Therefore, apart from the center, NGC 6946 is almost transparent to photons with λ ≃ 6563 Å propagating toward us.
The τHα derived can then be used to correct the Hα emission for attenuation by dust, taking into account the effective fraction of dust actually absorbing the Hα photons. Since these photons are usually emitted from sources within the galaxy, the total dust thickness τHα only provides an upper limit. Following Dickinson et al. (2003), we set the effective thickness to τeff = fd × τHα with fd being the dust fraction actually absorbing the Hα; the attenuation factor for the Hα flux is then e− τeff. At our resolution of 18″≃ 530 pc, one may assume that the Hα emitting ionized gas is uniformly mixed with the dust, which would imply fd ≃ 0.5. Considering the fact that the ionized gas has a larger extent than the dust, Dickinson et al. (2003) found a smaller effective factor (fd = 0.33) based on a cosecant law modeling. We also adopt fd = 0.33 for NGC 6946. We note that this choice barely influences the thermal fraction of the radio emission, due to the small τHα (Sect. 3.2). Of course, it would be preferable not to use a uniform value fd for the whole galaxy, but one that is adapted to the geometry (well mixed diffuse medium or shell-like in Hii regions, Witt & Gordon 2000) and the dust column density. However, this would require specifying the location of the stellar sources and the absorbing dust along the line of sight and solving the radiative transfer problem with massive numerical computations which is far from our first order approximation.
In another approach, assuming that the dust is mainly heated by the massive stars, we corrected the Hα emission by combining it with the TIR (integrated dust luminosity in the 8–1000 μm wavelength range): Hαcorr = Hαobs + 0.0024 TIR (Kennicutt et al. 2009). Interestingly, this approach is linearly correlated with the de-reddening using τeff (Fig. 2), with an offset of 0.19 dex and a dispersion of 0.14 dex. Figure 2 shows that at the highest luminosities, the corrected Hα values agree, corresponding to the calibration of the second approach specifically to star-forming regions. Outside of these regions, the Hα-TIR ratio approach overestimates the correction applied to the observed Hα, probably because of contributions from other dust-heating sources. Masking out the diffuse emission in the inter-arm regions and outer disk (i.e., considering only the spiral arms and SF regions), both the offset and dispersion reduces to 0.11 dex and hence both methods agree within the uncertainties (~20% due to calibration). This likely indicates that the diffuse dust is not heated by the UV radiation of ionizing stars.
 |
Fig. 2 Hα luminosity de-reddened based on τeff versus de-reddening using the TIR luminosity. Also shown are the lines of 1:1 correspondence (dashed) and Y = X − 0.19 (solid). |
 |
Fig. 3 Free-free (left) and synchrotron emission (right) from NGC 6946 at 3.5 cm (top) and 20 cm (bottom). The angular resolution is 18″ (shown in the lower left corner of the panels) with a grid size of 6″. The bars at the right of the images show the intensity values in mJy/beam. Note that the areas are not the same at 20 cm and 3.5 cm due to their different observed fields. At 20 cm the synchrotron emission is overlaid with contours of linearly polarized intensity (Beck & Hoernes 1996). The contour levels are 70, 120, 160 μJy/beam. |
3.2. Distribution of the free-free and synchrotron emission
Using the corrected Hα emission from the first approach, we derive the intrinsic Hα intensity, I0, according to I = I0 e− τeff. Integration of the de-reddened Hα map out to a radius of 11.9 kpc (414″) yields a luminosity of LHα = (3.46 ± 0.05) × 1041 erg s-1 that is higher than the foreground-corrected luminosity by ≃20%. A similar increase in the Hα flux has been derived in other nearby galaxies, M 33 (≃13%, Tabatabaei et al. 2007b) and M 31 (≃30%, Tabatabaei & Berkhuijsen 2010).
Dickinson et al. (2003) showed that the Hα emitting medium in our Galaxy is optically thick to ionizing Lyman photons (case B, Osterbrock 1989) not only for Hii regions (τLyα ~ 103 − 1010) but also for faint Hα features at intermediate and high Galactic latitudes (τLyα ~ 1 − 30). Assuming the same condition applies for NGC 6946, the emission measure (EM) follows from the Hα intensity (in units of erg cm-2 s-1 sr-1) via the expression (Valls-Gabaud 1998): 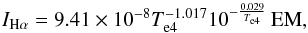 (2)where the electron temperature, Te4, is in units of 104 K, and EM in cm-6 pc. The emission measure is related to the continuum optical thickness, τc, of the ionized gas by
(2)where the electron temperature, Te4, is in units of 104 K, and EM in cm-6 pc. The emission measure is related to the continuum optical thickness, τc, of the ionized gas by 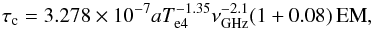 (3)with a ≃ 1 (Dickinson et al. 2003). The factor (1 + 0.08) takes into account the contribution from singly ionized He. The brightness temperature of the radio continuum (free-free) emission, Tb, then follows from
(3)with a ≃ 1 (Dickinson et al. 2003). The factor (1 + 0.08) takes into account the contribution from singly ionized He. The brightness temperature of the radio continuum (free-free) emission, Tb, then follows from 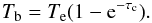 (4)Equation (4) with Eqs.(2) and (3) gives:
(4)Equation (4) with Eqs.(2) and (3) gives: 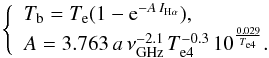 (5)Hence, the free-free emission can be derived separately at each radio wavelength. The resulting distributions of the intensity of the free-free emission in mJy/beam at 3.5 and 20 cm are shown in (Fig. 3, left panels) for3Te = 104 K. Using a constant electron temperature is supported by the shallow metallicity gradient found in this galaxy (Moustakas et al. 2010). Subtracting the free-free emission from the observed radio continuum emission results in a map of the synchrotron emission (Fig. 3, right panels).
(5)Hence, the free-free emission can be derived separately at each radio wavelength. The resulting distributions of the intensity of the free-free emission in mJy/beam at 3.5 and 20 cm are shown in (Fig. 3, left panels) for3Te = 104 K. Using a constant electron temperature is supported by the shallow metallicity gradient found in this galaxy (Moustakas et al. 2010). Subtracting the free-free emission from the observed radio continuum emission results in a map of the synchrotron emission (Fig. 3, right panels).
The synchrotron maps exhibit diffuse emission extending to large radii indicating diffusion and propagation of the CREs. Strong synchrotron emission emerges from the galaxy center, giant star-forming regions, and spiral arms, which could be due to stronger magnetic fields and/or young-energetic CREs close to the star-forming regions. Interestingly, the so called “magnetic arms” traced by the linearly polarized intensity (Beck & Hoernes 1996) are clearly visible in the 20 cm synchrotron map. The fact that they are less prominent at 3.5 cm implies that these arms are filled by older and lower energetic CREs (see Sect 4.2). The thermal free-free map, on the other hand, exhibits narrow spiral arms dominated by the star-forming regions.
Global radio continuum flux densities and thermal fractions in NGC 6946.
Integrating the observed, synchrotron and free-free maps in the plane of the galaxy (i = 38°) around the center out to a radius of 324′′ (9.2 kpc), we obtain the total flux densities and thermal fractions at 3.5 and 20 cm (Table 3). The thermal fractions are about 18% and 7% at 3.5 and 20 cm, respectively. As mentioned before, we assumed a dust attenuation factor of fd = 0.3. For a uniform distribution of dust and ionized gas (fd = 0.5), the thermal fractions increase to about 21% and 8% at 3.5 and 20 cm, respectively.
 |
Fig. 4 Synchrotron spectral index map of NGC 6946 overlaid with contours of the linearly polarized emission at 6 cm (top) tracing the ordered magnetic field in the sky plane with the same levels as in Fig. 3 and of bright Hα sources (bottom). The Hα contour levels are 18, 24, 35, and 47% of the maximum intensity. The 9 giant Hii regions are indicated (Table 4). The bars at the right of the images show the values of the synchrotron spectral index. |
 |
Fig. 5 Histogram of the observed radio continuum (gray) and synchrotron spectral index (black) in NGC 6946. |
4. Synchrotron spectral index
Using the nonthermal radio fluxes at 3.5 and 20 cm, we obtained the spectral index of the nonthermal radio emission. This was only computed for pixels with flux densities of at least three times the rms noise at both frequencies. The synchrotron spectral index, αn, shows a smooth variation across the disk of NGC 6946 (Fig. 4). The greenish color in Fig. 4 corresponds to the synchrotron emission with flat spectrum (αn ≲ 0.7), and the reddish color to the regions with a steep spectrum (αn ≳ 0.9), i.e. emission from lower-energy CREs. The flat spectrum is found in giant Hii regions and the steep spectrum in the inter-arm regions, the eastern part of the central galaxy, and the south of the major axis where αn = 1.0 ± 0.1. As shown in the histogram representation (Fig. 5), the median value of αn across the galaxy is 0.81 with a dispersion of 0.18. Figure 5 also presents a histogram of the “observed” spectral index α (obtained using the observed radio data at 3.5 and 20 cm, i.e., contaminated by the free-free emission), for comparison, with α ≃ 0.7 on the average and with a dispersion of 0.16.
4.1. Synchrotron spectral index versus star formation
In the star-forming regions, the synchrotron spectrum is relatively flat with an average index of αn = 0.65 ± 0.10, the typical spectral index of young CREs in SF regions (in supernova remnants, αn is about 0.5 on the average and could even be flatter, see e.g. Gordon et al. 1999; Reynolds et al. 2012; Longair 1994, and references therein). Table 4 lists αn in 9 giant Hii regions annotated in Fig. 4, (called Enuc following the nomenclature and location presented in Murphy et al. 2010). Enuc2 and Enuc3 have a relatively steep spectrum which could be due to an energy loss of CREs in a magneto-ionic medium along the line of sight seen at the position of these Hii regions. This is possible for Enuc3 since this source is adjacent to the strong northern magnetic arm (see below). In the neighborhood of the Enuc2, however, no strong polarized emission is detected. The estimated spectral index of this source could be affected by an underestimate of the observed 3.5 cm emission, since this source sits on the edge of the 3.5 cm observed field (primary beam).
Considering synchrotron, inverse-Compton, ionization, and bremsstrahlung cooling mechanisms of CREs as well as using a prescription for the escape of these particles, Murphy et al. (2010) modeled the radio SEDs and found an αn ≃ 0.8 for the giant Hii regions in Table 4, which is steeper than our finding and equals to the average αn for the entire galaxy. One contributing factor to their steeper indices could be a result of assuming a fixed ISM density for the extranuclear regions of 0.1 cm-3 (motivated by their beam size area of 30″~ 0.9 kpc), leading to dominant synchrotron and IC losses rather than the ionization and bremsstrahlung cooling mechanisms of CREs (and hence a rather steep spectrum for these objects). In the present work, we determine αn at a smaller beam size of ~0.5 kpc (the scale of the giant SF regions in NGC 6946 Kennicutt & Evans 2012) and without any assumption on the ISM density and/or cooling mechanism of CREs. On these scales, more energetic CREs and/or stronger magnetic fields close to the SF regions provide the synchrotron emission with a flatter αn on the average.
Table 4 also lists the thermal fractions at 3.5 cm and 20 cm in these extranuclear Hii complexes. The thermal fractions at 3.5 cm are higher than those at 20 cm by a factor of about two (apart from Enuc4).
4.2. Synchrotron spectral index versus magnetic fields
The magnetic fields in NGC 6946 have been extensively studied by Beck & Hoernes (1996), Rohde et al. (1999), and Beck (2007). The contours in Fig. 4 show the linearly polarized intensity (PI) at 6.3 cm which determines the strength of the ordered magnetic field in the plane of the sky (see e.g. Tabatabaei et al. 2008). Interestingly, there is a good correspondence between the steep synchrotron emission and the PI, particularly along the northern magnetic arm (Beck & Hoernes 1996) and also along the strong ordered magnetic field in the central disk (anisotropic turbulent magnetic field, Beck 2007). In these regions, the spectral index of αn = 1.0 ± 0.1 indicates that CREs suffer strong synchrotron losses propagating along NGC 6946’s ordered magnetic field.
Overall, the synchrotron spectral index map agrees with the energy loss theory of relativistic electrons propagating away from their origin in star-forming regions in the ISM (e.g. see Chapter 18 of Longair 1994; Biermann et al. 2001). The difference in αn in star-forming regions and along the magnetic arms in NGC 6946 is similar to that predicted by Fletcher et al. (2011) for the spiral galaxy M 51.
5. Maps of total and turbulent magnetic fields
The strength of the total magnetic field Btot can be derived from the total synchrotron intensity. Assuming equipartition between the energy densities of the magnetic field and cosmic rays (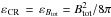 ):
): ![\begin{eqnarray} {B}_{\rm tot}= C(\alpha_{\rm n}, K, L) \big[I_{\rm n} \big]^{\frac{1}{\alpha_{\rm n}+3}}, \label{eq:Btoteq} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20249-12/aa20249-12-eq104.png) (6)where In is the nonthermal intensity and C is a function of αn, K the ratio between the number densities of cosmic ray protons and electrons, and L the pathlength through the synchrotron emitting medium (see Beck & Krause 2005; Tabatabaei et al. 2008). Using the maps of In and αn obtained from the TRT method and assuming that the magnetic field is parallel to the plane of the galaxy (inclination of i = 38° and position angle of the major axis of PA = 242°), Btot is derived across the galaxy. In our calculations, we apply values of K ≃ 100 (Beck & Krause 2005) and L ≃ 1 kpc/cos i. Figure 6 shows strong Btot in the central region of the galaxy, the arms and the star-forming regions.
(6)where In is the nonthermal intensity and C is a function of αn, K the ratio between the number densities of cosmic ray protons and electrons, and L the pathlength through the synchrotron emitting medium (see Beck & Krause 2005; Tabatabaei et al. 2008). Using the maps of In and αn obtained from the TRT method and assuming that the magnetic field is parallel to the plane of the galaxy (inclination of i = 38° and position angle of the major axis of PA = 242°), Btot is derived across the galaxy. In our calculations, we apply values of K ≃ 100 (Beck & Krause 2005) and L ≃ 1 kpc/cos i. Figure 6 shows strong Btot in the central region of the galaxy, the arms and the star-forming regions.
 |
Fig. 6 Strength of the total Btot (top) and turbulent Btur (bottom) magnetic fields in NGC 6946. The bars at the top of each image show the magnetic field strength in μ Gauss. |
As a fraction of the polarized intensity PI is related to the strength of the ordered magnetic field, and the nonthermal intensity In to the total magnetic field in the plane of the sky, In − (PI/0.75) gives the nonthermal emission due to the turbulent magnetic field Btur4. Using this intensity with Eq. (6) yields the distribution of Btur across the galaxy. Similar to Btot, Btur is higher in places of star-forming regions (Fig. 6, bottom). We note that any ordered field which is not resolved and depolarized within the beam would contribute to the turbulent magnetic field. In other words, we cannot distinguish between unresolved structures of the ordered field and truly turbulent fields for structures smaller than the beam.
The magnetic field strength estimated using the “standard method” for thermal/nonthermal separation, i.e. assuming a fixed synchrotron spectral index (see Appendix A), is similar to the TRT estimate (within 10% difference) in the spiral arms, and is underestimated by 35% in the giant Hii regions, and 45% in the nucleus. This is because, in those regions, In is smaller and αn is larger based on the standard method.
Radio-IR relations on pixel-by-pixel basis in N6946.
6. Radio-FIR Correlation
The radio correlations with both monochromatic and bolometric FIR observations are obtained using three different approaches: classical pixel-to-pixel (Pearson correlation), wavelet multi-scale (Frick et al. 2001), and the q-ratio method (Helou et al. 1985). Although the main goal of this paper is to investigate the synchrotron-FIR correlation, we also present the correlations between the emissions of the thermal free-free and each of the monochromatic FIR bands.
6.1. Classical correlation
The pixel-to-pixel correlation is the simplest measure of the correlation between two images, f1(x,y) and f2(x,y), with the same angular resolution and the same number of pixels using Pearson’s linear correlation coefficient, rc5: 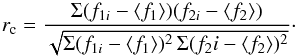 (7)When the two images are identical, rc = 1. The correlation coefficient is rc = −1 for images that are perfectly anti-correlated. The formal error on the correlation coefficient depends on the strength of the correlation and the number of independent pixels, n, in an image:
(7)When the two images are identical, rc = 1. The correlation coefficient is rc = −1 for images that are perfectly anti-correlated. The formal error on the correlation coefficient depends on the strength of the correlation and the number of independent pixels, n, in an image: 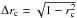 /
/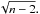
We calculated the correlations between both the radio free-free/synchrotron and the FIR 70, 100, 160, and 250 μm maps, restricting the intensities to >3 × rms noise. We obtained sets of independent data points (n) i.e. a beam area overlap of <20%, by choosing pixels spaced by more than one beamwidth. Since the correlated variables do not directly depend on each other, we fitted a power law to the bisector in each case (Isobe et al. 1990; Hoerneset al. 1998). The Student’s t-test is also calculated to indicate the statistical significance of the fit. For a number of independent points of n > 100, the fit is significant at the 3σ level if t > 3 (e.g. Wall 1979). Errors in the slope b of the bisector are standard deviations (1 σ).
The results for both radio wavelengths are presented in Table 5. The calculated Student’s t-test values are large (>33) indicating that the fitted slopes are statistically significant. With coefficients of rc ≥ 0.8, good correlations hold between the FIR bands and observed radio (RC)/free-free emission. The FIR correlation coefficients with the synchrotron emission are slightly lower than those with the free-free emission.
The synchrotron emission is slightly better correlated with the 250 μm emission (as a proxy for cold dust) than with the 70 μm emission (as a proxy for warm dust). On the contrary, a free-free–cold/warm dust differentiation is only hinted, but not yet clear given the errors from the rc values.
The free-free emission exhibits an almost linear correlation with the warmer dust emission at 70 and 100 μm (with a slope of b ≃ 0.9). The correlation becomes more and more sub-linear with dust emission probed at 160 and 250 μm.
The synchrotron emission, on the other hand, tends to show a linear correlation with colder rather than warmer dust (with a super-linear correlation). A similar trend is also seen between the observed RC and FIR bands.
Super-linear radio-FIR correlations have been also found for samples of galaxies by Price & Duric (1992) and Niklas (1997), which were attributed to the non-linearity of the synchrotron-FIR correlation and/or to the fact that colder dust may not be necessarily heated by the young massive stars. A better synchrotron-cold than -warm dust correlation was also found in M 31 (Hoerneset al. 1998) and in a sample of late-type galaxies (Xu et al. 1994).
One possible issue is that our use of the dust mass to de-redden the Hα emission, and thus the free-free emission, is somehow influencing the correlations. To test this, we re-derive the free-free emission using the observed Hα emission (not corrected for extinction) and re-visit the thermal/nonthermal correlations with the FIR bands. The results are given in parenthesis in Table 5. The differences are less than 4% and within the errors.
The synchrotron emission based on the standard method also shows a decrease of the slope with increasing FIR wavelength (Table 6), similar to the TRT based study. However, the expected better linearity of the free-free-warmer dust is not seen using the standard thermal/nonthermal separation method. As shown in Sect. 5, in our resolved study, this method results in an excess of the free-free diffuse emission in the inter-arm regions where there is no warm dust and TIR counterparts. This is most probably caused by neglecting variations of αn locally across the galaxy, since in global studies, the standard separation method leads to a linear thermal radio-FIR correlation (e.g. Niklas 1997). Based on the standard method, the separated RC components are not as tightly correlated with the FIR bands as the observed RC-FIR correlations.
Same as Table 5 for the 3.5 cm free-free (FF)/synchrotron (SYN) emission separated using the standard method (see Appendix A).
6.2. Multi-scale correlation
Classical cross-correlations contain all scales that exist in a distribution. For example, the high-intensity points represent high-emission peaks on small spatial scales belonging to bright sources, whereas low-intensity points represent weak diffuse emission with a large-scale distribution, typically. However, such a correlation can be misleading when a bright, extended central region or an extended disk exists in the galactic image. In this case, the classical correlation is dominated by the large-scale structure, e.g. the disc of the galaxy, while the (more interesting) correlation on the scale of the spiral arms can be much worse. The classical correlation provides little information in the case of an anti-correlation on a specific scale (Frick et al. 2001). Using the “wavelet cross-correlation” introduced by Frick et al. (2001), one can calculate the correlation between different emissions as a function of the angular scale of the emitting regions. The wavelet coefficients of a 2D continuous wavelet transform are given by: 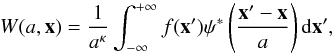 (8)where f(x) is a two-dimensional function (an image), ψ(x) is the analyzing wavelet, the symbol ∗ denotes the complex conjugate, x = (x,y) defines the position of the wavelet and a defines its scale. κ is a normalization parameter (we use κ = 2, which is equivalent to energy normalization). Following Frick et al. (2001) and, e.g., Laine et al. (2010), we use the “Pet Hat” function as the analyzing wavelet ψ(x) to have both a good scale resolution and a good spatial resolution. The wavelet cross-correlation coefficient at scale a is defined as
(8)where f(x) is a two-dimensional function (an image), ψ(x) is the analyzing wavelet, the symbol ∗ denotes the complex conjugate, x = (x,y) defines the position of the wavelet and a defines its scale. κ is a normalization parameter (we use κ = 2, which is equivalent to energy normalization). Following Frick et al. (2001) and, e.g., Laine et al. (2010), we use the “Pet Hat” function as the analyzing wavelet ψ(x) to have both a good scale resolution and a good spatial resolution. The wavelet cross-correlation coefficient at scale a is defined as ![\begin{equation} r_{\rm w}(a)=\frac{\int \int W_{1}(a,{\vec x})~W^{\ast}_{2}(a,{\vec x}) {\rm d}{\vec x}}{[M_{1}(a)M_{2}(a)]^{1/2}}, \end{equation}](/articles/aa/full_html/2013/04/aa20249-12/aa20249-12-eq145.png) (9)where the subscripts refer to two images of the same size and linear resolution and
(9)where the subscripts refer to two images of the same size and linear resolution and 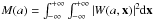 is the wavelet equivalent of the power spectrum in Fourier space. The value of rw varies between − 1 (total anti-correlation) and +1 (total correlation). The correlation coefficient of | rw | = 0.5 is translated as a marginal value for acceptance of the correlation between the structures at a given scale. The error in rw is estimated by the degree of correlation and the number of independent points (n) as
is the wavelet equivalent of the power spectrum in Fourier space. The value of rw varies between − 1 (total anti-correlation) and +1 (total correlation). The correlation coefficient of | rw | = 0.5 is translated as a marginal value for acceptance of the correlation between the structures at a given scale. The error in rw is estimated by the degree of correlation and the number of independent points (n) as 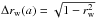 /
/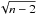 , where n ~ LxLy/a2, and (Lx,Ly) are the map sizes in (x,y). Thus, toward larger scales, n decreases and the errors increase.
, where n ~ LxLy/a2, and (Lx,Ly) are the map sizes in (x,y). Thus, toward larger scales, n decreases and the errors increase.
To prevent a strong influence of the nucleus on the wavelet analysis, the central 2 kpc was subtracted from the PACS and SPIRE maps as well as the radio maps of NGC 6946. Then, the maps were decomposed using Eq. (8) into 12 angular scales (a) between 32′′(~0.9 kpc) and 313′′ (~9 kpc)6. The derived wavelet coefficients W(a,x) of the radio and FIR maps were then used in Eq. (9) in order to derive the radio-FIR correlation coefficient rw on the 12 scales of decomposition. Figure 7 shows rw between the maps of the FIR bands and the 20 cm synchrotron, free-free, and observed RC versus spatial scale a.
The total RC-FIR and the synchrotron-FIR correlations are higher for scales >4–5 kpc, the scale of the diffuse central disk. On smaller scales the synchrotron-FIR correlations fluctuate (within the errors) close to the threshold value rw = 0.5.
On the smallest scale of 0.9 kpc, corresponding to the width of the complexes of giant molecular clouds (GMCs) and star formation within spiral arms (typical width of spiral arms in the galaxy ~1.6−2 kpc, Frick et al. 2001), the synchrotron-colder dust correlation (e.g. 250 μm, rw = 0.53 ± 0.02) is slightly better than the synchrotron-warmer dust one (70 μm, rw = 0.45 ± 0.02). Right after a small maximum on scales of spiral arms (~1.6−2 kpc), a small minimum in the RC/synchrotron-FIR correlation occurs at a ~ 2.5 kpc, the scale covering the width of the spiral arms plus diffuse emission in between the arms. Hence, the minimum could be due to the diffuse nature of the nonthermal emission caused by the propagation of CREs. The existence of the “magnetic arms” where there is no significant FIR emission, could also cause the general weaker correlation on scales of their widths, i.e., <3 kpc (see Sect. 7.7).
The FIR bands are better correlated with free-free than with synchrotron emission on a ≤ 3 kpc, as expected (note that this difference is not that obvious in the classical correlation at 20 cm). Moreover correlations show a split in terms of the FIR band, with warmer dust having a better correlation than colder dust. Such a split is again not obtained from the classical correlation. This occurs because the classical correlation is biased toward large scales (due to the bright disk of NGC 6946), where the cold/warm dust split is less pronounced (or disappears in the free-free-FIR plot, Fig. 7 middle).
 |
Fig. 7 Scale-by-scale correlation between the FIR emission and the observed 20 cm RC (top), the free-free (middle), and the synchrotron (bottom) emissions in NGC 6946. The horizontal line shows rw = 0.5, the threshold for detecting a correlation. Larger rw(a) corresponds to more highly correlated structures. These figures illustrate that, on scales smaller than 4 kpc, the FIR-synchrotron correlation is weaker than the FIR-free-free correlation. |
6.3. FIR/radio ratio map
To determine variations in the radio-FIR correlation across the disk of NGC 6946, we constructed a logarithmic FIR/radio ratio map using the 20 cm “synchrotron” map and a FIR42−122μm (following Helou et al. 1985) luminosity map derived by integrating the spectral energy distribution (SED) pixel-by-pixel (Aniano et al. 2012). According to the convention of Helou et al. (1985), q is defined as: 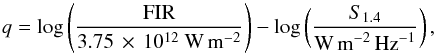 with S1.4 the synchrotron 20 cm flux. The resulting map is shown in Fig. 8. Only pixels detected above the 3σ level in each radio and FIR map were considered. The mean q across the galaxy is 2.22 ± 0.10 with 0.10 the standard deviation. In star-forming regions we find q = 2.30–2.40 which agrees well with the value derived by Yun et al. (2001) for a sample of nearby galaxies (with a mean value of q = 2.34). In the inter-arm regions, q decreases to values lower than 2.0. Hence, spiral arms are easily discernible in the q map.
with S1.4 the synchrotron 20 cm flux. The resulting map is shown in Fig. 8. Only pixels detected above the 3σ level in each radio and FIR map were considered. The mean q across the galaxy is 2.22 ± 0.10 with 0.10 the standard deviation. In star-forming regions we find q = 2.30–2.40 which agrees well with the value derived by Yun et al. (2001) for a sample of nearby galaxies (with a mean value of q = 2.34). In the inter-arm regions, q decreases to values lower than 2.0. Hence, spiral arms are easily discernible in the q map.
 |
Fig. 8 Synchrotron-FIR correlation (q) overlaid with contours of the star formation traced by free-free emission with contour levels of 20, 50, 100, 200, 400 μJy/beam (top), the ordered magnetic field traced by the linearly polarized intensity PI with contour levels of 85, 120, 160 μJy/beam (middle) and the turbulent magnetic field (Isyn − PI/0.75) with contour levels of 0.3, 0.6, 1, 2, 25, 32 mJy/beam (bottom) in NGC 6946. |
The free-free emission provides a proper measure for the present-day SFR (e.g. Murphy et al. 2011). The upper panel in Fig. 8 shows a good correlation between q and the free-free emission (contours), in agreement with the important role of SF in controling the radio-FIR correlation7. Besides SF, magnetic fields also seem to play a role as suggested by Fig. 8 (middle) where we observe a correspondence between small q values and peaks of the polarized intensity. Furthermore, there is a good agreement between high q values and the turbulent magnetic field (Fig. 8 bottom). Is there any dependency or competition between SF and magnetic fields in controling the radio-FIR correlation? A more quantitative comparison between q, SFR, and magnetic fields is given in Sect. 7.
7. Discussion
In the following, we discuss the variations in the synchrotron-FIR correlation across the disk of NGC 6946 as a function of radiation field (important for the dust heating), star formation and magnetic fields. We further investigate possible connections between SF and the ISM components, magnetic fields and gas. This will help us to understanding the origin of the observed synchrotron-FIR correlation in this galaxy.
7.1. Correlations versus radiation field
The spatial variations in q may mean that the slope of the correlation is not constant. The higher q, e.g., in the arms rather than in the inter-arm regions can be translated as a larger slope (b) of the synchrotron-FIR correlation in the arms than in the inter-arm regions (a larger arm/inter-arm slope was also found in M 51 by Dumas et al. 2011). Similarly, the good correspondence between q and star formation (Sect. 7.3) implies that the slope of the synchrotron-FIR correlation is higher in SF regions and lower in between the arms and outer disk. However, if we consider that the synchrotron-FIR correlation originates from massive SF, no correlation would be expected in regions devoid of SF. Such information on the quality of the correlation cannot be extracted from the q map. In order to investigate both the slope and the quality of the correlation, i.e. the correlation coefficient rc, in SF regions and regions with no SF, we derive the classical correlations in regimes of well-defined properties.
The radiation field is one of the properties which sets the dust heating. Since it is fed by UV photons from the SF regions as well as photons from old and low mass stars (that contribute significantly to the diffuse ISRF), the radiation field could provide a proper defining parameter here. Taking advantage of the radiation field map (see Fig. 1, right), we derive the radio-FIR correlation separately for regions where the main heating source of the dust is either SF or the diffuse ISRF. Along the spiral arms and in the central disk, the radiation field has U > 1.3 U⊙, with U⊙ being the corresponding radiation field in the solar neighborhood, and it is smaller between the arms and in the outer disk (see Fig. 1). Hence, U = 1.3 U⊙ is our criterion8 to differentiate regimes with ISRF-fed from SF-fed radiation fields. Table 7 lists the results of the 20 cm synchrotron-FIR correlation analysis for both monochromatic and bolometric FIR emissions in the two defined regimes.
The slope b of the correlations is indeed shallower in the ISRF than that in the SF regime, in agreement with the q map. However, apart from the synchrotron correlation with the warm dust (70 μm) emission, the correlations in the ISRF regime are as good as those in the SF regime (compare rc values). This is also the case for the bolometric FIR-synchrotron correlation.
It is worth mentioning that, among the FIR bands, the 100 μm emission has about the same slope as the bolometric FIR versus the synchrotron emission. This can be explained by the fact that the peak of the FIR SED occurs around 100 μm in this galaxy (Dale et al. 2012).
Synchrotron-FIR/gas correlation in different regimes of radiation fields UISRF and USF.
7.2. Correlations versus magnetic fields
In the inter-arm regions of NGC 6946, the two magnetic arms are well traced in the 20 cm synchrotron map (Fig. 3) and show lower q values. A lower q or a smaller FIR/synchrotron ratio indicates that the synchrotron emission is less influenced than the FIR emission by the absence of SF in the inter-arm regions. This can be explained by different dependencies of the FIR and synchrotron emission on SF, or that other mechanisms than SF regulate the synchrotron emission. The synchrotron emission is a function of the total magnetic field strength and CRE density. Thus, using the synchrotron emission as a tracer of SF implies that both the magnetic field and the CRE density are related to SF. This seems plausible since supernovae produce CREs and induce a turbulent magnetic field via strong shocks in SF regions (e.g. Reynolds et al. 2012). However, CREs diffuse and propagate away from their birth places into the magnetized ISM on large scales, where the total magnetic field is dominated by the uniform or ordered field. The origin of the ordered magnetic field can be linked to the dynamo effect on galactic scales (e.g. Beck et al. 1990, 1996) and is not correlated with SF9 (e.g. Chyży 2008; Krause 2009; Fletcher et al. 2011). Therefore in NGC 6946, magnetic arms seem to compensate for the lack of synchrotron emission in the inter-arms as shown by the anti-correlation between q and the linearly polarized intensity PI contours in Fig. 8 (middle panel).
It is also instructive to investigate the role of the magnetic fields responsible for the synchrotron emission in places with high q (and high SF). Figures 6 and 8 show a good correspondence between high q regions and Btur, Btot. The scatter plot in Fig. 9a shows that q versus Btot and Btur obeys the following power-law relations: 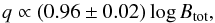 (10)and
(10)and 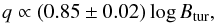 (11)obtained using the bisector method. Both fits have a dispersion of 0.07 dex. Hence, the FIR-to-synchrotron flux ratio linearly changes with the total magnetic field strength. Studying similar linearity and also the flatter q-Btur correlation in other galaxies would be of high interest.
(11)obtained using the bisector method. Both fits have a dispersion of 0.07 dex. Hence, the FIR-to-synchrotron flux ratio linearly changes with the total magnetic field strength. Studying similar linearity and also the flatter q-Btur correlation in other galaxies would be of high interest.
7.3. Correlations versus star formation
We now aim to characterize the relation between q and SF. We first derive the SF surface density (ΣSFR) using the de-reddened Hα map. The diffuse emission is excluded by masking regions where the free-free 20 cm flux falls below a threshold value (0.05 mJy, that is the minimum flux of the detected Hii regions by Lacey et al. 1997). The nucleus was also subtracted as the optically thin condition does not hold there (τHα > 1) and also because of its anomalous properties (for details see Murphy et al. 2011). The de-reddened Hα luminosity is converted to SFR using the relation calibrated by Murphy et al. (2011) for NGC 6946: 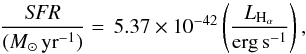 (12)where LHα is the Hα luminosity density. ΣSFR (in units of M⊙ yr-1 kpc-2) is then calculated. The power-law behavior of q versus ΣSFR is given by:
(12)where LHα is the Hα luminosity density. ΣSFR (in units of M⊙ yr-1 kpc-2) is then calculated. The power-law behavior of q versus ΣSFR is given by: 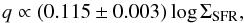 (13)with a Pearson correlation coefficient of rc = 0.8 and a dispersion of 0.05 dex (Fig. 9b). Hence, the FIR-to-synchrotron flux ratio changes with a much flatter power-law index with ΣSFR than with Btot or Btur.
(13)with a Pearson correlation coefficient of rc = 0.8 and a dispersion of 0.05 dex (Fig. 9b). Hence, the FIR-to-synchrotron flux ratio changes with a much flatter power-law index with ΣSFR than with Btot or Btur.
 |
Fig. 9 Radio-IR correlation (q-parameter) versus total and turbulent magnetic field strength a) and star formation surface density ΣSFRb). The magnetic field strength-ΣSFR relation is shown for the total, turbulent c), and the ordered magnetic field strength measured by the degree of polarization d). The lines in the upper panels are the bisector fits. The solid lines in c) and d) show the ordinary least square fit, and the dashed line the bisector fit. In panel d), the binned data points (diamonds) are fitted for ΣSFR ≳0.01 M⊙ yr-1 kpc-2 (solid line). In panels a) and c), the total magnetic field is shifted up by 0.3 units for clarity. The nucleus is not included in these analysis. |
7.4. Connection between star formation and magnetic fields
As discussed above, star formation can regulate the magnetic field in galaxies. Therefore, understanding their relationship is important. In Fig. 9c, we show a good correlation between ΣSFR and both Btot (rc = 0.69 ± 0.03) and Btur (rc = 0.67 ± 0.03). The bisector fit leads to a power-law proportionality for both Btot and Btur vs. ΣSFR: ![\begin{eqnarray} &&{\rm log}\,{B}_{\rm tot} \propto ( 0.14\pm 0.01)\,{\rm log} \, \Sigma_{\rm SFR}, \\[4mm] &&{\rm log}\,{B}_{\rm tur} \propto ( 0.16\pm 0.01)\,{\rm log} \,\Sigma_{\rm SFR}, \end{eqnarray}](/articles/aa/full_html/2013/04/aa20249-12/aa20249-12-eq202.png) with dispersions of 0.08 and 0.06 dex, respectively. Equation (14) reflects a process where the production of the total magnetic field scales with SF activity. This process probably has a common origin with the production of Btur as indicated by the similar slopes in Eqs. (14) and (15). Feedback mechanisms associated with star formation, such as supernova and strong shocks, produce an increase in turbulence. These could amplify small-scale magnetic fields by a turbulent dynamo mechanism where kinetic energy converts to magnetic energy (e.g. Beck et al. 1996; Gressel et al. 2008).
with dispersions of 0.08 and 0.06 dex, respectively. Equation (14) reflects a process where the production of the total magnetic field scales with SF activity. This process probably has a common origin with the production of Btur as indicated by the similar slopes in Eqs. (14) and (15). Feedback mechanisms associated with star formation, such as supernova and strong shocks, produce an increase in turbulence. These could amplify small-scale magnetic fields by a turbulent dynamo mechanism where kinetic energy converts to magnetic energy (e.g. Beck et al. 1996; Gressel et al. 2008).
On the other hand, there is no correlation between Bord (as traced by polarized intensity) and ΣSFR for the whole range of parameters (rc = 0.14 ± 0.02, see the crosses in Fig. 9d). However, a weak anti-correlation (rc = −0.25 ± 0.5) with a slope of b = −0.24 ± 0.1 is found for high ΣSFR (≳0.01 M⊙ yr-1 kpc-2), after binning the data points with a width of 0.5 (see the red diamonds in Fig. 9d). An anti-correlation for large ΣSFR is also visible when comparing the PI and the SF contours in Fig. 8, where no polarized emission is associated with the optical spiral arms. Using the wavelet analysis, an anti-correlation between PI and Hα emission was already found by Frick et al. (2001) on scales equivalent to the width of the spiral arms. All taken together, this suggests that the production of Bord could be suppressed along the spiral arms and in SF regions. An efficient dynamo action in the inter-arm regions could produce a regular field that is anti-proportional to ΣSFR, as shown for NGC 6946 (see Beck 2007; Rohde et al. 1999).
Comparison with a similar study in another spiral galaxy, NGC 4254, is instructive. This galaxy is a member of the Virgo galaxy cluster that is experiencing a gravitational encounter at the cluster’s periphery (e.g. Chyży et al. 2007), or ram pressure due to the galaxy’s motion through the intracluster medium (Murphy et al. 2009), or both of them (Vollmer et al. 2005). Both tidal forces and ram pressures can compress or shear the magnetic fields. Interestingly, NGC 4254 also shows two different trends of Bord vs. ΣSFR, with no general correlation between them (Chyży 2008). The division of the two-way behavior, however, occurs at a larger ΣSFR (≃0.02 M⊙ yr-1 kpc-2) than in NGC 6946. Moreover, in NGC 4254, the slope of Btur − ΣSFR relation (0.26 ± 0.01) is larger than that of Btot − ΣSFR relation (0.18 ± 0.01), unlike in NGC 6946. The slope of Btur − ΣSFR relation is also larger in NGC 4254 than in NGC 6946 (0.16 ± 0.01, see Eq. (15)). Hence, although the two galaxies resemble each other in their general magnetic field-ΣSFR behavior, they differ in the details of these connections. These differences could be related to different contributions of Bord and Btur to Btot, as a similar scaling relation holds between Btot and ΣSFR in these galaxies. Hence, investingating Bord-to-Btur ratio (Bord/Btur) could be instructive. In NGC 4254, Bord/Btur shows a general decreasing trend with increasing ΣSFR for the whole range of values (see Fig. 7b of Chyży 2008). In NGC 6946, such a decreasing trend is indicated only for ΣSFR ≳ 0.01 M⊙ yr-1 kpc-2 (Fig. 10). For small ΣSFR values, Bord/Btur is larger in NGC 4254 than in NGC 6946.
In the Virgo Cluster galaxy NGC 4254, the strongest ordered field is found in the outer arms, dominated by anisotropic turbulent field and is probably a product of shearing/stretching forces caused by weak gravitational interaction (Chyży 2008) and/or ram pressure (Murphy et al. 2009) in the cluster environment. Such forces can transform Btur into Bord in the outer arms of NGC 4254 where ΣSFR is low (particularly in the southern arm). This could cause the steeper log (Btur) − log (ΣSFR) than log (Btot) − log (ΣSFR) relation in NGC 4254.
In spite of the magnetic arms, NGC 6946 yields smaller values of Bord/Btur at low SFR compared to NGC 4254 because it does not experience shearing due to tidal forces and/or ram pressures inserted by a cluster environment. The total field has similar properties in both galaxies (same slope), because the shearing does not change the total field strength. It only transforms a turbulent field into an ordered field. This could explain the flatter slope of log (Btur) − log (ΣSFR) in NGC 6946 than that in NGC 4254.
Therefore, we might expect that, in normal galaxies like NGC 6946, the slope of log (B) vs. log (ΣSFR) is similar for both Btur and Btot, while it is steeper for Btur than for Btot in galaxies interacting with the cluster environment (like NGC 4254).
 |
Fig. 10 Ratio of the Ordered-to-turbulent magnetic field strengths Bord/Btur vs. star formation surface density ΣSFR in NGC 6946. The dashed line shows the corresponding fitted line in NGC 4254 shifted by 0.2 along the x-axis (y = −0.32 x − 0.7, see Fig. 7b in Chyży 2008). |
7.5. Correlations with neutral gas
Some of the radio-FIR correlation models are based on a coupling between the magnetic field B and gas density ρ (Helou & Bicay 1993; Niklas & Beck 1997; Hoerneset al. 1998; Murgia et al. 2005). Physically, the B-ρ coupling could be caused by the amplification of the Magneto Hydrodynamic (MHD) turbulence until energy equipartition is reached (Groves et al. 2003). This model has the advantage of 1) producing the radio-FIR correlation where the FIR is dominated by dust heated by older stellar populations or the ISRF (e.g. Hoerneset al. 1998) and 2) naturally producing a local radio-FIR correlation, breaking down only on scales of the diffusion length of the CREs ldif (as discussed in Niklas & Beck 1997).
Table 7 shows that the total molecular and atomic gas surface density ΣGas in M⊙ pc-2 is correlated with the synchrotron emission in both the SF and the ISRF regimes. The correlation, in the ISRF regime, is however not as tight as in the SF regime (see rc values in Table 7) because the inter-arm regions (heated by the ISRF) are filled with low-density atomic HI gas which appears to have a weaker correlation with synchrotron emission compared to dense molecular gas (Beck 2007). In M 51, Tilanus et al. (1988) found a much weaker correlation between the diffuse HI gas and the synchrotron emission.
A tight correlation between ΣGas and the total magnetic field holds for the entire galaxy (Fig. 11). The total magnetic field Btot vs. ΣGas follows a power-law relation, 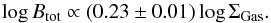 (16)The dispersion of the fit is about 0.04. In the ISRF regime, the Btot − ΣGas correlation is weaker than in the SF regime, although the power-law indices are similar (Table 7).
(16)The dispersion of the fit is about 0.04. In the ISRF regime, the Btot − ΣGas correlation is weaker than in the SF regime, although the power-law indices are similar (Table 7).
Niklas & Beck (1997) suggested that the tight radio-FIR correlation can be reached by considering the coupling between the FIR emission and the gas density via the Kennicutt-Schmidt (KS) relation between ΣSFR and ΣGas (Schmidt 1959; Kennicutt 1998). Interestingly, in NGC 6946, not only does the KS relation hold, but also it is very similar in the ISRF and SF regimes (Table 7 and Fig. 12). Hence, it seems that in the ISRF regime, the lower gas density and the weaker radiation field conspire to hold the KS relation but with a weaker ΣSFR − ΣGas correlation. In the SF regime, the ΣSFR − ΣGas power-law index of ~1.3 agrees with Kennicutt (1998). The KS index in both regimes agrees with the global value of 1.46 ± 0.29 for NGC 6946 presented in Bigiel et al. (2008).
 |
Fig. 11 Correlation between the magnetic field and the total gas surface density ΣGas. Also shown is the bisector fit. The nucleus is not included in this analysis. |
An equipartition between the CRE and magnetic field energy densities is needed in the B-ρ model of Niklas & Beck (1997). This implies that the energy density of CREs (and the synchrotron luminosity) is determined by the field strength alone, and neither the CRE production rate nor the CRE escape probability affects it. On small spatial scales, however, e.g. in supernova remnants, the energy density of the particles may exceed strongly the energy density of the magnetic field. A static pressure equilibrium could then be achieved when the components of the ISM have been relaxed on larger scales (e.g. determined by a scale height of gas clouds of a few 100 pc). Hence, the local synchrotron-FIR correlation should break down on small spatial scales where equipartition is not valid anymore. Looking for such a break in the synchrotron-FIR correlation in NCG 6946, we refer to our scale-by-scale correlation study. Figure 7 shows that the smallest scale on which the synchrotron –70 μm correlation holds, i.e. rw ~ 0.5, is a ~ 1.7 kpc (on scales smaller, rw < 0.5 and hence it is below the threshold value for the acceptability of the correlation). This scale can be translated as ldif or the scale of the static pressure equilibrium, according to the B-ρ model (Niklas & Beck 1997). However, this is not certain, since the colder dust traced by the longer FIR wavelengths do not show similar break rw < 0.5 when correlating with the synchrotron emission. Nevertheless, the synchrotron –70 μm correlation has been used in previous studies to determine the CRE diffusion length. For instance, using the Spitzer MIPS 70 μm data, Murphy et al. (2008) estimated ldif in a sample of nearby galaxies by applying an image-smearing method. Using the same FIR wavelength (70 μm), our derived ldif agrees with the best-fitted disk value of Murphy et al. (2008) in NGC 6946, ldif = 1.6 ± 0.1 kpc, although the two methods are different.
 |
Fig. 12 Correlations between the ΣSFR [M⊙ yr-1 kpc-2] and the total gas surface density ΣGas [M⊙ pc-2] for the ISRF (left) and SF regimes (right) as defined by U > 1.3 U⊙. Also shown are the bisector fits. The nucleus is not included in this analysis. |
7.6. The origin of the radio-FIR correlation in NGC 6946
The proposed models to explain the radio-FIR correlation in galaxies include:
-
a)
The calorimeter model of Völk (1989). Thismodel assumes that CREs are completely trapped in their hostgalaxies and that the galaxies are optically thick for thedust-heating stellar UV photons. In the case of complete CREtrapping, a synchrotron spectral index of αn ≥ 1.0 is expected, i.e.synchrotron and inverse Compton losses are the dominantcooling mechanism of CREs.
-
b)
The optically-thin model of Helou & Bicay (1993) and Niklas & Beck (1997). The dust-heating UV photons and the cosmic rays are assumed to have a common origin in massive star formation similar to the model of Völk (1989), but in this case both photons and cosmic rays can escape the galaxy. Although different distribution for the CREs energy density is applied by Helou & Bicay (1993) and Niklas & Beck (1997) (also see Hoerneset al. 1998; Murgia et al. 2005), the basic condition of B-ρ coupling is a common assumption in these models, as discussed in Sect. 7.5.
-
c)
The calorimeter model of Lacki et al. (2010) in starbursts, in which cosmic ray protons lose all of their energy and produce secondary electrons and positrons whose synchrotron emission keeps the radio-FIR correlation linear. This was motivated by Thompson et al. (2006) who suggested that Bremsstrahlung and ionization losses are more important in starburst galaxies leading to a flat αn (≃0.75). According to Lacki et al. (2010), the CRE density is not proportional to the SFR in starbursts, in contrast to both the calorimeter model of Völk (1989) and the “optically-thin” models of Helou & Bicay (1993) and Niklas & Beck (1997), who explained the observed non-linear synchrotron-FIR correlation in the Shapley-Ames galaxies (presented in Niklas 1997) by assuming a SFR related synchrotron emission and B-ρ coupling.
In NGC 6946, the complete CRE trapping assumed in the model (a) does not apply, since depending on the location, the synchrotron spectral index changes between a flatter αn ≃ 0.6 (in the star-forming regions) and a steeper αn ≃ 1 (in regions of strong ordered magnetic field, Sect. 4). This indicates the presence of various loss mechanisms of the CREs energy leading to a flatter nonthermal spectrum (mean αn ≃ 0.8) than that produced by the efficient synchrotron and inverse Compton losses (αn = 1.0–1.2) for theentire galaxy.
Although NGC 6946 is classified as a normal star-forming galaxy, it would be instructive to see its position in respect to the model (c). The synchrotron-FIR correlation is non-linear with the warmer dust globally (Table 5), or the dust heated by the SF (Table 7). On the contrary, a linearity is found for the colder dust globally (Table 5), or the dust heated by the ISRF (Table 7). The linearity of the correlation cannot be explained by secondary electrons & positrons suggested for dense gas condition in starbursts, due to the low gas density of the ISRF regime in NGC 6946 (in agreement with Murphy 2009).
As shown in Sect. 7.5, we already obtained indications for a B − ρ coupling in NGC 6946 which is in favor of the model (b). How this model could also reproduce the observed slope of the synchrotron-FIR correlation in the SF and the ISRF regimes are detailed as follows:
In the SF regime, the KS relation gives 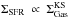 , with the KS index of 1.3 ± 0.05 (Table 7). Our data show that the FIR luminosity is proportional to ΣSFR with a slope of 0.95 ± 0.05. Hence,
, with the KS index of 1.3 ± 0.05 (Table 7). Our data show that the FIR luminosity is proportional to ΣSFR with a slope of 0.95 ± 0.05. Hence, 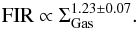 We note that the same proportionality is derived by directly correlating between the FIR luminosity and ΣSFR, as expected. From Eq. (6), the equipartition magnetic field is given by:
We note that the same proportionality is derived by directly correlating between the FIR luminosity and ΣSFR, as expected. From Eq. (6), the equipartition magnetic field is given by: 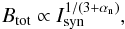 with αn = 0.8 ± 0.1 (Sect. 4). In Sect. 8.2, we found that
with αn = 0.8 ± 0.1 (Sect. 4). In Sect. 8.2, we found that 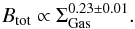 Following Niklas & Beck (1997) and Hoerneset al. (1998), we assume that the scale height of the neutral gas is equal to that of the dust and is constant. Thus, ΣGas can be replaced by the gas volume density in the above proportionalities resulting in
Following Niklas & Beck (1997) and Hoerneset al. (1998), we assume that the scale height of the neutral gas is equal to that of the dust and is constant. Thus, ΣGas can be replaced by the gas volume density in the above proportionalities resulting in 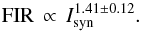 (17)This is in excellent agreement with the observed synchrotron-FIR correlation in the SF regime with the slope of bSF = 1.33 ± 0.04 (Table 7).
(17)This is in excellent agreement with the observed synchrotron-FIR correlation in the SF regime with the slope of bSF = 1.33 ± 0.04 (Table 7).
A similar calculation for the ISRF regime leads to 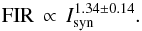 (18)The slope is higher than the observed slope of bSF = 1.05 ± 0.04 by about 2σ errors (28%).
(18)The slope is higher than the observed slope of bSF = 1.05 ± 0.04 by about 2σ errors (28%).
Xu et al. (1994) found a linear correlation between the 20 cm synchrotron and cold dust emission in a sample of late-type spirals. They explained this correlation by considering intermediate mass stars (5–20 M⊙) as a heating source of cold dust and synchrotron emission, since these stars are supernova progenitor as well. It is also likely that, in NGC 6946 which is a late-type spiral with a good 20 cm synchrotron-cold dust correlation (e.g. see Table 5), the intermediate mass stars provide the non-ionizing UV photons to heat the cold dust (which emit at longer FIR wavelengths). As such, these UV photons provide the bulk of the ISRF in NGC 6946.
In the previous sections, we showed that the local radio-FIR correlation varies as a function of not only SFR but also dust heating sources, magnetic fields, and gas density; i.e., the ISM properties. The SF and ISM are continuously influencing each other: Stars form within the dense and cold regions of the ISM, molecular clouds, and replenish the ISM with matter and energy. Hence, the local radio-FIR correlation is a probe for the SF − ISM interplay which is partly explained through scaling relations such as the KS relation between ΣSFR and gas surface density, and the relation between ΣSFR and the magnetic field strengths (Sect. 7.4).
The global radio-FIR correlation is known to be a tracer of SF. Among the SF-based theories to explain the global radio-FIR correlation, our local studies match with those considering a coupling between the magnetic field and gas density, as the radio-FIR correlation also holds in regions with no massive SF, e.g. in the inter-arm regions and the outer disk (Sect. 7.1). This shows that a balance between the gas and magnetic field/CRE pressure is an unavoidable condition for the correlation. Apart from this, the global radio-FIR correlation as a tracer of SF still applies since the integrated radio and FIR fluxes are weighted toward more luminous regions of galaxies, i.e. the SF regions.
7.7. ISM and propagation of CREs
Propagating through the ISM, CREs can experience various energy losses via ionization, bremsstrahlung, adiabatic, synchrotron, and inverse-Compton losses that change the power-law index of the energy distribution of these particles or equivalently the nonthermal spectral index, αn. The maps of the synchrotron spectral index (Sect. 4), magnetic fields (Sect. 5), and radiation field (Sect. 3), provide direct information on the main cooling mechanisms of CREs, as well as the cooling timescale and diffusion scalelength of CREs in NGC 6946. As shown in Fig. 4, there is a difference in the spectral indices of Δαn ≃ 0.5 between the star-forming regions and the magnetic arms/inter-arm regions. This is expected if the main mechanisms of energy losses for the electrons are synchrotron emission and inverse Compton scattering (Longair 1994). The CRE cooling timescale tcool (in units of yr) associated with the two dominant processes can be derived from the following formula (Murphy et al. 2008): 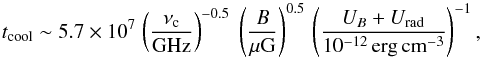 (19)where νc ~ BE2 is the critical frequency at which a CRE emits most of its energy E. UB = B2/(8π) is the magnetic field energy density, and Urad is the radiation energy density.
(19)where νc ~ BE2 is the critical frequency at which a CRE emits most of its energy E. UB = B2/(8π) is the magnetic field energy density, and Urad is the radiation energy density.
Using a simple random walk equation, CREs will diffuse over a distance lcool = (DE tcool)0.5 before losing all of their energy to synchrotron and inverse Compton losses, with DE being the energy-dependent diffusion coefficient. Assuming that the diffusion length scale of 1.7 kpc, obtained from the synchrotron-FIR correlation (Sect. 7.5), is equivalent to the cooling scale length lcool, DE can be estimated independently. Mathis et al. (1983) determined the radiation field energy density in starlight of Urad = 8.64 × 10-13 U erg cm-3. However, Urad should also include the dust emission energy density, UFIR = 5 × 10-13 U erg cm-3 as well as the cosmic microwave background radiation energy density, UCMB = 4.17 × 10-13 erg cm-3 (Draine 2011). Therefore, we use a more general form of Urad = (4.17 + 13.64 U) × 10-13 erg cm-3. For the entire galaxy, U ≃ 2 U⊙ and B ≃ 18 μG. Thus, UB ≃ 1.3 × 10-11 erg cm-3 and Urad ≃ 3.1 × 10-12 erg cm-3. Substituting these values in Eq. (19) results in tcool ≃ 1.3 × 107 yr. The CRE diffusion coefficient is then DE ≃ 6.8 × 1028 cm2 s-1. Assuming that DE changes with energy as DE = D0 (E/GeV)0.5 (e.g. Ginzburg et al. 1980), we derive the normalization factor D0 = 4.6 × 1028 cm2 s-1 for the 2.2 GeV CREs.
As discussed in Sect. 6.2, the drop in the synchrotron-FIR correlation on the larger scales of about 2.5 kpc is related to a lack of FIR emission from the magnetic arms (in the inter-arm regions), where diffused CREs experience synchrotron loss. Hence, we assume that the cooling length scale is lcool ≃ 2.5 kpc in the magnetic arms, where the radiation field is U ≃ U⊙ and the magnetic field B ≃ 15 μG. These lead to a cooling time scale of tcool = 1.7 × 107 yr and a diffusion coefficient of D0 = 7.0 × 1028 cm2 s-1 for the 2.4 GeV CREs.
The above estimates of the CRE diffusion coefficient agree with both observational (Strong & Moskalenko 1998; Dahlem et al. 1995) and theoretical (e.g. Roediger et al. 2007) estimates of DE ≃ (1 − 10) × 1028 cm2 s-1 and is about 10 times larger than the diffusion coefficient estimated on small scales in the turbulent medium near 30Dor (Murphy et al. 2012). These demonstrate the effect of the ISM and CRE cooling on the synchrotron-FIR correlation on kpc-scales. On these (i.e., ≳1 kpc) scales, the CRE population is likely to be dominated by old/diffuse particles accelerated in past generations of star formation. These particles may even be re-accelerated by passing shocks in the ISM, and thus will have little memory of their original birth sites in star-forming regions. Consequently, the propagation of these particles is very sensitive to the ISM conditions.
On sub-kpc scales, however, the CRE population is more likely to be dominated by younger CREs, which are still close to their production sites in star-forming complexes. The energy distribution of these particles is more influenced by the age and activity of their acceleration sources rather than the conditions of the quasi-state ISM. This is in agreement with Murphy et al. (2008) who showed that the current diffusion length of CREs from star-forming structures is largely set by the age of the star-formation activity rather than the cooling mechanisms in the general ISM.
8. Summary
Highly resolved and sensitive Herschel images of NGC 6946 at 70, 100, 160, and 250 μm enable us to study the radio-FIR correlation, its variations and dependencies on star formation and ISM properties across the galactic disk. Our study includes different thermal/nonthermal separation methods. The radio-FIR correlation is calculated using the classical pixel-by-pixel correlation, wavelet scale-by-scale correlation, and the q-method. The most important findings of this study are summarized as follows:
-
The slope of the radio-FIR correlation across the galaxy varies asa function of both SFR density and magnetic field strength. Thetotal and turbulent magnetic field strengths are correlated with ΣSFRwith a power-law index of 0.14 and 0.16, respectively (Eqs. (14),(15)). This indicates efficient production of turbulent magneticfields with increasing turbulence in actively starforming regions,in general agreement with Chyży (2008).
-
In regions where the main heating source of dust is the general ISRF, the synchrotron emission correlates better with the cold dust than with the warm dust. However, there is no difference between the quality of the correlations for colder/warmer dust in regions of a strong radiation field powered by massive stars. This is expected if warmer dust is mainly heated by SF regions (where synchrotron emission is produced by young CREs/turbulent magnetic field), and colder dust by a diffuse ISRF across the disk (where synchrotron emission produced by old, diffused CREs/large-scale magnetic field).
-
The synchrotron-FIR correlation in strong radiation fields can be well explained by the optically-thin models where massive stars are the common source of the radio and FIR emission. The intermediate-mass stars seem to be a more appropriate origin for the observed synchrotron-FIR correlation in the ISRF regime.
-
The synchrotron spectral index map indicates a change in the cooling of CREs when they propagate from their place of birth in star-forming regions across the disk of NGC 6946. Young CREs emitting synchrotron emission with a flat spectrum, αn = 0.6 ± 0.1, are found in star-forming regions. Diffused and older CREs (with lower energies) emit synchrotron emission with a steep spectrum, αn = 1.0 ± 0.1, along the so-called “magnetic arms” (indicating strong synchrotron losses) in the inter-arm regions. The mean synchrotron spectral index is αn = 0.8 ± 0.1 across the disk of NGC 6946.
-
The cooling scale length of CREs determined using the multi-scale analysis of the synchrotron-FIR correlation provides an independent measure of the CRE diffusion coefficient. Our determined value of D0 = 4.6 × 1028 cm2 s-1 for the 2.2 GeV CREs agrees with the observed values in the Milky Way. This agreement suggests that, reversing our argument and assuming Milky Way values for DE, the cooling scale length of CREs due to the synchrotron and inverse-Compton energy losses appear to be consistent with scales on which the radio-FIR correlation is weak on kpc scales. This indicates that the interstellar magnetic fields can affect the propagation of the old/diffuse CREs on large scales.
Smaller values of Te are reported from the measurements in the Milky Way (e.g. Haffner et al. 1999; Madsen et al. 2006). Assuming Te = 7000 K, the thermal fraction would decrease by about 23%.
In a completely ordered magnetic field, the maximum degree of linear polarization is about 0.75 (e.g. Westfold 1959).
The wavelet analysis was performed using the code described by Dumas et al. (2011).
This is determined by considering the radiation field in the solar neighborhood as a proxy to the diffuse ISRF optimized for enough number of points in between the arms and outer disk of NGC 6946 at 70 μm (a 5σ level statistically significant correlation or t = 11 for 70 μm–synchrotron correlation).
The ordered magnetic field can also be produced by compressions and shear of the anisotropic or turbulent field in dense gas, known to be the origin of the strong ordered field in the central 6 kpc gas concentration of NGC 6946 (Beck 2007).
Acknowledgments
We are grateful to A. Ferguson for kindly providing us with the Hα data. The combined molecular and atomic gas data were kindly provided by F. Walter. F.S.T. acknowledges the support by the DFG via the grant TA 801/1-1.
References
- Aniano, G., Draine, B. T., Gordon, K. D., & Sandstrom, K. 2011, PASP, 123, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Aniano, G., Draine, B. T., Calzetti, D., et al. 2012, ApJ, 756, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, R., Sargent, A. I., Scoville, N. Z., Lo, K. Y., & Scott, S. L. 1985, ApJ, 298, L21 [Google Scholar]
- Beck, R. 1991, A&A, 251, 15 [NASA ADS] [Google Scholar]
- Beck, R. 2007, A&A, 470, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., & Hoernes, P. 1996, Nature, 379, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Wielebinski, R., & Kronberg, P. P. 1990, Galactic and intergalactic magnetic fields; Proc. 140th IAU Symp., Heidelberg, Germany, June 19–23, 1989 [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Wilson, C. D., Pohlen, M., et al. 2010, A&A, 518, L65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berkhuijsen, E. M., Beck, R., & Hoernes, P. 2003, A&A, 398, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biermann, P. L., Langer, N., Seo, E.-S., & Stanev, T. 2001, A&A, 369, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Boomsma, R., Oosterloo, T. A., Fraternali, F., van der Hulst, J. M., & Sancisi, R. 2008, A&A, 490, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boulanger, F., & Perault, M. 1988, ApJ, 330, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Chyży, K. T. 2008, A&A, 482, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., Bomans, D. J., Krause, M., et al. 2007, A&A, 462, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, J. G., Persson, S. E., & Searle, L. 1984, ApJ, 281, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Crosthwaite, L. P., & Turner, J. L. 2007, AJ, 134, 1827 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlem, M., Lisenfeld, U., & Golla, G. 1995, ApJ, 444, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Helou, G., Contursi, A., Silbermann, N. A., & Kolhatkar, S. 2001, ApJ, 549, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Aniano, G., Engelbracht, C. W., et al. 2012, ApJ, 745, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Davies, R. D., & Davis, R. J. 2003, MNRAS, 341, 369 [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Dumas, G., Schinnerer, E., Tabatabaei, F. S., et al. 2011, AJ, 141, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, A. M. N., Wyse, R. F. G., Gallagher, J. S., & Hunter, D. A. 1998, ApJ, 506, L19 [Google Scholar]
- Fletcher, A., Beck, R., Shukurov, A., Berkhuijsen, E. M., & Horellou, C. 2011, MNRAS, 412, 2396 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Frick, P., Beck, R., Berkhuijsen, E. M., & Patrickeyev, I. 2001, MNRAS, 327, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, V. L., Khazan, I. M., & Ptuskin, V. S. 1980, Ap&SS, 68, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, S. M., Duric, N., Kirshner, R. P., Goss, W. M., & Viallefond, F. 1999, ApJS, 120, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Pérez-González, P. G., Misselt, K. A., et al. 2004, ApJS, 154, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., Elstner, D., Ziegler, U., & Rüdiger, G. 2008, A&A, 486, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Groves, B. A., Cho, J., Dopita, M., & Lazarian, A. 2003, PASA, 20, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Haffner, L. M., Reynolds, R. J., & Tufte, S. L. 1999, ApJ, 523, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., & Bicay, M. D. 1993, ApJ, 415, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., Soifer, B. T., & Rowan-Robinson, M. 1985, ApJ, 298, L7 [Google Scholar]
- Hoernes, P., Berkhuijsen, E. M., & Xu, C. 1998, A&A, 334, 57 [NASA ADS] [Google Scholar]
- Hughes, A., Wong, T., Ekers, R., et al. 2006, MNRAS, 370, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., Sharina, M. E., & Huchtmeier, W. K. 2000, A&A, 362, 544 [NASA ADS] [Google Scholar]
- Kennicutt, R. C., Jr., 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., Jr., & Evans, II, N. J. 2012, Ann. Rev. A&A, 50, 531 [Google Scholar]
- Kennicutt, R. C., Jr.,Lee, J. C., Funes, S. J., et al. 2008, ApJS, 178, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr.,Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, U., Wielebinski, R., & Beck, R. 1984, A&A, 135, 213 [NASA ADS] [Google Scholar]
- Krause, M. 2009, in Rev. Mex. Astron. Astrofis. Conf. Ser., 36, 25 [Google Scholar]
- Lacey, C., Duric, N., & Goss, W. M. 1997, ApJS, 109, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lacki, B. C., Thompson, T. A., & Quataert, E. 2010, ApJ, 717, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Laine, S., Krause, M., Tabatabaei, F. S., & Siopis, C. 2010, AJ, 140, 1084 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Bigiel, F., et al. 2009, AJ, 137, 4670 [NASA ADS] [CrossRef] [Google Scholar]
- Longair, M. S. 1994, High energy astrophysics, 2, Stars, the galaxy and the interstellar medium [Google Scholar]
- Madsen, G. J., Reynolds, R. J., & Haffner, L. M. 2006, ApJ, 652, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Moustakas, J., Kennicutt, Jr., R. C., Tremonti, C. A., et al. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Murgia, M., Helfer, T. T., Ekers, R., et al. 2005, A&A, 437, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, E. J. 2009, ApJ, 706, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Helou, G., Braun, R., et al. 2006, ApJ, 651, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Helou, G., Kenney, J. D. P., Armus, L., & Braun, R. 2008, ApJ, 678, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Kenney, J. D. P., Helou, G., Chung, A., & Howell, J. H. 2009, ApJ, 694, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Helou, G., Condon, J. J., et al. 2010, ApJ, 709, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Porter, T. A., Moskalenko, I. V., Helou, G., & Strong, A. W. 2012, ApJ, 750, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Niklas, S. 1997, A&A, 322, 29 [NASA ADS] [Google Scholar]
- Niklas, S., & Beck, R. 1997, A&A, 320, 54 [NASA ADS] [Google Scholar]
- Osterbrock, D. E. 1989, in Astrophysics of gaseous nebulae and active galactic nuclei, ed. M. Valley (CA, University Science Books), 422 [Google Scholar]
- Osterbrock, D. E., & Stockhausen, R. E. 1960, ApJ, 131, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price, R., & Duric, N. 1992, ApJ, 401, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, S. P., Gaensler, B. M., & Bocchino, F. 2012, Space Sci. Rev., 166, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Roediger, E., Brüggen, M., Rebusco, P., Böhringer, H., & Churazov, E. 2007, MNRAS, 375, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rohde, R., Beck, R., & Elstner, D. 1999, A&A, 350, 423 [NASA ADS] [Google Scholar]
- Roussel, H. 2012, submitted [arXiv:1205.2576] [Google Scholar]
- Roussel, H., Wilson, C. D., Vigroux, L., et al. 2010, A&A, 518, L66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubin, R. H. 1968, ApJ, 154, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Schinnerer, E., Murphy, E., et al. 2010, ApJ, 714, L190 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Böker, T., Emsellem, E., & Lisenfeld, U. 2006, ApJ, 649, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. D. T., Draine, B. T., Dale, D. A., et al. 2007, ApJ, 656, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., & Moskalenko, I. V. 1998, ApJ, 509, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Tabatabaei, F. S., & Berkhuijsen, E. M. 2010, A&A, 517, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabatabaei, F. S., Beck, R., Krause, M., et al. 2007a, A&A, 466, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabatabaei, F. S., Beck, R., Krügel, E., et al. 2007b, A&A, 475, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabatabaei, F. S., Krause, M., Fletcher, A., & Beck, R. 2008, A&A, 490, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, T. A., Quataert, E., Waxman, E., Murray, N., & Martin, C. L. 2006, ApJ, 645, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Tilanus, R. P. J., Allen, R. J., van der Hulst, J. M., Crane, P. C., & Kennicutt, R. C. 1988, ApJ, 330, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Tsai, C.-W., Turner, J. L., Beck, S. C., et al. 2006, AJ, 132, 2383 [NASA ADS] [CrossRef] [Google Scholar]
- Valls-Gabaud, D. 1998, PASA, 15, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J. 1989, A&A, 218, 67 [NASA ADS] [Google Scholar]
- Vollmer, B., Huchtmeier, W., & van Driel, W. 2005, A&A, 439, 921 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wall, J. V. 1979, QJRAS, 20, 138 [Google Scholar]
- Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Westfold, K. C. 1959, ApJ, 130, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, A. N., & Gordon, K. D. 2000, ApJ, 528, 799 [Google Scholar]
- Xu, C. 1990, ApJ, 365, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C., Lisenfeld, U., & Voelk, H. J. 1994, A&A, 285, 19 [NASA ADS] [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Thermal/nonthermal separation using the standard method
Tabatabaei et al. (2007b) presented a detailed comparison of the TRT thermal/nonthermal separation method to a more conventional method, the so called “standard method”, for M 33. The standard method requires accurate absolute measurements of the brightness temperature at high and low radio frequencies and assumes a priori knowledge of αn. An incomplete frequency coverage of the radio images makes it difficult to find variations in αn, technically, and hence in most cases the thermal/nonthermal components are decomposed assuming a constant αn. Although this assumption does not allow for the study of the change in the CREs energy when they propagate away from SF regions, the standard separation method is often used as it can produce thermal and nonthermal maps using radio continuum data at only two frequencies (at high and low radio band) and more straightforwardly than using, e.g., the TRT method. Here, we derive the thermal/nonthermal distributions from the standard method for NGC 6946. Comparing the results of the standard and the TRT methods could be instructive for similar studies in future.
For a total spectral index, α, obtained from the observed flux densities at frequencies ν1 and ν2 and constant value of the nonthermal spectral index αn, the thermal fraction at frequency ν1 is given by 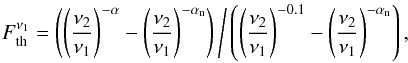 (A.1)(Klein et al. 1984). Then the thermal flux density at frequency ν1,
(A.1)(Klein et al. 1984). Then the thermal flux density at frequency ν1, 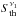 , is obtained from
, is obtained from 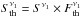 , and the nonthermal flux density
, and the nonthermal flux density 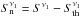 . Using the data at 3.5 and 20 cm for the above formula, and assuming the frequently adopted index αn ≃ 1 (e.g. Klein et al. 1984; Berkhuijsen et al. 2003), the corresponding free-free and synchrotron maps are derived (see also Beck 2007). Figure A.1 shows the resulting maps at 3.5 cm divided by those obtained in Sect. 3 (the standard-to-TRT ratio maps).
. Using the data at 3.5 and 20 cm for the above formula, and assuming the frequently adopted index αn ≃ 1 (e.g. Klein et al. 1984; Berkhuijsen et al. 2003), the corresponding free-free and synchrotron maps are derived (see also Beck 2007). Figure A.1 shows the resulting maps at 3.5 cm divided by those obtained in Sect. 3 (the standard-to-TRT ratio maps).
 |
Fig. A.1 Top: ratio map of the standard-to-TRT based free-free intensity overlaid with contours of the TIR emission. The contour levels are 9, 15, 20, 130, 200 L⊙ kpc-2. Bottom: the same for the synchrotron component. The ratio values are indicated by the bars at the right of each image. |
The standard-to-TRT free-free ratio fluctuates around one in the spiral arms and the central disk indicated by the TIR contours. In the nucleus and its surroundings, however, the ratio exceeds 2. A striking excess of free-free emission from the standard method occurs between the arms in the west and the south. We note that, in these regions, there is no significant emission of Hα as a tracer of the ionized gas, nor 24 or 70 μm as tracers of warm dust, and even from the TIR as a tracer for SF. Hence, the strong diffuse free-free emission in those regions is not real.
The standard-to-TRT synchrotron ratio map resembles the αn map (Fig. A.1). It is close to unity in regions where the assumed αn is close to that obtained from the TRT model. The synchrotron emission is underestimated in regions with αn flatter than the assumed αn = 1. The lack of synchrotron emission is particularly seen in regions with an excess of free-free emission in the west/south of the galaxy discussed above. The synchrotron emission from the SF regions and the nucleus is also underestimated as αn < 1 for those regions (Sect. 4).
All Tables
Same as Table 5 for the 3.5 cm free-free (FF)/synchrotron (SYN) emission separated using the standard method (see Appendix A).
Synchrotron-FIR/gas correlation in different regimes of radiation fields UISRF and USF.
All Figures
 |
Fig. 1 Left: dust optical depth at Hα wavelength τHα overlaid with contours of the Hα emission from NGC 6946. Contour levels are 1, 3, 6, 15, 30, 40 μerg s-1 cm-2 sr-1. The bar at the right shows the values of τHα. Right: radiation field U map (mass-weighted mean starlight heating intensity) of NGC 6946 in units of radiation field in solar neighborhood U⊙ (Aniano et al. 2012), indicated by the bar at the right of the image. The beam area is shown in the lower left corners. |
| In the text | |
 |
Fig. 2 Hα luminosity de-reddened based on τeff versus de-reddening using the TIR luminosity. Also shown are the lines of 1:1 correspondence (dashed) and Y = X − 0.19 (solid). |
| In the text | |
 |
Fig. 3 Free-free (left) and synchrotron emission (right) from NGC 6946 at 3.5 cm (top) and 20 cm (bottom). The angular resolution is 18″ (shown in the lower left corner of the panels) with a grid size of 6″. The bars at the right of the images show the intensity values in mJy/beam. Note that the areas are not the same at 20 cm and 3.5 cm due to their different observed fields. At 20 cm the synchrotron emission is overlaid with contours of linearly polarized intensity (Beck & Hoernes 1996). The contour levels are 70, 120, 160 μJy/beam. |
| In the text | |
 |
Fig. 4 Synchrotron spectral index map of NGC 6946 overlaid with contours of the linearly polarized emission at 6 cm (top) tracing the ordered magnetic field in the sky plane with the same levels as in Fig. 3 and of bright Hα sources (bottom). The Hα contour levels are 18, 24, 35, and 47% of the maximum intensity. The 9 giant Hii regions are indicated (Table 4). The bars at the right of the images show the values of the synchrotron spectral index. |
| In the text | |
 |
Fig. 5 Histogram of the observed radio continuum (gray) and synchrotron spectral index (black) in NGC 6946. |
| In the text | |
 |
Fig. 6 Strength of the total Btot (top) and turbulent Btur (bottom) magnetic fields in NGC 6946. The bars at the top of each image show the magnetic field strength in μ Gauss. |
| In the text | |
 |
Fig. 7 Scale-by-scale correlation between the FIR emission and the observed 20 cm RC (top), the free-free (middle), and the synchrotron (bottom) emissions in NGC 6946. The horizontal line shows rw = 0.5, the threshold for detecting a correlation. Larger rw(a) corresponds to more highly correlated structures. These figures illustrate that, on scales smaller than 4 kpc, the FIR-synchrotron correlation is weaker than the FIR-free-free correlation. |
| In the text | |
 |
Fig. 8 Synchrotron-FIR correlation (q) overlaid with contours of the star formation traced by free-free emission with contour levels of 20, 50, 100, 200, 400 μJy/beam (top), the ordered magnetic field traced by the linearly polarized intensity PI with contour levels of 85, 120, 160 μJy/beam (middle) and the turbulent magnetic field (Isyn − PI/0.75) with contour levels of 0.3, 0.6, 1, 2, 25, 32 mJy/beam (bottom) in NGC 6946. |
| In the text | |
 |
Fig. 9 Radio-IR correlation (q-parameter) versus total and turbulent magnetic field strength a) and star formation surface density ΣSFRb). The magnetic field strength-ΣSFR relation is shown for the total, turbulent c), and the ordered magnetic field strength measured by the degree of polarization d). The lines in the upper panels are the bisector fits. The solid lines in c) and d) show the ordinary least square fit, and the dashed line the bisector fit. In panel d), the binned data points (diamonds) are fitted for ΣSFR ≳0.01 M⊙ yr-1 kpc-2 (solid line). In panels a) and c), the total magnetic field is shifted up by 0.3 units for clarity. The nucleus is not included in these analysis. |
| In the text | |
 |
Fig. 10 Ratio of the Ordered-to-turbulent magnetic field strengths Bord/Btur vs. star formation surface density ΣSFR in NGC 6946. The dashed line shows the corresponding fitted line in NGC 4254 shifted by 0.2 along the x-axis (y = −0.32 x − 0.7, see Fig. 7b in Chyży 2008). |
| In the text | |
 |
Fig. 11 Correlation between the magnetic field and the total gas surface density ΣGas. Also shown is the bisector fit. The nucleus is not included in this analysis. |
| In the text | |
 |
Fig. 12 Correlations between the ΣSFR [M⊙ yr-1 kpc-2] and the total gas surface density ΣGas [M⊙ pc-2] for the ISRF (left) and SF regimes (right) as defined by U > 1.3 U⊙. Also shown are the bisector fits. The nucleus is not included in this analysis. |
| In the text | |
 |
Fig. A.1 Top: ratio map of the standard-to-TRT based free-free intensity overlaid with contours of the TIR emission. The contour levels are 9, 15, 20, 130, 200 L⊙ kpc-2. Bottom: the same for the synchrotron component. The ratio values are indicated by the bars at the right of each image. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


