| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201220444 | |
| Published online | 31 January 2013 | |
Catching the fish – Constraining stellar parameters for TX Piscium using spectro-interferometric observations⋆
1
Department of AstrophysicsUniversity of Vienna,
Türkenschanzstraße 17,
1180
Vienna,
Austria
e-mail: daniela.klotz@univie.ac.at
2
Department of Physics and Astronomy, Division of Astronomy and
Space Physics, Uppsala University, Box 516, Uppsala
75120,
Sweden
3
Department of Physics and Astronomy G. Galilei, University of Padova, Vicolo dell’Osservatorio 3, 35122
Padova,
Italy
4
Belgian Institute for Space Aeronomy (BIRA-IASB),
Ringlaan 3 Avenue Circulaire,
1180
Brussels,
Belgium
5
Instituut voor Sterrenkunde, KULeuven, Celestijnenlaan
200D, 3001
Heverlee,
Belgium
Received: 26 September 2012
Accepted: 21 December 2012
Context. Stellar parameter determination is a challenging task when dealing with galactic giant stars. The combination of different investigation techniques has proven to be a promising approach.
Aims. We analyse archive spectra obtained with the Short Wavelength Spectrometer (SWS) onboard ISO, and new interferometric observations from the Very Large Telescope MID-infrared Interferometric instrument (VLTI/MIDI) of a very well studied carbon-rich giant: TX Psc. The aim of this work is to determine stellar parameters using spectroscopy and interferometry.
Methods. The observations are used to constrain the model atmosphere, and eventually the stellar evolutionary model in the region where the tracks map the beginning of the carbon star sequence. Two different approaches are used to determine stellar parameters: (i) the “classic” interferometric approach where the effective temperature is fixed by using the angular diameter in the N-band (from interferometry) and the apparent bolometric magnitude; (ii) parameters are obtained by fitting a grid of state-of-the-art hydrostatic models to spectroscopic and interferometric observations.
Results. We find good agreement between the parameters of the two methods. The effective temperature and luminosity clearly place TX Psc in the carbon-rich AGB star domain in the H-R-diagram. Current evolutionary tracks suggest that TX Psc became a C-star just recently, which means that the star is still in a “quiet” phase compared to the subsequent strong-wind regime. This agrees with the C/O ratio being only slightly greater than one.
Key words: stars: AGB and post-AGB / stars: atmospheres / stars: fundamental parameters / techniques: interferometric / techniques: spectroscopic / stars: carbon
© ESO, 2013
1. Introduction
The asymptotic giant branch (AGB) is the late evolutionary stage of low- to intermediate- mass stars (1−8 M⊙). On the early-AGB the carbon-to-oxygen-ratio is lower than one. After several thermal pulses, the atmospheres of objects with masses between 1−4 M⊙ will very likely turn from oxygen-rich into carbon-rich because of the third dredge-up (Iben & Renzini 1983). Good estimates of stellar parameters are needed for a profound understanding of the evolution of this stage. Their determination is a challenging task because of the complexity of the atmospheres of these objects. It is demonstrated that the combined use of spectroscopic and interferometric observing techniques can efficiently help ascertain stellar parameters (e.g. Wittkowski et al. 2001, 2008, 2011; Neilson & Lester 2008; Paladini et al. 2011; Sacuto et al. 2011a; Martí-Vidal et al. 2011). At the same time these observations provide constraints for existing model atmospheres: e.g. COMARCS (Aringer et al. 2009), Höfner et al. (2003), PHOENIX (Hauschildt et al. 1999), ATLAS (e.g. Kurucz 1993), and CODEX (Ireland et al. 2008, 2011).
TX Psc is one of the brightest and closest carbon-rich AGB stars. It is listed as an irregular variable in the General Catalogue of Variable stars (Samus et al. 2009) with a mean brightness of ~5 mag and a peak-to-peak amplitude of 0.4 mag in the V-band (Jorissen et al. 2011). Distance estimates range from 275 to 315 pc (van Leeuwen 2007; Claussen et al. 1987; Bergeat & Chevallier 2005). Different ISO/SWS spectra of TX Psc (Jørgensen et al. 2000; Gautschy-Loidl et al. 2004) show that there is a difference in the 3 μm feature between 1996 and 1997. With the help of plane-parallel, hydrostatic models Jørgensen et al. (2000) interpret this difference as a change in temperature of ~100 K. The photometry and spectra have been successfully modelled by Gautschy-Loidl et al. (2004) with dust-free dynamical models that reproduce the region between 1−5 μm. They claim that the region between 8−9 μm is affected almost solely by CS. The authors suggest that observations from 8−9 μm show the deep photosphere, while the expected absorption of HCN and C2H2 originating in the higher layers is not observed. As this object is almost (carbon) dust-free we may infer it became a carbon star quite recently. Therefore, this star is a perfect candidate to constrain the region where the transition from oxygen- to carbon-rich occurs.
In this work we present a study of the atmosphere and a stellar parameter determination for TX Psc. We combine spectro-interferometric observations of VLTI/MIDI and spectroscopic observations from ISO/SWS and compare them to geometric, hydrostatic, and evolutionary models.
A description of observations and data reduction is given in Sect. 2. Models and approaches to derive synthetic observables are presented in Sect. 3. The stellar parameters are derived in Sect. 4 and compared to state-of-the-art evolutionary tracks in Sect. 5. A summary of the results is given in Sect. 6.
2. Observations and data reduction
Sections 2.1 and 2.2 discuss the interferometric and spectroscopic observations obtained with VLTI/MIDI and ISO/SWS, respectively. Section 2.3 discusses possible cycle-to-cycle and intra-cycle variability of the data.
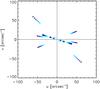 |
Fig. 1 N-band spectrally dispersed uv-coverage of the MIDI observations of TX Psc. Colour levels range from 8−11.5 μm (black to blue, respectively) with a step size of 0.5 μm. North is up and east is left. |
2.1. MIDI visibilities and spectra
TX Psc was observed in 2004 with the 8.2 m Unit Telescopes (UTs) and in 2005, 2006, and 2011 with the 1.8 m Auxiliary Telescopes (ATs) of the Very Large Telescope Interferometer MIDI (Leinert et al. 2003). MIDI covers the N-band and provides spectrally dispersed visibilities, differential phases, and fluxes (resolution R = 230 for observations in 2004, R = 30 for observations in 2005, 2006, and 2011). The journal of available MIDI observations is given in Table 1. The uv-coverage is plotted in Fig. 1.
Journal of MIDI observations of TX Psc sorted for projected baseline length.
Data are reduced using MIA+EWS 1.7.11 (Jaffe 2004; Ratzka 2005; Leinert et al. 2004). Observations are not used if one or more of the selection criteria discussed in Klotz et al. (2012a) are violated (observations that are not boldfaced in Table 1). Uniform-disk angular diameters and IRAS 12 μm flux of the calibrator targets are given in Table 2.
Since only one suitable calibrator is available per observation, a standard multiplicative error of 10% is assumed for the calibrated visibilities (Chesneau 2007). Some calibrated visibilities at baselines shorter than ~30 m are significantly noisier and sometimes more than unity after 11.5 μm. Therefore, in the following, spectro-interferometric observations are only considered for wavelengths shorter than 11.5 μm.
For the calibrated spectra, additional selection criteria are applied (Chesneau 2007): (i) the airmass difference between science and calibrator observations is <0.2, (ii) the spectral type of the calibrator is not later than M0. Considering these criteria, five spectra are derived (flagged with “a” in Table 1).
TX Psc is almost unresolved for baselines shorter than 32 m. Therefore, we expect that the star is unresolved by the single-dish UTs. Thus, most of the mid-infrared (mid-IR) flux is located within the field-of-view (FoV) of the UTs and consequently also in the FoV of the ATs and ISO, which makes the spectra fully comparable to each other.
2.2. ISO spectra
Three spectra of TX Psc were observed with the Short Wavelength Spectrometer (SWS, de Graauw et al. 1996) onboard of ISO (Sloan et al. 2003; Jørgensen et al. 2000). Two spectra have a resolution of R ~ 200 and range from 2.36−45.35 μm. The other spectrum ranges from 2.45−45.20 μm and has a resolution of R ~ 2000 that has been binned to the resolution of the other spectra. For the ISO spectra a multiplicative error of ± 10% is assumed from 2.38−4.05 μm and ± 5% afterwards (Sloan et al. 2003).
2.3. Interferometric and spectroscopic variability
In the left-hand panel of Fig. 2, the calibrated MIDI spectra are overplotted to the ISO/SWS spectra. The flux level of the MIDI observations is the same (within the error bars) as the ISO/SWS spectra taken on 26 Nov. 1996 and 11 Dec. 1997. This suggests that no significant cycle-to-cycle variation is expected in the mid-IR. The right-hand plot of Fig. 2 shows part of the lightcurve of TX Psc in V taken from AAVSO. The spectra from 26 Nov. 1996 and 11 Dec. 1997 were observed at a “local” visual maximum and minimum, respectively. In the following we use these two spectra to derive the parameters of the star at different phases. Because we do not have any information on the V magnitude of the spectrum from 24 May 1997, this spectrum is not used in subsequent sections. Additionally, the phase for all the MIDI observations is unknown. However, AAVSO visual estimates from one specific observer revealed that none of the MIDI observations were taken at visual minima or maxima.
Simulations with dust-free model atmospheres show that the effect of pulsation on the N-band UD-radius is less than 0.1 mas at 1 kpc (Paladini et al. 2009). This would be ~0.3 mas for a star at the distance of TX Psc. This value is beyond the limit of resolution of MIDI. Therefore, we do not expect any observed intra-cycle variability effect that is greater than the errors. This allows combining all calibrated visibilities for further analysis.
Properties of the calibrator targets.
3. Model description
In the following we present the different classes of models and the derivation of synthetic observables that are compared to observations in Sect. 4.
3.1. Hydrostatic models
Observed spectra and visibilities are compared to the grid of spherical hydrostatic model atmospheres and the spectra of Aringer et al. (2009). These models are computed with COMARCS and are generated by assuming hydrostatic local thermal and chemical equilibrium. The molecular and atomic opacities are treated in the opacity sampling (OS) approximation. The parameters that characterize a model are: effective temperature Teff, metallicity Z, surface gravity g, mass M, and carbon-to-oxygen ratio C/O.
For this work we limit the sample to models that have solar metallicity because the effect of metallicity is expected to be small for low-resolution spectroscopy. Additionally, there is no indication of non-solar metallicity from other properties of this star.
 |
Fig. 2 Left: MIDI flux (error bars) for different dates. Overplotted are the three ISO/SWS spectra (full lines) of TX Psc. Right: AAVSO V-band light curve of TX Psc. Vertical lines mark the observation date of the ISO spectra. Colours are the same as in the left figure. |
The spectra cover the following parameters: 2400 ≤ Teff ≤ 4000 K in steps of 100 K; Z/Z⊙ = 1; −1.0 ≤ log (g[cm s-2] ) ≤ + 0.0; M/M⊙ = 1,2; C/O = 1.05,1.10,1.40,2.00. To get precise estimates of Teff, additional model atmospheres were produced that resulted in a grid spacing of ΔT = 10 K. All the main molecular opacities typical of C-stars were included: CO (Goorvitch & Chackerian 1994), C2 (Querci et al. 1974), HCN (Harris et al. 2006), CN (Jørgensen 1997) in the form of line lists, and C2H2 and C3 (Jorgensen et al. 1989) as OS data. CS is not included due to the lack of line lists and OS data. Synthetic spectra with a resolution of 18 000 are computed in the wavelength range 0.8−25 μm. The spectra are convolved to get the same resolution as the observed data.
Among the output of the spherical radiative transfer code COMA is the monochromatic spatial intensity profile. This profile is used to calculate a synthetic visibility profile in the mid-IR for a subset of the models in the grid. A detailed description of the computation of the visibility profiles is given in Paladini et al. (2009).
3.2. Evolutionary tracks
The luminosity and effective temperature that are determined from hydrostatic models are compared to thermally-pulsing (TP) AGB evolutionary tracks from Marigo et al. (in prep.). We selected TP-AGB sequences with an initial scaled-solar chemical composition (Z = 0.014, Y = 0.273), where Z denotes the mass fraction of metals and Y of helium. TP-AGB evolutionary calculations were carried out from the first thermal pulse – extracted from the PARSEC database of stellar models (Bressan et al. 2012) – to the complete ejection of the envelope due to stellar winds. The TP-AGB tracks are based on numerical integrations of complete envelope models in which, for the first time, molecular chemistry and gas opacities were computed on-the-fly with the ÆSOPUS code (Marigo & Aringer 2009). This guarantees full consistency of the envelope structure with the surface chemical abundances that may significantly vary due to the third dredge-up episodes and hot-bottom burning. The transition from C/O < 1 to C/O > 1 is followed accurately, in particular in the narrow range from 0.95 ≈ C/O ≈ 1.05, where an abrupt change in the molecular chemistry and opacity is expected to occur (see Figs. 11 and 16 in Marigo & Aringer 2009). This point is particularly relevant in the context of the present work, since TX Psc is found to have a surface C/O slightly above unity.
4. Stellar parameter determination
Stellar parameters for TX Psc were determined by a number of authors. A summary is given in Table 3. In the following two different approaches are used to determine the stellar parameters of TX Psc: (i) in Sect. 4.1 we use the “classical approach” of interferometrists where spectro-interferometric observations are used to determine the effective temperature Teff; (ii) in Sect. 4.2 we follow the approach of Paladini et al. (2011, P11 hereafter) where spectroscopic/interferometric measurements are compared to hydrostatic models to determine Teff and the C/O ratio and to constrain mass and log g.
 |
Fig. 3 Left: calibrated visibilities (symbols) versus baseline length for three different wavelengths. The lines represent the best-fitting UD-model at the given wavelength. Right: spectrally dispersed angular diameter plus errors from the best-fitting UD-model (dark grey shaded area). The light grey shaded area marks the region that is omitted for the mean diameter estimation. |
Published stellar parameters of TX Psc.
4.1. Approach 1: geometric models
Interferometry is a powerful tool for constraining the morphology and size of stars and their environments. A deviation from spherical symmetry for the circumstellar environment of TX Psc was detected by several authors at different spatial scales and wavelengths (e.g. Cruzalèbes et al. 1998; Ragland et al. 2006; Sacuto et al. 2011b; Jorissen et al. 2011; Hron et al., in prep.). Clearly, the circumstellar environment of TX Psc is very complex, and most likely unrelated effects shape the morphology in different regions, resulting in a wide variety of structures. To study the geometry of the innermost region of the star in the N-band, the geometrical model fitting tool GEM-FIND (Klotz et al. 2012b) was used to fit the MIDI interferometric observations of TX Psc. A spherical UD-model is able to reproduce the calibrated visibilities; i.e., TX Psc can be assumed to be spherically symmetric in the mid-IR on the spatial scales probed by our MIDI observations. The reason the asymmetrical structures detected by other works are not observed is that they were either detected at distances outside the FoV of MIDI or on smaller spatial scales beyond the detection limit of MIDI. This is supported by the differential phase measurements of MIDI, which do not show any deviation from zero. The calibrated visibilities are plotted together with the best-fitting UD-model in the left-hand panel of Fig. 3 for three different wavelengths.
The right-hand panel of Fig. 3 shows the wavelength dispersed diameter calculated with the UD-model (dark grey shaded area). The star appears larger between 8 and 9 μm. According to Gautschy-Loidl et al. (2004) CS affects this wavelength range. Because of this molecular contamination, this region is omitted, and a mean angular diameter of θ = 10.51 ± 0.70 mas is calculated by averaging the diameter from 9 μm to 11.5 μm.
 |
Fig. 4 Rosseland radius of the synthetic models versus the derived mid-IR UD-radius of the same models (crosses). The blue line is a linear fit to the data. |
4.1.1. Effective temperature
The temperature can be determined using the apparent bolometric magnitude mbol and the angular Rosseland diameter θross. The apparent bolometric magnitude mbol = 2.26 mag was derived by F. Kerschbaum by fitting a combination of blackbodies to near-IR and IRAS data2.
Various definitions for the radius can be found (cf. reviews by Baschek et al. 1991; Scholz 2003), where the most commonly used radius in atmospheric modelling is the Rosseland radius. It is defined by the distance between the centre of the star and the layer having Rosseland optical depth 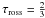 . This radius, however, is not an observable quantity and observed radii have to be converted by using model considerations. In the following we derive this conversion factor for hydrostatic C-stars by using a subset of the hydrostatic models in the grid of Aringer et al. (2009) to derive a mean UD-radius in the mid-IR (9−11.5 μm). This mean UD-radius is plotted versus the Rosseland radius of the corresponding hydrostatic model in Fig. 4. There is a clear correlation between the two radii, yielding
. This radius, however, is not an observable quantity and observed radii have to be converted by using model considerations. In the following we derive this conversion factor for hydrostatic C-stars by using a subset of the hydrostatic models in the grid of Aringer et al. (2009) to derive a mean UD-radius in the mid-IR (9−11.5 μm). This mean UD-radius is plotted versus the Rosseland radius of the corresponding hydrostatic model in Fig. 4. There is a clear correlation between the two radii, yielding 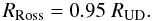 (1)This implies that for a hydrostatic C-star the Rosseland radius can be approximated by the mid-IR UD-radius if the derived correction factor of 0.95 is applied.
(1)This implies that for a hydrostatic C-star the Rosseland radius can be approximated by the mid-IR UD-radius if the derived correction factor of 0.95 is applied.
Applying this correction factor yields an angular Rosseland diameter θRoss = 9.99 mas. The distance-independent effective temperature can be derived with the bolometric magnitude. Using the three different distance estimates d that are available for TX Psc (see Table 3), a linear radius and luminosity can be calculated. Table 4 lists the derived and calculated stellar parameters of approach 1. Errors on the temperature are determined by using the errors on θUD and by assuming an arbitrary error of ± 0.1 for mbol that accounts for the stellar variability and the fitting error. These values agree with those in the literature (see Table 3).
Stellar parameters derived from observations (middle block) and calculated (right block) using approach 1.
4.2. Approach 2: hydrostatic models
The short-wavelength part of the ISO spectrum of TX Psc is dominated by the 3 μm feature which has contributions from HCN and C2H2. The 5 μm feature, on the other hand, is due to C3 and the fundamental band of CO. The region from 7 to 8 μm is dominated by HCN and C2H2, and according to Gautschy-Loidl et al. (2004), the region from 8 to 9 μm is affected by CS opacity. The low variability in the V-band (ΔV ~ 0.4 mag) justifies the use of hydrostatic models in both the near- and mid-IR. Additionally, hydrostatic models are able to reproduce large parts of the overall ISO as well as MIDI spectra. This indicates that the circumstellar environment of TX Psc is optically thin and contains almost no dust.
In Sects. 4.2.1 and 4.2.2 low-resolution spectroscopic observations are compared with synthetic spectra of hydrostatic models to fix the fundamental stellar parameters C/O ratio and Teff. The overall energy distribution as well as the bands of the molecules that are present from 2.3−6 μm put strong constraints on these parameters (Jørgensen et al. 2000; Loidl et al. 2001; P11).
Low-resolution spectroscopy does not allow mass and log g to be ascertained (Figs. 6−10 in P11). To determine these parameters Sect. 4.2.3 follows the approach described in P11: spectro-interferometric observations are compared to models of fixed Teff and C/O ratio but varying log g and mass.
4.2.1. C/O ratio
Jørgensen et al. (2000) found the ratio between the 3 μm feature (HCN and C2H2) and the 5.1 μm feature (CO and C3) to be a sensitive measure of the C/O ratio. To be independent of distance, each model spectrum is normalized to the ISO flux at 2.9 μm (local minimum of molecular absorption, Aringer et al. 2009). A χ2 test is applied between 2.9−6.0 μm to compare the observed ISO spectra (26 Nov. 1996 and 11 Dec. 1997) to the models. For both ISO spectra, we find that the best solution is obtained with a C/O ratio of 1.05. Considering all solutions lying within the 68% confidence level, a C/O ratio of 1.1 can be defined as an upper limit. Due to the coarse grid spacing for C/O, this value is not a strict upper limit and no lower limit can be assigned. Figures 5 and 6 show the ISO/SWS spectrum plotted with models of different temperatures and C/O ratios. The upper panels draw the region around the 3 μm and 5.1 μm feature on a larger scale. These plots demonstrate that a synthetic spectrum with a C/O ratio that is higher than or equal to 1.4 is not able to reproduce the observations, because it over-evaluates the depth of the 5.1 μm feature. This finding is consistent with the C/O ratios given in the literature (see Table 3).
 |
Fig. 5 ISO/SWS spectrum of TX Psc at visual minimum from 11 Dec. 1997 (black line) plotted with hydrostatic models (coloured lines) of different temperatures and C/O ratios. The best-fitting model is plotted in green. Model spectra are normalized to the flux of the corresponding ISO spectrum at 2.9 μm. |
4.2.2. Effective temperature
We expect the 3 μm feature to be a good temperature indicator for hydrostatic stars (P11). Consequently, to determine the temperature for TX Psc, a χ2 test is used to compare the observed ISO spectra and the model spectra between 2.9−3.6 μm. Only model spectra lying within the confidence level of C/O (1.05, 1.1; see Sect. 4.2.1) are used for this test.
The large grid of models allows Teff to be determined very precisely. All solutions lying within the 68% confidence level have a temperature of 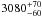 and
and 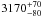 K for the visual minimum and maximum, respectively. The upper left-hand panel of Figs. 5 and 6 show that models with higher/lower temperatures do not reproduce the depth of the 3 μm feature. The temperature derived with approach 1 in Sect. 4.1.1 is within the errors of the temperature that is derived here for the visual minimum and maximum.
K for the visual minimum and maximum, respectively. The upper left-hand panel of Figs. 5 and 6 show that models with higher/lower temperatures do not reproduce the depth of the 3 μm feature. The temperature derived with approach 1 in Sect. 4.1.1 is within the errors of the temperature that is derived here for the visual minimum and maximum.
We confirm the finding of Jørgensen et al. (2000) that the difference in the two ISO spectra can be explained by a temperature change. The lightcurve suggests that this difference is due to variability effects, but time-series spectroscopy is needed to confirm this finding.
4.2.3. Surface gravity and mass
Interferometric observations are compared to the synthetic visibilities of hydrostatic models of varying log g and mass using a χ2 test. All synthetic visibilities were computed for the best-fitting values of Teff and C/O-ratio from Sects. 4.2.1 and 4.2.2. Synthetic visibilities were derived at three different distances: 275 pc, 280 pc, and 315 pc (van Leeuwen 2007; Claussen et al. 1987; Bergeat & Chevallier 2005, respectively). In Fig. 7 the wavelength-dispersed calibrated visibilities are plotted together with the synthetic visibilities of the best-fitting models. The region between 8−9 μm is not considered in the fitting, because the hydrostatic models do not include the CS opacity data.
 |
Fig. 7 Wavelength-dispersed calibrated visibilities plus errors (dark grey shaded area) plotted with the best-fitting synthetic visibilities of hydrostatic models (full lines). To show the degeneracy between mass and log g one model with 3 M⊙ is overplotted (dotted line). |
Stellar parameters derived from observations (middle block) and calculated (right block) using approach 2.
The middle block of Table 5 gives the best-fitting stellar parameters for a given distance that were determined using approach 2. It is clear from the table and from Fig. 7 that, given the error bars on the visibilities, there is a degeneracy between log g and mass. Since the distance defines the level of visibility, there is also a degeneracy between distance and log g. From current TP-AGB evolutionary calculations (e.g. Karakas et al. 2002; Marigo & Girardi 2007; Marigo et al., in prep.), we expect that a 1 M⊙ TP-AGB star with solar metallicity does not make the transition to the C-rich domain. This suggests that the log g values in Table 5 found for M = 2 M⊙ are the more reliable ones. But considering the degeneracy and the limited mass sampling (M = 1,2 M⊙) in the grid, models with higher masses would also reproduce the observed visibilities. To support this statement, one additional model with 3 M⊙ is calculated and overplotted in Fig. 7. The models are almost indistinguishable.
The right-hand part of Table 5 gives stellar parameters that are calculated from the derived log g, mass, and effective temperature. The luminosities are significantly higher than the L = 5200 L⊙ used by Gautschy-Loidl et al. (2004), but comparable to the L = 7700 L⊙ derived by Claussen et al. (1987). The luminosities and radii are also in perfect agreement with the ones determined with approach 1 (see Sect. 4.1).
4.2.4. Photometric constraints on the best model
The best-fitting hydrostatic models of visual minimum/ maximum (model with lowest 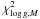 in Table 5) are overplotted to the ISO and MIDI spectra, as well as to photometric measurements in Fig. 8. Photometric measurements from Johnson et al. (1966), Mendoza & Johnson (1965), and Catchpole et al. (1979) were observed with the Johnson filter system. Zero points to convert these measurements from magnitudes to Jansky were taken from Cox (2000). These zero points are also used to convert observations from Bergeat et al. (1976) and Bergeat & Lunel (1980) because the authors claim that their filter system is similar to the Johnson filter system. Zero points for 2MASS photometry (Cutri et al. 2003) are given in Cohen et al. (2003). Olofsson et al. (1993) and Kerschbaum et al. (1996) used the ESO filter system. Zero points were taken from Le Bertre (1988) and Wamsteker (1981). Noguchi et al. (1981) used their own filter system, and the corresponding zero points are given in their paper.
in Table 5) are overplotted to the ISO and MIDI spectra, as well as to photometric measurements in Fig. 8. Photometric measurements from Johnson et al. (1966), Mendoza & Johnson (1965), and Catchpole et al. (1979) were observed with the Johnson filter system. Zero points to convert these measurements from magnitudes to Jansky were taken from Cox (2000). These zero points are also used to convert observations from Bergeat et al. (1976) and Bergeat & Lunel (1980) because the authors claim that their filter system is similar to the Johnson filter system. Zero points for 2MASS photometry (Cutri et al. 2003) are given in Cohen et al. (2003). Olofsson et al. (1993) and Kerschbaum et al. (1996) used the ESO filter system. Zero points were taken from Le Bertre (1988) and Wamsteker (1981). Noguchi et al. (1981) used their own filter system, and the corresponding zero points are given in their paper.
 |
Fig. 8 Best-fitting hydrostatic models for the visual minimum (black line) and maximum (grey line). Superimposed are the ISO spectra of visual minimum (green line) and visual maximum (blue line), MIDI spectra (violet lines) and photometric measurements of different works (orange symbols). Model spectra are normalized to the flux of the corresponding ISO spectrum at 2.9 μm. |
 |
Fig. 9 Zoom into the AGB region of the H-R diagram. Lines denote solar metallicity evolutionary tracks (Marigo et al., in prep.) and numbers indicate the mass on the early-AGB. Yellow/grey lines mark the region of carbon-rich AGB stars with C/O > 1.0. Black lines mark the region of oxygen-rich AGB stars (C/O ≤ 1). For better visibility, the track of the 2 M⊙ model is plotted with a dotted line. Different coloured symbols refer to the luminosity and effective temperature determined in this work (for the two different approaches A1 and A2 at visual minimum/maximum). |
5. Comparison with evolutionary tracks
We follow the approach described in P11 and compare the stellar parameters with new evolutionary tracks of thermally pulsing AGB stars (Marigo et al., in prep.). Figure 9 depicts evolutionary tracks in the region of AGB stars in the H-R diagram. Overplotted are the determined luminosity and temperature for TX Psc for the two approaches. Only the best-fitting luminosity (see Table 5) at d = 280 pc is plotted for TX Psc. Errors for the luminosity are assumed to lie in the order ~40% (uncertainty on the given distance measurement).
We note an encouraging agreement between the observed location of TX Psc in the H-R diagram and the predicted ranges of luminosity and effective temperature for a carbon-rich star with solar-metallicity and C/O within a narrow interval (i.e. 1 < C/O ≤ 1.1). As we see in Fig. 9, the TP-AGB evolutionary tracks in the C-rich regime extend to much lower effective temperatures than the derived values for TX Psc. This cooling is mainly driven by the increase in the C/O ratio after each dredge-up episode, as well as by the progressive strengthening of the mass-loss efficiency. The relatively warm effective temperature of TX Psc suggests that this star is observed close after the transition into the C-star domain, in an early “quiet” stage in which the strong wind has not yet developed. This picture is nicely supported by the observational findings already discussed in the previous sections.
It is visible from the evolutionary tracks that an AGB star with solar metallicity will turn into a carbon-rich AGB star only for masses around 2 M⊙ and higher. Also, the position of TX Psc in Fig. 9 suggests that the mass lies between 2 and 3 M⊙. This does not agree with the best-fitting models having 1 M⊙ (Sect. 4.2.3), but is in good agreement with the models having 2 M⊙.
6. Conclusion
In this work we determined stellar parameters for TX Psc by comparing observations to geometric models (Klotz et al. 2012b), state-of-the-art hydrostatic model atmospheres (Aringer et al. 2009) and evolutionary models (Marigo et al., in prep.). Two different approaches were used to fix the parameters:
-
A1.
Spectro-interferometric observations were used todetermine a wavelength-dispersed uniform disk diameter. Acorrection factor for hydrostatic C-stars was derived fromhydrostatic models to convert the UD diameter to the Rosselandradius, which was then used to determine the effectivetemperature Teff.
-
A2.
Spectroscopic measurements were compared to synthetic spectra from hydrostatic models to determine Teff and C/O ratio. The mass and log g were constrained by comparing spectro-interferometric observations with synthetic visibility profiles from hydrostatic models.
The main advantage of approach 1 is the distance-independent determination of Teff. On the other hand, conversion of the UD-radius to the Rosseland radius and the use of the apparent bolometric magnitude introduces uncertainties. Approach 2 allows to constrain not only Teff, but also C/O, log g and M. One of the disadvantages of this technique is the unknown error that is introduced by the model. Additionally, the uncertainty in distance, which is needed to constrain log g and M, and the degeneracy between these two parameters limits the accuracy of the parameter determination. This suggests that high-resolution spectroscopy is needed to fully distinguish between mass and log g. There is very good agreement between the best-fitting hydrostatic model atmosphere and observations (interferometry, spectroscopy, and photometry).
Our spectro-interferometric results are also an important tool to constrain and validate stellar AGB models, which are still subject to severe uncertainties. We found that present TP-AGB tracks with a detailed treatment of molecular opacities nicely reproduce the derived Teff,L,C/O values for TX Psc.
Method described in Kerschbaum & Hron (1996) and references therein; near-IR data from the IRAS catalogue and Fouque et al. (1992).
Acknowledgments
The authors thank Angela Baier for fruitful discussions on ISO spectra and Walter Nowotny for helpful discussions of SEDs and photometric filter systems. This work is supported by the Austrian Science Fund FWF under project number AP23006. B.A. acknowledges support from Austrian Science Fund (FWF) Projects AP23006 & AP23586 and from contract ASI-INAF I/009/10/0. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France. We acknowledge the variable star observations from the AAVSO International Database that were used in this research.
References
- Aringer, B., Girardi, L., Nowotny, W., Marigo, P., & Lederer, M. T. 2009, A&A, 503, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baschek, B., Scholz, M., & Wehrse, R. 1991, A&A, 246, 374 [NASA ADS] [Google Scholar]
- Bergeat, J., & Chevallier, L. 2005, A&A, 429, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergeat, J., & Lunel, M. 1980, A&A, 87, 139 [NASA ADS] [Google Scholar]
- Bergeat, J., Sibille, F., Lunel, M., & Lefevre, J. 1976, A&A, 52, 227 [NASA ADS] [Google Scholar]
- Bergeat, J., Knapik, A., & Rutily, B. 2001, A&A, 369, 178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Catchpole, R. M., Robertson, B. S. C., Lloyd-Evans, T. H. H., et al. 1979, South African Astron. Obs. Circ., 1, 61 [Google Scholar]
- Chesneau, O. 2007, New Astron. Rev., 51, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Claussen, M. J., Kleinmann, S. G., Joyce, R. R., & Jura, M. 1987, ApJS, 65, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., Wheaton, W. A., & Megeath, S. T. 2003, AJ, 126, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. 2000, Allen’s Astrophysical Quantities (Springer) [Google Scholar]
- Cruzalèbes, P., Lopez, B., Bester, M., Gendron, E., & Sams, B. 1998, A&A, 338, 132 [NASA ADS] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog II/246 [Google Scholar]
- de Graauw, T., Haser, L. N., Beintema, D. A., et al. 1996, A&A, 315, L49 [NASA ADS] [Google Scholar]
- de Vegt, C. 1974, A&A, 34, 457 [NASA ADS] [Google Scholar]
- Dunham, D. W., Evans, D. S., Silverberg, E. C., & Wiant, J. R. 1975, MNRAS, 173, 61 [NASA ADS] [Google Scholar]
- Dyck, H. M., van Belle, G. T., & Benson, J. A. 1996, AJ, 112, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Fouque, P., Le Bertre, T., Epchtein, N., Guglielmo, F., & Kerschbaum, F. 1992, A&AS, 93, 151 [NASA ADS] [Google Scholar]
- Gautschy-Loidl, R., Höfner, S., Jørgensen, U. G., & Hron, J. 2004, A&A, 422, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goorvitch, D., & Chackerian, Jr., C. 1994, ApJS, 91, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, G. J., Pavlenko, Y. V., Jones, H. R. A., & Tennyson, J. 2003, MNRAS, 344, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, G. J., Tennyson, J., Kaminsky, B. M., Pavlenko, Y. V., & Jones, H. R. A. 2006, MNRAS, 367, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., Ferguson, J., Baron, E., & Alexander, D. R. 1999, ApJ, 525, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Höfner, S., Gautschy-Loidl, R., Aringer, B., & Jørgensen, U. G. 2003, A&A, 399, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, Jr., I., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, M. J., Scholz, M., & Wood, P. R. 2008, MNRAS, 391, 1994 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, M. J., Scholz, M., & Wood, P. R. 2011, MNRAS, 418, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W. J. 2004, in SPIE Conf. Ser. 5491, ed. W. A. Traub, 715 [Google Scholar]
- Johnson, H. L., Mitchell, R. I., Iriarte, B., & Wisniewski, W. Z. 1966, Commun. Lunar and Plan. Lab., 4, 99 [Google Scholar]
- Jørgensen, U. G. 1997, in IAU Symp. 178, ed. E. F. van Dishoeck, 441 [Google Scholar]
- Jorgensen, U. G., Almlöf, J., & Siegbahn, P. E. M. 1989, ApJ, 343, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, U. G., Hron, J., & Loidl, R. 2000, A&A, 356, 253 [NASA ADS] [Google Scholar]
- Jorissen, A., Mayer, A., van Eck, S., et al. 2011, A&A, 532, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karakas, A. I., Lattanzio, J. C., & Pols, O. R. 2002, PASA, 19, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Kerschbaum, F., & Hron, J. 1996, A&A, 308, 489 [NASA ADS] [Google Scholar]
- Kerschbaum, F., Lazaro, C., & Habison, P. 1996, A&AS, 118, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klotz, D., Sacuto, S., Kerschbaum, F., et al. 2012a, A&A, 541, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klotz, D., Sacuto, S., Paladini, C., Hron, J., & Wachter, G. 2012b, SPIE Conf., 8445, 84451 [CrossRef] [Google Scholar]
- Kurucz, R. 1993, Limbdarkening for 2 km s-1 grid (No. 13): [+0.0] to [− 5.0], Kurucz CD-ROM No. 17 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lambert, D. L., Gustafsson, B., Eriksson, K., & Hinkle, K. H. 1986, ApJS, 62, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Lasker, B. M., Bracker, S. B., & Kunkel, W. E. 1973, PASP, 85, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bertre, T. 1988, A&A, 190, 79 [NASA ADS] [Google Scholar]
- Leinert, C., Graser, U., Przygodda, F., et al. 2003, Ap&SS, 286, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., van Boekel, R., Waters, L. B. F. M., et al. 2004, A&A, 423, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loidl, R., Lançon, A., & Jørgensen, U. G. 2001, A&A, 371, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., & Aringer, B. 2009, A&A, 508, 1539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., & Girardi, L. 2007, A&A, 469, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martí-Vidal, I., Marcaide, J. M., Quirrenbach, A., et al. 2011, A&A, 529, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendoza V., E. E., & Johnson, H. L. 1965, ApJ, 141, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Neilson, H. R., & Lester, J. B. 2008, A&A, 490, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noguchi, K., Kawara, K., Kobayashi, Y., et al. 1981, PASJ, 33, 373 [NASA ADS] [Google Scholar]
- Ohnaka, K., Tsuji, T., & Aoki, W. 2000, A&A, 353, 528 [NASA ADS] [Google Scholar]
- Olofsson, H., Eriksson, K., Gustafsson, B., & Carlstroem, U. 1993, ApJS, 87, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Paladini, C., Aringer, B., Hron, J., et al. 2009, A&A, 501, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paladini, C., van Belle, G. T., Aringer, B., et al. 2011, A&A, 533, A27 (P11) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Querci, F., Querci, M., & Tsuji, T. 1974, A&A, 31, 265 [NASA ADS] [Google Scholar]
- Quirrenbach, A., Mozurkewich, D., Hummel, C. A., Buscher, D. F., & Armstrong, J. T. 1994, A&A, 285, 541 [NASA ADS] [Google Scholar]
- Ragland, S., Traub, W. A., Berger, J.-P., et al. 2006, ApJ, 652, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Ratzka, T. 2005, Ph.D. Thesis, Max-Planck-Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany [Google Scholar]
- Richichi, A., Chandrasekhar, T., Lisi, F., et al. 1995, A&A, 301, 439 [NASA ADS] [Google Scholar]
- Sacuto, S., Aringer, B., Hron, J., et al. 2011a, A&A, 525, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacuto, S., Jorissen, A., Cruzalèbes, P., et al. 2011b, in Why Galaxies Care about AGB Stars II: Shining Examples and Common Inhabitants, eds. F. Kerschbaum, T. Lebzelter, & R. F. Wing, ASP Conf. Ser., 445, 171 [Google Scholar]
- Samus, N. N., Durlevich, O. V., et al. 2009, VizieR Online Data Catalog: B/gcvs [Google Scholar]
- Scholz, M. 2003, in SPIE Conf. Ser. 4838, ed. W. A. Traub, 163 [Google Scholar]
- Sloan, G. C., Kraemer, K. E., Price, S. D., & Shipman, R. F. 2003, ApJS, 147, 379 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wamsteker, W. 1981, A&A, 97, 329 [NASA ADS] [Google Scholar]
- Wittkowski, M., Hummel, C. A., Johnston, K. J., et al. 2001, A&A, 377, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Driebe, T., et al. 2008, A&A, 479, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Ireland, M., et al. 2011, A&A, 532, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Stellar parameters derived from observations (middle block) and calculated (right block) using approach 1.
Stellar parameters derived from observations (middle block) and calculated (right block) using approach 2.
All Figures
 |
Fig. 1 N-band spectrally dispersed uv-coverage of the MIDI observations of TX Psc. Colour levels range from 8−11.5 μm (black to blue, respectively) with a step size of 0.5 μm. North is up and east is left. |
| In the text | |
 |
Fig. 2 Left: MIDI flux (error bars) for different dates. Overplotted are the three ISO/SWS spectra (full lines) of TX Psc. Right: AAVSO V-band light curve of TX Psc. Vertical lines mark the observation date of the ISO spectra. Colours are the same as in the left figure. |
| In the text | |
 |
Fig. 3 Left: calibrated visibilities (symbols) versus baseline length for three different wavelengths. The lines represent the best-fitting UD-model at the given wavelength. Right: spectrally dispersed angular diameter plus errors from the best-fitting UD-model (dark grey shaded area). The light grey shaded area marks the region that is omitted for the mean diameter estimation. |
| In the text | |
 |
Fig. 4 Rosseland radius of the synthetic models versus the derived mid-IR UD-radius of the same models (crosses). The blue line is a linear fit to the data. |
| In the text | |
 |
Fig. 5 ISO/SWS spectrum of TX Psc at visual minimum from 11 Dec. 1997 (black line) plotted with hydrostatic models (coloured lines) of different temperatures and C/O ratios. The best-fitting model is plotted in green. Model spectra are normalized to the flux of the corresponding ISO spectrum at 2.9 μm. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but at visual maximum from 21 Nov. 1996. |
| In the text | |
 |
Fig. 7 Wavelength-dispersed calibrated visibilities plus errors (dark grey shaded area) plotted with the best-fitting synthetic visibilities of hydrostatic models (full lines). To show the degeneracy between mass and log g one model with 3 M⊙ is overplotted (dotted line). |
| In the text | |
 |
Fig. 8 Best-fitting hydrostatic models for the visual minimum (black line) and maximum (grey line). Superimposed are the ISO spectra of visual minimum (green line) and visual maximum (blue line), MIDI spectra (violet lines) and photometric measurements of different works (orange symbols). Model spectra are normalized to the flux of the corresponding ISO spectrum at 2.9 μm. |
| In the text | |
 |
Fig. 9 Zoom into the AGB region of the H-R diagram. Lines denote solar metallicity evolutionary tracks (Marigo et al., in prep.) and numbers indicate the mass on the early-AGB. Yellow/grey lines mark the region of carbon-rich AGB stars with C/O > 1.0. Black lines mark the region of oxygen-rich AGB stars (C/O ≤ 1). For better visibility, the track of the 2 M⊙ model is plotted with a dotted line. Different coloured symbols refer to the luminosity and effective temperature determined in this work (for the two different approaches A1 and A2 at visual minimum/maximum). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


