| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 5 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219726 | |
| Published online | 05 February 2013 | |
On the relation between continuum brightness and magnetic field in solar active regions
1 Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
2 Technische Universität Braunschweig, Institut für Theoretische Physik, Mendelssohnstrasse 3, 38106 Braunschweig, Germany
Received: 31 May 2012
Accepted: 12 December 2012
Context. Variations of solar irradiance are mainly determined by the changing coverage of the visible solar disk with magnetic flux concentrations. The relationship between brightness and field strength is an important ingredient for models and reconstructions of irradiance variations.
Aims. We assess the effect of limited observational resolution on the relationship between brightness and magnetic field by comparing comprehensive MHD simulations with observational results.
Methods. Simulations of magnetoconvection representing the near-surface layers of a plage region were used to determine maps of the continuum brightness and Stokes profiles for the Fe i line at 630.22 nm. After convolving with instrumental profiles, synthetic observations of the magnetic field were generated by applying a Stokes inversion code. We compare the resulting relation between brightness and apparent vertical magnetic field to the corresponding outcome derived from real observations of a plage region with the Hinode satellite.
Results. Consideration of the image smearing effects due to the limited resolution of the observations transform the largely monotonic relation between brightness and field strength at the original resolution of the simulations into a profile with a maximum at intermediate field strength, which is in good agreement with the observations.
Conclusions. Considering the effect of limited observational resolution renders the relation between brightness and magnetic field from comprehensive MHD simulations consistent with observational results. This is a necessary prerequisite for the utilization of simulations for models and reconstruction of solar irradiance variations.
Key words: Sun: surface magnetism / Sun: photosphere / Sun: faculae, plages
© ESO, 2013
1. Introduction
The relation between the local values of brightness and magnetic field strength at the solar surface is a crucial ingredient for quantitative models and reconstructions of solar (ir)radiance (Fröhlich & Lean 2004; Domingo et al. 2009; Schnerr & Spruit 2011; Ball et al. 2012). Comprehensive numerical simulations of near-surface magneto-convection can be used to study the effect of the magnetic field on the local radiance, including spatial scales that are not resolved by observations. This concerns the fine structure of faculae, the “quiet” network, and possibly also the turbulent field, whose variations may contribute to long-term irradiance changes (e.g., Krivova et al. 2010, 2011; Vieira et al. 2011).
A necessary condition for simulations to become a reliable tool to calibrate irradiance models and reconstructions is their consistency with observational results. For pixel-based values, a comparison of the mean relations between the disk-center brightness contrast (with respect to the average quiet Sun) and the magnetic field strength from observations and simulations at their respective spatial resolution reveals a striking disagreement. The simulations basically show a monotonic increase of contrast with field strength (Vögler et al. 2005), while the observations exhibit a maximum contrast (which may even be negative) at intermediate field strength (or magnetogram signal) and a decrease towards stronger field values (e.g., Title et al. 1992; Topka et al. 1992; Lawrence et al. 1993; Narayan & Scharmer 2010; Kobel et al. 2011), even if dark pores are explicitely excluded. On the other hand, if only bright features are considered, observers find increasing brightness (or saturation) with growing field strength (Viticchié et al. 2010; Berger et al. 2007). This suggests that the pixel-based observational results are heavily affected by instrumental effects resulting from finite telescope aperture, optical abberations, straylight, and atmospheric seeing for ground-based instruments (e.g., Title & Berger 1996).
Röhrbein et al. (2011) made a first attempt to evaluate the importance of finite-resolution effects on the pixel-based relation between brightness and field strength (for brevity, henceforth referred to as the I − B relation). They convolved maps of field strength and bolometric intensity from MHD simulations with an Airy function, thus mimicking finite telescope aperture. It turned out that the smearing of strong magnetic field at the bright edges of magnetic structures renders the I − B relation from monotonic to a profile with a local maximum that is qualitatively consistent with the observational results.
Here we extend the study of Röhrbein et al. (2011) and provide a quantitative comparison between observation and simulation. To this end, on the basis of simulation results, we emulated the steps connecting the physical quantities in the solar atmosphere to the final mean I − B relation derived from spectro-polarimetric observations. This means calculating maps of continuum intensity and synthetic Stokes profiles, convolving them with a realistic point spread function, rebinning to detector pixel size, and applying an inversion algorithm to retrieve the magnetic field. The resulting pixel-based mean I − B relation can then be quantitatively compared with the corresponding observational result.
 |
Fig. 1 Upper row: maps of the normalized continuum intensity near 630 nm at original resolution of the MHD simulation (left panel) and after convolving with the Hinode/SP PSF and rebinning to SP detector pixels (right panel). Yellow contours outline the areas identified by the pore exclusion procedure. Lower row: maps of the vertical magnetic field component at local optical depth τ630 = 0.1 for original resolution of the simulation (left panel) and of the line-of-sight magnetic field derived from the inversion of synthetic Stokes profiles (right panel). |
2. Methods
2.1. Observational data
We used a spectropolarimetric scan of active region NOAA 10940 started on February 1, 2007, at 12:14:05 near solar disk center with the Hinode/SP instrument (Kosugi et al. 2007; Tsuneta et al. 2008; Suematsu et al. 2008; Lites et al. 2001; Ichimoto et al. 2008). The data set consists of maps of the four Stokes parameters in the wavelength range around the Fe i 630.15 nm and 630.25 nm lines. We selected a slightly enlarged subarea (70′′ × 70′′) of the scan used by Kobel et al. (2011, see their Fig. 1, upper panel) to determine the I − B relation for small-scale magnetic features (i.e., excluding pores) in a plage region.
The data were treated in exactly the same way as described by Kobel et al. (2011) in order to obtain maps of the magnetic field and of the intensity in the red continuum of the 630.25 nm line. This included an inversion of the Stokes spectra with the VFISV code developed by Borrero et al. (2011), which provides the “apparent” strength of the line-of-sight component of the field, BLOS = Bαcosγ, where B is the “intrinsic” field strength, α is the fractional amount of light that comes from the magnetized plasma, and γ is the inclination angle with respect to the observer (here, the vertical direction). The factor α is introduced in an attempt to take account of the effects of local straylight and of non-magnetized plasma in the resolution element. The average of BLOS over the selected plage area of the scan is ⟨BLOS⟩ = 166.6 G.
2.2. MHD simulation
We considered a simulation with the MURaM code (Vögler 2003; Vögler et al. 2005). The setup was the same as that used in Röhrbein et al. (2011), except that we here used non-gray radiative transport by opacity binning with 4 bins (Vögler et al. 2004). The simulation domain was threaded by a prescribed vertical magnetic flux corresponding to a horizontally averaged vertical field of 200 G, which is roughly consistent with the value of ⟨BLOS⟩ inferred for the observation. The computational domain covered 24 Mm × 24 Mm in the horizontal directions and 1400 km in the vertical, resolved into a mesh with 1152 × 1152 × 100 grid points. This corresponds to an area of 32′′ × 32′′ on the sun and to a height range covering the uppermost convection zone and the photospheric layers. The mean level of the (Rosseland) optical depth unity was located about 400 km below the upper boundary of the computational domain.
2.3. Synthetic observations
Based on a snapshot taken after the MHD simulation had reached a statistically stationary state, we reproduced the steps leading from the physical quantities in the solar atmosphere to the final observational data products, i.e., the continuum intensity near the Fe i 630.22 nm line, I, and the apparent line-of-sight magnetic field strength, BLOS.
The first step in the synthesis was the calculating the profiles of the four Stokes parameters for the 630.22 nm line and the nearby continuum with a wavelength resolution of 7.5 mÅ. For each resolution element of the simulation, the radiative transfer equation for polarized light was integrated along a vertical line of sight (corresponding to disk-center observations) with the SPINOR code (e.g., Frutiger et al. 2000), using oscillator strengths taken from the VALD database (Piskunov et al. 1995) and log ε = 7.46 for the iron abundance (Asplund 2000).
The next step was to apply the spatial point spread function (PSF) derived for Hinode/SP (Danilovic et al. 2008) to the maps of synthesized Stokes profiles in order to account for the instrumental image degradation. The rms contrast of the continuum intensity was brought into agreement with the value of 6.6% from the Hinode plage observation by assuming a slight defocus of the telescope (for details, see Danilovic et al. 2008). In wavelength space, the Stokes profiles were convolved with a Gaussian of 25 mÅ FWHM and resampled to a wavelength spacing of 21.5 mÅ, which corresponds to the wavelength resolution and size of the CCD detector pixels of the Hinode/SP instrument. Furthermore, noise of 10-3Ic was added.
Finally, the line-of-sight magnetic field strength, BLOS, was determined for each 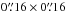 observational pixel by applying the inversion code VFISV (Borrero et al. 2011) in exactly the same way as done for the real observational data. It suffices to consider BLOS since the magnetic field is almost vertical in the height range relevant for line formation. The “intrinsic” field sometimes also derived from inversions strongly depends on assumptions regarding a mixture of magnetic and non-magnetic areas within a pixel (“filling factor”) or on assumptions regarding the nature of false light (“local straylight”). Comparing the actual magnetic field in the simulations with the results of an inversion of synthesized Stokes profiles, we found that the derived “intrinsic” field in many cases deviates grossly from the actual field, especially in regions of weak field.
observational pixel by applying the inversion code VFISV (Borrero et al. 2011) in exactly the same way as done for the real observational data. It suffices to consider BLOS since the magnetic field is almost vertical in the height range relevant for line formation. The “intrinsic” field sometimes also derived from inversions strongly depends on assumptions regarding a mixture of magnetic and non-magnetic areas within a pixel (“filling factor”) or on assumptions regarding the nature of false light (“local straylight”). Comparing the actual magnetic field in the simulations with the results of an inversion of synthesized Stokes profiles, we found that the derived “intrinsic” field in many cases deviates grossly from the actual field, especially in regions of weak field.
3. Results
Figure 1 shows a comparison of the simulation results at their original resolution to the synthetic Hinode/SP observations. The continuum intensity maps (upper panels) clearly show the effect of the image degradation: the bright structures in the intergranular lanes are much less conspicuous owing to reduced contrast. The yellow contours in the degraded intensity map (upper right panel of Fig. 1) indicate the result of the pore exclusion procedure following Kobel et al. (2011): first, regions of at least 4 pixels size showing an intensity contrast I/ ⟨I⟩ < − 0.15 (where ⟨I⟩ is the average over all pixels with BLOS < 100 G) and a field strength BLOS above 900 G were selected; these regions were then extended until BLOS became smaller than 200 G and excluded from the determination of the I − B relation. Since there are only some micropores in the simulation, the pore exclusion had almost no effect on the resulting I − B relation.
 |
Fig. 2 Probability distribution functions (normalized to unit area) of apparent vertical field, BLOS (>50 G; bin size 50 G), resulting from the inversion procedure (after removal of the pores). The solid curve corresponds to the MHD simulations, the dashed curve to the Hinode/SP observations. |
The lower panels of Fig. 1 show a map of the vertical field component at continuum optical depth τ630 = 0.1 directly from the simulation (left panel) in comparison with the map of BLOS from the inversion of the synthetic Stokes profiles (right panel). Orozco Suárez et al. (2010) showed that Milne-Eddington inversions fairly well represent the conditions in the atmospheric layers around the τ630 = 0.1 level. The maps indicate that the morphology of the magnetic structures is well preserved in the maps of BLOS, albeit somewhat smeared owing to instrumental image degradation. The latter is also mainly responsible for the generally lower values of the “apparent” field strength derived from the inversion. Compared to a map of the original simulated field smeared with the Hinode PSF, the differences between original smeared and inferred field strength do not exceed about 200 G for strong fields, which is consistent with the result of Orozco Suárez et al. (2010, see their Fig. 8).
 |
Fig. 3 Bin-averaged continuum intensity contrast near 630 nm vs. magnetic field strength. The bin size is 25 G. Shown are observational Hinode/SP data (red curve), simulation data (intrinsic vertical field) at original resolution (solid black curve, values taken at optical depth 0.1), inverted apparent magnetic field at original simulation resolution (dashed black curve), and synthetic Hinode/SP observations derived from the simulations (green curve). The shift between the solid and dashed black curves (the inverted field being somewhat weaker than the original field for the same contrast value) indicates that the inversion effectively samples the magnetic field at a level somewhat above the surface of optical depth 0.1. |
 |
Fig. 4 Probability distribution functions (normalized to unit area) of the continuum intensity contrast (bin size 0.01) from MHD simulations (solid curves, corresponding to the green curve in Fig. 3) and observations (dashed curves, corresponding to the red curve in Fig. 3). The upper left panel shows the PDF for all pixels, while the plots in the other panels give the PDFs for various ranges of BLOS (indicated by the insets) obtained from inversions, omitting the pixels corresponding to pores. |
Figure 2 gives a comparison of the probability distribution functions (PDFs) of BLOS from the inversion of the observed Stokes profiles (dashed line) and from the synthetic Stokes profiles based on the simulation data (solid line), respectively, after removal of the pores. The general agreement of the two curves indicates that the simulation covers the observed field distribution reasonably well.
Figure 3 shows the mean contrast curves for the inverted observational Hinode/SP data (red), for the original simulation data without inversion (solid black), for the inverted apparent magnetic field at original resolution (dashed black), and for the inverted synthetic Hinode/SP observations derived from the simulations (green). To derive these curves, the average continuum intensity was calculated by combining the pixel-based data into bins of 25 G width each. The observational (red) curve agrees well with the third-order polynomial fit determined by Kobel et al. (2011) for the same data set. Comparing the black curve and the green curve confirms the result of Röhrbein et al. (2011): image smearing effects transform the monotonic I − B relation (for field strengths above a few hundred G) into a relation with a local maximum at intermediate apparent field strength. The dashed black curve shows that the inversion procedure to obtain the apparent field alone does not change the monotonic relation between brightness and magnetic field. As studied in detail in Röhrbein et al. (2011), this change results mainly from the smearing of the magnetic field. The bright small-scale magnetic flux concentrations with kG fields are surrounded by areas of much weaker field (typically of the order of 100–200 G), so that the image smearing results in strongly reduced values of the field strength. At the same time, the intensity outside the bright small flux concentrations only drops to intergranular values, so that its relative change between flux concentrations and their surroundings is much lower than that of the magnetic field. As a consequence, the intensity of the bright small flux concentrations is less much affected by smearing than the magnetic field (see also Fig. 4 of Röhrbein et al. 2011), so that pixels corresponding to bright flux concentrations are preferentially moved to the left of the contrast-BLOS plane. This explains the enhanced mean contrast in the range | BLOS | ≲ 700 G after image smearing. The kG field in the dark interior of micropores and magnetic knots is much less affected by image degradation since these structures are bigger than the bright small-scale flux concentrations. As a result of the different effect of smearing on small bright and bigger dark flux concentrations, the average contrast curve turns over for higher field strength (see also Fig. 6 of Röhrbein et al. 2011). Note that the curve for the synthetic observations ends at about 1100 G because, owing to the limited size of the computational box, the number of pixels with higher field strength is insufficient for statistically meaningful averages.
The “fishhook” shape of the curves for low field values reflects the transition from very weakly magnetized regions (granules, newly formed intergranular lanes) with field strengths below 150 G to the flux of a few hundred G advected into the intergranular lanes that still has too low field strength to affect the local brightness (Schnerr & Spruit 2011).
In order to further evaluate the correspondence of the simulation results to the observations, in Fig. 4 we consider the intensity distributions for different ranges of BLOS. The PDFs agree rather well and thus support the validity of the simulations. The PDFs agree particularly well for weak field (0 G < BLOS < 200 G) and strong field 700 G < BLOS < 1500 G. In the latter case, dark pixels with contrast values below − 0.2 are somewhat underrepresented in the simulations, but this has a negligible effect on the mean contrast curves shown in Fig. 3. The slight shift between the curves for the interval 200 G < BLOS < 700 G (lower left panel) reflects the difference between the mean contrast curves from observation and simulation in Fig. 3. The origin of this deviation probably can be traced back to the assumption used in this simulation that the total outgoing radiative energy flux should match that of the average value for the quiet Sun (by adjusting the entropy of the inflowing plasma at the bottom of the computational box). Hence, the excess emission in the bright magnetic elements is compensated by slightly darker granules. The underrepresentation of bright pixels compared to the observation (see upper left panel of Fig. 4) indicates that this assumption may not be adequate. In fact, simulations with the inflow entropy fixed to the quiet-Sun value yield an increase of the integrated outgoing radiative flux by about 2.5% relative to the quiet Sun for a mean vertical field of 200 G (Vögler 2005). Using this value for the normalization of the intensity contrast in the simulation would bring the contrast curves in Fig. 3 into much closer agreement. In addition, instrumental straylight affects mainly the small-scale bright magnetic elements with strong field. Since the straylight has so far not been fully characterized in the observations, it could not be modelled in our analysis.
4. Conclusion
If the steps leading from physical properties in the solar atmosphere to the results of observational data analysis are consistently applied to models from comprehensive MHD simulations, thus providing synthetic observations, the resulting pixel-based average I − B relation is quantitatively consistent with that derived from real Hinode/SP observations. The remaining differences can be explained by slightly different values of the total outgoing radiative flux and instrumental straylight and/or defocus effects in the observations (Danilovic et al. 2008).
This correspondence between simulation and observational results is a necessary condition for using MHD simulations to calibrate quantitative models and reconstructions of solar
irradiance variations. However, further analysis, such as the center-to-limb variation of the contrast (cf. Afram et al. 2011) and a detailed consideration of the size distribution of magnetic elements (particularly concerning small pores) as a function of the mean flux density, is required before such a calibration can be realized.
Acknowledgments
D.R. acknowledges a Ph.D. fellowship of the International Max Planck Research School on Physical Processes in the Solar System and Beyond. P. Kobel kindly provided a version of the VFSIV code adapted for Hinode/SP data. Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway).
References
- Afram, N., Unruh, Y. C., Solanki, S. K., et al. 2011, A&A, 526, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M. 2000, A&A, 359, 755 [NASA ADS] [Google Scholar]
- Ball, W. T., Unruh, Y. C., Krivova, N. A., et al. 2012, A&A, 541, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, T. E., Rouppe van der Voort, L., & Löfdahl, M. 2007, ApJ, 661, 1272 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., Tomczyk, S., Kubo, M., et al. 2011, Sol. Phys., 273, 267 [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domingo, V., Ermolli, I., Fox, P., et al. 2009, Space Sci. Rev., 145, 337 [Google Scholar]
- Fröhlich, C., & Lean, J. 2004, A&ARv, 12, 273 [Google Scholar]
- Frutiger, C., Solanki, S. K., Fligge, M., & Bruls, J. H. M. J. 2000, A&A, 358, 1109 [NASA ADS] [Google Scholar]
- Ichimoto, K., Lites, B., Elmore, D., et al. 2008, Sol. Phys., 249, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Kobel, P., Solanki, S. K., & Borrero, J. M. 2011, A&A, 531, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Krivova, N. A., Solanki, S. K., & Unruh, Y. C. 2011, J. Atm. Terr. Phys., 73, 223 [Google Scholar]
- Krivova, N. A., Vieira, L. E. A., & Solanki, S. K. 2010, J. Geophys. Res., 115, 12112 [CrossRef] [Google Scholar]
- Lawrence, J. K., Topka, K. P., & Jones, H. P. 1993, J. Geophys. Res., 98, 18911 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Elmore, D. F., & Streander, K. V. 2001, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236, 33 [NASA ADS] [Google Scholar]
- Narayan, G., & Scharmer, G. B. 2010, A&A, 524, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., Vögler, A., & Del Toro Iniesta, J. C. 2010, A&A, 518, A2 [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Röhrbein, D., Cameron, R., & Schüssler, M. 2011, A&A, 532, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schnerr, R. S., & Spruit, H. C. 2011, A&A, 532, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suematsu, Y., Tsuneta, S., Ichimoto, K., et al. 2008, Sol. Phys., 249, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Title, A. M., & Berger, T. E. 1996, ApJ, 463, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Title, A. M., Topka, K. P., Tarbell, T. D., et al. 1992, ApJ, 393, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Topka, K. P., Tarbell, T. D., & Title, A. M. 1992, ApJ, 396, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., Bruls, J. H. M. J., & Schüssler, M. 2004, A&A, 421, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieira, L. E. A., Solanki, S. K., Krivova, N. A., & Usoskin, I. 2011, A&A, 531, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viticchié, B., Del Moro, D., Criscuoli, S., & Berrilli, F. 2010, ApJ, 723, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A. 2003, Ph.D. Thesis, University of Göttingen, Germany, http://webdoc.sub.gwdg.de/diss/2004/voegler (in English) [Google Scholar]
- Vögler, A. 2005, Mem. Soc. Astron. Italiana, 76, 842 [Google Scholar]
All Figures
 |
Fig. 1 Upper row: maps of the normalized continuum intensity near 630 nm at original resolution of the MHD simulation (left panel) and after convolving with the Hinode/SP PSF and rebinning to SP detector pixels (right panel). Yellow contours outline the areas identified by the pore exclusion procedure. Lower row: maps of the vertical magnetic field component at local optical depth τ630 = 0.1 for original resolution of the simulation (left panel) and of the line-of-sight magnetic field derived from the inversion of synthetic Stokes profiles (right panel). |
| In the text | |
 |
Fig. 2 Probability distribution functions (normalized to unit area) of apparent vertical field, BLOS (>50 G; bin size 50 G), resulting from the inversion procedure (after removal of the pores). The solid curve corresponds to the MHD simulations, the dashed curve to the Hinode/SP observations. |
| In the text | |
 |
Fig. 3 Bin-averaged continuum intensity contrast near 630 nm vs. magnetic field strength. The bin size is 25 G. Shown are observational Hinode/SP data (red curve), simulation data (intrinsic vertical field) at original resolution (solid black curve, values taken at optical depth 0.1), inverted apparent magnetic field at original simulation resolution (dashed black curve), and synthetic Hinode/SP observations derived from the simulations (green curve). The shift between the solid and dashed black curves (the inverted field being somewhat weaker than the original field for the same contrast value) indicates that the inversion effectively samples the magnetic field at a level somewhat above the surface of optical depth 0.1. |
| In the text | |
 |
Fig. 4 Probability distribution functions (normalized to unit area) of the continuum intensity contrast (bin size 0.01) from MHD simulations (solid curves, corresponding to the green curve in Fig. 3) and observations (dashed curves, corresponding to the red curve in Fig. 3). The upper left panel shows the PDF for all pixels, while the plots in the other panels give the PDFs for various ranges of BLOS (indicated by the insets) obtained from inversions, omitting the pixels corresponding to pores. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


