| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913423 | |
| Published online | 18 January 2013 | |
Spectral diagnostic of a microflare. Evidences of resonant scattering in C IV 1548 Å, 1550 Å lines
1
Research Center for Astronomy and Applied Mathematics, Academy of
Athens,
4 Soranou Efessiou Str.,
11527
Athens,
Greece
e-mail: cgontik@academyofathens.gr
2
NASA Marshall Space Flight Center, VP 62,
Huntsville, AL
35812,
USA
3
University of Ioannina, Dept Physics-Section Astrogeophysics,
451 10
Ioannina,
Greece
Received: 8 October 2009
Accepted: 3 December 2012
Aims. We study a microflare, classified as a GOES-A1 after background subtraction, which was observed in active region NOAA 8541 on May 15, 1999.
Methods. We used TRACE filtergrams to study the morphology and time evolution. SUMER spectral lines were used to diagnose the chromospheric plasma (Si ii 1533 Å), transition region plasma (C iv 1548, 1550 Å), and coronal plasma (Ne viii 770 Å).
Results. In the 171 Å and 195 Å filtergrams, we measure apparent mass motions along two small loops that compose the microflare from the eastern toward the western footpoints. In SUMER, the microflare is detected as a small (47 Mm2), bright area at the western footpoints of the TRACE loops. The spectral profiles recorded over the bright area are complex. The Si ii 1533 Å line is self-reversed owing to opacity, and the coronal Ne viii line profile is composed of two Gaussian components, one of them systematically redshifted. The C iv 1548 Å and 1550 Å profiles are badly distorted because of the temporary depression of the detector local gain caused by the very high count rates reached in the flaring region and we can only confirm the presence of strong blueshifts of ≃ –200 km s-1. Few, unaffected C iv profiles show two spectral components. In the northern part of the bright area, all SUMER spectral lines have at least one blueshifted spectral component. In the southern region of the bright area the spectral lines are redshifted. Adjacent to the microflare we measure, for the first time on the solar disk, an intensity ratio of the 1548 Å line to 1550 Å line with values of three to four, indicating that resonance scattering prevails in the lines formation. Moreover, the scattering region is found to be cospatial to a solar pore.
Conclusions. The blueshifts in the footpoints of the microflare and the apparent mass motions observed with TRACE can be explained by a gentle chromospheric evaporation triggered by the microflare. The redshifted spectral components can be explained as cooling material that is falling back on the solar surface. The presence of resonant scattering can be explained by the low electron density expected in the transition region of a solar pore, combined with the high photon flux coming from the nearby microflare. We estimate that the lower limit of the electron density in the pore lies in the range 108 cm-3 to 109 cm-3.
Key words: Sun: activity / Sun: corona / Sun: flares
© ESO, 2013
1. Introduction
Microflares are transient events with X-ray peak emission 10-3 to 10-6 times the emission of regular flares. They are believed to have the same physical characteristics of large flares but on a smaller scale (Kamio et al. 2011; Brosius & Holman 2009; Berkebile-Stoiser et al. 2009). Moreover, in several cases, large flares consist of an avalanche of several microflares (Berghmans et al. 2001). First observed in EUV by Skylab as transients, microflares were systematically studied in X-rays with later missions, such as the Solar Maximum Mission (SMM), the Soft X-ray Telescope (SXT) on the Yohkoh satellite, and, more recently, with the Extreme ultraviolet Imaging Telescope (EIT) onboard the Solar and Heliospheric Observatory (SOHO), the Transition Region And Coronal Explorer (TRACE), the Ramaty High Energy Solar Spectroscopic Imager (RHESSI), Hinode (Hannah et al. 2008), and the Atmospheric Imaging Assembly (AIA) on the Solar Dynamic Observatory (SDO; Brosius & Holman 2012). They are characterized by a duration of one to ten minutes, a size of 6 Mm2 to 300 Mm2, and radiative losses of 1024 ergs to 1026 ergs (Berghmans & Clette 1999).
In the standard flare model, energy stored in the magnetic field is released into the corona. This energy flows into the chromosphere through either streaming electrons or conduction. The heating of the chromosphere causes an immediate increase in intensity that correlates with the hard X-ray light curve (Kane & Donnelly 1971; Brekke et al. 1996). Measured temperatures and Doppler shifts can be used to confirm the theory of chromospheric evaporation (Hudson 2007 and references therein). According to numerical simulations (Fisher et al. 1985), gentle evaporation associated with small flares results in blueshifted spectral lines emitted from plasma with chromospheric to coronal temperatures (Brosius & Phillips 2004; Milligan et al. 2006b). Explosive evaporation is characterized by redshifted chromospheric and transition region spectral lines and by blueshifted coronal spectral lines (Chen & Ding 2010; Brosius & Holman 2009; Falchi et al. 2006; Milligan et al. 2006a; Teriaca et al. 2006).
A characteristic of chromospheric evaporation is also the presence of multiple component profiles in the transition region and coronal spectral lines (Brosius & Holman 2010; Brosius 2003; Doschek et al. 1977). In Brosius (2003), a flare observed by CDS with good temporal resolution revealed that transition region and coronal lines were initially described well by a single blueshifted Gaussian function indicating strong evaporation. As the flare progressed, additional redshifted components emerged thanks to the draining plasma, dubbed “warm rain”. In Berkebile-Stoiser et al. (2009), the multiple-component spectral lines during a microflare were observed all along the flaring structure instead of just at the footpoints, and they interpreted this observation as a twist along the flare loop.
The modeling of flares’ impulsive phases has to include several phenomena such as plasma heating through high-energy electron beams and conduction fronts, the radiative transfer in the heated chromosphere and the generation of plasma flows (e.g., Allred et al. 2005; Liu et al. 2009). In order to model properly the emitted transition region spectral lines one has to take also into account the deviation from ionization equilibrium present in flare plasmas (Bradshaw et al. 2004). Sarro et al. (1999) reproduced the C iv 1548 Å spectra observed in explosive events using time dependent hydrodynamic calculations of a loop by taking into account departures from ionization equilibrium for the carbon ions. Their C iv 1548 Å line profiles have multiple peaks indicating strong red and blueshifts.
The strong increase of photon flux during flares enhances the importance of photo-excitation and photo-ionization for many plasma conditions. Two examples are the influence on the low chromospheric continuum (Machado & Henoux 1982) and on the excitation of helium spectral lines (Andretta et al. 2008). The enhancement of electron density caused by the chromospheric evaporation increases the importance of collisional excitation so that photo-excitation remains unnoticed in most cases. Judge & Pietarilla (2004) predict that scattering regions will appear as bright halos in He i and C ii lines around transient brightenings. The strong photon flux generated during a flare interacting with the plasma of a close-by sunspot can increase the spectral lines intensity of H2 (Jordan et al. 1978; Innes 2008) due to fluorescence. Moreover, the strong intensity of the C iv 1548 Å line emitted from a flare excited CO lines emitted from a close-by sunspot (Jordan et al. 1979).
In this study we analyze spectral data of a microflare recorded by SUMER (Solar Ultraviolet Measurement of Emitted Radiation), in combination with images of the event taken with TRACE. In Sect. 2, we present the observations and the data treatment and in Sect. 3 we describe the analysis of the TRACE images and the SUMER spectra over the microflare. In Sect. 3.4, we analyze a region adjacent to the microflare where we measure resonance scattering in the C iv lines. In Sect. 4, we discuss the dynamics of the microflare and in Sect. 5 we summarize our results.
 |
Fig. 1 TRACE 171 Å filtergram recorded on 14:27:39 UT. The arrow is pointing at the microflare while the frame indicates the field of view of the SUMER raster. |
2. Observations
The microflare under study took place in NOAA Active Region 8541 on 15 May 1999, between 14:25 and 14:29 UT. It was located at (x,y) = (320′′, 370′′) from the disk center (see Fig. 1). On 15 May 1999, the mean X-ray background flux measured in the 1–8 Å band, by the Geostationary Operational Environmental Satellites, GOES-8 and 10 was of ≃ 4 × 10-7 W m-2. At 14:27:43 UT, a small enhancement of the X-ray flux on the order of 10-8 W m-2 was measured after the background subtraction (see Sect. 3). Therefore the event can be classified as an A1-class microflare. This microflare was observed by TRACE and the SUMER spectrometer on SOHO.
SUMER recorded this event while performing a raster in a west-to-east direction over a 159″ × 120″ field of view centered at (331′′, 384′′) with a 30 s exposure time. The SUMER slit was oriented in the north-south direction. The size of SUMER’s raster field of view is shown in Fig. 1. The microflare was recorded at three consecutive slit exposures between 14:26 UT and 14:28 UT. SUMER transmitted spectral windows of the detector around the Si ii 1533 Å spectral line (formed at 104.1 K), the C iv 1548 Å and 1550 Å spectral lines (formed at 105 K), and the Ne viii 770 Å spectral line (formed at 105.8 K and observed in second order), as well as a low chromosphere continuum section between the Si ii 1526.7 Å line (formed at 104.1 K) and 1528.7 Å. The temperatures given above for each spectral line correspond to the maximum ion population for ionization equilibrium conditions (Arnaud & Rothenflug 1985). TRACE observed the microflare in 12 EUV images of 171 Å and 195 Å coronal filtergrams plus UV images recorded in the 1216 Å and 1600 Å filtergrams and in the White Light (WL) filter. MDI observed the active region with the full disk magnetograms taken with a cadence of 96 min. One of the magnetograms was recorded at 14:24:03 UT, a few seconds before the event. We also used a series of full disk Hα filtergrams recorded with the heliograph of the Meudon observatory in Paris, France in the core of the Hα line with a 0.5 Å spectral width. The spatial resolution of the Hα filtergrams is of 1.95′′, the time cadence is 65 s and the exposure time of each individual filtergram is 60 s.
 |
Fig. 2 Evolution of the flaring loops as seen in the 171 Å (first row) and 195 Å (second row) filtergrams. In Panel b), the isocontour defines the maximum area reached by the bright loops. Two arrows are pointing to the main flaring loops while the letters A and B to their east and west footpoints, respectively. Letters C and D mark the size of a secondary structure activated during the microflare. The third row shows the TRACE white light (Panel i)), 1600 Å (Panel j)), and 1216 Å (Panel k)) filtergrams and the SUMER recorded continuum in the 1527 Å to 1528 Å range (Panel l)). The last row shows the four MDI magnetograms recorded from 11:12 to 16:00. In Panel m), the dotted curve represents the flaring loops as in Panel b). In Panel n), four numbered arrows are pointing to the magnetic structures under the microflare as explained in the text. The bright feature in Panels j), k), and l) corresponds to the loops west footpoint-A as seen by the overplotted 171-loops isocontours. An arrow is pointing to a dark pore (Panel i)) cospatial to a positive magnetic structure (Panel n)), and cospatial to the scattering region (Panel l)) that is presented in Sect. 3.4. The size of each image is of 55″ × 55″ and the EUV intensities are in logarithmic scale. |
Standard corrections were applied to the SUMER data including dead time correction, flatfield subtraction, local gain correction, and correction of geometric distortions. Two further corrections where applied to the dopplergrams calculated from the SUMER spectral lines. A long term variation of the Doppler shift in SUMER measurements on the order of ≃ 0.6 pixel/h is caused by thermo-elastic modifications of the instrument (see Rybák et al. 1999, see Fig. 2 in Peter 1999; Davey et al. 2005). This effect is also apparent in the dopplergram of our 52.5 min long raster. Moreover, the correction of the geometric distortions is not complete and presents residual Doppler shifts of instrumental origin, on the order of ± 2 km s-1, (see Dammasch et al. 1999, their Fig. 6; Davey et al. 2005). We calculated the mean Doppler shift, of the Si ii 1533 Å line, along the slit for each raster step, forming the Doppler shift trend during the raster. This function, after being smoothed with a box-car method, was subtracted accordingly from the Doppler shifts across the slit, for the dopplergrams of the three spectral lines. Similarly, by calculating the mean Si ii Doppler shift across the slit we estimated the residuals from the geometrical correction to be applied to Doppler values along the slit. We computed these corrections using the dopplergram of the Si ii line, which has the lower relative solar Doppler shifts in these active region data, to avoid the influence of true Doppler shifts during these corrections (Davey et al. 2005). These corrections are on the order of ± 2 km s-1.
The dispersion axis of the SUMER spectra needs to be calibrated in order to know the zero-point Doppler shift of each spectral line. The SUMER data set included three reference (full detector) spectra in the range of 1524 Å to 1564 Å recorded by SUMER at the active region between 12:58 UT and 13:02 UT, one and a half hour before the microflare. We used these spectra to determine the dispersion of the detector and apply the same dispersion to the microflare data. We cannot calibrate directly the spectra of the microflare as the raster includes only spectral windows of about 2 Å (about 1 Å in second order). For each reference observation, we summed the individual spectra along the slit to increase the signal to noise ratio and we analyzed these three reference spectra for calibration purposes. A large explosive event, recorded during reference observations, could affect the velocity calibration and, therefore, was not included in the sum along the slit.
To calibrate the dispersion axis of these three spectra we used the Si i lines with wavelengths 1542.428 Å, 1543.725 Å, 1544.186 Å, 1547.13 Å, 1552.209 Å, 1553.370 Å, (Sandlin et al. 1986; Teriaca et al. 1999) as reference lines assuming they have a negligible Doppler shift. We also used the C i lines 1541.520 Å, 1542.175 Å, and 1543.959 Å as reference lines assuming that they are redshifted by 1.5 km s-1 (Teriaca et al. 1999). We finally used the Si ii lines 1526.708 Å and 1533.432 Å as reference lines assuming that they are redshifted by 3.8 km s-1 (Achour et al. 1995 measurement in an active region). After the application of a linear fit to the position of the reference spectral lines, the standard deviation of the residuals of their position is of 0.3 spectral pixels, which corresponds to 2.5 km s-1. This is larger than the residuals found in the literature for the same kind of measurements for Quiet Sun (like in Dadashi et al. 2011). We attempted to obtain calibrated Doppler shifts for the Si ii 1526 Å and 1533 Å lines, using Si i lines, in the 1527 Å to 1535 Å part of the spectrum as reference. We found the two Si ii lines blueshifted by –3 km s-1 to –5 km s-1 depending on the employed reference lines. The spectrum is taken over an active region where the spectral lines of neutral elements could have non-negligible Doppler shifts (see Teriaca et al. 2008). This must explain the 0.3 spectral pixels spread in the residuals of the reference lines mentioned above, and also the blueshifts found in the Si ii lines while in the literature these lines are always found to be redshifted. Therefore, we preferred to use the values found in the literature for the Si ii lines and have them as reference lines. From the calibration of the dispersion axis of the spectra we found that the Ne viii 770.428 Å is redshifted by ≃ 0.5 km s-1 and that the C iv 1548 Å and 1550 Å lines are redshifted by ≃ 6 km s-1. The error associated with this method is mostly caused by the linear fit which calculates the dispersion axis to the spectrum and is on the order of ± 6 km s-1. The error due to the Gaussian fit on the major spectral lines (Ne viii , C iv ) is negligible. This wavelength calibration is more accurate than the one used in Gontikakis et al. 2006 where the Si ii lines are assumed to have negligible Doppler shifts.
The TRACE 171 Å and 195 Å filtergrams were not corrected for cosmic rays around the microflare, as the correcting algorithm confuses the microflare with a cosmic ray hit. TRACE coronal images were coaligned with the SUMER Ne viii intensity image. The 1600 Å and 1216 Å TRACE images were coaligned with the MDI magnetograms and the SUMER Si ii intensity image.
3. Results
3.1. Event morphology and time evolution
The images in Fig. 2a to Fig. 2k show the microflare observed throughout the TRACE filtergrams. The cadence is of approximately 30 s between images recorded from different coronal filters. The coronal images in the first two rows of Fig. 2 show that the microflare is supported mainly by a system of two parallel loops of ≃ 20 Mm length. These loops are indicated by arrows in Fig. 2b; their footpoints are also marked as A and B. West of footpoint B, a small complex structure is also part of the microflare; its edges are marked with the letters C and D. The loops appear to fill from footpoint B to footpoint A in the 171 Å filtergrams (Figs. 2a and b) and the 195 Å filtergrams (Figs. 2e–g) until 14:27:39 UT, the time of the maximum brightness. Then they appear to drain simultaneously (Figs. 2c, d, and h). The size of the microflare at its maximum brightness is of 120 Mm2. After the intensity peak, the intensity decreases but the bright features are still visible three minutes later. The total duration of the event is of four minutes. The event morphology is very similar in 171 Å and 195 Å with a correlation larger than 80%.
Figures 2j and k show the 1600 Å and 1216 Å filtergrams recorded at 12:26:08 UT and 12:26:20 UT respectively. These images show a bright flaring area, composed of two separate small patches, located at the west footpoint of the 171 Å loops (see the 171 Å loops isocontour overplotted in Fig. 2k). From this patch emerge some faint loop like structures (which are more sharply visible in the 1600 Å image) having a similar morphology with the 171 Å and 195 Å loops. The spectral channel of the 1600 Å filtergrams includes the 1548 Å and 1550 Å lines (see Handy et al. 1999). The bright flaring area and the loop like structures in the 1600 Å filtergram are mostly due to photons emitted from the C iv 1548 Å and 1550 Å spectral lines and correspond to transition region plasma.
The last row in Fig. 2 shows a series of MDI magnetograms with a 96 min cadence. In Fig. 2m, we see that the A footpoints of the 171 Å loops, (the dotted curve), are anchored to a negative flux forming a small sunspot (see the white light filtergram in Fig. 2i). Cospatial with footpoint B, where we have the bright flaring area in the chromospheric filtergrams, the magnetograms show a negative and an adjacent positive structure. In Fig. 2n, the arrow with number 3 is pointing to the positive structure while the arrow with number 2 is pointing to the negative structure.
The microflare is triggered due to magnetic cancellation between the negative and positive magnetic structures. Indeed, in Fig. 2n, taken two minutes before the microflare, the negative structure magnetic field intensity is in the range of –290 to –100 Gauss. In Fig. 2p, showing the magnetogram taken 1:30 h after the microflare, the negative structure magnetic field intensity is only of –90 Gauss, and its area is about 50% smaller. The negative structure is connected with a positive structure indicated with arrow 4 in Fig. 2n. These two structures, named 2 and 4, are coaligned with the footpoints of the small loop indicated in Fig. 2b with the letters C and D. However, it is also possible that the negative structure 2 is magnetically connected with the small positive structure 3 to form a small dipole. A plausible explanation of our event is that one of the small magnetic structures (2, 3) and (2, 4) or both of them, interact with the larger loops (A, B; seen in the 171 Å images) through magnetic reconnection.
The positive magnetic structure indicated with arrow number 1 in Fig. 2n is of +290 Gauss and is cospatial to a dark pore visible in the white light TRACE filtergram (see Fig. 2i). The dark pore has 15% lower intensity than its surroundings, has a size of 1.5′′ and lies south of the flaring bright area seen in Figs. 2j and k. The solar pore is visible in two other white light images recorded by TRACE at 14:15:57 UT and 14:36:26 UT. The importance of the dark pore for our analysis is presented in Sect. 3.4.
The lightcurves of the microflare in the 171 Å and 195 Å filtergrams are found from summing the counts in the pixels inside the isocontour in Fig. 2b and are shown in Fig. 3a. The intensity isocontour in Fig. 2b corresponds to 10% of the peak intensity of the microflare. In the same panel we added the lightcurve from the Hα filtergrams. The Hα lightcurve was formed by summing the Hα intensity from pixels of the filtergrams where a surge-like feature, roughly cospatial to the 171 Å loops, develops during the time of the microflare. In Fig. 3a we see that the Hα lightcurve peak intensity appears just before the 171 Å peak intensity which is also before the peak intensity of the 195 Å lightcurve. However, the time delay of the peak intensities is smaller than the cadence of the instruments and is not meaningful. Figure 3b shows that the light curve of GOES-8 at 1–8 Å has a maximum flux at 14:27:43 UT, 20 s before the maximum intensity recorded in the 195 Å TRACE filtergram. The high cross correlation factors derived from the light curves and the morphology between 171 Å and 195 Å images classify the event as a loop flare according to the criteria of Aschwanden et al. (2000).
We measured the variation of the position of the intensity peaks along the loop as a function of time in order to estimate their propagation speed, which we interpreted as mass motion (see Figs. 3c and d). The derived velocities range from 10 km s-1 to 60 km s-1 for the 171 Å filtergram and from 20 km s-1 to 70 km s-1 for the 195 Å filtergram. The motions are from the west footpoint toward the loop top and then the east loop footpoint. The loop intensity decrease starts at the loop top (Figs. 2c, d, and h) and propagates towards the footpoints but this motion is more difficult to quantify.
 |
Fig. 3 Panel a) shows the light curves from 171 Å (solid line with diamonds), 195 Å (dashed line with triangles), and from Hα (solid line with crosses) filtergrams. The vertical segments show the duration of SUMER observation. Panel b) shows the GOES 8 flux in the 1–8 Å band. The time duration of Panel a) is shown as two vertical segments while an arrow is pointing at the microflare event at 14:27:43 UT. Panel c) shows the 171 Å intensity distribution along the TRACE loops (see Fig. 2b) for two different times. The x-axis shows the distance along the loop where zero is at the east (A) footpoint and the maximum value at the west (B) footpoint. Panel d) shows the 195 Å intensity variation at three different times. Panels c) and d) show bright structures moving from the west to the east footpoints interpreted as mass motions from which we measure velocities of 20 km s-1 to 70 km s-1. |
SUMER recorded the event during the rising phase of TRACE lightcurves between 14:26:14 UT and 14:27:34 UT (Fig. 3). In SUMER images, the microflare appears as a bright area similar to the 1600 Å filtergram (Fig. 2l). Figures 4 and 6a, b show images and dopplergrams from three of the spectral lines recorded by SUMER. In these panels, the field of view is centered on the bright area mentioned above. In Fig. 4a, the isocontour from the TRACE 171 Å loops (Fig. 2b) is plotted for comparison. The analysis of the SUMER images and spectra is described in the next two sections.
3.2. Si II and Ne VIII spectra
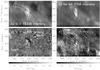 |
Fig. 4 Intensity maps and dopplergrams of the Si ii 1533 Å line in Panels a) and c) and of the Ne viii 770 Å line in Panels b) and d). Each panel size is of 60″ × 40″ centered on the bright area at the footpoint B of the 171 Å loops. In Panels a) and d), the 171 Å intensity isocontour of the microflare loops (see Fig. 2b) is overplotted in white. Moreover, the two regions with black isocontours show the areas where the Si ii line has self-reversed spectral profiles. In Panels b) and c), the black isocontour corresponds to the Si ii 1533 Å intensity. In the dopplergrams, the bright area is separated in a blueshifted north part (black) and a redshifted south part (white) indicated with arrows in Panel c). Over the bright area, two Gaussian components are required to fit the Ne VIII profiles. Thus, in panels b) and d), the intensities and Doppler shifts above this area are those from the high intensity and narrower component (see text). In Panel d), the white isocontour indicates the parts where the secondary low intensity component is redshifted while the two crosses show the only pixels where the secondary component is blueshifted. Intensities are in logarithmic scale. |
The SUMER spectra were analyzed by performing Gaussian fits with a constant background. The number of Gaussian functions necessary to perform the fit was selected initially by visual inspection of the data but also in order to minimize the reduced chi-square function 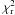 which is defined as
which is defined as 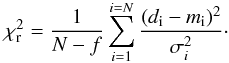 (1)In Eq. (1), (Peter 2010), N is the number of data points in each spectral profile and varies from 47 to 49 depending on the spectral line, f is the number of free parameters and equals four and seven, for a fit with one or two Gaussians respectively. The numerator of the summed fractions equals the squared differences of the data points di minus the corresponding value mi modeled with the Gaussian fit. The denominator of the summed fractions
(1)In Eq. (1), (Peter 2010), N is the number of data points in each spectral profile and varies from 47 to 49 depending on the spectral line, f is the number of free parameters and equals four and seven, for a fit with one or two Gaussians respectively. The numerator of the summed fractions equals the squared differences of the data points di minus the corresponding value mi modeled with the Gaussian fit. The denominator of the summed fractions 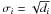 corresponds to the Poisson weighting for the SUMER measurements. Most of the
corresponds to the Poisson weighting for the SUMER measurements. Most of the 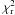 derived values for the fits are on the order of one.
derived values for the fits are on the order of one.
Figures 4a and c shows the intensity and Doppler map of the Si ii 1533 Å line after performing a single Gaussian fit. The intensity image shows the bright area having the same shape as the SUMER continuum (Fig. 2l) and TRACE 1216 Å and 1600 Å filtergrams (Figs. 2j and k). In the Doppler map the bright area is divided in a north blueshifted and a south redshifted regions. In the northern region, 8 pixels have velocities in the range (–2.5 km s-1 to –10 km s-1) and correspond to upward motions, while in the southern region 26 pixels have velocities in the range 2 km s-1 to 16 km s-1 corresponding to downward motions. The above Doppler values are obtained after adding a mean velocity of 3.8 km s-1, taken from Achour et al. (1995), to each Doppler shift. A net blueshift in the northern region persist also if we add, instead, a mean velocity of 6.4 km s-1, found on an active region from Teriaca et al. (1999).
In the 14 profiles distributed in two small regions shown in Figs. 4a, c with two black isocontours, the Si ii presents double spectral peaks. These peaks are very narrow as their width is of one to two spectral pixels and they are found in a short spectral distance of four to five spectral pixels (see Fig. 5a).
An effort to fit these spectral peaks with two Gaussians gave poor results because the double Gaussian fit could not reach the low intensity dip between the two intensity peaks. Therefore, the Doppler shifts from these double-peaked profiles where computed with a single Gaussian fit. The single Gaussian fits to five of these reversed profiles gave blueshifts that belong to the eight blueshifted profiles located in the northern region. The Gaussian fits to five other self-reversed profiles gave redshifts belonging to the 26 redshifted profiles of the southern region. These double-peaked profiles correspond to a self-reversal caused by the high optical thickness of the spectral line in these areas. The self-reversed profiles of the Si ii 1533 Å line have been observed with Skylab at the limb (Nicolas et al. 1977) and studied with radiative transfer calculations (Lanzafame 1994). Other Si ii spectral profiles as in Fig. 5b do not present important distortions from a single Gaussian profile. The peak intensity of the Si ii spectral profile over the microflare equals 83 counts during the 30 s exposure time and is roughly four times higher than the peak intensity of the mean active region spectral profile.
 |
Fig. 5 Spectral profiles of the Si ii 1533 Å line (Panels a) and b)) and Ne viii 770 Å (Panels c) and d)). The left Si ii profile is self-reversed due to opacity while the right one is well fitted with a single Gaussian fit. The Ne viii profiles are fitted with a narrow, high-intensity Gaussian component and a broad, low-intensity Gaussian component. |
The intensities and Doppler shifts of the Ne viii line are mapped in Fig. 4b and d respectively. The 60% of the spectral profiles over the microflare are better described with a double Gaussian fit. The first Gaussian component is narrow with a high intensity, while the second component has two to four times lower intensities with broader profiles (see Figs. 5c and d). In Fig. 4b and d, the intensities and Doppler shifts derived from the narrow component Gaussian fit are represented over the microflare while the intensities and Doppler shifts of the surrounding area, are computed with a single Gaussian fit.
The broad component is redshifted by 20 km s-1 to 60 km s-1 while we found only two cases presenting blueshifts of ≃−30 km s-1 (see Fig. 5c) in the blueshifted region. Very often the red part of the broad profiles is missing due to the short range of the spectral windows (see Fig. 5d). In these truncated cases we can only confirm that there is a second component and that it is redshifted but we cannot measure the Doppler shift.
The northern blueshifted and southern redshifted regions are also present but with a different shape than the ones in the Si ii dopplergram. The measured Doppler shifts are –15 km s-1 to –5 km s-1 for the north and 5 km s-1 to 20 km s-1 in the south region for the Ne viii line. The peak intensity of the Ne viii microflare mean spectral profile equals 732 counts and is 18 times higher than the peak intensity of the spectral profile averaged over the active region.
3.3. C IV 1548 Å and 1550 Å spectra
In the microflare area, the average peak intensity of the C iv 1548 Å spectral profile is 6250 counts and is 57 times larger than the peak intensity of the spectral profile over the mean active region. Most of the C iv 1548 Å peak intensities are higher than 50 counts/s. At such rates, the gain of the SUMER detector is locally reduced to a level that the spectral profiles become unrecoverable (L. Teriaca, priv. comm.)1. The mentioned critical rate is taken before the correction for the local gain of the detector. The over-exposed profiles are composed of a saturated core with two or three spectral peaks and are physically meaningless. The wing of these profiles, where the count rate is lower than the critical rate, can be meaningful. We perform a Gaussian fit analysis only for profiles where the maximum count rate is below 35 counts/s before the application of the local gain correction. The same threshold of 35 counts/s was applied for the case of the C iv 1550 Å spectral line. Only five C iv 1548 Å profiles and 20 C iv 1550 Å profiles have peak intensities below 35 counts/s while SUMER recorded over the microflare 42 individual profiles. In Fig. 6, we show two typical microflare spectral profiles for both the 1548 Å and the 1550 Å lines. Panels (c) and (d) are taken in the west part of the microflare. Panels (e) and (f) are taken in the central part of the microflare where the detector is over-exposed. In panels (e) and (f), the part of the profiles with intensity higher than the dashed horizontal line cannot be trusted. In panels (c) and (d), where the spectra are not over-exposed, we present the curves from a double Gaussian fit.
Moreover, in Fig. 6, panels a) and b) show, respectively, the intensity map and dopplergram of the bright area in the C iv 1550 Å line. The over-exposed area in Fig. 6 is represented with white color as if it is “burned” in both panels. In the microflare area that is not over-exposed, we performed a double Gaussian fit and we represent the dominant Gaussian component intensity and Doppler shift in panels (a) and (b), respectively. The rest of the two images were computed using a single Gaussian fit.
For the Gaussian fit of the C iv 1548 Å line, we ignored the presence of the chromospheric Si i lines at 1547.13 Å, 1547.45 Å and 1548.72 Å, while for the Gaussian fit of the C iv 1550 Å line, we ignored the Fe ii 1550.26 Å and Si i 1551.24 Å lines. (The line identifications were found in Curdt et al. 2001; Peter 2000.)
The meaningful profiles of the C iv lines that we analyzed are recorded at the west SUMER slit position observing the microflare. These profiles were recorded at the very beginning of the microflare and are blueshifted. The narrow components have upflows on the order of –20 km s-1 to –5 km s-1, while for the broad Gaussian component, the upflows are in the range –10 km s-1 to –50 km s-1. The measured line widths are from 40 km s-1 to 50 km s-1 for the narrow component while for the broad component the range of the width is of 80 km s-1 to 140 km s-1. The over-exposed profiles are so broad that they cover the 2 Å range of the SUMER spectral windows. The continuum, which can be easily measured in the 1528 Å spectral window is much lower than the counts measured in the red wing of the over-exposed profiles. Therefore, in these profiles we see emission from the C iv lines blueshifted to about –200 km s-1.
 |
Fig. 6 Panels a) and b) show the C iv 1550 Å intensity and dopplergram, respectively. The other panels show individual spectral profiles of the C iv 1548 Å line (panels c) and e)) and C iv 1550 Å (panels d) and f)) lines. The position of the profile in arcseconds is shown at the top left of each panel and is indicated with letters (corresponding to the panels) in the intensity image. The histogram line represents the data. In panels c) and d), the solid lines represent the fit function and the two Gaussian components. In panels e) and f), the profiles are recorded in the central bright area. The detector is over-exposed for the parts of the profiles above the horizontal dashed lines. The non-overexposed part of these profiles, shows blueshifts on the order of –200 km s-1 at the microflare. |
From the width of the broad component we can compute the nonthermal velocity ξ. Assuming an ion temperature of T = 105 K for the C iv ions we can write: 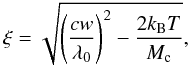 (2)where c is the speed of light, w the measured line width from the Gaussian fits, λ0 = 1548 Å, kB the Boltzmann constant and Mc the carbon atomic mass. Most values of ξ are in the range 80 km s-1 to 140 km s-1. These values are 1.7 to 3 times higher than the velocity of sound for 105 K which is vs = 48 km s-1. On the other hand, the nonthermal velocity of the narrow components are in the range 30 km s-1 to 45 km s-1.
(2)where c is the speed of light, w the measured line width from the Gaussian fits, λ0 = 1548 Å, kB the Boltzmann constant and Mc the carbon atomic mass. Most values of ξ are in the range 80 km s-1 to 140 km s-1. These values are 1.7 to 3 times higher than the velocity of sound for 105 K which is vs = 48 km s-1. On the other hand, the nonthermal velocity of the narrow components are in the range 30 km s-1 to 45 km s-1.
3.4. Resonant scattering deduced from the C IV intensity line ratio
The two C iv form a doublet. The 1548 Å line originates from the atomic transition 2s 2S1/2 → 2p 2P3/2, which we refer as the transition from ground level 1 to level 3 and the 1550 Å line originates from the atomic transition 2s 2S1/2 → 2p 2P1/2, which we refer as the transition from ground level 1 to level 2. For typical conditions in the transition region, the emissivity of the C iv lines is dominated by collisions and, for optically thin conditions, the line intensity ratio is I13/I12 = 2, where I13 is the total specific intensity of the 1548 Å line, I12 the total specific intensity of the 1550 Å line and the 13 and 12 indexes refer to the corresponding transitions. When the optical thickness becomes important, 1548 Å photons are scattered out of the line of sight and the line ratio has values between one and two (Dere & Mason 1993).
In a location having a surface of 17 Mm2 corresponding to 34 SUMER spatial pixels centered 5 Mm south of the bright area, the total intensity ratio of 1548 Å over 1550 Å has values of three to five. This is the first time, to our knowledge, that a value substantially higher than two for the ratio of the C iv lines is measured on the disk. The excess in the ratio values is caused by resonance scattering contribution to the formation of the two C iv spectral lines (A.H. Gabriel, priv. comm.). We call the area presenting the enhanced line ratio the scattering region. In Fig. 7a, the scattering region is represented as black isocontours delineating regions with lines ratio higher than three over the C iv 1548 Å line intensity image. The black isocontours are not closed lines to avoid the adjacent overexposed part of the C iv line profiles.
In Fig. 7c, one can see two individual spectral profiles of the C iv 1548 Å and 1550 Å lines, respectively, taken at the same spatial pixel of the scattering region; these have a line ratio equal to 3.7 and are redshifted by ≃ 20 km s-1. The profiles in Fig. 7c are typical of the scattering region. In Fig. 7c, data are represented with a histogram and a solid line curve represents a single Gaussian fit to the data. Figure 7b shows the line ratio calculated along the slit in a north-south direction across the scattering region. The line ratio is calculated by dividing the total intensities derived from the single Gaussian fit to the profiles (Fig. 7c). The four curves in Fig. 7b, correspond to four subsequent slit positions. Curves with x-crosses, squares, triangles and plus signs correspond to values selected at Solar X = 318′′, 319′′, 320′′ and 321′′, respectively. The ratio is computed from profiles where the count rate at the peak intensity, before the application of the local gain, is below 35 counts/s. In these positions we can trust the line ratio values. However, two ratio values are between four and five for Solar X = 320′′. Assuming a 10% error on the coefficients used to correct profile intensities from the local gain of the detector, gives an average error of 10% to the integrated intensities used to the calculated the line ratio. Moreover, the relative error on the line ratios is assumed to be 20%.
Figure 7b shows, also, the peak intensity of the I13 profiles (dashed line with squares) across the scattering region from north to south along the slit position Solar-X = 319′′. The peak intensity becomes higher than 1000 counts for Solar-Y larger than 364′′ while when Solar-Y = 367′′ the C iv 1548 Å profiles are multipeaked due to over-exposure and the line ratio is meaningless. SUMER recorded a raster with the same characteristics (same f.o.v., and same spectral lines) as the one studied in this paper during from 13:04 UT to 13:57 UT. During this first raster, SUMER recorded the (320′′, 370′′) location at 13:28 UT before the onset of the microflare and the area did not present any particular brightening. The C iv lines ratio at this location was on the order of two. This indicates that the high line ratio found in this study is directly related to the high intensity produced at the microflare. Figure 7d shows a calculation of the electron density in the scattering region with a method that is discussed in the next section.
 |
Fig. 7 Panel a) shows the C iv 1548 Å intensity image of the microflare. The isocontours delineate the scattering region but do not overlap with the white, over-exposed area. Panel b) shows the lines ratio across the scattering region along the slit from Solar Y = 360′′ to 368′′ for four slit positions. Curves with x-crosses triangles, squares and crosses correspond to values selected at the Solar X = 318′′, 319′′, 320′′ and 321′′ slit positions, respectively. Moreover, in Panel b), the dashed line shows the peak intensity of the C iv 1548 Å line profiles from Solar Y = 360′′ to 368′′ at Solar X = 319′′. Panel c) shows the individual profiles (histogram lines) of the C iv 1548 Å and 1550 Å lines from the same spatial pixel of the scattering region with the Gaussian fit. Panel d) shows the calculated electron density according to Eq. (5) for the line ratios of panel b). |
3.5. Estimation of the electron density at the scattering region
For resonant, optically thin lines with a high oscillator strength as is the case of the 1548 Å, 1550 Å lines, the total specific intensity can be described as the sum of two terms (Kohl & Withbroe 1982; Noci et al. 1987). 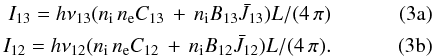 In the above equations, the first term on the right hand side is due to electron collisions while the second term is due to resonant scattering. We assumed that all C iv ions are at the ground level and we replaced n1, which is the C iv ions population in the ground state with ni, the total population of C iv ions. The quantities ni and the electron density, ne, are averaged along the line-of-sight section, L, crossing the transition region. B13 = 5.18 × 109 [s-1/(erg s-1 cm-2 sr-1 Hz-1)], B12 = 2.59 × 109 [s-1/(erg s-1 cm-2 sr-1 Hz-1)] and C13 [cm3/s], C12 [cm3/s] are the two Einstein absorption coefficients and the two collisional excitation rate coefficients, respectively. The collisional excitation is computed with the assumption of a Maxwellian electron distribution (Aggarwal & Keenan 2004) and is a function of the electron temperature.
In the above equations, the first term on the right hand side is due to electron collisions while the second term is due to resonant scattering. We assumed that all C iv ions are at the ground level and we replaced n1, which is the C iv ions population in the ground state with ni, the total population of C iv ions. The quantities ni and the electron density, ne, are averaged along the line-of-sight section, L, crossing the transition region. B13 = 5.18 × 109 [s-1/(erg s-1 cm-2 sr-1 Hz-1)], B12 = 2.59 × 109 [s-1/(erg s-1 cm-2 sr-1 Hz-1)] and C13 [cm3/s], C12 [cm3/s] are the two Einstein absorption coefficients and the two collisional excitation rate coefficients, respectively. The collisional excitation is computed with the assumption of a Maxwellian electron distribution (Aggarwal & Keenan 2004) and is a function of the electron temperature.
The mean intensities, 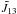 and
and 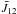 , in [erg s-1 cm-2 sr-1 Hz-1] units, in the radiative excitation rates (Noci et al. 1987) are expressed as
, in [erg s-1 cm-2 sr-1 Hz-1] units, in the radiative excitation rates (Noci et al. 1987) are expressed as 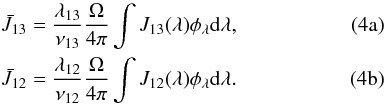 In the above equations J13(λ) and J12(λ) are the exciting radiation fields (Rutten 2003) illuminating the resonant region, φλ [1/Å] is the normalized absorption profile, and Ω is the solid angle subtending the area from which the exciting radiation originates.
In the above equations J13(λ) and J12(λ) are the exciting radiation fields (Rutten 2003) illuminating the resonant region, φλ [1/Å] is the normalized absorption profile, and Ω is the solid angle subtending the area from which the exciting radiation originates.
Dividing Eqs. (3a), (3b) for I13 and I12, supposing that ν13 = ν12 and solving for ne gives, 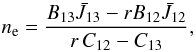 (5)where r = I13/I12 is the total intensity ratio. When the resonant scattering terms in Eqs. (3a), (3b) are negligible, the ratio r equals the ratio of the collision excitation rates C13/C12 = g3/g2 = 2 where g2 and g3 are the statistical weights of levels 2 and 3, respectively. Therefore, when r = 2, Eq. (5) is irrelevant as well as the estimation of the electron density.
(5)where r = I13/I12 is the total intensity ratio. When the resonant scattering terms in Eqs. (3a), (3b) are negligible, the ratio r equals the ratio of the collision excitation rates C13/C12 = g3/g2 = 2 where g2 and g3 are the statistical weights of levels 2 and 3, respectively. Therefore, when r = 2, Eq. (5) is irrelevant as well as the estimation of the electron density.
Using Eq. (5), we estimated the electron density across the scattering region along a north-south direction as a function of the electron temperature. In order to calculate the electron density, we need to estimate the mean intensities 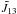 and
and 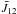 . We considered that φλ is a Gaussian function, having a width equal to a thermal component at T = 105 K plus a nonthermal component, ξ (Noci et al. 1987). In our case we used a value ξ = 29 km s-1, which is the mean nonthermal velocity computed from the Gaussian fits of the scattering region line profiles and is also found from nonthermal line measurements of the C iv 1548 Å line emitted in an active region (Teriaca et al. 1999). In that way, the spectral width of the ion’s mean absorption profile corresponds to the spread of their velocities. We also assumed that φλ is centered on the C iv lines rest wavelengths, ignoring the mean plasma velocity of the scattering region relative to the flaring region.
. We considered that φλ is a Gaussian function, having a width equal to a thermal component at T = 105 K plus a nonthermal component, ξ (Noci et al. 1987). In our case we used a value ξ = 29 km s-1, which is the mean nonthermal velocity computed from the Gaussian fits of the scattering region line profiles and is also found from nonthermal line measurements of the C iv 1548 Å line emitted in an active region (Teriaca et al. 1999). In that way, the spectral width of the ion’s mean absorption profile corresponds to the spread of their velocities. We also assumed that φλ is centered on the C iv lines rest wavelengths, ignoring the mean plasma velocity of the scattering region relative to the flaring region.
We assumed that the photons exciting the C iv ions in the scattering region originate from the bright area. To estimate the incident intensity profile J12(λ), we selected a spatial pixel showing a typical C iv 1550 Å microflare profile with high, but not too distorted, intensities in the bright area (Fig. 7a). The 1548 Å line profile at the same spatial pixel is corrupted, so that we assumed that J13(λ) = 2J12(λ).
The factor 2 in the previous equation means that the electron density is high at the microflare and the scattering effects are negligible. However, this assumption means that ratios higher than four in the scattering region are impossible. Thus, values above four would imply that the ratio in the exciting region is higher than two or, more probably, that the above ratios are indeed not higher than four when considering the rather high uncertainties. A difficult parameter to estimate is the solid angle Ω which subtends the illuminating area as we do not know the exact geometry of the microflare. We estimated the solid angle subtending the bright area as Ω = π/2 sr. This represents the one eighth of a sphere oriented towards the microflare and must be an upper limit of the solid angle. Another possibility would be to consider Ω = S/D2 where S = 47 Mm2 is the surface of the bright area recorded with SUMER and D the mean distance of each position in the scattering region from the bright area. For this last possibility, Ω mean value is of 0.6 sr. We believe that in the second estimation of the solid angle we underestimate the size of the microflare illuminating region as we ignore the altitude reached by the bright C iv plasma during this eruption. In Fig. 7d the electron density of the scattering region is in the range 2 × 108 cm-3 to 109 cm-3 and is calculated for a solid angle Ω = π/2. For Ω = S/D2, these values are in the range 6 × 107 cm-3 to 2 × 108 cm-3 which are too low to be accepted for active region densities. Another reason for the low electron density values is that we underestimate the intensity of the microflare profiles used for the incident intensity, perhaps by some numerical factor of two to even four because of the over- exposure of the detector. The measured electron densities are dependent on temperature through the collision coefficients C12 and C13 in Eq. (5). The presented electron densities are calculated for a temperature of 105 K which is the most probable for C iv ions. For a temperature of 80 000 K, the electron densities raise by 20%.
We also performed an error propagation analysis on Eq. (5) (Beers 1957, p. 26) assuming the dependence of the electron density on the lines ratio (with a 20% relative error) and on the 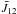 which, in the present study is known within a numerical factor, say from three to five, to include the errors on the solid angle and on the microflare true brightness. The computed mean error bar on the electron density is of 2 × 109 cm-3 which is higher than our measured electron densities.
which, in the present study is known within a numerical factor, say from three to five, to include the errors on the solid angle and on the microflare true brightness. The computed mean error bar on the electron density is of 2 × 109 cm-3 which is higher than our measured electron densities.
3.6. Relation of the scattering region to the solar pore
The reason for the low estimated collisional processes may be explained by the presence of a solar pore cospatial to the scattering region (see Fig. 2j). Solar pores are small sunspots deprived from penumbra. Their magnetic field strength is on the order of 1–2 kGauss (Keppens & Martinez Pillet 1996). However, from the MDI magnetogram we find a magnetic field of just ≃ 290 Gauss under the solar pore. This low magnetic field strength of the solar pore is caused by a low filling factor as the 1.97′′ spatial resolution of the magnetogram is larger than the size of the solar pore. Studies of the transition region above sunspots have shown that the electron density on the order of 1010 cm-3 which is 10 times smaller than in the surrounding plage (Tian et al. 2009). We expect that the observed solar pore has electron densities of the same order, or even higher, than the ones measured in Tian et al. (2009). However, we measure electron densities that are one or two orders of magnitude lower (108 to 109 cm-3). Therefore, our measurements are lower limits of the solar pore electron density as we underestimate the illumination coming from the microflare due to the detector over-exposure and due to the uncertainty on the solid angle estimation. However, this result supports the low collisional rate estimation and suggests that a scattering region is part of the solar pore transition region.
4. Discussion
In this section, we give an interpretation to the Doppler shifts measured with SUMER connected to the findings from the other instruments. The blueshifts correspond to upflows created by the reconnection event that takes place between the two opposite-sign magnetic structures observed by MDI (see the last row of Fig. 2).
It is difficult to tell if the blueshifts are tracing plasma ejected directly from the reconnection site, which is the interpretation given to the Doppler shifts observed for explosive events (Innes et al. 1997) and jets (Gontikakis et al. 2009) or if it is plasma ejected due to chromospheric evaporation. The high intensity increase measured at the bright area in all spectral lines, and mostly in the transition region lines of C iv , indicates the mechanism of chromospheric evaporation, where chromospheric plasma is heated to coronal temperatures through the transition region. On the other hand, observations of explosive events do not show a strong increase in intensity. The finding of an A-event in the GOES-8 lightcurve indicates the formation of hot coronal plasma as expected for a small flare. Finally, the Si ii line profile is self-reversed on the flaring area due to high opacity. This fact can be explained by the process of chromospheric evaporation which supplies plasma to the corona through the upper chromosphere where Si ii 1533 Å is formed. A plausible interpretation of the measured redshifts is that they trace the motion of cooling plasma back to the solar surface.
The spatial distribution of the Doppler shifts depends on the morphology of the plasma features that are very difficult to discern due to their small size except perhaps for the 171 Å loops of Fig. 2b. The C iv spectral profiles are over-exposed over the microflare. Their spectral blue wing is very bright but not over-exposed indicating strong blueshifts.
The Ne viii line, as seen in Figs. 4 and 5, presents a narrow and high intensity component that is mostly blueshifted in the north-east part of the microflare, and redshifted in the south-west part. It also presents a broader and low intensity mostly redshifted component.
The Ne viii line and the 171 Å and 195 Å emission very often represent the same plasma (Winebarger et al. 2002; Gontikakis et al. 2006) so that the upward proper motions measured along the 171 Å and 195 Å loops seem consistent with the blueshifts, cospatial to the TRACE loops, measured in the Ne viii line. On the other hand, the redshifted component, not present in the apparent mass motions measured by TRACE perhaps due to its low intensity, must represent cooling material. Blueshifts are also measured in the Si ii line for the northern region. The measurement of upward motions from the chromosphere up to the corona indicates a gentle chromospheric evaporation. The high intensity and nonthermal velocity of the broad spectral component measured in the C iv lines (see Figs. 6a, b) must be a direct evidence of the heating process during the microflare indicating the presence of turbulence or wave heating (Peter 2000) at the footpoints of the flaring loops.
The southern region is redshifted for the Ne viii and Si ii spectral lines observed with SUMER while the C iv lines are useless. The southern region of the microflare is dominated by cooling plasma moving toward the solar surface at coronal and chromospheric temperatures.
Concerning the resonant scattering studied through the C iv lines, let us mention that the use of resonant doublet lines ratio is an important diagnostic for the velocity of the solar wind (Kohl & Withbroe 1982; Noci et al. 1987). This is the first time, to our knowledge, that the C iv 1548 Å over 1550 Å line ratio is observed to be significantly higher than two indicating resonant scattering taking place on the solar disk. There are three more regions of resonant scattering in the same SUMER raster. The first of them, centered at (264′′, 437′′) is associated with a jet emerging also from a microflare (see Gontikakis et al. 2009) and has a C iv ratio between 3 and 3.5 for three spatial pixels. The second region, centered at (290′′, 383′′) close to a small bright feature (see Fig. 2l), has a C iv ratio between 3 and 3.5 for four spatial pixels. These resonant scattering regions, which are produced by close-by bright areas where the C iv profiles are over-exposed, are also co-located with small sunspots or pores which appear in the TRACE white light and have a smaller surface than the one studied in this work. Finally, we report a third, three pixels size scattering area, where the line ratio is between 2.9 and 3.1, at (348′′, 402′′) adjacent to a small bright structure where the profiles do not suffer from over-exposure like the other regions.
5. Conclusions
We present a multiwavelength study of a typical microflare using SUMER spectra and TRACE images. The detection of a simultaneous A1-class event, and the strong correlations computed from the morphology and lightcurves of the TRACE 171 Å and 195 Å filtergrams confirm that the event is a small flare (Aschwanden et al. 2000).
SUMER, simultaneously with the bright small flaring loops seen in TRACE 171 Å and 195 Å filtergrams, observed a small bright area in all spectral windows from the low chromospheric continuum up to the coronal Ne viii line. The small area is located at the western footpoints of the bright TRACE loops. The same bright area is also prominent in the TRACE 1216 Å and 1600 Å filtergrams, simultaneously with SUMER.
The analysis of the SUMER dopplergrams, in conjunction with the morphology and time evolution of the TRACE 171 Å and 195 Å filters, indicates that we observe a gentle chromospheric evaporation in the northern region of the bright area. This process appears as upward proper motions along the flaring loops in 171 Å and 195 Å filters as well as blueshifted spectral components in the northern region of the bright area in the coronal Ne viii 770 Å line, (with one blueshifted spectral component) the transition region C iv 1548, 1550 Å lines (with enhanced blueshifted wings) and in the chromospheric Si ii 1533 Å line.
Together with this chromospheric evaporation, we also observe cooling plasma moving toward the solar surface. This plasma appear as a secondary spectral component of the Ne viii spectral line. The blueshifted and redshifted spectral components appear in the same spectral individual profiles which mean that uplift motions due to chromospheric evaporation and the cooling down motions toward the solar surface are within ≃ 1′′ in space and within 30 s in time which correspond to the space and time resolutions of the SUMER instrument respectively.
In the southern part of the bright region the spectral lines have redshifted spectral components with the exception of the C iv profiles that are unreliable due to the detector over-exposure. A possible interpretation for the dynamic of this region is that the plasma at higher or lower temperature exhibit motions toward the solar surface due to cooling.
Moreover, in SUMER observations, we detect a region which is south and adjacent to the bright flaring area where the C iv 1548 Å, 1550 Å line intensity ratio presents values from three to five. These values are much higher than the value of two, which is expected for the C iv lines ratio emitted by an optically thin plasma where collisional excitation dominates. We suggest these ratios are produced because radiation scattering prevails over electrons impacts in the lines formation. A further quantitative analysis is impossible due to the detector over-exposure caused by the high intensity of the microflare in the C iv lines.
The scattering region is cospatial with a solar pore visible in the TRACE white light image. Electron density measurements above sunspots umbrae using transition region spectral lines have shown electron densities 10 times smaller than the electron density of the surrounding active region (Tian et al. 2009). Therefore the reason for such low electron densities is that the scattering region is above a small sunspot. The measurement of resonant scattering in the C iv 1548 Å was possible because of the low electron density above the solar pore which was illuminated with the high intensity produced by the microflare.
A possible diagnostic potential of resonant scattering observed on the solar disk, as reported here, could be to deduce path lengths of the scattering regions (L in Eqs. (3a), (3b)) and thus of filling factors. To exploit the potentialities of on-disk resonant scattering as a diagnostic tool, an instrument capable of observing over a high dynamic range with higher spatial and temporal resolution is clearly needed. The capability of observe diverse doublets formed at different temperatures together with density and temperature diagnostics would also be a dramatic advantage. A spectrometer like Large European Module for solar Ultraviolet Research (LEMUR; Teriaca et al. 2012), proposed for the Japanese Solar C mission would fulfill these requirements. The use of resonance doublets observed on the solar disk in parallel with other wavelengths, such as RHESSI X-ray spectra should be done systematically and might be very important for the study of solar flares.
Acknowledgments
SOHO is a mission of international cooperation between ESA and NASA. The SUMER project is financially supported by DLR, CNES, NASA and the ESA PRODEX program (Swiss contribution). C.G. acknowledge discussions with J.-C. Vial, A. H. Gabriel, W. Curdt, and M. K. Georgoulis. We thank J.-M. Malherbe for providing the Hα filtergrams from the Meudon Heliograph. Last, but not least, we would like to thank the referee, L. Teriaca, who helped very much the present work with his comments. This research has been supported in part by the European Union (European Social Fund ESF) and in part by the Greek Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF) – Research Funding Program: Thales. “Hellenic National Network for Space Weather Research”–MIS 377274. S.P. acknowledges support from an FP7 Marie Curie Grant (FP7-PEOPLE-2010-RG/268288).
References
- Achour, H., Brekke, P., Kjeldseth-Moe, O., & Maltby, P. 1995, ApJ, 453, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Allred, J. C., Hawley, S. L., Abbett, W. P., & Carlsson, M. 2005, ApJ, 630, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Andretta, V., Mauas, P. J., Falchi, A., & Teriaca, L. 2008, ApJ, 681, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Aggarwal, K. M., & Keenan, F. P. 2004, Phys. Scripta, 69, 385 [Google Scholar]
- Arnaud, M., & Rothenflug, R. 1985, A&AS, 60, 425 [NASA ADS] [Google Scholar]
- Aschwanden, M. J., Nightingale, R. W., Tarbell, T. D., & Wolfson, C. J. 2000, ApJ, 535, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, Y. 1957, Introduction to the theory of error (Addison-Wesley Publ.) [Google Scholar]
- Bevington, P. R. 1969, Data reduction and error analysis for the physical sciences (New York: McGraw-Hill) [Google Scholar]
- Berghmans, D., & Clette, F. 1999, Sol. Phys., 186, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Berghmans, D., McKenzie, D., & Clette, F. 2001, A&A, 369, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berkebile-Stoiser, S., Gomory, P., Veronig, A. M., Rybák, J., & Sutterlin, P. 2009, A&A, 505, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., Del Zanna, G., & Mason, H. E. 2004, A&A, 425, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brekke, P., Rottman, G. J., Fontenla, J. M., & Judge, P. G. 1996, ApJ, 468, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Brosius, J. W. 2003, ApJ, 586, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Brosius, J. W., & Holman, G. D. 2009, ApJ, 692, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Brosius, J. W., & Holman, G. D. 2010, ApJ, 720, 1472 [NASA ADS] [CrossRef] [Google Scholar]
- Brosius, J. W., & Holman, G. D. 2012, A&A, 540, 24 [Google Scholar]
- Brosius, J. W., & Phillips, 2004, ApJ, 613, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, F., & Ding, M. D. 2010, ApJ, 724, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Yun, H. S., & Poland, A. I. 1998, ApJ, 114, 151 [Google Scholar]
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dadashi, N., Teriaca, L., & Solanki, S. K. 2011, A&A, 534, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dammasch, I. E., Wilhelm, K., Curdt, W., & Hassler, D. M. 1999, A&A, 346, 285 [NASA ADS] [Google Scholar]
- Davey, A. R., McIntosh, S. W., & Hassler, D. M. 2005, ApJS, 165, 386 [Google Scholar]
- Del Zanna, G., Landini, M., & Mason, H. E. 2002, A&A, 385, 968 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., & Mason, H. E. 1993, Sol. Phys., 144, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Doschek, G. A., Feldman, U., & Rosenberg, F. D. 1977, ApJ, 215, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, J. G., & Phillips, H. J. H. 1992, A&A, 257, 773 [NASA ADS] [Google Scholar]
- Falchi, A., Teriaca, L., & Maltagliati, L. 2006, Sol. Phys., 239, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., Mandelbaum, P., Seely, J. L., Doschek, G. A., & Gursky, H. 1992, ApJS, 81, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985, ApJ, 289, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Gontikakis, C., Dara, H. C., Zachariadis, Th. G., et al. 2006, Sol. Phys., 233, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Gontikakis, C., Archontis, V., & Tsinganos, K. 2009, A&A, 506, 45 [Google Scholar]
- Handy, B. N., Tarbell, T. D., Wolfson, C. J., Korendyke, C. M., & Vourlidas, A. 1999, Sol. Phys., 190, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Hannah, I. G., Krucker, S., Hudson, H. S., Christe, S., & Lin, R. P. 2008, A&A, 481, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hudson, H. S. 2007, ASP Conf. Ser. 368, eds. P. Heinzel, I. Dorotovic, & R. J. Rutten, 365 [Google Scholar]
- Innes, D. E. 2008, A&A, 481, 41 [Google Scholar]
- Innes, D. E., Inhester, B., Axford, W. I., & Wilhelm, K. 1997, Nature, 386, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Jordan, C., Brueckner, G. E., Bartoe, J.-D. F., Sandlin, G. D., & VanHoosier, M. E. 1978, ApJ, 226, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Jordan, C., Bartoe, J.-D. F., Brueckner, G. E., et al. 1979, MNRAS, 187, 473 [NASA ADS] [Google Scholar]
- Judge, P. G., & Pietarila, A. 2004, ApJ, 606, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Kamio, S., Curdt, W., Teriaca, L., & Innes, D. E. 2011, A&A, 529, 21 [Google Scholar]
- Kane, S. R., & Donnelly, R. F. 1971, ApJ, 164, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., & Martínez Pillet, V. 1996, A&A, 316, 229 [NASA ADS] [Google Scholar]
- Kjeldseth-Moe, O., Brylindsen, N., Brekke, P., Maltby, P., & Brueckner, G. E. 1993, Sol. Phys., 145, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, J. L., & Withbroe, G. L. 1982, ApJ, 256, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzafame, A. C. 1994, A&A, 287, 972 [NASA ADS] [Google Scholar]
- Lites, B. W., & Cook, J. W. 1979, ApJ, 228, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Petrosian, V., & Mariska, J. T. 2009, ApJ, 702, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Machado, M. E., & Henoux, J.-C. 1982, A&A, 108, 61 [NASA ADS] [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [Google Scholar]
- Milligan, R. O., Gallagher, P. T., Mathioudakis, M., et al. 2006a, ApJ, 638, 117 [Google Scholar]
- Miligan, R. O., Gallagher, P. T., Mathioudakis, M., & Keenan, F. P. 2006b, ApJ, 642, 169 [Google Scholar]
- Nicolas, K. R., Brueckner, G. E., Tousey, R., et al. 1977, Sol. Phys., 55, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Noci, G., Kohl, J. L., & Withbroe, G. L. 1987, ApJ, 315, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H. 1999, ApJ, 516, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H. 2000, A&A, 360, 761 [NASA ADS] [Google Scholar]
- Peter, H. 2010, A&A, 724, 640 [Google Scholar]
- Porter, J. G., Fontenla, J. M., & Simnett, G. M. 1995, ApJ, 438, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, K. J. H., Bromage, G. E., & Doyle, J. G. 1992, A&A, 385, 731 [Google Scholar]
- Sandlin, G. D., Bartoe, J.-D., F., Brueckner, G. E., Tousey, R., & VanHoosier, M. E. 1986, ApJS, 61, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Sarro, L. M., Erdélyi, R., Doyle, J. G., & Pérez, M. E. 1999, A&A, 351, 721 [NASA ADS] [Google Scholar]
- Spadaro, D., Antiochos, S. K., & Mariska, J. T. 1991, ApJ, 382, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Rubio da Costa, F., Fletcher, L., Labrosse, N., & Zuccarello, F. 2009, A&A, 507, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rutten, R. J. 2003, Radiative Transfer in Stellar Atmospheres, Utrecht University lecture notes, 8th edn. [Google Scholar]
- Rybák, J., Curdt, W., Kučera, A., Schüdle, U., & Wöhl, H. 1999, in The 9th European Meeting on Solar Physics, ed. A. Wilson (Noordwijk: ESA: ESA-448), 361 [Google Scholar]
- Teriaca, L., Banerjee, D., & Doyle, J. G. 1999 A&A, 349, 636 [Google Scholar]
- Teriaca, L., Falchi, A., Falchiani, R., Cauzzi, G., & Maltagliati, L. 2006, A&A, 455, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teriaca, L., Curdt, W., & Solanki, S. K. 2008, A&A, 491, 5 [Google Scholar]
- Teriaca, L., Andretta, V., Auchére, F., et al. 2012, Exp. Astron, 34, 273 [Google Scholar]
- Tian, H., Curdt, W., Teriaca, L., Landi, E., & Marsch, E. 2009, A&A, 505, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winebarger, A. R., Warren, H., Van Ballegooijen, A., DeLuca, E. E., & Golub, L. 2002, ApJ, 567, 89 [Google Scholar]
All Figures
 |
Fig. 1 TRACE 171 Å filtergram recorded on 14:27:39 UT. The arrow is pointing at the microflare while the frame indicates the field of view of the SUMER raster. |
| In the text | |
 |
Fig. 2 Evolution of the flaring loops as seen in the 171 Å (first row) and 195 Å (second row) filtergrams. In Panel b), the isocontour defines the maximum area reached by the bright loops. Two arrows are pointing to the main flaring loops while the letters A and B to their east and west footpoints, respectively. Letters C and D mark the size of a secondary structure activated during the microflare. The third row shows the TRACE white light (Panel i)), 1600 Å (Panel j)), and 1216 Å (Panel k)) filtergrams and the SUMER recorded continuum in the 1527 Å to 1528 Å range (Panel l)). The last row shows the four MDI magnetograms recorded from 11:12 to 16:00. In Panel m), the dotted curve represents the flaring loops as in Panel b). In Panel n), four numbered arrows are pointing to the magnetic structures under the microflare as explained in the text. The bright feature in Panels j), k), and l) corresponds to the loops west footpoint-A as seen by the overplotted 171-loops isocontours. An arrow is pointing to a dark pore (Panel i)) cospatial to a positive magnetic structure (Panel n)), and cospatial to the scattering region (Panel l)) that is presented in Sect. 3.4. The size of each image is of 55″ × 55″ and the EUV intensities are in logarithmic scale. |
| In the text | |
 |
Fig. 3 Panel a) shows the light curves from 171 Å (solid line with diamonds), 195 Å (dashed line with triangles), and from Hα (solid line with crosses) filtergrams. The vertical segments show the duration of SUMER observation. Panel b) shows the GOES 8 flux in the 1–8 Å band. The time duration of Panel a) is shown as two vertical segments while an arrow is pointing at the microflare event at 14:27:43 UT. Panel c) shows the 171 Å intensity distribution along the TRACE loops (see Fig. 2b) for two different times. The x-axis shows the distance along the loop where zero is at the east (A) footpoint and the maximum value at the west (B) footpoint. Panel d) shows the 195 Å intensity variation at three different times. Panels c) and d) show bright structures moving from the west to the east footpoints interpreted as mass motions from which we measure velocities of 20 km s-1 to 70 km s-1. |
| In the text | |
 |
Fig. 4 Intensity maps and dopplergrams of the Si ii 1533 Å line in Panels a) and c) and of the Ne viii 770 Å line in Panels b) and d). Each panel size is of 60″ × 40″ centered on the bright area at the footpoint B of the 171 Å loops. In Panels a) and d), the 171 Å intensity isocontour of the microflare loops (see Fig. 2b) is overplotted in white. Moreover, the two regions with black isocontours show the areas where the Si ii line has self-reversed spectral profiles. In Panels b) and c), the black isocontour corresponds to the Si ii 1533 Å intensity. In the dopplergrams, the bright area is separated in a blueshifted north part (black) and a redshifted south part (white) indicated with arrows in Panel c). Over the bright area, two Gaussian components are required to fit the Ne VIII profiles. Thus, in panels b) and d), the intensities and Doppler shifts above this area are those from the high intensity and narrower component (see text). In Panel d), the white isocontour indicates the parts where the secondary low intensity component is redshifted while the two crosses show the only pixels where the secondary component is blueshifted. Intensities are in logarithmic scale. |
| In the text | |
 |
Fig. 5 Spectral profiles of the Si ii 1533 Å line (Panels a) and b)) and Ne viii 770 Å (Panels c) and d)). The left Si ii profile is self-reversed due to opacity while the right one is well fitted with a single Gaussian fit. The Ne viii profiles are fitted with a narrow, high-intensity Gaussian component and a broad, low-intensity Gaussian component. |
| In the text | |
 |
Fig. 6 Panels a) and b) show the C iv 1550 Å intensity and dopplergram, respectively. The other panels show individual spectral profiles of the C iv 1548 Å line (panels c) and e)) and C iv 1550 Å (panels d) and f)) lines. The position of the profile in arcseconds is shown at the top left of each panel and is indicated with letters (corresponding to the panels) in the intensity image. The histogram line represents the data. In panels c) and d), the solid lines represent the fit function and the two Gaussian components. In panels e) and f), the profiles are recorded in the central bright area. The detector is over-exposed for the parts of the profiles above the horizontal dashed lines. The non-overexposed part of these profiles, shows blueshifts on the order of –200 km s-1 at the microflare. |
| In the text | |
 |
Fig. 7 Panel a) shows the C iv 1548 Å intensity image of the microflare. The isocontours delineate the scattering region but do not overlap with the white, over-exposed area. Panel b) shows the lines ratio across the scattering region along the slit from Solar Y = 360′′ to 368′′ for four slit positions. Curves with x-crosses triangles, squares and crosses correspond to values selected at the Solar X = 318′′, 319′′, 320′′ and 321′′ slit positions, respectively. Moreover, in Panel b), the dashed line shows the peak intensity of the C iv 1548 Å line profiles from Solar Y = 360′′ to 368′′ at Solar X = 319′′. Panel c) shows the individual profiles (histogram lines) of the C iv 1548 Å and 1550 Å lines from the same spatial pixel of the scattering region with the Gaussian fit. Panel d) shows the calculated electron density according to Eq. (5) for the line ratios of panel b). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


