| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219601 | |
| Published online | 11 December 2012 | |
TASTE
III. A homogeneous study of transit time variations in WASP-3b⋆,⋆⋆,⋆⋆⋆
1 Dipartimento di Fisica e AstronomiaUniversità degli Studi di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
e-mail: valerio.nascimbeni@unipd.it
2 INAF – Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
3 Departamento de Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Canary Islands, Spain
4 Universidad de Monterrey, Departamento de Física y Matemáticas, Av. I. Morones Prieto 4500 Pte., San Pedro Garza García, Nuevo León, 66238, México
5 Instituto de Astrofísica de Canarias, Vía Láctea s/n, E38200 La Laguna, Tenerife, Canary Islands, Spain
6 Astronomical Observatory of the Autonomous Region of the Aosta Valley, Loc. Lignan 39, 11020 Nus (AO), Italy
Received: 15 May 2012
Accepted: 8 October 2012
The TASTE project is searching for low-mass planets with the transit timing variation (TTV) technique by gathering high-precision, short-cadence light curves for a selected sample of transiting exoplanets. It has been claimed that the “hot Jupiter” WASP-3b could be perturbed by a second planet. Presenting eleven new light curves (secured at the IAC80 and UDEM telescopes) and re-analyzing thirty-eight archival light curves in a homogeneous way, we show that new data do not confirm the previously claimed TTV signal. However, we bring evidence that measurements are not consistent with a constant orbital period, though no significant periodicity can be detected. Additional dynamical modeling and follow-up observations are planned to constrain the properties of the perturber or to put upper limits to it. We provide a refined ephemeris for WASP-3b and improved orbital/physical parameters. A contact eclipsing binary, serendipitously discovered among field stars, is reported here for the first time.
Key words: techniques: photometric / planetary systems / stars: individual: WASP-3
This article is based on observations made with the IAC80 telescope operated on the island of Tenerife by the Instituto de Astrofísica de Canarias (IAC) in the Spanish Observatorio del Teide.
Tables 1 and 3 and Appendix A are available in electronic form at http://www.aanda.org
Photometric data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/549/A30
© ESO, 2012
1. Introduction
Most of the extrasolar planets discovered so far are massive, gaseous giant planets. The present trend is to probe ever smaller masses, with the final aim of detecting temperate “super-Earths” or Earth-sized rocky planets (1−10 M⊕, 1−3 R⊕) around solar-type stars. The signal expected from a true Earth analog orbiting a Sun twin is extremely small: ~80 ppm for the photometric transit, and ~10 cm/s for the radial velocity (RV) Doppler shift. In the conventional framework both measurements are required to derive the planetary radius and mass (Rp, Mp), i.e., the basic quantities necessary to confirm the planetary status of the transiting body, and to characterize it. Achieving a photometric precision of ~20 ppm (which would allow the detection of an Earth-like planet at 4σ level) over the timescale of a transit is within reach of space-based telescopes only, while a long-term ≲ 20 cm/s RV accuracy is still too ambitious even for the most stable spectrographs, such as HARPS.
A few indirect techniques have been developed to obtain an estimate of Mp (or upper limits to it) for a non-transiting planet without the need of RV measurements, the most promising of which is the transit timing variation (TTV) method. By monitoring a known transiting planet with high-precision photometry, the central instant T0 of each individual transit can be estimated. The gravitational perturbation of a previously unknown third body, which is not necessarily transiting, can cause a significant variation of the orbital period P (Holman & Murray 2005). The effect is greatly increased if the perturber is locked in a low-order mean-motion resonance with the transiting planet (Agol et al. 2005). The Asiago Search for Transit timing variation of Exoplanets (TASTE) project was started in 2010 to search for TTVs with several ground-based, medium-class facilities on a sample of carefully selected targets (Nascimbeni et al. 2011a).
The TTV technique has been exploited and already gave interesting results on a number of Kepler mission candidates. Some candidate planets in multiple systems were validated through TTV analysis (Lissauer et al. 2011). In the past few years, some authors have claimed TTV detections also from ground-based facilities, but none is confirmed so far. Among these claims, WASP-10b (Maciejewski et al. 2011), WASP-5b (Fukui et al. 2011), the intriguing case of HAT-P-13b, which was monitored also by TASTE (Pál et al. 2011; Nascimbeni et al. 2011b; Southworth et al. 2012), and the subject of the present investigation: WASP-3b (Maciejewski et al. 2010).
WASP-3b is a typical short-period (P ≃ 1.8468 days) “hot Jupiter” (1.31 Rjup, 1.76 Mjup), hosted by an F7-8 dwarf. It was discovered by Pollacco et al. (2008). Analyzing an O−C (observed − calculated) diagram computed by comparing the T0 of fourteen transits with the value predicted by a linear ephemeris, Maciejewski et al. (2010) claimed the detection of a sinusoidal modulation with a period of PTTV ≃ 127.4 days and a semi-amplitude of ~0.0014 days ≃2 min. They interpreted this signal as the effect of an outer perturber, identifying three possible orbital solutions in the range 6 − 15 M⊕ and P = 3.03 − 3.78 days. No independent confirmation of this claim has been published so far, though both Littlefield (2011) and Sada et al. (2012) discussed the consistence of their data with that TTV modulation.
In this paper we present (Sect. 2) eleven unpublished transits of WASP-3b: six of them have been gathered at the IAC-80 telescope and five at the UDEM 0.36 m (Universidad de Monterrey, Mexico). We also sifted the literature in search of all the archival photometric data useful for a TTV study (Sect. 3). In Sects. 4 and 5 we describe how both new and archival light curves, for a total of forty-nine transits, were reduced and analyzed in a homogeneous way with the same software tools to provide a consistent estimate of the planetary parameters and their uncertainties. This is crucial especially for T0, whose estimate has been shown to be easily biased by the employed analysis technique (Fulton et al. 2011; Southworth et al. 2012). In addition to T0, we also refined the orbital and physical parameters of WASP-3b, and computed an updated ephemeris (Eq. (10)) for any future study on this target. In Sect. 5.2 we demonstrate that the TTV claimed by Maciejewski et al. (2010) is not supported by our analysis; instead it is probably due to small-sample statistics. Yet, we point out that the revised O − C diagram displays a complex, non-periodic structure and is not compatible with a constant orbital period. Finally, in Sect. 6 we discuss the possible origin of this TTV signal, and show that careful dynamical modeling and additional photometric and RV follow-up is required to confirm the hypothesis and constrain the mass and period of the possible perturber(s).
2. TASTE observations
2.1. IAC-80 observations
We observed six transits of WASP-3b between 2011 May 7 and Aug. 2, employing the CAMELOT camera mounted on the IAC80 telescope. A log summarizing dates and other quantities of interest is reported in Table 1. Individual transits are identified by an ID code ranging from N1 to N6. IAC80 is a 0.8 m Cassegrain reflector installed at the Teide Observatory (Tenerife, Canary Islands) that is operated by Instituto de Astrofísica de Canarias (IAC). CAMELOT is a conventional imager with a  field of view (FOV), equipped with an E2V 42-40 2048 × 2048 CCD detector, corresponding to a 0.304′′ pixel scale. The software clock interrogated to save the timestamps in the image headers is automatically synchronized with the GPS time signal.
field of view (FOV), equipped with an E2V 42-40 2048 × 2048 CCD detector, corresponding to a 0.304′′ pixel scale. The software clock interrogated to save the timestamps in the image headers is automatically synchronized with the GPS time signal.
All observations were carried out with a standard Bessel R filter and the same instrumental setup. Windowing and 2 × 2 binning were employed to increase the duty-cycle of the photometric series, as described in Nascimbeni et al. (2011a). A 10.4′ × 3.2′ read-out window was chosen to image the target and a previously selected set of reference stars in a region of the detector free from cosmetic defects. The one-amplifier readout was preferred to prevent gain offsets between different channels. Stars were intentionally defocused to a full width at half-maximum (FWHM) of 10−13 binned pixels (≃6.0−8.0′′) to avoid saturation and minimize systematic errors due to intra-pixel and pixel-to-pixel inhomogeneities (Southworth et al. 2009). Exposure time was set to 20 s (N1-4) or 15 s (N5-6), resulting in a net cadence τ = 19−25 s and a ~75−87% duty-cycle, with the only exception of N3. On that night, due to software problems, the images were read unbinned and in unwindowed readout mode, decreasing both signal-to-noise ratio (S/N) and duty-cycle.
The weather was photometric on all nights, except for a few thin veils during N3. Our initial goal was to start the series one hour before the first contact of the transit, and to stop one hour after the last contact, but the amount of pre-transit photometry is only a few minutes for the N4 and N6 light curves, and the N1 series was interrupted twenty minutes earlier because of twilight.
2.2. UDEM observations
We observed five transits of WASP-3b between 2008 Sep. 3 and 2010 Aug. 15 with the Universidad de Monterrey (UDEM) 0.36-m reflector. UDEM is a small private college observatory with the Minor Planet Center Code 720 and is located in the suburbs of Monterrey, México. The data were acquired using standard Bessel I- and Sloan z-band filters with a 1280 × 1024 pixel CCD camera at 1.0′′ pixel scale, resulting in a FOV of ~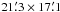 . The observations were slightly defocused to improve the photometric precision and avoid saturation. On-axis guiding was used to maintain pointing stability. Exposure times were set to 30 s for I and 40 s for z. All images were binned 2 × 2 to facilitate rapid readout (~3 s). Each observing session lasted about 4.5 h in order to accommodate the transit event and also to cover about one hour before ingress and one hour after egress. The computer clock was reset to UTC via Internet at the beginning of every observing session to the nearest second.
. The observations were slightly defocused to improve the photometric precision and avoid saturation. On-axis guiding was used to maintain pointing stability. Exposure times were set to 30 s for I and 40 s for z. All images were binned 2 × 2 to facilitate rapid readout (~3 s). Each observing session lasted about 4.5 h in order to accommodate the transit event and also to cover about one hour before ingress and one hour after egress. The computer clock was reset to UTC via Internet at the beginning of every observing session to the nearest second.
 |
Fig. 1 Light curves of WASP-3b. The ID code of each transit matches the corresponding entry in Table 1. Data points are plotted with the original cadence, except for G1/G2 and Z1/E7, which are binned on 30 s and 300 s intervals for clarity, respectively. The red line is the best-fit model found by JKTEBOP. Transits are offset in magnitude by integer multiples of 0.025. |
3. Archival light curves
All available archival data were searched for any light curve useful for a TTV analysis, i.e., complete transits of WASP-3b with a suitable S/N. Partial transits were rejected, except for a few cases with high S/N and without obvious presence of “red noise” after a visual inspection. We define red noise, following Pont et al. (2006), as correlated noise with a covariance between data points on time-scales on the same order of the duration of our transit signal. The transit itself must be modeled and removed from a light curve in order to study the statistical properties of its noise content. Thus, first we analyze the whole sample of light curves in Sect. 5.1, then we discuss how to select a high-quality subset for furter analysis in Sect. 5.2 (“ALL” vs. “SELECTED”).
Hereafter we refer to each light curve with the corresponding alphanumeric ID code reported in Table 1. Overall, thirty-eight archival light curves were (re-)analyzed in the present study:
-
Gibson et al. (2008): two transits in 2008 (G1-2) observed with the RISE camera mounted at the 2.0 m Liverpool Telescope. Both nights were photometric. The second series (G2) ended just before the last contact. The RISE camera filter has a custom wideband 500 − 700 nm, approximately covering both the Johnson R and V passbands.
-
Tripathi et al. (2010): five transits in 2008/2009 (T1-5) from two different telescopes (Fred Lawrence Whipple Observatory FLWO-1.2 m and University of Hawaii UH-2.2 m) and in three Sloan passbands (g, i, z), gathered to complement their high-precision RV measurements. The first two FLWO i transits (T1-2) are partial, the first one missing the first contact by only few minutes.
-
Damasso et al. (2010): one complete transit observed in 2009 (D1), with a commercial 0.25 m reflector in a nonstandard R band, as a part of the feasibility study for a project dedicated to the search for transiting rocky planets around M dwarfs.
-
Maciejewski et al. (2010): six complete transits in the R band from two different telescopes (M1-3 at Rohzen-0.6 m, M4-6 at Jena-0.9 m). The first five observations (M1-5) were carried out on focused images, a practice resulting in a possible increase of the content of red noise.
-
Christiansen et al. (2011): six complete (C1-4, C7-8) and two partial (C5-6) transits, extracted from an 18-day photometric series secured by the High Resolution Imager (HRI) mounted on the spacecraft EPOXI, as part of the EPOCh project. No filter was employed.
-
Littlefield (2011): three transits observed with an 11′′ Schmidt-Cassegrain reflector and without filter (L1-3). These three light curves correspond to the first, third, and fifth ligh curve presented in the original paper. The S/N of the other curves is too low to include them in the present study.
-
Zhang et al. (2011): one 2009 transit in the V band from the Weihai-1.0 m telescope (Z1).
-
Sada et al. (2012): four transits secured in 2009 − 2011 by different telescopes: S1 and S3-4 at the 0.5 m Visitor Center telescope at Kitt Peak National Observatory (KPNO), in the Sloan z band; S2 at the KPNO 2.1 m reflector in the J band, exploiting the FLAMINGO infrared imager.
The first two follow-up light curves of WASP-3b were published by Pollacco et al. (2008): one transit observed at the IAC80 (alternating V and I filters) and one at the Keele-0.6 m (R band), both in 2007. Unfortunately, the original light curves are not retrievable anymore and we did not include them in this study. A T0 data point is determined by the first term of their published ephemeris: 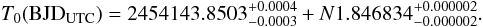 (1)One should be careful, however, because this T0 (corresponding to 2007 Feb. 12) is not an independent measurement of a single transit event. Instead, it comes from an ensemble analysis of SuperWASP, IAC80 and Keele-0.6 m data. For this reason we adopted T0 from Eq. (1) as our first data point in the determination of our new ephemeris, but not in our subsequent TTV analysis (Sect. 5.2). The epoch N of each reported observation in our set is defined according to the ephemeris in Eq. (1), i.e., as the number of transits elapsed since 2007 Feb. 12.
(1)One should be careful, however, because this T0 (corresponding to 2007 Feb. 12) is not an independent measurement of a single transit event. Instead, it comes from an ensemble analysis of SuperWASP, IAC80 and Keele-0.6 m data. For this reason we adopted T0 from Eq. (1) as our first data point in the determination of our new ephemeris, but not in our subsequent TTV analysis (Sect. 5.2). The epoch N of each reported observation in our set is defined according to the ephemeris in Eq. (1), i.e., as the number of transits elapsed since 2007 Feb. 12.
All timestamps were converted to BJD(TDB), i.e., based on barycentric dynamical time following the prescription by Eastman et al. (2010). Each light curve was calibrated in time by identifying the time standard reported in the data headers and (when clarifications were necessary) contacting the authors. Generally speaking, even when the authors report a reliable synchronization source (GPS, NTP, etc.) for their data, it is impossible to carry out an external confirmation of that. The only exception, discussed in Sect. 6, is when two or more independent observations of the same event were performed. Though we did not find any reason to doubt the accuracy of the absolute time calibration of these data, it is worth noting that most of these observations were not performed with the specific goal of a TTV analysis. Thus, the precision achievable on T0 could be limited by sub-optimal choices made about the instrumental setup. For instance, it is widely known that a “long” (in our case, τ ≳ 60 s) exposure time is one of those limiting factors (Kipping 2010).
When required, light curves in flux units were converted into magnitudes and normalized to zero by fitting a low-order polynomial function to the off-transit data points. In a few cases, the tabulated photometric errors are underestimated up to about 50%, as confirmed by the reduced 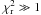 (χ2 being defined as the χ2 divided by the number of degrees of freedom of the fit). This is not unusual in high-precision photometry owing to effects that are not accounted for by standard noise models (Howell 2006): poorly modeled scintillation, high-frequency systematics mimicking random errors, stellar microvariability for both target and comparison stars, etc. We dealt with this by rescaling the errors by a factor of
(χ2 being defined as the χ2 divided by the number of degrees of freedom of the fit). This is not unusual in high-precision photometry owing to effects that are not accounted for by standard noise models (Howell 2006): poorly modeled scintillation, high-frequency systematics mimicking random errors, stellar microvariability for both target and comparison stars, etc. We dealt with this by rescaling the errors by a factor of  , following a common practice (Winn et al. 2007; Gibson et al. 2009). When the photometric errors were not published, the error was assumed to be constant and equal to the scatter σ of the off-transit polynomial-corrected curve. We define the scatter as the 68.27th percentile of the residual distribution from the median, after a 5σ iterative clipping. This measurement is much more robust against outliers than the classical RMS.
, following a common practice (Winn et al. 2007; Gibson et al. 2009). When the photometric errors were not published, the error was assumed to be constant and equal to the scatter σ of the off-transit polynomial-corrected curve. We define the scatter as the 68.27th percentile of the residual distribution from the median, after a 5σ iterative clipping. This measurement is much more robust against outliers than the classical RMS.
4. Data reduction
4.1. IAC80 photometry
The six IAC80 light curves (N1-6) were reduced with the STARSKY photometric pipeline presented in Nascimbeni et al. (2011a,b) but here upgraded with some improvements. The present version v1.1.002 adopts a new, fully empirical weighting scheme to carry out differential photometry. Reference stars were previously weighted by the amount of scatter measured on their light curves after being registered to the total reference magnitude mi (that is, the weighted mean of the instrumental magnitudes of all comparison stars; Broeg et al. 2005). That was an iterative process. Instead, the updated version first extracts the off-transit part of the series, then constructs a set of “intermediate” light curves of the reference stars by subtracting the magnitude of each of them to the off-transit magnitude of the target. Ideally, those curves should be flat and their RMS should be equal to the quadratic sum 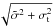 , where σt is the theoretical photometric noise expected on the target (calculated as in Nascimbeni et al. 2011a) and
, where σt is the theoretical photometric noise expected on the target (calculated as in Nascimbeni et al. 2011a) and  the intrinsic noise of the reference star, defined as at the end of Sect. 3. We therefore estimated the latter as
the intrinsic noise of the reference star, defined as at the end of Sect. 3. We therefore estimated the latter as  . The individual weights for a given comparison star are then assumed to be
. The individual weights for a given comparison star are then assumed to be  . The output of this weighting algorithm is checked during each run against two other weighting schemes: (1) equal weights, i.e., unweighted; and (2) using weights derived from the expected theoretical noise computed for the reference stars. The DSYS and PSYS parameters (as defined in Nascimbeni et al. 2011b) allow us to diagnose “bad” reference stars, and to set their weights to zero. For all the N1-N6 transits, the same set of eleven reference stars was employed for consistency reasons. None of them shows signs of variability or higher-than-expected scatter.
. The output of this weighting algorithm is checked during each run against two other weighting schemes: (1) equal weights, i.e., unweighted; and (2) using weights derived from the expected theoretical noise computed for the reference stars. The DSYS and PSYS parameters (as defined in Nascimbeni et al. 2011b) allow us to diagnose “bad” reference stars, and to set their weights to zero. For all the N1-N6 transits, the same set of eleven reference stars was employed for consistency reasons. None of them shows signs of variability or higher-than-expected scatter.
A second improvement to STARSKY is a new algorithm developed to deal with light curves with red noise caused by veils, trails, or thin clouds. This happens when the cloud possesses a structure at angular scales on the same order as the FOV, and/or it is moving fast. Even differential photometry can be affected by these events, as the change of transparency can affect the target and the reference stars by a different amount. Of course, this systematic effect is correlated on with the rapidity of transparency changes. and this correlation can be exploited to discard the affected frames. A quantity that we called “numerical derivative of the absolute flux” (NDAF) is evaluated for each frame i of the series 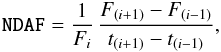 (2)where Fi is the weighted instrumental flux of the reference stars (Fi = 10 − 0.4mi, mi defined as above), and ti is the JD time at the mid-exposure. When NDAF deviates more than 4σ from its average along the series, the frame is discarded. The first and last frame are ignored by our algorithm.
(2)where Fi is the weighted instrumental flux of the reference stars (Fi = 10 − 0.4mi, mi defined as above), and ti is the JD time at the mid-exposure. When NDAF deviates more than 4σ from its average along the series, the frame is discarded. The first and last frame are ignored by our algorithm.
STARSKY outputs light curves extracted from a set of different photometric apertures. These curves are then detrended by a routine that searches for linear and polynomial correlations between the off-transit flux and several combinations of external parameters such as the position of the star on the detector, the airmass, the FWHM of the stellar profiles, the mean sky level, the reference flux Fi, and time. In the following, we describe the reason why we searched for a linear correlation between differential flux and airmass X. We considered the case of two stars (target “t” and reference “r”) with out-of-atmosphere magnitudes mt and mr and color ξt and ξr, respectively. Given the extinction coefficient k and the extinction color term k′, the measured differential magnitude Δm is the difference between the observed magnitudes 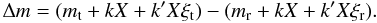 (3)By grouping the involved terms, and taking into account that X is the only quantity that shows short-term variations,
(3)By grouping the involved terms, and taking into account that X is the only quantity that shows short-term variations, 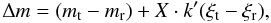 (4)it is easy to see that systematic effects caused by differential extinction on the “true” (intrinsic) differential magnitude (mt − mr) are linearly proportional to X.
(4)it is easy to see that systematic effects caused by differential extinction on the “true” (intrinsic) differential magnitude (mt − mr) are linearly proportional to X.
Eventually, we chose the light curve with the smallest amount of scatter σ and the lowest level of red noise estimated from the β parameter as defined by Winn et al. (2008). The overall S/N of an observation can be quantified by rescaling the unbinned photometric σ of the light curve (with a net cadence τ) on a standard 120-s timescale, that is, by calculating 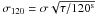 . With the only exception of N3, the final IAC80 light curves have σ120 = 0.67 − 0.95 mmag (Table 1, Fig. 2), only slightly higher than that achieved by Gibson et al. (2008), Tripathi et al. (2010) and Christiansen et al. (2011), with space-based or much larger facilities. N6 shows a large amount of red noise of unknown origin, which is probably related to color-dependent systematics caused by variable atmospheric extinction. For the above-mentioned reasons, N3 and N6 were employed in the determination of our new ephemeris, but not in our TTV analysis (Sect. 5).
. With the only exception of N3, the final IAC80 light curves have σ120 = 0.67 − 0.95 mmag (Table 1, Fig. 2), only slightly higher than that achieved by Gibson et al. (2008), Tripathi et al. (2010) and Christiansen et al. (2011), with space-based or much larger facilities. N6 shows a large amount of red noise of unknown origin, which is probably related to color-dependent systematics caused by variable atmospheric extinction. For the above-mentioned reasons, N3 and N6 were employed in the determination of our new ephemeris, but not in our TTV analysis (Sect. 5).
4.2. UDEM photometry
Standard dark-current subtraction and twilight sky flat-field division process were performed for calibration on each image of the UDEM light curves (U1-5). Aperture differential photometry was carried out on the target star and 4 − 6 comparison stars of similar magnitude ( | Δm | ≲ 1.5). The apertures used varied for each date due to defocus and weather conditions, but they were optimized to minimize the scatter of the resulting light curves. We found that the best results were obtained by averaging the ratios of WASP-3b to each comparison star. This produced smaller scatter than the method of ratioing the target star to the sum of all the comparison stars. We estimated the formal error for each photometric point as the standard deviation of the ratio to the individual comparison stars, divided by the square root of their number (error of the mean).
After normalizing the target star to the comparison stars and averaging, some long-term systematics as a function of time were found. This is perhaps caused by differential extinction between the transit and comparison stars, which generally have different and unknown spectral types. This variation was removed by fitting a linear airmass-dependent function to the out-of-transit baseline of the light curve.
Orbital/physical parameters of WASP-3b estimated from individual data (sub-)sets.
5. Data analysis
5.1. Fitting of the transit model
We chose to analyze all new and archival light curves employing the same software tools and algorithms. Our goal was to obtain a homogeneous estimate of the physical/orbital parameters of WASP-3b. In particular we were interested for our TTV analysis in estimating the T0 of each transit and its associated error in the most accurate way, avoiding biases caused by different techniques. We avoided estimating T0 through heuristic algorithms that assume a symmetric light curve, such as that developed by Kwee & van Woerden (1956). The main reason is that they do not fit for any quantity other than T0. Even more important, they are not robust against outliers, they provide values of T0 known to be biased (Kipping 2010) and errors on T0 known to be underestimated (Pribullaet al. 2012).
JKTEBOP2 (Southworth et al. 2004) is a code that models the light curve of a binary system by assuming both components as biaxial ellipsoids and performing a numerical integration in concentric annuli over the surface of each component. JKTEBOP version 25 was run to fit a model light curve over our data and to derive the four main photometric parameters of the transit: the orbital inclination i, the ratio of the fractional radii kr = Rp/R ⋆ , the sum of the fractional radii Σr = Rp/a + R ⋆ /a (R ⋆ is the stellar radius, Rp the planetary radius, and a the orbital semi-major axis), and the mid-transit time T0. We chose to fit i, kr, Σr independently for each data set, because in a perturbed system i and Σr could change over a long timescale, while kr is an important diagnostic of light curve quality: when the photometric aperture is contaminated with flux from neighbors, the transit is diluted and kr becomes smaller. Moreover, an independent fit allows us to highlight correlations between i, kr, Σr and to derive more reliable global results, as discussed at the end of this section.
We set a quadratic law to model the limb-darkening (LD) effect, naming u1 the linear term and u2 the quadratic term: Iμ/I0 = 1 − u1(1 − μ) − u2(1 − μ)2 and μ = cosγ, where I0 is the surface brightness at the center of the star and γ is the angle between a line normal to the stellar surface and the line of sight of the observer. Southworth (2010), among others, has shown that fixing the values of both u1 and u2 should be avoided, as it could lead to an underestimate of the errors. On the other hand, most light curves have an S/N too low to let both u1 and u2 free, and the resulting best-fit results can be unphysical. We set the quadratic term u2 always fixed to its theoretical value interpolated from the tables computed by Claret (2000; BVRcIc bands), and Claret (2004; Sloan ugriz), adopting the stellar parameters of WASP-3 derived by Pollacco et al. (2008). For all light curves from nonstandard photometry, that is, unfiltered CCD photometry (C1-8, L1-3, E1) or from wide-band R + V photometry (G1-2), estimating first-guess LD coefficients is not trivial. As for G1-2, we interpolated u1 = 0.24 and u2 = 0.38 from the tables by Claret (2000) by taking the average of the values tabulated for the Johnson-V and Cousin-R bands, as done by Gibson et al. (2008). We did the same for C1-8, L1-3, and E1, assuming that the quantum efficiency of a typical unfiltered CCD usually peaks somewhere in between those two bands.
Then one of the three following procedures was applied:
- 1.
On the data sets with a high overall S/N and with two or more transits gathered with the same instrument and filter (G1-2; T1-3; T5-T6; M1-3; M4-5; C1-8; L1-3; N1-5) we first fitted a model with free i, kr, Σr, T0 (and u1 fixed at its theoretical value) to the “best” individual light curves to derive a preliminary estimate of their T0. For “best” we mean complete transits with high S/N: our choice is summarized in Table 2, fourth column. Then we phased those curves setting T0 = 0. The free parameters i, kr, Σr, u1 were fitted again on the stacked light curve to obtain a high-S/N “reference” model of the transit by integrating the information contained in the whole set. We fixed i, kr, Σr, u1 to their best-fit values, and fitted a model with only T0 as free parameter on all individual transits, including the low-S/N or partial ones.
- 2.
On T4, a high-S/N but single light curve, we carried out one simultaneous fit with i, kr, Σr, T0, and u1 as free parameters.
- 3.
In all other cases, the data quality did not allow us to constrain u1 to values with physical meaning, thus u1 was fixed to its theoretical value along with u2. Each transit was then fitted individually to derive i, kr, Σr, and T0.
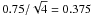 mmag. By taking also into account that our observations do not always cover the same orbital phases, we are confident that the level of red noise in the IAC80 photometry is very low.
mmag. By taking also into account that our observations do not always cover the same orbital phases, we are confident that the level of red noise in the IAC80 photometry is very low.
As the formal errors derived by least squares techniques are known to be underestimated in presence of correlated noise, we took advantage of two techniques implemented in JKTEBOP to estimate realistic errors: a Monte Carlo test (MC) and a bootstrapping method based on the cyclic permutations of the residuals (RP or “prayer bead” algorithm, Southworth 2008). The errors on all parameters obtained with the RP algorithm are on average significantly larger for most of the archival light curves, suggesting a non-negligible amount of red noise. We thus conservatively adopted the RP results in our subsequent analysis. Mean values and error bars can be estimated in two different ways: (1) as the arithmetic mean of the RP distribution associated to its standard error ± σ; and (2) as the median of the RP distribution along with its 15.87th (σ − ) and 84.13th percentile (σ + ). The first estimate assumes a Gaussian distribution, while the latter is purely empirical: they should match in absence of red noise.
We adopted as final results the RP median and uncertainties σ + , σ − for every fitted parameter except T0. The estimated T0 is analyzed in Sect. 5.2 with periodogram techniques that cannot deal with asymmetric error bars, thus for this parameter we adopted the RP means with Gaussian errors ± σ. The best-fit values of Σr, kr, i and u1 modeled on each individual data set are summarized in Table 2. We also show the theoretical value of the linear LD coefficient u1, th as interpolated from Claret (2000, 2004). On all subsets, u1 and u1, th agree within ~ 1σ. This holds even for C1-8, L1-3, and G1, demonstrating that assumptions previously made on nonstandard “clear” or R + V photometry are reasonable.
 |
Fig. 2 Construction of the best-fit model from the four best light curves of WASP-3b observed at IAC80 (on 2011 May 7, May 21, Jun. 26, Jul. 20). The ID# of each transit (N1, N2, N4, N5) matches the corresponding entry in Table 1. Small gray dots represent the data points with the original cadence, while blue circles are binned on 120 s intervals. The red line is the best-fit from JKTEBOP (Table 2). Left panel: individual light curves. Transits are offset in magnitude by a multiple of 0.02 for clarity. Middle panel: residuals from the best-fit model. The reported scatter is evaluated on the binned points as the 68.27th percentile from the median value. Right panel: stack of all four IAC80 light curves with the best-fit model superimposed. The derived parameters are quoted in Table 2. |
 |
Fig. 3 Geometrical parameters of WASP-3b estimated from individual data (sub-)sets (Table 2) plotted as black labeled circles in their two-dimensional parameter space to highlight the sizeable correlation between Σr, kr, and i. The blue dashed line in each plot is a weighted linear fit of all points; the blue triangles and the associated error ellipse correspond to the weighted mean ± 1σ computed on the marginal distribution of Σr, kr, and i (last but one row of Table 2). The red continuous line and squares are computed in the same way as the blue ones, but after removing the outlier labeled “3” from the set (T1,T3; last row of Table 2). |
In an unperturbed system, the transit parameters Σr, kr, and i are purely geometrical and should not depend on wavelength or observing technique. Even if the system is suspected of being perturbed, one can check the long-term consistency of Σr, kr, and i by comparing the best-fit values estimated for independent data sets (Table 2). It is then possible to integrate all extracted information to obtain final quantities of higher precision. We computed the weighted means of all subset estimates of Σr, kr, and i listed in Table 2, obtaining the result shown in the last but one line of the same table ( ⟨ weighted mean ⟩ 1). As pointed out from previous works (e.g., Southworth 2008), these three quantities are correlated with each other, as becomes evident by plotting their individual estimate on planes projected from the three-dimensional parameter space (Σr, kr, i) (Fig. 3). Apart from this, the consistency among all measurements is assessed within the error bars, and we conclude that no variation of Σr, kr, or i is detectable over the timescale covered by our data. The data point extracted from subset T1,T3 appears as the only probable outlier in two correlation plots out of three. We re-evaluated the weighted mean after removing that point ( ⟨ weighted mean ⟩ 2 in Table 2). The resulting averages are quite similar to those evaluated without removing the outlier, but the uncertainty on kr is smaller. We adopt the second mean as final estimate:  More in general, results obtained from subsets T1-3 (Sloan i) and T5-6 (Sloan g) slightly but significantly disagree with each other, which was already noted by Tripathi et al. (2010), who attributed this to the presence of residual red noise.
More in general, results obtained from subsets T1-3 (Sloan i) and T5-6 (Sloan g) slightly but significantly disagree with each other, which was already noted by Tripathi et al. (2010), who attributed this to the presence of residual red noise.
5.2. TTV analysis
The best-fit T0 values for each transit after uniform conversion to BJD(TDB) are shown in Table 3 along with their estimated ± 1σ uncertainties (second column). For completeness we also tabulated the median value of T0 estimated from the distribution of the RP residuals (third column of Table 3) along with its 15.87th (σ − ) and 84.13th percentile (σ + ).
To check which light curves within our sample are significantly affected by red noise, we considered the two diagnostic parameters β and Σ. The first one is defined as in Winn et al. (2008): the light curve is averaged over M bins containing N unbinned points each, then β is calculated as 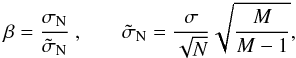 (8)that is, β is the ratio between the scatter σN measured on a given temporal scale Δt = Nτ, and the expected noise
(8)that is, β is the ratio between the scatter σN measured on a given temporal scale Δt = Nτ, and the expected noise  estimated by rescaling the unbinned scatter σ assuming Gaussian statistics. Ideally, we expect β ≃ 1 for independent and random errors (i.e., pure “white noise”), higher values indicating red noise at time scales ~Δt. The time scales around Δt ≃ 25 min are the most important ones for our purposes, because they correspond to the duration of the ingress/egress part of the WASP-3b light curve. As shown by Doyle & Deeg (2004), those are the parts with the highest information content about T0. We chose to compute β on a set of averaging times between Δt = 20 and 30 min, then we took their arithmetic mean as a final estimate for β.
estimated by rescaling the unbinned scatter σ assuming Gaussian statistics. Ideally, we expect β ≃ 1 for independent and random errors (i.e., pure “white noise”), higher values indicating red noise at time scales ~Δt. The time scales around Δt ≃ 25 min are the most important ones for our purposes, because they correspond to the duration of the ingress/egress part of the WASP-3b light curve. As shown by Doyle & Deeg (2004), those are the parts with the highest information content about T0. We chose to compute β on a set of averaging times between Δt = 20 and 30 min, then we took their arithmetic mean as a final estimate for β.
The second diagnostic is Σ. We mentioned above that the distribution of the RP residuals around the best-fit value should be symmetric if the noise budget is dominated by white noise. Hence a “skewed” distribution could highlight a significant amount of red noise. The opposite is not always true: short-term systematics (Δt ≲ τ) do not necessarily lead to skewed RP residual distributions. We parametrized this “skewness” with the ratio Σ between the largest and the smallest error bar σ of a given data point 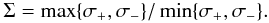 (9)In principle, Σ ≃ 1 for well-behaved transits, and Σ ≫ 1 for transits dominated by long-term systematics. Table 3 lists Σ for all employed T0. We found 1.01 < Σ < 1.63 for the eleven TASTE transits (N1-6, U1-5). Instead, a few archival data points show unusually high values (e.g., Σ = 8.07 for T2). We investigated this issue by comparing the most significant T0 published in the literature (T1-5; G1-2; C1-8; M1-6) with those derived by our reanalysis (Fig. 4, third panel from the top). We concluded that the vast majority of the published estimate agree within the error bars with ours. Notable exceptions are T1, T2, and G2: they all are partial transits, and T2, G2 have also large Σ. This is exactly what we expected. It indeed demonstrates that when a light curve lacks the off-transit part, its normalization becomes difficult, and even a very small difference in the adopted technique can lead to significantly different T0 measurements. We emphasize this conclusion because many TTV studies employ partial transits (some of them even for the most part: among others, Pál et al. 2011 and Fulton et al. 2011). While this is fine when estimating the orbital and physical parameters of the planet, we demonstrated that partial light curves should be included with extreme caution in a TTV analysis. We note that, on average, our error bars are larger than the published ones – sometimes by a factor of two –, confirming our concern that most measurements carried out in the past have been published with underestimated errors due to neglected red noise.
(9)In principle, Σ ≃ 1 for well-behaved transits, and Σ ≫ 1 for transits dominated by long-term systematics. Table 3 lists Σ for all employed T0. We found 1.01 < Σ < 1.63 for the eleven TASTE transits (N1-6, U1-5). Instead, a few archival data points show unusually high values (e.g., Σ = 8.07 for T2). We investigated this issue by comparing the most significant T0 published in the literature (T1-5; G1-2; C1-8; M1-6) with those derived by our reanalysis (Fig. 4, third panel from the top). We concluded that the vast majority of the published estimate agree within the error bars with ours. Notable exceptions are T1, T2, and G2: they all are partial transits, and T2, G2 have also large Σ. This is exactly what we expected. It indeed demonstrates that when a light curve lacks the off-transit part, its normalization becomes difficult, and even a very small difference in the adopted technique can lead to significantly different T0 measurements. We emphasize this conclusion because many TTV studies employ partial transits (some of them even for the most part: among others, Pál et al. 2011 and Fulton et al. 2011). While this is fine when estimating the orbital and physical parameters of the planet, we demonstrated that partial light curves should be included with extreme caution in a TTV analysis. We note that, on average, our error bars are larger than the published ones – sometimes by a factor of two –, confirming our concern that most measurements carried out in the past have been published with underestimated errors due to neglected red noise.
We considered two different samples of measurements for our TTV analysis. The first (“ALL”) includes all the 49 T0 listed in Table 3, plus the T0 from the ephemeris Eq. (1) from Pollacco et al. (2008). The second sample (“SELECTED”) is a high-quality subset of 36 values, selected by excluding Eq. (1) (it does not correspond to an independent measurement of one single transit) and other 13 data points using the following rejection criteria:
- 1.
partial light curve: data points lacking between the first and the last contact;
- 2.
large scatter: σ30 > 1 mmag (σ30 defined as the RMS of the residuals after averaging over 30-min bins);
- 3.
red noise: Σ > 2 or β > 1.2;
- 4.
presence of systematics during or close to the transit ingress/egress, as determined by visual inspection of the residuals.
The first step to plot an O − C diagram is to calculate a “reference” linear ephemeris to predict T0 at any given epoch. We set the new zero epoch at N2, i.e., our most accurate light curve. The ALL sample was employed to fit a linear model by ordinary weighted least squares, obtaining 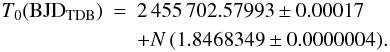 (10)The uncertainties were evaluated from the covariance matrix of the fit, and were both rescaled by
(10)The uncertainties were evaluated from the covariance matrix of the fit, and were both rescaled by  to take into account the real dispersion of the data points around our best-fit ephemeris. In Fig. 4 are plotted the O − C diagrams for ALL (first panel from top) and SELECTED samples (second panel, with a smaller baseline). In both diagrams, the reduced
to take into account the real dispersion of the data points around our best-fit ephemeris. In Fig. 4 are plotted the O − C diagrams for ALL (first panel from top) and SELECTED samples (second panel, with a smaller baseline). In both diagrams, the reduced 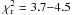 suggests that the measurements do not fully agree with the linear ephemeris in Eq. (10). Yet, there is no evident periodic pattern in our diagrams. We investigated the possibility that this statistically significant scatter is caused by a genuine TTV, either the TTV claimed by Maciejewski et al. (2010) or a different one.
suggests that the measurements do not fully agree with the linear ephemeris in Eq. (10). Yet, there is no evident periodic pattern in our diagrams. We investigated the possibility that this statistically significant scatter is caused by a genuine TTV, either the TTV claimed by Maciejewski et al. (2010) or a different one.
 |
Fig. 4 First panel from the top: O − C diagram for all data points tabulated in Table 3. Second panel: same as above for points selected as in the last column of Table 3. Third panel: comparison between the original T0 published by the respective authors (white circles with gray error bars; Table 1) and as re-estimated in this work (red triangles and bars) for the subset of high-precision light curves identified in the horizontal axis. Fourth panel: GLS periodogram for the complete sample (red line, highest peak at A) and the selected sample (black line, highest peak at S). The periodicity claimed by Maciejewski et al. (2010) is marked with the M label. |
We exploited two algorithms to search for periodic signals: the generalized Lomb-Scargle periodogram (GLS; Zechmeister & Kürster 2009) and the “fast χ2” algorithm (Fχ2; Palmer 2009). Both these techniques are able to deal with irregularly sampled data with nonuniform weights, and minimize aliasing effects caused by the window function. In addition to this, Fχ2 can also search for an arbitrary number of harmonics.
We searched for periodic signals with GLS in the period range P = 4−1000 d, the lower limit being imposed by the Nyquist sampling criterion to avoid aliasing (Horne & Baliunas 1986). The resulting periodograms for both samples are plotted in the fourth panel of Fig. 4. In neither case a prominent peak is visible. The ALL and SELECTED periodograms are quite similar, and their highest peaks stand at P(A) ≃ 6.41 d and P(S) ≃ 11.29 d, respectively. The formal false-alarm probability (FAP) as defined by Zechmeister & Kürster (2009) is 0.023 (2.28σ) for the ALL power peak and 0.076 (1.77σ) for the SELECTED peak, i.e., only marginally significant. However, the formal FAP is derived under the assumption of pure Gaussian noise, which is not our case. To take into account the intrinsic dispersion of our data, we investigated whether these peaks are statistically significant with a resampling algorithm. We generated 10 000 synthetic O−C diagrams with the same temporal coordinates of actual data points by randomly scrambling the O−C values at each generation. A GLS periodogram was then evaluated on each of them with the same settings as applied on real data. The power of the highest peak found in the real data for ALL and SELECTED samples lies at the 12th (−1.17σ) and 38th percentile (−0.31σ) of the distribution of the maximum-power peaks in the synthetic, randomly permutated diagrams. We conclude that neither peak can be considered as statistically significant. In particular, the P(M) ≃ 127 days periodicity claimed by Maciejewski et al. (2010) is not consistent with our data. Instead of a peak, the periodogram range where the P(M) peak is expected is characterized by an extremely low GLS power (fourth panel of Fig. 4, blue region). On the other hand, tests on synthetic O−C diagrams with the same sampling and noise properties of our sample demonstrate that a P = P(M), Δ(O−C) = 0.0014 day signal corresponding to the Maciejewski et al. (2010) claim would be easily detectable from our data.
 |
Fig. 5 Period analysis carried out on the same set of O − C data points analyzed by Maciejewski et al. (2010). Upper left panel: O−C diagram for the selected points. Upper right panel: GLS periodogram as a function of frequency ν, adopting the same plotting limits as Maciejewski et al. (2010). Bottom panel: GLS periodogram as a function of period, adopting wider limits on frequency according to the Nyquist criterion (see text for details). The red vertical line marks the peak claimed by Maciejewski et al. (2010). |
We set Fχ2 to search for periodicities with one or two harmonics in the same frequency range. Results from both samples are quite similar to those obtained above with GLS, with nonsignificant power peaks at periods very close to those previously found in the GLS periodogram.
We also carried out our analysis on a subset of data points corresponding to those analyzed by Maciejewski et al. (2010) by employing the same tools as for our full data set (Fig. 5). When plotted adopting the same frequency limits, the resulting periodogram (and the peak corresponding to the maximum power) perfectly matches those published by Maciejewski et al. (2010, upper right panel of Fig. 5). On the other hand, the upper limit in frequency set by Maciejewski et al. (2010; 0.038P-1) is too low according to the Nyquist criterion. In the range 0.038 < ν < 0.5P-1 many other maxima are as high as the 0.0145P-1 peak (lower panel of Fig. 5). Following a statistical test similar to the one above described, we discard that peak as not significant and consider it to be caused by to small-sample statistics.
6. Discussion and conclusions
We analyzed eleven unpublished light curves of WASP-3b and re-analyzed another thirty-eight archival light curves with the same software tools and procedures. We derived improved orbital and physical parameters for this target (Table 2), and computed a refined ephemeris (Eq. (10)). All individual measurements of the central instant T0 were compared with the new ephemeris to search for changes in the orbital period P of the transiting planet. We conclude that available observations of WASP-3b, spanning more than four years, are not consistent with a linear ephemeris (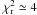 ). A possible explanation for this scatter is the presence of a perturbing body in the WASP-3 planetary system.
). A possible explanation for this scatter is the presence of a perturbing body in the WASP-3 planetary system.
It is known that the impact of red noise on high-precision transit photometry is still not fully understood. Previous claims of TTVs have been disproved on this basis (Southworth et al. 2012; Fulton et al. 2011). Could the observed scatter in the O − C diagram of WASP-3b be explained in terms of underestimated observational errors or calibration problems? The absolute time calibration of each archival light curve cannot be independently checked. In principle one should trust the authors about that. However, we point out two main clues supporting the auto-consistence of the overall data, and hence the hypothesis of a genuine TTV:
-
on three different epochs (N = 444, 486, 653 following the Pollacco et al. 2008 ephemeris) multiple observations of the same transit are available. Because they were carried out by different authors at different facilities, they should represent independent measurements of the same quantity. All these data points (marked with a star in the first column of Table 3) agree with each other within their 1σ error bars, suggesting that the uncertainties on T0 are correctly evaluated by our pipeline;
-
some anomalous patterns in the O−C diagrams are confirmed by several different data sets. For instance, nearly all points gathered in 2009 within the range N = 440−510 lie ahead of the T0 predicted by our baseline ephemeris (O−C < 0). The only exception is U4, which essentially lies at O−C ~ 0 within its error bar. The weighted mean of these twelve measurements from eight different authors is O−C = −0.00118 ± 0.00016 days. This implies a 7.2σ deviation from a constant orbital period. These patterns can also be detected in high-precision data subsets, such as ours. Among the four best IAC80 transits, the first two (N1-2) are delayed by 4.3σ (i.e., O−C = 48 ± 11 s) compared with the prediction, while the second two (N4-5) are ahead of the ephemeris by 2.8σ (O−C = 35 ± 13 s).
Veras et al. (2011) demonstrated that some orbital configurations, especially close to (but not exactly in) mean-motion resonances, can induce quasi-periodic or even chaotic TTVs. In other non-exotic configurations, the periodicity would manifest itself only at time scales >10 yr (Veras et al. 2011). Also when more than one perturber is present whose orbital periods are not commensurable, as in the case of our inner solar system, the resulting TTV would be in general aperiodic (Holman & Murray 2005).
If WASP-3b belongs to one of these cases, careful dynamical modeling and additional follow-up is required to confirm the hypothesis and to constrain the mass and period of the possible perturber(s). Photometric monitoring is still ongoing within the TASTE project, and high-precision RV measurements are planned with HARPS-N. As stressed by Meschiari & Laughlin (2010) and Payne & Ford (2011), photometric TTVs and RVs are highly complementary in breaking the degeneracies that are common in the inverse dynamical problem.
We note that recently Montalto et al. (2012) reported an independent analysis of the WASP-3 system, presenting also novel photometric data. We did not include these data in our work, nevertheless the conclusions reached by those authors appear very similar to ours.
Online material
Summary of the light curves of WASP-3b analyzed in this work.
Central instants of WASP-3b transits estimated from all individual light curves.
Appendix A: A new eclipsing variable
A star in the WASP-3 field (UCAC3 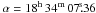 ,
, 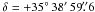 , epoch 2000.0; Zacharias et al. 2010), initially chosen as reference star, was found to be variable and was excluded from the reference list. A complete light curve of this variable was assembled by registering the magnitudes on the N1-2 and N4-N6 frames on a common zero point (Fig. A.1, upper panel). When folded on the P ≃ 0.3524 day peak detected in the Lomb-Scargle periodogram, the binned curve shows a periodical pattern with equal maxima and slightly different minima, typical of contact eclipsing binaries (W UMa-type; Fig. A.1, lower panel). We derived the following ephemeris, setting Φ = 0 at the phase of primary minimum and estimating uncertainties through a bootstrapping algorithm:
, epoch 2000.0; Zacharias et al. 2010), initially chosen as reference star, was found to be variable and was excluded from the reference list. A complete light curve of this variable was assembled by registering the magnitudes on the N1-2 and N4-N6 frames on a common zero point (Fig. A.1, upper panel). When folded on the P ≃ 0.3524 day peak detected in the Lomb-Scargle periodogram, the binned curve shows a periodical pattern with equal maxima and slightly different minima, typical of contact eclipsing binaries (W UMa-type; Fig. A.1, lower panel). We derived the following ephemeris, setting Φ = 0 at the phase of primary minimum and estimating uncertainties through a bootstrapping algorithm: ![\appendix \setcounter{section}{1} \begin{eqnarray} T_0 (\mathrm{BJD}_\mathrm{TDB}) &=& 2\,455\,776.48932\pm0.00024 \nonumber \\[3mm] && + \,\Phi \, (0.3523683\pm0.0000018). \end{eqnarray}](/articles/aa/full_html/2013/01/aa19601-12/aa19601-12-eq414.png) (A.1)This variable star appears to be unpublished, and we submitted it to the International Variable Star Index (identifier: VSX J183407.3+353859). Colors from catalog magnitudes: V = 15.63, R = 14.99 (NOMAD; Zacharias et al. 2004), J = 14.64, H = 14.34, Ks = 14.21 (2MASS; Skrutskie et al. 2006), and proper motions μαcosδ = −32 mas/yr, μδ = 19 mas/yr (UCAC3) suggest that this object could be a binary with both components of late-G spectral type.
(A.1)This variable star appears to be unpublished, and we submitted it to the International Variable Star Index (identifier: VSX J183407.3+353859). Colors from catalog magnitudes: V = 15.63, R = 14.99 (NOMAD; Zacharias et al. 2004), J = 14.64, H = 14.34, Ks = 14.21 (2MASS; Skrutskie et al. 2006), and proper motions μαcosδ = −32 mas/yr, μδ = 19 mas/yr (UCAC3) suggest that this object could be a binary with both components of late-G spectral type.
 |
Fig. A.1 Light curve of a previously unreported R ~ 15 variable star in the WASP-3 field, classified as a contact eclipsing binary (see text for details). Top panel: unbinned data points folded on the best-fit period P = 0.353626 days. Different nights are coded in different colors. Bottom panel: same as above, binned on 0.02 intervals in phase. |
Acknowledgments
This work was partially supported by PRIN INAF 2008 “Environmental effects in the formation and evolution of extrasolar planetary system”. V.N. and G.P. acknowledge partial support by the Università di Padova through the “progetto di Ateneo #CPDA103591”. V.G. acknowledges support from PRIN INAF 2010 “Planetary system at young ages and the interactions with their active host stars”. Some tasks of our data analysis have been carried out with the VARTOOLS (Hartman et al. 2008) and Astrometry.net codes (Lang et al. 2010). This research has made use of the International Variable Star Index (VSX) database, operated at AAVSO, Cambridge, Massachusetts, USA.
References
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Broeg, C., Fernández, M., & Neuhäuser, R. 2005, Astron. Nachr., 326, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Christiansen, J. L., Ballard, S., Charbonneau, D., et al. 2011, ApJ, 726, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damasso, M., Giacobbe, P., Calcidese, P., et al. 2010, PASP, 122, 1077 [Google Scholar]
- Doyle, L. R., & Deeg, H.-J. 2004, in Bioastronomy 2002: Life Among the Stars, eds. R. Norris, & F. Stootman, IAU Symp., 213, 80 [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Fukui, A., Narita, N., Tristram, P. J., et al. 2011, PASJ, 63, 287 [NASA ADS] [Google Scholar]
- Fulton, B. J., Shporer, A., Winn, J. N., et al. 2011, AJ, 142, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Pollacco, D., Simpson, E. K., et al. 2008, A&A, 492, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibson, N. P., Pollacco, D., Simpson, E. K., et al. 2009, ApJ, 700, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Gaudi, B. S., Holman, M. J., et al. 2008, ApJ, 675, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B. 2006, Handbook of CCD astronomy, eds. R. Ellis, J. Huchra, S. Kahn, G. Rieke, & P. B. Stetson [Google Scholar]
- Kipping, D. M. 2010, MNRAS, 408, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Kwee, K. K., & van Woerden, H. 1956, Bull. Astron. Inst. Netherlands, 12, 327 [Google Scholar]
- Lang, D., Hogg, D. W., Mierle, K., Blanton, M., & Roweis, S. 2010, AJ, 139, 1782 [Google Scholar]
- Lissauer, J. J., Fabrycky, D. C., Ford, E. B., et al. 2011, Nature, 470, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Littlefield, C. 2011, ArXiv e-prints [Google Scholar]
- Maciejewski, G., Dimitrov, D., Neuhäuser, R., et al. 2010, MNRAS, 407, 2625 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, G., Dimitrov, D., Neuhäuser, R., et al. 2011, MNRAS, 411, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Meschiari, S., & Laughlin, G. P. 2010, ApJ, 718, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Montalto, M., Gregorio, J., Boué, G., et al. 2012, MNRAS, accepted [arXiv:1211.0218] [Google Scholar]
- Nascimbeni, V., Piotto, G., Bedin, L. R., & Damasso, M. 2011a, A&A, 527, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nascimbeni, V., Piotto, G., Bedin, L. R., et al. 2011b, A&A, 532, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pál, A., Sárneczky, K., Szabó, G. M., et al. 2011, MNRAS, 413, L43 [NASA ADS] [Google Scholar]
- Palmer, D. M. 2009, ApJ, 695, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Payne, M. J., & Ford, E. B. 2011, ApJ, 729, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Poddaný, S., Brát, L., & Pejcha, O. 2010, New A, 15, 297 [Google Scholar]
- Pollacco, D., Skillen, I., Collier Cameron, A., et al. 2008, MNRAS, 385, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Zucker, S., & Queloz, D. 2006, MNRAS, 373, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Pribulla, T., Vaňko, M., Ammler-von Eiff, M., et al. 2012, Astron. Nachr., 333, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Sada, P. V., Deming, D., Jennings, D. E., et al. 2012, PASP, 124, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2010, MNRAS, 408, 1689 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2004, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Hinse, T. C., Burgdorf, M. J., et al. 2009, MNRAS, 399, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Bruni, I., Mancini, L., & Gregorio, J. 2012, MNRAS, 2177 [Google Scholar]
- Tripathi, A., Winn, J. N., Johnson, J. A., et al. 2010, ApJ, 715, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Veras, D., Ford, E. B., & Payne, M. J. 2011, ApJ, 727, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Holman, M. J., Henry, G. W., et al. 2007, AJ, 133, 1828 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Holman, M. J., Torres, G., et al. 2008, ApJ, 683, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2004, in Am. Astron. Soc. Meet. Abstr., BAAS, 36, 1418 [Google Scholar]
- Zacharias, N., Finch, C., Girard, T., et al. 2010, AJ, 139, 2184 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, J.-C., Cao, C., Song, N., Wang, F.-G., & Zhang, X.-T. 2011, Chin. Astron. Astrophys., 35, 409 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Orbital/physical parameters of WASP-3b estimated from individual data (sub-)sets.
All Figures
 |
Fig. 1 Light curves of WASP-3b. The ID code of each transit matches the corresponding entry in Table 1. Data points are plotted with the original cadence, except for G1/G2 and Z1/E7, which are binned on 30 s and 300 s intervals for clarity, respectively. The red line is the best-fit model found by JKTEBOP. Transits are offset in magnitude by integer multiples of 0.025. |
| In the text | |
 |
Fig. 2 Construction of the best-fit model from the four best light curves of WASP-3b observed at IAC80 (on 2011 May 7, May 21, Jun. 26, Jul. 20). The ID# of each transit (N1, N2, N4, N5) matches the corresponding entry in Table 1. Small gray dots represent the data points with the original cadence, while blue circles are binned on 120 s intervals. The red line is the best-fit from JKTEBOP (Table 2). Left panel: individual light curves. Transits are offset in magnitude by a multiple of 0.02 for clarity. Middle panel: residuals from the best-fit model. The reported scatter is evaluated on the binned points as the 68.27th percentile from the median value. Right panel: stack of all four IAC80 light curves with the best-fit model superimposed. The derived parameters are quoted in Table 2. |
| In the text | |
 |
Fig. 3 Geometrical parameters of WASP-3b estimated from individual data (sub-)sets (Table 2) plotted as black labeled circles in their two-dimensional parameter space to highlight the sizeable correlation between Σr, kr, and i. The blue dashed line in each plot is a weighted linear fit of all points; the blue triangles and the associated error ellipse correspond to the weighted mean ± 1σ computed on the marginal distribution of Σr, kr, and i (last but one row of Table 2). The red continuous line and squares are computed in the same way as the blue ones, but after removing the outlier labeled “3” from the set (T1,T3; last row of Table 2). |
| In the text | |
 |
Fig. 4 First panel from the top: O − C diagram for all data points tabulated in Table 3. Second panel: same as above for points selected as in the last column of Table 3. Third panel: comparison between the original T0 published by the respective authors (white circles with gray error bars; Table 1) and as re-estimated in this work (red triangles and bars) for the subset of high-precision light curves identified in the horizontal axis. Fourth panel: GLS periodogram for the complete sample (red line, highest peak at A) and the selected sample (black line, highest peak at S). The periodicity claimed by Maciejewski et al. (2010) is marked with the M label. |
| In the text | |
 |
Fig. 5 Period analysis carried out on the same set of O − C data points analyzed by Maciejewski et al. (2010). Upper left panel: O−C diagram for the selected points. Upper right panel: GLS periodogram as a function of frequency ν, adopting the same plotting limits as Maciejewski et al. (2010). Bottom panel: GLS periodogram as a function of period, adopting wider limits on frequency according to the Nyquist criterion (see text for details). The red vertical line marks the peak claimed by Maciejewski et al. (2010). |
| In the text | |
 |
Fig. A.1 Light curve of a previously unreported R ~ 15 variable star in the WASP-3 field, classified as a contact eclipsing binary (see text for details). Top panel: unbinned data points folded on the best-fit period P = 0.353626 days. Different nights are coded in different colors. Bottom panel: same as above, binned on 0.02 intervals in phase. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


