| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 45 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201219078 | |
| Published online | 11 January 2013 | |
The Infrared Telescope Facility (IRTF) spectral library:
Spectral diagnostics for cool stars
1
Dipartimento di Fisica e Astronomia “G. Galilei”Università di
Padova, vicolo dell’Osservatorio
3, 35122
Padova, Italy
e-mail: mary.cesetti@unipd.it
2
INAF – Osservatorio Astronomico di Padova,
vicolo dell’Osservatorio 5,
35122
Padova,
Italy
3
European Southern Observatory, Ave. Alonso de Còrdova 3107, Casilla 19, 19001
Santiago,
Chile
Received:
20
February
2012
Accepted:
12
November
2012
Context. The near-infrared (NIR) wavelength range offers some unique spectral features, and it is less prone to the extinction than the optical one. Recently, the first flux calibrated NIR library of cool stars from the NASA Infrared Telescope Facility (IRTF) have become available, and it has not been fully exploited yet.
Aims. We want to develop spectroscopic diagnostics for stellar physical parameters based on features in the wavelength range 1−5 μm. In this work we test the technique in the I and K bands. The study of the Y, J, H, and L bands will be presented in the following paper.
Methods. An objective method for semi-empirical definition of spectral features sensitive to various physical parameters is applied to the spectra. It is based on sensitivity map – i.e., derivative of the flux in the spectra with respect to the stellar parameters at a fixed wavelength. New optimized indices are defined and their equivalent widths (EWs) are measured.
Results. The method is applied in the I- and K-band windows of the IRTF stellar spectra to verify the new technique by comparing the results with the known behavior of well-studied spectral features. A number of sensitive features to the effective temperature and surface gravity are re-identified or newly identified clearly showing the reliability of the sensitivity map analysis.
Conclusions. The sensitivity map allows to identify the best bandpass limits for the line and nearby continuum. It reliably predicts the trends of spectral features with respect to a given physical parameter but not their absolute strengths. Line blends are easy to recognize when blended features have different behavior with respect to some physical stellar parameter. The use of sensitivity map is therefore complementary to the use of indices. We give the EWs of the new indices measured for the IRTF star sample. This new and homogeneous set of EWs will be useful for stellar population synthesis models and can be used to get element-by-element abundances for unresolved stellar population studies in galaxies.
Key words: infrared: stars / line: identification / stars: abundances / supergiants / stars: late-type / stars: fundamental parameters
© ESO, 2013
1. Introduction
The interpretation of the spectral absorption features in the integrated light of galaxies requires the understanding of the behavior of these features in the spectra of the stars as function of their effective temperature Teff, surface gravity log (g), and metal abundance (usually parametrized with the Iron abundance [Fe/H] and the ratio [α/Fe] of alpha-elements to Iron). This explains why some major observational and theoretical efforts are invested into the development of extensive stellar libraries for population synthesis e.g., (Burstein et al. 1984; Worthey et al. 1994; Trager et al. 1998; Tripicco & Bell 1995; Korn et al. 2005). The knowledge derived from the analysis of the stellar spectra is promptly transferred to the galaxy integrated light because Teff and log (g) are related to the age of the dominant stellar population, and [Fe/H] is related to the overall galactic chemical abundance.
Usually, first the sensitivity of the spectral absorption features to the physical parameters of stars is empirically investigated, and then stellar photosphere models are adopted to explain the behavior of the features within the theory of line formation. The former step is typically limited to looking for correlations between of the line strengths and Teff, log (g), or [Fe/H]. A notable exception is the work by Worthey et al. (1994, see their Tables 2 and 3) who determined the derivatives of these relations and adopted them as sensitivity indices for individual lines in order to compare the relative sensitivity of various features to the physical parameters of the stellar population.
Prompted by this idea, we attempt here to develop it further to its logical conclusion by defining the sensitivity map, that is a continuous derivative across the stellar spectra of stars for different Teff, log (g), or [Fe/H] spanning the full range of parameters for a given wavelength.
This new method allowed us to characterize the behavior of the individual spectral features and it is an useful and objective tool to define at the best the spectral indices more sensible to physical stellar parameters. Moreover, it accounts for the variable sensitivity of individual lines. It was developed in order to explore near-infrared (NIR) spectral ranges, which have never been used for stellar population analysis before (i.e., 1−1.8 μm). First we applied it to some well-understood features, such as the calcium triplet (CaT hereafter) at 0.85 μm and CO band at 2.29 μm, to demonstrate its feasibility. In this paper we also present the sensitivity map for a number of other NIR indices with respect to spectral type (SpT hereafter) and surface gravity. In a forthcoming paper we will extend such an analysis to other spectral ranges to define new indices, optimized for stellar population analysis. The new set of NIR indices will be useful for both stellar and extragalactic astrophysics.
The structure of the paper is as follows. Section 2 gives a short description of the adopted Infrared Telescope Facility (IRTF) spectral library. Section 3 summarizes the physical parameters of the stars in the library. The method used to create the sensitivity map is described in Sect. 4. The absorption features and line indices in the I band and their use as spectral diagnostics are discussed in Sects. 5 and 6, respectively. Sections 7 and 8 are devoted to K-band indices. Section 9 discusses and summarizes the results.
2. The IRTF spectral library
The IRTF spectral library (Cushing et al. 2005; Rayner et al. 2009), which is the first NIR library of flux-calibrated stellar spectra and extends the optical library described in Gorgas et al. (1993), contains 210 cool stars. The spectra were taken with the cross-disperser medium-resolution infrared spectrograph SpeX (Rayner et al. 2003) mounted at the 3.0-m NASA Infrared Telescope Facility (IRTF) on Mauna Kea, Hawaii. The observations were carried out with two different set-ups with a resolving power R ≈ 2000 at 0.8−2.4 μm and R ≈ 2500 at 2.4−5 μm, respectively. Several spectral orders were simultaneously recorded during a single exposure with significant wavelength overlap between the adjacent orders making it easier to preserve the continuum shape. It results to be reliable to within a few percent, as verified by generating a set of synthetic Two-Micron All Sky Survey (2MASS) colors from the spectra (Rayner et al. 2009). Therefore, the IRTF library allowed us to measure the strong and broad molecular absorption bands that are common in the NIR.
Most of the stars were observed in the 0.8−2.5 μm range, and for a small fraction of them the wavelength coverage extends up to 5 μm. The wide wavelength range permits to connect some well-studied regions as the I and K bands, with the relatively unexplored J, H, and L bands. The sample contains the F, G, K, M, and L stars, spanning luminosity classes from I to V. It also includes some AGB, carbon, and S stars. The SpTs were derived from optical spectra in the framework of the MK classification system (Rayner et al. 2009).
The sample is limited to bright stars (Fig. 1), guaranteeing high signal-to-noise ratio (S/N) even in the thermal infrared region (~2.3−5 μm). It is S/N ≥ 100 across most of the wavelength range, with the exception of regions with poor atmospheric transmission and with λ > 4 μm. The brightness limit has a downside. Indeed, most of the sample stars are located nearby in the Milky Ways disk, and they have near-solar chemical composition. The abundance distribution of the sample stars with known [Fe/H] (Cayrel de Strobel et al. 1997) is shown in Fig. 1(a) of Rayner et al. (2009), and it is representative for the stars in the solar neighborhood (Nordström et al. 2004).
3. Physical parameters of the sample stars
The sample stars span a wide range in SpTs and luminosity classes. The photospheric data for the sample stars are taken from literature. This is an inhomogeneous compilation, and in an effort to homogenize the data as much as possible (at least in terms of abundance estimate methods) we used spectroscopic determinations when possible. We adopted the metallicities based on narrow-band photometry when these were the only ones available in the literature. The K-band absolute luminosities were calculated by convolving the spectra with a filter transmission curve. If log (Teff) was not available from literature, we estimated it from the SpT-Teff relation by Carroll & Ostlie (1996). Part of the sample lacks gravity determination. The parallaxes were obtained from the Hipparcos catalog (Perryman et al. 1997). All the collected parameters of the IRTF stars are listed in Table 3.
Figure 1 shows how the sample stars populate the log (g) − log (Teff) and log (LK) − log (Teff) planes. Their metallicity distribution is shown in Fig. 2. The average [Fe/H] is about −0.1 dex with a dispersion of 0.2 dex, which is typical of the solar neighborhood.
 |
Fig. 1 Surface gravity log (g) (top panel) and K-band flux log (FK) (bottom panel) as a function of effective temperature log (Teff) for the sample stars. |
 |
Fig. 2 Metallicity distribution of the sample stars with spectroscopic measurements of [Fe/H]. |
4. Method
This section presents the empirical method we used to identify the most sensitive line-strength indices to a particular stellar physical parameter, and the procedure to define them. The method is free from any a priori assumption and it can be applied to any star or line-strength index. But here it was constrained to the range of SpTs, luminosity classes, and spectral coverage spanned by the IRTF library. Our goal is to find proxies for Teff, log (g) and [Fe/H], except for that the temperature is replaced by SpT, as it is more readily available. We numbered the SpT assigning value of 0 to F0 stars, 1 to G0, 2 to K0, etc., with decimals for the subtypes (e.g., F5 = 0.5; G8 = 1.8; M0.5 = 3.05). In the first application described in this work we considered the spectral ranges that include the CaT and CO bands that have already been widely used for stellar population analysis (e.g., Jones et al. 1984; Armandroff & Da Costa 1991; Mayya 1997; Ivanov et al. 2000; Vazdekis et al. 2003; Mármol-Queraltó et al. 2008). They provided a test-bed for verifying the method.
 |
Fig. 3 I-band model spectrum of supergiant stars obtained by fitting at each wavelength the flux-normalized (at 0.88 μm) sample spectra along SpTs. The model spectrum for different SpTs is offset for displaying purposes and the SpT is given. The green and red regions mark the bandpasses of the newly defined indices and their adjacent continuum, respectively (see Table 1). In particular the light green, green and dark green regions mark the Pa, Ca, Mg and FeClTe features, respectively. Some relevant absorption features are marked. |
 |
Fig. 6 I-band sensitivity map for SpT of supergiant stars. The sensitivity map for different SpTs is offset for displaying purposes and the SpT is given. Symbols are as in Fig. 3. |
The first step was to homogenize the spectra re-binning them with a step of 3.872 × 10-4 μm pixel-1. The supergiants, giants, and dwarfs were analyzed separately. After experimenting with absolute flux calibrated spectra and continuum-normalized spectra we opted the latter because the normalization lowered the scatter in the final results. The spectra were normalized to unity at λ = 0.88 μm and 2.20 μm for the analysis of the I and K bands, respectively. Both these wavelength regions were chosen because they were free of relevant absorption features.
Next, for each wavelength bin we derived a second-order polynomial least-square fit of the normalized intensity as a function of SpT. The fit was performed under the IDL1 environment using a specially developed script. An independent fit is obtained for each wavelength bin. The choice of the second-order is discussed in Sect. 9. We defined as model spectrum the combined fitting functions for all wavelengths. Such a fit was introduced to provide continuity across the entire parameter space, otherwise, the sensitivity could be evaluated only for discrete values of the physical parameter (the SpT in this case) for which stellar spectra were available.
Finally, we calculated the derivative of the model spectrum with respect to the SpT by building the so-called sensitivity map. A spectral index is sensitive to the SpT if the derivative with respect to the SpT of the model spectrum at the index central wavelength is different from the derivative of the surrounding region. The wavelength regions where such a strong difference is observed are characterized by sharp features in the sensitivity map and can be easily identified. Cuts of the fit and sensitivity map for a fixed SpT in the I band are shown for sample supergiants in Figs. 3 and 6, respectively.
To study the features sensitive to gravity we divided the sample into four SpT bins (F, G, K, and M; the L stars in the sample have no gravity measurements and therefore were excluded). In each bin we sorted the flux-normalized spectra in a sequence of increasing log (g). We then followed the same steps as for the SpT, except for that the fit and derivative were performed along the log (g) axis. Figures 9 and 10 show the results of the analysis for fixed surface gravity in the I band for the F and G stars and the K and M stars, respectively.
5. Spectral indices in the I band
5.1. Main I-band spectral features
Here we shortly summarize the main I-band (0.80−0.90 μm) spectral features in later type stars. The spectra of F stars are dominated by the neutral hydrogen (H i) absorption lines of the Paschen series. Their strength decreases with increasing wavelength. The Paschen series becomes weaker progressing from supergiants through giants to dwarfs, and from F to late-type G stars. The absorption lines of neutral metals are stronger in G stars than in F stars, and reach a maximum depth in the spectra of K and M stars. The lines of ionized metals (the strongest feature is CaT at 0.86 μm) weaken towards later SpTs. The molecular absorption increases in later types, affecting significantly the slope of the local continuum. In M stars the titanium oxide (TiO) bands are significant and blend with CaT, which is weaker than in earlier types. Progressing from M to L stars, the metal oxides (TiO and VO) are replaced by metal hydrides (CrH at 0.8611 μm and FeH at 0.8692 μm) as the main molecular species (Rayner et al. 2009).
The CaT was used in different studies over a wide range of atmospheric parameters and was applied to both individual stars and integrated stellar populations in different environments, the calibration is both empirical (i.e., Cenarro et al. 2002) and theoretical (i.e., Du et al. 2012). Several definitions for the CaT index exist: the classical approach consists in establishing a central bandpass covering the spectral feature, and one or more adjacent bandpasses to trace the reference level of the local continuum. Cenarro et al. (2001b, Cen01 hereafter) analyzed previous CaT index definitions and defined a new one, which was specifically designed to avoid contamination from molecular bands and to cover the line wings completely. The latter is an important issue, because the main contributors to the strength of the CaT lines are their wings, whereas the core is not very sensitive to the atmospheric and stellar parameters (Erdelyi-Mendes & Barbuy 1991). The Ca ii lines are heavily affected by metallicity and gravity: their strengths increase as metallicity increases and gravity decreases. For a detailed discussion see Sect. 2 of Cen01. To summarize, the CaT in cool stars (~F7–M0) follows a complex behavior with varying temperature, metallicity, and gravity.
5.2. Sensitivity map for the spectral type
The I-band model spectrum and sensitivity map for the different SpTs (i.e., for different Teff) are shown in Figs. 3–5 and in Figs. 6–8 for supergiant, giant, and dwarf stars, respectively. The different plots are shown with a constant vertical offset for display purposes and the position of the CaT band, Paschen lines, the Mg and the FeClTi band are marked.
The analysis of the supergiant stars can be used to summarize the features present in the I band (Fig. 6). The H i lines from the Paschen series correspond to positive peaks in the sensitivity map over about the F0–K0 SpT range. Their equivalent width (EW hereafter) decreases with SpT, because the flux within the absorption line is growing more rapidly than the flux of the surrounding continuum. From about K0.0 to about K8.6 the sensitivity of the Paschen lines to the SpT is negligible, and from about K8.6 to about M7.1 the sensitivity map shows negative peaks at the Paschen lines because these features decrease toward later types over this range of SpTs. The CaT generally shows just the opposite trend, but with asymmetric sensitivity map because the features are contaminated by H i, so there is a superposition of a negative and a positive peak. Higher-resolution spectroscopy with sufficient S/N to allow line decomposition is required when CaT is used as a diagnostic tool. The Magnesium sensitivity map show negative peaks for stars of all spectral types and luminosity classes.
The samples of giant and dwarf stars show similar behavior (Figs. 7 and 8) but the H i lines are less-sensitive temperature indicators than in supergiant stars. As a result, the variation of the CaT comes across clearer, with symmetric, less contaminated peaks. Some cases of contamination are still present, e.g., Pa4 at 0.886 μm is affected by Ni and Fe absorption lines. This index should only be used for hotter stars that show no TiO in their atmospheres. Finally, the variations of molecular features are particularly strong in giant stars, and affect most of the continuum in I band, confirming that they are good temperature indicators. The FeClTi band shows no variation in dwarf stars.
5.3. Sensitivity map for the surface gravity
The I-band sensitivity map of the surface gravity is displayed in Figs. 9 and 10 for the F and G stars and the K and M stars, respectively. For the purpose of this analysis the sample was divided according to SpT and the L stars were excluded because of insufficient gravity coverage. As expected, the CaT band shows the strongest variation across all the SpTs, with positive peaks at the core of the lines, consistent with CaT becoming weaker moving from supergiant and giant towards dwarf stars. The sensitivity to surface gravity (i.e., the strongest peaks) decreases for stars with lowest log (g). The Paschen lines follow a similar trend but they are useful only in F and, to some degree, in G stars, disappearing in K and M stars, as discussed in the previous section. The Mg line and FeClTi band show no noticeable variation. The change in the overall shape of the sensitivity map in K and M stars for low log (g) stars is probably due to the broad molecular features.
 |
Fig. 9 I-band sensitivity map for surface gravity of F (top) and G-type stars (bottom). The sensitivity map for different gravity values is offset for displaying purposes and the central values of the corresponding log (g) bins are given. Symbols are as in Fig. 3. |
 |
Fig. 11 Equivalent width of the I-band indices as function of spectral type (top panels) and effective temperature (bottom panels). The different symbols correspond to the supergiant (circles), giant (triangles), and dwarf stars (squares), respectively. For each index on the right side of the plot the median of the errors is shown (top panels). |
 |
Fig. 12 Equivalent width of the I-band indices as function of surface gravity (top panels) and metallicity (bottom panels). Symbols for supergiant, giant, and dwarf stars and errors are as in Fig. 11. Different colors in top panels correspond to F (blue), G (green), K (grey), and M stars (pink), respectively. |
5.4. Definition of new I-band indices
The sensitivity map helped us to identify 11 I-band features that can be used to measure the SpT and log (g). We defined spectral indices in order to quantitatively analyze the relation between the EW of these features and stellar physical parameters. The indices consist of a central bandpass covering the feature of interest, and two other adjacent bandpasses, at the red and blue sides, tracing the local continuum. The central bandpass was selected to include the peak of the sensitivity map and the continuum bandpasses were placed on spectral regions where the sensitivity map is (nearly) constant. For a perfectly uniform stellar library the central bandpass can be defined to guarantee optimal extraction, but this was not possible in the NIR region so we were conservative and defined slightly wider bandpasses to assure that the spectral features were fully encompassed. If possible, the combined width of the continuum bandpasses was equal or larger than the width of the central bandpass to avoid S/N being degraded. For the Ca ii feature the central bandpass overlaps with the Cen01 definition, whereas the continuum bandpasses are different. Six indices were defined to characterize the Paschen series: three have narrower bandpasses than in Cen01 and three have new bandpasses. The Mg feature has the central bandpass overlapping with the Rayner et al. (2009) definition, whereas the continuum bandpasses are different. Finally, we defined a new index centered at 0.9090 μm to measure the combined contribution of Fe i, Cl i, and Ti i. The bandpasses of the I-band indices are listed in Table 1.
Definition of the bandpasses of the I-band indices.
The EW is defined as 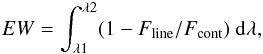 (1)where Fline is
the flux density of the observed spectrum F(λ) inside
the line bandpass between λ1 and
λ2, Fcont is the value of the
local continuum at the central wavelength of the line bandpass as obtained by linearly
interpolating between the two continuum bandpasses, and
Δλ = λ2 − λ1 is
the width of the line bandpass. The measurements were performed under the IDL environment
using a specially developed script. The EW is measured directly on the observed spectrum.
To derive the EW errors we first computed the rms of the residual of the spectrum and the
continuum (where the continuum is assumed to be the straight line interpolating the two
continuum bandpasses) in the two continuum regions. We then estimated the EW errors by
means of Monte Carlo simulations on the observed spectrum taking as noise the root mean
square (rms) above derived. We also measured the CaT, PaT and CaT* indices as defined by
Cen01. The results are listed in Tables 4 and 5.
(1)where Fline is
the flux density of the observed spectrum F(λ) inside
the line bandpass between λ1 and
λ2, Fcont is the value of the
local continuum at the central wavelength of the line bandpass as obtained by linearly
interpolating between the two continuum bandpasses, and
Δλ = λ2 − λ1 is
the width of the line bandpass. The measurements were performed under the IDL environment
using a specially developed script. The EW is measured directly on the observed spectrum.
To derive the EW errors we first computed the rms of the residual of the spectrum and the
continuum (where the continuum is assumed to be the straight line interpolating the two
continuum bandpasses) in the two continuum regions. We then estimated the EW errors by
means of Monte Carlo simulations on the observed spectrum taking as noise the root mean
square (rms) above derived. We also measured the CaT, PaT and CaT* indices as defined by
Cen01. The results are listed in Tables 4 and 5.
6. Spectral diagnostics in the I band
6.1. Spectral diagnostics for the spectral type
The new I-band indices are plotted as a function of the SpT and Teff in Fig. 11. The plots confirm that the CaT lines are not sensitive to the SpT for stars from F to early-M type, (although they have some sensitivity to the luminosity class, i.e., log (g), see Sect. 6.2) and show a marked decrease for SpT later than M, vanishing beyond the M5 type. The negative values are due to the broad TiO bands affecting the continuum, particularly in the dwarf and, to some extent, in giant stars.
Pa1 shows negligible variation with SpT, whereas Pa2 and the other H i lines decrease, most notably from F to early-G stars. The sharp rise beyond the M type is due to molecular contamination, which is strongest in Pa4. The scatter is the largest for the reddest lines, probably due to the increasing of the sky background and worsening of the atmospheric transmission. Mg shows a constant increasing with SpT. Finally, the FeClTi band appears insensitive to the SpT for all luminosity classes.
We conclude that the sensitivity map method correctly recovers the different behavior of Mg, CaT and Paschen lines and it allows to determine the SpT of stars. However, we notice that the CaT in supergiant stars is characterized by a larger scatter than in dwarf and giant stars. This is not due to a metallicity effect (see Sect. 6.2).
6.2. Spectral diagnostics for the surface gravity and metallicity
The Paschen indices show no trend with surface gravity. The sensitivity map indicates a mild decrease of the Paschen lines with increasing log (g) for F and G stars, but the large EW scatter for the hotter sample stars prevented us from measuring any gradient. K and M stars are characterized by a smaller EW scatter and we found constant Paschen values as expected. The Mg and FeClTi feature do not show any correlation with surface gravity as expected from the sensitivity map.
Weak trends are observed for Ca1 and FeClTi but the narrow metallicity range of the stellar library prevented us from drawing firm conclusions whether these indices can be used to derive [Fe/H]. The CaT index is indeed a well understood metallicity indicator (Terlevich et al. 1989; Tolstoy et al. 2009), although it degenerates at higher metallicities (Vazdekis et al. 2003).
7. Spectral indices in the K band
7.1. Main K-band spectral features
The same analysis described in the previous sections for the I band was carried out for the K band (1.92−2.40 μm), which also contains some well-studied features. The most prominent are the series of Ca i lines at 1.95 μm, Na i doublet at 2.21 μm, Ca i doublet at 2.26 μm, and the series of first-overtone bandheads of 12CO extending redward of 2.29 μm and of 13CO extending redward of 2.34 μm (Cushing et al. 2005). The F stars show H i absorption lines of the Bracket series. They are the Brδ at 1.94 μm, which falls in a wavelength region of moderate telluric absorption and Brγ at 2.16 μm. The metal features and the CO are known to increase with SpT, whereas the H i lines decrease with SpT (e.g., Ivanov et al. 2000). Finally, broad water-absorption bands appear on both sides of the K band in late-M type stars and they smoothly decrease in strength from supergiants through giants to dwarfs (e.g., Lançon et al. 2007).
7.2. Sensitivity map for the spectral type
The K-band model spectrum and sensitivity map as a function of SpT are shown in Figs. 13–15 and in Figs. 16–18 for supergiant, giant, and dwarf stars, respectively. Each luminosity class was considered separately. The analysis of the supergiant stars can be used to summarize the features present in the K band as done for the I band. The bluest part of the K band contains a complex of Fe i and Ca i lines at about 1.95–1.99 μm. The sensitivity map shows dips with variable strength, corresponding to an increase of the line strengths from F0 to late-F stars, a plateau for the F–G types, and a further increase for SpTs from K5 to M7.
The sensitivity map of the Si i features shows a dip for the F stars and it is flat – within the scatter – for later SpTs, indicating that the line looses its sensitivity to Teff for redder stars. The Brγ has a peak which decreases with SpT from F0.0 to K8.6, because the flux in the line rises towards later types faster than the neighboring continuum, making the line weaker. Brδ also corresponds to a peak in the sensitivity map and the line almost completely disappears after K2-5 type. The blend of Mg i at 2.106 μm and Al i at 2.110 μm exhibits a shallow dip in the sensitivity map, i.e. it increases mildly with the SpT. The EWs of the Na i doublet at 2.21 μm and Ca i doublet at 2.26 μm follow the pattern of the previously discussed Ca lines. The two Fe i at 2.23 and 2.24 μm are not sensitive to the SpT in the range between F and K and they increase only for M stars. The Mg i at 2.28 μm shows no marked variations for different SpTs. The 12CO at 2.29 μm shows a dip in the sensitivity map and it strongly increases with the SpT.
Summarizing, the spectral features in the supergiant, giant, and dwarf stars show similar behavior – perhaps, with slightly different strengths of the gradients. A difference may be noted in the overall shape of the derivatives due to the broad water vapor absorption at the blue and the red edges of the K band in the late-K and M-type dwarf stars.
7.3. Sensitivity map for the surface gravity
The K-band sensitivity map as a function of surface gravity is plotted in Figs. 19 and 20 for the F and G stars and the K and M stars, respectively. The sample is divided according the SpT and the L stars are excluded, as done in the I band. The peaks at the Brδ and Brγ lines are the most prominent features for the F and G stars. They indicate that flux at the core of the lines increases faster than the continuum flux with increasing gravity, i.e., the lines become weaker for more compact stars. Mg, and to lesser extent Na, follow opposite trends, as indicated by the small dips at these lines. The H i lines nearly disappear in the K and M stars and the peaks corresponding to the CO bandheads become the strongest features in the sensitivity map, being characterized by a strong decrease towards lower surface gravity. The Ca and Fe lines in the range 1.95−1.99 μm show small dips which indicate a mild increase with increasing log (g). On the contrary, the prominent Na and Ca doublets appear insensitive to the stellar gravity.
7.4. Definition of new K-band indices
The sensitivity map allowed us to identify 16 K-band features that could be used as indicators of the SpT and/or log (g). Eight of them, falling in the spectral range λ = 2.10−2.30 μm, correspond to absorption lines already studied. We followed the previous definition of the line-strength indices by Ivanov et al. (2004) for Mg i at 2.11 μm and Brγ, by Silva et al. (2008) for Fe i at 2.23 μm, Fe i at 2.24 μm, and Mg i at 2.28 μm, and by Cesetti et al. (2009) for the Ca i and Na i doublets and the 12CO absorption band at 2.29 μm. For some of them in literature are present multiple index definitions. In this case we preferred to use the index definition more suitable for extragalactic studies. This is the case of Ca i, Na i, and 12CO. The features for λ > 2.29 μm are not considered in the analysis due to the difficulty of defining a reliable continuum on the red side of the features. Eight indices, falling in the wavelength range λ = 1.92−2.01 μm are defined by adopting the common continuum passband. The estimated continuum in the wavelength range of the absorption features is shown with a straight line in Figs. 13–15. All the above definitions are listed in Table 2. The indices were measured for all the sample stars and their EWs are listed in Tables 6 and 7.
8. Spectral diagnostics in the K band
8.1. Spectral diagnostics for the spectral type
The new K-band indices are plotted as a function of spectral type in Fig. 21. All indices within the 1.92−2.01 μm range suffer from large scatter – not surprising, given their weakness and the poor atmospheric transmission in this spectral region – but a general increase of most Ca and Fe lines towards later type stars is observed. The Ca2 and Ca3 indices have a turnover at early- to mid-M stars, but their scatter is significant. The Brδ index decreases in hotter stars stars until hitting a turnover at early- to mid-K stars.
The Mg lines increase with SpT from F to K, but for later-type stars the trend flattens or even reverts, and dwarf stars show abnormal scatter. The Na, Ca, and Fe indices follow similar pattern but the strength of the lines makes it more pronounced, especially the turnover for K8-M0 supergiants. The Brγ index decreases nearly monotonically towards later SpTs. The 12CO index is insensitive to SpT for F and early-G stars and it increases for later SpTs. Moreover, it is also able to distinguish between luminosity classes: the index is progressively weaker ranging from supergiant, to giant, and to dwarf stars. The same results were obtained in the analysis of the spectral diagnostics for the Teff.
With the exception of a few features, the behavior of indices is similar for stars of the three luminosity classes.
Definition of the bandpasses of the K-band indices.
8.2. Spectral diagnostics for surface gravity and metallicity
We also studied how the indices vary as function of the surface gravity and metallicity (Fig. 22). Most features show no significant changes within the errors with two exceptions. The molecular CO band is sensitive to log (g), as expected. The metal lines of K and M stars peak at the extremely high gravity. This effect did not appear for the I-band indices and it is probably due to a combination of two factors: in late-type dwarfs the Teff and log (g) are correlated (i.e., the start are ordered along the main sequence) and the features do show temperature dependence, as demonstrated in Fig. 21. The large scatter of Na and Ca indices for low gravity K stars is puzzling.
 |
Fig. 13 I-band model spectrum of supergiant stars obtained by fitting at each wavelength the flux-normalized (at 2.20 μm) sample spectra along SpTs. The model spectrum for different SpTs is offset for displaying purposes and the SpT is given. The green regions mark the bandpasses of the newly defined indices and, the red and grey regions, mark their adjacent continuum as defined in this paper and in literature respectively (see Table 2). Some relevant absorption features are marked. |
 |
Fig. 16 K-band sensitivity map for SpT of supergiant stars. The sensitivity map for different SpTs is offset for displaying purposes and the SpT is given. Symbols are as in Fig. 13. |
 |
Fig. 19 K-band sensitivity map for surface gravity of F (top) and G-type stars (bottom). The sensitivity map for different gravity values is offset for displaying purposes and the central values of the corresponding log (g) bins are given. Symbols are as in Fig. 16. |
Finally, no trend is observed with [Fe/H] for any of the investigated lines, as expected for the narrow metallicity range of the sample.
9. Discussion and conclusions
The Cenarro et al. (2001a, 2002) library, which is limited to the I-band spectral region, is characterized by a larger number of stars (706 stars with Teff = 3300−25 000 K) compared to and our sample (198 stars with Teff = 2600−7200 K) and by a higher spectral resolution. This gives us the opportunity to check if our results are affected by poor stellar parameter sampling, spectral resolution, and differences in data reduction.
Spectra direct comparison. We compared directly spectra from the IRTF and Cenarro et al. (2001a, 2002) libraries, rebinning the latter to the resolution of the IRTF spectra. Two extreme cases were considered: the M supergiant Betelgeuse (HD 39801), one of the brightest stars in both samples, and a flaring K3 dwarf HD 219134. In Fig. 23 we show for each star the two spectra superimposed and their difference. In the case of HD 219134 we notice a slight difference in the continuum slope. We therefore compared the two spectra also after the continuum normalization (Fig. 23 bottom panel). We see that no telluric corrections residuals are present and the strength of the individual spectral features are the same. We therefore are confident that the IRTF and Cenarro et al. (2001a, 2002) libraries are consistent.
 |
Fig. 23 Direct comparison of the spectra of Betelgeuse (HD 39801, top panel) and HD 219134 (middle panel) from the libraries of Rayner et al. (2009, solid lines) and Cenarro et al. (2001a, 2002, dotted lines). In the bottom panel the continuum normalized spectra of HD 219134 are shown. In each panel the difference of the two corresponding spectra are plotted (shifted by +0.4 for displaying purposes) and the rms value is given. |
 |
Fig. 24 EW of the CaT (top panel), PaT (middle panel), and CaT* index (bottom panel) as a function of θ = 5040/Teff for the stars of the IRTF sample (filled symbols) and the sample by Cenarro et al. (2002, open symbols) sample. The different symbols correspond to the supergiant (stars), giant (triangles), and dwarf stars (squares), respectively. |
Calcium triplet comparison. Indices as the CaT were extensively studied both with empiric that theoretic methods. A comprehensive study was done by Cen01 that extensively studied the behavior of this spectral feature in respect to Teff, log (g), and [Fe/H]. We compare our sample CaT behavior with Cen01 adopting their definition of the CaT* index that removes the Paschen line contamination. The CaT* is defined as: CaT ∗ = CaT−0.93 × PaT, where the CaT = Ca1 + Ca2 + Ca3 and PaT = Pa1 + Pa2 + Pa3 indices measure the strength of the raw CaT and three Paschen lines. We limited the comparison to stars within the same metallicity range as in Cenarro et al. (2002). Different luminosity classes were analyzed separately. The comparison of the samples shows excellent agreement and similar scatter (Fig. 24).
Sensitivity map comparison. We tested if the library limited number of stars and systematic errors in the stellar parameters can affect the sensitivity maps. This has been done by deriving the sensitivity maps with the Cenarro et al. (2001a, 2002) library. The maps are remarkably similar.
We demonstrated that the study of derivatives yields qualitatively consistent results with respect to the direct investigation of the behaviour of line-strength indices. However, it is not possible to predict the strength of a gradient and the intrinsic scatter of the correlations. The latter is due to the smoothing applied to the data using a second-degree polynomial as fitting function in the derivation of the model spectrum. In fact, the introduction of the fitting function was necessary to fill gaps in the parametric space due to irregular sampling and to smooth the data before perform its derivative.
 |
Fig. 25 Equivalent width of the Ca1 index as a function of spectral type for the observed and model spectrum of the sample stars. The different symbols correspond to the measurements in the observed spectra of the supergiant (circles), giant (triangles), and dwarf stars (squares), respectively. The different lines are for measurements in the model spectrum of of the supergiant (dotted line), giant (dashed line), and dwarf stars (solid line), respectively. |
 |
Fig. 26 I-band indices sensitivity to the velocity dispersion broadening. The indices relative variations for different luminosity classes and spectral types are shown: supergiants (solid line), giants (dashed line) and dwarfs (dotted line). |
To address this problem we measured the EWs on both the model and observed spectra. Let us consider, as an example, the case of Ca1 dependence on SpT. The EWs of the observed spectra are characterized by a significant scatter which is different for the three luminosity classes, whereas the EWs measured on the model spectrum change smoothly with SpT (Fig. 25). This means that, although for each wavelength an independent fit is applied along the SpT direction, the different fits maintain a degree of coherence along the wavelength direction such that a smooth trend of the EW is observed when it is measured on the model spectrum. On the other hand the EWs of the model spectrum do follow the trend measured on real data with different degrees of goodness. In this respect, the choice of the degree of the fitting function plays a relevant role. The introduction of a higher-order polynomial generally allows a better description of the data but the noise on the derivative increases severely limiting its effectiveness in defining indices. Our conclusion is that a second-order polynomial leads to a sensitivity map that qualitatively predict the variation of a spectral feature with respect to a given physical parameter. Therefore the sensitivity map is useful as an objective tool to define the best bandpasses for the spectral feature and their adjacent continuum, whereas the measurements on the real spectra yield more reliable correlations between the EWs and the stellar physical parameters. Last but not least, the index definitions derived from the sensitivity map depend on the spectral resolution of the library.
Sensitivity of indices to velocity dispersion broadening. A straightforward application of the indices system is the study of the unresolved stellar population in galaxies. It is therefore important to investigate how our measurements are affected by the unavoidable velocity broadening due to the internal galaxy kinematics.
We broadened all the spectra by convolving them with a Gaussian of σ varying from 115 to 400 km s-1, in steps of 25 km s-1. The indices were measured for all the broadened spectra and a third-order polynomial fit was done to the relative changes of each index value as a function of velocity dispersion. Figures 26 and 27 illustrate the Δ(Index)/Index(σ0) values for the different luminosity classes and spectral types. It has to be noted that some indices have a low EW value, typically ≲1 Å for some of the spectral types considered. The EW of these indices shows a large variation even for small values of σ and goes to zero for σ > 200−300 km s-1. The faint indices are not shown in Fig. 26 and 27. The analysis shows that there is a very strong correlation between the line strength and the effect of the broadening, being the strongest lines less affected. This is true in both bands. The K-band indices are generally more affected by broadening due to the intrinsic faintness of the lines.
This work extended the previously defined sensitivity indices (Worthey et al. 1994) to a broader concept of sensitivity map and tested if they allows us to identify the spectral features that can be used as a proxy for Teff, log (g), and [Fe/H]. This empirical method is applied to I- and K-band absorption features for the star spectra of the IRTF library (Cushing et al. 2005; Rayner et al. 2009). The main results are:
-
sensitivity map allows to fine tune the best definition for the line-strength indices (i.e., the bandpass limits for the line and nearby continuum);
-
sensitivity map reliably predicts the variation of a spectral feature with respect to a given physical parameter but not its absolute strength;
-
spectral line blends are obvious on sensitivity map when the blended features are characterized by a different behavior with respect to some physical stellar parameters;
-
the EWs of new indices were measured for the IRTF star sample, and they will be useful for stellar population synthesis models and can be used to get element-by-element abundances for unresolved stellar population studies in galaxies;
-
a systematic search for reliable Teff, log (g), and [Fe/H] for the IRTF sample stars was carried out and the available physical parameters are reported.
We develop a fast and efficient method to identify those features that are sensible to different physical stellar parameters. The method is free from any assumption and it can be applied to any star or line-strength index. In a forthcoming paper we will extend such an analysis to Y, J, H, and L bands to define new indices. A straightforward next step is the extensive use of the sensitivity map in the upcoming X-Shooter Spectral Library (XLS, Chen et al. 2011).
Tables 3−7 that follow are an important part of the project, but they are placed here because they are large.
Physical parameters of the stars of the IRTF library.
EW of the I-band indices. Part 1.
EW of the I-band indices. Part 2.
EW of the K-band indices. Part 1.
EW of the K-band indices. Part 2.
Acknowledgments
M.C. acknowledges the European Southern Observatory for hospitality at Santiago Headquarters while this paper was in progress. This work was supported by Padua University through the grants CPDA089220/08, 60A02-5934/09, and 60A02-1283/10 and by Italian Space Agency through the grant ASI-INAF I/009/10/0. M.C. acknowledges financial support from Padua University grant CPDR095001/09 and CPDR115539/11. L.M. acknowledges financial support from Padua University grant CPS0204.
References
- Andrievsky, S. M., Egorova, I. A., Korotin, S. A., & Burnage, R. 2002, A&A, 389, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ArellanoFerro, A. 2010, Mex. Astron. Astrofis., 46, 331 [NASA ADS] [Google Scholar]
- Armandroff, T. E., & Da Costa, G. S. 1991, AJ, 101, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Balachandran, S. 1990, ApJ, 354, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Barbuy, B., & Erdelyi-Mendes, M. 1989, A&A, 214, 239 [NASA ADS] [Google Scholar]
- Boesgaard, A. M., & Friel, E. D. 1990, ApJ, 351, 467 [Google Scholar]
- Boesgaard, A. M., & Lavery, R. J. 1986, ApJ, 309, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Boesgaard, A. M., & Tripicco, M. J. 1986, ApJ, 303, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Burstein, D., Faber, S. M., Gaskell, C. M., & Krumm, N. 1984, ApJ, 287, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, J. S., Sellgren, K., & Balachandran, S. C. 2000, ApJ, 530, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, B. W., & Ostlie, D. A. 1996, An Introduction to Modern Astrophysics [Google Scholar]
- Castro, S., Porto de Mello, G. F., & da Silva, L. 1999, MNRAS, 305, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Cayrel de Strobel, G., Knowles, N., Hernandez, G., & Bentolila, C. 1981, A&A, 94, 1 [NASA ADS] [Google Scholar]
- Cayrel de Strobel, G., Soubiran, C., Friel, E. D., Ralite, N., & Francois, P. 1997, A&AS, 124, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cenarro, A. J., Cardiel, N., Gorgas, J., et al. 2001a, MNRAS, 326, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Cenarro, A. J., Gorgas, J., Cardiel, N., et al. 2001b, MNRAS, 326, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Cenarro, A. J., Gorgas, J., Cardiel, N., Vazdekis, A., & Peletier, R. F. 2002, MNRAS, 329, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Cenarro, A. J., Peletier, R. F., Sanchez-Blazquez, P., et al. 2007, VizieR Online Data Catalog: J/MNRAS/374/664 [Google Scholar]
- Cesetti, M., Ivanov, V. D., Morelli, L., et al. 2009, A&A, 497, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y., Trager, S., Peletier, R., & Lançon, A. 2011, J. Phys. Conf. Ser., 328, 012023 [NASA ADS] [CrossRef] [Google Scholar]
- Cornide, M., & Rego, M. 1984, Ap&SS, 105, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Cottrell, P. L., & Sneden, C. 1986, A&A, 161, 314 [NASA ADS] [Google Scholar]
- Cushing, M. C., Rayner, J. T., & Vacca, W. D. 2005, ApJ, 623, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Du, W., Luo, A. L., & Zhao, Y. H. 2012, AJ, 143, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Edvardsson, B., Gustafsson, B., & Nissen, P. E. 1984, The Messenger, 38, 33 [NASA ADS] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Erdelyi-Mendes, M., & Barbuy, B. 1991, A&A, 241, 176 [NASA ADS] [Google Scholar]
- Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
- Gehren, T. 1981, A&A, 100, 97 [NASA ADS] [Google Scholar]
- Gonzalez, G., Wallerstein, G., & Saar, S. H. 1999, ApJ, 511, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Gorgas, J., Faber, S. M., Burstein, D., et al. 1993, ApJS, 86, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Goss, W. M., Ekers, R. D., Skellern, D. J., & Smith, R. M. 1982, MNRAS, 198, 259 [NASA ADS] [Google Scholar]
- Gratton, R. G., & Sneden, C. 1991, A&A, 241, 501 [NASA ADS] [Google Scholar]
- Gray, R. O., Graham, P. W., & Hoyt, S. R. 2001, AJ, 121, 2159 [NASA ADS] [CrossRef] [Google Scholar]
- Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holmberg, J., Nordstroem, B., & Andersen, J. 2008, VizieR Online Data Catalog: V/128 [Google Scholar]
- Ivanov, V. D., Rieke, G. H., Groppi, C. E., et al. 2000, ApJ, 545, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, V. D., Rieke, M. J., Engelbracht, C. W., et al. 2004, ApJS, 151, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Jasniewicz, G., Recio-Blanco, A., de Laverny, P., Parthasarathy, M., & de Medeiros, J. R. 2006, A&A, 453, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, J. E., Alloin, D. M., & Jones, B. J. T. 1984, ApJ, 283, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Kipper, T. 2008, Baltic Astron., 17, 87 [Google Scholar]
- Korn, A. J., Maraston, C., & Thomas, D. 2005, A&A, 438, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovtyukh, V. V. 2007, MNRAS, 378, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Krishnaswamy, K., & Sneden, C. 1985, PASP, 97, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Kučinskas, A., Hauschildt, P. H., Ludwig, H., et al. 2005, A&A, 442, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambert, D. L., & Ries, L. M. 1981, ApJ, 248, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Lançon, A., Hauschildt, P. H., Ladjal, D., & Mouhcine, M. 2007, A&A, 468, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lèbre, A., Palacios, A., Do Nascimento, Jr., J. D., et al. 2009, A&A, 504, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2005, ApJ, 628, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E. 1982, ApJ, 256, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Bond, H. E. 1980, ApJ, 241, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Heiter, U. 2007, AJ, 133, 2464 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Wepfer, G. G. 1995, AJ, 110, 2425 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubimkov, L. S., Lambert, D. L., Rostopchin, S. I., Rachkovskaya, T. M., & Poklad, D. B. 2010, MNRAS, 402, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Malkan, M. A., Hicks, E. K., Teplitz, H. I., et al. 2002, ApJS, 142, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Mallik, S. V. 1998, A&A, 338, 623 [NASA ADS] [Google Scholar]
- Mármol-Queraltó, E., Cardiel, N., Cenarro, A. J., et al. 2008, A&A, 489, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayya, Y. D. 1997, ApJ, 482, L149 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A. 1990, ApJS, 74, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Mirtorabi, M. T., Wasatonic, R., & Guinan, E. F. 2003, AJ, 125, 3265 [NASA ADS] [CrossRef] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrin, M.-N. 1983, A&A, 128, 347 [NASA ADS] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Randich, S., Gratton, R., Pallavicini, R., Pasquini, L., & Carretta, E. 1999, A&A, 348, 487 [NASA ADS] [Google Scholar]
- Rayner, J. T., Toomey, D. W., Onaka, P. M., et al. 2003, PASP, 115, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJS, 185, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silva, D. R., Kuntschner, H., & Lyubenova, M. 2008, ApJ, 674, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., & Lambert, D. L. 1986, ApJ, 311, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., & Lambert, D. L. 1990, ApJS, 72, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Bienayme, O., Mishenina, T. V., & Kovtyukh, V. V. 2008, VizieR Online Data Catalog: J/A+A/480/91 [Google Scholar]
- Soubiran, C., Le Campion, J., Cayrel de Strobel, G., & Caillo, A. 2010, VizieR Online Data Catalog: B/pastel [Google Scholar]
- Spite, M., & Spite, F. 1980, A&A, 89, 118 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., & Schordan, P. 2000, Astron. Nachr., 321, 277 [Google Scholar]
- Takeda, Y., Sato, B., & Murata, D. 2008, PASJ, 60, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Terlevich, E., Diaz, A. I., & Terlevich, R. 1989, Ap&SS, 157, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Tomkin, J., & Lambert, D. L. 1999, ApJ, 523, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Worthey, G., Faber, S. M., Burstein, D., & Gonzalez, J. J. 1998, ApJS, 116, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tripicco, M. J., & Bell, R. A. 1995, AJ, 110, 3035 [Google Scholar]
- Vazdekis, A., Cenarro, A. J., Gorgas, J., Cardiel, N., & Peletier, R. F. 2003, MNRAS, 340, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Venn, K. A. 1995, ApJS, 99, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Faber, S. M., Gonzalez, J. J., & Burstein, D. 1994, ApJS, 94, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Zboril, M., & Byrne, P. B. 1998, MNRAS, 299, 753 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Surface gravity log (g) (top panel) and K-band flux log (FK) (bottom panel) as a function of effective temperature log (Teff) for the sample stars. |
| In the text | |
 |
Fig. 2 Metallicity distribution of the sample stars with spectroscopic measurements of [Fe/H]. |
| In the text | |
 |
Fig. 3 I-band model spectrum of supergiant stars obtained by fitting at each wavelength the flux-normalized (at 0.88 μm) sample spectra along SpTs. The model spectrum for different SpTs is offset for displaying purposes and the SpT is given. The green and red regions mark the bandpasses of the newly defined indices and their adjacent continuum, respectively (see Table 1). In particular the light green, green and dark green regions mark the Pa, Ca, Mg and FeClTe features, respectively. Some relevant absorption features are marked. |
| In the text | |
 |
Fig. 4 As in Fig. 3 but for giant stars. |
| In the text | |
 |
Fig. 5 As in Fig. 3 but for dwarf stars. |
| In the text | |
 |
Fig. 6 I-band sensitivity map for SpT of supergiant stars. The sensitivity map for different SpTs is offset for displaying purposes and the SpT is given. Symbols are as in Fig. 3. |
| In the text | |
 |
Fig. 7 As in Fig. 6 but for giant stars. |
| In the text | |
 |
Fig. 8 As in Fig. 6 but for dwarf stars. |
| In the text | |
 |
Fig. 9 I-band sensitivity map for surface gravity of F (top) and G-type stars (bottom). The sensitivity map for different gravity values is offset for displaying purposes and the central values of the corresponding log (g) bins are given. Symbols are as in Fig. 3. |
| In the text | |
 |
Fig. 10 As in Fig. 9 but for K (top) and M-type stars (bottom). |
| In the text | |
 |
Fig. 11 Equivalent width of the I-band indices as function of spectral type (top panels) and effective temperature (bottom panels). The different symbols correspond to the supergiant (circles), giant (triangles), and dwarf stars (squares), respectively. For each index on the right side of the plot the median of the errors is shown (top panels). |
| In the text | |
 |
Fig. 12 Equivalent width of the I-band indices as function of surface gravity (top panels) and metallicity (bottom panels). Symbols for supergiant, giant, and dwarf stars and errors are as in Fig. 11. Different colors in top panels correspond to F (blue), G (green), K (grey), and M stars (pink), respectively. |
| In the text | |
 |
Fig. 13 I-band model spectrum of supergiant stars obtained by fitting at each wavelength the flux-normalized (at 2.20 μm) sample spectra along SpTs. The model spectrum for different SpTs is offset for displaying purposes and the SpT is given. The green regions mark the bandpasses of the newly defined indices and, the red and grey regions, mark their adjacent continuum as defined in this paper and in literature respectively (see Table 2). Some relevant absorption features are marked. |
| In the text | |
 |
Fig. 14 As in Fig. 13 but for giant stars. |
| In the text | |
 |
Fig. 15 As in Fig. 13 but for dwarf stars. |
| In the text | |
 |
Fig. 16 K-band sensitivity map for SpT of supergiant stars. The sensitivity map for different SpTs is offset for displaying purposes and the SpT is given. Symbols are as in Fig. 13. |
| In the text | |
 |
Fig. 17 As in Fig. 16 but for giant stars. |
| In the text | |
 |
Fig. 18 As in Fig. 16 but for dwarf stars. |
| In the text | |
 |
Fig. 19 K-band sensitivity map for surface gravity of F (top) and G-type stars (bottom). The sensitivity map for different gravity values is offset for displaying purposes and the central values of the corresponding log (g) bins are given. Symbols are as in Fig. 16. |
| In the text | |
 |
Fig. 20 As in Fig. 19 but for K (top) and M-type stars (bottom). |
| In the text | |
 |
Fig. 21 As in Fig. 11 but for K-band indices. |
| In the text | |
 |
Fig. 22 As in Fig. 12 but for K-band indices. |
| In the text | |
 |
Fig. 23 Direct comparison of the spectra of Betelgeuse (HD 39801, top panel) and HD 219134 (middle panel) from the libraries of Rayner et al. (2009, solid lines) and Cenarro et al. (2001a, 2002, dotted lines). In the bottom panel the continuum normalized spectra of HD 219134 are shown. In each panel the difference of the two corresponding spectra are plotted (shifted by +0.4 for displaying purposes) and the rms value is given. |
| In the text | |
 |
Fig. 24 EW of the CaT (top panel), PaT (middle panel), and CaT* index (bottom panel) as a function of θ = 5040/Teff for the stars of the IRTF sample (filled symbols) and the sample by Cenarro et al. (2002, open symbols) sample. The different symbols correspond to the supergiant (stars), giant (triangles), and dwarf stars (squares), respectively. |
| In the text | |
 |
Fig. 25 Equivalent width of the Ca1 index as a function of spectral type for the observed and model spectrum of the sample stars. The different symbols correspond to the measurements in the observed spectra of the supergiant (circles), giant (triangles), and dwarf stars (squares), respectively. The different lines are for measurements in the model spectrum of of the supergiant (dotted line), giant (dashed line), and dwarf stars (solid line), respectively. |
| In the text | |
 |
Fig. 26 I-band indices sensitivity to the velocity dispersion broadening. The indices relative variations for different luminosity classes and spectral types are shown: supergiants (solid line), giants (dashed line) and dwarfs (dotted line). |
| In the text | |
 |
Fig. 27 As in Fig. 26 but for the K-band indices. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


