| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219702 | |
| Published online | 23 November 2012 | |
Chandra observations of dying radio sources in galaxy clusters ⋆
1 INAF – Osservatorio Astronomico di Cagliari, Loc. Poggio dei Pini, Strada 54, 09012 Capoterra (CA), Italy
e-mail: matteo@oa-cagliari.inaf.it
2 NASA Goddard Space Flight Center, Code 662, Greenbelt, MD 20771, USA
3 INAF – Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna, Italy
Received: 29 May 2012
Accepted: 12 October 2012
Context. The dying radio sources represent a very interesting and largely unexplored stage of the active galactic nucleus (AGN) evolution. They are considered to be very rare, and almost all of the few known ones were found in galaxy clusters. However, considering the small number detected so far, it has not been possible to draw any firm conclusions about their X-ray environment.
Aims. We present X-ray observations performed with the Chandra satellite of the three galaxy clusters Abell 2276, ZwCl 1829.3+6912, and RX J1852.1+5711, which harbor at their center a dying radio source with an ultra-steep spectrum that we recently discovered.
Methods. We analyzed the physical properties of the X-ray emitting gas surrounding these elusive radio sources. We determined the global X-ray properties of the clusters, derived the azimuthally averaged profiles of metal abundance, gas temperature, density, and pressure. Furthermore, we estimated the total mass profiles.
Results. The large-scale X-ray emission is regular and spherical, suggesting a relaxed state for these systems. Indeed, we found that the three clusters are also characterized by significant enhancements in the metal abundance and declining temperature profiles toward the central region. For all these reasons, we classified RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912 as cool-core galaxy clusters.
Conclusions. We calculated the non-thermal pressure of the radio lobes assuming that the radio sources are in the minimum energy condition. For all dying sources we found that this is on average about one to two orders of magnitude lower than that of the external gas, as found for many other radio sources at the center of galaxy groups and clusters. We found marginal evidence for the presence of X-ray surface brightness depressions coincident with the fossil radio lobes of the dying sources in A2276 and ZwCl 1829.3+691. We estimated the outburst age and energy output for these two dying sources. The energy power from the AGN outburst is significantly higher than the X-ray luminosity in both clusters. Indeed, it is sufficient that a small fraction of this power is dissipated in the intra-cluster medium to reheat the cool cores.
Key words: X-rays: galaxies: clusters / galaxies: active / galaxies: clusters: general
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Dying radio sources represent the last stage in the life-cycle of radio galaxies. During their active stage, which may last several 107 years, the strong synchrotron sources associated with elliptical galaxies are powered with energy from the active galactic nucleus (AGN) via jets of plasma. In this stage, the total spectra of the radio sources are usually well approximated by a power law over a wide range of frequencies. However, when the activity in the nucleus stops or falls to such a low level that the plasma outflow can no longer be sustained, the radio source undergoes a period of fading (dying phase) before it disappears completely. In the dying phase, the radio core, well-defined jets, and compact hot-spots will disappear because they are the structures produced by continuing activity. However, the radio lobes, which accumulated the relativistic particles produced during the active phase, may still remain detectable for a longer time. An example of such a source was given in Cordey (1987). It is also possible that radio galaxies may be active intermittently. In this scenario, one expects to observe fossil radio plasma remaining from an earlier active epoch, along with newly restarting jets. The best case for fading radio lobes seen with a currently active galaxy is 3C 338 (see Gentile et al. 2007, for a recent work).
In principle, every radio galaxy must inevitably enter the fading phase. Nevertheless, dying radio sources are very rare objects. Only a few percent of the radio sources in the B2 and 3C samples have the characteristics of a dying radio galaxy (Giovannini et al. 1988). A possible explanation for the rarity of dying radio galaxies may be the strong spectral evolution that occurs in the source during the fading phase. Without fresh particle injection, the high-frequency radio spectrum develops an exponential cutoff due to the radiative losses (e.g. Komissarov & Gubanov 1994). At this point, the adiabatic expansion of the radio lobes will concur to shift this spectral break to lower frequencies and the source will quickly disappear from the sky.
However, if the adiabatic expansion of the fading radio lobes is somehow reduced, or even stopped after attaining the pressure equilibrium, there is still the chance to detect the dying source, at least at lowest radio frequencies. Indeed, due to their ultra-steep and curved radio spectra, dying radio galaxies are more easily detected in low-frequency selected samples. The Westerbork Northern Sky Survey (WENSS; Rengelink et al. 1997) at 325 MHz and the B2 survey at 408 MHz (Colla et al. 1970, 1972, 1973) are particularly well-suited to search for these elusive fossil radio sources. Parma et al. (2007) discovered nine new dying sources by cross-correlating the WENSS with the NRAO VLA Sky Survey (NVSS; Condon et al. 1998). Another two dying galaxies (the central radio source in Abell 2622 and MKW03s) and one possibly restarting source (MKW07) were found by Giacintucci et al. (2007) in a low-frequency survey of nearby galaxy clusters performed with the Giant Metrewave Radio Telescope. Five more dying radio galaxies with extremely steep spectra have been found in the WENSS and the B2 catalogs by Murgia et al. (2011).
These studies demonstrate that the dying sources could be among the most promising targets for the upcoming next generation of low-frequency interferometers. Owing to their high sensitivity and angular resolution, LOFAR, LWA, and in the future SKA, represent the ideal instruments to discover and study these elusive objects in detail. In the meantime, we can begin to address a few significant points. One is the X-ray environment of the dying sources discovered so far. The gaseous environment in which radio galaxies are embedded may play a fundamental role in the later stages of the radio source life. It seems that there is a tendency for dying sources to reside in dense environments. Parma et al. (2007) found that about half of the dying sources of their sample are located in galaxy clusters, while only a few appear to be isolated. The five dying galaxies presented in Murgia et al. (2011) are not an exception to the rule: each source is located, at least in projection, at the center of an X-ray emitting cluster or galaxy group. The galaxy clusters are Abell 2276, ZwCl 1829.3+6912, RX J1852.1+5711, ZwCl 0107.5+3212, and Abell 2162 for the radio sources WNB 1734+6407, WNB 1829+6911, WNB 1851+5707, B2 0120+33, and B2 1610+29.
Coordinates and distances of the three galaxy clusters studied in this work.
Although no firm conclusions can be drawn because of the small number statistics involved, the results in Murgia et al. (2011) suggest that the probability for a dying radio source to be found in a cluster is as high as ~86%. The simplest interpretation for the tendency of dying galaxies to be found in clusters is that the low-frequency radio emission from the fading radio lobes lasts longer if their expansion is somewhat reduced or even stopped by the pressure of a particularly dense intra-cluster medium. Another possibility is that the occurrence of dying sources is intrinsically higher in galaxy clusters.
To investigate these hypotheses, we need to compare in detail the actual fading radio structures with the properties of the X-ray emitting gas. However, the X-ray environment of dying sources is poorly known in general. For instance, only 2 out of a total of 14 dying radio sources in clusters presented in Parma et al. (2007) and Murgia et al. (2011) have well-measured X-ray properties. This is not surprising since these samples have been selected originally in the radio band and thus adequate X-ray follow-up is required. We had the chance to observe three of these clusters, Abell 2276, ZwCl 1829.3+6912, and RXC J1852.1+5711, with the Chandra satellite. Very little is known about these galaxy clusters. In this paper we report the results we obtained from the study of the Chandra data.
In Sect. 2 we described the X-ray observations and data reduction. In Sect. 3 we present the X-ray analysis results. The implications of these results are discussed in Sect. 4. and a final summary of the conclusions is given in Sect. 5. In addition, we report the details of the minimum energy calculation in the appendix.
Throughout this paper we assume a ΛCDM cosmology with H0 = 71 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7. Unless otherwise stated, reported uncertainties are at 1σ confidence level.
 |
Fig. 1 Background-subtracted and exposure-corrected Chandra ACIS-I image in the 0.5−7 keV band of RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912. In the left-column panels the adaptively smoothed Chandra images are shown with the VLA radio contours at 1.4 GHz overlaid. A zoom of the central regions of the galaxy clusters are shown in the right-column panels. Red tones represent the Chandra image smoothed with a Gaussian kernel with σ = 2″ while the blue tones represent the optical images from the DSS (RX J1852.1+5711 and ZwCl 1829.3+6912) and SDSS (A2276). |
2. Chandra observations and data reduction
We observed the galaxy clusters Abell 2276, ZwCl 1829.3+ 6912, and RX J1852.1+5711 with the Chandra satellite using the ACIS-I detector. The basic properties of the three galaxy clusters are reported in Table 1 while the summary of observing exposure times, ID, and dates is given in Table 2.
The data calibration was performed with the help of the Chandra’s data analysis system CIAO (Fruscione et al. 2006). The photon list was filtered for bad events following the standard procedures. In particular, we removed bad pixels and columns, events with ASCA grades 1, 5, and 7. Data were taken in VFAINT mode and we filtered the event file to exclude bad events associated with cosmic ray afterglows.
We examined the light curve of the X-rays from the portions of the detector free from the cluster or point sources. We excluded all time intervals where the background fluctuations were stronger than ± 20% of the average. We discarded a few percent of total exposure time for each cluster.
The background was modeled using a composite blank-field background data set corresponding to the period of the observations, cleaned and normalized as described by Markevitch et al. (2003).
Chandra ACIS-I observations summary.
For each of the three galaxy clusters, we generated an approximate exposure map from the aspect histogram file and the instrument map by assuming a mono-energetic distribution of source photons at the same energy as the count rate histogram peak.
3. X-ray analysis results
For the data analysis we made use of the XSPEC package (Arnaud 1996).
Global spectral properties derived from the fit of the APEC model.
3.1. Large-scale X-ray emission and global physical properties
The Chandra X-ray images in the 0.5−7 keV band of the three galaxy clusters are shown in Fig. 1. In the left-column panels the adaptively smoothed Chandra images of the large-scale X-ray emission are shown with the VLA radio contours at 1.4 GHz overlaid (see Murgia et al. 2011, for the details about the radio data). The dying radio sources are all located at the center of the clusters. In the right-column panels of Fig. 1, we show the zoom of the central regions of the galaxy clusters where the blue tones represent the optical images from the Digitized Sky Surveys (DSS) and Sloan Digital Sky Survey (SDSS).
We extracted the global spectra of the three galaxy clusters from a circular region of RE = 250 kpc in radius centered on the X-ray peak. We masked the X-ray point sources and fitted the global spectra with a single-temperature APEC (astrophysical plasma emission code; Smith et al. 2001) model and Galactic absorption. We let the total Galactic H i column density (NH) vary in the fit procedure. The best-fit parameters are summarized in Table 3 where, for comparison, we also report the Galactic NH derived by radio surveys1.
3.1.1. RX J1852.1+5711
The large-scale X-ray emission can be traced out to more than about two arcminutes from the cluster center and is quite regular and symmetric in shape. The most striking feature seen in the X-ray image is a strong peak of emission at the cluster center. The bright X-ray core hosts the complex radio source WNB1851+5707. Spectral studies based on VLA radio data suggest that WNB1851+5707 is in reality composed by two distinct dying radio galaxies: WNB1851+5707a, the amorphous radio source at cluster center, and WNB1851+5707b, the fainter double-structure source a few tens of kpc to the N-E of the core (Murgia et al. 2011). The two hosting galaxies have nearly the same redshifts, which additionally supports that they are spatially nearby and not positionally coincident just because of a projection effect. This association is intriguing given the rarity of this kind of sources. At the edge of the bright X-ray core two narrow head-tail radio sources, apparently traveling in opposite direction with respect to the intra-cluster medium, are visible (see Fig. 1 top panel).
3.1.2. Abell 2276
The overall cluster X-ray emission is very regular and spherical with a clear enhancement at the cluster center. A zoom of the core is presented in the middle-right panel of Fig. 1. Abell 2276 hosts the dying source WNB1734+6407 (Murgia et al. 2011). Characterized by two relaxed lobes lacking jets and hot-spots, the radio morphology of WNB1734+6407 can be considered the prototype of fossil radio galaxies. The VLA images also reveal a slightly extended core component in coincidence with the cD galaxy at the peak of the X-ray emission. This feature has a quite steep radio spectrum and its nature remains unclear. The SDSS image shows a chain of three smaller satellite galaxies trailing the cD galaxy about 20 kpc to the south of the core.
 |
Fig. 2 Azimuthally averaged radial profiles of the gas metal abundance (left panel) and temperature (right panel). In the right-column panels the open symbols refer to the deprojected temperature profiles while the dotted lines are the best fit of the polytropic model to the four more external annuli, see text. |
 |
Fig. 3 Azimuthally averaged SX profiles in the 0.5 − 7 keV band along with the best fit of the isothermal β-model (dashed line) and double β-model (continuous line). |
3.1.3. ZwCl 1829.3+6912
The large-scale X-ray emission has an ellipsoidal shape, slightly flattened in the N-S direction. A bright peak is present at the center. The cluster hosts the restarting radio source WNB 1829+6911 (Murgia et al. 2011). The radio source is characterized by an active core, associated to the cD galaxy, and a fossil structure extended about 100 kpc in the E-W direction, following the elongation of the surrounding large-scale X-ray emission.
3.2. Metal abundance and temperature profiles
We fitted the metal abundance and the plasma temperature using six concentric annuli centered on the cluster core using an APEC model with the Galactic absorption fixed to the value found from fit of the global X-ray spectrum (see Table 3).
The radial profiles of the metal abundance (in the XSPEC default system; Anders & Grevesse 1989) are shown in the left panel of Fig. 2, while the radial profiles of the gas temperature are presented in the right-column panels of Fig. 2. We tried to deproject the temperature profile using the PROJCT model of XSPEC. The statistical quality of our data was not sufficient to permit a detailed deprojection of the metal abundance. Therefore, we kept this parameter fixed to the projected value in each annulus. The deprojected temperature profiles are represented by the open dots in the right-column panels of Fig. 2. Although the error bars are large, we note that toward the cluster center the deprojected temperature profiles are steeper and the gas temperature is lower in the central bins, as expected.
3.3. Density profile modeling
We extracted the radial profiles of the cluster X-ray surface brightness (SX) by azimuthally averaging the counts in concentric annuli of about 2″ in width centered on the cD galaxy. We cut out the unrelated sources in the field of view and attempted to model the observed SX profiles by first assuming that the intra-cluster medium is in pressure equilibrium and isothermal at the global temperature reported in Table 3. The temperature radial profiles suggest that the isothermal assumption is applicable for Abell 2276 while it could be inappropriate to describe the central regions of RX J1852.1+5711 and ZwCl 1829.3+6912. For this reason, at the end of this section we also compare the results of the isothermal model fitting with the deprojection analysis.
Under the assumptions of spherical symmetry, we first attempted to model the observed SX profiles by assuming the isothermal β-model for the gas density: ![\begin{equation} n_{\rm H}(R)=n_{\rm H,0}\left[1+(R/R_{\rm c})^2\right]^{-3\beta/2}, \label{betamod} \end{equation}](/articles/aa/full_html/2012/12/aa19702-12/aa19702-12-eq43.png) (1)where R is the distance from the cluster center while Rc is the core radius, β the index, and nH,0 the central density (Cavaliere & Fusco-Femiano 1976).
(1)where R is the distance from the cluster center while Rc is the core radius, β the index, and nH,0 the central density (Cavaliere & Fusco-Femiano 1976).
Results of the surface brightness profile fit of the β-model.
The model is calculated in a two-dimensional image with the same pixel size as the observed image. For each pixel in the model image, we computed the expected X-ray surface brightness profile by integrating the emission measure along the line of sight: 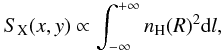 (2)here
(2)here 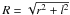 , where
, where 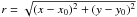 is the projected distance from the X-ray peak whose position, (x0,y0), has been kept fixed during the fit.
is the projected distance from the X-ray peak whose position, (x0,y0), has been kept fixed during the fit.
The model is filtered (multiplied) by the mono-energetic exposure map and the background is added before the radial binning is performed. Finally, the expected SX radial profile is compared to the observed one by azimutally averaging the model and the data with the same set of annuli and by minimizing the χ2 statistic: ![\begin{equation} \chi^2=\sum \left[(C_{\rm obs}-C_{\rm mod})/Err(C_{\rm obs})\right]^2, \label{chi2} \end{equation}](/articles/aa/full_html/2012/12/aa19702-12/aa19702-12-eq62.png) (3)here Cobs and Cmod are the observed and model counts in each annulus, respectively, and we summed over all annuli.
(3)here Cobs and Cmod are the observed and model counts in each annulus, respectively, and we summed over all annuli.
Results of the surface brightness profile fit of the double β-model.
Since we fixed the position of the X-ray centroid, the β-model has three remaining free parameters: the core radius, the index β, and the normalization. The APEC normalization provided by XSPEC is 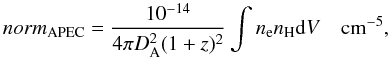 (4)where DA is the angular distance to the source. Indeed, we can obtain the central gas density nH,0 from APEC normalization of the global spectrum listed in Table 3 and the values of β and Rc found from the fit of the SX profile, by computing the emission measure integral
(4)where DA is the angular distance to the source. Indeed, we can obtain the central gas density nH,0 from APEC normalization of the global spectrum listed in Table 3 and the values of β and Rc found from the fit of the SX profile, by computing the emission measure integral 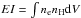 :
: 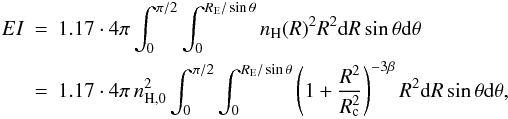 (5)where RE = 250 kpc is the radius of the extraction region of the global spectrum and we assumed that ne = 1.17nH.
(5)where RE = 250 kpc is the radius of the extraction region of the global spectrum and we assumed that ne = 1.17nH.
The best fits of the β-model to the observed SX profiles are presented as dashed lines in Fig. 3 while the best-fit parameters are listed in Table 4.
While it is clear that the β-model gives a good representation of the SX profiles in the external regions of the clusters, it is far from a good fit in the inner 10 kpc. The brightness excess of the cool cores of the clusters we considered in this work cannot be described by the simple β-model. Indeed, we also consider the empirical double β-model presented by Pratt & Arnaud (2002): ![\begin{eqnarray} R<R_{\rm cut}&&n_{\rm H}(R)=n_{\rm Hin,0}\left[1+(R/R_{\rm c,in})^2\right]^{-3\beta_{\rm in}/2}\\ R>R_{\rm cut}&&n_{\rm H}(R)=n_{\rm Hout,0}\left[1+(R/R_{\rm c,out})^2\right]^{-3\beta_{\rm out}/2}.\nonumber \label{doublebeta} \end{eqnarray}](/articles/aa/full_html/2012/12/aa19702-12/aa19702-12-eq89.png) (6)The model assumes that both the inner and outer gas density profile can be described by a β-model, but with different parameters. However, the density profile (and its derivate) must be continuous across Rcut to ensure the continuity of the total mass profile. From this condition it follows that
(6)The model assumes that both the inner and outer gas density profile can be described by a β-model, but with different parameters. However, the density profile (and its derivate) must be continuous across Rcut to ensure the continuity of the total mass profile. From this condition it follows that ![\begin{equation} n_{\rm Hout,0}=n_{\rm Hin,0}\frac{\left[1+(R_{\rm cut}/R_{\rm c,in})^2\right]^{-3\beta_{\rm in}/2}}{\left[1+(R_{\rm cut}/R_{\rm c,out})^2\right]^{-3\beta_{\rm out}/2}} \end{equation}](/articles/aa/full_html/2012/12/aa19702-12/aa19702-12-eq90.png) (7)and
(7)and 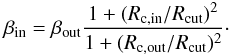 (8)We fitted the double β-model by varing Rcut, βout, Rc,in, and Rc,out, and the model normalization. Similarly as for the single β-model, the value of the central gas density, nHin,0, is obtained through the APEC normalization of the global spectrum in Eq. (4) and the volume integral in Eq. (5).
(8)We fitted the double β-model by varing Rcut, βout, Rc,in, and Rc,out, and the model normalization. Similarly as for the single β-model, the value of the central gas density, nHin,0, is obtained through the APEC normalization of the global spectrum in Eq. (4) and the volume integral in Eq. (5).
The best fits of the double β-model to the observed SX profiles are presented as continuous lines in Fig. 3 while the best-fit parameters are listed in Table 5. The double β-model gives a good representation of the SX profile also in the inner central 10 kpc and represents a statistically significant improvement over the single β-model.
The internal core radius in RXJ1852.1+5711 is of about Rc,in ≃ 2 kpc, while it is somewhat larger in A2276 and ZwCl 1829.3+6912, Rc,in ≃ 8 and 9 kpc, respectively. The rapid increase in the gas density observed for R < Rc,in could be interpreted as the result of the cooling flow process where the dense intra-cluster medium may have already mixed with the progenitor X-ray coronas associated to the cD galaxies (Sun et al. 2007).
These calculations are based on the assumption that the emissivity of the gas simply scales as density squared. To estimate the effect of temperature variations on the value of the electron density, we calculated the electron number density directly from the deprojected spectral analysis (Sect. 3.2) and compared this with the model electron number density obtained from the fit of the isothermal models to the X-ray surface brightness. The left-column panels of Fig. 4 show that the deprojected electron density (represented by the open dots) agrees remarkably well with that obtained from the model analysis.
The gas pressure can be related to density and temperature via the ideal gas law: 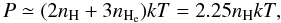 (9)where we neglected the contribution from elements heavier than helium and adopted nHe/nH = 0.083 for the number density of helium relative to hydrogen, which is obtained from the primordial mass fraction of helium and by assuming the abundance of heavier elements to be 0.3 − 0.5 solar.
(9)where we neglected the contribution from elements heavier than helium and adopted nHe/nH = 0.083 for the number density of helium relative to hydrogen, which is obtained from the primordial mass fraction of helium and by assuming the abundance of heavier elements to be 0.3 − 0.5 solar.
In the right-column panels of Fig. 4, we compare the deprojected gas pressure with the prediction of the isothermal models. The gas pressure is derived for both the β-model and the double β-model by assuming for the gas temperature the global values reported in Table 3.
 |
Fig. 4 Radial profiles of gas density (left-column panels) and pressure (right-column panels). The open dots represent the result of the deprojected spectral analysis while the dashed and continuous line represent the trend of the isothermal β-model and double β-model, respectively. The shaded areas represent the range of non-thermal pressure of the radio lobes under the minimum energy assumption, see Sect. 4.2. |
We note that the gas pressure at the cluster center predicted by isothermal models is higher than the deprojected value in RX J1852.1+5711 and ZwCl 1829.3+6912. In fact, for these two clusters we observe a much stronger drop of the temperature in the central bins. For Abell 2276 the temperature drop at the center is less prominent and thus we observe for this cluster a better agreement between the pressure profiles derived from the isothermal model fit and the values obtained through the deprojection analysis.
3.4. Total mass profiles
We calculated the profiles of total mass under the assumption of hydrostatic equilibrium. For a spherically symmetric distribution of gas the total mass profile is given by 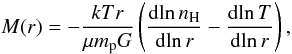 (10)where mp is the proton mass, G the gravitational constant, and μ = 0.6. If the gas density profile is described by the β-model
(10)where mp is the proton mass, G the gravitational constant, and μ = 0.6. If the gas density profile is described by the β-model 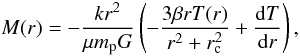 (11)while for the double β-model we have
(11)while for the double β-model we have 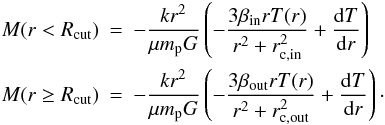 (12)The total mass profiles for the isothermal models are shown in Fig. 5. We also calculated the mass profile from the deprojected gas temperature and density obtained in Sect. 3.3. We excluded the cool core from the total mass calculation and evaluated the radial temperature gradient, dT/dr, by fitting a polytropic relation of the form
(12)The total mass profiles for the isothermal models are shown in Fig. 5. We also calculated the mass profile from the deprojected gas temperature and density obtained in Sect. 3.3. We excluded the cool core from the total mass calculation and evaluated the radial temperature gradient, dT/dr, by fitting a polytropic relation of the form 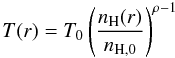 (13)to the deprojected temperature measured in the four external annuli, where for the density profile nH(r) we adopted the best fit of the double β-model. The fit is shown as a dotted curve in the right-column plots of Fig. 2. We found a polytropic index of ρ = 1.17, 1.15, and 1.06 for RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912. The total masses derived from the deprojected temperature profile are shown as dots in Fig. 5. The profiles of total mass derived from the two isothermal models are very similar and they both agree well with the masses estimated from the polytropic temperature model in the four external annuli. Extrapolating the profiles up to r500 (i.e. the radius at which the mean mass density is 500 times the critical density), we found a total mass of 1.0, 1.3, and 2.0 × 1014 M⊙ for RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912, respectively. These values are in roughly agree with the total mass observed for galaxy clusters of this temperature (e.g. Finoguenov et al. 2001).
(13)to the deprojected temperature measured in the four external annuli, where for the density profile nH(r) we adopted the best fit of the double β-model. The fit is shown as a dotted curve in the right-column plots of Fig. 2. We found a polytropic index of ρ = 1.17, 1.15, and 1.06 for RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912. The total masses derived from the deprojected temperature profile are shown as dots in Fig. 5. The profiles of total mass derived from the two isothermal models are very similar and they both agree well with the masses estimated from the polytropic temperature model in the four external annuli. Extrapolating the profiles up to r500 (i.e. the radius at which the mean mass density is 500 times the critical density), we found a total mass of 1.0, 1.3, and 2.0 × 1014 M⊙ for RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912, respectively. These values are in roughly agree with the total mass observed for galaxy clusters of this temperature (e.g. Finoguenov et al. 2001).
4. Discussion
 |
Fig. 5 Total mass profiles for the isothermal β-model and double β-model shown as dashed and continuous lines, respectively. The dots represent the total mass profile derived from the measured deprojected temperature profile by fixing the density profile to the best fit of the double β-model. The arrows indicate the radii at overdensities of 500 and 200 times the critical density. |
We characterized with data from the Chandra satellite the X-ray emission of three clusters from the Murgia et al. (2011) sample: RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912, which host a their center the dying sources WNB 1851+5707, WNB 1734+6407, and WNB 1829+6911. From the X-ray analysis presented in Sect. 3, we can conclude that the physical state of the intra-cluster medium in the three galaxy clusters presents quite similar properties. The large-scale X-ray emission is regular and spherical, suggesting a relaxed state for these systems. The most striking feature revealed from the Chandra images is a peak of emission at the center of the clusters that cannot be parametrized by the isothermal β-model. In fact, we found that the three systems are also characterized by strong enhancements in the central abundance and declining temperature profiles toward the central region. For all these reasons, we classify RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912 as cool-core galaxy clusters. We used the density profile derived in Sect. 3.3 together with the deprojected gas temperature to estimate the central cooling time as 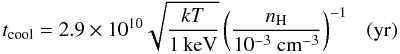 (14)from Pratt & Arnaud (2002). For RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912 we found a central cooling time of tcool = 1.3, 3.3, and 2.7 Gyr. According to Hudson et al. (2010), the central cooling time is the best parameter to segregate cool-core from non-cool-core clusters. In particular, these authors found from their statistical analysis results that clusters whose central cooling time is shorter than the critical value tcool < 7.7 Gyr are classifiable as cool-cores. Indeed, given their comparatively short central cooling time, we can confirm that all three clusters studied here belong to the category of the cool-core systems.
(14)from Pratt & Arnaud (2002). For RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912 we found a central cooling time of tcool = 1.3, 3.3, and 2.7 Gyr. According to Hudson et al. (2010), the central cooling time is the best parameter to segregate cool-core from non-cool-core clusters. In particular, these authors found from their statistical analysis results that clusters whose central cooling time is shorter than the critical value tcool < 7.7 Gyr are classifiable as cool-cores. Indeed, given their comparatively short central cooling time, we can confirm that all three clusters studied here belong to the category of the cool-core systems.
It is of interest to compare these results with the X-ray properties of galaxy clusters that host dying sources known in the literature. The prototypical restarting radio source 3C 338 is associated to the cD galaxy of nearby rich cluster Abell 2199 (z = 0.0309). The cluster has been studied with Chandra by Johnstone et al. (2002), who found evidence for radial gradients in temperature and metallicity in the X-ray emitting gas. The temperature decreases toward the central region of the cluster, which is where the radiative cooling time drops below 1 Gyr. As seen in Chandra images, the radio lobes associated with the AGN significantly affect the X-ray gas, inflating cavities or bubbles in the dense intra-cluster medium. Overall, the X-ray properties of Abell 2199 are similar to those we found for the more distant galaxy cluster ZwCl 1829.3+6912. The radio morphologies of the two radio sources are also similar: they both posses a restarting nucleus surrounded by dying radio lobes produced in an earlier phase of activity. Among the dying sources studied by Murgia et al. (2011) there is B2 0120+33, which is identified with the galaxy NGC 507, the dominant, massive elliptical galaxy of a nearby (z = 0.01646) group/poor cluster (the so-called Pisces cluster). The X-ray halo of NGC 507 has been studied with ROSAT HRI and Chandra ACIS-S data by Paolillo et al. (2003), who found that the halo core has a complex morphology with a main X-ray emission peak, coincident with the center of the optical galaxy, and several secondary peaks. The authors found that the energy input by the central radio source was strong enough to prevent gas cooling. Indeed, the X-ray properties of the clusters examined in this works do not seem to be peculiar compared to those of the few examples already known in the literature. Although the poor statistics prevents a quantitative analysis, there is a tendency for dying sources to be preferentially found in relaxed galaxy clusters.
4.1. Are there X-ray cavities associated to the fossil radio lobes?
It is well established that the central gas in many cool-core systems that host active radio sources is not smoothly distributed, see e.g. the notable cases of Hydra A (McNamara et al. 2000) and MS 0735+7421 (McNamara et al. 2005). The comparison of radio and X-ray images obtained at similar angular resolution has revealed that AGN jets are the cause of highly disturbed structures in the cores of many clusters, including shocks, ripples, and density discontinuities. The most remarkable structures are the so-called cavities (or radio bubbles), depressions in the X-ray surface brightness that are approximately coincident with the radio lobes. The cavities form as the jets propagate in opposite directions outward from the cD galaxy, inflating the lobes of radio plasma and pushing aside the X-ray emitting gas. It is hypothesized that the depressions are nearly devoided of X-ray emitting gas. X-ray cavities are common in cool-core clusters; they are present in more than 70% of these systems (Dunn et al. 2005). There are, hoverer, “ghost cavities”, i.e., X-ray depressions with no detectable radio emission. The interpretation is that these structures have been created by the AGN in the more distant past and their radio emission had faded over the time (Bîrzan et al. 2004). In the view of these findings, it is important to discuss if there is evidence of X-ray cavities associated to our dying radio sources. The fading lobes are not powered by the AGN anymore, but their radio emission is still barely detectable. Indeed, dying sources might be an intermediate evolutionary stage in between active and ghost cavities.
 |
Fig. 6 Unsharp mask images obtained from the 0.5 − 7 keV band by subtracting the best fit of the circularly symmetric double-β model from the count image smoothed with a 1′′ Gaussian kernel, and then dividing by the sum of the two. |
The galaxy clusters in our study are somewhat more distant compared to the clusters in which most X-ray cavities have been found so far. Thus, detecting the X-ray depression is difficult because of the low contrast of our images. For this reason, we have produced unsharp mask images by subtracting from the observed counts images the best fit of the double-β model to the radially averaged SX profiles found in Sect. 3.3. Figure 6 shows the results obtained from the 0.5 − 7 keV band by subtracting the circularly symmetric double-β model from an image smoothed with a 1′′ Gaussian kernel then dividing by the sum of the two. Point sources were removed from the images and replaced with values interpolated from surrounding background regions using the CIAO task dmfilth. There is no evidence for cavities associated to the radio lobes of WNB 1851+5707 in the unsharp mask image of RX J1852.1+5711 shown in the left panel of Fig. 6. The unsharp image of Abell 2276 is presented in the middle panel of Fig. 6. For this cluster there is a hint of an X-ray depression associated to the south lobe of WNB 1734+6407. Finally, the unsharp image of ZwCl 1829.3+6912 is shown in the right panel of Fig. 6. There is marginal evidence for a cavity in correspondence to the west lobe of WNB 1829+6911. The depression seems roughly to follow the morphology of the radio lobe. We considered whether we can detect a cavity given the sensitivity of our observations. For that purpose, we simulated the expected X-ray depressions that correspond to the radio lobes of WNB 1734+6407 in A2276. We chose this cluster for the simulations because the geometry of the problem is simpler to study. We assumed that the gas distribution in the cluster atmosphere is described by the double-β model found in Sect. 3. Furthermore, we assumed that the fossil lobes of the dying source have an ellipsoidal shape and are completely devoid of X-ray emitting material. The results are presented in Fig. 7 for three inclinations of the radio source with respect to the observer. The top panels shows the expected depressions in the X-ray surface brightness for i = 0° (left-column panels), i = 22.5° (middle-column panels), and i = 45° (right-column panels). If the source lies on the plane of the sky (i = 0°), the cavities are intrinsically closer to the cluster’s core and thus they are more prominent since they remove dense gas. If the radio source is inclined toward the observer, the cavities are at a larger intrinsic distance from the core, the removed gas is more rarefied and thus the cavities appear less prominent. We quantified the expected fractional depression in the X-ray counts over the area of the radio lobes. We constructed synthetic count images by sampling from a Poisson distribution whose mean is given by the models shown in the top panel of Fig. 7. We filtered the synthetic images by the exposure map, added the blank-field background counts, and calculated an expected fractional depression in the X-ray counts of 22%, 15%, and 9% for i = 0°, 22.5°, and 45°. We compared these numbers with the observed counts over the region of the south lobe of WNB 1734+6407. For the north lobe the situation is less clear, but this region of the ACIS-I chip is heavily affected by bad columns. Over the region of the south lobe, we measured a fractional depression in the X-ray counts of 19 ± 13%, which is compatible with the predicted value for the source aligned to the plane of the sky. We note, however, that the uncertainty in the source counts is large and thus it is difficult to draw a definitive conclusion. For a less favorable orientation of the radio source (i > 20°) the cavities would be hardly discernible in our image. This is also illustrated in the bottom panels of Fig. 7, where we show the unsharp mask images corresponding to the three simulated values for the source’s inclination.
We did not perform any simulations for ZwCl 1829.3+691. However, for the west lobe of the dying source WNB 1829+6911 we measured a depression in the X-ray counts of 13 ± 7%. The X-ray cavity appears to follow the shape of the radio lobe. For the east lobe no statistical significant depression is detected.
In summary, we investigated the presence of X-ray cavities associated to the radio lobes of our dying sources. We found hints of possible cavities in A2276 and ZwCl 1829.3+691, but the evidence is weak. However, while cavities are not clearly seen, their presence cannot be excluded either. For the case of A2276, we showed through simulations that if the radio source is on the plane of the sky, the effect of the cavities is consistent with the faint depressions observed in the X-ray surface brightness while the cavities would be hardly discernible in our image if the radio source were significantly inclined toward the observer. Additional, more sensitive observations are necessary to confirm the presence of these features unambiguously.
 |
Fig. 7 Simulated cavities in A2276 for the double-β model (top panels). The synthetic unsharp mask images are shown in the bottom panels. We expect a depression in the X-ray surface brightness of 22%, 15%, and 9% for i = 0°, 22.5°, and 45°. |
Non-thermal pressure of radio lobes in the three galaxy clusters assuming minimum energy.
4.2. Pressure balance
The gas pressure in the immediate regions of the dying sources is close to Pth ~ 10-10 dyne/cm-2 for all three clusters.
We calculated the non-thermal pressure of the radio lobes as 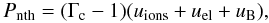 (15)where Γc = 4/3 is the adiabatic index of the material in the lobes while uions, uel, and uB are the energy densities of relativistic ions, electrons, and magnetic field. Under the hypothesis that the radio source is in a minimum energy condition, we can compare the non-thermal pressure of the radio plasma, Pnth = umin/3, to that of the external medium. The electron energy spectrum is taken to be a power law whose slope is derived from the spectral modeling presented in Murgia et al. (2011) while the volume of the emitting regions is estimated from the radio images assuming a unity filling factor. We also assumed an isotropic electron population spiralling in a completely disordered magnetic field and averaged the synchrotron emissivity over all possible orientations of the field with respect to the line-of-sight (see the appendix for details). For steep electron energy spectra the electron energy density depends critically on the low-energy cut off, γmin, whose value is rather uncertain. Traditionally, the energy spectrum is truncated at the energy of the electrons radiating at the lower end of the radio band, νlow = 10 MHz (see e.g., Pacholczyk 1970). This choice minimizes the source energetics required by the observed radiation in the radio band. However, it has been pointed out that it would miss the contribution from lower energy electrons (Brunetti et al. 1997; Beck & Krause 2005). Indeed, we also calculated uel by extrapolating the power law energy spectrum to γmin = 1. Another poorly known variable is the relative energy density of relativistic ions to that of electrons, k = uions/uel. We adopted k = 1 as reference value.
(15)where Γc = 4/3 is the adiabatic index of the material in the lobes while uions, uel, and uB are the energy densities of relativistic ions, electrons, and magnetic field. Under the hypothesis that the radio source is in a minimum energy condition, we can compare the non-thermal pressure of the radio plasma, Pnth = umin/3, to that of the external medium. The electron energy spectrum is taken to be a power law whose slope is derived from the spectral modeling presented in Murgia et al. (2011) while the volume of the emitting regions is estimated from the radio images assuming a unity filling factor. We also assumed an isotropic electron population spiralling in a completely disordered magnetic field and averaged the synchrotron emissivity over all possible orientations of the field with respect to the line-of-sight (see the appendix for details). For steep electron energy spectra the electron energy density depends critically on the low-energy cut off, γmin, whose value is rather uncertain. Traditionally, the energy spectrum is truncated at the energy of the electrons radiating at the lower end of the radio band, νlow = 10 MHz (see e.g., Pacholczyk 1970). This choice minimizes the source energetics required by the observed radiation in the radio band. However, it has been pointed out that it would miss the contribution from lower energy electrons (Brunetti et al. 1997; Beck & Krause 2005). Indeed, we also calculated uel by extrapolating the power law energy spectrum to γmin = 1. Another poorly known variable is the relative energy density of relativistic ions to that of electrons, k = uions/uel. We adopted k = 1 as reference value.
The internal pressure ranges are reported in Table 6 and plotted as shaded regions in the right-column panels of Fig. 4. The lower and upper bound of the range correspond to νlow = 10 MHz and γmin = 1, respectively. For all the dying sources, we found that Pnth is on average about one to two orders of magnitude lower than that of the external gas. The gap is reduced for γmin = 1, but still remains significant, especially for the dying source in RX J1852.1+571 and ZwCl 1829.3+691. This discrepancy is known for a long time (e.g. Morganti et al. 1988) and has been found for many other radio sources at the center of galaxy groups and clusters (Croston et al. 2008). Several hypotheses can be put forward to explain why Pth > Pnth:
-
(i)
the source is not in the minimum energy condition;
-
(ii)
there is a large number of “uncounted” electrons radiating at frequencies well below the explored radio band;
-
(iii)
there is a large contribution to the non-thermal energy by protons or other heavy relativistic particles, i.e., k ≫ 1;
-
(iv)
ambient thermal material entered the radio lobes, providing an additional source of pressure;
-
(v)
the volume filling-factor of the radio emitting plasma is smaller than unity.
Distinguishing among these possibilities is not trivial since we cannot even exclude that they are acting in combination. However, one can attempt to discuss them separately. Scenario (i) require that either the magnetic field energy density or the relativistic particle energy density are much higher than the equipartition value. To sustain an external pressure as high as Pth ~ 10-10 dyne/cm-2, a magnetic field strength of 90 μG is needed. This would imply extremely severe radiative losses for the synchrotron electrons. Especially for a dying source, where the energy supply from the AGN is switched off, the electron energy spectrum will be burned out rapidly in the absence of any compensating re-acceleration mechanism. Indeed, this scenario could be potentially less problematic if the deviation from equipartition is caused by a higher energy density in relativistic particles.
Scenario (ii) postulates the presence of a bulk of low-energy electrons in the source that radiate below the observable radio band. We already showed that extending the energy spectrum down to γmin = 1 is not sufficient to fill the pressure gap. Thus, for this scenario to work, there would have to be a pile-up of low-energy electrons further in excess of the extrapolation of the power law energy spectrum. On the other hand, according to scenario (iii) the radio lobes may contain a high percentage of relativistic protons. To fill the pressure gas it is required that k ~ 100 ÷ 1000. These values are in the range found for central sources in clusters (Bîrzan et al. 2008) and suggest that these radio lobes have been inflated by heavy jets. However, the matter content of AGN jets is still extremely controversial and the various attempts to determine the jet composition by indirect means led to contradictory conclusions (see e.g. Marsher et al. 2007). According to scenario (iv) there could be a significant amount of thermal material inside the radio lobes to account for a large part of the total pressure. The entrainment of surrounding material may occur in the radio jets during the active phase (Laing et al. 1999), and it cannot be ruled out that sources close to pressure balance, such as our dying sources, could be more susceptible to turbulence and higher entrainment rates. Finally, as outlined in scenario (v), the radio emitting volume could be much lower than assumed either because the magnetic fields is highly filamentary and/or the shape of the radio lobes is not ellipsoidal but rather flattened to a lenticular shape or bent in a toroidal shape as they rise through the external medium (Churazov et al. 2001).
4.3. Outburst age and energetics
The injection of energy by the AGN is the favored solution to the cooling problem in relaxed galaxy clusters. The synchrotron plasma is less dense than the intra-cluster medium and so the radio lobes are expected to detach from the core and rise up buoyantly through the cluster (e.g. Dunn & Fabian 2006). It is well known that the energy radiated away through the synchrotron emission is only a tiny fraction of the total outburst energy. The mechanical work done by the radio source dominates the outburst energetic and can be inferred directly for those clusters where an X-ray cavity is detected in correspondence of the radio lobe. Indeed, we attempted to estimate the outburst energetics of the dying sources in Abell 2276 and ZwCl 1829.3+691, the two clusters for which we have a putative cavity detection. If radio lobes are inflated sub-sonically, the energy necessary to form the cavity can be evaluated as the sum of the internal energy and the work done against Pth, the external pressure of the thermal gas, 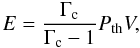 (16)where V is the volume of the cavity while Γc is the adiabatic index of the fluid in the radio lobe. For a relativistic fluid Γc = 4/3 the outburst energy contained in the cavity is E = 4PthV. To estimate the rate at which the AGN energy input is dissipated into the intra-cluster medium we need to estimate the age of the outburst.
(16)where V is the volume of the cavity while Γc is the adiabatic index of the fluid in the radio lobe. For a relativistic fluid Γc = 4/3 the outburst energy contained in the cavity is E = 4PthV. To estimate the rate at which the AGN energy input is dissipated into the intra-cluster medium we need to estimate the age of the outburst.
In A2276 the dying lobes are detached from the AGN and are likely rising in the cluster atmosphere pushed by the buoyant force. Assuming that the density of the relativistic fluid in the lobe is negligible with respect to that of the external medium, the buoyancy velocity of the lobes can be estimated as 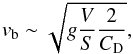 (17)where g is the gravitational acceleration, S is lobe cross section, and CD the drag coefficient (Churazov et al. 2001).
(17)where g is the gravitational acceleration, S is lobe cross section, and CD the drag coefficient (Churazov et al. 2001).
 |
Fig. 8 Comparison of radiative and buoyancy ages as a function of the magnetic field for the dying source WNB 1734+6407 in A2276. The radiative age (green line and shaded region) is derived from the spectral break measured by Murgia et al. (2011). The horizontal blue dashed line and shaded region is the buoyancy age for the south lobe. The two ages match at 65 Myr for B ≃ 12 μG. This value for the source’s magnetic field (dotted line) fits within the equipartition range for k = 1 pictured by the vertical shaded region in red. |
For the putative cavity that corresponds to the south radio lobe in A2276 we assumed an ellipsoidal geometry with major and minor semi-axes of a = 30 and b = 21 kpc, respectively. We calculated the gravitational acceleration from the total mass profile of the cluster (see Sect. 3.4) and, from the volume V = (4/3)πab2 and the cross-section S = πab of the cavity, we found vb ≃ 600–850 km s-1 for CD ≈ 1.0–0.5.
The sound speed in the intra-cluster medium is 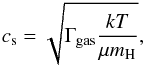 (18)where Γgas = 5/3. At the center of A2276, T ≃ 3 keV, and hence cs ≃ 895 km s-1, which implies that the radio bubble is effectively rising sub-sonically.
(18)where Γgas = 5/3. At the center of A2276, T ≃ 3 keV, and hence cs ≃ 895 km s-1, which implies that the radio bubble is effectively rising sub-sonically.
Since the cavity is located at about r ≃ 21–69 kpc from the cluster center, we obtain a buoyancy age of about tb ≃ 65 ± 46 Myr by assuming a constant rising speed. Despite the large uncertainties involved, this age is on the same order as the radiative age of trad ≃ 86 Myr estimated by Murgia et al. (2011) from the analysis of the total radio spectrum of the dying source and by assuming Bmin = 10 μG. We investigate this point in more detail in Fig. 8, where we show the comparison of radiative and buoyancy ages as a function of the source’s magnetic field. The trend of the radiative age (green line and shaded region) is derived from ![\begin{equation} t_{\rm rad}= 1590 \frac{B^{0.5}} {\left(B^{2}+B_{\rm IC}^2\right)\left[(1+z)\nu_{\rm break}\right]^{0.5}} ~~~~\rm (Myr), \label{trad} \end{equation}](/articles/aa/full_html/2012/12/aa19702-12/aa19702-12-eq181.png) (19)where the magnetic field is measured in μG, BIC = 3.25(1 + z)2 is the equivalent inverse Compton field associated to the cosmic background radiation, and
(19)where the magnetic field is measured in μG, BIC = 3.25(1 + z)2 is the equivalent inverse Compton field associated to the cosmic background radiation, and 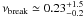 GHz is the spectral break measured in the total radio spectrum by Murgia et al. (2011). The horizontal blue dashed line is the buoyancy age for the south lobe. The two ages match at 65 Myr for B ≃ 12 μG. This value for the source’s magnetic field fits within the equipartition range Bmin = 5.5–22.7 μG for k = 1 pictured by the vertical shaded region in red. This means that if the source is in the minimum energy condition, the pressure equilibrium with the external medium, Pnth ~ 10-10 dyne/cm2, cannot be attained even supposing that k ≫ 1. In fact, the relativistic particles energy density should be on the same order of the magnetic field energy density, i.e., (1 + k)uel ≃ uB ~ 5.7 × 10-12 dyne/cm2, see Eq. (A.13). Indeed, a possibility is that k ~ 20 and the source is not in the minimum energy condition because the energy density is dominated by non-radiating relativistic particles. Alternatively, the source is in the minimum energy condition with k = 1 and the pressure equilibrium is sustained by thermal material entrained in the radio lobes.
GHz is the spectral break measured in the total radio spectrum by Murgia et al. (2011). The horizontal blue dashed line is the buoyancy age for the south lobe. The two ages match at 65 Myr for B ≃ 12 μG. This value for the source’s magnetic field fits within the equipartition range Bmin = 5.5–22.7 μG for k = 1 pictured by the vertical shaded region in red. This means that if the source is in the minimum energy condition, the pressure equilibrium with the external medium, Pnth ~ 10-10 dyne/cm2, cannot be attained even supposing that k ≫ 1. In fact, the relativistic particles energy density should be on the same order of the magnetic field energy density, i.e., (1 + k)uel ≃ uB ~ 5.7 × 10-12 dyne/cm2, see Eq. (A.13). Indeed, a possibility is that k ~ 20 and the source is not in the minimum energy condition because the energy density is dominated by non-radiating relativistic particles. Alternatively, the source is in the minimum energy condition with k = 1 and the pressure equilibrium is sustained by thermal material entrained in the radio lobes.
Whatever the reason, by assuming a similar energy output for the north cavity, the total power deposited by the AGN at the center of A2276 is estimated to be about QAGN = 2 × 4Pth/tb ~ 5 × 1044 erg/s. The energy power from the AGN outburst is almost one order of magnitude higher than the X-ray luminosity of A2276. Indeed, it is sufficient that a small fraction of this power is dissipated in the intra-cluster medium to reheat the cool core of the cluster.
In ZwCl 1829.3+691 a cavity is detected in the west lobe of the dying source WNB 1829+6911 at a distance of about 40 kpc from the core. We performed a similar calculation as for A2276 and found a buoyancy age of about tb ~ 58 Myr. According to Murgia et al. (2011) the radiative age is much longer trad ~ 218 Myr. However, a detailed comparison is more difficult in this case since the dying source has a restarting core whose spectrum overlaps that of the fossil outburst. Nevertheless, the total power deposited by the AGN is estimated to be about QAGN ~ 2.6−10 × 1044 erg/s. Thus, in this case the energy power from the AGN outburst is also far in excess of the X-ray luminosity of the cluster and thus sufficient to reheat the cool core.
5. Conclusion
We presented X-ray observations performed with the Chandra satellite of the three galaxy clusters Abell 2276, ZwCl 1829.3+6912, and RX J1852.1+5711, which harbor at their center a dying radio source with an ultra-steep spectrum.
We analyzed the physical properties of the X-ray emitting gas that surrounds these elusive radio sources and concluded that the physical state of the intra-cluster medium in the three galaxy clusters presents quite similar properties.
The large-scale X-ray emission is regular and spherical, suggesting a relaxed state for these systems. In fact, we found that the three systems are also characterized by strong enhancements in the central abundance and declining temperature profiles toward the central region. For all these reasons, we classify RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912 as cool-core galaxy clusters.
We found only marginal evidence for the presence of X-ray cavities associated to the fossil radio lobes in two of our galaxy clusters, namely A2276 and ZwCl 1829.3+691.
We compared the pressure of the intra-cluster medium with the non-thermal pressure of the radio lobes assuming that the radio sources are in the minimum energy condition. For all dying sources we found that this is on average about one to two orders of magnitude lower than that of the external gas, as found for many other radio sources at the center of galaxy groups and clusters.
We estimated the outburst age and energy output for the dying sources in Abell 2276 and ZwCl 1829.3+691, the two clusters for which we have a putative cavity detection.
For WNB 1734+6407, the dying source at the center of A2276, the radiative age obtained from the analysis of the radio spectrum matches the buoyancy age estimated from the X-ray analysis if the source is in the minimum energy condition. Indeed, the pressure equilibrium with the external medium is reached because the energy density of non-radiating particles (either relativistic or at thermal energies) is much higher than the magnetic field energy density.
We calculated the mechanical work done by the radio bubbles on the external gas and divided by the age of the radio source. The energy power from the AGN outburst is significantly higher than the X-ray luminosity in both clusters. Indeed, it is sufficient that a small fraction of this power is dissipated in the intra-cluster medium to reheat the cool cores.
Online material
Appendix A: Minimum energy calculation for an isotropic electron population with a power law spectrum in a disordered magnetic field
The total non-thermal energy density of the radio lobes is written as the sum of the ions, electrons, and magnetic field contributions: 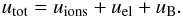 (A.1)The energy density in non-radiating particles is set simply proportional to that of electrons
(A.1)The energy density in non-radiating particles is set simply proportional to that of electrons 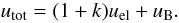 (A.2)The electron energy spectrum (number density of electrons with a Lorentz factor between γ and γ + dγ) is taken to be a power law
(A.2)The electron energy spectrum (number density of electrons with a Lorentz factor between γ and γ + dγ) is taken to be a power law 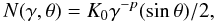 (A.3)where the electron’s Lorentz factor γ is in the range from γmin to γmax and we assumed an isotropic distribution of the pith angle θ between the local direction of the magnetic field and the electron velocity. Thus, the electron energy density is
(A.3)where the electron’s Lorentz factor γ is in the range from γmin to γmax and we assumed an isotropic distribution of the pith angle θ between the local direction of the magnetic field and the electron velocity. Thus, the electron energy density is 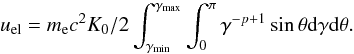 (A.4)The radio emissivity as a function of the pitch angle in a uniform magnetic field of strength B is given by
(A.4)The radio emissivity as a function of the pitch angle in a uniform magnetic field of strength B is given by 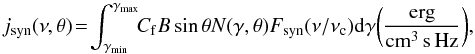 (A.5)where Fsyn(ν/νc) is the synchrotron kernel (see e.g. Blumenthal & Gould 1970; Rybicki & Lightman 1979), while
(A.5)where Fsyn(ν/νc) is the synchrotron kernel (see e.g. Blumenthal & Gould 1970; Rybicki & Lightman 1979), while 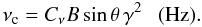 (A.6)The constants Cf = 2.3444 × 10-22 (erg Gauss-1) and Cν = 4.1989 × 106 (Gauss-1 s-1) depend only on fundamental physical constants.
(A.6)The constants Cf = 2.3444 × 10-22 (erg Gauss-1) and Cν = 4.1989 × 106 (Gauss-1 s-1) depend only on fundamental physical constants.
We now suppose that the magnetic field is completely tangled in an infinitesimally small scale compared to the source’s size. With this assumption, the synchrotron luminosity, after averaging Eq. (A.5) over all possible magnetic field directions with respect to the line-of-sight (LOS), is 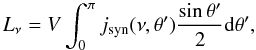 (A.7)\newpage\noindentwhere V is the source’s volume, see also the discussion in Murgia et al. (2010). In the power law regime, νmin ≪ ν ≪ νmax, we obtain the well-known formula for the synchrotron monochromatic power
(A.7)\newpage\noindentwhere V is the source’s volume, see also the discussion in Murgia et al. (2010). In the power law regime, νmin ≪ ν ≪ νmax, we obtain the well-known formula for the synchrotron monochromatic power 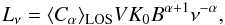 (A.8)where α = (p − 1)/2 while
(A.8)where α = (p − 1)/2 while 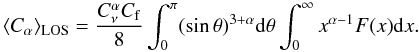 (A.9)In the literature an idealized situation is often assumed in which the source’s magnetic field lies in the plane of the sky. In this case, due to the high beaming of the synchrotron radiation, only electrons with pith angle θ = 90° can be observed and the constant in Eq. (A.8) has to be replaced by
(A.9)In the literature an idealized situation is often assumed in which the source’s magnetic field lies in the plane of the sky. In this case, due to the high beaming of the synchrotron radiation, only electrons with pith angle θ = 90° can be observed and the constant in Eq. (A.8) has to be replaced by 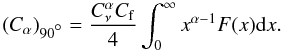 (A.10)The synchrotron radiation is then amplified by 60 − 70% with respect to the more realistic situation in which the field direction is disordered in the source.
(A.10)The synchrotron radiation is then amplified by 60 − 70% with respect to the more realistic situation in which the field direction is disordered in the source.
For α in the range between 0.5 and 1.0, Eq. (A.9) can be approximated by the polynomial expansion: 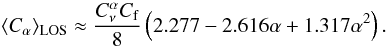 (A.11)Substituting Eq. (A.8) in (A.4), we found that the source’s non-thermal energy is minimum for
(A.11)Substituting Eq. (A.8) in (A.4), we found that the source’s non-thermal energy is minimum for ![\appendix \setcounter{section}{1} \begin{equation} B_{\rm min}=\left[\frac{4\pi m_{\rm e}c^2 (1+\alpha) (1+k) \nu^{\alpha}}{\langle C_{\alpha} \rangle_{\rm LOS} }\left(\frac{\gamma_{\rm max}^{1-2\alpha}-\gamma_{\rm min}^{1-2\alpha}}{1-2\alpha}\right) \frac{L_{\nu}}{V}\right] ^{1/(3+\alpha)}\cdot \label{bmin} \end{equation}](/articles/aa/full_html/2012/12/aa19702-12/aa19702-12-eq214.png) (A.12)For this value of the magnetic field strength the energy is nearly equipartitioned between particles and field:
(A.12)For this value of the magnetic field strength the energy is nearly equipartitioned between particles and field: 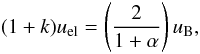 (A.13)so that the total minimum energy density is
(A.13)so that the total minimum energy density is 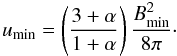 (A.14)
(A.14)
NH web tool at http://heasarc.gsfc.nasa.gov
Acknowledgments
We acknowledge the referee for helpful and constructive comments that improved the paper. F.G. and M.M. are grateful for the hospitality of the Harvard-Smithsonian Center for Astrophysics, where part of this research was done. Support was provided by Chandra grant GO9-0133X, NASA contract NAS8-39073, and the Smithsonian Institution. We acknowledge financial contribution from the agreement ASI-INAF I/009/10/0. The National Radio Astronomy Observatory is operated by Associated Universities, Inc., under contract with the National Science Foundation. This research made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. The optical DSS2 red images were taken from: http://archive.eso.org/dss/dss. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This research made use of Montage, funded by the National Aeronautics and Space Administration’s Earth Science Technology Office, Computation Technologies Project, under Cooperative Agreement Number NCC5-626 between NASA and the California Institute of Technology. Montage is maintained by the NASA/IPAC Infrared Science Archive.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arnaud, K. A. 1996, Astronomical Data Analysis Software and Systems V, 101, 17 [NASA ADS] [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Bîrzan, L., Rafferty, D. A., McNamara, B. R., Wise, M. W., & Nulsen, P. E. J. 2004, ApJ, 607, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Bîrzan, L., McNamara, B. R., Nulsen, P. E. J., Carilli, C. L., & Wise, M. W. 2008, ApJ, 686, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Setti, G., & Comastri, A. 1997, A&A, 325, 898 [NASA ADS] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- Churazov, E., Brüggen, M., Kaiser, C. R., Böhringer, H., & Forman, W. 2001, ApJ, 554, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Colla, G., Ficarra, A., Formiggini, L., et al. 1970, A&AS, 1, 281 [NASA ADS] [Google Scholar]
- Colla, G., Fanti, C., Fanti, R., et al. 1972, A&AS, 7, 1 [NASA ADS] [Google Scholar]
- Colla, G., Fanti, C., Fanti, R., et al. 1973, A&AS, 11, 291 [NASA ADS] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cordey, R. A. 1987, MNRAS, 227, 695 [NASA ADS] [Google Scholar]
- Croston, J. H., Hardcastle, M. J., Birkinshaw, M., Worrall, D. M., & Laing, R. A. 2008, MNRAS, 386, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Dunn, R. J. H., & Fabian, A. C. 2006, MNRAS, 373, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Dunn, R. J. H., Fabian, A. C., & Taylor, G. B. 2005, MNRAS, 364, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Reiprich, T. H., & Böhringer, H. 2001, A&A, 368, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fruscione, A., McDowell, J. C., Allen, G. E., et al. 2006, Proc. SPIE, 6270 [Google Scholar]
- Gentile, G., Rodríguez, C., Taylor, G. B., et al. 2007, ApJ, 659, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Giacintucci, S., Venturi, T., Murgia, M., et al. 2007, A&A, 476, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giovannini, G., Feretti, L., Gregorini, L., & Parma, P. 1988, A&A, 199, 73 [NASA ADS] [Google Scholar]
- Hudson, D. S., Mittal, R., Reiprich, T. H., et al. 2010, A&A, 513, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, R. M., Allen, S. W., Fabian, A. C., & Sanders, J. S. 2002, MNRAS, 336, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Komissarov, S. S., & Gubanov, A. G. 1994, A&A, 285, 27 [NASA ADS] [Google Scholar]
- Kraft, R. P., Forman, W. R., Churazov, E., et al. 2004, ApJ, 601, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A., Parma, P., de Ruiter, H. R., & Fanti, R. 1999, MNRAS, 306, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., Gómez, J. L., et al. 2007, ApJ, 665, 232 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., Wise, M., Nulsen, P. E. J., et al. 2000, ApJ, 534, L135 [CrossRef] [Google Scholar]
- McNamara, B. R., Nulsen, P. E. J., Wise, M. W., et al. 2005, Nature, 433, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Markevitch, M., Bautz, M. W., Biller, B., et al. 2003, ApJ, 583, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Morganti, R., Fanti, R., Gioia, I. M., et al. 1988, A&A, 189, 11 [NASA ADS] [Google Scholar]
- Murgia, M., Eckert, D., Govoni, F., et al. 2010, A&A, 514, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murgia, M., Parma, P., Mack, K.-H., et al. 2011, A&A, 526, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pacholczyk, A. G. 1970, Series of Books in Astronomy and Astrophysics (San Francisco: Freeman) [Google Scholar]
- Parma, P., Murgia, M., de Ruiter, H. R., et al. 2007, A&A, 470, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., & Arnaud, M. 2002, A&A, 394, 375 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rengelink, R. B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979 (New York: Wiley-Interscience), 393 [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Jones, C., Forman, W., et al. 2007, ApJ, 657, 197 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Non-thermal pressure of radio lobes in the three galaxy clusters assuming minimum energy.
All Figures
 |
Fig. 1 Background-subtracted and exposure-corrected Chandra ACIS-I image in the 0.5−7 keV band of RX J1852.1+5711, Abell 2276, and ZwCl 1829.3+6912. In the left-column panels the adaptively smoothed Chandra images are shown with the VLA radio contours at 1.4 GHz overlaid. A zoom of the central regions of the galaxy clusters are shown in the right-column panels. Red tones represent the Chandra image smoothed with a Gaussian kernel with σ = 2″ while the blue tones represent the optical images from the DSS (RX J1852.1+5711 and ZwCl 1829.3+6912) and SDSS (A2276). |
| In the text | |
 |
Fig. 2 Azimuthally averaged radial profiles of the gas metal abundance (left panel) and temperature (right panel). In the right-column panels the open symbols refer to the deprojected temperature profiles while the dotted lines are the best fit of the polytropic model to the four more external annuli, see text. |
| In the text | |
 |
Fig. 3 Azimuthally averaged SX profiles in the 0.5 − 7 keV band along with the best fit of the isothermal β-model (dashed line) and double β-model (continuous line). |
| In the text | |
 |
Fig. 4 Radial profiles of gas density (left-column panels) and pressure (right-column panels). The open dots represent the result of the deprojected spectral analysis while the dashed and continuous line represent the trend of the isothermal β-model and double β-model, respectively. The shaded areas represent the range of non-thermal pressure of the radio lobes under the minimum energy assumption, see Sect. 4.2. |
| In the text | |
 |
Fig. 5 Total mass profiles for the isothermal β-model and double β-model shown as dashed and continuous lines, respectively. The dots represent the total mass profile derived from the measured deprojected temperature profile by fixing the density profile to the best fit of the double β-model. The arrows indicate the radii at overdensities of 500 and 200 times the critical density. |
| In the text | |
 |
Fig. 6 Unsharp mask images obtained from the 0.5 − 7 keV band by subtracting the best fit of the circularly symmetric double-β model from the count image smoothed with a 1′′ Gaussian kernel, and then dividing by the sum of the two. |
| In the text | |
 |
Fig. 7 Simulated cavities in A2276 for the double-β model (top panels). The synthetic unsharp mask images are shown in the bottom panels. We expect a depression in the X-ray surface brightness of 22%, 15%, and 9% for i = 0°, 22.5°, and 45°. |
| In the text | |
 |
Fig. 8 Comparison of radiative and buoyancy ages as a function of the magnetic field for the dying source WNB 1734+6407 in A2276. The radiative age (green line and shaded region) is derived from the spectral break measured by Murgia et al. (2011). The horizontal blue dashed line and shaded region is the buoyancy age for the south lobe. The two ages match at 65 Myr for B ≃ 12 μG. This value for the source’s magnetic field (dotted line) fits within the equipartition range for k = 1 pictured by the vertical shaded region in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


