| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219702 | |
| Published online | 23 November 2012 | |
Online material
Appendix A: Minimum energy calculation for an isotropic electron population with a power law spectrum in a disordered magnetic field
The total non-thermal energy density of the radio lobes is written as the sum of the ions, electrons, and magnetic field contributions: 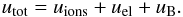 (A.1)The energy density in non-radiating particles is set simply proportional to that of electrons
(A.1)The energy density in non-radiating particles is set simply proportional to that of electrons  (A.2)The electron energy spectrum (number density of electrons with a Lorentz factor between γ and γ + dγ) is taken to be a power law
(A.2)The electron energy spectrum (number density of electrons with a Lorentz factor between γ and γ + dγ) is taken to be a power law 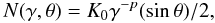 (A.3)where the electron’s Lorentz factor γ is in the range from γmin to γmax and we assumed an isotropic distribution of the pith angle θ between the local direction of the magnetic field and the electron velocity. Thus, the electron energy density is
(A.3)where the electron’s Lorentz factor γ is in the range from γmin to γmax and we assumed an isotropic distribution of the pith angle θ between the local direction of the magnetic field and the electron velocity. Thus, the electron energy density is 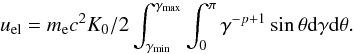 (A.4)The radio emissivity as a function of the pitch angle in a uniform magnetic field of strength B is given by
(A.4)The radio emissivity as a function of the pitch angle in a uniform magnetic field of strength B is given by  (A.5)where Fsyn(ν/νc) is the synchrotron kernel (see e.g. Blumenthal & Gould 1970; Rybicki & Lightman 1979), while
(A.5)where Fsyn(ν/νc) is the synchrotron kernel (see e.g. Blumenthal & Gould 1970; Rybicki & Lightman 1979), while 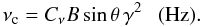 (A.6)The constants Cf = 2.3444 × 10-22 (erg Gauss-1) and Cν = 4.1989 × 106 (Gauss-1 s-1) depend only on fundamental physical constants.
(A.6)The constants Cf = 2.3444 × 10-22 (erg Gauss-1) and Cν = 4.1989 × 106 (Gauss-1 s-1) depend only on fundamental physical constants.
We now suppose that the magnetic field is completely tangled in an infinitesimally small scale compared to the source’s size. With this assumption, the synchrotron luminosity, after averaging Eq. (A.5) over all possible magnetic field directions with respect to the line-of-sight (LOS), is 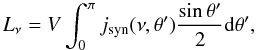 (A.7)\newpage\noindentwhere V is the source’s volume, see also the discussion in Murgia et al. (2010). In the power law regime, νmin ≪ ν ≪ νmax, we obtain the well-known formula for the synchrotron monochromatic power
(A.7)\newpage\noindentwhere V is the source’s volume, see also the discussion in Murgia et al. (2010). In the power law regime, νmin ≪ ν ≪ νmax, we obtain the well-known formula for the synchrotron monochromatic power  (A.8)where α = (p − 1)/2 while
(A.8)where α = (p − 1)/2 while 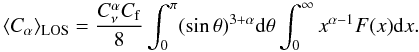 (A.9)In the literature an idealized situation is often assumed in which the source’s magnetic field lies in the plane of the sky. In this case, due to the high beaming of the synchrotron radiation, only electrons with pith angle θ = 90° can be observed and the constant in Eq. (A.8) has to be replaced by
(A.9)In the literature an idealized situation is often assumed in which the source’s magnetic field lies in the plane of the sky. In this case, due to the high beaming of the synchrotron radiation, only electrons with pith angle θ = 90° can be observed and the constant in Eq. (A.8) has to be replaced by 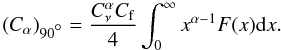 (A.10)The synchrotron radiation is then amplified by 60 − 70% with respect to the more realistic situation in which the field direction is disordered in the source.
(A.10)The synchrotron radiation is then amplified by 60 − 70% with respect to the more realistic situation in which the field direction is disordered in the source.
For α in the range between 0.5 and 1.0, Eq. (A.9) can be approximated by the polynomial expansion: 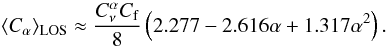 (A.11)Substituting Eq. (A.8) in (A.4), we found that the source’s non-thermal energy is minimum for
(A.11)Substituting Eq. (A.8) in (A.4), we found that the source’s non-thermal energy is minimum for 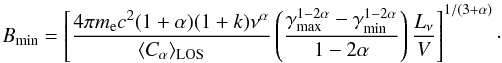 (A.12)For this value of the magnetic field strength the energy is nearly equipartitioned between particles and field:
(A.12)For this value of the magnetic field strength the energy is nearly equipartitioned between particles and field: 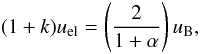 (A.13)so that the total minimum energy density is
(A.13)so that the total minimum energy density is 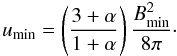 (A.14)
(A.14)
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


