| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219780 | |
| Published online | 07 November 2012 | |
Detection of Neptune-size planetary candidates with CoRoT data
Comparison with the planet occurrence rate derived from Kepler
1
Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de
Marseille) UMR 7326,
13388
Marseille,
France
e-mail: aldo.bonomo@oamp.fr
2
INAF – Osservatorio Astronomico di Torino, via Osservatorio 20, 10025
Pino Torinese,
Italy
3
Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université
Pierre & Marie Curie, 98bis boulevard Arago, 75014
Paris,
France
4
Observatoire de Haute-Provence, Université Aix-Marseille
& CNRS, 04870 St.
Michel l’ Observatoire, France
5
Institute of Planetary Research, German Aerospace Centre, Rutherfordstrasse 2,
12489
Berlin,
Germany
6
INAF – Osservatorio Astrofisico di Catania, via S. Sofia, 78,
95123
Catania,
Italy
7
School of Physics and Astronomy, Raymond and Beverly Sackler
Faculty of Exact Sciences, Tel Aviv University, Tel Aviv, Israel
8
Oxford Astrophysics, Denys Wilkinson Building, Keble Road, Oxford
OX1 3RH,
UK
9
Observatoire de l’Université de Genève, 51 chemin des
Maillettes, 1290
Sauverny,
Switzerland
10
LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules
Janssen, 92195
Meudon,
France
Received:
8
June
2012
Accepted:
13
September
2012
Context. The CoRoT space mission has been searching for transiting planets since the end of December 2006. It has led to the detection of about twenty Jupiter-size planets and three planets with radius Rp ≲ 5 R⊕. The latter are CoRoT-7b, the first super-Earth observed in transit, and two validated Neptunes, CoRoT-24b and c, in a multiple system.
Aims. We aim to investigate the capability of CoRoT to detect small-size transiting planets in short-period orbits, and to compare the number of CoRoT planets with 2.0 ≤ Rp ≤ 4.0 R⊕ with the occurrence rate of small-size planets provided by the distribution of Kepler planetary candidates.
Methods. We performed a test that simulates transits of super-Earths and Neptunes in real CoRoT light curves of six long observational runs and searches for them blindly by using the transit detection pipeline developed at the Laboratoire d’Astrophysique de Marseille.
Results. The CoRoT detection rate of planets with radius between 2 and 4 R⊕ and orbital period P ≤ 20 days is 59% (31%) around stars brighter than r′ = 14.0 (15.5). The vast majority of the missed planets went undetected because of a low transit signal-to-noise ratio (S/N). However, in some cases, additional instrumental or astrophysical noise may prevent even transits with relatively high S/N, i.e. S/N ≥ 10, from being revealed. By properly taking the CoRoT detection rate for Neptune-size planets (2 ≤ Rp ≤ 4 R⊕) and the transit probability into account, we found that according to the Kepler planet occurrence rate, CoRoT should have discovered 12 ± 2 Neptunes orbiting G and K dwarfs with P ≤ 17 days in six observational runs. This estimate must be compared with the validated Neptune CoRoT-24b and five CoRoT planetary candidates in the considered range of planetary radii, the nature of which is still unsolved. We thus found a disagreement with expectations from Kepler at 3σ or 5σ, assuming a blend fraction of 0% (six Neptunes) and 100% (one Neptune) for these candidates.
Conclusions. This underabundance of CoRoT Neptunes with respect to Kepler may be due to a) an underestimate of the uncertainty on the Kepler planet occurrence; b) an underestimate of the false-positive probability of the Kepler small-size planetary candidates; c) an overestimate of our prediction of CoRoT Neptunes related to the number of G and K dwarfs observed by CoRoT; or d) different stellar populations probed by the two space missions. Regardless of the origin of the disagreement, which needs to be investigated in more detail, the noticeable deficiency of CoRoT Neptunes at short orbital periods seems to indirectly support the general trend found in Kepler data, i.e. that the frequency of small-size planets increases with increasing orbital periods and decreasing planet radii.
Key words: planetary systems / techniques: photometric / stars: statistics / stars: solar-type
© ESO, 2012
1. Introduction
More than 750 exoplanets have been found since the discovery of the extrasolar planet 51 Peg b around a solar-like star by Mayor & Queloz (1995). Most of them are gaseous giant planets, but much effort is currently put into detecting small-size planets, such as Neptunes, super-Earths, and Earth-sized planets, with radial-velocity and space-based transit surveys.
About a hundred low-mass planets have been recently discovered by the HARPS and HIRES radial-velocity surveys (e.g., Mayor et al. 2011; Howard et al. 2010, and references therein). From these early discoveries, low-mass planets seem to be abundant. Focusing on 376 solar-type stars (from late-F to late-K dwarfs) observed with the HARPS spectrograph, Mayor et al. (2011) found that about 28 ± 5% of them host a planet with a minimum mass Msini = 3 to 30 M⊕ and orbital period P < 50 days. With a more limited sample of G and K dwarfs observed with the HIRES spectrograph, Howard et al. (2010) reported an occurrence rate of 18 ± 5%, slightly lower than the rate of Mayor et al. (2011), for the same mass domain and period range.
The observed occurrence rate of low-mass planets around dwarf stars, its dependence on the properties of the host stars (metallicity, stellar mass, etc.) and on the planetary parameters (mass, semi-major axis, and eccentricity) represent a powerful test for models of planet formation and migration (e.g., Mordasini et al. 2009a,b, 2012, and references therein; Mayor et al. 2011).
In addition to their contribution to general statistics, transiting low-mass planets are extremely interesting to study because one can measure their radius and mass free of the sini degeneracy if radial-velocity variations induced by the planet on its parent star or transit timing variations in a multiple system are observed. This enables a detailed characterisation of small-size planets and studies of their internal structure.
The transits of small-size planets can be observed from the ground only if their host stars have sizes considerably smaller than that of the Sun. This is, for example, the case of the super-Earth or mini-Neptune GJ 1214b (Charbonneau et al. 2009). In general, we have to move to space to detect small-size planets around solar-like stars as the photometric precision from the ground is insufficient.
1.1. The CoRoT space mission
The CoRoT space mission is the pioneer for the detection of transiting planets from space. It is operated by CNES1, with contributions from Austria, Belgium, Brazil, ESA, Germany and Spain (Baglin 2003). CoRoT was launched at the end of December 2006 on a polar orbit at an altitude of ~900 km. With its 27 cm telescope, it has been monitoring the optical flux of thousands of stars with 11 < V < 17 for ~150 days at the longest, in several fields of view pointing mainly in two different directions: one towards the Aquila and the other one towards the Monoceros constellation. The field of view of the telescope for the exoplanet science was ~4 deg2 before one DPU on board was lost through technical problems on 8 March 2009. Since then, only one CCD dedicated to exoplanet science is currently working, giving a halved field of view of 1.38 deg2. We refer the reader to Auvergne et al. (2009) for a detailed description of the instrument.
To date, CoRoT has led to the detection of three small-size planets with Rp ≲ 5 R⊕: CoRoT-7b, the first super-Earth observed in transit (Léger et al. 2009), and two transiting Neptunes, CoRoT-24b and CoRoT-24c, in a multiplanet system (Alonso et al. 2012). For the last two planets, radial-velocity observations performed with the HARPS spectrograph did not have sufficient precision to derive their masses, given that their parent star is faint. However, by using a procedure similar to that described in Torres et al. (2011), these candidates have been “validated” as low-mass planets (Alonso et al. 2012). This means that the probability that the observed transits are due to astrophysical false positives, such as blended eclipsing binaries, is very low. In other words, the planet scenario is most likely true (Torres et al. 2011).
1.2. The Kepler space mission
The other space-based mission aimed at detecting planetary transits is the NASA Kepler mission, launched in April 2009 in a heliocentric orbit. It performs photometric observations of ~156 000 stars with 9 < V < 16 in a fixed stellar field of 115 deg2 located in the Cygnus constellation (Borucki et al. 2006; Koch et al. 2010). With its 95 cm telescope and 42 back-illuminated CCDs, it reaches a photometric precision of ~50 ppm on a mV = 11.5 star for a ~30 min integration time, while the corresponding rms of CoRoT is ~200 ppm. Moreover, since Kepler has been observing always the same stellar field, as time goes by, it has the capability of detecting shallower and shallower transits because the signal-to-noise ratio (S/N) scales as the square root of the number of transits. Thanks to the unprecedented photometric precision of the instrument, the Kepler team found 2321 planetary candidates in the first sixteen months of data (Batalha et al. 2012). The vast majority of them have radii below the Neptune radius.
Up to now, the Kepler team has announced the discovery of 42 planets with radius smaller than 5 R⊕, many of which belong to multiple systems2. We recall the exceptional discoveries of the Kepler-11 and Kepler-20 systems with six and five small-size planets, respectively. In many cases, for instance Kepler-20, the planets have been only “validated” because their mass has not been measured either through radial-velocity observations or transit timing variations (e.g., Torres et al. 2011; Fressin et al. 2011). Kepler-20e with Rp = 0.87 R⊕ is the smallest planet found by the Kepler team (Fressin et al. 2012).
From stellar population synthesis and Galactic structure models, Morton & Johnson (2011) claimed that more than 90% of Kepler planetary candidates are very likely real planets. Based on this fiducial lower limit, Howard et al. (2012) have performed detailed statistical studies on the Kepler planetary candidates. After correcting for the alignment probability, these authors derived an occurrence rate of 13 ± 1% for planets with radius 2 ≤ Rp ≤ 4 R⊕, orbiting G and K dwarfs in P < 50 days. Moreover, Howard and coworkers found that the planet occurrence increases with decreasing planet radius and increasing orbital period.
1.3. Outline and purpose of the present work
In the present work, we first of all aim to investigate the capability of CoRoT of detecting small-size planetary transits. To that purpose, we simulated planetary transits of super-Earths and Neptunes in real CoRoT light curves of G and K dwarfs and searched for them blindly, that is, without knowing in advance in which light curves the transits had been simulated (Sect. 2). We used the transit detection pipeline currently operating at the Laboratoire d’Astrophysique de Marseille (Sect. 3), which is in charge of the CoRoT alarm mode. This allowed us to derive the CoRoT detection rate for planets with different sizes, from 1.3 to 5.0 R⊕ (Sect. 4.1), and to investigate the obstacles to the detection of small-size planets with CoRoT (Sect. 4.2). By deriving the CoRoT detection rate of planets with radii from 2.0 to 4.0 R⊕, we compared the number of small-size planets discovered by CoRoT with expectations from the Kepler occurrence rate provided by Howard et al. (2012), after taking the transit probability into account (Sect. 4.3).
2. Simulations
We made use of real light curves (N2 level data) of the CoRoT long runs lasting more than 110 days, i.e. LRa01 (Carone et al. 2012), LRa02, LRa03 (Cavarroc et al. 2012), LRa04, LRc01 (Cabrera et al. 2009), and LRc023. They refer to six different fields of view observed by CoRoT. For all runs except for LRa03 and LRa04, both of the two CCDs dedicated to exoplanet science were operating. Out of the ~55 000 stars observed in the above-mentioned long runs, almost 14 000 were classified as dwarfs with spectral type G and K, according to the photometric classification of Exodat (Deleuil et al. 2009). The remaining targets were ranked as either evolved or hotter stars. Among the ~14 000 G and K dwarfs, only those brighter than r′ = 15.5 were selected, that is, 9526 stars. From this sample, light curves of binaries or planetary candidates found by the CoRoT detection team were excluded. This yields 9333 light curves for our blind test.
Here we must point out that from a comparison between the Exodat photometric classification and a massive spectral analysis of more than 1000 CoRoT stars with FLAMES/GIRAFFE multi-fiber observations, Gazzano et al. (2010) found that the former tends to systematically underestimate the number of dwarfs, while there is a fairly good agreement between the spectral types determined by the two methods. Figure 8 in Gazzano et al. (2010) clearly shows this behaviour for the LRa01 and LRc01 stellar fields: the spectral analysis found 52% of the dwarfs while only 32% of the stars were classified as such by the photometric classification, which is a difference of a factor 1.7. The number of subgiants identified by both methods is similar, while the amount of giants was clearly overestimated by Exodat. However, since the classification based on spectroscopy is only available for about a thousand targets in the LRa01 and LRc01, we could only rely on the Exodat classification for the light curve selection. Nevertheless, we will consider a correction factor to take the underestimate of dwarf stars by the Exodat classification into account in Sect. 4.3.
The choice of restricting ourselves to the light curves of G and K dwarfs allows us to compare the rate of small-size planets detected by CoRoT with the statistics provided by the distribution of Kepler planetary candidates. In addition, G and K main-sequence stars with r′ ≤ 15.5 are the most interesting targets for the detection of small-size planets. The fainter the stars and/or the bigger their radius, the more difficult the discovery of Neptunes and super-Earths.
Simulated transits of small-size planets, super-Earths and Neptunes, with radius Rp ranging between 1.3 and 5.0 R⊕ and orbital period P from 0.7 up to 20 days were inserted into the selected 9333 CoRoT light curves. A flat distribution was adopted both for the planetary radius and the orbital period. To obtain a sufficiently large statistics for the detection of super-Earths, we repeated our experiment twice. First we simulated only transits of planets with 1.3 < Rp ≤ 2.5 R⊕ in the 9333 light curves. Then, we inserted transits of bigger planets with 2.5 < Rp ≤ 5.0 R⊕ into the same original light curves.
We used the universal transit modeler (Deeg 2009) to simulate the planetary transits assuming, for simplicity, circular planetary orbits, the stellar radius and mass of a G2V star for the G dwarfs, i.e. R ⋆ = 1 R⊙ and M ⋆ = 1 M⊙, and those of a K2V star for the K ones: R ⋆ = 0.8 R⊙ and M ⋆ = 0.7 M⊙ (Cox 2000). A linear limb-darkening law was adopted with the linear coefficient for the CoRoT bandpass u = 0.62 or 0.69 for the G or K spectral types, respectively (Sing 2010). The impact parameter was chosen at random between 0 and 1 to take the distribution of the orbital inclination into account. The initial epoch of the transits was also chosen randomly.
Our simulations do not take planets around one component of a binary or triple physical system into account. Such planets would be more difficult to detect because their transit depth is diluted by the stellar companion(s). However, for the time being, it is not clear how the frequency of small-size planets is affected by the multiplicity of stellar systems and as long as we lack this information, we will consider only single stars. Moreover, even the distribution of the planetary radii of Kepler candidates, which was used by Howard et al. (2012) to determine the planet occurrence as a function of orbital period, implicitly assumes that they orbit single stars (Borucki et al. 2011; Batalha et al. 2012).
Another possible cause of dilution of the transit depth is the contamination of background stars inside the CoRoT aperture mask of a star (Deeg et al. 2009). However, this can be readily neglected for our study, because this contamination is typically only ~5% of the flux collected by CoRoT for a given star (e.g., Bonomo et al. 2010 ).
3. Data analysis
3.1. The LAM transit detection pipeline
Transits were searched for by means of the transit detection pipeline developed at the Laboratoire d’Astrophysique de Marseille (LAM). The CoRoT detection team uses seven different techniques to detrend the light curves and search for transits (Cabrera et al. 2009). Blind tests organized within the CoRoT consortium to compare their performance on real CoRoT light curves have shown that the LAM pipeline and two other algorithms have the best performance and a similar detection rate (Barge, priv. comm.). Our pipeline consists of eight steps:
-
a)
Outliers caused by proton impacts during the passage of thesatellite across the South Atlantic Anomaly (Auvergneet al. 2009) are filtered out with a5-sigma clipping.
-
b)
Data points oversampled at 32 s are re-binned at 512 s.
-
c)
Low-frequency variations (i.e., stellar variability) are removed with a high-pass filter, consisting of a sliding median filter with a window extension of 0.5 days (see Sect. 3.3 for a discussion on the choice of the filtering time scale).
-
d)
High-frequency variations are removed with a low-pass filter, consisting of a Savitzky-Golay filter (Press et al. 1992) with a time scale of ~1 h. Most of these high-frequency variations are related to the signal at the satellite orbit of 6184 s (1.72 h).
-
e)
Jumps/discontinuities that are mainly caused by hot pixels (Srour et al. 2003; cf. Auvergne et al. 2009, for the specific case of CoRoT) or pointing displacements are automatically detected. After that, data points that fall 0.4 days before and after the time of a given hot pixel are removed. These discontinuities in CoRoT light curves may represent a major concern for detecting shallow planetary transits (see below Sect. 4.2). Indeed, after the filtering process (steps a-b-c-d), they give rise to dips in the residuals that can be erroneously identified as transits by the detection algorithms, such as the box fitting least squares (BLS, Kovács et al. 2002). The detection of hot pixels is carried out by using a sliding window of eight data points sampled at 512 s and computing the standard error of the mean inside the moving window. When a discontinuity takes place in the light curve, the standard error suddenly increases, allowing the hot pixel detection as soon as it exceeds a given threshold (see Fig. 1). The latter was fixed at four standard deviations of the set of the mean standard errors obtained for each position of the eight-point sliding window. This method allows us to detect approximately 60–70% of the most evident hot pixels. After detecting a discontinuity in the light curve, we prefer to remove data points in its vicinity. Indeed, after a simple adjustment of the light curve without any clearing of data points in the vicinity of a hot pixel, high-frequency variations could still remain and hinder the transit detection. Figure 1 shows one of the light curves selected for our blind test that is affected by a clear jump (top panel) and other less evident discontinuities. Into this light curve of a r′ = 12.8 G dwarf, namely LRc01_E1_0331, transits of a super-Earth with Rp = 2.14 R⊕ and P = 9.8 days were inserted. The red arrow indicates the discontinuity identified by our pipeline. In the middle panel, the high- and low-pass filtered light curve (3.1.b-c-d) is displayed. An artificial dip followed by a jump is seen at the time of the hot pixel as a result of the filtering process. Other artificial flux drops caused by small undetected discontinuities are also discernible. Even though the low-pass filter reduces the rms of the light curve, the individual planetary transits are not visible in the light curve. The artificial dip produced by the hot pixel identified by our pipeline is corrected after step 3.1.e (bottom panel). Despite several artificial dips, in this case the transit signal is easily detected: the highest peak at the orbital frequency and those corresponding to its harmonics in the BLS spectrum are shown in Fig. 2.
-
f)
Transits are searched for by means of the BLS algorithm with the directional correction (cf. Tingley 2003). The period search was carried out from Pmin = 0.4 up to Pmax = 30 days. The fractionary length of the transit was varied between 0.006 and 0.09, adopting a number of phase bins nbins = 240 (Kovács et al. 2002). The frequency sampling δν was optimised according to the criterion given by Schwarzenberg-Czerny & Beaulieu (2006): δν = 1/(Pmax·nbins). This criterion ensures that the simulated planets do not remain undetected because of an inappropriate frequency sampling.

Fig. 1 Top panel: the CoRoT light curve LRc01_E1_0331, filtered from cosmic rays (Sect. 3.1.a), containing simulated transits of a super-Earth with an orbital period of 9.8 days. The red arrow indicates the jump produced by a hot pixel and correctly identified by our pipeline. Middle panel: high- and low-pass filtered light curve after steps b), c), and d). Planetary transits by the super-Earth are not visible to the naked eye. Other artificial dips are produced by undetected small discontinuities. Bottom panel: light curve after removal of data points in the vicinity of the identified discontinuity (Sect. 3.1.e).

Fig. 2 Top panel: BLS spectrum of the filtered light curve LRc01_E1_0331, containing simulated transits by a super-Earth with orbital period P = 9.8 days (see bottom panel of Fig. 1). The highest peak corresponds to the inserted transit signal, which is thus easily detected. Its harmonics are also clearly visible. Bottom panel: phase-folded light curve at the period and epoch found by the BLS (Sect. 3.1.g).
-
g)
The light curve phase-folded at the period and epoch found by the BLS (Fig. 2, bottom panel) is visually inspected if events with signal detection efficiency greater or equal than 6 have been detected. Events below this threshold are generated by pure noise with very high probability (Kovács et al. 2002). In addition, a visual inspection of the original light curve filtered from outliers (Sect. 3.1.a) is fundamentally important for checking whether a given transit-like feature could be caused by undetected hot pixels. The visual inspection checks that there are no hot pixels at any epochs of the detected transits or, if any are found, that after their removal, the planetary transit is still detectable and visible in the folded light curve. A complementary method is checking possible depth differences when folding the filtered light curve at twice the period found by the BLS. Indeed, significant depth differences can arise when the transit-like feature is produced by a discontinuity in the light curve.
-
h)
The filtering of an instrumental effect due to the perturbation associated with the Earth’s rotation at the frequency of one day-1 and its harmonics is carried out. This effect is caused by variations of the Earth’s infrared emission that produce temperature changes, even though the way in which these variations affect the onboard instrumentation is not well understood yet. Such a perturbation gives rise to quasi-sinusoidal signals with a period of 12, 24, or 36 h, affecting all CoRoT light curves, although not in the same way: there is probably a dependence on the position of the star on the CCD. Mostly, the Earth’s perturbation can be neglected and does not affect the transit detection. In a few cases, however, it does have an effect and may lead to a missed detection. To show this, we display in the top panel of Fig. 3 the BLS spectrum of the light curve of the r′ = 15.0 star LRa01_E1_2996, in which we simulated transits of a super-Earth with radius Rp = 1.56 R⊕ and period P = 2.1 days. We see that the peak related to the 12 h instrumental effect exceeds the power of the transit signal, which impedes the transit detection. Indeed, from the visual inspection of the phase-folded light curve (Sect. 3.1.g), only a sinusoidal variation with a peak-to-peak amplitude of ~6 × 10-4 appears (see bottom panel of Fig. 3). To filter this out, we smoothed the quasi-sinusoid in phase to determine its amplitude, period, and initial phase, and subtracted it from the initial temporal series processed up to step e). After which, carrying out again the BLS allows us to detect the transit signal because this signal becomes the dominant peak in the BLS spectrum (Fig. 4).
 |
Fig. 3 Top panel: BLS spectrum of the filtered light curve LRa01_E1_2996, containing simulated transits by a super-Earth with orbital period P = 2.1 days. The 12 h instrumental effect overcomes the planetary signal, which impedes its detection. Bottom panel: phase-folded light curve at the period and epoch found by the BLS, displaying the quasi-sinusoidal variation caused by the Earth’s perturbation (see text for more details). |
3.2. Why use a simple median filter?
Our choice of using a simple median filter to remove stellar variability is motivated by two reasons: the first is the work by Bonomo et al. (2009), who showed that iterative median filters (Aigrain & Irwin 2004), with an appropriate choice of the window extension, perform very well for detections of planetary transits; the second is that simple median filters are less sensitive to discontinuities and/or jumps in the light curves. Indeed, more sophisticated filters, such as harmonic fitting (Moutou et al. 2005; Bonomo & Lanza 2008) or wavelet filters (Jenkins 2002), give rise to deeper artificial flux drops and oscillations in the vicinity of an undetected hot pixel. These flux drops, once again, can be erroneously identified as transits by the BLS.
3.3. Optimising the extension of the median filter window
In the same way as in Bonomo et al. (2009), to find the optimal window extension of the sliding median filter, we performed the transit search on the light curves of a subset of 500 light curves of our blind test by using five different extensions: 0.3, 0.5, 0.75, 1.0, and 1.25 days. We found that the maximum detection rate was reached with a window extension of 0.5 days, which apparently contradicts the results of Bonomo et al. (2009). These authors showed with extensive simulations of light curves with solar-like variability and planetary transits that one should use the longest possible window extension allowed by the stellar activity level to maximise the transit detection. However, their light curves were not affected by the instrumental effects that are present in CoRoT data. In other words, the short extension of 0.5 days allows a better filtering of the CoRoT light curves, which are usually affected by sudden jumps and jitter noise (Sect. 3.1.e). The longer the median filter window, the stronger the filtered light curves are affected by residual instrumental effects that hamper the transit detection.
One may argue that, on the other hand, for long transits, a strong filtering with such a short extension could reduce the transit signal. However, longer windows did not increase the detection rate in our exercise as we were searching for small-size planets around solar-like stars in short-period orbits, with transit durations of typically less than 5–6 h.
 |
Fig. 4 Top panel: the same as Fig. 3 after filtering the 12 h instrumental signal (see Sect. 3.1.h). The planetary signal is now correctly detected as the most significant peak. Bottom panel: phase-folded light curve at the period and epoch found by the BLS, distinctly showing the transit signature. |
 |
Fig. 5 Distribution of the simulated planets in the r′ magnitude vs. orbital period diagram. Green and black dots indicate detected and missed planets, respectively. Left: simulations with 1.3 ≤ Rp ≤ 2.5 R⊕. Right: simulations with 2.5 < Rp ≤ 5.0 R⊕. See text for explanation. |
Percentage of detected simulated planets with orbital period 0.7 ≤ P ≤ 20 days for different values of planetary radius.
3.4. The CoRoT alarm mode
The CoRoT alarm mode is a CNES operational task that is operated at the LAM. It is responsible for detecting transits in CoRoT light curves while observations of a given stellar field are ongoing and uses the so-called N1 level data (Surace et al. 2008). As soon as transits in a light curve are detected by the alarm mode, the temporal sampling of that light curve is changed from 512 s to 32 s. This is very important for the transit modelling, which requires the transit ingress and egress to be well sampled (e.g., Kipping 2010), the study of transit timing variations (e.g., Csizmadia et al. 2010), and the detection of the secondary eclipse (e.g., Alonso et al. 2009). Additionally, the alarm mode can trigger the ground-based follow-up of the most interesting planetary candidates as soon as possible, which is required to unveil their nature and, if they turn out to be planets, derive the orbital parameters. If a planetary candidate is not detected by the alarm mode, it can be discovered by the other detection algorithms of the CoRoT team that search for transits on the more precise N2 level data (Cabrera et al. 2009). However, in this case, the ground-based follow-up has to wait for about six months before the target becomes observable again.
With the exception of CoRoT-21b, all CoRoT planets, including the super-Earth CoRoT-7b, were detected by the alarm mode. A replacement of the previous variability filter, a gauging filter developed by Guis & Barge (2005), with the one described in Sects. 3.1.a–d, allowed us to increase the number of planetary candidates found by the alarm mode by ~20–30%. This is mainly because the gauging filter is very sensitive to discontinuities caused by hot pixels and shows that light curve filtering is crucial for detecting planetary transits, in particular the small-size ones. CoRoT-21b was missed by the previous version of the alarm mode pipeline that used the gauging filter. The replacement of the variability filter took place in February 2009 during the long run LRa02.
The current alarm mode pipeline is a simplified version of the one described in Sect. 3.1. In particular, it performs neither the automatic correction of light curve discontinuities (Sect. 3.1.e) nor the filtering of the instrumental effect mentioned in Sect. 3.1.h. Indeed, the task of the alarm mode is, in principle, the detection of naked-eye transits, hence the complete LAM detection pipeline (Sect. 3.1) is used only to search for small-size planets with N2 data. Nevertheless, even with this simplified detection pipeline, the alarm mode enables detecting many small-size planetary candidates with transits embedded in the noise. As an example, it led to the detection of the Neptune CoRoT-24c (Alonso et al. 2012), with a transit S/N lower than CoRoT-7b by about a factor of three since it orbits a faint star with r′ = 15.11 in almost 12 days.
4. Results and discussion
4.1. CoRoT detection rate of super-Earths and Neptunes
With our LAM transit detection pipeline (Sect. 3.1), we searched for the simulated transits blindly, that is, without knowing in advance into which light curves the transits had been inserted (Sect. 2). Figure 5 shows our results in terms of detected planets in the r′ magnitude vs. orbital period diagram. The green and black dots indicate the detected and undetected events, respectively. We considered an event as “detected” when the BLS algorithm correctly found the period of the simulated transits and the signal detection efficiency was ≥ 6. In the left panel of Fig. 5, we clearly notice that only few planets with radius Rp ≤ 2.5 R⊕, i.e. 6%, were correctly found. The vast majority of them orbit relatively bright stars and/or have short orbital periods, i.e. P < 5 days. In contrast, the right panel shows that about 50% of the simulated planets with larger radius, 2.5 < Rp ≤ 5.0 R⊕, were correctly detected. In the latter case, the majority of the missed events are the simulated transits with relatively long orbital periods, P > 13 days, which were inserted in faint stars with r′ > 14.5 (see Fig. 5, right panel).
Table 1 reports the percentage of detections of the simulated transits with orbital period 0.7 ≤ P ≤ 20 days for different intervals of planetary radii. The associated errors were estimated with binomial statistics. Below 2 R⊕, the detection rate ξCoRoT is very low, ξCoRoT ~ 3% by taking all the stars of our blind tests into account, and ξCoRoT ~ 11% by considering only those brighter than r′ = 14.0. For the biggest planets with 4.0 ≤ Rp ≤ 5.0 R⊕, ξCoRoT ~ 2/3 (9/10) for r′ ≤ 15.5 (≤ 14.0). By taking small-size planets with radii between 2 and 4 R⊕ into account, which is the smallest range considered by Howard et al. (2012) to determine the planet occurrence rate, our detection rate is 30.6 ± 0.5% and 58.9 ± 1.3% for stars brighter than r′ = 15.5 and 14.0, respectively. For this range of planetary radius, Table 2 lists the fraction of detected planets in eight bins of orbital period, along with their own uncertainties estimated, once again, with binomial statistics.
Percentage of detected simulated planets with radius 2 ≤ Rp ≤ 4 R⊕ as a function of orbital period.
For each simulated transiting planet we computed a posteriori the signal-to-noise ratio
as 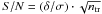 ,
where δ is the transit depth, ntr the number
of data points inside the transit bottom part, and σ the total noise of
the 512 s sampled light curves. The latter is estimated as
,
where δ is the transit depth, ntr the number
of data points inside the transit bottom part, and σ the total noise of
the 512 s sampled light curves. The latter is estimated as
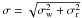 ,
where σw is the point-to-point scatter of the out-of-transit
light curve and σr its correlated noise (e.g., Pont et al. 2006). σw was
evaluated in a robust way as σw = 1.4826·MAD, where MAD stands
for median absolute deviation, to exclude possible outliers, after removing low-frequency
variations on time scales longer than 12 h. σr was estimated
by comparing the expected white noise at seven different time scales, from 25 min (3 data
points) up to 2.1 h (15 data points), with the standard deviation of the sliding average
over the same time scales (evaluated, once again, in a robust way). Since the white noise
decreases with the square root of the number of measurements, the maximum of the
quadrature differences between the expected white noise and the measured noise, computed
for the seven temporal windows, was set to σr. Figure 6 is an example of the estimated noise in a typical CoRoT
light curve used in our blind test. In agreement with estimates of the correlated noise in
CoRoT light curves by Aigrain et al. (2009), we
found that its contribution is in general low, ~1/4 of the total noise.
,
where σw is the point-to-point scatter of the out-of-transit
light curve and σr its correlated noise (e.g., Pont et al. 2006). σw was
evaluated in a robust way as σw = 1.4826·MAD, where MAD stands
for median absolute deviation, to exclude possible outliers, after removing low-frequency
variations on time scales longer than 12 h. σr was estimated
by comparing the expected white noise at seven different time scales, from 25 min (3 data
points) up to 2.1 h (15 data points), with the standard deviation of the sliding average
over the same time scales (evaluated, once again, in a robust way). Since the white noise
decreases with the square root of the number of measurements, the maximum of the
quadrature differences between the expected white noise and the measured noise, computed
for the seven temporal windows, was set to σr. Figure 6 is an example of the estimated noise in a typical CoRoT
light curve used in our blind test. In agreement with estimates of the correlated noise in
CoRoT light curves by Aigrain et al. (2009), we
found that its contribution is in general low, ~1/4 of the total noise.
 |
Fig. 6 Measured noise (square) and expected white noise (diamond) of a typical CoRoT light curve used in our blind test as a function of the number of photometric measurements sampled at 512 s. In this case, the highest difference is found at 3 measurements, as indicated by the arrow. |
 |
Fig. 7 Radius of the simulated planets as a function of the S/N of their transits. As in Fig. 5, green and black dots indicate the identified and missed planets, respectively. The vast majority of the discovered transits have S/N > 8 (red dashed line). Note that the x-scale in the left and right panels is different. See text for discussion about the transits with S/N ≥ 15 that should be easily detectable but were missed in our blind test. |
Figure 7 displays the radius of the simulated planets in terrestrial units as a function of the signal-to-noise ratio of their transits. As in Fig. 5, green dots indicate the correctly identified planets while the black dots the missed ones. Figure 7 shows that the vast majority of detected transits have S/N > 8 and that CoRoT is able to detect transiting small-size planets with an S/N much lower than CoRoT-7b, i.e. ~1/4·S/NCoRoT−7b.
4.2. Obstacles in detecting small-size planets in CoRoT data
The vast majority of undetected planets in our blind test were missed because their transits have a low S/N. However, some events with a relatively high S/N, which should have been quite easily identified, were also missed. This motivated us to investigate additional obstacles that may contribute to a missed detection. For this reason, we carefully looked at the few events with S/N > 15 that went undetected (see Fig. 7). They represent only 5% of the total number of simulated planets with S/N > 15 because 95% of them were correctly found.
The first obstacle has been mentioned already (Sects. 3.1.e, h) and consists of light curve discontinuities mainly caused by hot pixels or pointing displacements that were not identified by our pipeline because of their low amplitude. Another obstacle is the stellar variability in the case of fast rotators with rotation period Prot < 2−3 days. In this case, the variability is much stronger than the transit signal. Even a very strong filtering is unable to reveal the transits because it simultaneously reduces their depth, which prevents us from detecting them. We found that ~70% of the missed transits with S/N > 15 went undetected by our pipeline owing to unidentified, hence uncorrected light curve discontinuities, and ~30% because of stellar variability.
While such obstacles are not a major concern for events with S/N > 15 since, as already mentioned, only 5% of such planets were not detected, they certainly have a stronger impact on signals near the detection threshold, i.e. S/N ~ 10. Therefore, we suspect they are very likely responsible for the 20% of small planets with S/N ≥ 10 that were not found by our pipeline.
Finally, we recall that the instrumental signal caused by Earth’s perturbation on 12 or 24 h time scale can in some cases also impede the detection of small-size planets, if it is not adequately filtered. However, this filtering is implemented in our automatic pipeline (Sect. 3.1.h).
4.3. Comparison between discovered and expected CoRoT planets with Rp = 2–4 R⊕
After deriving the CoRoT detection rate of small-size planets from our blind test, we are now able to estimate the expected number of CoRoT planets with radius between 2 and 4 R⊕ from the statistics provided by the distribution of the Kepler planetary candidates. Assuming that these candidates are real planets (Morton & Johnson 2011), Howard et al. (2012) found, by studying their occurrence rate around G and K dwarfs after correcting for the alignment probability, that “the planet occurrence increases substantially with decreasing planet radius and increasing orbital period” (see their Figs. 5 and 6). They empirically determined the planet occurrence as a function of planetary radius and orbital period up to 50 days (cf. their Eqs. (4) and (8)). In the remainder of the paper we consider only planets with 2 ≤ Rp ≤ 4 R⊕ and 1.2 ≤ P ≤ 17.0 days to choose the same bins of planetary radius and orbital period as Howard et al. (2012, see their Figs. 4 and 7). Integrating between 1.2 and 17.0 days gives an occurrence rate of 5.5 ± 0.5%.
Kepler planet frequency f(R,P), CoRoT detection ξCoRoT(R,P) rate, and number of expected CoRoT Neptunes nCoRoT [2−4 R⊕] for each cell of Rp and P as in Fig. 4 of Howard et al. (2012).
The expected number of CoRoT planets with radii of
2−4 R⊕ and orbital periods up to 17 days can be
estimated as ![\begin{eqnarray} \label{pl_corot} n_{{\rm CoRoT} [2{-}4~R_{\oplus}]}&=& n_{\rm \star [GV-KV]}\nonumber \\ &&\times \int^{4}_{2} \int^{17.0}_{1.2} f(R, P) p_{\rm tr}(P) \xi_{\rm CoRoT}(R, P) {\rm d}R~{\rm d}P, \end{eqnarray}](/articles/aa/full_html/2012/11/aa19780-12/aa19780-12-eq151.png) (1)
(1)
where n ⋆ [GV−KV] is the number of G
and K main-sequence stars with r′ ≤ 15.5 in the six CoRoT long
runs used in our blind test (Sect. 2), i.e. those
lasting more than 110 days, hence more suited to the search for small-size planets;
f(R,P) is the frequency of planets as a function of
planetary radius and orbital period determined by Howard
et al. (2012); ![\hbox{$p_{\rm tr}(P)=[(4 \pi^2 R_{\star}^{3})/(GM_{\star}P^2)]^{1/3}$}](/articles/aa/full_html/2012/11/aa19780-12/aa19780-12-eq153.png) is the
transit probability assuming for simplicity
R ⋆ = R⊙,
M ⋆ = M⊙,
and circular orbits; ξCoRoT(R,P) is the CoRoT
detection rate, which was derived from our blind test and is a function of planetary
radius and orbital period. The integral
is the
transit probability assuming for simplicity
R ⋆ = R⊙,
M ⋆ = M⊙,
and circular orbits; ξCoRoT(R,P) is the CoRoT
detection rate, which was derived from our blind test and is a function of planetary
radius and orbital period. The integral 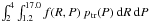 represents the fraction of
transiting Neptune-size planets with P ≤ 17 days according to the
Kepler planet occurrence (we recall that 20 days is the maximum allowed
period in our blind test). The integral in Eq. (1), by containing also the factor
ξCoRoT(R,P), gives the percentage of such
planets detectable by CoRoT. Multiplying the integral by
n ⋆ [GV−KV] simply allows one to
estimate the number of Neptune-size planets that CoRoT should have discovered
(nCoRoT [2−4 R⊕] , see
Eq. (1)). This was evaluated by computing
the integrand function and multiplying it by
n ⋆ [GV−KV] for each of the “cells”
that range from 2 to 4 R⊕ and from 1.2 to 17.0 days in
Fig. 4 of Howard et al. (2012, see Table 3). The values
calculated for each cell were then added.
represents the fraction of
transiting Neptune-size planets with P ≤ 17 days according to the
Kepler planet occurrence (we recall that 20 days is the maximum allowed
period in our blind test). The integral in Eq. (1), by containing also the factor
ξCoRoT(R,P), gives the percentage of such
planets detectable by CoRoT. Multiplying the integral by
n ⋆ [GV−KV] simply allows one to
estimate the number of Neptune-size planets that CoRoT should have discovered
(nCoRoT [2−4 R⊕] , see
Eq. (1)). This was evaluated by computing
the integrand function and multiplying it by
n ⋆ [GV−KV] for each of the “cells”
that range from 2 to 4 R⊕ and from 1.2 to 17.0 days in
Fig. 4 of Howard et al. (2012, see Table 3). The values
calculated for each cell were then added.
Because G and K dwarfs are underestimated in the Exodat photometric classification, as pointed out by Gazzano et al. (2010), n ⋆ [GV−KV] was increased by a factor 1.7: n ⋆ [GV−KV] = 9526 × 1.7 = 16 194 (see Sect. 2 and Fig. 8 in Gazzano et al. 2010). Moreover, a conservative arbitrary error of 30% on this quantity was considered because the work by Gazzano et al. (2010) inevitably relies on a limited number of stars, ~1000. In this way, the number of CoRoT planets nCoRoT [2−4 R⊕] expected from the planet occurrence rate determined by Howard et al. (2012) was estimated to be 12 ± 2 (Eq. (1)). The error was evaluated with a Monte Carlo method and is related to the uncertainties on n ⋆ [GV−KV] , f(R,P), and ξCoRoT(R,P). The error on f(R,P) was computed with binomial statistics in the same way as described in Howard et al. (2012), Sect. 3 (see Table 3).
We point out that our estimate of nCoRoT [2−4 R⊕] might be slightly underestimated because in our simulations the stellar radius and mass were fixed to those of a G2V or K2V star for the G and K dwarfs, respectively4. G stars of later spectral types would give rise to deeper, hence more easily detectable transits. Therefore, it is likely that our detection rate ξCoRoT(R,P) is moderately underestimated. However, this effect is partly compensated for by the slightly lower transit probability for such stars.
After estimating nCoRoT [2−4 R⊕] , a comparison with the CoRoT Neptunes and Neptune-size planetary candidates is interesting. For that purpose, the N2 light curves of the six observational runs considered for our blind test were analysed with the LAM pipeline (Sect. 3.1). All small-size candidates previously detected by the alarm mode (Sect. 3.4) and the other six detection algorithms used by the CoRoT team, including those discovered by Ofir et al. (2010), were correctly found. The CoRoT Neptune-size planetary candidates, regardless of their priority and stellar classification, constitute a substantial fraction of the total number of candidates (Deleuil et al., in prep.; see, e.g., Fig. 14 in Carone et al. 2012 ).
Since the statistics provided by Howard et al. (2012) does not take planets smaller than 2 R⊕ into account because of the current incompleteness of Kepler candidates, we excluded CoRoT-7b from this comparison. By considering only the range between 2 and 4 R⊕, we discarded also CoRoT-8b (Bordé et al. 2010) and CoRoT-24c (Alonso et al. 2012) because all of them have radii larger than 4 R⊕. The only CoRoT validated planet in this range is CoRoT-24b, which has a radius of 3.7 ± 0.4 R⊕ and an orbital period of 5.11 days (Alonso et al. 2012). We also checked the CoRoT Neptune-size candidates that were not identified as false positives from the light curve analysis and follow-up ground-based observations (Deeg et al. 2009; Moutou et al. 2009). The nature of these candidates is unknown, however, because no radial-velocity variation was detected with the HARPS spectrograph given that they orbit faint stars (r′ ≳ 13). Therefore, they could be either real planets, in which case only an upper limit can be put on their mass, or blended eclipsing binaries not identifiable from the CoRoT light curves. For uniformity with our study, we selected the Neptune-size candidates orbiting stars with r′ ≤ 15.5 that are classified as G or K dwarfs by Exodat, in the long runs LRa01, LRa02, LRa03, LRa04, LRc01, and LRc02. We ended up with three candidates and also added two more candidates whose stars were misclassified as giants by the Exodat photometric classification but were recognised to be G8V and K3V stars, respectively, thanks to low-resolution reconnaissance spectroscopy. However, we point out that the transits of two of them are V-shaped, which would indicate they are more likely blends.
In the most favourable case that all these candidates are real planets, which cannot be stated with certainty as they have not been properly validated, there would be six CoRoT Neptunes. This therefore disagrees with the expectation from the Kepler mission, i.e. nCoRoT [2−4 R⊕] = 12 ± 2, at 3σ. The disagreement would obviously get worse if a significant fraction of the Neptune candidates were actually blends, up to 5σ for a blend fraction of 100%.
Such a disagreement may be due to several reasons. First of all, the uncertainty on f(R,P) might be underestimated because the errors on the size of the Kepler planetary candidates were not taken into consideration by Howard et al. (2012). Such errors are related to the uncertainties on the stellar radii in the KIC catalogue which are typically ~30% (Brown et al. 2011). Secondly, the false-positive probability (FPP) of Kepler small-size planetary candidates in single systems might be higher than predicted by Morton & Johnson (2011). This has been suggested by Colón et al. (2012), who followed-up four Kepler candidates with radii smaller than 5 R⊕ and orbital periods less than 6 days with multicolour photometry. Half of them turned out to be false positives (Colón et al. 2012). However, Spitzer observations of a bigger sample of Kepler candidates would indicate, on the contrary, a low FPP (Désert et al. 2012). An FPP higher than estimated by Morton & Johnson (2011) may have led Howard et al. (2012) to overestimate the planet occurrence of small-size planets, although at least the Kepler planetary candidates in multiple systems are in all likelihood real planets (Latham et al. 2011; Lissauer et al. 2012). An alternative reason might be that a wrong value was adopted for n ⋆ [GV−KV] but the latter should be sufficiently accurate after correcting for the systematic effects of the photometric stellar classification and adding an arbitrary error of 30%. Lastly, the disagreement could also be related to the different stellar populations observed by CoRoT and Kepler. In any case, this disagreement needs to be investigated in more detail in subsequent papers as its explanation goes beyond the scope of the present work.
Despite the above-mentioned disagreement and the fact that the exact number of CoRoT Neptunes cannot be precisely determined for the moment, we point out that their noticeable deficiency seems to agree with the general trend found in Kepler data, i.e. that the frequency of small-size planets increases with increasing orbital periods and decreasing planet radii (Howard et al. 2012). If transiting planets with 2.0 ≤ Rp ≤ 4.0 R⊕ were numerous at short-orbital period, a significant fraction of them would have been detected by CoRoT, up to 59% (31%) for G and K dwarfs brighter than r′ = 14.0 (15.5) (Table 1).
5. Summary and prospects
We performed a blind test that consisted in simulating transits of small-size planets, super-Earths and Neptunes, in real CoRoT light curves of G and K dwarfs, and searching for them blindly. In this way, we investigated the capability of CoRoT of detecting small-size planets in short-period orbits. In particular, we showed that CoRoT can detect small planets with an S/N as low as ~1/4 that of CoRoT-7b. We found that the CoRoT detection rate is 59% (31%) for planets with radii between 2 and 4 R⊕ orbiting stars with r′ ≤ 14.0 (≤ 15.5) in P ≤ 20 days. The vast majority of missed planets went undetected because of a low S/N of their transits. However, in some cases, additional instrumental or astrophysical noise may also prevent transits with relatively high S/N, i.e. S/N ≥ 10, from being revealed. This noise is mainly caused by uncorrected light curve discontinuities produced by hot pixels and pointing displacements, or short-term (< 2−3 days) stellar variability.
By properly taking the CoRoT detection rate for Neptune-size planets (2 ≤ Rp ≤ 4 R⊕) and the transit probability into account, CoRoT should have discovered 12 ± 2 Neptunes with P ≤ 17 days around G and K dwarfs of six observational runs, according to the Kepler planet occurrence rate (Howard et al. 2012). However, between one and six CoRoT Neptunes were found in these runs, depending on the fraction of Neptune-size candidates that are actually blends. The reason of this disagreement still needs to be investigated. In any case, by noticing the scarcity of close-in Neptune-size planets found by CoRoT, our results seem to indirectly support the reality of the trend found in Kepler data, i.e. that the frequency of small-size planets increases with increasing orbital periods and decreasing planet radii (Howard et al. 2012).
At the end of the CoRoT mission, repeating this comparison by including the next CoRoT long runs and new detected or validated CoRoT Neptunes will certainly prove instructive. Moreover, the radial-velocity follow-up of Kepler small-size planetary candidates with the high-resolution spectrograph HARPS-N, mounted at the Telescopio Nazionale Galileo (La Palma, Spain), will also unveil their FPP, while determining the mass of several of them. The FPP of Kepler candidates is of fundamental importance for studies on the planet occurrence rate and could be then compared with the theoretical estimate of Morton & Johnson (2011) adopted by Howard et al. (2012).
Data available at http://idoc-corot.ias.u-psud.fr/
Acknowledgments
A. S. Bonomo gratefully acknowledges support through INAF/HARPS-N fellowship and CNES grant. A. S. Bonomo, C. Moutou, M. Deleuil, F. Bouchy, and A. Santerne acknowledge support from the “Programme National de Planétologie” (PNP) of CNRS/INSU and the French National Research Agency (ANR-08-JCJC-0102-01). The authors wish to thank R. F. Díaz for interesting and useful discussions.
References
- Aigrain, S., & Irwin, M. 2004, MNRAS, 350, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Aigrain, S., Pont, F., Fressin, F., et al. 2009, A&A, 506, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, R., Alapini, A., & Aigrain, S. 2009, A&A, 506, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, R., Guenther, E. W., Almenara, J.-M., et al. 2012, A&A, submitted [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baglin, A. 2003, Adv. Space Res., 31, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N., Rowe, J. F., Bryson, S. T., et al. 2012, ApJS, submitted [arXiv:1202.5852] [Google Scholar]
- Bonomo, A. S., & Lanza, A. F. 2008, A&A, 482, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonomo, A. S., Aigrain, S., Bordé, P., & Lanza, A. F. 2009, A&A, 495, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonomo, A. S., Santerne, A., Alonso, R., et al. 2010 A&A, 520, A65 [Google Scholar]
- Bordé, P., Bouchy, F., Deleuil, M., et al. 2010, A&A, 520, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2006, in Planetary Systems and Planets in Systems, eds. S. Udry, W. Benz, & R. von Steiger, ISSI Scientific Reports Series, 207 [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2011, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Latham, D. W., Everett, M. E., et al. 2011, AJ, 142, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera, J., Fridlund, M., Ollivier, M., et al. 2009, A&A, 506, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carone, L., Gandolfi, D., Cabrera, J., et al. 2012, A&A, 538, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavarroc, C., Moutou, C., Gandolfi, D., et al. 2012, Ap&SS, 337, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cox, A. N. 2000, Allen’s Astrophysical Quantities (New York: Springer) [Google Scholar]
- Colón, K. D., Ford, E. B., & Morehead, R. C. 2012, MNRAS, submitted [arXiv:1207.2481v1] [Google Scholar]
- Csizmadia, Sz., Renner, S., & Barge, P. 2010, A&A, 510, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeg, H. 2009, in Transiting Planets, Proc. IAU Symp., 253, 388 [NASA ADS] [Google Scholar]
- Deeg, H. J., Gillon, M., Shporer, A., et al. 2009, A&A, 506, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deleuil, M., Meunier, J. C., Moutou, C., et al. 2009, AJ, 138, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J. M., Charbonneau, D., Fressin, F., & Torres, G. 2012, in AAS Meeting, 219 [Google Scholar]
- Fressin, F., Torres, G., Désert, J.-M., et al. 2011, ApJS, 197, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Fressin, F., Torres, G., Rowe, J. F., et al. 2012, Nature, 482, 195 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gazzano, J.-C., de Laverny, P., Deleuil, M., et al. 2010, A&A, 523, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guis, V., & Barge, P. 2005, PASP, 117, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A. W., Marcy, G. W., Johnson, J. A., et al. 2010, Science, 330, 653 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2011, ApJS, 201, 15 [Google Scholar]
- Jenkins, J. M. 2002, ApJ, 575, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. 2010, MNRAS, 408, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Latham, D. W., Rowe, J. F., Samuel, N. Q., et al. 2011, ApJ, 732, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Lissauer, J. J., Marcy, G. J., Rowe, J., et al. 2012, ApJ, 750, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009a, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009b, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., Klahr, H., & Henning, T. 2012, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, T. D., & Johnson, J. A. 2011, ApJ, 738, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Moutou, C., Pont, F., Barge, P., et al. 2005, A&A, 437, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Pont, F., Bouchy, F., et al. 2009, A&A, 506, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofir, A., Alonso, R., Bonomo, A. S., et al. 2012, MNRAS, 404, L99 [Google Scholar]
- Pont, F., Zucker, S., & Queloz, D. 2006, MNRAS, 373, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in C, The art of scientific computing (Cambridge: University Press), 2nd edn. [Google Scholar]
- Schwarzenberg-Czerny, A., & Beaulieu, J.-Ph. 2006, MNRAS, 365, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K. 2010, A&A, 510, A21 [Google Scholar]
- Srour, J. R., Marshall, C. J., & Marshall, P. W. 2003, IEEE Trans. Nucl. Sci., 50, 653 [Google Scholar]
- Surace, C., Alonso, R., Barge, P., et al. 2008, in Advanced Software and Control for Astronomy II, eds. A. Bridger, & N. M. Radziwill, Proc. SPIE Conf. Ser., 7019, 70193B [Google Scholar]
- Tingley, B. 2003, A&A, 408, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, G., Fressin, F., Batalha, N. M., et al. 2011, ApJ, 727, 24 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Percentage of detected simulated planets with orbital period 0.7 ≤ P ≤ 20 days for different values of planetary radius.
Percentage of detected simulated planets with radius 2 ≤ Rp ≤ 4 R⊕ as a function of orbital period.
Kepler planet frequency f(R,P), CoRoT detection ξCoRoT(R,P) rate, and number of expected CoRoT Neptunes nCoRoT [2−4 R⊕] for each cell of Rp and P as in Fig. 4 of Howard et al. (2012).
All Figures
 |
Fig. 1 Top panel: the CoRoT light curve LRc01_E1_0331, filtered from cosmic rays (Sect. 3.1.a), containing simulated transits of a super-Earth with an orbital period of 9.8 days. The red arrow indicates the jump produced by a hot pixel and correctly identified by our pipeline. Middle panel: high- and low-pass filtered light curve after steps b), c), and d). Planetary transits by the super-Earth are not visible to the naked eye. Other artificial dips are produced by undetected small discontinuities. Bottom panel: light curve after removal of data points in the vicinity of the identified discontinuity (Sect. 3.1.e). |
| In the text | |
 |
Fig. 2 Top panel: BLS spectrum of the filtered light curve LRc01_E1_0331, containing simulated transits by a super-Earth with orbital period P = 9.8 days (see bottom panel of Fig. 1). The highest peak corresponds to the inserted transit signal, which is thus easily detected. Its harmonics are also clearly visible. Bottom panel: phase-folded light curve at the period and epoch found by the BLS (Sect. 3.1.g). |
| In the text | |
 |
Fig. 3 Top panel: BLS spectrum of the filtered light curve LRa01_E1_2996, containing simulated transits by a super-Earth with orbital period P = 2.1 days. The 12 h instrumental effect overcomes the planetary signal, which impedes its detection. Bottom panel: phase-folded light curve at the period and epoch found by the BLS, displaying the quasi-sinusoidal variation caused by the Earth’s perturbation (see text for more details). |
| In the text | |
 |
Fig. 4 Top panel: the same as Fig. 3 after filtering the 12 h instrumental signal (see Sect. 3.1.h). The planetary signal is now correctly detected as the most significant peak. Bottom panel: phase-folded light curve at the period and epoch found by the BLS, distinctly showing the transit signature. |
| In the text | |
 |
Fig. 5 Distribution of the simulated planets in the r′ magnitude vs. orbital period diagram. Green and black dots indicate detected and missed planets, respectively. Left: simulations with 1.3 ≤ Rp ≤ 2.5 R⊕. Right: simulations with 2.5 < Rp ≤ 5.0 R⊕. See text for explanation. |
| In the text | |
 |
Fig. 6 Measured noise (square) and expected white noise (diamond) of a typical CoRoT light curve used in our blind test as a function of the number of photometric measurements sampled at 512 s. In this case, the highest difference is found at 3 measurements, as indicated by the arrow. |
| In the text | |
 |
Fig. 7 Radius of the simulated planets as a function of the S/N of their transits. As in Fig. 5, green and black dots indicate the identified and missed planets, respectively. The vast majority of the discovered transits have S/N > 8 (red dashed line). Note that the x-scale in the left and right panels is different. See text for discussion about the transits with S/N ≥ 15 that should be easily detectable but were missed in our blind test. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


