| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 16 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201218767 | |
| Published online | 26 October 2012 | |
Do high-velocity clouds trace the dark matter subhalo population?⋆
University of ViennaDepartment of AstrophysicsTuerkenschanzstr. 17 1180 Vienna Austria
e-mail: sylvia.ploeckinger@univie.ac.at; gerhard.hensler@univie.ac.at
Received: 2 January 2012
Accepted: 13 August 2012
Context. Within the cosmological concordance model, cold dark matter (CDM) subhalos form the building blocks that merge hierarchically into more massive galaxies. This concept requires that massive galaxies are even nowadays surrounded by numerous subhalos. Since intergalactic gas is accreted by massive galaxies, observable e.g. as high-velocity clouds (HVCs) around the Milky Way, with extremely low metallicities, these can represent the baryonic content of primordial dark matter (DM) subhalos. Another possibility of their origin is that they stem from disrupted satellite galaxies, but in this case, these gas clouds move unaccompanied by a bound DM structure.
Aims. HVCs are mainly observed at significant distances from the galactic disk, while those closer to the disk have lower infall speed on average and larger but not yet solar element abundances. This can be caused by interactions with the hot halo gas: decelerated by ram pressure and metal-enriched by the more abundant gas in the galactic halo. Since HVCs are observed with long gas tails and with irregular substructures, numerical models of gas clouds passing through hot halo gas are performed to explore their structure and compare them with observations. If HVCs are engulfed by DM subhalos, their gas must leave the DM gravitational potential and reflect this in their dynamics. On the other hand, the evolution and survival of pure gas models must be tested to distinguish between DM-dominated and DM-free clouds and to draw conclusions about their origins.
Methods. A series of high-resolution hydrodynamical simulations using the adaptive-mesh refinement code FLASH V3.2 were performed for typical HVC masses, distances, and infall velocities.
Results. The models demonstrate that purely baryonic HVCs with low masses are disrupted by ram-pressure stripping and Kelvin-Helmholtz instabilities, while more massive ones survive, losing their initially spherical shape, developing significant substructures including cometary elongations in the column density distribution (“head-tail structure”). In contrast, HVCs with DM subhalos survive with more than 90% of their gas mass still bound and spherically shaped, approaching like bullets the Galactic disk. In addition, we find that velocity gradients along the cometary head-tail structures does not necessarily offer a possibility of distinguishing between DM-dominated and purely gaseous HVCs. Comparison of models with observations let us conclude that HVCs are not embedded in a DM substructure and do not trace the cosmological subhalo population.
Key words: ISM: clouds / Galaxy: halo / Galaxy: evolution / dark matter
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
In his general investigation of a possible Galactic corona, Spitzer (1956) was the first to predict the existence of high-velocity clouds (HVCs). A few years later the systematic search for neutral hydrogen clouds succeeded when E. Raimond observed the 21 cm line of neutral hydrogen at high velocities (Muller 1963).
Although the possibilities in observations, the theoretical understanding of the interstellar medium (ISM), and the facilities for numerical simulations have increased dramatically, yet half a century later, the formation and evolution of HVCs are still being discussed. The theories on their origin not only vary in small details but also lead to completely different pictures of the observed clouds, with tremendous consequences for galaxy formation and evolution. They are approaching the Galactic disk with high velocities and, depending on their distance, have to pass the hot coronal gas of the Milky Way halo.
Their radial velocities lie above or around the escape velocity of the Milky Way, and their rotation component is incompatible with the Galactic rotation (Blitz et al. 1999). This obtrudes the extragalactic origin of these gas clouds, excluding the widely discussed possibility of ejecta from galactic fountains (Shapiro & Field 1976; Bregman 1980).
This issue leaves two further fundamental possibilities open. They are either 1) relics of cosmological structure formation in a cold dark matter (CDM) cosmology (Connors et al. 2006) and therefore distant “building blocks” from galaxy formation in the Local Group (Blitz et al. 1999) or 2) remnants of galaxy collisions, from tidal disruption of dwarf galaxies (Putman et al. 2004), or/and from close-by tidal interactions of satellite galaxies (Gardiner & Noguchi 1996; Bland-Hawthorn et al. 1998). The main difference that distinguishes between both sources is their dark matter (DM) content: in case 1) clouds should be strongly dominated by DM, but not in 2). Decisive conclusions could be drawn from detailed observations in connection with complex numerical simulations, accounting for their distances, physical state, dynamical structure, and chemical abundances.
Distances and abundances of HVC and IVC.
2. State of the art
2.1. Observations
2.1.1. Distances, all-sky surveys, general properties
Detailed studies measure distances of a few kpc for the extended HVC complexes (Thom et al. 2006; Wakker et al. 2008), e.g. Complex C with a distance of d = 10 ± 2.5 kpc (Thom et al. 2008). For the massive Complex H, a distance of 27 kpc (Lockman 2003) and a mass of 2 × 107 M⊙ (Simon et al. 2006) is derived. Beside such large complexes that cover around 40% of the sky for a resolution limit of NHI ≥ 7 × 1017 cm-2 (Murphy et al. 1995), isolated, compact gas cloudlets have also been found with a small angular extent (Braun & Burton 1999). The first all-sky study of this subpopulation, called compact high velocity clouds (CHVCs), was presented by de Heij et al. (2002a) as a combination of data extracted by de Heij et al. (2002b) from the Leiden Dwingeloo Survey for the northern hemisphere and from the HI Parkes All Sky Survey (HIPASS), extracted by Putman et al. (2002) for the southern hemisphere. Owing to the compactness of CHVCs, the lack of distance indicators, and the poor knowledge about their physical environment, direct distance measurements are difficult.
Observations of M 31 have shown recently that HVC-analogs are clustered around their host galaxy with a maximum distance between 50 kpc (Thilker et al. 2004) and 60 kpc (Westmeier et al. 2005b). Most recently, Richter et al. (2011) have studied Ca II absorbers at low redshift and propose that the characteristic radial extent of HVC analogs with log N(HI) ≥ 17.4 in galaxies with z < 0.5 is RHVC ≈ 55 kpc.
Another remarkable property of HVCs is a two-phase structure with a cold, dense core and a warmer, more tenuous envelope, which has already been discussed by Wakker & Schwarz (1991) for clumps in the larger complexes, and this is still supported by more recent observations of smaller cloudlets as in Ben Bekhti et al. (2006). Giovanelli et al. (2010) presented ALFALFA (Arecibo Legacy Fast ALFA) observations of ultra-compact high velocity clouds (UCHVCs) at assumed extragalactic distances. The derived masses of the measures UCHVCs at a distance of 1 Mpc are below 106 M⊙, which explains the nondetection by previous HI surveys, such as Pisano et al. (2007).
2.1.2. Dark matter minihalo and ram pressure stripping
If the CHVCs permeate intergalactic space, their origin allows two possibilities: they are disrupted remnants from galaxy collisions and were formed in the tidal tails, or else they represent the relics of structure formation in a CDM cosmology. The latter possibility would provide the requested link to the postulated DM building blocks of hierarchical galaxy formation which means that this baryonic cloud mass should be harbored by a so-called DM mini-halo. Nichols & Bland-Hawthorn (2009) have investigated the orbit of the Smith Cloud under the consideration that the cloud is confined by a DM halo.
Detailed observations of HVCs show a head-tail structure in the hydrogen column density distribution in both over-densities within the large complexes (Brüns et al. 2000) and single CHVCs, as presented for example by Brüns et al. (2001) and Ben Bekhti et al. (2006). In agreement with theoretical and numerical studies, these structural properties are unambiguously indicative of gas clouds moving through a surrounding plasma. It is expected that, if the force due to ram pressure exceeds the gravitational restoring force that keeps the cloud material via self-gravity together, material is stripped off the cloud (Gunn & Gott 1972). This leads to a head-tail structure of the cloud, which is observed with radio observations of the 21cm line of neutral hydrogen (Brüns et al. 2000; Putman et al. 2002; Westmeier et al. 2005a). Furthermore, the mixing of hot halo and cool cloudy gas might be responsible for the observed ionization stages in the hot halo (Spitzer 1996).
Observationally derived structure parameters allow the conclusion that CHVCs are bound by a DM halo of significant mass (Braun & Burton 2000). While the gravitational potential in the vicinity of the HVC is dominated by the combined gravitational potentials of the cloud itself and the host galaxy, a DM halo around the CHVC enlarges the total mass of the cloud-halo system and therefore also the volume in which the cloud potential exceeds the potential of the major galaxy, so that HVC material is gravitationally stronger bound to the cloud.
Initial parameters of the high-velocity clouds in different simulations.
In addition, whether HVCs represent the baryonic content of cosmological DM sub-halos or not, should become visible during the ram pressure stripping (RPS) action on their passage through the hot halo gas. The gravitational acceleration in the vicinity of the HVC is dominated by the self-gravity of the cloud and the external gravitational potential of its host galaxy. At first, the cloud gas is confined within the equipotential of cloud and galaxy potential. Once the stripped-off material runs over this region, it gains an additional acceleration in comparison to the material that is stripped off but still gravitationally bound to the cloud. This effect is expected to be hardly noticeable if the HVC’s total mass is only determined by its gas mass, because the potential of the massive host galaxy mass would strongly dominate the self-gravity of the cloud. If the cloud is embedded in a DM subhalo, the total mass of the HVC and therefore its self-gravity is much higher and could make this effect visible in velocity–position space as a sharp change in the velocity gradient along the head-tail structure of the cloud, as observations obtrude (Brüns et al. 2000, 2001; Ben Bekhti et al. 2006).
2.2. Numerical simulations
2.2.1. Ram pressure stripping
Quilis & Moore (2001) used hydrodynamical simulations to study the behavior of CHVCs passing through the dilute hot halo gas of a typical disk galaxy at large distances. The main purpose of their numerical models was to compare the emerging head-tail structure with observations, in order to draw conclusions on the necessity of a DM component and on a possible lower density limit for the surrounding intergalactic medium (IGM).
They found head-tail structures in environments with a density higher than 10-4 cm-3. The lifetimes in simulations without a DM halo are very short, only ≈10 Myr, while the tails in their DM-dominated clouds survive for ≈1 Gyr.
Although the authors have simulated a grid of HVC models, it is worth pointing out that there is no comparison of the same cloud with and without DM, as we discuss in this work, but the authors study two different scenarios: HVCs as close-by structures at a distance of 1−10 kpc and masses between 10 and 100 M⊙ vs. very distant DM-dominated clouds at a distance of 300 kpc, a radius of 1 kpc, and a mass of more than 107 M⊙, unlike the typical maximum distance of around 55 kpc (Richter et al. 2011).
A snapshot of the DM-dominated cloud modeled over 300 Myr (Fig. 2 of Quilis & Moore 2001) with a constant velocity of 200 km s-1 travels over a distance of 60 kpc through the galactic halo, i.e. must have faced changes in the ambient densities, a tidal field, and an acceleration by the host galaxy. Owing to the lack of self-gravity, low-mass DM-free gas clouds are disrupted very quickly so that the evolution is only shown after 3 Myr (Quilis & Moore 2001, Fig. 3). The DM-free clouds in the simulation runs presented in this work can easily survive for 100 Myr, not only because of the included self-gravity but also thanks to the much higher masses and distances, in agreement with recent observations.
Heitsch & Putman (2009) have shown with grid-based hydrodynamic simulations that smaller clouds with HI masses <104.5 M⊙ will lose their HI content during their paths of 10 kpc at maximum (for typical relative velocities and halo densities). They propose that the stripped material that is usually gas in the warm and ionized phase can contribute to the extended layer of warm, ionized gas at lower galactic heights (Reynolds 1993; Gaensler et al. 2008) and later on recool and form smaller HI cloudlets, which are classified as low or intermediate velocity clouds (LVC, IVCs).
2.2.2. Heat conduction
Owing to the large temperature gradient between the cloud and the surrounding halo gas, saturated heat conduction should be an important process of energy transport between the gas phases, leading to the classical two-phase structure. Furthermore, heat conduction stabilizes clouds with head-tail structures and extend their lifetimes (Vieser & Hensler 2007b). In addition, Vieser & Hensler (2007a) have shown that in models that combine heating, cooling and saturated heat conduction with self-gravity, condensation of halo gas on the cloud surface can dominate evaporation and lead to a net accretion of ambient gas.
For the warm cosmic rain theory by Heitsch & Putman (2009), this means that the stripped off material is not only warmer and more highly ionized than the cold core of HVCs, but it also would have other significant consequences. On average HVCs contain much smaller element abundances than the Milky Way ISM (see Table 1), which clearly advocates for their primordial origin. HVCs affected by heat conduction and stripping in the presumably metal-rich halo gas are expected to also have a higher metallicity because the stripped cloud surface consists not only of cloud gas but also of accreted halo gas. If part of the LVC and IVCs are the decelerated survivors of disrupted or ablated HVCs they should have a higher metallicity than the less processed HVCs, which is observationally confirmed (Table 1). Since IVCs/LVCs rain down with velocities below escape velocity, an origin in the galactic fountain cannot be ruled out. The cores of HVCs, which survive ram-pressure stripping, can be decelerated by either the drag of the hot halo gas or other processes like the buffering of plane-parallel galactic magnetic field lines that have to couple to the HVC plasma (Zimmer et al. 1997). This effect would contribute to the heating of the halo gas (Jelínek & Hensler 2011).
In a recent study about the origin of the HVCs, Binney et al. (2009) have suggested that they can be formed by thermal instability in the warm-hot Galactic halo medium. For Milky Way sized halos, however, they find that this happens only in regions outside of 100 kpc and for an almost perfectly flat entropy profile, when thermal instabilities are not damped by a combination of buoyancy and thermal conduction. They conclude that it is therefore a rather unlikely formation scenario for HVCs.
2.3. General questions
Since differences in the ram-pressure stripped gas and in the head-tail structure have not yet been explored with respect to their possible origins, we here present numerical models of HVCs with and without a stabilizing DM subhalo based on the following questions. Is it possible for the cloud with DM to keep the gas longer bound as without? Does a DM halo suppress hydrodynamical instabilities? Is a cloud without a DM halo already disrupted and does it lose most of its gas owing to the ram pressure produced by its supersonic motion (up to more than 400 km s-1) through the hot gaseous halo of its host galaxy or in the outskirts of the dilute halo gas? Can we distinguish from the observed velocity–position distribution of the head-tail structure whether the observed cloud contains DM? If they are embedded in a DM halo, are HVCs the low mass extensions of gas rich subhalos with (ultra faint) dwarf galaxies as their higher mass analogs? Moreover, if they are DM-free and a significant fraction of the few observed satellite galaxies have a tidal origin (Bournaud & Duc 2006; Okazaki & Taniguchi 2000), where are all the DM satellites we see in large cosmological simulations?
 |
Fig. 1 Initial density (top panel) and pressure (lower panel) distribution of the model setups described in Table 2. |
 |
Fig. 2 Column density distribution of the gas cloud overlaid with equipotential lines for Setup 2-DD (see Table 2 for its parameters) at a maximum refinement level of 7 (effective spatial resolution: 5 pc): without DM halo (left panels, Run VI) and with DM halo of scale radius r0 = 250 pc (right panels, Run IX). The contour lines of the grayscale Hi column density distribution range between log (NHi) = 18.8...21.2 cm-2 in steps of 0.3 dex. Overlaid are the equipotential lines of the total gravitational potential by the gaseous cloud, the DM subhalo of the cloud (if present), and the external galaxy (see text) in steps of 2.5 × 1011 cm2 g-2. In red, the equipotential line of the innermost Lagrangian point is depicted. Top panels show the initial distributions, bottom panels after a simulation time of 100 Myr. (Step-like contour lines reflect the coarser grid farther away from the cloud.) |
2.4. Paper structure
This paper has the following structuring. First the numerical method and the model setup of both the host galaxy and the HVCs are presented. In Sect. 3.4 we discuss the size of the Roche-lobes in this two-body system and the consequences for the gas that is lost by RPS. The effect of RPS that leads to the observed cometary appearance of the clouds is discussed in Sect. 3.5, while further possible mass-loss procedures are mentioned in Sect. 3.7.
Because HVCs do not necessarily fall directly towards the observer or radially into the center of the Milky Way, we take a close look at the line-of-sight problem in Sect. 4.2. Not only does the column density distribution varies when changing the inclination between object and observer, but the velocity measurements also can only cover the radial velocity. Therefore the whole phase-space distribution of the observed clouds is highly sensitive to line-of-sight effects. For all performed simulations we processed the data in a way that simulates different line-of-sight directions to look for signatures that are dependent on the line of sight. Finally, the dependency of the results on parameters, such the initial velocity (see Sect. 4.3.1) and the DM mass (see Sect. 4.3.2) and shape (Sect. 4.3.3) are discussed.
We have included not only a self-gravitating gas cloud and a static gravitational potential that represents a DM mini-halo, but also an external gravitational potential, which gives us the opportunity to study the equipotential lines of the combined potential of the galaxy and the HVC.
The initial distance between the HVC and the external mass was chosen to be 50 kpc, which leads to cloud masses ranging from 105 to 106 solar masses. Outside of 60 kpc, the HVCs are either fully ionized and therefore not visible in neutral hydrogen or HVCs origin from an interaction scenario like the Magellanic Stream, which would also explain the typical maximum distance of around 50−60 kpc.
3. Models
3.1. Numerical methods
To resolve hydrodynamical instabilities and turbulence in the stripped-off gas, but not to waste computational time and spatial resolution by the dynamics outside of the clouds, an adaptive-mesh algorithm is a proper choice. For all simulations in this project the hydrodynamic code FLASH3.2 developed by Fryxell et al. (2000) is used, which already provides a fast multigrid Poisson solver that is based on Ricker (2008) and adapted for the FLASH grid structure by the Flash Center.
 |
Fig. 3 HVC model with an initial gas mass of Mgas = 4.4 × 105 M⊙ (Setup 2-DD): color-coded pressure distribution (logarithmic scale [dyne cm-2]) through the midplane (z = 0) of the 3D simulation box overlaid with Hi column density contours between log (NHI) = 18.5...21.5 cm-2 in steps of 0.5 dex, 100 Myr after the onset. Upper left panel: cloud without DM (Run VI), upper right panel: cloud embedded in an NFW halo (see Sect. 4.3.3); lower panels: clouds with Burkert halos with r0 = 150 pc (Run VII, left panel) and r0 = 250 pc (Run IX, right panel), respectively. The red contour depicts the (Ekin + Ei) = −Epot boundary and encloses all material, both from the cloud and from the hot halo gas, which is gravitationally bound to the HVC. The velocity vectors indicate a maximum velocity of 215 km s-1 and their lengths are linearly scaled. |
3.2. Initial setup
The initial setup for every run is an isothermal cloud in hydrostatic equilibrium with temperature Tgas, radius Rgas, and mass Mgas embedded in a Burkert (1995) halo with a scale radius of r0 and a mass MDM. The baryon-to-total mass ratio for the cloud is given by Mgas/Mtot and the relative velocity between the cloud, and the ambient medium is given as vw.
The simulation of an object moving towards the center of an external gravitational potential representing the host galaxy is performed in such a way that the rest frame remains at the cloud’s mass center. This leads to a wind-tunnel setup with an increasing wind velocity, because the gravitational attraction of the host galaxy increases as the cloud approaches. Since observations do not show any star formation in HVCs, whether nowadays or at any point in the past, the simulated cloud should not collapse because of self-gravity during the simulation time, but also not expand and dissolve at the simulated heights because we focus on the compact, isolated subclass of the HVCs. Therefore we assume an initial hydrostatic equilibrium:  (1)where Φ(r) is the gravitational potential of the cloud. Since the cloud is spherically symmetric in the beginning, the pressure distribution is:
(1)where Φ(r) is the gravitational potential of the cloud. Since the cloud is spherically symmetric in the beginning, the pressure distribution is:  (2)where ρ(r) is the gas density and M(r) the enclosed mass within the radius r.
(2)where ρ(r) is the gas density and M(r) the enclosed mass within the radius r.
We intend to compare clouds that are embedded in a DM halo to clouds that only consist of baryonic matter. In these two cases the initial pressure, hence density distribution, is different since the enclosed mass contains both dark and baryonic matter. Subsequently, other parameters as the cloud radius and the cloud mass differ between the cases with and without a DM subhalo.
To avoid effects that are of the different initial distributions we set up clouds that are in hydrostatic equilibrium with the gaseous part only (Setups 2 and 3) as well as clouds that are stable under both the baryonic and the DM mass (Setup 2-D, Setup 2-DD, and Setup 3-D) and performed simulations with and without a DM subhalo for each setup (see Table 2 and Fig. 1 for details).
Stability studies without wind are performed to ensure that the timescale of the changes due to the deviation from the hydrostatic equilibrium is negligible, i.e. much larger with respect to the ram-pressure timescale.
The cloud is embedded in a homogeneous medium with a temperature of THIM = 106 K and a density of ρHIM = 4 × 10-4 H cm-3, which represents the hot galactic halo. While observationally determined values for the outer halo of the Milky Way are rare, Quilis & Moore (2001) have shown that head-tail features only appear if the external medium has a density higher than 10-4 cm-3 and a relative velocity of 200 km s-1. The cloud’s pressure is integrated following Eq. (2) down to a radius where the pressure of the cloud equals the pressure of the ambient medium.
Since our study aims at exploiting whether HVCs would represent the extension of DM-dominated baryon assemblies from dwarf galaxies to the lower masses, it seems reasonable to also choose the empirically derived profile by Burkert (1995) as DM density distribution:  (3)with the empirical correlation between ρ0 and r0 of
(3)with the empirical correlation between ρ0 and r0 of  (4)In contrast to the mostly referred to DM profile, the so-called NFW profile (Navarro et al. 1997), which was initially derived from large-scale cosmological simulations, with the characteristic cuspy center (see also Moore et al. 1999; Navarro et al. 2004), the observed rotation curves of dwarf galaxies show nearly solid body rotation, which is preferably fitted with a central core in the DM distribution (e. g. Burkert 1995; de Blok & Bosma 2002; Gentile et al. 2005; de Blok 2005). The resulting DM halos in more recent high-resolution cosmological simulations (Navarro et al. 2010) support central cores that can also be derived from a global DM-radius relation from spirals to dwarf spheroidal galaxies (Walker et al. 2010). For further discussions of this topic see Sect. 4.3.3.
(4)In contrast to the mostly referred to DM profile, the so-called NFW profile (Navarro et al. 1997), which was initially derived from large-scale cosmological simulations, with the characteristic cuspy center (see also Moore et al. 1999; Navarro et al. 2004), the observed rotation curves of dwarf galaxies show nearly solid body rotation, which is preferably fitted with a central core in the DM distribution (e. g. Burkert 1995; de Blok & Bosma 2002; Gentile et al. 2005; de Blok 2005). The resulting DM halos in more recent high-resolution cosmological simulations (Navarro et al. 2010) support central cores that can also be derived from a global DM-radius relation from spirals to dwarf spheroidal galaxies (Walker et al. 2010). For further discussions of this topic see Sect. 4.3.3.
 |
Fig. 4 Projected velocity-space distribution of Setup 3 without a DM halo at a maximum refinement level of 7. Top left panel: contour lines of the column density distribution (in z direction) at log (NHI) = 18.8 ... 21.2 Hcm-2 steps of 0.6 dex 100 Myr after the simulation onset. Both the x- and the y-coordinates correspond to the Cartesian grid of the 3D data cube. Radial velocities measurable along the line-of-sight (dashed line) in different directions of angle α = 0 deg,15 deg, and 30 deg with respect to the x-direction are shown in the 3 frames from bottom left (α = 0deg), through top right (α = 15deg) to bottom right (α = 30deg). Along the abscissa, projected distances perpendicular to the line-of-sight (dotted line) through the mass center (x = 0) are shown. All cells with densities n > 0.01 H cm-3 are included and re-arranged to represent the column density distribution in the observed position-velocity space (leading to the bubbled contour structure). The contour lines of the line-of-sight column densities indicate log (NHI) = 18, 19, 20,and21 H cm-2. The measured maximum velocities differ accordingly from 215 (for α = 0deg) to 188 km s-1 (α = 30deg). |
We decided to run all our simulations up to a given simulation time of 100 Myr, so that we can neglect the change in the ambient pressure, while the effects of the time-dependent external potential are described well in our simulations. The distance of the CHVC on the radial trajectory is in our case between 30 kpc and 50 kpc. We expect that for clouds closer than that, the simplification of a radial infall is not valid anymore, and an eccentric orbit close to the disk would lead to tidal stretching of the clouds as observed in the large complexes closer to the Galactic disk.
To cover a wide range of parameter space, but in a reasonable expense of computational time, and to perceive clear differences between DM-dominated and pure gas clouds, we only use two different scale radii (r0 = 150 pc and r0 = 250 pc) for the DM profile. In combination with a sample of baryonic masses, we obtain setups with very different baryon-to-total mass ratios fb = Mb/Mtot including both very low and very high baryon contents.
The larger DM halo with r0 = 250 pc has a total DM mass that is more than three times higher than that of the smaller DM halo with r0 = 150 pc. Owing to the different scale radii and the core shape of the potential, the ratio of the enclosed mass of the central part does not represent the full mass ratio of the total halos. But within 400 pc, a typical extent of the head-tail structure, the larger halo has already 70% more DM mass enclosed than the smaller one, also leading to a difference in the gradient of the DM potential of 70%. If the simulations were very sensitive to the scale radius of the surrounding DM halo, we would expect a significant difference in the results.
Hoeft et al. (2006) have studied structure formation by means of hydrodynamic simulations for different spatial resolutions and find that low-mass halos below a critical total mass of Mc(z = 0) = 6.5 × 109h-1 M⊙ can be baryon poor with fb as low as 0.01. We cover the full range from baryon poor halos over halos with the universal baryon-to-total mass ratio derived by WMAP3 data (fb ≈ 0.17, Komatsu et al. 2011) to systems with fb as high as 0.39 (Setup 3) to investigate the influence of a DM subhalo in a RPS scenario. The latter fb anticipates that the outermost part of the DM subhalo is already distorted by the Galactic tidal force.
3.3. Parameter variants
For a better comparison between the simulation runs with and without DM content for every mass range runs with different stability setups are performed. One setup represents an initial distribution in hydrostatic equilibrium for a self-gravitating gas cloud (Setups 2 and 3), while another setup is stable in a static run that also includes DM with a mass of 4.93 × 106M⊙ and a scale radius of 150 pc for setups 2-D and 3-D and with a DM mass of 1.63 × 107M⊙ and a scale radius of 250 pc for setup 2-DD (see Table 3). For all these initial distributions, we performed runs with and without a DM halo. This leads to configurations that are not in perfect hydrostatic equilibrium (see Sect. 3.1 for details). In Table 2 a summary of the used parameters can be found.
 |
Fig. 5 As in Fig. 3. The initial gas mass is Mgas = 3.1 × 106M⊙ (Setup 3). Upper panel: DM-free cloud (Run XIV); lower panel: cloud with DM subhalo of r0 = 150 pc (Run XVII). |
3.4. External gravitational potential
Observations of individual CHVCs by Brüns et al. (2001) and Ben Bekhti et al. (2006) show not only a head-tail structure in the column density distribution but also a clear change in the velocity gradient along the elongated density contours. Since the gravitational potential in the vicinity of the HVCs is dominated by its own mass and the external gravitational field of its host galaxy, this system can be considered as a two-body interaction. Therefore the area within the equipotential line through the Lagrangian point 1 (in binary systems called “Roche lobe”) determines the region in which the cloud material is gravitationally bound to the HVC. Ram pressure leads to an elongation of the gas density profile in the wind direction, and as soon as gas has crossed the Roche lobe, it becomes unbound from the HVC and should therefore be exposed to an additional acceleration visible in the immediate change of the velocity gradient. Since the size of the Roche lobe is dependent on the mass of the HVC, the observed position of the velocity gradient change can help distinguish whether HVCs contain a significant fraction of DM or not.
In our simulations the cloud will start at an initial distance of 50 kpc to an external point mass of MGal = 1011 M⊙ which represents the host galaxy. Xue et al. (2008) have derived the Milky Way DM halo mass from the kinematics of blue horizontal branch stars in the galactic halo. They fitted both an unaltered NFW profile and an adiabatically contracted NFW halo and find virial masses between ![\hbox{$M_{\rm vir} = [0.82^{+0.21}_{-0.18}\, ...\, 1.21^{+0.40}_{-0.30}] \times 10^{12} \Msun$}](/articles/aa/full_html/2012/11/aa18767-12/aa18767-12-eq92.png) with virial radii in the range of
with virial radii in the range of ![\hbox{$r_{\rm vir} = [258^{+20}_{-21}\,...\,293^{+31}_{-26}]\,\rm kpc$}](/articles/aa/full_html/2012/11/aa18767-12/aa18767-12-eq93.png) . We compared the gravitational acceleration in the cloud region of the external point mass with MGal = 1011 M⊙ to the NFW profile represented by [Mvir = 0.82 × 1012 M⊙, rvir = 258 kpc, c = 12.2] and found that the relative difference is as small as 1−3%, which is much less than the difference between the models by Xue et al. (2008).
. We compared the gravitational acceleration in the cloud region of the external point mass with MGal = 1011 M⊙ to the NFW profile represented by [Mvir = 0.82 × 1012 M⊙, rvir = 258 kpc, c = 12.2] and found that the relative difference is as small as 1−3%, which is much less than the difference between the models by Xue et al. (2008).
The equipotential lines, together with the column density distribution of the isothermal gas distribution initially as well as after 100 Myr of simulation time, are shown in Fig. 2 for Setup 2-DD with (Run VIII and IX) and without DM (Run V).
In all setups the gaseous parts of the clouds exceed the smallest Lagrangian equipotential surface in at least one direction. In the setups without the additional mass of a DM halo, the L1 surface lies completely within the cloud. The Roche lobes indicated in Fig. 2 become smaller with time, not because of the mass loss, but because the cloud approaches the galaxy mass with an initial velocity of 200 km s-1 and reaches a distance of around 30 kpc after the simulation time of 100 Myr.
Including an external mass in our simulations does not only affect the region where the cloud material is bound to the objects, but also influences the motion of the HVC. Thanks to the gravitation by a host galaxy, the cloud is accelerated towards the external point mass. Benjamin & Danly (1997) have shown that clouds reach a terminal velocity on their way to the galactic disk, where the acceleration due to gravitational force is equal to the drag force caused by the different densities of the hydrostatic layers of the galactic disk. Their model is valid for distances up to 10 kpc, and they did not take the change in the area that is exposed to drag into account. In our setup the cloud travels in galactic heights between 30 kpc (after 100 Myr of simulation time) and 50 kpc (initial distance), where the change of the hot halo gas density is negligible. The stronger gravitational acceleration at smaller distances and, in many cases, the shrinkage of the cloud surface that is exposed to drag due to RPS, together with a constant ambient medium do not lead to a terminal velocity in our models as assumed by Benjamin & Danly (1997).
3.5. Ram-pressure stripping
We calculated the analytical stripping radius Rstrip as the radius where the force due to ram pressure Fram equals the gravitational restoring force Fgrav. For radii larger than Rstrip the gravitational energy of the cloud mass is not strong enough to keep the gas bound so that it is stripped off due to the relative motion of the hot ambient gas. Gunn & Gott (1972) derived Rstrip for the instantaneous RPS of a gaseous disk moving face-on through the intra-cluster medium (ICM). McCarthy et al. (2008) modified the original Gunn & Gott (1972) formulation to determine the stripping radius for spherically symmetric density distributions. Their stripping condition then reads analogously as  (5)where ρamb here is the density of the surrounding halo material, vrel the relative velocity between the cloud and the ambient medium, gmax(R) the maximum restoring acceleration in wind direction, and Σgas(R) the surface density of the gas projected in wind direction. Here R is the distance from the cloud center perpendicular to the direction of the ram pressure. For a schematic diagram see Fig. 3 of McCarthy et al. (2008). To calculate Rstrip, where
(5)where ρamb here is the density of the surrounding halo material, vrel the relative velocity between the cloud and the ambient medium, gmax(R) the maximum restoring acceleration in wind direction, and Σgas(R) the surface density of the gas projected in wind direction. Here R is the distance from the cloud center perpendicular to the direction of the ram pressure. For a schematic diagram see Fig. 3 of McCarthy et al. (2008). To calculate Rstrip, where  (6)at any time, we use the 3D data cube and drill bars out of the cloud in the streaming direction of the halo gas with a cross section of one grid cell at the highest resolution and calculate the righthand side directly from the gravitational potential and the gas density that is already stored in each grid cell. The ram pressure (lefthand side) would be constant for a standard windtunnel setup. In our case ρamb stays constant over the simulation time but the relative velocity is increasing because of the gravitational attraction of the external mass. In our setups the velocity increases by about 6% in 100 Myr leading to an increase in the ram pressure by ≈12.4%. Therefore the whole condition for RPS shown in Eq. (6) is not constant in time because both the velocity vrel, affecting the ram pressure term, as well as the density distribution of the cloud changes, leading to a different column density distribution Σgas(R) and subsequently to a different gravitational restoring force.
(6)at any time, we use the 3D data cube and drill bars out of the cloud in the streaming direction of the halo gas with a cross section of one grid cell at the highest resolution and calculate the righthand side directly from the gravitational potential and the gas density that is already stored in each grid cell. The ram pressure (lefthand side) would be constant for a standard windtunnel setup. In our case ρamb stays constant over the simulation time but the relative velocity is increasing because of the gravitational attraction of the external mass. In our setups the velocity increases by about 6% in 100 Myr leading to an increase in the ram pressure by ≈12.4%. Therefore the whole condition for RPS shown in Eq. (6) is not constant in time because both the velocity vrel, affecting the ram pressure term, as well as the density distribution of the cloud changes, leading to a different column density distribution Σgas(R) and subsequently to a different gravitational restoring force.
3.6. Numerical resolution
In numerical simulations, reliable results should not depend on the spatial resolution but only on the included physics. To make certain that the results are valid for our setup, we checked for convergence in performing the same simulation run for different levels of refinement. We expect differences, as well in the apparent substructure of the cloud, as in the overall dynamical properties for models with low refinement levels, compared to runs with sufficiently small grid sizes. Especially, mass loss procedures as RPS and Kelvin-Helmholtz instabilities are highly sensitive to the physical size of a single cell. In addition the equipotential volume within the cloud, i.e. where the cloud gas is gravitationally bound, gets smaller when the cloud approaches the external center-of-mass and is therefore likely not to be properly resolved in low-resolution runs.
 |
Fig. 6 Comparison of the temporal evolution of cloud radius (full-drawn lines) vs. semi-analytically (Eq. (6)) determined stripping radius (dashed lines) for Setup 3 without a DM halo and for different refinement levels “Ref n” (for details see text). |
In Fig. 6 the evolution of both the cloud radius and the stripping radius is shown for different levels of refinement. For the low-resolution runs with 643 cells (Ref 4) and 1283 cells (Ref 5), the calculated stripping radius suffers from the poorly resolved gravitational potential within the cloud. Therefore the maximum restoring acceleration gmax is underestimated. For higher resolution runs with 2563 cells (Ref 6) and 5123 cells (Ref 7), results converge. Comparing the analytically determined stripping radius to the cloud radius for the same resolution, it is evident that the evolution of the cloud radius follows the changes in the stripping radius. Therefore, dynamical stripping due to ram pressure is the dominant mass loss procedure in the considered scenario.
3.7. Further mass-loss processes
Even though we performed highly refined simulations with a resolution as low as 5 pc, it is not easily possible to take processes into account that are happening on subgrid scale. In this section, we discuss the relative importance of other than the above described mass-loss processes, as namely Kelvin-Helmholtz (KH) instability (Sec. 3.7.1), Rayleigh-Taylor (RT) instability (Sect. 3.7.2), mass loss due to intrinsic velocity dispersion (Sect. 3.7.3), and tidal disruption (Sect. 3.7.4).
3.7.1. Kelvin Helmholtz instability
KH instability (for detailed analysis, see Chandrasekhar 1961) can occur when a velocity shear is present within a continuous fluid or when there is sufficient velocity difference across the interface between two fluids. It can be an important process that leads to high mass loss owing to so-called KH stripping of cloud material. Stability analysis of the KH instability shows a condition for the growth of perturbation in dependence on the wavenumber k = 2π/λ. Perturbations with a wavenumber of k ≤ kmin are damped, while perturbations with k > kmin are enhanced (see Eq. (7)). The critical value kmin can be derived from  (7)
(7)
with αi = ρi/(ρ1 + ρ2) (i = 1, 2), where gz is the gravitational acceleration perpendicular to the relative motion, ρ1 and ρ2 are the densities e.g. of cloud and hot gas at the edge of the cloud, and (v1 − v2) = vrel is the relative velocity between the cloud and the ambient hot gas. For the initial values of setup 2-DD, kmin = 0.59 kpc-1, which corresponds to a wavelength of λmax = 10.8 kpc. Therefore all perturbations with a wavelength shorter than λmax lead to KH instability.
On the other hand, the KH timescale τKH can be estimated as the time after which the whole cloud mass Mgas is removed from the cloud by the continuous mass loss due to KH instability. The mass-loss rate is given by Nulsen (1982) with ṀKH = πr2ρamb × vrel, where r is the cloud radius and ρamb the ambient density of the hot halo gas. The KH timescale is given by  (8)Inserting typical values for our models, the KH timescale is 5.8 Gyr, which is much longer than our simulation time of 100 Myr. Starting at 50 kpc with a typical velocity of 200 km s-1, the cloud reaches the galactic disk after 240 Myr. Therefore, stripping by KH instability does not play a major role in the evolution of HVCs.
(8)Inserting typical values for our models, the KH timescale is 5.8 Gyr, which is much longer than our simulation time of 100 Myr. Starting at 50 kpc with a typical velocity of 200 km s-1, the cloud reaches the galactic disk after 240 Myr. Therefore, stripping by KH instability does not play a major role in the evolution of HVCs.
3.7.2. Rayleigh Taylor instability
For an accelerated cloud with a higher density than the ambient medium the conditions for a RT instability are also fulfilled (Chandrasekhar 1961). Stabilizing mechanisms that can suppress RT instabilities are magnetic fields (Chandrasekhar 1961), heat conduction (Vieser & Hensler 2007b), and self-gravity. Roediger & Hensler (2008) investigated the conditions for RT instabilities in a self-gravitating cloud. They find that without magnetic fields, the expression for whether a RT instability is present at a radius R from the cloud center is equivalent to the expression for RPS. Subsequently, in regions where RT instabilities are suppressed, the cloud is also stable against RPS, while in regions with greater distance to the center, the gravitational restoring force is weaker, which leads to both RPS and the occurrence of RT instabilities.
3.7.3. Velocity dispersion
As shown in Fig. 2 a significant fraction of the cloud mass is located outside the Roche lobe at any time. Therefore, this gas is gravitationally unbound to the cloud and very likely to be lost within a few dynamical timescales τdyn, owing to the thermal pressure. For a temperature of 1000 K (Setup 2, 2-D and 2-DD), the mean thermal velocity of the hydrogen atoms within the cloud is σH = 5 km s-1 and for a temperature of 2000 K (Setup 3 and 3-D) σH = 7 km s-1. The dynamical timescale, determined by τdyn = Dgas/σH, where Dgas = 2Rgas is therefore between ≈50 Myr (Setup 2-D) and ≈105 Myr (Setup 3). This is of course only valid for regions outside the Roche lobe and for a constant temperature and cloud diameter over time, which is not realistic. It still provides a first estimate that the simulation time of 100 Myr is close to the dynamical timescale or twice of it, and therefore this process is dominated by the ram pressure, which is happening on a much shorter timescale.
Unlike all other effects mentioned before, this mass-loss process is not only valid for the gaseous component but also for the DM subhalo that is surrounding the gas cloud. As a typical velocity for the DM minihalo, Burkert (1995) finds v0 = 17.7(r0/kpc)2/3 km s-1, while the virial radius as the extension of the halo is given by Rvir = 3.4 × r0 (Burkert 1995). Subsequently, the dynamical timescale for the DM component is τdyn ≈ 210 Myr for the r0 = 150 pc halo and τdyn ≈ 250 Myr for the r0 = 250 pc halo. This is more than twice the simulation time in both cases, which allows us to use a DM halo that is static with respect to the cloud center and is therefore accelerated, together with the gaseous component in the direction of the external mass.
3.7.4. Tidal disruption
On their journey to the galactic disk of their host galaxy, high velocity clouds would not only be ram pressure stripped but also tidally stretched in the gravitational field of the galaxy. According to Blitz et al. (1999) the already disrupted clouds would correspond to the large HVC complexes with large angular extents and distances of a few kpc. A useful estimate for the cloud’s tidal radius is provided by the Jacobian limit (Binney & Tremaine 1988) rJ: ![\begin{equation} r_{\rm J} = \pm D \left [ \frac{m}{M(3+m/M)}\right ]^{1/3} \end{equation}](/articles/aa/full_html/2012/11/aa18767-12/aa18767-12-eq144.png) (9)where D is the distance between the two mass centers, m the HVC mass, and M the galaxy mass. Initially at a distance of 50 kpc all cloud radii lie well within the Jacobian limit. For Setup 2-DD, for example, the Jacobian limit is 4.5 times more than the cloud radius without a DM subhalo, 10.3 times with a r = 150 pc halo, or 15 times with a r = 250 pc halo. After the simulation time of 100 Myr and even with an assumed extreme mass loss of 50% the Jacobian limit is still between two and seven times more than the initial cloud radius. In addition, also the virial radius of the DM minihalo always remains within the Jacobian limit. Therefore we conclude that tidal disruption does not play any role on radial orbits and at these distances from the galactic center.
(9)where D is the distance between the two mass centers, m the HVC mass, and M the galaxy mass. Initially at a distance of 50 kpc all cloud radii lie well within the Jacobian limit. For Setup 2-DD, for example, the Jacobian limit is 4.5 times more than the cloud radius without a DM subhalo, 10.3 times with a r = 150 pc halo, or 15 times with a r = 250 pc halo. After the simulation time of 100 Myr and even with an assumed extreme mass loss of 50% the Jacobian limit is still between two and seven times more than the initial cloud radius. In addition, also the virial radius of the DM minihalo always remains within the Jacobian limit. Therefore we conclude that tidal disruption does not play any role on radial orbits and at these distances from the galactic center.
4. Results
4.1. Head-tail structure
For all simulation runs without DM, it is possible to reproduce the observed and expected head-tail structure in the density distribution of the cloud. For a better comparison with observations, the 3D density is integrated in z-direction in order to get a 2D column density distribution. Iso-density contours are shown in Fig. 2, as well as in Figs. 3 and 5. Whilethe iso-density contours are distorted in runs without an additional DM potential, even close to the cloud’s mass center, they stay very circular in models in which the cloud is embedded in a DM subhalo. A remarkable difference not only in the head-tail structure between simulations with and without DM can be found in the results of Setup 2-DD (Fig. 3) where the cloud without DM is totally disrupted while there is hardly any difference in the column density distribution between the runs with DM halo. We conclude that while the existence of a DM halo has a large impact on the head-tail structure of the HVCs, it is not very sensitive to the parameters of the DM halo as MDM, r0 and to whether the DM density profile has a core or a cusp in the center (see Sect. 4.3.3).
4.2. Line-of-sight effects
Because the HVC motion is by far not radially towards the observer, but might happen ballistically, we have chosen different line-of-sight angles and integrated the radial velocity components from a virtual observer. To create a plot in the velocity–position space, the velocity is affected by not only the line-of-sight effect but also the spatial coordinate (see. Fig. 4 for further explanations).
We find that different velocity gradients along the head-tail structure of the gas cloud can be easily created only by changing the inclination of the line-of-sight aspect angle. For inclinations of 15 deg and 30 deg, changes in the velocity gradient also appear, as observed in different HVCs. These changes appear in Setup 3 at distances from the cloud center of about 300 pc, which is far outside the Roche lobe. Therefore the “knees” in phase space according to the different velocity gradients are not directly connected to the Roche lobe, which is at a distance of less than 100 pc (Setup 3) after 100 Myr of simulation time.
For comparison between our models and HVCs observations (e.g. by Brüns et al. 2000, 2001; Ben Bekhti et al. 2006), the head-tail structure as a simple horizontal cut through the HVCs is not an appropriate measure for deciding about the existence of a DM subhalo. In the present paper, we limit ourselves to radially infalling HVCs, while we suggest that inclined HVC motions – and most probably with a significant perpendicular velocity component – could lead to the observed knee in the velocity–position distribution.
Since we investigate the location of the HVC in velocity–position phase space, we also check the final model for convergence with runs on higher resolution. The line-of-sight dependent contour plots shown in Fig. 4 are analyzed in more detail for runs with different refinement levels. The mean velocity is calculated in bins of the initial cell size for each refinement and shown for an angle of α = 30deg in Fig. 7 for refinement levels 4, 5, 6, and 7. While the gradient of the velocity in the tail part is very different between refinement runs 4, 5, and 6 the result is nicely converging between refinement 6 and 7.
To compare all simulation runs for their behavior in phase space for different line-of-sight directions and independence on their DM content the plots for Setups 2, 2-D, 3, and 3-D are shown in Figs. A.2–A.5.
 |
Fig. 7 The average line-of-sight velocity under an inclination angle of α = 30deg in each position bin after 100 Myr of simulation time for four different levels of refinement. |
4.3. Parameter study
4.3.1. Effect of the initial wind velocity
While all models mentioned before start with an initial wind velocity of 200 km s-1, i.e. supersonic motion with respect to the ambient medium of Mach 1.7, in this section, we present models of Setup 2-DD without DM halo and with a DM halo of r0 = 250 pc at an initial velocity of 250 km s-1 (Mach 2.1) in order to investigate the effects caused by different relative velocities vrel.
The gas clouds, however, are not directly experiencing the full wind speed due to a quickly forming bow shock that leads to a post-shock region with subsonic velocity. Figure 8 demonstrates that only a small difference in the evolution of the stripping radii exists between the runs with the different velocities.
4.3.2. The dark matter mass
Setup 2-DD represents a cloud that is in hydrostatic equilibrium under its total mass, consisting of the gas (Mgas = 4.4 × 105 M⊙) and a DM minihalo with a scale radius of r0 = 250 pc and a mass of MDM = 1.63 × 107M⊙. Simulations with DM minihalos of r0 = 150 pc and r0 = 250 pc are performed, as well as one model simulation with only a pure gas cloud (see Fig. 3). The maximum refinement level for all three runs is set to 7, leading to an effective resolution of 5 pc. (For further information about Setup 2-DD see Table 2.) While the cloud is disrupted in the run without DM and significantly decelerated after no more than 70 Myr, both clouds with the Burkert DM halo remain almost unaffected by ram pressure with only small mass loss. They do not show significant differences, even though the total DM mass with r0 = 250 pc is more than three times higher than that of the halo with r0 = 150 pc.
The time evolution of the model without a DM subhalo is shown by its column density distribution in Fig. A.1 (Appendix). Until 50 Myr the ram pressure affects only the outer HVC shells, while the main HVC body remains untouched. In this run the central part of the gas cloud is highly compressed by means of the strong drag force and (starting after 60 Myr) the peak density is shifted away from the simulation rest frame, i.e., is decelerated.
Owing to the very high pressure in the head part of the cloud, the gas starts to re-expand (perpendicularly to the cloud’s motion according to the Bernoulli effect) and to form a bow-like structure in front of its mass center (between 70 and 100 Myr). This feature shows a compressed leading edge but low density in the region behind. Its relatively large extent makes it very likely to be disrupted by both Rayleigh-Taylor instability and RPS in a short time.
The highest gas mass fraction in our models is applied to Setup 3, where the DM mass is only 1.6 times higher than the gas mass. Even this light DM halo has a strong impact on the stability of the cloud. While the extent of the HVC perpendicular to the wind direction has decreased remarkably within 100 Myr in the simulation run without DM, the cloud with the surrounding DM halo conserves the initially spherical-symmetric shape much better (see Fig. 5). The mass loss after 100 Myr is for both runs, with and without DM, of a few percent. In Setup 3 without a DM halo, the ratio between bound mass and total mass equals 0.966, which means that the mass loss is twice more than in the simulation run with a DM halo, where the fraction of bound mass is 98.31%. This means that the self-gravity of a gas cloud of 3.1 × 106M⊙ alone is strong enough to keep most of the material bound in the first 100 Myr and cannot be neglected in simulations.
We determined the bound mass by comparing the sum of kinetic and internal energy to the corrected potential energy for every cell within the computational domain. Because we are interested in the binding energy to the cloud or cloud-halo system rather than to the external point mass, the total gravitational potential is reduced by the potential that is produced by the host galaxy. Every cell in which the binding energy dominates contributes to the bound mass.
For Setup 2-DD without a DM halo (Run VI), 95.72% of the initial cloud mass is still bound after 100 Myr. The same setup but embedded in an r0 = 150 pc (Run VII) or r0 = 250 pc (Run IX) halo, reduces the amount of mass loss by a factor of 7−8 and leads to a bound mass of 99.39% (r0 = 150 pc) and 99.49% (r0 = 250 pc) of the initial gas mass after 100 Myr.
 |
Fig. 8 Semi-analytically derived stripping radius for Setup 2-DD with DM minihalos of r0 = 150 pc (full-drawn line, Run VI) and r0 = 250 pc for an initial relative velocity of 200 km s-1 (dashed line, Run IX) and 250 km s-1 (dotted line, Run XI). |
4.3.3. The dark matter density profile
The DM density distribution, especially in low mass system, is still under discussion (e.g. Neto et al. 2007; Retana-Montenegro et al. 2012; Navarro et al. 2010; Amorisco & Evans 2012; Walker & Peñarrubia 2011; Tal et al. 2012; Salvador-Solé et al. 2012). To provide a full sample, we started an additional run with an NFW (Navarro et al. 1997) DM density profile to numerically investigate possible differences in the ram-pressure stripping.
We resimulated Run IX, with an NFW halo that shows a cuspy density profile, unlike the centrally flat Burkert halo. We decided to set up an NFW halo with the same total DM mass as in Run IX (M200 = 1.63 × 107 M⊙) so that we can compare the differences that appear due to the shape of the DM halo. The virial radius of this NFW halo r200 = 5.5 kpc and the circular velocity at r200 is: v200 = 3.57 km s-1. For a full description of the DM density profile, 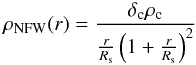 (10)with δc the overdensity relative to the critical density of the universe ρc = 3H2/(8πG) (with H = 65 km s-1 Mpc-1), the concentration parameter c, in addition to the virial mass M200, is needed. This parameter differs significantly from object to object and does not show a clear correlation with the mass of the object. Fitting rotation curves from galaxies from the THINGS survey shows concentration parameter in large varieties (Chemin et al. 2011) and vary between c = [1···30] for dwarf galaxies (van den Bosch & Swaters 2001).
(10)with δc the overdensity relative to the critical density of the universe ρc = 3H2/(8πG) (with H = 65 km s-1 Mpc-1), the concentration parameter c, in addition to the virial mass M200, is needed. This parameter differs significantly from object to object and does not show a clear correlation with the mass of the object. Fitting rotation curves from galaxies from the THINGS survey shows concentration parameter in large varieties (Chemin et al. 2011) and vary between c = [1···30] for dwarf galaxies (van den Bosch & Swaters 2001).
Using a concentration parameter of c = 22, which lies well within the measured range, leads to a scale radius of Rs = r200/c = 0.25 kpc, which is the same as in the comparison halo with a Burkert profile. With the concentration parameter c, the overdensity δc is determined by ![\begin{equation} \delta_{\rm c} = \frac{200}{3} \frac{c^3}{[ln(1+c)- c/(1+c)]} \cdot \end{equation}](/articles/aa/full_html/2012/11/aa18767-12/aa18767-12-eq169.png) (11)The radial distribution of the DM density, as well as the circular velocity of both the Burkert and the NFW halos is shown in Fig. 9.
(11)The radial distribution of the DM density, as well as the circular velocity of both the Burkert and the NFW halos is shown in Fig. 9.
The results (see Fig. 3) demonstrate that the final column density distribution and therefore the existence of a head-tail structure are highly dependent neither on the DM mass (see also Sect. 4.3.2) nor on the shape of the DM potential.
 |
Fig. 9 Comparison of the DM density profile (bottom) and the circular velocity profile (top) for DM halos with a scale radius of 250 pc and a mass of 1.63 × 107 M⊙. The solid line shows the Burkert profile (central core profile), and the dashed line represents an NFW profile with a cusp in the center. |
5. Conclusions
In summary, the following major conclusions can be drawn from the series of model runs we have presented. While it is possible to reproduce the observed change in the velocity gradient, this feature is not directly connected to the Roche lobe and therefore the position of the observed “knee” in velocity–position phase space cannot help distinguish between DM dominated and pure gas clouds. For a variety of initial distributions, we can create these phase-space distributions by changing the inclination of the line-of-sight. In a further study, clouds with a significant azimuthal motion must be tested with respect to their velocity gradient of the stripped gas, for which we expect a more significantly observable velocity “knee”.
We simulated DM-embedded clouds with baryonic-to-total mass ratios between 0.03 and 0.39 and found that the results only marginally depend on the DM mass and profile and that already a DM halo with a mass of 1.6 times the baryonic mass stabilizes the gas cloud against ram-pressure disruption.
After 100 Myr the column-density distributions of the clouds with DM halo can be distinguished from pure gas clouds. While the isodensity lines of the core of gas clouds without an additional DM gravitational potential are losing their initial shape after half the simulation time and show a lot of substructures, HVCs remain spherical and centrally concentrated for all DM-dominated models, even if the DM content is low as in Setup 3. Furthermore, an extended head-tail structure at galactic heights between 30 and 50 kpc can only be reproduced for DM-free clouds.
In our simulations, clouds with DM – with baryonic masses ranging from a few times 105 to a few times 106 M⊙ – approach the galactic disk like bullets with high velocities, while DM-free clouds are already decelerated and distorted at higher galactic heights. Observed HVCs with distances up to 30 kpc, like e.g. Complexes C and H, reveal a very heterogeneous multiphase internal gas structure without any central concentration, which we only obtain in simulations without DM.
Furthermore, because there are no HVCs observed very close to the Milky Way disk (only LVCs exist) and because high-speed infalling Hi gas is not observed in galaxies with extended Hi envelopes, as in NGC 2403 (Fraternali et al. 2002), we conclude that HVCs are decelerated to LVCs or disrupted on their infall into galactic halos, unlike the simulated “bullets” of clouds that have an accompanying DM minihalo.
Our DM-free models can explain both the proximity of the large HVC complexes to the galactic disk even though they start their journey from a height of 50 kpc above the plane, and their morphologies, such as from elongated shapes for more massive clouds to head-tail structures and the inherent amount of substructures.
Our conclusions contain the following further serious consequences for the cosmological model and for our understanding of cosmological structure formation.
-
1.
Since HVCs are DM-free, they cannot be the cosmologicalsmall-scale relics expected from the ΛCDM structure.
-
2.
Since HVCs have typical distances to the disk of their host galaxy of not more than 50 - 60 kpc and do not populate the intergalactic space frequently enough, it is obtruding that, if they are DM-free, they develop out of stripped-off gas of satellite galaxies or in condensations of diffuse intergalactic medium due to thermal instability rather than in an cosmological background.
Online material
 |
Fig. A.1 Setup 2-DD. Time evolution of the column density and the equipotential distribution. Contours as in Fig 2. From top to bottom, on the lefthand side the panels show snapshots at 0, 20, 30, 40, and 50 Myr and on the righthand at 60, 70, 80, 90, and 100 Myr after the simulation onset. |
 |
Fig. A.2 Setup 2 with (red contour lines) and without a DM halo (black contour lines) at a maximum refinement level of 6. In the top left panel the contour lines represent the column density distribution log (NHI) = 18.8 ... 21.2 Hcm-2 in 0.6 dex after 100 Myr of simulation time. For the line-of-sight plots in the panels on the right side and the panel at the bottom left, contour lines are at log (NHI) = 18, 19, 20,and21 H cm-2. The angle α determines the inclination of the line of sight, for details see caption of Fig. 4. |
Acknowledgments
The authors acknowledge support with FLASH by Elke Rödiger and Nigel Mitchell and helpful discussions with Bastian Arnold and Simone Recchi. The software used in this work was in part developed by the DOE-supported ASC / Alliance Center for Astrophysical Thermonuclear Flashes at the University of Chicago. Part of this study was funded by the project no. HE1487/36 (S.P.) within the DFG Priority Program “Witnesses of Cosmic History: Formation and evolution of galaxies, their central black holes, and their environment”. The numerical simulations are performed at the HPC astro-cluster of the Institute of Astronomy and at the Vienna Scientific Cluster (VSC1) under project no. 70128. The publication is supported by the Austrian Science Fund (FWF). The authors gratefully acknowledge helpful comments by the referee that led to further clarifications.
References
- Amorisco, N. C., & Evans, N. W. 2012, MNRAS, 419, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Ben Bekhti, N., Brüns, C., Kerp, J., & Westmeier, T. 2006, A&A, 457, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benjamin, R. A., & Danly, L. 1997, ApJ, 481, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1988, Galactic Dynamics (Princeton Series in Astrophysics) [Google Scholar]
- Binney, J., Nipoti, C., & Fraternali, F. 2009, MNRAS, 397, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., Veilleux, S., Cecil, G. N., et al. 1998, MNRAS, 299, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., Spergel, D. N., Teuben, P. J., Hartmann, D., & Burton, W. B. 1999, ApJ, 514, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., & Duc, P.-A. 2006, A&A, 456, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braun, R., & Burton, W. B. 1999, A&A, 341, 437 [NASA ADS] [Google Scholar]
- Braun, R., & Burton, W. B. 2000, A&A, 354, 853 [NASA ADS] [Google Scholar]
- Bregman, J. N. 1980, ApJ, 236, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Brüns, C., Kerp, J., Kalberla, P. M. W., & Mebold, U. 2000, A&A, 357, 120 [NASA ADS] [Google Scholar]
- Brüns, C., Kerp, J., & Pagels, A. 2001, A&A, 370, L26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burkert, A. 1995, ApJ, 447, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and hydromagnetic stability (Oxford: Clarendon) [Google Scholar]
- Chemin, L., de Blok, W. J. G., & Mamon, G. A. 2011, AJ, 142, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, J. A., Shull, J. M., & Giroux, M. L. 2007, ApJ, 657, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Connors, T. W., Kawata, D., Bailin, J., Tumlinson, J., & Gibson, B. K. 2006, ApJ, 646, L53 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G. 2005, ApJ, 634, 227 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., & Bosma, A. 2002, A&A, 385, 816 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Heij, V., Braun, R., & Burton, W. B. 2002a, A&A, 392, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Heij, V., Braun, R., & Burton, W. B. 2002b, A&A, 391, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraternali, F., van Moorsel, G., Sancisi, R., & Oosterloo, T. 2002, AJ, 123, 3124 [NASA ADS] [CrossRef] [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Madsen, G. J., Chatterjee, S., & Mao, S. A. 2008, PASA, 25, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Gardiner, L. T., & Noguchi, M. 1996, MNRAS, 278, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Burkert, A., Salucci, P., Klein, U., & Walter, F. 2005, ApJ, 634, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Kent, B. R., & Adams, E. A. K. 2010, ApJ, 708, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Gott, J. R. I. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., & Putman, M. E. 2009, ApJ, 698, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, M., Yepes, G., Gottlöber, S., & Springel, V. 2006, MNRAS, 371, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Jelínek, P., & Hensler, G. 2011, Comput. Phys. Comm., 182, 1784 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J. 2003, ApJ, 591, L33 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Frenk, C. S., Font, A. S., et al. 2008, MNRAS, 383, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
- Muller, C. A. 1963, Nature, 200, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. M., Lockman, F. J., & Savage, B. D. 1995, ApJ, 447, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Hayashi, E., Power, C., et al. 2004, MNRAS, 349, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Ludlow, A., Springel, V., et al. 2010, MNRAS, 402, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Neto, A. F., Gao, L., Bett, P., et al. 2007, MNRAS, 381, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Nichols, M., & Bland-Hawthorn, J. 2009, ApJ, 707, 1642 [NASA ADS] [CrossRef] [Google Scholar]
- Nulsen, P. E. J. 1982, MNRAS, 198, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Okazaki, T., & Taniguchi, Y. 2000, ApJ, 543, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Pisano, D. J., Barnes, D. G., Gibson, B. K., et al. 2007, ApJ, 662, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Putman, M. E., de Heij, V., Staveley-Smith, L., et al. 2002, AJ, 123, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Putman, M. E., Thom, C., Gibson, B. K., & Staveley-Smith, L. 2004, ApJ, 603, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Quilis, V., & Moore, B. 2001, ApJ, 555, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Retana-Montenegro, E., van Hese, E., Gentile, G., Baes, M., & Frutos-Alfaro, F. 2012, A&A, 540, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, R. J. 1993, in Back to the Galaxy, eds. S. S. Holt, & F. Verter, AIP Conf. Ser., 278, 156 [Google Scholar]
- Richter, P., Krause, F., Fechner, C., Charlton, J. C., & Murphy, M. T. 2011, A&A, 528, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, P. M. 2008, ApJS, 176, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Roediger, E., & Hensler, G. 2008, A&A, 483, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvador-Solé, E., Viñas, J., Manrique, A., & Serra, S. 2012, MNRAS, 423, 2190 [NASA ADS] [CrossRef] [Google Scholar]
- Sembach, K. R., Gibson, B. K., Fenner, Y., & Putman, M. E. 2002, ApJ, 572, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, P. R., & Field, G. B. 1976, ApJ, 205, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D., Blitz, L., Cole, A. A., Weinberg, M. D., & Cohen, M. 2006, ApJ, 640, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, Jr., L. 1956, ApJ, 124, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, Jr., L. 1996, ApJ, 458, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Tal, T., Wake, D. A., & van Dokkum, P. G. 2012, ApJ, 751, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Braun, R., Walterbos, R. A. M., et al. 2004, ApJ, 601, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Thom, C., Putman, M. E., Gibson, B. K., et al. 2006, ApJ, 638, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Thom, C., Peek, J. E. G., Putman, M. E., et al. 2008, ApJ, 684, 364 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, F. C., & Swaters, R. A. 2001, MNRAS, 325, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Vieser, W., & Hensler, G. 2007a, A&A, 475, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieser, W., & Hensler, G. 2007b, A&A, 472, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakker, B. P. 2001, ApJS, 136, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P., & Schwarz, U. J. 1991, A&A, 250, 484 [NASA ADS] [Google Scholar]
- Wakker, B. P., York, D. G., Wilhelm, R., et al. 2008, ApJ, 672, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., & Peñarrubia, J. 2011, ApJ, 742, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., McGaugh, S. S., Mateo, M., Olszewski, E. W., & Kuzio de Naray, R. 2010, ApJ, 717, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Westmeier, T., Brüns, C., & Kerp, J. 2005a, in Extra-Planar Gas, ed. R. Braun, ASP Conf. Ser., 331, 105 [NASA ADS] [Google Scholar]
- Westmeier, T., Brüns, C., & Kerp, J. 2005b, A&A, 432, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xue, X. X., Rix, H. W., Zhao, G., et al. 2008, ApJ, 684, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Zimmer, F., Lesch, H., & Birk, G. T. 1997, A&A, 320, 746 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Initial density (top panel) and pressure (lower panel) distribution of the model setups described in Table 2. |
| In the text | |
 |
Fig. 2 Column density distribution of the gas cloud overlaid with equipotential lines for Setup 2-DD (see Table 2 for its parameters) at a maximum refinement level of 7 (effective spatial resolution: 5 pc): without DM halo (left panels, Run VI) and with DM halo of scale radius r0 = 250 pc (right panels, Run IX). The contour lines of the grayscale Hi column density distribution range between log (NHi) = 18.8...21.2 cm-2 in steps of 0.3 dex. Overlaid are the equipotential lines of the total gravitational potential by the gaseous cloud, the DM subhalo of the cloud (if present), and the external galaxy (see text) in steps of 2.5 × 1011 cm2 g-2. In red, the equipotential line of the innermost Lagrangian point is depicted. Top panels show the initial distributions, bottom panels after a simulation time of 100 Myr. (Step-like contour lines reflect the coarser grid farther away from the cloud.) |
| In the text | |
 |
Fig. 3 HVC model with an initial gas mass of Mgas = 4.4 × 105 M⊙ (Setup 2-DD): color-coded pressure distribution (logarithmic scale [dyne cm-2]) through the midplane (z = 0) of the 3D simulation box overlaid with Hi column density contours between log (NHI) = 18.5...21.5 cm-2 in steps of 0.5 dex, 100 Myr after the onset. Upper left panel: cloud without DM (Run VI), upper right panel: cloud embedded in an NFW halo (see Sect. 4.3.3); lower panels: clouds with Burkert halos with r0 = 150 pc (Run VII, left panel) and r0 = 250 pc (Run IX, right panel), respectively. The red contour depicts the (Ekin + Ei) = −Epot boundary and encloses all material, both from the cloud and from the hot halo gas, which is gravitationally bound to the HVC. The velocity vectors indicate a maximum velocity of 215 km s-1 and their lengths are linearly scaled. |
| In the text | |
 |
Fig. 4 Projected velocity-space distribution of Setup 3 without a DM halo at a maximum refinement level of 7. Top left panel: contour lines of the column density distribution (in z direction) at log (NHI) = 18.8 ... 21.2 Hcm-2 steps of 0.6 dex 100 Myr after the simulation onset. Both the x- and the y-coordinates correspond to the Cartesian grid of the 3D data cube. Radial velocities measurable along the line-of-sight (dashed line) in different directions of angle α = 0 deg,15 deg, and 30 deg with respect to the x-direction are shown in the 3 frames from bottom left (α = 0deg), through top right (α = 15deg) to bottom right (α = 30deg). Along the abscissa, projected distances perpendicular to the line-of-sight (dotted line) through the mass center (x = 0) are shown. All cells with densities n > 0.01 H cm-3 are included and re-arranged to represent the column density distribution in the observed position-velocity space (leading to the bubbled contour structure). The contour lines of the line-of-sight column densities indicate log (NHI) = 18, 19, 20,and21 H cm-2. The measured maximum velocities differ accordingly from 215 (for α = 0deg) to 188 km s-1 (α = 30deg). |
| In the text | |
 |
Fig. 5 As in Fig. 3. The initial gas mass is Mgas = 3.1 × 106M⊙ (Setup 3). Upper panel: DM-free cloud (Run XIV); lower panel: cloud with DM subhalo of r0 = 150 pc (Run XVII). |
| In the text | |
 |
Fig. 6 Comparison of the temporal evolution of cloud radius (full-drawn lines) vs. semi-analytically (Eq. (6)) determined stripping radius (dashed lines) for Setup 3 without a DM halo and for different refinement levels “Ref n” (for details see text). |
| In the text | |
 |
Fig. 7 The average line-of-sight velocity under an inclination angle of α = 30deg in each position bin after 100 Myr of simulation time for four different levels of refinement. |
| In the text | |
 |
Fig. 8 Semi-analytically derived stripping radius for Setup 2-DD with DM minihalos of r0 = 150 pc (full-drawn line, Run VI) and r0 = 250 pc for an initial relative velocity of 200 km s-1 (dashed line, Run IX) and 250 km s-1 (dotted line, Run XI). |
| In the text | |
 |
Fig. 9 Comparison of the DM density profile (bottom) and the circular velocity profile (top) for DM halos with a scale radius of 250 pc and a mass of 1.63 × 107 M⊙. The solid line shows the Burkert profile (central core profile), and the dashed line represents an NFW profile with a cusp in the center. |
| In the text | |
 |
Fig. A.1 Setup 2-DD. Time evolution of the column density and the equipotential distribution. Contours as in Fig 2. From top to bottom, on the lefthand side the panels show snapshots at 0, 20, 30, 40, and 50 Myr and on the righthand at 60, 70, 80, 90, and 100 Myr after the simulation onset. |
| In the text | |
 |
Fig. A.2 Setup 2 with (red contour lines) and without a DM halo (black contour lines) at a maximum refinement level of 6. In the top left panel the contour lines represent the column density distribution log (NHI) = 18.8 ... 21.2 Hcm-2 in 0.6 dex after 100 Myr of simulation time. For the line-of-sight plots in the panels on the right side and the panel at the bottom left, contour lines are at log (NHI) = 18, 19, 20,and21 H cm-2. The angle α determines the inclination of the line of sight, for details see caption of Fig. 4. |
| In the text | |
 |
Fig. A.3 As in Fig. A.2 but for Setup 2-D. |
| In the text | |
 |
Fig. A.4 As in Fig. A.2 but for Setup 3. |
| In the text | |
 |
Fig. A.5 As in Fig. A.2 but for Setup 3-D. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


