| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219580 | |
| Published online | 18 October 2012 | |
The reawakening of the sleeping X-ray pulsar XTE J1946+274
1
Dr. Karl Remeis-Observatory & ECAP, Universität Erlangen
Nürnberg, Sternwartstr.
7, 96049
Bamberg,
Germany
e-mail: Sebastian.Mueller@sternwarte.uni-erlangen.de
2
CEA Saclay, DSM/IRFU/SAp-UMR AIM (7158) CNRS/CEA/Université Paris
7, Diderot,
91191
Gif-sur-Yvette,
France
3
CRESST and NASA Goddard Space Flight Center, Greenbelt, MD 20771,
USA and Center for Space Science and Technology, UMBC, Baltimore, MD
21250,
USA
4
Department of Physics, Florida International
University, Miami,
FL
33199,
USA
5
ISDC Data Center for Astrophysics, University of
Geneva, 16 chemin
d’Écogia, 1290
Versoix,
Switzerland
6
Center for Astronomy and Space Sciences, University of
California, San
Diego, La Jolla,
CA
92093,
USA
7
Institut für Astronomie und Astrophysik, Universität
Tübingen, Sand 1,
72076
Tübingen,
Germany
Received: 11 May 2012
Accepted: 29 August 2012
We report on a series of outbursts of the high-mass X-ray binary XTE J1946+274 in 2010/2011 observed with INTEGRAL, RXTE, and Swift. We discuss possible mechanisms resulting in the extraordinary outburst behavior of this source. The X-ray spectra can be described by standard phenomenological models, enhanced by an absorption feature of unknown origin at about 10 keV and a narrow iron Kα fluorescence line at 6.4 keV, which are variable in flux and pulse phase. We find possible evidence for a cyclotron resonance scattering feature at about 25 keV at the 93% level. The presence of a strong cyclotron line at 35 keV seen in data from the source’s 1998 outburst that was confirmed by a reanalysis of these data can be excluded. This result indicates that the cyclotron line feature in XTE J1946+274 is variable between individual outbursts.
Key words: X-rays: binaries / accretion, accretion disks
© ESO, 2012
1. Introduction
Owing to the ~1012 G strong magnetic field at the magnetic poles of many accreting neutron stars in high-mass X-ray binaries, cyclotron resonance scattering features (CRSFs or cyclotron lines) are observable in the X-ray spectra of these sources. These lines originate from photons generated in the accretion column of a magnetized neutron star that interact with electrons in the column, since their motion perpendicular to the B-field is quantized into Landau-levels with energy differences 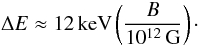 (1)To date, CRSFs have been reported for about 20 X-ray pulsars (Caballero & Wilms 2011).
(1)To date, CRSFs have been reported for about 20 X-ray pulsars (Caballero & Wilms 2011).
The 15.8 s pulsar XTE J1946+274 was first detected in 1998 (Smith & Takeshima 1998; Wilson et al. 1998). It is a transient X-ray source with a Be-type companion (Verrecchia et al. 2002). This type of main-sequence B stars shows Balmer emission lines caused by a quasi-Keplerian equatorial disk near the Be star (see, e.g., Hanuschik 1996; Slettebak 1988). Interaction between this disk and the orbiting neutron star can lead to violent X-ray outbursts that in turn result in the appearance of bright X-ray sources in the sky.
The initial outburst of XTE J1946+274 in 1998 lasted for about three months. Heindl et al. (2001) reported on the discovery of a CRSF at an energy near 35 keV during this outburst, which was followed by several fainter outbursts separated by ~80 d (Campana et al. 1999). This separation was later established by Wilson et al. (2003) as half of the ~170 d orbital period. The occurrence of two outbursts per orbit could be related to the misalignment of the Be star’s angular momentum and the orbital plane of the neutron star. While we look nearly onto the pole of the Be star, the orbital inclination is ≳46° (Wilson et al. 2003).
After a phase of nearly periodic flaring between 1998 and 2001, XTE J1946+274 went into quiescence until 2010 June, when a new sequence of outbursts started (see, e.g., Müller et al. 2010). The principal outburst behavior in 2010 was the same as that observed in the 1990s, with two outbursts per orbit. As shown in Fig. 1, however, the five outbursts seen during 2010 are neither clearly connected to the times of periastron and apastron passages (based on the orbital ephemeris from Wilson et al. 2003), nor to any other specific orbital phase. This new outburst episode ended in 2011 June and the source was back in quiescence at the time of writing.
In this paper, we report on INTEGRAL, Swift, and RXTE observations of the first and the third outburst of this series in 2010 June/July and 2010 November/December, respectively. In Sect. 2 we give a summary of the observations. In Sect. 3 we describe the continuum model and study the time and pulse-phase-resolved behavior of the spectra. Summary and conclusions are given in Sect. 4.
 |
Fig. 1 15–50 keV Swift/BAT light curve of the 2010/2011 outburst series. The times of periastron and apastron passages are marked by P and A, respectively. These epochs and the corresponding uncertainties were calculated using the orbital solution from Wilson et al. (2003). The insets provide a closer view on the first (Jun./Jul.) and the third (Nov./Dec.) outburst. The blue, red, and green arrows in these insets indicate the observations times for PCA, ISGRI, and XRT, respectively. Epochs over which data were summed for the time resolved spectral analysis are indicated with I to VI. |
2. Observations and data reduction
Summary of observations.
The 2010/2011 outburst series started on 2010 June 4, when Swift/BAT detected an increase of the X-ray flux of XTE J1946+274, rising to 40 mCrab (15–50 keV) within three days (Krimm et al. 2010). This first outburst lasted about 60 d and reached a flux of ~140 mCrab (see Fig. 1). The subsequent four outbursts lasted between 30 and 50 d each, reaching almost the same maximum flux level between 40 and 60 mCrab. The separation of the outbursts is between 60 and 90 d. A peculiar behavior was observed during the third outburst where the primary maximum was followed by another brightening, reaching again luminosities of up to ~50 mCrab (Fig. 1, inset).
We present data from the Proportional Counter Array (PCA, Jahoda et al. 2006) onboard the Rossi X-ray Timing Explorer (RXTE, Bradt et al. 1993), the INTEGRAL Soft Gamma-Ray Imager (ISGRI, Lebrun et al. 2003) onboard the INTErnational Gamma-Ray Astrophysics Laboratory (INTEGRAL, Winkler et al. 2003), and the X-ray Telescope (XRT, Burrows et al. 2005) onboard the Swift Gamma-Ray Burst Explorer (Gehrels 2004). Data were reduced with the standard analysis pipelines, based on heasoft (v. 6.10 and 6.11) and INTEGRAL OSA v. 9.0. XTE J1946+274 was monitored by RXTE regularly during the first and the third outburst. The source was also sporadically in the field of view of INTEGRAL during the first and the third outburst. Swift pointings were available only during the main and secondary peak of the third outburst. Table 1 contains a log of the observations with these satellites, which are also indicated in Fig. 1.
Results of the time resolved spectral analysis.
The PCA consisted of five proportional counter units (PCUs) with a field of view of ~1°, sensitive between 2 and 90 keV. Since PCU2 is known to be the best-calibrated one (Jahoda et al. 2006), only data from the top layer of this PCU were used. We obtained 2–60 keV light curves with 0.125 s resolution, spectra in the standard2f mode, and pulse-phase-resolved spectra using GoodXenon data. The light curves were corrected to the barycenter of the solar system using faxbary1. The PCA background model SkyVLE was used for PCA background subtraction. Due to large uncertainties in the orbital parameters (Wilson et al. 2003) no correction could be performed for the neutron star’s orbital motion. The lack of sufficient statistics prevented us from improving the existing orbital solution. Data from the High Energy X-ray Timing Experiment (HEXTE, Rothschild et al. 1998) onboard RXTE were excluded from our analysis since both HEXTE clusters were not rocking at the time of the observations. The resulting uncertainties in the background determination are too large for the purposes of this paper.
The CdTe detector of INTEGRAL/ISGRI covers the energy range from ~18 keV to 1 MeV (Lebrun et al. 2003). Thanks to the large field of view of INTEGRAL, XTE J1946+274 was detected several times during its recent outbursts between 2010 June and 2011 April in observations pointed at Cyg X-1. We extracted ISGRI pulse-phase-averaged spectra for all observations of XTE J1946+274 using the standard spectral extraction method of OSA 9 described in the INTEGRAL documentation2. We selected those observations of XTE J1946+274 for which it was less than 12° off-axis.
To cover the soft X-ray band we used data from Swift/XRT, a 600 × 600 pixel CCD covering a field of view of 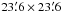 in the energy range 0.2–10 keV. We extracted the data in windowed timing mode. For the source region we chose a circle around the source with a radius of ~1′. The background was extracted using circles of the same radius at two off-source positions about
in the energy range 0.2–10 keV. We extracted the data in windowed timing mode. For the source region we chose a circle around the source with a radius of ~1′. The background was extracted using circles of the same radius at two off-source positions about 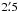 away from the source.
away from the source.
In the spectral analysis, we used data between 1.5 keV and 7.0 keV for XRT. We binned the XRT and PCA data to a signal-to-noise ratio (S/N) of ten. Due to calibration problems of the PCA at the Xe L-edge, we excluded PCA data below 4.5 keV from our analysis. Discarding bins with S/N < 10 results in an upper energy limit of typically 40 keV for the PCA. ISGRI covers the high-energy band between 20 keV and 100 keV. We added a systematic error in quadrature to the PCA and the ISGRI spectra using canonical values of 0.5% and 2.0%, respectively (see Jahoda et al. 2006, and the IBIS analysis user manual).
3. Spectral analysis
We performed all fits using the Interactive Spectral Interpretation System (ISIS, Houck & Denicola 2000). To improve the S/N of individual spectra, we averaged the data over six data blocks in time, taking into account the flux level and instrument availability. These epochs I–VI are defined in Table 2 and shown in Fig. 1. The spectra in epochs I and II cover the first outburst at the maximum and fading phase, respectively. Epochs III–V follow the maximum and the fading phase of the third outburst. The flux in the maximum level of this outburst (epoch III) is comparable to the fading phase of the first outburst (epoch II). The last set of observations is summarized in epoch VI. These XRT data cover the fading phase of the flare immediately after the third outburst. Before defining these epochs we confirmed that the spectral variability during these epochs is negligible.
3.1. Spectral model
As shown, e.g., by Becker & Wolff (2007), the X-ray spectra of accretion-powered X-ray pulsars can be roughly described by a powerlaw with a high-energy cutoff. In practical data modeling, this continuum has been approximated by several different continuum models (see, e.g., Kreykenbohm et al. 2002, for a summary). Here we describe the data using the so-called Fermi-Dirac cutoff (FDCO, Tanaka 1986), given by ![\begin{equation} \mathrm{FDCO}(E)\propto E^{-\Gamma}\times\left[1+\exp\left(\frac {E-E_{\mathrm{cut}}}{E_{\mathrm{fold}}}\right)\right]^{-1}, \end{equation}](/articles/aa/full_html/2012/10/aa19580-12/aa19580-12-eq128.png) (2)which has been successfully applied to other accreting X-ray pulsars such as Vela X-1 (Kreykenbohm et al. 2008). This continuum is modified by the CRSF, modeled as a line with a Gaussian optical depth profile
(2)which has been successfully applied to other accreting X-ray pulsars such as Vela X-1 (Kreykenbohm et al. 2008). This continuum is modified by the CRSF, modeled as a line with a Gaussian optical depth profile ![\begin{equation} \label{gauabs} \exp(-\tau(E)),\ \mathrm{with} \ \tau(E)=\tau_\mathrm{CRSF}\times\exp\left[-\frac{1}{2}\left(\frac{E-E_\mathrm{CRSF}}{\sigma_\mathrm{CRSF}}\right)^2\right]\cdot \end{equation}](/articles/aa/full_html/2012/10/aa19580-12/aa19580-12-eq129.png) (3)The equivalent width of this feature will be denoted with WCRSF in the following. The spectra of some X-ray pulsars, including XTE J1946+274, also contain an absorption- or emission-like feature in the range 8–12 keV (Coburn 2001). The origin of this so-called 10 keV feature is still unclear; however, since it appears always at about the same energy, it is probably not related to the magnetic field strength of the neutron star. We modeled this feature as a broad Gaussian absorption feature, which we also did for the CRSF (Eq. (3)) with the centroid energy, EG, the width, σG, optical depth, τG, and equivalent width, WG. Finally, interstellar absorption was modeled with an updated version of TBabs3, using abundances by Wilms et al. (2000) and cross sections by Verner & Yakovlev (1995).
(3)The equivalent width of this feature will be denoted with WCRSF in the following. The spectra of some X-ray pulsars, including XTE J1946+274, also contain an absorption- or emission-like feature in the range 8–12 keV (Coburn 2001). The origin of this so-called 10 keV feature is still unclear; however, since it appears always at about the same energy, it is probably not related to the magnetic field strength of the neutron star. We modeled this feature as a broad Gaussian absorption feature, which we also did for the CRSF (Eq. (3)) with the centroid energy, EG, the width, σG, optical depth, τG, and equivalent width, WG. Finally, interstellar absorption was modeled with an updated version of TBabs3, using abundances by Wilms et al. (2000) and cross sections by Verner & Yakovlev (1995).
In modeling the data, we took into account that the cross-normalization of the different instruments used is not entirely known and the source might also slightly change in flux between the different observations. These effects were taken into account by cross calibration constants cXRT and cISGRI, using the PCA as the reference instrument. Furthermore, the PCA background was allowed to vary slightly in count rate. To account for these imperfections in modeling the background, we introduced the constant cb.
Finally, the data modeling was affected by the proximity of the source to the plane of the Galaxy. Galactic ridge emission (GRE, see, e.g., Worrall et al. 1982; Warwick et al. 1985) manifests itself through an emission feature at ~6–7 keV in the PCA spectrum caused by unresolved Fe Kα fluorescence lines. These lines are not present in the XRT data in epochs III and IV and therefore must be caused by diffuse emission that is picked up by the PCA only, owing to its larger field of view. In our modeling of the PCA data we therefore introduced a model for the Galactic ridge emission based on that of Ebisawa et al. (2007), who described the ridge emission as the sum of two bremsstrahlung components and an iron line complex modeled by three Gaussian lines at 6.4 keV, 6.67 keV, and 7.0 keV, with equivalent width ratios of 85:458:129, respectively. Since we used the PCA data down to 4.5 keV only, we did not account for the two soft bremsstrahlung components and modeled the Galactic ridge emission as the sum of three narrow Gaussians, with fixed energies and equivalent-width ratios according to Ebisawa et al. (2007). This component was applied only to the PCA data and absorbed by the interstellar medium using the Galactic NH as determined from the Leiden/Argentine/Bonn (LAB) Survey of Galactic H i, NH = 9.4 × 1021 cm-2 (Kalberla et al. 2005). We determined the flux of the Galactic ridge emission from simultaneous fits to the XRT and PCA data from epochs III and IV. In epoch IV, residuals around 6–7 keV are only visible in the PCA, while in XRT neither residuals from this emission, nor from a source-intrinsic iron Kα line are detected. Thus, the residuals in the epoch IV PCA spectrum must be caused by Galactic ridge emission. In epoch III, on the other hand, we find weak evidence for the presence of a source intrinsic iron Kα line in the XRT spectrum. The unabsorbed flux of the 6.4 keV iron line of the Galactic ridge emission in both spectra is consistent with each other ((7.2 ± 2.0) × 10-5 photons s-1 cm-2, and (6.6 ± 2.0) × 10-5 photons s-1 cm-2 for epoch III and IV, respectively). While these values are slightly higher than the 1.22 × 10-5 photons s-1 cm-2 reported by Ebisawa et al. (2007), the difference is still within the typical variation of the Galactic ridge emission over the Galactic plane (Yamauchi et al. 2009). Since the flux of the Galactic ridge emission is constant over time, we added this model component with parameters fixed to the mean value as obtained from epochs III and IV to the PCA spectra of all epochs. We find that for the late part of the outburst, the ridge contributes 1.5% of the 3–10 keV flux and 8% in the Fe band (6–7 keV). To estimate the significance of the Galactic ridge emission, we performed Monte Carlo simulations of the best-fit model without this feature to create a set of 1000 synthetic spectra. We then performed the fit allowing all model parameters, including the Galactic ridge emission, to vary. For the two epochs III and IV none of these simulations led to a fake spectrum for which the improvement in χ2 was as high as in the real data, i.e., the probability that the Galactic ridge emission is real is greater than 99.9 % (>3.3σ). The remaining residuals at 6.4 keV can be explained by a narrow source intrinsic iron Kα flourescence line. We modeled this feature by a thin Gaussian emission line with fixed centroid energy EFe = 6.4 keV and width σFe = 10-4 keV. The flux, AFe, (and thus equivalent width, WFe) were allowed to vary.
In summary, the model can be written as 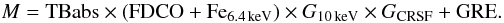 (4)
(4)
3.2. Time-resolved spectroscopy
In this section we describe the time-resolved behavior of the spectral parameters. For each of the six epochs we fitted the respective spectra separately, including the Galactic ridge emission as a constant component as discussed above. Example spectra of two epochs together with the best model fit are shown in Fig. 2. The free fit parameters are summarized in Table 2 and are displayed in Fig. 3. We calculated fluxes in the energy band 10–20 keV for the epochs I–V. In order to be able to compare the source fluxes of all epochs, but avoid excessive extrapolation of the models, we also derived the fluxes in the energy band 7–15 keV. We excluded the contribution from the Galactic ridge emission from this flux.
 |
Fig. 2 Panels a) and b) show two example spectra of XTE J1946+274. Epoch I is the spectrum with the highest count rate while epoch IV is the only data set for which all instruments are available. Histograms show the best-fit continuum. Panels c)–k) show the behavior of the residuals when the additional components of the spectral model are added one by one. Numbers at the bottom right of each panel indicate the best-fit statistics, χ2/d.o.f. c) and d) best fit using the Fermi-Dirac cutoff only; e) and f) residuals after adding the 10 keV feature to the continuum model; g) and h) residuals after adding the Galactic ridge emission to the PCA (for epoch I the flux of this model component was fixed to the result obtained from epochs III and IV); i) and j) residuals after adding the Fe Kα line to the model. Since in the model fit of epoch IV the depth of the CRSF is zero; panel j) displays the final result for epoch IV. In panel k) the CRSF was added to the data for epoch I. See also text for a discussion of the statistical significances of the Galactic ridge emission, the 10 keV feature, and the CRSF. |
The resulting 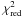 for all fits does not exceed 1.3 (see Table 2). For epoch I, the value of
for all fits does not exceed 1.3 (see Table 2). For epoch I, the value of 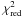 is rather high. Here, the highest contribution to
is rather high. Here, the highest contribution to 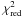 comes from residuals of the ISGRI data, which are caused by calibration problems, therefore we accept this fit. Not all model components are necessary to describe the data in the spectra with low statistics, e.g., epoch V provides a statistically too low
comes from residuals of the ISGRI data, which are caused by calibration problems, therefore we accept this fit. Not all model components are necessary to describe the data in the spectra with low statistics, e.g., epoch V provides a statistically too low 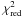 of 0.78. The reason for including these components in these fits even though the components overdetermine the fit model, is that this way it can be shown that these spectra are at least consistent with the full model. In addition, we note that an overestimation of the systematic error would also yield a χred that is too low. In epoch VI only XRT data are available and the continuum parameters are poorly constrained from these data alone. We therefore fixed Efold and Ecut to the value obtained from epoch I because a change of these parameters mainly affects energies not covered by XRT. However, possible influences of these fixed parameters to the free fit parameters NH and Γ might affect the results.
of 0.78. The reason for including these components in these fits even though the components overdetermine the fit model, is that this way it can be shown that these spectra are at least consistent with the full model. In addition, we note that an overestimation of the systematic error would also yield a χred that is too low. In epoch VI only XRT data are available and the continuum parameters are poorly constrained from these data alone. We therefore fixed Efold and Ecut to the value obtained from epoch I because a change of these parameters mainly affects energies not covered by XRT. However, possible influences of these fixed parameters to the free fit parameters NH and Γ might affect the results.
The behavior of the photon index, Γ, the cutoff energy, Ecut, and the folding energy, Efold, yields information about the evolution of the spectral continuum. In most cases there are no or only slight variations of these parameters apparent. However, we know from previous observations that these parameters can also be significantly correlated to each other. We therefore also derived a model-independent illustration of the spectral changes by dividing the background-subtracted PCA spectra from epochs II–V by the spectrum from epoch I (see Fig. 4). The ratios II/I, III/I, and IV/I appear to be mainly constants, meaning that the variations of the continuum parameters in epochs I–IV are probably artificial and caused by cross correlations. In contrast to this, ratio V/I shows a spectral softening for epoch V, caused by a real change of the continuum parameters.
Except for epochs covered by XRT, the hydrogen column density NH is poorly determined and the best-fit parameters are consistent with constant NH. In addition to the line caused by Galactic ridge emission, an Fe Kα fluorescence line at 6.4 keV is required during the first outburst and the maximum phase of the third outburst (epochs I–III). The flux of this line is correlated with the X-ray flux of the source, as expected for a fluorescent line. Furthermore, for these epochs at highest luminosities (I–III), the equivalent width WFe stays roughly constant. In the fading phase of the third outburst and its subsequent flare (epochs IV–VI), this feature is consistent with zero, meaning that the additional emission at these energies can be explained by the Galactic ridge emission. To estimate the significance of the Fe Kα line, we performed similar Monte Carlo simulations as those done for the Galactic ridge emission. For epochs I and II, the probability that there is a source-intrinsic Fe Kα line is greater than 99.9 % (>3.3σ). During epochs III and IV, where the source was much fainter, these simulations show that the probability for Fe line emission from the source is 98.5% (2.4σ) and 62.0% (0.9σ), i.e., here the Fe line region is dominated by Galactic ridge emission.
 |
Fig. 3 Results of time-resolved spectroscopy. The units are as follows: FX in 10-2 photons s-1 cm-2 in the 7–15 keV energy band, NH in 1022 cm-2, Efold and Ecut in keV, and AFe in 10-4 photons s-1 cm-2. |
 |
Fig. 4 a) PCA spectra of time bins I–V (shifted in y-direction for clarity). b) Ratio of the background-corrected time-resolved spectra. |
We found no evidence for the centroid energy, the width, and the optical depth of the 10 keV feature to be variable over time. Owing to the lack of statistics, the width of the feature, σG, in epoch III and IV cannot be constrained and was therefore fixed to the mean value obtained from epochs I and II, i.e., σG = 2.0 keV. In epoch V, also owing to the lack of statistics, this feature is not required to describe the data. We therefore omitted it from our model in this epoch, and also from epoch VI, where our coverage reaches only below 7 keV.
One of the most interesting questions is whether there is a cyclotron line as in the 1998 outburst (Heindl et al. 2001). We found a possible CRSF at ~25 keV during epochs I–IV, i.e., the epochs where good coverage exists above 10 keV. The statistics during the maximum of the first outburst (epoch I) are sufficient to obtain CRSF parameters that are well constrained. As is fairly common for CRSF fits (Coburn 2001), the width and depth of the line are strongly correlated. We therefore set a lower limit of 0.5 keV for the width, which is comparable to the resolution of the PCA at these energies. Monte Carlo simulations as described above lead to a 93% (1.81σ) probability that the CRSF found in epoch I is real.
 |
Fig. 5 PCA-pulse profile of epoch I (in the full PCA energy band, i.e., 2–60 keV), shown twice for clarity. The count rate in each bin is normalized to its variance relative to the mean pulse profile count rate. The phase bins are marked as follows. MP: main peak, SP: secondary peak, off: off state. |
The dependence of the CRSF’s parameters to the choice of the approach of modeling the continuum is an important point that has to be discussed as well. The results presented here were obtained by first adding the 10 keV feature to the model, and then accounting for the CRSF. Reversing this procedure for epoch I, we find another minimum of 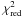 , leading to different cyclotron line parameters, i.e.,
, leading to different cyclotron line parameters, i.e., 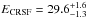 keV,
keV, 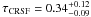 , and
, and 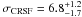 keV. The main problem for this alternative approach is the need of fixing parameters to certain values for the final fit. For example, allowing σCRSF for the final fit to vary leads to an unrealistically broad CRSF that effectively models part of the exponential rollover and not the line. Furthermore, the quality of this fit is slightly worse (χ2 ≈ 97 vs. χ2 ≈ 86). We note that there is a third solution in which the centroid energy of the CRSF agrees with Heindl et al. (2001). However, in contrast to Heindl et al. (2001), this third solution has an unphysically broad and shallow shape and is thus not physically meaningful. All results presented in this paper are based on the approach of first adding the 10 keV feature, and then the CRSF. Finally, we note that there are two other solutions, in which the CRSF is located at 30 keV and 40 keV and a line width of less than 1 keV. These two solutions are indeed physically meaningful, but a Monte Carlo estimation of the significances of these features yields probabilities of 85% (1.44σ) and 86% (1.48σ), respectively, much lower than for the solution with the CRSF at 25 keV. Furthermore, these two solutions are supported only by about three data bins per instrument (the 40 keV solution even only by ISGRI), while the 25 keV solution is based on a much larger number of spectral bins.
keV. The main problem for this alternative approach is the need of fixing parameters to certain values for the final fit. For example, allowing σCRSF for the final fit to vary leads to an unrealistically broad CRSF that effectively models part of the exponential rollover and not the line. Furthermore, the quality of this fit is slightly worse (χ2 ≈ 97 vs. χ2 ≈ 86). We note that there is a third solution in which the centroid energy of the CRSF agrees with Heindl et al. (2001). However, in contrast to Heindl et al. (2001), this third solution has an unphysically broad and shallow shape and is thus not physically meaningful. All results presented in this paper are based on the approach of first adding the 10 keV feature, and then the CRSF. Finally, we note that there are two other solutions, in which the CRSF is located at 30 keV and 40 keV and a line width of less than 1 keV. These two solutions are indeed physically meaningful, but a Monte Carlo estimation of the significances of these features yields probabilities of 85% (1.44σ) and 86% (1.48σ), respectively, much lower than for the solution with the CRSF at 25 keV. Furthermore, these two solutions are supported only by about three data bins per instrument (the 40 keV solution even only by ISGRI), while the 25 keV solution is based on a much larger number of spectral bins.
Including a CRSF in the fainter observations in epochs II–IV does not significantly improve the fits. All observations are in principle consistent with the presence of a weak line as that seen in epoch I. Including such a feature in the spectral modeling for consistency, fixing the centroid energy and width, and leaving the optical depth/the equivalent width of the line as a free parameter effectively gives an upper limit for the depth of the line in these observations. As expected, the limit for τCRSF increases for the fainter phases of the outburst (Table 2). We found no evidence for the equivalent width WCRSF to be variable over time.
Results of the pulse-phase-resolved spectral analysis.
3.3. Pulse-phase-resolved spectroscopy
Spectral parameters are known to be variable as a function of pulse phase, e.g., the parameters of cyclotron lines (e.g., 1A 1118−61; Suchy et al. 2011). To investigate these changes, we performed pulse-phase-resolved spectroscopy on epoch I with the PCA, based on a pulse period ephemeris found by epoch folding. Epoch I provides the best statistics for this analysis. The ephemeris can be described with a constant spin-up, Ṗpulse = (− 3.0 ± 0.3) × 10-9 s s-1 with pulse period between 15.755 s and 15.767 s. The uncertainties of the pulse periods were typically less than 0.003 s. Since it was not possible to correct the light curve for the orbital motion of the system, this spin-up trend might be caused by orbital effects and not by transfer of angular momentum of the accreted matter onto the neutron star. We extracted pulse-phase-resolved spectra using individual pulse periods following this ephemeris. The resulting pulse profile (Fig. 5) shows a double-peaked structure typical for these sources (see, e.g., Bildsten et al. 1997).
As in the time-resolved case, we used the FDCO model to fit the phase-resolved spectra using three phase bins as indicated in Fig. 5: the main peak (MP), the secondary peak (SP), and the off state (off). The pulse phases of the bins are summarized in Table 3. Constant Galactic ridge emission is taken into account in the same way as for the pulse-averaged analysis. The background scaling factor for the PCA cb is assumed to be equal to the result from the pulse-averaged analysis and was therefore frozen to this value. Initial fits of the pulse-phase-resolved spectra lead to large unconstraints in NH and the width of the 10 keV feature σG. These values were therefore frozen to the results form the phase-averaged analysis. The S/N ratio in the spectra from the individual pulse phases is too low to allow us to study the behavior of the CRSF. Similar to the flux-dependent analysis, we froze the CRSF centroid energy and width to the result from the pulse-averaged analysis and allowed only the optical depth/the equivalent width to vary (because of the marginal significance of the CRSF no other attempt was made to study a phase dependence of the cyclotron line).
 |
Fig. 6 a) PCA spectra of the three phase bins together with the pulse-phase-averaged spectrum (shifted in y-direction for clarity). b) Ratio of the background-corrected pulse-phase-resolved spectra. |
Figure 6 shows the ratios of background-corrected pulse-phase-resolved spectra. The ratio MP/off appears to be mainly constant, while the other two ratios reveal more complex shapes. This constant ratio agrees with the spectral parameters of the main peak and the off state. These parameters show almost no or only slight differences to each other. The ratio MP/SP, a falling line, can be explained by a change in photon index. This explanation is confirmed from the spectral analysis. While Ecut and Efold show only small differences, the photon index Γ is significantly lower in the secondary peak, i.e., the spectrum in this phase bin is harder than in the other phase bins. The centroid energy of the 10 keV feature does not vary with pulse phase while its depth weakens during the main peak. The equivalent width remains constant in the main and the secondary peak, while it shows a higher value in the off state. Finally, there is neither evidence for changes of the Fe line flux nor for the equivalent width over the pulse phase.
4. Results and conclusions
4.1. Outburst series
We analyzed quasi-simultaneous XRT, ISGRI, and PCA observations of two outbursts of XTE J1946+274 during a series in the second half of 2010.
Before the onset of this outburst series, XTE J1946+274 was in a state of quiescence for almost one decade, i.e., about 20 orbits of the neutron star. Even though the formation, structure, and dynamics of Be disks are even today far from being completely understood (see, e.g., Draper et al. 2011, and references therein), the missing mass accretion onto the neutron star during that time is probably due to the absence of a sufficiently large Be disk during that time. A new outburst was only possible once the disk had been replenished and accretion could be triggered.
This series shows similar behavior as the one observed in 1998, e.g., two outbursts are observed per orbital period. The outbursts of XTE J1946+274 could also be similar to those seen in GX 301−2, which have been extensively modeled by Leahy (2002). These authors suggested that an additional stream of matter is flowing from the primary, and that a second outburst per orbit could be caused by the passage of the neutron star through this stream. These flux peaks of GX 301−2 occur near the apsides of this system.
However, the outbursts of XTE J1946+274 do not clearly coincide with the times of periastron and apastron passages of the neutron star (Fig. 1). This could be explained by 3D simulations, which show that the disturbance of the Be disk by the gravitational field of the neutron star could lead to a strong asymmetric structure of the circumstellar material, which could also lead to multiple X-ray outbursts during one orbital period (see, e.g., Okazaki et al. 2011).
Alternatively, the outbursts can be triggered by the neutron star passing through the Be disk owing to a misalignment of the orbit and the Be star’s equatorial plane (Wilson et al. 2003).
Another possible explanation for the irregularity of the outbursts is that they are triggered by density variations in the Be disk and not by orbital effects alone. This assumption could be verified by regular optical monitoring of the Balmer Hα line, which is an indicator for the presence of such a disk (see, e.g., Grundstrom et al. 2007, and references therein).
4.2. Spectroscopic results
An absorbed Fermi-Dirac cutoff powerlaw together with an iron Kα fluorescence line, an iron line complex between 6 and 7 keV caused by Galactic ridge emission, a Gaussian-like absorption feature around 10 keV, and a cyclotron line at ~25 keV reproduce the observations well in terms of 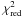 . We found time- as well as pulse-phase-dependent variability of the continuum parameters of XTE J1946+274. In the time-resolved case, these changes might be caused by different accreting mechanisms depending on the mass transfer onto the neutron star. The periodically changing line of sight with respect to the X-ray emitting region, caused by the rotation of the neutron star, is likely responsible for the variabilities observed in the pulse-phase-resolved analysis. Furthermore, this rotation together with differences in the accretion geometries at the two magnetic poles of the neutron star might lead to the asymmetric pulse profile of the X-ray pulsar (see Fig. 5).
. We found time- as well as pulse-phase-dependent variability of the continuum parameters of XTE J1946+274. In the time-resolved case, these changes might be caused by different accreting mechanisms depending on the mass transfer onto the neutron star. The periodically changing line of sight with respect to the X-ray emitting region, caused by the rotation of the neutron star, is likely responsible for the variabilities observed in the pulse-phase-resolved analysis. Furthermore, this rotation together with differences in the accretion geometries at the two magnetic poles of the neutron star might lead to the asymmetric pulse profile of the X-ray pulsar (see Fig. 5).
Studying the behavior of the spectral shape is problematic because the spectral parameters photon index Γ, folding energy Efold, and the cutoff energy Ecut, which describe the broadband shape of the X-ray spectrum, show strong cross correlations. To account for this, we calculated ratios of the spectra for the time-resolved and the pulse-phase-resolved studies. In the time-resolved case, we found clear deviations from a constant ratio for epoch V. During epochs I–IV, the overall spectral shape seems to remain relatively constant. In the pulse-phase-resolved analysis, the spectrum of the secondary peak turns out to be significantly harder than those from the main peak and the off state. These properties of X-ray spectra are caused for instance by the temperature of the visible part of the X-ray emitting region, in particular the accretion column.
 |
Fig. 7 Flux of the iron Kα fluorescence line against the 7−15 keV flux. The crosses correspond to the data from the 2010 outburst, and the diamond to the average spectrum of the 1998 outburst, obtained by reextracting and analyzing the old PCA and HEXTE data from 1998. |
 |
Fig. 8 a) Difference of χ2 of the best fit of epoch I with frozen CRSF parameters (Fig. 2k) and the χ2 of the best fit without CRSF. The centroid energy was varied in steps of 1 keV. The red dashed-dotted curve displays the χ2 of the best fit when using τCRSF and σCRSF from Heindl et al. (2001). For the light blue solid curve the parameters from this work were used. The dark blue dashed-double-dotted curve shows this difference when the width as well as the depth (the upper limit has been set to 3) of the CRSF are allowed to vary, i.e., the same situation as in Fig. 2. The two additional minima in χ2 are discussed in Sect. 3.2. The horizontal dashed line indicates Δχ2 = 0, and the horizontal dotted line seperates the logarithmic and linear scaling in y-direction. The vertical dashed lines shows the position of the CRSF derived in Heindl et al. (2001) and this work. b), c) Results for the optical depth and width of the CRSF, respectively, when these parameters were allowed to vary. The plateau of the curve displayed in panel b at ~60–70 keV is caused by the upper limit for τCRSF of 3. |
Another feature required to achieve a good fit is a source-intrinsic Gaussian iron Kα emission line at 6.4 keV. The disagreement in the strength of the required emission in this energy range between PCA and XRT in initial fits can be solved by inducing the emission of the Galactic ridge. The strength of the Galactic ridge emission is about four times larger than found in other regions of the Galaxy (Ebisawa et al. 2007). This difference is consistent, however, with the typical spatial variations of the ridge emission (Yamauchi et al. 2009). Furthermore, Kühnel et al. (in prep.) found an emission strength consistent with our result for GRO J1008−57.
After taking into account the contribution from the Galactic ridge emission, the flux of the source intrinsic Fe Kα emission line was correlated with the X-ray flux FX (see Fig. 7), as also observed in other X-ray transients (see, e.g., Inoue 1985). The Fe Kα line is significantly detected at source fluxes (7–15 keV) greater than about 0.035 photons s-1 cm-2. At fluxes below this value, the source intrinsic line is consistent with zero. The equivalent width WFe stays constant for high luminosities, i.e., epochs I–III. Reanalyzing the earlier RXTE data (Heindl et al. 2001) with the continuum model employed here yielded an equivalent width that also agrees with the result from the 1998 outburst (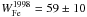 eV). The different values for WFe for the fainter observations, where the Fe Kα line is only marginally detected, can be caused by the uncertainties of the Galactic ridge emission, which significantly contributes to the data at these energies. In the pulse-phase-resolved analysis we found no evidence for variability of the line flux. This result indicates that it is emitted in a region that is quite extended compared to the distance traveled by light during one pulse period. The equivalent width shows no variation either, while rather a variation is expected for this parameter when the respective model component remains constant at varying flux levels. However, this can be explained by the quite large relative uncertainty of WFe, which is on the same order of magnitude as the respective variations.
eV). The different values for WFe for the fainter observations, where the Fe Kα line is only marginally detected, can be caused by the uncertainties of the Galactic ridge emission, which significantly contributes to the data at these energies. In the pulse-phase-resolved analysis we found no evidence for variability of the line flux. This result indicates that it is emitted in a region that is quite extended compared to the distance traveled by light during one pulse period. The equivalent width shows no variation either, while rather a variation is expected for this parameter when the respective model component remains constant at varying flux levels. However, this can be explained by the quite large relative uncertainty of WFe, which is on the same order of magnitude as the respective variations.
The 10 keV feature is present during all epochs and pulse phases. It shows relatively constant results for line energy, width, and depth in the time-resolved case. The reanalysis of the 1998 data yields an equivalent width of 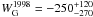 eV, which also equals the results for the current outburst. While we found almost no connection of the parameters of this feature with the luminosity, its optical depth and equivalent width varies with pulse phase. WG is constant during the main and the secondary peak, but it strongly increases during the off state. This behavior indicates that the fractional amount of absorbed flux related to the continuum level is constant for the main and the secondary peak and changes in the off state. This behavior of the 10 keV feature could give rise to speculations about possible physical processes as, e.g., pulse-phase-dependent absorbing processes, which could produce such a feature. On the other hand, the residuals around 10 keV could also be caused by the failing of the spectral broadband continuum models, which in turn would result in a wrong description of the data around these energies. More quantitative analyses of this feature, also from other sources where it occours in emission, are urgently needed to reveal the true nature of this enigmatic feature.
eV, which also equals the results for the current outburst. While we found almost no connection of the parameters of this feature with the luminosity, its optical depth and equivalent width varies with pulse phase. WG is constant during the main and the secondary peak, but it strongly increases during the off state. This behavior indicates that the fractional amount of absorbed flux related to the continuum level is constant for the main and the secondary peak and changes in the off state. This behavior of the 10 keV feature could give rise to speculations about possible physical processes as, e.g., pulse-phase-dependent absorbing processes, which could produce such a feature. On the other hand, the residuals around 10 keV could also be caused by the failing of the spectral broadband continuum models, which in turn would result in a wrong description of the data around these energies. More quantitative analyses of this feature, also from other sources where it occours in emission, are urgently needed to reveal the true nature of this enigmatic feature.
4.3. Cyclotron resonance scattering feature
We found weak evidence for the presence of the CRSF, first discovered by Heindl et al. (2001) during the 1998 outburst series. The cyclotron line improved the model fit for the high S/N epoch I spectrum, where PCA and ISGRI data are available. Later spectra are consistent with the presence of a CRSF with unchanged parameters, but the line is not formally detected in these observations because of their lower S/N ratio. We stress that due to its relative weakness, including the CRSF in our fits does not affect our results for the continuum parameters or for the pulse-phase-resolved analysis.
If the identification of the line is correct, its depth in 2010 was significantly lower than that measured in the 1998 outburst (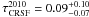 vs.
vs. 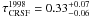 , Heindl et al. 2001). Furthermore, the centroid energy of the CRSF in 2010 (
, Heindl et al. 2001). Furthermore, the centroid energy of the CRSF in 2010 (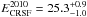 keV) is significantly lower than in 1998 (
keV) is significantly lower than in 1998 (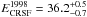 keV, Heindl et al. 2001). Reanalyzing the earlier RXTE data as described above yields CRSF parameters that are consistent with those found by Heindl et al. (2001). Furthermore, the equivalent width in 1998 was also significantly larger than in the current data (
keV, Heindl et al. 2001). Reanalyzing the earlier RXTE data as described above yields CRSF parameters that are consistent with those found by Heindl et al. (2001). Furthermore, the equivalent width in 1998 was also significantly larger than in the current data (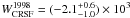 eV).
eV).
One reason why constraining the CRSF is so much easier in the 1998 data is because while the exposure times of the 1998 and the 2010 data are comparable, the 10–20 keV X-ray flux of the 1998 observation is ~40% higher than in the 2010 observation (~9.6 × 10-2 photons s-1 cm-2 vs. ~6.9 × 10-2 photons s-1 cm-2). However, fits to the 2010 data in which we fixed the CRSF parameters to their 1998 values did not yield a satisfactory description of the data (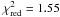 ). Could this indicate that the energy of the line has varied? Assuming that the CRSF width and depth remained the same, we searched for a line similar to that found in the 1998 data. Varying the CRSF energy in steps of a 1 keV and refitting the continuum parameters did not yield any satisfactory results, with best-fit
). Could this indicate that the energy of the line has varied? Assuming that the CRSF width and depth remained the same, we searched for a line similar to that found in the 1998 data. Varying the CRSF energy in steps of a 1 keV and refitting the continuum parameters did not yield any satisfactory results, with best-fit 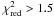 over the 20 to 60 keV band (see Fig. 8, red curve). This result indicates that irrespective of the difference in the S/N ratio between both data sets, the CRSF must have varied between both outbursts, and a strong line as that seen in 1998 is not consistent with the data analyzed here.
over the 20 to 60 keV band (see Fig. 8, red curve). This result indicates that irrespective of the difference in the S/N ratio between both data sets, the CRSF must have varied between both outbursts, and a strong line as that seen in 1998 is not consistent with the data analyzed here.
Taking the 2010 CRSF values at face value, a possible explanation for the difference between the 1998 and 2010 outbursts could be the flux dependence that is seen in some other CRSF sources (see, e.g., Caballero & Wilms 2011, for a recent discussion). XTE J1946+274 could therefore be a cyclotron source with an overall positive correlation between the X-ray flux and the CRSF energy, similar to Her X-1 (Staubert et al. 2007). In models for the change in cyclotron line energy in neutron stars this change is generally interpreted as a change in height of the line-producing region because the accretion column changes with mass accretion rate (and thus luminosity). Using the dipole approximation and assuming that in 1998 the CRSF was emitted from the neutron star’s surface (rNS = 10 km and mNS = 1.4 M⊙) yields a height difference of 1.2 km for the regions where the CRSF is generated. This agrees with typical estimates of several kilometers for the height of the accretion columns (see, e.g., Basko & Sunyaev 1976). Becker et al. (2012) showed that a positive correlation between flux and energy is possible in the luminosity range where the stopping in the accretion column is dominated by Coulomb braking. For cyclotron line energies around 30 keV Coulomb braking is the dominating braking process in the luminosity range 1–5 × 1037 erg s-1. For higher luminosities, radiation braking dominates. XTE J1946+274’s peak outburst luminosity of 4.5 × 1037 erg s-1 is barely consistent with this range, but because the source seems to be located at the transition between Coulomb and radiation braking and was brighter in 1998, the very strong change in CRSF energy seems unlikely to be due to a pure mass accretion rate effect.
In conclusion, while the possibility of a luminosity dependent CRSF is intriguing, the poor S/N ratio of the 2010 data does not allow a definitive answer concerning the luminosity dependence of the CRSF. Additional longer monitoring observations of XTE J1946+274 during its next outburst episode are urgently needed to resolve this question.
Acknowledgments
The authors thank Jérôme Rodriguez for his help with the INTEGRAL observations, and the schedulers of RXTE and Swift for their role in making this campaign possible. We thank the anonymous referee for his/her thorough review of this paper and his/her constructive comments. We thank John E. Davis for the development of the SLxfig module, which was used to create all figures in the paper. We acknowledge funding by the Bundesministerium für Wirtschaft und Technologie under Deutsches Zentrum für Luft- und Raumfahrt grants 50 OR 0808, 50 OR 0905, and 50 OR 1113. I.C. acknowledges financial support from the French Space Agency CNES through CNRS. This research is also based on observations with INTEGRAL, an ESA project with instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain), Czech Republic, and Poland, and with the participation of Russia and the USA.
References
- Basko, M. M., & Sunyaev, R. A. 1976, MNRAS, 175, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., & Wolff, M. T. 2007, ApJ, 654, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., Klochkov, D., Schönherr, G., et al. 2012, A&A, 544, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Bradt, H. V., Rothschild, R. E., & Swank, J. H. 1993, A&AS, 97, 355 [NASA ADS] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, I., & Wilms, J. 2011, Mem. SA It., in press [Google Scholar]
- Campana, S., Israel, G., & Stella, L. 1999, A&A, 352, L91 [NASA ADS] [Google Scholar]
- Coburn, W. 2001, Ph.D. Thesis, Univ. of California, San Diego [Google Scholar]
- Draper, Z. H., Wisniewski, J. P., Bjorkman, K. S., et al. 2011, ApJ, 728, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Ebisawa, K., Yamauchi, S., Tanaka, Y., Koyama, K., & Suzaku Team 2007, Progr. Theor. Phys. Suppl., 169, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 2004, in Proc. 5th INTEGRAL Workshop on the INTEGRAL Universe, eds. V. Schönfelder, G. Lichti, & C. Winkler, ESA SP, 552, 777 [Google Scholar]
- Grundstrom, E. D., Boyajian, T. S., Finch, C., et al. 2007, ApJ, 660, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuschik, R. W. 1996, A&A, 308, 170 [NASA ADS] [Google Scholar]
- Heindl, W. A., Coburn, W., Gruber, D. E., et al. 2001, ApJ, 563, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. C., & Denicola, L. A. 2000, in Astronomical Data Analysis Software and Systems IX, eds. N. Manset, C. Veillet, & D. Crabtree, ASP Conf. Ser., 216, 591 [Google Scholar]
- Inoue, H. 1985, Space Sci. Rev., 40, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreykenbohm, I., Coburn, W., Wilms, J., et al. 2002, A&A, 395, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreykenbohm, I., Wilms, J., Kretschmar, P., et al. 2008, A&A, 492, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krimm, H. A., Barthelmy, S. D., Baumgartner, W., et al. 2010, ATel, 2663 [Google Scholar]
- Leahy, D. A. 2002, A&A, 391, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, S., Kühnel, M., Pottschmidt, K., et al. 2010, ATel, 3077 [Google Scholar]
- Okazaki, A. T., Nagataki, S., Naito, T., et al. 2011, in IAU Symp. 272, eds. C. Neiner, G. Wade, G. Meynet, & G. Peters (Cambridge), 628 [Google Scholar]
- Rothschild, R. E., Blanco, P. R., Gruber, D. E., et al. 1998, ApJ, 496, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Slettebak, A. 1988, PASP, 100, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. A., & Takeshima, T. 1998, ATel, 36 [Google Scholar]
- Staubert, R., Shakura, N. I., Postnov, K., et al. 2007, A&A, 465, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suchy, S., Pottschmidt, K., Rothschild, R. E., et al. 2011, ApJ, 733, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, Y. 1986, in Radiation Hydrodynamics in Stars and Compact Objects, eds. D. Mihalas, & K. H. Winkler (New York: Springer), IAU Colloq., 89, 198 [Google Scholar]
- Verner, D. A., & Yakovlev, D. G. 1995, A&AS, 109, 125 [NASA ADS] [Google Scholar]
- Verrecchia, F., Israel, G. L., Negueruela, I., et al. 2002, A&A, 393, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warwick, R. S., Turner, M. J. L., Watson, M. G., & Willingale, R. 1985, Nature, 317, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. A., Finger, M. H., Wilson, R. B., & Scott, D. M. 1998, IAU Circ., 7014 [Google Scholar]
- Wilson, C. A., Finger, M. H., Coe, M. J., & Negueruela, I. 2003, ApJ, 584, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Worrall, D. M., Marshall, F. E., Boldt, E. A., & Swank, J. H. 1982, ApJ, 255, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Yamauchi, S., Ebisawa, K., Tanaka, Y., et al. 2009, PASJ, 61, 225 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 15–50 keV Swift/BAT light curve of the 2010/2011 outburst series. The times of periastron and apastron passages are marked by P and A, respectively. These epochs and the corresponding uncertainties were calculated using the orbital solution from Wilson et al. (2003). The insets provide a closer view on the first (Jun./Jul.) and the third (Nov./Dec.) outburst. The blue, red, and green arrows in these insets indicate the observations times for PCA, ISGRI, and XRT, respectively. Epochs over which data were summed for the time resolved spectral analysis are indicated with I to VI. |
| In the text | |
 |
Fig. 2 Panels a) and b) show two example spectra of XTE J1946+274. Epoch I is the spectrum with the highest count rate while epoch IV is the only data set for which all instruments are available. Histograms show the best-fit continuum. Panels c)–k) show the behavior of the residuals when the additional components of the spectral model are added one by one. Numbers at the bottom right of each panel indicate the best-fit statistics, χ2/d.o.f. c) and d) best fit using the Fermi-Dirac cutoff only; e) and f) residuals after adding the 10 keV feature to the continuum model; g) and h) residuals after adding the Galactic ridge emission to the PCA (for epoch I the flux of this model component was fixed to the result obtained from epochs III and IV); i) and j) residuals after adding the Fe Kα line to the model. Since in the model fit of epoch IV the depth of the CRSF is zero; panel j) displays the final result for epoch IV. In panel k) the CRSF was added to the data for epoch I. See also text for a discussion of the statistical significances of the Galactic ridge emission, the 10 keV feature, and the CRSF. |
| In the text | |
 |
Fig. 3 Results of time-resolved spectroscopy. The units are as follows: FX in 10-2 photons s-1 cm-2 in the 7–15 keV energy band, NH in 1022 cm-2, Efold and Ecut in keV, and AFe in 10-4 photons s-1 cm-2. |
| In the text | |
 |
Fig. 4 a) PCA spectra of time bins I–V (shifted in y-direction for clarity). b) Ratio of the background-corrected time-resolved spectra. |
| In the text | |
 |
Fig. 5 PCA-pulse profile of epoch I (in the full PCA energy band, i.e., 2–60 keV), shown twice for clarity. The count rate in each bin is normalized to its variance relative to the mean pulse profile count rate. The phase bins are marked as follows. MP: main peak, SP: secondary peak, off: off state. |
| In the text | |
 |
Fig. 6 a) PCA spectra of the three phase bins together with the pulse-phase-averaged spectrum (shifted in y-direction for clarity). b) Ratio of the background-corrected pulse-phase-resolved spectra. |
| In the text | |
 |
Fig. 7 Flux of the iron Kα fluorescence line against the 7−15 keV flux. The crosses correspond to the data from the 2010 outburst, and the diamond to the average spectrum of the 1998 outburst, obtained by reextracting and analyzing the old PCA and HEXTE data from 1998. |
| In the text | |
 |
Fig. 8 a) Difference of χ2 of the best fit of epoch I with frozen CRSF parameters (Fig. 2k) and the χ2 of the best fit without CRSF. The centroid energy was varied in steps of 1 keV. The red dashed-dotted curve displays the χ2 of the best fit when using τCRSF and σCRSF from Heindl et al. (2001). For the light blue solid curve the parameters from this work were used. The dark blue dashed-double-dotted curve shows this difference when the width as well as the depth (the upper limit has been set to 3) of the CRSF are allowed to vary, i.e., the same situation as in Fig. 2. The two additional minima in χ2 are discussed in Sect. 3.2. The horizontal dashed line indicates Δχ2 = 0, and the horizontal dotted line seperates the logarithmic and linear scaling in y-direction. The vertical dashed lines shows the position of the CRSF derived in Heindl et al. (2001) and this work. b), c) Results for the optical depth and width of the CRSF, respectively, when these parameters were allowed to vary. The plateau of the curve displayed in panel b at ~60–70 keV is caused by the upper limit for τCRSF of 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


