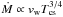| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 21 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219528 | |
| Published online | 01 October 2012 | |
The progenitor mass of the Type IIP supernova SN 2004et from late-time spectral modeling⋆
1
Department of Astronomy, The Oskar Klein CentreStockholm
University,
10601
Stockholm,
Sweden
e-mail: andersj@astro.su.se
2
Astrophysics Research Centre, School of Maths and Physics, Queen’s
University Belfast, Belfast
BT7 1NN,
UK
3
Department of Physics (Astrophysics), University of
Oxford, DWB, Keble
Road, Oxford
OX1 3RH,
UK
4
ESO, Karl-Schwarzschild-Strasse 2, 85748
Garching,
Germany
Received: 3 May 2012
Accepted: 8 August 2012
SN 2004et is one of the nearest and best-observed Type IIP supernovae, with a progenitor detection as well as good photometric and spectroscopic observational coverage well into the nebular phase. Based on nucleosynthesis from stellar evolution/explosion models we apply spectral modeling to analyze its 140−700 day evolution from ultraviolet to mid-infrared. We find a MZAMS = 15 M⊙ progenitor star (with an oxygen mass of 0.8 M⊙) to satisfactorily reproduce [O i] λλ6300, 6364 and other emission lines of carbon, sodium, magnesium, and silicon, while 12 M⊙ and 19 M⊙ models under- and overproduce most of these lines, respectively. This result is in fair agreement with the mass derived from the progenitor detection, but in disagreement with hydrodynamical modeling of the early-time light curve. From modeling of the mid-infrared iron-group emission lines, we determine the density of the “Ni-bubble” to ρ(t) ≃ 7 × 10-14 × (t/100 d)-3 g cm-3, corresponding to a filling factor of f = 0.15 in the metal core region (V = 1800 km s-1). We also confirm that silicate dust, CO, and SiO emission are all present in the spectra.
Key words: supernovae: general / supernovae: individual: SN 2004et / line: formation / line: identification / radiative transfer
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Stars with zero age main sequence (ZAMS) mass greater than about 8 M⊙ end their lives as core-collapse supernovae (SNe). Over half of these events (per unit volume) are classified as Type IIP (Li et al. 2011), showing hydrogen lines, as well as a 3−4 month plateau in the light curve, implying the presence of a massive hydrogen envelope. After the plateau phase, the core of the SN becomes visible, glowing from radioactive input by 56Co. As long as the ejecta remain opaque to the gamma-rays emitted in the decay, the light curve follows the exponential decay of 56Co, with an e-folding time of 111.4 days. The spectrum evolves from being dominated by absorption lines and lines exhibiting P-Cygni profiles superimposed upon a blackbody-like continuum to strong emission lines and a weaker continuum. As the temperature falls, thermal emission eventually shifts into the infrared, but ultraviolet/optical features remain, caused by non-thermal ionizations and excitations.
From hydrodynamical modeling, the progenitors of Type IIP SNe are believed to be red supergiants (RSGs; Chevalier 1976; Falk & Arnett 1977). The rapidly growing image archives have improved the prospects of confirming this by identifying SN progenitors in imaging surveys. Such identifications have now been made for the Type IIP SNe SN 2003gd, SN 2004A, SN 2004et, SN 2005cs, SN 2008bk, SN 2008cn, and SN 2009md (Smartt 2009; Elias-Rosa et al. 2009; Fraser et al. 2011, and references therein). For SN 2003gd, the progenitor identification was verified by follow-up observations showing that the candidate had disappeared (Maund & Smartt 2009). In the cases where multiple-band detections were made, the progenitors have shown properties consistent with the RSG hypothesis, except for SN 2008cn, where the progenitor was yellow1 (Elias-Rosa et al. 2009).
The estimated luminosity of the progenitor allows its ZAMS mass to be determined from stellar evolution models. The resulting values are consistently found to be below 20 M⊙, with a statistical analysis yielding a range of 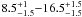 M⊙ for the progenitor population (Smartt et al. 2009), although dust effects may produce a somewhat higher upper boundary (Walmswell & Eldridge 2012). The fate of stars in the 20−25/30 M⊙ range then remains unclear, as standard stellar evolution models predict also these to evolve to RSGs and explode as Type IIP SNe (e.g., Heger & Langer 2000; Meynet & Maeder 2003; Eldridge et al. 2008). Models including rotation show that stars with initial mass greater than 20 M⊙ and time-averaged equatorial velocities of ≳ 200 km s-1 could lose much of their hydrogen envelope and move bluewards in the HR diagram (e.g. Meynet & Maeder 2003). While this is immediately attractive as an explanation for the lack of luminous RSGs as Type IIP progenitors, one must account for the broad observed distribution of equatorial velocities (e.g. Hunter et al. 2008) as well as the lack of detection of blue, luminous progenitors for Type IIn/Ib/Ic SNe (Smartt 2009).
M⊙ for the progenitor population (Smartt et al. 2009), although dust effects may produce a somewhat higher upper boundary (Walmswell & Eldridge 2012). The fate of stars in the 20−25/30 M⊙ range then remains unclear, as standard stellar evolution models predict also these to evolve to RSGs and explode as Type IIP SNe (e.g., Heger & Langer 2000; Meynet & Maeder 2003; Eldridge et al. 2008). Models including rotation show that stars with initial mass greater than 20 M⊙ and time-averaged equatorial velocities of ≳ 200 km s-1 could lose much of their hydrogen envelope and move bluewards in the HR diagram (e.g. Meynet & Maeder 2003). While this is immediately attractive as an explanation for the lack of luminous RSGs as Type IIP progenitors, one must account for the broad observed distribution of equatorial velocities (e.g. Hunter et al. 2008) as well as the lack of detection of blue, luminous progenitors for Type IIn/Ib/Ic SNe (Smartt 2009).
Another method to derive information about the exploded star is through radiation-hydrodynamical modeling of the bolometric light curve. Litvinova & Nadezhin (1983, 1985) presented scaling relations from fits to a grid of Type IIP SN models allowing for the determination of the explosion energy, ejecta mass, and progenitor radius from the observed plateau length, V-band magnitude, and photospheric velocity. However, the neglect of 56Ni in these models renders them viable only for SNe with very small 56Ni masses. Eastman et al. (1994) found that a (typical) 56Ni mass of 0.06 M⊙ extends the plateau by 40%, and Kasen & Woosley (2009) found a prolongation by 20−30% for 56Ni-masses of 0.05−0.1 M⊙. Since the ejecta mass has a strong scaling with the plateau length (to the power 2.9) in the Litvinova & Nadezhin (1985) relations, a significant overestimate of the ejecta mass results.
More reliable results can be obtained by fitting hydrodynamical models including 56Ni to the whole light curve evolution. Such modeling has been undertaken for SN 1999em (Baklanov et al. 2005; Utrobin 2007; Bersten et al. 2011), SN 2003Z (Utrobin et al. 2007), SN 2004et (Utrobin & Chugai 2009), SN 2005cs (Utrobin & Chugai 2008), and SN 2009kf (Utrobin et al. 2010), obtaining ejecta masses Mej = 14−28 M⊙. As discussed by Utrobin & Chugai (2009) and Maguire et al. (2010, M10 hereafter), these ejecta masses are generally too high to be consistent with the initial masses determined from direct observations of SN progenitors, as well as for what is expected from stellar evolution in general. Recently, Inserra et al. (2011) and Inserra et al. (2012), using the radiation hydrodynamics code of Pumo & Zampieri (2011), determined lower ejecta masses of Mej = 5−7.5 and Mej = 8−12 M⊙ for the Type IIP SNe 2007od and SN 2009bw.
A third method for diagnosing the progenitor mass is through late-time spectral modeling. In the nebular phase (t ≳ 150 days), the inner ejecta become visible, and the various nuclear burning zones can be analysed. Stellar evolution models predict the metal core mass to strongly increase with progenitor ZAMS mass (e.g. Woosley & Weaver 1995), making it possible to distinguish between different progenitors by determining the nucleosynthesis yields. Emission lines of carbon, oxygen, neon, sodium, magnesium, silicon, and sulphur are the main signatures that can potentially constrain the progenitor mass.
Despite being the most common core-collapse SN class, there are so far only a handful of Type IIP SNe that have extensive temporal and spectral coverage in the nebular phase, and not much information has as yet been derived from these observations. The best existing datasets are for SN 1990E (Schmidt et al. 1993; Gomez & Lopez 1993; Benetti et al. 1994), SN 1999em (Leonard et al. 2002a; Elmhamdi et al. 2003), SN 1999gi (Leonard et al. 2002b), SN 2002hh (Pozzo et al. 2006), SN 2004dj (Chugai et al. 2005), SN 2004et (Sahu et al. 2006, M10), SN 2005cs (e.g. Pastorello et al. 2009), 2007it (Andrews et al. 2011), and 2007od (Inserra et al. 2011). Of these, only SN 1999em was well monitored also in the near-infrared (NIR).
Apart from the sparsity of data, spectral analysis needs complex tools to model the transformation of energy from radioactive decay to emergent UVOIR radiation. Temperature and NLTE solutions for a large number of zones and elements, including non-thermal heating/ionization/excitation rates, and multi-line radiative transfer are the fundamental ingredients that must be calculated, together making up millions of constraints whose self-consistent solution must be iteratively sought. In addition, molecules, dust, and time-dependent effects may cause further complications.
So far, SN 1987A is the only Type II SN for which detailed spectral modeling has been undertaken. Despite being a Type IIpec rather than a Type IIP, it was probably similar to a Type IIP in the nebular phase, since the nucleosynthesis is largely unaffected by the late-time evolution of the envelope. Xu & McCray (1991) and Kozma & Fransson (1992) obtained the solutions for the ionization, excitation, and heating produced by the gamma-rays and positrons, which is the first step in the nebular phase modeling. The evolution of individual lines were analyzed in a series of papers by Xu et al. (1992) (hydrogen), Li & McCray (1992) (oxygen), Li et al. (1993) (iron, cobalt, nickel), Li & McCray (1993) (calcium), and Li & McCray (1995) (helium). The thermal evolution of the envelope was modeled in detail by de Kool et al. (1998), and Kozma & Fransson (1998a,b, in the following KF98a,b) computed the spectra from detailed explosion models to study the evolution of temperature, ionization, and line fluxes in the 200−800 day range. Kjær et al. (2010) and Jerkstrand et al. (2011, J11 hereafter) analyzed the spectrum in the 44Ti-powered phase (t ≳ 5 years), including the effects of multi-line radiative transfer.
Modeling of other objects includes the work by Dessart & Hillier (2011), who compared the emergent spectra of Type IIP explosion models to SN 1999em, assuming complete thermalization of the gamma-rays, but performing a detailed radiative transfer calculation.
In this paper we undertake a detailed analysis of one of the brightest and best-observed Type IIP SNe to date, SN 2004et. This SN has been subject to progenitor analysis, hydrodynamical modeling, and some qualitative spectral analysis. Li et al. (2005) identified a progenitor candidate in ground-based pre-explosion images. However, Crockett et al. (2011) showed that this candidate was still visible in 2007 (3 years after explosion), and that the source in the original images was a composite of two or three sources. They identified an excess flux in the pre-explosion images contributed by the true SN progenitor, and for two different assumptions about the late-time SN flux determined MZAMS = 8 and 10 M⊙, with an error of +5/−1 M⊙. With new post-explosion imaging and updated methods to determine bolometric corrections and synthetic colors from model spectra, Fraser et al. (in prep.) have revised this to 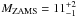 M⊙. The best estimates for luminosity, temperature, and radius are log (L/L⊙) = 4.8, T = 3600 K, and R0 = 650 R⊙.
M⊙. The best estimates for luminosity, temperature, and radius are log (L/L⊙) = 4.8, T = 3600 K, and R0 = 650 R⊙.
Through radiation-hydrodynamical modeling, Utrobin & Chugai (2009) derived a large ejecta mass of Mej = 24.5 ± 1 M⊙, the highest value for any Type IIP modeled in detail so far. They also determined a progenitor radius R0 = 1500 ± 140 R⊙, explosion energy E = 2.3 ± 0.3 B (1 B = 1051 erg) and 56Ni mass M(56Ni) = 0.068 ± 0.009M⊙.
Spectroscopic analysis is so far limited to some qualitative results from the nebular spectrum by Sahu et al. (2006, S06 hereafter) and M10. S06 found the [O i] λλ6300, 6364 luminosity to be of comparable to the one in SN 1987A, and from the similar 56Ni mass they conclude that SN 2004et should have a similar oxygen mass. From this follows a similar progenitor mass, which was 16−22 M⊙ for SN 1987A (Arnett et al. 1989). M10 found the [O i] λλ6300, 6364 flux normalized to the 56Ni mass to be 15% lower than in SN 1987A at 285 days, and assuming all other things equal the oxygen mass would then be smaller by the same factor. With the strong dependency of oxygen production on progenitor mass (e.g. Woosley & Weaver 1995), SN 2004et would then be expected to have a progenitor mass only slightly lower than SN 1987A.
Taken together with the progenitor analysis and light curve modeling, there are therefore conflicting results for how massive the progenitor of SN 2004et was. The aim in this paper is to shed more light on this issue by modeling the photometric and spectroscopic nebular phase data. To this end, we use the spectral synthesis code described in J11 (see also Maurer et al. 2011 for testing of the code), with some modifications described in Appendix B. We compare the model spectra produced by using three different explosion models as input (from MZAMS = 12, 15 and 19 M⊙ progenitors), and investigate which produces best agreement with observations. This paper is complemented by a more general discussion of the nebular phase spectra of Type IIP SNe in Maguire et al. (2012, in the following M12).
2. Observational summary
SN 2004et was discovered on Sep. 27 2004 (Zwitter et al. 2004), with the explosion date determined to Sep. 22 (Li et al. 2005). The host galaxy was the nearby (5.5 Mpc) starburst galaxy NGC 6946, which has hosted nine SNe since 1917. The SN was classified as a Type IIP, showing broad P-Cygni Balmer lines (Zwitter et al. 2004; Filippenko et al. 2004). Intensive photometric and spectroscopic monitoring was initiated, and is described in S06, Misra et al. (2007, M07 hereafter), Kotak et al. (2009, K09 hereafter) and M10. The luminosity was among the highest of all Type IIP events, both on the 110 day plateau and in the radioactive tail phase (M10).
The SN was detected at radio wavelengths on October 5 2004 (Stockdale et al. 2004), implying the presence of significant amounts of circumstellar material. Follow-up observations were made with MERLIN (Beswick et al. 2004), GMRT (M07) and VLBI (Martí-Vidal et al. 2007). X-ray and radio emission (Rho et al. 2007; Martí-Vidal et al. 2007) indicate the presence of a progenitor wind. A mass loss rate of Ṁ = 10-5 M⊙ yr-1 was estimated from the radio turn-on time, assuming a wind velocity of vw = 10 km s-1 and a circumstellar temperature of Tcs = 105 K (Chevalier et al. 2006)2, whereas Rho et al. (2007) found Ṁ = 2 × 10-6 M⊙ yr-1 from modeling of the X-ray emission.
K09 obtained Spitzer mid-infrared (MIR) spectra at 5−35 μm for seven epochs between 295 and 1385 days, as well as optical Keck spectra at days 823, 933 and 1146. The late optical spectra appear to be dominated by circumstellar interaction in the form of wide (HWZI = 8500 km s-1), box-shaped Hα, [Ca ii] λ7300, and [O i] λλ6300, 6364, as well as narrow (70 km s-1) Hα and [N ii] λλ6548, 6583. Spectroscopic identification of silicate dust is reported, with a mass of a few times 10-4 M⊙. Further MIR data and analysis is presented by Fabbri et al. (2011, F11 hereafter).
2.1. Distance and extinction
We adopt a distance of 5.5 Mpc for NGC 6946, as determined using the H i Tully-Fisher relation (Pierce 1994), and in agreement with the average value of several other distance determinations (Schmidt 1993; Schoniger & Sofue 1994; Karachentsev et al. 2000; Sahu et al. 2006).
We adopt an extinction of EB − V = 0.41, based on the sum of local and foreground Na i D absorption lines (Zwitter et al. 2004). The galactic foreground extinction toward NGC 6946 is EB − V = 0.34 (Schlegel et al. 1998).
2.2. Metallicity
Metallicity measurements would traditionally come from the [O ii] and [O iii] line fluxes in nebular or H ii regions at, or close to the SN position (e.g., Smartt et al. 2009; Modjaz et al. 2011). From the radial position of SN 2004et (rg = 0.92r25), and the gradient of Pilyugin et al. (2004), Smartt et al. (2009) estimated the oxygen abundance of the progenitor to 12 + log O/H = 8.3 dex, which is a factor of about two lower than solar metallicity. However the determination of absolute oxygen abundances from the strong line ratio of [O ii] and [O iii] has been plagued by large differences between the calibrations employed. As Moustakas et al. (2010) show, the oxygen abundance at the position of SN 2004et determined by two physically motivated calibrations is 8.9 and 8.3 dex. This large difference of a factor four makes it difficult for us to choose a specific stellar metallicity for the progenitor model. The solar value of 8.7 dex (Asplund et al. 2009) is intermediate between the two and as we have no clear way of distinguishing between the discrepant results we employ a solar metallicity model. We discuss the influence of metallicity on the modeling in the discussion (Sect. 5).
2.3. Photometry
We use UBVRI photometry presented by S06, M07, M10 and F11. S06 obtained photometry for 8−541 days, M07 for 14−90 and 370−470 days, and M10 for 7−1214 days. F11 obtained VRI photometry for 79−1412 days.
For nebular-phase NIR photometry, we use M10 measurements of J and H magnitudes on days 134 and 141, and JHK magnitudes from F11 for days 268, 317, 390, and 652. We also use day 307 JHK observations by M10, which due to their importance for the only NIR spectrum taken were recalibrated with an extended set of reference stars. The raw data were reduced following standard procedures with the addition of corrections for quadrant crosstalk and field distortion. We determined color constants from standard fields and approximate S-corrections from the standard star spectrum and the filter transmission curves, to as accurately as possible transform from the instrumental system to the standard (2MASS) system. We find J = 15.70 ± 0.03, H = 15.48 ± 0.02, and K = 15.12 ± 0.03.
In the MIR, we use 3.6 μm, 4.5 μm, and 24 μm Spitzer photometry from K09.
2.4. Spectroscopy
We use a set of sixteen optical, one near-infrared, and three mid-infrared spectra from S06, K09, and M10, a summary of which can be seen in Table 1. We recalibrated the NIR TNG/Amici spectrum (day 307) using the new photometry reductions described above. The prism used in these observations has very low resolution preventing wavelength calibration using lamp or sky lines because of line blending. Instead the observatory provides a pixel to wavelength mapping to be calibrated using known features in the spectrum by applying a constant pixel shift. We used this method to calibrate the spectrum by alignment of the strongest lines to the model spectra. The raw data were reduced following standard procedures with the addition of corrections for quadrant cross talk and the spectrum then extracted and corrected for telluric absorption using the standard star spectrum. The absolute flux calibration was performed by a least squares fit of synthetic and measured J and H magnitudes (spectral response in the K-band region involves significantly higher uncertainties).
All spectra displayed in the paper have been corrected for the host galaxy recession velocity of 48 km s-1 (Sandage & Tammann 1981). The optical and NIR spectra have been corrected for extinction with EB−V = 0.41 (Sect. 2.1) and the Cardelli et al. (1989) extinction law. No correction was applied to the MIR data, for which the extinction is negligible.
Summary of spectroscopic observations used in this paper.
3. Modeling
The spectral synthesis code we use is described in detail in J11. In summary, we compute the energy deposition by radioactive isotopes by performing an effective opacity transfer of the gamma-rays, and assuming on-the-spot deposition for the leptons and X-rays. The relative fractions of the energy going into heating, ionization, and excitation are calculated as described in Kozma & Fransson (1992), and the equations of statistical and thermal equilibrium (including non-thermal heating/ionization/excitation, collisional (thermal) excitation/de-excitation, radiative excitation/de-excitation, photoionization, radiative recombination, charge transfer, photoelectric heating, free-free heating, line cooling, recombination cooling, and free-free cooling) are then iterated with a Monte Carlo simulation of the radiation field until convergence has been achieved. The radiative transfer treatment uses the Sobolev approximation. The method is a quasi-Λ-iteration, but differs in that it treats continuum and part of the line scattering on-the-fly in each radiation field simulation, rather than including them in the emissivity functions. This improves the convergence properties by allowing photons to travel longer distances than one mean-free-path in each iteration. The emergent spectrum is obtained by binning the escaping Monte Carlo packets, and smoothing with a Gaussian of FWHM = 600 km s-1.
The code has been updated in some respects compared to the version used in J11. Because the computations here are for earlier epochs than in J11, photoexcitation/de-excitation rates in the NLTE solutions cannot be approximated to zero. We therefore implemented a modified Monte Carlo operator to allow for partial deposition of photo-excitation energy along the photon trajectories (we keep the coupling partial to avoid approaching a classic Λ-iteration, and keep the NLTE solutions limited in size). The details of the new treatment can be found in Appendix B. We have also added electron scattering, as well as the influence of line overlap on Lyα and Lyβ Sobolev escape probabilities, also detailed in Appendix B.
3.1. Explosion model and zoning
As input we use the 12 M⊙, 15 M⊙, and 19 M⊙ explosion models computed by Woosley & Heger (2007, WH07 hereafter), which are non-rotating stars of solar metallicity evolved with the KEPLER hydrodynamics code and then exploded with a piston, endowing a final kinetic energy of 1.2 B to the ejecta. The mass-loss prescription in these models is based on the empirically established relations by Nieuwenhuijzen & de Jager (1990), both for the main sequence and the RSG phase. The mass loss for the three stars are 1.2, 2.3, and 3.8 M⊙.
We divide the ejecta into eight distinct zone types: Fe/He, Si/S, O/Si/S, O/Ne/Mg, O/C, He/C, He/N, and H, named after their dominant constituents. The mass of the Fe/He zone is set to give a total 56Ni-mass of 0.062 M⊙ in the ejecta (see Sect. 3.3). Table 2 shows the zone masses in the three models we use, and Tables A.1–A.3 in the appendix show their detailed composition.
Zone masses (in M⊙) of the three different explosion models used.
The explosion models are 1D, and therefore lack the macroscopic mixing which is known to occur (e.g., Kifonidis et al. 2006; Hammer et al. 2010). We therefore distribute the zones over a core, where each zone is distributed as Ncl spherical clumps, completely macroscopically mixed in velocity, and an envelope, where the zones are concentric shells, with no mixing. The Fe/He, Si/S, O/Si/S, O/Ne/Mg, O/C, and He/C zones exist only in the core, whereas the He/C, He/N, and H zones exist partially in the core (fractions xHe for the He zones and xH for the H zone), and partially in the envelope (fractions 1 − xHe and 1 − xH). The first two shells in the envelope are the unmixed He/C and He/N zones. External to these zones are logarithmically spaced (Vi/Vi−1 = 1.2) shells of the H-zone material. The velocities of the two unmixed He-shells are set so their densities equal that of the first hydrogen shell.
The density of the H-envelope is set to follow the density profile of the input model, but scaled down with a constant to account for the mixing of material into into the core. This downscaling was about 10% for all three models. The envelope is terminated at 104 km s-1, as the density decreases steeply beyond a few thousand km s-1, and little line or continuum opacity remains at higher velocities than this in the nebular phase.
Although our artificial mixing alters the velocity field for each species compared to the 1D input models, the explosion energy of 1.2 B is preserved to within 3% in all models. Figure 1 shows the velocity field for the 15 M⊙ model that we use, compared to the 1D hydro simulation.
 |
Fig. 1 The density profile in the 1D hydrodynamical model (solid lines) and in the artificially mixed model used in this paper (dashed lines). Note that in the artificially mixed model, the zones in the core are distributed as clumps with individual filling factors, the densities plotted are the densities within each clump. |
3.2. Model parameters
The parameters of the model are the velocity dividing the core and the envelope (Vcore), the fractions of the He and H zones mixed into the core (xHe and xH), the filling factors of the different zones in the core (fFe/He, fSi/S, fO/Si/S, fO/Ne/Mg, fO/C, fHe/C, fHe/N, fH), the number of clumps per zone in the core (Ncl), and the dust optical depth function (τd(t)), which we assume to be gray. Most of these parameters can be constrained from observations or theoretical arguments, as described below.
3.2.1. Core velocity Vcore
The core velocity is to first order found by inspecting the line widths of [O i] λλ6300, 6364 and [Fe ii] λ7155, which were mainly emitted from the core in SN 1987A (KF98b). The wings of these lines may, however, be produced by primordial oxygen and iron in the envelope (M12), and are therefore unsuitable markers of the core width. A more relevant starting point is the half-width-at-half-maximum, HWHM, which is ~1200 km s-1 for the [O i] λλ6300, 6364 lines (M12). Inspection of the [Fe ii] λ7155 line gives similar values. The emission line profile from a homogeneous sphere expanding homologously is parabolic with VHWHM = 0.71Vcore, so Vcore can be estimated to 1700 km s-1. We find that a value Vcore = 1800 km s-1 best reproduces the line profiles, and is chosen for the modeling.
3.2.2. In-mixing fractions xHe and xH
Several 2D and 3D hydrodynamical calculations have shown that 1−2 M⊙ of the H-envelope gets mixed with core material in the explosion (Herant & Benz 1991; Mueller et al. 1991; Herant & Woosley 1994; Kifonidis et al. 2006; Hammer et al. 2010). This was also found from modeling of the Hα evolution in SN 1987A (KF98b). Herant & Woosley (1994) obtain 1.4 M⊙ of H (20% of the total) and 1.3 M⊙ of He (85% of the total) inside 1800 km s-1, for the 2D explosion of a 12 M⊙ RSG. The 3D explosion simulation of a 15.5 M⊙ blue supergiant by Hammer et al. (2010) shows 60% of the He and and 15% of the H mixed inside Vcore = 1800 km s-1. Based on this we adopt xHe = 0.60 and xH = 0.15.
3.2.3. Filling factors
The filling factor of the iron zone is determined by the energy input from the 56Ni decay during the first weeks, creating an “iron bubble” in the core (Woosley 1988; Herant & Benz 1991; Basko 1994). As we show in Sect. 4.4, analysis of the Fe/Ni/Co fine-structure lines can be used to determine the filling factor of this zone. We find fFe/He ≈ 0.15, which is used throughout the rest of the paper.
The oxygen density can be derived from the evolution of the [O i] λ6300/6364 line ratio, which is found to be similar to the one in SN 1987A (M12). We therefore use the same value for the oxygen density as derived for SN 1987A, nO = 6.2 × 10 cm-3 at 100 days (Spyromilio & Pinto 1991; Li & McCray 1992). This determines fO/Si/S, fO/Ne/Mg, and fO/C, giving a scaling proportional to the oxygen mass.
The Si/S zone was found by J11 to have expanded to a low density in SN 1987A, and is given a density ten times lower than the oxygen zone density.
The remaining core volume is divided between the mixed-in He/C, He/N, and H components to give them equal number densities.
The resulting filling factors for the three models are listed in Table 3.
Filling factors used for the core zones the three models.
3.2.4. Number of clumps Ncl
Several arguments suggest that the number of clumps produced in SN explosions is high. For SN 1987A, Chugai (1994) could reproduce the statistical fluctuations in the [O i] λλ6300, 6364 lines with 2000 clumps. Multi-dimensional models indicate strong mixing and a high degree of fragmentation (Kifonidis et al. 2006; Hammer et al. 2010). The strong O i λ1.129 μm line observed in SN 1987A requires synthesized3 oxygen to be mixed with hydrogen down to very small scales in order for the Bowen fluorescence to occur before Lyβ is converted to Paα (Oliva 1993), also supporting a large number of clumps. Based on these results, we choose the number of clumps Ncl = 103 for our modeling here.
3.2.5. Dust
Both S06 and M10 note that the [O i] λ6300 and Hα lines show shifts to the blue at around 300 days, and conclude that dust formed at this time. We have extended this analysis of the dust formation process by measuring the position of the line peaks for Na i λ58964, [O i] λ6300, Hαλ6563, [Fe ii] λ7155 and [Ca ii] λ73035, for all epochs in the 163–465 day range.
We measured the positions of the peaks in two ways; first by determining the wavelength of the maximum (within ±2000 km s-1 of the rest wavelength), and secondly by fitting a second-order polynomial to the part of the line that is within 15% of the peak flux. The two methods gave similar results. The resulting measurements with the second method are plotted in Fig. 2, together with straight-line fits.
 |
Fig. 2 Velocity shifts of the peaks of the strongest emission lines in the observed spectra as function of time. The symbols are estimates of the peak positions from fitting a parabola to the part of the line with a flux higher than 85% of the peak value (95% for [Fe ii] λ7155). The lines are linear fits to the measured values. |
All emission lines show a continuous blue-shifting trend with time. However, all lines, except [O i] λ6300, show a redshift of a few hundred km s-1 at early epochs. One possibility is that the SN has a higher recession velocity than the galactic one of 45 km s-1. However, positioned far out from the center in a galaxy seen almost face-on, a peculiar velocity of several hundred kilometers per second is unlikely. Another possibility is that these redshifts are due to electron scattering in the ejecta, whose optical depth is of order unity in the early nebular phase (Chugai 1977; Dessart & Hillier 2011). However, while electron scattering will produce a distinct red wing in the line profile (Auer & van Blerkom 1972; Chugai 1977; Fransson & Chevalier 1989), Fransson & Chevalier (1989) did not find any redshift of the peak in their simulations. We therefore favor a third possibility, that a fundamental asymmetry of the ejecta is the explanation.
Whatever the reason is for the early red-shifts, later on the line peaks change into blue-shifts, which is most likely caused by dust. The average value of the slope of the linear fits is −2.0 km s-1/day. Denoting the velocity shift as function of time by ΔV(t), and taking the dust formation to begin at day 250, we then write 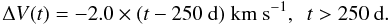 (1)The dust optical depth τd(t) can then be estimated from the formula for a uniformly emitting and absorbing sphere of velocity Vd (Lucy et al. 1991):
(1)The dust optical depth τd(t) can then be estimated from the formula for a uniformly emitting and absorbing sphere of velocity Vd (Lucy et al. 1991): ![\begin{equation} \frac{\Delta V(t)}{V_{\rm d}} = -1 + \frac{\ln\left[{1+\tau_{\rm d}(t)}\right]}{\tau_{\rm d}(t)}\cdot \label{formula:taud} \end{equation}](/articles/aa/full_html/2012/10/aa19528-12/aa19528-12-eq139.png) (2)The solution for τd(t), for Vd = 1800 km s-1, is plotted in Fig. 3 (red dashed line).
(2)The solution for τd(t), for Vd = 1800 km s-1, is plotted in Fig. 3 (red dashed line).
 |
Fig. 3 The (gray) dust optical depth function τd(t) derived from the observed dust luminosity (blue, solid), from the blue-shifts of line profiles (red, dashed), and the one we use for our modeling here (black, dot-dashed). |
The dust hypothesis is supported by Spitzer observations of a warm MIR-continuum at 500 K (K09, F11). In K09, a triple-component black-body fit reveals a steadily increasing fraction of the 56Co-deposition being re-radiated by a warm component, which is attributed to dust formed in the ejecta. By equating 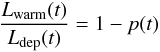 (3)where Lwarm(t) is the luminosity of the warm component, Ldep(t) is the energy deposition, and p(t) is the escape probability from a uniformly emitting sphere with constant opacity (Osterbrock & Ferland 2006),
(3)where Lwarm(t) is the luminosity of the warm component, Ldep(t) is the energy deposition, and p(t) is the escape probability from a uniformly emitting sphere with constant opacity (Osterbrock & Ferland 2006), ![\begin{equation} p(t) = \frac{3}{4\tau_{\rm d}(t)}\left[1 - \frac{1}{2\tau_{\rm d}(t)^2}+\left(\frac{1}{\tau_{\rm d}(t)}+\frac{1}{2\tau_{\rm d}(t)^2}\right){\rm e}^{-2\tau_{\rm d}(t)}\right] ,\label{eq:escapeprob} \end{equation}](/articles/aa/full_html/2012/10/aa19528-12/aa19528-12-eq145.png) (4)the dust optical depth function τd(t) can be determined. The resulting values (with Lwarm(t) and Ldep(t) taken from K09) are plotted in Fig. 3 (blue, solid line)6, and are compared with the values derived from the line-shifts. Within the errors expected from the uniform sphere assumption, the independent derivations agree reasonably well.
(4)the dust optical depth function τd(t) can be determined. The resulting values (with Lwarm(t) and Ldep(t) taken from K09) are plotted in Fig. 3 (blue, solid line)6, and are compared with the values derived from the line-shifts. Within the errors expected from the uniform sphere assumption, the independent derivations agree reasonably well.
For our modeling, we employ a functional form for the dust optical depth lying between the Spitzer and line-shift fits, given by 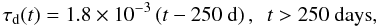 (5)shown as the black dot-dashed line in Fig. 3. The extrapolation after 500 days is uncertain, but is not relevant for any of the conclusions in this paper.
(5)shown as the black dot-dashed line in Fig. 3. The extrapolation after 500 days is uncertain, but is not relevant for any of the conclusions in this paper.
3.3. 56Ni mass
The 56Ni mass can be determined by comparing the estimated bolometric luminosity in the early tail-phase with the theoretical value of fully trapped 56Co deposition, which is given by 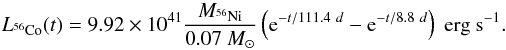 (6)Apart from the assumption of full trapping, one also has to assume that the deposited energy is instantaneously re-emitted, and that no other energy source has any influence.
(6)Apart from the assumption of full trapping, one also has to assume that the deposited energy is instantaneously re-emitted, and that no other energy source has any influence.
We used the UBVRIH photometry from day 142 (M10), together with an extrapolation outside the H-band (see below) to estimate the bolometric luminosity at this epoch. The linearly interpolated, dereddened UBVRIH flux at 142 days is 1.82 × 1041 erg s-1. The UBVRIJHKLMN1N2N3Q0 photometry of SN 1987A at day 135 (Hamuy et al. 1988; Bouchet et al. 1989) shows 26% of the total (linearly interpolated) U − Q0 flux to be outside the U − H range. Assuming a fraction of 0.26 also for SN 2004et, the extrapolated bolometric U − Q0 flux is 2.46 × 1041 erg s-1. From Eq. (6), this corresponds to a 56Ni mass of 0.062 M⊙. This is in good agreement with values derived by S06, M07, and M10.
3.4. Molecules
There are now a handful of detections of CO in core-collapse SNe, suggesting that its formation is common (e.g. Gerardy et al. 2000, 2002). In SN 1987A, CO emission was detected already in the photospheric phase, and persisted to over 600 days (Spyromilio et al. 1988; Bouchet & Danziger 1993).
Also SiO was formed in SN 1987A, detected from day ~250 and persisting to over 600 days (Roche et al. 1991; Bouchet & Danziger 1993). It has fewer detections in other SNe compared to CO, likely because it lacks a strong spectral feature in the NIR.
The 2.3 μm first overtone band of CO was detected in SN 2004et in the NIR spectrum taken at 307 days (M10). No earlier nebular NIR spectra exist to determine exactly when this feature emerged.
The 8 μm fundamental band of SiO was detected in the first Spitzer spectrum at day 295 (K09). It could then be followed until at least day 450, after which it became difficult to distinguish. No spectra covering the fundamental band of CO (4.6 μm) were taken, but its presence is revealed by the photometry (see Sect. 4.3.3).
 |
Fig. 4 Normalized photometric evolution (all magnitudes have been subtracted by t/102 d to normalize to the 56Co decay) of the (reddened) 12 M⊙ (blue, dot-dashed), 15 M⊙ (black, solid), and 19 M⊙ (green, dashed) models, compared to observations (red points). T.P. means “this paper”. The M10s, S06s, and TPs data points are synthetic photometry from the observed spectra. |
Models show that CO forms in the O/C zone, and SiO forms in the O/Si/S zone, with little formation of either in the O/Ne/Mg zone (Liu & Dalgarno 1995). Our models do not include molecules, and because these likely determine the temperature of the O/C and O/Si/S zones (Liu & Dalgarno 1995), we need some prescription for how to set these temperatures.
Spyromilio et al. (1988) found, assuming LTE and optically thin conditions, the temperature of the CO clumps in SN 1987A to decline from 3000 K to 1200 K between 192 and 350 days. Liu et al. (1992) found that inclusion of optical depth and NLTE effects gave a temperature evolution of 4000−1900 K. We assume that the temperature in the CO zone follows a linear interpolation of this result, but levels off at 1000 K at late times 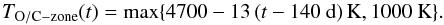 (7)For SiO, Liu & Dalgarno (1994) found a temperature evolution from 2000 K to 1000 K between 257 and 519 days in SN 1987A. We use the same interpolation method here
(7)For SiO, Liu & Dalgarno (1994) found a temperature evolution from 2000 K to 1000 K between 257 and 519 days in SN 1987A. We use the same interpolation method here 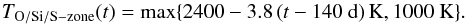 (8)Our results are not sensitive to the exact prescription for the temperature of these zones as they have too small mass and are too cold (assuming that some level of molecular cooling occurs) for any significant atomic thermal emission.
(8)Our results are not sensitive to the exact prescription for the temperature of these zones as they have too small mass and are too cold (assuming that some level of molecular cooling occurs) for any significant atomic thermal emission.
4. Results
4.1. Temperature evolution
For later guidance in the interpretation of line fluxes, Fig. 5 shows the model temperature evolution for the different zones, for the 15 M⊙ model. These results may also be of use in interpreting thermal emission line luminosities in other SNe with similar 56Ni mass.
4.2. Photometric evolution
Figure 4 shows the observed (normalized) U, B, V, R, I, J, H and K photometric evolution compared to the models. For clarity we have divided all fluxes with the exponential decay factor for 56Co, which in magnitudes corresponds to a subtraction by t/98 d. This reduces the span of magnitudes from ~8 to ~2, allowing greater detail to be seen.
In addition to the observed photometry, we also plot photometry obtained by convolving the observed spectra with the standard filter functions (filled (black) symbols). As is clear from the R-band and I-band plots, significant differences may occur here, due to the difficulty of transforming from telescope filters to standard filters for sources with strong emission lines, such as nebular phase SNe.
The models differ little in the U-band, all agreeing well with the data. The agreement (to within 20%) is quite striking, considering the enormous complexity of the radiative transfer in the UV. The relative brightening with time (up to the on-set of gamma-ray leakage at ~400 days) is due to decreasing line-blocking.
 |
Fig. 5 Evolution of model temperatures in the various core zones in the 15 M⊙ model. |
In the B-band, the models are also similar, reproducing the general time-evolution well. As in the U-band, the relative flux initially increases as line blocking decreases in efficiency. The small differences between the models in both U and B can be understood as a consequence of most of the radiation here originating from far out in the envelope (which has a similar structure in all models), the core being highly opaque due to line blocking.
From the V-band and on, line blocking is less efficient, and differences due to the different cores start to emerge. In V, the 12 and 15 M⊙ models are in good agreement with the observations at all times, whereas the 19 M⊙ model is too bright. The V-band includes Na i λλ5890, 5896 and [O i] λλ6300, 6364, and it is mainly too strong emission in these that cause the overproduction in the high-mass model (Sect. 4.3).
The R-band behaves similarly to the V-band. The band is dominated by Hα, but is also influenced by [O i] λλ6300, 6364, especially at late times. The fluxes in both lines are too strong in the 19 M⊙ model (see below), overproducing the R-band. The 12 and 15 M⊙ models are better, but still show some discrepancies as they also over-produce Hα (Sect. 4.3).
The I-band shows significant differences between the observed photometry and the synthetic photometry from the observed spectra, up to half a magnitude during the first year. The I-band is influenced by the [Ca ii] 7291, 7323 doublet as well as the Ca ii IR triplet, both lying on the edge of the filter. As mentioned before, this implies that SN I-band photometry has to be used with considerable caution.
 |
Fig. 6 Optical (dereddened) spectrum at 401 days (red) compared to the 12 M⊙ (blue) and 19 M⊙ (green) models. |
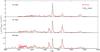 |
Fig. 7 Observed (dereddened) spectra (red) and 15 M⊙ model spectra at 212, 401, and 465 days (black). All spectra have been smoothed with a Gaussian of FWHM = 600 km s-1 to improve the S/N. |
In the NIR, the J and H data points at 134 and 141 days are important in showing that the models reproduce the flux reasonably well also in the NIR in the full gamma-ray trapping phase, which together with the good agreement in the other bands provide confirmation that the 56Ni mass is well determined. For the K-band, one should be aware that our models do not include the CO first overtone at 2.3 μm (which lies at the edge of the band), so we expect the models to be on the low side.
It is clear that the progenitor mass has its strongest influence on the V, R, and H bands, which are therefore valuable observables in the nebular phase. In U, B, I, J, and K, the differences are smaller.
4.3. Spectral evolution
4.3.1. Optical
Figure 6 shows the optical model spectra for the 12 and 19 M⊙ models compared to the observed (dereddened) spectrum at 401 days. It is clear that the main influence of the progenitor mass are the Na i λλ5890, 5896 and [O i] λλ6300, 6364 lines. The observed spectrum shows fluxes in these lines that fall in between the 12 M⊙ and 19 M⊙ models.
Also Hα, [Ca ii] λλ7291, 7323, and the Ca ii IR triplet fluxes differ between the models, although by less. These lines are mainly formed in the hydrogen zone, and are therefore not direct indicators of the core mass, but rather depend on the quite uncertain pre-SN mass loss and the explosive mixing.
The spectrum below 6000 Å is a complex mix of mainly iron-group lines formed by scattering and fluorescence in the hydrogen envelope. Because of the similar envelopes in the models, the model spectra differ by little in this spectral region. One exception is the Mg i] λ4571 line, which arises from the metal core.
 |
Fig. 8 Observed (dereddened) line fluxes (red points), normalized to the bolometric flux of 0.062 M⊙ of 56Co at a distance of 5.5 Mpc, compared to model values (12 M⊙: black, solid, 15 M⊙: blue, dot-dashed, 19 M⊙: green, dashed). See the text (Sect. 4.3.1) for details on the line flux measurements. |
 |
Fig. 9 Near-infrared (dereddened) spectrum at 307 days (red) compared to the 12 M⊙ (blue), 15 M⊙ (black), and 19 M⊙ (green) models. The boxed regions at 1.5−1.2 μm and 1.4−1.7 μm show particular sensitivity to the core mass. Note that CO emission is not included in the model spectra. |
The 15 M⊙ model spectra at 212, 401, and 465 days are plotted in Fig. 7. We see that this model is generally successful in reproducing the observed spectra, and in particular reproduces the [O i] λλ6300, 6364 lines well at all epochs. This is further corroborated by Fig. 8, where we plot the evolution of Mg i] λ4571, Na i λλ5890, 5896, [O i] λλ6300, 6364, [Ne ii] λ12.81 μm, Hα, [Fe ii] λλ7155, 7172, [Ca ii] λλ7291, 7323, and the Ca ii IR triplet, from the observed spectra as well as from the three different models. Both observed and modeled fluxes have been normalized to the bolometric flux of 0.062 M⊙ of 56Co, assuming a distance of 5.5 Mpc. The resulting numbers therefore represent the fraction of the radioactive decay energy re-emerging in the various lines. The optical line flux measurements were done by integrating the spectra over Vcut = ±2700 km s-1 and subtracting the continuum level, which was taken as the linear interpolation of the minimum flux values on the right and lefthand side, within Vcont = ±1.25Vcut = ±3375 km s-1. These velocity limits were found to give reasonable extractions of the line fluxes for all lines and epochs, except for Hα for which we used Vcut = ±7200 km s-1 and Vcont = 1.25Vcut = ±9000 km s-1 to include the broad wings. Because we perform the same operation on model and observed spectra, the choice is not critical for the comparison.
Diagnostic lines of the core mass.
The most important lines as diagnostics of the core mass are [O i] λλ6300, 6364. These lines are distinct at most epochs, relatively undisturbed by line-blending and line blocking (there is, however, some iron line emission blended with them, see Dessart & Hillier 2011), and have at least half their flux coming from synthesized oxygen (M12). In addition, oxygen is mainly neutral in the core, while magnesium and sodium are mainly ionized, meaning that the thermal emission by O i is quite insensitive to the ionization balance. In all models, the thermal emission by [O i] λλ6300, 6364 from the O/Ne/Mg zone corresponds to 50−60% of the heating of this zone, at all times after 300 days. Combined with the constraints on the density that the 6300/6364 flux ratio provides (M12), the doublet lines are excellent diagnostics of the core mass. The main complication is that primordial oxygen in the hydrogen zone contributes to the emission as well (M12). In the 15 and 19 M⊙ models, however, there is so much synthesized oxygen that this contribution is quite small.
Also the Mg i] λ4571 line is a potentially useful diagnostic of the O/Ne/Mg zone. According to the models, this is the strongest optical Mg i line, followed by Mg i λλ5167, 5172, 5183, which is too weak to be detected. The Mg i] λ4571 line is, however, also rather weak and difficult to extract. The first clear detection is in the spectrum taken at 284 days. Before that, complex line blending and blocking makes it difficult to distinguish, and even later it is possible that the emission is blended. The last spectrum at day 465 has too poor signal-to-noise ratio (S/N) to assess the line.
None of the models produce any distinct Mg i] λ4571 until 200−300 days after explosion, in agreement with the observations. The evolution after that is in best agreement with the 15 M⊙ model, but the model differences are quite small. Observations after 500 days would have allowed a more conclusive comparison between the models to have been made with regard to this line.
Mg ii is the dominant ion in the O/Ne/Mg zone at all epochs, so the Mg i lines have strong contributions by recombination. The transition has a thermal emission of about 10% of the [O i] λλ6300, 6364 emission. This is not enough to account for the luminosity of the line (Fig. 8), so recombinations indeed dominate the emission.
The Na i D resonance lines are optically thick quite far out in the H-envelope (to 6200 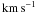 at day 300). The lines are therefore formed by a combination of P-Cygni scattering and by emission by synthesized sodium in the core. The D lines are responsible for some of the cooling of the O/Ne/Mg zone, but most of the emission is recombination. The observed flux is in good agreement with the 12 and 15 M⊙ models, but is strongly overproduced by the 19 M⊙ model. Less influenced by line blocking and blending than the Mg i] λ4571 line, but still sensitive to charge transfer (J11) as well as the hydrogen envelope properties (through the scattering), this line is intermediate to the Mg i] λ4571 and [O i] λλ6300, 6364 lines in model parameter sensitivity.
at day 300). The lines are therefore formed by a combination of P-Cygni scattering and by emission by synthesized sodium in the core. The D lines are responsible for some of the cooling of the O/Ne/Mg zone, but most of the emission is recombination. The observed flux is in good agreement with the 12 and 15 M⊙ models, but is strongly overproduced by the 19 M⊙ model. Less influenced by line blocking and blending than the Mg i] λ4571 line, but still sensitive to charge transfer (J11) as well as the hydrogen envelope properties (through the scattering), this line is intermediate to the Mg i] λ4571 and [O i] λλ6300, 6364 lines in model parameter sensitivity.
We do not reproduce the [Ne ii] 12.81 μm line well with any of the models. We discuss this line more in the section about the MIR lines.
Diagnostic lines of the hydrogen and helium zones.
In addition to the the hydrogen and helium lines, also many metal lines are dominated by emission from the hydrogen and helium zones. The strongest lines from these zones are discussed in detail in M12, and we will therefore here only make some specific points relevant for this paper.
The hydrogen envelope mass is similar in the three models, 7.7−9.5 M⊙ (Table 2). We also assume the fraction mixed into the core to be the same in all models (xH = 0.15). There are therefore no major differences in the H-zone lines between the models. Still, as Fig. 8 shows, the lines from this zone do differ somewhat, as the hydrogen and helium zones have different densities for their in-mixed components, and are also exposed to different amounts of gamma-rays as well as diffuse radiation, depending on the metal content of the core.
Hα is formed by recombinations following photoionizations in the Balmer continuum up to ~500 days, and recombinations following non-thermal ionizations from the ground state after that. With less core material to absorb the gamma-rays in the lower-mass models, the Hα flux is somewhat higher, although the hydrogen mass is smaller. The observed flux is lower than in all models. As most of the model flux comes from the in-mixed hydrogen component, a reduction in in-mixing below 15% would likely improve the fits. Note, however, that the Hα flux in SN 1987A was about a factor of two weaker than expected (from the other hydrogen recombination lines) in the 200−500 day range (Xu et al. 1992), still without an explanation.
The [Ca ii] λλ7291, 7323 lines are significant coolants of the hydrogen zone (Li & McCray 1993, KF98b, M12). The models differ by little, both agreeing reasonably well with the data. The ratio of the Ca ii triplet lines to the 7291, 7323 Å lines depends on the temperature and density (Fransson & Chevalier 1989; Ferland & Persson 1989; Li & McCray 1993). Our models give a slightly too high triplet to 7291, 7323 Å ratio, which indicates that our density in the Ca ii emitting gas may be too high.
4.3.2. Near-infrared
Figure 9 shows the day 307 NIR spectrum compared to the models. It is clear that the core mass has a significant influence on the spectral features at 1.15−1.2 μm and 1.4−1.7 μm. The plateau-like feature at 1.15−1.2 μm is a blend of C i λ1.176, 1.181 μm (C/O zone + He/C zone), Mg i λ1.183 μm (O/Ne/Mg zone), Si i λ1.200 μm (Si/S zone + O/Si/S zone), as well as several Fe i lines from both the Fe/He zone and from the O/Ne/Mg zone. The 1.4−1.7 μm range contains emission by C i λ1.454 μm (C/O zone + He/C zone), Mg i λ1.504 μm (O/Ne/Mg zone), [Si i] λ1.607, 1.645 μm (Si/S zone), and [Fe ii] λ1.534 μm, 1.600 μm, 1.644 μm, 1.681 μm (Fe/He zone). As an important complement to the optical analysis, we find that the 15 M⊙ model produces better fits than the 12 and 19 M⊙ models for these metal emission lines as well.
The O i + Na i feature at 1.13 μm may seem to suggest a higher-mass progenitor than 19 M⊙. However, the O i λ1.129 μm line (which dominates the blend) is produced by H i Lyβ branching into O i λ1025.76 2p4(3P) − 3d(3Do), and Oliva (1993) found that much of this branching must occur over zone boundaries, with Lyβ photons scattering into regions of synthesized oxygen while trapped between n = 1 and n = 3 in H i. Our modeling does not treat such line overlap between zones (although we do treat the overlap within each zone, see Appendix B.5), and we can therefore not properly model the line.
The strongest feature in the NIR is He i λ1.083 μm + [S i] λ1.082 μm, which is a bit too strong in the models. Of the hydrogen lines, both Paα and Paβ are also overproduced. Together with the overproduction of Hα, this suggests that the He and H content of the models may be too large, and/or too strongly mixed into the radioactive core.
4.3.3. Mid-infrared
As shown by K09, and discussed in Sect. 3.2, the mid-IR is dominated by a combination of warm dust emission from the ejecta and cold dust emission from the circumstellar environment, with superimposed atomic and molecular emission lines from the ejecta. To reproduce the spectrum in this region it is therefore necessary to include these dust components. For this we repeat the modeling in K09, although with slightly different parameters, since we here include also the detailed contribution by atomic emission (which was approximated as a hot blackbody in K09).
For ejecta dust extinction we use the smoothed Draine & Lee model with “astronomical” silicate (Draine & Lee 1984; Laor & Draine 1993) and use the escape probability formalism (Eq. (4)). As parameters at 350 and 451 days we find temperatures of 700 and 600 K, and optical depths at 10 μm of 2.1 and 3.2, respectively, to be good choices for reproducing the observed spectrum. These values are similar to the ones derived by K09. For the circumstellar dust component, we assume a blackbody SED, and obtain a good fit at 350 days with T = 50 K and L = 3 × 1038 erg s-1.
We also add a component of vibrational-rotational SiO lines from the fundamental band at 7−9 μm. These are calculated from a NLTE solution of the SiO molecule, including the first 100 rotational levels of the v = 0 to v = 3 vibrational levels, with collision rates from Varambhia et al. (2009) and Liu & Dalgarno (1994), and radiative transition rates from Drira et al. (1997). The parameters for this component are the temperature, the electron density, and the total luminosity. For the electron density we take ne = 7 × 107 cm-3 at 350 days and ne = 2.6 × 107 cm-3 at 451 days, as given by the models for the O/Si/S zone. Because of the limited S/N and resolution of the spectra, the shape of the P and R branches of the v = 1 to v = 0 bands are not well defined. We therefore use a temperature similar to that in SN 1987A of 1500 K (Liu & Dalgarno 1994). We assume a velocity equal to that of the core velocity. For the luminosity, we find that LSiO = 9.9 × 1037 erg s-1 at 350 days and LSiO = 4.3 × 1037 erg s-1 at 451 days reproduce the observed spectra in the 7−9 μm range well.
 |
Fig. 10 Observed MIR spectrum at 350 days (red, solid line), compared to model spectra of the 15 M⊙ model (black, solid). To simulate the instrument response, the model has been convolved with a Gaussian of FWHM = λ/R, where the resolving power R was taken to be 60. Also shown are the dust component (pink, dashed), the observed photometry at 3.6 and 4.5 μm (red stars), and the corresponding model photometry for the model (black circles). The observed photometry is at 361 days, and has been rescaled with the 56Co decay factor to 350 days (exp−11/111.5). |
Figures 10 shows the Spitzer spectrum at 350 days (red line), together with the 15 M⊙ model spectrum including the ejecta dust, circumstellar dust, and SiO components described above (black line). It is clear that above 8 μm, dust emission dominates the atomic emission. At shorter wavelengths, however, the atomic emission is about as strong as the dust emission. It is also clear that CO 4.55 μm fundamental band emission is present, as there is not enough emission by dust and atoms in the 4−5 μm range to account for the photometric 4.5 μm observations. To reach the observed flux, we need LCO = 6.0 × 1038 erg s-1 at 350 days, and for 295 and 451 days we need LCO = 4.1 × 1038 erg s-1 and LCO = 2.1 × 1038 erg s-1, respectively. That significant amounts of CO have formed is also evidenced by the presence of the first overtone band at 2.3 μm (Fig. 9). The presence of both CO and SiO emission supports our assumption of molecular cooling occurring in the O/Si/S and O/C zones (see also Sect. 4.4.1).
The atomic lines we identify using our model spectra are labeled in Fig. 10. Most lines do not differ significantly between the models, as they mainly originate in the Fe/He or H zones. The only line sensitive to the core mass is [Ne ii] λ12.81 μm. This line, arising in our models mainly from the He/C zone, but also from the O/Ne/Mg zone, is too strong in all models, suggesting that the neon content in this zone is too high, that we have mixed the He/C zone too strongly into the radioactive core, or that our ionization solution overproduces singly ionized neon.
In our models, the [Ar ii] λ6.985 μm line is not emitted by synthesized argon, but by primordial argon in the He zone. Here, argon is singly ionized and is responsible for about 1% of the cooling. The synthesized argon is located mainly in the Si/S zone, but is here only ionized to ~10-4−10-3, and provides only ~10-4 of the cooling, which is dominated by [S i] and [Ca ii].
4.4. Determination of the iron zone filling factor
As demonstrated for SN 1987A, the infrared iron-group lines are useful as diagnostics of the physical conditions in the 56Ni “bubble”, resulting from radioactive 56Ni heating (Moseley et al. 1989; Haas et al. 1990; Spyromilio & Graham 1992; Roche et al. 1993; Li et al. 1993). A complication is, however, that there are varying contributions to these lines from primordial iron from the H and He zones (KF98b, M12). In addition, the studies mentioned make several assumptions about the ionization balance and optical depths. More reliable results require calculation of these quantities.
Because both the Fe/He and H/He zones are similar in the various models, the iron-group lines differ little between them, and we consider only the 15 M⊙ model. The electron density in the Fe/He zone at 350 days is of order 109 cm-3 in the model, much higher than the critical densities for forbidden fine-structure lines (~105 cm-3), so all lines arising from the lower multiplets are in LTE. We find, for all possible filling factors of the iron clumps, optical depths much higher than unity for the [Fe ii] λ17.94 μm and [Fe ii] λ25.99 μm lines. These lines are thus both in LTE and optically thick. The general expression for line luminosity, in the Sobolev approximation, is 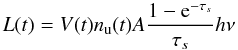 (9)where V(t) is the zone volume, nu(t) is the number density of the upper level, A is the transition probability, and τs is the Sobolev optical depth. For an optically thick line in LTE, Eq. (9) becomes
(9)where V(t) is the zone volume, nu(t) is the number density of the upper level, A is the transition probability, and τs is the Sobolev optical depth. For an optically thick line in LTE, Eq. (9) becomes 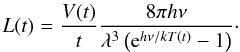 (10)Since hν ≪ kT for the MIR lines, the line luminosity is then
(10)Since hν ≪ kT for the MIR lines, the line luminosity is then 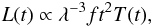 (11)where f is the filling factor. Since we, at a given time t, can compute the temperature T(t) for any given filling factor f, we are therefore in a good position to determine the latter by comparing model line luminosities to the observed ones.
(11)where f is the filling factor. Since we, at a given time t, can compute the temperature T(t) for any given filling factor f, we are therefore in a good position to determine the latter by comparing model line luminosities to the observed ones.
 |
Fig. 11 Model Fe/Ni/Co line fluxes relative to observed values, at 295 days. The 15 M⊙ model has been used. |
Figures 11–13 show the model fluxes of the Fe/Co/Ni MIR lines relative to the measured fluxes, as a function of fFe/He. When we vary fFe/He, we add/subtract the corresponding amount to fH. We measure the line fluxes as described in Sect. 4.3.1, using Vcut = ±6400 km s-1 (=±3σ for R = 60), and Vcont = 1.25Vcut = ±8000 km s-1. The model spectra were convolved to the Spitzer resolution (R = 60), before this operation. For each epoch we only plot the lines with clear detections.
The MIR lines behave quite consistently, many of them being optically thick and in LTE. The filling factor-dependency is generally weaker than Eq. (11) suggests, as there is also an (almost constant) component from the He/H zones. We find that we can fit the Fe/Ni/Co lines only if fFe/He = 0.1−0.2. At larger values, the singly ionized lines become too strong, and in addition doubly ionized lines ([Fe iii] λ22.94 μm, [Co iii] λ11.89 μm, [Co iii] λ16.39 μm) emerge in the model. These lines are not observed, and we therefore rule out a filling factor larger than fFe/He ≈ 0.3. Values much smaller than fFe/He ≈ 0.1 can also be ruled out, as the singly ionized lines are then too weak, and unobserved neutral lines in the optical/NIR (Fe i] 4s(a5F) − 4s4p(z7Do) transitions between 8000−8500 Å and [Fe i] 4s2(a5D) − 4s(a5F) transitions at 1.36, 1.44 and 1.53 μm), are strong. A filling factor of fFe/He = 0.1−0.2 is also supported by the [Fe ii] λ7155 line, whose behavior agrees well with the MIR lines, removing any uncertainty regarding the MIR calibration for our conclusions.
As is seen in the figures, [Fe ii] λ24.52 μm is not reproduced well by any filling factor. This line is, however, weak and in a noisy part of the spectrum. Also the [Fe ii] λ25.99 μm line shows poorer agreement compared to the shorter wavelength lines.
Our result here is close to the fFe/He value derived for SN 1987A by KF98b (fFe/He ≈ 0.2). The value derived by Li et al. (1993) (fFe/He > 0.3) is likely too large as they ignore the primordial Fe emission. We find that for fFe/He = 0.15 and t = 350 days, the contribution by primordial iron-group elements in the H and He zones to the line fluxes is 30−40% for the [Fe ii] lines, and 20% for [Ni ii] λ6.636 μm. The contribution by primordial cobalt is low (<1%) as the solar abundance of cobalt is very low. The [Co ii] λ10.52 μm line thus comes from the radioactive 56Co, but being optically thick (up to 500 days) does not allow an independent determination of the 56Co mass. Also the [Co ii] λ14.74 and 15.46 μm lines have significant optical depth (τ ≈ 1 at 350 days).
The [Ni ii] λ6.634 μm line arises mainly from stable 58Ni in the Fe/He zone, with some contribution from 57Ni. We find that the [Ni ii] 6.634 line is well produced by the amount of 58Ni in the explosion models (M(58Ni)/M(56Ni) ≈ 0.04).
4.4.1. Molecules
Figures 14–15 show the estimated total luminosities of CO and SiO (Sect. 4.3.3), compared to the heating of the O/C and O/Si/S zones in the three models. If molecules are responsible for all of the cooling in these zones, these values should match for the model with the correct O/Si/S and O/C zone masses.
For SiO, no observations of the overtone exist, and for CO, we have only one observation. The CO overtone luminosity at the other epochs is assumed to scale to the day 307 luminosity in the same manner as in SN 1987A (Bouchet & Danziger 1993). It contributes less than 10% to the total luminosity at 350 and 450 days.
 |
Fig. 14 Observed flux in the CO fundamental band (hollow squares), first overtone (diamond), and estimated total (filled squares), compared to the total heating of the O/C zone in the various models. For the estimated total emission, correction for the internal dust extinction has been taken into account. All values have been normalized to the decay of 0.062 M⊙ of 56Co. |
The CO emission falls in between the 12 and 15 M⊙ models, behaving consistently with the optical emission lines. This result is also important in ruling out CO as a possibility for a more massive progenitor to still produce weak [O i] 6300, 6364 Å emission from the O/Ne/Mg zone. The observed CO flux in such a case would be much stronger.
The SiO emission is about a factor of 2–3 below the total heating of the O/Si/S zone in all of the models. As for CO, this is important for constraining the possible cooling channels of the O/Ne/Mg zone. Note that O/Si/S zone does not grow monotonically with progenitor mass, being larger in the 15 M⊙ model than in the 19 M⊙ one (Table 2).
It is possible that SiO only does part of the cooling of the O/Si/S zone. However, with the large partition function of molecules, one would expect it to dominate the cooling. The determination of the SiO fundamental band flux is complicated by the silicate dust feature at the same wavelength, possibly explaining the discrepancy. It is also likely that the silicate dust, which presumably forms in the same zone as the SiO, produces stronger extinction there than for the spectrum as a whole, and/or does some of the cooling.
5. Discussion
In evaluating the robustness of linking the nebular spectra to a progenitor mass, there are several aspects to consider. Our models test specific stellar evolution/explosion models (in our case the models by WH07), and the zone masses and compositions in these may vary depending on the assumptions about convection, rotation, and nuclear burning rates (see e.g., Schaller et al. 1992; Woosley & Weaver 1995; Thielemann et al. 1996; Woosley et al. 2002; Hirschi et al. 2004). It is beyond the scope of this paper to test all types of models with respect to variation in these parameters. However, an attempt to judge the influence of some of them is warranted.
The influence of metallicity on the total nucleosynthesis yield is quite weak, although it does affect specific elements in particular zones (WW95). Estimates of the metallicity in the region of SN 2004et indicate that it is likely within a factor two from solar (Sect. 2.2), and such a variation should not have any strong impact on the stellar evolution or SN spectral formation. Although it was found by M12 that emission by primordial metals in the hydrogen envelope can be significant contributors to the nebular spectrum, this emission will change little with metallicity as long as the relative amounts of metals are roughly the same. The fraction of cooling done by each element will then roughly stay the same, although a slight temperature increase will occur for lower metallicities due to the fewer number of coolants available. We therefore do not think that the assumption of solar metallicity is crucial for any of our conclusions.
Rotation can enhance the nucleosynthesis yield for a given stellar mass (e.g. Hirschi et al. 2004). For rapidly rotating progenitor models, our best fit would (most likely) have been a lower-mass star. With regard to this parameter, we can therefore say that 15 M⊙ is an upper limit to the progenitor mass. One should note, however, that the progenitor analyses (e.g. Crockett et al. 2011) also assume non-rotating stars, so if one postulates rotation, best-fitting progenitor models also go down in mass (rotation boosts luminosity in the late evolutionary stages).
Assumptions about the symmetry, mixing, and fragmentation of the explosion also influence the model outputs. The observed line profiles constrain the velocity range of the material, however, and furthermore do not indicate any extreme asymmetries in the SN. As gamma-rays scatter around the whole ejecta in the nebular phase, neither is it obvious that even strong asymmetries will significantly change the energy deposition in the various zones.
Our results here are in fair agreement with the progenitor analysis of SN 2004et, which has given 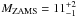 M⊙ (Fraser et al., in prep.). On the other hand, hydrodynamical modeling by Utrobin & Chugai (2009) gave an ejecta mass of 24.5 M⊙, over a factor two larger than the ejecta mass of our best-fitting model here (10.9 M⊙), as well as any final mass in standard stellar evolution models (the maximum ejecta mass with standard mass-loss rates is ~14 M⊙ (Kasen & Woosley 2009), and will be even lower if strong pulsation-driven mass-loss occurs in the RSG phase (Yoon & Cantiello 2010). The discrepancy between the hydrodynamical modeling and the progenitor analysis/nebular-phase spectral analysis is important to understand. More independent analyses in all three fields are needed to make progress here. A possible concern regarding the hydrodynamical modeling by Utrobin & Chugai (2009) is that non-evolutionary progenitor models are used.
M⊙ (Fraser et al., in prep.). On the other hand, hydrodynamical modeling by Utrobin & Chugai (2009) gave an ejecta mass of 24.5 M⊙, over a factor two larger than the ejecta mass of our best-fitting model here (10.9 M⊙), as well as any final mass in standard stellar evolution models (the maximum ejecta mass with standard mass-loss rates is ~14 M⊙ (Kasen & Woosley 2009), and will be even lower if strong pulsation-driven mass-loss occurs in the RSG phase (Yoon & Cantiello 2010). The discrepancy between the hydrodynamical modeling and the progenitor analysis/nebular-phase spectral analysis is important to understand. More independent analyses in all three fields are needed to make progress here. A possible concern regarding the hydrodynamical modeling by Utrobin & Chugai (2009) is that non-evolutionary progenitor models are used.
We also mention the results in Chevalier et al. (2006), who estimated a progenitor mass of ~20 M⊙ by linking the estimated mass-loss rate from radio observations to standard mass-loss laws and stellar evolution models. This result relies on several assumptions (wind velocity, shell velocity, circumstellar temperature, and dominance of free-free opacity), and in addition the mass-loss laws have standard deviations of a factor 2−3. Rho et al. (2007) derived a lower mass-loss rate of 2 × 10-6 M⊙ yr-1, which corresponds to a MZAMS = 15 M⊙ progenitor.
Comparing with other nebular-phase analysis of SN 2004et, we reach a similar conclusion as S06 and M10 do by simply comparing the [O i] doublet to SN 1987A, that the oxygen mass is somewhat lower than in SN 1987A, and the progenitor thereby a bit less massive (assuming similar rotation etc.). We have here, however, put this result on a much firmer footing by computing detailed models and finding consistent results from several other lines. One should also bear in mind the contribution by primordial oxygen that complicates such simple comparisons (M12). The comparison to SN 1987A works quite well in this case as these two SN both have large masses of synthesized oxygen, similar velocities, and similar 56Ni-masses. One should note though, that the progenitor mass of SN 1987A cannot be taken to be known better than in the range 16−22 M⊙ (Arnett et al. 1989). Since modeling of SN 1987A would require only small changes to the parameters used here, we would most likely find a mass on the lower side of this range.
Dessart et al. (2010) find, using models without any macroscopic mixing, a correlation between the width of the oxygen lines and the progenitor mass (for a fixed explosion energy). For an explosion energy of 2.3 B, they find that the progenitor mass of SN 2004et should be less than 18 M⊙, which is in agreement with our result here.
For a more general comparison of our modeling with other work, we consider the results in Dessart & Hillier (2011), who compute model spectra for 15 and 25 M⊙ progenitors, also taken from WH07. These authors include a full NLTE and radiative transfer treatment, and in this sense their work is complementary to ours. They do, however, assume some microscopic mixing to occur, which may have important effects on the cooling and ionization balance, and therefore also on the emerging spectrum. At 300 days, the difference in the flux of the [O i] doublet appears to differ by the same amount as the 56Ni mass in the two models (factor 1.9), a result possibly in disagreement with our model, but since we use the same 56Ni mass for all models we cannot say with certainty. At 1000 days the more massive star shows about a factor of 3.6 stronger [O i] λλ6300, 6364 emission, or a factor 1.9 stronger per unit 56Co mass.
In M12, it was shown that the diversity of line emission in a sample of Type IIP SNe is quite small. One reason for this was found to be that the large hydrogen envelopes in these objects add significant contribution to all metal emission lines, mitigating the impact of varying core masses. Despite this damping effect, our modeling here suggests that stars at and above 19 M⊙ should produce Na i λλ5890, 5890, [O i] λλ6300, 6364, [Ne ii] λ12.81 μm, [Si i] λ1.60, 1.64 μm about a factor two stronger than lower-mass progenitors (15 M⊙ and below). None of the SNe in the M12 sample, including SN 1987A, show such strong oxygen emission. Future detailed modeling of individual objects (making sure the “missing flux” cannot be accounted for in other lines such as CO), and a larger sample size, will show if these high-mass stars are indeed missing from the Type IIP group.
6. Conclusions
-
We have shown that nebular-phase spectral modeling can be used to constrain the progenitor masses of Type IIP supernovae. Lines showing significant dependency on the progenitor mass are [O i] λλ6300, 6364, Na i λλ5890, 5896, Mg i] λ4571, Mg i λ1.503 μm, C i λ1.176 μm, C i λ1.454 μm, Si i λ1.20 μm, [Si i] λλ1.607, 1.645 μm, and [Ne ii] λ12.81 μm.
-
The nebular-phase optical and near-infrared emission lines of SN 2004et are well reproduced by model spectra of a MZAMS = 15 M⊙ (non-rotating) progenitor star, with an oxygen mass of 0.8 M⊙. Spectra from 12 and 19 M⊙ progenitors under- and overproduce most of the nebular phase lines, respectively, with particular discrepancy for the high-mass model. This result is in fair agreement with the analysis of pre-explosion imaging (
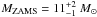 , Fraser et al., in prep.), but in disagreement with the progenitor mass inferred from hydrodynamical modeling (MZAMS > 25 M⊙, Utrobin & Chugai 2009).
, Fraser et al., in prep.), but in disagreement with the progenitor mass inferred from hydrodynamical modeling (MZAMS > 25 M⊙, Utrobin & Chugai 2009). -
In the 300−600 day range, we find that the [O i] 6300, 6364 doublet emits 1, 2, and 4−6% of the 56Co decay energy for 12, 15, and 19 M⊙ progenitor stars. This result may be used for a coarse diagnosis of other Type IIP SNe with similar 56Ni mass (0.06 M⊙).
-
By modeling the mid-infrared iron-group lines observed with Spitzer, we determine a filling factor f = 0.15 for the Fe/Co/Ni clumps in the ejecta, corresponding to a density ρ(t) = 7 × 10-14 × (t/100 d)-3 g cm-3. This is similar to the filling factor derived for SN 1987A by Kozma & Fransson (1998b), whereas Li et al. (1993) likely overestimate the filling factor due to neglect of emission by primordial iron in the hydrogen zone.
-
By our calculation of the atomic emission lines and continua, we can confirm the contribution by a silicate dust feature to the mid-infrared spectrum, first identified by Kotak et al. (2009), as well as the presence of SiO and CO fundamental band emission in the spectrum. The CO luminosity matches the total heating of the O/C zone in a 12−15 M⊙ progenitor.
Online material
Appendix A: Chemical composition of explosion models
Tables A.1–A.3 show the chemical composition of the three explosion models we use (taken from Woosley & Heger 2007).
Chemical composition (mass fractions) of the 12 M⊙ model used.
Appendix B: Code updates compared to J11
B.1. Photoexcitation/deexcitation rates
Because the computations here are for earlier epochs than in J11, photoexcitation/deexcitation rates in the NLTE solutions have to be included. We therefore implemented a modified Monte Carlo operator to allow for partial deposition of photoexcitation energy along the photon trajectories. A photon packet of comoving energy E and frequency ν, coming into resonance with a transition l → u of atom k, where the upper level 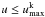 (=the number of levels included in the NLTE solution of atom k), now increases the number of photoabsorbed packages by
(=the number of levels included in the NLTE solution of atom k), now increases the number of photoabsorbed packages by 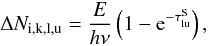 (B.1)where i is the zone index and
(B.1)where i is the zone index and 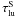 the Sobolev optical depth. The packet then continues (undeflected) with energy
the Sobolev optical depth. The packet then continues (undeflected) with energy 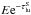 . For lines with
. For lines with 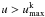 , we retain the treatment described in J11 (scattering/fluorescence is treated explicitly in the transfer). rescaled so that no photoexcitation energy is deposited).
, we retain the treatment described in J11 (scattering/fluorescence is treated explicitly in the transfer). rescaled so that no photoexcitation energy is deposited).
The values for 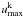 should be chosen large enough to reasonably well sample the total number of photoexcitations from each level, but small enough to ensure stability and keep computation times limited (matrix inversion times in the statistical equilibrium solutions scale as
should be chosen large enough to reasonably well sample the total number of photoexcitations from each level, but small enough to ensure stability and keep computation times limited (matrix inversion times in the statistical equilibrium solutions scale as 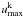 cubed). The
cubed). The 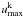 values used here can be found in Table B.2. We have chosen to set
values used here can be found in Table B.2. We have chosen to set 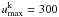 for all iron-group elements (except Fe i, Fe ii and Cr ii, where we solve for more levels), and
for all iron-group elements (except Fe i, Fe ii and Cr ii, where we solve for more levels), and 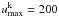 for the non-iron-group elements.
for the non-iron-group elements.
In the Sobolev approximation, the photoexcitation rates to be used in the statistical equilibrium equations are given by (Castor 1970) 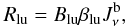 (B.2)\vadjust{\eject\vspace*{11cm}}where Blu is the Einstein coefficient for photoexcitation, βlu is the escape probability, and
(B.2)\vadjust{\eject\vspace*{11cm}}where Blu is the Einstein coefficient for photoexcitation, βlu is the escape probability, and 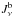 is the far blue-wing mean intensity (before Jν is affected by the line). The deexcitation rate is related by detailed balance
is the far blue-wing mean intensity (before Jν is affected by the line). The deexcitation rate is related by detailed balance 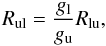 (B.3)where gl and gu are the statistical weights.
(B.3)where gl and gu are the statistical weights.
Overlapping lines may cause 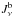 to significantly vary with the choice of the blue frequency. We therefore do not compute the photoexcitation rates from this equation, but by adding the contributions from Eq. (B.1). Since stimulated emission is treated as negative absorption in the Sobolev optical depth, Eq. (B.1) gives only the net number of photons absorbed in the line; absorptions minus stimulated emissions. The actual number of absorptions occurring is therefore higher by a factor (1 − glnu/gunl)-1, where nl and nu are the populations of levels l and u, so the estimator for the photoexcitation rate is
to significantly vary with the choice of the blue frequency. We therefore do not compute the photoexcitation rates from this equation, but by adding the contributions from Eq. (B.1). Since stimulated emission is treated as negative absorption in the Sobolev optical depth, Eq. (B.1) gives only the net number of photons absorbed in the line; absorptions minus stimulated emissions. The actual number of absorptions occurring is therefore higher by a factor (1 − glnu/gunl)-1, where nl and nu are the populations of levels l and u, so the estimator for the photoexcitation rate is 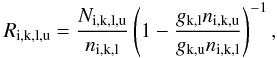 (B.4)where Ni,k,l,u is the total number of packets absorbed in the transition in the Monte Carlo simulation.
(B.4)where Ni,k,l,u is the total number of packets absorbed in the transition in the Monte Carlo simulation.
For lines with 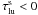 , we allow lasering to occur in the transfer by using the same formalism as for normal positive optical depths (Eq. (B.1)). In these cases we compute the deexcitation rate as
, we allow lasering to occur in the transfer by using the same formalism as for normal positive optical depths (Eq. (B.1)). In these cases we compute the deexcitation rate as 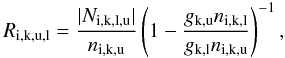 (B.5)and then use Eq. (B.3) to get the excitation rate.
(B.5)and then use Eq. (B.3) to get the excitation rate.
B.2. Charge transfer
We now generalize the treatment of the O ii + C i → O i(2p(1D)) + C ii reaction in J11, by assuming that all charge transfer reactions occur to the state (either in the recombining or in the ionizing element) that gives the smallest energy defect.
B.3. Photoionization rates and photoelectric heating rates
We have also modified the estimators for the photoionization rates and the photoelectric heating rates. Whereas the previous treatment did not allow splitting of packets upon continuum interaction, a photon packet passing a region of optical depth τ, of which photoionization by atom k, level l, contributes 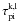 , now adds a contribution
, now adds a contribution 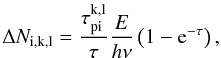 (B.6)to the number of photons Ni,k,l absorbed in the corresponding continuum. The heating rate is increased by
(B.6)to the number of photons Ni,k,l absorbed in the corresponding continuum. The heating rate is increased by  (B.7)where Vi is the volume of the zone, and χk,l is the ionization potential.
(B.7)where Vi is the volume of the zone, and χk,l is the ionization potential.
B.4. Electron scattering
We implement electron scattering in the following way. The total continuum optical depth to the next point of interest (a zone boundary, a line, or a photoionization threshold) is 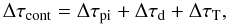 (B.8)where Δτpi is the photoionization optical depth, Δτd is the dust optical depth, and ΔτT is the Thomson optical depth. The fraction of photons absorbed in photoionization continua is
(B.8)where Δτpi is the photoionization optical depth, Δτd is the dust optical depth, and ΔτT is the Thomson optical depth. The fraction of photons absorbed in photoionization continua is 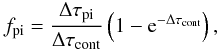 (B.9)the fraction absorbed by dust is
(B.9)the fraction absorbed by dust is 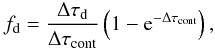 (B.10)the fraction that Thomson scatter is
(B.10)the fraction that Thomson scatter is 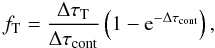 (B.11)and the fraction that do not interact is
(B.11)and the fraction that do not interact is 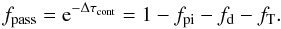 (B.12)We let the fractions fpi and fd be absorbed in photoionization continua and by dust, respectively. We then let the remaining fraction (fT + fpass) Thomson scatter with probability
(B.12)We let the fractions fpi and fd be absorbed in photoionization continua and by dust, respectively. We then let the remaining fraction (fT + fpass) Thomson scatter with probability 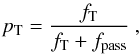 (B.13)and continue through with probability 1 − pT. If Thomson scattering occurs, we draw a position for the scattering from
(B.13)and continue through with probability 1 − pT. If Thomson scattering occurs, we draw a position for the scattering from ![\appendix \setcounter{section}{2} \begin{equation} \Delta \tau = -\ln\left[1 + z\left({\rm e}^{-\Delta \tau_{\rm cont}}-1\right)\right]~, \end{equation}](/articles/aa/full_html/2012/10/aa19528-12/aa19528-12-eq534.png) (B.14)and a new direction cosine μ from
(B.14)and a new direction cosine μ from 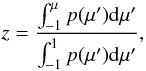 (B.15)where z is a uniform random number between 0 and 1, and p(μ′) is the Rayleigh phase function
(B.15)where z is a uniform random number between 0 and 1, and p(μ′) is the Rayleigh phase function 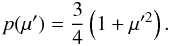 (B.16)We treat the scattering as coherent in the fluid frame, i.e. we ignore the small energy shifts occurring due to the thermal motions of the electrons, as well as the Compton shift.
(B.16)We treat the scattering as coherent in the fluid frame, i.e. we ignore the small energy shifts occurring due to the thermal motions of the electrons, as well as the Compton shift.
Transitions into which (part of the) Lyα flux is allocated.
B.5. Line overlap
When the density is high, the line escape probabilities may be enhanced from their Sobolev values βS by overlapping continua and lines, so that 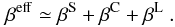 (B.17)We take the βC term into account as described in J11. In this paper, we also take the βL term into account for Lyα and Lyβ, which are important for the spectral formation in Type II SNe.
(B.17)We take the βC term into account as described in J11. In this paper, we also take the βL term into account for Lyα and Lyβ, which are important for the spectral formation in Type II SNe.
Lyα reaches optical depths as high as τS = 1010−1011 in the early nebular phase, and may branch into several iron-group lines around 1215.67 Å before escaping the resonance layer. Preliminary simulations (which we hope to expand on in a future publication) show that at typical conditions in the early nebular phase, the branching probability is 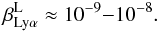 (B.18)Here we use
(B.18)Here we use 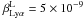 . We assume that the absorbing lines are the ones which, at 300 days in the core H region, are optically thick and within 100 Doppler widths (on the red side) of the Lyα rest wavelength, with allocation to these transitions in equal proportions. The lines, which fall in the 1215.67−1220 Å range, are listed in Table B.1.
. We assume that the absorbing lines are the ones which, at 300 days in the core H region, are optically thick and within 100 Doppler widths (on the red side) of the Lyα rest wavelength, with allocation to these transitions in equal proportions. The lines, which fall in the 1215.67−1220 Å range, are listed in Table B.1.
Model atoms used.
The O i λ1025.76 2p4(3P) − 3d(3Do) transition lies within the Doppler core of Lyβ. If the O i λ1.129 μm 3p(3P) − 3d(3Do) transition is optically thin, and complete l-mixing in both H i n = 3 and O i 3d3D is assumed, the branching probability for O i fluorescence is7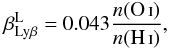 (B.19)where n(O i) and n(H i) are the number densities of O i and H i. At solar metallicity n(O)/n(H) = 4.9 × 10-4, so
(B.19)where n(O i) and n(H i) are the number densities of O i and H i. At solar metallicity n(O)/n(H) = 4.9 × 10-4, so 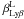 = 2.1 × 10-5, which is the value we use.
= 2.1 × 10-5, which is the value we use.
B.6. Photoionization cross sections
For excited states with unknown photoionization cross sections, we use the hydrogenic approximation (Rybicki & Lightman 1979) 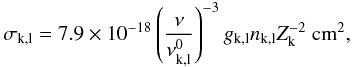 (B.20)where
(B.20)where 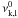 is the ionization threshold, gk,l is the Gaunt factor (which we set to unity for all levels), Zk is the effective nuclear charge (number of protons minus number of screening electrons), and nk,l is the effective principal quantum number
is the ionization threshold, gk,l is the Gaunt factor (which we set to unity for all levels), Zk is the effective nuclear charge (number of protons minus number of screening electrons), and nk,l is the effective principal quantum number 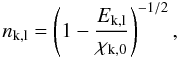 (B.21)where Ek,l is the level energy and χk,0 is the ground state ionization potential.
(B.21)where Ek,l is the level energy and χk,0 is the ground state ionization potential.
We use a threshold for how many levels to compute photoionization cross sections for. For this paper this limit was set to 50 levels. Tests showed that contributions by levels above this were small for all epochs modeled.
B.7. Free-bound emissivities
For hydrogen, we use detailed emissivity functions obtained by applying the Milne relations to the photoionization cross sections, which we obtain from Verner et al. (1996) for n = 1, and Bethe & Salpeter (1957) for n = 2. For n = 3 and higher we use the hydrogenic approximation.
For all other atoms k we use a simplified prescription, where recombination to level l gives an emissivity of 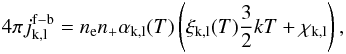 (B.22)is emitted over a box-shaped profile between 0.5−1.5 kT. Here αk,l(T) is the specific recombination coefficient, and ξk,l(T) is taken as 0.55 for all atoms, levels, and temperatures, the value for hydrogen at a few thousand K (Spitzer 1948).
(B.22)is emitted over a box-shaped profile between 0.5−1.5 kT. Here αk,l(T) is the specific recombination coefficient, and ξk,l(T) is taken as 0.55 for all atoms, levels, and temperatures, the value for hydrogen at a few thousand K (Spitzer 1948).
B.8. Collision strengths
For transitions with unknown collision strengths we use van Regemorter’s formula (van Regemorter 1962) for allowed lines (taken as fosc > 10-3), and 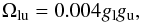 (B.23)for forbidden lines (Axelrod 1980).
(B.23)for forbidden lines (Axelrod 1980).
B.9. Model atoms
Table B.2 lists the model atoms used. Compared to J11, we now include more levels in the NLTE solutions, and have also added Fe iii and Co iii8. We have added collision strengths for Ni ii (Cassidy et al. 2010, 2011, we use the values at 5000 K). The sources for the rest of the atomic data are given in J11.
Acknowledgments
We thank the referee for many useful ideas for improving the manuscript. We thank A. Heger for providing the explosion models, and M. Fraser for helpful discussion. Thanks to S. Gelato for advice on code development. This work has been supported by the Swedish Research Council and the Swedish National Space Board. We have made use of the SUSPECT database.
References
- Andrews, J. E., Sugerman, B. E. K., Clayton, G. C., et al. 2011, ApJ, 731, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D., Bahcall, J. N., Kirshner, R. P., & Woosley, S. E. 1989, ARA&A, 27, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, L. H., & van Blerkom, D. 1972, ApJ, 178, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Axelrod, T. S. 1980, Ph.D. Thesis, AA (California Univ., Santa Cruz.) [Google Scholar]
- Baklanov, P. V., Blinnikov, S. I., & Pavlyuk, N. N. 2005, Astron. Lett., 31, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Basko, M. 1994, ApJ, 425, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Benetti, S., Cappellaro, E., Turatto, M., et al. 1994, A&A, 285, 147 [NASA ADS] [Google Scholar]
- Bersten, M. C., Benvenuto, O., & Hamuy, M. 2011, ApJ, 729, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Beswick, R. J., Muxlow, T. W. B., Argo, M. K., Pedlar, A., & Marcaide, J. M. 2004, IAU Circ., 8435, 3 [Google Scholar]
- Bethe, H. A., & Salpeter, E. E. 1957, Quantum Mechanics of One- and Two-Electron Atoms, eds. H. A., Bethe, & E. E. Salpeter [Google Scholar]
- Bouchet, P., & Danziger, I. J. 1993, A&A, 273, 451 [NASA ADS] [Google Scholar]
- Bouchet, P., Slezak, E., Le Bertre, T., Moneti, A., & Manfroid, J. 1989, AAps, 80, 379 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cassidy, C. M., Ramsbottom, C. A., Scott, M. P., & Burke, P. G. 2010, A&A, 513, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassidy, C. M., Ramsbottom, C. A., & Scott, M. P. 2011, ApJ, 738, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I. 1970, MNRAS, 149, 111 [NASA ADS] [Google Scholar]
- Chevalier, R. A. 1976, ApJ, 207, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., Fransson, C., & Nymark, T. K. 2006, ApJ, 641, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Chugai, N. N. 1977, Sov. Astron. Lett., 3, 241 [NASA ADS] [Google Scholar]
- Chugai, N. N. 1994, ApJ, 428, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Chugai, N. N., Fabrika, S. N., Sholukhova, O. N., et al. 2005, Astron. Lett., 31, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Crockett, R. M., Smartt, S. J., Pastorello, A., et al. 2011, MNRAS, 410, 2767 [NASA ADS] [CrossRef] [Google Scholar]
- de Kool, M., Li, H., & McCray, R. 1998, ApJ, 503, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., & Hillier, D. J. 2011, MNRAS, 410, 1739 [NASA ADS] [Google Scholar]
- Dessart, L., Livne, E., & Waldman, R. 2010, MNRAS, 408, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Drira, I., Hure, J. M., Spielfiedel, A., Feautrier, N., & Roueff, E. 1997, A&A, 319, 720 [NASA ADS] [Google Scholar]
- Eastman, R. G., Woosley, S. E., Weaver, T. A., & Pinto, P. A. 1994, ApJ, 430, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Izzard, R. G., & Tout, C. A. 2008, MNRAS, 384, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Elias-Rosa, N., Van Dyk, S. D., Li, W., et al. 2009, ApJ, 706, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Elmhamdi, A., Danziger, I. J., Chugai, N., et al. 2003, MNRAS, 338, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Fabbri, J., Otsuka, M., Barlow, M. J., et al. 2011, MNRAS, 418, 1285 (F11) [NASA ADS] [CrossRef] [Google Scholar]
- Falk, S. W., & Arnett, W. D. 1977, ApJS, 33, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., & Persson, S. E. 1989, ApJ, 347, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V., Foley, R. J., Treu, T., & Malkan, M. A. 2004, IAU Circ., 8414, 1 [NASA ADS] [Google Scholar]
- Fransson, C., & Chevalier, R. A. 1989, ApJ, 343, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, M., Ergon, M., Eldridge, J. J., et al. 2011, MNRAS, 417, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Gerardy, C. L., Fesen, R. A., Höflich, P., & Wheeler, J. C. 2000, AJ, 119, 2968 [NASA ADS] [CrossRef] [Google Scholar]
- Gerardy, C. L., Fesen, R. A., Nomoto, K., et al. 2002, PASJ, 54, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, G., & Lopez, R. 1993, MNRAS, 263, 767 [NASA ADS] [Google Scholar]
- Haas, M. R., Erickson, E. F., Lord, S. D., et al. 1990, ApJ, 360, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, N. J., Janka, H., & Müller, E. 2010, ApJ, 714, 1371 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Suntzeff, N. B., Gonzalez, R., & Martin, G. 1988, AJ, 95, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Herant, M., & Benz, W. 1991, ApJ, 370, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Herant, M., & Woosley, S. E. 1994, ApJ, 425, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2004, AAp, 425, 649 [Google Scholar]
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inserra, C., Turatto, M., Pastorello, A., et al. 2011, MNRAS, 417, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Inserra, C., Turatto, M., Pastorello, A., et al. 2012, MNRAS, 422, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Jerkstrand, A., Fransson, C., & Kozma, C. 2011, A&A, 530, A45 (J11) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., Sharina, M. E., & Huchtmeier, W. K. 2000, AAp, 362, 544 [Google Scholar]
- Kasen, D., & Woosley, S. E. 2009, ApJ, 703, 2205 [NASA ADS] [CrossRef] [Google Scholar]
- Kifonidis, K., Plewa, T., Scheck, L., Janka, H.-T., & Müller, E. 2006, AAp, 453, 661 [NASA ADS] [Google Scholar]
- Kjær, K., Leibundgut, B., Fransson, C., Jerkstrand, A., & Spyromilio, J. 2010, AAp, 517, A51 [Google Scholar]
- Kotak, R., Meikle, W. P. S., Farrah, D., et al. 2009, ApJ, 704, 306 (K09) [NASA ADS] [CrossRef] [Google Scholar]
- Kozma, C., & Fransson, C. 1992, ApJ, 390, 602 (KF92) [NASA ADS] [CrossRef] [Google Scholar]
- Kozma, C., & Fransson, C. 1998a, ApJ, 496, 946 (KF98 a) [NASA ADS] [CrossRef] [Google Scholar]
- Kozma, C., & Fransson, C. 1998b, ApJ, 497, 431 (KF98 b) [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, D. C., Filippenko, A. V., Gates, E. L., et al. 2002a, PASP, 114, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, D. C., Filippenko, A. V., Li, W., et al. 2002b, AJ, 124, 2490 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., & McCray, R. 1992, ApJ, 387, 309 [CrossRef] [Google Scholar]
- Li, H., & McCray, R. 1993, ApJ, 405, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., & McCray, R. 1995, ApJ, 441, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., McCray, R., & Sunyaev, R. A. 1993, ApJ, 419, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Van Dyk, S. D., Filippenko, A. V., & Cuillandre, J.-C. 2005, PASP, 117, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Leaman, J., Chornock, R., et al. 2011, MNRAS, 412, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinova, I. I., & Nadezhin, D. K. 1983, Ap&SS, 89, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinova, I. Y., & Nadezhin, D. K. 1985, Sov. Astron. Lett., 11, 145 [NASA ADS] [Google Scholar]
- Liu, W., & Dalgarno, A. 1994, ApJ, 428, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., & Dalgarno, A. 1995, ApJ, 454, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Dalgarno, A., & Lepp, S. 1992, ApJ, 396, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B., Danziger, I. J., Gouiffes, C., & Bouchet, P. 1991, in Supernovae, ed. S. E. Woosley, 82 [Google Scholar]
- Maguire, K., di Carlo, E., Smartt, S. J., et al. 2010, MNRAS, 404, 981 (M10) [NASA ADS] [CrossRef] [Google Scholar]
- Maguire, K., Jerkstrand, A., Smartt, S. J., et al. 2012, MNRAS, 420, 3451 (M12) [NASA ADS] [CrossRef] [Google Scholar]
- Martí-Vidal, I., Marcaide, J. M., Alberdi, A., et al. 2007, AAp, 470, 1071 [Google Scholar]
- Maund, J. R., & Smartt, S. J. 2009, Science, 324, 486 [NASA ADS] [PubMed] [Google Scholar]
- Maurer, I., Jerkstrand, A., Mazzali, P. A., et al. 2011, MNRAS, 418, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misra, K., Pooley, D., Chandra, P., et al. 2007, MNRAS, 381, 280 (M07) [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Kewley, L., Bloom, J. S., et al. 2011, ApJ, 731, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Moseley, S. H., Dwek, E., Silverberg, R. F., et al. 1989, ApJ, 347, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Kennicutt, Jr., R. C., Tremonti, C. A., et al. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Mueller, E., Fryxell, B., & Arnett, D. 1991, AAp, 251, 505 [Google Scholar]
- Nieuwenhuijzen, H., & de Jager, C. 1990, AAp, 231, 134 [Google Scholar]
- Oliva, E. 1993, AAp, 276, 415 [NASA ADS] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei (Astrophysics of gaseous nebulae and active galactic nuclei, 2nd. edn., eds. D. E. Osterbrock, & G. J. Ferland (Sausalito, CA: University Science Books) [Google Scholar]
- Pastorello, A., Valenti, S., Zampieri, L., et al. 2009, MNRAS, 394, 2266 [NASA ADS] [CrossRef] [Google Scholar]
- Pierce, M. J. 1994, ApJ, 430, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Vílchez, J. M., & Contini, T. 2004, A&A, 425, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozzo, M., Meikle, W. P. S., Rayner, J. T., et al. 2006, MNRAS, 368, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Pumo, M. L., & Zampieri, L. 2011, ApJ, 741, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Rho, J., Jarrett, T. H., Chugai, N. N., & Chevalier, R. A. 2007, ApJ, 666, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Roche, P. F., Aitken, D. K., & Smith, C. H. 1991, MNRAS, 252, 39 [NASA ADS] [Google Scholar]
- Roche, P. F., Aitken, D. K., & Smith, C. H. 1993, MNRAS, 261, 522 [NASA ADS] [Google Scholar]
- Rybicki, G., & Lightman, A. 1979, Radiative Processes in Astrophysics (Wiley) [Google Scholar]
- Sahu, D. K., Anupama, G. C., Srividya, S., & Muneer, S. 2006, MNRAS, 372, 1315 (S06) [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Tammann, G. A. 1981, A revised Shapley-Ames Catalog of bright galaxies, ed. A. Sandage, & G. A. Tammann, [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, B. P. 1993, Ph.D. Thesis, Harvard University [Google Scholar]
- Schmidt, B. P., Kirshner, R. P., Schild, R., et al. 1993, AJ, 105, 2236 [NASA ADS] [CrossRef] [Google Scholar]
- Schoniger, F., & Sofue, Y. 1994, AAp, 283, 21 [Google Scholar]
- Smartt, S. J. 2009, ARA&A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J., Eldridge, J. J., Crockett, R. M., & Maund, J. R. 2009, MNRAS, 395, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, Jr., L.1948, ApJ, 107, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Spyromilio, J., & Pinto, P. A. 1991, in European Southern Observatory Astrophysics Symposia, eds. I. J. Danziger, & K. Kjaer, 423, 37 [Google Scholar]
- Spyromilio, J., & Graham, J. R. 1992, MNRAS, 255, 671 [NASA ADS] [Google Scholar]
- Spyromilio, J., Meikle, W. P. S., Learner, R. C. M., & Allen, D. A. 1988, Nature, 334, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Stockdale, C. J., Weiler, K. W., van Dyk, S. D., et al. 2004, IAU Circ., 8415, 1 [Google Scholar]
- Thielemann, F., Nomoto, K., & Hashimoto, M. 1996, ApJ, 460, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Utrobin, V. P. 2007, AAp, 461, 233 [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2008, AAp, 491, 507 [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2009, AAp, 506, 829 [Google Scholar]
- Utrobin, V. P., Chugai, N. N., & Pastorello, A. 2007, AAp, 475, 973 [Google Scholar]
- Utrobin, V. P., Chugai, N. N., & Botticella, M. T. 2010, ApJ, 723, L89 [NASA ADS] [CrossRef] [Google Scholar]
- van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Varambhia, H. N., Gupta, M., Faure, A., Baluja, K. L., & Tennyson, J. 2009, J. Phys. B Atomic Molecul. Phys., 42, 095204 [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Walmswell, J. J., & Eldridge, J. J. 2012, MNRAS, 419, 2064 [Google Scholar]
- Woosley, S. E. 1988, ApJ, 330, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Heger, A. 2007, Phys. Rep., 442, 269 (WH07) [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJs, 101, 181 (WW95) [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y. M., & McCray, R. 1991, in Supernovae, ed. S. E. Woosley, 444 [Google Scholar]
- Xu, Y., McCray, R., Oliva, E., & Randich, S. 1992, ApJ, 386, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Cantiello, M. 2010, ApJ, 717, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Zwitter, T., Munari, U., & Moretti, S. 2004, IAU Circ., 8413, 1 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The density profile in the 1D hydrodynamical model (solid lines) and in the artificially mixed model used in this paper (dashed lines). Note that in the artificially mixed model, the zones in the core are distributed as clumps with individual filling factors, the densities plotted are the densities within each clump. |
| In the text | |
 |
Fig. 2 Velocity shifts of the peaks of the strongest emission lines in the observed spectra as function of time. The symbols are estimates of the peak positions from fitting a parabola to the part of the line with a flux higher than 85% of the peak value (95% for [Fe ii] λ7155). The lines are linear fits to the measured values. |
| In the text | |
 |
Fig. 3 The (gray) dust optical depth function τd(t) derived from the observed dust luminosity (blue, solid), from the blue-shifts of line profiles (red, dashed), and the one we use for our modeling here (black, dot-dashed). |
| In the text | |
 |
Fig. 4 Normalized photometric evolution (all magnitudes have been subtracted by t/102 d to normalize to the 56Co decay) of the (reddened) 12 M⊙ (blue, dot-dashed), 15 M⊙ (black, solid), and 19 M⊙ (green, dashed) models, compared to observations (red points). T.P. means “this paper”. The M10s, S06s, and TPs data points are synthetic photometry from the observed spectra. |
| In the text | |
 |
Fig. 5 Evolution of model temperatures in the various core zones in the 15 M⊙ model. |
| In the text | |
 |
Fig. 6 Optical (dereddened) spectrum at 401 days (red) compared to the 12 M⊙ (blue) and 19 M⊙ (green) models. |
| In the text | |
 |
Fig. 7 Observed (dereddened) spectra (red) and 15 M⊙ model spectra at 212, 401, and 465 days (black). All spectra have been smoothed with a Gaussian of FWHM = 600 km s-1 to improve the S/N. |
| In the text | |
 |
Fig. 8 Observed (dereddened) line fluxes (red points), normalized to the bolometric flux of 0.062 M⊙ of 56Co at a distance of 5.5 Mpc, compared to model values (12 M⊙: black, solid, 15 M⊙: blue, dot-dashed, 19 M⊙: green, dashed). See the text (Sect. 4.3.1) for details on the line flux measurements. |
| In the text | |
 |
Fig. 9 Near-infrared (dereddened) spectrum at 307 days (red) compared to the 12 M⊙ (blue), 15 M⊙ (black), and 19 M⊙ (green) models. The boxed regions at 1.5−1.2 μm and 1.4−1.7 μm show particular sensitivity to the core mass. Note that CO emission is not included in the model spectra. |
| In the text | |
 |
Fig. 10 Observed MIR spectrum at 350 days (red, solid line), compared to model spectra of the 15 M⊙ model (black, solid). To simulate the instrument response, the model has been convolved with a Gaussian of FWHM = λ/R, where the resolving power R was taken to be 60. Also shown are the dust component (pink, dashed), the observed photometry at 3.6 and 4.5 μm (red stars), and the corresponding model photometry for the model (black circles). The observed photometry is at 361 days, and has been rescaled with the 56Co decay factor to 350 days (exp−11/111.5). |
| In the text | |
 |
Fig. 11 Model Fe/Ni/Co line fluxes relative to observed values, at 295 days. The 15 M⊙ model has been used. |
| In the text | |
 |
Fig. 12 Same as Fig. 11, for 350 days. |
| In the text | |
 |
Fig. 13 Same as Fig. 11, for 451 days. |
| In the text | |
 |
Fig. 14 Observed flux in the CO fundamental band (hollow squares), first overtone (diamond), and estimated total (filled squares), compared to the total heating of the O/C zone in the various models. For the estimated total emission, correction for the internal dust extinction has been taken into account. All values have been normalized to the decay of 0.062 M⊙ of 56Co. |
| In the text | |
 |
Fig. 15 Same as Fig. 14, for SiO. The overtone band is unobserved, and is assumed to be zero. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.