| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219387 | |
| Published online | 11 October 2012 | |
Constraining the fraction of Compton-thick AGN in the Universe by modelling the diffuse X-ray background spectrum
1
Institute of Astronomy & Astrophysics, National Observatory of
Athens,
I. Metaxa & V. Pavlou 1,
15236
Penteli,
Greece
e-mail: age@mpe.mpg.de
2
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse 1,
85748
Garching bei München,
Germany
3
INAF - Osservatorio Astronomico di Bologna, via Ranzani
1, 40127
Bologna,
Italy
Received: 11 April 2012
Accepted: 2 September 2012
This paper investigates which constraints can be placed on the fraction of Compton-thick active galactic nuclei (AGN) in the Universe from modelling the spectrum of the diffuse X-ray background (XRB). We present a model for the synthesis of the XRB that uses as input a library of AGN X-ray spectra generated by Monte Carlo simulations. This is essential to account for the Compton scattering of X-ray photons in a dense medium and the impact of that process on the spectra of heavily obscured AGN. We identify a small number of input parameters to the XRB synthesis code that encapsulate the minimum level of uncertainty in reconstructing the XRB spectrum. These are the power-law index and high-energy cutoff of the intrinsic X-ray spectra of AGN, the level of the reflection component in AGN spectra, and the fraction of Compton-thick AGN in the Universe. We then map the volume of the space allowed to these parameters by current observational determinations of the XRB spectrum in the range 3−100 keV. One of the least-constrained parameters is the fraction of Compton-thick AGN. Statistically acceptable fits to the XRB spectrum at the 68% confidence level can be obtained for Compton-thick AGN fractions in the range 5−50%. This is because of degeneracies among input parameters to the XRB synthesis code and uncertainties in the modelling of AGN spectra (e.g. level of reflection fraction). The most promising route for constraining the fraction of Compton-thick AGN in the Universe is via the direct detection of those sources in high-energy (≳ 10 keV) surveys. We show that the observed fraction of Compton-thick sources identified in the Swift/BAT serendipitous survey limits the intrinsic fraction of Compton-thick AGN, at least at low redshift, to 10−20% (68% confidence level). We also make predictions on the number density of Compton-thick sources that current and future X-ray missions are expected to discover. Testing those predictions with data will place tight constraints on the intrinsic fraction of Compton-thick AGN as a function of redshift.
Key words: X-rays: diffuse background / X-rays: general
© ESO, 2012
1. Introduction
The origin of the diffuse X-ray background (XRB) has been at the centre of high-energy astrophysical research since its discovery (Giacconi et al. 1962). Already by the early 90s numerous X-ray experiments have constrained the most salient spectral features of the XRB, the power-law spectral energy distribution with photon index Γ = 1.4 in the energy interval 2−10 keV and the peak at 20−30 keV (e.g. Marshall et al. 1980; Gruber et al. 1999). At the same time, observations at energies below about 10 keV demonstrated that at least a fraction of the XRB intensity is composed of point sources, some of which were identified with broad-line quasi-stellar objects (QSOs, e.g. Shanks et al. 1991). However, early suggestions that the XRB is the result of the superposition of active galactic nuclei (AGN) across cosmic time stumbled upon the steeper X-ray spectra of UV-bright (unobscured) QSOs compared to the XRB spectrum below 10 keV (Fabian & Barcons 1992). This led to suggestions that Seyfert-2 AGN, which were observed to have flatter X-ray spectra compared to UV bright QSOs, could potentially be major contributors to the XRB (Setti & Woltjer 1989; Awaki et al. 1991). Progress in the interpretation of the X-ray spectra of AGN (e.g. Williams et al. 1992; Nandra & Pounds 1992; Turner et al. 1993; Nandra et al. 1993; Nandra & Pounds 1994) coupled with improved constraints on their cosmological evolution (Stocke et al. 1991; Maccacaro et al. 1991; Shanks et al. 1991; Boyle et al. 1993) led to the seminal work of Comastri et al. (1995). They demonstrated that AGN under the unification paradigm (Antonucci 1993) could reproduce the XRB spectrum up to about 100 keV. A key prediction of that model was the high incidence of obscured accreting supermassive black holes (SMBHs) in the Universe, including a fraction (≈ 25% of total population) of luminous Compton-thick ones (NH > 1024 cm-2).
Observations with the XMM-Newton and Chandra confirmed some of these predictions, lending support to the basic assumptions of the Comastri et al. (1995) model. Deep surveys carried out by those telescopes resolved almost the entire XRB intensity into point sources up to energies of few keV (e.g. Worsley et al. 2005). Moreover, follow-up observations suggested that the majority of those sources are AGN (e.g. Bauer et al. 2004). Analysis of their X-ray spectra also demonstrated that in most of them the direct X-ray emission is reprocessed by gas and dust clouds with column densities NH ≈ 1022−1024 cm-2 (Tozzi et al. 2006; Akylas et al. 2006). X-ray surveys by those telescopes revealed an unexpected dependence of the obscured (NH > 1022 cm-2) AGN fraction on accretion luminosity, which implies deviations from the basic unification paradigm (Ueda et al. 2003; La Franca et al. 2005; Akylas et al. 2006; Hasinger 2008; but see Dwelly et al. 2005; Dwelly & Page 2006).
In the wake of those developments, Gilli et al. (2007) revised the Comastri et al. (1995) XRB synthesis model by including the knowledge accumulated by the XMM-Newton and Chandra observations both on the evolution of the X-ray luminosity function and the dependence of the obscured AGN fraction on luminosity. Large numbers of Compton-thick sources with column densities 1024−26 cm-2 (equal number to that of Compton-thin AGN) were required by the revised model. Most of them were predicted to lie close to, or below, the sensitivity limits of the deepest current X-ray surveys. Attempts to identify this hidden population either directly at X-rays (e.g. Tozzi et al. 2006; Georgantopoulos et al. 2009; Comastri et al. 2011; Feruglio et al. 2011) or the mid-infrared (e.g. Fiore et al. 2009) suggested agreement, at least to the first approximation, with the Gilli et al. (2007) predictions. At the same time, however, criticism has been raised on the large percentage of Compton-thick AGN adopted by that model. Studies selecting local AGN either at hard X-ray energies ≳ 15 keV (e.g. Beckmann et al. 2009; Tueller 2011; Burlon et al. 2011), or via optical spectroscopy (e.g. Akylas & Georgantopoulos 2009) or at the mid-infrared (e.g. Brightman & Nandra 2011) determined intrinsic Compton-thick fractions in the range 15−25% of the AGN population.
It has also been pointed out that observational uncertainties as well as aliases among the large number of parameters that are unavoidably adopted in XRB synthesis codes, make it hard to draw robust conclusions on the space density of Compton-thick AGN in the Universe. Treister et al. (2009), for example, showed that the current level of uncertainty in the normalisation of the XRB intensity limits the predictive power of XRB synthesis codes on the fraction of Compton-thick AGN. Moreover, certain AGN spectral components are not yet well understood, e.g. the strength of the radiation reflected off the torus or the accretion disk in the line of sight. Tuning this parameter in XRB synthesis models to values allowed by current observational constraints can change the required number of Compton-thick sources (Treister et al. 2009). Draper & Ballantyne (2009) also highlighted the significance of unobscured AGN populations for the interpretation of the hard (>10 keV) X-ray background. These authors estimated the contribution to the XRB of blazars with X-ray spectra dominated by synchrotron radiation. Including those sources can reduce the fraction of Compton-thick QSOs required by the Gilli et al. (2007) model by about 20%.
In light of those studies, it is interesting to revisit the question of whether the XRB hump at 20−30 keV requires the presence of Compton-thick AGN. This paper takes a critical approach to this problem by presenting an XRB synthesis code that uses state-of-the-art numerical simulations to model the high-energy spectra of AGN (Brightman & Nandra 2011). A feature of those simulations is the realistic modelling of the Compton scattering of photons in a dense medium, which has a strong impact on the X-ray spectra of AGN at obscurations close to and above the Compton-thick limit, NH = 1024 cm-2. We then identify four input parameters to the XRB synthesis code (one of which is the number of Compton-thick AGN, others relate to the AGN spectral characteristics), which encapsulate the minimum level of uncertainty in reconstructing the XRB spectrum. Instead of fixing those parameters to literature values, we allow them to vary within plausible intervals. We then map the volume of the space allowed to those parameters by current observational determinations of the XRB intensity. This approach allows us to investigate in a quantitative way degeneracies among the AGN spectral parameters and their impact on the determination of the Compton-thick AGN fraction from measurements of the XRB spectrum. Finally, we demonstrate how current data and future X-ray missions can provide significant progress in our understanding of the origin and composition of XRB, by directly constraining the fraction of Compton-thick AGN across cosmic time. In our calculations we adopt H0 = 70 km s-1 Mpc-1, ΩM = 0.3 and ΩΛ = 0.7.
2. The X-ray background model
The synthesis of the XRB spectrum requires assumptions to be made on (i) the shape of the spectral energy distribution of AGN at X-rays; (ii) the volume density of AGN in the Universe as a function of accretion luminosity and redshift; (iii) the distribution of AGN in obscuration, which is often parametrised by the hydrogen column density, NH. Each component of the XRB synthesis model is described below.
2.1. AGN X-ray spectral energy distribution
Active galactic nuclei have complex spectra at high energies that depend on the properties of the SMBH (mass, spin), the rate at which matter accretes onto it, and on the overall structure and distribution of material in its vicinity (e.g. torus). Observations and theoretical work suggest that the components needed to reconstruct the X-ray spectra of AGN include (i) a power-law with an exponential cutoff at high energies, which represents the intrinsic AGN radiation; (ii) photoelectric absorption and Compton scattering; (iii) emission lines, the most prominent of which is the FeKα at 6.4 keV; (iv) reflection of the direct AGN radiation on an optical thick medium; (v) an excess emission over the power-law extrapolation at soft energies (<1−2 keV); and (vi) a possible contribution from radio jets.
The intrinsic AGN X-ray spectrum can be parameterised by a power-law with photon index Γ and an exponential decline at high energies with e-folding parameter EC. This functional form is the result of comptonisation processes. Low-energy photons (UV, soft X-rays), possibly associated with the accretion disk, are upscattered to hard X-ray energies by the energetic particles of a hot corona that surrounds the innermost regions of SMBHs (e.g. Haardt & Maraschi 1991). In this standard model, the photon index Γ is related to the temperature, the optical depth and overall structure of the matter close to the central engine (e.g. Murphy & Yaqoob 2011). The energy cut-off depends on the temperature of the thermal hot electrons that are responsible for the Compton-scattering of the accretion disk seed photons.
The direct X-ray emission of AGN is modified by cold material in the vicinity of the SMBH, such as the putative torus of gas and dust clouds. X-ray photons that intersect such clouds are absorbed with an efficiency that depends on the density and the chemical composition of obscuring screen. When the column density of the absorbing screen increases, Compton-scattering of X-ray photons on the electrons of the intervening material becomes increasingly important relative to photoelectric absorption. The net result is that the direct emission, at least below about 10 keV, is significantly suppressed. The Compton-scattering optical depth is defined τ ≃ σTNH, where σT is the Thomson-scattering cross section and NH the hydrogen column density of the material. Compton-scattering dominates the fate of the X-ray photons emitted by the central engine at τ ≳ 1 or equivalently NH = σT-1 = 1.5 × 1024 cm-2. The impact of photoelectric absorption and Compton-scattering on the intrinsic AGN spectrum is accounted for in a self-consistent way using the numerical simulations of Brightman & Nandra (2011). We used their model that describes the transmission spectrum from an isotropic source located at the centre of a uniform spherical distribution of matter. Input parameters of the simulations are the Γ and EC of the intrinsic AGN spectrum, the column density NH, and metal abundance of the obscuring material. For simplicity we fixed abundances to solar values.
Observations also show the presence of a prominent iron Kα line in the spectra of AGN at an energy of 6.4 keV (Nandra & Pounds 1994). This can be produced as direct AGN emission intersects optically thick material, such as the accretion disk or the torus, and is Compton-backscattered into the line of sight. The same processes produces a reflection continuum component (George & Fabian 1991; Murphy & Yaqoob 2011), which becomes increasingly important at energies >8 keV. The numerical simulations of Brightman & Nandra (2011) include the Kα emission of iron as well as the transitions from several other elements. There is no reflection component in the spherical symmetric model of Brightman & Nandra (2011). We chose to describe this component using the simulations of Magdziarz & Zdziarski (1995) as implemented in the pexrav model of xspec. We parameterise the reflection emission by its strength fREF relative to the direct AGN radiation integrated in the rest-frame 2−10 keV band. Other XRB synthesis models (e.g. Gilli et al. 2007; Treister et al. 2009) measure the amplitude of the reflection component with the parameter R, which denotes the solid angle subtended by the reflecting material. For comparison R = 0.5 (Treister et al. 2009) corresponds to fREF = 2.
Ideally, the modelling of AGN X-ray spectra should also include a soft-excess component. For type-1 AGN this is suggested to be relativistically blurred photoionized disc reflection emission (e.g. Crummy et al. 2006). In type-2 AGN, the soft excess is proposed to be scattered radiation in the line of sight that is not absorbed by the torus (e.g. Turner et al. 1997). When synthesising the XRB spectrum, we chose not to include the above components because we are primarily interested in the intensity of the XRB spectrum at ≳ 2 keV. The contribution of the soft excess is likely to be small at those energies. These components become important, however, when using the XRB synthesis code to make predictions on the expected number of AGN, particularly heavily obscured ones, as a function of X-ray flux at relatively soft energies (e.g. 0.5−2 keV). For this application we included a soft-excess scattered-light component in the spectra of type-2 AGN. It follows the same functional form as the direct AGN radiation (power-law plus high-energy cutoff) with a normalisation fixed to 3 per cent of the intrinsic AGN spectrum in the 2−10 keV band. This is the same as the strength of the soft-excess component for the type-2 AGN adopted by Gilli et al. (2007).
About 10% of the AGN have powerful radio jets that may also contribute to or even dominate the emission at X-ray wavelengths. Although we did not directly include such a spectral component, we used the results of Draper & Ballantyne (2009) to account for the contribution of blazars to the XRB spectrum.
Given our assumptions for the main emission components of AGN, the key parameters for modelling their intrinsic X-ray spectra are Γ, EC, and the strength of the reflection component, fREF. X-ray spectroscopy of individual AGN provides constraints on those parameters. There are, however, degeneracies among the different emission components which when combined with observational limitations, do not allow a description of the typical spectral characteristics of AGN at the accuracy level required for the synthesis of the XRB. For example, the average photon index of AGN is determined to be in the range 1.8−2.0 with a standard deviation around the mean of about 0.15−0.30 (Nandra & Pounds 1994; Dadina 2008; Beckmann et al. 2009; Brightman & Nandra 2011; Ricci et al. 2011; Burlon et al. 2011). Observational constraints on the cutoff energy range from as low as 50 keV (e.g. Molina et al. 2009) to about ~300 keV (Dadina 2008). The strength of the reflection component also varies among different studies, with observational constraints ranging from fREF = 0.01 to 0.1 (Ricci et al. 2011) (corresponding to a reflection parameter R ~ 0.2−2). A possible dependence of the reflection of the source characteristics, i.e. type-1 vs. type-2 AGN, may explain the wide range of values (Ricci et al. 2011), although such a trend remains to be established.
2.2. The AGN X-ray luminosity function
For the X-ray luminosity function (XLF) of AGNs and its evolution with redshift we used the parameterisation of Ueda et al. (2003). They estimated the AGN XLF in the rest-frame 2−10 keV energy range using a combination of hard-band (>2 keV) surveys conducted with the HEAO-1, ASCA, and Chandra missions. Here, we adopted the luminosity-dependent density evolution of the luminosity function, which provides a better fit to the Ueda et al. (2003) data. In this parameterisation the cutoff redshift after which the evolution of AGN stops increases with luminosity. We preferred to use the Ueda et al. (2003) XLF over more recent determinations (e.g. Aird et al. 2010) because the former include a self-consistent estimation of the fraction of Compton-thin AGN (NH = 1022−1024 cm-2).
2.3. The distribution of AGN in hydrogen column density
It is assumed that AGN are distributed uniformly in the hydrogen column density logarithmic intervals, log NH = 20−22 and 22−24 (cm-2). The AGN NH distribution, f(NH), is therefore approximated by a step function with a fixed ratio, ℛ, between absorbed (NH = 1022−1024 cm-2) and unabsorbed (NH < 1022 cm-2) sources. The parameter ℛ is a function of X-ray luminosity as parameterised by Akylas et al. (2006). It increases from ℛ ≈ 0.4 at LX(2−10 keV) ≈ 1045 erg s-1 to ℛ ≈ 0.8 at LX(2−10 keV) ≈ 1042 erg s-1. For comparison, the corresponding fractions in the Gilli et al. (2007) model are ℛ ≈ 0.45 and 0.75 at the above luminosities. The adopted parametrisation for the luminosity dependence of the obscured AGN fraction is also similar to that of Ueda et al. (2003). We chose to use the Akylas et al. (2006) results because they are using X-ray spectral analysis, not hardness ratios, to determine the column density of individual AGN in their sample. It should be emphasised that our results and conclusions would not change if we used the Ueda et al. (2003) functional form for the LX dependence of ℛ.
Compton-thick AGN are not included in the Ueda et al. (2003) XLF, or indeed any XLF determination based on observations in the 0.5−10 keV spectral band. This is because for NH ≳ 1024 cm-2, the bulk of the direct AGN emission at rest-frame energies ≲ 10−20 keV is suppressed. These heavily obscured sources are therefore too faint in the 0.5−10 keV spectral window of Chandra and XMM-Newton. Their identification is therefore hard even in the deepest current X-ray survey fields (e.g. Tozzi et al. 2006; Georgantopoulos et al. 2009). As a result, the fraction of Compton-thick AGN remains uncertain (see Comastri et al. 2011, and references therein). We introduced the parameter fCT, which is defined as the fraction of Compton-thick AGN (NH > 1024 cm-2) relative to mildly obscured Compton-thin sources (NH = 1022−1024 cm-2). We then added this fraction of Compton-thick AGN to the XLF of Ueda et al. (2003). It is therefore assumed that Compton-thick sources follow the same XLF as mildly obscucred systems.
Range of parameters used in modelling the XRB.
3. Adopted parameters
Modelling the XRB involves many parameters, some of which are reasonably well-constrained (e.g. the XLF of Compton thin AGN at least out to z = 2−3), while others have larger uncertainties (e.g. AGN X-ray spectrum). We identified four parameters that are important for shaping the XRB spectrum and for which sufficiently accurate observational determinations are still not available. These are the photon index, Γ, and the high-energy cutoff, Ec, of the intrinsic AGN spectrum, the fraction of the reflection component in AGN X-ray spectra, fREF, and the fraction of Compton-thick sources, fCT, among AGN. Instead of fixing those parameters to plausible values, we adopted the alternative approach of leaving them free to study the region of the four-dimensional parameter space, which is consistent with current observational data. These include measurements of the XRB spectrum itself and the fraction of Compton-thick AGN detected by high-energy (≳ 10 keV) missions.
We emphasise that the list of free parameters we chose is far from exhaustive. For example, a possible redshift dependence of the fraction of obscured AGN (e.g. La Franca et al. 2005; Treister & Urry 2006; Della Ceca et al. 2008), which is not included in our modelling, would imprint on the predicted XRB spectrum. Similarly, the results of the synthesis code depend on the spread of the Γ distribution, which we fixed to 0.15 following the BeppoSAX results of Dadina (2008). Another limitation of our modelling is that we assumed that all AGN have the same values of Ec and fREF, when a distribution of values might be more realistic. Nevertheless, by investigating the impact of observational uncertainties of a few parameters on the reconstruction of the XRB spectrum, one can assess whether observations of the diffuse X-ray background intensity can place reliable constraints on AGN properties. Table 1 shows the adopted range of values for each of the four parameters of interest as well as the step size used to sample the parameter space.
For synthesising the XRB spectrum, the assumed XLF and NH function were integrated in redshift, luminosity, and hydrogen column density to estimate the expected number of AGN at a given bin of redshift, luminosity, and NH. The integration was carried out in the luminosity and column density intervals LX(2−10 keV) = 1040−1047 erg s-1, NH = 1020−1025 cm-2. The redshift range adopted was z = 0−7. Limiting the integration to z = 4, to explore the impact of a possible exponential decline in the AGN XLF at z ≳ 3−4 (e.g. Brusa et al. 2009; Civano et al. 2011), changes the estimated intensity of the XRB spectrum by less than 1%. The step in z and LX is logarithmic and variable in size, taking a minimum value of dlog z = 0.1 at z = 1.5 and dlog LX = 0.3 at log LX(2−10 keV) = 43.8 erg s-1 and increasing at lower/higher redshift/luminosities. This significantly improves the computing performance of the code without loss of accuracy because the XRB is dominated by AGN at z ≈ 1−2 and LX(2−10 keV) ≈ 1043−1045 erg s-1 (e.g. Aird et al. 2010). The NH step size is fixed to Δlog NH = 0.5 cm-2.
At each z, LX and NH bin the observed shape of the AGN spectrum at energies 3−100 keV was determined using the simulations of Brightman & Nandra (2011) to model the effect of photoelectric absorption and Compton-scattering for a given intrinsic photon index Γ and high-energy cutoff Ec. A Gaussian distribution of photon indices was adopted, with a fixed spread of σ = 0.15 around the mean. Reflection was also added to the AGN spectrum using the pexrav model of xspec and assuming a fixed fraction fREF of this component relative to the direct AGN emission in the 2−10 keV band. The resulting spectrum was then normalised to the number of AGN within a given z, LX and NH bin as determined from the integration of the XLF. Adding the normalised spectra from all z, LX and NH bins yields the XRB intensity as a function of energy for a given set of parameters Γ, Ec, fREF and fCT. Figure 1 shows an example of a model spectrum produced by our code.
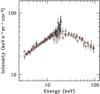 |
Fig. 1 Red curve: an example of an XRB spectrum produced by our synthesis model for parameters Γ = 1.88, EC = 230 keV, fREF = 0.055 and fCT = 0.1. The points are the observational constraints on the intensity of the XRB at different energies from the studies discussed in the text. Comparison of the model curve with the data yields a χ2 of 70.8 for 86 degrees of freedom (90 data points minus four free parameters). |
 |
Fig. 2 Left: confidence intervals for the model parameters Γ, EC, fREF and fCT used to synthesise the XRB spectrum. The (blue) thick continuous line corresponds to the 68 per cent confidence level (Δχ2 = 4.72 for four parameters). The (red) thin dotted line marks the 95th percentile (Δχ2 = 9.70 for four parameters). Right: same as right panel but including to our XRB synthesis results the contribution of blazars, as modelled by Draper & Ballantyne (2009). |
The standard χ2 statistic was estimated for each set of parameters (Γ, Ec, fREF, fCT) by comparing the model predictions with observations at discrete energies. In this exercise we used measurements of the intensity of the XRB estimated by Revnivtsev et al. (2003, RXTE/PCA, 3−, Churazov et al. (2007, INTEGRAL, 5−, Ajello et al. (2008b, Swift/BAT, 15−, Moretti et al. (2009, Swift/XRT 1.5− and Türler et al. (2010, INTEGRAL/IBIS, 20−. These measurements are plotted in Fig. 1. Observational studies on the XRB spectrum that provide confidence intervals, not discrete data points (e.g. ASCA; Gendreau et al. 1995; Kushino et al. 2002; Chandra, Hickox & Markevitch 2006; XMM-Newton, Lumb et al. 2002; De Luca & Molendi 2004; BeppoSAX, Vecchi et al. 1999) were not used in the analysis. The 1 keV normalisations of the XRB spectrum determined from those studies are in the range 9.6−12 keV keV-1 cm-2 s-1 sr-1. This should be compared with the 1 keV normalisation of 12.2 keV keV-1 cm-2 s-1 sr-1 determined by the Swift/XRT, which was used as a constraint in our analysis. Also, the XRB measurements from the HEAO-1 mission (Marshall et al. 1980) were not compared with the model predictions since there is a controversy over the absolute flux calibration of that mission, which may result in a systematic underestimation of the XRB intensity level (e.g. Ueda et al. 2003; Worsley et al. 2005; Treister & Urry 2005). Indeed, almost all measurements of the XRB intensity at 1 keV lie above the HEAO-1 estimate by factors of up to 1.5. Stray-light affecting focusing X-ray telescopes, unlike the HEAO-1, may also be responsible for the discrepancy. Nevertheless, INTEGRAL and Swift/BAT, which have similar optics to HEAO-1, also found a higher normalisation for the XRB intensity (Churazov et al. 2007; Moretti et al. 2009).
 |
Fig. 3 Joint constraints on the parameters Γ, EC, fREF and fCT based on both the XRB spectrum and the fraction of Compton-thick of AGN in the Swift/BAT AGN survey (Burlon et al. 2011). Left: the (blue) thick continuous line marks the region of the parameter space which is consistent at the 68% confidence level with both the observed XRB spectrum and the fraction of Swift/BAT Compton-Thick AGN. The (red) thin dotted line marks the region which is consistent with those observations at the 95% confidence level. Right: same as left panel including the contribution of blazars, as modeled by Draper & Ballantyne (2009), to the XRB synthesis results. |
 |
Fig. 4 The observed fraction of Compton-thick AGN in the spectral bands 0.5−2, 0.5−8, 2−10 and 20−40 keV. Our model predictions for an intrinsic Compton-thick AGN fraction of 5, 15, 25% correspond to the the red dotted, blue short-dashed and green long dashed curves, respectively. The black solid lines are the predictions of the X-ray background synthesis model of Gilli et al. (2007). The magenta dot-dashed lines are the predictions of the Ballantyne et al. (2011) model. The inset plots show the predictions for the cumulative number counts of Compton-thick AGN. The curves are the same as in the main panels. The observational datapoints are from Tozzi et al. (2006) (2−10 keV), Brightman & Ueda (2012) (0.5−8 keV), Krivonos et al. (2007) adapted from Treister et al. (2009) (20−40 keV). |
The comparison between model and observations is limited to the energy range 3−100 keV. Below about 3 keV sources other than AGN also contribute to the XRB, i.e. X-ray emission from our Galaxy, groups, and clusters (Blanchard et al. 1992). At energies above 100 keV processes that are not modelled in this paper, such as inverse-Compton scattering of photons in relativistic jets of radio-loud AGN, dominate (see Draper & Ballantyne 2009). These processes are also expected to have a small contribution to the XRB below 100 keV (Giommi et al. 2006; Ajello et al. 2009). We approximated their impact by adding to the XRB spectrum estimated by our synthesis code the Blazar contribution as modelled by Draper & Ballantyne (2009), assuming a duty cycle of 13% for the BL Lacs. In that model the blazar contribution to the XRB is 12% in the 0.5−2 keV band, 7% in the 2−10 keV band, 9% in the 15−55 keV band and close to 100% in the MeV region. The χ2 statistic was re-estimated for each set of our model parameters (Γ, Ec, fREF, fCT), including the contribution of blazars.
The XRB synthesis code also produces predictions on the number density of AGN samples that fulfill different selection criteria in luminosity, redshift, and/or obscuration. The observed fraction of Compton-thick AGN as a function of flux limit and detection energy band provides constraints on the parameters of the XRB synthesis model that are independent of those obtained from the XRB spectrum. In this exercise we used the fraction of Compton-thick AGN detected in the 15−55 keV energy band by the Swift/BAT survey (Ajello et al. 2008a). The sky coverage sensitivity curve corresponding to the 5σ detection threshold of the Swift/BAT sample was folded in our XRB synthesis code to predict the fraction of Compton-thick sources in that survey for the grid of model parameters presented in Table 1. This was then compared with the observations using binomial distribution confidence intervals. There are 197 AGN in the Swift/BAT sample of which nine (4.5%) are classified Compton-thick (Burlon et al. 2011). The 68 and 95% binomial confidence intervals for the Compton-thick fraction are 0.031−0.060 and 0.016−0.074, respectively.
4. Results
Figure 2 plots the two-dimensional projections of the four-dimensional parameter space, which is consistent with the XRB observations. All possible pairs of the parameters Γ, Ec, fREF, and fCT are shown in different panels. The contours correspond to the 68 and 95% confidence intervals. In the case of four degrees of freedom these correspond to Δχ2 relative to the minimum χ2 value of 4.72 and 9.70, respectively. The right set of panels in Fig. 2 include the contribution of blazars to the XRB as modelled by Draper & Ballantyne (2009).
The parameter space shown in Fig. 2 is complex. Firstly, there are degeneracies among parameters, such as Γ and EC, with higher values of the photon index also requiring higher cutoff energies to provide acceptable fits to the XRB observations. There are also effects related to the resolution of the parameter grid. These are manifested by wiggles in the contours e.g. in the plots of fCT vs. EC or fREF vs. EC. Increasing the sampling rate of the parameters (i.e. smaller step size in Table 1) would smoothen the contours at the expense of computation time.
Despite this limitation, the XRB spectrum does place constraints on some of the four parameters plotted in Fig. 2. For example, there is a relatively narrow region of the Γ-EC parameter space that is consistent with the observations at the 68 or the 95% confidence interval. In contrast, all plots that include the fCT parameter (top row of panels in Fig. 2) have confidence contours that cover most of the grid space. Therefore the parameter that is least sensitive to the XRB spectrum (and hence least constrained) is the fraction of Compton-thick AGN. For any value of fCT there are combinations of the other three parameters that yield acceptable fits to the XRB spectrum at the 68 or 95% confidence intervals.
Including blazars into the X-ray background synthesis modelling reduces the volume of the parameter space, which is consistent with the XRB spectrum at the 68% confidence level. This trend is more pronounced for fCT. Blazars have hard X-ray spectra, dominated by synchrotron emission, and therefore their net impact on the XRB modelling is the reduction of the fraction of Compton-thick sources needed to reproduce the shape and overall normalisation of the XRB spectrum (Draper & Ballantyne 2009). Nevertheless, blazars appear to have a small impact on the 95% confidence level contours of Fig. 2, which remain wide, especially for panels that include the fCT parameter.
Figure 3 shows how the (Γ, EC, fREF, fCT) parameter space is modified by considering the joint constraints from both the XRB spectrum and the observed fraction of Compton-thick AGN in the Swift/BAT survey (Burlon et al. 2011). As expected, the most affected parameter is fCT, which is limited to the range 10−20% (68 per cent confidence level). This is similar to the Compton-thick AGN fraction in the local Universe estimated by optical and IR surveys (Akylas & Georgantopoulos 2009; Brightman & Nandra 2011).
5. Predictions on the properties of Compton-thick AGN
Current and future (e.g. NUSTAR, Harrison et al. 2010; eROSITA; Predehl et al. 2011) high-energy missions have among their prime scientific goals the direct identification of Compton-thick AGN to constrain their cosmological evolution. This section presents the predictions of our model on the number density and redshift distribution of Compton-thick AGN at different energy bands and depths.
Figure 4 plots as a function of flux the observed fraction and cumulative number counts of Compton-thick sources determined by our XRB synthesis code for different values of the parameter fCT. The curves in that figure were constructed by fixing Γ = 1.9 and then setting Ecut, fREF to the values that yield the minimum χ2 for the XRB spectrum (see Table 2). Predictions are presented in the 0.5−2, 0.5−8, 2−10 and 20−40 keV bands. The redshift distributions of the Compton-thick AGN at different flux limits in those bands are shown in Fig. 5. The curves in that figure correspond to the model of Table 2 with fCT = 15%.
The 0.5–2 keV band is not an obvious choice of energy interval for Compton-thick AGN searches. However, many current (e.g. XMM-Newton, Chandra) and future (e.g. eROSITA) missions have their highest throughput in that energy range. Therefore, the deepest current images of the X-ray sky, in terms of resolving the highest fraction of the XRB, are in the 0.5−2 keV band. The detectability of Compton-thick AGN in the 0.5−2 keV band depends on both the assumed fCT and the adopted level of the soft component (e.g. scattered radiation) of the AGN spectra. The latter parameter has a strong impact on the number density of Compton-thick AGN predicted by our model.
 |
Fig. 5 The differential redshift distribution of Compton-thick AGN (dN/dz) predicted by our model in the spectral bands 0.5−2, 0.5−8, 2−10 and 20−40 keV. The different curves correspond to flux limits of 10-13 (black dash-dotted), 10-14 (blue large-dashed), 10-15 (cyan small-dashed), 10-16 (red dotted) and 10-17 erg s-1 cm-2 (red continuous). |
The choice of the 0.5−8 keV band is motivated by recent results on the number density of Compton-thick AGN in that spectral band by Brightman & Ueda (2012). They used the 4 Ms Chandra Deep Field South data in combination with the spectral models of Brightman & Nandra (2011), which account for Compton-scattering and the geometry of the circumnuclear material, to identify Compton-thick AGN to the flux limit fX(0.5−8 keV) ≈ 10-16 erg s-1 cm-2. Figure 4 shows that the cumulative number counts of those sources are consistent with the fCT = 25% model curve. We chose to compare our model predictions with the observed cumulative number count distribution of Compton-thick sources rather than their fraction relative to the overall AGN population. This is to avoid any uncertainties in the determination of the number density as a function of flux of the overall AGN population with LX(2−10 keV) > 1042 erg s-1 adopted by Brightman & Ueda (2012) to normalise the Compton-thick number counts. In the context of our model the fraction fCT ≈ 25% implied by the Brightman & Ueda (2012) results is consistent at the 95% confidence level with the observed fraction of Compton-thick sources in the Swift/BAT AGN sample in the local Universe (see Fig. 3). This tentatively suggests a redshift dependence of the fCT, given the mean expected redshift, z ≈ 1, of the Brightman & Ueda (2012) Compton-thick AGN sample (see Fig. 5).
The 2−10 keV band is routinely used to search for heavily obscured AGN. This is because photons at this energy interval are least affected by moderate obscuring column densities, while the sensitivity of imaging telescopes, such as XMM-Newton and Chandra, at this energy range remains relatively high. The detectability of Compton-thick AGN in the 2−10 keV band depends on the level of the reflection component of the AGN spectra.
The 20−40 keV band encompasses the peak of the XRB spectrum and will be explored to unprecedented depths (~10-14 erg s-1 cm-2) with the imaging optics of the NUSTAR mission (Nuclear Spectroscopic Telescope Array, Harrison et al. 2010). The Compton-thick AGN fraction predictions in that band are more directly related to fCT and are least dependent on other input parameters to the XRB synthesis code, such as the level of the reflection component. At the confusion flux limit of NUSTAR, fX(20−40 keV) ≈ 10-14 erg s-1 cm-2, we predict a fraction of Compton-thick AGN between 2 to 10%, depending on fCT. Figure 5 shows that the redshift distribution of those sources is expected to peak at z ≈ 0.6.
Although the efficiency of finding Compton-thick AGN is highest in the 20−40 keV band, the largest numbers of such sources will be produced by wide-area surveys at lower energies. At the flux limit fX(0.5−2) ≈ 10-14 erg s-1 cm-2 of the eROSITA All Sky Survey for example, the predicted number density of Compton-thick AGN is 0.2−0.9 deg-2. This translates into a total of 900 to 4000 Compton-thick AGN in the 0.5−2 keV eROSITA source catalogue. Figure 5 shows that the mean expected redshift of these sources is z ≈ 0.3. In the 2−10 keV band, eROSITA will achieve a sensitivity of about 3 × 10-13 erg s-1 cm-2. A total of about 70 to 280 Compton-thick AGN are expected at that flux limit over the whole sky. The relatively small field of view of NUSTAR (6 arcmin radius) and the fact that it is confusion limited at fX(20−40) ≈ 10-14 erg s-1 cm-2 (about 100 ks exposure), means that this mission will detect up to a few hundred Compton-thick AGN, depending on the adopted survey strategy. A limitation of the eROSITA data, however, is that the detected sources will typically have limited number of counts. The identification of the Compton-thick AGN among the eROSITA X-ray source population will therefore be challenging.
6. Discussion
We presented a synthesis model for the XRB that uses the results of state-of-the-art Monte Carlo simulations for the key spectral components of AGN. This was used to reconstruct the XRB spectrum for a wide range of values of the parameters (i) Γ, the exponent of the intrinsic AGN power-law; (ii) EC, the high-energy cutoff of the AGN spectra; (iii) fREF, the level of reflection in the spectra of AGN; and (iv) fCT, the fraction of Compton thick sources. We then define the volume of the four-dimensional parameter space for which the model XRB spectra are consistent with the observed one.
A result from Figs. 2 and 3 is that there are no solutions consistent with the observed XRB spectrum for Γ ≳ 1.98 (better than 95 per cent confidence level), under the assumptions of the model and for the range of parameter values explored. Therefore, within the context of the model, this is an upper limit to the intrinsic power-law index of AGN.
It is also interesting in Fig. 2 that the intensity of the integrated XRB spectrum does not provide any meaningful constraints on the space density of Compton-thick AGN in the Universe. Our analysis shows that a wide range of values of the Compton-thick fraction, fCT, yields acceptable fits to the XRB spectrum. This is because of degeneracies among input parameters to the XRB synthesis code. Also the parameters that describe the shape of the AGN spectra (e.g. reflection fraction, high energy cutoff) are still not adequately constrained by observations and therefore the range of plausible values remains wide. Figure 3 shows that the most solid limits on the fraction of Compton-thick AGN comes from the direct detection of such sources.
This is also demonstrated in Fig. 4, which plots the model expectations for the observed fraction and the number-count distribution of Compton thick AGN as a function of flux at different energy bands. The number counts of Compton thick AGN in the Chandra Deep Field South (Brightman & Ueda 2012) suggest fCT ≈ 25 per cent at z ≈ 1, in agreement at the 95 per cent confidence level with the Swift/BAT results in the local Universe.
Figure 4 also compares our predictions on the number density of Compton-thick AGN with the X-ray background synthesis models of Gilli et al. (2007)1 and Draper & Ballantyne (2010). The former model is built on the same basic principles (e.g. AGN unification paradigm) as the XRB code presented in this paper. There are important differences between the two codes however, in e.g. the adopted X-ray luminosity function, the overall fraction of Compton-thick AGN, and the level of the reflection component. Only mildly Compton-thick AGN, log NH = 24−25 cm-2, are included in the Gilli et al. (2007) predictions plotted in Fig. 4 to facilitate the comparison with our results. Contrary to other XRB synthesis codes, Draper & Ballantyne (2010) postulated that the physical parameter that is more relevant to obscuration and Compton-thickness is the accretion rate onto the SMBH. This is motivated by numerical simulations, which suggest that the AGN obscuration is related to the evolutionary status of the SMBH, and by observational constraints on the accretion properties of nearby Compton-thick QSOs. This model assumes that the fraction of Compton-thick AGN (log NH = 24−25 cm-2) is a strong function of accretion rate. They dominate at both high (λ > 0.9; fCT ≈ 0.86) and low (λ < 0.01; fCT ≈ 0.60) Eddington ratios, while they are absent at intermediate Eddington ratios.
In all panels of Fig. 4 the Gilli et al. (2007) and Draper & Ballantyne (2010) results predict a very different flux dependence of the observed Compton-thick fraction and number count distribution. In the 0.5−8 or 2−10 keV bands for example, the differences are caused by the adopted fCT and the treatment of the reflection spectral component in the different codes. We assigned the same fREF to all AGN, whereas in Gilli et al. (2007) the level of reflection depends on the obscuration and accretion luminosity. As a result, the Gilli et al. (2007) predictions cut through our curves in Fig. 4. At faint fluxes, below about 10-16 erg s-1 cm-2, their curve lies well above our predictions because of the higher fraction of Compton-thick AGN adopted by their model. The Draper & Ballantyne (2010) model predicts more Compton-thick AGN relative to the Gilli et al. (2007) and our predictions. The hump in their number-count predictions marks the change in the dominant Compton-thick population from high Eddington ratio sources at bright fluxes to slowly accreting systems.
The detectability of Compton-thick AGN in the 0.5−2 keV band depends quite strongly on the level of the soft spectral component. It is not surprising that in Fig. 4 there is fair agreement between our fCT = 25% model and that of Gilli et al. (2007) down to fX(0.5−2 keV) ≈ 10-16 erg s-1 cm-2, although the latter assumes a much higher fraction of Compton-thick AGN. This is because both models use the same level of scattered radiation (3%) to model the soft component of AGN. The upturn in the fraction of the Compton-thick AGN at fX(0.5−2 keV) ≲ 10-16 erg s-1 cm-2 in the Gilli et al. (2007) models is caused by the increasing contribution of high redshift sources for which the reflection component is redshifted into the 0.5−2 keV band.
Finally, the detection rate of Compton-thick AGN in the 20−40 keV band is more directly related to the total number of sources in the parent population and less sensitive to the spectral characteristics of AGN (e.g. level of scattered radiation or reflection fraction). Our estimates for the observed fraction of Compton-thick AGN in that band are therefore consistently below those of Gilli et al. (2007) and Draper & Ballantyne (2010) because these authors assume a higher intrinsic fraction of Compton-thick AGN.
7. Conclusions
A model for the synthesis of the XRB was presented, which used as input an AGN X-ray spectral library generated by Monte Carlo simulations to account for the impact of Compton-scattering and photoelectric absorption. We then explored whether the input parameters to the XRB synthesis code can be constrained by observations of the XRB intensity as a function of energy. Four parameters were used in this exercise, the power-law index and high-energy cutoff of the intrinsic X-ray spectrum of AGN, the level of the reflection component in AGN spectra, and the intrinsic fraction of Compton-thick AGN. We mapped the volume of this four-dimensional space that is consistent with observational determinations of the XRB spectrum in the energy interval 3−100 keV and found that one of the least constrained model parameters is the fraction of Compton-thick AGN in the Universe. Acceptable fits to the XRB spectrum (68% confidence level) can be obtained for Compton-thick AGN fractions in the range 5−50%. This is because of aliases among input parameters to the XRB synthesis code as well as because of uncertainties in our current understanding of AGN spectra (e.g. level of reflection). The most stringent constraints on the fraction of Compton-thick AGN in the Universe comes from the direct detection of such sources in high-energy surveys, such as those carried out by Swift/BAT and INTEGRAL. These observations suggest a Compton-thick fraction, at least in the local Universe, of 10−20% at the 68% confidence level. We also predicted the number counts of Compton-thick AGN as a function of flux and energy band. These predictions can be tested by current and upcoming X-ray missions to set tight constraints on the space density of Compton-thick AGN as a function of redshift.
Acknowledgments
We thank the anonymous referee for constructive comments and suggestions. A.G. acknowledges financial support from the Marie-Curie Reintegration Grant PERG03-GA-2008-230644. I.G. acknowledges support by the European Community through the Marie Curie fellowship FP7-PEOPLE-IEF-2008 Prop. 235285 under the Seventh Framework Programme (FP7/2007-2013).
References
- Aird, J., Nandra, K., Laird, E. S., et al. 2010, MNRAS, 401, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Greiner, J., Kanbach, G., et al. 2008a, ApJ, 678, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Greiner, J., Sato, G., et al. 2008b, ApJ, 689, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Costamante, L., Sambruna, R. M., et al. 2009, ApJ, 699, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Akylas, A., & Georgantopoulos, I. 2009, A&A, 500, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akylas, A., Georgantopoulos, I., Georgakakis, A., Kitsionas, S., & Hatziminaoglou, E. 2006, A&A, 459, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Awaki, H., Koyama, K., Inoue, H., & Halpern, J. P. 1991, PASJ, 43, 195 [NASA ADS] [Google Scholar]
- Ballantyne, D. R., Draper, A. R., Madsen, K. K., Rigby, J. R., & Treister, E. 2011, ApJ, 736, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, F. E., Vignali, C., Alexander, D. M., et al. 2004, Adv. Space Res., 34, 2555 [NASA ADS] [CrossRef] [Google Scholar]
- Beckmann, V., Soldi, S., Ricci, C., et al. 2009, A&A, 505, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanchard, A., Wachter, K., Evrard, A. E., & Silk, J. 1992, ApJ, 391, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Boyle, B. J., Griffiths, R. E., Shanks, T., Stewart, G. C., & Georgantopoulos, I. 1993, MNRAS, 260, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Brightman, M., & Nandra, K. 2011, MNRAS, 413, 1206 [CrossRef] [Google Scholar]
- Brightman, M., & Ueda, Y. 2012, MNRAS, 423, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Brusa, M., Comastri, A., Gilli, R., et al. 2009, ApJ, 693, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Burlon, D., Ajello, M., Greiner, J., et al. 2011, ApJ, 728, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Sunyaev, R., Revnivtsev, M., et al. 2007, A&A, 467, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Civano, F., Brusa, M., Comastri, A., et al. 2011, ApJ, 741, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., Setti, G., Zamorani, G., & Hasinger, G. 1995, A&A, 296, 1 [NASA ADS] [Google Scholar]
- Comastri, A., Ranalli, P., Iwasawa, K., et al. 2011, A&A, 526, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crummy, J., Fabian, A. C., Gallo, L., & Ross, R. R. 2006, MNRAS, 365, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Dadina, M. 2008, A&A, 485, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Luca, A., & Molendi, S. 2004, A&A, 419, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Ceca, R., Caccianiga, A., Severgnini, P., et al. 2008, A&A, 487, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draper, A. R., & Ballantyne, D. R. 2009, ApJ, 707, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Draper, A. R., & Ballantyne, D. R. 2010, ApJ, 715, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Dwelly, T., & Page, M. J. 2006, MNRAS, 372, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Dwelly, T., Page, M. J., Loaring, N. S., et al. 2005, MNRAS, 360, 1426 [Google Scholar]
- Fabian, A. C., & Barcons, X. 1992, ARA&A, 30, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Daddi, E., Fiore, F., et al. 2011, ApJ, 729, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Fiore, F., Puccetti, S., Brusa, M., et al. 2009, ApJ, 693, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Gendreau, K. C., Mushotzky, R., Fabian, A. C., et al. 1995, PASJ, 47, L5 [NASA ADS] [Google Scholar]
- Georgantopoulos, I., Akylas, A., Georgakakis, A., & Rowan-Robinson, M. 2009, A&A, 507, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Giacconi, R., Gursky, H., Paolini, F. R., & Rossi, B. B. 1962, Phys. Rev. Lett., 9, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giommi, P., Colafrancesco, S., Cavazzuti, E., Perri, M., & Pittori, C. 2006, A&A, 445, 843 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruber, D. E., Matteson, J. L., Peterson, L. E., & Jung, G. V. 1999, ApJ, 520, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F., Boggs, S., Christensen, F., et al. 2010, in AAS/High Energy Astrophysics Division #11, BAAS, 42, 737 [Google Scholar]
- Hasinger, G. 2008, A&A, 490, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hickox, R. C., & Markevitch, M. 2006, ApJ, 645, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Krivonos, R., Revnivtsev, M., Lutovinov, A., et al. 2007, A&A, 475, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kushino, A., Ishisaki, Y., Morita, U., et al. 2002, PASJ, 54, 327 [NASA ADS] [CrossRef] [Google Scholar]
- LaFranca, F., Fiore, F., Comastri, A., et al. 2005, ApJ, 635, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Lumb, D. H., Warwick, R. S., Page, M., & De Luca, A. 2002, A&A, 389, 93 [Google Scholar]
- Maccacaro, T., della Ceca, R., Gioia, I. M., et al. 1991, ApJ, 374, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, F. E., Boldt, E. A., Holt, S. S., et al. 1980, ApJ, 235, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Molina, M., Bassani, L., Malizia, A., et al. 2009, MNRAS, 399, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Pagani, C., Cusumano, G., et al. 2009, A&A, 493, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, K. D., & Yaqoob, T. 2011, MNRAS, 415, 3962 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., & Pounds, K. A. 1992, Nature, 359, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., & Pounds, K. A. 1994, MNRAS, 268, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., Fabian, A. C., George, I. M., et al. 1993, MNRAS, 260, 504 [NASA ADS] [Google Scholar]
- Predehl, P., Andritschke, R., Becker, W., et al. 2011, in SPIE Conf. Ser., 8145 [Google Scholar]
- Revnivtsev, M., Gilfanov, M., Sunyaev, R., Jahoda, K., & Markwardt, C. 2003, A&A, 411, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricci, C., Walter, R., Courvoisier, T. J.-L., & Paltani, S. 2011, A&A, 532, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Setti, G., & Woltjer, L. 1989, A&A, 224, L21 [NASA ADS] [Google Scholar]
- Shanks, T., Georgantopoulos, I., Stewart, G. C., et al. 1991, Nature, 353, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Stocke, J. T., Morris, S. L., Gioia, I. M., et al. 1991, ApJS, 76, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, P., Gilli, R., Mainieri, V., et al. 2006, A&A, 451, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treister, E., & Urry, C. M. 2005, ApJ, 630, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Treister, E., & Urry, C. M. 2006, ApJ, 652, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Treister, E., Urry, C. M., & Virani, S. 2009, ApJ, 696, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Tueller, J. 2011, in Amer. Astron. Soc. Meeting Abstracts #218, 115.02 [Google Scholar]
- Türler, M., Chernyakova, M., Courvoisier, T. J.-L., et al. 2010, A&A, 512, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, T. J., Nandra, K., George, I. M., Fabian, A. C., & Pounds, K. A. 1993, ApJ, 419, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, T. J., George, I. M., Nandra, K., & Mushotzky, R. F. 1997, ApJS, 113, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Akiyama, M., Ohta, K., & Miyaji, T. 2003, ApJ, 598, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Vecchi, A., Molendi, S., Guainazzi, M., Fiore, F., & Parmar, A. N. 1999, A&A, 349, L73 [NASA ADS] [Google Scholar]
- Williams, O. R., Turner, M. J. L., Stewart, G. C., et al. 1992, ApJ, 389, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Worsley, M. A., Fabian, A. C., Bauer, F. E., et al. 2005, MNRAS, 357, 1281 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Red curve: an example of an XRB spectrum produced by our synthesis model for parameters Γ = 1.88, EC = 230 keV, fREF = 0.055 and fCT = 0.1. The points are the observational constraints on the intensity of the XRB at different energies from the studies discussed in the text. Comparison of the model curve with the data yields a χ2 of 70.8 for 86 degrees of freedom (90 data points minus four free parameters). |
| In the text | |
 |
Fig. 2 Left: confidence intervals for the model parameters Γ, EC, fREF and fCT used to synthesise the XRB spectrum. The (blue) thick continuous line corresponds to the 68 per cent confidence level (Δχ2 = 4.72 for four parameters). The (red) thin dotted line marks the 95th percentile (Δχ2 = 9.70 for four parameters). Right: same as right panel but including to our XRB synthesis results the contribution of blazars, as modelled by Draper & Ballantyne (2009). |
| In the text | |
 |
Fig. 3 Joint constraints on the parameters Γ, EC, fREF and fCT based on both the XRB spectrum and the fraction of Compton-thick of AGN in the Swift/BAT AGN survey (Burlon et al. 2011). Left: the (blue) thick continuous line marks the region of the parameter space which is consistent at the 68% confidence level with both the observed XRB spectrum and the fraction of Swift/BAT Compton-Thick AGN. The (red) thin dotted line marks the region which is consistent with those observations at the 95% confidence level. Right: same as left panel including the contribution of blazars, as modeled by Draper & Ballantyne (2009), to the XRB synthesis results. |
| In the text | |
 |
Fig. 4 The observed fraction of Compton-thick AGN in the spectral bands 0.5−2, 0.5−8, 2−10 and 20−40 keV. Our model predictions for an intrinsic Compton-thick AGN fraction of 5, 15, 25% correspond to the the red dotted, blue short-dashed and green long dashed curves, respectively. The black solid lines are the predictions of the X-ray background synthesis model of Gilli et al. (2007). The magenta dot-dashed lines are the predictions of the Ballantyne et al. (2011) model. The inset plots show the predictions for the cumulative number counts of Compton-thick AGN. The curves are the same as in the main panels. The observational datapoints are from Tozzi et al. (2006) (2−10 keV), Brightman & Ueda (2012) (0.5−8 keV), Krivonos et al. (2007) adapted from Treister et al. (2009) (20−40 keV). |
| In the text | |
 |
Fig. 5 The differential redshift distribution of Compton-thick AGN (dN/dz) predicted by our model in the spectral bands 0.5−2, 0.5−8, 2−10 and 20−40 keV. The different curves correspond to flux limits of 10-13 (black dash-dotted), 10-14 (blue large-dashed), 10-15 (cyan small-dashed), 10-16 (red dotted) and 10-17 erg s-1 cm-2 (red continuous). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


