EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 546 (October 2012) A&A, 546 (2012) A43 Full HTML
Free Access
Issue
A&A
Volume 546, October 2012
Article Number A43
Number of page(s) 19
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201219310
Published online 05 October 2012

© ESO, 2012

1. Introduction

So far, more than 700 exoplanets have been confirmed and thousands of transiting candidates identified by the space telescope Kepler (Batalha et al. 2012). Among them, hot Jupiters are a class of gas giants with orbital periods of a few days or less. They are found around  ~0.5% of KGF stars (Howard et al. 2010, 2012). About 10% of them transit their host star, and their atmospheric composition and physical structure can be studied by transit spectroscopy (e.g. Charbonneau et al. 2000, 2008; Richardson et al. 2007; Tinetti et al. 2007; Sing et al. 2008; Swain et al. 2008a,b, 2009a,b; Huitson et al. 2012).

Although current observations are still limited and subjected to divergent interpretations, future instruments such as E-ELT, JWST (Gardner et al. 2006), EChO (Tinetti et al. 2012), and FINESSE (Swain 2010) should provide better constraints on both the chemical composition and the temperature profiles of the nearby hot Jupiters like HD 189733b and HD 209458b. They will also be able to study more distant targets and deliver statistically significant trends about the nature of their atmospheres. Chemical modeling will be an important component of these studies. It will point to key observations able to distinguish between various hypotheses and will be used to analyze the observations and to constrain, for instance, the atmospheric elemental abundances.

The first models of hot Jupiter atmospheres assumed chemical equilibrium (e.g. Burrows & Sharp 1999; Seager & Sasselov 2000; Sharp & Burrows 2007; Barman 2007; Burrows et al. 2007, 2008; Fortney et al. 2008a). However, strongly irradiated atmospheres are unlikely to be at chemical equilibrium. Their intense UV irradiation (typically 10 000 times the flux received on the top of the atmosphere of Jupiter) and strong dynamics result in photolyses and diffusion/advection timescales that are comparable to or shorter than the chemical ones. Deviations from the thermodynamic equilibrium have been discussed with timescale arguments (e.g. Lodders & Fegley 2002; Fortney et al. 2006, 2008b; Visscher et al. 2006, 2010; Madhusudhan & Seager 2010) or modeled with a few reactions describing the CO-CH4 conversion coupled with the dynamics (Cooper & Showman 2006). A more detailed modeling requires the use of a photochemical kinetic network. A kinetic network is, in practice, a list of reactions and associated rate coefficients able to quantitatively describe (within a certain accuracy) the kinetics of a pool of species, usually the most abundant ones. Constructing such a network of reactions implies answering two major questions. One has to do with the completeness of the network: what are the species and the reactions connecting them that must be included? The other issue is the availability of the kinetic data, because the literature and databases may not provide the rate coefficients for some of the needed reactions or may provide conflicting values with no recommendation. These two issues are tightly connected and both depend on the considered range of temperatures and pressures. Eventually, and regardless of the methodology adopted to select the reactions and their rates, it is the ability to predict experimentally-controled abundances that can validate the network or not.

To investigate the consequences of the strong UV incident flux on neutral species, photochemical models have been developed (Liang et al. 2003, 2004). Based on kinetics model dedicated to Jupiter’s low-temperature atmosphere, these models however neglected endothermic reactions, which are in fact fairly efficient in such hot atmospheres. Line et al. (2010) have introduced some endothermic reactions to a similar Jovian photochemical scheme but most of the pre-existing reactions were not reversed. They were therefore not able to reproduce the thermodynamic equilibrium, which occurs in the deep atmospheres of hot Jupiters. Zahnle et al. (2009a,b) developed a photochemical model that considers the reversal of their whole set of two-body exothermic reactions. They selected their rate constants in the NIST database1 based on the following criteria: relevance of temperature conditions, date of review, date of the experiment, and date of the theoretical study (in order of preference). Moses et al. (2011) developed a model that considered the reversal of all the reactions, including three-body reactions, ensuring reproduction of the thermodynamical equilibrium from the top to the deepest layers of the atmosphere. Their chemical scheme is derived from the Jupiter and Saturn models (Gladstone et al. 1996; Moses 1996; Moses et al. 1995b,a, 2000a,b) with further updates on the basis of combustion-chemistry literature. In the same manner, Line et al. (2011) developed a fully reversible kinetic model, to study the hot Neptune GJ 436b. None of these works discuss the validation of the chemical scheme against experiments. In addition, that computed abundances evolve towards the composition predicted by equilibrium calculations (at given pressure P and temperature T with no external irradiation or mixing) is by no means a validation of the kinetic network. Indeed, any network containing at least as many independent, reversible reactions as modeled species, in which the rates for the backward processes are derived from equilibrium constants and forward rates, will evolve toward the equilibrium predicted with the same equilibrium constants, regardless of the quantitative values of the forward rates, as illustrated in Fig. 1.

thumbnail Fig. 1

Abundances of NH3 as a function of time computed with two kinetic schemes that are fully reversed according to equilibrium constants but that differs by their nitrogen chemistry (nominal and GRIMECH as defined in Sects. 2.1.2 and 3.3). While they both converge towards the equilibrium (dotted line), they exhibit very different evolution. Initial condition is a mixture of H2, CH4, O2, N2, and He with solar elemental abundances.

Fortunately, and thanks to the physical conditions and elemental composition of hot Jupiter (and hot Neptune) atmospheres, we benefit from decades of intensive work in the field of combustion, which includes a vast amount of experiments, the development of comprehensive mechanisms2, and the systematic comparison between the two. Therefore, we propose in the present work a new mechanism dedicated to the chemical modeling of hot atmospheres that is not adapted from previous Solar System photochemical models but instead derives from industrial applications (mainly combustion in car engines). Details about this chemical network and its range of validity are presented in Sect. 2.1.

We use this chemical network in a 1D model that includes photolyses and vertical transport, which has been previously used to study the atmospheric photochemistry of various objects in the Solar System: Neptune (Dobrijevic et al. 2010a), Titan (Hébrard et al. 2006, 2007), Saturn (Dobrijevic et al. 2003; Cavalié et al. 2009), and Jupiter (Cavalié et al. 2008) as well as extrasolar terrestrial planets (Selsis et al. 2002). We model the photochemistry of two hot Jupiters: HD 209458b and HD 189733b (Sect. 2.5). We study the departure from thermodynamic equilibrium and compare our results with those of Moses et al. (2011) (Sect. 3). We also investigate how including different reaction networks specific to nitrogen-bearing species influences the model results (Sect. 3.3) and the planetary synthetic spectra (Sect. 3.3.1).

2. The model

2.1. Kinetic network: from car engine to hot Jupiters

Significant progress has been made during the past decade in the development of validated combustion mechanisms. In the context of limiting the environmental impact of transportation, there is indeed a need for developing detailed chemical kinetic models that are more predictive and more accurate for the combustion of fuels. One part of the studies undertaken in the LRGP (Laboratoire Réactions et Génie des Procédés, Nancy, France) concerns engine-fuel adaptation to improve the efficiency of engines and to limit the emission of pollutants. Gasoline and diesel fuels contain many molecules belonging to several major hydrocarbon families. Biofuels contain also oxygenated species, such as alcohols and methyl esters. Oxidation and combustion of these complex blends occur by radical chain reactions involving hundreds of molecular and radical species and several thousand elementary reactions in the case of pure reference fuels, such as n-heptane, iso-octane, or cetane. The primary focus of the currently developed chemical models is to simulate the main combustion parameters (auto-ignition delay times, laminar flame speed, heat release), which are needed for the design of engines or burners, to estimate the fuel consumption, and to model the formation of some of the main regulated pollutants (carbon monoxide, nitrogen oxides, unburned hydrocarbons, and particulate matter). Most of these kinetic models were developed for industrial applications and have been validated in a range of temperatures, from 300 to approximately 2500 K, and for pressures from 0.01 bar to some hundred bar. What is worth noticing is the similarity of these temperature and pressure ranges with the conditions prevailing in hot Jupiters atmospheres, in the very layers where they influence the observed molecular features. In addition, combustion mechanisms mainly deal with molecules made of C, H, O, and N, which are also the main constituents of the molecules and radicals in these atmospheres. For this reason, we have decided to implement such a mechanism, which has already been applied successfully to many cases and systematically validated (Bounaceur et al. 2007), to study the atmosphere of hot Jupiters.

In this study we have used a C/H/O/N mechanism, whose core is a C0–C2 mechanism that includes all the reactions required to model the kinetic evolution of radicals and molecules containing fewer than three carbon atoms. This mechanism also contains some species with more than two carbon atoms, which are necessary to model the abundance of C0–C2 species. This mechanism does not include nitrogen species, except N2 as a third body. Because nitrogen species, such as N2, NH3, HCN, and CN, are expected to be important constituents of hot Jupiter atmospheres, we completed this C0-C2 base with a validated submechanism specifically constructed to model nitrogen species and all the cross-term reactions involved (for instance, reactions between alkanes and NOx). These mechanisms do not use rate coefficients that have been adjusted by optimization procedures in order to fit experiments. Their values are those recommended for the individual processes by the main kinetics databases for combustion (Tsang & Hampson 1986; Manion et al. 2008; Smith et al. 1999; Baulch et al. 2005). The list of the reactions and their rate coefficients are available in the online database KIDA: KInetic Database for Astrochemistry3 (Wakelam et al. 2012). The final mechanism includes 957 reversible and 6 irreversible reactions (see Sect. 2.1.3), involving 105 neutral species (molecule or radical). Helium is also included in this mechanism and plays the role of third body in some reactions.

2.1.1. C0–C2 reaction base

The C0–C2 reaction base we use was developed for industrial applications, was first presented by Barbé et al. (1995), and has been continuously updated (Fournet et al. 1999; Bounaceur et al. 2010). This mechanism is designed to reproduce the kinetics of species with fewer than three carbons. It includes all the unimolecular or bimolecular reactions involving radicals or molecules containing no more than two carbon atoms. This mechanism was built by using a reaction grid, as proposed by Tsang & Hampson (1986). All unimolecular and bimolecular elementary forward reactions involving the considered reacting species were systematically written. Reacting species include 46 compounds (19 molecules and 27 radicals), which were ranked according to the molecular formula OxCyHz (with x varying from 0 to 3, y from 0 to 2, and z from 0 to 6): CO, H2, H2O, O2, H2O2, CH4, H2CO, CH3OH, CO2, CH3OOH, C2H2, C2H4, C2H6, CH2CO, CH3CHO, C2H5OH, C2H5OOH, CH3COOOH, cC2H4O (Ethylene Oxide), C, CH, 1CH2 (singlet),3CH2 (triplet), O(3P), H, OH, OOH, CH3, HCO, CH2OH, CH3O, CH3OO, C2H, C2H3, C2H5, CHCO, CH2CHO, CH3CO, C2H5O, C2H4OOH, C2H5OO, CH3COOO, CH3OCO, CO2H, 1-C2H4OH and 2-C2H4OH (ethyl radical isomers, 1-hydroxy, and 2-hydroxy). This ranking permits the part of the mechanism related to pyrolysis reactions to be separated easily from the one related to oxidation or combustion. The mechanism also includes 14 species containing three or four carbon atoms: C3H8, C4H8, C4H10, C2H5CHO, C3H7OH, C3H7O, C4H9O, C2H6CO, C3H8CO, C2H3CHO, n-C3H7, i-C3H7 (isopropyl and n-propyl radical isomers), 1-C4H9 and 2-C4H9 (1-butyl and 2-butyl radical isomers).

This C0–C2 mechanism has been widely validated in the 300–2500 K, 0.01–100 bar range for several types of reactors, such as shock-tubes, perfectly stirred reactors, plug-flow reactors, rapid compression machines, and laminar flames (e.g. Battin-Leclerc et al. 2006; Bounaceur et al. 2007; Anderlohr et al. 2010; Bounaceur et al. 2010; Wang et al. 2010). Obviously, it is not possible to describe all these validations in detail, but we can mention, for instance, the very recent work of Dirrenberger et al. (2011) who has studied the laminar burning velocity of several mixtures including air, hydrogen, and components of natural gas experimentally and modeled it with success. Laminar burning velocities are important parameters in many areas of combustion science, such as the design of burners and the prediction of explosions. They also play an essential role in determining several important aspects of the combustion process in spark ignition engines. These experiments were done in specific mixtures, containing nitrogen in the sole form of N2 and in which nitrogen species produced from N2 (NOx in the typical mixtures used in combustion) do not significantly affect the outcome, in order to validate the C0–C2 mechanism itself. Therefore, a model including only the C0–C2 base would not be accurate to predict the abundance of C0–C2 species in this range of P and T when applied to mixtures containing or producing (by reaction with N2) significant levels of nitrogen species other than N2.

2.1.2. Nitrogen reaction base

In our nominal model, the subnetwork for the nitrogen bearing species was derived from Konnov (2000, 2009) and Coppens et al. (2007). It is based on a comprehensive analysis of the combustion chemistry of nitrogen oxides (Konnov & De Ruyck 1999a), ammonia (Konnov & De Ruyck 2000b), hydrazine (Konnov & De Ruyck 2001b), and modeling of nitrogen oxides formation in different combustion systems (Konnov & De Ruyck 1999b, 2000a, 2001a). The mechanism was tested at the California Institute of Technology, USA, and found to be suitable for steady one-dimensional detonation and constant volume explosion simulations (Schultz & Shepherd 1999). It was also preferred by the researchers at the University of Bielefeld, Germany, to analyze flame structure and NO reburning in C3 flames (Atakan & Hartlieb 2000). In addition, we consider a few additional pathways for HCN oxidation from Dagaut et al. (2008).

Validations of our nominal subnetwork for nitrogen-bearing species were made on the basis of experimental data obtained, for instance, by oxidation of HCN in a silica jet-stirred reactor (JSR) at atmospheric pressure and from 1000 to 1400 K (Dagaut et al. 2008), or by studying laminar flame speeds in NH3–N2O mixtures (Brown & Smith 1994). The nitrogen mechanism includes 42 species (molecule or radical): NO3, HONO2, CH3ONO, CH3NO2, HNO2, CH3NO, NO2, HONO, HCNN, HCNO, N2O, NCO, HNO, HOCN, NNH, H2CN, N(4S), CN, HNCO, NO, NH, NH2, HCN, NH3, N2, N2O4, N2O3, N2H2, N2H3, N2H4, HNNO, HNOH, HNO3, NH2OH, H2NO, CNN, H2CNO, C2N2, HCNH, HNC, HON and NCN.

For comparison, we also used other nitrogen submechanisms, which are presented in Sect. 3.3 with the corresponding results.

Because the mechanism we use was created from individual processes and validated without any optimization of their reaction coefficients, its application outside the condition range of validation is not problematic. This is a problem, for instance, with the well-known combustion mechanism GRI-Mech 3.04 (Smith et al. 1999), proposed by Gas Research Institute, which is an optimized mechanism designed to model natural gas combustion. Optimization makes the model extremely accurate within the optimization domain, but its application beyond is risky (Battin-Leclerc et al. 2011).

2.1.3. Reversible reactions: kinetics vs. thermodynamics

For most reversible reactions, rate coefficients are only available for the exothermic (forward) direction. The rate constant for the endothermic (reverse) direction, kr(T), is then calculated as the ratio between the forward rate constant kf(T) and the equilibrium constant Keq(T), calculated with thermodynamical data, as explained in Appendix A. However, rate coefficients have sometimes been measured for both directions. In such cases, the ratio kf(T)/kr(T) departs from Keq(T) because different uncertainties affect the rate coefficients and the thermodynamic data. The computation of kr(T) using Keq(T) ensures the consistency between kinetics and thermodynamics by making the kinetic model evolve strictly toward the thermodynamic equilibrium that we calculate. Nevertheless, this choice may not always be the best. It results in the propagation into kr(T) of both the errors affecting kf(T) and Keq(T). Indeed, thermodynamic parameters used to calculate Keq(T) are not free of error, and are regularly updated just as kinetic data. In the field of combustion, for small species, such as CH4, CH3, and OH, it is common to use experimentally measured kinetic rates, rather than thermodynamical reversal, when they are available in the relevant temperature range. There is no obvious rule in this matter, but validation of the mechanism with out-of-equilibrium experiments seems the only practical way to chose between different rates. This is the criterion that we use, and our nominal network uses thermodynamical reversal for most of the reactions but not for three important ones. These reactions affect the unimolecular initiations (or thermal dissociation reactions) of methane into methyl and hydrogen radicals, 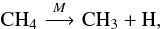(1)

of ethane into two methyl radicals, 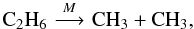(2)

and of hydrogen peroxide into two hydroxyl radicals, (3)At high temperature, chemical kinetics is very sensitive to these three reactions, which have been widely studied experimentally (Baulch et al. 1994; Golden 2008; Troe 2011). Therefore, we use the kinetic data measured experimentally for the forward and the reverse directions instead of calculating the reverse rate constants using thermodynamic parameters.

2.1.4. Excitation of oxygen and nitrogen atoms

Photodissociations produce excited states of oxygen (O(1D)) and nitrogen (N(2D)) that are not treated in the original combustion mechanisms. Therefore, we added 19 reversible reactions to the C/H/O/N mechanism, which describe the kinetics of O(1D) and N(2D), including radiative and collisional desexcitation. These reactions rates are taken (or have been estimated) from Okabe (1978), Herron (1999), Umemoto et al. (1998), Balucani et al. (2000a), Sato et al. (1999), Balucani et al. (2000b), and Sander et al. (2011).

2.2. Test of the chemical scheme with a 0D model

In addition to our 1D model, we have also developed a simple 0D model that computes the chemical evolution of a mixture at constant temperature and pressure. It includes neither mixing with another mixture nor photolyses. We used this 0D model to compare the composition found at steady state with the abundances at thermodynamic equilibrium (calculated with the code TECA, described in Appendix B) for several couples of pressure-temperature. Figure 2 illustrates this comparison with four species. First, we used a version of our nominal scheme in which all the reactions are reversed, in agreement with their equilibrium constant. The computed abundances converge exactly towards the equilibrium values with negligible numerical differences. Then, we used our nominal model in which some reactions are not reversed according to their equilibrium constant but using rate coefficients measured experimentally. In this case, the abundances reached at steady state departs from the predicted equilibrium. This departure remains very small: below 1% for most species and always below 5%. However, one can see that the kinetic evolution can be significantly different, both in terms of abundances and timescales.

thumbnail Fig. 2

Comparison between the thermodynamic equilibrium (dotted line) and the evolution of some molecular abundances in the 0D model, with two different schemes: the thermochemically reversed model (solid line) and the nominal model (dashed line) as a function of integration time at different temperature-pressure points. Initial condition is a mixture of H2, CH4, O2, N2, and He with solar elemental abundances.

2.3. The 1D model

To model the chemical composition of the atmosphere of the hot Jupiters HD 209458b and HD 189733b, we use our 1D time-dependent model, described in Dobrijevic et al. (2010a). As an input of the model, we give a pressure-temperature profile for the atmosphere of the planet being studied. This profile is then divided into discrete uniform layers with a thickness 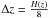, where H(z) is the pressure scale height. The grid contains  ~300 layers. Then the 1D kinetic model resolves the continuity equation (Eq. (4)) as a function of time, for each species and atmospheric layer, until a steady state is reached. 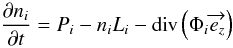(4)where ni the number density of the species i (cm-3), Pi its production rate (cm-3   s-1), Li its loss rate (s-1), and Φi its vertical flux (cm-2   s-1) that follows the diffusion equation, (5)where K is the eddy diffusion coefficient (cm2   s-1), Di is the molecular diffusion coefficient (cm2   s-1), and Hi the scale height of the species i.

At both upper and lower boundaries, we impose a zero flux for each species.

2.4. Photochemistry

We add a set of 34 photodissociations to the thermochemical scheme, which are presented in Appendix D. As we can see in Fig. 3, for HD 209458b and HD 189733b, UV flux penetrates down to a pressure of about 1 bar, where the temperature is higher than 1500 K. At these temperature and pressure, endothermic reactions do matter, which implies that photochemistry and thermochemistry are coupled in such highly irradiated atmospheres. We used absorption cross sections at the highest available temperature (i.e. 370 K at maximum, which is low compared to the temperatures in the atmosphere of hot Jupiters (see Fig. 4)).

thumbnail Fig. 3

Penetration of UV flux in the atmosphere of HD 209458b and HD 189733b at the steady state in function of wavelength. Plots represent the level where the optical depth τ = 1. The name of the compounds responsible for the main absorption at different wavelengths is indicated.

To calculate the photodissociation rates in all the layers of the atmosphere, we computed the stellar UV flux as a function of pressure and wavelength, taking molecular absorption by 22 species (Appendix D) and Rayleigh scattering into account. Actinic fluxes are calculated with a resolution of 1 nm (which is also the resolution we adopted for the absorption cross-sections), assuming a plane parallel geometry and an incidence angle θ of 48° (as done in Moses et al. 2011, because  ⟨ cosθ ⟩  = 2/3   (θ ≃ 48°) is the projected-area weighted average of the cosine of the stellar zenith angle over the planetary disk in secondary-eclipse conditions). Multiple Rayleigh scattering is coupled with absorption through a simple two-stream iterative algorithm (Isaksen et al. 1977).

thumbnail Fig. 4

Pressure-temperature profiles (left) and eddy diffusion profiles (right) of HD 189733b and HD 209458b (from Moses et al. 2011).

2.5. Application to hot Jupiters: HD 209458b and HD 189733b

HD 209458b and HD 189733b are transiting planets around nearby bright stars. Their atmospheres have been studied by their transmission spectrum obtained during the primary transit and their day-side emission spectrum measured at the secondary eclipse. These observations can be used to constrain the thermal profile (Swain et al. 2009a; Madhusudhan & Seager 2009) and to detect the spectral signature of atmospheric compounds (Charbonneau et al. 2002; Tinetti et al. 2007; Swain et al. 2008b; Grillmair et al. 2008; Langland-Shula et al. 2009; Swain et al. 2009a,b; Beaulieu et al. 2010).

In this preliminary study, we do not compare the results of our model with these observations for two reasons. First, there is no consensus yet on the actual constraints that can be drawn from these measurements. Secondly, such a comparison would imply addressing the effects of circulation on the composition and exploring all the range of possible elemental abundances for these objects. Several recent works claim that observations of some hot Jupiters imply enhanced elemental C/O ratios (Madhusudhan et al. 2011a,b). With C/O ratios close or above unity, species with more than two carbon atoms will be important, and our C0–C2 network does not allow us to study them. For these reasons, we are implementing a C0–C6 mechanism and a coupling with atmospheric circulation, which will be described in further studies. At this stage, our main goal is to compare the results of our model with already published works, in particular Moses et al. (2011, hereafter M11). We could also have compared our results with those of Zahnle et al. (2009a), who explored a broader range of conditions, included sulfur-bearing species and various elemental compositions. We decided to restrict our comparison with M11 because their model, like ours, only includes species made of C, H, O, and N (and He), and also because M11 have already made a comparison between their results and those of Zahnle et al. (2009a) showing only little discrepancies when the same conditions are considered. We used the same conditions (P-T profiles, eddy diffusion, elemental abundances) as in M11, so that differences should only come from kinetics (and photochemistry in the upper atmosphere), which represents the novelty of our approach.

2.5.1. Physical properties and composition

The physical properties of HD 209458b have been refined by Rowe et al. (2008) and are presented in Table 1, with some properties of the host star. Properties of HD 189733b and HD 189733 come from Southworth (2008, 2010).

Table 1

Properties of the systems HD 209458 and HD 189733.

To compare the outcomes of the two models (Sect. 3.2), we used the temperature and eddy diffusion profiles published in M11 (Fig. 4). Also following M11, we assumed protosolar elemental abundances (Lodders & Palme 2009) for both planets, with 20% of depletion for oxygen (sequestered along with silicates and metals). We started our time-dependent modeling with the thermodynamic equilibrium abundances calculated with TECA (an equilibrium model described in Appendix B) at each level of the atmosphere.

2.5.2. UV spectral irradiance

As HD 209458 is a G0 star (Table 1), we use the UV spectral irradiance of the Sun for this star. For the star HD 189733, a K1–K2 star (Table 1), the UV spectrum has been provided to us by Ignasi Ribas (priv. comm.). It is based on FUSE and HST observations of the star ϵ Eridani, a proxy of HD 189733 (similar type, age, and metallicity), in the 90−330 nm range. Between 0.5 and 90 nm, it is based on data from the X-exoplanets Archive at the CAB (Sanz-Forcada et al. 2011). Above 330 nm, we use a synthetic spectrum calculated with the stellar atmosphere code Phoenix (Hauschildt et al. 1999). This model for the UV spectrum of HD 189733 differs slightly from the one chosen in M11. We also tested our model with the spectrum used by M11 and found negligible differences at the pressure levels we model.

thumbnail Fig. 5

Steady-state composition of HD 209458b (left) and HD 189733b (right) calculated with our nominal model (color lines), compared to the thermodynamic equilibrium (thin black lines).

thumbnail Fig. 6

Steady-state composition of HD 209458b (left) and HD 189733b (right) calculated with our nominal model without photodissociation (color lines), compared to the thermodynamic equilibrium (thin black lines).

3. Results

3.1. Nominal model

First of all, we checked that our kinetic model reproduces the thermodynamic equilibrium, in the absence of vertical mixing and photodissociation. We obtained differences lower than a few percent, as found with the 0D model (see Sect. 2.2). For both planets, the homopause is always found above the 1 × 10-5 mbar level, which is beyond the range of pressure that we model. As a consequence, and although it is included, molecular diffusion does not affect our results.

Figure 5 shows the steady-state composition of the atmosphere of HD 209458b and HD 189733b, with vertical transport and photodissociations, while in Fig. 6, photodissociations have been removed. Comparing Figs. 5 and 6 shows us the influence of photolyses. Although HD 209458b receives a higher UV flux than HD 189733b, we can see that UV photons have little effect on the composition of HD 209458b, while they have significant influence on the chemistry of HD 189733b. This is because the temperature is higher in HD 209458b so that the chemical timescales are significantly shorter than the lifetime of species against photolyses, so in HD 209458b, kinetics dominate over photodissociations, even at high altitude. In HD 189733b, however, photodissociations affect the composition down to about the 10 mbar level. This is particularly noticeable for H and OH abundances. The production of H is dominated by the photolysis of H2 for pressures lower than 1 μbar. Below this level, and for pressures higher than 0.1 mbar, H is produced by the photodissociation of H2O, with a minor contribution of the photodissociations of NH3 and HCN. The abundance of OH follows the profile of H, and increases for pressures lower than 10 mbar. There is a photochemical enhancement of HCN above the 10 mbar pressure level, as discussed in M11. CH4 is destroyed by photolyses for pressures lower than 0.01 mbar. NH3 is photodissociated down to levels as deep as 1 bar, but vertical transport compensates for this destruction for pressures higher than 0.1 mbar. Above that level, the amount of NH3 decreases with altitude due to photolyses. Photochemistry has a negligible effect on CO2, as noted by Zahnle et al. (2009a).

thumbnail Fig. 7

Comparison between the abundance profiles found by our nominal model (color lines) and by Moses et al. (2011) (thin black lines), for the two planets (HD 209458b (left) and HD 189733b (right)).

For HD 209458b, we can see in Fig. 6 that mixing quenches NH3 and HCN at 1 bar and CH4 at 400 mbar. These species are transported up to the  ~1 mbar pressure level, but because the temperature increases with altitude at this level, they tend to come back to their thermochemical equilibrium values, so their abundances decrease again. For the other molecules, such as H2, H and CO2, at the thermodynamic equilibrium, there is a steep variation in composition (smoothed by vertical mixing) corresponding to the strong temperature gradient of the upper atmosphere.

Vertical quenching has an effect on a larger part of the atmosphere of HD 189733b. Both NH3 and HCN are quenched at 5 bar, CH4 at 1 bar, H at 40 mbar, and CO2 at 20 mbar. Quenching contaminates the composition up to very low-pressure levels (10-4 mbar).

thumbnail Fig. 8

Abundances of CH4, HCN, NH3, and CH3 in HD 209458b (left) and HD 189733b (right) with the four different models, compared to the results of Moses et al. (2011).

thumbnail Fig. 9

Abundances of C2H2, H, OH, and H2O in HD 209458b (left) and HD 189733b (right) with the four different models, compared to the results of Moses et al. (2011).

3.2. Comparison with Moses et al. (2011)

3.2.1. Equilibrium

Overall, the composition we calculate at thermodynamic equilibrium (which is our initial condition) is very close to what is obtained by M11 except for HCN for which there is a difference that can reach  ~30% at 100 bars and 1545 K. To check our calculations we also did a comparison with the code STANJAN5 and found negligible discrepancies for the species we compared, including HCN at this pressure and temperature. The difference with M11 probably comes from the coefficients used for the NASA polynomials (see Appendix A). Although the difference remains small for equilibrium calculations, we should keep in mind that it may significantly affect the kinetics of HCN and related species through the calculation of the rate for backward reactions and vertical quenching.

3.2.2. Steady state

In Fig. 7, we compare our results at steady state with those of M11. Differences between M11 and our nominal model are also shown species by species in Figs. 8 and 9. Discrepancies between the two models can be due to the different chemical schemes and, at levels where the results are sensitive to photochemistry, to possible differences in the UV fluxes, cross sections, and photodissociation quantum yields. An influence of the numerical implementation (such as the discretization of the atmosphere, the solver for the continuity equations, or the treatment of the UV transfer) is also possible.

In the lower atmosphere of HD 189733b and for most of the atmosphere of HD 209458b, photolyses have a negligible influence and departures should be caused by the kinetics. For these regions we find very similar results for species that remain at their equilibrium abundance (H, OH, CO, CO2, H2O, for instance), which only confirms, as stated before, that our thermodynamic equilibrium codes are in good agreement. For species quenched by mixing, however, significant deviations appear, in particular for NH3, HCN, and CH4. Their quenching occurs at different pressure levels and, thus, for different abundances that will then contaminate a large fraction of the atmosphere above. The discrepancies are much more significant in the case of HD 189733b, due to higher sensitivity to kinetics. Although the kinetic network is certainly the main reason for these departures, it is also true that quenching can be quite sensitive to the resolution of the pressure (or altitude) grid, in particular when there is a steep gradient of temperature which is the case in the convective zone (P >100 bar). For this reason, we impose the thickness of individual layers to be smaller than 1/8th of the local scale height, which results in  ~300 layers for the pressure range that we model. Although we do not know what resolution is used in M11, it seems more likely that the deviation comes from differences in the kinetic network itself. As explained in the Introduction, we use a chemical scheme validated for the species represented and for most of the range of temperature and pressure of the modeled atmospheres. M11, on the other hand, use a chemical scheme derived from Jupiter and Saturn models (Gladstone et al. 1996; Moses 1996; Moses et al. 1995b,a, 2000a,b) completed by high-temperature kinetics from combustion-chemistry literature (Baulch et al. 1992, 1994, 2005; Atkinson et al. 1997, 2006; Smith et al. 1999; Tsang 1987, 1991; Dean & Bozzelli 2000), which has not, to our knowledge, been validated against experiments. We also note departures in the upper atmosphere, where photolyses are important. In particular, H and OH exhibit similar profiles than those of M11 in HD 189733b, but shifted by about one order of magnitude in abundance for pressures lower than 50 mbar. CH4 is also affected. We checked that these differences are not due to using different stellar fluxes by switching between the flux we use and the one used in M11 (for HD 209458b, we both use the solar UV flux). At these altitudes, we note significant sensitivity of the mixing ratio of these species to the Rayleigh scattering, so the treatment of the scattering could explain at least part of this disagreement. Again, and although we do not know the details of the photochemical data and radiative transfer used in M11, we assume that kinetics explain the differences.

3.3. Other networks for nitrogen species

The main differences between M11 and our results are related to the quenching of NH3 and HCN. As mentioned in M11, the chemistry of nitrogen compounds has been less studied than carbon species and chemical networks have been subjected to less validation. However, NOx, HCN, CN, and NH3 are important species in applied combustion (gas fuel, for instance, can contain high concentrations of ammonia), and should be reproduced well within the temperature and pressure range of the validation. Quenching is found to occur within 1 to 10 mbars, corresponding to the range of validation in terms of pressure. An originality of our network compared to other schemes used in combustion is that it is not optimized to increase the agreement between modeling and experiments. In other words, the rate coefficients of the individual processes were not altered compared to their original measurement or estimate. The application of the network is therefore not strictly restricted to the validation domain.

Other submechanisms are available to model the kinetics of nitrogen-bearing species. They were constructed based on different approaches (optimization, specific domain of application, reduced number of reactions). To test our model against other nitrogen schemes, we replaced our nitrogen reaction base by nitrogen submechanisms taken from other C/H/O/N mechanisms:

  • GRIMECH, mechanism based on GRI-Mech 3.0 (Smith et al. 1999) with several reactions involving NOx compounds added with respect to the mechanisms of Glaude et al. (2005), as recommended and done by Anderlohr et al. (2009). It includes 162 reversible reactions involving 26 nitrogen compounds. The GRI-Mech 3.0 is a mechanism designed to model natural gas combustion, including NO formation and reburn chemistry. As already mentioned in Sect. 2.1.2, it has been optimized as a global mechanism; i.e., some rate coefficients have been modified (compared to the literature) in order to fit the results of a pool of experiments with conditions and compositions specific to combustion. The individual processes were not studied separately in all the pressure and temperature range. Applying this mechanism beyond its domain of optimization/validation is a risky extrapolation. Mixing ratios of oxidants, for instance, are very low in hot Jupiter atmospheres compared with the experiments used to optimize/validate GRI-Mech 3.0. While doing the present study, we noticed that two reactions from the GRIMECH mechanism had wrong rates so we corrected them. These erroneous rate constants, which can be traced back to the NIST Chemical Kinetics Database (Manion et al. 2008), were identified by systematically comparing reaction rate constants with collision limit values and energy barriers with the enthalpy budget of the reaction. The first reaction is 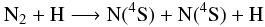(6)for which the rate given by NIST is kf(T) = 1.26 × 10-9   T-0.20 e−27,254/T cm3 molecule-1 s-1 (with T in Kelvin), although this expression corresponds in fact to the reaction 7, the thermal dissociation of NH through collisions with atomic nitrogen (Caridade et al. 2005): (7)The above expression overestimates by many orders of magnitude the rate constant of the reaction, whose activation energy must be around 100 000 K, as implied by the bond energy of molecular nitrogen and by measurements of the thermal dissociation of N2 through collisions with various bodies.

    thumbnail Fig. 10

    Synthetic day-side (left) and transmission (right) spectra of HD 189733b with the nominal mechanism (green curve) compared to the one corresponding to the GRIMECH mechanism (red curve) and to the thermochemical equilibrium (blue curve). The dark curve is obtained when NH3 is removed from the model. The day-side fluxes are given as brightness temperatures (Tb). Because of the reflection component, note that the link between Tb and the atmospheric thermal profile is altered below 2 μm. The transmission spectrum is given as the apparent planetary radius. The data points obtained from various observations are also shown.

    We finally adopted a more general form for the dissociation of N2, 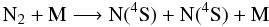(8)with the reaction rate constant kf(T) = 1.661 × 104   T-3.30 e−11,310/T cm3 molecule-1 s-1 (Thielen & Roth 1986). This rate had a strong influence on our results. Using the wrong rate has a strong effect on the atmospheric profiles of NH3 and HCN. The second reaction is 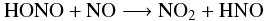(9)for which the reaction rate constant given by NIST (kf(T) = 7.34 × 10-20   T2.64 e−2034/T cm3 molecule-1 s-1) was in fact the rate of the reverse of reaction (9), as calculated by Mebel et al. (1998). In our model, we use instead the reaction 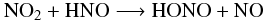(10)with the reaction rate constant kf(T) = 1.00 × 10-12 e−1000/T cm3 molecule-1 s-1 (Tsang & Herron 1991). When this paper is published, these rates should be corrected in the NIST Chemical Kinetics Database, but one should check that the wrong rates are not used in modeling.

  • GDF-Kin, a mechanism optimized for natural gas combustion modeling (Turbiez et al. 1998; De Ferrieres et al. 2008) that includes less individual processes: 180 reversibles reactions involving 22 nitrogen species. Several experimental data on natural gas combustion have been acquired in partnership with Gaz de France to develop this mechanism. The NOx chemistry has been included in GDF-Kin 3.0 (El Bakali et al. 2006). We used the update version GDF-Kin 5.0 (Lamoureux et al. 2010), in which five reactions involving NCN were refined in order to better reproduce the kinetics of this species. It is validated for temperatures between 400 and 2200 K and pressures between 0.04 and 10 bars.

  • DEAN, taken from Dean & Bozzelli (2000). This book that presents a catalog of reactions is used by Moses et al. (2011), at least for some reactions. The mechanism derived from this work includes 370 reversible reactions involving 49 nitrogen species and one C/H/O species that is not included in our C0–C2 scheme: HCOH. The purpose of the work of Dean and Bozzelli was to list gas phase reactions involving nitrogen-bearing species that could be important for high-temperature combustion modeling and to provide the associated rate coefficients based on an analysis of elementary reaction data, when available, or on estimations from thermochemical kinetics principles otherwise. This mechanism was developed on the basis of analysis of individual reactions rather than by attempting to reproduce any specific set of experiments. It is clearly written in this book that “Although we show in the chapter that this mechanism provides a reasonable description of some aspects of high-temperature nitrogen chemistry, we have not attempted a comprehensive comparison”. Therefore, this kinetic network should be viewed as a database of reaction rate constants rather than a validated mechanism, in the absence of validation.

The impact of the different nitrogen submechanisms on the abundance profiles of various species is illustrated in Figs. 8 and 9. Thermodynamic equilibrium is the same for all schemes (for the species in common).

First, we restrict our analysis to pressures higher than  ~1 mbar in order not to mix effects of kinetic rates with possible differences in the photochemical data or modeling. For HD 209458b, the main species that are significantly affected at these pressure levels by the change of nitrogen scheme are HCN and NH3. This is not surprising since these are the most abundant nitrogen species departing from equilibrium due to quenching, and the pressure level at which the quenching occurs depends on the kinetic network adopted. These two species (but also others) show even larger differences in the case of HD 189733b, since the lower temperatures of this atmosphere enhance the differences due to the kinetics. Departures between schemes are expected to become even larger for cooler atmospheres. None of the tested schemes shows an general improvement of the agreement with M11. Similar NH3 quenching is found by M11 and with DEAN for both planets, which makes sense because M11 use Dean & Bozzelli (2000) as a source of reactions and associated rates for N-bearing compounds. This similarity is also found for HCN but only at pressures higher than 1 bar. At higher altitudes, the HCN profiles from M11 become closer to the result with GRIMECH. For both planets and both HCN and NH3, profiles obtained with GDF-Kin are bracketed by those from the nominal model and DEAN, while GRIMECH gives significantly higher abundances than all other models in the quenching region. With GRIMECH, we also notice that NH3 becomes the main nitrogen-bearing species from the bottom of the atmosphere up to 0.03 mbar because of vertical mixing, whereas thermodynamics predicts that N2 should be the main nitrogen-bearing species.

Understanding the roots of theses discrepancies would require an in-depth study of the sensitivities of these schemes to reaction cycles, as a function of temperature and pressure, which is far beyond the scope of this study and would require tools that may have to be developed specifically for such large networks. To illustrate this difficulty we tried to identify the reaction that dominates the production rate of NH3 for HD 189733b, at 100 mbar. We found it to be the same for all mechanisms: (11)whose rate constant is similar in all schemes, and is calculated reversing the reaction: (12)which dominates the destruction of NH3, also in all the schemes. The following rates are found in the different schemes:

  • Nominal, Dean, GRIMECH:9.00 × 10-19   T2.4 e−4990/T cm3 molecule-1 s-1, derived from Ko et al. (1990).

  • GDF-Kin: 1.056 × 10-18   T2.39 e−5114/T cm3 molecule-1 s-1 from Michael et al. (1986).

We could think that these slight differences are responsible for the different results. However, NH3 does not display the same abundance when using Dean and GRIMECH mechanisms, even though they share the same rate constant. Moreover, nulling the rate constant of this reaction in the nominal scheme does not affect the quenching level of NH3 or its abundance for pressures higher than 10 mbar. We can therefore eliminate this hypothesis. Key reactions are in fact usually those that limit the rate of a cycle and that do not dominate the production or destruction of a given species. Finding those limiting processes in complex networks is a field of research in itself.

Identifying key pathways and their limiting reactions require dedicated algorithms (Lehmann 2004; Grenfell et al. 2006; Dobrijevic et al. 2010b; Stock et al. 2011, 2012) whose adaptation to the large networks we consider will require further work.

For hydrocarbons (see for instance CH4, C2H2, and CH3), all the models we tested cluster to the same profiles for pressures below 1 mbar. This shows that N-bearing species have little influence on hydrocarbon chemistry at these altitudes. (This would no longer be true at higher temperature and for higher C/O ratios since HCN would become a major reservoir of both N and C.) M11 systematically finds higher mixing ratios for hydrocarbons (but within one order of magnitude) above the quenching level of CH4 (1–10 bar), probably due to kinetic differences in the C0–C2 mechanism.

At lower pressure, Figs. 8 and 9 show large differences that are no longer due to quenching. At pressures lower than 1 mbar, the abundances of hydrocarbons depend on the nitrogen network used. It is particularly striking for C2H2 in HD 189733b, where DEAN and GRIMECH, on the one hand, and the nominal model, GDF-Kin and M11, on the other hand, seem to cluster in two different regimes, exhibiting two to three orders of magnitude differences at 0.1–0.001 mbar. Departures between network results can come from differences in the kinetic network (different reactions, different rates, different minor species included) but also in photochemistry. Indeed, some UV-absorbing species are not included in all the models, such as N2H4, HNO3, C2N2, and N2O4, which have absorption domains that overlap that of C2H2.

3.3.1. Corresponding emission and transmission spectra

To calculate the planetary transmission and emission+reflection spectra of HD 189733b (Fig. 10) and HD 209458b, we used a line-by-line radiative transfer model from 0.3 to 25 μm (Iro et al. 2005; Iro & Deming 2010). The opacity sources included in the model are the main molecular constituents: H2O, CO, CH4, NH3, Na, K, and TiO; collision-induced absorption by H2 and He; Rayleigh diffusion; and H− bound-free and 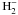free-free. For absorbing species not included in our kinetic model (Na, K, and TiO), chemical equilibrium is assumed. The current model does not account for clouds. For the reflected component, we used synthetic stellar spectra generated from ATLAS6. The main difference from the static model described in Iro et al. (2005) is the addition of NH3 for which we used the HITRAN 2008 database (Rothman et al. 2009). Planetary parameters are taken from Table 1.

We applied this model for the compositions obtained with the two nitrogen mechanisms, which give the most opposite results (Nominal and GRIMECH), as well as for chemical equilibrium. The GRIMECH scheme gives the highest abundance for ammonia: ten times more NH3 than the nominal model for HD 209458b and one hundred times more than the nominal model for HD 189733b. As a consequence, features of this molecule become noticeable on both the emission and transmission spectra at 1.9, 2.3, 3.0, 4.0, 6.1, and 10.5 μm. The most prominent feature is found for HD 189733b at 10.5 μm. NH3 features are also visible on the spectra of HD 209458b, but so slightly that it would not be observable.

At the moment, our radiative transfer model does not include the contribution of HCN to the opacities. Based on the HCN abundances and associated spectra found by M11, we can expect the spectra to be also sensitive to the HCN abundance. Indeed, at the altitudes probed by the observations, there is nearly two orders of magnitude less HCN with our nominal model than with GRIMECH, and GRIMECH gives HCN abundances similar to that of M11. Therefore, the signature of HCN found by M11 at 14 μm should also become noticeable with the GRIMECH version of our scheme.

Some observational data are superimposed on the spectra (Charbonneau et al. 2008; Grillmair et al. 2008; Swain et al. 2009b, for emission spectrum) and (Knutson et al. 2007, 2009; Swain et al. 2008b; Beaulieu et al. 2008; Sing et al. 2009; Désert et al. 2009; Agol et al. 2010, for transmission spectrum), but we do not discuss the agreement between observations and synthetic spectra, as we did not attempt to fit the observable using different thermal profiles.

4. Discussion

To study HD 209458b and HD 189733b, we used the pressure-temperature and eddy diffusion profiles from M11. These profiles were derived from general circulation models of Showman et al. (2009). This choice is motivated by the comparison with M11 and also because the actual physical structure of these atmospheres is not yet well constrained by observations; however, Huitson et al. (2012) have recently published thermal profiles for both planets, as inferred from transit spectroscopy. It seems that HD 189733b could be warmer than HD 209458b between 10-5 and 10-3 bar. Considering the large uncertainties affecting their physical conditions, our models should not be considered as predictions of the composition of hot Jupiters but more as a step in developing chemical models of these objects and model intercomparison.

In addition, circulation is not included in either our model or, to our knowledge, in other current photochemical models of hot Jupiters, although it has a significant influence on the chemical composition of the atmospheres owing, for instance, to the strong longitude dependency of the temperature. We will study the influence of the horizontal transport on the composition of the atmosphere of HD 209458b in a forthcoming paper (Agúndez et al. 2012).

Because modeled abundances depend significantly on the reaction network (in particular for NH3, HCN, and some hydrocarbons), we recommend using a network that has been validated (but not optimized) against experiments for conditions as close as possible to those of application. We do not claim that the network we release is a definitive one, but it will necessarily evolve as new experimental results and kinetic/thermodynamic data become available. Detailed nitrogen chemistry, for instance, has been implemented in combustion networks only recently and will be subject to further evolution. Missing elements should also be added to the network, sulfur being the most obvious one. Since the scheme has not been optimized, adding new species and reactions to the network we release is possible. Moreover, although the range of P, T, and the elements considered in combustion model do fit well with the study of hot Jupiter atmospheres, the ratio between hydrogen and the other elements does not. For this reason, among others, it is important to avoid using optimized networks that would prevent modeling of such hydrogen-rich mixtures. Also, our current network, which cannot be used to study the abundance of species with more than two carbon atoms, is probably insufficient to study atmospheres with C/O ratios close to or above unity. For this reason we are currently working on an extended network that can model species up to six carbon atoms.

Hot Jupiter atmospheres represent an extreme case of planetary atmospheres in terms of both high temperatures and low metallicity. With the progress of observations, cooler and heavier atmospheres are or will be soon (with JWST, EChO, Finesse, E-ELT) accessible to characterization. Cooler atmospheres will depart more from equilibrium and will thus be more sensitive to the details of the kinetics. Molecules that remain minor constituents of hot Jupiter atmospheres will become more abundant in cooler atmospheres and have an increased influence on their spectral appearance and thermal structure, making the use of validated schemes even more relevant. More metallic atmospheres should be found as we explore the exoplanet realm towards smaller objects with higher core/envelope masses, and eventually terrestrial objects. While some uncertainties still exist when applying our network to hydrogen-rich atmospheres, atmospheres with a decreasing hydrogen-to-heavy elements ratio become closer to the conditions of validation (by their equivalence ratios, to use combustion terms). Even hot Jupiters can be significantly enriched (by factor of 10 or more) in heavy elements compared to their parent stars, which could, for instance, explain the high observed abundances of CO2 (Zahnle et al. 2009a).

5. Conclusion

We have constructed a chemical scheme to study the atmospheric composition of hot Jupiters. Compared to existing models we chose to use one that

  • is derived from mechanisms that are intensively used for industrial applications (in particular car engine simulations);

  • has been subjected to in-depth validation protocols in a broad range of temperatures, pressures and compositions;

  • is based on individual rate coefficients that have not been altered to optimize the agreement between the collective behavior of the network and experiments (contrary to most mechanisms in combustion). This allows users to apply the network slightly beyond its validation domain and to add species and reactions;

  • uses experimental measurements for some of the endothermic reactions when robust data are available but still reproduces thermodynamic equilibrium with excellent accuracy.

We developed a 1D photochemical model based on this kinetic scheme, which includes vertical transport (mixing and molecular diffusion) and photodissociations. We applied this model to the hot Jupiters HD 209458b and HD 189733b and compared our results with those of Moses et al. (2011). Qualitatively, we find similar conclusions: photodissociations do not have a significant impact on the atmospheric composition of HD 209458b, with the high temperatures we assume. It remains at the thermodynamic equilibrium for pressures higher than 1 bar. For lower pressures, vertical transport affects the abundances of HCN, NH3, CH4, and some of the minor associated species. For HD 189733b, we assume significantly lower temperatures and find the atmospheric composition to be more sensitive to photolyses and vertical transport, with all species affected, except the main reservoirs, H2, H2O, CO, and N2. Quantitatively, however, we find significant differences (up to several orders of magnitude in the case of HD 189733b) in the abundances that are likely to be due to the different chemical schemes used. These differences are smaller for HD 209548b because kinetics have less influence. The quenching of HCN and NH3, as well as CH4 to a less extent, is particularly affected, as well as most species sensitive to photochemistry in the upper atmosphere. Despite being large in terms of abundances, these differences do not produce strong effects on the spectra, with the exception of NH3 at 10.5 μm. Comparing different schemes with observations will thus have to await more accurate spectroscopic observations (JWST, E-ELT, EChO). Until them, experimental validation appears mandatory.

To illustrate the sensitivity to the kinetic scheme, we implemented different available nitrogen schemes that are either optimized (GRIMECH, GDFKin) or not validated (Dean). We studied the extent of the possible results, and found large differences whenever disequilibrium chemistry is at work. Changing the nitrogen scheme strongly affects the quenched species (HCN, NH3) and most species (including hydrocarbons) in the upper atmosphere of HD 189733b. For HD 209458b, deviations are again less noticeable since the atmosphere departs less from equilibrium. We therefore emphasize the need to use validated and nonoptimized chemical schemes. This is already true for hot Jupiters but is even more crucial in the case of cooler atmospheres (GJ1614b, GJ3470b, for instance), which depart more from thermodynamic equilibrium and are more sensitive to kinetics.

Our nominal scheme can be downloaded from the KIDA database7 (Wakelam et al. 2012). The scheme is designed to reproduce the kinetic evolution of species with fewer than two carbon atoms. To study atmospheres with C/O ratios higher than solar (close to or above 1), we are currently developing a C0–C6 scheme that will be able to describe the kinetics of species up to six carbon atoms. One of the next improvements to our model should be the addition of sulfur. Because the kinetics of nitrogen species is an active field of research, we expect regular updates of the network (which would be notified and available on KIDA).

Any conclusions from this study of the chemical composition of hot Jupiters, which derive from models using an average 1D vertical profile, will probably have to be revisited with the effects of atmospheric circulation.

Online material

Appendix A: Thermochemical data

Thermochemical properties, such as enthalpies of formation, entropies, and heat capacities are very important to ensure the consistency between the rate parameters of the forward and reverse elementary reactions. They are also useful for estimating the heat release rate. Thermochemical data for all molecules or radicals have been estimated and stored as 14 NASA polynomial coefficients, according to the McBride et al. (1993) formalism. The NASA polynomials take the following form: 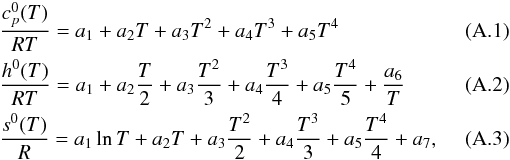where ai, i ∈  [1,7] , are the numerical NASA coefficients for the fourth-order polynomial. Each species is characterized by fourteen numbers. The first seven numbers are for the high-temperature range, generally from 1000 to 5000 K, and the following seven numbers are the coefficients for the low-temperature range, generally from 300 to 1000 K. When these parameters are not available in the literature (McBride et al. 1993) or in databases8, which is the most frequent case for species present in automotive fuels, they have to be estimated. In this case, these data were automatically calculated using the software THERGAS (Muller et al. 1995), which was developed in the LRGP laboratory and is based on the group and bond additivity methods proposed by Benson (1976) and updated based on the data of Domalski & Hearing (1996). The enthalpies of formation of alkyl radicals have been also updated according to the values of bond dissociation energies published by Tsang & Hampson (1986) and by Luo (2003) and following the recommendations of Benson & Cohen (1997).

An elementary reversible reaction i involving L chemical species can be represented in the general form 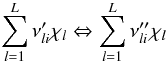(A.4)where 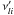are the forward stoichiometric coefficients, and 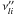are the reverse ones. χl is the chemical symbol of the lth species.

The kinetic data associated to each reaction are expressed with a modified Arrhenius law 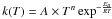where T is the temperature, Ea the activation energy of the reaction, A the pre-exponential factor, and n a coefficient that allows the temperature dependence of the pre-exponential factor. If the rate constant associated to the forward reaction is kfi(T), then the one associated to the reverse reaction is kri(T), verifying 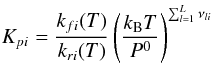(A.5)where Kpi is the equilibrium constant, when the activity of the reactants is expressed in pressure units (Benson 1976): 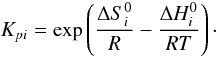(A.6)Here, 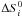and are the variation in entropy and enthalpy occurring when passing from reactants to products in the reaction i, P0 is the standard pressure (P0 = 1.01325 bar), kB is the Boltzmann’s constant, and νl are the stoichiometric coefficients of the L species involved in reaction i: 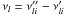. Combined with Eqs. (A.2) and (A.3), 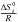and 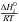can be calculated with the NASA coefficients: 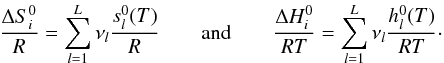(A.7)Finally, we can calculate the reverse reaction rate for the reaction i: 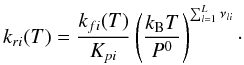(A.8)

Appendix B: Chemical equilibrium calculation

To compute the equilibrium abundance of the species in a definite system considered as an ideal gas, we have developed a thermodynamical equilibrium calculator TECA. TECA is software that allows equilibrium calculation for a complex mixture. More specifically, for a given initial state of an ideal-gas mixture, the chemical-equilibrium program is able to determine the gas composition at a defined temperature and pressure. This calculation is based on the principle of the minimization of Gibbs energy (e.g. Gibbs 1873; White et al. 1958; Eriksson & Rosen 1971; Smith & Missen 1982; Reynolds 1986): 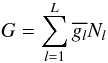(B.1)where L is the total number of species, the partial free energy of the species l, and Nl the number of moles of the species l.

The partial free energy of a compound l, behaving as an ideal gas, is given by (B.2)where gl(T,P) is the free energy of the species l at the temperature T and the pressure P of the system and R is the ideal gas constant.

For an ideal gas, gl(T,P) is given by 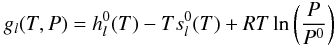(B.3)where 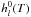and 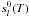are respectively, the standard-state enthalpy and entropy of the species l at the temperature T of the system.

The enthalpy and the entropy are expressed as NASA polynomials as described above.

Appendix C: Pressure-dependent reactions

Table C.1

Some examples of reactions with pressure-dependent rate constants present in the kinetic model.

Under some conditions, several reactions do not have the same rate constant depending on whether they occur under low or high pressure (respectively k0(T) and k∞(T)). In this case, between these two limits what is called a fall-off zone appears. This is typically the case in reactions requiring a collisional body to proceed, such as thermal dissociation or recombination (three-body) reactions. In the present kinetic model, we have different types of reactions with pressure-dependent rate constants (Table C.1). In some cases, some species act more efficiently as collisional bodies than do others. Then, when available from the literature, collisional efficiencies are used to specify the increased efficiency of the lth species in the ith reaction (see for example reaction (2) in Table C.1).

For the pressure-dependent reactions, the rate constant at any pressure is taken to be (C.1)where the reduced pressure Pr is given by (C.2)and  [M]  is the concentration of the mixture, weighted by the efficiency of each compound, αl, in the reaction studied: (C.3)where  [Xl]  is the concentration of the species k.

As shown in Table C.1, three methods of representation of the rate expression in the fall-off region are used (enhanced collisional body efficiencies of certain species are presented below the reaction):

In the Lindenman form, F is unity (F = 1).

In the Troe form F is given by (C.4)with and (C.5)the four parameters a, T***, T* and T** must be specified but it is often the case that the parameter T** is not used because of the lack of data.

The approach taken at the Stanford Research Institute (SRI) by Stewart et al. (1989) is in many ways similar to that taken by Troe, but the blending function F is approximated differently. Here, F is given by (C.6)where 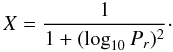(C.7)

Appendix D: Photodissociations

Table D.1

Photodissociations scheme used in the model.

2

In the field of combustion, a mechanism or reaction base is a network of reactions able to describe the kinetic evolution of a given pool of species. The mechanism includes the list of reactions and the associated rate coefficients, in a modified Arrhenius form, as well as the thermodynamic data for all the species involved in these reactions, which are required to calculate the equilibrium constants of the reactions and the rates of the reverse reactions.

9

M=CH4 has specific coefficients

Acknowledgments

We thank Ignasi Ribas for providing the UV flux of ϵ Eridani, proxy of HD 189733 and Anthony M. Dean for providing the list of rate coefficients from his book in an electronic form. F.S., O.V., E.H., and M.A. acknowledge support from the European Research Council (ERC Grant 209622: E3ARTHs).

References

  1. Agol, E., Cowan, N., Knutson, H., et al. 2010, ApJ, 721, 1861 [NASA ADS] [CrossRef] [Google Scholar]
  2. Agúndez, M., Venot, O., Iro, N., et al. 2012, A&A, submitted [Google Scholar]
  3. Akimoto, H., Obi, K., & Tanaka, I. 1965, J. Chem. Phys., 42, 3864 [NASA ADS] [CrossRef] [Google Scholar]
  4. Anderlohr, J., Bounaceur, R., Pires Da Cruz, A., & Battin-Leclerc, F. 2009, Combustion and Flame, 156, 505 [CrossRef] [Google Scholar]
  5. Anderlohr, J., Pires da Cruz, A., Bounaceur, R., & Battin-Leclerc, F. 2010, Combustion Sci. Techn., 182, 39 [CrossRef] [Google Scholar]
  6. Atakan, B., & Hartlieb, A. 2000, Appl. Phys. B: Lasers Opt., 71, 697 [NASA ADS] [CrossRef] [Google Scholar]
  7. Atkinson, R., Baulch, D., Cox, R., et al. 1997, J. Phys. Chem. Ref. Data, 26, 1329 [NASA ADS] [CrossRef] [Google Scholar]
  8. Atkinson, R., Baulch, D., Cox, R., et al. 2006, Atmos. Chem. Phys., 6, 3625 [Google Scholar]
  9. Au, J., Cooper, G., Burton, G., Olney, T., & Brion, C. 1993, Chem. Phys., 173, 209 [NASA ADS] [CrossRef] [Google Scholar]
  10. Balucani, N., Alagia, M., Cartechini, L., et al. 2000a, J. Am. Chem. Soc., 122, 4443 [CrossRef] [Google Scholar]
  11. Balucani, N., Cartechini, L., Alagia, M., Casavecchia, P., & Volpi, G. 2000b, J. Phys. Chem. A, 104, 5655 [CrossRef] [Google Scholar]
  12. Barbé, P., Battin-Leclerc, F., & Côme, G. 1995, J. Chim. Phys., 92, 1666 [Google Scholar]
  13. Barman, T. 2007, ApJ, 661, L191 [NASA ADS] [CrossRef] [Google Scholar]
  14. Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2012, ApJS, submitted [arXiv:1202.5852] [Google Scholar]
  15. Battin-Leclerc, F., Bounaceur, R., Belmekki, N., & Glaude, P. 2006, Int. J. Chem. Kin., 38, 284 [CrossRef] [Google Scholar]
  16. Battin-Leclerc, F., Blurock, E., Bounaceur, R., et al. 2011, Chem. Soc. Rev., 40, 4762 [CrossRef] [Google Scholar]
  17. Baulch, D., Cobos, C., Cox, R., et al. 1992, J. Phys. Chem. Ref. Data, 21, 411 [NASA ADS] [CrossRef] [Google Scholar]
  18. Baulch, D., Cobos, C., Cox, R., et al. 1994, J. Phys. Chem. Ref. Data, 23, 847 [NASA ADS] [CrossRef] [Google Scholar]
  19. Baulch, D., Bowman, C., Cobos, C., et al. 2005, J. Phys. Chem. Ref. Data, 34, 757 [NASA ADS] [CrossRef] [Google Scholar]
  20. Beaulieu, J., Carey, S., Ribas, I., & Tinetti, G. 2008, ApJ, 677, 1343 [NASA ADS] [CrossRef] [Google Scholar]
  21. Beaulieu, J., Kipping, D., Batista, V., et al. 2010, MNRAS, 409, 963 [NASA ADS] [CrossRef] [Google Scholar]
  22. Benson, S. W. 1976, Thermochemical Kinetics: methods for the estimation of thermochemical data and rate parameters, second edition (New York: John Wiley) [Google Scholar]
  23. Benson, S. W., & Cohen, N. 1997, In Peroxyl Radicals (New York: John Wiley) [Google Scholar]
  24. Bounaceur, R., Glaude, P., Fournet, R., et al. 2007, Int. J. Vehicle Design, 44, 124 [CrossRef] [Google Scholar]
  25. Bounaceur, R., Herbinet, O., Fournet, R., et al. 2010, SAE Tech. Paper, 01 [Google Scholar]
  26. Brown, M. J., & Smith, D. B. 1994, 25th Symposium (International) on Combustion, 25, 1011 [Google Scholar]
  27. Burrows, A., & Sharp, C. 1999, ApJ, 512, 843 [NASA ADS] [CrossRef] [Google Scholar]
  28. Burrows, A., Hubeny, I., Budaj, J., Knutson, H., & Charbonneau, D. 2007, ApJ, 668, L171 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  29. Burrows, A., Budaj, J., & Hubeny, I. 2008, ApJ, 678, 1436 [NASA ADS] [CrossRef] [Google Scholar]
  30. Burton, G., Chan, W., Cooper, G., & Brion, C. 1993, Chem. Phys., 177, 217 [NASA ADS] [CrossRef] [Google Scholar]
  31. Caridade, P., Rodrigues, S., Sousa, F., & Varandas, A. 2005, J. Phys. Chem. A, 109, 2356 [CrossRef] [Google Scholar]
  32. Cavalié, T., Billebaud, F., Biver, N., et al. 2008, Planet. Space Sci., 56, 1573 [NASA ADS] [CrossRef] [Google Scholar]
  33. Cavalié, T., Billebaud, F., Dobrijevic, M., et al. 2009, Icarus, 203, 531 [NASA ADS] [CrossRef] [Google Scholar]
  34. Chan, W., Cooper, G., & Brion, C. 1992, Chem. Phys., 168, 375 [NASA ADS] [CrossRef] [Google Scholar]
  35. Chan, W., Cooper, G., & Brion, C. 1993a, Chem. Phys., 170, 111 [NASA ADS] [CrossRef] [Google Scholar]
  36. Chan, W., Cooper, G., & Brion, C. 1993b, Chem. Phys., 178, 387 [NASA ADS] [CrossRef] [Google Scholar]
  37. Chan, W., Cooper, G., Sodhi, R., & Brion, C. 1993c, Chem. Phys, 170, 81 [Google Scholar]
  38. Chang, A. H. H., Mebel, A. M., Yang, X.-M., Lin, S. H., & Lee, Y. T. 1998, J. Chem. Phys., 109, 2748 [NASA ADS] [CrossRef] [Google Scholar]
  39. Charbonneau, D., Brown, T., Latham, D., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  40. Charbonneau, D., Brown, T., Noyes, R., & Gilliland, R. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
  41. Charbonneau, D., Knutson, H., Barman, T., et al. 2008, ApJ, 686, 1341 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  42. Chen, F., & Wu, C. 2004, J. Quant. Spectr. Rad. Trans., 85, 195 [Google Scholar]
  43. Chen, F., Judge, D., Wu, C., & Caldwell, J. 1999, Planet. Space Sci., 47, 261 [NASA ADS] [CrossRef] [Google Scholar]
  44. Cheng, B., Lu, H., Chen, H., et al. 2006, ApJ, 647, 1535 [NASA ADS] [CrossRef] [Google Scholar]
  45. Cody, R., Sabetydzvonik, M., & Jackson, W. 1977, J. Chem. Phys., 66, 2145 [NASA ADS] [CrossRef] [Google Scholar]
  46. Cooper, C., & Showman, A. 2006, ApJ, 649, 1048 [NASA ADS] [CrossRef] [Google Scholar]
  47. Cooper, G., Burton, G., & Brion, C. 1995a, J. Electron Spectros. Rel. Phen., 73, 139 [Google Scholar]
  48. Cooper, G., Olney, T., & Brion, C. 1995b, Chem. Phys., 194, 175 [NASA ADS] [CrossRef] [Google Scholar]
  49. Cooper, G., Anderson, J., & Brion, C. 1996, Chem. Phys., 209, 61 [NASA ADS] [CrossRef] [Google Scholar]
  50. Coppens, F., De Ruyck, J., & Konnov, A. 2007, Combustion and Flame, 149, 409 [CrossRef] [Google Scholar]
  51. Dagaut, P., Glarborg, P., & Alzueta, M. 2008, Progress in Energy and Combustion Science, 34, 1 [CrossRef] [Google Scholar]
  52. De Ferrieres, S., El Bakali, A., Lefort, B., Montero, M., & Pauwels, J. 2008, Combustion and Flame, 154, 601 [CrossRef] [Google Scholar]
  53. Dean, A., & Bozzelli, J. 2000, Springer-Verlag Inc, 125 [Google Scholar]
  54. Désert, J., Lecavelier des Etangs, A., Hébrard, G., et al. 2009, ApJ, 699, 478 [NASA ADS] [CrossRef] [Google Scholar]
  55. Dirrenberger, P., Le Gall, H., Bounaceur, R., et al. 2011, Energy & Fuels, 15, 3875 [Google Scholar]
  56. Dobrijevic, M., Ollivier, J., Billebaud, F., Brillet, J., & Parisot, J. 2003, A&A, 398, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Dobrijevic, M., Cavalié, T., Hébrard, E., et al. 2010a, Planet. Space Sci., 1555 [Google Scholar]
  58. Dobrijevic, M., Hébrard, E., Plessis, S., et al. 2010b, Adv. Space Res., 45, 77 [NASA ADS] [CrossRef] [Google Scholar]
  59. Domalski, E. S., & Hearing, E. D. 1996, J. Phys. Chem. Ref. Data, 25, 1 [NASA ADS] [CrossRef] [Google Scholar]
  60. El Bakali, A., Pillier, L., Desgroux, P., et al. 2006, Fuel, 85, 896 [CrossRef] [Google Scholar]
  61. Eng, R., Lambert, H., Fei, R., Carrington, T., & Filseth, S. 1996, Chem. Phys. Lett., 261, 651 [NASA ADS] [CrossRef] [Google Scholar]
  62. Eriksson, G., & Rosen, E. 1971, Acta Polytechnica Scandinavica – Chemical Including Metallurgy Series, 2 [Google Scholar]
  63. Fahr, A., Hassanzadeh, P., & Atkinson, D. 1998, Chem. Phys., 236, 43 [NASA ADS] [CrossRef] [Google Scholar]
  64. Fillion, J., Ruiz, J., Yang, X., et al. 2004, J. Chem. Phys., 120, 6531 [NASA ADS] [CrossRef] [Google Scholar]
  65. Fortney, J., Cooper, C., Showman, A., Marley, M., & Freedman, R. 2006, ApJ, 652, 746 [NASA ADS] [CrossRef] [Google Scholar]
  66. Fortney, J., Lodders, K., Marley, M., & Freedman, R. 2008a, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
  67. Fortney, J., Marley, M., Saumon, D., & Lodders, K. 2008b, ApJ, 683, 1104 [NASA ADS] [CrossRef] [Google Scholar]
  68. Fournet, R., Baugé, J., & Battin-Leclerc, F. 1999, Int. J. Chem. Kin., 31, 361 [Google Scholar]
  69. Gans, B., Boye-Peronne, S., Broquier, M., et al. 2011, Phys. Chem. Chem. Phys., 13, 8140 [CrossRef] [Google Scholar]
  70. Gardner, J. P., Mather, J. C., Clampin, M., et al. 2006, Space Sci. Rev., 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
  71. Gibbs, J. 1873, A method of geometrical representation of the thermodynamic properties of substances by means of surfaces (Connecticut Academy of Arts and Sciences) [Google Scholar]
  72. Gladstone, G., Allen, M., & Yung, Y. 1996, Icarus, 119, 1 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  73. Glaude, P., Marinov, N., Koshiishi, Y., Matsunaga, N., & Hori, M. 2005, Energy & Fuels, 19, 1839 [CrossRef] [Google Scholar]
  74. Golden, D. 2008, Int. J. Chem. Kin., 40, 310 [CrossRef] [Google Scholar]
  75. Grenfell, J., Lehmann, R., Mieth, P., Langematz, U., & Steil, B. 2006, J. Geophys. Res., 111, D17311 [NASA ADS] [CrossRef] [Google Scholar]
  76. Grillmair, C., Burrows, A., Charbonneau, D., et al. 2008, Nature, 456, 767 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  77. Hampson Jr, R., & McNesby, J. 1965, J. Chem. Phys., 42, 2200 [NASA ADS] [CrossRef] [Google Scholar]
  78. Hauschildt, P., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
  79. Hébrard, E., Dobrijevic, M., Bénilan, Y., & Raulin, F. 2006, J. Photochem. Photobiol. C: Photochem. Rev., 7, 211 [CrossRef] [Google Scholar]
  80. Hébrard, E., Dobrijevic, M., Bénilan, Y., & Raulin, F. 2007, Planet. Space Sci., 55, 1470 [NASA ADS] [CrossRef] [Google Scholar]
  81. Herron, J. 1999, J. Phys. Chem. Ref. Data, 28, 1453 [NASA ADS] [CrossRef] [Google Scholar]
  82. Hochanadel, C., Sworski, T., & Ogren, P. 1980, J. Phys. Chem., 84, 231 [CrossRef] [Google Scholar]
  83. Holland, D., Shaw, D., Hayes, M., et al. 1997, Chem. Phys., 219, 91 [NASA ADS] [CrossRef] [Google Scholar]
  84. Howard, A., Marcy, G., Johnson, J., et al. 2010, Science, 330, 653 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  85. Howard, A., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
  86. Huebner, W., Keady, J., & Lyon, S. 1992, Solar photo rates for planetary atmospheres and atmospheric pollutants (Kluwer Academic Pub) [Google Scholar]
  87. Huestis, D. L., & Berkowitz, J. 2010, Adv. Geosci., 25, 229 [Google Scholar]
  88. Huffman, R. 1969, Canadian J. Chem., 47, 1823 [CrossRef] [Google Scholar]
  89. Huitson, C. M., Sing, D. K., Vidal-Madjar, A., et al. 2012, MNRAS, 422, 2477 [NASA ADS] [CrossRef] [Google Scholar]
  90. Iida, Y., Carnovale, F., Daviel, S., & Brion, C. 1986, Chem. Phys., 105, 211 [NASA ADS] [CrossRef] [Google Scholar]
  91. Iro, N., & Deming, L. D. 2010, ApJ, 712, 218 [NASA ADS] [CrossRef] [Google Scholar]
  92. Iro, N., Bézard, B., & Guillot, T. 2005, A&A, 436, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Isaksen, I. S. A., Midtbo, K. H., Sunde, J., & Crutzen, P. J. 1977, Geophys. Norvegica, 31, 11 [Google Scholar]
  94. Ityakov, D., Linnartz, H., & Ubachs, W. 2008, Chem. Phys. Lett., 462, 31 [NASA ADS] [CrossRef] [Google Scholar]
  95. Jackson, W., & Halpern, J. 1979, J. Chem. Phys., 70, 2373 [NASA ADS] [CrossRef] [Google Scholar]
  96. Kameta, K., Machida, S., Kitajima, M., et al. 1996, J. Electron Spectroscopy and Related Phenomena, 79, 391, Proceedings of the 11th International Conference on Vacuum Ultraviolet Radiation Physics [Google Scholar]
  97. Kameta, K., Kouchi, N., Ukai, M., & Hatano, Y. 2002, J. Electr. Spectr. Rel. Phenom., 123, 225 [CrossRef] [Google Scholar]
  98. Khamaganov, V., Karunanandan, R., Rodriguez, A., & Crowley, J. 2007, Phys. Chem. Chem. Phys., 9, 4098 [CrossRef] [Google Scholar]
  99. Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  100. Knutson, H., Charbonneau, D., Cowan, N., et al. 2009, ApJ, 690, 822 [NASA ADS] [CrossRef] [Google Scholar]
  101. Ko, T., Marshall, P., & Fontijn, A. 1990, J. Phys. Chem., 94, 1401 [CrossRef] [Google Scholar]
  102. Konnov, A. A. 2000, in 28th Symposium (Int.) on Combustion. Abstr. Symp. Pap, 317 [Google Scholar]
  103. Konnov, A. A. 2009, Combustion and Flame, 156, 2093 [CrossRef] [Google Scholar]
  104. Konnov, A. A., & De Ruyck, J. 1999a, Combustion Sci. Techn., 149, 53 [CrossRef] [Google Scholar]
  105. Konnov, A. A., & De Ruyck, J. 1999b, in Mediterranean Combustion Symposium, 679 [Google Scholar]
  106. Konnov, A. A., & De Ruyck, J. 2000a, in 16th International Symposium on Gas Kinetics, Cambridge, Abstr. Symp. Pap. PC10 [Google Scholar]
  107. Konnov, A. A., & De Ruyck, J. 2000b, Combustion Sci. Techn., 152, 23 [CrossRef] [Google Scholar]
  108. Konnov, A. A., & De Ruyck, J. 2001a, Combustion and Flame, 125, 1249 [CrossRef] [Google Scholar]
  109. Konnov, A. A., & De Ruyck, J. 2001b, Combustion and Flame, 124, 106 [CrossRef] [Google Scholar]
  110. Lamoureux, N., Desgroux, P., El Bakali, A., & Pauwels, J. 2010, Combustion and Flame, 157, 1929 [Google Scholar]
  111. Langland-Shula, L., Vogt, S., Charbonneau, D., Butler, P., & Marcy, G. 2009, ApJ, 696, 1355 [NASA ADS] [CrossRef] [Google Scholar]
  112. Lee, L. 1980, J. Chem. Phys., 72, 6414 [NASA ADS] [CrossRef] [Google Scholar]
  113. Lee, A., Yung, Y., Cheng, B., et al. 2001, ApJ, 551, L93 [NASA ADS] [CrossRef] [Google Scholar]
  114. Lehmann, R. 2004, J. Atmos. Chem., 47, 45 [Google Scholar]
  115. Liang, M., Parkinson, C., Lee, A., Yung, Y., & Seager, S. 2003, ApJ, 596, L247 [NASA ADS] [CrossRef] [Google Scholar]
  116. Liang, M., Seager, S., Parkinson, C., Lee, A., & Yung, Y. 2004, ApJ, 605, L61 [NASA ADS] [CrossRef] [Google Scholar]
  117. Lias, S. G., Collin, G. J., Rebbert, R. E., & Ausloos, P. 1970, J. Chem. Phys., 52, 1841 [NASA ADS] [CrossRef] [Google Scholar]
  118. Lindemann, F., Arrhenius, S., Langmuir, I., et al. 1922, Tran. Faraday Soc., 17, 598 [CrossRef] [Google Scholar]
  119. Line, M., Liang, M., & Yung, Y. 2010, ApJ, 717, 496 [NASA ADS] [CrossRef] [Google Scholar]
  120. Line, M., Vasisht, G., Chen, P., Angerhausen, D., & Yung, Y. 2011, ApJ, 738, 32 [NASA ADS] [CrossRef] [Google Scholar]
  121. Lodders, K., & Fegley, B. 2002, Icarus, 155, 393 [NASA ADS] [CrossRef] [Google Scholar]
  122. Lodders, K., & Palme, H. 2009, Meteor. Planet. Sci. Suppl., 72, 5154 [Google Scholar]
  123. Loison, J.-C., Kable, S. H., Houston, P. L., & Burak, I. 1991, J. Chem. Phys., 94, 1796 [NASA ADS] [CrossRef] [Google Scholar]
  124. Luo, Y. 2003, Handbook of bond dissociation energies in organic compounds (CRC) [Google Scholar]
  125. Madhusudhan, N., & Seager, S. 2009, ApJ, 707, 24 [NASA ADS] [CrossRef] [Google Scholar]
  126. Madhusudhan, N., & Seager, S. 2010, ApJ, 725, 261 [NASA ADS] [CrossRef] [Google Scholar]
  127. Madhusudhan, N., Harrington, J., Stevenson, K., et al. 2011a, Nature, 469, 64 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  128. Madhusudhan, N., Mousis, O., Johnson, T., & Lunine, J. 2011b, ApJ, 743, 191 [NASA ADS] [CrossRef] [Google Scholar]
  129. Manion, J. A., Huie, R. E., Levin, R. D., et al. 2008, NIST Chemical Kinetics Database, NIST Standard Reference Database 17 [Google Scholar]
  130. McBride, B., Gordon, S., & Reno, M. 1993, NASA Technical Memorandum, 4513 [Google Scholar]
  131. McNesby, J., Tanaka, I., & Okabe, H. 1962, J. Chem. Phys., 36, 605 [NASA ADS] [CrossRef] [Google Scholar]
  132. Mebel, A. M., Lin, M. C., & Morokuma, K. 1998, Int. J. Chem. Kin., 30 [Google Scholar]
  133. Meller, R., & Moortgat, G. 2000, J. Geophys. Res., 105, 7089 [Google Scholar]
  134. Merienne, M., Jenouvrier, A., Coquart, B., & Lux, J. 1997, J. Atmos. Chem., 27, 219 [CrossRef] [Google Scholar]
  135. Michael, J., Sutherland, J., & Klemm, R. 1986, J. Phys. Chem., 90, 497 [CrossRef] [Google Scholar]
  136. Moses, J. I. 1996, in The Collision of Comet Shoemaker-Levy 9 and Jupiter, eds. H. A. Weaver, K. S. Noll, P. D. Feldman (Cambridge, UK: Cambridge Univ. Press) [Google Scholar]
  137. Moses, J., Allen, M., & Gladstone, G. 1995a, Geophys. Res. Lett., 22, 1601 [NASA ADS] [CrossRef] [Google Scholar]
  138. Moses, J., Allen, M., & Gladstone, G. 1995b, Geophys. Res. Lett., 22, 1597 [NASA ADS] [CrossRef] [Google Scholar]
  139. Moses, J., Bézard, B., Lellouch, E., et al. 2000a, Icarus, 143, 244 [NASA ADS] [CrossRef] [Google Scholar]
  140. Moses, J., Lellouch, E., Bézard, B., et al. 2000b, Icarus, 145, 166 [NASA ADS] [CrossRef] [Google Scholar]
  141. Moses, J., Visscher, C., Fortney, J., et al. 2011, ApJ, 737, 15 [NASA ADS] [CrossRef] [Google Scholar]
  142. Mota, R., Parafita, R., Giuliani, A., et al. 2005, Chem. Phys. Lett., 416, 152 [NASA ADS] [CrossRef] [Google Scholar]
  143. Mount, G., & Moos, H. 1978, ApJ, 224, L35 [NASA ADS] [CrossRef] [Google Scholar]
  144. Muller, C., Michel, V., Scacchi, G., & Côme, G. 1995, J. Chim. Phys., 92, 1154 [Google Scholar]
  145. Okabe, H. 1978, Photochemistry of small molecules (Wiley New York) [Google Scholar]
  146. Okabe, H. 1981, J. Chem. Phys., 75, 2772 [NASA ADS] [CrossRef] [Google Scholar]
  147. Okabe, H. 1983, J. Chem. Phys., 78, 1312 [NASA ADS] [CrossRef] [Google Scholar]
  148. Olney, T., Cann, N., Cooper, G., & Brion, C. 1997, Chem. Phys., 223, 59 [NASA ADS] [CrossRef] [Google Scholar]
  149. Orkin, V., Huie, R., & Kurylo, M. 1997, J. Phys. Chem. A, 101, 9118 [CrossRef] [Google Scholar]
  150. Parkes, D., Paul, D., Quinn, C., & Robson, R. 1973, Chem. Phys. Lett., 23, 425 [NASA ADS] [CrossRef] [Google Scholar]
  151. Reynolds, W. C. 1986, Technical Report (Stanford: Stanford University) [Google Scholar]
  152. Richardson, L., Deming, D., Horning, K., Seager, S., & Harrington, J. 2007, Nature, 445, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  153. Rothman, L. S., Gordon, I. E., Barbe, A., et al. 2009, J. Quant. Spectr. Rad. Trans., 110, 533 [Google Scholar]
  154. Rowe, J., Matthews, J., Seager, S., et al. 2008, ApJ, 689, 1345 [NASA ADS] [CrossRef] [Google Scholar]
  155. Samson, J., & Cairns, R. 1964, J. Geophys. Res., 69, 4583 [NASA ADS] [CrossRef] [Google Scholar]
  156. Samson, J., & Haddad, G. 1994, JOSA B, 11, 277 [Google Scholar]
  157. Sander, S. P., Friedl, R. R., Barker, J. R., et al. 2011, NASA/JPL Publication [Google Scholar]
  158. Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A&A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  159. Sato, K., Misawa, K., Kobayashi, Y., et al. 1999, J. Phys. Chem. A, 103, 8650 [CrossRef] [Google Scholar]
  160. Schultz, E., & Shepherd, J. 1999, California Institute of Technology, Graduate Aeronautical Laboratories, Technical Report FM99-5 [Google Scholar]
  161. Seager, S., & Sasselov, D. 2000, ApJ, 537, 916 [NASA ADS] [CrossRef] [Google Scholar]
  162. Selsis, F., Despois, D., & Parisot, J. 2002, A&A, 388, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  163. Sharp, C., & Burrows, A. 2007, ApJS, 168, 140 [NASA ADS] [CrossRef] [Google Scholar]
  164. Showman, A., Fortney, J., Lian, Y., et al. 2009, ApJ, 699, 564 [NASA ADS] [CrossRef] [Google Scholar]
  165. Sing, D., Vidal-Madjar, A., Désert, J., Etangs, A., & Ballester, G. 2008, ApJ, 686, 658 [NASA ADS] [CrossRef] [Google Scholar]
  166. Sing, D., Désert, J., des Etangs, A., et al. 2009, A&A, 505, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  167. Smith, G., Golden, D., Frenklach, M., et al. 1999, URL: http://www.me.berkeley.edu/gri_mech [Google Scholar]
  168. Smith, W., & Missen, R. 1982, Chemical reaction equilibrium analysis: theory and algorithms (New York: Wiley) [Google Scholar]
  169. Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
  170. Southworth, J. 2010, MNRAS, 408, 1689 [NASA ADS] [CrossRef] [Google Scholar]
  171. Stark, G., Smith, P. L., Huber, K. P., et al. 1992, J. Chem. Phys., 97, 4809 [NASA ADS] [CrossRef] [Google Scholar]
  172. Stark, G., Yoshino, K., Smith, P. L., & Ito, K. 2007, J. Quant. Spectros. Rad. Trans., 103, 67 [Google Scholar]
  173. Stewart, P., Larson, C., & Golden, D. 1989, Combustion and Flame, 75, 25 [CrossRef] [Google Scholar]
  174. Stock, J., Grenfell, J., Lehmann, R., Patzer, A., & Rauer, H. 2011, Planet. Space Sci., 68, 18 [NASA ADS] [CrossRef] [Google Scholar]
  175. Stock, J., Boxe, C., Lehmann, R., et al. 2012, Icarus, 219, 13 [NASA ADS] [CrossRef] [Google Scholar]
  176. Stockwell, W., & Calvert, J. 1978, J. Photochem., 8, 193 [CrossRef] [Google Scholar]
  177. Swain, M. R. 2010, in BAAS, 42, AAS/Division for Planetary Sciences Meeting Abstracts, 42, 1064 [Google Scholar]
  178. Swain, M., Bouwman, J., Akeson, R., Lawler, S., & Beichman, C. 2008a, ApJ, 674, 482 [NASA ADS] [CrossRef] [Google Scholar]
  179. Swain, M., Vasisht, G., & Tinetti, G. 2008b, Nature, 452, 329 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  180. Swain, M., Tinetti, G., Vasisht, G., et al. 2009a, ApJ, 704, 1616 [NASA ADS] [CrossRef] [Google Scholar]
  181. Swain, M., Vasisht, G., Tinetti, G., et al. 2009b, ApJ, 690, L114 [NASA ADS] [CrossRef] [Google Scholar]
  182. Thielen, K., & Roth, P. 1986, AIAA journal, 24, 1102 [NASA ADS] [CrossRef] [Google Scholar]
  183. Tinetti, G., Vidal-Madjar, A., Liang, M., et al. 2007, Nature, 448, 169 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  184. Tinetti, G., Beaulieu, J. P., Henning, T., et al. 2012, Exper. Astron., in press [arXiv:1112.2728] [Google Scholar]
  185. Troe, J. 1983, Berichte der Bunsengesellschaft Phys. Chem., 87, 161 [CrossRef] [Google Scholar]
  186. Troe, J. 2011, Combustion and Flame, 158, 594 [CrossRef] [Google Scholar]
  187. Tsang, W. 1987, J. Phys. Chem. Ref. Data, 16, 471 [NASA ADS] [CrossRef] [Google Scholar]
  188. Tsang, W. 1991, J. Phys. Chem. Ref. Data, 20, 221 [NASA ADS] [CrossRef] [Google Scholar]
  189. Tsang, W., & Hampson, R. 1986, J. Phys. Chem. Ref. Data, 15, 1087 [NASA ADS] [CrossRef] [Google Scholar]
  190. Tsang, W., & Herron, J. 1991, J. Phys. Chem. Ref. Data, 20, 609 [NASA ADS] [CrossRef] [Google Scholar]
  191. Turbiez, A., Pauwels, J., Desgroux, P., et al. 1998, in 27th Symposium (international) on Combustion [Google Scholar]
  192. Umemoto, H., Nakae, T., Hashimoto, H., & Kongo, K. 1998, J. Chem. Phys., 109, 5844 [NASA ADS] [CrossRef] [Google Scholar]
  193. Vaghjiani, G. L. 1993, J. Chem. Phys., 98, 2123 [NASA ADS] [CrossRef] [Google Scholar]
  194. Vaghjiani, G. 1995, Int. J. Chem. Kin., 27, 777 [CrossRef] [Google Scholar]
  195. Van Dishoeck, E., & Dalgarno, A. 1984, Icarus, 59, 305 [NASA ADS] [CrossRef] [Google Scholar]
  196. Vandaele, A., Hermans, C., Simon, P., et al. 1998, J. Quant. Spectros. Rad. Trans., 59, 171 [NASA ADS] [CrossRef] [Google Scholar]
  197. Visscher, C., Lodders, K., & Fegley, Jr., B. 2006, ApJ, 648, 1181 [NASA ADS] [CrossRef] [Google Scholar]
  198. Visscher, C., Lodders, K., & Fegley, Jr., B. 2010, ApJ, 716, 1060 [NASA ADS] [CrossRef] [Google Scholar]
  199. Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
  200. Wang, H., Warner, S., Oehlschlaeger, M., et al. 2010, Combustion and Flame, 157, 1976 [CrossRef] [Google Scholar]
  201. White, W., Johnson, S., & Dantzig, G. 1958, J. Chem. Phys., 28, 751 [NASA ADS] [CrossRef] [Google Scholar]
  202. Wu, C., Chen, F., & Judge, D. 2001, J. Geophys. Res., 106, 7629 [NASA ADS] [CrossRef] [Google Scholar]
  203. Wu, C., Chen, F., & Judge, D. 2004, J. Geophys. Res., 109, E07S15 [Google Scholar]
  204. Zahnle, K., Marley, M., Freedman, R., Lodders, K., & Fortney, J. 2009a, ApJ, 701, L20 [NASA ADS] [CrossRef] [Google Scholar]
  205. Zahnle, K., Marley, M. S., & Fortney, J. J. 2009b, ApJL, submitted [arXiv:0911.0728] [Google Scholar]

All Tables

Table 1

Properties of the systems HD 209458 and HD 189733.

In the text
Table C.1

Some examples of reactions with pressure-dependent rate constants present in the kinetic model.

In the text
Table D.1

Photodissociations scheme used in the model.

In the text

All Figures

thumbnail Fig. 1

Abundances of NH3 as a function of time computed with two kinetic schemes that are fully reversed according to equilibrium constants but that differs by their nitrogen chemistry (nominal and GRIMECH as defined in Sects. 2.1.2 and 3.3). While they both converge towards the equilibrium (dotted line), they exhibit very different evolution. Initial condition is a mixture of H2, CH4, O2, N2, and He with solar elemental abundances.
In the text
thumbnail Fig. 2

Comparison between the thermodynamic equilibrium (dotted line) and the evolution of some molecular abundances in the 0D model, with two different schemes: the thermochemically reversed model (solid line) and the nominal model (dashed line) as a function of integration time at different temperature-pressure points. Initial condition is a mixture of H2, CH4, O2, N2, and He with solar elemental abundances.
In the text
thumbnail Fig. 3

Penetration of UV flux in the atmosphere of HD 209458b and HD 189733b at the steady state in function of wavelength. Plots represent the level where the optical depth τ = 1. The name of the compounds responsible for the main absorption at different wavelengths is indicated.
In the text
thumbnail Fig. 4

Pressure-temperature profiles (left) and eddy diffusion profiles (right) of HD 189733b and HD 209458b (from Moses et al. 2011).
In the text
thumbnail Fig. 5

Steady-state composition of HD 209458b (left) and HD 189733b (right) calculated with our nominal model (color lines), compared to the thermodynamic equilibrium (thin black lines).
In the text
thumbnail Fig. 6

Steady-state composition of HD 209458b (left) and HD 189733b (right) calculated with our nominal model without photodissociation (color lines), compared to the thermodynamic equilibrium (thin black lines).
In the text
thumbnail Fig. 7

Comparison between the abundance profiles found by our nominal model (color lines) and by Moses et al. (2011) (thin black lines), for the two planets (HD 209458b (left) and HD 189733b (right)).
In the text
thumbnail Fig. 8

Abundances of CH4, HCN, NH3, and CH3 in HD 209458b (left) and HD 189733b (right) with the four different models, compared to the results of Moses et al. (2011).
In the text
thumbnail Fig. 9

Abundances of C2H2, H, OH, and H2O in HD 209458b (left) and HD 189733b (right) with the four different models, compared to the results of Moses et al. (2011).
In the text
thumbnail Fig. 10

Synthetic day-side (left) and transmission (right) spectra of HD 189733b with the nominal mechanism (green curve) compared to the one corresponding to the GRIMECH mechanism (red curve) and to the thermochemical equilibrium (blue curve). The dark curve is obtained when NH3 is removed from the model. The day-side fluxes are given as brightness temperatures (Tb). Because of the reflection component, note that the link between Tb and the atmospheric thermal profile is altered below 2 μm. The transmission spectrum is given as the apparent planetary radius. The data points obtained from various observations are also shown.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.