| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202142816 | |
| Published online | 10 August 2022 | |
A mini-chemical scheme with net reactions for 3D general circulation models
I. Thermochemical kinetics★
1
Atmospheric, Ocean, and Planetary Physics, Department of Physics, University of Oxford,
UK
e-mail: shang-min.tsai@physics.ox.ac.uk
2
Center for Space and Habitability, University of Bern,
Gesellschaftsstrasse 6,
3012
Bern, Switzerland
Received:
2
December
2021
Accepted:
7
April
2022
Context. Growing evidence has indicated that the global composition distribution plays an indisputable role in interpreting observational data. Three-dimensional general circulation models (GCMs) with a reliable treatment of chemistry and clouds are particularly crucial in preparing for upcoming observations. In attempts to achieve 3D chemistry-climate modeling, the challenge mainly lies in the expensive computing power required for treating a large number of chemical species and reactions.
Aims. Motivated by the need for a robust and computationally efficient chemical scheme, we devise a mini-chemical network with a minimal number of species and reactions for H2-dominated atmospheres.
Methods. We apply a novel technique to simplify the chemical network from a full kinetics model, VULCAN, by replacing a large number of intermediate reactions with net reactions. The number of chemical species is cut down from 67 to 12, with the major species of thermal and observational importance retained, including H2O, CH4, CO, CO2, C2H2, NH3, and HCN. The size of the total reactions is also greatly reduced, from ~800 to 20. We validated the mini-chemical scheme by verifying the temporal evolution and benchmarking the predicted compositions in four exoplanet atmospheres (GJ 1214b, GJ 436b, HD 189733b, and HD 209458b) against the full kinetics of VULCAN.
Results. The mini-network reproduces the chemical timescales and composition distributions of the full kinetics well within an order of magnitude for the major species in the pressure range of 1 bar–0.1 mbar across various metallicities and carbon-to-oxygen (C/O) ratios.
Conclusions. We have developed and validated a mini-chemical scheme using net reactions to significantly simplify a large chemical network. The small scale of the mini-chemical scheme permits simple use and fast computation, which is optimal for implementation in a 3D GCM or a retrieval framework. We focus on the thermochemical kinetics of net reactions in this paper and address photochemistry in a follow-up paper.
Key words: planets and satellites: atmospheres / planets and satellites: composition / methods: numerical
Table of the reaction rates is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/664/A82
© S.-M. Tsai et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The field of exoplanet research is now entering the stage of probing the spatial distribution of atmospheric composition (Venot et al. 2018; Ehrenreich et al. 2020). Upcoming observatories, such as the James Webb Space Telescope (Venot et al. 2020a; Drummond et al. 2020) and the Atmospheric Remote-sensing Infrared Exoplanet Large-survey (Moses et al. 2022; Tinetti et al. 2021), will have the ability to provide accurate spectral data and map out the compositional variation across the globe of the planet. Chemical kinetics models (e.g., Kasting et al. 1979; Yung et al. 1984; Moses et al. 2011; Venot et al. 2012; Hu et al. 2012; Miguel & Kaltenegger 2014; Molaverdikhani et al. 2019; Hobbs et al. 2019; Tsai et al. 2021a) have played an instrumental role in understanding the fundamental processes that shape the atmospheric compositions. However, these models are commonly limited to a 1D column approach. Studies using 3D models, such as Drummond et al. (2018), Mendonça et al. (2018), and Drummond et al. (2020), have demonstrated the importance of horizontal transport on tidally locked exoplanets. Considering the effects of global circulation is critical to understanding the chemical and thermal feedbacks and interpreting phase-resolved observational data. In addition, retrieval works (Taylor et al. 2020; Feng et al. 2020; Irwin et al. 2020; Pluriel et al. 2020, 2022) have shown that atmospheric retrievals can suffer biases when neglecting the 3D nature of the planets. Pseudo-2D models that employ a rotating 1D column have started to emerge (Agúndez et al. 2014; Venot et al. 2020b; Baeyens et al. 2021; Moses et al. 2022; Roth et al. 2021) and have significantly improved 1D models by including horizontal interconnection; however, the circulation is considerably simplified, with a globally uniform jet and the chemical-radiative feedback excluded. In order to study their interactions in depth and to be in position for the prospective observations, a self-consistent 3D general circulation model (GCM) that couples chemistry, radiation, and circulation is desired.
The endeavor of coupling the gaseous chemistry to a 3D GCM began with the chemical relaxation method (Cooper & Showman 2006) and was later followed by Drummond et al. (2018) and Mendonça et al. (2018). The relaxation method (Cooper & Showman 2006; Tsai et al. 2018) is analogous to Newtonian cooling as the radiative heating in idealized GCMs, which is the simplest and the least computationally demanding to implement in a 3D model. However, it is challenging to generalize the relaxation method to incorporate photochemistry since a predetermined photochemical equilibrium state is required in principle. Motivated by the need for a more efficient scheme, Venot et al. (2019) developed a reduced chemical scheme, cutting back from 105 species and about 2000 reactions in the original network (Venot et al. 2012) to 30 species and 362 reactions. The size of the scheme from Venot et al. (2019) is close to that in Tsai et al. (2017), which is probably the lower size limit needed to maintain accuracy for conventional kinetics. Venot et al. (2020a) further updated the methanol (CH3OH) chemistry and added acetylene (C2H2) to extend the valid domain for warm carbon-rich atmospheres. However, the C-H-O network in Tsai et al. (2017) does not include nitrogen chemistry, whereas the new reduced scheme in Venot et al. (2020a) now involves 44 species and 582 reactions, and photochemistry is not considered in any of the above schemes. Chen et al. (2019, 2021) have recently applied an Earth-based chemistry-climate model (Marsh et al. 2013) that employs the MOZART chemical module (Kinnison et al. 2007) to explore the chemistry-climate interaction and the impact of stellar flares on exoplanets around M stars. The setup provides insights into potential Earth twins but is restricted to atmospheres with Earthlike compositions. Compared to the development of atmospheric chemistry modules for Earth-climate models (e.g., Kinnison et al. 2007; Derwent et al. 2021) and the progress of simulating aerosols (Lee et al. 2016; Lines et al. 2018; Steinrueck et al. 2021), a robust chemical scheme with photochemistry capacity is still lacking and urgently needed in exoplanet science.
In this work we present a novel design of the chemical scheme, aiming to tackle the aforementioned problems. The chemical network is composed of a few elementary reactions that treat radical species and a handful of net reactions that greatly reduce the kinetics mechanisms. Our C-H-N-O thermochemical network without photochemistry consists of only 12 species and 10 forward reactions. The scheme is validated for a wide range of temperatures, pressures, and elemental abundances and has the capacity to include photochemistry. The scheme is suitable for applications that require minimal computing time, such as 3D GCMs and atmospheric retrievals. We focus on the method and validation of the net-reaction mechanisms in this paper and will address photochemistry in a follow-up paper.
2 Method
2.1 Making use of Net Reactions
The principal mechanisms governing chemical species are often understood by the associated cycles (also referred to as schemes, e.g., Moses et al. 2011, and pathways, e.g., Venot et al. 2020a; Tsai et al. 2021a). The chemical conversions generally consist of more than one intermediate reaction step, for example, the ozone cycle on Earth (e.g., Jacob 2011) and the CH4–CO interconversion on Jupiter (Prinn & Barshay 1977; Visscher et al. 2010) and brown dwarfs (Zahnle & Marley 2014). It is essential in kinetics simulations to include all reactions relevant to the application, supplied with correct rate coefficients. The chemical cycles naturally emerge as an outcome of this bottom-up approach. In this work, we followed Tsai et al. (2018) and applied Dijkstra’s algorithm (Dijkstra 1959) to identify the fastest conversion pathways for different atmospheric conditions systematically. Taking one of the CH4–CO conversion pathways in a warm H2 atmosphere as an example,
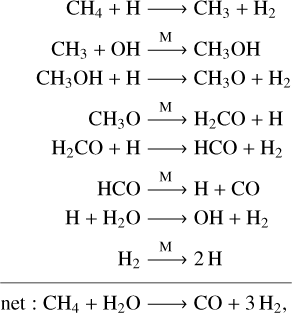 (1)
(1)
where CH4 + H2O → CO + 3 H2 with an unspecified rate coefficient is simply a mathematical “summary” of the above eight reactions that compose the pathway sequence. An attractive property of the pathway is that the overall timescale of the conversion is controlled by the slowest reaction, the rate-limiting step (Moses et al. 2011; Tsai et al. 2018), which is readily determined once the pathway is identified. The rate-limiting step per se contains sufficient information for computing the rate of change without getting into the details of each elementary reaction. We constructed the network with a top-down design, as opposed to the bottom-up structure used in conventional kinetics. The crux of the mini-network is to replace hundreds of elementary reactions in a full network with just a few net reactions. The effective rates of these net reactions are subsequently determined by the corresponding rate-limiting steps.
We emphasize that the pathways and their rate-limiting steps depend strongly on the atmospheric temperature, pressure, and elemental abundances. As a result, the rate coefficient of these net reactions can no longer be expressed by the modified Arrhenius equation, which is generally a function that depends solely on temperature1 (i.e., k = ATb exp 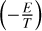 ). Instead, the effective rate coefficients of a schematic net reaction A + B → C + D dictated by the rate-limiting step is expressed as
). Instead, the effective rate coefficients of a schematic net reaction A + B → C + D dictated by the rate-limiting step is expressed as
![$ k = {{{\rm{rat}}{{\rm{e}}_{{\rm{RLS}}}}} \over {\left[ {\rm{A}} \right]\left[ {\rm{B}} \right]}}, $](/articles/aa/full_html/2022/08/aa42816-21/aa42816-21-eq3.png) (2)
(2)
where rateRLS is the reaction rate (molecules cm−3 s−1) of the rate-limited step in the entailed pathway, and [A], [B] is the mole fraction of the reactants A, B. All quantities in Eq. (2) are evaluated in chemical equilibrium for the given temperature, pressure, and elemental abundances (see the discussion regarding adopting equilibrium abundances in Tsai et al. 2018). Hence, the rate coefficient (Eq. (2)) is now a function of temperature, pressure, and elemental abundances. We then derived the rate coefficients of the backward net reactions by reversing those of the forward reactions to ensure thermochemical equilibrium can be consistently achieved (Tsai et al. 2017), the same way as with elementary reactions.
Following the same example, Pathway (1) presents the pathway of CH4–C0 conversion at T = 1000 K and P =1 bar, where CH3 + OH → [M]CH3OH is the rate-liming step. At the same pressure but with the temperature increased to 1500 K, the pathway switches to
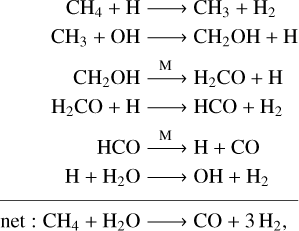 (3)
(3)
where CH3 + OH → CH2OH + H is now the rate-liming step. Accordingly, the rate coefficient of the net reaction CH4 + H2O → CO + 3H2 at T = 1000 K and P = 1 bar is
![$ k = {{{k_1}\left[ {{\rm{C}}{{\rm{H}}_3}} \right]\left[ {{\rm{OH}}} \right]{\rm{M}}} \over {\left[ {{\rm{C}}{{\rm{H}}_4}} \right]\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}, $](/articles/aa/full_html/2022/08/aa42816-21/aa42816-21-eq5.png) (4)
(4)
while that at T = 1500 K and P = 1 bar is
![$ k = {{{k_2}\left[ {{\rm{C}}{{\rm{H}}_3}} \right]\left[ {{\rm{OH}}} \right]} \over {\left[ {{\rm{C}}{{\rm{H}}_4}} \right]\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}, $](/articles/aa/full_html/2022/08/aa42816-21/aa42816-21-eq6.png) (5)
(5)
where k1 and k2 are the rate coefficients of 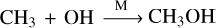 and CH3 + OH → CH2OH + H, respectively.
and CH3 + OH → CH2OH + H, respectively.
Based on the major pathways of the key molecules (Moses et al. 2011; Tsai et al. 2018, 2021b; Venot et al. 2020a), we employed six essential net reactions to govern the main species in the C-H-N-O thermochemical kinetics. Firstly, CH4 + H2O → CO + 3H2 and 2 NH3 → N2 + 3H2 describe the CH4–CO and NH3–N2 interconversions, respectively. The 2CH4 → C2H2 + 3 H2 reaction is identified as the main channel for C2H2 production at low temperature and high pressure and CO + CH4 → C2H2 + H2 + O at high temperature and low pressure, where CO is the main carbon-bearing molecule. Similarly, CH4 + NH3 → HCN + 3 H2 and CO + NH3 → HCN + H2O are employed for HCN production at low temperature and high pressure and at high temperature and low pressure, respectively. Additionally, four elementary reactions involve fast-reacting radicals: OH, H, and O are included to complete the mini-network. Specifically, OH + H2 → H2O + H is a key reaction for the formation of water in a hydrogen-rich environment (e.g., Liang et al. 2003; Tsai et al. 2021b), and OH + CO → H + CO2 is responsible for the interconversion between CO and CO2 (e.g., Yung & DeMore 1999; Gao et al. 2015). The above two reactions are necessary for correctly computing H2O and CO2. Lastly, O + H2 → OH + H contributes to tracking atomic O and 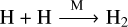 to hydrogen dissociation and recombination, which are included to be in position for the implementation with photochemistry.
to hydrogen dissociation and recombination, which are included to be in position for the implementation with photochemistry.
All the elementary and net reactions employed in our mininetwork are listed in Table 1 and encompass 12 species: H, H2, OH, H2O, CO, CO2, O, CH4, C2H2, NH3, N2, and HCN. The topology of the mini-network and the full network that the mini-network is condensed from is illustrated in Fig. 1, where the degree means the number of reaction connections to other species and the eigenvector centrality measures the influence of the species by taking both quantity (number of reaction links) and quality (rates of reactions and connections to reactive species) into account. In the mini-network, H lost its high centrality in the full network since most of the elementary reactions involving H are now concealed in the net reactions. Similarly, the fast cycles between CH3 and CH4 and those between NH3 and NH2 are implicitly packed in the net reactions. Our mini-network keeps most of the major species with the highest centrality in the full kinetics; CH3 and NH2 are excluded for the sake of simplicity, and N2 is included as a major nitrogen-bearing molecule.
The numerical rate coefficients of the net reactions as a function of temperature and pressure for given elemental abundances can be generated using the full chemical scheme in advance and thus do not add extra computational cost when applying the mini-scheme. Figure 2 illustrates the wide range of rate coefficients of the net reactions CH4 + H2O → CO + 3 H2 across temperatures and pressures for solar metallicity. We tabulated the rate coefficients for temperatures and pressures in the range 300–3000 K and 103–10−6 bar for a grid of metallicities (0.1× solar, solar, 10× solar, 100× solar, and 500× solar) and carbon-to-oxygen ratios (C/O = 0.25, solar, C/O = 1, C/O = 2). The numerical tables of net reactions in the mini-chemical scheme are available in the supplementary files, and a part of the table for CH4 + H2O → CO + 3 H2 is shown in Table 2 for demonstration. The application should be restricted to the tested range of elemental ratios, and since the conversion pathways that control the effective rate coefficients of the net reaction can be sensitive to the atmospheric condition, these rate coefficients should ideally be made from the first principle for a specific elemental abundance ratio2. We end this section by noting that although the same pathway analysis in Tsai et al. (2018) is applied, the crucial difference is that the chemical sources and sinks are approximated by a linear expansion in the chemical relaxation method in Tsai et al. (2018), whereas exactly the same format of rate equations that allows nonlinear dynamics as the standard kinetics is utilized in this work.
Elementary and net reactions included in the C-H-N-O chemical kinetics.
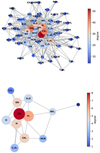 |
Fig. 1 Visualization of the full chemical network from VULCAN (top) and the mini-network (bottom). Each species is represented by a node, with the color varying with the degree and the size varying with centrality. The shorter length of the edges (lines) indicates faster rates between two species (not to linear scale). The graphs are for Τ = 1000 Κ, Ρ = 1 bar, and chemical equilibrium composition. |
 |
Fig. 2 Effective rate constants (cm3 molecules−1 s−1) for the net reaction CH4 + H20 → CO + 3 H2. |
2.2 Validation Setup
2.2.1 0D Evolution in Time
We set up a 0D kinetics model to compare the temporal evolution computed by the mini-network and that from the full C-H-N-O kinetics of VULCAN (Tsai et al. 2021a)3. The 0D model is initialized with prescribed gas mixtures at a fixed temperature and pressure, which evolve with time toward thermochemical equilibrium, analogous to the experimental setup of a cell for monitoring the evolution of the gas mixture (Peng et al. 2014; Fleury et al. 2019). The initial gas mixtures are H2, He, CH4, H2O, and NH3, partitioned by solar elemental abundances, except that CH4 and NH3 are replaced by CO and N2, respectively, in the CH4- and NH3-dominated regime (low temperatures and high pressures) to clearly show the changes in time. The C-, Ο-, and N-bearing molecules are scaled accordingly when the metallicity varies, and we keep oxygen fixed when changing the C/O ratio.
2.2.2 1 D Vertical Profiles
Since the observable abundances in planetary atmospheres are usually governed by the transport-induced quenching process (e.g., Baxter et al. 2021; Kawashima et al. 2021), determining the quench levels (Visscher & Moses 2011; Moses 2014; Tsai et al. 2017) is the key aspect in ID chemical kinetics modeling. To verify that our mini-chemical scheme can correctly reproduce the quenching behavior predicted in 1D models, we adopted the pressure–temperature (P–T) profiles of the planets GJ 1214b, GJ 436b, HD 189733b, and HD 209458b as inputs to validate the mini-network. These chosen atmospheres have equilibrium temperatures from about 500 to 1700 K, representative of the vertical-mixing-dominated regime. We computed the radiative-convective equilibrium temperature profiles of GJ 1214b and GJ 436b using the radiative-transfer model HELIOS (Malik et al. 2019), while those of HD 189733b and HD 209458b are taken from Moses et al. (2011). The inverted temperature profile of HD 209458b is adopted for validating the scheme with a thermal inversion and for comparison with previous works (Tsai et al. 2017; Venot et al. 2019), but we note that emission observations show no evidence of a thermal inversion of HD 209458b (e.g., Diamond-Lowe et al. 2014; Schwarz et al. 2015; Line et al. 2016). All the P–T profiles are shown in Fig. 3. We varied the uniform eddy diffusion coefficients (Kzz) from 105 to 1011 cm2 s−1, evenly spaced on a log 10 scale, to explore diverse quench levels for each planet.
3 Results
3.1 0D Validation: The Same Chemical Timescales Produced Even with Different Paths
Figure 4 compares the temporal evolution of the major species computed by the mini-networks and full chemical kinetics (VULCAN). In most cases, the mini-network manifests the same temporal path as the full kinetics. At high temperatures and low pressures (T ≳ 1500 Κ and Ρ ≲ 1 mbar), the evolution from the mini-network can start to take somewhat different paths (e.g., CH4 and NH3 in the upper-right panel of Fig. 4). This is likely due to more participation of small molecules and atoms in this regime, such as C and CN, that are not included in the mini-network. Despite different paths, these species still achieve the equilibrium state around the same time as those in the full kinetics. Defining the timescale as the time it takes for the composition to approach the equilibrium value within 0.1%, we evaluated the relative errors (|tnet–tfull|/tfull × 100%) of the chemical timescales for the main species (H2O, CH4, CO, CO2, NH3, HCN, and N2) in solar metallicity. We find a maximum relative error of 135% and a mean relative error of 43% in the most relevant range of 1000 K≤T≤ 2500 Κ and 10−4 bar ≤ Ρ ≤ 1000 bar. The 0D tests show that the mini-network scheme can successfully reproduce the chemical timescale from the full kinetics.
Selected portion of the table of the rate constants for the net reaction CH4 + H2O → CO + 3 H2.
 |
Fig. 3 Adopted pressure-temperature profiles of GJ 1214b, GJ 436b, HD 189733b, and HD 209458b, for validating the mini-chemical scheme. |
3.2 1D validation: Reproducing Correct Quench Levels
The vertical distributions of the main compositions computed by the two chemical networks of each planet with different vertical mixing for solar metallicity are summarized in Fig. 5. Among the explored eddy diffusion coefficients from 105 to 1011 cm2 s−1 we present the resulting profiles that are sensitive to the change for clarity. Specifically, Kzz = 105, 107, 109, 1011 (cm2 s−1) are shown for GJ 1214b, Kzz=106, 107, 108, 109 (cm2 s−1) for GJ 436b, Kzz = 105, 107, 109, 1011 (cm2 s−1) for HD 189733b, and Kzz= 107, 109, 1010, 1011 (cm2 s−1) for HD 209458b. First of all, transport-induced quenching is correctly reproduced by the mini-network, that is, the quench levels of CO on the cooler planets GJ 1214b and GJ 436b and those of CH4 on the hotter planets HD 189733b and HD 209458b agree well between two networks. For species that react fast with the major species, such as C2H2 and HCN, the noncon-stant mixing ratio profiles, as they follow their parent molecules before they themselves are quenched at lower pressure (e.g., Moses et al. 2011; Tsai et al. 2017), are also well captured by the mini-network.
Of all the species in the mini-network, C2H2 appears to have the largest deviation, up to about a factor of three on GJ 1214b, which can be attributed to the combination of its low abundance and the simplification of hydrocarbon kinetics. The mini-network is able to correctly reproduce the vertical quenching of the main species and notably the abundance profiles, with the second equilibrium region present in the upper atmosphere due to thermal inversion on HD 209458b. The maximum errors4 of the main species with mixing ratios not lower than 10−20 in the region of observational interest (1 bar–0.1 mbar) computed by the mini-chemical scheme for the whole range of eddy diffusion coefficients are listed in Table 3. Errors greater than 100% all occur with volume mixing ratios smaller than 10−10. We find the discrepancies for the main species abundances between the mini-network and the full kinetics to always be less than an order of magnitude and rarely exceeding a factor of two, consistent with the 0D validation in Sect. 3.1.
A self-contained way to evaluate the errors with respect to the presumed uncertainty factors in the reaction rates of the full kinetics is to perform an uncertainty propagation analysis (Dobrijevic et al. 2010; Wakelam et al. 2010). Venot et al. (2019) determined a tighter constraint of 10% for their GJ 436b model using the Monte Carlo uncertainty propagation (Hébrard et al. 2015), with the uncertainty factor derived from the combustion study. However, in practice, it is not uncommon to have models with different sets of kinetics data that differ by an order of magnitude (Moses 2014; Tsai et al. 2021a) when the overall aspects of uncertainties are taken into account. Therefore, at least before the kinetics discrepancies are fully resolved, we consider an order of magnitude of error to be acceptable for exoplanet application.
 |
Fig. 4 Time evolution of the main species in the 0D model computed with the full C-H-N-O kinetics (solid) and the mini-network (dashed) for solar metallicity with various temperatures and pressures. Open circles plotted at the end of each run indicate the thermochemical equilibrium abundances. |
Maximum errors in percent of the compositions in the pressure range of 1 bar – 0.1 mbar computed by the mini-network for solar elemental abundances, with the largest errors among the four planets shown in bold.
3.3 Varying Metallicity and C/O Ratio
While the rate coefficients of net reactions depend on the elemental abundances, the approach is general in principle. The same procedure may be applied to construct a mini-network with relevant elementary and net reactions for arbitrary elemental composition. Here, we vary the metallicity and C/O to test the validity of our mini-network designed for H2-dominated composition. First, Fig. A.1 illustrates how the rate coefficients of CH4 + H2O → CO+3 H2 and 2 NH3 → N2 + 3 H2 vary with metallicity and C/O ratio. The rate coefficients of CH4 → CO and NH3 → N2 generally increase with metallicity, while no consistent trends are found for the C/O ratio. Next, Figs. A.2–A.5 showcase the same 0D and 1D validation with 500 times solar metallicity and solar composition but with C/O = 2. The maximum errors are also listed in Tables A.1 and A.2. We find the scheme to be less accurate with higher metallicity when the atmosphere becomes less H2-dominated. Therefore, we restricted the valid range of our mini-network to not exceed 500 times solar metallicity. Of all the explored cases, C2H2 remains associated with the largest error, and less abundant species tend to have larger errors too. For instance, CH4 and NH3 produce bigger errors in hotter planets, HD 189733b and HD 209458b, whereas C2H2 is more accurate in warm conditions, where it is favored. Compared to the updated reduced chemical scheme in Venot et al. (2020a, which has a new CH3OH mechanism and includes C2H2), the mini-network achieves comparable accuracy (≲10%) for GJ 436b with a solar metallicity, except for C2H2. The same trend of increased errors with higher metallicity is also found in the reduced chemical scheme of Venot et al. (2020a). For the hot Jupiters HD 189733b and HD 209458b, the mini-network produces more significant errors in C2H2, while the reduced network in Venot et al. (2020a) appears to produce larger errors in NH3. Overall, the agreement between our mini-chemical scheme and the full kinetics remains well under an order of magnitude, similar to the accuracy of the reduced scheme (with 44 species and 582 reactions) from Venot et al. (2020a).
4 Conclusions
We have devised a novel chemical scheme that utilizes net reactions to significantly reduce the size of a chemical network. We have validated the new scheme across a wide range of temperatures and pressures by comparing the chemical timescales from the mini-network and the full kinetics model VULCAN (Tsai et al. 2017, 2021a). The mini-network scheme is able to reproduce the quenching behavior of major species well under an order of magnitude in the benchmark exoplanet atmospheres (GJ 1214b, GJ 436b, HD 189733b, and HD 209458b). The tabulated rates of the net reactions from 300 Κ ≤ Τ ≤ 3000 Κ and 10−6 bar ≤ Ρ ≤ 103 bar for the valid ranges of metallic-ities (0.1–500 times solar) and C/O (0.25–2 times solar) are available in the supplementary files. The presented scheme is robust yet simple to adopt and fast to run. The mini-network takes about 1.5 × 10−3 s to integrate an atmospheric cell for one time step (tested on a 2015 laptop with 2.2 GHz Intel Core i7 using SciPy linear algebra routines). For comparison, its computational time is about 25 times faster than the original C-H-N-O network in Tsai et al. (2021b) and about 10 times faster than a network with a size similar to that of Venot et al. (2019)5. We hope that it will encourage the field of research to incorporate a more realistic chemical mechanism in 3D models and retrieval frameworks.
We reiterate that, unlike the relaxation method (Cooper & Showman 2006; Drummond et al. 2018; Tsai et al. 2018), the mini-chemical network keeps the same form of rate equations as the standard kinetics. In addition to the major molecules of observational interest or radiative importance, key radical species are also included. This allows us to extend the scheme to incorporate photochemistry, where radical species are produced by photodissociation. We will present the detailed treatment of photochemistry in a follow-up paper.
 |
Fig. 5 Vertical composition distributions computed by the mini-chemical scheme (dashed) compared with those computed by the full chemical kinetics VULCAN (solid) for the four planets with temperature profiles in Fig. 3. The dark to light colors represent increasing vertical mixing (see the text for the specific values of Kzz used). |
Acknowledgements
S.-M.T. thanks F. Selsis for the project collaboration that sparks the mini-network conception and T. Fisher for comments on the graph analysis. S.-M.T. acknowledges support from the European community through the ERC advanced grant EXOCONDENSE (#740963; PI: R.T. Pierrehumbert).
Appendix A Validation for Non-solar Elemental Abundances
 |
Fig. A.1 Rate coefficients of the net reactions CH4 + H2O → CO + 3 H2 and 2 NH3 → N2 + 3 H2 at 2000 Κ and 0.01 bar as a function of metallicity (left) and C/O (right). |
References
- Agúndez, M., Venot, O., Selsis, F., & Iro, N. 2014, ApJ, 781, 68 [Google Scholar]
- Baeyens, R., Decin, L., Carone, L., et al. 2021, MNRAS, 505, 5603 [NASA ADS] [CrossRef] [Google Scholar]
- Baulch, D. L., Cobos, C. J., Cox, R. A., et al. 1992, J. Phys. Chem. Ref. Data, 21, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Baxter, C., Désert, J.-M., Tsai, S.-M., et al. 2021, A&A, 648, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, H., Wolf, E. T., Zhan, Z., & Horton, D. E. 2019, ApJ, 886, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H., Zhan, Z., Youngblood, A., et al. 2021, Nat. Astron., 5, 298 [Google Scholar]
- Cooper, C. S., & Showman, A. P. 2006, ApJ, 649, 1048 [CrossRef] [Google Scholar]
- Derwent, R. G., Parrish, D. D., Archibald, A. T., et al. 2021, Atmos. Environ., 248, 118248 [NASA ADS] [CrossRef] [Google Scholar]
- Diamond-Lowe, H., Stevenson, K. B., Bean, J. L., Line, M. R., & Fortney, J. J. 2014, ApJ, 796, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, E. W. 1959, Numerische Mathematik, 1, 269 [CrossRef] [Google Scholar]
- Dobrijevic, M., Cavalié, T., Hébrard, E., et al. 2010, Planet. Space Sci., 58, 1555 [CrossRef] [Google Scholar]
- Drummond, B., Mayne, N. J., Manners, J., et al. 2018, ApJ, 855, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Drummond, B., Hébrard, E., Mayne, N. J., et al. 2020, A&A, 636, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrenreich, D., Lovis, C., Allart, R., et al. 2020, Nature, 580, 597 [Google Scholar]
- Feng, Y. K., Line, M. R., & Fortney, J. J. 2020, AJ, 160, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Fleury, B., Gudipati, M. S., Henderson, B. L., & Swain, M. 2019, ApJ, 871, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, P., Hu, R., Robinson, T. D., Li, C., & Yung, Y. L. 2015, ApJ, 806, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Gardiner, W. C. 1984, Combustion Chemistry (New York: Springer) [CrossRef] [Google Scholar]
- Hébrard, Tomlin, A. S., Bounaceur, R., & Battin-Leclerc, F. 2015, Proc. Combustion Inst., 35, 607 [CrossRef] [Google Scholar]
- Hobbs, R., Shorttle, O., Madhusudhan, N., & Rimmer, P. 2019, MNRAS, 487, 2242 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, R., Seager, S., & Bains, W. 2012, ApJ, 761, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, P. G. J., Parmentier, V., Taylor, J., et al. 2020, MNRAS, 493, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Jacob, D. J. 2011, Introduction to Atmospheric Chemistry (Princeton: Princeton University Press) [Google Scholar]
- Jacobs, T. A., Giedt, R. R., & Cohen, N. 1965, J. Chem. Phys., 43, 3688 [NASA ADS] [CrossRef] [Google Scholar]
- Kasting, J. F., Liu, S. C., & Donahue, T. M. 1979, J. Geophys. Res. Oceans, 84, 3097 [NASA ADS] [Google Scholar]
- Kawashima, Yui, & Min, Michiel. 2021, A&A, 656, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kinnison, D. E., Brasseur, G. P., Walters, S., et al. 2007, J. Geophys. Res. Atmos., 112, D20302 [CrossRef] [Google Scholar]
- Lam, K.-Y., Davidson, D. F., & Hanson, R. K. 2013, Int. J. Chem. Kinetics, 45, 363 [CrossRef] [Google Scholar]
- Lee, E., Dobbs-Dixon, I., Helling, C., Bognar, K., & Woitke, P. 2016, A&A, 594, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, M.-C., Parkinson, C. D., Lee, A. Y.-T., Yung, Y. L., & Seager, S. 2003, ApJ, 596, L247 [NASA ADS] [CrossRef] [Google Scholar]
- Line, M. R., Stevenson, K. B., Bean, J., et al. 2016, AJ, 152, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Lines, S., Mayne, N. J., Boutle, I. A., et al. 2018, A&A, 615, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malik, M., Kitzmann, D., Mendonça, J. M., et al. 2019, AJ, 157, 170 [Google Scholar]
- Marsh, D. R., Mills, M. J., Kinnison, D. E., et al. 2013, J. aim., 26, 7372 [Google Scholar]
- Mendonça, J. M., Tsai, S.-M., Malik, M., Grimm, S. L., & Heng, K. 2018, ApJ, 869, 107 [CrossRef] [Google Scholar]
- Miguel, Y., & Kaltenegger, L. 2014, ApJ, 780, 166 [Google Scholar]
- Molaverdikhani, K., Henning, T., & Mollière, P. 2019, ApJ, 883, 194 [Google Scholar]
- Moses, J. I. 2014, Philos. Trans. R. Soc. London Ser. A, 372, 20130073 [NASA ADS] [Google Scholar]
- Moses, J. I., Visscher, C., Fortney, J. J., et al. 2011, ApJ, 737, 15 [Google Scholar]
- Moses, J. I., Tremblin, P., Venot, O., & Miguel, Y. 2022, Exp. Astron., 53, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Z., Carrasco, N., & Pernot, P. 2014, Geo. Res. J., 1-2, 33 [Google Scholar]
- Pluriel, W., Zingales, T., Leconte, J., & Parmentier, V. 2020, A&A, 636, A66 [EDP Sciences] [Google Scholar]
- Pluriel, W., Leconte, J., Parmentier, V., et al. 2022, A&A, 658, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prinn, R. G., & Barshay, S. S. 1977, Science, 198, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, A., Drummond, B., Hébrard, E., et al. 2021, MNRAS, 505, 4515 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, H., Brogi, M., de Kok, R., Birkby, J., & Snellen, I. 2015, A&A, 576, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinrueck, M. E., Showman, A. P., Lavvas, P., et al. 2021, MNRAS, 504, 2783 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J., Parmentier, V., Irwin, P. G. J., et al. 2020, MNRAS, 493, 4342 [NASA ADS] [CrossRef] [Google Scholar]
- Tinetti, G., Eccleston, P., Haswell, C., et al. 2021, ArXiv e-prints [arXiv:2104.04824] [Google Scholar]
- Tsai, S.-M., Lyons, J. R., Grosheintz, L., et al. 2017, ApJS., 228, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tsai, S.-M., Kitzmann, D., Lyons, J. R., et al. 2018, ApJ, 862, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Tsai, S.-M., Malik, M., Kitzmann, D., et al. 2021a, ApJ, 923, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Tsai, S.-M., Innes, H., Lichtenberg, T., et al. 2021b, ApJ, 922, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Venot, O., Hébrard, E., Agúndez, M., et al. 2012, A&A, 546, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venot, O., Drummond, B., Miguel, Y., et al. 2018, Exp. Astron., 46, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Venot, Bounaceur, R., Dobrijevic, M., et al. 2019, A&A, 624, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venot, O., Cavalié, T., Bounaceur, R., et al. 2020a, A&A, 634, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venot, O., Parmentier, V., Blecic, J., et al. 2020b, ApJ, 890, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Visscher, C., & Moses, J. I. 2011, ApJ, 738, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Visscher, C., Moses, J. I., & Saslow, S. A. 2010, Icarus, 209, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Smith, I. W. M., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [CrossRef] [Google Scholar]
- Yung, Y. L., & DeMore, W. B. 1999, Photochemistry of Planetary Atmospheres (Oxford: Oxford University Press) [Google Scholar]
- Yung, Y. L., Allen, M., & Pinto, J. P. 1984, ApJS, 55, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Zahnle, K. J., & Marley, M. S. 2014, ApJ, 797, 41 [CrossRef] [Google Scholar]
All Tables
Selected portion of the table of the rate constants for the net reaction CH4 + H2O → CO + 3 H2.
Maximum errors in percent of the compositions in the pressure range of 1 bar – 0.1 mbar computed by the mini-network for solar elemental abundances, with the largest errors among the four planets shown in bold.
All Figures
 |
Fig. 1 Visualization of the full chemical network from VULCAN (top) and the mini-network (bottom). Each species is represented by a node, with the color varying with the degree and the size varying with centrality. The shorter length of the edges (lines) indicates faster rates between two species (not to linear scale). The graphs are for Τ = 1000 Κ, Ρ = 1 bar, and chemical equilibrium composition. |
| In the text | |
 |
Fig. 2 Effective rate constants (cm3 molecules−1 s−1) for the net reaction CH4 + H20 → CO + 3 H2. |
| In the text | |
 |
Fig. 3 Adopted pressure-temperature profiles of GJ 1214b, GJ 436b, HD 189733b, and HD 209458b, for validating the mini-chemical scheme. |
| In the text | |
 |
Fig. 4 Time evolution of the main species in the 0D model computed with the full C-H-N-O kinetics (solid) and the mini-network (dashed) for solar metallicity with various temperatures and pressures. Open circles plotted at the end of each run indicate the thermochemical equilibrium abundances. |
| In the text | |
 |
Fig. 5 Vertical composition distributions computed by the mini-chemical scheme (dashed) compared with those computed by the full chemical kinetics VULCAN (solid) for the four planets with temperature profiles in Fig. 3. The dark to light colors represent increasing vertical mixing (see the text for the specific values of Kzz used). |
| In the text | |
 |
Fig. A.1 Rate coefficients of the net reactions CH4 + H2O → CO + 3 H2 and 2 NH3 → N2 + 3 H2 at 2000 Κ and 0.01 bar as a function of metallicity (left) and C/O (right). |
| In the text | |
 |
Fig. A.2 Same as Fig. 4 but for 500 times solar metallicity. |
| In the text | |
 |
Fig. A.3 Same as Fig. 4 but for solar metallicity and C raised to C/O = 2. |
| In the text | |
 |
Fig. A.4 Same as Fig. 5 but for 500 times solar metallicity. |
| In the text | |
 |
Fig. A.5 Same as Fig. 5 but for solar metallicity with C/O = 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


