| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201218966 | |
| Published online | 08 October 2012 | |
Supernova Type Ia progenitors from merging double white dwarfs
Using a new population synthesis model⋆
1
Department of Astrophysics/IMAPPRadboud University Nijmegen,
PO Box 9010
6500 GL,
Nijmegen,
The Netherlands
e-mail: s.toonen@astro.ru.nl
2
Instituut voor Sterrenkunde, KU Leuven, Celestijnenstraat 200D,
3001
Leuven,
Belgium
3
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden, The
Netherlands
Received:
6
February
2012
Accepted:
20
July
2012
Context. The study of Type Ia supernovae (SNIa) has lead to greatly improved insights into many fields in astrophysics, e.g. cosmology, and also into the metal enrichment of the universe. Although a theoretical explanation of the origin of these events is still lacking, there is a general consensus that SNIa are caused by the thermonuclear explosions of carbon/oxygen white dwarfs with masses near the Chandrasekhar mass.
Aims. We investigate the potential contribution to the supernova Type Ia rate from the population of merging double carbon-oxygen white dwarfs. We aim to develop a model that fits the observed SNIa progenitors as well as the observed close double white dwarf population. We differentiate between two scenarios for the common envelope (CE) evolution; the α-formalism based on the energy equation and the γ-formalism that is based on the angular momentum equation. In one model we apply the α-formalism throughout. In the second model the γ-formalism is applied, unless the binary contains a compact object or the CE is triggered by a tidal instability for which the α-formalism is used.
Methods. The binary population synthesis code SeBa was used to evolve binary systems from the zero-age main sequence to the formation of double white dwarfs and subsequent mergers. SeBa has been thoroughly updated since the last publication of the content of the code.
Results. The limited sample of observed double white dwarfs is better represented by the simulated population using the γ-formalism for the first CE phase than the α-formalism. For both CE formalisms, we find that although the morphology of the simulated delay time distribution matches that of the observations within the errors, the normalisation and time-integrated rate per stellar mass are a factor ~7−12 lower than observed. Furthermore, the characteristics of the simulated populations of merging double carbon-oxygen white dwarfs are discussed and put in the context of alternative SNIa models for merging double white dwarfs.
Key words: binaries: close / stars: evolution / white dwarfs / supernovae: general
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Type Ia supernovae (SNIa) are one of the most energetic explosive events known. They have been of great importance in many fields, most notably as a tool in observational cosmology. They have been used very successfully as standard candles on cosmological distance scales (e.g. Riess et al. 1998; Perlmutter et al. 1999), owing to the special property of great uniformity in the light curves (e.g. Phillips 1993). The SNIa also strongly affect the Galactic chemical evolution through the expulsion of iron (e.g. van den Bergh & Tammann 1991). Despite their significance, Type Ia supernovae are still poorly understood theoretically.
Supernovae Type Ia are generally thought to be caused by thermonuclear explosions of carbon/oxygen (CO) white dwarfs (WDs) with masses near the Chandrasekhar mass Mch ≈ 1.4 M⊙ (e.g. Nomoto 1982). Various progenitor scenarios have been proposed. The standard scenarios can be divided into two schools of thoughts: the single-degenerate (SD) (Whelan & Iben 1973) and double-degenerate (DD) scenario (Webbink 1984; Iben & Tutukov 1984). In the SD scenario, a CO WD explodes as an SNIa if its mass approaches Mch through accretion from a non-degenerate companion. In the DD scenario, two CO WDs can produce an SN Ia while merging if their combined mass is larger than Mch.
However, observationally as well as theoretically, the exact nature of the SNIa progenitors remains unclear. The explosion mechanism is complex due to the interaction of hydrodynamics and nuclear reactions. Several models exist that vary for example between a detonation or deflagration disruption or vary between explosions at the Chandrasekhar mass or sub-Chandrasekhar masses (see e.g. Hillebrandt & Niemeyer 2000, for a review). It also remains unclear whether the DD and SD scenario both contribute to the SNIa rate or if one of the scenarios dominates. Both scenarios have problems in matching theories with observations. A serious concern about the DD scenario is whether the collapse of the remnant would lead to a supernova or to a neutron star through accretion-induced collapse (see Nomoto & Iben 1985; Saio & Nomoto 1985; Piersanti et al. 2003; Yoon et al. 2007; Pakmor et al. 2010, 2012; Shen et al. 2012). Although in the SD channel the models for the explosion process need to be fine-tuned to reproduce the observed spectra and light curves, an SNIa like event is more easily reproduced in the simulations of the explosion process. One problem in the SD scenario is that the white dwarfs should go through a long phase of supersoft X-ray emission, although it is unclear if there are enough of these sources to account for the SNIa rate (see Di Stefano 2010; Gilfanov & Bogdán 2010; Hachisu et al. 2010). Moreover, archival data of known SNIa have not shown this emission unambiguously, but there is may be one case (see Voss & Nelemans 2008; Roelofs et al. 2008; Nielsen et al. 2010). Furthermore, SNIa that take place more than a few 109 years after the starburst (see e.g. Maoz et al. 2010) are hard to create in this channel (e.g. Yungelson & Livio 2000; Han & Podsiadlowski 2004).
To use SNIa as proper standard candles, we need to know what SNIa are, when they happen and what their progenitors are. Therefore, we study the binary evolution of low- and intermediate mass stars. In a forthcoming paper (Bours et al., in prep.) we study the SD-scenario by looking into the poorly understood physics of accretion onto white dwarfs. In this paper we focus on the DD scenario and the effect of the as yet very uncertain phases of common envelope (CE) evolution on the double white dwarf (DWD) population. These DWD systems are interesting sources for studying various phases of stellar evolution, in our case the CE evolution. Gravitational wave emission is also important as this affects the binary system by decreasing the orbital period and eventually leading to a merger (Kraft et al. 1962; Peters 1964), or possible a SNIa. The DWDs are expected to be the dominant source (Evans et al. 1987; Nelemans et al. 2001a) of gravitational waves for the future space-born gravitational wave observatories such as eLISA (Amaro-Seoane et al. 2012a,b).
We study the population of merging DWDs that might lead to a SNIa from a theoretical point of view. We incorporated results from observations where possible. We use the population synthesis code SeBa for simulating the stellar and binary evolution of stellar systems that leads to close DWDs. In Sect. 2 we describe the code and the updates since the last publication of SeBa. A major influence on the merging double-degenerate population is the poorly understood CE phase (Paczynski 1976; Webbink 1984; Nelemans et al. 2000). We adopt two different models for the CE. In Sect. 3 we describe these models and their implications for the observations of close DWDs. In Sect. 4 we discuss the binary paths leading to SNIa for each model. The SNIa rates and time-integrated numbers are derived in Sect. 5. The properties of the population of merging DWDs are discussed in the context of the classical and alternative sub- and super-Chandrasekhar SNIa explosion models in Sect. 6. A discussion and conclusion follows in Sect. 7.
 |
Fig. 1 Simulated population of visible double white dwarfs as a function of orbital period and mass of the brighter white dwarf. Left: the stellar evolution tracks according to EFT are used; right: HPT (using model γα, see Sect. 3). The intensity of the grey scale corresponds to the density of objects on a linear scale. The same grey scale is used for both plots. Observed binary white dwarfs are overplotted with filled circles. Thick points taken are from Marsh et al. (2011), thinner points from Tovmassian et al. (2004); Napiwotzki et al. (2005); Kulkarni & van Kerkwijk (2010); Brown et al. (2010, 2011); Marsh et al. (2011); Kilic et al. (2011a,c,b), see Sect. 2.1 for a discussion. |
2. SeBa – a fast stellar and binary evolution code
We present an update to the software package SeBa (Portegies Zwart & Verbunt 1996; Nelemans et al. 2001b) for fast stellar and binary evolution computations. Stars are evolved from the zero-age main sequence (ZAMS) until remnant formation and beyond. Stars are parametrised by mass, radius, luminosity, core mass, etc. as functions of time and initial mass. Mass loss from winds, which is substantial e.g. for massive stars and post main-sequence stars, is included. Binary interactions such as mass loss, mass transfer, angular momentum loss, CE, magnetic braking, and gravitational radiation are taken into account with appropriate recipes at every timestep (Portegies Zwart & Verbunt 1996; Portegies Zwart & Yungelson 1998). Following mass transfer in a binary, the donor may turn into a helium-burning star without hydrogen envelope. When the mass transfer leads to a merger between the binary stars, we estimate the resulting stellar product and follow the evolution further. Note that we do not solve the equations of stellar structure. The stellar tracks instead assume stellar models in hydrostatic equilibrium. When this is not the case, however the gas envelope surrounding the core may puff outward (see Appendix A.2 for details on the formalism). In our simulation the mass transfer rate is calculated from the relevant timescales (see Appendix A.3) and not from than the stellar radii. Therefore binary evolution is not critically dependent on out-of-equilibrium parameter values.
The philosophy of SeBa is to not a priori define the binary’s evolution, but rather to determine this at runtime depending on the parameters of the stellar system. When more sophisticated models become available of processes that influence stellar evolution, these can be included, and the effect can be studied without altering the formalism of binary interactions. An example is the accretion efficiency onto the accretor star during mass transfer. Instead of prescribing a specific constant percentage of the transferred matter to be accreted (and the rest to be lost from the system), the efficiency depends on the properties of the accreting star, such as the thermal timescale, the radius and the Roche lobe of the accretor (see Appendix A.2 for details). Another example is the stability of mass transfer. In our simulations the stability and rate of mass transfer are dependent on the reaction to mass change of the stellar radii and the corresponding Roche lobes. The advantage of this is that the (de)stabilising effect of non-conservativeness of stable mass transfer (see Soberman et al. 1997) is taken into account automatically. There is no need to make the assumption in the stability calculation that stable mass transfer is conservative, as with methods that depend on the mass ratio (Hjellming & Webbink 1987; Tout et al. 1997; Hurley et al. 2002).
Since the last publication of the code content, many changes have been made. We briefly discuss the most important changes below, and provide more detail in Appendix A. First, the wind mass loss prescriptions that we implemented are mostly based on the recommendations by Hurley et al. (2000). The specific prescriptions for different types of stars are described in Appendix A.1. Second, a summary of the treatment of accretion onto different stars can be found in Appendix A.2. The accretion procedure previously used in SeBa is complemented with a procedure for accretion from a hydrogen-poor star. We assume that for ordinary stars, helium-rich matter is accreted directly to the core of the star. The mass accretion process onto white dwarfs is updated with new efficiencies of mass retention on the surface of the white dwarf. For hydrogen accretion we have the option to choose between the efficiencies of Hachisu et al. (2008) and Prialnik & Kovetz (1995). Helium retention can be modelled according to Kato & Hachisu (1999, with updates from Hachisu et al. 1999) or Iben & Tutukov (1996). In this research we used the efficiencies of Hachisu et al. (2008), Kato & Hachisu (1999), and Hachisu et al. (1999). For a study of different retention efficiencies and the effect on the Supernova Type Ia rate using the new version of SeBa, see Bours et al. (in prep.) Third, the stability of mass transfer is based on the adiabatic and thermal response of the donor star to mass loss and the response of the Roche lobe. The adjustment of the Roche lobe is dependent on the mass transfer rate, which in turn sets the efficiency of accretion onto the accretor star, see Appendix A.3. Fourth, regarding the stellar tracks, previously, stellar evolution has been based on evolutionary tracks described by analytic formulae given by Eggleton et al. (1989, hereafter EFT) with updates from Tout et al. (1997) and helium star evolution as described by Portegies Zwart & Verbunt (1996) based on Iben & Tutukov (1985). In the new version, the evolution of ordinary stars and hydrogen-poor stars is based on Hurley et al. (2000, hereafter HPT). We do not adopt the HPT tracks for remnants, instead we maintain our prescription (Portegies Zwart & Verbunt 1996; Nelemans et al. 2001b), which includes processes such as natal kick velocities to compact objects in supernovae explosions.
2.1. Impact on the population of double white dwarfs
Figure 1 shows the visible close DWD population simulated by SeBa. On the left a simulation is shown of the previous version of SeBa that a.o. uses the EFT tracks and on the right we show the current version using the HPT tracks. Initial parameters are distributed according to the distributions described in Table 1. Primary masses are drawn from 0.96−11 M⊙ to include all stars that evolve into a white dwarf in a Hubble time. For the mass ratio and eccentricity we cover the full range 0−1, and the orbital separation out to 106 R⊙. We assumed solar metallicity, unless specified otherwise. In the normalisation of the simulation we assumed that primary masses lie in the range 0.1−100 M⊙. Our method to estimate the visible population of DWDs is described in Nelemans et al. (2004), in which the Galactic star formation history is based on Boissier & Prantzos (1999) and WD cooling according to Hansen (1999). We assume a magnitude limit of 21. In Fig. 1, the observed DWDs are overplotted with filled circles. The systems are described by Marsh (2011) and references therein, as well as Tovmassian et al. (2004) and Rodríguez-Gil et al. (2010). Additionally, we included 19 newly discovered DWDs from Kulkarni & van Kerkwijk (2010); Brown et al. (2010, 2011); Marsh et al. (2011); Kilic et al. (2011a,c) and Kilic et al. (2011b). These new systems are displayed with smaller circles and thinner lines to separate them from the previously found systems. We did this because the observational biases are very different. The previously found systems were selected from a magnitude-limited sample down to 16−17 mag. The new systems are much fainter at about 20 mag. Moreover, most of the new systems are discovered as part of the ELM survey (Brown et al. 2010). This survey focuses on finding extremely low-mass white dwarfs from follow-up observations of spectroscopically selected objects from the Sloan Digital Sky Survey. Therefore, the set of new systems is biased to lower masses. One should take this bias into account while comparing with the simulations and not take the combined set of observed systems as a representative sample of the DWD population. Kilic et al. (2011a) showed in their Fig. 12 a visualisation of the population of visible DWDs simulated by SeBa, where this selection effect has been taken into account.
Distributions of the initial binary parameter mass, mass ratio, orbital separation and eccentricity.
The locations of the observed DWDs in Fig. 1 correspond reasonably well to the predictions of both models. The overall structure of the simulated populations from both models are similar. At masses of ~0.5 M⊙ and periods of 1−10 h, there is a very pronounced region in the plot from the EFT tracks that seems to be missing in the HPT plot. However, this is not really the case. These systems mainly consist of one helium (He) WD and one CO WD. Masses of CO WDs span a wider range of values in the HPT tracks, which distributes the pronounced region in EFT over a larger region in mass and period in HPT.
For a single burst of star formation the number of created DWDs within 13.5 Gyr and with
an orbital period P < 1000 h for the HPT and EFT
stellar tracks is very similar;
6.9 × 10-3 per M⊙ of created stars for
both models. The time-integrated merger rate is 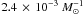 for HPT and
for HPT and 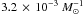 for EFT. The current merger rate in the Milky Way according to the HPT and EFT stellar
tracks is very similar; 1.4 × 10-2 yr-1 for HPT
and 1.2 × 10-2 yr-1 for EFT, for which we have assumed
a star formation history as in Nelemans et al.
(2004) based on Boissier & Prantzos
(1999).
for EFT. The current merger rate in the Milky Way according to the HPT and EFT stellar
tracks is very similar; 1.4 × 10-2 yr-1 for HPT
and 1.2 × 10-2 yr-1 for EFT, for which we have assumed
a star formation history as in Nelemans et al.
(2004) based on Boissier & Prantzos
(1999).
Classically, the population of double He dwarfs is thought to dominate in number over the other types of close DWDs. Using the EFT tracks for a single burst of star formation, we predict a percentage of [He-He, He-CO, CO-CO] = [60%, 17%, 21%] and a negligible number of DWDs containing oxygen/neon (ONe) dwarfs. For the HPT tracks, the percentage of double He dwarfs decreases to 38%. The population consists of [He-He, He-CO, CO-CO] = [38%, 27%, 33%] and 2% CO-ONe dwarfs. The decrease in number of He WDs is caused by a difference in the stellar tracks related to helium ignition under degenerate conditions. As shown by Han et al. (2002), degenerate stars do not ignite helium at a fixed core mass, but instead the core mass at helium ignition is a decreasing function of the ZAMS mass of the star. Taking this into account, more WDs in close binaries are labelled CO WDs.
3. Two models for common envelope evolution
Close DWDs are believed to encounter at least two phases of mass transfer in which one of the stars loses its hydrogen envelope. In at least one of these phases mass transfer from the evolving more massive star to the less massive companion is dynamically unstable (Paczynski 1976; Webbink 1984) which leads to a common envelope. The core of the donor and companion spiral inward through the envelope, expelling the gaseous envelope around them. Because of the loss of significant amounts of mass and angular momentum, the CE phase plays an essential role in binary star evolution in particular the formation of short-period systems that contain a compact object.
Despite of the importance of the CE phase and the enormous efforts of the community, all
effort so far have not been successful in understanding the phenomenon. Several
prescriptions for CE evolution have been proposed. The α-formalism (Webbink 1984) is based on the conservation of orbital
energy. The α-parameter describes the efficiency with which orbital energy
is consumed to unbind the CE according to 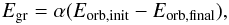 (1)where
Eorb is the orbital energy and Egr
is the binding energy between the envelope mass Menv and the
mass of the donor M. Egr is often approximated
by
(1)where
Eorb is the orbital energy and Egr
is the binding energy between the envelope mass Menv and the
mass of the donor M. Egr is often approximated
by 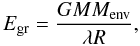 (2)where R is
the radius of the donor star and λ depends on the structure of the donor.
We assume αλ = 2. Nelemans et al.
(2000) deduced this value from reconstructing the last phase of mass transfer for
10 known DWDs using the unique core-mass – radius relation for giants.
(2)where R is
the radius of the donor star and λ depends on the structure of the donor.
We assume αλ = 2. Nelemans et al.
(2000) deduced this value from reconstructing the last phase of mass transfer for
10 known DWDs using the unique core-mass – radius relation for giants.
To explain the observed distribution of DWDs, Nelemans
et al. (2000) proposed an alternative formalism. According to
this γ-formalism, mass transfer is unstable and non-conservative. The
mass-loss reduces the angular momentum of the system in a linear way according to
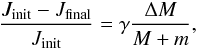 (3)where Jinit
resp. Jfinal is the angular momentum of the pre- and post-mass
transfer binary respectively, and m is the mass of the companion. We
assumed γ = 1.75, see Nelemans et al.
(2001b).
(3)where Jinit
resp. Jfinal is the angular momentum of the pre- and post-mass
transfer binary respectively, and m is the mass of the companion. We
assumed γ = 1.75, see Nelemans et al.
(2001b).
 |
Fig. 2 Simulated population of visible double white dwarfs as a function of orbital period and mass ratio, where mass ratio is defined as the mass of the brighter white dwarf divided by that of the dimmer white dwarf. In the left model γα is used, in the right model αα. The intensity of the grey scale corresponds to the density of objects on a linear scale. The same grey scale is used for both plots. Observed binary white dwarfs are overplotted with filled circles, see Fig. 1 for references. |
 |
Fig. 3 Simulated population of visible double white dwarfs as a function of orbital period and the combined mass of the two dwarfs. On the left the common envelope is parametrised according to model γα, on the right according to model αα (see Sect. 3). The intensity of the grey scale corresponds to the density of objects on a linear scale. The same grey scale is used for both plots. Observed binary white dwarfs are overplotted with filled circles, see Fig. 1 for references. The Chandrasekhar mass limit is indicated with the dotted line. The dashed line roughly demarks the region in which systems merge within a Hubble time. Systems located to the left of the dashed line and above the dotted line are supernova type Ia progenitors in the standard picture. |
We adopt two evolutionary models that differ in their treatment of the CE phase. In
model αα the α-formalism is used to determine the
outcome of every CE. For model γα the γ-prescription is
applied unless the binary contains a compact object or the CE is triggered by a tidal
instability (rather than dynamically unstable Roche lobe overflow, see Appendix A.3). Typically, the second CE (with a giant donor and
white dwarf companion) is described by the α-formalism, which gives
consistent results when compared with the observations (Nelemans et al. 2000). If the first phase of mass transfer is unstable, it
typically evolves through a γ-CE. In model γα
and αα, if both stars are evolved when the CE develops, we assumed that
both cores spiral-in (see Nelemans et al. 2001b). The
envelopes are expelled according to 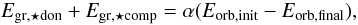 (4)analogous to Eq. (1), where
Egr, ⋆ don represents the
binding energy of the envelope of the donor star
and Egr, ⋆ comp of the
companion star.
(4)analogous to Eq. (1), where
Egr, ⋆ don represents the
binding energy of the envelope of the donor star
and Egr, ⋆ comp of the
companion star.
The motivation for the alternative formalism is the large amount of angular momentum available in binaries with similar-mass objects. The physical mechanism behind the γ-description remains unclear however. Interesting to note here is that recently Woods et al. (2010, 2012) suggested a new evolutionary model to create DWDs. It differs from standard assumptions in the first phase of mass transfer. These authors find that mass transfer between a red giant and a main-sequence star can be stable and nonconservative. The effect on the orbit is a modest widening, with a result alike to the γ-description.
3.1. Impact on the population of double white dwarfs and type Ia supernova progenitors
Figure 2 shows the mass ratio of the visible population (see Sect. 2.1) of DWDs versus the orbital period according to model γα and αα. Overlayed with filled circles are the observed populations. For systems for which only a lower limit to the mass of the companion is known, we show a plausible range of mass ratios of that system with an arrow. The arrow is drawn starting from the maximum mass ratio, which corresponds to an inclination of 90 degrees. It extends to a companion mass that corresponds to an inclination of 41 degrees. Within this range of inclinations there is a 75% probability that the actual mass ratio lies along the arrow. The filled circles overplotted on the arrow indicate the mass ratio for the median for random orientations, i.e., 60 degrees.
Using model αα, the DWDs cluster around a mass ratio of q ~ 0.5, while model γα shows a wider range in mass ratio. This agrees better with the observed binaries. The different mass ratio distributions are inherent to the models and only slightly dependent on the CE efficiency. This is because in the first CE phase, the γ-CE allows for widening or very mild shrinkage of the orbit, whereas in the α-prescription the orbit will always shrink. The resulting orbital separation determines when the secondary will fill its Roche lobe, and the corresponding core mass of the secondary, which determines the mass ratio distribution of the prospective DWD.
In Fig. 3 the population of observed and simulated DWDs are shown as a function of combined mass of the two WDs for the two models of CE evolution. The left upper corner bounded by the dotted and dashed lines contains SNIa progenitors. In Fig. 3 there are two systems that have a probability to fall in this region. These systems are the planetary nebulae nuclei with WD companions TS 01 (PN G135.9+55.9) (Tovmassian et al. 2004; Napiwotzki et al. 2005; Tovmassian et al. 2010) and V458 Vul (Rodríguez-Gil et al. 2010). An immediate precursor of a DWD that is possibly a progenitor candidate for a SN Ia via the DD channel has also been observed; a subdwarf with a white dwarf companion, KPD 1930+2752 (Maxted et al. 2000; Geier et al. 2007).
In our model of the visible population of DWDs (see Sect. 2.1), the percentage of merging DWDs with a total mass exceeding the Chandrasekhar is 1.2% for model γα and 4.3% for model αα. Including only double CO WDs, the percentage is 0.9 and 2.9%, respectively. Because the number of observed close DWDs until today is low, we do not expect to observe many SNIa progenitors (see also Nelemans et al. 2001b). Therefore a comparison of the SNIa progenitors with population synthesis by a statistical approach is unfortunately not yet possible. We find it important to compare the observed close DWD population with the simulated one, since these systems go through similar evolutions and are strongly influenced by the same processes. Although the observed population mostly consists of He DWDs and He-CO DWDs instead of CO DWDs required for SNIa progenitors, at this time the population of all close DWDs are the closest related systems that are visible in bulk.
4. Evolutionary paths to supernova type Ia from the double degenerate channel
In this section we discuss the most common binary scenarios that leads to a potential supernova type Ia in the DD channel. We assume that every merger of two carbon/oxygen white dwarf with a mass exceeding 1.4 M⊙ will lead to a supernova. The contribution of merging systems that contains a helium white dwarf that surpasses the Chandrasekhar mass is negligible. In the canonical scenario a DWD is formed through two consecutive CEs. This we label the “common envelope channel”. In accordance with Mennekens et al. (2010), we find that there are other channels that can lead to a SNIa as well. We find that the common envelope scenario can account for less than half of the supernova progenitors in a single burst of star formation, 34% for model γα and 45% for model αα. We distinguish between three scenarios labelled “common envelope”, “stable mass transfer” and “formation reversal”. The names of the first two tracks refer to the first phase of mass transfer, whereas “formation reversal” applies to the reversed order in which the two white dwarf are formed, see Sect. 4.3). The stable mass transfer channel accounts for 52% and 32% assuming model γα and αα, respectively, for a single burst of star formation. The formation reversal channel accounts for a lower percentage of all SNIa, 14% for model γα and 23% for model αα for a single starburst. Note that the importance of the stable mass transfer channel strongly depends on the assumed amount of mass loss and angular momentum loss.
In population synthesis studies all known information about binary evolution is combined, and different evolutionary paths emerge out of these quite naturally. As noted by Mennekens et al. (2010), the significant contribution to the SNIa rate from other channels than the common envelope channel complicates the use of analytical formalisms for determining the distribution of SNIa delay times. The SNIa delay time of a binary is the time of the SNIa since the formation of the system. This is commonly used to compare observational and synthetic rates to constrain different physical scenarios (e.g. Yungelson & Livio 2000; Ruiter et al. 2009; Mennekens et al. 2010, see also Sect. 5 in this paper). During a CE phase the companion is assumed to be hardly affected e.g. by accretion. If this is not the case, as in stable mass transfer, the assumption that the formation timescale of the DWD is approximately the main-sequence lifetime of the least massive component is not valid any more. Furthermore, the in-spiral timescale from DWD formation to merger due to gravitational waves is strongly dependent on the orbital separation at DWD formation. This can be very different for systems that undergo stable mass transfer instead of a CE evolution. Concluding, the delay time, which is the sum of the DWD formation and in-spiral timescale can be significantly different when these tracks are not properly taken into account.
 |
Fig. 4 Evolutionary track for the merger of two carbon/oxygen white dwarfs of a combined mass that exceeds the Chandrasekhar mass. In this scenario the first phase of mass transfer is dynamically unstable which results in a common envelope. In this figure we show a representative example of model γα, see Sect. 3. ZAMS stands for zero age main sequence and CE for common envelope. G is a giant star, MS a main-sequence star, He MS a helium MS and WD a white dwarf. |
4.1. Common envelope channel
In the canonical path, both stars lose their hydrogen envelopes through two consecutive common envelopes. An example of a typical evolution is shown in Fig. 4. In this example two zero-age main-sequence stars of 6 M⊙ and 4 M⊙ are in an orbit of 125 days. When the initially more massive star (hereafter primary) ascends the giant branch, it fills its Roche lobe and a CE commences. The primary loses its hydrogen envelope, but does not become a WD immediately and a helium star is born. The primary becomes a white dwarf of about solar mass. When the initially less massive star (hereafter secondary) evolves off the main sequence and its radius significantly increases, another common envelope occurs. As a result, the orbit shrinks. The secondary evolves further as a helium star without a hydrogen envelope until it eventually turns into a white dwarf. For model αα the orbit decreases more severely in the first phase of mass transfer. Therefore the initial periods in this channel are higher, by a factor ~1.5−3 and the primaries are typically more evolved giants when the donors fill their Roche lobes. In this evolution channel both the primary and secondary can fill their Roche lobes as helium giants. If this happens, mass transfer is usually dynamically stable, but the effect on the orbit is small.
A variation of this evolution can occur when the secondary has reached the giant stages of its evolution when the primary fills its Roche lobe. This happens for systems of nearly equal masses. We assume both stars lose their envelope in the CE phase according to Eq. (4), in which the orbit is severely decreased. This variation contributes 23% of the systems in the common envelope channel for model γα and 10% for model αα.
With the α-CE prescription it is likely to have another variation on the evolution, in which the primary becomes a white dwarf immediately after the first phase of mass transfer. This can happen when the primary fills its Roche lobe very late on the asymptotic giant branch when the star experiences thermal pulses. These systems have initial periods that are a factor 5 lger than in the standard CE channel using model αα. This subchannel contributes 43% to the CE channel for model αα. When using the γα-model for the CE, the contribution from this subchannel is 20%. However, these systems are not formed through a standard γ-CE because the orbit does not shrink severely enough to obtain a significant contribution. Instead these systems are formed through a double-CE as described by Eq. (4). For model αα the double-CE mechanism is important in only 18% of the 43%.
 |
Fig. 5 Two evolutionary tracks for the merger of two carbon/oxygen white dwarfs of a combined mass exceeding the Chandrasekhar mass. In these scenarios the first phase of mass transfer is dynamically stable. On the left an example of the stable mass transfer channel is shown, on the right the formation reversal channel. In the latter scenario the first phase of mass transfer is dynamically stable which results in a low-mass helium-star with a long lifetime. The initially less massive star becomes the first formed white dwarf. The top and bottom parts of the figure have different scales due to a common envelope phase, denoted as CE in the figure. Abbreviations are as in Fig. 4. Additionally sRLOF stands for stable Roche lobe overflow, HG is a Hertzsprung-gap star and He G a helium giant. |
4.2. Stable mass transfer channel
In this channel the initial masses of the stars and the initial orbits are smaller than for the common envelope channel. Typical values are a primary mass of 5 M⊙, a secondary mass of 3 M⊙ and an orbital separation of 40 R⊙ (assuming a circular orbit). The primary fills the Roche lobe as a Hertzsprung gap star and mass transfer occurs stably. Which fraction of transferred mass is actually accreted by the secondary and how much is lost from the system depends on the mass and radius of the secondary and the secondary’s Roche lobe (see Appendix A.2 for more details). In Fig. 5a an example of a typical evolution is shown. When the secondary fills its Roche lobe, a CE commences. In this channel the tidal instability (see Appendix A.3) is important. In one third of the systems the CE occurs because of a tidal instability, the other part is caused by a dynamical instability. The secondary turns into a hydrogen-deficient helium-burning star in a system in which the period has decreased by one or two orders of magnitude. As in the previous channel, the primary and secondary can fill their Roche lobe as helium giants. If the primary fills its Roche lobe, mass transfer is usually dynamically stable and has little effect on the orbit. If the secondary fills its Roche lobe, mass transfer can be stable or unstable. In the example of Fig. 5a when the secondary fills its Roche lobe again as it ascends the helium giant branch, the mass transfer is unstable and the orbital separation decreases by a factor ~5.
4.3. Formation reversal channel
We present a scenario in which in the first mass transfer a helium star (sdB star) is formed that becomes a white dwarf only after the companion has become a white dwarf1. A typical example of an evolution like this is shown in Fig. 5b. The first phase of mass transfer is stable, like the stable mass transfer track. However, the resulting helium stars in this channel have low masses in the range of 0.5−0.8 M⊙ and long lifetimes of ~108 yr. The first mass transfer occurs approximately conservatively. As a consequence, the subsequent evolution of the high-mass secondary (5−8 M⊙) accelerates. When the secondary fills its Roche lobe, mass transfer is tidally unstable (see Appendix A.3). The secondary loses its hydrogen and helium envelope in two consecutive CEs and becomes a white dwarf. Subsequently, the original primary evolves of the helium main-sequence and becomes a white dwarf.
To our knowledge, this track has not been studied in detail before. Therefore we evaluated this track by performing detailed numerical calculations using the ev binary stellar-evolution code originally developed by Eggleton (Eggleton 1971, 1972; Yakut & Eggleton 2005, and references therein) and updated as described in Pols et al. (1995) and Glebbeek et al. (2008). The code solves the equations of stellar structure and evolution for the two components of a binary simultaneously. The simulation showed that indeed the evolution of the secondary can be accelerated through accretion so that the secondary can stop helium burning prior to the primary.
5. Delay time distribution
One way to constrain the population of SNIa progenitors is through the delay time distribution (DTD), where the delay times is the time between the formation of the binary system and the SNIa event. In a simulation of a single burst of star formation the DTD gives the SNIa rate as a function of time after the starburst. The DTD is linked to the nuclear timescales of the progenitors and the binary evolution timescales up to the merger. We assumed a 50% binary fraction and initial parameters are distributed according to the distributions described in Table 1.
In Fig. 6 we compare the delay time distribution for
the two different models of CE evolution. The sharp cut-off near 13.5 Gyr is artificial,
because evolution was only allowed to proceed for 13.5 Gyr. The delay time distribution
shows that these mergers are expected to take place in young as well as old populations. The
peak in the supernova Ia rate is at ~150 Myr for both models. The median delay time
is 0.7 Gyr for model αα and 1.0 Gyr for model γα. The
normalisations of the delay time distribution of model αα
and γα are comparable. The time-integrated number of SNe Ia per unit
formed stellar mass is 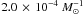 and
and 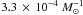 for model γα and αα, respectively. From the Lick
Observatory Supernova Search, Maoz et al. (2011)
inferred a value of
for model γα and αα, respectively. From the Lick
Observatory Supernova Search, Maoz et al. (2011)
inferred a value of 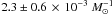 ,
which is a factor 7−12 higher than the predictions from our models.
,
which is a factor 7−12 higher than the predictions from our models.
 |
Fig. 6 Merger rate of double carbon/oxygen white dwarfs with a total mass above the Chandrasekhar mass as a function of delay time. Rates are in yr-1 per 1010 M⊙ formed stellar mass of the parent galaxy. Solar metallicity (Z = 0.02) is assumed. Delay times are shown for two different prescriptions of the CE phase. In black we plot model γα and in grey model αα, see Sect. 3. Overplotted with black circles are the observed values of the SNIa rate of Totani et al. (2008), Maoz et al. (2010), Maoz & Badenes (2010) and Maoz et al. (2011; for a review Maoz & Mannucci 2012). For comparison the grey circles show the observations scaled down by a factor 10. |
The morphologies of the DTD of model γα and αα resemble each other in that they show a strong decline with delay time, although with a slightly different slope. The αα model shows higher rates at short delay times, whereas the rate for model γα shows higher rates at long delay times. This is because the α-CE causes a stronger decrease of the orbital separation than the γ-CE in the first phase of mass transfer. The observed rates from Totani et al. (2008), Maoz et al. (2010), Maoz & Badenes (2010), and Maoz et al. (2011; see Maoz & Mannucci 2012, for a review), shown in Fig. 6, are much higher than the predicted rates from both models. To compare the morphological shapes of the DTDs more easily, we scaled down the observations by a factor 10 in Fig. 6 in light grey. The shape of the observed DTD fits the synthetic DTDs well. At long delay times >6 Gyr, the flattening of the DTD is better reproduced by the γα-model.
We have a last remark about Fig. 6, about the datapoint from Maoz et al. (2010) at 185 Myr and a rate of 0.165 yr-1 (1010 M⊙)-1. If this datapoint is true, it could indicate a steep rise of the delay time distribution at the shortest delay times. Neither model γα, or αα reproduces the steep rise indicated by this point. At short delay times the contribution to the SNIa rate from other channels might be significant, for instance the contribution from helium donors in the SD channel. Wang et al. (2009), Ruiter et al. (2009) and Claeys et al. (2011) showed that at delay times of ~100 Myr, the DTD from helium donors in the SD channel peaks, although rates at this delay time vary between 10-4−10-2 yr-1 (1010 M⊙)-1. Hydrogen donors in the SD channel are a possible contributor to the SNIa rate as well, but there is a strong disagreement over the DTD from this channel (see for example Nelemans et al. 2012, for an overview). In that paper it was shown that the simulated peaks of the DTDs lie anywhere between 0.1 to 3 Gyr and the peak rates vary between 10-6−10-2 yr-1 (1010 M⊙)-1.
 |
Fig. 7 Merger rate of double carbon/oxygen white dwarfs with a total mass above the Chandrasekhar mass as a function of delay time for a metallicity of 0.001. Rates are in yr-1 per 1010 M⊙ per formed stellar mass of the parent galaxy. Delay times are shown for two different prescriptions of the CE phase. In black model we plot γα and in grey model αα, see Sect. 3. |
If we do not assume an instantaneous burst of star formation, but instead convolve the DTD with a star formation rate, we can estimate the SNIa rate from double degenerates for spiral galaxies like the Milky Way. If we assume a Galactic star formation rate as in Nelemans et al. (2004) based on Boissier & Prantzos (1999), model αα gives 8.3 × 10-4 SNIa yr-1. Model γα gives a Galactic rate of 5.8 × 10-4 SNIa yr-1. The reason for the relatively high Galactic rate for model γα in comparison with model αα relative to the integrated rates is that the peak of star formation occurs at long delay times where the DTD of model γα dominates over model αα. The empirical SN Ia rate from Sbc-type galaxies like our own (Cappellaro & Turatto 2001) is 4 ± 2 × 10-3 yr-1, which is a factor ~5−7 higher than the simulated rates.
When convolving the DTD with a star formation history, one should also take into account a
metallicity dependence of the stars. To study the effect of metallicity on the SNIa rate, we
simulated a delay time distribution from a single burst of stars of
metallicity Z = 0.001. The important part of the DTDs in this respect are
the long delay times because this is where the fraction of metal poor stars is highest. The
DTD of model γα for Z = 0.001 is lower at long delay times
and higher at short delay times than the same CE model for solar metallicities. The
time-integrated number of SNe Ia per unit formed stellar mass
is 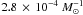 for model γα. This is an increase of ~60% with respect
to Z = 0.02. The integrated rate for model αα
for Z = 0.001 is
for model γα. This is an increase of ~60% with respect
to Z = 0.02. The integrated rate for model αα
for Z = 0.001 is 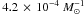 ,
which is an increase of ~30% with respect to Z = 0.02. The DTD
for Z = 0.001 is roughly similar in morphological shape to that
for Z = 0.02, see Fig. 7. The DTDs
of both metallicities for model αα are similar at long delay times, and
consequently the effect on the Galactic SNIa rate is expected to be marginal.
,
which is an increase of ~30% with respect to Z = 0.02. The DTD
for Z = 0.001 is roughly similar in morphological shape to that
for Z = 0.02, see Fig. 7. The DTDs
of both metallicities for model αα are similar at long delay times, and
consequently the effect on the Galactic SNIa rate is expected to be marginal.
 |
Fig. 8 Simulated distribution of the population of merging double CO white dwarfs from a single burst of star formation as a function of delay time and total mass of the system. On the left model γα is used for the common envelope parametrisation, on the right model αα (see Sect. 3). The intensity of the grey scale corresponds to the density of objects on a linear scale in units of number of systems per 105 M⊙. The black line corresponds to a combined mass of 1.4 M⊙. |
6. Population of merging double white dwarfs
In this section we discuss the properties of the population of SNIa progenitors from merging DWD and place it in the context of recent studies of the SNIa explosion itself. Figure 8 shows the combined mass of the system as a function of delay time for merging CO DWDs. It shows that for classical SNIa progenitors, the number of merging events decreases with time and that the number decreases faster with time for model αα than for model γα, as discussed in Sect. 5. Moreover, the figure shows that mergers near the Chandrasekhar mass are most common, independent of delay time.
Fryer et al. (2010) showed that if super-Chandrasekhar mergers of CO DWDs of ~2 M⊙ produce thermonuclear explosions, the light curves are broader than the observed SNIa sample. These authors argued that these mergers cannot dominate the current SNIa sample. We find indeed in both models that mergers with combined masses ~2 M⊙ are much less common than mergers in systems with a combined mass near the Chandrasekhar mass limit.
 |
Fig. 9 Simulated population of merging double CO white dwarfs from a single burst of star formation as a function of the masses of the two white dwarfs. Mmassive is the mass of the most massive white dwarf, Mnon−massive corresponds to the least massive white dwarf. On the left model γα is used for the common envelope parametrisation, on the right model αα (see Sect. 3). The intensity of the grey scale corresponds to the density of objects on a linear scale in units of number of systems per 105 M⊙. To increase the contrast, we placed an upper limit on the intensity, which effects only one bin for model γα and two bins for model αα. The black solid line corresponds to a combined mass of 1.4 M⊙. The dashed and dashed-dotted line correspond to a mass ratio q = m/M of 1 and 0.8, respectively. The mass ratio distribution, which is important e.g. in the scenarios proposed by Pakmor et al. (2010) and van Kerkwijk et al. (2010) are very different for model γα and αα. |
Where Fryer et al. (2010) studied a merger of
a 1.2 M⊙ CO WD with
a 0.9 M⊙ CO WD, Pakmor
et al. (2010) focused on mergers of nearly equal mass WDs. In their scenario both
WDs are distorted in the merger process and the internal structure of the merger remnant is
quite different. Pakmor et al. (2010) argued that
these mergers become hot enough to ignite carbon burning if the WD masses
exceed M ≳ 0.9 M⊙. They found that these
systems resemble subluminous SNIa such as SN 1991bg. Li
et al. (2001) found 1991bg-like supernovae account for 16 ± 6% of all SNIa.
From an improved sample Li et al. (2011) found a
percentage of 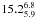 . If we assume that
1991bg-like events account for 15% of all SNIa and the time-integrated of all SNIa types
is
. If we assume that
1991bg-like events account for 15% of all SNIa and the time-integrated of all SNIa types
is 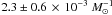 (Maoz et al. 2011), the time-integrated rate should
be
(Maoz et al. 2011), the time-integrated rate should
be 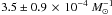 .
When we include the error of 6% on the fraction of 1991bg-like events with respect to all
SNIa, the rate is
.
When we include the error of 6% on the fraction of 1991bg-like events with respect to all
SNIa, the rate is 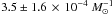 .
If we assume in a simplistic way that all CO DWD mergers
of q = M2/M1 > 0.92
and M1 > 0.9
(where M1 is the most massive WD
and M2 the least massive WD) would lead to a 1991bg-like
event, the time-integrated number of events is
.
If we assume in a simplistic way that all CO DWD mergers
of q = M2/M1 > 0.92
and M1 > 0.9
(where M1 is the most massive WD
and M2 the least massive WD) would lead to a 1991bg-like
event, the time-integrated number of events is 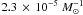 according to model γα and
according to model γα and 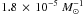 assuming model αα. While the SNIa rate from the classical progenitors from
modelγα is comparable to that of model αα, the
population of DWDs is very different. In Sect. 3.1 we
showed that the type of CE parametrisation introduces a bias in the mass ratio distribution
of observed DWDs, which mostly consist of (double) He DWDs and He-CO DWDs. In Fig. 9 we show that this is also the case for the population of
merging CO DWDs. Although the mass ratio distribution is not important for the standard DD
scenario, it is important for the scenario proposed by Pakmor et al. (2010). If the standard scenario and the scenario proposed by Pakmor et al. (2010) hold, SN 1991bg-like events are more
common in model γα. We have to make a side remark on the expected delay
times of this scenario. The median delay times are 180 Myr for model γα
and 150 Myr for model αα. The timescales are short because generally, more
massive WDs have more massive progenitor stars, whose evolutionary timescales are short
compared to those of less massive stars. Observations show, however, that subluminous SNIa
are associated with old stellar populations ~5−12 Gyr (Howell 2001).
assuming model αα. While the SNIa rate from the classical progenitors from
modelγα is comparable to that of model αα, the
population of DWDs is very different. In Sect. 3.1 we
showed that the type of CE parametrisation introduces a bias in the mass ratio distribution
of observed DWDs, which mostly consist of (double) He DWDs and He-CO DWDs. In Fig. 9 we show that this is also the case for the population of
merging CO DWDs. Although the mass ratio distribution is not important for the standard DD
scenario, it is important for the scenario proposed by Pakmor et al. (2010). If the standard scenario and the scenario proposed by Pakmor et al. (2010) hold, SN 1991bg-like events are more
common in model γα. We have to make a side remark on the expected delay
times of this scenario. The median delay times are 180 Myr for model γα
and 150 Myr for model αα. The timescales are short because generally, more
massive WDs have more massive progenitor stars, whose evolutionary timescales are short
compared to those of less massive stars. Observations show, however, that subluminous SNIa
are associated with old stellar populations ~5−12 Gyr (Howell 2001).
In our simulations the majority of merging CO DWDs have combined masses below the
Chandrasekhar mass, see Fig. 8. Sub-Chandrasekhar
models have long been proposed in order to raise total number of SNIa to match observations.
Sim et al. (2010) found that if sub-Chandrasekhar
WDs can be detonated, especially in the
range ~1.0−1.2 M⊙, the explosions match several
observed properties of SNIa reasonably well. In the hypothetical situation that all double
CO WDs that merge lead to an SNIa event, the integrated rate
is 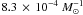 for model γα and
for model γα and 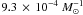 for model αα. This is still a factor 3 lower than the observed rate
of
for model αα. This is still a factor 3 lower than the observed rate
of 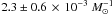 (Maoz et al. 2011). Only if we assume that all
mergers between a CO WD and a CO or He WD lead to an SNIa, the rates
of
(Maoz et al. 2011). Only if we assume that all
mergers between a CO WD and a CO or He WD lead to an SNIa, the rates
of 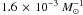 and
and 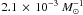 for model γα and αα, respectively, match the observed
rate.
for model γα and αα, respectively, match the observed
rate.
The challenge for sub-Chandrasekhar models is how to detonate the white dwarf. A scenario
for this was recently suggested by van Kerkwijk et al.
(2010). In this scenario two CO WDs with nearly equal masses merge. The merger
remnant itself is too cold and insufficiently dense to produce an SNIa by itself, as noted
by Pakmor et al. (2010). van Kerkwijk et al. (2010) proposed that accretion of the thick disk
that surrounds the remnant leads to an SNIa through compressional heating. If we
simplistically assume that every merger of a double CO DWD
with q > 0.8
and M1 + M2 < 1.4
leads to an SNIa, the time-integrated number per unit formed mass
is 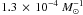 for model γα and
for model γα and 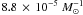 for model αα. Relaxing the condition
of M1 + M2 < 1.4
to all masses,
for model αα. Relaxing the condition
of M1 + M2 < 1.4
to all masses, 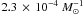 for model γα and
for model γα and 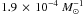 for model αα. As in the scenario proposed by Pakmor et al. (2010), when a scenario is biased to merging systems of
high-mass ratio, the relative contribution from this scenario in the γα
model is higher than the αα model.
for model αα. As in the scenario proposed by Pakmor et al. (2010), when a scenario is biased to merging systems of
high-mass ratio, the relative contribution from this scenario in the γα
model is higher than the αα model.
7. Conclusion and discussion
We studied the population of SNIa progenitors from merging double CO WDs with a combined mass exceeding the Chandrasekhar mass, the so-called DD progenitors. We considered two prescriptions of the CE phase. The CE evolution is a crucial ingredient in the formation of close double degenerate compact objects, but the process itself is still poorly understood. The first model assumes the α-formalism for all CE. The second model is a combination of the α-formalism and the γ-formalism (see Sect. 3). Typically, the first CE is described by the γ-scenario and the second by the α-formalism, if mass transfer is unstable.
We applied the updated version of the population synthesis code SeBa to simulate the population of DWDs and SNIa progenitors. At present, close DWDs (of all WD types) are the closest related systems to the DD SNIa progenitors that are visible in bulk. The mass ratio distribution of the DWDs in model αα is inconsistent with the observations. Using model γα the simulated population of DWDs compares well with observations, nevertheless, this is what the γ-formalism was designed to do.
Recently, Webbink (2008) and Zorotovic et al. (2010) claimed that the predictive power of the γ-scenario is more restricted. They suggested that the α-scenario is valid when sources of an energy other than the binding energy of the envelope is available, such as, the energy released by recombination in the common envelope. This could explain the high value of α found by Nelemans et al. (2000) for the second CE, but certainly does not solve the problem for the first CE for which Nelemans et al. (2000) found a value of α < 0.
The delay time distributions from our two models show the characteristic shape of a strong decay with time. This strong decay is expected when the delay time is dominated by the gravitational wave timescale (tgr ∝ a4) and the distribution of orbital separations at DWD formation is similar to the initial (ZAMS) distribution of N(a)da ∝ a-1da (Abt 1983). The DTD from model γα fits the shape of the observed DTD best. Mennekens et al. (2010) also showed a DTD using the γ-scenario for the CE phase. They found that the DD DTD lies almost an order of magnitude lower in absolute rate than when using the α-scenario. However, they used the γ-formalism for all CE phases. In our prescription (see Sect. 3) the γ-formalism is typically used in the first CE phase only. The reason for this is that in equal mass systems there is more angular momentum compared to unequal mass systems with similar orbits. Mennekens et al. (2010) and also Yungelson & Livio (2000); Ruiter et al. (2009) and Claeys et al. (2011) showed DD DTDs using the α-scenario (however their CE-prescriptions may differ slightly from Eq. (2)). Surprisingly, but as realised before, even though different groups used different binary evolution codes with different versions of the α-CE and CE efficiencies, the DTDs of the DD channel are very uniform in that they show a strong decline with time (see for example Nelemans et al. 2012, for an overview).
Usually in synthetic DTD studies, the shape and normalisation of the DTD are discussed separately. This might not be valid any more, as more and more observed rates are available and the conversion from observational units to synthetic units (e.g. the star formation history (SFH) and rate in per K-band luminosity instead of per M⊙ of created stars) is better understood. For example, the SFH is often convolved with the DTD to estimate the SNIa rate in spiral galaxies like our Milky Way. The problem with this is that different assumptions for the Galactic SFH can significantly alter the theoretical Galactic SNIa rate. Since the SNIa rate follows the SFH with typical delay times of a few Gyr, the synthetic Galactic SNIa rate is very sensitive to the assumed SFH at recent times. When a constant SFH (of ≳3 M⊙ yr-1) is assumed, the SNIa rate is artificially enhanced compared with detailed SFHs that show a peak in the star formation at a few Gyr and a decline to 1 M⊙ yr-1 at recent times, see e.g. Nelemans et al. (2004). In the observed SNIa rates of Maoz & Badenes (2010) and Maoz et al. (2011) the detailed SFH of every individual galaxy or galaxy subunit was taken into account to reconstruct the DTD. Therefore it is no longer necessary to convolve the theoretical SNIa rate from a burst of star formation with an approximate SFH. The theoretical calculations of the SNIa rate from a single starburst can directly be compared with observations.
We found that the normalisation of the DTD of model αα
and γα do not differ much, even though the CE evolution is very
different. The time-integrated number of SNIa in model αα
(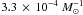 )
is 70% larger as in model γα (
)
is 70% larger as in model γα (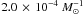 ).
But most importantly, the simulated time-integrated numbers do not match the observed number
of
).
But most importantly, the simulated time-integrated numbers do not match the observed number
of 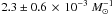 by (Maoz et al. 2011) by a factor of ~7−12. If
our understanding of binary evolution and initial parameter distributions is correct, the
standard DD channel is not a major contributor to the SNIa rate.
by (Maoz et al. 2011) by a factor of ~7−12. If
our understanding of binary evolution and initial parameter distributions is correct, the
standard DD channel is not a major contributor to the SNIa rate.
For the SNIa model proposed by Pakmor et al. (2010),
in which carbon burning is ignited in the merger process of two massive white dwarfs of
nearly equal mass, we found an SNIa rate of 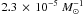 for model γα and
for model γα and 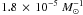 for model αα. Pakmor et al. (2010)
founds that these systems resemble subluminous SNIa such as SN 1991bg. Assuming the fraction
of 1991bg-like events to all SNIa events is 15 ± 6% (Li
et al. 2001, 2011), the observed event rate
is
for model αα. Pakmor et al. (2010)
founds that these systems resemble subluminous SNIa such as SN 1991bg. Assuming the fraction
of 1991bg-like events to all SNIa events is 15 ± 6% (Li
et al. 2001, 2011), the observed event rate
is 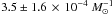 .
van Kerkwijk et al. (2010) proposed a model in
which sub-Chandrasekhar WDs can explode as an SNIa. In this scenario two white dwarfs of
nearly equal mass merge, though carbon ignition occurs only after the merger when the thick
disk surrounding the remnant is accreted onto it. The event rate
is
.
van Kerkwijk et al. (2010) proposed a model in
which sub-Chandrasekhar WDs can explode as an SNIa. In this scenario two white dwarfs of
nearly equal mass merge, though carbon ignition occurs only after the merger when the thick
disk surrounding the remnant is accreted onto it. The event rate
is 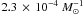 for model γα and
for model γα and 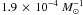 for model αα. When only taking into account systems with a combined mass
below 1.4 M⊙, the rates
are
for model αα. When only taking into account systems with a combined mass
below 1.4 M⊙, the rates
are 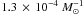 and
and 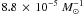 ,
respectively. In the scenario proposed by Pakmor et al.
(2010) and in the scenario by van Kerkwijk et al.
(2010), systems are required to have high mass ratios. We showed that the mass
ratio distribution of DWDs depends on the prescription for the CE. When
the γ-scenario is used, the average mass ratio of DWDs lies closer to
one, which increases the SNIa rate in the above described scenario with respect to
the α-scenario. The rates of the channel proposed by van Kerkwijk et al. (2010) for systems with
sub-Chandrasekhar masses are on the same order of magnitude as the rates of the standard DWD
channel. Therefore the combination of the two models is not sufficient to explain the
observed rates. For our synthetic rates of the DD scenario to match the observed SNIa rates,
within our current model of binary evolution, the parameter space of the DD progenitors has
to be increased severely, e.g. to include all CO-CO and CO-He mergers, which seems unlikely.
,
respectively. In the scenario proposed by Pakmor et al.
(2010) and in the scenario by van Kerkwijk et al.
(2010), systems are required to have high mass ratios. We showed that the mass
ratio distribution of DWDs depends on the prescription for the CE. When
the γ-scenario is used, the average mass ratio of DWDs lies closer to
one, which increases the SNIa rate in the above described scenario with respect to
the α-scenario. The rates of the channel proposed by van Kerkwijk et al. (2010) for systems with
sub-Chandrasekhar masses are on the same order of magnitude as the rates of the standard DWD
channel. Therefore the combination of the two models is not sufficient to explain the
observed rates. For our synthetic rates of the DD scenario to match the observed SNIa rates,
within our current model of binary evolution, the parameter space of the DD progenitors has
to be increased severely, e.g. to include all CO-CO and CO-He mergers, which seems unlikely.
Alternatively (and if contributions from channels other than the DD are minor), our model underpredicts the fraction of standard DD SNIa progenitors in the entire DWD population. Our model of the visible population of DWDs predicts 0.9−2.9% of the visible DWDs (depending on the model) to be SNIa progenitors. To match the observed rate of Maoz et al. (2011), 10−30% (excluding any errors on the observed and synthetic values) of the observed DWDs should lie in the SNIa progenitor region (upper left corner of Fig. 3). With 46 observed DWDs so far, 4−15 SNIa progenitors are expected without taking non-uniform selection effects into account. So far, only two systems have been found that possibly are SNIa progenitors, which makes it improbable, but not impossible, that our model underpredicts the number of DD SNIa progenitors. When the population of observed DWDs is increased, the fraction of SNIa progenitors amongst DWDs will give more insight into the validity of our knowledge of binary evolution of massive DWDs.
Concluding, although the shape of the DD DTD fits the observed DTD beautifully, the normalisation does not. An important point is that we did not optimise our model to fit the observed DTD in shape or number. We showed that the normalisation can be influenced by the metallicity; ~30−60% depending on the model for Z = 0.001 with respect to Z = 0.02. Furthermore, the normalisation depends on the initial mass function, the percentage of single stars, and the initial distribution of mass ratios and orbital periods. In this paper and in Nelemans et al. (2012) we assumed the percentage of single stars to be 50%. Results from e.g. Kouwenhoven et al. (2007) and Raghavan et al. (2010) showed that the binary fraction might be as high as 70% or more for A- and B-type stars, potentially raising the synthetic SNIa rate by a factor <2. Preliminary results show that the initial distribution of mass ratio and orbital separation affects the slope of the DTD, still the strong decline with time remains. Moreover, the integrated rates are not affected by factors sufficient to match the observed rate. Additional research is needed to study if the normalisation can be raised sufficiently to match the observed rate. If not, the main contribution to the SNIa rate comes from other channels, such as the SD scenario (e.g. supersoft sources), double detonating sub-Chandrasekhar accretors (see e.g. Kromer et al. 2010), or Kozai oscillations in triple systems (Shappee & Thompson 2012; Hamers et al. in prep.).
Online material
Appendix A: Most important changes to the population synthesis code SeBa
A.1. Treatment of wind mass-loss
Each star may lose mass in the form of a stellar wind. In a binary system the stellar wind matter from a binary component can be accreted by the companion star or lost from the system (see Appendix A.2). This influences the binary parameters via the loss of mass and angular momentum from the system. We assume that the matter that is lost from the system carries a specific angular momentum equal to that of the star from which it originates. Furthermore, we assume that wind accretion onto the binary companion is Bondi-Hoyle accretion (Bondi & Hoyle 1944), as re-formulated by Livio & Warner (1984). The wind mass loss prescriptions for different types of stars used in SeBa are updated e.g. to include metallicity dependency where possible. The prescriptions correspond to some degree to the recommendations by Hurley et al. (2000). If multiple mass loss predictions are applicable to a star, we take the one that predicts the maximum mass loss rate.
-
For all types of luminous stars (L > 4000 L⊙) from the main sequence (MS) to the asymptotic giant branch (AGB) we apply the empirical mass loss rate by Nieuwenhuijzen & de Jager (1990) given by
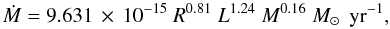 (A.1)where
Ṁ is the mass accretion rate, R the stellar
radius in R⊙, L the luminosity in
L⊙ and M the stellar mass
in M⊙. We assume that the formalism of Nieuwenhuijzen & de Jager (1990) is
dependent on the initial metallicity
as Ṁ(z) = (z/z⊙)1/2 Ṁ(z⊙)
(see Kudritzki et al. 1987).
(A.1)where
Ṁ is the mass accretion rate, R the stellar
radius in R⊙, L the luminosity in
L⊙ and M the stellar mass
in M⊙. We assume that the formalism of Nieuwenhuijzen & de Jager (1990) is
dependent on the initial metallicity
as Ṁ(z) = (z/z⊙)1/2 Ṁ(z⊙)
(see Kudritzki et al. 1987). -
For a massive MS star we give preference to the rates of Vink et al. (2000, 2001). Where they do not apply, the rates of Nieuwenhuijzen & de Jager (1990) are used. Massive MS suffer from strong winds driven by radiation pressure in lines and in the continuum. Vink et al. (2000, 2001) take into account multiple scattering effects of photons. They find good agreement between observations and theoretical mass-loss rates.
-
For stars in giant phases we adopt the empirical relation found by Reimers (1975),
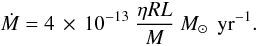 (A.2)We assume a
numerical prefactor of η = 0.5, see Maeder & Meynet (1989) and Hurley et al. (2000).
(A.2)We assume a
numerical prefactor of η = 0.5, see Maeder & Meynet (1989) and Hurley et al. (2000). -
AGB stars can experience severe mass-loss caused by radiation pressure on dust that condensates in the upper atmosphere of the stars. Empirically, the mass-loss rate has been coupled to the period of large-amplitude radial pulsations Ppuls (Vassiliadis & Wood 1993):
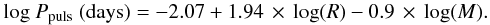 (A.3)We apply
mass-loss to the envelope according to the prescription of Vassiliadis & Wood (1993). During the superwind
phase the radiation pressure driven wind is modelled by
(A.3)We apply
mass-loss to the envelope according to the prescription of Vassiliadis & Wood (1993). During the superwind
phase the radiation pressure driven wind is modelled by 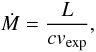 (A.4)where
c represents the speed of light
and vexp the stellar wind expansion velocity. The
latter is given by:
(A.4)where
c represents the speed of light
and vexp the stellar wind expansion velocity. The
latter is given by: 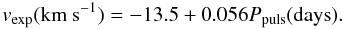 (A.5)Furthermore,
vexp is constrained to the
range 3.0–15.0 km s-1. Before the superwind phase, the mass loss
rate increases exponentially with Ppuls as
(A.5)Furthermore,
vexp is constrained to the
range 3.0–15.0 km s-1. Before the superwind phase, the mass loss
rate increases exponentially with Ppuls as
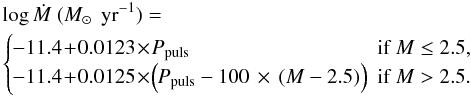 (A.6)The
mass loss rate of Vassiliadis & Wood
(1993) is given by the minimum of Eqs. (A.4) and (A.6).
(A.6)The
mass loss rate of Vassiliadis & Wood
(1993) is given by the minimum of Eqs. (A.4) and (A.6). -
Luminous blue variables (LBVs) are extremely massive and luminous stars near the Humphreys-Davidson limit (Humphreys & Davidson 1994) with enormous mass-loss rates. We use the LBV mass loss prescription and implementation suggested by Hurley et al. (2000):
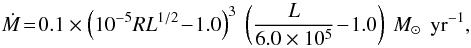 (A.7)if
L > 6.0 × 105 L⊙
and 10-5RL1/2 > 1.0.
(A.7)if
L > 6.0 × 105 L⊙
and 10-5RL1/2 > 1.0.
-
Wolf-Rayet stars are stars in a stage of evolution following the LBV phase where weak or no hydrogen lines are observed in their spectra. Like Hurley et al. (2000) we include a Wolf-Rayet-like mass-loss for stars with a small hydrogen-envelope mass (μ < 1.0 from their Eq. (97)). The prescription itself, however, is different. We model it according to Nelemans & van den Heuvel (2001):
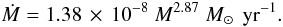 (A.8)This is a fit
to observed mass-loss rates from Nugis &
Lamers (2000). We multiply with a factor (1 − μ) to
smoothly switch on mass loss.
(A.8)This is a fit
to observed mass-loss rates from Nugis &
Lamers (2000). We multiply with a factor (1 − μ) to
smoothly switch on mass loss. -
In addition to the evolution of ordinary hydrogen rich stars, the evolution of helium burning stars with hydrogen poor envelopes is simulated as well. For helium main-sequence stars with a mass M > 2.5 M⊙ we assume the same relation as for Wolf-Rayet-like stars. For helium giants, either on the equivalent of the Hertzsprung or giant branch, we describe mass loss in a very general way similar to Nelemans et al. (2001b). We presume 30% of the mass of the envelope Menv will be lost during the naked helium giant phase with a rate that increases in time according to
![\appendix \setcounter{section}{1} \begin{equation} \Delta M_{\rm wind} = 0.3 M_{\rm env} \left[ \left(\frac{t+\Delta t}{t_{\rm f}}\right)^{6.8}-\left(\frac{t}{t_{\rm f}}\right) ^{6.8}\right], \label{eq:Mwindheg} \end{equation}](/articles/aa/full_html/2012/10/aa18966-12/aa18966-12-eq133.png) (A.9)where
ΔMwind is the amount of mass lost in the wind in
M⊙ in a timestep Δt,
tf is the duration of the helium giant phase
and t the time since the beginning of the phase.
(A.9)where
ΔMwind is the amount of mass lost in the wind in
M⊙ in a timestep Δt,
tf is the duration of the helium giant phase
and t the time since the beginning of the phase.
A.2. Accretion onto stellar objects
Roche lobe overflow mass transfer and subsequent accretion can substantially alter the stars and the binary orbit. Mass accretion can affect the structure of the receiver star and its subsequent evolution. When more mass is transferred than the accretor can accrete, we assume that the non-accreted matter leaves the system with an angular momentum of 2.5 times the specific angular momentum of the binary (Portegies Zwart & Verbunt 1996; Nelemans et al. 2001b). For compact accretors we assume the matter leaves the system with the specific angular momentum of the compact remnant. In this section we discuss the limiting accretion rate, the response of the accretor to regain equilibrium, and the subsequent evolution of the new object for different types of accretors.
A.2.1. Accretion onto ordinary stars
For ordinary stars from MS to AGB stars, we distinguish between two types of accretion; accretion from a hydrogen-rich or a helium-rich envelope. Hydrogen-rich accretion can occur for example when a donor star ascends the giant branch and fills its Roche lobe. After it loses its hydrogen envelope, it can become a helium-burning core. When this helium star ascends the helium equivalent of the giant branch, a fraction of the helium-rich envelope can be transferred onto the accretor. We name this type of accretion “helium accretion”. We assume that the accreted helium settles and sinks to the core instantaneously. The helium accretion rate is limited by the Eddington limit. Hydrogen is accreted onto the envelope of the receiver star. The accretion rate is bounded by the star’s thermal timescale times a factor that is dependent of the ratio of Roche lobe radius of the receivers to its effective radius, as described by Portegies Zwart & Verbunt (1996). The formalism is proposed by Pols & Marinus (1994), which is based on Kippenhahn & Meyer-Hofmeister (1977); Neo et al. (1977) and Packet & De Greve (1979). If the mass transfer rate is higher than the maximum mass accretion rate, the excess material is assumed to leave the binary system.
Because of the accretion, the star falls temporarily out of thermal equilibrium. While regaining equilibrium, the gas envelope surrounding the core puffs outward. Because we do not solve the equations of stellar structure and the stellar evolution tracks describe single stars in equilibrium, we add a procedure to account for a temporal increase in radius as in Portegies Zwart & Verbunt (1996). This is important for example to determine if an accretor star fills its Roche lobe. It also affects the magnetic braking process and the Darwin-Riemann instability through the increased stellar angular momentum. Note that the mass transfer rate is not dependent on the stellar radius in our simulations, so that the binary evolution is not critically dependent on out-of-equilibrium parameter values.
Accretion can also affect the structure of the receiver star and its subsequent evolution. It is modelled by changing the stellar track and moving along the track. The former is described by the track mass, which is equivalent to the zero-age main-sequence mass that the star would have had without interaction. The latter is described by the relative age trel of the star. We distinguish two cases:
-
Rejuvenation of an MS star. Accretion onto an MS star rejuvenates the star. The star evolves similarly to a younger star of its new mass and its MS lifetime can be extended. It would show up in a Hertzsprung-Russell diagram as a bluestraggler. For hydrogen accretion the track mass is always updated and the renewed relative age of the star
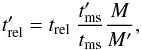 (A.10)where primes
denote quantities after a small amount of mass accretion,
tms the main-sequence lifetime,
and M the mass of the star. For helium accretion we assume
the mass accretes to the core instantaneously and the track mass is increased
accordingly. These stars appear older than for hydrogen accretion because more
hydrogen has been burned previously. The rejuvenation process is described by
(A.10)where primes
denote quantities after a small amount of mass accretion,
tms the main-sequence lifetime,
and M the mass of the star. For helium accretion we assume
the mass accretes to the core instantaneously and the track mass is increased
accordingly. These stars appear older than for hydrogen accretion because more
hydrogen has been burned previously. The rejuvenation process is described by
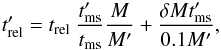 (A.11)where we
assume 10% of the mass of the star will be burned during the MS phase.
(A.11)where we
assume 10% of the mass of the star will be burned during the MS phase. -
Rejuvenation of a giant. During the giant phases the envelope is discoupled from the core in terms of stellar structure. The evolution of the star will therefore not be influenced directly by small amounts of hydrogen accretion to the envelope. The track is only updated when the new mass is larger than the track mass to account for severe hydrogen accretion. The mass before accretion can be much lower than the track mass because of wind mass loss, which can be strong for giants. For helium accretion to the core, the track is always updated. An exception to this is the early AGB where the helium core does not grow. In this stage there is a one-to-one relation between the helium core mass and the track mass (Eq. (66) in Hurley et al. 2000). When a giant accretor star moves to a new evolutionary track, we need to determine the location of the star along this track. In a more physical picture this means determining the relative age of the star trel. For a giant its evolution is mainly determined by its core. Therefore for a given evolutionary track and core mass, the relative age is effectively constrained. For both types of accretion, we insist that the star stays in its same evolutionary state after its mass increase. When no solution can be found for trel, the relative age is set to the beginning or end of the current evolutionary state and the track mass is varied to find a fitting track that ensures mass conservation.
A.2.2. Accretion onto helium-burning cores
For accretion onto helium-burning stars that have lost their hydrogen envelopes, accretion is limited by the Eddington limit. Helium accretion onto a helium main-sequence star is similar as hydrogen accretion onto normal main-sequences stars. We assume that the star evolves similarly to a younger star of its new mass according to Eq. (A.10) where tms should be replaced by the helium main-sequence life time. We assume that for helium giants the envelope is discoupled from the core in terms of stellar structure, as with hydrogen-rich giants. Therefore we assume that the evolution of the giant is not affected and only update the track when the new mass is larger than the track mass.
The effect of hydrogen accretion onto helium stars is more complicated. If the hydrogen layer is sufficiently thick, the layer can ignite. This can significantly increase the radius of the star and essentially turn it into a born-again star on the horizontal or asymptotic giant branch. We studied the effect of hydrogenaccretion to helium stars with stellar models simulated by the stellar evolution code STARS. This code models stellar structure and evolution in detail by solving the stellar structure equations. The code is based on Eggleton (1971) and includes updated input physics as described in Hu et al. (2010). The models do not include atomic diffusion. For mass accretion rates at ten percent of the Eddington rate of the accretor for ~104−105 yr, the accreted hydrogen layer ignites. Helium stars that are more massive than ~0.55 M⊙ resemble horizontal branch stars after accretion, but most of the luminosity still comes from helium burning. For lower mass helium stars this is not the case, because the corresponding horizontal branch stars (<3.5 M⊙) can have ignited helium in a degenerate core, which strongly affects the characteristics of the star. For both mass ranges, the accretor expands by a factor ~10−100 compared to the original helium star. Because hydrogen accretion to helium stars is not very likely, we model this very simply. When more than 5% of the total mass is accreted, the radius of the star is increased by a factor 50. With few exceptions, this leads to a merger of the two components.
The effect of hydrogen accretion to helium giants is not known very well and additional research is necessary. For now, because it is very unlikely to happen, we treat it in the same way as helium accretion onto the envelope of the giant.
A.2.3. Accretion onto remnants
White dwarf, neutron star and black hole accretors can accrete with a maximum rate of the Eddington limit. If more mass is transferred, the surplus material leaves the system with the specific angular momentum of the compact remnant. For neutron stars and black holes we assume that the transferred mass is temporarily stored in a disk. From this disk, mass will flow onto the surface of the remnant with ten percent of the Eddington limit. We assume that a neutron star collapses onto a black hole when its mass exceeds 1.5 M⊙.
For white dwarfs, the accretion process is more complicated because of possible thermonuclear runaways in the accreted material on the surface of the white dwarf. In SeBa there are several options to model the effectiveness of the white dwarf to retain the transferred material. For hydrogen accretion we can choose between the efficiencies of Hachisu et al. (2008) and Prialnik & Kovetz (1995). For helium retention, the option is between Kato & Hachisu (1999) (with updates from Hachisu et al. 1999) and Iben & Tutukov (1996).
A.3. Stability of mass transfer
A semi-detached system can become unstable in two ways. In a mass transfer instability, the Roche-lobe-filling star expands faster than the Roche lobe itself on the relevant timescale. In the other case tidal interactions lead to an instability (Darwin 1879).
A.3.1. Tidal instability
A tidal instability can take place in systems of extreme mass ratios. When there is
insufficient orbital angular momentum Jb that can be
transferred onto the mass-losing star, the star cannot stay in synchronous rotation.
Tidal forces will cause the companion to spiral into the envelope of the donor star.
The tidal instability occurs when the angular momentum of the
star  , where
, where
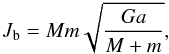 (A.12)where
Jb is the orbital angular momentum of the circularised
binary, a is the orbital separation, M the mass of
the donor star and m the mass of the accretor star. The angular
momentum J ⋆ of a star with
radius R is given by
(A.12)where
Jb is the orbital angular momentum of the circularised
binary, a is the orbital separation, M the mass of
the donor star and m the mass of the accretor star. The angular
momentum J ⋆ of a star with
radius R is given by 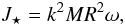 (A.13)where
k2 is the gyration radius described by Nelemans et al. (2001b) and ω is
the angular velocity of the donor star, which is assumed to be synchronised with the
orbit. It is given
by ω = 2π/Pb,
where Pb is the orbital period. We model the inspiral
according to the standard α-CE (see Sect. 3). Owing to the expulsion of the envelope, the binary may evolve
to a more stable configuration or merge. If the mass-losing star is a main-sequence
star, we assume that the instability always leads to a merger.
(A.13)where
k2 is the gyration radius described by Nelemans et al. (2001b) and ω is
the angular velocity of the donor star, which is assumed to be synchronised with the
orbit. It is given
by ω = 2π/Pb,
where Pb is the orbital period. We model the inspiral
according to the standard α-CE (see Sect. 3). Owing to the expulsion of the envelope, the binary may evolve
to a more stable configuration or merge. If the mass-losing star is a main-sequence
star, we assume that the instability always leads to a merger.
A.3.2. Mass transfer instability
The stability of mass transfer from Roche lobe overflow and its consequences on the
binary depend on the response of the radius and the Roche lobe of the donor star to
the imposed mass loss (e.g. Webbink 1985;
Hjellming & Webbink 1987, hereafter
HW87, Pols & Marinus 1994; Soberman et al. 1997). We distinguish four modes
of mass transfer; on the dynamical, thermal, nuclear timescale of the donor or on
the angular-momentum-loss timescale. The response of the accretor star to the mass
that is transferred onto it and the effect of this on the orbit is described in
Appendix A.2. The response of the donor star
to mass loss is to readjust its structure to recover hydrostatic and thermal
equilibrium. The dynamical timescale to recover hydrostatic equilibrium is short
compared to the thermal timescale. For mass transfer to be dynamically stable, the
dynamical timescale of the star is important. The change in radius due to adiabatic
adjustment of hydrostatic equilibrium is expressed as a logarithmic derivative of
the radius with respect of mass,
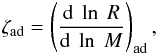 (A.14)where
M and R are the mass and radius of the donor
star. The assumed values of ζad are shown in Table A.1.
(A.14)where
M and R are the mass and radius of the donor
star. The assumed values of ζad are shown in Table A.1.
The response of the Roche lobe RL of the donor star is
expressed as the logarithmic derivative of the Roche lobe radius with respect to
mass: 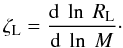 (A.15)The value of
ζL is calculated numerically by transferring a test
mass of 10-5M⊙.
Because ζL = ζL(M1,M2,a),
ζL is dependent on the mass accretion efficiency of
the secondary, and therefore on the mass accretion rate of the test mass. For
instance, for high mass ratios q ≫ 1 the loss of some mass and
corresponding angular momentum can have a stabilising effect on the
mass-transferring binary. To determine the dynamical stability of mass transfer, we
assume that the mass transfer rate of the test mass is on the thermal timescale of
the donor star:
(A.15)The value of
ζL is calculated numerically by transferring a test
mass of 10-5M⊙.
Because ζL = ζL(M1,M2,a),
ζL is dependent on the mass accretion efficiency of
the secondary, and therefore on the mass accretion rate of the test mass. For
instance, for high mass ratios q ≫ 1 the loss of some mass and
corresponding angular momentum can have a stabilising effect on the
mass-transferring binary. To determine the dynamical stability of mass transfer, we
assume that the mass transfer rate of the test mass is on the thermal timescale of
the donor star: 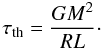 (A.16)
(A.16)
-
When ζL > ζad, mass transfer is dynamically unstable. We model this as a CE phase, as described in Sect. 32.
Table A.1Values of the adiabatic ζad and thermal ζeq response of the radius to mass loss for different types of stars.
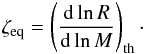 (A.18)The assumed
values for ζeq are described in Table A.1.
(A.18)The assumed
values for ζeq are described in Table A.1.
To calculate the response of the Roche
lobe ζL,eq, we assume that the mass
transfer rate of the test mass is on the nuclear evolution timescale:
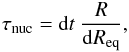 (A.19)where
R represents the equilibrium radius of the star according to the
single-star tracks. dReq is the change
in R in a short timestep dt without binary
interactions.
(A.19)where
R represents the equilibrium radius of the star according to the
single-star tracks. dReq is the change
in R in a short timestep dt without binary
interactions.
-
2.
When ζL,eq < min(ζeq,ζad) mass transfer is driven by the expansion of the stellar radius due to its internal evolution.
-
3.
When ζL,eq > min(ζeq,ζad), the mass transfer is thermally unstable and proceeds on the thermal time scale of the donor.
-
4.
The previous modes of mass transfer are caused by an expanding donor star. The final mode is caused by shrinking of the orbit caused by angular momentum loss. We assume that this mode takes place when the corresponding timescale τJ is shorter than the timescales at which the other three modes of mass transfer take place. Angular momentum loss can happen due to gravitational wave radiation
 (Kraft et al. 1962) and magnetic
braking
(Kraft et al. 1962) and magnetic
braking 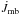 (Schatzman 1962; Huang 1966; Skumanich 1972; Verbunt
& Zwaan 1981). Mass transfer proceeds on the time scale on
which these processes occur:
(Schatzman 1962; Huang 1966; Skumanich 1972; Verbunt
& Zwaan 1981). Mass transfer proceeds on the time scale on
which these processes occur:
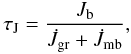 (A.20)where
Jb is the angular momentum of the circularized
binary given by Eq. (A.12).
Next we discuss the assumptions and implications
of
(A.20)where
Jb is the angular momentum of the circularized
binary given by Eq. (A.12).
Next we discuss the assumptions and implications
of 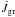 and
and 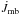 .
Gravitational wave radiation most strongly influences close binaries since it
is a strong function of orbital separation. The change in orbital
separation ȧ averaged over a full orbit is given by (Peters 1964)
.
Gravitational wave radiation most strongly influences close binaries since it
is a strong function of orbital separation. The change in orbital
separation ȧ averaged over a full orbit is given by (Peters 1964)
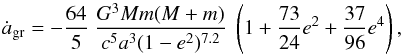 (A.21)where
(A.21)where
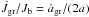 .
Magnetic braking mostly affects low-mass stars within the mass range
of 0.6 ≲ M/M⊙ ≲ 1.5.
These stars suffer from winds that are magnetically coupled to the star.
Although the mass loss in this process is negligible, the associated angular
momentum loss can be severe (Rappaport et al.
1983):
.
Magnetic braking mostly affects low-mass stars within the mass range
of 0.6 ≲ M/M⊙ ≲ 1.5.
These stars suffer from winds that are magnetically coupled to the star.
Although the mass loss in this process is negligible, the associated angular
momentum loss can be severe (Rappaport et al.
1983):
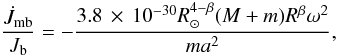 (A.22)where
β is a parameter that represents the dependence of the
braking on the radius of the donor star. We take β = 2.5.
(A.22)where
β is a parameter that represents the dependence of the
braking on the radius of the donor star. We take β = 2.5.
This track is a close analogy of the track proposed by Sipior et al. (2004) regarding recycled pulsars. In the scenario proposed by these authors the end states of the two components are reversed, resulting in a neutron star that forms prior to a black hole. However, in our scenario the name “formation reversal” applies to the evolutionary timescales of the primary and secondary. Although the primary first evolves off the main sequence, the secondary becomes a remnant first.
When the timescale of the CE phase becomes relevant, we assume that it proceeds on a
time scale τ given by the geometric mean of the
thermal τth and dynamical τd
timescales of the donor (see Paczyiński &
Sienkiewicz 1972): 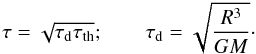 (A.17)
(A.17)
Acknowledgments
We thank Haili Hu, Marc van der Sluys and Lev Yungelson for providing results from their detailed stellar and binary evolution models. We also thank Dan Maoz for providing us his data of the observed SNIa rate and Frank Verbunt for his software to make the Roche lobe plots. This work was supported by the Netherlands Research Council NWO (grants VIDI [# 639.042.813], VICI [# 639.073.803], AMUSE [# 614.061.608] and Little Green Machine) and by the Netherlands Research School for Astronomy (NOVA).
References
- Abt, H. A. 1983, ARA&A, 21, 343 [Google Scholar]
- Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2012a, GW Notes, submitted [arXiv:1201.3621] [Google Scholar]
- Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2012b, Class. Quant. Grav., 29, 124016 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Kilic, M., Allen de Prieto, C., & Kenyon, S. J. 2010, ApJ, 723, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Kilic, M., Hermes, J. J., et al. 2011, ApJ, 737, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellaro, E., & Turatto, M. 2001, in The Influence of Binaries on Stellar Population Studies, ed. D. Vanbeveren (Dordrecht: Kluwer Academic Publishers), ASSL, 264, 199 [Google Scholar]
- Claeys, J. S. W., Pols, O. R., Vink, J., & Izzard, R. G. 2011 [arXiv:1101.5601] [Google Scholar]
- Darwin, G. 1879, Phil. Trans. Roy. Soc., 170, 447 [Google Scholar]
- Di Stefano, R. 2010, ApJ, 712, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
- Eggleton, P. P., Fitchett, M. J., & Tout, C. A. 1989, ApJ, 347, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. R., Iben, Jr., I., & Smarr, L. 1987, ApJ, 323, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., Ruiter, A. J., Belczynski, K., et al. 2010, ApJ, 725, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Geier, S., Nesslinger, S., Heber, U., et al. 2007, A&A, 464, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilfanov, M., & Bogdán, Á. 2010, Nature, 463, 924 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Glebbeek, E., Pols, O. R., & Hurley, J. R. 2008, A&A, 488, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hachisu, I., Kato, M., Nomoto, K., & Umeda, H. 1999, ApJ, 519, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 2008, ApJ, 679, 1390 [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 2010, ApJ, 724, L212 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, P. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S. 1999, ApJ, 520, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A. 2001, ApJ, 554, L193 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, H., Glebbeek, E., Thoul, A. A., et al. 2010, A&A, 511, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huang, S.-S. 1966, Ann. Astrophys., 29, 331 [NASA ADS] [Google Scholar]
- Humphreys, R. M., & Davidson, K. 1994, PASP, 106, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1985, ApJS, 58, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1996, ApJS, 105, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 1999, ApJ, 513, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Brown, W. R., Allen de Prieto, C., et al. 2011a, ApJ, 727, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Brown, W. R., Hermes, J. J., et al. 2011b, MNRAS, 418, L157 [NASA ADS] [Google Scholar]
- Kilic, M., Brown, W. R., Kenyon, S. J., et al. 2011c, MNRAS, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Meyer-Hofmeister, E. 1977, A&A, 54, 539 [NASA ADS] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraft, R. P., Mathews, J., & Greenstein, J. L. 1962, ApJ, 136, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Kromer, M., Sim, S. A., Fink, M., et al. 2010, ApJ, 719, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R. P., Pauldrach, A., & Puls, J. 1987, A&A, 173, 293 [NASA ADS] [Google Scholar]
- Kulkarni, S. R., & van Kerkwijk, M. H. 2010, ApJ, 719, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Filippenko, A. V., Treffers, R. R., et al. 2001, ApJ, 546, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Leaman, J., Chornock, R., et al. 2011, MNRAS, 412, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Warner, B. 1984, The Observatory, 104, 152 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 1989, A&A, 210, 155 [NASA ADS] [Google Scholar]
- Maoz, D., & Badenes, C. 2010, MNRAS, 407, 1314 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Mannucci, F. 2012, PASA, 29, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Sharon, K., & Gal-Yam, A. 2010, ApJ, 722, 1879 [Google Scholar]
- Maoz, D., Mannucci, F., Li, W., et al. 2011, MNRAS, 412, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R. 2011, Class. Quant. Grav., 28, 094019 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R., Gänsicke, B. T., Steeghs, D., et al. 2011, ApJ, 736, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Marsh, T. R., & North, R. C. 2000, MNRAS, 317, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Mennekens, N., Vanbeveren, D., De Greve, J. P., & De Donder, E. 2010, A&A, 515, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napiwotzki, R., Tovmassian, G., Richer, M. G., et al. 2005, in Planetary Nebulae as Astronomical Tools, eds. R. Szczerba, G. Stasińska, & S. K. Gorny, AIP Conf. Ser., 804, 173 [Google Scholar]
- Nelemans, G., & van den Heuvel, E. P. J. 2001, A&A, 376, 950 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelemans, G., Verbunt, F., Yungelson, L. R., & Portegies Zwart, S. F. 2000, A&A, 360, 1011 [NASA ADS] [Google Scholar]
- Nelemans, G., Yungelson, L. R., & Portegies Zwart, S. F. 2001a, A&A, 375, 890 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001b, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelemans, G., Yungelson, L. R., & Portegies Zwart, S. F. 2004, MNRAS, 349, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Toonen, S., & Bours, M. 2012 [arXiv:1204.2960] [Google Scholar]
- Neo, S., Miyaji, S., Nomoto, K., & Sugimoto, D. 1977, PASJ, 29, 249 [NASA ADS] [Google Scholar]
- Nielsen, M., Nelemans, G., & Voss, R. 2010, in AIP Conf. Ser., 1273, eds. K. Werner, & T. Rauch, 279 [Google Scholar]
- Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
- Nomoto, K. 1982, ApJ, 257, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., & Iben, Jr., I. 1985, ApJ, 297, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
- Packet, W., & De Greve, J. P. 1979, A&A, 75, 255 [NASA ADS] [Google Scholar]
- Paczyiński, B., & Sienkiewicz, R. 1972, Acta Astron., 22, 73 [NASA ADS] [Google Scholar]
- Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan (Dordrecht: Kluwer), IAU Symp., 73, 75 [Google Scholar]
- Pakmor, R., Kromer, M., Röpke, F. K., et al. 2010, Nature, 463, 61 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., et al. 2012, ApJ, 747, L10 [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Gagliardi, S., Iben, Jr., I., & Tornambé, A. 2003, ApJ, 598, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., & Marinus, M. 1994, A&A, 288, 475 [NASA ADS] [Google Scholar]
- Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., & Verbunt, F. 1996, A&A, 309, 179 [NASA ADS] [Google Scholar]
- Portegies Zwart, S. F., & Yungelson, L. R. 1998, A&A, 332, 173 [NASA ADS] [Google Scholar]
- Prialnik, D., & Kovetz, A. 1995, ApJ, 445, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rappaport, S., Verbunt, F., & Joss, P. C. 1983, ApJ, 275, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1975, Mem. Soc. Roy. Sci. Liège, 8, 369 [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Gil, P., Santander-García, M., Knigge, C., et al. 2010, MNRAS, 407, L21 [NASA ADS] [Google Scholar]
- Roelofs, G., Bassa, C., Voss, R., & Nelemans, G. 2008, MNRAS, 391, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Belczynski, K., & Fryer, C. 2009, ApJ, 699, 2026 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Nomoto, K. 1985, A&A, 150, L21 [NASA ADS] [Google Scholar]
- Schatzman, E. 1962, Ann. Astrophys., 25, 18 [Google Scholar]
- Shappee, B. J., & Thompson, T. A. 2012, ApJ, submitted [arXiv:1204.1053] [Google Scholar]
- Shen, K. J., Bildsten, L., Kasen, D., & Quataert, E. 2012, ApJ, 748, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Sim, S. A., Röpke, F. K., Hillebrandt, W., et al. 2010, ApJ, 714, L52 [Google Scholar]
- Sipior, M. S., Portegies Zwart, S., & Nelemans, G. 2004, MNRAS, 354, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620 [NASA ADS] [Google Scholar]
- Totani, T., Morokuma, T., Oda, T., Doi, M., & Yasuda, N. 2008, PASJ, 60, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Tout, C. A., Aarseth, S. J., Pols, O. R., & Eggleton, P. P. 1997, MNRAS, 291, 732 [NASA ADS] [Google Scholar]
- Tovmassian, G., Yungelson, L., Rauch, T., et al. 2010, ApJ, 714, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Tovmassian, G. H., Napiwotzki, R., Richer, M. G., et al. 2004, ApJ, 616, 485 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S., & Tammann, G. A. 1991, ARA&A, 29, 363 [NASA ADS] [CrossRef] [Google Scholar]
- van Kerkwijk, M. H., Chang, P., & Justham, S. 2010, ApJ, 722, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voss, R., & Nelemans, G. 2008, Nature, 451, 802 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wang, B., Chen, X., Meng, X., & Han, Z. 2009, ApJ, 701, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1985, Stellar evolution and binaries, eds. J. E. Pringle, & R. A. Wade, 39 [Google Scholar]
- Webbink, R. F. 2008, in ASSL 352, eds. E. F. Milone, D. A. Leahy, & D. W. Hobill (Berlin: Springer), 233 [Google Scholar]
- Whelan, J., & Iben, Jr., I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. E., Ivanova, N., van der Sluys, M., & Chaichenets, S. 2010, in AIP Conf. Ser. 1314, eds. V. Kologera, & M. van der Sluys, 24 [Google Scholar]
- Woods, T. E., Ivanova, N., van der Sluys, M., & Chaichenets, S. 2012, ApJ, 744, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Yakut, K., & Eggleton, P. P. 2005, ApJ, 629, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., Podsiadlowski, P., & Rosswog, S. 2007, MNRAS, 380, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Yungelson, L. R., & Livio, M. 2000, ApJ, 528, 108 [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Distributions of the initial binary parameter mass, mass ratio, orbital separation and eccentricity.
Values of the adiabatic ζad and thermal ζeq response of the radius to mass loss for different types of stars.
All Figures
 |
Fig. 1 Simulated population of visible double white dwarfs as a function of orbital period and mass of the brighter white dwarf. Left: the stellar evolution tracks according to EFT are used; right: HPT (using model γα, see Sect. 3). The intensity of the grey scale corresponds to the density of objects on a linear scale. The same grey scale is used for both plots. Observed binary white dwarfs are overplotted with filled circles. Thick points taken are from Marsh et al. (2011), thinner points from Tovmassian et al. (2004); Napiwotzki et al. (2005); Kulkarni & van Kerkwijk (2010); Brown et al. (2010, 2011); Marsh et al. (2011); Kilic et al. (2011a,c,b), see Sect. 2.1 for a discussion. |
| In the text | |
 |
Fig. 2 Simulated population of visible double white dwarfs as a function of orbital period and mass ratio, where mass ratio is defined as the mass of the brighter white dwarf divided by that of the dimmer white dwarf. In the left model γα is used, in the right model αα. The intensity of the grey scale corresponds to the density of objects on a linear scale. The same grey scale is used for both plots. Observed binary white dwarfs are overplotted with filled circles, see Fig. 1 for references. |
| In the text | |
 |
Fig. 3 Simulated population of visible double white dwarfs as a function of orbital period and the combined mass of the two dwarfs. On the left the common envelope is parametrised according to model γα, on the right according to model αα (see Sect. 3). The intensity of the grey scale corresponds to the density of objects on a linear scale. The same grey scale is used for both plots. Observed binary white dwarfs are overplotted with filled circles, see Fig. 1 for references. The Chandrasekhar mass limit is indicated with the dotted line. The dashed line roughly demarks the region in which systems merge within a Hubble time. Systems located to the left of the dashed line and above the dotted line are supernova type Ia progenitors in the standard picture. |
| In the text | |
 |
Fig. 4 Evolutionary track for the merger of two carbon/oxygen white dwarfs of a combined mass that exceeds the Chandrasekhar mass. In this scenario the first phase of mass transfer is dynamically unstable which results in a common envelope. In this figure we show a representative example of model γα, see Sect. 3. ZAMS stands for zero age main sequence and CE for common envelope. G is a giant star, MS a main-sequence star, He MS a helium MS and WD a white dwarf. |
| In the text | |
 |
Fig. 5 Two evolutionary tracks for the merger of two carbon/oxygen white dwarfs of a combined mass exceeding the Chandrasekhar mass. In these scenarios the first phase of mass transfer is dynamically stable. On the left an example of the stable mass transfer channel is shown, on the right the formation reversal channel. In the latter scenario the first phase of mass transfer is dynamically stable which results in a low-mass helium-star with a long lifetime. The initially less massive star becomes the first formed white dwarf. The top and bottom parts of the figure have different scales due to a common envelope phase, denoted as CE in the figure. Abbreviations are as in Fig. 4. Additionally sRLOF stands for stable Roche lobe overflow, HG is a Hertzsprung-gap star and He G a helium giant. |
| In the text | |
 |
Fig. 6 Merger rate of double carbon/oxygen white dwarfs with a total mass above the Chandrasekhar mass as a function of delay time. Rates are in yr-1 per 1010 M⊙ formed stellar mass of the parent galaxy. Solar metallicity (Z = 0.02) is assumed. Delay times are shown for two different prescriptions of the CE phase. In black we plot model γα and in grey model αα, see Sect. 3. Overplotted with black circles are the observed values of the SNIa rate of Totani et al. (2008), Maoz et al. (2010), Maoz & Badenes (2010) and Maoz et al. (2011; for a review Maoz & Mannucci 2012). For comparison the grey circles show the observations scaled down by a factor 10. |
| In the text | |
 |
Fig. 7 Merger rate of double carbon/oxygen white dwarfs with a total mass above the Chandrasekhar mass as a function of delay time for a metallicity of 0.001. Rates are in yr-1 per 1010 M⊙ per formed stellar mass of the parent galaxy. Delay times are shown for two different prescriptions of the CE phase. In black model we plot γα and in grey model αα, see Sect. 3. |
| In the text | |
 |
Fig. 8 Simulated distribution of the population of merging double CO white dwarfs from a single burst of star formation as a function of delay time and total mass of the system. On the left model γα is used for the common envelope parametrisation, on the right model αα (see Sect. 3). The intensity of the grey scale corresponds to the density of objects on a linear scale in units of number of systems per 105 M⊙. The black line corresponds to a combined mass of 1.4 M⊙. |
| In the text | |
 |
Fig. 9 Simulated population of merging double CO white dwarfs from a single burst of star formation as a function of the masses of the two white dwarfs. Mmassive is the mass of the most massive white dwarf, Mnon−massive corresponds to the least massive white dwarf. On the left model γα is used for the common envelope parametrisation, on the right model αα (see Sect. 3). The intensity of the grey scale corresponds to the density of objects on a linear scale in units of number of systems per 105 M⊙. To increase the contrast, we placed an upper limit on the intensity, which effects only one bin for model γα and two bins for model αα. The black solid line corresponds to a combined mass of 1.4 M⊙. The dashed and dashed-dotted line correspond to a mass ratio q = m/M of 1 and 0.8, respectively. The mass ratio distribution, which is important e.g. in the scenarios proposed by Pakmor et al. (2010) and van Kerkwijk et al. (2010) are very different for model γα and αα. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


