| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201218966 | |
| Published online | 08 October 2012 | |
Online material
Appendix A: Most important changes to the population synthesis code SeBa
A.1. Treatment of wind mass-loss
Each star may lose mass in the form of a stellar wind. In a binary system the stellar wind matter from a binary component can be accreted by the companion star or lost from the system (see Appendix A.2). This influences the binary parameters via the loss of mass and angular momentum from the system. We assume that the matter that is lost from the system carries a specific angular momentum equal to that of the star from which it originates. Furthermore, we assume that wind accretion onto the binary companion is Bondi-Hoyle accretion (Bondi & Hoyle 1944), as re-formulated by Livio & Warner (1984). The wind mass loss prescriptions for different types of stars used in SeBa are updated e.g. to include metallicity dependency where possible. The prescriptions correspond to some degree to the recommendations by Hurley et al. (2000). If multiple mass loss predictions are applicable to a star, we take the one that predicts the maximum mass loss rate.
-
For all types of luminous stars (L > 4000 L⊙) from the main sequence (MS) to the asymptotic giant branch (AGB) we apply the empirical mass loss rate by Nieuwenhuijzen & de Jager (1990) given by
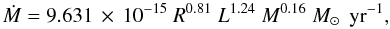 (A.1)where
Ṁ is the mass accretion rate, R the stellar
radius in R⊙, L the luminosity in
L⊙ and M the stellar mass
in M⊙. We assume that the formalism of Nieuwenhuijzen & de Jager (1990) is
dependent on the initial metallicity
as Ṁ(z) = (z/z⊙)1/2 Ṁ(z⊙)
(see Kudritzki et al. 1987).
(A.1)where
Ṁ is the mass accretion rate, R the stellar
radius in R⊙, L the luminosity in
L⊙ and M the stellar mass
in M⊙. We assume that the formalism of Nieuwenhuijzen & de Jager (1990) is
dependent on the initial metallicity
as Ṁ(z) = (z/z⊙)1/2 Ṁ(z⊙)
(see Kudritzki et al. 1987). -
For a massive MS star we give preference to the rates of Vink et al. (2000, 2001). Where they do not apply, the rates of Nieuwenhuijzen & de Jager (1990) are used. Massive MS suffer from strong winds driven by radiation pressure in lines and in the continuum. Vink et al. (2000, 2001) take into account multiple scattering effects of photons. They find good agreement between observations and theoretical mass-loss rates.
-
For stars in giant phases we adopt the empirical relation found by Reimers (1975),
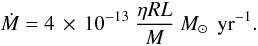 (A.2)We assume a
numerical prefactor of η = 0.5, see Maeder & Meynet (1989) and Hurley et al. (2000).
(A.2)We assume a
numerical prefactor of η = 0.5, see Maeder & Meynet (1989) and Hurley et al. (2000). -
AGB stars can experience severe mass-loss caused by radiation pressure on dust that condensates in the upper atmosphere of the stars. Empirically, the mass-loss rate has been coupled to the period of large-amplitude radial pulsations Ppuls (Vassiliadis & Wood 1993):
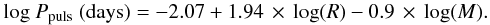 (A.3)We apply
mass-loss to the envelope according to the prescription of Vassiliadis & Wood (1993). During the superwind
phase the radiation pressure driven wind is modelled by
(A.3)We apply
mass-loss to the envelope according to the prescription of Vassiliadis & Wood (1993). During the superwind
phase the radiation pressure driven wind is modelled by 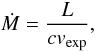 (A.4)where
c represents the speed of light
and vexp the stellar wind expansion velocity. The
latter is given by:
(A.4)where
c represents the speed of light
and vexp the stellar wind expansion velocity. The
latter is given by: 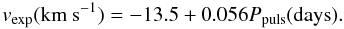 (A.5)Furthermore,
vexp is constrained to the
range 3.0–15.0 km s-1. Before the superwind phase, the mass loss
rate increases exponentially with Ppuls as
(A.5)Furthermore,
vexp is constrained to the
range 3.0–15.0 km s-1. Before the superwind phase, the mass loss
rate increases exponentially with Ppuls as
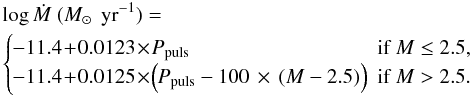 (A.6)The
mass loss rate of Vassiliadis & Wood
(1993) is given by the minimum of Eqs. (A.4) and (A.6).
(A.6)The
mass loss rate of Vassiliadis & Wood
(1993) is given by the minimum of Eqs. (A.4) and (A.6). -
Luminous blue variables (LBVs) are extremely massive and luminous stars near the Humphreys-Davidson limit (Humphreys & Davidson 1994) with enormous mass-loss rates. We use the LBV mass loss prescription and implementation suggested by Hurley et al. (2000):
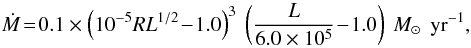 (A.7)if
L > 6.0 × 105 L⊙
and 10-5RL1/2 > 1.0.
(A.7)if
L > 6.0 × 105 L⊙
and 10-5RL1/2 > 1.0.
-
Wolf-Rayet stars are stars in a stage of evolution following the LBV phase where weak or no hydrogen lines are observed in their spectra. Like Hurley et al. (2000) we include a Wolf-Rayet-like mass-loss for stars with a small hydrogen-envelope mass (μ < 1.0 from their Eq. (97)). The prescription itself, however, is different. We model it according to Nelemans & van den Heuvel (2001):
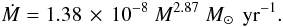 (A.8)This is a fit
to observed mass-loss rates from Nugis &
Lamers (2000). We multiply with a factor (1 − μ) to
smoothly switch on mass loss.
(A.8)This is a fit
to observed mass-loss rates from Nugis &
Lamers (2000). We multiply with a factor (1 − μ) to
smoothly switch on mass loss. -
In addition to the evolution of ordinary hydrogen rich stars, the evolution of helium burning stars with hydrogen poor envelopes is simulated as well. For helium main-sequence stars with a mass M > 2.5 M⊙ we assume the same relation as for Wolf-Rayet-like stars. For helium giants, either on the equivalent of the Hertzsprung or giant branch, we describe mass loss in a very general way similar to Nelemans et al. (2001b). We presume 30% of the mass of the envelope Menv will be lost during the naked helium giant phase with a rate that increases in time according to
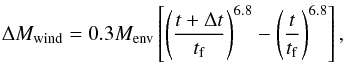 (A.9)where
ΔMwind is the amount of mass lost in the wind in
M⊙ in a timestep Δt,
tf is the duration of the helium giant phase
and t the time since the beginning of the phase.
(A.9)where
ΔMwind is the amount of mass lost in the wind in
M⊙ in a timestep Δt,
tf is the duration of the helium giant phase
and t the time since the beginning of the phase.
A.2. Accretion onto stellar objects
Roche lobe overflow mass transfer and subsequent accretion can substantially alter the stars and the binary orbit. Mass accretion can affect the structure of the receiver star and its subsequent evolution. When more mass is transferred than the accretor can accrete, we assume that the non-accreted matter leaves the system with an angular momentum of 2.5 times the specific angular momentum of the binary (Portegies Zwart & Verbunt 1996; Nelemans et al. 2001b). For compact accretors we assume the matter leaves the system with the specific angular momentum of the compact remnant. In this section we discuss the limiting accretion rate, the response of the accretor to regain equilibrium, and the subsequent evolution of the new object for different types of accretors.
A.2.1. Accretion onto ordinary stars
For ordinary stars from MS to AGB stars, we distinguish between two types of accretion; accretion from a hydrogen-rich or a helium-rich envelope. Hydrogen-rich accretion can occur for example when a donor star ascends the giant branch and fills its Roche lobe. After it loses its hydrogen envelope, it can become a helium-burning core. When this helium star ascends the helium equivalent of the giant branch, a fraction of the helium-rich envelope can be transferred onto the accretor. We name this type of accretion “helium accretion”. We assume that the accreted helium settles and sinks to the core instantaneously. The helium accretion rate is limited by the Eddington limit. Hydrogen is accreted onto the envelope of the receiver star. The accretion rate is bounded by the star’s thermal timescale times a factor that is dependent of the ratio of Roche lobe radius of the receivers to its effective radius, as described by Portegies Zwart & Verbunt (1996). The formalism is proposed by Pols & Marinus (1994), which is based on Kippenhahn & Meyer-Hofmeister (1977); Neo et al. (1977) and Packet & De Greve (1979). If the mass transfer rate is higher than the maximum mass accretion rate, the excess material is assumed to leave the binary system.
Because of the accretion, the star falls temporarily out of thermal equilibrium. While regaining equilibrium, the gas envelope surrounding the core puffs outward. Because we do not solve the equations of stellar structure and the stellar evolution tracks describe single stars in equilibrium, we add a procedure to account for a temporal increase in radius as in Portegies Zwart & Verbunt (1996). This is important for example to determine if an accretor star fills its Roche lobe. It also affects the magnetic braking process and the Darwin-Riemann instability through the increased stellar angular momentum. Note that the mass transfer rate is not dependent on the stellar radius in our simulations, so that the binary evolution is not critically dependent on out-of-equilibrium parameter values.
Accretion can also affect the structure of the receiver star and its subsequent evolution. It is modelled by changing the stellar track and moving along the track. The former is described by the track mass, which is equivalent to the zero-age main-sequence mass that the star would have had without interaction. The latter is described by the relative age trel of the star. We distinguish two cases:
-
Rejuvenation of an MS star. Accretion onto an MS star rejuvenates the star. The star evolves similarly to a younger star of its new mass and its MS lifetime can be extended. It would show up in a Hertzsprung-Russell diagram as a bluestraggler. For hydrogen accretion the track mass is always updated and the renewed relative age of the star
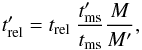 (A.10)where primes
denote quantities after a small amount of mass accretion,
tms the main-sequence lifetime,
and M the mass of the star. For helium accretion we assume
the mass accretes to the core instantaneously and the track mass is increased
accordingly. These stars appear older than for hydrogen accretion because more
hydrogen has been burned previously. The rejuvenation process is described by
(A.10)where primes
denote quantities after a small amount of mass accretion,
tms the main-sequence lifetime,
and M the mass of the star. For helium accretion we assume
the mass accretes to the core instantaneously and the track mass is increased
accordingly. These stars appear older than for hydrogen accretion because more
hydrogen has been burned previously. The rejuvenation process is described by
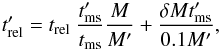 (A.11)where we
assume 10% of the mass of the star will be burned during the MS phase.
(A.11)where we
assume 10% of the mass of the star will be burned during the MS phase. -
Rejuvenation of a giant. During the giant phases the envelope is discoupled from the core in terms of stellar structure. The evolution of the star will therefore not be influenced directly by small amounts of hydrogen accretion to the envelope. The track is only updated when the new mass is larger than the track mass to account for severe hydrogen accretion. The mass before accretion can be much lower than the track mass because of wind mass loss, which can be strong for giants. For helium accretion to the core, the track is always updated. An exception to this is the early AGB where the helium core does not grow. In this stage there is a one-to-one relation between the helium core mass and the track mass (Eq. (66) in Hurley et al. 2000). When a giant accretor star moves to a new evolutionary track, we need to determine the location of the star along this track. In a more physical picture this means determining the relative age of the star trel. For a giant its evolution is mainly determined by its core. Therefore for a given evolutionary track and core mass, the relative age is effectively constrained. For both types of accretion, we insist that the star stays in its same evolutionary state after its mass increase. When no solution can be found for trel, the relative age is set to the beginning or end of the current evolutionary state and the track mass is varied to find a fitting track that ensures mass conservation.
A.2.2. Accretion onto helium-burning cores
For accretion onto helium-burning stars that have lost their hydrogen envelopes, accretion is limited by the Eddington limit. Helium accretion onto a helium main-sequence star is similar as hydrogen accretion onto normal main-sequences stars. We assume that the star evolves similarly to a younger star of its new mass according to Eq. (A.10) where tms should be replaced by the helium main-sequence life time. We assume that for helium giants the envelope is discoupled from the core in terms of stellar structure, as with hydrogen-rich giants. Therefore we assume that the evolution of the giant is not affected and only update the track when the new mass is larger than the track mass.
The effect of hydrogen accretion onto helium stars is more complicated. If the hydrogen layer is sufficiently thick, the layer can ignite. This can significantly increase the radius of the star and essentially turn it into a born-again star on the horizontal or asymptotic giant branch. We studied the effect of hydrogenaccretion to helium stars with stellar models simulated by the stellar evolution code STARS. This code models stellar structure and evolution in detail by solving the stellar structure equations. The code is based on Eggleton (1971) and includes updated input physics as described in Hu et al. (2010). The models do not include atomic diffusion. For mass accretion rates at ten percent of the Eddington rate of the accretor for ~104−105 yr, the accreted hydrogen layer ignites. Helium stars that are more massive than ~0.55 M⊙ resemble horizontal branch stars after accretion, but most of the luminosity still comes from helium burning. For lower mass helium stars this is not the case, because the corresponding horizontal branch stars (<3.5 M⊙) can have ignited helium in a degenerate core, which strongly affects the characteristics of the star. For both mass ranges, the accretor expands by a factor ~10−100 compared to the original helium star. Because hydrogen accretion to helium stars is not very likely, we model this very simply. When more than 5% of the total mass is accreted, the radius of the star is increased by a factor 50. With few exceptions, this leads to a merger of the two components.
The effect of hydrogen accretion to helium giants is not known very well and additional research is necessary. For now, because it is very unlikely to happen, we treat it in the same way as helium accretion onto the envelope of the giant.
A.2.3. Accretion onto remnants
White dwarf, neutron star and black hole accretors can accrete with a maximum rate of the Eddington limit. If more mass is transferred, the surplus material leaves the system with the specific angular momentum of the compact remnant. For neutron stars and black holes we assume that the transferred mass is temporarily stored in a disk. From this disk, mass will flow onto the surface of the remnant with ten percent of the Eddington limit. We assume that a neutron star collapses onto a black hole when its mass exceeds 1.5 M⊙.
For white dwarfs, the accretion process is more complicated because of possible thermonuclear runaways in the accreted material on the surface of the white dwarf. In SeBa there are several options to model the effectiveness of the white dwarf to retain the transferred material. For hydrogen accretion we can choose between the efficiencies of Hachisu et al. (2008) and Prialnik & Kovetz (1995). For helium retention, the option is between Kato & Hachisu (1999) (with updates from Hachisu et al. 1999) and Iben & Tutukov (1996).
A.3. Stability of mass transfer
A semi-detached system can become unstable in two ways. In a mass transfer instability, the Roche-lobe-filling star expands faster than the Roche lobe itself on the relevant timescale. In the other case tidal interactions lead to an instability (Darwin 1879).
A.3.1. Tidal instability
A tidal instability can take place in systems of extreme mass ratios. When there is
insufficient orbital angular momentum Jb that can be
transferred onto the mass-losing star, the star cannot stay in synchronous rotation.
Tidal forces will cause the companion to spiral into the envelope of the donor star.
The tidal instability occurs when the angular momentum of the
star 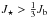 , where
, where
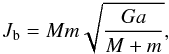 (A.12)where
Jb is the orbital angular momentum of the circularised
binary, a is the orbital separation, M the mass of
the donor star and m the mass of the accretor star. The angular
momentum J ⋆ of a star with
radius R is given by
(A.12)where
Jb is the orbital angular momentum of the circularised
binary, a is the orbital separation, M the mass of
the donor star and m the mass of the accretor star. The angular
momentum J ⋆ of a star with
radius R is given by 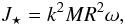 (A.13)where
k2 is the gyration radius described by Nelemans et al. (2001b) and ω is
the angular velocity of the donor star, which is assumed to be synchronised with the
orbit. It is given
by ω = 2π/Pb,
where Pb is the orbital period. We model the inspiral
according to the standard α-CE (see Sect. 3). Owing to the expulsion of the envelope, the binary may evolve
to a more stable configuration or merge. If the mass-losing star is a main-sequence
star, we assume that the instability always leads to a merger.
(A.13)where
k2 is the gyration radius described by Nelemans et al. (2001b) and ω is
the angular velocity of the donor star, which is assumed to be synchronised with the
orbit. It is given
by ω = 2π/Pb,
where Pb is the orbital period. We model the inspiral
according to the standard α-CE (see Sect. 3). Owing to the expulsion of the envelope, the binary may evolve
to a more stable configuration or merge. If the mass-losing star is a main-sequence
star, we assume that the instability always leads to a merger.
A.3.2. Mass transfer instability
The stability of mass transfer from Roche lobe overflow and its consequences on the
binary depend on the response of the radius and the Roche lobe of the donor star to
the imposed mass loss (e.g. Webbink 1985;
Hjellming & Webbink 1987, hereafter
HW87, Pols & Marinus 1994; Soberman et al. 1997). We distinguish four modes
of mass transfer; on the dynamical, thermal, nuclear timescale of the donor or on
the angular-momentum-loss timescale. The response of the accretor star to the mass
that is transferred onto it and the effect of this on the orbit is described in
Appendix A.2. The response of the donor star
to mass loss is to readjust its structure to recover hydrostatic and thermal
equilibrium. The dynamical timescale to recover hydrostatic equilibrium is short
compared to the thermal timescale. For mass transfer to be dynamically stable, the
dynamical timescale of the star is important. The change in radius due to adiabatic
adjustment of hydrostatic equilibrium is expressed as a logarithmic derivative of
the radius with respect of mass,
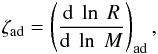 (A.14)where
M and R are the mass and radius of the donor
star. The assumed values of ζad are shown in Table A.1.
(A.14)where
M and R are the mass and radius of the donor
star. The assumed values of ζad are shown in Table A.1.
The response of the Roche lobe RL of the donor star is
expressed as the logarithmic derivative of the Roche lobe radius with respect to
mass: 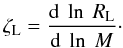 (A.15)The value of
ζL is calculated numerically by transferring a test
mass of 10-5M⊙.
Because ζL = ζL(M1,M2,a),
ζL is dependent on the mass accretion efficiency of
the secondary, and therefore on the mass accretion rate of the test mass. For
instance, for high mass ratios q ≫ 1 the loss of some mass and
corresponding angular momentum can have a stabilising effect on the
mass-transferring binary. To determine the dynamical stability of mass transfer, we
assume that the mass transfer rate of the test mass is on the thermal timescale of
the donor star:
(A.15)The value of
ζL is calculated numerically by transferring a test
mass of 10-5M⊙.
Because ζL = ζL(M1,M2,a),
ζL is dependent on the mass accretion efficiency of
the secondary, and therefore on the mass accretion rate of the test mass. For
instance, for high mass ratios q ≫ 1 the loss of some mass and
corresponding angular momentum can have a stabilising effect on the
mass-transferring binary. To determine the dynamical stability of mass transfer, we
assume that the mass transfer rate of the test mass is on the thermal timescale of
the donor star: 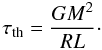 (A.16)
(A.16)
-
When ζL > ζad, mass transfer is dynamically unstable. We model this as a CE phase, as described in Sect. 32.
Table A.1Values of the adiabatic ζad and thermal ζeq response of the radius to mass loss for different types of stars.
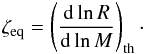 (A.18)The assumed
values for ζeq are described in Table A.1.
(A.18)The assumed
values for ζeq are described in Table A.1.
To calculate the response of the Roche
lobe ζL,eq, we assume that the mass
transfer rate of the test mass is on the nuclear evolution timescale:
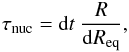 (A.19)where
R represents the equilibrium radius of the star according to the
single-star tracks. dReq is the change
in R in a short timestep dt without binary
interactions.
(A.19)where
R represents the equilibrium radius of the star according to the
single-star tracks. dReq is the change
in R in a short timestep dt without binary
interactions.
-
2.
When ζL,eq < min(ζeq,ζad) mass transfer is driven by the expansion of the stellar radius due to its internal evolution.
-
3.
When ζL,eq > min(ζeq,ζad), the mass transfer is thermally unstable and proceeds on the thermal time scale of the donor.
-
4.
The previous modes of mass transfer are caused by an expanding donor star. The final mode is caused by shrinking of the orbit caused by angular momentum loss. We assume that this mode takes place when the corresponding timescale τJ is shorter than the timescales at which the other three modes of mass transfer take place. Angular momentum loss can happen due to gravitational wave radiation
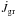 (Kraft et al. 1962) and magnetic
braking
(Kraft et al. 1962) and magnetic
braking 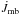 (Schatzman 1962; Huang 1966; Skumanich 1972; Verbunt
& Zwaan 1981). Mass transfer proceeds on the time scale on
which these processes occur:
(Schatzman 1962; Huang 1966; Skumanich 1972; Verbunt
& Zwaan 1981). Mass transfer proceeds on the time scale on
which these processes occur:
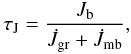 (A.20)where
Jb is the angular momentum of the circularized
binary given by Eq. (A.12).
Next we discuss the assumptions and implications
of
(A.20)where
Jb is the angular momentum of the circularized
binary given by Eq. (A.12).
Next we discuss the assumptions and implications
of 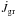 and
and 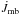 .
Gravitational wave radiation most strongly influences close binaries since it
is a strong function of orbital separation. The change in orbital
separation ȧ averaged over a full orbit is given by (Peters 1964)
.
Gravitational wave radiation most strongly influences close binaries since it
is a strong function of orbital separation. The change in orbital
separation ȧ averaged over a full orbit is given by (Peters 1964)
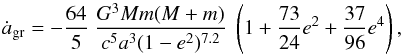 (A.21)where
(A.21)where
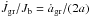 .
Magnetic braking mostly affects low-mass stars within the mass range
of 0.6 ≲ M/M⊙ ≲ 1.5.
These stars suffer from winds that are magnetically coupled to the star.
Although the mass loss in this process is negligible, the associated angular
momentum loss can be severe (Rappaport et al.
1983):
.
Magnetic braking mostly affects low-mass stars within the mass range
of 0.6 ≲ M/M⊙ ≲ 1.5.
These stars suffer from winds that are magnetically coupled to the star.
Although the mass loss in this process is negligible, the associated angular
momentum loss can be severe (Rappaport et al.
1983):
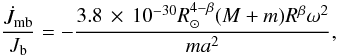 (A.22)where
β is a parameter that represents the dependence of the
braking on the radius of the donor star. We take β = 2.5.
(A.22)where
β is a parameter that represents the dependence of the
braking on the radius of the donor star. We take β = 2.5.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


