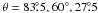| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 16 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201219480 | |
| Published online | 18 September 2012 | |
X-ray bursting neutron star atmosphere models using an exact relativistic kinetic equation for Compton scattering⋆,⋆⋆
1
Institut für Astronomie und Astrophysik, Kepler Center for Astro and
Particle Physics, Universität Tübingen,
Sand 1,
72076
Tübingen,
Germany
e-mail: suleimanov@astro.uni-tuebingen.de; werner@astro.uni-tuebingen.de
2
Kazan Federal University, Kremlevskaja str. 18, 420008
Kazan,
Russia
3 Astronomy Division, Department of Physics, PO Box 3000, 90014
University of Oulu, Finland
e-mail: juri.poutanen@oulu.fi
Received:
25
April
2012
Accepted:
13
July
2012
Context. Theoretical spectra of X-ray bursting neutron star (NS) model atmospheres are widely used to determine the basic NS parameters such as their masses and radii. Compton scattering, which plays an important role in spectra formation at high luminosities, is often accounted for using the differential Kompaneets operator, while in other models a more general, integral operator for the Compton scattering kernel is used.
Aims. We construct accurate NS atmosphere models using for the first time an exact treatment of Compton scattering via the integral relativistic kinetic equation. We also test various approximations to the Compton scattering redistribution function and compare the results with the previous calculations based on the Kompaneets operator.
Methods. We solve the radiation transfer equation together with the hydrostatic equilibrium equation accounting exactly for the radiation pressure by electron scattering. We use the exact relativistic angle-dependent redistribution function as well as its simple approximate representations.
Results. We thus construct a new set of plane-parallel atmosphere models in local thermodynamic equilibrium (LTE) for hot NSs. The models were computed for six chemical compositions (pure H, pure He, solar H/He mix with various heavy elements abundances Z = 1, 0.3, 0.1, and 0.01 Z⊙, and three surface gravities log g = 14.0, 14.3, and 14.6. For each chemical composition and surface gravity, we compute more than 26 model atmospheres with various luminosities relative to the Eddington luminosity LEdd computed for the Thomson cross-section. The maximum relative luminosities L/LEdd reach values of up to 1.1 for high gravity models. The emergent spectra of all models are redshifted and fitted by diluted blackbody spectra in the 3−20 keV energy range appropriate for the RXTE/PCA. We also compute the color correction factors fc.
Conclusions. The radiative acceleration grad in our luminous, hot-atmosphere models is significantly smaller than in corresponding models based on the Kompaneets operator, because of the Klein-Nishina reduction of the electron scattering cross-section, and therefore formally “super-Eddington” model atmospheres do exist. The differences between the new and old model atmospheres are small for L/LEdd < 0.8. For the same grad/g, the new fc are slightly larger (by approximately 1%) than the old values. We also find that the model atmospheres, the emergent spectra, and the color correction factor computed using angle-averaged and approximate Compton scattering kernels differ from the exact solutions by less than 2%.
Key words: radiative transfer / scattering / methods: numerical / stars: atmospheres / stars: neutron / X-rays: stars
Appendices are available in electronic form at http://www.aanda.org
Tables D.1–D.3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/545/A120
© ESO, 2012
1. Introduction
X-ray bursting neutron stars (NSs) are members of low-mass X-ray binaries with quasi-periodical thermonuclear flashes on their surfaces (see reviews by Lewin et al. 1993; Strohmayer & Bildsten 2006). Thermonuclear burning occurs at the bottom of the freshly accreted matter and can be so powerful that the luminosity reaches the Eddington limit. These bursts lead to photospheric radius expansion (PRE) and are a potentially powerful tool for determining the NS masses and radii (Ebisuzaki 1987; Damen et al. 1990; van Paradijs et al. 1990). The knowledge of NS basic parameters is extremely important for establishing the physical properties (equation of state) of supra-nuclear dense matter in the NS inner cores (see Lattimer & Prakash 2007, for a review).
The precise radius determination of the NSs from X-ray bursts is impossible without
accurate spectral models. The observed spectra of X-ray bursts are often well-fitted by a
blackbody (Galloway et al. 2008). Theoretical models
of hot NS atmospheres show (London et al. 1986; Lapidus et al. 1986; Pavlov et al. 1991) that the emergent spectra are close to diluted blackbody
spectra 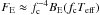 owing to strong energy
exchange caused by Compton scattering. The color correction factor
fc ≡ Tc/Teff,
which relates the color temperature of the spectrum Tc to the
effective temperature of the atmosphere Teff, takes values of
about 1.3−1.9. Theoretical dependences of the color correction factor on luminosity for
various chemical compositions and gravities were computed by Suleimanov et al. (2011b, hereafter SPW11). The atmosphere models used in their
work were based on the Kompaneets operator (Kompaneets
1957) description of Compton scattering. This approach was also used in most
previous studies (London et al. 1986; Lapidus et al. 1986; Ebisuzaki 1987; Pavlov et al. 1991). The
Kompaneets operator describes Compton scattering in the non-relativistic, isotropic,
diffusion approximation, which should still be rather adequate for hot NS model atmospheres
with typical effective temperatures below ~2 keV. On the other hand, Madej and
collaborators (Madej 1991; Madej et al. 2004; Majczyna et al.
2005) used the integral description of Compton scattering employing the
angle-averaged redistribution function (RF) derived by Guilbert (1981). A fully relativistic treatment of Compton scattering becomes
important at luminosities close to the Eddington values, because of the reduction of the
effective cross-section and the corresponding drop in the radiation pressure force. This
obviously changes the maximum value of the luminosity where hydrostatic equilibrium can
still be achieved, i.e. the actual value of the Eddington luminosity. This has important
implications for the method of determining the NS masses and radii from PRE bursts, which is
based on the Eddington luminosity (see Suleimanov et al.
2011a, hereafter S11). It is therefore, necessary to check the validity of model
atmospheres and spectral properties computed with the Kompaneets operator by comparing the
results with more accurate models based on an exact treatment of Compton scattering using
relativistic kinetic equations.
owing to strong energy
exchange caused by Compton scattering. The color correction factor
fc ≡ Tc/Teff,
which relates the color temperature of the spectrum Tc to the
effective temperature of the atmosphere Teff, takes values of
about 1.3−1.9. Theoretical dependences of the color correction factor on luminosity for
various chemical compositions and gravities were computed by Suleimanov et al. (2011b, hereafter SPW11). The atmosphere models used in their
work were based on the Kompaneets operator (Kompaneets
1957) description of Compton scattering. This approach was also used in most
previous studies (London et al. 1986; Lapidus et al. 1986; Ebisuzaki 1987; Pavlov et al. 1991). The
Kompaneets operator describes Compton scattering in the non-relativistic, isotropic,
diffusion approximation, which should still be rather adequate for hot NS model atmospheres
with typical effective temperatures below ~2 keV. On the other hand, Madej and
collaborators (Madej 1991; Madej et al. 2004; Majczyna et al.
2005) used the integral description of Compton scattering employing the
angle-averaged redistribution function (RF) derived by Guilbert (1981). A fully relativistic treatment of Compton scattering becomes
important at luminosities close to the Eddington values, because of the reduction of the
effective cross-section and the corresponding drop in the radiation pressure force. This
obviously changes the maximum value of the luminosity where hydrostatic equilibrium can
still be achieved, i.e. the actual value of the Eddington luminosity. This has important
implications for the method of determining the NS masses and radii from PRE bursts, which is
based on the Eddington luminosity (see Suleimanov et al.
2011a, hereafter S11). It is therefore, necessary to check the validity of model
atmospheres and spectral properties computed with the Kompaneets operator by comparing the
results with more accurate models based on an exact treatment of Compton scattering using
relativistic kinetic equations.
Here we construct new models of hot NS atmospheres based on an exact treatment of Compton scattering that employs a fully relativistic, angle-dependent RF (Aharonian & Atoyan 1981; Prasad et al. 1986; Nagirner & Poutanen 1994; Poutanen & Svensson 1996). In Sect. 2, we present the main equations describing the atmosphere models as well as the methods for their solution. We also compare atmosphere models based on various RFs for Compton scattering and using the Kompaneets operator. In Sect. 3, we present a new set of atmosphere models, emergent spectra, and the color correction factors. We compare them to previous results obtained with the Kompaneets operator. In Sect. 4, we discuss applications of the new models to the observations of X-ray bursts and determination of the NS masses and radii. We summarize in Sect. 5. In Appendix A we derive the exact RF for Compton scattering. The details of the method of solution of the radiative transfer equation are presented in Appendix B. Comparison with the previous attempts to compute atmosphere models using integral approach to Compton scattering are given in Appendix C. And, finally, Appendix D presents the spectral characteristics of the models.
2. Method of atmosphere modeling
2.1. Main equations
A method for modeling hot X-ray bursting NS atmospheres that employs the Kompaneets operator for Compton scattering was described in detail in SPW11. Here we repeat the basic assumptions and emphasize the differences arising because of the new treatment of Compton scattering as well as radiation transfer.
We compute models in hydrostatic and radiative equilibrium in a plane-parallel
approximation. The main input parameters are the chemical composition (particularly the
hydrogen mass fraction X), the surface gravity 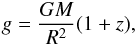 (1)and the relative NS
luminosity
l = L/LEdd,
where LEdd is the Eddington luminosity measured at the
NS surface
(1)and the relative NS
luminosity
l = L/LEdd,
where LEdd is the Eddington luminosity measured at the
NS surface 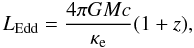 (2)for the Thomson
scattering opacity
(2)for the Thomson
scattering opacity 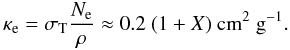 (3)Here
σT = 6.65 × 10-25 cm2 is the Thomson
cross-section, ρ is the gas density, and
Ne is the electron number density. The gravitational redshift
is related to the NS parameters as
(3)Here
σT = 6.65 × 10-25 cm2 is the Thomson
cross-section, ρ is the gas density, and
Ne is the electron number density. The gravitational redshift
is related to the NS parameters as 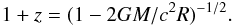 (4)We assume that the
flux is constant throughout the NS surface. Our calculations are valid for a patch on the
NS surface if instead of the relative luminosity we consider the relative flux,
(4)We assume that the
flux is constant throughout the NS surface. Our calculations are valid for a patch on the
NS surface if instead of the relative luminosity we consider the relative flux,
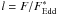 ,
as a parameter, where
,
as a parameter, where 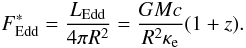 (5)The effective
temperature Teff can be expressed via l as
(5)The effective
temperature Teff can be expressed via l as
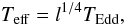 (6)where the Eddington
temperature TEdd is the maximum possible effective temperature
on the NS surface, which is evaluated using the Thomson scattering opacity
(6)where the Eddington
temperature TEdd is the maximum possible effective temperature
on the NS surface, which is evaluated using the Thomson scattering opacity 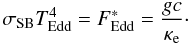 (7)The structure of the
atmosphere for an X-ray bursting NS is described by a set of differential equations. The
first one is the hydrostatic equilibrium equation
(7)The structure of the
atmosphere for an X-ray bursting NS is described by a set of differential equations. The
first one is the hydrostatic equilibrium equation 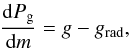 (8)where
grad is the radiative acceleration and
Pg is the gas pressure and the column
density m is defined as
(8)where
grad is the radiative acceleration and
Pg is the gas pressure and the column
density m is defined as
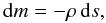 (9)where s
is the vertical distance.
(9)where s
is the vertical distance.
The second equation is the radiation transfer equation for the specific
intensity I(x,μ) accounting for Compton scattering
(see Appendix A for derivation). In the
plane-parallel approximation, it has the form 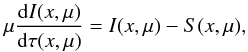 (10)where
(10)where
![\begin{equation} \rmd\tau (x,\mu) = \left[\sigma(x,\mu)+k(x)\right]\, \rmd m, \end{equation}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq41.png) (11)μ = cosθ
is the cosine of the angle between the surface normal and the direction of radiation
propagation,
x = hν/mec2
is the photon energy in units of electron rest mass,
and k(x) is the “true” absorption opacity. The
electron scattering opacity accounting for the induced scattering is
(11)μ = cosθ
is the cosine of the angle between the surface normal and the direction of radiation
propagation,
x = hν/mec2
is the photon energy in units of electron rest mass,
and k(x) is the “true” absorption opacity. The
electron scattering opacity accounting for the induced scattering is 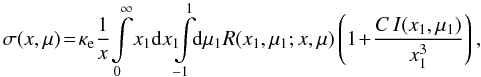 (12)and
(12)and 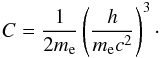 (13)The source
function is a sum of the thermal part and the scattering part
(13)The source
function is a sum of the thermal part and the scattering part 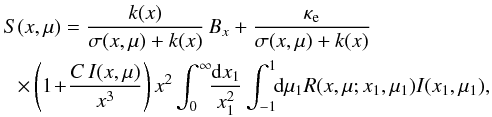 (14)where
(14)where
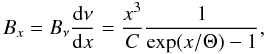 (15)with
Bν being the Planck function and
(15)with
Bν being the Planck function and
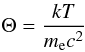 (16)the
electron temperature.
(16)the
electron temperature.
The RF
R(x,μ;x1,μ1)
describes the probability that a photon with the dimensionless
energy x1 propagating in the direction corresponding
to μ1 is scattered to energy x and in a
direction corresponding to μ. This function is found by integrating over
the azimuthal angle ϕ of the
RF R(x,x1,η),
which depends on the cosine of the angle between the directions of the photon propagation
before and after scattering η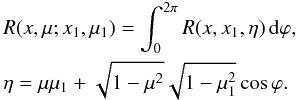 (17)\arraycolsep1.75ptThe
RF depends on the depth s through the electron temperature and satisfies
the relation (see Eq. (A.7))
(17)\arraycolsep1.75ptThe
RF depends on the depth s through the electron temperature and satisfies
the relation (see Eq. (A.7))
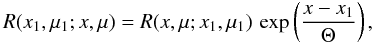 (18)which is the
consequence of the detailed balance relation (Pomraning
1973; Nagirner & Poutanen 1994,
see Appendix A). This implies that the source
function given by Eq. (14) equals the
Planck function for the photon field described by the Bose-Einstein distribution of any
chemical potential.
(18)which is the
consequence of the detailed balance relation (Pomraning
1973; Nagirner & Poutanen 1994,
see Appendix A). This implies that the source
function given by Eq. (14) equals the
Planck function for the photon field described by the Bose-Einstein distribution of any
chemical potential.
In this paper, we use two RFs for Compton scattering. The first one is the fully
relativistic exact RF valid for any photon energy and electron temperature (Aharonian & Atoyan 1981; Nagirner & Poutanen 1993, 1994; Poutanen & Svensson 1996,
see Eqs. (A.18) and (A.22) in Appendix A.2). The second one is an approximate RF corresponding to the
isotropic scattering in the electron rest frame (Eq. (A.26) in Appendix A.2), which is
accurate at temperatures below about 100 keV and non-relativistic photon energies (Arutyunyan & Nikogosyan 1980; Poutanen 1994; Poutanen
& Svensson 1996). In both cases, we also consider the angle-averaged RFs
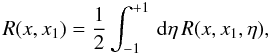 (19)substituting it
instead of the angle-dependent RF into Eq. (18).
(19)substituting it
instead of the angle-dependent RF into Eq. (18).
The formal solution of the radiation transfer Eq. (10) is obtained using the short-characteristic method (Olson & Kunasz 1987) in three angles in each hemisphere, and the full solution is found with an accelerated Λ-iteration method (see details in Appendix B).
The radiation pressure acceleration grad is computed using
the RF as ![\begin{eqnarray} g_{\rm rad} &\!=\!& \frac{\rmd P_{\rm rad}}{\rmd m} = \frac{2\pi}{c} \,\frac{\rmd}{\rmd m}\, \int^{\infty}_{0} \rmd x \, \int^{+1}_{-1}\mu^2 I(x,\mu)\, \rmd\mu \nonumber\\ &\!=\!& \frac{2\pi}{c} \int^{\infty}_{0} \!\! \rmd x \int^{+1}_{-1}\!\! \left[\sigma(x,\mu) \!+\! k(x)\right] \left[I(x,\mu)\!-\!S(x,\mu)\right] \,\, \mu \, \rmd\mu, \label{eq:grad} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq63.png) (20)where
the derivative with respect to m is replaced by the first moment of the
radiation transfer Eq. (10). When the
source functions and the opacities are isotropic, this expression is reduced to the
standard definition
(20)where
the derivative with respect to m is replaced by the first moment of the
radiation transfer Eq. (10). When the
source functions and the opacities are isotropic, this expression is reduced to the
standard definition ![\begin{equation} g_{\rm rad} = \frac{4\pi}{c} \, \int^{\infty}_{0} \left[\sigma(x) + k(x)\right] H_x(m) \ \rmd x, \label{eq:grad_stan} \end{equation}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq64.png) (21)where
(21)where
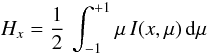 (22)is the first moment of
specific intensity.
(22)is the first moment of
specific intensity.
These equations are completed by the energy balance equation ![\begin{equation} \int^{\infty}_{0} {\rm d}x \, \int^{+1}_{-1} \left[\sigma(x,\mu) + k(x)\right] \left[I(x,\mu)-S(x,\mu)\right] \, \, {\rm d}\mu = 0, \label{eq:econs} \end{equation}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq66.png) (23)the ideal gas law
(23)the ideal gas law
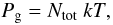 (24)where
Ntot is the number density of all particles, and the
particle and charge conservation equations. In our calculations, we assumed local
thermodynamic equilibrium (LTE), therefore the number densities of all ionization and
excitation states of all elements were calculated using the Boltzmann and Saha equations.
We accounted for the pressure ionization effects on hydrogen and helium populations using
the occupation probability formalism (Hummer &
Mihalas 1988) as described by Hubeny et al.
(1994). In addition to electron scattering, we took into account the free-free
opacity as well as the bound-free transitions for all ions of the 15 most abundant
chemical elements (H, He, C, N, O, Ne, Na, Mg, Al, Si, S, Ar, Ca, Fe, Ni) (see Ibragimov et al. 2003) using opacities from Verner & Yakovlev (1995).
(24)where
Ntot is the number density of all particles, and the
particle and charge conservation equations. In our calculations, we assumed local
thermodynamic equilibrium (LTE), therefore the number densities of all ionization and
excitation states of all elements were calculated using the Boltzmann and Saha equations.
We accounted for the pressure ionization effects on hydrogen and helium populations using
the occupation probability formalism (Hummer &
Mihalas 1988) as described by Hubeny et al.
(1994). In addition to electron scattering, we took into account the free-free
opacity as well as the bound-free transitions for all ions of the 15 most abundant
chemical elements (H, He, C, N, O, Ne, Na, Mg, Al, Si, S, Ar, Ca, Fe, Ni) (see Ibragimov et al. 2003) using opacities from Verner & Yakovlev (1995).
2.2. Method of solution
To solve the above equations, we used our version of the computer code ATLAS (Kurucz 1970, 1993), modified to deal with high temperatures (Suleimanov & Poutanen 2006; Suleimanov & Werner 2007). The code was further developed to account for Compton scattering using the RF approach.
In our computations, we used 300–360 logarithmically equidistant frequency points in the
range 1014−1020 Hz (≈ 4 × 10-4−400 keV) for the
luminous model atmospheres (l ≥ 0.1),
and 1014−1019 Hz
for l < 0.1. The calculations were performed at
a set of 98 depth points mi distributed equidistantly on the
logarithmic scale from 10-6 to
mmax = 106 g cm-2. The appropriate
value of mmax was chosen to satisfy the condition
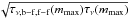 > 1
at all frequencies,
where τν,b−f, f−f is
the optical depth computed with the true opacity only (bound-free and free-free
transitions, without scattering). This requirement was necessary for satisfying the inner
boundary condition of the radiation transfer problem.
> 1
at all frequencies,
where τν,b−f, f−f is
the optical depth computed with the true opacity only (bound-free and free-free
transitions, without scattering). This requirement was necessary for satisfying the inner
boundary condition of the radiation transfer problem.
The course of the calculations was the same as for the method that adopts the Kompaneets
operator (SPW11). First, a starting grey atmosphere model was calculated and opacities at
all depth points and all frequencies were obtained. The solution of the radiative transfer
Eq. (10) was checked for the energy
balance Eq. (23), together with the
surface flux condition 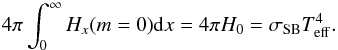 (25)The relative flux
error
(25)The relative flux
error 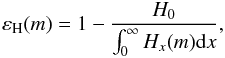 (26)and the energy
balance error
(26)and the energy
balance error ![\begin{equation} \varepsilon_{\Lambda}(m) = \frac{1}{2}\! \int^{\infty}_{0} \!\! \! {\rm d}x \!\! \int^{+1}_{-1} \!\! \left[\sigma(x,\mu) + k(x)\right] \left[I(x,\mu)-S(x,\mu)\right] {\rm d}\mu \label{eq:econs1} \end{equation}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq85.png) (27)were calculated as
functions of depth. Temperature corrections were then evaluated using three different
procedures. In the upper atmospheric layers, we used the integral Λ-iteration method,
modified for Compton scattering, based on the energy balance Eq. (23). The temperature correction for a
particular depth was found as
(27)were calculated as
functions of depth. Temperature corrections were then evaluated using three different
procedures. In the upper atmospheric layers, we used the integral Λ-iteration method,
modified for Compton scattering, based on the energy balance Eq. (23). The temperature correction for a
particular depth was found as ![\begin{equation} \Delta T_{\Lambda} = - \varepsilon_{\Lambda}(m) \ \left(\int_0^{\infty} \left[ \frac{\Lambda_{\rm d}(x)-1}{1-\alpha(x)\Lambda_{\rm d}(x)} \right] k(x)\, \frac{{\rm d}B_x}{{\rm d}T}\, {\rm d}x \right) ^{-1}, \end{equation}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq86.png) (28)where
α(x) = σCS(x)/(k(x) + σCS(x)),
and Λd(x) is the diagonal matrix element of the Λ-operator.
Here σCS(x) is the Compton scattering
opacity averaged over the relativistic Maxwellian electron distribution (see Eq. (A16) in
Poutanen & Svensson 1996, which is
equivalent to Eq. (12) if one ignores the
induced scattering). In the deep layers, we used the Avrett-Krook flux correction based on
the relative flux error εH(m). Finally,
the third procedure was the surface correction based on the emergent flux error (see Kurucz 1970, for a detailed description of
the methods).
(28)where
α(x) = σCS(x)/(k(x) + σCS(x)),
and Λd(x) is the diagonal matrix element of the Λ-operator.
Here σCS(x) is the Compton scattering
opacity averaged over the relativistic Maxwellian electron distribution (see Eq. (A16) in
Poutanen & Svensson 1996, which is
equivalent to Eq. (12) if one ignores the
induced scattering). In the deep layers, we used the Avrett-Krook flux correction based on
the relative flux error εH(m). Finally,
the third procedure was the surface correction based on the emergent flux error (see Kurucz 1970, for a detailed description of
the methods).
The iteration procedure is repeated until the relative flux error is smaller than 0.1%, and the relative flux derivative error is smaller than 0.01%. As a result, we obtain a self-consistent NS model atmosphere, together with the emergent spectrum of radiation. We note that this accuracy is unachievable for luminous models with grad ≈ g, and that these models can have larger relative flux errors, up to 2−3%.
2.3. Accuracy of computation
To compute a new extended set of hot NS model atmospheres, we accelerated the convergence of the iterations of the radiation transfer equation by using the source function from the previous temperature iteration as the first approximation (see Appendix B). However, in every fifth temperature iteration the radiation transfer equation was solved using the pure thermal source function as a first approximation. We compared a pure hydrogen model atmosphere computed for Teff = 1.8 × 107 K and log g = 14.0 (the fiducial model) using this accelerated approach with the model computed without acceleration. The temperature structures differ by less than 0.3%, and the differences between the emergent spectra are about 1% in the 3−20 keV energy range (typical of RXTE/PCA) and larger in the Wien tail (Fig. 1).
 |
Fig. 1 Emergent spectrum (top panel) and temperature structure (bottom panel) of the fiducial model (pure hydrogen, Teff = 1.8 × 107 K, log g = 14.0) computed using three different methods. In accurate method 1 every Λ-iteration starts from the thermal part of the source function (solid curves give the results for the relative accuracy of 10-4). In accelerated method 2, the Λ-iterations start from the source function taken from previous temperature iteration, but at every fifth temperature correction they start from the thermal part of the source function (dashed curves show results for the relative accuracy of 10-4). Method 3 is the same as method 2, but for the relative accuracy of 10-5 (dot-dashed curve). In the top lower panel, the ratios of the spectra for methods 2 and 3 to the spectrum computed with method 1 are shown. The ratio of the temperature structures computed using methods 2 and 1 is shown in the bottom lower panel. |
As a convergence criterion for the solution of the radiation transfer equation, we chose the maximum relative error of 10-4 in the mean intensity at all depths and energies. To determine the uncertainty in the final spectrum caused by this criterion, we compared the emergent spectra computed for the same model atmosphere with the accuracies of 10-4 and 10-5 (see top panel of Fig. 1). We see that the relative error is smaller than 1% at all energies, which is then the intrinsic accuracy of our model spectra. We note that a similar error is introduced into the angular dependence of the specific intensities by ignoring polarization (see e.g. Chandrasekhar 1960,compare his Tables XV and XXIV).
2.4. Various RFs and the Kompaneets operator
 |
Fig. 2 Left panels present the emergent spectrum (top panel) and the temperature structure (bottom panel) of the fiducial model computed using four different RFs: (a) exact angle-dependent (solid curves), (b) exact angle-averaged (dashed curves), (c) approximate angle-dependent (dot-dashed curves), and (d) approximate angle-averaged (dotted curves). In the top lower sub-panel, the ratios of the spectra (b), (c), and (d) to the spectrum for case (a) are shown. In the bottom lower sub-panel, the ratio of the temperature structures (b), (c), and (d) to that of case (a) are shown. Right panels present the emergent spectrum (top panel) and the temperature structure (bottom panel) of the fiducial model computed using an exact angle-dependent RF (solid curves) and the Kompaneets operator (dashed curves). |
 |
Fig. 3 Comparison of the emergent spectra (top panel) and the temperature structures (bottom panel) computed using the present code with the exact RF (solid curves) and the previous code employing the Kompaneets operator (dashed curves). The models for various relative luminosities are marked by corresponding numbers next to the curves. Left panels are for pure H and right panels are for the solar abundances. |
A comparison of model atmospheres, which were computed using our new code with four different RFs (exact angle-dependent, exact angle-averaged, approximate angle-dependent, and approximate angle-averaged) is shown in the left panels of Fig. 2. The model computed using the approximate angle-dependent RF is almost indistinguishable from the reference model calculated using the exact angle-dependent RF. This is unsurprising, because the approximate function matches the accurate one very well up to the temperatures of about 100 keV. Similar results were obtained by Poutanen & Svensson (1996) for the Comptonization spectra in the optically thin slabs. The differences are smaller than 1% for the emergent spectra and below 0.3% for the temperature structure. Deviations of model atmospheres computed using the angle-averaged RF of the reference model are more significant, at about 2% for both the temperature structure and spectra.
The model atmosphere calculated employing the Kompaneets operator has more significant differences from the reference model (see right panels in Fig. 2), of up to 10% in the temperature structure and about 3−4% in the emergent flux at 1 keV. The deviations are much smaller (<1%) near the spectral maximum and larger in the Wien tail. A rather good agreement between model atmospheres computed with the relativistic exact angle-dependent RF and the non-relativistic angle-independent Kompaneets operator again is unsurprising, because temperatures of the upper atmosphere layers where the emergent spectra form are sufficiently low (~2−4 keV) and relativistic corrections are small.
3. New grid of models
3.1. General properties
We computed a new set of hot NS model atmospheres using the exact relativistic angle-dependent RF. The models were calculated for six chemical compositions (pure hydrogen, pure helium, and solar hydrogen/helium mix with various heavy element abundances: of solar and 0.3, 0.1 and 0.01 of solar). For every chemical composition, 26−28 models with relative luminosities spanning the interval from l = 0.001 to 1.06−1.10 for three values of the surface gravity (log g = 14.0, 14.3 and 14.6) were calculated. Because the radiative acceleration in our models is smaller than in the models based on the Thomson opacity owing to the Klein-Nishina reduction in the cross-section (see below), there exist formally “super-Eddington” (relative to LEdd) models. The Klein-Nishina reduction depends on the electron temperature, which is higher for larger surface gravities, therefore the limiting luminosity is higher for larger log g.
Examples of emergent spectra and temperature structures for the models with log g = 14.0 and various chemical compositions (pure hydrogen and solar mix) are shown in Fig. 31. The corresponding emergent spectra and temperature structures computed with the old code employing the Kompaneets operator are also shown. At low luminosities, the models are very close to each other, which is expected as at low temperatures the diffusion (Kompaneets) approximation is an accurate representation of Compton scattering. For models close to the Eddington limit, the treatment of the radiative acceleration becomes important. Contribution of the radiation force to the hydrostatic equilibrium grad/g is smaller in the new models despite l being the same for both model sets. It is well-known that the model spectra with large contributions of radiative acceleration are harder, and their surface temperatures are higher (London et al. 1986; Lapidus et al. 1986; Ebisuzaki 1987; Pavlov et al. 1991). In complete agreement with this, the old models with large l are harder and hotter than new models. However, for the same grad/g the new model spectra are hotter. Normalizing the spectra to the maximum flux and plotting them against the scaled photon energies E/kTeff, one also sees that the new spectra are harder (see Fig. 4).
3.2. Limb-darkening
 |
Fig. 4 Comparison of the emergent spectra (top panel) and the temperature structures (bottom panel) of the new (solid curves) and the old (dashed curves) models with the same grad/g. The models are computed for pure hydrogen as well as solar abundance. The models have different effective temperatures, therefore the spectra are normalized to the maximum flux and plotted against the scaled photon energy. For clarity, the spectra of solar abundance models are shifted by a factor of three, and the relative temperatures are shifted by adding one. |
 |
Fig. 5 Comparison of the emergent specific intensity for pure hydrogen (top panel) and solar abundance models (bottom panel) with the electron-scattering limb-darkening law (dashed curves) for two relative luminosities of l = 0.1 and 0.8. The l = 0.8 models are multiplied by a factor of three for clarity. The lower sub-panels show the ratios of the corresponding models. |
 |
Fig. 6 Comparison of the emergent specific intensity at three angles (from the Gaussian
quadrature μ = 0.113,0.5,0.887,
i.e. |
Knowledge of the angular distribution of the emergent radiation is important when only part of the star is visible (for example, is partially blocked by the accretion disk), or when there are inhomogeneities at the NS surface related, for example, to the varying gravitational acceleration due to the rapid rotation. Computation of the amplitude of reflection from the accretion disk also requires that information. The limb-darkening law (i.e. angular dependence of the intensity) for the radiation emerging from the optically thick electron-scattering-dominated atmosphere is described by the H(0)(μ) function (Chandrasekhar & Breen 1947; Chandrasekhar 1960; Sobolev 1949, 1963). A simple approximation to this function is I(μ) ≈ 1 + 2.06 μ. Our simulations show that the intensity closely (within a couple of per cents) follows the H(0)(μ) function around the peak of the spectrum, in the observed energy range (see Fig. 5). At photon energies below 1 keV, the computed angular distribution becomes more isotropic, because there free-free absorption dominates over electron scattering and the upper atmosphere layers are almost isothermal. The low-inclination intensity is above and the high-inclination intensity is below the electron-scattering limb-darkening law at energies above the peak, because the temperature of the layer where the photons originate drops with the inclination. The iron absorption edge at ~9 keV significantly affects the angular distribution for the solar abundance models (Fig. 5, bottom panel). Above the edge, radiation becomes more directed along the surface normal.
The angular distribution of the intensity also depends on the specific form of the RF used in the calculations. The approximate angle-dependent gives results very close to the reference intensity spectra, within 2% for the largest angle θ (see Fig. 6, top panel). The exact, but angle-averaged, RF, does not give such accurate results (see Fig. 6, bottom panel).
3.3. Color correction factors
 |
Fig. 7 Relative deviations of the new, exact RF-based (solid curves) and old Kompaneets-based (dashed curves) spectra from the best-fit diluted blackbodies versus photon energy for hydrogen (top panel) and solar H/He mixture with Z = 0.3 Z⊙ (bottom panel) low gravity (log g = 14.0) models. Corresponding relative luminosities and the effective temperatures are given at the curves. The vertical dotted line shows the lower boundary of the energy band, where the fitting procedures were performed. For clarity, models with l = 0.1 and 0.5 are shifted up by 0.2 and 0.1, respectively. |
 |
Fig. 8 Color correction factors fc,1 (computed using method 1 from SPW11) for model atmospheres of two chemical compositions (pure hydrogen and solar hydrogen/helium mix with 30% of solar heavy-element abundance) and different log g as functions of the relative luminosity l (top panel) or grad/g (bottom panel). The new models based on the exact RF are shown by the solid curves, and the old models, based on the Kompaneets operator, by dashed curves. |
Color-correction and dilution factors from the blackbody fits to the spectra of hydrogen atmosphere models at log g = 14.0.
All computed emergent spectra of the new atmosphere models were fitted by a diluted
blackbody spectrum 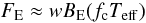 (29)using five
different fitting procedures described in SPW11. We calculated the color
correction fc and dilution w factors in the
energy band (3−20) × (1 + z) keV corresponding to the observed range
of the RXTE/PCA detector. We calculated redshifts
from log g by adopting a NS mass equal
to 1.4 M⊙ (see Eqs. (1) and (4)):
for log g = 14.0, 14.3, and 14.6, we get R = 14.80,
10.88, 8.16 km and z = 0.18, 0.27, 0.42, respectively. Varying the mass
in the interval 1−2 M⊙ has a smaller than 0.1% effect on
the color corrections (SPW11). The results of the fitting procedures are presented in
Table 1 (see also Appendix D).
(29)using five
different fitting procedures described in SPW11. We calculated the color
correction fc and dilution w factors in the
energy band (3−20) × (1 + z) keV corresponding to the observed range
of the RXTE/PCA detector. We calculated redshifts
from log g by adopting a NS mass equal
to 1.4 M⊙ (see Eqs. (1) and (4)):
for log g = 14.0, 14.3, and 14.6, we get R = 14.80,
10.88, 8.16 km and z = 0.18, 0.27, 0.42, respectively. Varying the mass
in the interval 1−2 M⊙ has a smaller than 0.1% effect on
the color corrections (SPW11). The results of the fitting procedures are presented in
Table 1 (see also Appendix D).
Deviations of the new model spectra from the best-fit diluted blackbodies are similar to those for the old spectra based on the Kompaneets operator (Fig. 7). Comparison of the new and old color correction factors is shown in Figs. 8 and 9. Although the old fc − l dependences for different gravities were almost identical at high luminosities, we see that now these dependences deviate, because of the dependence of the limiting relative luminosity on log g. However, the old and new color-correction factors have very similar dependences on grad/g for all log g and chemical compositions (see Figs. 8 and 9), with the new fc being about 1% larger. The difference grows at grad/g close to unity.
Pavlov et al. (1991) derived an approximate
analytical formula for the ratio of the surface model atmosphere temperature to the
effective one 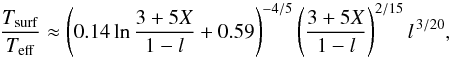 (30)which is correct for the
highly luminous (l > 0.9) model atmospheres. The
numerical constants 0.14 and 0.59 were found from the fitting of their model atmospheres
based on the Kompaneets operator description of Compton scattering. If the models were
instead computed using an exact RF for Compton scattering, it is obvious
that l should be substituted by the relative radiation
acceleration grad/g. We
fit our color correction factors computed using the first fitting procedure (see SPW11)
with a formula similar to Eq. (30) and
found numerical constants that also depend on the chemical composition
(30)which is correct for the
highly luminous (l > 0.9) model atmospheres. The
numerical constants 0.14 and 0.59 were found from the fitting of their model atmospheres
based on the Kompaneets operator description of Compton scattering. If the models were
instead computed using an exact RF for Compton scattering, it is obvious
that l should be substituted by the relative radiation
acceleration grad/g. We
fit our color correction factors computed using the first fitting procedure (see SPW11)
with a formula similar to Eq. (30) and
found numerical constants that also depend on the chemical composition ![\begin{eqnarray} \fc &\approx& \left( \left[ 0.102+0.008X \right] \ln \frac{3+5X}{1-g_{\rm rad}/g} + 0.63-0.06X \right) ^{-4/5} \nonumber \\ &&\times \, \left( \frac{3+5X}{1-g_{\rm rad}/g} \right) ^{2/15} (g_{\rm rad}/g )^{3/20}. \label{eq:fcfit} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq134.png) (31)This
approximation works well for
grad/g > 0.8
(see Fig. 10).
(31)This
approximation works well for
grad/g > 0.8
(see Fig. 10).
3.4. Radiative acceleration
The radiative acceleration can formally be represented as a product of the flux and the
temperature-dependent effective opacity 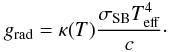 (32)This expression can
alternatively be written as
(32)This expression can
alternatively be written as 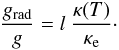 (33)In diffusion
approximation, κ(T) is given by the Rosseland mean
opacity. When electron scattering dominates, it is often approximated (neglecting the
electron degeneracy) as (Paczynski 1983)
(33)In diffusion
approximation, κ(T) is given by the Rosseland mean
opacity. When electron scattering dominates, it is often approximated (neglecting the
electron degeneracy) as (Paczynski 1983)
![\begin{equation} \kappa (T) = \kappaR (T) \approx \kappae \left[1+\left(\frac{kT}{38.8\ {\rm keV}} \right)^{0.86} \right]^{-1}\cdot \label{eq:pacz} \end{equation}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq139.png) (34)This approximation is
based on calculations by Buchler & Yueh
(1976), who underestimated the opacity at low temperatures, where certain
approximations were made because of severe numerical problems. A better approximation in
the range 2−50 keV that is of interest here is (J. Poutanen et al., in prep.)
(34)This approximation is
based on calculations by Buchler & Yueh
(1976), who underestimated the opacity at low temperatures, where certain
approximations were made because of severe numerical problems. A better approximation in
the range 2−50 keV that is of interest here is (J. Poutanen et al., in prep.)
![\begin{equation} \kappaR (T) \approx \kappae \left[1+\left(\frac{kT}{39.4\ {\rm keV}} \right)^{0.976} \right]^{-1}\cdot \label{eq:rossel} \end{equation}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq140.png) (35)It is clear that the
radiative acceleration decreases in the deep, hotter atmosphere layers and the ratio of
radiation pressure force to the surface gravity decreases inwards (see Fig. 11). The radiative acceleration is smaller than that
corresponding to the Thomson opacity, even in the upper atmosphere layers. The actual
radiative acceleration in the surface layers (see top panel in Fig. 11) computed from the models using Eq. (20) is perfectly described by Eqs. (35) and (33)
throughout the whole atmosphere (compare dotted and solid curves at the top panel in
Fig. 11), while Paczynski’s approximation
underestimates it.
(35)It is clear that the
radiative acceleration decreases in the deep, hotter atmosphere layers and the ratio of
radiation pressure force to the surface gravity decreases inwards (see Fig. 11). The radiative acceleration is smaller than that
corresponding to the Thomson opacity, even in the upper atmosphere layers. The actual
radiative acceleration in the surface layers (see top panel in Fig. 11) computed from the models using Eq. (20) is perfectly described by Eqs. (35) and (33)
throughout the whole atmosphere (compare dotted and solid curves at the top panel in
Fig. 11), while Paczynski’s approximation
underestimates it.
Radiative acceleration computed using the angle-averaged RFs is larger than that computed using angle-dependent RFs (see bottom panel in Fig. 11), because the high-energy photons scatter on the relatively cold electrons in a predominantly forward direction, reducing the magnitude of the momentum transfer in comparison with the isotropic case.
Radiative acceleration in the surface layers that we obtain from the models can be
expressed through Teff and fc as
![\begin{equation} \kappa (T=\fc T_{\rm eff}) = \kappae\ \left[1+\left(\frac{kT}{38.8\ {\rm keV}} \right)^{\alpha_{\rm g}} \right]^{-1}, \label{eq:grfit} \end{equation}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq141.png) (36)where
αg = 1.01 + 0.067(log g − 14.0) (see
Fig. 12). The
relation grad/g − l
also slightly depends on the chemical composition, but the dependence on the surface
gravity is stronger.
(36)where
αg = 1.01 + 0.067(log g − 14.0) (see
Fig. 12). The
relation grad/g − l
also slightly depends on the chemical composition, but the dependence on the surface
gravity is stronger.
The relation of the effective temperature to the effective opacity given by Eq. (36) allows us to estimate grad/g for the given model parameters (l,Teff) without actually computing the atmosphere models. We can make a first guess of fc, substitute T = fcTeff to Eq. (36), then use this κ in Eq. (33), find a new fc through Eq. (31), and iterate.
4. Application to observations
In our previous works (S11 and SPW11), we suggested a new method for the determination of
NS radii and masses. It is based on the spectral (blackbody)
normalization K at late phases of PRE X-ray bursts depending on the color
correction factor only 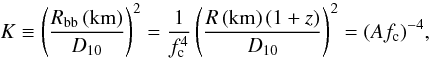 (37)where
D10 = D/10 kpc is the
distance. The observed
relation K−1/4 − Fbb
between the blackbody flux Fbb and
normalization K can be fitted by the theoretical
dependence fc − l obtained from the
atmosphere models. The fit gives two parameters: the value of
A = [R (km) (1 + z)/D10]−1/2
and the observed Eddington flux
FEdd = LEdd(1 + z)-2/(4πD2).
The distance-dependent quantities A and FEdd
can be combined to the distance-independent Eddington temperature which is the apparent
effective temperature corresponding to LEdd
(37)where
D10 = D/10 kpc is the
distance. The observed
relation K−1/4 − Fbb
between the blackbody flux Fbb and
normalization K can be fitted by the theoretical
dependence fc − l obtained from the
atmosphere models. The fit gives two parameters: the value of
A = [R (km) (1 + z)/D10]−1/2
and the observed Eddington flux
FEdd = LEdd(1 + z)-2/(4πD2).
The distance-dependent quantities A and FEdd
can be combined to the distance-independent Eddington temperature which is the apparent
effective temperature corresponding to LEdd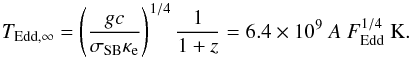 (38)If the distance to the
source is known (for example, for sources in globular clusters), we can plot three curves on
the M − R plane corresponding to the values
of A, FEdd, and
TEdd,∞. Two crossing points give two pairs
of NS mass and radius values that satisfy the observed data.
(38)If the distance to the
source is known (for example, for sources in globular clusters), we can plot three curves on
the M − R plane corresponding to the values
of A, FEdd, and
TEdd,∞. Two crossing points give two pairs
of NS mass and radius values that satisfy the observed data.
 |
Fig. 10 Color correction factor fc versus grad/g for models of various chemical compositions. Solid curves are the results of calculations based on the exact Compton RF, the dotted curves give the approximation (31). For clarity, the curves for pure H models (shown for three log g) are shifted up by +0.2. |
 |
Fig. 11 Top panel: comparison of the relative radiative acceleration in pure hydrogen atmospheres (solid curves) with our approximation given by Eq. (35) (dotted curves, which nearly coincide with solid curves) and with Paczynski’s approximation (34) (dashed curves). Bottom panel: comparison of the relative radiative acceleration for the fiducial model computed with different RFs: exact and approximate, angle-dependent, and angle-averaged. The relative radiative acceleration for Thomson scattering is also shown. |
 |
Fig. 12 Dependence of the relative radiative acceleration grad/g on l. Symbols represent the results of calculations based on the exact Compton RF, the solid curves give the approximation (36). The dot-dashed curve is the l = grad/g relation. |
It is now important to understand how the new models affect results based on formulae that use the Thomson cross-section for electron scattering. We have seen that owing to the Klein-Nishina reduction in the cross-section, the actual Eddington limit is reached at luminosities of 6−10% higher than LEdd and the shape of the fc − l relation differs somewhat from the Kompaneets-based results. As an illustration, we consider a long PRE X-ray burst of 4U 1724–307 in the globular cluster Terzan 2 studied by S11, who obtained a rather large NS radius for this source (R ≥ 14 km). We now use new sets of theoretical relations fc − l that we fit to the observed relation K−1/4 − Fbb, taking pure hydrogen models as an example. We note that the new relations significantly depend on the surface gravity (see Fig. 8, top panel), therefore, in principle, it would be possible also to find the surface gravity that provides the best fit to the observed relation. This is, however, difficult in practise, because a change in log g can be compensated for by varying FEdd.
 |
Fig. 13 Top panel: the fit of the X-ray burst data for 4U 1724–307 by the theoretical models for the NS atmosphere. The circles indicate the observed dependence of K−1/4 versus F for the long burst (S11) and the solid curve corresponds to the best-fit theoretical model for a pure hydrogen atmosphere and log g = 14.0. Vertical dotted and dashed lines show the best-fit value for FEdd for the old and new models. Bottom panel: constraints on mass and radius of the NS in 4U 1724–307. The new (solid) and the old (dashed) curves corresponding to TEdd,∞ are shown. The dash-dotted curve corresponds to the new best-fit parameter A for the distance to the source of 5.3 kpc. |
The theoretical fc–l curve for log g = 14.0 gives the best fit to the data (Fig. 13) for A = 0.168 and FEdd = 4.93 × 10-8 erg s-1 cm-2. The corresponding old, Kompaneets-based values are 0.170 and 5.25 × 10-8, respectively. This small change in the best-fit parameters leads to a small decrease of TEdd,∞ from 1.64 × 107 K to 1.60 × 107 K and a corresponding increase in the NS radii (see Fig. 13, bottom panel). Interestingly, the new TEdd,∞ curve crosses with the curve log g = 14.0 at the NS mass close to 1.5 M⊙, and the curve A = 0.168 also passes through the same crossing point when D10 = 0.53 (i.e. 5.3 kpc, the distance to Terzan 2, Ortolani et al. 1997). The uncertainties in the obtained values arising owing to uncertainties in the data are very close to the differences between the old and the new values of the best-fit parameters (see Table 1 in S11).
A few attempts to find NS mass and radius from the direct fitting of the observed X-ray burst spectrum by NS atmosphere model spectra were performed (Majczyna & Madej 2005; Miller et al. 2011; Kuśmierek et al. 2011). They have proposed finding the best fit for a fixed log g by varying the relative luminosity l (or effective temperature Teff) and the gravitational redshift z. The best-fit between all trial log g values then gives the desired log g and z. Thereafter, the NS mass and radius can be found using Eqs. (1) and (4). Unfortunately, the curves on the M − R plane corresponding to the fixed values of log g and z cross at very small angles (see Fig. 1 in SPW11). Therefore, the uncertainties are expected to be large. More importantly, the model spectra are very close to the blackbody in the observed RXTE/PCA energy band. This means that for an arbitrary product fcTeff (i.e. color temperature of the theoretical spectrum) we can find the redshift z that makes the combination fcTeff/(1 + z) equal to the observed color temperature Tbb, and in turn this method extremely unreliable.
5. Summary
We have considered hot NS model atmospheres taking into account Compton scattering using the relativistic kinetic equation with the exact angle-dependent RF and cross-section (Nagirner & Poutanen 1994; Poutanen & Svensson 1996), accounting also for the induced scattering. We have developed a method to solve the obtained radiation transfer equation using a short characteristic method with the accelerated Λ-iteration. We have implemented this solution in our computer code for the model atmosphere calculations (SPW11).
We have examined the properties of the new model atmospheres. The main difference in comparison with the old models computed with the Kompaneets operator concerns radiative acceleration. In the new approach, the Klein-Nishina reduction in the electron scattering cross-section leads to a decrease in the radiative acceleration relative to that for the Thomson scattering cross-section. The grid of model atmospheres was extended to higher effective temperatures up to luminosities formally exceeding the Eddington limit LEdd computed for the Thomson cross-section. The role of the radiation pressure reduces in the deeper, hot, optically thick layers due to the same effect.
We computed a new set of 484 hot NS model atmospheres. Following SPW11, we computed the models for six different chemical compositions (pure hydrogen, pure helium, solar hydrogen/helium mix with various abundances of heavy elements Z = 1, 0.3, 0.1, and 0.01 Z⊙) and three surface gravities (log g = 14.0,14.3, and 14.6). The relative luminosities range from l = 0.001 to 1.06−1.1 (depending on log g). The new models with l < 0.8 are almost identical to the old models based on the Kompaneets operator approach. At higher l, the deviations are more significant due to a different treatment of the radiative acceleration. The difference between the new and old models is small if instead of l one uses the relative radiative acceleration grad/g as a parameter.
The spectra of the new and old models deviate by less than 5% in the region around the spectral peak, and the deviation grows at higher energies. We have also tested various approximate and angle-averaged RFs for Compton scattering and found that they produce spectra that deviate from the exact solution typically by less than 2%. The comparison of our spectra to the models computed using Madej’s code (Madej 1991; Madej et al. 2004; Majczyna et al. 2005) revealed dramatic differences in the spectral shape. We attribute these differences to their usage of the incorrect RF from Guilbert (1981) and/or to the non-convergence of their radiation transfer calculations.
The spectra of all our models were fitted by the diluted blackbody spectra in the RXTE/PCA energy band (3−20 keV) using the same five fitting procedures as in SPW11. The new fc − l relations are similar in shape to the old relations, but depend significantly on the surface gravity. However, the dependences of the color correction on grad/g are almost indistinguishable, with the new fc being larger by approximately 1%. The color corrections with the corresponding dilution factors, the theoretical emergent spectral energy distributions, and specific intensities at various angles for all models are available at CDS.
In the present paper, we have also tested how the new fc − l relations affect the determination of the NS masses and radii derived from the spectral evolution observed during the cooling stages of PRE bursts. We found that the best-fit NS radius increases by about 10% from the value obtained using the old model based on the Kompaneets equation (S11). We note that bursting NSs are rapidly rotating and accounting for the latitudinal variation in gravity and the Doppler effect will affect the estimated NS radius. This will be a subject of a separate publication.
Online material
Appendix A: Relativistic kinetic equation for Compton scattering and the RFs
For completeness let us rederive here the exact relativistic expressions for the Compton scattering RFs. For the detailed derivation, see Nagirner & Poutanen (1993) and Poutanen & Vurm (2010), where more general problems have been solved. In the first paper, the redistribution matrices describing Compton scattering of polarized radiation in terms of Stokes parameters were derived, while in the second the RFs for anisotropic electron distribution have been obtained. We start from the relativistic kinetic equation (RKE) for photons that describes Compton scattering.
A.1. Radiative transfer equation
A description of interactions between photons and electrons via Compton scattering
accounting for the induced scattering and electron degeneracy can be provided by the
explicitly covariant RKE for photons (Buchler &
Yueh 1976; de Groot et al. 1980; Nagirner & Poutanen 1993, 1994) ![\appendix \setcounter{section}{1} \begin{eqnarray} \fourx \cdot \unb \noccx(\vecx) &=& \frac{\re^2}{2} \frac{2}{\lambdac^3} \int \frac{\rmd \vecp}{\gamma} \frac{\rmd \vecp_1}{\gamma_1} \frac{\rmd \vecx_1}{x_1} \: F \: \delta^4(\fourp_1 + \fourx_1 - \fourp - \fourx) \nonumber \\ &&\times \, \left\{ \noccx(\vecx_1) [1+\noccx(\vecx)] \nocce(\vecp_1) [1-\nocce(\vecp)] \right. \nonumber\\ \label{eq:rke} &&- \left. \,\noccx(\vecx) [1+\noccx(\vecx_1)] \nocce(\vecp) [1-\nocce(\vecp_1)] ) \right\}, \end{eqnarray}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq180.png) (A.1)where
(A.1)where
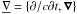 is the four-gradient,
re is the classical electron radius,
λC = h/mec is
the Compton wavelength, F is the Klein-Nishina reaction rate (Berestetskii et al. 1982)
is the four-gradient,
re is the classical electron radius,
λC = h/mec is
the Compton wavelength, F is the Klein-Nishina reaction rate (Berestetskii et al. 1982) 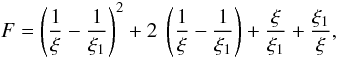 (A.2)and
(A.2)and  (A.3)are the
four-products of the corresponding momenta (second equalities in Eq. (A.3) arising from the four-momentum
conservation law represented by the delta-function in Eq. (A.1)). Here we define the dimensionless
photon four-momentum as
(A.3)are the
four-products of the corresponding momenta (second equalities in Eq. (A.3) arising from the four-momentum
conservation law represented by the delta-function in Eq. (A.1)). Here we define the dimensionless
photon four-momentum as  ,
where ω is the unit vector in the photon propagation
direction and
x ≡ hν/mec2.
The photon distribution is described by either the occupation
number n or the specific intensity (per dimensionless energy
interval)
I(x) = x3n(x)/C,
where the constant C is given by Eq. (13). The dimensionless electron four-momentum is
,
where ω is the unit vector in the photon propagation
direction and
x ≡ hν/mec2.
The photon distribution is described by either the occupation
number n or the specific intensity (per dimensionless energy
interval)
I(x) = x3n(x)/C,
where the constant C is given by Eq. (13). The dimensionless electron four-momentum is
 ,
where Ω is the unit vector along the electron
momentum, γ and
,
where Ω is the unit vector along the electron
momentum, γ and 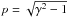 are the electron Lorentz factor and its momentum in units
of mec, and β is the
velocity in units of c. The electron distribution is described by the
occupation number
are the electron Lorentz factor and its momentum in units
of mec, and β is the
velocity in units of c. The electron distribution is described by the
occupation number 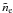 .
For the isotropic electron distribution, we use the electron distribution function
.
For the isotropic electron distribution, we use the electron distribution function
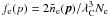 , normalized
to unity
, normalized
to unity 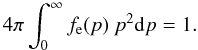 (A.4)In the following, we
consider a steady state and ignore electron degeneracy, because in the upper
atmosphere layers, where the radiation spectrum is formed, electrons are
non-degenerate. We define the RF as
(A.4)In the following, we
consider a steady state and ignore electron degeneracy, because in the upper
atmosphere layers, where the radiation spectrum is formed, electrons are
non-degenerate. We define the RF as 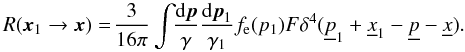 (A.5)For the relativistic
Maxwellian distribution of temperature
Θ = kTe/mec2
(Jüttner 1911; Synge 1957),
(A.5)For the relativistic
Maxwellian distribution of temperature
Θ = kTe/mec2
(Jüttner 1911; Synge 1957), 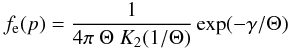 (A.6)(where
K2 is the modified Bessel function), the RF satisfies
the symmetry property
(A.6)(where
K2 is the modified Bessel function), the RF satisfies
the symmetry property 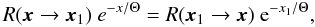 (A.7)which follows
from its definition in Eq. (A.5) and
the energy conservation
γ1 = γ + x − x1,
or from the detailed balance condition (see Eq. (8.2) in Pomraning 1973). Using this result it is easy to show that the
Bose-Einstein distribution
n(x) = 1/(exp { [x − μ] /Θ } − 1)
with any chemical potential is a solution of the RKE (A.1).
(A.7)which follows
from its definition in Eq. (A.5) and
the energy conservation
γ1 = γ + x − x1,
or from the detailed balance condition (see Eq. (8.2) in Pomraning 1973). Using this result it is easy to show that the
Bose-Einstein distribution
n(x) = 1/(exp { [x − μ] /Θ } − 1)
with any chemical potential is a solution of the RKE (A.1).
In the absence of strong magnetic field, the medium is isotropic, therefore the RF
depends only on the photon energies and the scattering angle (where η
is its cosine), i.e. we can write
R(x1 → x) = R(x,x1,η).
The kinetic Eq. (A.1) can then be
recast in a standard form of the radiative transfer equation ![\appendix \setcounter{section}{1} \begin{eqnarray} \lefteqn { \frac{\vomega \cdot \vnabla \noccx(\vecx) }{\sigmat \: \Ne} \!= \! - \noccx(\vecx) \frac{1}{x} \int_{0}^{\infty} \!\! x_1 \rmd x_1 \int \rmd ^2 \vomega_1 \: R(x_1,x,\eta) [1+\noccx(\vecx_1)] } \nonumber \\ \label{eq:rte2} &&\qquad\quad\; + [1+\noccx(\vecx)] \frac{1}{x} \int_{0}^{\infty} \!\! x_1 \rmd x_1\!\! \int \!\! \rmd ^2 \vomega_1 \: R(x,x_1,\eta) \noccx(\vecx_1). \end{eqnarray}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq210.png) (A.8)For
the plane-parallel atmosphere, this reduces to
(A.8)For
the plane-parallel atmosphere, this reduces to ![\appendix \setcounter{section}{1} \begin{eqnarray} \lefteqn { \mu \frac{\rmd \noccx(x,\mu)}{ \rmd \taut} \!=\! \noccx(x,\mu) \frac{1}{x} \int_{0}^{\infty} \!\!\!\! x_1 \rmd x_1 \!\! \int_{-1}^{1} \!\! \rmd \mu_1 \: R(x_1,\mu_1;x,\mu) [1+\noccx(x_1,\mu_1)] } \nonumber \\ & - & [1+\noccx(x,\mu)] \frac{1}{x} \int_{0}^{\infty} \!\!\!\! x_1 \rmd x_1\!\! \int_{-1}^{1} \!\! \rmd \mu_1 \: R(x,\mu;x_1,\mu_1)\noccx(x_1,\mu_1), \label{eq:rte_plane} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq211.png) (A.9)where
dτT = − σTNeds = κe dm,
μ and μ1 are the cosines of the angle
relative to the normal,
(A.9)where
dτT = − σTNeds = κe dm,
μ and μ1 are the cosines of the angle
relative to the normal, 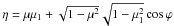 and
and
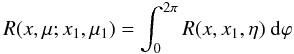 (A.10)is the
azimuth-integrated RF. Rewriting Eq. (A.9) in terms of the intensity I(x,μ), we
get the radiative transfer Eq. (10)
that accounts for electron scattering with the scattering opacity and the source
function given by Eqs. (12) and (14), respectively.
(A.10)is the
azimuth-integrated RF. Rewriting Eq. (A.9) in terms of the intensity I(x,μ), we
get the radiative transfer Eq. (10)
that accounts for electron scattering with the scattering opacity and the source
function given by Eqs. (12) and (14), respectively.
A.2. Redistribution functions
The expression (A.5) for the RF can
be simplified by taking the integral over p with the
help of the three-dimensional delta-function and using the identity
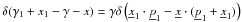
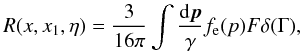 (A.11)where we have
dropped the subscript 1 from the electron quantities and
(A.11)where we have
dropped the subscript 1 from the electron quantities and
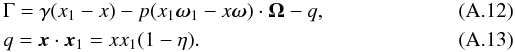 \arraycolsep1.75ptTo
integrate over angles in Eq. (A.11),
we follow the recipe proposed by Aharonian &
Atoyan (1981) (see also Prasad et al.
1986; Poutanen & Vurm 2010),
choosing the polar axis along the direction of the transferred momentum
\arraycolsep1.75ptTo
integrate over angles in Eq. (A.11),
we follow the recipe proposed by Aharonian &
Atoyan (1981) (see also Prasad et al.
1986; Poutanen & Vurm 2010),
choosing the polar axis along the direction of the transferred momentum
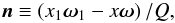 (A.14)where
(A.14)where
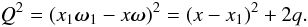 (A.15)Thus, the integration
variables become
cosα = n·Ω
and the azimuth Φ. The RF (A.11) can
then be written as
(A.15)Thus, the integration
variables become
cosα = n·Ω
and the azimuth Φ. The RF (A.11) can
then be written as 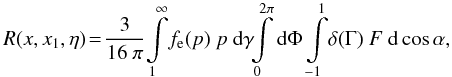 (A.16)where now
(A.16)where now
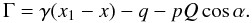 (A.17)Integrating over
cosα using the delta-function, we get
(A.17)Integrating over
cosα using the delta-function, we get 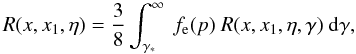 (A.18)where the
integration over the electron distribution can been done numerically. Here we
introduce the RF for monoenergetic electrons
(A.18)where the
integration over the electron distribution can been done numerically. Here we
introduce the RF for monoenergetic electrons 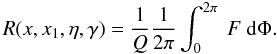 (A.19)We need to
substitute
(A.19)We need to
substitute 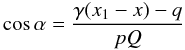 (A.20)into
the expression for F. The condition |cosα| ≤ 1
provides the constraint
(A.20)into
the expression for F. The condition |cosα| ≤ 1
provides the constraint 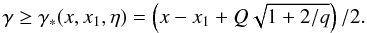 (A.21)Integrating
over azimuth Φ in Eq. (A.19) gives the
exact analytical expression for the RF that is valid for any photon and electron
energy (Aharonian & Atoyan 1981; Nagirner & Poutanen 1994; Poutanen & Vurm 2010), which we use in our
calculations
(A.21)Integrating
over azimuth Φ in Eq. (A.19) gives the
exact analytical expression for the RF that is valid for any photon and electron
energy (Aharonian & Atoyan 1981; Nagirner & Poutanen 1994; Poutanen & Vurm 2010), which we use in our
calculations 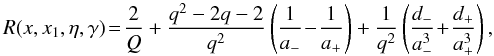 (A.22)where
(A.22)where
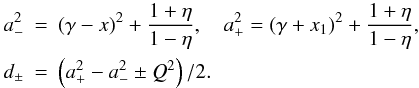 (A.23)We
note that the RF (A.19) satisfies the
detailed balance condition (Nagirner &
Poutanen 1994)
(A.23)We
note that the RF (A.19) satisfies the
detailed balance condition (Nagirner &
Poutanen 1994) 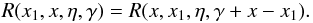 (A.24)The RF (A.11) is related to the scattering
kernel (8.13) of Pomraning (1973) as
R(x,x1,η) = σs(x1 → x,η)x1/x.
The form given by Eq. (A.16) is
equivalent to Eq. (A.4) of Buchler & Yueh
(1976). The derived RF for monoenergetic electrons (A.22) is equivalent to Eq. (A.5) of Buchler & Yueh (1976) and Eq. (14) of Aharonian & Atoyan (1981).
(A.24)The RF (A.11) is related to the scattering
kernel (8.13) of Pomraning (1973) as
R(x,x1,η) = σs(x1 → x,η)x1/x.
The form given by Eq. (A.16) is
equivalent to Eq. (A.4) of Buchler & Yueh
(1976). The derived RF for monoenergetic electrons (A.22) is equivalent to Eq. (A.5) of Buchler & Yueh (1976) and Eq. (14) of Aharonian & Atoyan (1981).
A very simple approximate expression for the RF can be obtained by assuming that the
scattering in the electron rest frame proceeds in the Thomson regime (i.e. coherent)
and is isotropic. This is equivalent to substituting F
by 4/3 in Eq. (A.19). We then get (Arutyunyan &
Nikogosyan 1980; Poutanen 1994; Poutanen & Svensson 1996) 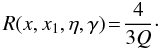 (A.25)Integrating
it over the Maxwellian distribution (A.6) gives
(A.25)Integrating
it over the Maxwellian distribution (A.6) gives 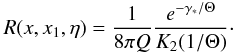 (A.26)This
approximate RF is also used in the calculations. We note that this RF also satisfies
the detailed balance condition (A.7).
(A.26)This
approximate RF is also used in the calculations. We note that this RF also satisfies
the detailed balance condition (A.7).
Appendix B: Method for solving the radiation transfer equation
The formal solution of the radiative transfer equation gives a relation between the
outward I + (x,μ) and the inward
I−(x,μ) = I(x, − μ)
intensities at some depth point i (on the optical depth
grid 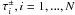 )
with the adjacent intensities
)
with the adjacent intensities ![\appendix \setcounter{section}{2} \begin{eqnarray} I^+_i(x,\mu) &=& I^+_{i+1}(x,\mu) \exp[-(\tau^+_{i+1}-\tau^+_i)/\mu] \\ \nonumber && + \int^{\tau^+_{i+1}}_{\tau^+_i}\,S^+(t,x,\mu)\exp[-(t-\tau^+_i)/\mu]\,{\rm d}t/\mu, \\ I^-_i(x,\mu) &=& I^-_{i-1}(x,\mu) \exp[-(\tau^-_{i}-\tau^-_{i-1})/|\mu|] \\ \nonumber && +\int^{\tau^-_{i}}_{\tau^-_{i-1}}\,S^-(t,x,\mu)\exp[-(\tau^-_i-t)/|\mu]\,{\rm d}t/|\mu|. \end{eqnarray}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq242.png) The
integrals can be replaced by the sums using the parabolic approximation
The
integrals can be replaced by the sums using the parabolic approximation
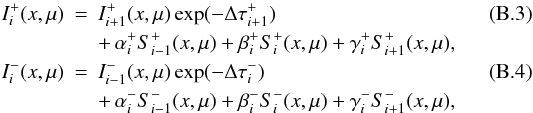 where
where
![\appendix \setcounter{section}{2} \begin{eqnarray} && \Delta\tau^{\pm}_i = (\tau^{\pm}_{i}-\tau^{\pm}_{i-1})/|\mu|, \\ \nonumber && \alpha^-_i = e^-_{0,i} + \frac{e^-_{2,i}-(\Delta\tau^-_{i+1} +2\Delta\tau^-_{i})\,e^-_{1,i}}{\Delta\tau^-_{i}(\Delta\tau^-_{i+1}+\Delta\tau^-_{i})}, \\ \nonumber && \beta^-_i = ([\Delta\tau^-_{i} +\Delta\tau^-_{i+1}]\,e^-_{1,i}-e^-_{2,i})/(\Delta\tau^-_{i}\Delta\tau^-_{i+1}), \\ \nonumber && \gamma^-_i = (e^-_{2,i}-\Delta\tau^-_{i}\,e^-_{1,i})/[\Delta\tau^-_{i+1}(\Delta\tau^-_{i+1}+\Delta\tau^-_{i})], \\ \nonumber && \alpha^+_i = (e^+_{2,i+1}-\Delta\tau^+_{i+1}\,e^+_{1,i+1})/(\Delta\tau^+_{i}[\Delta\tau^+_{i+1}+\Delta\tau^+_{i}]), \\ \nonumber && \beta^+_i = ([\Delta\tau^+_{i} +\Delta\tau^+_{i+1}]\,e^+_{1,i+1}-e^+_{2,i+1})/(\Delta\tau^+_{i}\Delta\tau^+_{i+1}), \\ \nonumber && \gamma^+_i = e^+_{0,i+1} +\frac{e^+_{2,i+1}-(\Delta\tau^+_{i} +2\Delta\tau^+_{i+1})\,e^+_{1,i+1}}{\Delta\tau^+_{i+1}(\Delta\tau^+_{i+1}+\Delta\tau^+_{i})}, \end{eqnarray}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq244.png) (B.5)\arraycolsep1.75ptand
(B.5)\arraycolsep1.75ptand
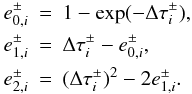 (B.6)At
the first depth point, the coefficients are
(B.6)At
the first depth point, the coefficients are
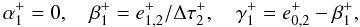 (B.7)and at the last
point they are
(B.7)and at the last
point they are 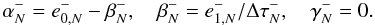 (B.8)We note that the
inward and the outward opacities along the same ray are different (see Eq. (12)).
(B.8)We note that the
inward and the outward opacities along the same ray are different (see Eq. (12)).
 |
Fig. B.1 Comparison of the emergent spectra from a hot electron slab back-irradiated by a blackbody computed using the compps code and the code presented here. |
The formal solution for a given source function starts for the inward intensities from
the outer boundary condition (the lack of incoming radiation at the surface)
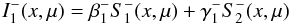 (B.9)up to the last depth
point N. The intensities at the innermost depth point are found using
the inner boundary condition, which is taken from the diffusion approximation
(B.9)up to the last depth
point N. The intensities at the innermost depth point are found using
the inner boundary condition, which is taken from the diffusion approximation
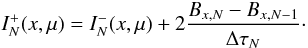 (B.10)The full solution is
found iteratively using an accelerated Λ-iteration. At the first iteration, the thermal
part of the source function is taken. For the subsequent iteration n,
the intensities obtained from the previous iteration n − 1 are used to
compute the current source functions
(B.10)The full solution is
found iteratively using an accelerated Λ-iteration. At the first iteration, the thermal
part of the source function is taken. For the subsequent iteration n,
the intensities obtained from the previous iteration n − 1 are used to
compute the current source functions 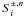 .
Iterations are continued until the relative change becomes smaller than the
predetermined accuracy
.
Iterations are continued until the relative change becomes smaller than the
predetermined accuracy ![\appendix \setcounter{section}{2} \begin{equation} \max \left[\frac{J^{n}_i(x)}{J^{n-1}_i(x)}-1\right] < 10^{-4}, \end{equation}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq254.png) (B.11)where
Ji(x) are the mean
intensities. This solution method of the radiation transfer equation was tested for a
rather optically thin (Thomson optical depth τT = 2) and hot
(kTe = 60 keV) electron slab
back-illuminated by soft blackbody photons of
kTBB = 1 keV. The solution for the
emergent intensities obtained at five angles using our method were compared with the
solution obtained with the Comptonization code compps (Poutanen & Svensson 1996, see Fig. B.1).
(B.11)where
Ji(x) are the mean
intensities. This solution method of the radiation transfer equation was tested for a
rather optically thin (Thomson optical depth τT = 2) and hot
(kTe = 60 keV) electron slab
back-illuminated by soft blackbody photons of
kTBB = 1 keV. The solution for the
emergent intensities obtained at five angles using our method were compared with the
solution obtained with the Comptonization code compps (Poutanen & Svensson 1996, see Fig. B.1).
 |
Fig. B.2 The maximum relative change in the solution of the radiation transfer equation at the final temperature correction computed by different versions of the accelerated Λ-iteration. |
In the optically thick case (τT ≫ 1), which is typical of
NS atmospheres, the convergence of the solution can be accelerated using the following
procedure. The difference between the formal solution obtained in the current
iteration I ± ,n,FS and the solution at
iteration n − 1 is increased by some factor
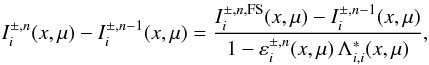 (B.12)where
(B.12)where
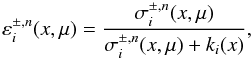 (B.13)and
(B.13)and
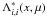 is the diagonal term of the
approximate Λ-operator
is the diagonal term of the
approximate Λ-operator ![\appendix \setcounter{section}{2} \begin{eqnarray} \Lambda^*_{i,i}(x,\mu) &=& \frac{1}{4}[\beta^+_i(x,\mu)+\beta^-_i(x,\mu)]\, \nonumber \\ &&\times \, x^2\,\int_0^\infty \frac{{\rm d}x_{\rm 1}}{x^2_{\rm 1}} \int_{-1}^1 {\rm d}\mu_{\rm 1} R(x, \mu;x_{\rm 1},\mu_1). \end{eqnarray}](/articles/aa/full_html/2012/09/aa19480-12/aa19480-12-eq264.png) (B.14)The
acceleration is not high (about 30–40%) and the number of necessary iterations is still
large (see Fig. B.2). However, in the process of
the model atmosphere computation it is possible to use the source function from the
previous temperature iteration as the starting approximation for the current source
function (see details in Sect. 2). In this case,
the acceleration depends on the value of the temperature
corrections ΔTi. At the first few
temperature iterations, when ΔTi are large,
the acceleration is insignificant, but at later iterations, when
ΔTi are relatively small,
the accelerated Λ-iterations converge very quickly (Fig. B.2).
(B.14)The
acceleration is not high (about 30–40%) and the number of necessary iterations is still
large (see Fig. B.2). However, in the process of
the model atmosphere computation it is possible to use the source function from the
previous temperature iteration as the starting approximation for the current source
function (see details in Sect. 2). In this case,
the acceleration depends on the value of the temperature
corrections ΔTi. At the first few
temperature iterations, when ΔTi are large,
the acceleration is insignificant, but at later iterations, when
ΔTi are relatively small,
the accelerated Λ-iterations converge very quickly (Fig. B.2).
Appendix C: Comparison with Madej’s code
 |
Fig. C.1 Left panels: comparison of emergent spectra and temperature structures of the models computed by our code (solid curves) and Madej’s code (dashed curves), when electron scattering is approximated by coherent Thomson scattering. Right panels: same as left, but when the exact RF was used to compute Compton scattering. The spectrum computed by us using the Madej’s temperature structure is shown by the dotted curve and the spectrum computed with a relative accuracy of 10-2 is presented by dash-dots. |
The only other attempt to compute NS atmospheres using an integral approach to Compton scattering going beyond the Kompaneets approximation was that of J. Madej et al. (Madej 1991; Madej et al. 2004; Majczyna et al. 2005). They used an angle-averaged RF for Compton scattering derived by Guilbert (1981). It is important to compare our results with those obtained by Madej’s code for the same input parameters. We selected our fiducial model as a testbed and computed two models. In the first, we approximated electron scattering by coherent Thomson scattering. In the second, the exact fully relativistic RF for Compton scattering was used. Calculations for identical parameters were performed with Madej’s code (J. Madej & A. Różańska, priv. comm.). A comparison between the results is shown in Fig. C.1.
We see that the Thomson scattering models are very close to each other, in terms of both the spectra and the temperature structures (Fig. C.1, left panels). However, the models with Compton scattering differ substantially (Fig. C.1, right panels). Temperatures in the upper layers with column densities less than 103 g cm-2 are lower in our model by up to 5−15%, and our spectrum (solid curve) is much more peaked and softer than that computed by Madej’s code (dashed curve). We also note that our spectrum is very close to the diluted blackbody spectra, which cannot be said about Madej’s spectrum.
We can suggest two hypotheses to explain the discrepancies. First, there is a difference in the RF used by the two codes. We employed the exact relativistic RF (see Appendix A.2), which had been extensively studied and tested against Monte-Carlo simulations (Stern et al. 1995; Zdziarski et al. 2000). Madej and collaborators (Madej 1991; Madej et al. 2004; Majczyna et al. 2005) used the (angle-averaged) RF derived by Guilbert (1981) (see his Eqs. (8) and (10)), which differs from the correct expression (A.19) by an additional factor [1 − (β·n)(n·ω1)] /(1 − β·ω1), which appeared from an error in the Jacobian. Guilbert’s RF also does not satisfy the detailed balance condition (A.24) and therefore the RF integrated over the electron distribution does not satisfy the condition (A.7) either. Because the energy transfer by Compton scattering scales as β2, the error on the order of β obviously invalidates all the results obtained with this RF.
Second, some of the discrepancies could be connected to a difference in the computation of the radiation transfer and the atmosphere modeling. We illustrate this in Fig. C.1 (top right panel). Using our radiation transfer code, we computed the spectrum using the temperature structure from Madej’s calculations. When calculations proceeded until the accuracy of 10-4 was reached (dotted curve), the spectrum was much above our benchmark spectrum, i.e. it had a much higher effective (and color) temperature. If calculations were stopped at a lower accuracy of 10-2 (dash-dotted curve), the spectrum was found to be similar to Madej’s spectrum. This suggests that the radiation transfer iterations with Madej’s code did not sufficiently converge.
Madej et al. use the partial linearization method described in Mihalas (1978, p. 179) and modified to include Compton scattering. Their radiation transfer equation is rewritten to include the linearized part of the radiative equilibrium equation. The solution of this generalized radiation transfer equation satisfies simultaneously the radiative equilibrium to the first order. Using the computed radiation field, the temperature correction for the current temperature structure of the atmosphere is found. This procedure is iterated until some convergence criterion is satisfied, for example, the emergent bolometric flux is accurate to within 0.1%. In this method, the accuracy of the current solution of the radiation transfer equation is on the order ΔT/T, which is about 10-2−10-3 at the last iteration. We have shown above that this internal accuracy is insufficient to obtain the exact solution of the radiation transfer equation when Compton scattering is taken into account. We note that using this method is not possible to solve the radiation transfer equation for a given atmosphere model or, for example, for a homogeneous isothermal slab. This means that it cannot be checked independently of the atmosphere modeling.
Appendix D: Atmosphere model spectra and color-corrections
Table D.1 gives the color-correction and dilution factors from the blackbody fits to 484 atmosphere model spectra (fluxes), which in their turn are given in Table D.2. Table D.3 contains the emergent specific intensities at three angles. Tables D.1−D.3 are only available in electronic form at the CDS. The Xspec code utilizing the models is available from the authors on request.
The spectral energy distributions of fluxes and specific intensities for all models are described in Appendix D.
Acknowledgments
The work is supported by the German Research Foundation (DFG) grant SFB/Transregio 7 Gravitational Wave Astronomy, Russian Foundation for Basic Research (grant 12-02-97006-r-povolzhe-a), the Jenny ja Antti Wihuri foundation, and the Academy of Finland (grant 127512). We also acknowledge the support of the International Space Science Institute (Bern, Switzerland), where part of this investigation was carried out. We are grateful to Jerzy Madej and Agata Różańska for kindly providing us with the results of their atmosphere calculations.
References
- Aharonian, F. A., & Atoyan, A. M. 1981, Ap&SS, 79, 321 [NASA ADS] [Google Scholar]
- Arutyunyan, G. A., & Nikogosyan, A. G. 1980, Sov. Phys. Dokl., 25, 918 [Google Scholar]
- Berestetskii, V. B., Lifshitz, E. M., & Pitaevskii, L. P. 1982, Quantum electrodynamics (Oxford: Pergamon Press) [Google Scholar]
- Buchler, J. R., & Yueh, W. R. 1976, ApJ, 210, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1960, Radiative transfer (New York: Dover) [Google Scholar]
- Chandrasekhar, S., & Breen, F. H. 1947, ApJ, 105, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Damen, E., Magnier, E., Lewin, W. H. G., et al. 1990, A&A, 237, 103 [NASA ADS] [Google Scholar]
- de Groot, S. R., van Leeuwen, W. A., & van Weert, C. G. 1980, Relativistic kinetic equation (Amsterdam: North-Holland) [Google Scholar]
- Ebisuzaki, T. 1987, PASJ, 39, 287 [NASA ADS] [Google Scholar]
- Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Guilbert, P. W. 1981, MNRAS, 197, 451 [NASA ADS] [Google Scholar]
- Hubeny, I., Hummer, D., & Lanz, T. 1994, A&A, 282, 151 [NASA ADS] [Google Scholar]
- Hummer, D., & Mihalas, D. 1988, ApJ, 331, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Ibragimov, A. A., Suleimanov, V. F., Vikhlinin, A., & Sakhibullin, N. A. 2003, Astron. Rep., 47, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Jüttner, F. 1911, Ann. Phys. Chem., 34, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Kompaneets, A. S. 1957, Sov. Phys.–JETP, 4, 730 [Google Scholar]
- Kurucz, R. L. 1970, SAO Special Report, 309 [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid, Kurucz CD-ROM No. 13, Cambridge, Mass.: Smithsonian Astrophysical Observatory [Google Scholar]
- Kuśmierek, K., Madej, J., & Kuulkers, E. 2011, MNRAS, 415, 3344 [NASA ADS] [CrossRef] [Google Scholar]
- Lapidus, I. I., Syunyaev, R. A., & Titarchuk, L. G. 1986, Sov. Astron. Lett., 12, 383 [NASA ADS] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2007, Phys. Rep., 442, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G., van Paradijs, J., & Taam, R. E. 1993, Space Sci. Rev., 62, 223 [NASA ADS] [CrossRef] [Google Scholar]
- London, R. A., Taam, R. E., & Howard, W. M. 1986, ApJ, 306, 170 [Google Scholar]
- Madej, J. 1991, ApJ, 376, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Madej, J., Joss, P. C., & Różańska, A. 2004, ApJ, 602, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Majczyna, A., & Madej, J. 2005, Acta Astron., 55, 349 [NASA ADS] [Google Scholar]
- Majczyna, A., Madej, J., Joss, P. C., & Różańska, A. 2005, A&A, 430, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihalas, D. 1978, Stellar atmospheres, 2nd edn. (San Francisco: W. H. Freeman and Co.) [Google Scholar]
- Miller, M. C., Boutloukos, S., Lo, K. H., & Lamb, F. K. 2011, in Fast X-ray timing and spectroscopy at extreme count rates, PoS (HTRS 2011) 024 [Google Scholar]
- Nagirner, D. I., & Poutanen, J. 1993, A&A, 275, 325 [NASA ADS] [Google Scholar]
- Nagirner, D. I., & Poutanen, J. 1994, Astrophys. Space Phys. Rev., 9, 1 [NASA ADS] [Google Scholar]
- Olson, G. L., & Kunasz, P. B. 1987, J. Quant. Spec. Radiat. Transf., 38, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Ortolani, S., Bica, E., & Barbuy, B. 1997, A&A, 326, 614 [NASA ADS] [Google Scholar]
- Paczynski, B. 1983, ApJ, 267, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlov, G. G., Shibanov, I. A., & Zavlin, V. E. 1991, MNRAS, 253, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Pomraning, G. C. 1973, The Equations of Radiation Hydrodynamics (Oxford: Pergamon) [Google Scholar]
- Poutanen, J. 1994, Ph.D. Thesis, Univ. Helsinki [Google Scholar]
- Poutanen, J., & Svensson, R. 1996, ApJ, 470, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., & Vurm, I. 2010, ApJS, 189, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Prasad, M. K., Kershaw, D. S., & Beason, J. D. 1986, Appl. Phys. Lett., 48, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolev, V. V. 1949, Uch. Zap. Leningrad Univ., 16 [Google Scholar]
- Sobolev, V. V. 1963, A treatise on radiative transfer (Princeton: Van Nostrand) [Google Scholar]
- Stern, B. E., Poutanen, J., Svensson, R., Sikora, M., & Begelman, M. C. 1995, ApJ, 449, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T., & Bildsten, L. 2006, in Compact stellar X-ray sources, eds. W. Lewin, & M. van der Klis (Cambridge: Cambridge University Press), Cambridge Astrophys. Ser., 39, 113 [Google Scholar]
- Suleimanov, V., & Poutanen, J. 2006, MNRAS, 369, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Suleimanov, V., & Werner, K. 2007, A&A, 466, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suleimanov, V., Poutanen, J., Revnivtsev, M., & Werner, K. 2011a, ApJ, 742, 122 (S11) [NASA ADS] [CrossRef] [Google Scholar]
- Suleimanov, V., Poutanen, J., & Werner, K. 2011b, A&A, 527, A139 (SPW11) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Synge, J. L. 1957, The Relativistic Gas (Amsterdam: North-Holland Publication) [Google Scholar]
- van Paradijs, J., Dotani, T., Tanaka, Y., & Tsuru, T. 1990, PASJ, 42, 633 [NASA ADS] [Google Scholar]
- Verner, D. A., & Yakovlev, D. G. 1995, A&AS, 109, 125 [NASA ADS] [Google Scholar]
- Zdziarski, A. A., Poutanen, J., & Johnson, W. N. 2000, ApJ, 542, 703 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Color-correction and dilution factors from the blackbody fits to the spectra of hydrogen atmosphere models at log g = 14.0.
All Figures
 |
Fig. 1 Emergent spectrum (top panel) and temperature structure (bottom panel) of the fiducial model (pure hydrogen, Teff = 1.8 × 107 K, log g = 14.0) computed using three different methods. In accurate method 1 every Λ-iteration starts from the thermal part of the source function (solid curves give the results for the relative accuracy of 10-4). In accelerated method 2, the Λ-iterations start from the source function taken from previous temperature iteration, but at every fifth temperature correction they start from the thermal part of the source function (dashed curves show results for the relative accuracy of 10-4). Method 3 is the same as method 2, but for the relative accuracy of 10-5 (dot-dashed curve). In the top lower panel, the ratios of the spectra for methods 2 and 3 to the spectrum computed with method 1 are shown. The ratio of the temperature structures computed using methods 2 and 1 is shown in the bottom lower panel. |
| In the text | |
 |
Fig. 2 Left panels present the emergent spectrum (top panel) and the temperature structure (bottom panel) of the fiducial model computed using four different RFs: (a) exact angle-dependent (solid curves), (b) exact angle-averaged (dashed curves), (c) approximate angle-dependent (dot-dashed curves), and (d) approximate angle-averaged (dotted curves). In the top lower sub-panel, the ratios of the spectra (b), (c), and (d) to the spectrum for case (a) are shown. In the bottom lower sub-panel, the ratio of the temperature structures (b), (c), and (d) to that of case (a) are shown. Right panels present the emergent spectrum (top panel) and the temperature structure (bottom panel) of the fiducial model computed using an exact angle-dependent RF (solid curves) and the Kompaneets operator (dashed curves). |
| In the text | |
 |
Fig. 3 Comparison of the emergent spectra (top panel) and the temperature structures (bottom panel) computed using the present code with the exact RF (solid curves) and the previous code employing the Kompaneets operator (dashed curves). The models for various relative luminosities are marked by corresponding numbers next to the curves. Left panels are for pure H and right panels are for the solar abundances. |
| In the text | |
 |
Fig. 4 Comparison of the emergent spectra (top panel) and the temperature structures (bottom panel) of the new (solid curves) and the old (dashed curves) models with the same grad/g. The models are computed for pure hydrogen as well as solar abundance. The models have different effective temperatures, therefore the spectra are normalized to the maximum flux and plotted against the scaled photon energy. For clarity, the spectra of solar abundance models are shifted by a factor of three, and the relative temperatures are shifted by adding one. |
| In the text | |
 |
Fig. 5 Comparison of the emergent specific intensity for pure hydrogen (top panel) and solar abundance models (bottom panel) with the electron-scattering limb-darkening law (dashed curves) for two relative luminosities of l = 0.1 and 0.8. The l = 0.8 models are multiplied by a factor of three for clarity. The lower sub-panels show the ratios of the corresponding models. |
| In the text | |
 |
Fig. 6 Comparison of the emergent specific intensity at three angles (from the Gaussian
quadrature μ = 0.113,0.5,0.887,
i.e. |
| In the text | |
 |
Fig. 7 Relative deviations of the new, exact RF-based (solid curves) and old Kompaneets-based (dashed curves) spectra from the best-fit diluted blackbodies versus photon energy for hydrogen (top panel) and solar H/He mixture with Z = 0.3 Z⊙ (bottom panel) low gravity (log g = 14.0) models. Corresponding relative luminosities and the effective temperatures are given at the curves. The vertical dotted line shows the lower boundary of the energy band, where the fitting procedures were performed. For clarity, models with l = 0.1 and 0.5 are shifted up by 0.2 and 0.1, respectively. |
| In the text | |
 |
Fig. 8 Color correction factors fc,1 (computed using method 1 from SPW11) for model atmospheres of two chemical compositions (pure hydrogen and solar hydrogen/helium mix with 30% of solar heavy-element abundance) and different log g as functions of the relative luminosity l (top panel) or grad/g (bottom panel). The new models based on the exact RF are shown by the solid curves, and the old models, based on the Kompaneets operator, by dashed curves. |
| In the text | |
 |
Fig. 9 Same as Fig. 8, but for different chemical compositions and log g = 14.0. |
| In the text | |
 |
Fig. 10 Color correction factor fc versus grad/g for models of various chemical compositions. Solid curves are the results of calculations based on the exact Compton RF, the dotted curves give the approximation (31). For clarity, the curves for pure H models (shown for three log g) are shifted up by +0.2. |
| In the text | |
 |
Fig. 11 Top panel: comparison of the relative radiative acceleration in pure hydrogen atmospheres (solid curves) with our approximation given by Eq. (35) (dotted curves, which nearly coincide with solid curves) and with Paczynski’s approximation (34) (dashed curves). Bottom panel: comparison of the relative radiative acceleration for the fiducial model computed with different RFs: exact and approximate, angle-dependent, and angle-averaged. The relative radiative acceleration for Thomson scattering is also shown. |
| In the text | |
 |
Fig. 12 Dependence of the relative radiative acceleration grad/g on l. Symbols represent the results of calculations based on the exact Compton RF, the solid curves give the approximation (36). The dot-dashed curve is the l = grad/g relation. |
| In the text | |
 |
Fig. 13 Top panel: the fit of the X-ray burst data for 4U 1724–307 by the theoretical models for the NS atmosphere. The circles indicate the observed dependence of K−1/4 versus F for the long burst (S11) and the solid curve corresponds to the best-fit theoretical model for a pure hydrogen atmosphere and log g = 14.0. Vertical dotted and dashed lines show the best-fit value for FEdd for the old and new models. Bottom panel: constraints on mass and radius of the NS in 4U 1724–307. The new (solid) and the old (dashed) curves corresponding to TEdd,∞ are shown. The dash-dotted curve corresponds to the new best-fit parameter A for the distance to the source of 5.3 kpc. |
| In the text | |
 |
Fig. B.1 Comparison of the emergent spectra from a hot electron slab back-irradiated by a blackbody computed using the compps code and the code presented here. |
| In the text | |
 |
Fig. B.2 The maximum relative change in the solution of the radiation transfer equation at the final temperature correction computed by different versions of the accelerated Λ-iteration. |
| In the text | |
 |
Fig. C.1 Left panels: comparison of emergent spectra and temperature structures of the models computed by our code (solid curves) and Madej’s code (dashed curves), when electron scattering is approximated by coherent Thomson scattering. Right panels: same as left, but when the exact RF was used to compute Compton scattering. The spectrum computed by us using the Madej’s temperature structure is shown by the dotted curve and the spectrum computed with a relative accuracy of 10-2 is presented by dash-dots. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.