| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219184 | |
| Published online | 10 September 2012 | |
Distribution of the heavy elements throughout the extended narrow-line region of the Seyfert galaxy NGC 7212⋆
1
Dipartimento di Fisica e AstronomiaUniversity of Padova,
Vicolo dell’Osservatorio 2,
35122
Padova,
Italy
e-mail: valentina.cracco@unipd.it
2
School of Physics and Astronomy, Tel-Aviv
University, 69978
Tel-Aviv,
Israel
Received: 7 March 2012
Accepted: 4 July 2012
The latest observations of line and continuum spectra emitted from the extended narrow-line region (ENLR) of the Seyfert 2 galaxy NGC 7212 are analysed using models that account for photoionization from the active galactic nucleus (AGN) and shocks. The results show that relatively high (500–800 km s-1) shock velocities appear at the edge of the cone and beyond. The model-inferred AGN flux, which is lower than 10-11 photons cm-2 s-1 eV-1 at the Lyman limit, is more typical of low-luminosity AGN than Seyfert 2 galaxies. The preshock densities are characteristic of the ENLR and range between 80–150 cm-3. Nitrogen and sulphur are found to be depleted by a factor lower than 2, particularly at the eastern edge. Oxygen is depleted at several locations. The Fe/H ratio is approximately solar, whereas the Ne/H relative abundance is unusually high, 1.5–2 times the solar value. Modelling the continuum spectral energy distribution (SED), we have found radio synchrotron radiation generated by the Fermi mechanism at the shock front, whereas the X-rays are produced by the bremsstrahlung from a relatively high temperature plasma.
Key words: radiation mechanisms: general / shock waves / ISM: abundances / galaxies: Seyfert / galaxies: individual: NGC 7212
Table 2 is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Morphological and spectroscopic studies of Seyfert galaxies have shed light on the nature of active galactic nuclei (AGN). Specifically, the spectra of type 2 Seyferts are generally dominated by strong forbidden and permitted lines that reveal the physical properties of the extended narrow-line region (ENLR). The spectra indicate that radiation from the AGN dominates the radiation field; however, line ratios corresponding to low ionization levels and neutral lines could be explained by underlying shock wave hydrodynamics. The full width at half maximum (FWHM) of the lines reveals velocities of up to 1000 km s-1. Modelling of line and continuum spectra observed in many single regions throughout the ENLR provided a new dimension to our knowledge. For instance, the complex nature of NGC 7130, in terms of the intermingled activity of starbursts, shocks, and of an active nucleus and their mutual location, could be traced by Contini et al. (2002a). In these objects, e.g. NGC 4388 (Ciroi et al. 2003) or Mrk 298 (Radovich et al. 2005), the relative importance of the radiation flux from the AGN, of shocks, and of radiation from starbursts could be determined in the different regions of the galaxy. This method, which is useful for isolated galaxies, becomes fundamental for the analysis of Seyfert nuclei in merging systems that originate from collisions, even for multiple (generally double) nuclei that are not yet clearly identified as such by the observations. For instance, the biconical structure of the high-excitation region that emerges from the toroidal obscuring material can be fragmented by collision, and patches of highly ionized material can appear at the edges of the ENLR, as e.g. in NGC 3393 (Cooke et al. 2000). The interaction of the ENLR galactic matter with fast shocks, star formation, dust grain destruction etc. are amply analysed and summarised by Ramos Almeida et al. (2009) for NGC 7212 and other Seyfert 2 galaxies.
NGC 7212 (z = 0.0266) belongs to a compact group of interacting galaxies, with two galaxies in a clear ongoing merger (Wasilewski 1981). Spectropolarimetry studies show the presence of a hidden broad line region (BLR) (Tran & Kay 1992), clumpy nuclear morphology, and irregular diffuse emission. Muñoz Marín et al. (2007) also claimed that these galaxies manifest some cases in which in addition to the extended emission, the UV light stems from the knots or clumps that are likely produced by star clusters. These authors identified the bright clumps to the south as star-forming regions with a certain contribution from the AGN. Exploring whether photoionization or shocks dominate in NGC 7212, Bianchi et al. (2006) found a striking resemblance of the [O III] structure with soft X-ray emission, a clear indication that shocks are at work.
In an accompanying paper, Cracco et al. (2011) presented new observations of NGC 7212 and suggested that its ENLR gas has an external origin, likely due to gravitational interaction effects that act in this triple system. The optical spectra described in detail by Cracco et al. are rich in number of lines: e.g. oxygen from three ionization levels ([O III]5007, [O II]3727 and [O I]6300), He II 4686 and He I 5876, [Ne III]3869, [N II]6548, 6583, the two [S II] lines 6716 and 6731, lines from higher ionization levels, e.g. [Ar IV]4713 and [Fe VII]6087, in addition to Hβ and Hα. The line ratios constrain the physical conditions of the emitting gas and the relative abundances. These authors pointed out for the first time the presence of an extended ionization cone in NGC 7212, with high values of [O III]/Hβ, up to 3.6 kpc. Indeed, the Veilleux & Osterbrock (1987) diagnostic diagrams indicate that the main source of ionization, at least in the entire field of view of the integral field spectra, is the AGN. However, high values of [N II]/Hα and [S II]/Hα are observed towards the region of gravitational interaction between the interacting galaxies, suggesting a possible combination of ionization by the active nucleus and shocks. On the other hand, no contribution from stellar ionization is required to explain the observed emission line ratios. An archival broad-band Hubble Space Telescope (HST) image of NGC 7212 obtained with the F606W filter reveals a structure composed of clouds or filaments (see Fig. 19 in Cracco et al. 2011). The evidence of dust located in the ENLR also supports the idea that the gas in the cone has a filamentary structure. In addition, comparing the more significant line ratios (e.g. [O III]/Hβ, [O II]/Hβ, [N II]/Hα, etc.) with diagnostic diagrams, Cracco et al. found depletion of heavy elements such as N and O relative to solar.
The emission line profiles of [O III] inside the ionization cone display blue wings in the northern side of the cone, and red wings in the southern side, while in the nucleus the profiles are symmetric. This suggests the presence of gas in radial motions, which is confirmed also by the analysis of high-resolution echelle spectra characterised by multiple kinematical components at different velocities. If radial motions are acting in the ENLR of NGC 7212, shock ionization is expected to play a significant role.
Moreover, it is well known that the higher the flux from the photoionizing source, the stronger the [O III] lines are, while emission lines such as [O II], [N II], etc., namely low-ionization level lines, are significant when the gas is affected by strong shock. Consequently, we decided to reproduce the observational data presented by Cracco et al. (2011) by means of models that account for the coupled effect of photoionization and shock, improving their interpretation, and adding information concerning the physical and chemical conditions throughout the galaxy.
The structure of the paper is as follows: observations of the optical spectra are described in Sect. 2. In Sect. 3 the models and the modelling method are explained. Modelling results of the line and continuum spectra are presented in Sects. 4 and 5, respectively. Discussion and concluding remarks follow in Sects. 6 and 7.
2. Observations
Cracco et al. (2011) present integral field spectra taken with the Multi Pupil Fiber Spectrograph (MPFS; Afanasiev et al. 2001) at the Special Astrophysical Observatory (SAO RAS). They obtained 256 simultaneous spectra arranged in an array of 16 × 16 spatial elements in the range 3800–7300 Å, with a resolution of 6 Å. The field of view was 16 × 16 square arcsec, seeing was about 1.5′′. At the distance of the galaxy the spatial scale is 0.513 kpc arcsec-1 (H0 = 75 km s-1 Mpc-1), yielding a field of view of 8.2 × 8.2 kpc2.
The data were reduced with p3d (Sandin et al. 2010) and corrected for reddening, atmospheric absorption bands, and atmospheric refraction with iraf1. The stellar component was subtracted with starlight (Cid Fernandes et al. 2005, 2007) and finally the spectra were measured with pan. Spectra are numbered from 1 to 256 and their positions in the field of view are reported in Fig. 1. For more details about reduction and calibration procedures, see Cracco et al. (2011).
 |
Fig. 1 2D map of the stellar continuum at 5500 Å. The numbers identify the spectra in Fig. 7. The image size is 16 × 16 square arcsec. North is up and east is to the left. |
 |
Fig. 2 Maps of the line ratios to Hβ. From left to right: [O III], [Fe VII] and [N II] (top); [O II], [S II]6716 and He II (middle); [O I], [S II]6731 and He I (bottom). Spatial scale is 1 arcsec px-1. North is up and east is to the left. |
In Fig. 2 we show a few significant observed line ratios throughout the observed region to obtain a first hint about the ionization conditions of the emitting gas. The diagrams of the left column describe the spatial distribution of [O III], [O II], and [O I] line ratios to Hβ. It can be noticed that photoionization from the AGN dominates in the central regions where the [O III]/Hβ and the [O II]/Hβ show smooth opposite trends. However, throughout all the ENLR, [O I]6300/Hβ line ratios show moderate fluctuations (Fig. 2) ranging between ~0.3–0.6. These line ratios are relatively low, implying that the spectra correspond to matter-bound clumps. Such a narrow range is unusual in matter fragmented by the underlying turbulence that accompanies relatively high velocity shocks. Eventually, [O I]/Hβ can be about 0, where the emitting cloud is so thin that there is not enough gas at temperatures ≤ 104 K. The [O I]/Hβ line ratios observed in NGC 7212 may suggest that the contribution from the galactic interstellar medium (ISM), that is, ionized gas not perturbed by high-velocity shocks, emerges at some locations in the ENLR.
In this work, we have tried to fit the [O I] lines consistently with [O III] and [O II]. Only in a few cases did the fit of the three oxygen ionization level lines to Hβ require certain ISM contribution, even when accounting for the typical observational errors of 0.12, 0.18 and 0.32, for [O II]/Hβ, [O III]/Hβ and [O I]/Hβ, respectively.
3. The models
Complex line profiles, as those observed in each position of NGC 7212, indicate a complex network of emitting clouds. The models help to separate the contributions of the different heating and ionizing sources (e.g. photoionization from the AGN, diffuse secondary radiation, shock waves, etc.) to each spectrum by reproducing most of the observed line intensity ratios. In this way we obtain the physical conditions that prevail in each position.
3.1. Analysis of the spectra
The clumpy and irregular morphology of NGC 7212 and the relative broad FWHM of the spectral lines indicate that in addition to the photoionization flux from the AGN, shocks are heating and ionizing the ENLR gas. We chose the shock velocity on the basis of both a close approximation to the observed FWHM of the line profiles and the best fit to the observed line intensities. Indeed, we consider that the FWHM roughly represents the shock velocity. Therefore, we present both the spectra calculated by high and low velocity shocks, when different profiles are intermingled in one spectrum and show a broad component compared with the bulk of the narrow profiles observed throughout the ENLR.
The physical parameters are combined throughout the calculation of forbidden and permitted lines (see Osterbrock 1989) emitted from a shocked nebula.
In pure photoionization models, the density n is constant throughout the nebula, while in a shock wave regime, n is calculated downstream by the compression equation in each single slab. Compression depends on n, the magnetic field B and the shock velocity Vs. In models accounting for the shocks, both the electron temperature Te and the electron density ne are far from constant throughout each cloud, showing the characteristic profiles in the downstream region (see Sect. 4.2.5). Therefore, even sophisticated calculations approximately reproduce the highly inhomogeneous conditions of the gas, giving rise to some discrepancies between the calculated and observed line ratios.
The ranges of the physical conditions in the nebula were inferred, as an initial guess, from the observed lines (e.g. the shock velocity from the FWHM) and from the characteristic line ratios (e.g. ne and Te). The physical parameters revealed by the observations indicate that a steady-state situation can be applied (Cox 1972) in NGC 7212. In this case, the time t required for a parcel of gas to cross the cooling region from the shock front to the recombination zone, for shock waves with Vs = 100 km s-1, is found to be approximately 1000/ne yr (calculated by the recombination coefficients), such that for an electron density ne = 100 cm-3, t = 10 yr. Shock velocities are not likely to change appreciably in such a short time, and therefore the steady-state calculation may be regarded as adequate.
3.2. The code: input parameters
We calculated the line and continuum spectra emitted by the gas downstream of the shock front with suma2. The code simulates the physical conditions in an emitting gaseous cloud under the coupled effect of photoionization from an external radiation source and shocks. The line and continuum emission from the gas are calculated consistently with dust-reprocessed radiation in a plane-parallel geometry.
The input parameters that refer to the shock are the shock velocity Vs, the pre-shock density n0, and the pre-shock magnetic field B0. The input parameters related to the radiation field are the power-law flux from the active nucleus F in number of photons cm-2 s-1 eV-1 at the Lyman limit, if the photoionization source is an active nucleus, and the spectral indices αUV = −1.5 and αX = −0.7. F is combined with the ionization parameter U by U = (F/(n c (α − 1)) ((EH)−α + 1 − (EC)−α + 1) (Contini & Aldrovandi 1983), where EH is H ionization potential and EC is the high-energy cutoff, n the density, α the spectral index, and c the speed of light. The secondary diffuse radiation emitted from the slabs of gas heated by the shocks is also calculated. The flux from the active centre and the secondary radiation are calculated by radiation transfer throughout the slabs downstream.
The dust-to-gas ratio (d/g) and the abundances of He, C, N, O, Ne, Mg, Si, S, A, and Fe relative to H are also accounted for. They affect the calculation of the cooling rate. The dust grains are heated radiatively by photoionization and collisionally by the shock. The distribution of the grain radii downstream results from sputtering. The geometrical thickness of the emitting nebula (D), determines whether the model is radiation-bound or matter-bound.
The input parameters that provide the best fit of the line ratios establish the physical conditions in each of the observed positions.
3.3. The code: calculation process
The calculations initiate at the shock front where the gas is compressed and are adiabatically thermalised, reaching a maximum temperature in the immediate post-shock region (T ~ 1.5 × 105 (Vs/100 km s-1)2). T decreases downstream following recombination. The cooling rate is calculated in each slab. The downstream region is cut up into a maximum of 300 plane-parallel slabs with different geometrical widths calculated automatically, to account for the temperature gradient (Contini 1997, and references therein).
In each slab, compression is calculated by the Rankine-Hugoniot equations for the conservation of mass, momentum and energy throughout the shock front. Compression (n/n0) downstream ranges between 4 (the adiabatic jump) and ≥ 10, depending on Vs and B0. The stronger the magnetic field, the lower the compression downstream, while a higher shock velocity corresponds to a higher compression.
The ionizing radiation from an external source is characterised by its spectrum and by the flux intensity. The flux is calculated at 440 energies from a few eV to keV. Owing to radiative transfer, the spectrum changes throughout the downstream slabs, each of them contributing to the optical depth. In addition to the radiation from the primary source, the effect of the diffuse radiation created by the gas line and continuum emission is also taken into account, using 240 energies to calculate the spectrum.
For each slab of gas, the fractional abundance of the ions of each chemical element is obtained by solving the ionization equations. These equations account for the ionization mechanisms (photoionization by the primary and diffuse radiation, and collisional ionization) and recombination mechanisms (radiative, dielectronic recombinations), as well as charge transfer effects. The ionization equations are coupled to the energy equation if collision processes dominate, and to the thermal balance if radiative processes dominate. The latter balances the heating of the gas due to the primary and diffuse radiations reaching the slab with the cooling due to recombinations and collisional excitation of the ions followed by line emission, dust collisional ionization and thermal bremsstrahlung. The coupled equations are solved for each slab, providing the physical conditions necessary for calculating the slab optical depth, as well as its line and continuum emissions. The slab contributions are integrated throughout the cloud.
In particular, the absolute line fluxes corresponding to the ionization level i of element K are calculated by the term nK(i), which represents the density of the ion i. We consider that nK(i) = X(i) [K/H] nH, where X(i) is the fractional abundance of the ion i calculated by the ionization equations, [K/H] is the relative abundance of the element K to H and nH is the density of H (in number cm-3). In models including shock, nH is calculated by the compression equation (Cox 1972) in each slab downstream. Accordingly, the abundances of the elements are given relative to H as input parameters.
Dust grains are coupled to the gas across the shock front by the magnetic field (Viegas & Contini 1994). They are heated by radiation from the AGN and collisionally by the gas to a maximum temperature, which is a function of the shock velocity, of the chemical composition and of the radius of the grains, up to the evaporation temperature (Tdust ≥ 1500 K). The grain radius distribution downstream is determined by sputtering, which depends on the shock velocity and on the density. Throughout shock fronts and downstream, the grains might be destroyed by sputtering.
Summarizing, the code starts by adopting an initial Te (~104 K) and the input parameters for the first slab (Sects. 3.1 and 3.2). It then calculates the density from the compression equation, the fractional abundances of the ions from each level for each element, line emission, free-free emission and free-bound emission. It re-calculates Te by thermal balancing or the enthalpy equation, and calculates the optical depth of the slab and the primary and secondary fluxes. Finally, it adopts the parameters found in slab i as initial conditions for slab i + 1. The line intensities and the bremsstrahlung are calculated from the gas that emits the spectrum. The data are observed at Earth, therefore they diverge by a factor that depends on the distance of the nebula from the active centre (r), and on the distance (d) of the galaxy to Earth (r2/d2). We then calculated the line ratios to a specific line (in the present case Hβ, which is a strong line), and compared them with the observed line ratios.
4. Modelling the NGC 7212 spectra
The spectra are rich in number of lines, therefore the calculated spectra are strongly constrained by the observed line ratios. The line ratios are different in each of the observed spectra, revealing different physical conditions from region to region. At each stage of the modelling process, if a satisfactory fit is not found for all the lines, a new iteration is initiated with a different set of input parameters. When a ratio was not reproduced, we checked how it depends on the physical parameters and decided accordingly how to change them. Each ratio has a different weight, but we generally considered that the observed spectrum was satisfactorily fitted by a model when the strongest line ratios were reproduced by the calculation within a 20% discrepancy and weak line ratios within 50%.
We ran a grid of models (~100 for each position) to select the most appropriate one. The fit was successful in 111 out of the 256 spectra, since they were the most complete in number of lines. Figure 3 shows a map of the signal-to-noise ratio (S/N) of the stellar continuum with the number of the modelled spectrum overlaid. Most of these spectra have an S/N higher than 6. The final gap between observed and calculated line ratios is due to random and systematic observational errors as well as to the uncertainties of the atomic parameters adopted by the code, such as recombination coefficients, collision strengths etc., which are continuously updated, and to the choice of the model. Models are generally allowed to reproduce the data within a factor of 2. This leads to input parameter ranges of a few per cent.
 |
Fig. 3 2D map of the S/N of the stellar continuum. The numbers indicate the successfully modelled spectra. |
4.1. First step: choice of physical parameters
In the first iterations, we tried to reproduce the [O III]5007+4959/Hβ line ratio (5007+4959 will be referred to in the following as 5007+; the + indicates that the doublet 5007, 4959 is summed up), the highest ratio in general, by readjusting F and Vs (Vs, however, is constrained through a small range by the observed FWHM). The higher F, the higher the [O III]/Hβ and the [O III]/[O II] line ratios (see Fig. 4), as well as He II/Hβ. Moreover, a high F maintains the gas ionized far from the source, yielding enhanced [O I] and [S II] lines. We recall that these lines behave similarly because the first ionization potential of S (10.36 eV) is lower than that of O (13.61 eV).
Then, we considered the [O II]3727+ doublet. If the flux from the active centre is low (F ≤ 109 ph cm-2 s-1 eV-1), a shock-dominated regime is found, which is characterised by relatively high [O II]/[O III] (≥ 1, as can be seen in Fig. 4). These lines can be drastically reduced by collisional deexcitation at high electron densities (ne > 3000 cm-3).
The gas density is a crucial parameter. In each cloud, it reaches its upper limit downstream and remains nearly constant, while the electron density decreases following recombination. A high density, increasing the cooling rate, speeds up the recombination process of the gas, enhancing the low-ionization lines. Indeed, each line is produced in a region of gas at a different ne and Te, depending on the ionization level and the atomic parameters characteristic of the ion. The density n, which can be roughly inferred from the [S II]6716/6731 doublet ratio, is related with n0 by compression downstream (n/n0), which ranges between ~4 and ~100, depending on Vs and B0. The [S II] lines are also characterised by a relatively low critical density for collisional deexcitation. In NGC 7212 the [S II]6716/6731 line ratios are ~1 in all observed positions, constraining the choice of n0. In some cases the [S II]6716/6731 line ratio varies from > 1 to < 1 throughout a relatively small region, since the [S II] line ratios depend on both the temperature and electron density of the emitting gas (Osterbrock 1989). The median error of the modelled ratios is about 10%, and 90% of this sample has an error lower than 30%.
 |
Fig. 4 Correlation of the input parameters with calculated [O III]5007+/[O II]3727+ line ratios. |
Physical parameters resulting from modelling the observed spectra.
 |
Fig. 5 Top: histograms of the shock velocities (left), pre-shock density (middle) and the AGN ionizing flux (right). Bottom: 2D maps of the same parameters. The units are km s-1 (left), cm-3 (middle) and ph cm-2 s-1 eV-1 (right). Spatial scale is 1 arcsec px-1. Contours of the stellar continuum are overplotted onto the map of the ionizing flux. North is up and east is to the left. |
We fitted the lines of a single spectrum adopting an n0 that was combined with the other input parameters, including the pre-shock magnetic field B0. The magnetic field has an important role in models accounting for the shock. The stronger B0, the lower the compression. Therefore, lower densities are compensated for by a lower magnetic field. If n0 in one spectrum is inconsistent with n0 calculated in the surrounding regions, we can reduce the n0 divergence by changing the magnetic field, because n0 and B0 are strongly (anti)correlated. This procedure would lead to a smoother distribution of n0 throughout the ENLR of NGC 7212, which is not expected however, because collisions and merging phenomena render the density field inhomogeneous. Accordingly, we adopted a constant B0 = 10-4 G, which is suitable for the ENLR of AGN (Beck 2011). This choice is slightly unrealistic but it is justified because the preshock densities range between values within a factor of 2 (~80–150 cm-3, Table 1). Table 1 shows that B0 could be modified in regions 103–105, 121–122, 132–133, and 156–157. These regions are too few to yield a trend for B0 throughout the ENLR. Moreover, B0 fluctuations would not affect the ensemble of the results.
The final choice of a model was dictated by [O I]6300+/Hβ, which was calculated consistently with [O III]/Hβ and [O II]/Hβ. The geometrical thickness (D) of the emitting clouds was mainly determined by [O I]/Hβ because [O I] is emitted from gas at relatively low temperature, at the cloud edge opposite the shock front.
A first analysis of the data shows that the models are mostly matter-bound, namely, the integration of the calculated line fluxes downstream is interrupted at such a distance from the shock front that all line ratios of a single spectrum are satisfactorily reproduced (by 10 per cent for the strongest ones). The low [O I]6300/Hβ (≤ 0.6, Fig. 2) observed by Cracco et al. are hardly reproduced by radiation-bound models, which are revealed in a few cases (represented by the maximum D in Fig. 4). The [S II]6716, 6731 lines are also emitted by relatively cool gas. Therefore, their ratios to Hβ are determined by [O I]/Hβ.
So far, the results of modelling correspond to the set of input parameters presented in Table 1. The relative maps are shown in Fig. 5. The uncertainties of the input parameters are approximately 10%. Indeed, a change of 10% corresponds to variations of the resulting line ratios within 20% for the strongest lines to up to 50% for the weakest lines. For all models we used solar abundances. In Table 2 we compare the spectra calculated in each position with the observed corrected line ratios to Hβ. Each of the observed line ratios is followed by the calculation results. The numbers in the first column refer to Fig. 1. Not all the lines used for modelling are included in Table 2. We have focused on [O III]5007+, [Ne III]3869+, [O II]3727+, [O I]6300+, He II 4686, He I 5876, [N II]6548+, [S II]6716, 6731. For all spectra, we assumed that the reddening corrected ratio is Hα/Hβ = 2.8, model calculations give Hα/Hβ ~ 2.9 and Hγ/Hβ ~ 0.46.
Table 2 and Fig. 6 show that the observed [O III]/Hβ, [O II]/Hβ and [O I]/Hβ are reproduced by the models with relatively high precision (the discrepancy is <20%).
The Ne/H relative abundance used in the calculation of the spectra is 10-4. Comparison with the data shows that Ne/H higher by a factor of 1.5–2 should be adopted. This would approach the Ne/H = 1.95 × 10-4 solar value calculated by Bahcall et al. (2005). Table 2 shows that [Fe VII]6087/Hβ is not negligible in some regions, in the nucleus and in the regions to the east of the nucleus, even if the iron line is faint and the median error is about 0.3.
The modelled He I/Hβ and He II/Hβ ratios agree with the observed values within their large error bars. [N II]/Hβ, [S II]/Hβ line ratios show a large scatter (see Fig. 6), which does not depend on the observational errors. We point out that at this stage of modelling, we considered solar abundances. We will now determine the metallicity relative to N and S by constraining in the following calculations the relative abundances of N/H and S/H to obtain a perfect fit of calculated to observed line ratios.
 |
Fig. 6 Comparison between the observed and the calculated emission line ratios for the lines in Table 2. σ is the median error for the observed ratios. The solid line is the 1:1 line. |
4.2. Second step: relative abundances
The ratios of calculated to observed [S II]/Hβ and [N II]/Hβ in each position are shown in Table 2. Unfortunately, there are no data for S lines from higher ionization levels, which could indicate whether the choice of the model is misleading, or different relative abundances should be adopted. Since sulphur can be easily depleted from the gaseous phase and trapped into dust grains and molecules, we considered that the [S II]/Hβ line ratios indicate the S/H relative abundance.
 |
Fig. 7 Variations of calculated/observed line ratios as a function of the number of spectra (see Fig. 1). Left: [N II]/Hβ (red asterisks), [O II]/Hβ (blue asterisks); middle: [O I]/Hβ (green asterisks), [S II]6716+6731/Hβ (black asterisks); right: He II/Hβ (magenta asterisks). |
The same is valid for the [N II] lines. The observations do not contain any other strong line of N, which could confirm whether the discrepancy between the calculated and the observed [N II]/Hβ line ratios can be resolved by changing the N/H relative abundance or the other input physical parameters. Solar nitrogen is less abundant than other solar elements such as oxygen, neon, etc., therefore it is not an efficient coolant, namely, it does not strongly affect the cooling rate of the gas downstream. Varying N/H will change only the [N II]/Hβ line ratio, but not the other line ratios, while if changing O/H the whole input parameter set must be readjusted.
4.2.1. [N II] and [O II]
Table 2 and Fig. 6 show that the lines that systematically disagree with the observations are the [N II] doublet at 6548+6584 Å. The doublet is summed up in the table. In the calculations we adopted solar N/H value 9.1 × 10-5 (Allen 1976). Table 2 shows that the observed [N II]/Hβ line ratios are mostly overpredicted by the models. The discrepancies between observed and calculated values are shown in Fig. 7. [N II] lines come from the same region of the gas that emits the [O II] lines. [O II]/Hβ line ratios depend on the physical parameters and are constrained by [O III]/Hβ and [O I]/Hβ, therefore the discrepancy in the [N II]/Hβ line ratios can be explained by abnormal N/H relative abundances. In the left diagram of Fig. 7 ([N II]/Hβ)calc/([N II]/Hβ)obs and ([O II]/Hβ)calc/([O II]/Hβ)obs are plotted in the different positions. If discrepancies between calculation and observation were due to the model, both [N II]/Hβ and [O II]/Hβ would show the same variations. Contrariwise, in positions beyond 100 (regions to the east of the nucleus) the [N II]/Hβ calculated line ratios overpredict the data by a factor of at least 1.5, whereas the observed [O II]/Hβ are always well reproduced by the models. This indicates that N/H should be depleted by a factor of at least 1.5, while O/H is almost solar. The map showing the N/H depletion and excess (Table 3) appears in Fig. 8.
Calculated relative abundances.
4.2.2. [S II] and [O I]
From the last two columns of Table 2 we can realize that the doublet ratios [S II]6716/6731 ~ 1, indicative of the emitting gas density, are relatively low (≤ 103 cm-3). The [S II] and [O I] lines are emitted from relatively cool gas in similar physical conditions. In Fig. 7 (middle diagram) both ([S II]/Hβ)calc/([S II]/Hβ)obs and ([O I]/Hβ)calc/([O I]/Hβ)obs ratios show up. Table 2 and Fig. 6 suggest that [S II] line ratios to Hβ calculated adopting solar abundances are acceptable, except in some positions. At the north-east of the nucleus the calculated [S II]/Hβ ratios overpredict the data and at other positions they even underpredict them (see Fig. 7). The map of the S/H depletion and excess (Table 3) is shown in Fig. 8. Eventually, the [S II] observed lines include a large contribution from the ISM cool gas. The [S II]4070+ lines are not included in Table 2 because they do not appear in all spectra and because they are blended with other lines at nearby wavelengths. However, model results indicate that the [S II]4070+/Hβ ratios are relatively high for high velocities and reproduce the data in a few positions.
 |
Fig. 8 Obs/calc maps of nitrogen (left), oxygen (middle) and sulphur (right). Values lower than 1 indicate depletion. Spatial scale is 1 arcsec px-1. North is up and east is to the left. |
4.2.3. He II and the oxygen lines
The first cycle of calculations yields He II/Hβ line ratios generally lower than those observed. Indeed, higher He II/Hβ can be obtained by increasing the photoionization flux, which spoils the goodness of fit of the [O III]/Hβ and [O II]/Hβ line ratios, however. Another option is to reduce the geometrical thickness of some of the clouds, excluding the cooling region. Accounting only for the high-temperature zone close to the shock front downstream, only the He II lines would be strong. Summing up the spectra of these thinner clouds with the other ones would give high He II/Hβ ratios. The three most important line ratios [O III]/Hβ, [O II]/Hβ and [O I]/Hβ are all well-fitted by adopting the solar O/H relative abundance, 6.6 × 10-4 (Allen 1976). However, Cracco et al. (2011) compared the line ratios with models calculated by pure photoionization and found a low metallicity in NGC 7212. Oxygen is a strong coolant. Decreasing O/H in the models will induce a lower cooling rate downstream, yielding a larger zone of hot gas capable of emitting higher He II/Hβ. Moreover, the He II line sits on top of the [Fe III] multiplet, whose most prominent lines are at 4658 Å and 4702 Å. The lines are blended with He II in high-velocity regimes. Consequently, we adopted in the next cycle of calculations a lower O/H relative abundance in positions where the observed He II/Hβ lines ratios were underpredicted. This required an adjustment of the input parameters also regarding the physical conditions. Finally, we added the [Fe III]/Hβ line ratios to He II/Hβ, which can be as high as He II/Hβ in some positions. The comparison of calculated with observed He II/Hβ improved (Fig. 7, right diagram) except in some positions, e.g. 109, 124, 200, where observational errors are high (larger than 60%). In particular, we obtained O/H = 3.6 × 10-4 in positions 60 and 115, 4.6 × 10-4 in positions 116, 141, 187, 188, 203 and 4 × 10-4 in 213. Moreover, O/H = 3 × 10-4 was used in positions 125, 140, and 2.6 × 10-4 in position 133. Interestingly, most of these positions refer to relatively high shock velocities (see Table 1). For all other positions, the solar O/H value was adopted. The map of the oxygen depletion is shown in Fig. 8.
4.2.4. HeI/Hβ line ratios
The HeI/Hβ diagram in Fig. 6 and the results in Table 2 show that the calculated HeI/Hβ line ratios mostly range between 0.11 and 0.13, while the observations range between 0.04 and 0.4. To understand the results, we show in Fig. 9 the profile of the temperature and of HI, HeI and HeII fractional abundances as a function of distance from the shock front, which corresponds to the cloud edge reached by the flux from the AGN. We have chosen position 53, which shows a strong F and a relatively low Vs. The temperature maximum between 1018 and 3 × 1018 cm is real and not due to the calculation approximation. It arises when hydrogen becomes neutral, followed by the decrease of the density of electrons, which, colliding with the heavy elements, produce cooling downstream (Williams 1967). The calculations of the He ion fractional abundances follow the temperature fluctuations by small variations, while the HI fluctuation is imperceptible, so the HeI/Hβ calculated range is small. On the other hand, the observational error of HeI reaches 79%.
 |
Fig. 9 Profile of HI (solid line), HeI (dot-dashed) and HeII (dashed) fractional abundances as a function of distance from the shock front for position 53. |
4.2.5. [Fe II]
Rodríguez-Ardila et al. (2004) studied the [Fe II] line emission in AGN and found that [Fe II]/Paβ increases from pure photoionization to a shock excitation regime. For instance, [Fe II] emission and double profiles are due to jet-gas interaction in Mrk 78 (Whittle et al. 1988; Ramos Almeida et al. 2006) and [Fe II] lines are strong in the radio-jet interaction region in Mrk 34 (Jackson & Beswick 2007). This could indicate the importance of the shocks for strong [Fe II] lines. The iron first-ionization potential (7.9 eV), which corresponds to the [Fe II] lines, is lower than that of O+ and H+. Therefore [Fe II] lines are mainly emitted from cool recombined gas. Collisional ionization coefficients are low at those low temperatures (≤ 104 K), therefore strong [Fe II] lines in the shock-dominated case (as for supernovae) are due to diffuse secondary radiation, which in turn is high because it is emitted from shock-heated gas slabs.
In HII regions, on the other hand, the black body flux is rapidly reduced by radiation transfer throughout the gas and the temperature drop, therefore the [Fe II] lines are weak. In Fig. 10 (top diagram) we illustrate the temperature and electron density profiles downstream in positions 140 (left) and 149 (right). We have chosen these positions because they have very different shock velocities and are reached by different flux intensities. Nevertheless, the spectra are sufficiently well reproduced by the models. The O0/O, O + /O and O2 + /O fractional abundances and the fractional abundances of significant Fe ions are described in the middle and the bottom diagrams, respectively.
 |
Fig. 10 Pos. 140 (left), pos. 149 (right); top diagram: the electron temperature (solid line) and electron density (dashed line) downstream; middle diagram: the fractional abundances of O0 (green), O+ (black), O2+ (red); bottom diagram: the fractional abundances of Fe+ (black), Fe2+ (red), Fe3+ (magenta), Fe4+ (cyan), Fe5+ (yellow), Fe6+ (blue). |
5. The continuum SED
We checked the models by comparing them with the observed spectral energy distribution (SED) of the continuum, shown in Fig. 11. The data (represented by black crosses) were extracted from the NASA/IPAC extragalactic database (NED) and are detailed in Table 4. They were taken with different apertures, and therefore they cover different regions of the galaxy. However, for apertures of a few arcsec, the emission is very likely dominated by the AGN. We expected the same for the hard X-ray emission, even if the aperture is large. Some problems can arise in the soft X-ray and infrared domains, where the fluxes are emitted by a large part of the galaxy and additional contributions, e.g. supernova remnants and dust, may be non-negligible.
Most of the AGN emission in the optical-UV range is hidden by the molecular dusty torus, which makes the black-body flux from the old stellar population visible, here reproduced by black-body radiation at T = 5000 K. The archival GALEX data in the UV follow the black-body old star radiation. Nevertheless, the power-law flux from the AGN and the shocks heat the gas, which contributes to the SED by its reprocessed bremsstrahlung emission.
 |
Fig. 11 Comparison of the continuum SED with the model results. Black crosses: data from NED; black encircled crosses: the data from the NED believed to be dominated by the AGN; red asterisks: data from Sargsyan (2011); black squares: data from GALEX archive; green: synchrotron radiation; red: the dust-reprocessed radiation flux calculated by models 71 (solid line) and 107 (dashed line); blue: the bremsstrahlung for position 71 (solid line) and for position 107 (dashed line). Black line: the black-body flux from the background stars. |
List of photometric data extracted from NED.
Figure 11 shows that the data cover the X-ray domain, indicating the presence of high-temperature regions. The bremsstrahlung at high frequencies depends on the temperature of the gas in the downstream region behind the shock front. The higher the shock velocity, the higher the temperature of the gas downstream. Thus, the bremsstrahlung peaks at high frequencies for models calculated with high Vs. To reproduce soft X-ray emission (0.5–2 keV) we adopted the result of the model calculated with a shock velocity Vs = 550 km s-1, corresponding to position 71. NGC 7212 is a Compton-thick source (Bennert et al. 2006) with reflected hard X-rays (2–10 keV) coming directly from the AGN. Yet, hard X-rays could be contributed by shocks corresponding to Vs = 800 km s-1, as found in position 107. Models with lower velocities do not contribute to the continuum SED at high frequencies.
The IR shows a composite black-body radiation from dust grains at different temperatures. Dust grains are heated radiatively by the flux from the active centre and collisionally by the gas. The data in the near IR domain are reproduced by dust-reprocessed radiation downstream of the highest velocity models adopting a dust-to-gas ratio d/g ~ 2 × 10-4 and 4 × 10-5 (by mass) in positions 71 and 107, respectively. We stress, for comparison, that in the ISM d/g ~ 4 × 10-3–4 × 10-4 (Contini & Contini 2007).
The data in the radio range show the characteristic power-law of the synchrotron radiation created by the Fermi mechanism at the shock front. The free-free and free-bound continuum radiation flux are calculated consistently with the line emission fluxes for each model. The bremsstrahlung emitted from the gas has the same frequency distribution in the IR-radio range for different models (see Contini et al. 2004) when free-free self-absorption is negligible (at rather low densities).
6. Discussion
6.1. Comparison with other observations
Comparison between our model and the Bennert et al. (2006) nuclear optical spectrum.
To confirm the ranges of the parameters obtained by reproducing Cracco et al. (2011) data, we present in Table 5 the results from modelling of the Bennert et al. (2006) nuclear optical spectrum, corresponding to an aperture of 1′′. We find a shock velocity of 370 km s-1, slightly higher than that inferred from the average observed FWHM (250 km s-1) provided by these authors. Near-IR spectroscopic data are reported by Ramos Almeida et al. (2009) for five Seyfert galaxies showing jet-gas interaction, including NGC 7212. Its IR nuclear spectrum (1.5′′-aperture) is presented in Table 6. The line ratios are well reproduced with a model very similar to those that reproduce the Cracco et al. (2011) optical spectra. The contemporary fit of neutral and coronal lines in different ranges requires composite models (see, e.g. Rodríguez-Ardíla et al. 2005).
The shock velocities adopted to fit the Bennert et al. and Ramos Almeida et al. nuclear spectra were compared to the values obtained by the present modelling of the Cracco et al. spectra in a region of 3″ × 3″ centred on the nucleus. This region was chosen to take into account possible effects of slit misalignenment with respect to the active nucleus. The values are similar: 370, 500, and 110–550 km s-1, respectively. The densities are 190, 200, and 70–120 cm-3, respectively. We recall that the densities in the present modelling are preshock, corresponding to densities downstream higher by a factor of 4–10, depending on the shock velocity. The fluxes are also similar: log F = 10.85, 10, and 10–10.8, respectively. A difference of factor ~100 is apparent in the geometrical thickness of the clouds. Those referring to IR spectra by Ramos Almeida et al. are approximately 3 × 1015 cm, while the others are about 2 × 1017 cm. It seems that observable coronal lines are emitted from very thin clouds, to prevent recombination of the Si, S, etc.
6.2. The physical picture of the NLR
The 2D maps in Fig. 5 depict the distribution of the shock velocity Vs (left panel), of the preshock density n0 (central panel) and of the flux from the active nucleus F (right panel). They refer to the shock regime. High-velocity shocks (600–800 km s-1) delineate the region where matter external to the ENLR collides with the ENLR gas. The highest velocities are found in the eastern regions, where the maps show low n0 values. Matter is faster throughout the less dense gas regions, as expected from the mass conservation equation at the shock front. This confirms the presence of shocks. The preshock densities demonstrate a narrow maximum near the eastern edge, which most probably obstructs the spreading of the high-velocity shock. The histograms in Fig. 5 illustrate the distributions of the values, Vs, n0 and log F.
Explaining the ionization of the perturbed gas in radio galaxies, Tadhunter et al. (2000) discussed why the perturbed gas varies significantly in surface luminosity from object to object, while the quiescent gas does not. The correlation between F and Hβ absolute flux calculated at the nebula is shown in Fig. 12, as well as the correlation of the shock velocity with Hβ. Hβ is chosen to represent the surface luminosity at the emitting nebula. Extrapolating from many different objects to different regions in the same galaxy, Fig. 12 shows that the luminosity of each region in NGC 7212 is strongly linked with the AGN flux reaching it. The Hβ line emission is strong from regions at temperatures T ≥ 104 K. The correlation with Vs is less straightforward. Indeed, at temperatures higher than 104 K collisional parameters are much more important than the radiation ones, but, a higher Vs generates higher densities downstream and consequently a higher cooling rate, which results in a reduced H recombination zone. Accordingly, we can hardly recognize the shocks resulting from collisions by means of the object luminosity, but they can be found out by analysing line ratios and profiles.
 |
Fig. 12 Shock velocities vs. Hβ calculated flux (top panel); fluxes from the active centre vs. Hβ calculated flux (bottom panel). Red: models calculated with high Vs (> 700 km s-1); blue: the other models. |
The shock velocities calculated in the observed positions throughout the NGC 7212 ENLR roughly show the regions in which collision of matter from the ENLR with matter from outside the cone occurred. We found that the velocities are lower than 200 km s-1, and the preshock densities are relatively low (~100 cm-3) in all the positions representing the ENLR matter uncontaminated by high-density debris from the BLR. These velocities refer to a smooth regime. Tadhunter et al. (2000) used the term “quiescent” to mean “in a quasi-stable dynamical configuration in a galaxy”, that is, within a factor of 2 of the rotational velocity. The high velocities, on the other hand, refer to shocks.
We confirm that shocks are strong beyond the edges of the cone that is overplotted in Fig. 13 on the shock velocities in the contour map of the photoionization cone. Our calculations reveal that high-velocity shocks are located at the edge of the ionization cone and beyond it, in agreement with the large FWHM of the line profiles, 500–800 km s-1. Interestingly, patches of highly ionized clumps were observed also outside the ENLR of NGC 3393 (Cooke et al. 2000) where merging is confirmed by the binary black hole system observed in the nucleus (Fabbiano et al. 2011). Tables 1 and 2 show that where the highest Vs are found (e.g. in position 108), the contribution of spectra calculated with relatively low velocity – most likely emitted from the ENLR or even from the ISM of the host galaxy – cannot be excluded. The relative contribution of the two spectra to each of the observed one is revealed by the complex FWHM of the line profiles corresponding to the different ions, in agreement with the multiple kinematics found by Cracco et al. (2011). For instance, the [S II]6716+ lines have a strong contribution from low-velocity gas.
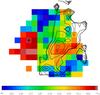 |
Fig. 13 2D map of the shock velocity in km s-1 with the contour map of the photoionization cone ([O III]/Hβ) overplotted. Spatial scale is 1 arcsec px-1. |
6.3. The distribution of metallicities
We calculated the relative abundances to H of the heavy elements throughout the galaxy, particularly those identified with metallicity (e.g. oxygen in the present case), because metallicity is sensitive not only to star formation, but is also affected by the presence of infalls and outflows, i.e. by the interaction between the merging galaxy and the intergalactic medium (Sommariva et al. 2011). By adopting models that account for both shock and photoionization, we found that O/H is solar in almost all positions corresponding to “quiet” gas if we employed the solar relative abundance O/H = 6.6 × 10-4 reported by Allen (1976). However, O/H becomes about 0.77 solar, when we referred to the solar abundance O/H = 8.5 × 10-4 calculated by Anders & Grevesse (1989) and Feldman (1992). Sub-solar O/H values as low as 2.6 × 10-4 (Fig. 8) were found only in some positions far from the centre. On the other hand, Cracco et al. (2011) found sub-solar O/H throughout all observed positions using pure photoionization models. Indeed, the suma modelling is based on both the [O III] and [O II] lines. The [O III] line intensity depends strongly on the flux from the active centre, while the [O II] line is also affected by the shock velocity. Moreover, we improved the modelling procedure, by accounting for the complete spectrum in each position.
In agreement with Cracco et al. (2011), we found that nitrogen is depleted by factors lower than 2 in extended regions of the cone, which correspond to relatively low shock velocities. In the regions characterised by high shock velocities (Fig. 5), N/H is roughly solar. S/H shows some depletion in the same external south-east regions. N/H is generally high in AGN (e.g. Contini et al. 2002a; Ciroi et al. 2003). A low N/H may indicate inclusion of N into molecules in the ISM and/or acquisition of external gas in the merging process. In Sect. 5 we found that the dust-to-gas ratio is relatively low in NGC 7212, showing that dust grains and molecules can be destroyed by the itense radiation from the AGN and by relative strong shocks. We conclude that sub-solar N/H is another indication of external gas acquisition.
It is generally known that bursts of star formation are triggered by galaxy-galaxy mergers (Somerville et al. 2001). As mentioned in Sect. 1, Muñoz Marín et al. (2007) claimed that interacting galaxies can show UV-light coming from knots produced by star clusters. These authors identified some bright clumps at the south of NGC 7212 as star-forming regions. However, the contribution of the starbursts to the [O III] 5007 emission line flux is less than 20%, lower than that of the AGN, which agrees with the result that NGC 3393 (Contini 2012) is another Seyfert galaxy belonging to a merger system.
 |
Fig. 14 N/O vs. O/H diagram adapted from Mouhcine & Contini (2002, see their Fig. 1). The blue area represents a sample of UV-selected galaxies, the red area includes starburst nucleus galaxies (SBNGs) selected in the optical or in the infrared, and the magenta area represents H ii galaxies. The results of our model calculations are overplotted (black circles). |
The evidence for star formation motivated us to compare the N/O relative abundance as a function of metallicity calculated throughout the galaxy with the N/O vs. O/H diagram presented by Mouhcine & Contini (2002) in Fig. 14. The calculated N/O and O/H ratios lie in the zone covered by UV-selected galaxies and massive starbursts in the diagnostic diagram of Mouhcine & Contini (2002, Fig. 1, black squares and circles, respectively). Figure 14 shows a strong variation of N/O throughout NGC 7212, indicating a time delay between the release of oxygen and that of nitrogen (Contini et al. 2002b) in the regions characterised by O/H solar abundance. Positions showing an N/O overabundance (log (N/O) ≥ −0.86) (see also Fig. 8) may indicate mixing with external matter as a consequence of a minor merger.
7. Conclusions
We presented an analysis of the line spectra observed by Cracco et al. (2011) in the different positions throughout the ENLR of NGC 7212, adopting calculation models that account for the coupled effect of shocks and photoionization. The results yield new reliable estimates about the intensity and distribution of the flux from the AGN, the velocity field, the preshock density, the relative abundances, etc.
In Seyfert galaxies the radiation from the active nucleus is the main photoionization mechanism. The AGN in NGC 7212 is characterised by a flux intensity lower than 1011 photons cm-2 s-1 eV-1, at the Lyman limit, similar to that of low-luminosity AGN (e.g. Contini 2004), rather than to Seyfert 2 (e.g. Contini et al. 2002a; Ciroi et al. 2003). The AGN flux peaks in correspondence with the maximum starlight flux. In the ENLR of NGC 7212, as in most Seyfert galaxies, the single lines show complex profiles. This indicates that the hydrodynamical field is complex. Shock waves created by winds and jets from the stars and/or by collision of matter are generally present. Characteristic of shocked clouds is the profile of the density downstream, where the gas cools due to recombination processes. Compression speeds up recombination, enhancing the intensity of lines corresponding to low-ionization levels. The spectra emitted by shocked gas are therefore different from those emitted from clouds heated and ionized by radiation from an external source. The relative importance of photoionization and shocks in NGC 7212 throughout most of the 256 spatial elements simultaneously observed by MPFS results from the consistent modelling of line and continuum spectra. Each spectrum stems from a complex grid of models that account for the parameter in various ranges. The parameters are constrained by the He II/Hβ line ratios (F), by [S II]6716/6731 (n0), by [O III]:[O II]:[O I] (Vs and F), etc. The shock velocity is also constrained by the continuum SED.
In conclusion, the interaction of galaxy-galaxy or of a galaxy with matter from the interstellar or intracluster medium can reveal shocks by line ratios that cannot be readily explained by pure photoionization models (e.g. Villar-Martín et al. 1999), by high electron temperatures leading to X-ray emission, and by radio synchrotron radiation. Radiation and collisional processes are strongly intermingled in ionizing the gas (e.g. Contini 1997). The degree to which shocks contribute to the gas ionization in the different regions of NGC 7212 can be found only by consistent modelling of line and continuum spectra. Our results agree with Tadhunter et al. (2000), who claimed that shocks contribute significantly to the ionization of the ENLR of Seyfert galaxies, even if photoionization contributes substantially in most of AGNs (Robinson et al. 1987; Villar-Martín et al. 1997).
Online material
Comparison between calculated and observed line ratios.
See http://wise-obs.tau.ac.il/marcel/suma/index.htm for a detailed description.
Acknowledgments
We are greatful to the anonymous referee for useful comments and suggestions whi ch improved the quality of the paper. This research has made use of the NASA Astrophysics Data System (ADS) and the NED, operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with NASA. We are grateful to M. Mouhcine for allowing us to reproduce Fig. 14.
References
- Afanasiev, V. L., Dodonov, S. N., & Moiseev, A. V. 2001, in Stellar Dynamics: From Classic to Modern, eds. by L.P. Ossipkov, & I.I. Nikiforov (Saint Petersburg: Sobolev Astronomical Institute), Proc. Int. Conf., 103 [Google Scholar]
- Allen, C. W. 1976, Astrophysical Quantities, London: Athlone, 3rd edition [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Bahcall, J. N., Basu, S., & Serenelli, A. M. 2005, ApJ, 631, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2011, in the Central Kiloparsec in Galactic Nuclei – Astronomy at High Angular Resolution 2011, J. Phys. Conf. Ser. (IOP Publishing) [arXiv:1112.1823] [Google Scholar]
- Becker, R. H., White, R. L., & Edwards, A. L. 1991, ApJS, 75, 1 [Google Scholar]
- Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006, A&A, 456, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., Guainazzi, M., & Chiaberge, M. 2006, A&A, 448, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- CidFernandes, R., Asari, N. V., Sodré, L., et al. 2007, MNRAS, 375, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ciroi, S., Contini, M., Rafanelli, P., & Richter, G. M. 2003, A&A, 400, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, A. J., Baldwin, J. A., Ferland, G. J., Netzer, H., & Wilson, A. S. 2000, ApJS, 129, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, M. 1997, A&A, 323, 71 [NASA ADS] [Google Scholar]
- Contini, M. 2004, MNRAS, 354, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, M. 2012, MNRAS, 425, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, M., & Aldrovandi, S. M. V. 1983, A&A, 127, 15 [NASA ADS] [Google Scholar]
- Contini, M., & Contini, T. 2007, AN, 328, 953 [NASA ADS] [Google Scholar]
- Contini, M., Radovich, M., Rafanelli, P., & Richter, G. M. 2002a, ApJ, 572, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, T., Treyer, M. A., Sullivan, M., & Ellis, R. S. 2002b, MNRAS, 330, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, M., Viegas, S. M., & Prieto, M. A. 2004, MNRAS, 348, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Cracco, V., Ciroi, S., Di Mille, F., et al. 2011, MNRAS, 418, 2630 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, J. N., Bash, F. N., Bozyan, F. A., Torrence, G. W., & Wolfe, C. 1996, AJ, 111, 1945 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U. 1992, Phy. Scr., 46, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Guainazzi, M., Matt, G., & Perola, G. C. 2005, A&A, 444, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, N., & Beswick, R. J. 2007, MNRAS, 376, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Levenson, N. A., Heckman, T. M., Krolik, J. H., Weaver, K. A., & Życki, P. T. 2006, ApJ, 648, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Moshir, M., et al. 1990, IRAS Faint Source Catalogue [Google Scholar]
- Mouhcine, M., & Contini, T. 2002, A&A, 389, 106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muñoz Marín, V. M., González Delgado, R. M., Schmitt, H. R., et al. 2007, AJ, 134, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, in Research supported by the University of California (CA: University Science Books) [Google Scholar]
- Peng, Z., Gu, Q., Melnick, J., & Zhao, Y. 2006, A&A, 453, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Radovich, M., Ciroi, S., Contini, M., et al. 2005, A&A, 431, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramos Almeida, C. Pérez García, A. M., Acosta-Pulido, J. A., et al. 2006, ApJ, 645, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C. Pérez García, A. M., & Acosta-Pulido, J. A. 2009, ApJ, 694, 1379 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, A., Binette, L., Fosbury, R. A. E., & Tadhunter, C. N. 1987, MNRAS, 227, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Ardila, A., Pastoriza, M. G., Viegas, S., Sigut, T. A. A., & Pradhan, A. K. 2004, A&A, 425, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-Ardila, A., Contini, M., & Viegas, S. M. 2005, MNRAS, 357, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Sandin, C., Becker, T., Roth, M. M., et al. 2010, A&A, 515, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sargsyan, L., Weedman, D., Lebouteiller, V., et al. 2011, ApJ, 730, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., Primack, J. R., & Faber, S. M. 2001, MNRAS, 320, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Tadhunter, C. N., Villar-Martin, M., Morganti, R., Bland-Hawthorn, J., & Axon, D. 2000, MNRAS, 314, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Tran, H. D., & Kay, L. E. 1992, AIPC, 254, 504 [NASA ADS] [Google Scholar]
- Ueda, Y., Ishisaki, Y., Takahashi, T., Makishima, K., & Ohashi, T. 2001, ApJS, 133, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Villar-Martín, M., Tadhunter, C., & Clark, N. 1997, A&A, 323, 21 [NASA ADS] [Google Scholar]
- Villar-Martín, M., Tadhunter, C., Morganti, R., Axon, D., & Koekemoer, A. 1999, MNRAS, 307, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Wasilewski, A. J. 1981, PASP, 93, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. E. 1967, ApJ, 147, 556 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. L., & Becker, R. H. 1992, ApJS, 79, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Whittle, M., Pedlar, A., Meurs, E. J. A., et al. 1988, ApJ, 326, 125 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison between our model and the Bennert et al. (2006) nuclear optical spectrum.
All Figures
 |
Fig. 1 2D map of the stellar continuum at 5500 Å. The numbers identify the spectra in Fig. 7. The image size is 16 × 16 square arcsec. North is up and east is to the left. |
| In the text | |
 |
Fig. 2 Maps of the line ratios to Hβ. From left to right: [O III], [Fe VII] and [N II] (top); [O II], [S II]6716 and He II (middle); [O I], [S II]6731 and He I (bottom). Spatial scale is 1 arcsec px-1. North is up and east is to the left. |
| In the text | |
 |
Fig. 3 2D map of the S/N of the stellar continuum. The numbers indicate the successfully modelled spectra. |
| In the text | |
 |
Fig. 4 Correlation of the input parameters with calculated [O III]5007+/[O II]3727+ line ratios. |
| In the text | |
 |
Fig. 5 Top: histograms of the shock velocities (left), pre-shock density (middle) and the AGN ionizing flux (right). Bottom: 2D maps of the same parameters. The units are km s-1 (left), cm-3 (middle) and ph cm-2 s-1 eV-1 (right). Spatial scale is 1 arcsec px-1. Contours of the stellar continuum are overplotted onto the map of the ionizing flux. North is up and east is to the left. |
| In the text | |
 |
Fig. 6 Comparison between the observed and the calculated emission line ratios for the lines in Table 2. σ is the median error for the observed ratios. The solid line is the 1:1 line. |
| In the text | |
 |
Fig. 7 Variations of calculated/observed line ratios as a function of the number of spectra (see Fig. 1). Left: [N II]/Hβ (red asterisks), [O II]/Hβ (blue asterisks); middle: [O I]/Hβ (green asterisks), [S II]6716+6731/Hβ (black asterisks); right: He II/Hβ (magenta asterisks). |
| In the text | |
 |
Fig. 8 Obs/calc maps of nitrogen (left), oxygen (middle) and sulphur (right). Values lower than 1 indicate depletion. Spatial scale is 1 arcsec px-1. North is up and east is to the left. |
| In the text | |
 |
Fig. 9 Profile of HI (solid line), HeI (dot-dashed) and HeII (dashed) fractional abundances as a function of distance from the shock front for position 53. |
| In the text | |
 |
Fig. 10 Pos. 140 (left), pos. 149 (right); top diagram: the electron temperature (solid line) and electron density (dashed line) downstream; middle diagram: the fractional abundances of O0 (green), O+ (black), O2+ (red); bottom diagram: the fractional abundances of Fe+ (black), Fe2+ (red), Fe3+ (magenta), Fe4+ (cyan), Fe5+ (yellow), Fe6+ (blue). |
| In the text | |
 |
Fig. 11 Comparison of the continuum SED with the model results. Black crosses: data from NED; black encircled crosses: the data from the NED believed to be dominated by the AGN; red asterisks: data from Sargsyan (2011); black squares: data from GALEX archive; green: synchrotron radiation; red: the dust-reprocessed radiation flux calculated by models 71 (solid line) and 107 (dashed line); blue: the bremsstrahlung for position 71 (solid line) and for position 107 (dashed line). Black line: the black-body flux from the background stars. |
| In the text | |
 |
Fig. 12 Shock velocities vs. Hβ calculated flux (top panel); fluxes from the active centre vs. Hβ calculated flux (bottom panel). Red: models calculated with high Vs (> 700 km s-1); blue: the other models. |
| In the text | |
 |
Fig. 13 2D map of the shock velocity in km s-1 with the contour map of the photoionization cone ([O III]/Hβ) overplotted. Spatial scale is 1 arcsec px-1. |
| In the text | |
 |
Fig. 14 N/O vs. O/H diagram adapted from Mouhcine & Contini (2002, see their Fig. 1). The blue area represents a sample of UV-selected galaxies, the red area includes starburst nucleus galaxies (SBNGs) selected in the optical or in the infrared, and the magenta area represents H ii galaxies. The results of our model calculations are overplotted (black circles). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


