| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201218812 | |
| Published online | 28 August 2012 | |
High angular resolution near-infrared integral field observations of young star cluster complexes in NGC 1365⋆
1 Observatório Nacional, Rua General José Cristino, 77, 20921-400 São Cristovão, Rio de Janeiro, Brazil
e-mail: egallian@on.br; etelles@on.br
2 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
e-mail: mkissler@eso.org
3 Observatoire de Haute-Provence, OAMP, 04870 Saint Michel l’Observatoire, France
e-mail: danielle.alloin@oamp.fr
Received: 11 January 2012
Accepted: 21 July 2012
This paper presents and examines new near-infrared integral field observations of the three so-called “embedded star clusters” located in the nuclear region of NGC 1365. Adaptive-optics-corrected K-band data cubes were obtained with the ESO/VLT instrument SINFONI. The continuum in the K-band and emission lines such as He I, Brγ, and several H2 lines were mapped at an achieved angular resolution of 0.2′′ over a field of 3 × 3′′2 around each source. We find that the continuum emission of the sources is spatially resolved. This means that they are indeed cluster complexes confined to regions of about 50 pc extension. We performed robust measurements of the equivalent width of the CO absorption band at 2.3 μm and of Brγ. For the main mid-infrared bright sources, the data only allow us to determine an upper limit to the equivalent width of the CO bands. Under the assumption of an instantaneously formed standard initial mass function Starburst99 model, the new measurements are found to be incompatible with previously published mid-infrared line ratios. We show that an upper mass limit of 25 to 30 M⊙, lower than the typically assumed 100 M⊙, allows one to simply remove this inconsistency. For such a model, the measurements are consistent with ages in the range of 5.5 Myr to 6.5 Myr, implying masses in the range from 3 to 10 × 106 M⊙. We detect extended gas emission both in H ii and H2. We argue that the central cluster complexes are the sources of excitation for the whole nebulae, through ionisation and shock heating. We detect a blue wing on the Brγ emission profile, suggesting the existence of gas outflows centred on the cluster complexes. We do not find any evidence for the presence of a lower mass cluster population, which would fill up a “traditional” power law cluster mass function.
Key words: Hii regions / infrared: galaxies / galaxies: groups: individual: NGC 1365
Figure 9 and Tables 1–4 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The knowledge about young star cluster populations in galaxies increased much since high angular resolution (~0.1′′) visible images could be obtained with the Hubble Space Telescope (see the reviews by Portegies Zwart et al. 2010; Larsen 2011, and references therein). In the infrared, images approaching such a high angular resolution can be achieved only from large aperture, hence ground-based telescopes. The high angular resolution infrared observations therefore suffer from the limitations inherent to the technique itself: only a few infrared transparent windows exist, and, due to the intense atmospheric emission, the sensitivity is relatively low. The few high angular resolution mid-infrared (MIR) studies of actively star-forming regions in external galaxies have been able to resolve them in hot spots, which generally have no counterpart in the visible, but are bright in the radio. These types of sources have been named “embedded clusters” (Gorjian et al. 2001; Plante & Sauvage 2002; Beck et al. 2002; Martín-Hernández et al. 2005; Galliano et al. 2005; Martín-Hernández et al. 2006; Wold & Galliano 2006; Gandhi et al. 2011). They correspond to the hypothetical first phase of a star cluster, when it is still embedded in its birth material. It is believed that this embedded phase only lasts for a few million years: the intense stellar winds and supernova activity provokes the expulsion of the remaining gas and quickly leads to the disruption of the cluster itself (see the review by Bastian 2011, and references therein).
Three examples of massive star clusters in this evolutionary stage have been discovered in the star-forming nuclear region of the strongly barred spiral NGC 1365 (Galliano et al. 2005, GA05). The relatively small distance of NGC 1365 (18.6 Mpc, 90 pc per arcsec), the fact that this galaxy has been extensively observed and modelled (see Lindblad 1999, for a review on the specific galaxy), and the fact that the galaxy hosts an active galactic nucleus (AGN) that can feed an adaptive optics (AO) system make these clusters preferred targets for detailed studies. They are located in the central star-forming region, close to, or within, a well-defined dust lane. They were named M4, M5 and M6, “M” standing for MIR (GA05).
Galliano et al. (2005) presented the discovery (with ESO/3.6 m/TIMMI2) of the bright MIR counterparts to previously known centimetre sources (Sandqvist et al. 1982; Saikia et al. 1994; Sandqvist et al. 1995; Forbes & Norris 1998), and interpreted them as “embedded star clusters”. (Galliano et al. 2008, hereafter GA08), complemented these observations with near-infrared (NIR) data (K and L images and spectra with ESO/VLT/ISAAC), as well as new MIR data (narrow 12.8 μm image and N-band spectra with ESO/VLT/VISIR). These sources are bright in the MIR continuum, nebular lines, cm continuum and are spatially associated to CO hot-spots (Sakamoto et al. 2007, hereafter SA07). In GA08, we determined masses of about several times 107 M⊙ for the stellar component of each cluster, which puts them in the range of the most massive known stellar clusters (Kissler-Patig et al. 2006). The masses were estimated using the dereddened Brγ fluxes, and a determination of the cluster ages. Because the hydrogen emission line fluxes dramatically decrease with time during the first ~10 Myr of a cluster life, the mass estimated using the nebular line flux is very sensitive to the age determination. In GA08, we proposed an age determination for the clusters using the ionised gas emission lines in the N-band. Three lines of different ionisation potential ([Ar III] 27.6 eV, [S IV] 34.8 eV and [Ne II] 21.6 eV) are located in the N-band. In the VISIR N-band spectra, only the lower ionisation line [Ne II] could be detected. The stellar population synthesis model for young and instantaneously formed clusters predicts a drop of more than two orders of magnitude in the stellar continuum for radiation capable of ionising [Ar III] and [S IV], while this drop is much smaller (one order of magnitude) for the [Ne II] ionising radiation (see Figs. 15–17 in GA08). From this argument, we estimated an age of about 7 Myr for the three sources, from which we derived the above mentioned masses. Some other observational facts supported our age estimate for the clusters. First, similar-quality MIR spectra of a younger massive embedded cluster (NGC 5253/C2 with ESO/3.6 m/TIMMI2 by Martín-Hernández et al. 2005) indeed display intense [S IV]. They show that [SIV] is much brighter than [NeII]. Also, the centimetre spectral indexes of embedded clusters in NGC 1365 reveal a significant share of non-thermal emission, possibly originating from a high supernovae rate. This points towards ages older than 3 Myr or 4 Myr (GA05). In contrast, younger (~1 Myr old) clusters have flat or even inverted spectra (Kobulnicky & Johnson 1999). The long-slit K-band ISAAC spectra published in GA08 also displayed the CO absorption bands at 2.3 μm. These features are only expected to appear with the first red super giant stars, hence not before 6 Myr. Nevertheless, since the ISAAC spectra have relatively low angular resolution, this argument was not considered to be robust because we could not infirm the possibility that the absorption came from the background or nearby sources. A more reliable analysis is presented here, and interestingly, does not confirm the presence of the CO absorption bands that originate from the clusters themselves.
Elmegreen et al. (2009) examined how these sources might have been formed. These authors showed that the extreme stellar masses derived for the clusters in GA08 are consistent with the properties of the galaxy: the large amounts of gas found in the central kpc region that was detected through HI (Jorsater & van Moorsel 1995) and CO observations (Sakamoto et al. 2007) are sufficient for the formation of a few 107 M⊙ clusters. Elmegreen et al. (2009) propose a scenario to explain the building-up of the nuclear mass, where gas loops in along dust filaments to feed the bar dust lane and finally flows inwards towards the nuclear region. The interaction between the dust filaments and the dust lane is possibly a trigger for the formation of star clusters, which then would move inwards following the gas flow and feed the central bulge.
In the present paper, we discuss a new dataset for these three targets, recorded with SINFONI, the adaptive optics near-infrared integral field instrument available at the VLT. The observations were obtained with the adaptive optics loop closed on the nucleus of the galaxy, and hence have an angular resolution that is close to the diffraction limit of the 8 m aperture telescope. Since the SINFONI data cubes contain very much information, we give priority to the detailed presentation of the data, including the publication of tables. We report about the collection and reduction of the data in Sect. 2. The data analysis including the different measurement procedures used are described in Sect. 3. In Sect. 4, the observational results are provided; they are discussed in Sect. 5, and our conclusions are given in Sect. 6.
2. Data collection and reduction
The dataset was obtained with SINFONI at the ESO/VLT in the night from 2005/12/04 to 2005/12/051. SINFONI is a NIR integral field spectrometer (SPIFFI) coupled to a visible curvature AO system. The wavefront was analysed directly on the AGN of the galaxy (type 1.5, R = 15.4). The following observing mode was selected: field of view of 3 × 3′′2 and spaxels of 0.100 × 0.050′′2, wavelength range from 1.95 μm to 2.45 μm and spectral resolution of 4000, corresponding to an instrumental broadening of FWHM = 5.5 Å (this translates into FWHM = 75 km s-1 or σ = 30 km s-1). Since the angular distance between the clusters is about 4′′, we had to point on each target separately. The total integration time for each pointing was set to 1800 s. The observations were carried out under regular and stable atmospheric conditions, with a seeing of 1.2′′, a Strehl ratio of 42%, leading to an angular resolution of about 0.2′′ (λ/D = 0.05′′ at 2.1 μm), measured on the data, as detailed in Sect. 3.2.
An attempt to fully reduce the data cubes using the ESO pipeline (Modigliani et al. 2007) was first performed, but left too strong sky line residuals on the final spectra. These residuals result from the change of sky line intensity between the observation of the object (OBS) and that of the sky (SKY). P-Cygni-like profile residuals are also observed in some cases. They are due to a slight shift in the wavelength calibration between the OBJ and SKY telescope positions. These effects are thoroughly discussed in Davies (2007) and specific routines have been developed to correct them. They were kindly provided to us by Davies and allowed to improve the sky subtraction. All details about these procedures can be found in Davies (2007).
We used the following tools in the reduction process: the ESO pipeline, the routines by Davies, our own IDL routines, and the data visualisation tool QFitsView, developed by Thomas Ott at MPE2.
The observation of each target was split into two blocks (two OBs), each of which is a sequence of six integrations alternating object and sky (OBJ-SKY-SKY-OBJ-OBJ-SKY). For each field, we hence had six pairs (OBJ+SKY) of cubes. A standard jittering procedure was used for each sequence.
The data reduction was performed as follows. First, the raw frames were cleaned from the bad lines that are created by the data processing hardcoded at the detector level. The correction was performed using the routine provided in the SINFONI data reduction cookbook. We then reduced the calibration frames using the pipeline. Second, pipeline basic reduction was applied to each individual science cube (and not to each individual pair of cubes, as would be the case for standard pipeline reduction): the data were flat-fielded and corrected for dead/hot pixels; interpolations to linear wavelength and spatial scales were applied, after which the slitlets were aligned and stacked to create the final cube. The reduced sky cubes were then subtracted from the corresponding object cube using the routines from Davies (2007). A sample of a spectrum without/with residual correction is displayed in Fig. 1. It shows that we did not entirely get rid of the artefact P-cygni like residuals. Hence, for enhancing the legibility of the data, we decided to perform a cosmetic step after the correction, that replaced the pixel values by the median value over the wavelength range of the main lines. These ranges are highlighted in grey on the spectra displayed in the paper. The only line of interest that is critically affected is H2 3–2 S(3).
 |
Fig. 1 Example of the sky-subtraction correction, for an average case. We display a portion of the 1′′ radius aperture spectrum of one of the M4 data cube pairs. On top, the P-Cygni-like residuals are stronger before correction, and below, after correction, the residuals have been attenuated. The emission line is Brγ. |
Then, for each pointing, the six sky-subtracted reconstructed cubes were combined. For this, relative astrometry was performed between the cubes, using the header information about the jitter sequences.
We simultaneously performed the relative wavelength response and telluric feature corrections using the ESO provided data products of 27 observations of telluric standard stars. A median response, corrected from the stellar features, was then computed using the stellar spectra published by Pickles (1998) that are available on the ESO website. A scaling factor, following the Iraf telluric routine, was applied to adjust the depth of the atmospheric features. We also used this set of standard star data to evaluate the uncertainty on the flux calibration, which we call hereafter “photometric uncertainty”, in contrast to “measurement uncertainty”. The standard deviation of the conversion factors for these star flux measurements is 40%. Because these observations were obtained on different nights, we can be confident that the “photometric calibration uncertainty”, due to both the uncertainty on the standard star fluxes and the sky transparency variations, is at most ± 20%.
To perform the relative registration of the cubes, we first built K-band images by convolving by the filter transmission, and then degraded the image and pixel size to adjust it to that of the ISAAC K-band image published by GA08. For each image, we ascertained the world coordinates of the brightest peak using the ISAAC image to register the cubes. We hence used the same astrometric reference as in GA08, where the [0′′; 0′′] coordinate was set to the peak of the AGN in the VISIR 12.8 μm image.
Once the registration was performed, we use the comparison between the degraded SINFONI K-band reconstructed images and the ISAAC images to perform the absolute flux calibration of the images. This choice implies that the flux measurements on the ISAAC and on the SINFONI data agree by definition.
The last step of the reduction is the correction of the wavelength calibration to set the radial velocities in the local standard of rest (LSR).
3. Data analysis
This section presents the methods used to extract the quantitative information from the dataset.
3.1. Map reconstruction
 |
Fig. 2 Gas emission around the extremely massive clusters in NGC 1365, observed with VLT/SINFONI. First row: Brγ flux, radial velocity, and velocity dispersion, from left to right. Second row, same for H2; third row, same for He I. The axes are in arcsec, north is up and east is left. |
 |
Fig. 3 Top row, left to right: reconstructed maps for K-band flux density, Brγ flux and H2 1–0 S(1) flux. The chosen apertures are drawn on the maps. The aperture labels are given for each map on the empty map below it for clarity. The label number is given in increasing Right Ascension. North is up and east is left, and the X and Y axes are in arcsec. |
The first step of the analysis of the reduced data cubes is reconstructing 2D maps from 3D cubes. For three chosen emission lines (He I 2.06 μm, H2 2.12 μm and Brγ 2.16 μm), we performed an automatic Gaussian fit for each spectrum of the cubes, and built 1) the radial velocity maps (Gaussian profile central wavelength); 2) the radial velocity dispersion maps (σ of the Gaussian); and 3) the Gaussian flux maps from the fit parameter values. These maps are displayed in Fig. 2: from left to right, line flux, line radial velocity, and line width. A K-band map is obtained by convolving each spectrum by the filter transmission curve. A narrow band (excluding any spectral feature) map is also computed; it shows that the difference to the full K-band map is negligible. Accordingly, we only considered the full K-band maps. The K-band reconstructed map is displayed in Fig. 3 in the top left frame. This figure will be described in Sect. 3.2, when we define the set of apertures used for performing the measurements.
The Brγ large-scale kinematics (radial velocities) are consistent with the CO kinematics. The Brγ velocities can be compared to the large-scale isovelocity contours in SA07, which clearly show a rotation pattern with non-circular motions. From their Table 5, the measured LSR velocities (at the peak of brightness temperature for 12CO(2–1) ) are 1560 km s-1, 1540 km s-1 and 1480 km s-1 for the CO knots associated with M4, M5 and M6. In the SINFONI data, for a 1.0′′ diameter aperture, we find 1555 km s-1, 1520 km s-1 and 1475 km s-1 for Brγ, and 1560 km s-1, 1530 km s-1, and 1470 km s-1 for H2 respectively. We measured these velocities with a simple Gaussian fit at the positions [0.41; 7.12], [2.80; 9.86], [4.80; 6.90]. These results indicate that the Brγ velocities are slightly blueshifted with respect to CO. The 12CO(2–1) FWHM are 70 km s-1, 60 km s-1 and 80 km s-1 respectively, while Brγ is broader with an FWHM of 145 km s-1, 145 km s-1 and 200 km s-1 respectively.
 |
Fig. 4 Light profiles (1D cuts through the images) for a telluric star, N1, M5 and N2. For the first three, we took cuts along PA = 0°, 45°, 90° and 135° (black crosses, cyan asterisk, purple triangle and brown diamond). The median profile is drawn with a black line, and the Lorentzian fit with a salmon line. For N2, we only have PA = 0° since it is on the edge of the image. The fit FWHM are 0.10′′, 0.23′′, 0.20′′ 0.25′′. |
3.2. Measurement procedures
To perform measurements on the data cubes, we chose to first define a set of significant apertures to reduce the amount of information to be analysed. We used the K-band, Brγ, and H2 reconstructed maps to select the positions of these apertures. We chose the most prominent sources in the three images, as well as a few other apertures that sample regions of lower surface brightness. These apertures are drawn and labelled over the reconstructed maps in Fig. 3, which show from left to right, the K-band, Brγ and H2 maps. Below each map we show the set of labels used for identifying the apertures: a number increasing with Right Ascension. Their radius of 0.1′′ allows one to sample single angular resolution elements. The measurements performed are consequently the least possibly affected by source mixing. Results for most measurements described below are given in Tables 1–4 and can be used for subsequent analysis. The line fluxes given in the tables have not been corrected for any extinction.
The uncertainties on the different measurements have two origins: the uncertainty due to the noise and the measurement procedure, and the uncertainty on the calibration of the data, which we called photometric uncertainty in Sect. 2. In the tables, we only give the measurement uncertainties. The total maximum uncertainties for the fluxes can be obtained by quadratically adding the ± 20% uncertainty derived in Sect. 2 to the measurement uncertainty.
To measure the angular resolution on each cube, we chose sources that are bright and narrow and measured their profiles on the K-band reconstructed image. We chose four sources: a telluric star, the K-band bright cluster N1 (to the west of M4), M5 and N2, the bright cluster on the southern part of the M6 field. The profile measurements are shown in Fig. 4. The cuts are obtained along PA = 0°, 45°, 90° and 135°, at the position of the source given in Table 1, and at the centre of light for the star. Since the data are AO-corrected, it is natural for the telluric star to have a narrower profile, because the Strehl ratio is higher. In the best case, the achieved resolution would hence be 0.1′′ FWHM. For our dataset, the values measured are 0.23′′, 0.20′′ 0.25′′, for the M4, M5 and M6 cubes, respectively, and are to be considered as upper limits, since we cannot be certain that the sources are not resolved. We used the fits of the spatial profiles for comparison with the profiles measured on the data. In Fig. 5, we compare the profiles of the main sources (M4, M5 and M6) for K-band, Brγ and H2 2–1 S(1) to the measured reference profiles to check if they are resolved.
The centre of each aperture was first chosen by eye on the reconstructed maps, and then taken as the centre of light in a box of 3 × 3 pixels around the initially chosen position. For apertures that coincide with emission peaks, the given aperture position is a measurement of the source position. For apertures defined on extended emission regions, the precise position is not meaningful. Different peak positions coming from measurements inside a single cube (for example the K-band peak and a Brγ peak) have a good relative registration precision, up to a fraction of pixel size (1/5 of a pixel corresponds to 0.01′′). Between cubes, the registration was performed using the ISAAC images, and hence has the precision of a fraction of an ISAAC pixel size (1/5 corresponds to 0.03′′).
The emission line fluxes through the given apertures are derived from automatic Gaussian+continuum fitting of the line profiles, carried out with the idl routine mpfitpeak by Markwardt (2009). We measured the following lines: Brδ, Brγ, He I, and H2 roto-vibrational 1–0 S(3), 1–0 S(2), 2–1 S(3), 1–0 S(1), 2–1 S(2), 1–0 S(0), and 2–1 S(1). The errors on the fluxes and widths were derived from the routine results, whereas the error on the line centre was simply taken to be 1/5 of the line FWHM. For the flux measurements for lines below 2 μm, the uncertainty is greater due to the uncertainty on the response, because of the poorer atmospheric transmission in this region. We evaluated the uncertainty using the spectrum of M6 (apertures 31 and 32), which displays a steep continuum. If we extrapolate the continuum slope down to 1.95 μm, we find 0.0015 mJy, while we measure 0.0025 mJy on the spectrum. This means that the error can be higher than 50%.
 |
Fig. 5 Profile cuts for M4, M5 and M6 (position given is the table for the light centre on the K-band image) along PA = 45°, 60°, and 110°. The dotted line is the comparison profile for each cube (as explained in the corresponding paragraph). It has been rescaled to give a meaningful comparison. |
We measured the equivalent width of the CO 2.29 μm absorption band (EW(CO)) using the following procedure. First, we built a spectrum of the background emission of the region. Using a histogram of the K-band flux density, we assumed that the pixels with less than 0.7 mJy arcsec-2 belong to the background. A median background spectrum was then built for each of the three cubes. For each aperture, we measured EW(CO) on the background-subtracted spectrum. The continuum fit was performed over three intervals between the bands, while the depth of the feature is measured between 23 050 Å and 23 160 Å. The measurement error given in Table 1 corresponds to ± 0.3σ of the continuum around the fit. If the continuum signal-to-noise ratio (S/N) was less than 3, we only considered the upper limit of the EW(CO) (feature width divided by 0.3σ).
At the defined aperture positions, we performed larger aperture background-subtracted flux measurements (aperture radius of 0.2′′ and background in an annulus between 0.2 and 0.6′′). We used the djs_phot for the measurement and error evaluation. From these two measurements, we extract what we refer to in the following as the equivalent width of Brγ: EW(Brγ).
We measured the slope of the continuum (after background subtraction) as the ratio between the fluxes measured through two artificial rectangle 200 Å broad filters, which do not include any spectral feature and are centred at 20 300 Å and 22 100 Å. For these flux densities, the error was set to half the dispersion of the continuum.
4. Observational results
This section describes the main observational results derived from the analysis of the data described above. These results are discussed in Sect. 5. First, we present the results related to the images reconstructed from the data cubes and then those derived from the spectral measurements.
4.1. Images
Figure 6 shows the zoomed 1.2 × 1.2′′2 fields around M4 (top row), M5 (middle row) and M6 (bottom row). From left to right we display (1) the HST “R-band” image (filter F606W); (2) the SINFONI K-band image; (3) the Brγ image and (4) the H2 1 − 0 S(1) image. The crosses mark the position of the Brγ peak as defined by the procedure described in Sect. 3.2. It is important to keep in mind that the pixels on the cubes before combination are rectangular spaxels, which appear as 0.05 × 0.1′′2 rectangular vertical pixels on the reconstructed images. This can give the illusion that some sources are extended in the north-south direction.
The cluster positions were defined in GA08 as the peak of [Ne II] 12.8 μm emission. Now, we can refine this positioning by taking the Brγ peak position on the 0.2′′ resolution images. The [Ne II] and the Brγ positions are consistent, and the difference for M5 arises because, at the resolution of SINFONI the source is resolved into two bright knots. The new positions for the clusters are [0.39′′; 7.13′′] for M4/source 10, [2.80′′; 9.80′′] for M5/source 18 and [4.78′′; 6.93′′] for M6/source 31. The absolute precision of this registration with respect to the AGN is 0.03′′ ( ± 0.015′′, see Sect. 3.2).
 |
Fig. 6 Zooms on the 1.2 × 1.2′′2 around M4 (first row), M5 (second row) and M6 (third row). For each source, from left to right we display the R-band image (HST), the K-band image emission, the Brγ emission and the H2 1–0S(1) emission. The crosses mark the position of the Brγ peak. North is up and east is left, and the X and Y axis are in arcsec. |
At the new achieved angular resolution, we see that the Brγ and H2 sources that seemed coincident in the former observations at lower resolution are in fact spatially distinct emission knots. It is expected that the formerly superposed Brγ and H2 knots are not anymore perfectly coincident when the angular resolution is sufficiently high. This has previously been observed with a similar technique in IIZw40 by Vanzi et al. (2008). In our case, the data show that M4 is marginally resolved in K and Brγ, while the associated H2 peak is resolved (FWHM ~ 0.3′′) and is shifted by about 0.1′′ to W-SW. A secondary H2 source (source 3) is detected about 0.5′′ to the east of M4, and has no counterpart in any other emission. M5 is clearly resolved into four sources (apertures 16, 18, 21, 22) following a cloverleaf configuration inside a circle of about 0.5′′ diameter. Apertures 18 and 21 correspond to an emission peak in K and Brγ. These sources are not resolved individually. The associated H2 emission lies outside this cloverleaf, in two resolved knots aligned along PA ~ 70° and at a distance of about 0.8′′ (apertures 23 and 15). M6 is detected and resolved in K and Brγ. It has an asymmetrical shape, with an extension towards the S-E, which can be seen as an extended wing in the profiles in Fig. 4. The source as a whole is detected in H2, but the maximum of H2 is displaced by about 0.1′′ to the south with respect to the Brγ emission.
Figure 2 shows the full combined gas emission reconstructed maps for Brγ (top row), H2 1–0 S(1) (middle row) and He I (bottom row). From left to right we display the line flux, line centre and σ maps. We detect extended emission on scales of several arcsec, both in Brγ and H2. They have the same global distribution, but differ at the sub-arcsec scale: M4 and M5 are located on a filament-like emitting structure oriented along PA ~ 45° and extending over about 7′′, with a width of about 1′′. A distinct and more symmetrical emission region of about 3′′ diameter is observed around M6. The bright emission peaks are localised well in the middle of the extended emission regions. Apart from M4, M5 and M6, and their closely associated sources, there are only few secondary weak peaks (apertures 4, 7, 13 and 28 for Brγ).
4.2. Spectra
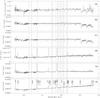 |
Fig. 7 Top to bottom: a) spectra of the background (defined in Sect. 3.2) + HR6705 in grey, b) aperture 0 + HR2508 in grey, c) aperture 26 + HR2508 in grey, and d) aperture 9 (M4), e) aperture 18 (M5) and f) aperture 31 (M6). d)–f) are not background subtracted. |
Figure 7 shows several full-wavelength range spectra of (a) the background as defined in Sect. 3.2, (b and c) the two brightest K-band clusters, and (d, e and f) M4, M5 and M6. Over the three first spectra, we plotted in grey normal star spectra taken from the library of Wallace & Hinkle (1997) for comparison. The line wavelengths given in the following are the rest wavelengths, the observed redshifted ones are about 0.01 μm longer.
The full-field combined K-band map is displayed on the left of Fig. 3. What we defined as background continuum in Sect. 3.2 appears in red (up to 0.7 mJy arcsec-2). The corresponding spectrum is given in Fig. 7a. Across this background, we mostly detect continuum sources along the border of the dust lane, on its western side. Only a few sources are detected on the dust lane itself, except for M6: we identified the sources corresponding to apertures 5, 12, 24 and 25. Two bright K-band clusters are observed: apertures 0 and 26. Their spectra are given in Figs. 7b, c.
The emission lines initially present on the background spectrum were removed artificially, and a pure continuum spectrum is left. In grey we overplot the spectrum of HR6705 (K5III). The next two spectra (apertures 0 and 26) correspond to the two brightest K-band sources. From these spectra, no emission lines were removed. The overplotted stellar templates are HR2508 (M1 + Ib-IIa). The spectral slopes of the templates were slightly reddened to adjust them to the observed ones. The spectra display strong CO absorption as well as metallic line absorptions. The next three spectra are M4, M5 and M6 (apertures 9, 18 and 31). The three sources show a rising continuum towards the red and several emission lines, labelled on the spectrum of M6: Brδ, Brγ, the 2.06 He I μm line and seven H2 roto-vibrational lines. For M5 and M6, a broad He I 2.11 μm observed close to the blue side of H2 1–0 S(1) is detected. The Gaussian fit FWHM is 50 Å and 38 Å for M5 and M6, respectively, while it is about 10 Å for the other lines. Weak He II absorption at 2.19 μm is detected for M5 and M6. For M6 only, we detect two weak [Fe III] emission lines at 2.22 μm and 2.24 μm. An unidentified emission line is detected on the spectrum of M6 at an observed wavelength of 22 097 Å, which corresponds to a rest wavelength of 21 990 Å.
 |
Fig. 8 Shape of the Brγ line. Top to bottom, left to right: apertures 9 (M4), 18 (M5), 31 (M6), 4, 13 and 28. The null velocity is chosen as the centre of the Gaussian fit of the line, and the continuum derived in the fit is subtracted. The crosses show the actual profile values for the positive velocities, which are also plotted for the negative velocities to show the asymmetry of the profile. |
For M4, M5 and M6, we detect an asymmetry in the Brγ profile. The same asymmetry is observed for He I 2.06 μm. Figure 8 displays the profiles for M4, M5 and M6 in the left column from top to bottom, and for a set of off-centred apertures (4, 13 and 28) in the right column. The intensities are shown on a logarithmic scale. The null velocity is computed as the central velocity of the Gaussian fit of the line. For the positive velocities, the crosses just show the data, and these are mirrored on the side of the negative velocities, from which one can appreciate the degree of asymmetry of the profile. Clearly, M4, M5 and M6 have an extended blue wing, while the spectra from the three other apertures display symmetrical profiles.
Figure 9 gathers a set of diagrams that plot various observables measured on the data following the procedures detailed in the former section. For all diagrams, the blue dots mark the bright Brγ sources, and the red dots mark the H2 emission knots. The purple labels refer to either the aperture numbers as defined in Fig. 3 or directly the source names for M4, M5 and M6. As detailed in Sect. 3.2, the equivalent width of the CO 2.29 μm band was measured through all defined apertures. The EW(CO) vs. the aperture number is plotted in Fig. 9a. Absorption is detected through all apertures, except for the Brγ peak sources M4, M5 and M6, for which the upper limit is a few Å. For the sources that are not bright in Brγ, the EW(CO) is about 20 ± 5 Å. Figure 9b shows as a histogram the number of apertures per EW(CO) bin and identifies two groups. In Fig. 9c, we plot the EW(CO) vs. the EW(Brγ). We see that the two groups are well identified in both quantities, with a well-defined anti-correlation between EW(Brγ) and EW(CO). M4-2 (or aperture 6, the K source right next to M4) has a high EW(CO), and its also high EW(Brγ) is likely due to its being superimposed over the extended Brγ emission from M4. The EW(Brγ) of the older sources range from 0 Å to 20 Å, and their EW(CO) from 15 Å to 25 Å. The other sources have higher EW(CO), ranging from 110 Å to 150 Å, and low EW(Brγ).
From the line analysis of our dataset, the only possibility to evaluate the extinction is to use the ratio between the two hydrogen lines that we can measure: Brδ and Brγ. Unfortunately, as stated in Sect. 3.2, the uncertainty on the flux calibration in the region of Brδ is greater than in the other regions of the spectral range. Indeed, if we blindly measure the Brδ fluxes, we find the Brδ/Brγ ratio to be higher than that of the theoretical case B (0.66). We decided to apply a correction factor of 0.0015/0.0025 = 0.6 to the Brδ fluxes (according to the continuum shape, as explained in Sect. 3.2). In Fig. 9d, we plot the continuum slope as defined in the previous section vs. the Brδ/Brγ. The correlation suggests that the origin of the continuum slope is the extinction. We transformed both quantities in Av in Fig. 9e. To derive the extinction from the continuum slope, we considered that the flatter source (N2 or source 26) has no extinction. We see that at least for the brightest Brγ sources (cyan dots), the values are well consistent and are in an Av range from 10 to 30 mag.
Figure 9 also displays three additional plots. Plot 9f shows that there is a possible correlation between the width and flux of Brγ. We will not discuss any implications of this because the apparent correlation is weak, but we think it is worth mentioning, given the number of results in the literature about the L-σ relation in dwarf galaxies (Bordalo & Telles 2011, and references therein). Plot 9g shows that the H2 and Brγ line widths are correlated, with H2 being narrower than Brγ (H2 ~ 0.85Brγ). Interestingly, in the “filament” joining M4 to M5, the Brγ FWHM values are about 10 Å, while they exceed 14 Å in the region of M6. This region of higher line width for both Brγ and H2 also displays a blueshift higher than in the surroundings, as can be seen in Fig. 2. The last plot (Fig. 9h) shows that the H2 line ratio 2–1 S(1)/1–0 S(1) does not depend on the aperture through which it is measured and has a value of ~0.2 ± 0.1. This is the ratio of the fluxes without any correction for extinction. The effect of extinction on this ratio is small since the lines are in the NIR and their wavelengths are close. For an Av of 30 mag, which represents the most extreme possibility according to Fig. 9e, an observed ratio of 0.2 implies an actual ratio of 0.15, within the error.
5. Discussion
In this section, we discuss the results derived from the dataset and presented above. The improvement of the spatial resolution with the SINFONI data allows us to re-examine the conclusions from GA08, some of which have been summarised in the introduction. First, we show that the new data allow us, contrary to GA05 and GA08, to resolve the K-band stellar continuum emission, and hence prove that the sources are no single clusters but rather cluster complexes. Then, we discuss the implications of the non-detection of the CO absorption bands, contrary to our previous work, derive new ages for the clusters, and discuss the apparent inconsistency with our previous estimate of 7 Myr, based on the MIR line ratios. In Sect. 5.2, we discuss the origin of the extended gas emission around the clusters, making full use of the integral field capacity of SINFONI.
5.1. Multiplicity and age
 |
Fig. 10 Starburst99 equivalent widths for Brγ emission on the left, and CO 2.29 μm absorption band on the right. |
First, the SINFONI data show that M4, M5 and M6, which we repeatedly referred to as clusters, are resolved in the K-band map at a resolution of 0.2′′, which corresponds to about 20 pc (Sect. 4.1 and Fig. 5). Since the K-band emission traces the stellar photospheres, these sources are very likely cluster complexes. For M4 and M6, we do not detect multiple sources, but resolve the peaks, hence we cannot formally refute the possibility that they are single large “clusters”. We note that the K-band source M4-2, which at first sight could be considered to belong to the M4 cluster complex, is indeed an older source, with deep CO absorption (see next paragraph). For M5, we detected four unresolved sources in an area of about 0.5 × 0.5′′2 = 45 × 45 pc2. The observational evidence that M4, M5 and M6 are cluster complexes is the crucial new piece of information that the SINFONI data reveal.
A second important piece of information is gained because the SINFONI data allow us to reliably probe the presence of the CO bands at high angular resolution, after careful evaluation of the background emission. Since the rapid evolution of very massive stars turns them into red supergiants in a few million years, the NIR continuum is dominated by them from 6–7 Myr onwards and the deep CO bands appear. Figure 10 shows the evolution predictions of EW(CO) between 0 and 10 Myr for a single, normal IMF, Z = 0.04, instantaneously formed cluster. It shows a steep rise between 6 and 7 Myr. As shown by Figs. 101 and 102 of Leitherer et al. (1999), the beginning of the steep rise of the CO depth will not depend on the precise values of these parameters, since it only depends on the evolution of very massive stars. For M4, M5 and M6, the measured upper limits on EW(CO) of 2 to 4 Å (Sect. 3.2 and Fig. 9a) formally imply an age upper limit of 6.5 Myr. For M5-2 and M5-4, we also have a lower limit for EW(CO) and the corresponding ages lie between 6 Myr and 7 Myr. According to Starburst99, EW(CO) should never exceed 17 Å. Figures 9a, b show higher values, but given the order of magnitude of the measurement error, this is not significant. The EW(CO) of the two brightest K-band sources (apertures 0 and 26) lie somewhere between 19 and 23 Å, and hence must be at the maximum of EW(CO), corresponding to an age between 8 and 30 Myr for instantaneous formation, and between about 10 Myr and 100 Myr for continuous formation.
Another common age indicator for very young clusters is the equivalent width of Brγ, EW(Brγ). This is valid under the hypothesis that we are able to actually measure the continuum from the ionising cluster only, and the Brγ flux emitted by the gas excited by this cluster only. Moreover, we must assume that the extinction towards the stars and the emitting gas is the same, which is not obvious since the spatial scale of the emitting gas is expected to be larger than that of the stars. For this last remark, we can object that this does not seem to be the case for the small apertures for the Brγ-emitting sources (M4, the components of M5 and M6) since we measure a very good correlation between the extinction derived from the K-band continuum slope and that derived from the Brδ/Brγ line ratio (Sect. 4.2 and Fig. 9e): the cyan dots lie close to the dotted line. Figure 9c plots the EW(CO) vs. the EW(Brγ) (measured following 3.2) and shows two groups, the older sources, with low EW(Brγ) and high EW(CO), and the younger sources with high EW(Brγ) and low EW(CO). For M4 and M6, EW(Brγ) is about 130 Å, and it is about 115 Å for the M5 sources. The measurement errors are small because of the measurement procedure, but, given the uncertainties mentioned above, the real uncertainty for the quantity that it makes sense to compare to model predictions must be larger. Nevertheless, even if we consider a large error of 50 Å, the formal ages implied by comparison with the Starburst99 models (Fig. 10) lie in the narrow range from 4.5 Myr to 5 Myr.
In this paragraph, we briefly state why other potentially powerful age indicators cannot be used in our particular case. (1) Wolf-Rayet features: we can easily see that WR features in the spectra of the clusters, if present, would be too faint to be detected. To estimate the flux of a WR in the K-band, we used the WR 102ca spectrum of Homeier et al. (2003), which is is at a distance of 8.5 kpc (quintuplet cluster) and has a flux of 0.04 Jy. According to Starburst99, the NGC 1365 7 Myr old clusters should contain about 1000 WR stars. At the distance of NGC 1365 (18 Mpc), this population would have a flux of only 0.01 mJy, undetectable in our data. (2) Broad-band colours: NGC 1365 has been extensively observed by HST, and hence images in different filters are available from the archive, and could be used to measure the broad-band colours of the clusters and derive ages. M4 and M6 are heavily obscured, and hence not detected in the visible, but M5 is detected. Unfortunately, GALEV models (Kotulla et al. 2009) show that we would need a 0.1mag precision on the Av of the cluster itself to distinguish between 4 Myr and 8 Myr clusters. (3) He I to Brγ ratio: in principle, this ratio would give information about the hardness of the UV continuum emitted by the cluster, and link it to its age (Doyon et al. 1992), but this has been demonstrated to be unreliable by Shields (1993) and Lumsden et al. (2003).
In summary, for a standard instantaneously formed Starburst99 model, there is inconsistency between the different mass estimates:
- 1.
The non-detection of the [ArIII] and [SIV] lines shows that the most massive, hence hard UV emitting stars, have died already, hence that the cluster is older than 7 Myr (Fig. 15 and Fig. 16 of GA08).
- 2.
The non-detection of the CO absorption bands shows the absence of red super giant stars, hence proves that the clusters are younger than 6 Myr.
- 3.
The EW(Brγ), even though we believe is not the most reliable age indicator in our case, is consistent with ages in the range 4.5 Myr to 5 Myr.
An easy way of making the Starburst99 model consistent with the observational constraints is to lower the upper mass cutoff of the IMF (Mmax) to values between 25 M⊙ to 30 M⊙. In this case, the cluster UV continuum is simply never sufficiently hard to maintain the ionisation of [Ar iii] and [S iv].
For Mmax = 25 M⊙ and Mmax = 30 Myr, we find that the observational constraints are consistent with age ranges of [6.2 − 6.4] Myr and [5.62 − 5.64] Myr, respectively. Hence, under the hypothesis of a “low” upper mass cutoff for the IMF, the ages derived might be only slightly lower than our first estimate in GA08, in the range [5.5 − 6.5] Myr. The corresponding mass estimates for the clusters would then be between 3 and 10 × 106 M⊙. We do not claim any evidence for a low upper mass cutoff IMF, but only show that the observational constraints are consistent with it, and inconsistent with the “standard” Starburst99 model. Given the large masses of these systems, the most massive stars cannot be absent just on the basis of stochastics and an astrophysical mechanism should be invoked to explain the possibility of an actual absence of stars with masses greater than 25 M⊙. This is beyond the scope of the current analysis.
In addition to the absolute ages of the cluster complexes, we note the presence of spectral features that might witness age differences between the clusters. We see that the slope (and extinction) increases between M5, M4 and M6. Interestingly, in the spectrum of M6, we detected weak [Fe III] lines that may reveal a slightly harder ionising field, hence a slightly younger age. The younger cluster complex being the most extincted is consistent with the idea of ongoing gas expulsion at that stage of evolution.
Even though we cannot derive any precise extinction from the SINFONI cubes, we estimated extinctions of about 10 to 30 mag through the small apertures, with a good consistency between the extinction from the gas emission lines and the star continuum (Sect. 4.2 and Fig. 9e). Galliano et al. (2008) derived comparatively low extinctions towards M4, M5 and M6 of 13.5, 3.2 and 8.5 mag, through much broader apertures.
In summary, the new dataset has highlighted that M4, M5 and M6 are cluster complexes, and provided evidence (EW(CO) and EW(Brγ) at high resolution) for ages (5.5 Myr to 6.5 Myr) that are slightly younger than previously derived (7 Myr). We showed that the inconsistency between the ages derived from the EW(CO) and EW(Brγ) on one side, and the MIR line ratios on the other, can be overcome by assuming an upper mass cutoff of 20 to 25 M⊙ for the IMF. We also showed that there is some indication for an age gradient across the sources, M6 being the youngest. The comparison between the old and the new extinction measurements strongly suggests that the extinction is patchy and higher towards the main sources.
5.2. The extended gas emission
In this subsection, we discuss the origin of the extended gas emission around the cluster complexes. A direct qualitative comparison between the maps for M4, M5 and M6 and the maps available for the well-known giant H ii region 30 Doradus in the LMC (Indebetouw et al. 2009; Pellegrini et al. 2010, 2011) can help in understanding the origin of the extended emission in the observed field. An impressive image of the whole Tarantula nebula was published in the ESO Photo-Release eso0216. It shows a nebula more than 300 pc across, which corresponds to an angular size of more than 3′′ at the distance of NGC 1365. The ionisation of the 30 Doradus nebula is dominated by photoionisation from the central cluster R136. This shows that even though the presence of more uniformly distributed lower mass and recently formed clusters in the region of extended gas emission cannot be excluded, such a configuration is not necessary to explain the extent of the emission. The region in which we observe M4, M5 and M6 possibly also only contains three giant HII regions, each dominated by a central cluster complex confined in a ~50 pc region. That the emission peaks are located well at the centre of the extended emission in the case of M6, and close to the symmetry axis of the “filament” joining M4 to M5, strengthens the idea that the stellar content is dominated by central cluster complexes. The observed slight shifts in position between the emission peaks (continuum, Brγ and H2) are indeed expected for a “30 Doradus”-like complex and clumpy gas structure for the following reason: at a resolution of about the total angular size of the emitting region, these emissions are coincident, but the stars (sources of continuum), the ionised gas (source of Brγ) and the warm gas (source of H2) occupy different regions of space, and may hence not be spatially coincident. This can be seen in the three colour image of R136 displayed in GA08 (Fig. 12), with the V-band emission tracing the stars, Hα the ionised gas, and 8 μm the warm dust. When observed at a sufficiently high resolution, the difference in position between the peaks of these components can be unveiled.
Indeed, the extended H2 emission is well consistent with the H ii emission on scales of several arcsec, while they do not coincide at a higher level of details. Figure 3 clearly shows that the H21–0 S(1)/Brγ ratio increases with distance to the central sources. We may wonder whether this is a sign of local excitation of the H2 emission. The K-band spectra show a series of H2 lines both for para- and ortho-hydrogen. The excitation mechanism for these lines can give clues about the presence of an underlying population of smaller mass clusters. The low 2–1 S(1)/1–0 S(1) ~ 0.2 ratio observed (Fig. 9h) usually traces thermally excited H2 in shocks. However, for high densities of about 105 cm-3 and for an intense incident FUV radiation field, collisional de-excitation of UV-pumped molecules thermalises the lower energy levels (Burton et al. 1990; Hollenbach & Natta 1995; Davies et al. 2003; Martín-Hernández et al. 2008). That the central UV sources possibly maintain ionisation of hydrogen at large distances suggests that the gas distribution is very clumpy, hence that the density is high. The only quantitative indication of the gas density comes from the observed ratio of the two forbidden [Fe III] lines (3G5–3H6 at rest 2.2183 μm and 3G4–3H4 at rest 2.2427 μm) detected in the spectra of M5 and M6 (apertures 18 and 31). We measured 0.38 ± 0.05 for M6 and ≤ 0.5 for M5. If we compare this to the model predictions from Keenan et al. (1992) reported in Gilbert et al. (2000), we find a density of 105 cm-3. This means that we cannot decide between the two excitation mechanisms from the 2–1 S(1)/1–0 S(1) ratio only. As explained in Davies et al. (2003), while the ν = 2 vibrational levels are thermalised at high density, the ν = 3 level is expected to retain a fluorescent population until even higher densities. In the transitions involving the ν = 3 level, the data only leave upper limits for 3–2 S(2), 3–2 S(4) and 3–2 S(5) while the 3–2 S(3) line is blended with a skyline. For M6 (aperture 31), we found 1 − 0 S(1)/3–2 S(2) > 20, and for the “pure” H2 source (aperture 15), close to M5, we found a lower limit of 35. Considering a ratio 3–2 S(2)/3–2 S(1) equal to the standard para-ortho ratio of 1/3 (see next paragraph), gives 1−0 S(1)/3−2 S(1) > 7 and 12, respectively. According to Martín-Hernández et al. (2008), for densities of about 105 cm-3, the fluorescent ratio retains values lower than 8. The measured lower limits hence suggest that the H2 emission is thermally excited in shocks.
As discussed by Martín-Hernández et al. (2008), an additional diagnostic can be obtained by the measurement of the ortho-to-para ratio of the H2 molecules. Where shock excitation is dominant, this ratio Φ, based on the statistical weights of the nuclear spins, is 3 (Smith et al. 1997). It can take other values in the case of fluorescent excitation (Sternberg & Neufeld 1999). Following Smith et al. (1997) and Martín-Hernández et al. (2008), we can measure the ortho-to-para ratio for the ν = 1 states (Φ1) measuring the fluxes of 1–0 S(0), 1–0 S(1) and 1–0 S(2). The measured values of Φ1 tend to be similar in all apertures, and slightly lower but consistent with 3, with a median of 2.4 and an error of ± 0.7. As reported by Martín-Hernández et al. (2008), ratios in the range 1.5–2.2 have been measured in PDRs. Hence, the measured values are consistent with shock excitation, but have a median that could indicate part of fluorescent excitation.
The different diagnostics for the excitation of H2 suggest a picture in which shocks are the dominant mechanism, while fluorescence, probably also present, is marginal. That shock excitation at large distance from the central complexes is taking place might signal the presence of a lower mass population of young clusters. However, we can also predict the origin of these shocks in gas outflows produced by the central complexes themselves, without the need of invoking another “hidden” cluster population. The blue wing of the Brγ line detected at the location of M4, M5 and M6 and displayed in Fig. 8 is possibly the evidence of such an outflow. The comparison with line profiles extracted away from the main sources, which are free of this asymmetry suggests that the outflows are indeed centred on the main sources M4, M5 and M6. The associated velocities are some hundreds of km s-1, which means that given the size of the giant H ii regions and their age, there has been enough time for gas heating through shocks to occur. The non-detection of the red wing can be simply attributed to extinction.
In summary, we find that the new data are consistent with a picture in which the central cluster complexes constitute the source of excitation of the whole nebula through ionisation and shocks produced by gas outflows. Even though we do not discard it, we find no need to invoke a lower mass cluster population to interpret the data at hand.
6. Conclusions
Thanks to the integral field capacity of SINFONI, along with the improved angular resolution achieved with the adaptive optics, our knowledge and understanding of the three bright MIR/radio “embedded clusters” M4, M5 and M6 located in NGC 1365 nuclear region has greatly improved.
First, the gain in angular resolution in the new K-band maps (compared to the former ISAAC K-band maps) allowed us to resolve the sources. This proves that they are not single clusters, but instead cluster complexes of several tens of parsec size.
The possibility to resolve the spectral features at a high angular resolution allowed us to perform precise measurements of both the equivalent width of the 2.3 μm CO absorption bands and that of the Brγ emission line, uncontaminated by background or close-by surrounding emission. The unexpected non-detection of the CO bands together with the measured values of EW(Brγ) suggest ages that are younger than previously derived. These new measurements, within the framework of a “standard” Starburst99 cluster model, are incompatible with the MIR line ratios discussed in our previous paper. We do not have any reliable explanation for this apparent inconsistency yet. But we note that it is a hint for an upper mass cutoff of the star cluster IMF lower than usually assumed with values below 30 M⊙. In this case, the complexes would only be slightly younger (5.5 to 6.5 Myr) than derived in our former work, with corresponding masses of [3–10] × 106 M⊙ per complex. If we had kept a standard IMF, and simply discarded our previous estimate, we would have found ages of 4 Myr, resulting in much lower masses, of about 106 M⊙.
The complete dataset available for these sources and the extended emission around them suggests that this gas-rich region (SA07) consists of three co-eval multiple “30 Doradus”-type giant H ii regions, each powered by a central star cluster complex. There is a weak observational indication for a slight age gradient among them, with the youngest (M6) displaying a steeper K-band slope and the presence of weak higher ionisation lines. A few secondary Brγ maxima are detected, and witness the presence of at least some lower mass clusters or cluster complexes, but we found no compelling need to invoke a fully populated power law cluster mass distribution to interpret the data at hand. The angular resolution achieved is sufficiently high to show that the distributions of the Brγ and H2 line emission are not coincident, indicating a patchy gas distribution, where the ionised gas is probably seen on the surface of denser knots, and reveals complex kinematics (line asymmetry and broad width). The colder H2 emitting gas is distributed all over the region, and appears to be predominantly thermally excited in shocks, rather than fluorescence in photo-dissociation regions. We interpret the observed extended blue wing in the Brγ profiles as a signature of gas outflows from the main cluster complexes, and suggest that these outflows would be the natural source of shock excitation of molecular hydrogen over the entire region.
Online material
 |
Fig. 9 Set of plots showing different relations between observables. The plots are described in Sect. 4.2. In all plots, the cyan dots correspond to the sources M4, M5, M5-2 to M5-4 and M6. The red dots correspond to the apertures chosen in the H2 image. |
Acknowledgments
We warmly thank the ESO staff for data acquisition in service mode and for support in data reduction. We are also indebted to an anomymous referee for helpful comments.
References
- Bastian, N. 2011, in Stellar Clusters & Association: A RIA Workshop on Gaia, eds. E. J. Alfaro Navarro, A. T. Gallego Calvente, & M. R. Zapatero Osorio, 85 [Google Scholar]
- Beck, S. C., Turner, J. L., Langland-Shula, L. E., et al. 2002, AJ, 124, 2516 [NASA ADS] [CrossRef] [Google Scholar]
- Bordalo, V., & Telles, E. 2011, ApJ, 735, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, M. G., Hollenbach, D. J., & Tielens, A. G. G. M. 1990, ApJ, 365, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I. 2007, MNRAS, 375, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Sternberg, A., Lehnert, M., & Tacconi-Garman, L. E. 2003, ApJ, 597, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Doyon, R., Puxley, P. J., & Joseph, R. D. 1992, ApJ, 397, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Galliano, E., & Alloin, D. 2009, ApJ, 703, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., & Norris, R. P. 1998, MNRAS, 300, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, E., Alloin, D., Pantin, E., Lagage, P. O., & Marco, O. 2005, A&A, 438, 803 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, E., Alloin, D., Pantin, E., et al. 2008, A&A, 492, 3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandhi, P., Isobe, N., Birkinshaw, M., et al. 2011, PASJ, 63, 505 [Google Scholar]
- Gilbert, A. M., Graham, J. R., McLean, I. S., et al. 2000, ApJ, 533, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Gorjian, V., Turner, J. L., & Beck, S. C. 2001, ApJ, 554, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., & Natta, A. 1995, ApJ, 455, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Homeier, N. L., Blum, R. D., Conti, P. S., & Damineli, A. 2003, A&A, 397, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Indebetouw, R., de Messières, G. E., Madden, S., et al. 2009, ApJ, 694, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Jorsater, S., & van Moorsel, G. A. 1995, AJ, 110, 2037 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, F. P., Berrington, K. A., Burke, P. G., et al. 1992, ApJ, 384, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Kissler-Patig, M., Jordán, A., & Bastian, N. 2006, A&A, 448, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobulnicky, H. A., & Johnson, K. E. 1999, ApJ, 527, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Kotulla, R., Fritze, U., Weilbacher, P., & Anders, P. 2009, MNRAS, 396, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Larsen, S. S. 2011, ArXiv e-prints [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblad, P. O. 1999, A&ARv, 9, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Lumsden, S. L., Puxley, P. J., Hoare, M. G., Moore, T. J. T., & Ridge, N. A. 2003, MNRAS, 340, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Martín-Hernández, N. L., Schaerer, D., & Sauvage, M. 2005, A&A, 429, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín-Hernández, N. L., Schaerer, D., Peeters, E., Tielens, A. G. G. M., & Sauvage, M. 2006, A&A, 455, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín-Hernández, N. L., Bik, A., Puga, E., Nürnberger, D. E. A., & Bronfman, L. 2008, A&A, 489, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Modigliani, A., Hummel, W., Abuter, R., et al. 2007 [arXiv:astro-ph/0701297] [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., & Ferland, G. J. 2010, ApJS, 191, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., & Ferland, G. J. 2011, ApJ, 738, 34 [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
- Plante, S., & Sauvage, M. 2002, AJ, 124, 1995 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Saikia, D. J., Pedlar, A., Unger, S. W., & Axon, D. J. 1994, MNRAS, 270, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K., Ho, P. T. P., Mao, R.-Q., Matsushita, S., & Peck, A. B. 2007, ApJ, 654, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Sandqvist, A., Jorsater, S., & Lindblad, P. O. 1982, A&A, 110, 336 [NASA ADS] [Google Scholar]
- Sandqvist, A., Joersaeter, S., & Lindblad, P. O. 1995, A&A, 295, 585 [NASA ADS] [Google Scholar]
- Shields, J. C. 1993, ApJ, 419, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. D., Davis, C. J., & Lioure, A. 1997, A&A, 327, 1206 [NASA ADS] [Google Scholar]
- Sternberg, A., & Neufeld, D. A. 1999, ApJ, 516, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzi, L., Cresci, G., Telles, E., & Melnick, J. 2008, A&A, 486, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wallace, L., & Hinkle, K. 1997, ApJS, 111, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Wold, M., & Galliano, E. 2006, MNRAS, 369, L47 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Example of the sky-subtraction correction, for an average case. We display a portion of the 1′′ radius aperture spectrum of one of the M4 data cube pairs. On top, the P-Cygni-like residuals are stronger before correction, and below, after correction, the residuals have been attenuated. The emission line is Brγ. |
| In the text | |
 |
Fig. 2 Gas emission around the extremely massive clusters in NGC 1365, observed with VLT/SINFONI. First row: Brγ flux, radial velocity, and velocity dispersion, from left to right. Second row, same for H2; third row, same for He I. The axes are in arcsec, north is up and east is left. |
| In the text | |
 |
Fig. 3 Top row, left to right: reconstructed maps for K-band flux density, Brγ flux and H2 1–0 S(1) flux. The chosen apertures are drawn on the maps. The aperture labels are given for each map on the empty map below it for clarity. The label number is given in increasing Right Ascension. North is up and east is left, and the X and Y axes are in arcsec. |
| In the text | |
 |
Fig. 4 Light profiles (1D cuts through the images) for a telluric star, N1, M5 and N2. For the first three, we took cuts along PA = 0°, 45°, 90° and 135° (black crosses, cyan asterisk, purple triangle and brown diamond). The median profile is drawn with a black line, and the Lorentzian fit with a salmon line. For N2, we only have PA = 0° since it is on the edge of the image. The fit FWHM are 0.10′′, 0.23′′, 0.20′′ 0.25′′. |
| In the text | |
 |
Fig. 5 Profile cuts for M4, M5 and M6 (position given is the table for the light centre on the K-band image) along PA = 45°, 60°, and 110°. The dotted line is the comparison profile for each cube (as explained in the corresponding paragraph). It has been rescaled to give a meaningful comparison. |
| In the text | |
 |
Fig. 6 Zooms on the 1.2 × 1.2′′2 around M4 (first row), M5 (second row) and M6 (third row). For each source, from left to right we display the R-band image (HST), the K-band image emission, the Brγ emission and the H2 1–0S(1) emission. The crosses mark the position of the Brγ peak. North is up and east is left, and the X and Y axis are in arcsec. |
| In the text | |
 |
Fig. 7 Top to bottom: a) spectra of the background (defined in Sect. 3.2) + HR6705 in grey, b) aperture 0 + HR2508 in grey, c) aperture 26 + HR2508 in grey, and d) aperture 9 (M4), e) aperture 18 (M5) and f) aperture 31 (M6). d)–f) are not background subtracted. |
| In the text | |
 |
Fig. 8 Shape of the Brγ line. Top to bottom, left to right: apertures 9 (M4), 18 (M5), 31 (M6), 4, 13 and 28. The null velocity is chosen as the centre of the Gaussian fit of the line, and the continuum derived in the fit is subtracted. The crosses show the actual profile values for the positive velocities, which are also plotted for the negative velocities to show the asymmetry of the profile. |
| In the text | |
 |
Fig. 10 Starburst99 equivalent widths for Brγ emission on the left, and CO 2.29 μm absorption band on the right. |
| In the text | |
 |
Fig. 9 Set of plots showing different relations between observables. The plots are described in Sect. 4.2. In all plots, the cyan dots correspond to the sources M4, M5, M5-2 to M5-4 and M6. The red dots correspond to the apertures chosen in the H2 image. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


