| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201218782 | |
| Published online | 26 September 2012 | |
Beyond the diffraction limit of optical/IR interferometers⋆,⋆⋆,⋆⋆⋆
I. Angular diameter and rotation parameters of Achernar from differential phases
1 Laboratoire J.-L. Lagrange, UMR 7293, Observatoire de la Côte d’Azur (OCA), Université de Nice-Sophia Antipolis (UNS), Centre National de la Recherche Scientifique (CNRS), Campus Valrose, 06108 Nice Cedex 2, France
e-mail: Armando.Domiciano@oca.eu
2 Centre de Recherche en Astronomie, Astrophysique et Géophysique (CRAAG), Route de l’Observatoire, BP 63, Bouzareah 16340, Alger, Algérie
3 Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo (USP), Rua do Matão 1226, Cidade Universitária, São Paulo 05508-900, Brazil
4 LESIA, Observatoire de Paris, CNRS UMR 8109, UPMC, Université Paris Diderot, 5 Place Jules Janssen, 92195 Meudon, France
5 INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
6 UJF-Grenoble 1 / CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
7 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received: 6 January 2012
Accepted: 26 July 2012
Context. Spectrally resolved long-baseline optical/IR interferometry of rotating stars opens perspectives to investigate their fundamental parameters and the physical mechanisms that govern their interior, photosphere, and circumstellar envelope structures.
Aims. Based on the signatures of stellar rotation on observed interferometric wavelength-differential phases, we aim to measure angular diameters, rotation velocities, and orientation of stellar rotation axes.
Methods. We used the AMBER focal instrument at ESO-VLTI in its high-spectral resolution mode to record interferometric data on the fast rotator Achernar. Differential phases centered on the hydrogen Br γ line (K band) were obtained during four almost consecutive nights with a continuous Earth-rotation synthesis during ~5 h/night, corresponding to ~60° position angle coverage per baseline. These observations were interpreted with our numerical code dedicated to long-baseline interferometry of rotating stars.
Results. By fitting our model to Achernar’s differential phases from AMBER, we could measure its equatorial radius Req = 11.6 ± 0.3 R⊙, equatorial rotation velocity Veq = 298 ± 9 km s-1, rotation axis inclination angle i = 101.5 ± 5.2°, and rotation axis position angle (from North to East) PArot = 34.9 ± 1.6°. From these parameters and the stellar distance, the equatorial angular diameter ⌀eq of Achernar is found to be 2.45 ± 0.09 mas, which is compatible with previous values derived from the commonly used visibility amplitude. In particular, ⌀eq and PArot measured in this work with VLTI/AMBER are compatible with the values previously obtained with VLTI/VINCI.
Conclusions. The present paper, based on real data, demonstrates the super-resolution potential of differential interferometry for measuring sizes, rotation velocities, and orientation of rotating stars in cases where visibility amplitudes are unavailable and/or when the star is partially or poorly resolved. In particular, we showed that differential phases allow the measurement of sizes up to ~4 times smaller than the diffraction-limited angular resolution of the interferometer.
Key words: stars: rotation / stars: individual: Achernar / methods: observational / methods: numerical / techniques: interferometric
Full Fig. 5 is available in electronic form at http://www.aanda.org
The FITS tables of the reduced data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/545/A130
© ESO, 2012
1. Introduction
By combining high angular and high spectral resolution, differential interferometry (DI; i.e., the measurement of wavelength-differential phases or wavelength-differential visibilities) yields physical parameters of sources with important wavelength-dependent spatial structures, even in cases where these sources are only poorly or partially resolved by the telescope (single-aperture) or the interferometer (multi-aperture).
Because they are self-calibrated and essentially seeing-independent, DI observables are usually more reliable than absolute visibility amplitude, which is the classical observable used to measure stellar angular diameters. Moreover, visibility amplitudes below ≃0.7 (well-resolved objects) are typically required to attain useful constraints (a few percent) on the angular diameters. This demands access to relatively long baselines (≃100−300 m) for optical/IR interferometers in order to measure angular diameters of ≃0.5−2 mas, a typical range of values for many bright stars. These observational constraints are relaxed in DI, where more precise and accurate stellar parameters can be measured for stars only slightly to partially resolved, corresponding to relatively high visibility amplitudes ≃0.6−0.9. Recently, Le Bouquin et al. (2009) used DI to measure the position angle (orientation on the plane of the sky) of the rotation axis of the fast rotator Fomalhaut.
Chelli & Petrov (1995) performed a theoretical study showing that DI can be used to measure stellar angular diameters, rotation velocities, and position angle of rotation axes. However, their study was based on a model of rotating spherical stars with homogeneous effective temperature and gravity, implying a constant local photospheric profile. Such formalism is thus more adapted to slowly rotating stars. It cannot be applied for fast rotators because the effective temperature and gravity, as well as the local profile, vary over the rotationally distorted stellar surface due to rotational flattening and gravity-darkening (also called von Zeipel effect; von Zeipel 1924). To interpret DI observations of rapidly rotating stars, it is thus necessary to use models including these two physical effects caused by high rotation velocities. In this work, we use our model for fast rotators CHARRON (Code for High Angular Resolution of Rotating Objects in Nature; Domiciano de Souza et al. 2012, 2002) to interpret differential phases of the rapidly rotating star Achernar (α Eridani). The observations were performed with the ESO VLTI/AMBER beam combiner (Petrov et al. 2007) centered on the hydrogen Br γ line (K band).
Achernar is a fast rotating Be star (Veqsini ≃ 225 km s-1 from spectroscopy; e.g., Vinicius et al. 2006) presenting a strong rotational flattening directly measured from VLTI/VINCI interferometry (Domiciano de Souza et al. 2003; Kervella & Domiciano de Souza 2006), which indicates that its rotation rate is close to the critical limit. Differential rotation (Jackson et al. 2004) and/or a small residual disk (Carciofi et al. 2008) are additional effects invoked to explain the very strong flattening observed on Achernar. In any case, the rapid stellar rotation is mainly responsible for this flattening.
Because Achernar is bright and well-studied with an angular diameter interferometrically measured, it is an ideal target to investigate, from real observations, how differential phases can be used to measure sizes, rotation velocities, and orientation of rotating stars. In this work, we thus interpret AMBER differential phases of Achernar under the hypothesis that its strong geometrical deformation is essentially due to a fast (near-critical) uniform rotation. This hypothesis is supported by the fact that the Br γ line observed with AMBER is in clear absorption; also, linear polarimetry obtained at the Pico dos Dias Observatory, Brazil, produced a null result within the observational errors (P ≲ 0.01%; Faes & Carciofi 2012, priv. comm.) Both observables, obtained at contemporaneous epochs, indicate that Achernar had no disk (or a very tenuous one at most) during our AMBER observations.
Our model for fast rotators is briefly presented in Sect. 2 while the observations and data reduction are described in Sect. 3. The data analysis followed by the discussion and conclusions of this study are presented in Sects. 4 and 5.
 |
Fig. 1 Top: dependence of simulated differential phases φdiff on Req and on d (solid line: tested model; dashed line: reference model as described in Sect. 2). The parameters of the tested model are identical to those of the reference model, except that Req = 9 R⊙ (left) and d = 60 pc (right). The values of the tested and reference models differ by ≃20%; they are indicated in the upper left part of the figures. All φdiff models were calculated across the Br γ line with a spectral resolution of 12 000 at four projected baselines (Bproj = 75 m and 150 m, and PA = 45° and 90°), which are typical values attained with VLTI/AMBER. These wavelengths and baselines result in visibility amplitudes between 0.6 and 0.9 for the studied stellar models, corresponding to a partially resolved star. The horizontal dashed gray lines indicate the typical error bar of AMBER φdiff (σφ = ± 0.5°). The φdiff signature of stellar rotation appears as an s-shaped curve well visible inside Br γ, with an amplitude higher than σφ at all baselines. Bottom: difference between φdiff of the tested and reference models (solid minus dashed curves in the top panel). The continuum of all curves is equal to zero, but they were shifted for better readability. |
 |
Fig. 2 Similar to Fig. 1 but for the dependence of φdiff on Veqsini and i. The left panel shows that φdiff in Brγ is sensitive to a variation of 20% in Veqsini ( = 200 km s-1 for the tested model). The right panel shows that φdiff also depends on i (changing from 60° to 90°), but to a lesser extent when compared to Req, d, and Veqsini. |
 |
Fig. 3 Similar to Fig. 1 but for the dependence of φdiff on |
2. Differential phase modeling for fast rotating stars
We investigate here the dependence of the differential phase φdiff, close to and within the Br γ line, on the relevant physical parameters of a model for fast rotating stars.
Thanks to the Van Cittert-Zernike theorem (e.g., Born & Wolf 1980), the interferometric observables can be derived from the monochromatic intensity maps of the studied object. In the present work, these intensity maps are computed with the numerical program CHARRON (Domiciano de Souza et al. 2012). This code is an IDL1-based, faster (~0.5 min per model) version of the interferometry-oriented code for rotating stars presented by Domiciano de Souza et al. (2002).
The φdiff obtained with the AMBER data reduction algorithm are related to the object’s Fourier phase φobj by (e.g., Millour et al. 2011, 2006) 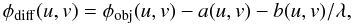 (1)where the spatial frequency coordinates u and v depend on the wavelength λ, the projected baseline length Bproj and the baseline position angle PA (from north to east; u = Bprojsin(PA)/λ and v = Bprojcos(PA)/λ). The parameters a and b correspond to an offset and a slope, given in appropriate units.
(1)where the spatial frequency coordinates u and v depend on the wavelength λ, the projected baseline length Bproj and the baseline position angle PA (from north to east; u = Bprojsin(PA)/λ and v = Bprojcos(PA)/λ). The parameters a and b correspond to an offset and a slope, given in appropriate units.
The high spectral resolution mode of AMBER (λ/Δλ ≃ 104) leads to a velocity resolution of ≃30 km s-1. Projected equatorial rotational velocities Veqsini above ~150 km s-1 would ensure that observations show ~10 individual φdiff values inside Br γ. In such cases, rapid rotation effects need to be accounted for when modeling phase signatures in order to be consistent with the physics of the studied star.
Many previous works have shown that the geometrical flattening and gravity-darkening are the main consequences of fast rotation measured by interferometry. Based on these works, the model of a uniformly rotating, gravity-darkened star in the Roche approximation was adopted in the present study (Domiciano de Souza et al. 2002). The most relevant physical parameters defining the model are: the rotation axis inclination angle i, the equatorial rotation velocity Veq (or alternatively Veqsini), the equatorial radius Req, the stellar mass M, the mean stellar effective temperature on the stellar surface  , and the gravity-darkening coefficient β. This set of input parameters defines the co-latitudinal (θ) dependent surface radius r(θ), the local effective gravity g(θ), the local effective temperature T(θ), the geometrical flattening (ratio of equatorial to polar radii)
, and the gravity-darkening coefficient β. This set of input parameters defines the co-latitudinal (θ) dependent surface radius r(θ), the local effective gravity g(θ), the local effective temperature T(θ), the geometrical flattening (ratio of equatorial to polar radii)  , the stellar surface area S, the luminosity
, the stellar surface area S, the luminosity  (σ is the Stefan-Boltzmann constant), among other quantities. The local effective temperature and gravity are related by the von Zeipel law: T(θ) ∝ g(θ)β.
(σ is the Stefan-Boltzmann constant), among other quantities. The local effective temperature and gravity are related by the von Zeipel law: T(θ) ∝ g(θ)β.
Two additional geometrical parameters required for calculating interferometric observables are the distance d and the position angle of the sky-projected rotation axis PArot. Further details on the adopted fast rotator model are given by Domiciano de Souza et al. (2002).
To study the dependence of φdiff on the model parameters, we define a reference stellar model similar to Achernar: Req = 11 R⊙, d = 50 pc, Veqsini = 250 km s-1, i = 60°, M = 6.1 M⊙, 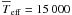 K, PArot = 0° (north direction), β = 0.25 (theoretical value for radiative stellar envelopes; von Zeipel 1924). These parameters correspond to Veq equal to 90% of the critical velocity Vcrit, Req/Rp = 1.4 and an equatorial angular diameter ⌀eq = 2Req/d = 2 mas. To be compatible with the AMBER observations presented in Sect. 3, the simulations were performed around the hydrogen Br γ line, considering an uncertainty in φdiff of σφ = 0.5°, Bproj = 75 m and 150 m, PA = 45° and 90°, and λ/Δλ = 12 000.
K, PArot = 0° (north direction), β = 0.25 (theoretical value for radiative stellar envelopes; von Zeipel 1924). These parameters correspond to Veq equal to 90% of the critical velocity Vcrit, Req/Rp = 1.4 and an equatorial angular diameter ⌀eq = 2Req/d = 2 mas. To be compatible with the AMBER observations presented in Sect. 3, the simulations were performed around the hydrogen Br γ line, considering an uncertainty in φdiff of σφ = 0.5°, Bproj = 75 m and 150 m, PA = 45° and 90°, and λ/Δλ = 12 000.
Figures 1 to 3 show several plots comparing φdiff from the reference model with those from models where the input parameters have been varied one by one. The characteristic s-shaped signature of rotation is seen at all φdiff curves inside Br γ. Our simulations indicate that φdiff is mostly sensitive to Req and d (defining the equatorial angular diameter ⌀eq), and to Veqsini (or Veq). For the adopted σφ and stellar model, these parameters can be determined within a ≃ 20% precision for a few observations, with the longest baselines at different PA. Figures 2 and 3 show that φdiff is also sensitive to i,  , and β, but to a lesser extent when compared to Req, d, and Veqsini.
, and β, but to a lesser extent when compared to Req, d, and Veqsini.
The strong dependence of φdiff on PArot can equally be seen in Figs. 1 to 3, which show that, for a given baseline, the amplitude of the s-shaped φdiff inside the line is stronger for PA = 90° (perpendicular to PArot) and weaker for PA = 45° (45° from PArot). Indeed, for uniform rotation, the φdiff amplitude decreases to zero when PA is parallel to PArot. This indicates that only the angular sizes in the equatorial directions are constrained directly from φdiff data alone and, consequently, this interferometric observable is not strongly sensitive to the apparent flattening of the star.
Of course, the uncertainties of the model parameters mentioned above are only indicative values. The actual precisions of the model parameters depend on the available baselines, observation errors, and parameter values. In the next section, we analyze real VLTI/AMBER observations using CHARRON and the results from the simulations presented above.
Log of the 28 VLTI/AMBER observations of Achernar with details on the dates, times, and baseline triplets.
3. VLTI/AMBER observations and data reduction
VLTI/AMBER observations of Achernar in high spectral resolution (λ/Δλ ≈ 12 000) centered on the Br γ line were carried out from October 25th to November 1th, 2009, during four nights with a different Auxiliary Telescope (AT) triplet configuration in each night (D0-H0-K0, D0-H0-G1, A0-G1-K0, and E0-G0-H0), providing good (u,v) coverage (Fig. 4). The calibrator δ Phe was observed interleaved with Achernar’s observations. δ Phe is a bright (K = 1.7) K0IIIb single star with a K band uniform-disk angular diameter of ⌀UD = 2.180 ± 0.023 mas (Bordé et al. 2002). Previous works showed that it is a trustable interferometric calibrator (e.g., Kervella & Domiciano de Souza 2006). The fringe tracker FINITO was used, providing a good locking ratio and fringe tracking performance. Individual exposure times ranged from 360 ms to 735 ms. The seeing varied from 0.8′′ to 1.2′′. The log of the observations with details on the dates, times, and baselines is given in Table 1.
 |
Fig. 4 Used VLTI baselines and (u,v) coverage of our VLTI/AMBER observations of Achernar. Earth-rotation synthesis spanning ~5 h/night provided this good (u,v) coverage. |
Data were reduced with amdlib software (version 3.1; Chelli et al. 2009; Tatulli et al. 2007). We adopted a frame selection based on fringe SNR and kept the 50% best frames. Data were calibrated using a dedicated script from Millour et al. (2008). Wavelength calibration was performed by fitting a Gaussian function to the line center of the AMBER spectra and correcting to the rest wavelength of Br γ.
After this initial data reduction, we obtain several VLTI/AMBER spectro-interferometric observables: source spectra, absolute and differential visibilities, differential phases, and closure phases. A high-frequency beating in wavelength was present in the calibrated data of all measurements (spectrum, visibilities, phases) due to a dichroic plate in the VLTI optical train in front of AMBER, routing the H band light to the IRIS image-tracker camera. Since this beating appears in a narrow frequency range in the wave-number domain, we removed it by applying a Fourier filtering to that specific wave-number domain. Moreover, a low-frequency beating was also present in our data due to the polarizing prisms of AMBER. This second beating was removed by subtracting a single sine wave fitted to the continuum close to Br γ.
Once the described data reduction steps are done, the differential phases φdiff show a clear signal in the Br γ line region corresponding to the expected s-shaped signature caused by stellar rotation (Fig. 5). Unfortunately, the commonly used visibility amplitudes could not be reliably calibrated due to a very chaotic transfer function. Additionally, no clear stellar signal was present in the Br γ line region in the differential visibilities. Finally, the closure phases are compatible with zero within the observational errors at all AT triplets and wavelengths (Br γ line included), not revealing any strong signatures of stellar rotation and/or asymmetries in the intensity distribution. At each AT triplet, the wavelength-averaged closure phase is always <0.8° (in absolute value), with a corresponding standard deviation several (~3−10) times higher. Such lack of stellar signatures in the closure phases is in agreement with (1) the Achernar’s inclination angle i being close to 90° (centrally-symmetric object; see Sect. 4) and with (2) the closure phases being less sensitive to the spatial intensity distribution than the differential phases for partially resolved objects. This last point is a consequence of the fact that, for poorly resolved objects, the closure phase is a third-order term of the Fourier transform of the spatial intensity distribution, while the differential phase is a first-order term (e.g., Lachaume 2003).
We thus concentrate hereafter our data analysis on the differential phase φdiff alone, which is the only available spectro-interferometric observable presenting a signal-to-noise ratio high enough to constrain the physical parameters of Achernar with a model-fitting algorithm. Most model-fitting algorithms, including the Levenberg-Marquardt algorithm used in the next section, assume that all data points are independent. To be consistent with this assumption, we did not use the φdiff observations at all wavelengths. Instead, we used only each third point (one wavelength over three), which ensures that all observations are independent with respect to the finite resolution of the AMBER spectrograph.
Our final data set consists of 84 (=28 × 3 baselines) φdiff(λ) curves centered on Br γ (from 2.159 to 2.172 μm) and presents ≃ 45 φdiff points for each of the 84 individual projected baselines. The median uncertainty of this data set is σφ,median = 0.6°.
4. Stellar parameters from VLTI/AMBER φdiff
The VLTI/AMBER φdiff observations of Achernar were analyzed with the numerical model CHARRON presented in Sect. 2. A χ2 minimization was performed using an IDL implementation of the Levenberg-Marquardt (LM) algorithm (Markwardt 2009, and references therein).
The free parameters for the model-fitting are Req, Veq, i, and PArot. Based on measurements from previous works and on the results of Sect. 2, the remaining model parameters were held fixed, namely:
-
d = 44.1 pc. For a consistent comparison of our results with previous works, we adopted the Hipparcos distance d = 44.1 pc from Perryman et al. (1997), instead of the more recent value of d = 42.7 pc from van Leeuwen (2007).
-
β = 0.20. Since Achernar is a hot B star with a mostly radiative envelope, the gravity-darkening parameter β should be close to 0.25. Recent interferometric observations of fast rotators (Che et al. 2011) and theoretical works (Claret 2012) suggest that the value β = 0.20 would be more adapted to Achernar’s spectral type. Gravity-darkening models from Espinosa Lara & Rieutord (2011) also indicate that β < 0.25 for fast rotators. Based on these works and on our results showing that φdiff is not strongly sensitive to β (Fig. 3), this parameter was fixed to 0.20 throughout the data analysis.
-
M = 6.1 M⊙. Value from Harmanec (1988), which was adopted by Domiciano de Souza et al. (2003) for Achernar.
-
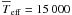 K. We adopt the value given by Vinicius et al. (2006), corresponding to the apparent temperature of Achernar. As shown in Fig. 3, φdiff does not depend strongly on
K. We adopt the value given by Vinicius et al. (2006), corresponding to the apparent temperature of Achernar. As shown in Fig. 3, φdiff does not depend strongly on  .
.
Figure 5 show the best-fit φdiff, together with the corresponding observations. The best-fit values of the free parameters found with the LM algorithm are given in Table 2. The uncertainties of the parameters estimated by the LM algorithm are ~1%. However, previous works have shown that the LM errors derived from the fit of spectro-interferometric data are often too optimistic and should be considered as lower limits (e.g., Niccolini et al. 2011; Domiciano de Souza et al. 2011). To obtain a more realistic estimation of the parameter uncertainties, we applied a Monte Carlo method, which consists in the analysis of artificial data sets generated from the real observations (Press et al. 2002). These artificial data sets have a random Gaussian distribution with a standard deviation given by the observed σφ and an average value given by the observed φdiff. By generating 300 artificial φdiff data sets and by performing a LM model-fit on each of these data sets, we determined the histogram distribution of each fitted parameter, which allowed us to estimate its uncertainty. The limits of the parameter distribution defining the uncertainties of the best-fit parameters given in Table 2 were chosen to correspond to the 68% confidence level of the commonly used standard deviation for normal distributions. We also present in Table 2 several stellar parameters derived from the best-fit parameters.
Parameters and uncertainties estimated from a Levenberg-Marquardt fit of our model to the VLTI/AMBER φdiff observed on Achernar.
 |
Fig. 5 The 84 VLTI/AMBER φdiff(λ) measured on Achernar around Br γ at 28 different observing times (format YYYY-MM-DDTHH_MM_SS) and, for each time, three different projected baselines and baseline position angles, as indicated in the plots. The dashed gray horizontal lines indicate the median ±σφ = ±0.6° of all observations. The smooth curves superposed to the observations are the best-fit φdiff obtained with a uniform-rotation, gravity-darkened Roche model, as described in Sect. 4. All the observed φdiff points are shown here, even if the fit has been performed using only each third wavelength point (cf. Sect. 4). All φdiff curves are equal to zero in the continuum, but they were shifted for better readability. The other panels are available in the electronic edition. |
5. Discussion and conclusions
The stellar parameters derived from the Achernar’s φdiff mostly agree with those from previous results. Our equatorial angular diameter ⌀eq = 2.45 ± 0.09 mas (or, alternatively, Req) is between the values reported by Kervella & Domiciano de Souza (2006, ⌀eq = 2.13 ± 0.05 and by Domiciano de Souza et al. (2003, ⌀eq = 2.53 ± 0.06, which were based on VLTI/VINCI observations. The relatively small differences between these three values can be explained, at least partially, by the fact that different approaches and models were used to interpret the interferometric observations. In particular, the smaller ⌀eq from Kervella & Domiciano de Souza (2006) is due to the use of a uniform brightness ellipse model, which is known to give smaller angular sizes than more realistic models, such as the one used in this work. The comparison with previous works also suggests that the uncertainty of ⌀eq derived from φdiff is of the same order as the uncertainties attained from visibility amplitudes.
The PArot derived here is ≃ 6° smaller than the values reported in these two previous works, meaning that these results agree within ≃ 3 − 4 sigma. The fact that the AMBER (u,v) coverage is more complete than the VLTI/VINCI (u,v) coverage suggests that the PArot from the present work is probably somewhat more accurate.
The derived Veqsini is larger than those obtained in other works based on spectroscopic data (e.g., Vinicius et al. 2006). These differences can be explained by gravity-darkening, which tends to decrease the Veqsini estimated from spectroscopy alone (e.g., Frémat et al. 2005). In any case, the derived rotation rate (Veq/Vcrit = 0.96 ± 0.03) agrees with the value reported by Carciofi et al. (2008), who obtained a lower limit for the rotational speed of Veq/Vcrit > 0.93, based on interferometric, spectroscopic, and polarimetric data.
The measured i ( = 101.5 ± 5.2°) is compatible with previous results, suggesting that 65° ≤ i ≤ 115° (Vinicius et al. 2006; Carciofi et al. 2007). We note that, although i = 101.5° and i = 78.5° ( = 180° − 101.5°) are indistinguishable from spectroscopic observations, they have different φdiff signatures when gravity-darkening is present. The measured inclination close to 90° (nearly a centrally-symmetric intensity distribution) is totally consistent with the observed closure phases, which show values compatible with zero within the error bars.
Following Vinicius et al. (2006), a somewhat higher  value could be adopted in our models, since this quantity is dependent on the rotation rate of the star and on the inclination angle i. We have thus checked the robustness of our results by performing an additional model-fitting fixing
value could be adopted in our models, since this quantity is dependent on the rotation rate of the star and on the inclination angle i. We have thus checked the robustness of our results by performing an additional model-fitting fixing 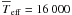 K, which corresponds to the average effective temperature of the visible stellar hemisphere given by Vinicius et al. (2006). In agreement with what was expected from Fig. 3, the values of the parameters obtained from the best fits with
K, which corresponds to the average effective temperature of the visible stellar hemisphere given by Vinicius et al. (2006). In agreement with what was expected from Fig. 3, the values of the parameters obtained from the best fits with 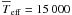 K (Table 2) and with
K (Table 2) and with 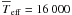 K are compatible within the parameter uncertainties.
K are compatible within the parameter uncertainties.
Finally, we also checked that compatible results, within uncertainties, are obtained from a fit performed over all wavelengths, instead of one-third of the φdiff(λ) points.
The present work shows that φdiff can be used to measure several parameters in fast rotators, in particular ⌀eq (or Req), PArot, Veq, and i. This is very useful, notably in cases when the visibility amplitude is too high (partially resolved objects), when it is poorly determined (large errors), and/or when it cannot be calibrated (as in the case of Achernar’s data). By analyzing VLTI/AMBER φdiff of Achernar, we have shown, using real observations, that the combination of high spatial and high spectral resolution allows one to go beyond diffraction-limited angular resolution of the interferometer, commonly defined as 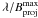 . The equatorial angular diameter of Achernar of ⌀eq = 2.45 ± 0.09 mas was measured from φdiff alone on Bproj between
. The equatorial angular diameter of Achernar of ⌀eq = 2.45 ± 0.09 mas was measured from φdiff alone on Bproj between  m and
m and  m at λ ≃ 2.2 μm. The derived ⌀eq is therefore ≃ 1.5 times smaller than the maximum available diffraction-limited angular resolution. Furthermore, our observations show that the Achernar’s diameter is already resolved at shorter baselines, with a clear signature of rotation seen (φdiff amplitudes ≳ σφ) at Bproj above ≃ 45 m (Fig. 5). Therefore, in these observations with Bproj ≃ 45 m, the measured diameter is even ≃ 4 times smaller than the corresponding diffraction-limited resolution of 10 mas.
m at λ ≃ 2.2 μm. The derived ⌀eq is therefore ≃ 1.5 times smaller than the maximum available diffraction-limited angular resolution. Furthermore, our observations show that the Achernar’s diameter is already resolved at shorter baselines, with a clear signature of rotation seen (φdiff amplitudes ≳ σφ) at Bproj above ≃ 45 m (Fig. 5). Therefore, in these observations with Bproj ≃ 45 m, the measured diameter is even ≃ 4 times smaller than the corresponding diffraction-limited resolution of 10 mas.
This super-resolution capacity provided by φdiff can be further improved if the observational uncertainties are smaller than those attained in the present work. In such cases, the angular diameters of even smaller and slower rotators can be measured, thanks to this powerful technique. The results obtained in this work from VLTI/AMBER differential phases open new perspectives to measure angular sizes of faint and/or angularly small stars, beyond the diffraction limit of optical/IR interferometers.
Online material
 |
Fig. 5 continued. |
 |
Fig. 5 continued. |
Available at http://www.jmmc.fr/aspro
Acknowledgments
This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, of NASA Astrophysics Data System Abstract Service, and of the Jean-Marie Mariotti Center Aspro service2. A.D.S. and A.C.C. thank the CNRS-PICS program for supporting our Brazilian-French collaboration and the present work. This research received the support of PHASE, the high angular resolution partnership between ONERA, Observatoire de Paris, CNRS, and University Denis Diderot Paris 7. A.C.C. acknowledges support from CNPq (grant 308985/2009-5) and Fapesp (grant 2010/19029-0). M.H. acknowledges the CRAAG and the EII/OPTICON Fizeau program for supporting his PhD thesis. We acknowledge the anonymous referee for her/his constructive comments and suggestions that helped us to improve this work.
References
- Bordé, P., Coudé du Foresto, V., Chagnon, G., & Perrin, G. 2002, A&A, 393, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Born, M., & Wolf, E. 1980, Principles of Optics Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 6th edn. [Google Scholar]
- Carciofi, A. C., Domiciano de Souza, A., Magalhães, A. M., Bjorkman, J. E., & Vakili, F. 2008, ApJ, 676, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Carciofi, A. C., Magalhães, A. M., Leister, N. V., Bjorkman, J. E., & Levenhagen, R. S. 2007, ApJ, 671, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Che, X., Monnier, J. D., Zhao, M., et al. 2011, ApJ, 732, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Chelli, A., & Petrov, R. G. 1995, A&AS, 109, 401 [NASA ADS] [Google Scholar]
- Chelli, A., Utrera, O. H., & Duvert, G. 2009, A&A, 502, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2012, A&A, 538, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Bendjoya, P., Niccolini, G., et al. 2011, A&A, 525, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Jankov, S., et al. 2003, A&A, 407, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Vakili, F., Jankov, S., Janot-Pacheco, E., & Abe, L. 2002, A&A, 393, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Zorec, J., & Vakili, F. 2012, SF2A Proc., in press [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frémat, Y., Zorec, J., Hubert, A., & Floquet, M. 2005, A&A, 440, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harmanec, P. 1988, Bull. Astron. Inst. Czechoslovakia, 39, 329 [Google Scholar]
- Jackson, S., MacGregor, K. B., & Skumanich, A. 2004, ApJ, 606, 1196 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., & Domiciano de Souza, A. 2006, A&A, 453, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lachaume, R. 2003, A&A, 400, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bouquin, J., Absil, O., Benisty, M., et al. 2009, A&A, 498, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 251 [Google Scholar]
- Millour, F., Vannier, M., Petrov, R. G., et al. 2006, in EAS Publ. Ser. 22, eds. M. Carbillet, A. Ferrari, & C. Aime, 379 [Google Scholar]
- Millour, F., Petrov, R. G., Vannier, M., & Kraus, S. 2008, in SPIE Conf. Ser., 7013, 41 [Google Scholar]
- Millour, F., Meilland, A., Chesneau, O., et al. 2011, A&A, 526, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niccolini, G., Bendjoya, P., & Domiciano de Souza, A. 2011, A&A, 525, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W., Teukolsky, S., Vetterling, W., & Flannery, B. 2002, Numerical Recipes in C: The art of scientific computing, 2nd edn. (Cambridge University Press) [Google Scholar]
- Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vinicius, M. M. F., Zorec, J., Leister, N. V., & Levenhagen, R. S. 2006, A&A, 446, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Log of the 28 VLTI/AMBER observations of Achernar with details on the dates, times, and baseline triplets.
Parameters and uncertainties estimated from a Levenberg-Marquardt fit of our model to the VLTI/AMBER φdiff observed on Achernar.
All Figures
 |
Fig. 1 Top: dependence of simulated differential phases φdiff on Req and on d (solid line: tested model; dashed line: reference model as described in Sect. 2). The parameters of the tested model are identical to those of the reference model, except that Req = 9 R⊙ (left) and d = 60 pc (right). The values of the tested and reference models differ by ≃20%; they are indicated in the upper left part of the figures. All φdiff models were calculated across the Br γ line with a spectral resolution of 12 000 at four projected baselines (Bproj = 75 m and 150 m, and PA = 45° and 90°), which are typical values attained with VLTI/AMBER. These wavelengths and baselines result in visibility amplitudes between 0.6 and 0.9 for the studied stellar models, corresponding to a partially resolved star. The horizontal dashed gray lines indicate the typical error bar of AMBER φdiff (σφ = ± 0.5°). The φdiff signature of stellar rotation appears as an s-shaped curve well visible inside Br γ, with an amplitude higher than σφ at all baselines. Bottom: difference between φdiff of the tested and reference models (solid minus dashed curves in the top panel). The continuum of all curves is equal to zero, but they were shifted for better readability. |
| In the text | |
 |
Fig. 2 Similar to Fig. 1 but for the dependence of φdiff on Veqsini and i. The left panel shows that φdiff in Brγ is sensitive to a variation of 20% in Veqsini ( = 200 km s-1 for the tested model). The right panel shows that φdiff also depends on i (changing from 60° to 90°), but to a lesser extent when compared to Req, d, and Veqsini. |
| In the text | |
 |
Fig. 3 Similar to Fig. 1 but for the dependence of φdiff on |
| In the text | |
 |
Fig. 4 Used VLTI baselines and (u,v) coverage of our VLTI/AMBER observations of Achernar. Earth-rotation synthesis spanning ~5 h/night provided this good (u,v) coverage. |
| In the text | |
 |
Fig. 5 The 84 VLTI/AMBER φdiff(λ) measured on Achernar around Br γ at 28 different observing times (format YYYY-MM-DDTHH_MM_SS) and, for each time, three different projected baselines and baseline position angles, as indicated in the plots. The dashed gray horizontal lines indicate the median ±σφ = ±0.6° of all observations. The smooth curves superposed to the observations are the best-fit φdiff obtained with a uniform-rotation, gravity-darkened Roche model, as described in Sect. 4. All the observed φdiff points are shown here, even if the fit has been performed using only each third wavelength point (cf. Sect. 4). All φdiff curves are equal to zero in the continuum, but they were shifted for better readability. The other panels are available in the electronic edition. |
| In the text | |
 |
Fig. 5 continued. |
| In the text | |
 |
Fig. 5 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


