| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219458 | |
| Published online | 17 July 2012 | |
Three ways to solve the orbit of KIC 11 558 725: a 10-day beaming sdB+WD binary with a pulsating subdwarf⋆,⋆⋆
1 Nordic Optical Telescope, Apartado 474, 38700 Santa Cruz de La Palma, Spain
e-mail: jht@not.iac.es
2 Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
3 Department of Physics, Astronomy, and Materials Science, Missouri State University, Springfield, MO 65804, USA
4 Instituto de Astrofísica de Andalucía (CSIC), Glorieta de la Astronomía s/n, 18008 Granada, Spain
5 Department of Physics and Astronomy, Aarhus University, 8000 Aarhus C, Denmark
6 Department of Astrophysics, IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
7 Department of Physics and Astronomy, Iowa State University, Ames, IA 50011, USA
8 Dr. Remeis Sternwarte Bamberg, Universität Erlangen-Nürnberg, Germany
9 Steward Observatory, University of Arizona, 933 North Cherry Avenue, Tucson, AZ 85721, USA
10 University of Ege, Department of Astronomy & Space Sciences, 35100 İzmir, Turkey
11 Australian Astronomical Observatory, PO Box 296, Epping, NSW 1710, Australia
12 SETI Institute/NASA Ames Research Center, Moffett Field, CA 94035, USA
Received: 23 April 2012
Accepted: 16 June 2012
The recently discovered subdwarf B (sdB) pulsator KIC 11 558 725 is one of the 16 pulsating sdB stars detected in the Kepler field. It features a rich g-mode frequency spectrum, with a few low-amplitude p-modes at short periods. This makes it a promising target for a seismic study aiming to constrain the internal structure of this star, and of sdB stars ingeneral. We have obtained ground-based spectroscopic radial-velocity measurements of KIC 11 558 725 based on low-resolution spectra in the Balmer-line region, spanning the 2010 and 2011 observing seasons. From these data we have discovered that KIC 11 558 725 is a binary with period P = 10.05 d, and that the radial-velocity amplitude of the sdB star is 58 km s-1. Consequently the companion of the sdB star has a minimum mass of 0.63 M⊙, and is therefore most likely an unseen white dwarf. We analyse the near-continuous 2010–2011 Kepler light curve to reveal the orbital Doppler-beaming effect, giving rise to light variations at the 238 ppm level, which is consistent with the observed spectroscopic orbital radial-velocity amplitude of the subdwarf. We use the strongest 70 pulsation frequencies in the Kepler light curve of the subdwarf as clocks to derive a third consistent measurement of the orbital radial-velocity amplitude, from the orbital light-travel delay. The orbital radius asdBsini = 11.5 R⊙ gives rise to a light-travel time delay of 53.6 s, which causes aliasing and lowers the amplitudes of the shortest pulsation frequencies, unless the effect is corrected for. We use our high signal-to-noise average spectra to study the atmospheric parameters of the sdB star, deriving Teff = 27 910 K andlog g = 5.41 dex, and find that carbon, nitrogen and oxygen are underabundant relative to the solar mixture. Furthermore, we analyse the Kepler light curve for its pulsational content and extract more than 160 significant frequencies.We investigate the pulsation frequencies for expected period spacings and rotational splittings. We find period-spacing sequences of spherical-harmonic degrees ℓ = 1 and ℓ = 2, and we associate a large fraction of the g-modes in KIC 11 558 725 with these sequences. From frequency splittings we conclude that the subdwarf is rotating subsynchronously with respect to the orbit.
Key words: stars: early-type / binaries: spectroscopic / subdwarfs / stars: oscillations / stars: individual: KIC11558725
Based on observations obtained by the Kepler spacecraft, the Kitt Peak Mayall Telescope, the Nordic Optical Telescope and the William Herschel Telescope.
Tables 1, 4, and 5 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The hot subdwarf B (sdB) stars populate an extension of the horizontal branch where the hydrogen envelope is of too low a mass to sustain hydrogen burning. These core helium burning stars must have suffered extensive mass loss close to the tip of the red giant branch in order to reach this core/envelope configuration. Binary interactions, either through stable Roche lobe overflow or common envelope ejection, are likely to be responsible for the majority of the sdB population (see Heber 2009, for a detailed review).
Several extensive radial-velocity surveys have targeted the sdB stars, with the most recent large sample explored by Copperwheat et al. (2011). They find that ~50% of all sdB stars reside in short-period binary systems with the majority of companions being white dwarf (WD) stars. A recent compilation of such short-period systems can be found in Appendix A of Geier et al. (2011), which lists a total of 89 systems. Adding 18 new systems from Copperwheat et al. (2011) brings the total well above a hundred sdBs with periods ranging from 0.07 to 27.8 d. These systems are all characterised by being single-lined binaries, i.e. only the sdB stars contribute to the optical flux, which directly constrains the companion to be either an M-dwarf or a compact stellar-mass object. Binaries with companions of type earlier than M are double-lined and also readily identifiable from a combination of optical and infrared photometry. Reed & Stiening (2004) find that ~50% of all sdB stars have IR excess and must have a companion no later than M2. Radial velocity studies targeting these double-lined stars have had a hard time detecting orbital periods, indicating that they must be exceedingly long. A recent breakthrough was made by Østensen & Van Winckel (2012) using high-resolution spectroscopy of a sample of eight bright subdwarf + main-sequence (MS) binaries detecting orbital periods spanning a range from ~500 to 1200 d with velocity amplitudes between 2 and 8 km s-1. The period distribution of these different types of binary systems are important in that they can be used to constrain a number of vaguely defined parameters used in binary population synthesis models, including the common envelope ejection efficiency, the mass and angular momentum loss during stable mass transfer, the minimum core mass for helium ignition, etc. The seminal binary population study of Han et al. (2002, 2003) successfully predicts many aspects of the sdB star population, but the key parameters have a wide range of possible values. A recent population synthesis study by Clausen et al. (2012) explores the possible populations of sdB+MS stars and demonstrates how the entire population can change with different parameter sets, but does not deal with sdB+WD binaries.
A theoretical prediction of the existence of pulsations in sdB stars, due to an opacity bump associated with iron ionisation in subphotospheric layers, was made by Charpinet et al. (1997). Since both p and g-mode pulsations were discovered in sdB stars (Kilkenny et al. 1997; Green et al. 2003), there has been a focus on the possibilities to derive the internal structure and to put constraints on the lesser known stages of the evolution by means of asteroseismology. Currently the immediate aims of asteroseismology of sdB stars are to derive the mass of the Helium-burning core and the mass of the thin Hydrogen envelope around the core (e.g. Randall et al. 2006), the rotational frequency and internal rotation profile (Charpinet et al. 2008), the radius, and the composition of the core (e.g. Van Grootel et al. 2010; Charpinet et al. 2011).
Recent observational success has been achieved from splendid light curves obtained by the CoRoT and Kepler spacecrafts, delivering largely uninterrupted time series with unprecedented accuracy for sdB stars. Overviews of the Kepler survey stage results for sdB stars were given by Østensen et al. (2010b, 2011), and case studies revealing dense pulsational frequency spectra are presented by Reed et al. (2010) and Baran et al. (2011). From Kepler data it has become clear that the g-modes in sdB stars can be identified from period spacings (Reed et al. 2011). Earth-size planets stripped from their outer layers have been found around the pulsating sdB star KIC 05807616 (KOI-55, KPD 1943+4058, Charpinet et al. 2011), the star being also the subject of the first seismic study of an sdB star in the Kepler field (Van Grootel et al. 2010).
Kepler sdB+dM binaries with pulsating subdwarf components have been presented by Kawaler et al. (2010), Østensen et al. (2010a), and by Pablo et al. (2011). White-dwarf companions in close Kepler binaries are presented by e.g. Bloemen et al. (2011, 2012) and Silvotti et al. (2012).
Our target, KIC 11 558 725 or J19265+4930, is one of the 16 pulsating sdB stars detected in the Kepler field. The Kepler magnitude of KIC 11 558 725 is 14.95, and the B-band magnitude is about 14.6, making it the third brightest in the sample. A first description of the spectroscopic properties, and the pulsational frequency spectrum as found from the 26 day Kepler survey dataset, was given by Østensen et al. (2011), with the source showing frequencies in the range of 78–391 μHz. Based on this relatively short data set already 36 frequencies were identified, showing the potential of this star for a seismic study. Subsequently, Baran et al. (2011) derived 53 frequencies in total from the Kepler survey data, and the frequencies were identified in terms of spherical-harmonic degrees by Reed et al. (2011). As a consequence, the star was observed by Kepler from Q6 onwards. At the time of writing, we have analysed data from the five quarters Q6 to Q10. We present the full frequency spectrum resulting from these 15 months of short-cadence Kepler observations.
In this paper we present our discovery of the binary nature of KIC 11 558 725 based on low-resolution spectroscopy. This object was sampled as part of a spectroscopic observing campaign to study the binary nature of the sdB population in the Kepler field, for which some preliminary results have already been presented by Telting et al. (2012). Part of the data from this campaign were presented in case studies on the close sdB+WD binary KIC 06614501 (Silvotti et al. 2012), and the p-mode pulsating sdB KIC 10139564 (Baran et al. 2012).
From our new spectra of KIC 11 558 725 we solve the orbital radial-velocity amplitude, and derive a lower limit of the companion of the sdB star, which is most likely an unseen white dwarf (Sect. 2). We use the average spectrum to study the atmospheric parameters in detail. We show that the orbital Kepler light curve reveals strong evidence for Doppler beaming that results in light variations at the 238 ppm level, consistent with theoretical predictions, again allowing us to make an independent measurement of the orbital radial-velocity amplitude (Sect. 3). We extract 166 pulsational frequencies from the Kepler light curve (Sect. 4), and show that the orbit has an appreciable effect through the light-travel time on the observed phases and frequencies of these pulsations, which in fact allows us to make a third independent measurement of the orbital-radial velocity amplitude (Sect. 5). In the final sections of this paper we discuss pulsational period spacings and frequency splittings, aiming to identify the spherical-harmonic degree of the modes and to disclose the rotation period of the subdwarf in KIC 11 558 725.
2. Spectroscopic observations
Over the 2010 and 2011 observing seasons of the Kepler field we obtained altogether 35 spectra of KIC 11 558 725.
Low-resolution spectra (R ≈ 2000–2500) have been collected using the Kitt Peak 4-m Mayall telescope with RC-Spec/ F3KB, the kpc-22b grating and a 1.5–2.0 arcsec slit, the 2.56-m Nordic Optical Telescope (NOT) with ALFOSC, grism #16 and a 0.5 arcsec slit, and the 4.2-m William Herschel Telescope (WHT) with ISIS, the R600B grating and 0.8–1.0 arcsec slit. Exposure times were 600 s at KP4m and WHT, and either 600 s or 300 s at the NOT. The resulting resolutions based on the width of arc lines is 1.7 Å for the KP4m and WHT setups, and 2.2 Å for the setup at the NOT. See Table 1 for an observing log.
The data were homogeneously reduced and analysed. Standard reduction steps within IRAF include bias subtraction, removal of pixel-to-pixel sensitivity variations, optimal spectral extraction, and wavelength calibration based on arc-lamp spectra. The target spectra and the mid-exposure times were shifted to the barycentric frame of the solar system. The spectra were normalised to place the continuum at unity by comparing with a model spectrum for a star with similar physical parameters as we find for the target (see Sect. 3.2). The mean spectra from each of the three telescopes are presented in Fig. 1.
 |
Fig. 1 Mean spectra from KP4m, NOT, WHT (bottom to top), offset in flux for clarity. The top panel is a zoom-in of the WHT spectrum, demonstrating some of the stronger lines of heavy elements, such as MgII 4481 Å and SiIII 4552, 4567 Å. |
Orbital solution of KIC 11 558 725.
2.1. Radial velocities and orbit solution
Radial velocities were derived with the FXCOR package in IRAF. We used the Hγ, Hδ, Hζ and Hη lines to determine the radial velocities (RVs), and used the spectral model fit (see next section) as a template. See Table 1 for the results, with errors in the radial velocities as reported by FXCOR. The errors reported by FXCOR are correct relative to each other, but may need scaling depending on, amongst other things, the parameter settings and the validity of the template as a model of the star. As our fit results in a χ2-value close to unity (see Table 2) we trust that scaling of the FXCOR errors is not necessary and that the derived errors of the fit parameters are adequate.
Assuming a circular orbit we find an orbital period of 10.0545(48) d, with a radial-velocity amplitude of 58.1(1.7) km s-1 for the subdwarf. See Table 2 for the complete parameter listing. The radial velocities and the derived solution are shown in Fig. 2. When fitting an eccentric radial-velocity curve the amplitude goes down to 56.8 km s-1, for eccentricity e = 0.063(33). Throughout this paper we regard the orbit as circular.
 |
Fig. 2 Radial-velocity curve from observations with the KP4m Mayall, the NOT, and the WHT. |
Given the solution presented in Table 2, the orbital radius of the sdB star can be approximated by asdBsin i = 11.5 R⊙, which corresponds to a light-travel time of 53.6(1.6) seconds between orbital phases corresponding to closest and furthest distance to the Sun.
The orbital solution combined with the mass function gives a lower limit for the mass of the companion of more than 0.63 M⊙, if one assumes a canonical mass of 0.48 M⊙ for the sdB star. As the spectrum does not reveal clear evidence for light contribution from a companion, it should be either an unseen compact object, or an unseen K star. As the 2MASS J = 15.38(5) and H = 15.35(9) magnitudes do not indicate a rising infrared flux that would reveal the presence of a K star in this system, we conclude that the unseen companion is most likely a white dwarf. If the inclination of the system is smaller than i ≲ 40 degrees then the companion may be a neutron star or black hole (i ≲ 25 degrees).
Assuming a radius for the sdB star of 0.2 R⊙, and assuming a white dwarf companion, one may expect to see eclipses only if the inclination angle is higher than i ≳ 88 degrees. We did not detect eclipses (see Fig. 3).
2.2. Atmospheric parameters
The spectra were shifted to remove the orbital motion, before being co-added to obtain high-S/N spectra (KP4m S/N = 175; NOT S/N = 145; WHT S/N = 305) with minimal orbital line broadening, for all three observatories. We derive the atmospheric parameters of the star from each of these mean spectra, and produce a weighted mean using the formal fitting errors as variance weights, as listed in Table 3. Our final adopted values are Teff = 27 910(210) K, log g = 5.410(15) dex and 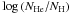 = − 3.116(18) dex, which are quite compatible with the parameters Teff = 27 400 K, log g = 5.37,
= − 3.116(18) dex, which are quite compatible with the parameters Teff = 27 400 K, log g = 5.37, 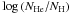 = − 2.8 found from the initial survey spectrum in Østensen et al. (2011). The errors on the adopted values are the errors on the weighted means, and reflect the spread of the individual measurements rather than the formal errors. Systematic errors related to model physics typically are of the order 500 K, 0.05, and 0.05, for Teff, log g, and
= − 2.8 found from the initial survey spectrum in Østensen et al. (2011). The errors on the adopted values are the errors on the weighted means, and reflect the spread of the individual measurements rather than the formal errors. Systematic errors related to model physics typically are of the order 500 K, 0.05, and 0.05, for Teff, log g, and 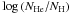 , respectively.
, respectively.
Atmospheric parameters of the subdwarf in KIC 11 558 725.
 |
Fig. 3 Top: the 461 day long Kepler light curve from quarters Q6 through Q10, folded on the orbital period and binned into 50 bins. Bottom: phased radial velocities from the spectra. |
Besides the lines of the hydrogen Balmer series and He i lines, clear lines of magnesium (4481 Å), and silicon (4552 Å, 4567 Å) are present. The high S/N mean WHT spectrum seen in the upper panel of Fig. 1 also allows the identification of a number of lines from O ii, N ii as well as the C ii doublet at 4267 Å and the C iii lines at 4647 and 4650 Å. By comparing the strength of these lines relative to LTE model spectra with explicit metal lines computed for the adopted parameters listed in Table 3, varying only the metallicity relative to solar, we find that oxygen is depleted to 4% of the solar abundance, nitrogen to 13%, and carbon to 1.6%. Such high depletion is normal in sdB stars due to gravitational settling, and large deviations from the solar mix for individual elements are also common (Heber et al. 2000).
3. The orbital light curve from Kepler photometry
We analysed the Kepler light curve of KIC 11 558 725 as obtained in quarters Q6–Q10, totalling roughly 15 months of data with 58.8 s sampling time (i.e. short-cadence data; see Gilliland et al. 2010). The photometric time series spans BJD 2 455 372 to 2 455 833, which is roughly the same range as our spectroscopic dataset. We analyse the light curve as transformed to fractional intensities ΔI/I.
At first we used the raw light curves produced by the Kepler data processing pipeline (SAP_FLUX; Jenkins et al. 2010). These light curves are extracted using a standard small pixel mask selected to minimise the noise in the output data. However, during the observations slight drifts were induced by guiding corrections and thermal effects in the focal plane, which implies that some light drifts in or out of the small pixel mask, causing trends that must be removed. For pulsations with much shorter timescales than the trends, this is not a problem, but with a 10 d orbital period in KIC 11 558 725, our concern was that the detrending could suppress the orbital beaming effect. We therefore analysed also the raw Kepler pixel data using a large custom pixel mask including all 20 to 23 pixels with target signal, as opposed to 4 to 6 pixels in the small pixel mask of the standard pipeline extraction. This recovers 36% more flux from the target and the monthly chunks can be detrended with simple linear trends. This approach gave a beaming amplitude that is 34% higher than our first estimate from the pipeline-reduced data. However, these large-aperture light curves are substantially more noisy and contain many more bad points. Hence we only use the raw, custom-mask pixel data to determine the amplitude of the Doppler beaming, but use the standard-mask pipeline-reduced raw data for our pulsation-frequency analysis in Sect. 4.
A Fourier analysis of the Kepler light curve reveals the orbital period to be 10.0516(27) d, in perfect agreement with the period found from spectroscopy. In Fig. 3 we show the Kepler light curve folded on the orbital period into 50 phase bins. A sine fit to the folded light curve, leaving only the amplitude as a free parameter, gives an amplitude of the orbital effects seen by Kepler of 238(6) ppm, and this amplitude is consistent with that derived from the Fourier analysis. The fit is shown as a solid line in the figure. We do not find orbital harmonics.
3.1. Doppler beaming
The high precision Kepler data permits us to accurately explore the low-amplitude Doppler beaming effect, something that is very hard to do with ground based data. This effect is induced by stellar motion in a binary orbit and causes brightness modulation (Rybicki & Lightman 1979). The Doppler beaming effect permits an estimate of the radial velocity without resorting to spectroscopic data. This effect was detected for the first time in Kepler data by van Kerkwijk et al. (2010) and for a planetary system in CoRoT data by Mazeh & Faigler (2010). A confirmation of the correspondence between Doppler beaming amplitudes and radial velocities was first established by Bloemen et al. (2011).
The light curve of KIC 11 558 725 displays a brightening of the sdB star at the orbital phases where the star is approaching us in its orbit (i.e. when itsorbital radial velocities are negative, see Fig. 3), and this is exactly the effect expected by Doppler beaming. Note that unlike KPD 1946+4330 (Bloemen et al. 2011), KIC 11 558 725 does not show any sign of ellipsoidal deformation which in the closest sdB+WD binaries produces a strong harmonic signal at Porb/2 (see also e.g. Silvotti et al. 2012). This is consistent with the much longer orbital period of KIC 11 558 725 as opposed to the 0.4 d period of KPD 1946+4330.
 |
Fig. 4 A dynamic Fourier spectrum from quarters Q6 through Q10 computed for 20 day stretches of data. The pronounced beatings show up as resolved frequencies in the Fourier spectrum of the complete data set. The horizontal lines reflect data gaps. |
In the case of Doppler beaming the observed flux from the target, Fλ, is related to the emitted spectrum and orbital velocity as 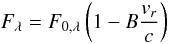 (1)and the beaming amplitude relates to the orbital radial-velocity amplitude K as
(1)and the beaming amplitude relates to the orbital radial-velocity amplitude K as 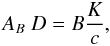 (2)where AB is the amplitude of the beaming signal in the light curve (see Fig. 3), and D the decontamination factor discussed below.
(2)where AB is the amplitude of the beaming signal in the light curve (see Fig. 3), and D the decontamination factor discussed below.
The beaming factor B contains three terms. For an approaching source a contribution of +1 comes from the enhanced photon arrival rate, and another term of +2 from the geometrical aberration of the wavefronts. The last term comes from the Doppler shift of the spectrum, which for a hot sdB star produces a negative effect as the blue-dominated flux gets blue-shifted out of the observed Kepler bandpass when the star is approaching. We compute this last term using TMAP model spectra (Werner et al. 2003) that cover the entire Kepler bandpass, following the procedure described in Bloemen et al. (2011).
With the beaming factor B = 1.403(5), and the spectroscopically derived orbital radial-velocity amplitude, we compute a predicted total beaming amplitude for the Kepler bandpass of 270 ppm. The observed beaming amplitude of AB = 238 ppm is 88% of the predicted value.
The Kepler pixels onto which our target is imaged suffer from contamination from neighbouring objects, and from passing charge from brighter sources when clocking out the CCD.
According to the Kepler Target catalogue1, the contamination factors for KIC 11 558 725 are 0.098 (Q6,Q10), 0.110 (Q7), 0.079 (Q8) and 0.106 (Q9), or 0.0982 on average, implying that all periodic amplitudes derived from these Kepler fluxes should be multiplied by D = 1/(1−0.0982) = 1.109 to get the intrinsic amplitudes of KIC 11 558 725. When applying this decontamination factor we find that the photometric amplitude of the Doppler beaming as seen by Kepler is consistent with the spectroscopically derived radial-velocity amplitude within the errors of the data. Given the observed amplitude AB, we use Eq. (2) to derive a value of K = 56.5(1.4) km s-1 for the orbital radial-velocity amplitude, from Doppler beaming.
The fact that this value is consistent with that of the spectroscopic value proves that the companion of the sdB does not significantly contribute to the observed Doppler beaming, consistent with a compact nature of the companion.
4. The pulsation spectrum
We are interested in the pulsation frequencies in KIC 11 558 725 for three reasons. Firstly, we intend to use the pulsations as clocks to derive the orbital light-travel time delay and consequently another independent determination of the orbital radial-velocity amplitude. Secondly, the pulsations may reveal the internal structure of the subdwarf through a detailed seismic study, for which we intend to derive mode identifications in Sect. 6. Furthermore, the frequency splittings may disclose the rotation period of the subdwarf.
To investigate the pulsational frequency spectrum we used the Kepler light curves as produced by the standard Kepler data processing pipeline. The fractional object intensities ΔI/I of quarters Q6–Q10 were first detrended, and subsequently outlying points were discarded leaving 625 617 data points with standard deviation σ = 2600 ppm. An iterative prewhitening process, involving a standard fast-fourier transform to find peaks and subsequent non-linear least-squares (NLLS) sine-curve fits to subtract the pulsational content mode by mode from the original data, was used to derive the frequency list of Table 4. In total we extracted 166 pulsational frequencies, in addition to the orbital frequency. The standard deviation of the data after removal of all significant periodic signals was σ = 1900 ppm.
The standard deviation in the Fourier amplitude spectrum of the original data amounts to σFT = 4.2 ppm, and we adopt 4σFT = 17 ppm as the threshold of significance of the peaks in the Fourier amplitude spectrum.
We note that the observed amplitudes in Table 4 have not been corrected for the Kepler decontamination factor D (see above), nor for the amplitude smearing due to the effective exposure time of 58.8 s. Both effects cause the observed amplitudes to be smaller than the intrinsic amplitudes, and the latter affects mostly the shortest periods (p-modes). For the strongest pulsation, with a period of 3641.1 s, the exposure time leads to a decrease of the amplitude of 4.3%, while for the shortest extracted period of 197.9 s the amplitude decrease is 14%.
To illustrate the fact that all pulsational frequencies are present throughout the Kepler run, we show a section of the Fourier transform in a dynamic form in Fig. 4. There is clear beating among the stronger frequencies; in fact, these beatings show up as resolved frequencies in the Fourier transform of the full Kepler data set, and may be attributed to the rotation of the subdwarf (Sect. 7).
4.1. Combination frequencies
We do not find evidence for harmonics of the pulsation frequencies. We do, however, find evidence for combination frequencies. When computing the residual frequency δf = f3 − f2 − f1 for all combinations of 168 frequencies in Table 4, we find 13 combinations that are consistent with a residual δf = 0 within the errors of the frequencies. Thirty-five different frequencies are involved in these 13 combinations. One of the combinations is an orbital alias discussed in Sect. 5.1. See Table 5 for the list of frequency combinations.
To investigate the significance of this, we take our observed frequencies and perturb each of them by a random offset which is big enough to upset real combinations, but small enough such that the distribution of these randomised frequencies looks like that of the observed distribution. We perturb the frequencies by ± 1 μHz. For each randomised frequency we adopt the frequency error of the original unperturbed peak. For 50 sets of such randomised frequencies, we find an average of 3.7 combinations that satisfy δf = 0 within the errors of the frequencies.
Hence, for the set of 13 combinations that we find in our 168 frequencies, we expect that about 4 are by-chance combinations. We assume that the combinations with the lowest-amplitude peaks are most likely to be by-chance combinations, as these peaks have the largest error on their frequency. These probable frequency combinations are marked in Table 4, and we take care when assigning these modes in period spacings and frequency multiplets.
5. Using the pulsations as clocks to derive the orbit
In analogy to the effect that the Earth’s orbit has on arrival times of a variational signal, and on the apparent frequencies of that signal, the orbit of the sdB alters the phases and frequencies of its pulsations as perceived by a distant observer.
As we already established in Sect. 2, the light-travel time between conjunctions is 53.6 s, which amounts to a significant phase change for the 300 s p-mode pulsations in this star. Similarly, the Doppler frequency change of the pulsations at orbital quadratures amounts to Δf = f ∗ K/c, which, with K = 58 km s-1, even for g-modes gives frequency shifts of 0.02 − 0.2 μHz. These are certainly measurable with our 460 day data set with frequency resolution of 0.025 μHz. If the orbit is known, one can simply correct for these effects by converting all observation timings to the centre-of-mass frame of the system, equivalent to the common approach of conversion of observation timings to the barycentric frame of the solar system.
If the orbit is not known, one can use the pulsations as clocks (see e.g. Hulse & Taylor 1975) to derive the light-travel time that corresponds to the radius of the orbit, which relates to the radial-velocity amplitude K that can be obtained from spectroscopy or the Doppler-beaming curve as 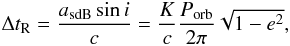 (3)where we introduce the Rømer delay, ΔtR, to represent the light-travel time.
(3)where we introduce the Rømer delay, ΔtR, to represent the light-travel time.
For a circular orbit, the light-travel delay as a function of the subdwarf’s position in its orbit can be written as 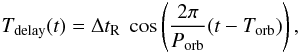 (4)where Torb is the time at which the subdwarf is closest to the Sun in its orbit, corresponding to the orbital phase listed in Table 2.
(4)where Torb is the time at which the subdwarf is closest to the Sun in its orbit, corresponding to the orbital phase listed in Table 2.
We did not detect any second- or third-harmonic peaks, neither for the orbit nor for the pulsations. Hence, for sinusoidal signals the Kepler light curve of KIC 11 558 725 can be approximated by 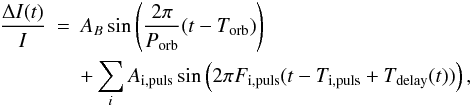 (5)where the first term describes the orbital beaming effect, and where all individual pulsations are affected by the same orbital light-travel delay Tdelay(t). Here, the phase of the individual pulsations, Ti,puls, is expressed in the time domain rather than as an angle. Note that the above sum of sine curves is equivalent to the model that we fit as part of the prewhitening procedure described in Sect. 4, with the addition of a phase delay that introduces just one extra parameter, i.e. the amplitude ΔtR of the light-travel delay.
(5)where the first term describes the orbital beaming effect, and where all individual pulsations are affected by the same orbital light-travel delay Tdelay(t). Here, the phase of the individual pulsations, Ti,puls, is expressed in the time domain rather than as an angle. Note that the above sum of sine curves is equivalent to the model that we fit as part of the prewhitening procedure described in Sect. 4, with the addition of a phase delay that introduces just one extra parameter, i.e. the amplitude ΔtR of the light-travel delay.
We apply the above Eq. (5) to derive a third independent measurement of the radial-velocity amplitude of the subdwarf in KIC 11 558 725. For this purpose, we included the above phase delay in our NLLS Levenberg-Marquardt routine, and fitted the above model (5) to the Kepler Q6–Q10 light curve. In the model we included the 70 strongest frequencies that are identified to be part of ℓ = 1 and ℓ = 2 sequences of the subdwarf (see next section), as to avoid possible pulsations from the unseen component in the binary.
Simultaneously fitting all 70 pulsational amplitudes, frequencies and phases, together with the Rømer delay and phase as free parameters, we find ΔtR = 26.5(1.5) s and Torb = 421.744(88) [BJD – 2 455 000], which is in perfect agreement with the spectroscopic parameters in Table 2, and the Doppler beaming amplitude. Given the observed Rømer delay ΔtR, we derive a value of K = 57.5(3.2) km s-1 for the orbital radial-velocity amplitude, from the light-travel time effect.
 |
Fig. 5 a) The pulsation spectrum KIC 11 558 725 as observed (upper panel), and after correcting for the Rømer delay (lower panel). The line in the upper panel indicates our 4-σ detection limit. b) The amplitude of five pulsation peaks as a function of Rømer correction. c) Same as a), but for a model light curve with the same duration and sampling frequency as the data in a). d) The predicted amplitude of the central peak and first alias as computed for a pure sine function distorted by an increasing Rømer delay. The upper curve indicates the total power of the central peak and the aliases. This sum departs from unity when the unaccounted-for second orbital alias pair starts to contribute. Entries in the legends have the same top-to-bottom order as the curves. |
5.1. Orbital aliases in the Fourier domain
Above we have solved the orbit by directly fitting the light curve with a parameterised model of the pulsations that includes the orbital light-travel delay. A different approach was recently investigated by Shibahashi & Kurtz (2012), who demonstrated how one can derive the orbit from the ratio of the amplitude of the central peak to the orbital aliases that the Rømer delay introduces in the observed Fourier spectrum.
In the case of KIC 11 558 725 we find that, of our 166 extracted pulsation frequencies, only afew of the strongest g-modes and a few of the highest-frequency pulsation modes in the weak p-mode regime have orbital aliases strong enough to be close to the amplitude level of significance.
Around the strongest g-modes the orbital sidelobes appear in frequency regions populated by weak unresolved structure and prewhitening residuals. A more clear example of the orbital sidelobes is given by the two peaks at 3073.5 and 3075.0 μHz, shown in the top panel of Fig. 5a. The sidelobes of each of the two central peaks can just be discerned close to the 4.0-σ line at a separation of Forb = 1.15 μHz. Since the amplitudes of these aliases are hardly significant, direct application of the ratio method of Shibahashi & Kurtz (2012) leads to inaccurate results for this particular dataset.
The two central peaks, however, are at ~16σ, and their amplitudes can be measured with very high precision. We can therefore exploit the energy theorem in Fourier analysis that implies that the total power in the Fourier transform should not change due to the time-distorting orbital motion. All the power observed in the sidelobes will therefore be restored into the central peak if the light curve is corrected for the light-travel time. In the bottom half of Fig. 5a we show that this is indeed the case. When we perform a light-travel time correction on the observation timings of the light curve, in the same way as the barycentric correction is done to remove the spacecraft orbit, then the orbital aliases in the Fourier domain disappear and the power is transferred to the central peak. For comparison, Fig. 5c shows a simulation using noise-free, evenly-sampled data modelled with and without an imposed Rømer delay.
Measured Rømer delay from high-frequency pulsations.
We can also use the amplitude of the central peak to measure the Rømer delay, and get another estimate of the radial-velocity amplitude. If we take our observed light curve and adjust the observation timings for various values of the Rømer delay, we find that the Fourier amplitudes of the pulsation peaks vary as shown in Fig. 5b. Clearly, all five modes reach maximum amplitude for roughly the same delay correction. The delays and peak amplitudes are given in Table 6, and if we take an average using the amplitudes as weights we find ΔtR = 26.4(0.7) s. The gain in amplitude for these modes is about 6%, when the optimal Rømer delay is applied.
 |
Fig. 6 Echelle diagrams of the ℓ = 1 and ℓ = 2 period-spacing sequences. The red rectangles depict the areas of acceptance to these sequences. Single frequencies are plotted in light green, doublets in black, and multiplets in blue (see Table 4). Modes marked with red circles form frequency combinations (Table 5). |
A model of how the observed amplitude of a pulsation peak taken to reside at 3073.5 μHz drops with increasing ΔtR is shown in Fig. 5d. The corrected amplitude of the central peak is found to be 6.1% higher in a simulated light curve with no Rømer delay than in one with a 26 s delay, as observed. The predicted amplitude of the orbital alias is found to be 25.2%. Rearranging Eq. (27) in Shibahashi & Kurtz (2012) in terms of this ratio, we find 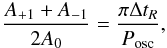 (6)which corresponds to 24.2% for ΔtR = 25 s and Posc = 325 s, which demonstrates that our numerical modelling (Fig. 5d) is consistent with their analytical derivation.
(6)which corresponds to 24.2% for ΔtR = 25 s and Posc = 325 s, which demonstrates that our numerical modelling (Fig. 5d) is consistent with their analytical derivation.
In Fig. 5d we show that the total power contained in the central peak and its aliases is preserved while applying observation-timing corrections. The curve drops off for large delays as we have only accounted for the first pair of a full comb of orbital aliases.
6. Pulsational period spacings
Recently, Reed et al. (2011) have revealed that g-modes in sdB stars show sequences with almost fixed period spacings. This is contrary to what models predicted up to now, i.e. strongly variable period spacings caused by mode trapping due to a highly stratified internal structure. The observed regular period spacings indicate that internal mixing processes must be considerably stronger than presumed. As the period spacings follow the asymptotic relation for g-modes, they change with the value of the spherical-harmonic degree ℓ of the modes. Hence, the spacings allow us to determine the ℓ-value of the modes directly.
Reed et al. (2011) already identified ℓ values for the pulsations that could be resolved in the Kepler survey data of KIC 11 558 725. They identified an ℓ = 1 sequence with period spacing ΔΠℓ = 1 = 246.8 s, and an ℓ = 2 sequence with period spacing ΔΠℓ = 2 = 142.6 s.
Here we use the same methods of Reed et al. (2011) to derive the period spacings, using the much longer Q6–Q10 data set. First we defined the period spacing for ℓ = 1, as marked in Table 4. This was achieved iteratively. As ℓ = 1 modes suffer the least geometric cancellation (see e.g. Reed et al. 2005), and hence should have highest amplitudes if all modes are driven at a similar level, we started off with the highest-amplitude modes. Subsequently we worked with an ℓ = 1 sequence consisting only of doublets, and finally all the ℓ = 1 periods marked in Table 4. For each step we derived mutually consistent values of the period spacing. We recover all the ℓ = 1 identifications from Reed et al. (2011) except for two periods not detected in the Q6 − Q10 data.
Including all 57 ℓ = 1 multiplet candidate peaks from Table 4 in a linear regression P(n) = C + n ∗ ΔΠℓ = 1, we find ΔΠℓ = 1 = 248.87(18) s with rms = 19 s. Here, the mode sequence number n should be equal to the radial number of nodes in the pulsation, n′, but shifted by a fixed offset that we cannot determine. When fitting for each of the 29 multiplets (mostly doublets) only the peak closest to this first fit, we obtain a consistent period spacing ΔΠℓ = 1 = 248.68(23) s, with rms = 14 s.
Given that for the asymptotic g-mode domain we expect 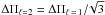 , we used a spacing of ΔΠℓ = 2 = 143 s as a starting point for the ℓ = 2 sequence. Again we iterated adding the highest-amplitude peaks and some frequency multiplets that cannot be ℓ = 1 modes. Including all 76 ℓ = 2 multiplet candidate peaks in a linear regression, we find ΔΠℓ = 2 = 143.44(08) s with rms = 16 s. When fitting for each of the 34 multiplets only the peak closest to this initial fit, we obtain a consistent period spacing ΔΠℓ = 2 = 143.37(10) s, with rms = 14 s.
, we used a spacing of ΔΠℓ = 2 = 143 s as a starting point for the ℓ = 2 sequence. Again we iterated adding the highest-amplitude peaks and some frequency multiplets that cannot be ℓ = 1 modes. Including all 76 ℓ = 2 multiplet candidate peaks in a linear regression, we find ΔΠℓ = 2 = 143.44(08) s with rms = 16 s. When fitting for each of the 34 multiplets only the peak closest to this initial fit, we obtain a consistent period spacing ΔΠℓ = 2 = 143.37(10) s, with rms = 14 s.
Of 166 pulsation frequencies, 23 have periods shorter than 900 s which we did not include as g-mode period-spacing candidates. From the 143 g-mode pulsations we find that 108 can be matched with either the ℓ = 1 or ℓ = 2 sequence, when accepting periods deviating up to ~35 s from the linear regression and allowing for any possible value of the azimuthal order m. We plot echelle diagrams for the ℓ = 1 and ℓ = 2 sequences in Fig. 6, and list all ℓ = 1 and ℓ = 2 matches in Table 4. Periods below 900 s that do match any of the ℓ = 1 or ℓ = 2 sequences are indicated as such in Table 4 for completeness.
Obviously, the period spacing in KIC 11 558 725 is not very strict, which makes conclusive identification of individual modes difficult, as by-chance identifications of modes that do not belong to a sequence are probable. However, the fact that the spacings vary within a sequence may hold information about the internal structure that can be derived from detailed seismic modelling. From Fig. 6 we find that between sequence numbers 8 and 18 in the ℓ = 1 sequence, corresponding to pulsation periods between 3300–5900 s, there is a remarkable bump away from the average spacing. Whereas the ℓ = 1 sequence shows coherence over a large period range, the ℓ = 2 sequence is dominated by a clumping of multiplet candidates in the period range 2900 − 3700 s.
Pulsation modes that could erroneously be accepted in any of the sequences may stem from any of the following: modes with higher degree ℓ that are strong enough to be picked-up by Kepler; modes in combination frequencies; modes that are tidally forced to have large amplitudes; modes that originate in the companion. If a mode in a combination frequency is due to non-linear or resonance effects between two other modes, its assignment to a period-spacing sequence may not be justified. Therefore we mark the modes that take part in frequency combinations (see Table 5) with a circle in Fig. 6.
 |
Fig. 7 Selected multiplets. The bottom 5 panels show the ~0.13 μHz splitting seen in some of the ℓ = 1 doublets. The strongest pulsations we detect in KIC 11 558 725 are amongst the ℓ = 1 peaks shown here. The top panels show sample regions with sequences of frequencies with splittings in the 0.37–0.58 μHz range. Amplitudes are given in ppm. The significance cut-off amplitude is 17 ppm. |
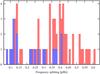 |
Fig. 8 Histogram of splittings listed in Table 4. The blue boxes reflect splittings from multiplets (mostly doublets) that were matched with the ℓ = 1 sequence in Sect. 6. |
Tidally forced oscillations can have large amplitudes when close to an eigenfrequency of the star, and can in principle be of any degree ℓ, although an ℓ = 2 excitation can be considered the most probable, in which case tidally induced pulsations should be part of the ℓ = 2 sequence. The error on the orbital frequency is not small enough to exclude some of the strongest pulsations in Table 4 from being a multiple of the orbital frequency. We note however, that for the observed frequencies in KIC 11 558 725 tidal forcing would occur at very high harmonics of the orbital frequency (i.e. > 300 for the strongest pulsation frequencies), which may diminish the forcing efficiency. Nevertheless, a recent case of tidally driven pulsations at high orbital harmonics (90th and 91st) is presented by Welsh et al. (2011).
Even though pulsating white dwarfs are rare as the instability strips are small, possible pulsations in the supposed white-dwarf companion could be picked up by Kepler. Assuming a white dwarf with a large radius 0.013 R⊙ (log (g) = 8.0, M = 0.63 M⊙), with a similar or somewhat cooler temperature as the subdwarf, and with intrinsic pulsation amplitudes at the 10–20% level, we conclude that such a white dwarf would contribute pulsation frequencies at observable amplitudes to the frequency spectrum of KIC 11 558 725, even if the white dwarf is not detected in our spectra, or in the available broad-band imaging. Hence we can not exclude this possibility, when trying to match period spacings or frequency splittings in KIC 11 558 725.
If any of the significant peaks we have detected were to originate from the white dwarf, their amplitudes would not be maximised by shifting to the rest frame of the sdB, as we demonstrated is the case for the short period peaks in Sect. 5.1. Rather, a Rømer delay with the opposite sign and an amplitude corresponding to the radial velocity of the white dwarf would have to be imposed to recover the full amplitude. Using the technique of Sect. 5.1 we found only one peak in Table 4 that shows an orbital phase behaviour that is opposite to that expected for the subdwarf, and hence could originate in the supposed white-dwarf companion: it is the peak with the shortest periodicity at 5053.5 μHz. As this peak is just at the detection limit we cannot rule out that it is just a random effect. If it persists in the next year of Kepler observations, it might turn out to be the first indication of an sdB+WD system where both stars are pulsating.
7. Frequency splittings and the rotation period
Fixed frequency splittings are expected as a consequence of rotation. To the first order in the rotation frequency Ω, the observed frequencies of the modes are altered by mΩ(1 − Cn′l), with m the azimuthal quantum number of the spherical harmonic. Hence, for non-radial modes of given degree ℓ, we expect frequency multiplets of 2ℓ+1 peaks to occur. However, not all peaks of a full multiplet need to be excited, and, furthermore, cancellation effects for a given inclination angle can favour the observability of some modes over others within a multiplet (see e.g. Reed et al. 2005).
In the case of KIC 11 558 725 the frequencies mostly do not appear as full multiplets, which makes the interpreting of the observed splittings difficult. See Table 4 for the observed splittings. We find many splittings in the range of 0.1–0.5 μHz. In Fig. 7 we show two sample frequency sequences that show a frequency splitting in the 0.4–0.55 μHz range, that seems typical for frequency groups that do not match the ℓ = 1 period spacing. We also show in Fig. 7 a series of doublets that match the ℓ = 1 period spacing, which all have a frequency splitting on the order of 0.13 μHz, and which in fact cause the prominent beating seen in Fig. 4. We also detect some doublets with spacings approximately twice this (~0.23 μHz) and we interpret the smaller frequency spacings as consecutive m while the larger spacings would be the | m | = 1 pairs. In Fig. 8 we present a histogram of the splittings listed in Table 4.
We tentatively identify this splitting of 0.13 μHz as the rotation frequency of the subdwarf in KIC 11 558 725. We regard this result as inconclusive as other doublets that seem to match the ℓ = 1 period spacing show a larger frequency splitting (>0.3 μHz). We note however that some of the peaks in these ℓ = 1 doublets also match the ℓ = 2 period spacing, and hence could be ℓ = 2 modes instead.
Assuming that the Ledoux constant Cn′l can be approximated by 1/(ℓ(ℓ+1)) as in the asymptotic g-mode regime, the observed frequency splitting of 0.13 μHz in the ℓ = 1 doublets leads to a rotation period of the subdwarf of 45 d. This consequently implies that the rotation of the subdwarf is not phase-locked with the orbit.
Even if we assume that the larger frequency splittings, in the 0.4–0.55 μHz range, belong to multiplets of ℓ > 1 modes and are due to rotation, we would still conclude with certainty that the subdwarf rotates subsynchronously with respect to the orbit. Here the case of a splitting of 0.55 μHz for a supposed ℓ = 2 multiplet provides the lower limit to the rotation period of 18 d.
Pablo et al. (2011, 2012) discuss the frequency splittings in the three of the four known Kepler sdB+dM systems, which all three have orbital periods on the order of ten hours. From the frequency splittings they derive that for each of their cases the subdwarf rotation is subsynchronous with respect to the orbit. Following their description of the Zahn (1975) synchronization timescale, we expect for KIC 11 558 725 a much longer synchronization timescale than for those sdB+dM systems, as the orbital period is much longer and the synchronization timescale scales with 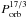 . In fact, we expect that the rotation period we measure now is a good indicator of the rotation period of the subdwarf after it just settled on the extreme horizontal branch.
. In fact, we expect that the rotation period we measure now is a good indicator of the rotation period of the subdwarf after it just settled on the extreme horizontal branch.
8. Summary and conclusions
From our new low-resolution spectroscopy we discovered that KIC 11 558 725 is a binary consisting of a B subdwarf and an unseen companion, likely a white dwarf. We found a circular orbit with Porb = 10.05 d, and a radial-velocity amplitude of 58 km s-1. From the high signal-to-noise average spectrum we redetermined the atmospheric parameters of the subdwarf: Teff = 27 910 K and log g = 5.41 dex.
Five quarters of short-cadence Kepler data of KIC 11 558 725 reveal Doppler beaming at the 238 ppm level. The amplitude of the Doppler-beaming modulation in the light curve corresponds to a radial-velocity amplitude that is fully consistent with that determined from the spectroscopic data.
We developed a new method that uses the pulsations as clocks to measure the orbital light-travel effect, or Rømer delay, directly from the Kepler light curve. The measured delay is again in perfect agreement with the spectroscopically determined radial-velocity amplitude. This method allows the light-travel delay to be measured on many pulsations simultaneously, allowing the determination to be accurate, and hence can be useful for stars that have many weak pulsation frequencies such as sdB stars.
For the 300 s p-modes in KIC 11 558 725 the pulsation amplitude varies slightly when transforming the observation timings to that of the center-of-mass of the binary. This effect will only show up for short-period pulsations in a long orbit. We have been able to measure the Rømer delay from this effect.
One may wonder if it is still necessary to use spectroscopy to solve orbits for targets in the Kepler field. For the case of KIC 11 558 725 the phasing of the spectroscopic results with respect to the Kepler light curve proved essential in order to establish that the light-curve modulation is due to Doppler beaming, and not due to reflected light from the companion or to a contaminating object in the course Kepler pixel aperture.In general, the Doppler beaming amplitude may not reflect the radial-velocity amplitude in case the companion significantly contributes to the observed combined beaming amplitude. However, the phase and amplitude of the light-travel delay as determined by using the pulsations as clocks provide the same orbital constraints as derived from spectroscopy.
We extracted 166 pulsation frequencies from the Kepler light curve, among which 13 are found to be possible combination frequencies. We found 6 p-modes, and 160 frequencies in the g-mode domain, demonstrating the potential for a seismic analysis of this star.
We showed that many of the pulsation frequencies match period spacings of ℓ = 1 and ℓ = 2 sequences, implying that the interior structure of the subdwarf cannot be heavily stratified. The period-spacing sequences will aid in the identification process of the modes in a future seismic study of this object.
Although we detect many pulsation frequencies, we see little evidence for complete multiplets. The frequency splittings are many in KIC 11 558 725 and are difficult to fit in a standard picture. We attribute the smallest splittings that we find to ℓ = 1 doublets, and derive a rotation period of 45 d. As a lower limit for the rotation period, we derive a value of 18 d, which implies that the subdwarf rotates subsynchronously with respect to the orbit.
KIC 11 558 725 is the first sdB pulsator in the Kepler sample with a confirmed compact stellar-mass companion. The 10 day orbit is in the long end of the period range of the ~100 known sdB binaries that have periods compatible with the common-envelope ejection scenario. Assuming a canonical sdB mass of 0.48 M⊙, we derived a lower limit for the mass of the companion of 0.63 M⊙. The distance between the two companions is ≳ 20 R⊙, which implies that if the sdB is a result of a common-envelope phase the progenitor must have been close to the maximum radius for a red giant, near the tip of the red-giant branch.
Online material
Log of the low-resolution spectroscopy of KIC 11 558 725.
Extracted pulsational frequencies.
Possible frequency combinations.
Acknowledgments
Based on observations made with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos (ORM) of the Instituto de Astrofisica de Canarias, and the William Herschel Telescope and Isaac Newton Telescope also at ORM, operated by the Isaac Newton Group. M.D.R. and L.F. were Visiting Astronomers to the Kitt Peak National Observatory, National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation. M.D.R. and L.F. were supported by the Missouri Space Grant Consortium funded by NASA. The authors gratefully acknowledge the Kepler team and all who have contributed to enabling the mission. Funding for the Kepler Mission is provided by NASA’s Science Mission Directorate. The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007–2013)/ERC grant agreement No. 227224 (prosperity), as well as from the Research Council of KU Leuven grant agreement GOA/2008/04. J.H.T. cordially thanks the Instituut voor Sterrenkunde, KU Leuven, for its hospitality.
References
- Baran, A. S., Kawaler, S. D., Reed, M. D., et al. 2011, MNRAS, 414, 2871 [NASA ADS] [CrossRef] [Google Scholar]
- Bloemen, S., Marsh, T. R., Østensen, R. H., et al. 2011, MNRAS, 410, 1787 [NASA ADS] [Google Scholar]
- Bloemen, S., Marsh, T. R., Degroote, P., et al. 2012, MNRAS, 422, 2600 [NASA ADS] [CrossRef] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 1997, ApJ, 483, L123 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charpinet, S., van Grootel, V., Reese, D., et al. 2008, A&A, 489, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 2011, Nature, 480, 496 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Clausen, D., Wade, R. A., Kopparapu, R. K., & O’Shaughnessy, R. 2012, ApJ, 746, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Copperwheat, C. M., Morales-Rueda, L., Marsh, T. R., Maxted, P. F. L., & Heber, U. 2011, MNRAS, 415, 1381 [NASA ADS] [CrossRef] [Google Scholar]
- Geier, S., Hirsch, H., Tillich, A., et al. 2011, A&A, 530, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilliland, R. L., Jenkins, J. M., Borucki, W. J., et al. 2010, ApJ, 713, L160 [NASA ADS] [CrossRef] [Google Scholar]
- Green, E. M., Fontaine, G., Reed, M. D., et al. 2003, ApJ, 583, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U., Reid, I. N., & Werner, K. 2000, A&A, 363, 198 [NASA ADS] [Google Scholar]
- Hulse, R. A., & Taylor, J. H. 1975, ApJ, 195, 51 [Google Scholar]
- Jenkins, J. M., Caldwell, D. A., Chandrasekaran, H., et al. 2010, ApJ, 713, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D., Reed, M. D., Østensen, R. H., et al. 2010, MNRAS, 409, 1509 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Koen, C., O’Donoghue, D., & Stobie, R. S. 1997, MNRAS, 285, 640 [Google Scholar]
- Mazeh, T., & Faigler, S. 2010, A&A, 521, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Østensen, R. H., & Van Winckel, H. 2012, in The Fifth Conference on Hot Subdwarf Stars and Related Objects, eds. D. Kilkenny, C. S. Jeffery, & C. Koen (San Francisco: ASP), ASP Conf. Ser., 452, 163 [Google Scholar]
- Østensen, R. H., Green, E. M., Bloemen, S., et al. 2010a, MNRAS, 408, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Silvotti, R., Charpinet, S., et al. 2010b, MNRAS, 409, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Silvotti, R., Charpinet, S., et al. 2011, MNRAS, 414, 2860 [NASA ADS] [CrossRef] [Google Scholar]
- Pablo, H., Kawaler, S. D., & Green, E. M. 2011, ApJ, 740, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Pablo, H., Kawaler, S. D., Reed, M. D., et al. 2012, MNRAS, 422, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Randall, S. K., Green, E. M., Fontaine, G., et al. 2006, ApJ, 645, 1464 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M. D., & Stiening, R. 2004, PASP, 116, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M. D., Brondel, B. J., & Kawaler, S. D. 2005, ApJ, 634, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M., Kawaler, S. D., Østensen, R. H., et al. 2010, MNRAS, 409, 1496 [Google Scholar]
- Reed, M. D., Baran, A., Quint, A. C., et al. 2011, MNRAS, 414, 2885 [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative processes in astrophysics (New York: Wiley-Interscience) [Google Scholar]
- Shibahashi, H., & Kurtz, D. W. 2012, MNRAS, 422, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Silvotti, R., Østensen, R. H., Bloemen, S., et al. 2012, MNRAS, in press [arXiv:1205.2457] [Google Scholar]
- Telting, J. H., Østensen, R. H., & Reed, M. D. 2012, in The Fifth Conference on Hot Subdwarf Stars and Related Objects, eds. D. Kilkenny, C. S. Jeffery, & C. Koen (San Francisco: ASP), ASP Conf. Ser., 452, 147 [Google Scholar]
- Van Grootel, V., Charpinet, S., Fontaine, G., et al. 2010, ApJ, 718, L97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Kerkwijk, M. H., Rappaport, S. A., Breton, R. P., et al. 2010, ApJ, 715, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, W. F., Orosz, J. A., Aerts, C., et al. 2011, ApJS, 197, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, K., Deetjen, J. L., Dreizler, S., et al. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner (San Francisco: ASP), ASP Conf. Ser., 288, 31 [Google Scholar]
- Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Mean spectra from KP4m, NOT, WHT (bottom to top), offset in flux for clarity. The top panel is a zoom-in of the WHT spectrum, demonstrating some of the stronger lines of heavy elements, such as MgII 4481 Å and SiIII 4552, 4567 Å. |
| In the text | |
 |
Fig. 2 Radial-velocity curve from observations with the KP4m Mayall, the NOT, and the WHT. |
| In the text | |
 |
Fig. 3 Top: the 461 day long Kepler light curve from quarters Q6 through Q10, folded on the orbital period and binned into 50 bins. Bottom: phased radial velocities from the spectra. |
| In the text | |
 |
Fig. 4 A dynamic Fourier spectrum from quarters Q6 through Q10 computed for 20 day stretches of data. The pronounced beatings show up as resolved frequencies in the Fourier spectrum of the complete data set. The horizontal lines reflect data gaps. |
| In the text | |
 |
Fig. 5 a) The pulsation spectrum KIC 11 558 725 as observed (upper panel), and after correcting for the Rømer delay (lower panel). The line in the upper panel indicates our 4-σ detection limit. b) The amplitude of five pulsation peaks as a function of Rømer correction. c) Same as a), but for a model light curve with the same duration and sampling frequency as the data in a). d) The predicted amplitude of the central peak and first alias as computed for a pure sine function distorted by an increasing Rømer delay. The upper curve indicates the total power of the central peak and the aliases. This sum departs from unity when the unaccounted-for second orbital alias pair starts to contribute. Entries in the legends have the same top-to-bottom order as the curves. |
| In the text | |
 |
Fig. 6 Echelle diagrams of the ℓ = 1 and ℓ = 2 period-spacing sequences. The red rectangles depict the areas of acceptance to these sequences. Single frequencies are plotted in light green, doublets in black, and multiplets in blue (see Table 4). Modes marked with red circles form frequency combinations (Table 5). |
| In the text | |
 |
Fig. 7 Selected multiplets. The bottom 5 panels show the ~0.13 μHz splitting seen in some of the ℓ = 1 doublets. The strongest pulsations we detect in KIC 11 558 725 are amongst the ℓ = 1 peaks shown here. The top panels show sample regions with sequences of frequencies with splittings in the 0.37–0.58 μHz range. Amplitudes are given in ppm. The significance cut-off amplitude is 17 ppm. |
| In the text | |
 |
Fig. 8 Histogram of splittings listed in Table 4. The blue boxes reflect splittings from multiplets (mostly doublets) that were matched with the ℓ = 1 sequence in Sect. 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


