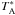| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219024 | |
| Published online | 23 August 2012 | |
The search for the magnetic precursor of C-type shocks in young molecular outflows
1
Centro de Astrobiología (CSIC/INTA), Instituto Nacional de Técnica
Aeroespacial,
Ctra de Torrejón a Ajalvir, km 4, 28850 Torrejón de
Ardoz,
Madrid,
Spain
e-mail: robertsj@cab.inta-csic.es
2
Harvard-Smithsonian Center for Astrophysics, 60 Garden St,
Cambridge,
MA
02138,
USA
3
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
4
LERMA, UMR 8112 du CNRS, Observatoire de Paris,
École Normale Supérieure, 24 rue
Lhomond, 75231
Paris Cedex 05,
France
Received:
12
February
2012
Accepted:
28
June
2012
The detection of very narrow SiO emission and the higher degree of excitation of the ion fluid compared to the neutral one towards the protostar L1448-mm have been interpreted as signatures of the magnetic precursor of C-shocks. Since this is the only source where these features have been observed together, we carried out a survey to map the J = 2 → 1 and 8 → 7 lines of SiO, and the J = 1 → 0 and 4 → 3 lines of H13CO+ (as the representative ion) and HN13C (as the representative neutral species) towards four class 0/I low-mass protostars known to have young outflows (L1448-IRS3, NGC 1333-IRAS 4A/B and SSV 13, VLA 1623 and IRAS 20353). As previously reported, towards L1448-IRS3 and NGC 1333 strong, narrow SiO 2 → 1 is detected, and we also find a velocity component towards each outflow which shows high a H13CO+ 4 → 3/1 → 0 integrated intensity ratio compared to that of HN13C. Towards VLA 1623, we find very weak, narrow SiO, and a component that is visible in H13CO+ but not at all in HN13C. For IRAS 20353, we find neither narrow SiO nor high H13CO+ 4 → 3/1 → 0 flux ratios.
Previous work explained the higher degree of excitation of H13CO+ by the selective excitation of ions by electrons, whose abundance is expected to increase at the precursor stage. Here, however, by considering a range of kinetic temperatures for the gas, we find that it is possible to fit the observations with a single temperature and density, without an increased electron abundance, despite the large differences in 4 → 3/1 → 0 ratio between the two molecules. The high H13CO+ 4 → 3/1 → 0 flux ratios may simply be due to protostellar heating. However, the hypothesis that narrow SiO is formed at the precursor stage of shocks remains plausible, since other explanations require either the presence of shocks with larger dynamical timescales, or predict the narrow SiO to have a larger spatial extent than it appears to have towards the sources L1448-IRS3 and VLA 1623. Larger scale maps of the narrow SiO emission are needed to confirm that it is confined to the regions around protostars (as would be expected in the precursor scenario), and mapping of different ion and neutral species is necessary to confirm whether there are indeed precursor regions surrounding young outflows where the ion and neutral species behave as separate fluids.
Key words: stars: formation / ISM: jets and outflows / shock waves / submillimeter: ISM / infrared: ISM
© ESO, 2012
1. Introduction
Molecular outflows are associated with the earliest stages of protostellar evolution, and play an important role in the star formation process by dispersing the surrounding natal core of the protostar, and by injecting turbulent energy into the molecular cloud. Shocks propagate at the interface between the outflow and the surrounding ambient material, dramatically modifying the density, temperature and chemistry of the unperturbed gas. In molecular dark clouds, where the fractional ionisation of the gas is very low (X(e) ≤ 10-7), when the magnetosonic speed is greater than the speed of the shock, the magnetic field is compressed ahead of the shock front, causing the charged fluid to accelerate and decouple from the neutral one (Mullan 1971; Draine 1980). The decoupled region ahead of the shock front is known as the magnetic precursor. If the magnetic field is sufficiently large, momentum transfer through collisions between the charged and neutral species in the precursor smooths out the discontinuity in the neutral fluid, resulting in a C-type (continuous) shock. The structure of a typical C-type shock is shown in Fig. 1 (reproduced from Jiménez-Serra et al. 2008). The shock structure was calculated using a parameterised model, with a shock velocity of 40 km s-1, magnetic field strength 450 μG, initial H2 density of 105 cm-3 and an ambient gas temperature of 10 K. In this case, since there is no longer a clear-cut shock front, we define the “precursor” as the region where the difference in velocity of the ion and neutral fluids is increasing, which roughly coincides with the region before the temperature of the neutrals reaches its maximum (Flower & Pineau des Forêts 2003). In the example in Fig. 1 the precursor length is 0.0005–0.001 pc.
 |
Fig. 1 Structure of a typical C-type shock from the parametric model of Jiménez-Serra et al. (2008). This model has a shock velocity of 40 km s-1, magnetic field strength of 450 μG, initial H2 density of 105 cm-3 and temperature of 10 K. The top panel shows the temperature of the ion and neutral fluids (Ti and Tn respectively) and the neutral gas density (nn). The bottom panel shows the ion and neutral fluid velocities (vi and vn) in a frame co-moving with the pre-shock gas, and vd is the velocity difference between the two fluids. |
As a consequence of the precursor interaction, the velocity decoupling between the ion and neutral fluids produces the sputtering of (mostly charged) dust grains, leading to the injection of large amounts of molecular material into the gas phase (see e.g. Caselli et al. 1997; Gusdorf et al. 2008; Jiménez-Serra et al. 2008). In addition, the densities (and fractional abundances) of the ion and electron fluids are expected to be enhanced by several orders of magnitude in the precursor, due to both the compression of the charged fluid and also UV fluorescence radiation which is generated after the collisional excitation of H2 at the precursor C-shock stage (see e.g. Flower et al. 1996; Flower & Pineau des Forêts 2003).
Observationally, there is currently evidence that points towards the detection of the signatures of the magnetic precursor of C-shock waves towards the very young outflow emanating from the L1448-mm source (dynamical age of few 1000 yr; Bachiller et al. 1990). Firstly, Jiménez-Serra et al. (2004) reported the detection of very narrow (linewidth of only ~0.6 km s-1) SiO emission arising from material at almost ambient velocities (the precursor component) towards L1448-mm. This narrow feature, which clearly differs from the broad SiO line profiles associated with high velocity post-shock gas (typical linewidths of Δν = 10–50 km s-1) (Martín-Pintado et al. 1992), could be the result of the sputtering of grain mantles at the precursor stage (Jiménez-Serra et al. 2008, 2009). By performing a multi-transition analysis of the ion and neutral molecular emission towards L1448-mm, Jiménez-Serra et al. (2006, hereafter JS06) reported the high degree of excitation of molecular ions such as H13CO+ with respect to neutral molecules such as HN13C (hereafter referred to as the “ion over-excitation”), in the precursor component (red-shifted by 0.5 km s-1 with respect to the ambient gas) towards this outflow. JS06 argued that the electron fractional abundance enhancement that is predicted at the precursor stage of C-shocks could cause the selective excitation of ions, because the collisional coefficients for electrons with molecular ions are larger than those with neutral species at low temperatures. For the case of H13CO+ and HN13C, at temperatures of 10–30 K, the collisional coefficients of H13CO+ with electrons are at least four times greater than those for HN13C with electrons for the J = 4 → 3 and 1 → 0 transitions, using the electron collisional coefficients from Faure et al. (2007) and Faure et al. (priv. comm.). More recently, Roberts et al. (2010) have shown that the ion over-excitation in the precursor component towards L1448-mm is restricted to the regions where narrow SiO is detected, and using observations of rarer isotopologues of H13CO+ and HN13C they found it unlikely that it is produced by a large optical depth effect if the emission is extended. Interferometric observations have also shown that the narrow SiO emission is very compact (size of ≤0.004 pc) and arises from regions at the interface between the post-shock gas and the ambient medium (Jiménez-Serra et al. 2011).
All this suggests that narrow SiO and the over-excitation of the ion fluid are the signatures of the interactions at work exclusively in the magnetic precursor of C-shocks. As a consequence, one would expect these features to be common towards other young molecular outflows around low-mass protostars. However, L1448-mm is the only object where narrow SiO emission and an ion over-excitation have been reported together so far.
In this paper, we present preliminary results from a multi-transition analysis of the SiO, H13CO+ and HN13C emission towards four other class 0/I protostars with young molecular outflows (NGC 1333-IRAS 4A/B and SSV 13, L1448-IRS3, VLA 1623 and IRAS 20353+6742 (hereafter IRAS 20353)), to see if these outflows also exhibit the features given above. We restrict our search to just low-mass protostars because in the case of high-mass objects, the strong UV field emanating from the protostar is likely to interfere in the study of the ion excitation and chemistry. For regions where we identify an H13CO+ over-excitation, we then use a large velocity gradient (LVG) excitation model to determine the physical conditions of the gas and to explore in detail the excitation of H13CO+ and HN13C. We compare the effects of both increasing kinetic temperature and electron fractional abundance on the excitation of the two molecules, to ascertain whether or not an electron abundance enhancement is needed to explain the observed differences in excitation.
These data belong to a larger program carried out with the IRAM 30 m and the JCMT telescopes, to on-the-fly map this emission across the entire outflowing regions. The complete dataset will be published in detail in a forthcoming paper. The observing strategy and details of the observations are reported in Sects. 2 and 3, and the results in Sect. 4. These results are analysed in detail by using our LVG code in Sect. 5, and the conclusions are presented in Sect. 6.
2. Observing strategy
The molecules H13CO+ and HN13C were chosen as the representative ion and neutral species because (i) the frequencies of their J = 1 → 0, 3 → 2 and 4 → 3 lines are such that they can be observed with few set-ups in the JCMT and IRAM 30 m telescopes, and most importantly; (ii) they both have similar critical densities and are likely to have reasonably similar molecular abundances in star forming molecular clouds, and hence are likely to trace the same gas. Table 1 shows the critical densities of the J = 1 → 0 and 4 → 3 transitions of H13CO+ and HN13C at various temperatures from 10 to 100 K, and shows that the 1 → 0 lines both trace gas with densities greater than a few times 105 cm-3, and the 4 → 3 lines both trace gas with densities greater than a few times 106–107 cm-3 for this temperature range. Gas-phase chemical models show that under dark cloud conditions, HCO+ and HNC should have abundances of similar orders of magnitude (Woodall et al. 2007), so assuming that there are no 13C fractionation effects, the abundances of H13CO+ and HN13C should also be similar to each other. We note however that the HN(13)C abundance is expected to drop rapidly for temperatures above 24 K, when it is converted into H(13)CN (Hirota et al. 1998). In addition, the critical densities of HN13C are generally about a factor of 2 higher than those of H13CO+ for the 1 → 0 and 4 → 3 transitions, so even for similar abundances one would expect the H13CO+ lines to be stronger and possibly more extended than those of HN13C.
Critical H2 densities in cm-3 of the 1 → 0 and 4 → 3 transitions of H13CO+ and HN13C at various temperatures.
The SiO 2 → 1 and 8 → 7 transitions were selected to probe the low- and high-excitation shocked gas possibly affected by the early interaction of the precursor of C-shocks.
3. Observations
The SiO J = 2 → 1,
H13CO+J = 1 → 0 and
HN13C J = 1 → 0 lines (all at ~87 GHz) were observed in
June 2010 with the receiver EMIR (Eight MIxer Receiver) at the IRAM (Instituto de
Radioastonomía Milimétrica) 30 m telescope, at Pico Veleta (Spain), towards the protostars
NGC 1333-IRAS 4A/B and SSV 13, L1448-IRS3, VLA 1623 and IRAS 20353. The beam size at this
frequency is ~29′′. We used the on-the-fly mapping, position switched observing
mode at a rate of 4′′ s-1, which covered total areas of approximately
6 arcmin squared. The central coordinates of the OTF maps were
(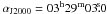 ,
δJ2000 =
,
δJ2000 = 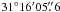 ) for NGC 1333,
(
) for NGC 1333,
(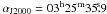 ,
,
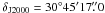 ) for L1448-IRS3,
(
) for L1448-IRS3,
(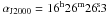 ,
,
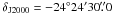 ) for VLA 1623,
and (
) for VLA 1623,
and (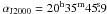 ,
,
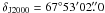 ) for IRAS 20353.
) for IRAS 20353.
The off reference positions with respect to the central coordinates of the maps were taken from the literature for L1448-IRS3 (JS06; (800′′, 0)) and NGC 1333 (Choi et al., 2004; (900′′, 0)). For VLA 1623 and IRAS 20353 off positions of (0, −800′′) and (−800′′, 0) were used, and were checked to be free of emission in the 1 → 0 lines down to an rms of ≤0.07 K at 0.1 km s-1 binning. The spectrometer (“back-end”) VESPA (VErsatile SPectrometer Array) was used, providing a spectral resolution of 40 kHz. This corresponds to a velocity resolution of ~0.14 km s-1 at 87 GHz. Pointing was checked on a nearby bright source every one to two hours, and the system temperatures ranged from 70 to 280 K.
The SiO J = 8 → 7, H13CO+J = 4 → 3 and HN13C J = 4 → 3 lines at 347–348 GHz were observed towards the same outflows using the HARP-B (Heterodyne ARray Program-B) receiver at the James Clerk Maxwell Telescope (JCMT) at Mauna Kea (Hawaii), in September 2010. We mapped this emission by using the HARP5 map-centred jiggle-map mode in position switching. The off positions used in the observations are the same as those above. The ACSIS (Auto-Correlation Spectrometer Imaging System) spectrometer provided resolutions of 61 kHz for H13CO+ 4 → 3 and HN13C 4 → 3, and 31 kHz for SiO 8 → 7, corresponding to velocity resolutions of 0.05 km s-1 and 0.03 km s-1 at 347 GHz, respectively. The beam size of the observations was 14′′. Pointing was checked every one to two hours on a nearby bright source, and system temperatures ranged from 230 to 395 K.
All the intensities were calibrated in units of antenna temperature, and for the LVG modelling we convert to TMB using beam efficiencies of 0.82 and 0.63 for the ~90 and ~350 GHz lines respectively.
4. Results
Maps of the SiO 2 → 1, H13CO+ 1 → 0, HN13C 1 → 0, and H13CO+ 4 → 3 integrated intensities are shown in Figs. 2 to 5 for each source. The emission was integrated over 5.5–9.5 km s-1 for NGC 1333, 0.5–7 km s-1 for L1448-IRS3, 2.5–4.6 km s-1 for VLA 1623, and 2–3.3 km s-1 for IRAS 20353. These velocity ranges were chosen such that they include all the narrow SiO, H13CO+ and HN13C emission. We do not show the HN13C 4 → 3 integrated intensities because it was not detected towards any of the sources above the 3σ limit.
 |
Fig. 2 Maps of the NGC 1333 region. Offsets are relative to the positions given in Sect. 3. a) Shows the Spitzer IRAC channel 2 emission (4.5 μm, retrieved from the Spitzer archive), and b) to e) show the integrated intensity maps of SiO 2 → 1, H13CO+ 1 → 0, HN13C 1 → 0, and H13CO+ 4 → 3. For maps b) to e) the contour levels start at 5σ, where σ is the estimated rms noise towards the centre of the map (it is higher towards the map edges). The values of σ (and contour step) in K km s-1 for these maps are: b) 0.044 (0.22), c) 0.094 (0.18), d) 0.056 (0.10), and e) 0.052 (0.26). Map f) shows the H13CO+ 4 → 3/1 → 0 integrated intensity ratio, with a lowest contour level of 0.1 and step 0.05. The grey-scale image is shown to make the map easier to read. The squares show the location of nearby protostars and the triangles show the Herbig-Haro 7–11 objects. The cross shows the location where we have extracted the single spectra. |
 |
Fig. 3 As in Fig. 2, but for L1448-IRS3. The values of σ (and contour step) in K km s-1 for maps b) to e) are: b) 0.016 (0.081), c) 0.013 (0.26), d) 0.028 (0.14), and e) 0.030 (0.15). The first contour level and step of the H13CO+ 4 → 3/1 → 0 integrated intensity ratio map f) are 0.08 and 0.04, respectively. |
 |
Fig. 4 As in Fig. 2, but for VLA 1623. The values of σ (and contour step) in K km s-1 for maps b) to e) are: b) 0.025 (0.027), c) 0.057 (0.54), d) 0.030 (0.15), and e) 0.065 (0.33). The first contour level and step of the H13CO+ 4 → 3/1 → 0 integrated intensity ratio map f) are 0.01 and 0.05, respectively. |
 |
Fig. 5 As in Fig. 2, but for IRAS 20353. For this source no SiO 2 → 1 was detected, and the H13CO+ 4 → 3/1 → 0 integrated intensity ratio map did not contain a sufficient number of valid pixels, therefore these maps are not shown. For maps b) to d) (showing the integrated intensities of only H13CO+ 1 → 0, HN13C 1 → 0 and H13CO+ 4 → 3), the values of σ (and contour step) in K km s-1 are: b) 0.034 (0.074), c) 0.067 (0.067), and d) 0.021 (0.014). Here the first contour level of H13CO+ 4 → 3 (map d)) is 3σ, as opposed to 5σ used in all the previous maps. |
We also plot the H13CO+ 4 → 3/1 → 0 integrated intensity ratio maps, which were calculated by regridding the H13CO+ 4 → 3 maps onto the same grid as the H13CO+ 1 → 0 maps using the task “reproject” from the CLASS analysis software included in the GILDAS package1, and then using the task “combine” to calculate their ratio. Pixels with an integrated intensity of less than 3σ (where σ is the map rms noise) in either molecule were considered invalid (apart from for NGC 1333 where we allow pixels with an H13CO+ 4 → 3 integrated intensity greater than 1σ to be used, because of the small spatial extent of the emission from this line). For IRAS 20353, even when using a threshold of 1σ for the 4 → 3 line there are insufficient valid pixels, therefore we do not show this map.
In addition, we also plot the Spitzer IRAC channel 2 (4.5 μm) map to put the observed regions into context. The 4.5 μm emission reveals any knots of shocked H2 gas (for example, south of L1448-IRS3, and towards the Herbig-Haro objects south-east of SSV 13 in the NGC 1333 region), and also reflection nebulae (for example, the strong emission north-east of VLA 1623, Dent et al. 1995) towards the sources. The locations of nearby protostars are marked with squares and Herbig-Haro objects with triangles, and the location of the offsets selected to study in more detail (see below) are marked by a cross on each map.
The maps of the H13CO+ 1 → 0 and HN13C 1 → 0 lines show that, in general, the spatial distribution of these two molecules are similar, adding confidence to our assumption that they trace the same gas. The H13CO+ 1 → 0 emission tends to be more widespread, owing to its lower critical density.
For each outflow, maps of the SiO 2 → 1 integrated intensity and H13CO+ 4 → 3/1 → 0 integrated intensity ratio were inspected to identify any offsets which showed both narrow SiO emission and any velocity components which have very high 4 → 3/1 → 0 integrated intensity ratios for H13CO+ compared to the upper limit for HN13C, as these may indicate the presence of the precursor (Jiménez-Serra et al. 2006). We selected a single offset from each outflow which best satisfied these criteria. The spectra from the selected offsets, smoothed to a velocity resolution of 0.1–0.15 km s-1, are shown in Fig. 6, and the observed parameters are given in Table 2. To take into account the different beam sizes of the observations, these spectra have been averaged by assuming a Gaussian taper, whose FWHM corresponds to the largest beam size of the observations (~29′′).
Observed parameters of the H13CO+, HN13C and SiO lines.
 |
Fig. 6 Spectra of the J = 1 → 0 and 4 → 3 lines of
H13CO+ and HN13C, and the
J = 2 → 1 and 8 → 7 lines of SiO towards the sources NGC 1333,
L1448-IRS3, VLA 1623 and IRAS 20353, for the positions selected in Sect. 4 (given at the top of each column). To account for
the different beam sizes, the spectra have been averaged by assuming a Gaussian taper,
whose FWHM corresponds to the largest beam size of the observations
(~29′′). The vertical axis is line intensity in Kelvin on the
|
Note that towards every outflow, Fig. 6 shows that at least two “ambient” velocity components are detected. Despite the fact that C-shock models predict that the ion and neutral velocities are continuous functions of time and space, Jiménez-Serra et al. (2009) showed that at early times the emission of H13CO+ and HN13C peak at two distinct velocity components as a consequence of the initial acceleration of ions by the precursor. The separate velocity components could have also formed by other dynamical processes. For example Langer et al. (1996) suggested that the 8 km s-1 structure observed towards NGC 1333 is a dense shell of gas, compressed by the outflows in the region.
In Table 3, we present the J = 4 → 3/1 → 0 integrated intensity ratios derived for every velocity component and molecule reported in Table 2 and Fig. 6. Below we discuss the results from the maps, and the individual spectra extracted from the positions which best satisfied our criteria for each outflow.
4.1. NGC 1333
NGC 1333 is a region of intense star formation located within the Perseus molecular cloud. Its distance is estimated to be between 220 (Cernis 1990) and 350 pc (Herbig & Jones 1983), and the complex has an ambient velocity of ~6–9 km s-1. The region we have observed encompasses the IRAS 4A/B class 0 protostars, as well as the SSV 13 ridge (IRAS 3) which contains at least one class 0 protostar (Bachiller et al. 1998; Sandell & Knee 2001). These protostars are all low-mass, with a total bolometric luminosity for the IRAS 4 system of 28 L⊙ (Sandell et al. 1991), and 69–90 L⊙ for the SSV 13 system (Sandell et al. 1990). Shocked gas traced by high velocity SiO emission indicates that the outflow emanating from IRAS 4 has a very young dynamical age of 3500 yr, and another outflow lobe, possibly generated by SSV 13, has a dynamical age of 11 000 yr (Lefloch et al. 1998b). These outflows have shaped the surrounding gas, forming a complicated structure of cavities and dense layers (Lefloch et al. 1998a).
Our observations (Fig. 2) show that, as reported by Lefloch et al. (1998b), the narrow SiO emission spreads around SSV 13 and the HH7-11 objects, and to the west of the IRAS 4A and 4B cores. The SiO emission towards the IRAS 4 cores is slightly narrower (Δv ~ 0.5 km s-1) than the emission surrounding SSV 13 (Δv ~ 1.5 km s-1). The H13CO+ 4 → 3 emission and H13CO+ 4 → 3/1 → 0 ratio have two peaks: one close to SSV 13 which is elongated towards the south, and another close to the IRAS 4A protostar. The regions where the H13CO+ 4 → 3/1 → 0 ratio is high do not follow the narrow SiO emission, which would not be expected if both these features were produced in the magnetic precursor. We selected the offset (85′′, −155′′), close to IRAS 4A, to study in more detail rather than the emission close to SSV 13, because it has both strong, narrow SiO emission and a high H13CO+J = 4 → 3/J = 1 → 0 ratio, whereas the emission towards SSV 13 has little or no narrow SiO emission.
Towards (85′′, −155′′), two components are clearly visible, at ~6.9 (referred to as C1 in Table 3) and ~7.8 km s-1 (C2 in Table 3). Langer et al. (1996) also observed components of emission in CS at similar velocities, and suggested that the ~8 km s-1 layer is a dense compressed shell surrounding a cavity created by the outflows. For the C1 component, we find that H13CO+ has a 4 → 3/1 → 0 ratio 5 times greater than that for HN13C. This is in contrast to component C2, where the upper limit of the HN13C 4 → 3/1 → 0 ratio is similar to that of H13CO+. C1 therefore appears to show an over-excitation of the ion fluid similar to that reported towards L1448-mm (JS06).
Like towards L1448-mm, narrow (~0.6 km s-1) SiO is also detected towards NGC 1333. However, this narrow SiO emission peaks at the C2 velocity component where no over-excitation of H13CO+ is reported. This behaviour differs from that observed towards L1448-mm, because the narrow SiO lines towards this outflow were detected at the velocity component which showed an over-excitation of the ion fluid.
Narrow SiO 8 → 7 was not detected, although the full spectrum (inset in Fig. 6) reveals a broad velocity wing with a terminal velocity of ~40 km s-1, most likely associated with the post-shock gas.
4.2. L1448-IRS 3
L1448-IRS3 is a class 0/I protostellar complex (Ciardi et al. 2003), also in Perseus, lying approximately 70′′ north west of the class 0 protostar L1448-mm. The total bolometric luminosity of the complex is 10 L⊙ (Bontemps et al. 1996), and the ambient velocity is ~4–4.7 km s-1. Bachiller et al. (1990) found that L1448-mm drives a highly collimated CO outflow, the northern lobe of which appears to impact with L1448-IRS3. In addition they found that L1448-IRS3 also appears to drive its own weaker outflow, with a dynamical age of ~2600 yr.
Figure 3 shows that the narrow SiO lies to the east of the L1448-IRS 3 complex. The emission close to L1448-IRS 3 is the narrowest (Δν ~ 0.5 km s-1), but going further east the width increases to Δν ~ 2 km s-1. The H13CO+ 4 → 3 emission and H13CO+ 4 → 3/1 → 0 ratio peak around the IRS3 complex, and could simply be a result of the high gas density of the protostars, but towards the east of the IRS 3 complex, where the narrow SiO emission is very strong, it is possible that the magnetic precursor is also contributing to the excitation of H13CO+. We therefore select the offset (14′′, 3′′) to study in detail because this position has the narrowest SiO emission, and also a very high H13CO+ 4 → 3/1 → 0 ratio. We note that, as for NGC 1333, the areas with high H13CO+ 4 → 3/1 → 0 ratio do not follow the narrow SiO emission.
Towards this offset, The H13CO+ and HN13C spectra, shown in Fig. 6, are best fit using three Gaussian components, centred at velocities ~4.0 (C1 in Table 3), ~4.7 (C2) and ~5.5 (C3) km s-1. The 4 → 3/1 → 0 integrated intensity ratios (Table 3) show that although component C3 has the largest 4 → 3/1 → 0 integrated intensity ratio, the largest difference between the H13CO+ and HN13C ratios is seen in C2. For this component the H13CO+ 4 → 3/1 → 0 ratio is ≳ 10 times greater than that for HN13C, similar to that found towards L1448-mm, again indicating an ion over-excitation towards this component. Narrow SiO 2 → 1 is also detected at the velocity of C2, although narrow SiO 8 → 7 is not, implying that the excitation of narrow SiO gas towards this source is relatively low.
4.3. VLA 1623
VLA 1623 is a class 0 protostar in the ρ-Ophiuchus region, at a distance of 160 pc and with a bolometric luminosity of 1 L⊙ (Bontemps et al. 1996). The ambient velocity is 3–3.5 km s-1. It drives a highly collimated and extended outflow, with an estimated dynamical age of ~3000 yr (André et al. 1990). Towards VLA 1623 (Fig. 4), the SiO emission is very weak (at its peak at offset (36′′, 36′′) it is only ~5σ), and is confined to a small region close to the starless core GPJ2008 Source 4 (Gurney et al. 2008) (we believe the peak in SiO integrated intensity towards the offset (10, −100′′) is due to high noise at the map edge). SiO 2 → 1 was not detected by Yu & Chernin (1997) towards this source, although Garay et al. (2002) detected weak emission towards a similar position as we have found. Note that this position does not lie along the main VLA 1623 outflow axis, which runs in an approximately south-east to north-west direction (Dent et al. 1995). 12CO observations of the GPL2008 source reveal an outflow, although it is possible that this outflow actually emanates from the VLA1623 protostar (Gurney et al. 2008).
The map of the H13CO+ 4 → 3/1 → 0 ratio is complicated because the H13CO+ 4 → 3 emission is quite extended, unlike for the other outflows where the emission is confined mainly to the areas around the protostars. The H13CO+ 4 → 3/1 → 0 ratio has two main peaks towards the offsets ~(50′′, 80′′) and ~(−10′′, −15′′). We select the offset (30′′, 71′′), which is close to one of the peaks in narrow SiO emission, and the H13CO+ 4 → 3/1 → 0 ratio is also close to its peak here. Furthermore, around this offset, we identified a component at ~2.6 km s-1 (component C1 in Table 3) which is seen in H13CO+, but is not seen at all in HN13C 1 → 0 (see Fig. 6 and Table 2). Table 3 shows that the excitation of H13CO+ in this component is higher than in the other component at ~3.5 km s-1 (C2) which is seen in both molecules. Note also that towards this source, the HN13C peaks about 50′′ north of the H13CO+, which could be a chemical effect, but could also be indicative of different conditions between the ion and neutral fluids.
Since the SiO 2 → 1 emission is very weak, the spectrum has been smoothed to a velocity resolution 0.5 km s-1, and therefore we cannot ascertain its velocity to enough accuracy to be able to tell if it lies at the velocity of C1 or C2. SiO 8 → 7 was not observed in this outflow due to time constraints.
4.4. IRAS 20353
IRAS 20353 is a class I protostar located within the L1152 isolated core (Bontemps et al. 1996), at a distance of 440 pc. It has a bolometric luminosity of 3.3 L⊙ (Myers et al. 1992), and an ambient velocity of ~3 km s-1. Bontemps et al. (1996) detected a bipolar CO outflow towards this source, which we estimate to have a dynamical age of 65 000 yr2. This age estimate is rather large in comparison to the other outflows in this study, but note that 65 000 yr is the age estimate of the shock at the outer boundary of the outflow lobes, so it is possible that there are younger shocks within the outflow lobes.
Towards IRAS 20353 (Fig. 5), no SiO 2 → 1 emission was detected. The H13CO+ 4 → 3 emission and the H13CO+ 4 → 3/1 → 0 ratio peak towards the central position of the protostar, so we studied the spectra from offset (0, 0) in more detail. This way we can investigate if excitation differences between ions and neutrals can be found even in the absence of narrow SiO.
Towards this offset, we identified two components of emission at 2.6 (C1) and 3.1 (C2) km s-1. Only the C1 component was detected in H13CO+ 4 → 3 (the peak at C2 looks like it is a noise spike), although the H13CO+ 4 → 3/1 → 0 integrated intensity ratio in this component is actually lower than the upper limit of the HN13C integrated intensity ratio (see Table 3). There is therefore no evidence of an over-excitation of H13CO+.
5. LVG modelling
Table 3 shows that towards both NGC 1333 and L1448-IRS3, there is one component of emission which has significantly larger (by ≥5–10 times) 4 → 3/1 → 0 integrated intensity ratios for H13CO+ compared to HN13C. Following the analysis of JS06, in Sect. 5.2 we first quantify the H13CO+ and HN13C excitation differences by estimating the H2 densities required to explain the line intensity ratios of Table 3, using the large velocity gradient (LVG) approximation. We assume collisional excitation by H2 only, and kinetic temperatures estimated from previous NH3 observations found in the literature. This is to ascertain whether there really is an over-excitation of H13CO+ under these conditions, or if it is just an effect of its lower critical density. In Sect. 5.3, we then investigate the possibility that an electron fractional abundance enhancement could be responsible for the difference in excitation between the two molecules towards NGC 1333 and L1447-IRS3, and we also explore the effect on the excitation of H13CO+ and HN13C of varying the gas temperature.
For all of the LVG modelling, we fit the peak intensities of the lines, and following the results given in Table 2 we adopt a line width of 0.8 km s-1 for all components. The H2 collisional coefficients used in the LVG model were taken from the Leiden Atomic and Molecular Database (Schöier et al. 2005), which uses the values from Flower (1999) for H13CO+ and Dumouchel et al. (2010) for HN13C. The electron collisional coefficients were from Faure et al. (priv. comm.) for H13CO+ and Faure et al. (2007) for HN13C.
5.1. A note about temperature
C-shock models predict that the ion and neutral fluid kinetic temperature can increase by several orders of magnitude throughout the propagation of a shock. However, since Jiménez-Serra et al. (2009) found that the narrow SiO line profile at ambient velocities towards L1448-mm can only be reproduced at very young shock ages (~3 yr), here we only consider very early stages of the precursor where both the ion and neutral fluids have moderate temperatures (≲150 K).
Derived H2 densities and column densities for H13CO+ and HN13C for each component observed towards the outflows.
A further complication is that in the magnetic precursor, the neutral, ion and electron
fluids are all predicted to have different kinetic temperatures: the ion fluid temperature
can be as much as 100 times greater than the neutral temperature, and the electron fluid
temperature is predicted to be in-between the ion and neutral temperatures (see e.g. Flower & Pineau des Forêts 2003). It is also
possible that the ion-neutral drift in the precursor could increase the effective
temperature of the ion-neutral collisions, similar to the mechanism described in
Federman et al. (1996). Strictly speaking, the
effective temperature, Teff, that should be used in the LVG
model for ion-neutral collisions is given by 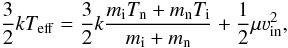 (1)where
mn (mi) is the mass of the
neutral (ion) species, Tn (Ti) is
the temperature of the neutral (ion) fluid, μ is the reduced mass of the
reacting molecules, νin is the ion-neutral drift velocity,
and k is the Boltzmann constant. The final term of Eq. (1) is the contribution to
Teff from the ion-neutral drift, and this is discussed in
more detail in Sect. 5.3.1.
(1)where
mn (mi) is the mass of the
neutral (ion) species, Tn (Ti) is
the temperature of the neutral (ion) fluid, μ is the reduced mass of the
reacting molecules, νin is the ion-neutral drift velocity,
and k is the Boltzmann constant. The final term of Eq. (1) is the contribution to
Teff from the ion-neutral drift, and this is discussed in
more detail in Sect. 5.3.1.
Considering H2–H13CO+ collisions, when Ti ≫ Tn, the first term on the right hand side of Eq. (1) tends to (3/2)k(mH2/mH13CO + )Ti (with mH13CO + ~ 15mH2). However, as mentioned above, here we only consider the early stages of the precursor when the ion fluid has not reached such high values. Under these conditions Tn is a good approximation for Teff (for Ti <10Tn, the [(miTn + mnTi)/mi + mn)] term in Eq. (1) approximates to Tn to within 60%).
We also use the neutral fluid temperature when considering collisions between electrons and H13CO+ and HN13C, although strictly speaking the electron temperature should be used. It is currently not possible in our LVG model to use a different kinetic temperature for electrons and for H2, but it is likely that including “hot” electrons would lead to higher 4 → 3/1 → 0 ratios in both molecules (and hence lower derived electron abundances). Furthermore, since the difference in electron collisional coefficients with H13CO+ and HN13C actually decreases for temperatures ≳ 30 K, the inclusion of hot electrons would probably decrease the excitation differences between H13CO+ and HN13C.
5.2. Quantifying the H13CO+ and HN13C excitation difference
5.2.1. NGC 1333 and L1448-IRS3
For these outflows the differences in integrated intensity ratios between ion and neutral species are similar to those found in L1448-mm, towards the positions where the precursor is believed to have been detected (see JS06, Tables 1 and 2). Since we expect the emission from these species to be optically thin, as was found to be the case for L1448-mm if the emission is extended (Roberts et al. 2010), the line intensity ratio between different transitions is directly related to the excitation temperature of the gas.
Here we estimate the H2 densities required to explain the line intensity ratios of Table 3, assuming collisional excitation by H2 only, and kinetic temperatures of 12 K for both NGC 1333 and L1448-IRS3. The kinetic temperature was estimated by taking the mean kinetic temperature of the NH3 cores identified by Rosolowsky et al. (2008) which lay within ~100′′ of the chosen offsets. The estimated H2 densities and column densities are given in Table 4.
We find that for component C1 of NGC 1333, which has a 4 → 3/1 → 0 integrated intensity ratio for H13CO+ ≥ 5 times greater than that for HN13C, the required H2 density to excite the H13CO+ is only ~2 times higher than the upper limit necessary to account for the HN13C excitation. This is in contrast to the results found by JS06 for L1448-mm, where the required H2 density for the precursor component was ≳ 10 times greater for H13CO+ compared to HN13C, even though the difference in 4 → 3/1 → 0 ratio between the two molecules was similar to that which we have found. We find a similar result for component C2 of L1448-IRS3, where despite the large difference in integrated intensity ratios between H13CO+ and HN13C, the H2 density required for H13CO+ is only ≳ 1.5 times greater than that for HN13C. For the other components in these outflows, the upper limit of the H2 densities required for HN13C are consistent with the H2 density derived for H13CO+.
A possible reason for the small difference in H2 densities for H13CO+ and HN13C, despite the large difference in observed integrated intensity ratios, is that the critical density of HN13C is somewhat higher than that for H13CO+. According to the data given in the LAMDA database (Schöier et al. 2005), at 10–20 K, the critical density of the H13CO+ 4 → 3 line is ~8.2 × 106 cm-3, whereas for same transition of HN13C it is more than double, at ~2.0 × 107 cm-3. A factor of two difference may seem unimportant, but it has a large effect on the densities required to excite the 4 → 3 lines of these molecules. As an example, assuming both molecules have a column density of 1 × 1012 cm-2, a line width of 0.8 km s-1, and kinetic temperature of 12 K, the H2 density required to excite H13CO+ to an intensity of 0.2 K is ~1.2 × 106 cm-3, whereas for HN13C the required density is ~1.2 × 107 cm-3, an order of magnitude greater. For the analysis of L1448-mm, where large differences in density required to excite the two molecules were found, JS06 derived the H2 densities using the 4 → 3/3 → 2 ratio for H13CO+, but since HN13C 4 → 3 and 3 → 2 lines were not detected in the precursor component, they used the upper limit of the 3 → 2/1 → 0 ratio to derive the HN13C densities. If we recalculate the H2 densities of JS06 using the 4 → 3/1 → 0 ratio in both lines3, for the (0, −10′′) offset we find that the H2 density required for H13CO+ is ~2.7 × 105 cm-3, and for HN13C it is ~4.9 × 105 cm-3. This shows that using this choice of transitions tends to give more similar densities for the two molecules, as expected from the 1 → 0 transition which mainly probes the outer envelope of the cloud. In contrast, the 3 → 2 and 4 → 3 transitions trace higher-density gas which is likely to be located closer to the regions affected by the outflows and the interaction of the precursor of C-shocks.
Nevertheless, by considering the 1σ error in the H13CO+ intensities for component C1 of NGC 1333 and component C2 of L1448-IRS3, the lower limits to the H2 densities required for H13CO+ (6.6 × 106 cm-3 for C1 of NGC 1333 and 1.6 × 106 cm-3 for C2 of L1448-IRS3) are still higher than the upper limit for the densities derived from HN13C, therefore there is still evidence to say that, for a gas temperature of 12 K, a single density cannot explain the excitation of both H13CO+ and HN13C for these components towards these outflows.
5.2.2. VLA 1623 and IRAS 20353
In Table 4 we have also included the estimated H2 densities and column densities for VLA 1623 and IRAS 20353, assuming kinetic temperatures of 17 K (Wootten et al. 1994) and 10 K (Benson 1991) for these outflows, respectively. For VLA 1623, since HN13C is not detected in C1, the component that could be associated with the precursor/shock, we cannot compare the excitation conditions between the two molecules. We do note, however, that the H2 density derived from H13CO+ is higher in C1 compared to C2, reflecting the higher excitation in component C1, which could possibly be associated with shocks or the precursor of shocks.
In IRAS 20353, as expected from the integrated intensity ratios, the densities needed to excite the H13CO+ fall within the upper limits of the densities required for HN13C, and there is no evidence of any over-excitation in either component.
5.3. The origin of the apparent H13CO+ over-excitation towards NGC 1333 and L1448-IRS3
As in JS06, we investigate the possibility that an electron fractional abundance enhancement in these components could be responsible for the difference in excitation between the two molecules, and we also explore the effect of increasing the gas temperature. We first investigate NGC 1333, taking the H2 density derived from H13CO+ in the C2 component (since it is lower than the upper limits inferred from HN13C), which was ~6 × 105 cm-3.
Figure 7 compares the effect of increasing the electron fractional abundance (with the temperature fixed at 12 K) and increasing the neutral gas temperature (with the electron fractional abundance fixed at 10-10) for both molecules on the 4 → 3/1 → 0 peak intensity ratio (keeping the column densities constant at N(H13CO+) = 8.8 × 1011 cm-2 and N(HN13C) = 5.1 × 1011 cm-2, the values given in Table 4 for component C1). It shows that by increasing the electron fractional abundance, the 4 → 3/1 → 0 ratio of H13CO+ increases rapidly for electron abundances greater than a few times 10-5. Counterintuitively, the 4 → 3/1 → 0 ratio of HN13C behaves similarly, even though the collisional coefficients for electrons with H13CO+ are >4 times greater than those with HN13C for these transitions at 12 K. The strong effect of electrons on HN13C could be explained by examining the collisional coefficients for each molecule with H2 and electrons: at 12 K, for the 4 → 3 transition of H13CO+ the collision rate with H2 is 4.0 × 10-10n(H2) s-1, and the collision rate with electrons is 1.4 × 10-5n(H2)X(e) s-1, meaning that the critical electron fractional abundance (which we define as the value for which the collisional rates for H2 and electrons are equal) is ~3 × 10-5. For HN13C the collisional rates are 1.1 × 10-10 n(H2) s-1 and 3.1 × 10-6 n(H2)X(e) s-1 with H2 and electrons respectively, meaning that the critical electron fractional abundance is also a few times 10-5. Consequently, electrons begin to affect both molecules once the electron abundance is ≳ 10-5.
 |
Fig. 7 Plot showing the effect of increasing electron fractional abundance (thick black curves, calculated using a constant kinetic temperature of 12 K) and kinetic temperature (dashed curves, calculated using a negligible electron abundance) on the 4 → 3/1 → 0 line intensity ratios of H13CO+ and HN13C, for gas with an H2 density of 6 × 105 cm-3 and H13CO+ and HN13C column densities of 8.8 × 1011 cm-2 and 5.1 × 1011 cm-2 respectively. The grey bar shows the observed H13CO+ 4 → 3/1 → 0 line intensity ratio towards NGC 1333, taking into account the 1σ errors in the observations. The thin black line shows the upper limit to the observed HN13C 4 → 3/1 → 0 line intensity ratio towards NGC 1333. |
We find that a fractional electron abundance of 8.8 × 10-4 is needed to reproduce the observed H13CO+ 4 → 3/1 → 0 ratio (assuming that the electron temperature is equal to the neutral temperature of 12 K). However, for this electron abundance the HN13C 4 → 3/1 → 0 is 0.31, almost double the observed upper limit. In addition, this electron fractional abundance exceeds the value of ≲10-5 predicted by C-shock models (Flower et al. 1996; Flower & Pineau des Forêts 2003). As pointed out by JS06, the cosmic abundance of atomic carbon (X(C) ~(2−3) × 10-4), the main repository of positive charge in dark clouds, provides a limit for the maximum electron abundance, which is also exceeded by this estimate.
On the other hand, Fig. 7 shows that increasing the kinetic temperature is more effective at increasing the 4 → 3/1 → 0 ratio for H13CO+ compared to HN13C. This can be explained by considering the critical densities of the molecules as follows: at densities much greater than the critical density, when collisions completely dominate, the excitation temperature of a transition tends towards the kinetic temperature for an optically thin transition (Green 1985), and the 4 → 3/1 → 0 ratio has a relatively strong temperature dependence, proportional to exp [− (ΔE43 − ΔE10)/kTkin] , where ΔEij is the energy difference between levels i and j, and Tkin is the gas kinetic temperature. At the other extreme, at low densities, radiative excitation dominates and the ratio is independent of the gas kinetic temperature. At a gas density of 6 × 105 cm-3, the excitation of both molecules is in-between the two regimes, but it appears that since the H13CO+ critical densities are a factor of two lower than for HN13C, the temperature dependence of H13CO+ is closer to the collisionally dominated regime, and hence stronger temperature dependence, than HN13C.
From Fig. 7, we see that in order to reproduce the 4 → 3/1 → 0 ratio of H13CO+, a temperature of ~27 K is needed. At this temperature, the 4 → 3/1 → 0 ratio of HN13C is ~0.10, which is below the observed upper limit of 0.17. The LVG model shows that the 4 → 3/1 → 0 ratios of both H13CO+ and HN13C are approximately constant with column density for column densities ≲1012 cm-2 (plot not shown), so by adjusting the column densities of H13CO+ and HN13C slightly, to 6.9 × 1011 cm-2 and 4.1 × 1011 cm-2 respectively, the absolute intensities of each line can be fitted to within 10%.
Repeating the analysis for L1448-IRS3, assuming a gas density of 1 × 106 cm-3 (as derived from the upper limit HN13C for the C2 component), we find that a temperature of 14 K or an electron fractional abundance of 5.4 × 10-5 can explain the H13CO+ 4 → 3/1 → 0 ratio. However, for both of these conditions, the HN13C 4 → 3/1 → 0 ratio is predicted to be slightly above the observed value (the temperature increase predicts a value 24% higher than the upper limit and the electron fractional abundance increase predicts a value 54% higher). This is probably because the density of the gas used was derived from HN13C upper limit, so of course if the temperature or electron density is increased, it will increase the excitation of HN13C so it will no longer fit the observations. In fact, since the density is only an upper limit, one finds that if the density is decreased to 3 × 105 cm-3, the H13CO+ ratio can be fitted with a temperature of 27 K, and under these conditions the HN13C ratio is only over-predicted by 10%. At this density, increasing the electron abundance to 3.7 × 10-4 can also fit the H13CO+ ratio, but in this case the HN13C ratio is over-predicted by 68%.
For both of these outflows, therefore, it seems that the over-excitation of H13CO+ can be explained best by a single density and a slightly raised temperature in the affected velocity component with respect to the other ones for both H13CO+ and HN13C. Given that using the same kinetic temperature and density for each species fits the observations reasonably well, we can not conclude that an electron fractional abundance increase is needed to explain the H13CO+ over-excitation. Nor can we unequivocally say that the H13CO+ and HN13C have different excitation conditions in the velocity components with the high 4 → 3/1 → 0 ratio for H13CO+ compared to HN13C. Therefore we can not confirm that the difference in 4 → 3/1 → 0 ratios is due to the magnetic precursor.
5.3.1. Considering the effect of ion-neutral drift
According to Eq. (1), the effective
temperature of the H2–H13CO+ collisions could be
enhanced by a factor of 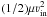 , due to
ion-neutral drift. If this were the case here, we would expect the temperature needed to
fit H13CO+ to be greater than that needed to fit HN13C.
For the case of NGC 1333, from Fig. 7 it is clear
that HN13C can have a temperature of anything ≲37 K for its 4 → 3/1 → 0
ratio to remain below the observed upper limit. It is therefore possible that
HN13C temperature could be lower than the ~27 K needed
to fit H13CO+. Similarly for L1448-IRS3, if the HN13C
temperature is kept at 12 K and the H13CO+ temperature is
increased by only a few degrees K, both lines can be fitted perfectly using the same gas
density. However, since C-shock models predict that the ion-neutral drift velocity could
be as high as ~30 km s-1 (Flower et al.
1996), this would lead to a Teff for
H2–H13CO+ collisions of ~68 000 K. Even at a more
modest ion-neutral drift velocity of 5 km s-1,
Teff would be as high as ~1900 K. One would therefore
expect the excitation of H13CO+ to be characterised by a much
higher effective temperature than the increases of 2–15 K which we have found.
, due to
ion-neutral drift. If this were the case here, we would expect the temperature needed to
fit H13CO+ to be greater than that needed to fit HN13C.
For the case of NGC 1333, from Fig. 7 it is clear
that HN13C can have a temperature of anything ≲37 K for its 4 → 3/1 → 0
ratio to remain below the observed upper limit. It is therefore possible that
HN13C temperature could be lower than the ~27 K needed
to fit H13CO+. Similarly for L1448-IRS3, if the HN13C
temperature is kept at 12 K and the H13CO+ temperature is
increased by only a few degrees K, both lines can be fitted perfectly using the same gas
density. However, since C-shock models predict that the ion-neutral drift velocity could
be as high as ~30 km s-1 (Flower et al.
1996), this would lead to a Teff for
H2–H13CO+ collisions of ~68 000 K. Even at a more
modest ion-neutral drift velocity of 5 km s-1,
Teff would be as high as ~1900 K. One would therefore
expect the excitation of H13CO+ to be characterised by a much
higher effective temperature than the increases of 2–15 K which we have found.
6. Discussion and conclusions
Following previous studies on L1448-mm (e.g. Jiménez-Serra et al. 2004; and JS06), which have interpreted the narrow SiO emission at ambient velocities and high line intensity ratios of ions compared to neutral species as signatures of the magnetic precursor of C-shocks, we have searched for these features towards four other young, low-mass protostars (class 0/I) with outflows. The sources NGC 1333, L1448-IRS3, and VLA 1623 all show narrow SiO 2 → 1 emission, and NGC 1333 and L1448-IRS3 also show velocity components with a much higher 4 → 3/1 → 0 integrated intensity ratio for H13CO+ compared to HN13C, similar to that seen towards L1448-mm. VLA 1623 showed a component in H13CO+ which is not seen at all in HN13C, even in the 1 → 0 line, which could either indicate a large difference in excitation conditions, or in abundances, between the two molecules.
JS06 explained the high 4 → 3/1 → 0 integrated intensity ratio of H13CO+ by the selective excitation of ions by electrons, which have an enhanced fractional abundance during the magnetic precursor stage of C-shocks. Our LVG analysis has found that for the sources NGC 1333 and L1448-IRS3, an increase in electron fractional abundance would cause the HN13C 4 → 3/1 → 0 intensity ratios to be increased beyond their observed upper limits. Instead we find that using a slightly higher kinetic temperature (an increase of ≲15 K) than the value estimated from previous NH3 observations can fit the intensities of both molecules well. It is also possible to fit the intensities with a higher temperature for H13CO+ than for HN13C, which would be expected in the magnetic precursor due to the increase in effective temperature of ion-neutral collisions. However, the estimated differences in temperature needed to fit the observations are much smaller than would be expected for the typical ion-neutral drift velocities predicted by C-shock models. Given that the H13CO+ 4 → 3 integrated intensity in Figs. 2 and 3 tends to peak towards the protostars, it could simply be that the high H13CO+ 4 → 3/1 → 0 ratio is caused by protostellar heating. However, since the errors involved in measuring the observations are large, we do not rule out the possibility that electrons play a part in the excitation of H13CO+. In fact, since C-shock models predict both a temperature and electron abundance increase (e.g. Flower et al. 1996), it is possible that a combination of temperature and electron abundance increase are responsible for the high H13CO+ 4 → 3/1 → 0 ratios. High-angular resolution interferometric observations are therefore required to separate the protostar and precursor contributions to the high 4 → 3/1 → 0 ratios observed towards these outflows.
Lefloch et al. (1998b) and Codella et al. (1999) suggested that the narrow, ambient SiO detected towards NGC 1333 could have been produced in post-shock gas which has decelerated to ambient velocities, rather than being produced at the magnetic precursor stage. Codella et al. (1999) estimated that for typical outflows this could take of the order 104 yr, but the dynamical timescales of the shocks towards L1448-IRS3 and VLA 1623 are much shorter than this. Furthermore, it seems that the SiO 2 → 1 emission towards these two outflows is on a much smaller scale than towards NGC 1333, which could indicate that the narrow SiO is produced by a smaller, local effect. In addition, towards VLA 1623, the narrow SiO lies in a small area off the outflow axis, so it might be difficult to explain how post-shock gas could arrive at that location. It is possible that the SiO is produced in the post shock gas from larger scale outflows that may exist in the region (Jiménez-Serra et al. 2010). If this is the case, one would not expect the narrow SiO to be compact and confined to regions near the protostars, as found towards L1448-mm (Jiménez-Serra et al. 2011). Large scale and high sensitivity maps would be useful to determine the absolute extent of the emission.
In summary, we cannot confirm that we have found the magnetic precursor towards these outflows, although the theory that ambient SiO is produced during the precursor stage of C-shocks remains very plausible. VLA 1623 appears to be a very promising outflow for further study, since the region of SiO 2 → 1 emission is small and weak it could be that it is in the early stages of formation, and there is a component of H13CO+ that is not seen in HN13C. Large scale interferometric maps of the narrow SiO, plus maps of several different ion and neutral species will be essential to provide conclusive detection of this phenomenon.
Bontemps et al. (1996) give a velocity range of 4–7.5 km s-1 for 12CO (2 → 1) in the redshifted outflow lobe detected in L1152. Subtracting the ambient source velocity of ~3 km s-1 gives a maximum velocity of ~4.5 km s-1. The red outflow lobe extends to an offset of approximately (−100′′, −100′′), which at the distance of the L1152 cloud, 440 pc, corresponds to approximately 0.30 pc. This gives a dynamical age estimate for the outflow of ~65 000 yr.
For this calculation we have converted to main beam temperatures and corrected for beam
dilution by multiplying the 4 → 3 intensities by a factor of
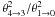 , where
θJup − Jlow is the beam size for the
transition Jup − Jlow. For the
observations presented in this paper, however, the beam size correction was performed by
averaging the spectra of the maps assuming a Gaussian taper of 29′′ for all
lines.
, where
θJup − Jlow is the beam size for the
transition Jup − Jlow. For the
observations presented in this paper, however, the beam size correction was performed by
averaging the spectra of the maps assuming a Gaussian taper of 29′′ for all
lines.
Acknowledgments
We would like to thank the anonymous referee for helpful comments on an earlier draft of this paper. This paper is based on observations from the IRAM 30 m Telescope and the James Clerk Maxwell Telescope (project M10BU04). The James Clerk Maxwell Telescope is operated by the Joint Astronomy Centre on behalf of the Science and Technology Facilities Council of the United Kingdom, The Netherlands Organisation for Scientific Research, and the National Research Council of Canada. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). This work has made use of the NASA/ IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This work has been partially supported by the Spanish Ministerio de Ciencia e Innovación under project ESP2007- 65812-C02-01, and by the Comunidad de Madrid Government under PRICIT project S-0505/ESP-0237 (ASTROCAM). A. Gusdorf acknowledges support by the grant ANR-09-BLAN-0231-01 from the French Agence Nationale de la Recherche as part of the SCHISM project.
References
- André, P., Martín-Pintado, J., Despois, D., & Montmerle, T. 1990, A&A, 236, 180 [NASA ADS] [Google Scholar]
- Bachiller, R., Martín-Pintado, J., Tafalla, M., Cernicharo, J., & Lazareff, B. 1990, A&A, 231, 174 [NASA ADS] [Google Scholar]
- Bachiller, R., Guilloteau, S., Gueth, F., et al. 1998, A&A, 339, L49 [NASA ADS] [Google Scholar]
- Benson, P. J. 1991, ASPC, 16, 21 [Google Scholar]
- Bontemps, S., André, P., Terebey, S., & Cabrit, S. 1996, A&A, 311, 858 [Google Scholar]
- Caselli, P., Hartquist, T. W., & Havnes, O. 1997, A&A, 322, 296 [NASA ADS] [Google Scholar]
- Cernis, K. 1990, Ap&SS, 166, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, M., Kamazaki, T., Tatematsu, K., & Panis, J.-F. 2004, ApJ, 617, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardi, D. R., Telesco, C. M., Williams, J. P., et al. 2003, ApJ, 585, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Codella, C., Bachiller, R., & Reipurth, B. 1999, A&A, 343, 585 [NASA ADS] [Google Scholar]
- Dent, W. R. F., Matthews, H. E., & Walther, D. M. 1995, MNRAS, 277, 193 [NASA ADS] [Google Scholar]
- Draine, B. T. 1980, ApJ, 241, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Dumouchel, F., Faure, A., & Lique, F. 2010, MNRAS, 406, 2488 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., Varambhia, H. N., Stoecklin, T., & Tennyson, J. 2007, MNRAS, 382, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Federman, S. R., Rawlings, J. M. C., Taylor, S. D., & Williams, D. A. 1996, MNRAS, 279, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R. 1999, MNRAS, 305, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2003, MNRAS, 343, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., Field, D., & May, P. W. 1996, MNRAS, 280, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Garay, G., Mardones, D., Rodríguez, L. F., Caselli, P., & Bourke, T. L. 2002, ApJ, 567, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Green, S. 1985, Il Nuovo Cimento C, 8, 435 [Google Scholar]
- Gurney, M., Plume, R., & Johnstone, D. 2008, PASP, 120, 873 [Google Scholar]
- Gusdorf, A., Cabrit, S., Flower, D. R., & Pineau des Forêts, G. 2008, A&A, 482, 809 [Google Scholar]
- Herbig, G. H., & Jones, B. F. 1983, AJ, 88, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, T., Yamamoto, S., Mikami, H., & Ohishi, M. 1998, ApJ, 503, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Martín-Pintado, J., Rodríguez-Franco, A., & Marcelino, N. 2004, ApJ, L49 [Google Scholar]
- Jiménez-Serra, I., Martín-Pintado, J., Viti, S., et al. 2006, ApJ, 650, L135 [JS06] [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Caselli, P., Martín-Pintado, J., & Hartquist, T. W. 2008, A&A, 482, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiménez-Serra, I., Martín-Pintado, J., Caselli, P., Viti, S., & Rodríguez-Franco, A. 2009, ApJ, 695, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Caselli, P., Tan, J. C., et al. 2010, MNRAS, 406, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Martín-Pintado, J., Winters, J.-M., Rodríguez-Franco, A., & Caselli, P. 2011, ApJ, 739, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., Castets, A., & Lefloch, B. 1996, ApJ, 471, 111 [Google Scholar]
- Lefloch, B., Castets, A., Cernicharo, J., Langer, W. D., & Zylka, R. 1998a, A&A, 334, 269 [Google Scholar]
- Lefloch, B., Castets, A., Cernicharo, P., & Loinard, L. 1998b, ApJ, 504, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Pintado, J., Bachiller, R., & Fuente, A. 1992, A&A, 254, 315 [NASA ADS] [Google Scholar]
- Mullan, D. J. 1971, MNRAS, 153, 145 [NASA ADS] [Google Scholar]
- Myers, P., Fuller, G., Mathieu, R., et al. 1987, ApJ, 319, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, J. F., Jiménez-Serra, I., Martín-Pintado, J., et al. 2010, A&A, 513, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosolowsky, E. W., Pineda, J. E., Foster, J. B., et al. 2008, ApJS, 175, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Sandell, G., & Knee, L. B. G. 2001, ApJ, 546, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Sandell, G., Aspin, C., Duncan, W. D., Robson, E. I., & Dent, W. R. F. 1990, A&A, 232, 347 [NASA ADS] [Google Scholar]
- Sandell, G., Aspin, C., Duncan, W. D., Russell, A. P. G., & Robson, E. I. 1991, ApJ, 376, 17 [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wootten, A., André, P., Despois, D., & Sargent, A. 1994, ASPC, 65, 294 [Google Scholar]
- Yu, T., & Chernin, L. M. 1997, ApJ, 479, L63 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Critical H2 densities in cm-3 of the 1 → 0 and 4 → 3 transitions of H13CO+ and HN13C at various temperatures.
Derived H2 densities and column densities for H13CO+ and HN13C for each component observed towards the outflows.
All Figures
 |
Fig. 1 Structure of a typical C-type shock from the parametric model of Jiménez-Serra et al. (2008). This model has a shock velocity of 40 km s-1, magnetic field strength of 450 μG, initial H2 density of 105 cm-3 and temperature of 10 K. The top panel shows the temperature of the ion and neutral fluids (Ti and Tn respectively) and the neutral gas density (nn). The bottom panel shows the ion and neutral fluid velocities (vi and vn) in a frame co-moving with the pre-shock gas, and vd is the velocity difference between the two fluids. |
| In the text | |
 |
Fig. 2 Maps of the NGC 1333 region. Offsets are relative to the positions given in Sect. 3. a) Shows the Spitzer IRAC channel 2 emission (4.5 μm, retrieved from the Spitzer archive), and b) to e) show the integrated intensity maps of SiO 2 → 1, H13CO+ 1 → 0, HN13C 1 → 0, and H13CO+ 4 → 3. For maps b) to e) the contour levels start at 5σ, where σ is the estimated rms noise towards the centre of the map (it is higher towards the map edges). The values of σ (and contour step) in K km s-1 for these maps are: b) 0.044 (0.22), c) 0.094 (0.18), d) 0.056 (0.10), and e) 0.052 (0.26). Map f) shows the H13CO+ 4 → 3/1 → 0 integrated intensity ratio, with a lowest contour level of 0.1 and step 0.05. The grey-scale image is shown to make the map easier to read. The squares show the location of nearby protostars and the triangles show the Herbig-Haro 7–11 objects. The cross shows the location where we have extracted the single spectra. |
| In the text | |
 |
Fig. 3 As in Fig. 2, but for L1448-IRS3. The values of σ (and contour step) in K km s-1 for maps b) to e) are: b) 0.016 (0.081), c) 0.013 (0.26), d) 0.028 (0.14), and e) 0.030 (0.15). The first contour level and step of the H13CO+ 4 → 3/1 → 0 integrated intensity ratio map f) are 0.08 and 0.04, respectively. |
| In the text | |
 |
Fig. 4 As in Fig. 2, but for VLA 1623. The values of σ (and contour step) in K km s-1 for maps b) to e) are: b) 0.025 (0.027), c) 0.057 (0.54), d) 0.030 (0.15), and e) 0.065 (0.33). The first contour level and step of the H13CO+ 4 → 3/1 → 0 integrated intensity ratio map f) are 0.01 and 0.05, respectively. |
| In the text | |
 |
Fig. 5 As in Fig. 2, but for IRAS 20353. For this source no SiO 2 → 1 was detected, and the H13CO+ 4 → 3/1 → 0 integrated intensity ratio map did not contain a sufficient number of valid pixels, therefore these maps are not shown. For maps b) to d) (showing the integrated intensities of only H13CO+ 1 → 0, HN13C 1 → 0 and H13CO+ 4 → 3), the values of σ (and contour step) in K km s-1 are: b) 0.034 (0.074), c) 0.067 (0.067), and d) 0.021 (0.014). Here the first contour level of H13CO+ 4 → 3 (map d)) is 3σ, as opposed to 5σ used in all the previous maps. |
| In the text | |
 |
Fig. 6 Spectra of the J = 1 → 0 and 4 → 3 lines of
H13CO+ and HN13C, and the
J = 2 → 1 and 8 → 7 lines of SiO towards the sources NGC 1333,
L1448-IRS3, VLA 1623 and IRAS 20353, for the positions selected in Sect. 4 (given at the top of each column). To account for
the different beam sizes, the spectra have been averaged by assuming a Gaussian taper,
whose FWHM corresponds to the largest beam size of the observations
(~29′′). The vertical axis is line intensity in Kelvin on the
|
| In the text | |
 |
Fig. 7 Plot showing the effect of increasing electron fractional abundance (thick black curves, calculated using a constant kinetic temperature of 12 K) and kinetic temperature (dashed curves, calculated using a negligible electron abundance) on the 4 → 3/1 → 0 line intensity ratios of H13CO+ and HN13C, for gas with an H2 density of 6 × 105 cm-3 and H13CO+ and HN13C column densities of 8.8 × 1011 cm-2 and 5.1 × 1011 cm-2 respectively. The grey bar shows the observed H13CO+ 4 → 3/1 → 0 line intensity ratio towards NGC 1333, taking into account the 1σ errors in the observations. The thin black line shows the upper limit to the observed HN13C 4 → 3/1 → 0 line intensity ratio towards NGC 1333. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.