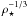| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201218817 | |
| Published online | 24 May 2012 | |
The TRAPPIST survey of southern transiting planets
I. Thirty eclipses of the ultra-short period planet WASP-43 b⋆,⋆⋆,⋆⋆⋆
1 Université de Liège, Allée du 6 août 17, Sart Tilman, Liège 1, Belgium
e-mail: michael.gillon@ulg.ac.be
2 Observatoire de Genève, Université de Genève, 51 chemin des Maillettes, 1290 Sauverny, Switzerland
3 Department of Astronomy and Astrophysics, University of California, Santa Cruz, CA 95064, USA
4 Department of Earth, Atmospheric and Planetary Sciences, Department of Physics, Massachusetts Institute of Technology, 77 Massachusetts Ave., Cambridge, MA 02139, USA
5 European Southern Observatory, Alonso de Cordova 3107, 19001 Casilla, Santiago, Chile
6 Astrophysics Group, Keele University, Staffordshire ST5 5BG, UK
7 School of Physics and Astronomy, University of St. Andrews, North Haugh, Fife, KY16 9SS, UK
8 Department of Physics and Astronomy, Vanderbilt University, Nashville, TN 37235, USA
Received: 13 January 2012
Accepted: 26 March 2012
We present twenty-three transit light curves and seven occultation light curves for the ultra-short period planet WASP-43 b, in addition to eight new measurements of the radial velocity of the star. Thanks to this extensive data set, we improve significantly the parameters of the system. Notably, the largely improved precision on the stellar density (2.41 ± 0.08 ρ⊙) combined with constraining the age to be younger than a Hubble time allows us to break the degeneracy of the stellar solution mentioned in the discovery paper. The resulting stellar mass and size are 0.717 ± 0.025 M⊙ and 0.667 ± 0.011 R⊙. Our deduced physical parameters for the planet are 2.034 ± 0.052 MJup and 1.036 ± 0.019 RJup. Taking into account its level of irradiation, the high density of the planet favors an old age and a massive core. Our deduced orbital eccentricity, 0.0035-0.0025+0.0060, is consistent with a fully circularized orbit. We detect the emission of the planet at 2.09 μm at better than 11-σ, the deduced occultation depth being 1560 ± 140 ppm. Our detection of the occultation at 1.19 μm is marginal (790 ± 320 ppm) and more observations are needed to confirm it. We place a 3-σ upper limit of 850 ppm on the depth of the occultation at ~0.9 μm. Together, these results strongly favor a poor redistribution of the heat to the night-side of the planet, and marginally favor a model with no day-side temperature inversion.
Key words: planetary systems / stars: individual: WASP-43 / techniques: photometric / techniques: radial velocities
Based on data collected with the TRAPPIST and Euler telescopes at ESO La Silla Observatory, Chile, and with the VLT/HAWK-I instrument at ESO Paranal Observatory, Chile (program 086.C-0222).
Tables 1 and 4 are available in electronic form at http://www.aanda.org
Photometry is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/542/A4
© ESO, 2012
1. Introduction
There are now more than seven hundreds planets known to orbit around other stars than our Sun (Schneider 2011). A significant fraction of them are Jovian-type planets orbiting within 0.1 AU of their host stars. Their very existence poses an interesting challenge for our theories of planetary formation and evolution, as such massive planets could not have formed so close to their star (D’Angelo et al. 2010; Lubow & Ida 2010). Long neglected in favor of disk-driven migration theories (Lin et al. 1996), the postulate that past dynamical interactions combined with tidal dissipation could have shaped their present orbit has raised a lot of interest recently (e.g. Fabrycky & Tremaine 2007; Naoz et al. 2011; Wu & Lithwick 2011), partially thanks to the discovery that a significant fraction of these planets have high orbital obliquities that suggest past violent dynamical perturbations (e.g. Triaud et al. 2010).
Not only the origin of these planets but also their fate raises many questions. Their relatively large mass and small semi-major axis imply tidal interactions with the host star that should lead in most cases to a slow spiral-in of the planet and to a transfer of angular momentum to the star (e.g. Barker & Ogilvie 2009; Jackson et al. 2009; Mastumura et al. 2010), the end result being the planet’s disruption at its Roche limit (Gu et al. 2003). The timescale of this final disruption depends mostly on the timescale of the migration mechanism, the tidal dissipation efficiency of both bodies, and the efficiency of angular momentum losses from the system due to magnetic braking. These three parameters being poorly known, it is desirable to detect and study in depth “extreme” hot Jupiters, i.e. massive planets having exceptionally short semi-major axes that could be in the final stages of their tidal orbital decay.
The WASP transit survey detected two extreme examples of such ultra-short period planets, WASP-18 b (Hellier et al. 2009) and WASP-19 b (Hebb et al. 2010), both having an orbital period smaller than one day. Thanks to their transiting nature, these systems were amenable for a thorough characterization that made possible a study of the effects of their tidal interactions (Brown et al. 2011). Notably, photometric observations of some of their occultations made possible not only to probe both planets’ dayside emission spectra but also to bring strong constraints on their orbital eccentricity (Anderson et al. 2010; Gibson et al. 2010; Nymeyer et al. 2011), a key parameter to assess their tidal history and energy budget. The same WASP survey has recently announced the discovery of a third ultra-short period Jovian planet called WASP-43 b (Hellier et al. 2011b, hereafter H11). Its orbital period is 0.81 d, the only hot Jupiter having a smaller period being WASP-19 b (0.79 d). Furthermore, it orbits around a very cool K7-type dwarf that has the lowest mass among all the stars orbited by a hot Jupiter (0.58 ± 0.05 M⊙, Teff = 4400 ± 200 K, H11), except for the recently announced M0 dwarf KOI-254 (0.59 ± 0.06 M⊙, Teff = 3820 ± 90 K, Johnson et al. 2012). Nevertheless, H11 presented another plausible solution for the stellar mass that is significantly larger, 0.71 ± 0.05 M⊙. This degeneracy translates into a poor knowledge of the physical parameters of the system.
With the aim to improve the characterization of this interesting ultra-short period planet, we performed an intense ground-based photometric monitoring of its eclipses (transits and occultations), complemented with new measurements of the radial velocity (RV) of the star. These observations were carried out in the frame of a new photometric survey based on the 60cm robotic telescope TRAPPIST1 (TRAnsiting Planets and PlanetesImals Small Telescope; Gillon et al. 2011a; Jehin et al. 2011). The concept of this survey is the intense high-precision photometric monitoring of the transits of southern transiting systems, its goals being (i) to improve the determination of the physical and orbital parameters of the systems, (ii) to assess the presence of undetected objects in these systems through variability studies of the transit parameters, and (iii) to measure or put an upper limit on the very-near-IR thermal emission of the most highly irradiated planets to constrain their atmospheric properties. We complemented the data acquired in the frame of this program for the WASP-43 system by high-precision occultation time-series photometry gathered in the near-IR with the VLT/HAWK-I instrument (Pirard et al. 2004; Casali et al. 2006) in our program 086.C-0222. We present here the results of the analysis of this extensive data set. Section 2 below presents our data. Their analysis is described in Sect. 3. We discuss the acquired results and drawn inferences about the WASP-43 system in Sect. 4. Finally, we give our conclusions in Sect. 5.
2. Data
2.1. TRAPPIST I+z filter transit photometry
We observed 20 transits of WASP-43 b with TRAPPIST and its thermoelectrically-cooled 2k × 2k CCD camera with a field of view of 22′ × 22′ (pixel scale = 0.65′′). All the 20 transits were observed in an Astrodon “I+z” filter that has a transmittance > 90% from 750 nm to beyond 1100 nm2, the red end of the effective bandpass being defined by the spectral response of the CCD. This wide red filter minimizes the effects of limb-darkening and differential atmospheric extinction while maximizing stellar counts. Its effective wavelength for Teff = 4400 ± 200 K is λeff = 843.5 ± 1.2 nm. The mean exposure time was 20 s. The telescope was slightly defocused to minimize pixel-to-pixel effects and to optimize the observational efficiency. We generally keep the positions of the stars on the chip within a box of a few pixels of side to improve the photometric precision of our TRAPPIST time-series, thanks to a “software guiding” system deriving regularly astrometric solutions on the science images and sending pointing corrections to the mount if needed. It could unfortunately not be used for WASP-43, because the star lies in a sky area that is not covered by the used astrometric catalog (GSC1.1). This translated into slow drifts of the stars on the chip, the underlying cause being the imperfection of the telescope polar alignment. The amplitudes of those drifts on the total duration of the runs were ranging between 15 and 85 pixels in the right ascension direction and between 5 and 75 pixels in the declination direction. Table 1 presents the logs of the observations. The first of these 20 transits was presented in H11.
After a standard pre-reduction (bias, dark, flatfield correction), the stellar fluxes were extracted from the images using the IRAF/DAOPHOT3 aperture photometry software (Stetson 1987). For each transit, several sets of reduction parameters were tested, and we kept the one giving the most precise photometry for the stars of similar brightness as WASP-43. After a careful selection of reference stars, differential photometry was then obtained. The resulting light curves are shown in Figs. 1 and 2.
 |
Fig. 1 Left: WASP-43 b transit photometry (12 first TRAPPIST transits) used in this work, binned per 2 min, period-folded on the best-fit transit ephemeris deduced from our global MCMC analysis (see Sect. 3.3), and shifted along the y-axis for clarity. The best-fit baseline+transit models are superimposed on the light curves. The fifth and ninth models (from the top) show some wiggles because of their position-dependent terms. Right: best-fit residuals for each light curve binned per interval of 2 min. |
 |
Fig. 2 Left: WASP-43 b transit photometry (8 last TRAPPIST transits + the 3 Euler transits) used in this work, binned per 2 min, period-folded on the best-fit transit ephemeris deduced from our global MCMC analysis (see Sect. 3.3), and shifted along the y-axis for clarity. The best-fit baseline+transit models are superimposed on the light curves (red = TRAPPIST I + z filter; green = Euler Gunn-r′ filter). The third, ninth and tenth models (from the top) show some wiggles because of their position-dependent terms. Right: best-fit residuals for each light curve binned per interval of 2 min. |
2.2. Euler Gunn-r′ filter transit photometry
Three transits of WASP-43 b were observed in the Gunn-r′ filter (λeff = 620.4 ± 0.5 nm) with the EulerCAM CCD camera at the 1.2-m Euler Swiss telescope, also located at ESO La Silla Observatory. EulerCAM is a nitrogen-cooled 4k × 4k CCD camera with a 15′ × 15′ field of view (pixel scale = 0.23′′). Here too, the telescope was slightly defocused to optimize the photometric precision. The mean exposure time was 85 s. The stars were kept approximately on the same pixels, thanks to a “software guiding” system similar to TRAPPIST’s but using the UCAC3 catalog. The calibration and photometric reduction procedures were similar to the ones performed on the TRAPPIST data. The logs of these Euler observations are shown in Table 1, while the resulting light curves are visible in Fig. 2. Notice that the first of these Euler transits was presented in H11.
2.3. TRAPPIST z′ filter occcultation photometry
Five occultations of WASP-43 b were observed with TRAPPIST in a Sloan z′ filter (λeff = 915.9 ± 0.5 nm). Their logs are presented in Table 1. The mean exposure time was 40 s. The calibration and photometric reduction of these occultation data were similar to the ones of the transits. Figure 3 shows the resulting light curves with their best-fit models.
 |
Fig. 3 Left: WASP-43 b occultation photometry, binned per intervals of 2 min, period-folded on the best-fit transit ephemeris deduced from our global MCMC analysis (see Sect. 3.3), and shifted along the y-axis for clarity. The best-fit baseline+occultation models are superimposed on the light curves (blue = TRAPPIST z′-filter; green = VLT/HAWK-I NB1190 filter; red = VLT/HAWK-I NB2090 filter). Right: same light curves divided by their best-fit baseline models. The corresponding best-fit occultation models are superimposed. |
2.4. VLT/HAWK-I 1.19 and 2.09 μm occultation photometry
We observed two occultations of WASP-43 b with the cryogenic near-IR imager HAWK-I at the ESO Very Large Telescope in our program 086.C-0222. HAWK-I is composed of four Hawaii 2RG 2048 × 2048 pixels detectors (pixel scale = 0.106′′), its total field of view on the sky being 7.5′ × 7.5′. We choose to observe the occultations within the narrow band filters NB2090 (λ = 2.095 μm, width = 0.020 μm) and NB1190 (λ = 1.186 μm, width = 0.020 μm), respectively. The small width of these cosmological filters minimizes the effect of differential extinction. Furthermore, they avoid the largest absorption and emission bands that are present in J and K bands, reducing thus significantly the correlated photometric noise caused by the complex spatial and temporal variations of the background due to the variability of the atmosphere. As this correlated noise is the main precision limit for ground-based near-IR time-series photometry, the use of these two narrow-band filters optimizes the photometric quality of the resulting light curves. This is especially important in the context of the challenging measurement of the emission of exoplanets.
The observation of the first occultation (NB2090 filter) took place on 2010 Dec. 9 from 5h37 to 9h07 UT. Atmospheric conditions were very good, with a stable seeing and extinction. Airmass decreased from 2.1 to 1.05 during the run. Each of the 185 exposures was composed of 17 integrations of 1.7 s each (the minimum integration time allowed for HAWK-I). We choose to do not apply a jitter pattern. Indeed, the background contribution in the photometric aperture is small enough to ensure that the low-frequency variability of the background cannot cause correlated noises with an amplitude larger than a few dozens of ppm in our light curves, making the removal of a background image unnecessary. Furthermore, staying on the same pixels during the whole run allows minimizing the effects of interpixel sensitivity inhomogeneity (i.e. the imperfect flat field). The analysis of HAWK-I calibration frames showed us that the detector is nearly linear up to 10–12 kADU. The peak of the target image was above 10 kADU in the first images, so a slight defocus was applied to keep it below this level during the rest of the run. The mean full-width at half maximum of the stellar point-spread function (PSF) was 7.3 pixels = 0.77′′, its standard deviation for the whole run being 0.57 pixels = 0.06′′. The pointing was carefully selected to avoid cosmetic defects on WASP-43 or on the comparison stars.
The second occultation (NB1190 filter) was observed on 2011 Jan. 9 from 4h57 to 9h27 UT. The seeing varied strongly during the all run (mean value in our images =0.76′′, with a standard deviation =0.19′′, minimum =0.51′′, maximum =1.22′′) while the extinction was stable during the first part of the run and slightly variable during the second part. No defocus was applied, the peak of the target being in the linear part of the detector dynamic in all images. Airmass decreased from 1.37 to 1.03, then increased to 1.13 during the run. Here too, no jitter pattern was applied. Each of the 241 exposures was composed of 17 integrations of 1.7 s.
After a standard calibration of the images (dark-subtraction, flatfield correction), a cosmetic correction was applied. This correction was done independently for each image and based on an automatic detection of the stars followed by a detection of outlier pixels. This latter was based on a comparison of the value of each pixel to the median value of the eight adjacent pixels. For a pixel within a stellar aperture, a detection threshold of 50-σ was used, while it was 5-σ for the background pixels. Outlier pixels had their value replaced by the median value of the adjacent pixels. At this stage, aperture photometry was performed with DAOPHOT for the target and comparison stars, and differential photometry was obtained for WASP-43. Table 1 presents the logs of our HAWK-I observations, while Fig. 3 shows the resulting light curves with their best-fit models.
2.5. Euler/CORALIE spectra and radial velocities
We gathered eight new spectroscopic measurements of WASP-43 with the CORALIE spectrograph mounted on Euler. The spectroscopic measurements were performed between 2011 Feb. 02 and March 12, the integration time being 30 min for all of them. RVs were computed from the calibrated spectra by weighted cross-correlation (Baranne et al. 1996) with a numerical spectral template. They are shown in Table 2. We analyzed these new RVs globally with the RVs presented in H11 and with our eclipse photometry (see Sect. 3.3).
3. Data analysis
Our analysis of the WASP-43 data was divided in two steps. First, we performed individual analyses of the 30 eclipse light curves, determining independently for each light curves the corresponding eclipse and physical parameters. The aim of this first step was searching for potential variability among the eclipse parameters (Sect. 3.2). We then performed a global analysis of the whole data set, including the RVs, with the aim to obtain the strongest constraints on the system parameters (Sect. 3.3).
CORALIE radial-velocity measurements for WASP-43.
3.1. Method and models
Our data analysis was based on the most recent version of our adaptive Markov chain Monte-Carlo (MCMC) algorithm (see Gillon et al. 2010, and references therein). To summarize, MCMC is a Bayesian stochastic simulation algorithm designed to deduce the posterior probability distribution functions (PDFs) for the parameters of a given model (e.g. Gregory 2005; Carlin & Louis 2008). Our implementation of the algorithm assumes as model for the photometric time-series the eclipse model of Mandel & Agol (2002) multiplied by a baseline model aiming to represent the other astrophysical and instrumental mechanisms able to produce photometric variations. For the RVs, the model is based on Keplerian orbits added to a model for the stellar and instrumental variability. Our global model can include any number of planets, transiting or not. For the RVs obtained during a transit, a model of the Rossiter-McLaughlin effect is also available (Giménez 2006). Comparison between two models can be performed based on their Bayes factor, this latter being the product of their prior probability ratio multiplied by their marginal likelihood ratio. The marginal likelihood ratio of two given models is estimated from the difference of their Bayesian Information Criteria (BIC; Schwarz 1978) which are given by the formula: 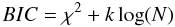 (1)where k is the number of free parameters of the model, N is the number of data points, and χ2 is the smallest chi-square found in the Markov chains. From the BIC derived for two models, the corresponding marginal likelihood ratio is given by e−ΔBIC/2.
(1)where k is the number of free parameters of the model, N is the number of data points, and χ2 is the smallest chi-square found in the Markov chains. From the BIC derived for two models, the corresponding marginal likelihood ratio is given by e−ΔBIC/2.
For each planet, the main parameters that can be randomly perturbed at each step of the Markov chains (called jump parameters) are
-
the planet/star area ratio dF = (Rp/R ⋆ )2, Rp and R ⋆ being respectively the radius of the planet and the star;
the occultation depth(s) (one per filter) dFocc;
the parameter b′ = acosip/R ⋆ which is the transit impact parameter in case of a circular orbit, a and ip being respectively the semi-major axis and inclination of the orbit;
the orbital period P;
the time of minimum light T0 (inferior conjunction);
the two parameters
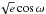 and
and 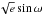 , e being the orbital eccentricity and ω being the argument of periastron;
, e being the orbital eccentricity and ω being the argument of periastron; the transit width (from first to last contact) W;
the parameter
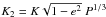 , K being the RV orbital semi-amplitude;
, K being the RV orbital semi-amplitude; the parameters
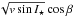 and
and 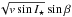 , vsinI ⋆ and β being respectively the projected rotational velocity of the star and the projected angle between the stellar spin axis and the planet’s orbital axis.
, vsinI ⋆ and β being respectively the projected rotational velocity of the star and the projected angle between the stellar spin axis and the planet’s orbital axis.
Uniform or normal prior PDFs can be assumed for the jump and physical parameters of the system. Negative values are not allowed for dF, dFocc, b′, P, T0, W and K2.
Two limb-darkening laws are implemented in our code, quadratic (two parameters) and non-linear (four parameters). For each photometric filter, values and error bars for the limb-darkening coefficients are interpolated in Claret & Bloemen’s tables (2011) at the beginning of the analysis, basing on input values and error bars for the stellar effective temperature Teff, metallicity [Fe/H] and gravity log g. For the quadratic law, the two coefficients u1 and u2 are allowed to float in the MCMC, using as jump parameters not these coefficients themselves but the combinations c1 = 2 × u1 + u2 and c2 = u1 − 2 × u2 to minimize the correlation of the obtained uncertainties (Holman et al. 2006). In this case, the theoretical values and error bars for u1 and u2 deduced from Claret’s tables can be used in normal prior PDFs. In all our analyses, we assumed a quadratic law and let u1 and u2 float under the control of the normal prior PDFs deduced from Claret & Bloemen’s tables. For the non-standard I + z filter, the modes of the normal PDFs for u1 and u2 were taken as the averages of the values interpolated from Claret’s tables for the standard filters Ic and z′, while the errors were computed as the quadratic sums of the errors for these two filters. The prior PDFs deduced for WASP-43 are shown in Table 3. They were computed for Teff = 4400 ± 200 K, log g = 4.5 ± 0.2 and [Fe/H] = −0.05 ± 0.17 (H11).
Prior PDF used in this work for the quadratic limb-darkening coefficients.
At the first step of the MCMC, the timings of the measurements are passed to the BJDTDB time standard, following the recommendation of Eastman et al. (2010) that outlined that the commonly-used BJDUTC time standard is not practical for high-precision timing monitoring as it drifts with the addition of one leap second roughly each year.
At each step of the Markov chains, the stellar density is derived from Kepler’s third law and the jump parameters dF, b′, W, 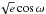 and
and 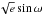 (Seager & Mallen-Ornelas 2003; Winn 2010). Using as input values the resulting stellar density and values for Teff and [Fe/H] drawn from their prior distributions, a modified version of the stellar mass calibration law deduced by Torres et al. (2010) from well-constrained detached binary systems (see Gillon et al. 2011b, for details) is used to derive the stellar mass. The stellar radius is then derived from the stellar density and mass. At this stage, the physical parameters of the planet (mass, radius, semi-major axis) are deduced from the jump parameters and stellar mass and radius. Alternatively, a value and error for the stellar mass can be imposed at the start of the MCMC analysis, In this case, a stellar mass value is drawn from the corresponding normal distribution at each step of the Markov chains, allowing the code to deduce the other physical parameters. We preferred here to use this second option, as WASP-43 was potentially lying at the lower edge of the mass range for which the calibration law of Torres et al. is valid, ~0.6 M⊙.
(Seager & Mallen-Ornelas 2003; Winn 2010). Using as input values the resulting stellar density and values for Teff and [Fe/H] drawn from their prior distributions, a modified version of the stellar mass calibration law deduced by Torres et al. (2010) from well-constrained detached binary systems (see Gillon et al. 2011b, for details) is used to derive the stellar mass. The stellar radius is then derived from the stellar density and mass. At this stage, the physical parameters of the planet (mass, radius, semi-major axis) are deduced from the jump parameters and stellar mass and radius. Alternatively, a value and error for the stellar mass can be imposed at the start of the MCMC analysis, In this case, a stellar mass value is drawn from the corresponding normal distribution at each step of the Markov chains, allowing the code to deduce the other physical parameters. We preferred here to use this second option, as WASP-43 was potentially lying at the lower edge of the mass range for which the calibration law of Torres et al. is valid, ~0.6 M⊙.
If measurements for the rotational period of the star and for its projected rotational velocity are available, they can be used in addition to the stellar radius values deduced at each step of the MCMC to derive a posterior PDF for the inclination of the star (Watson et al. 2010; Gillon et al. 2011b). We did not use this option here despite that the rotational period of the star was determined from WASP photometry to be 15.6 ± 0.4 days (H11), because the VsinI∗ measurement presented by H11 (4.0 ± 0.4 km s-1 ) was presented by these authors as probably affected by a systematic error due to additional broadening of the lines.
Several chains of 100 000 steps were performed for each analysis, their convergences being checked using the statistical test of Gelman & Rubin (1992). After election of the best model for a given light curve, a preliminary MCMC analysis was performed to estimate the need to rescale the photometric errors. The standard deviation of the residuals was compared to the mean photometric errors, and the resulting ratios βw were stored. βw represents the under- or overestimation of the white noise of each measurement. On its side, the red noise present in the light curve (i.e. the inability of our model to represent perfectly the data) was taken into account as described by Gillon et al. (2010), i.e. a scaling factor βr was determined from the standard deviations of the binned and unbinned residuals for different binning intervals ranging from 5 to 120 min, the largest values being kept as βr. At the end, the error bars were multiplied by the correction factor CF = βr × βw. For the RVs, a “jitter” noise could be added quadratically to the error bars after the election of the best model, to equal the mean error with the standard deviation of the best-fit model residuals. In this case, it was unnecessary.
Our MCMC code can model very complex trends for the photometric and RV time-series, with up to 46 parameters for each light curve and 17 parameters for each RV time-series. Our strategy here was first to fit a simple orbital/eclipse model and to analyze the residuals to assess any correlation with the external parameters (PSF width, time, position on the chip, line bisector, etc.), then to use the Bayes factor as indicator to find the optimal baseline function for each time-series, i.e. the model minimizing the number of parameters and the level of correlated noise in the best-fit residuals. For ground-based photometric time-series, we did not use a model simpler than a quadratic polynomial in time, as several effects (color effects, PSF variations, drift on the chip, etc.) can distort slightly the eclipse shape and can thus lead to systematic errors on the deduced transit parameters. This is especially important to include a trend in the baseline model for transit light curve with no out-of-transit data before or after the transit, and/or with a small amount of out-of-transit data. Having a rather small amount of out-of-transit data is quite common for ground-based transit photometry, as the target star is visible under good conditions (low airmass) during a limited duration per night. In such conditions, an eclipse model can have enough degrees of freedom to compensate for a small-amplitude trend in the light curve, leading to an excellent fit but also to biased results and overoptimistic error bars. Allowing the MCMC to “twist” slightly the light curve with a quadratic polynomial in time compensates, at least partially, for this effect.
For the RVs, our minimal baseline model is a scalar Vγ representing the systemic velocity of the star. It is worth noticing that most of the baseline parameters are not jump parameters in the MCMC, they are deduced by least-square minimization from the residuals at each step of the chains, thanks to their linear nature in the baseline functions (Bakos et al. 2009; Gillon et al. 2010).
3.2. Individual analysis of the eclipse time-series
As mentioned above, we first performed an independent analysis of the transits and occultations aiming to elect the optimal model for each light curve and to assess the variability and robustness of the derived parameters. For all these analyses, the orbital period and eccentricity were kept respectively to 0.813475 days and zero (H11), and the normal distribution N(0.58,0.052) M⊙ (H11) was used as prior PDF for the stellar mass. For the transit light curves, the jump parameters were dF, b′, W and T0. For the occultations, the only jump parameter was the occultation depth dFocc, the other system parameters being drawn at each step of the MCMC from normal distributions deduced from the values + errors derived in H11.
Table 1 presents the baseline function selected for each light curve, the derived factors βw, βr, CF, and the standard deviation of the best-fit residuals, unbinned and binned per 120 s. These results allow us to assess the photometric precision of the used instruments. The TRAPPIST data show mean values for βw and βr very close to 1, the I + z data having ⟨ βw ⟩ = 1.03 and ⟨ βr ⟩ = 1.05, while the z′ data have ⟨ βw ⟩ = 0.98 and ⟨ βr ⟩ = 1.11. This suggests that the photometric errors of each measurement are well approximated by a basic error budget (photon, read-out, dark, background, scintillation noises), and that the level of correlated noise in the data is small. Furthermore, we notice that most TRAPPIST light curves are well modeled by the “minimal model”, i.e. the sum of an eclipse model and a quadratic trend in time. Only one TRAPPIST transit light curve requires additional terms in x and y, while one occultation light curve acquired when the moon was close to full requires a linear term in background. The mean photometric errors per 2 min intervals can also be considered as very good for a 60 cm telescope monitoring a V = 12.4 star: 0.11% and 0.15% in the I + z and z′ filters, respectively, which is similar to the mean photometric error of Euler data, 0.12%. Euler data show also small mean values of ⟨ βw ⟩ = 1.27 and ⟨ βr ⟩ = 1.05. Their modeling requires PSF position terms for 2 out of 3 eclipses, despite the good sampling of the PSF and the active guiding system keeping the stars nearly on the same pixels. This could indicate that the flatfields’ quality is perfectible.
For the first HAWKI light curve, taken in the NB2090 filter, we notice that we have to account for a “ramp” effect (the log (t) term) similar to the well-documented sharp variation of the effective gain of the Spitzer/IRAC detector at 8 μm (e.g. Knutson et al. 2008), and also for a dependance of the measured flux with the exact position of the PSF center on the chip. This position effect could be decreased by spreading the flux on more pixels (defocus), but this would also increase the background’s contribution to the noise budget, potentially bringing not only more white noise but also some correlation of the measured counts with the variability of the local thermal structure. The photometric quality reached by these NB2090 data (βr = 1.09, mean error of 360 ppm per 2 min time interval), can be judged as excellent. For the NB1190 HAWKI data, we had to include a dependance in the PSF width in the model. This is not surprising, considering the large variability of the seeing during the run. We also notice for these data that our error budget underestimated strongly the noise of the measurements (βw = 2.22), suggesting an unaccounted noise source. Still, the reached photometric quality remains excellent (βr = 1, mean error of 470 ppm per 2 min time interval).
 |
Fig. 4 Correlation diagrams for the transit parameters deduced from the individual MCMC analysis of the 23 transit light curves. Top left: transit depth vs. transit impact parameter. Top right: transit duration vs. transit impact parameter. Bottom left: transit duration vs. transit depth. Bottom right: TTV (observed minus calculated transit timing) vs. transit duration. The filled black and open red symbols correspond, respectively, to the TRAPPIST and Euler light curves. |
 |
Fig. 5 Top: observed minus calculated transit timings obtained from the individual analysis of the transit light curves as a function of the transit epoch. The filled black and open red symbols correspond, respectively, to the TRAPPIST and Euler light curves. Bottom: same but deduced from the global analysis of all transits. |
Table 4 presents for each eclipse light curve the values and errors deduced for the jump parameters. Several points can be noticed.
-
The emission of the planet is clearly (10-σ) detected at 2.09 μm. At 1.19 μm, it is barely detected (~2.3-σ). It is not detected in any of the z′-band light curves.
-
The transit shape parameters b′, W, and dF, show scatters slightly larger than their average error, the corresponding ratio being, respectively, 1.24, 1.26, and 1.54. Furthermore, these parameters show significant correlation, as can be seen in Fig. 4.
-
Fitting a transit ephemeris by linear regression with the measured transit timings shown in Table 4, we obtained T(N) = 2 455 528.868289( ±0.000072) + N × 0.81347728(±0.00000060) BJDTDB. Table 4 shows (last column) the resulting transit timing residuals (observed minus computed, O–C). Figure 5 (upper panel) shows them as a function of the transit epochs. The scatter of these timing residuals is 2.1 times larger than the mean error, 18 s. No clear pattern is visible in the O–C diagram.
The apparent variability of the four transit parameters is present in both TRAPPIST and Euler results. The correlation of the derived transit parameters is not consistent with actual variations of these parameters and favors biases from instrumental and/or astrophysical origin. This apparent variability of the transit parameters could be explained by the variability of the star itself. Indeed, WASP-43 is a spotted star (H11), and occulted spots (and faculae) can alter the observed transit shape and bias the measured transit parameters (e.g. Huber et al. 2010; Berta et al. 2011). We do not detect clear spot signatures in our light curves, but our photometric precision could be not high enough to detect such low-amplitude structures, so we do not reject this hypothesis. On their side, unocculted spots should have a negligible impact on the measured transit depths, considering the low amplitude of the rotational photometric modulation detected in WASP data (6 ± 1 mmag). Still, they could alter the slope of the photometric baseline and make it more complex. We represent this baseline as an analytical function of several external parameters in our MCMC simulations, but the unavoidable inaccuracy of the chosen baseline model can also bias the derived results. As described in Sect. 2.1, no pointing corrections were applied during the TRAPPIST runs because of a stellar catalog problem. Even if the resulting drifts did not introduce clear correlations of the measured fluxes with PSF positions, they could have slightly affected the shape of the transits. These considerations reinforce the interest of performing global analysis of extensive data sets (i.e. many eclipses) in order to minimize systematic errors and to reach high accuracies on the derived parameters.
3.3. Global analysis of photometry and radial velocities
The global MCMC analysis of our data set was divided in three steps. For each step of the analysis, the MCMC jump parameters were dF, W, b′, T0, P, 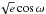 ,
, 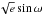 , three dFocc (for the z′, NB1190, and NB2090 filters), K2, and the limb-darkening coefficients c1 and c2 for the I + z and Gunn-r′ filters. No model for the Rossiter-McLaughlin was included in the global model, as no RV was obtained at the transit phase. For each light curve, we assumed the same baseline model than for the individual analysis. The assumed baseline for the RVs was a simple scalar (systemic velocity Vγ).
, three dFocc (for the z′, NB1190, and NB2090 filters), K2, and the limb-darkening coefficients c1 and c2 for the I + z and Gunn-r′ filters. No model for the Rossiter-McLaughlin was included in the global model, as no RV was obtained at the transit phase. For each light curve, we assumed the same baseline model than for the individual analysis. The assumed baseline for the RVs was a simple scalar (systemic velocity Vγ).
In a first step, we performed a chain of 100 000 steps with the aim to redetermine the scaling factors of the photometric errors. The deduced values are shown in Table 1. It can be noticed that the mean ⟨ βr ⟩ for the 20 transits observed by TRAPPIST in I + z filter is now 1.52, for 1.05 after the individual analysis of the lightcurves. We notice the same tendency for the Euler Gunn-r′ transits: ⟨ βr ⟩ goes up from 1.05 to 1.42. Considering the apparent variability of the transit parameters deduced from the individual analysis of the light curves and their correlations, our interpretation of this increase of the ⟨ βr ⟩ is that a part of the correlated noise (from astrophysical source or not) of a transit light curve can be “swallowed” in the transit+baseline model, leading to a good fit in terms of merit function but also to biased derived parameters. By relying on the assumption that all transits share the same profile, the global analysis allows to better separate the actual transit signal from the correlated noises of similar frequencies, leading to larger ⟨ βr ⟩ values. It is also worth noticing that the ⟨ βr ⟩ for the transits, 1.50, is larger than the one for the occultations, 1.12, which is consistent with the crossing of spots by the planet during transit, but can also be explained by the much larger number of transits than occultations.
In a second step, we used the updated error scaling factors and performed a MCMC of 100 000 steps to derive the marginalized PDF for the stellar density ρ ⋆ . This PDF was used as input to interpolate stellar tracks. As in Hebb et al. (2009), we used 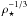 , mostly for practical reasons. Other inputs were the stellar effective and metallicity derived by H11, Teff = 4400 ± 200 K and [Fe/H] = −0.05 ± 0.17 dex. Those parameters were assumed distributed as a Gaussian. For each
, mostly for practical reasons. Other inputs were the stellar effective and metallicity derived by H11, Teff = 4400 ± 200 K and [Fe/H] = −0.05 ± 0.17 dex. Those parameters were assumed distributed as a Gaussian. For each 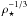 value from the MCMC, a random Gaussian value was drawn for stellar parameters. That point was placed among the Geneva stellar evolution tracks (Mowlavi et al. 2012) that are available in a grid fine enough to allow an MCMC to wander without computational systematic effects; a mass and age were interpolated. If the point fell off the tracks, it was discarded. Because of the way stars behave at these small masses, within the (
value from the MCMC, a random Gaussian value was drawn for stellar parameters. That point was placed among the Geneva stellar evolution tracks (Mowlavi et al. 2012) that are available in a grid fine enough to allow an MCMC to wander without computational systematic effects; a mass and age were interpolated. If the point fell off the tracks, it was discarded. Because of the way stars behave at these small masses, within the (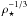 , Teff, [Fe/H]) space, the parameter space over which the tracks were interpolated covered stellar ages well above a Hubble time. A restriction on the age was therefore added. Only taking ages <12 Gyr, we obtained the distribution as shown in Fig. 6, refining the stellar parameters to Teff = 4520 ± 120 K and [Fe/H] = −0.01 ± 0.12 dex. The stellar mass is estimated to M ⋆ = 0.717 ± 0.025 M⊙. The output distribution is very close to Gaussian as displayed in Fig. 6. In addition the output
, Teff, [Fe/H]) space, the parameter space over which the tracks were interpolated covered stellar ages well above a Hubble time. A restriction on the age was therefore added. Only taking ages <12 Gyr, we obtained the distribution as shown in Fig. 6, refining the stellar parameters to Teff = 4520 ± 120 K and [Fe/H] = −0.01 ± 0.12 dex. The stellar mass is estimated to M ⋆ = 0.717 ± 0.025 M⊙. The output distribution is very close to Gaussian as displayed in Fig. 6. In addition the output 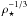 distribution has not been affected. Thus, our strongly improved precision on the stellar density combined with a constraint on the age (to be younger than a Hubble time) allows us to reject the main stellar solution proposed by H11 (M ⋆ = 0.58 ± 0.05 M⊙). Because the allowed (
distribution has not been affected. Thus, our strongly improved precision on the stellar density combined with a constraint on the age (to be younger than a Hubble time) allows us to reject the main stellar solution proposed by H11 (M ⋆ = 0.58 ± 0.05 M⊙). Because the allowed (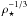 , Teff, [Fe/H]) space within the tracks still covers quite a large area, it is impossible at the moment to constrain the stellar age. The process is described in Triaud (2011, Ph.D. Thesis).
, Teff, [Fe/H]) space within the tracks still covers quite a large area, it is impossible at the moment to constrain the stellar age. The process is described in Triaud (2011, Ph.D. Thesis).
 |
Fig. 6 Main panel: modifield Herztsprung-Russell diagram showing the posterior PDF of |
We then performed a third MCMC step, using as prior distributions for M ⋆ , Teff, and [Fe/H], the normal distributions matching the results of our stellar modeling, i.e. N(0.717,0.0252) M⊙, N(4520,1202) K, and N( − 0.01,0.122) dex, respectively. The best-fit photometry and RV models are shown respectively in Figs. 7 and 8, while the derived parameters and 1-σ error bars are shown in Table 5.
 |
Fig. 7 Left: TRAPPIST I + z (top) and Euler Gunn-r′ (bottom) transit photometry period-folded on the best-fit transit ephemeris from the global MCMC analysis, corrected for the baseline and binned per 2 min intervals, with the best-fit transit models over-imposed. Right: same for the occultation photometry obtained by TRAPPIST in z′ filter (top), and by VLT/HAWK-I in NB1190 (middle) and NB2090 (bottom) filters, except that the data points are binned per 5 min intervals. |
Median and 1-σ limits of the posterior marginalized PDFs obtained for the WASP-43 system derived from our global MCMC analysis.
Global analysis of the 23 transits with free timings
As a complement to our global analysis of the whole data set, we performed a global analysis of the 23 transit light curves alone. The goal here was to benefit from the strong constraint brought on the transit shape by the 23 transits to derive more accurate transit timings and to assess the periodicity of the transit. In this analysis, we kept fixed the parameters T0 and P to the values shown in Table 5, and we added a timing offset as jump parameter for each transit. The orbit was assumed to be circular. The other jump parameters were dF, W, b′, and the limb-darkening coefficients c1 and c2 for both filters. The resulting transit timings and their errors are shown in Table 6. Fitting a transit ephemeris by linear regression with these new derived transit timings, we obtained T(N) = 2 455 528.868227( ± 0.000078) + N × 0.81347764( ± 0.00000065) BJDTDB. Table 6 shows (last column) the resulting transit timing residuals (observed minus computed, O–C). Figure 5 (lower panel) shows them as a function of the transit epochs. The scatter of these timing residuals is now 1.8 times larger than the mean error, 19 s. Comparing the errors on the timings derived from individual and global analysis of the transit photometry, one can notice that the better constraint on the transit shape for the global analysis improves the error of a few timings, but that most of them have a slightly larger error because of the better separation of the actual transit signal from the red noise (see above).
Median and 1-σ errors of the posterior PDFs deduced for the timings of the transits from their global analysis.
 |
Fig. 8 Euler/CORALIE RV measurements period-folded on the best-fit transit ephemeris from the global MCMC analysis, corrected for the systemic RV, with the best-fit orbital model overimposed. |
 |
Fig. 9 Planetary radii as a function of incident flux. WASP-43 b is shown as a black square. gray filled circles are Kepler planetary candidates (see Demory & Seager 2011). Transiting giant planets previously published, and mostly from ground-based surveys, are shown as gray triangles. The relevant parameters Rp, Rs, Teff and a have been drawn from http://www.inscience.ch/transits on August 29, 2011. |
4. Discussion
4.1. The physical parameters of WASP-43 b
Comparing our results for the WASP-43 system with the ones presented in H11, we notice that our derived parameters agree well with the second solution mentioned in H11, while being significantly more precise. WASP-43 b is thus a Jupiter-size planet, twice more massive than our Jupiter, orbiting at only ~0.015 AU from a 0.72 M⊙ main-sequence K-dwarf. Despite having the smallest orbital distance among the hot Jupiters, WASP-43 b is far from being the most irradiated known exoplanet, because of the small size and temperature of its host star. Assuming a solar-twin host star, its incident flux ~9.6 × 108 erg s-1 cm-2 would correspond to a P = 2.63 d orbit (a = 0.0374 AU), i.e. to a rather typical hot Jupiter. With a radius of 1.04 RJup, WASP-43 b lies toward the bottom of the envelope described by the published planets in the Rp vs. incident flux plane (Fig. 9). Taking into account its level of irradiation, the high density of the planet favors an old age and a massive core under the planetary structure models of Fortney et al. (2010). Our results are consistent with a circular orbit, and we can put a 3-σ upper limit < 0.03 to the orbital eccentricity. Despite its very short period, WASP-43 b has a semi-major axis approximatively twice larger than its Roche limit aR, which is typical for hot Jupiters (Ford & Rasio 2006; Mastumura et al. 2010). As noted by these authors, the inner edge of the distribution of most hot Jupiters at ~2 aR favors migrational mechanisms based on the scattering of planets on much wider orbit and the subsequent tidal shortening and circularization of their orbits. Thus, WASP-43 b does not appear to be a planet exceptionally close to its final tidal disruption, unlike WASP-19 b that orbits at only 1.2 aR (Hellier et al. 2011a).
4.2. The atmospheric properties of WASP-43 b
We have modeled the atmosphere of WASP-43 b using the methods described in Fortney et al. (2005, 2008) and Fortney & Marley (2007). In Fig. 10, we compare the planet-to-star flux ratio data to three atmosphere models. The coldest model (orange) uses a dayside incident flux decreased by 1/2 to simulate the loss of half of the absorbed flux to the night side of the planet. Clearly the planet is much warmer than this model. In blue and red are two models where the dayside incident flux is increased by a factor of 4/3 to simulate zero redistribution of absorbed flux (see, e.g., Hansen 2008). The red model features a dayside temperature inversion due to the strong optical opacity of TiO and VO gases (Hubeny et al. 2003; Fortney et al. 2006). The blue model is run in the same manner as the red model, but TiO and VO opacity are removed.
The blue and red models are constructed to maximize the emission from the dayside of the planet. Figure 10 shows that only such bright models could credibly match the data points. While a dayside with no temperature inversion is slightly favored by the 1.2 μm data point, it is difficult to come to a firm conclusion. Day-side emission measurements from Warm Spitzer will help to better constrain the atmosphere as well. They will also allow getting an even smaller upper-limit on the orbital eccentricity.
Fortney et al. model fits to near infrared photometry of other transiting planets (e.g., Croll et al. 2010) have generally favored inefficient temperature homogenization between the day and night hemispheres, although the warm dayside of WASP-43 b appears to be at the most inefficient end of this continuum. The apparent effeciency of temperature homogenization is expected to vary with wavelength. In particular, near infrared bands, at minima in water vapor opacity, are generally expected to probe deeper into atmospheres than the Spitzer bandpasses.
 |
Fig. 10 Model planet-to-star flux ratios compare to the three data points. The data are green diamonds with 1 − σ error bars shown. The orange model assumes planet-wide redistribution of absorbed flux. The red and blue models assume no redistribution of absorbed flux, to maximize the day-side temperature. The red model includes gaseous TiO and VO and has a temperature inversion. (See the figure inset.) The blue and orange models have TiO and VO opacity removed, and do not have a temperature inversion. For each model, filled circles are model fluxes averaged over each bandpass. The data slightly favor a model with no day-side temperature inversion. |
4.3. Transit timings
Dynamical constraints can be placed on short orbits companion planets from the 23 transits obtained in this study. The linear fit to the transit timings described above yields a reduced χ2 of 4.6 and the rms of its residuals is 38 s. Two transits (epochs 140 and 152) have a O–C different from zero at the ~4-σ level. The most plausible explanation for the significant scatter observed in the transit timings is systematic errors on the derived timings due to the influence of correlated noise. Another potential explanation is asymmetries in the transit light curves caused by the crossing of one or several star spots by the planet. In such cases, the fitted transit profile is shifted with time, producing timing variations.
We also explored the detectability domain of a second planet in the WASP-43 system. To this end, we followed Agol et al. (2005) and used the Mercury n-body integrator package (Chambers 1999). We simulated 3-body systems including a second companion with orbital periods ranging between 1.3 and 50 days, masses from 0.1 M⊕ to 2.0 MJup and an orbital eccentricities of ec = 0 and ec = 0.05. For each simulation, we computed the rms of the computed transits timings variations. The results are shown in Fig. 11 where the computed 1-σ (red) and 3-σ (black) detection thresholds are plotted for each point in the mass-period plane. We also added RV detectability threshold curves based on 5 (solid), 10 (dash) and 15 (dot) m s-1 semi-amplitudes (K).
Based on the present set of timings, the timings variations caused by a 5 Earth mass companion in 2:1 resonance would have been detected with 3-σ confidence, while unseen with radial velocities alone.
 |
Fig. 11 Detectivity domain for a putative WASP-43 c planet, assuming ec = 0 (black) and ec = 0.05 (red). The solid curves delimit the mass-period region where planets yield maximum TTV on WASP-43 b above 114 s (3-σ detection based on the present data). The dotted curves show the 1-σ threshold. Nearly horizontal solid, dashed and dotted lines shows RV detection limits for RV semi-amplitude K = 5, 10 and 15 m s-1 respectively. |
5. Conclusions
In this work we have presented 23 transit light curves and 7 occultation light curves for the ultra-short period planet WASP-43 b. We have also presented 8 new measurements of the radial velocity of the star. Thanks to this extensive data set, we have significantly improved the parameters of the system. Notably, our strongly improved precision on the stellar density (2.41 ± 0.08 ρ⊙) combined with a very reasonable constraint on its age (to be younger than a Hubble time) allowed us to break the degeneracy of the stellar solution mentioned by H11. The resulting stellar mass and size are 0.717 ± 0.025 M⊙ and 0.667 ± 0.011 R⊙. Our deduced physical parameters for the planet are 2.034 ± 0.052 MJup and 1.036 ± 0.019 RJup. Taking into account its level of irradiation, the high density of the planet favors an old age and a massive core. Our deduced orbital eccentricity, 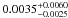 , is consistent with a fully circularized orbit.
, is consistent with a fully circularized orbit.
The parameters deduced from the individual analysis of the 23 transit light curves show some extra scatter that we attribute to the correlated noise of our data and, possibly, to the crossing of spots during some transits. This conclusion is based on the correlation observed among the transit parameters. These results reinforce the interest of performing global analysis of extensive data sets in order to minimize systematic errors and to reach high accuracies on the derived parameters.
We detected the emission of the planet at 2.09 μm at better than 11-σ, the deduced occultation depth being 1560 ± 140 ppm. Our detection of the occultation at 1.19 μm is marginal (790 ± 320 ppm) and more observations would be needed to confirm it. We place a 3-σ upper limit of 850 ppm on the depth of the occultation at ~0.9 μm. Together, these results strongly favor a poor redistribution of the heat from the dayside to the nightside of the planet, and marginally favor a model with no day-side temperature inversion.
Online material
WASP-43 b photometric eclipse time-series used in this work.
Median and 1-σ errors of the posterior PDFs deduced for the jump parameters from the individual analysis of the eclipse light curves.
Acknowledgments
TRAPPIST is a project funded by the Belgian Fund for Scientific Research (Fond National de la Recherche Scientifique, F.R.S-FNRS) under grant FRFC 2.5.594.09.F, with the participation of the Swiss National Science Fundation (SNF). M. Gillon and E. Jehin are FNRS Research Associates. We are grateful to ESO La Silla and Paranal staffs for their continuous support. We thank the anonymous referee for his valuable suggestions.
References
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, D. R., Gillon, M., Maxted, P., et al. 2010, A&A, 513, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bakos, G. Á., Torres, G., Pál, A., et al. 2009, ApJ, 710, 1724 [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barker, A. J., & Ogilvie, G. I. 2009, MNRAS, 395, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, Z. K., Charbonneau, D., Bean, J., et al. 2011, ApJ, 736, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, D. J. A., Collier Cameron, A., Hall, C., et al. 2011, MNRAS, 415, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Carlin, B. P., & Louis, T. A. 2008, Bayesian Methods for Data Analysis, third edition (Chapman & Hall/CRC) [Google Scholar]
- Casali, M., Pirard, J.-F., Kissler-Patig, M., et al. 2006, SPIE, 6269, 29 [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croll, B., Jayawardhana, R., Fortney, J. J., Lafrenière, D., & Albert, L. 2010, ApJ, 718, 920 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, G., Durisen, R. H., & Lissauer, J. J. 2010, Exoplanets, ed. S. Seager (University of Arizona Press), 319 [Google Scholar]
- Demory, B.-O., & Seager, S. 2011, ApJS, 197, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B., & Rasio, F. A. 2006, ApJ, 638, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., & Marley, M. S. 2007, ApJ, 666, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., Lodders, K., Saumon, D., & Freedman, R. S. 2005, ApJ, 627, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Saumon, D., Marley, M. S., Lodders, K., & Freedman, R. S. 2006, ApJ, 642, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., & Rubin, D. 1992, Statist. Sci., 7, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Aigrain, S., Pollaco, D. L., et al. 2010, MNRAS, 404, L14 [Google Scholar]
- Gillon, M., Lanotte, A. A., Barman, T., et al. 2010, A&A, 511, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Jehin, E., Magain, P., et al. 2011a, Detection and Dynamics of Transiting Exoplanets, Proceedings of OHP Colloquium, 23–27 August 2010, ed. F. Bouchy, R. F. Diaz, & C. Moutou (Platypus Press) [Google Scholar]
- Gillon, M., Doyle, A., Maxted, P., et al. 2011b, A&A, 533, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giménez, A. 2006, ApJ, 650, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C. 2005, Bayesian Logical Data Analysis for the Physical Sciences (Cambridge University Press) [Google Scholar]
- Gu, P.-G., Lin, D. N. C., & Bodenheimer, P. H. 2003, ApJ, 588, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S. 2008, ApJS, 179, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Hebb, L., Collier Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Hebb, L., Collier Cameron, A., Triaud, A. H. M. J., et al. 2010, ApJ, 708, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2009, Nature, 460, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2011a, ApJ, 730, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2011b, A&A, 535, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holman, M. J., Winn, J. N., Latham, D. W., et al. 2006, ApJ, 652, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., Burrows, A., & Sudarsky, D. 2003, ApJ, 594, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, H. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2010, A&A, 514, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, B., Barnes, R., & Greenberg, R. 2009, ApJ, 698, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Johnson, J. A., Gazak, J. Z., Apps, K., et al. 2012, AJ, 143, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2008, ApJ, 673, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & Ida, S. 2010, Exoplanets, ed. S. Seager (University of Arizona Press), 347 [Google Scholar]
- Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, 181 [Google Scholar]
- Mastumura, S., Peale, S. J., & Rasio, F. R. 2010, ApJ, 725, 1995 [NASA ADS] [CrossRef] [Google Scholar]
- Mowlavi, N., Eggenberger, P., Meynet, G., et al. 2012, A&A, 541, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naoz, S., Farr, W. M., Lithwick, Y., et al. 2011, Nature, 473, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Nymeyer, S., Harrington, J., Hardy, R., et al. 2011, ApJ, 742, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Pirard, J.-F., Kissler-Patig, M., Moorwood, A., et al. 2004, SPIE, 5492, 510 [Google Scholar]
- Schneider, J. 2011, http://exoplanet.eu/catalog-all.php [Google Scholar]
- Schwarz, G. E. 1978, Annals of Statistics, 6, 461 [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 111 [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Watson, C. A., Littlefair, S. P., Collier Cameron, A., et al. 2010, MNRAS, 408, 1606 [NASA ADS] [CrossRef] [Google Scholar]
- Triaud, A. H. M. J. 2011, Ph.D. Thesis, Geneva University, No. Sc. 4342, http://archive-ouverte.unige.ch/unige:18065 [Google Scholar]
- Triaud, A. H. M. J., Collier Cameron, A., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N. 2010, Exoplanets, ed. S. Seager (University of Arizona Press), 55 [Google Scholar]
- Wu, Y., & Lithwick, Y. 2011, ApJ, 735, 109 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Median and 1-σ limits of the posterior marginalized PDFs obtained for the WASP-43 system derived from our global MCMC analysis.
Median and 1-σ errors of the posterior PDFs deduced for the timings of the transits from their global analysis.
Median and 1-σ errors of the posterior PDFs deduced for the jump parameters from the individual analysis of the eclipse light curves.
All Figures
 |
Fig. 1 Left: WASP-43 b transit photometry (12 first TRAPPIST transits) used in this work, binned per 2 min, period-folded on the best-fit transit ephemeris deduced from our global MCMC analysis (see Sect. 3.3), and shifted along the y-axis for clarity. The best-fit baseline+transit models are superimposed on the light curves. The fifth and ninth models (from the top) show some wiggles because of their position-dependent terms. Right: best-fit residuals for each light curve binned per interval of 2 min. |
| In the text | |
 |
Fig. 2 Left: WASP-43 b transit photometry (8 last TRAPPIST transits + the 3 Euler transits) used in this work, binned per 2 min, period-folded on the best-fit transit ephemeris deduced from our global MCMC analysis (see Sect. 3.3), and shifted along the y-axis for clarity. The best-fit baseline+transit models are superimposed on the light curves (red = TRAPPIST I + z filter; green = Euler Gunn-r′ filter). The third, ninth and tenth models (from the top) show some wiggles because of their position-dependent terms. Right: best-fit residuals for each light curve binned per interval of 2 min. |
| In the text | |
 |
Fig. 3 Left: WASP-43 b occultation photometry, binned per intervals of 2 min, period-folded on the best-fit transit ephemeris deduced from our global MCMC analysis (see Sect. 3.3), and shifted along the y-axis for clarity. The best-fit baseline+occultation models are superimposed on the light curves (blue = TRAPPIST z′-filter; green = VLT/HAWK-I NB1190 filter; red = VLT/HAWK-I NB2090 filter). Right: same light curves divided by their best-fit baseline models. The corresponding best-fit occultation models are superimposed. |
| In the text | |
 |
Fig. 4 Correlation diagrams for the transit parameters deduced from the individual MCMC analysis of the 23 transit light curves. Top left: transit depth vs. transit impact parameter. Top right: transit duration vs. transit impact parameter. Bottom left: transit duration vs. transit depth. Bottom right: TTV (observed minus calculated transit timing) vs. transit duration. The filled black and open red symbols correspond, respectively, to the TRAPPIST and Euler light curves. |
| In the text | |
 |
Fig. 5 Top: observed minus calculated transit timings obtained from the individual analysis of the transit light curves as a function of the transit epoch. The filled black and open red symbols correspond, respectively, to the TRAPPIST and Euler light curves. Bottom: same but deduced from the global analysis of all transits. |
| In the text | |
 |
Fig. 6 Main panel: modifield Herztsprung-Russell diagram showing the posterior PDF of |
| In the text | |
 |
Fig. 7 Left: TRAPPIST I + z (top) and Euler Gunn-r′ (bottom) transit photometry period-folded on the best-fit transit ephemeris from the global MCMC analysis, corrected for the baseline and binned per 2 min intervals, with the best-fit transit models over-imposed. Right: same for the occultation photometry obtained by TRAPPIST in z′ filter (top), and by VLT/HAWK-I in NB1190 (middle) and NB2090 (bottom) filters, except that the data points are binned per 5 min intervals. |
| In the text | |
 |
Fig. 8 Euler/CORALIE RV measurements period-folded on the best-fit transit ephemeris from the global MCMC analysis, corrected for the systemic RV, with the best-fit orbital model overimposed. |
| In the text | |
 |
Fig. 9 Planetary radii as a function of incident flux. WASP-43 b is shown as a black square. gray filled circles are Kepler planetary candidates (see Demory & Seager 2011). Transiting giant planets previously published, and mostly from ground-based surveys, are shown as gray triangles. The relevant parameters Rp, Rs, Teff and a have been drawn from http://www.inscience.ch/transits on August 29, 2011. |
| In the text | |
 |
Fig. 10 Model planet-to-star flux ratios compare to the three data points. The data are green diamonds with 1 − σ error bars shown. The orange model assumes planet-wide redistribution of absorbed flux. The red and blue models assume no redistribution of absorbed flux, to maximize the day-side temperature. The red model includes gaseous TiO and VO and has a temperature inversion. (See the figure inset.) The blue and orange models have TiO and VO opacity removed, and do not have a temperature inversion. For each model, filled circles are model fluxes averaged over each bandpass. The data slightly favor a model with no day-side temperature inversion. |
| In the text | |
 |
Fig. 11 Detectivity domain for a putative WASP-43 c planet, assuming ec = 0 (black) and ec = 0.05 (red). The solid curves delimit the mass-period region where planets yield maximum TTV on WASP-43 b above 114 s (3-σ detection based on the present data). The dotted curves show the 1-σ threshold. Nearly horizontal solid, dashed and dotted lines shows RV detection limits for RV semi-amplitude K = 5, 10 and 15 m s-1 respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.