| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 26 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201118751 | |
| Published online | 13 June 2012 | |
Accurate and homogeneous abundance patterns in solar-type stars of the solar neighbourhood: a chemo-chronological analysis⋆
1
INPE, Divisão de Astrofísica, Av. dos Astronautas,
1758 São José dos Campos,
12201-970,
Brazil
e-mail: dasilvr2@gmail.com
2
UFRJ, Observatório do Valongo, Ladeira do Pedro Antônio 43, 20080-090
Rio de Janeiro,
Brazil
3
Observatório Nacional, Rua Gal. José Cristino 77, 20921-400
São Cristovão, Rio de Janeiro,
Brazil
Received:
28
December
2011
Accepted:
22
April
2012
Aims. We report the derivation of abundances of C, Na, Mg, Si, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Sr, Y, Zr, Ba, Ce, Nd, and Sm in a sample of 25 solar-type stars of the solar neighbourhood, correlating the abundances with the stellar ages, kinematics, and orbital parameters.
Methods. The spectroscopic analysis, based on data of high resolution and high signal-to-noise ratio, was differential to the Sun and applied to atomic line equivalent widths supplemented by the spectral synthesis of C and C2 features. We also performed a statistical study by using the method of tree clustering analysis, searching for groups of stars sharing similar elemental abundance patterns. We derived the stellar parameters from various criteria, with average errors of 30 K, 0.13 dex, and 0.05 dex, respectively, for Teff, log g, and [Fe/H]. The average error of the [X/Fe] abundance ratios is 0.06 dex. Ages were derived from theoretical HR diagrams and membership of the stars in known kinematical moving groups.
Results. We identified four stellar groups: one having, on average, over-solar abundances (⟨[X/H]⟩ = +0.26 dex), another with under-solar abundances (⟨ [X/H] ⟩ = −0.24 dex), and two with intermediate values (⟨ [X/H] ⟩ = −0.06 and +0.06 dex) but with distinct chemical patterns. Stars sharing solar metallicity, age, and Galactic orbit possibly have non-solar abundance ratios, a possible effect either of chemical heterogeneity in their natal clouds or migration. A trend of [Cu/Fe] with [Ba/Fe] seems to exist, in agreement with previous claims in the literature, and maybe also of [Sm/Fe] with [Ba/Fe]. No such correlation involving C, Na, Mn, and Zn is observed. The [X/Fe] ratios of various elements show significant correlations with age. [Mg/Fe], [Sc/Fe], and [Ti/Fe] increase with age. [Mn/Fe] and [Cu/Fe] display a more complex behaviour, first increasing towards younger stars up to the solar age, and then decreasing, a result we interpret as possibly related to time-varying yields of SN Ia and the weak s-process in massive stars. The steepest negative age relation is due to [Ba/Fe], but only for stars younger than the Sun, and a similar though less significant behaviour is seen for Zr, Ce, and Nd. [Sr/Fe] and [Y/Fe] show a linearly increasing trend towards younger stars. The [Cu/Ba] and [Sm/Ba] therefore decrease for younger stars. We found that [Ba/Mg], [Ba/Zn], and [Sr,Y,Ba/Sm] increase but only for stars younger than the Sun, whereas the [Sr/Mg], [Y/Mg], [Sr/Zn], and [Y/Zn] ratios increase linearly towards younger stars over the whole age range.
Key words: stars: solar-type / stars: fundamental parameters / stars: abundances
© ESO, 2012
1. Introduction
The Galactic chemical and dynamical history can be well framed by a series of average “laws” (see e.g. Edvardsson et al. 1993; McWilliam 1997), namely: the age-metallicity relation (which in principle is accessible by more than one chemical element), the [element/element] abundance ratios, the stellar metallicity frequency distribution, the Galactic metallicity gradient, and the star formation history, besides their mutual relationships as a function of space and time. The success of the Galactic chemical evolution models is to be judged by their ability to reproduce these constraints (see Allen & Porto de Mello 2011).
In recent years there has been growing recognition that, even though such average laws are meaningful and fundamental, there may be considerable underlying complexity in the real Galaxy that has gone at least partly unappreciated. In the present age of very large spectroscopic databases and precise abundances for numerous chemical elements, a successful model must harmonise stellar evolution inputs such as the initial mass function, the star-formation rate, and mass loss processes, connecting these to the specific properties of Galactic components, and a large diversity of spatial and temporal structures, differing timescales for stellar nucleosynthetic yields and their sensitivities to differing metallicities.
During the evolution of the Galactic disc, nucleosynthesis in successive generations of stars occurs together with dynamical interactions with the interstellar gas. The states of the Galaxy in past periods of its evolution are still preserved in the abundance distributions of solar-type stars, which constitute an ideal population to study the chemical evolution. These stars have an age dispersion comparable to the age of the Galaxy. They are similar to the Sun in many physical parameters, allowing the application of a differential analysis and the consequent minimisation of theoretical shortcomings of atmospheric models and systematic errors. In addition, their chemical composition does not change in consequence of the mixing processes in their surfaces, which means that the present abundance of a given element is the same as in the time of their formation (an exception are the abundances of Li, Be, and B, but these elements are not considered in this work). Therefore, the chemical abundance of solar-type stars, combined with kinematical, orbital, and evolutionary parameters (mass and age), provide a powerful tool to investigate the chemical and dynamical evolution of the Galaxy.
Over the last decade, several works have analysed the composition of disc dwarf stars of spectral types F and G (Chen et al. 2000; Reddy et al. 2003; Bensby et al. 2005; Chen et al. 2008; Neves et al. 2009). The metallicity ranges have become wider, the number of stars and elements studied has become larger, stars with and without detected planets have been compared, and the chemical distinction between thin and thick stellar population has been refined. Here we specifically ask, when regarded in as high a level of detail as possible with present techniques, to what extent the relative abundances of chemical elements can be traced as a function of age, the nature of underlying nucleosynthetic processes, and whether these properties can be statistically grouped for the nearby solar-type stars, defining “snapshots” relevant to the chemo-chronological evolution of the Galaxy.
In this work we present a multi-elemental spectroscopic analysis of a sample of 25 solar-type stars in the solar neighbourhood, all members of the thin disc stellar population (excepting one star in the transition between thin and thick discs). We have performed the determination of atmospheric parameters (effective temperature, metallicity, surface gravity, and micro-turbulence velocity), mass, age, kinematical and orbital parameters, and elemental abundances based on equivalent widths or spectral synthesis. Three different criteria were used to pin down the stellar effective temperatures, and they showed excellent internal consistency. We have also performed a statistical study of our abundance results using the method of tree clustering analysis (Everitt et al. 2001), through which we looked for stellar groups that share similar abundances in [X/H], where X represents one given element. Four groups were identified and then analysed in terms of their relations with [Fe/H], age, [Ba/Fe], kinematics, and Galactic orbits.
Despite the small range in metallicity, our sample stars cover a broad range in age, and possible trends with age were traced. The relation between [X/Fe] and [Ba/Fe] for a few elements has also been considered given the Ba-rich nature of some of our stars. In particular, we investigated previous correlations with Na and Cu suggested by Castro et al. (1999). Finally, considering the results of Rocha-Pinto et al. (2006) that, on average, metal-poor and old stars tend to have larger |Rm − R⊙| (where Rm is the mean orbital distance from the Galactic centre), we have looked for any relations involving the stellar groups of the clustering analysis and the kinematic and orbital parameters of the sample.
Though limited in size, our sample was carefully built up to undergo an homogeneous and detailed analysis, based on spectra with high resolution and high signal-to-noise ratio (S/N), in order to achieve a precision as high as possible in our determinations. Particular care was exercised to derive the stellar atmospheric parameters from different and independent criteria, in an attempt to limit the abundance uncertainties as much as possible.
In Sect. 2 we describe the observations and the reduction process. In Sect. 3 we present the methods used to derive the atmospheric parameters and the chemical abundances. The stellar evolution, kinematics, and orbits are presented in Sect. 4. The tree clustering method is described in Sect. 5, and all the results are discussed in Sect. 6. Finally, we present our conclusions in Sect. 7.
2. Observations and data reduction
The sample stars were selected from the Bright Star (Hoffleit & Jaschek 1982) and Hipparcos (ESA 1997) catalogues according to the following conditions:
-
i)
solar neighbourhood stars in a distance ≤40 pc;
-
ii)
stars brighter than V = 6.5 and with declination <+20°;
-
iii)
stars with effective temperature and metallicity distributed over about 5500 ≤ Teff ≤ 6100 K and −0.3 ≤ [Fe/H] ≤ 0.3 dex, respectively, which represents the colour index range 0.52 ≤ (B − V) ≤ 0.78 from the (B − V) calibration described in Sect. 3.4 (Eq. (3)); and
-
iv)
stars with no information of duplicity (capable of significantly affecting the spectroscopy) available in the astrometric and spectroscopic binary catalogues of Hoffleit & Jaschek (1982), Warren & Hoffleit (1987), Batten et al. (1989), and Duquennoy & Mayor (1991); the possibility of duplicity was afterward revised in the Washington Double Star Catalogue (Mason et al. 2001) and in the survey of Raghavan et al. (2010), and no close-in companions that could affect our analysis were found.
Based on these criteria, 99 F, G, and K dwarfs and subgiants were selected, out of which 25 stars were observed and analysed in this work. Our sample, shown in Table 1, contains F and G dwarf and subgiants stars from the thin disc stellar population, excepting the star HD 50806, which is probably in the transition between thin and thick discs.
The observations were carried out at the Cerro Tololo Inter-American Observatory (CTIO, Chile) in two different runs: i) 15 stars were observed in March 25−26, 1994 using the Cassegrain échelle spectrograph mounted on the 4 m telescope, with the red camera, 140 μm slit, and Tek CCD detector of 1024 × 1024 pixels (24 × 24 μm pixel size), and with a gain of 1 e−/ADU; the spectra have resolution R ~ 29 000 and cover the wavelength range 4370−6870 Å divided into 46 orders; and ii) 10 stars were observed in November 8−15, 1997 using the bench-mounted échelle spectrograph and a 750 mm folded Schmidt camera attached to the 1.5 m telescope; the same CCD was used; the spectra have resolution R ~ 46 000 and cover the wavelength range 4550−6520 Å divided into 37 orders.
The 25 sample stars.
The two subsamples, although observed in different conditions, were both selected based on the same criteria and will be treated as an homogeneous single sample. The spectra collected in the first run have, on average, signal-to-noise ratio (S/N = 395 ± 60) slightly larger than those of the second one (S/N = 320 ± 90) and, despite having smaller resolution, may provide smaller uncertainties in some parameters estimated here. Nevertheless, all spectra have S/N > 200 in the blue region, which warranties spectral line profiles good enough to the equivalent width measurements. Any differences in the error estimates are discussed throughout the paper whenever needed.
Two spectra of the sunlight reflected by Ganymede were also observed, one in each run. The S/N were estimated using continuum windows in the spectra selected by inspection of the solar flux atlas of Kurucz et al. (1984) (hereafter the Solar Flux Atlas) and the solar line identifications catalogue of Moore et al. (1966) (hereafter the Solar Lines Catalogue). The mean values ⟨ S/N ⟩ measured in the wavelength range 4500−5000 Å are listed in Table 1. For larger wavelengths the S/N are even higher, approaching twice that for λ4500 in the range 6000−6500 Å.
The spectra were reduced using IRAF1 routines for order identification and extraction, background subtraction (including bias and scattered light), flat-field correction, wavelength calibration, radial-velocity shift correction, and flux normalisation. The wavelength calibration was performed onto the stellar spectra themselves using lines selected by inspection of the Solar Flux Atlas and the Solar Lines Catalogue. The normalisation of the continuum is a very delicate and relevant step in the analysis procedure, since the accuracy of the equivalent width measurements is very sensitive to a faulty determination of the continuum level. Therefore, continuum windows free from telluric or photospheric lines were carefully selected also based on the Solar Flux Atlas and the Solar Lines Catalogue.
3. Spectroscopic analysis
A differential spectroscopic analysis relative to the Sun was performed to determine the atmospheric parameters and the chemical abundance of several elements in our sample. The analysis was based on the equivalent widths of atomic lines measured in the spectra, and on the spectral synthesis of carbon atomic and molecular lines. The two groups of stars (15 observed in the first and 10 in the second run) were treated in comparison with the Ganymede spectrum of their respective run.
3.1. Equivalent widths and atomic line parameters
Atomic lines of the elements Na, Mg, Si, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Sr, Y, Zr, Ba, Ce, Nd, and Sm were selected throughout the spectral range for equivalent width (EW) measurements. The lines were chosen based on the Solar Flux Atlas and the Solar Lines Catalogue, selecting only those for which the profiles were sufficiently clean from blends in order to provide reliable measurements. For both solar and stellar spectra, the EW values of more than 7500 lines of these elements (about 300 lines per star) were measured by hand by Gaussian function fit using IRAF routines.
 |
Fig. 1 Left panel: comparison of the EWs measured in this work in the Ganymede spectrum (second observation run) by Gaussian function fit to those measured by Meylan et al. (1993) in the Solar Flux Atlas by Voigt function fit; filled circles represent 145 lines of several elements; the linear regression (solid line) is the same expressed by Eq. (2). Right panel: comparison of the EWs listed in Table 8 of all lines in the Ganymede spectra in common to both runs after the conversions according to Eqs. (1) and (2); the coefficients of the linear regression (solid line) are shown. |
Strong line profiles are better described by Voigt functions than by Gaussian functions.
We show in Fig. 1 (left panel) a comparison of the
EWs measured in this work in the Ganymede spectrum of the second observation run (Gany 2)
by Gaussian function fit to those measured in the Solar Flux Atlas
(R > 500 000 and
S/N ~ 3000) by Voigt function fit (Meylan et al. 1993). A similar diagram was obtained
using the Ganymede spectrum of the first run (Gany 1) and the following relations
represent the linear least square regressions fitted to both diagrams: 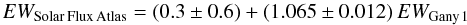 (1)
(1)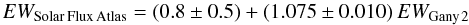 (2)where EW is given in mÅ. The standard
deviations and the cross-correlation coefficients are, respectively, σ =
3.4 mÅ and r = 0.991 for Eq. (1), and σ = 2.7 mÅ and r = 0.994 for
Eq. (2). Therefore, to reduce possible
systematic uncertainties and provide direct comparison with other works, all our EWs were
transformed to a common system using the regression coefficients of these equations
(the constant terms have no statistical significance within 2σ). The
regressions were derived in order to have a direct transformation to the Solar Flux Atlas
system. We also did the converse
(using EWGanymede vs.
EWSolar Flux Atlas diagrams) for
comparison, and the resulting regressions are comparable with those of Eqs. (1) and (2), within 1σ.
(2)where EW is given in mÅ. The standard
deviations and the cross-correlation coefficients are, respectively, σ =
3.4 mÅ and r = 0.991 for Eq. (1), and σ = 2.7 mÅ and r = 0.994 for
Eq. (2). Therefore, to reduce possible
systematic uncertainties and provide direct comparison with other works, all our EWs were
transformed to a common system using the regression coefficients of these equations
(the constant terms have no statistical significance within 2σ). The
regressions were derived in order to have a direct transformation to the Solar Flux Atlas
system. We also did the converse
(using EWGanymede vs.
EWSolar Flux Atlas diagrams) for
comparison, and the resulting regressions are comparable with those of Eqs. (1) and (2), within 1σ.
The wavelength and lower-level excitation potential (χ) of the atomic lines used were taken from the Solar Lines Catalogue. The oscillator strengths (gf) were computed using a solar model atmosphere applied to the EWs of Ganymede (converted using Eqs. (1) and (2)) in order to provide the standard solar abundances of Grevesse & Noels (1993). The adopted solar abundances are of course inconsequential in a differential analysis.
The solar and stellar model atmospheres were computed with a code kindly supplied by Dr. Monique Spite (Meudon Observatory, Paris) that interpolates the model-atmosphere grid from Edvardsson et al. (1993). We used an updated version of the original code from Spite (1967). The fundamental atmospheric parameters (effective temperature Teff, metallicity [Fe/H], surface gravity log g, and micro-turbulence velocity ξ) and the population ratio of helium and hydrogen atoms (nHe/nH) are taken as input. For the Sun, the adopted parameters are Teff = 5777 K, log g = 4.44, ξ = 1.3 km s-1, nHe/nH = 0.1, and log ϵ ⊙ = 7.50 (the solar Fe abundance).
The spectral lines used and their parameters are listed in Table 8, in which the EWs are the raw values (before the conversion). We do not list the EWs of the other stars but they are available upon request.
The atomic lines of the elements Mg, Sc, V, Mn, Co, and Cu have important hyperfine structure (HFS). Their gf values, listed in Table 9, were taken from Steffen (1985) and also revised according to the EWs of Ganymede and the standard solar abundances of Grevesse & Noels (1993), as done for the other elements. For the elements Zn, Sr, Y, Zr, Ce, Ba, and Nd, for which theoretical HFS exist, either their effects are negligible or the spectral lines used are too weak to depend on the HFS assumption. For the elements without HFS data listed in Steffen (1985), values of neighbouring multiplets were adopted. The only exception was the Mg line at λ5785.285, for which no HSF information was available. Its gf value, listed in Table 8, was obtained in the same way as those lines without HFS. This is not a strong line (EW < 60 mÅ) so that the error induced in the Mg abundance determination is not important. del Peloso et al. (2005) have recently shown that for Mn and Co the differences in their abundances computed using different values of HFS are not greater than 0.10 dex.
The HFS of Ba, and also its isotopic splitting, are of some importance only for the line at λ6496.9, and can be neglected for the lines at λ5853.7 and λ6141.7 (see Korotin et al. 2011). However, for the 25 stars of our sample we have found a good agreement among the abundances yielded by the three lines, with a mean standard deviation of 0.07 dex. Moreover, a test performed using only λ5853.7 and λ6141.7 indicated that the global behaviour and trends found in the abundance diagrams, as well as all our conclusions involving the Ba results would not change if only these two lines were used.
Concerning the fact that we used two spectrographs with different spectral resolutions, we performed a test in which we degraded the spectrum of Ganymede and of the metal-rich star HD 1835, both observed in the second observation run, to match the resolution of the first run. New values of EWs were then obtained, and no systematic differences were found when they are compared with the original measurements. Moreover, a comparison of the EWs of Ganymede listed in Table 8 and converted according to Eqs. (1) and (2) (see Fig. 1, right panel) demonstrates that the equivalent widths of the two observation runs were properly transformed to a common system, reinforcing our assumption of an homogeneous analysis.
3.2. Derivation of atmospheric parameters
In order to determine the fundamental atmospheric parameters we developed a code that
iteratively calculates these parameters for a given star based on initial input values.
The so called excitation effective temperature (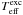 ) was calculated through the excitation
equilibrium of neutral iron by removing any dependence in a [Fe i/H] vs.
χ diagram. The micro-turbulence velocity was obtained by removing the
dependence of [Fe i/H] on EW, and the ionisation surface
gravity (log gion) was computed through the ionisation
equilibrium between Fe i and Fe ii. Finally, the metallicity was yielded
by the EW of Fe i lines.
) was calculated through the excitation
equilibrium of neutral iron by removing any dependence in a [Fe i/H] vs.
χ diagram. The micro-turbulence velocity was obtained by removing the
dependence of [Fe i/H] on EW, and the ionisation surface
gravity (log gion) was computed through the ionisation
equilibrium between Fe i and Fe ii. Finally, the metallicity was yielded
by the EW of Fe i lines.
The temperature used in our abundance analyses was the excitation effective temperature, which is a better representation of the temperature stratification of the line forming layers. In order to compute the stellar luminosity with more reliability by also accounting for any consequence due to small LTE departures, we also considered two other temperature indicators, which are described in Sect. 3.4.
Atmospheric parameters from our spectroscopic analysis.
Table 2 lists the spectroscopic atmospheric parameters of the programme stars. An estimate of their uncertainties was performed based on the analysis of HD 146233 and HD 26491, which are representative stars in our sample (from the first and second runs, respectively) with regard to their parameters and quality of the spectroscopic data. For both stars we have similar errors and they were obtained as follows:
-
i)
The uncertainty in
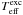 is related to the standard errorof
the angular coefficient of the linear regression fitted to the[Fe i/H] vs.
χ diagram. The temperature is changed until this coefficient is
of the same order of its error. The difference between the best value and the
previous one from the last iteration provides the
uncertainty σ(
is related to the standard errorof
the angular coefficient of the linear regression fitted to the[Fe i/H] vs.
χ diagram. The temperature is changed until this coefficient is
of the same order of its error. The difference between the best value and the
previous one from the last iteration provides the
uncertainty σ(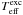 ) = 30 K;
) = 30 K; -
ii)
The uncertainty in metallicity is the standard deviation of the abundance yielded by individual Fe i lines, which is σ([Fe/H]) = 0.05 dex;
-
iii)
To estimate the uncertainty in log gion, its value is changed until the difference between the averaged abundance yielded by Fe i and Fe ii lines is of the order of their internal errors (~0.05 dex), which led to an uncertainty σ(log gion) = 0.13 dex;
-
iv)
The uncertainty in the micro-turbulence velocity is estimated regarding the [Fe i/H] vs. EW diagram. The ξ value is modified until the angular coefficient of the regression is of the same order of its error. An uncertainty σ(ξ) = 0.04 km s-1 was found for this parameter.
The spectroscopic atmospheric parameters were used to compute the model atmospheres, which in turn are required in the abundance determination. In our analysis, we used the model-atmosphere grid derived by Edvardsson et al. (1993) for stars with effective temperatures from 5250 to 6000 K, surface gravity from 2.5 to 5.0 dex, and metallicity from −2.3 to +0.3 dex (with small extrapolations when needed). These are 1D, plane-parallel, constant flux, line-blanketed, and LTE models computed over 45 layers.
The model atmospheres are, essentially, subject to errors in the atmospheric parameters, in the LTE simplifications, and in the thermal homogeneity assumption. However, the effects of non-LTE and thermal inhomogeneities are hopefully minor for the elements and the stellar types studied here, being more important for low metallicity and low surface gravity stars (Edvardsson et al. 1993; Asplund 2005). Possible errors induced by such simplified assumptions are dominated by other sources of uncertainties. In addition, in a differential analysis, the errors in the stellar atmospheric structure are of second order.
We also investigated what would be the effects on the derived abundances if another model-atmosphere grid were used. We compared Edvardsson and Kurucz models and, using the same equivalent widths, gf values, and atmospheric parameters obtained from a solar spectrum, we found that the differences in abundance [X/Fe] for most of the elements are of the order of 0.03 dex or smaller, achieving a maximum of 0.07 dex. We note that these values are for the Sun and represent the differences between the two sets of model atmospheres. The effects of these differences when computing the stellar abundances relative to the Sun are minimised in a differential approach.
3.3. Abundance determination and their uncertainties
The abundance of the elements studied was determined using an adapted version of a code also supplied by Dr. Monique Spite. The code takes into account the solar gf values and the stellar model atmospheres (computed using the atmospheric parameters of each star) to calculate the abundances that fits the equivalent widths measured in the spectra (transformed according to the procedure described in Sect. 3.1). The results of this abundance determination are presented and discussed in Sect. 6.
The main sources of uncertainties in the abundance determination come from the errors in the EWs (the most important), the gf values, the atmospheric parameters, and the adopted model atmospheres (these two latter are discussed in Sect. 3.2).
The uncertainties in the EWs were estimated as follows: by plotting the diagram
EWHD 26491 vs.
EWGanymede and computing the standard
deviation of the linear regression, we obtained σ = 2.9 mÅ. The solar EWs
were measured in the surrogate spectrum of the Sun collected under the same circumstances
as for the programme stars. Therefore, we assumed that σ is a quadratic
sum of the errors in EW of both objects and that they are similar to each other. Thus,
for the star HD 26491 the value of
σ(EW) is 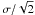 = 2.1 mÅ. Similarly, for the
star HD 146233 we obtained
σ(EW) = 1.7 mÅ. These values were adopted to represent
the uncertainties in EW of the two observation runs. Because the solar
gf values were computed to reproduce solar the equivalent widths,
the errors in EW contribute twice to the total uncertainty, with approximately the
same magnitude.
= 2.1 mÅ. Similarly, for the
star HD 146233 we obtained
σ(EW) = 1.7 mÅ. These values were adopted to represent
the uncertainties in EW of the two observation runs. Because the solar
gf values were computed to reproduce solar the equivalent widths,
the errors in EW contribute twice to the total uncertainty, with approximately the
same magnitude.
Each one in turn, EW, 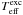 , [Fe/H], ξ, and
log gion are changed by 1σ in the sense of
increasing the abundance ratios and new abundances are computed for each element. The
differences between new and previous abundance values provide the errors induced by each
parameter and a quadratic sum of these errors yields the total uncertainty in the
elemental abundance ratios. The estimated errors (σest) are
listed in Table 3 for both HD 146233 and HD 26491, and they are compared to the dispersions around the
mean (σdisp) for elements with at least five lines measured
in the spectra. For these elements, the larger values were adopted to represent the
errors σ([X/Fe]) in each observation run.
Otherwise, σest was adopted.
, [Fe/H], ξ, and
log gion are changed by 1σ in the sense of
increasing the abundance ratios and new abundances are computed for each element. The
differences between new and previous abundance values provide the errors induced by each
parameter and a quadratic sum of these errors yields the total uncertainty in the
elemental abundance ratios. The estimated errors (σest) are
listed in Table 3 for both HD 146233 and HD 26491, and they are compared to the dispersions around the
mean (σdisp) for elements with at least five lines measured
in the spectra. For these elements, the larger values were adopted to represent the
errors σ([X/Fe]) in each observation run.
Otherwise, σest was adopted.
3.4. Photometric and Hα effective temperatures
The effective temperature of the sample stars were also obtained using some photometric
calibrations, providing the photometric effective
temperature (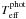 ). These calibrations, derived by Porto de
Mello et al. (in prep.) for the (B − V),
(BT − VT),
(b − y), and β colour indices,
are given by the following equations:
). These calibrations, derived by Porto de
Mello et al. (in prep.) for the (B − V),
(BT − VT),
(b − y), and β colour indices,
are given by the following equations: ![\begin{eqnarray} \label{cal_bv} &&T_{{\rm eff}\,(B-V)}^{\rm phot} = 7747 - 3016\,(B-V)\,\big\{1-0.15{\rm\,[Fe/H]}\big\} \\ \label{cal_btvt} &&T_{{\rm eff}\,(B_{\rm T}-V_{\rm T})}^{\rm phot} = 7551 - 2406\,(B_{\rm T}-V_{\rm T})\,\big\{1-0.2{\rm\,[Fe/H]}\big\} \\ \label{cal_by} &&T_{{\rm eff}\,(b-y)}^{\rm phot} = 8481 - 6516\,(b-y)\,\big\{1-0.09{\rm\,[Fe/H]}\big\} \\ \label{cal_beta} &&T_{{\rm eff}\,(\beta)}^{\rm phot} = 11654\,\big\{\,\beta - 2.349\big\}^{0.5} \end{eqnarray}](/articles/aa/full_html/2012/06/aa18751-11/aa18751-11-eq64.png) for Teff given in
K. The standard deviations of these calibrations are σ = 65, 64, 55,
and 70 K, respectively.
for Teff given in
K. The standard deviations of these calibrations are σ = 65, 64, 55,
and 70 K, respectively.
The (B − V) and (BT − VT) colour indices of our stars were taken from the Hipparcos Catalogue, and (b − y) and β from the literature (see Table 4), when available. For the star HD 33021, the β values adopted are only from Perry et al. (1987) because these authors made 41 measurements of this index. For the star HD 50806, only one reference for the β index was found, and the effective temperature from this index strongly disagrees with that obtained from the other colours and we thus discarded it.
Colour indices and photometric effective temperatures (given in K).
Table 4 lists the colour indices used and the
photometric effective temperature (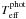 ) obtained, which is a mean of the
temperatures computed using the four calibrations, weighted by their variances. The
references for (b − y) and β are also
listed. The values of (b − y) from Gronbech & Olsen (1976), Olsen
(1983), Twarog (1980), and Schuster & Nissen (1988) were converted to the
Olsen (1993) system according to equations
provided by the latter author.
) obtained, which is a mean of the
temperatures computed using the four calibrations, weighted by their variances. The
references for (b − y) and β are also
listed. The values of (b − y) from Gronbech & Olsen (1976), Olsen
(1983), Twarog (1980), and Schuster & Nissen (1988) were converted to the
Olsen (1993) system according to equations
provided by the latter author.
The star HD 128620 is the primary component
(V = −0.01) of the α Cen triple system. The
Teff determination for very bright stars using photometric
colours is normally considered risky due to systematic effects that may affect the results
(such as non-linearity and detector dead time) and also, in the case of this system,
due to a possible contamination by the companion. For this reason, we preferred do not
include this star in our Teff estimates based on the
photometric indices. Nevertheless, our spectroscopic determination for
α Cen A, 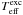 = 5857 ± 30 K, is in good agreement with
the photometric determination performed by Porto de Mello
et al. (2008), Teff = 5794 ± 34 K.
= 5857 ± 30 K, is in good agreement with
the photometric determination performed by Porto de Mello
et al. (2008), Teff = 5794 ± 34 K.
Concerning the uncertainties in 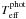 , on the one hand, the internal error of
the weighted mean, computed using the standard deviations in the four photometric
calibrations, is 31 K. On the other hand, the mean value of the standard deviations
around
, on the one hand, the internal error of
the weighted mean, computed using the standard deviations in the four photometric
calibrations, is 31 K. On the other hand, the mean value of the standard deviations
around 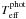 (i.e., the dispersion of the four values
of temperature around the weighted mean) is 41 K. Therefore, in this work we adopted
σ(
(i.e., the dispersion of the four values
of temperature around the weighted mean) is 41 K. Therefore, in this work we adopted
σ(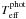 ) = 40 K as the internal uncertainty in our
photometric effective temperatures. This uncertainty intrinsically takes into account the
errors in the colour indices themselves.
) = 40 K as the internal uncertainty in our
photometric effective temperatures. This uncertainty intrinsically takes into account the
errors in the colour indices themselves.
The stellar effective temperature can also be estimated by modelling the wing profile of
the Hα line, which is very sensitive to changes in this parameter. Lyra & Porto de Mello (2005) applied this method to
solar neighbourhood stars, and values of 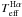 for our sample were used as a third
Teff indicator, with an uncertainty
σ(
for our sample were used as a third
Teff indicator, with an uncertainty
σ(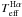 ) = 50 K.
) = 50 K.
3.5. Carbon abundance from spectral synthesis
The carbon abundance was derived using the spectral synthesis method applied to molecular lines of electronic-vibrational band heads of the C2 Swan System at λ5128 and λ5165, and also to C atomic lines at λ5052.2 and λ5380.3. To reproduce the atomic and molecular absorption lines in the observed spectra of the sample stars, the MOOG spectral synthesis code2, developed by Chris Sneden (University of Texas, USA), was used. The synthetic spectra were computed in steps of 0.02 Å, also taking into account the continuum opacity contribution in ranges of 0.5 Å. The Unsöld approximation multiplied by 6.3 was adopted in the calculations of the line damping parameters.
The model atmospheres are the same used in the spectroscopic analysis. They also include the micro-turbulence velocity and the elemental abundances of each star, both assumed to be constant in all layers. For any element X for which no abundance was determined in this work, we adopted the metallicity of the respective star to set the [X/H] ratio.
 |
Fig. 2 Spectral synthesis of the C2 molecular band regions (λ5128 and λ5165) and of the C atomic lines (λ5052.2 and λ5380.3) for Ganymede of the second observation run (top panels) and for one metal-rich star of the first run, HD 160691 (bottom panels). The solid lines represent three models with different values of [C/Fe]: −0.05 (red), 0.0 (green), and +0.05 dex (blue). The differences between observed (dots) and computed spectra (o−c) are also shown in the bottom of each panel. |
The atomic and molecular line parameters used to compute the synthetic spectra are: the central wavelength, the gf values, the lower-level excitation potential, and the constant of dissociation energy D0 (only for molecular features). Atomic and molecular data were taken, respectively, from the Vienna Atomic Line Database – VALD (Kupka et al. 1999, 2000; Piskunov et al. 1995; Ryabchikova et al. 1997) and from Kurucz (1992). In addition to C2, the spectral regions studied also include MgH molecular features that may contribute to the continuum formation. The oscillator strengths of C2 and MgH lines were revised according to the normalisation of the Hönl-London factors (Whiting & Nicholls 1974).
To account for the spectral line broadening, the synthetic spectra were computed by means
of the convolution with three input parameters: i) the spectroscopic instrumental
broadening; ii) the limb darkening of the stellar disc; and iii) a composite of velocity
fields, such as rotation velocity and macro-turbulence broadening,
named Vbroad. The instrumental broadening was estimated by
means of the FWHM of thorium lines present in Th-Ar spectra observed at the CTIO. The
linear limb-darkening coefficient (on average u ~ 0.7 for all the
sample stars) was individually estimated by interpolation of
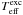 and log gion
in Table 1 of Díaz-Cordovéz et al. (1995). As a first estimate
of Vbroad, the projected rotation
velocity (vsini) of the stars was used, which was
computed based on the profile of four isolated Fe i lines
(λ5852.2, λ5855.1, λ5856.1, and
λ5859.6) in the spectra. Small corrections
in Vbroad were applied when needed according to an
eye-trained inspection of the synthetic spectra. The final values are listed in
Table 5, where they can be compared to the
stellar age and the chromospheric activity level.
and log gion
in Table 1 of Díaz-Cordovéz et al. (1995). As a first estimate
of Vbroad, the projected rotation
velocity (vsini) of the stars was used, which was
computed based on the profile of four isolated Fe i lines
(λ5852.2, λ5855.1, λ5856.1, and
λ5859.6) in the spectra. Small corrections
in Vbroad were applied when needed according to an
eye-trained inspection of the synthetic spectra. The final values are listed in
Table 5, where they can be compared to the
stellar age and the chromospheric activity level.
Figure 2 shows two examples of synthetic spectra of the C2 molecular band regions around λ5128 and λ5165, and of the C atomic lines at λ5052.2 and λ5380.3 for the sunlight spectrum reflected by Ganymede (second observation run) and for the metal-rich star HD 160691. The spectral synthesis was first applied to the Ganymede spectra of both runs, then the gf values of some atomic and molecular lines were revised when needed, and finally the synthesis was applied to the other stars, treated according to their observation runs. For each case, the best fit was obtained through the minimisation of the rms between observed and synthetic spectra.
In order to estimate the uncertainties in the [C/Fe] abundance determination, we
performed a spectral synthesis of the most prominent molecular band used
(λ5165) adopting model atmospheres perturbed by the errors estimated
for the atmospheric parameters. This procedure resulted in: ±0.03 dex due to the error
in 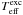 ; ± 0.01 dex due to the error in [Fe/H];
± 0.02 dex due to the error in ξ; and ± 0.03 dex due to the error
in log gion. The uncertainties related to errors
in Vbroad (~1.0 km s-1 or smaller) and in
the limb darkening coefficient are negligible. The quadratic sum of the individual
contributions (also including a global error of 0.05 dex estimated based on the
rms minimisation of the solar spectrum) yields a total uncertainty
σ([C/Fe]) = 0.07 dex.
; ± 0.01 dex due to the error in [Fe/H];
± 0.02 dex due to the error in ξ; and ± 0.03 dex due to the error
in log gion. The uncertainties related to errors
in Vbroad (~1.0 km s-1 or smaller) and in
the limb darkening coefficient are negligible. The quadratic sum of the individual
contributions (also including a global error of 0.05 dex estimated based on the
rms minimisation of the solar spectrum) yields a total uncertainty
σ([C/Fe]) = 0.07 dex.
4. Evolutionary, kinematic, and orbital parameters
4.1. Mass and age determination
The evolutionary parameters mass and age were obtained by interpolation in the Yonsei-Yale (Y2) evolutionary tracks and isochrones (Yi et al. 2001; Kim et al. 2002) drawn on the HR diagram and computed for different values of metallicity.
The luminosity used in the diagrams were calculated with parallaxes taken from the new
reduction of the Hipparcos data (van Leeuwen 2007),
bolometric corrections (BC) from Flower (1996), and
an absolute bolometric magnitude for the Sun 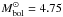 for
for
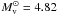 . We estimated, for these nearby stars with
precise parallaxes, a mean uncertainty of 0.01 dex
in log (L/L⊙).
. We estimated, for these nearby stars with
precise parallaxes, a mean uncertainty of 0.01 dex
in log (L/L⊙).
The effective temperature is a weighted mean (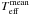 ) of the excitation, photometric, and
Hα temperatures. The weights are given
by 1/σ2 for
σ(
) of the excitation, photometric, and
Hα temperatures. The weights are given
by 1/σ2 for
σ(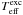 ) = 30 K,
σ(
) = 30 K,
σ(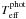 ) = 40 K, and
σ(
) = 40 K, and
σ(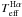 ) = 50 K, obtained as described in
Sects. 3.2 and 3.4. The uncertainty of the weighted mean is 22 K, calculated using these three
values of σ. On the other hand, the standard deviations of the three
values of temperature around the weighted mean is 29 K. Therefore, we conclude that our
estimates of effective temperature based on the three indicators agree with each other
very well (see the comparison in Fig. 3) and that the
mean value has a mean internal error
) = 50 K, obtained as described in
Sects. 3.2 and 3.4. The uncertainty of the weighted mean is 22 K, calculated using these three
values of σ. On the other hand, the standard deviations of the three
values of temperature around the weighted mean is 29 K. Therefore, we conclude that our
estimates of effective temperature based on the three indicators agree with each other
very well (see the comparison in Fig. 3) and that the
mean value has a mean internal error 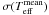 = 30 K.
= 30 K.
Porto de Mello et al. (2008) determined the
effective temperature of α Cen A (HD 128620) and B also using the excitation, photometric,
and Hα approaches. They found a good agreement for
α Cen A, a solar temperature star. However, for α Cen B
(Teff ~ 5200 K), the excitation effective temperature
is about 100−150 K higher than the photometric and the Hα counterparts,
which the authors attributed to non-LTE effects. Although the agreement for the coolest
and hottest stars in our sample is not that good, especially in the comparison of
excitation and Hα temperatures, Fig. 3 does not show any systematic difference among the three indicators, and the
differences are nonetheless within 2σ for all the
Teff range (only HD 115383 has 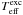 larger
than
larger
than 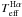 by 3σ). This confirms
that 1D LTE model atmospheres may adequately represent solar-type stars, at least in a
differential analysis relative to the Sun.
by 3σ). This confirms
that 1D LTE model atmospheres may adequately represent solar-type stars, at least in a
differential analysis relative to the Sun.
We remind that the temperature used in our abundance analyses (based on the equivalent widths or synthesis of spectral features) was the excitation effective temperature, which better characterises the temperature radial profile in the stellar photosphere and the formation of absorption lines in the emergent spectrum. On the other hand, to better represent the luminosity of a star and to account for any possible effect due to small deviations from LTE, we adopted the weighted mean of the three temperature indicators.
The stars were grouped according to their values of metallicity (12 groups from [Fe/H] = −0.32 to +0.32 dex) and then their masses and ages were computed using evolutionary tracks and isochrones for each stellar group. The difference in metallicity between each star and its respective HR diagram is not greater than 0.02 dex. A few examples for some metallicities are shown in Fig. 4. To reproduce the Sun’s position in the diagrams, adopting Teff = 5777 K and age = 4.53 Gy (Guenther & Demarque 1997), the evolutionary tracks and isochrones were displaced in log (Teff) and log (L/L⊙) by 0.001628 (~22 K in Teff) and 0.011, respectively. These values are, at any rate, of the same order or smaller than the uncertainties on these parameters.
As an independent check, we calculated the evolutionary surface gravity using the values
of mass and effective temperature obtained, which we
called gevol, using the following equation: 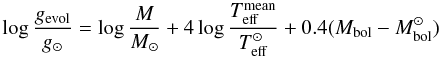 (7)where Mbol is the
absolute bolometric magnitude for the stars. The values
of log gevol are listed in Table 2 together with the ionisation surface gravity. They are in very good
agreement, having a dispersion of only 0.09 dex, smaller than the uncertainty of 0.13 dex
estimated for log gion.
(7)where Mbol is the
absolute bolometric magnitude for the stars. The values
of log gevol are listed in Table 2 together with the ionisation surface gravity. They are in very good
agreement, having a dispersion of only 0.09 dex, smaller than the uncertainty of 0.13 dex
estimated for log gion.
4.2. Galactic velocities, distance, and eccentricity
The kinematic properties of our sample were investigated by computing the Galactic velocity components ULSR, VLSR, and WLSR (see Fig. 5) with respect to the Local Standard of Rest (LSR). We developed a code that uses equations of Johnson & Soderblom (1987), parallaxes and proper motions both from the new reduction of the Hipparcos data, and radial velocities from Holmberg et al. (2007), Torres et al. (2006) for HD 114613, and Santos et al. (2004) for HD 160691. For the Sun, the adopted values of ULSR, VLSR, and WLSR are 10.0, 5.3, and 7.2 km s-1, respectively (Dehnen & Binney 1998).
The mean orbital distance from the Galactic centre (Rm) and the orbital eccentricity (e) were also considered in our analysis (see Fig. 5), where e = (Ra − Rp)/(Ra + Rp) and Rm = (Ra + Rp)/2 were computed using the perigalactic (Rp) and the apogalactic (Ra) orbital distances from the Geneva-Copenhagen survey (Holmberg et al. 2009). For the Sun, the adopted values are e = 0.06 and Rm = 8 kpc.
5. Tree clustering analysis
We looked for statistically significant abundance groups in our sample using a hierarchical clustering analysis. To avoid missing abundance values, the analysis uses only those elements having abundances measured for all stars and was applied to the [X/H] abundance space.
 |
Fig. 3 Comparisons of the three effective temperature indicators: the excitation vs. photometric (top panel), excitation vs. Hα (middle panel), and photometric vs. Hα (bottom panel) temperatures. The symbols represent the stellar groups defined in Sect. 5 (see Fig. 6). |
 |
Fig. 4 Evolutionary tracks (magenta solid lines) and isochrones (blue dots and dashed lines) from Yonsei-Yale, calculated for different values of metallicity, showing how to derive the stellar masses and ages. The ages in Gyr are indicated alongside the evolutionary tracks, for which the masses are indicated in M⊙. The Sun’s position for Teff = 5777 K is also shown in the solar metallicity panel (top-left corner). |
We used the complete linkage method for the hierarchical clustering (Everitt et al. 2001) and euclidean distances as measures of dissimilarities in this abundance space. A hierarchical clustering algorithm works by joining similar objects in a hierarchical structure. Initially, each object is assigned to its own cluster. The algorithm proceeds iteratively, joining the two most similar clusters in each pass until there is just a single cluster. The resulting hierarchy of clusters for our data is shown in Fig. 6 (upper panel) as a dendrogram. In this plot, the most similar objects are linked together in the bottom forming clusters, which are then iteratively linked together in pairs by similarity. The vertical axis in a dendrogram measures the dissimilarity between each individual or cluster. Since we used euclidean distances in the [X/H] abundance space, the units of this axis is dex, although it measures the total dissimilarity in this abundance space and not in a single variable.
 |
Fig. 5 Galactic velocity components (left and middle panels) and orbital eccentricity as a function of the mean orbital distance from the Galactic centre (right panel) for the sample stars and the Sun. The symbols represent the stellar groups defined in Sect. 5. |
 |
Fig. 6 Dendrogram (upper panel) and mean abundance ratios ⟨ [X/H] ⟩ (middle panel) and ⟨ [X/Fe] ⟩ (bottom panel) for the four stellar groups from the tree clustering analysis (Sect. 5). They are classified as metal-poor (▴), intermediate abundance (under solar △ or over solar °), or metal-rich (•) stars, and the same symbolism is adopted all over the paper. The dashed red line on the dendrogram represents a dissimilarity number of 0.9 dex. |
Clusters can be defined by specifying a reasonable total dissimilarity value for pruning the dendrogram. There is no unambiguous or optimal way for defining this pruning value, especially because the clusters found depend on the clustering method and cluster shapes. Since our sample is quite small, we arbitrarily decided to prune our dendrogram at the total dissimilarity of 0.9 dex, which is shown in Fig. 6 by the dashed red line. This pruning value was chosen in order to have four more or less equally populated clusters. Considering the size of our sample, less than four clusters would simply limit our discussion to poor against rich stars, while a larger number of clusters would make such an analysis meaningless.
The average ⟨ [X/H] ⟩ behaviour of the four clusters for each element considered in this analysis is shown in the middle panel of Fig. 6. Two of these clusters have over-solar abundances, with averages +0.26 and +0.06 dex for all the elements, whereas the two others have under-solar abundance values, with averages −0.06 and −0.24 dex. We can observe in the figure that the elemental abundance patterns of the metal-poor and metal-rich groups are distinct between each other. In particular, it seems to exit a chemical distinction even between the two intermediate groups: the under-solar intermediate group has an abundance pattern that roughly follows the element by element pattern of the metal-poor group, whereas the pattern of the over-solar intermediate group resembles the scaled-solar mixture.
The clustering analysis we have presented was tentatively based on biological ideas of evolving species, in the sense that the material the stars came from is continuously changing. For this reason we made use of [X/H] abundances ratios instead of [X/Fe]. We implicitly need the time evolution that [X/H] has, because we want a time hierarchy in the output groups. A similar analysis in the [X/Fe] space can still show groups, but the hierarchical relation between these groups in a dendrogram will not necessarily show evolutionary trends, because this variable is only indirectly linked with time. Notwithstanding, we have checked this, but the output groups show no meaningful interpretation in terms of chemical evolution or abundance ratio groups. The outcome could be different if the sample were larger, but this needs to be verified with another sample, what is beyond the scope of this paper. Nevertheless, we included in Fig. 6 (bottom panel) the average ⟨ [X/Fe] ⟩ behaviour of the stars clustered in the [X/H] parameter space. The small variation of ⟨ [X/Fe] ⟩ with respect to the solar values reinforces our point above: that for this specific small sample, the [X/Fe] parameter space is dynamically very narrow and does not favour a cluster analysis.
6. Results and discussion
Table 5 lists the evolutionary (mass and age), kinematic (ULSR, VLSR, and WLSR velocities), and orbital (mean orbital distance from the Galactic centre and orbital eccentricity) parameters computed for the programme stars. They are grouped following the tree clustering analysis performed in Sect. 5.
The uncertainties in the mass and age determination may vary widely depending on the stellar position in the HR diagram. We made an estimate of these errors for a few representative stars in our sample (cool and hot dwarfs and subgiants). We took into account the errors estimated for log (L/L⊙), log (Teff), and also [Fe/H] considering that the evolutionary tracks and isochrones are metallicity dependent. We found that the uncertainties in mass stand between 0.02 and 0.08 M⊙, whereas those in age vary from about 0.5 Gyr (or smaller) for evolved stars up to about 2.5 Gyr for cool main-sequence stars.
For HD 1835, HD 39587, HD 147513, and HD 181321 we determined an approximative value for their masses and an upper limit for their ages given their position in the HR diagram (close to the Zero Age Main Sequence). Indeed, these are very young stars: one of them, HD 1835, is likely a member of the Hyades star cluster (~600 Myr) according to López-Santiago et al. (2010); two others, HD 39587 (Soderblom & Mayor 1993; Fuhrmann 2004) and HD 147513 (Soderblom & Mayor 1993; Montes et al. 2001) belong to the Ursa Major moving group of ~300 Myr (see also Castro et al. 1999); and HD 181321 is a member of the Castor moving group (~200 Myr) according to Montes et al. (2001). For these four stars, we adopted the ages of their respective moving group in our study.
The stars HD 112164 and HD 160691, indicated by asterisks (*) in Table 5, are located in a region of the HR diagram where successive evolutionary tracks and isochrones are superposed (see example in Fig. 4). Therefore, their mass and age determination may yield larger uncertainties: ≲0.12 M⊙ and ≲0.7 Gyr for HD 112164, and ≲0.04 M⊙ and ≲1.0 Gyr for HD 160691.
The ULSR, VLSR, and WLSR velocities have a typical uncertainty of 0.3 km s-1 or smaller. An exception is the star HD 188376, for which the large errors (2.5, 1.1, and 1.8 km s-1, respectively) are due to a large uncertainty in its parallax.
The level of activity in the chromosphere of the stars, which is related to their age, was
also investigated. The table lists the flux in the centre of the Hα line
(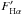 ), computed by Lyra & Porto de Mello (2005) and used as a chromospheric activity
indicator (the larger the value of
), computed by Lyra & Porto de Mello (2005) and used as a chromospheric activity
indicator (the larger the value of 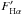 , the higher the level of chromospheric
activity). The uncertainty for this parameter
is 0.5 × 105 erg cm-2 s-1.
, the higher the level of chromospheric
activity). The uncertainty for this parameter
is 0.5 × 105 erg cm-2 s-1.
We note that a few stars in our sample have at least one planetary companion detected. They are HD 102365, HD 115617, HD 117176, HD 147513, and HD 160691 (see The Extrasolar Planets Encyclopaedia: http://exoplanet.eu). Comparisons of the properties of stars with and without planets are frequently published. In the analysis performed in this paper, however, no peculiar information distinguishing the two populations has been found.
6.1. Elemental abundances
Table 10 lists the chemical abundances relative to iron [X/Fe] obtained for the elements studied. For some elements of some stars, the abundance determination was not possible due to the poor quality or the weakness of their spectral lines (empty fields in the table). The carbon abundance ratios [C/Fe] are shown in Table 6.
We also computed the mean abundance ratios ⟨ [X/Fe] ⟩ of the following groups of elements: i) two groups of light metals: (Mg, Si) and (Ca, Sc, Ti); ii) two groups of the iron peak: (V, Cr, Co, Ni) and (Mn, Cu); iii) light elements from the s-process: (Sr, Y, Zr), to which we refer as ls; and iv) heavy elements from the s-process: (Ba, Ce, Nd), referred to as hs (see Table 7). They were grouped either because they have possibly the same nucleosynthetic origin or because they share a similar behaviour in the diagrams. The abundance ratio between heavy and light elements from the s-process, [hs/ls] = [hs/Fe]−[ls/Fe], was also calculated.
Figure 7 shows diagrams with the abundance ratios of the programme stars for individual elements and nucleosynthetic groups. The uncertainties are listed in Tables 3 and 7. As for the individual elements, the estimated errors are compared to the dispersions around the mean for groups having at least two elements. For each group of each observation run (represented by the stars HD 146233 and HD 26491), the larger values were adopted to be the uncertainties in the grouped abundance ratios. In Fig. 7, the stars are represented by different symbols according to the tree clustering analysis performed in Sect. 5.
The star HD 1835 is enriched in Ca, Sr, and Ba.
The mean value of all s-process elements also suggests an over-solar abundance.
Sm, the only r-process element analysed here, shows an under-solar abundance of −0.3 dex,
but with a large error. As already mentioned, this is a very young star, a probable member
of the Hyades star cluster of age ~600 Myr, which is in agreement with its high
level of chromospheric activity indicated by 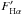 in Table 5.
in Table 5.
 |
Fig. 7 Abundance ratios [X/Fe] for individual elements (top of each panel) and ⟨ [X/Fe] ⟩ for the nucleosynthetic groups (bottom of each panel). The uncertainties adopted are those listed in Tables 3 and 7. The symbols represent the stellar classification defined in Sect. 5 (see Fig. 6). |
 |
Fig. 7 continued. |
Two other very young stars are HD 39587 and HD 147513, both members of the kinematic Ursa Major group. They are clearly overabundant in the s-process elements, especially Ba, and underabundant in C, which is in agreement with the results of Porto de Mello & da Silva (1997a) and Castro et al. (1999). These stars were proposed by Porto de Mello & da Silva (1997a) to be barium stars, originated in a phenomenon in which the more massive component of a binary system evolves as a thermally pulsing asymptotic giant branch (TP-AGB) star and the material produced in the He-burning envelope, enriched in s-process elements, is dredged-up to the surface and then accreted by its companion by wind mass transfer. The initially more massive star is now a white dwarf whereas the companion has become the primary barium star. At present, HD 39587 is a single-lined spectroscopic and astrometric binary, with a low mass companion of 0.15 M⊙ (König et al. 2002), and HD 147513 has a common proper motion companion, a DA2 white dwarf, at an angular separation of 345″ (Holberg et al. 2002). The barium-star scenario was not supported by Castro et al. (1999), who proposed that the two stars simply have usual Ba abundances for their age and that probably all the Ursa Major group members are Ba-enriched, either due to a primordial origin or because they are young (see discussion in Sect. 6.4).
Carbon abundance ratios derived from the spectral synthesis of the two atomic lines (λ5052.2 and λ5380.3) and the two C2 band heads (λ5128 and λ5165) studied.
Groups of chemical elements and uncertainties in the mean abundance ratios ⟨ [X/Fe] ⟩ .
HD 181321 and HD 188376 are two other Ba-rich stars. HD 188376 is the most evolved and massive star analysed here, clearly in the evolutionary stage of a subgiant. The other star, HD 181321, is the youngest and has the highest level of chromospheric activity in our sample. Indeed, our determination for Vbroad is 12.5 km s-1, indicating a fast-rotating star. It has solar atmospheric parameters, excepting a high value of micro-turbulence velocity (ξ = 2.3 km s-1). The kinematic and orbital parameters are also very close to the solar values. In other words, this star has, on the one hand, about the same effective temperature, metallicity, surface gravity, mass, Galactic orbit, and space velocities as the Sun. On the other hand, it is very young and significantly enriched in Ba, strengthening the relation between Ba abundance and age (see Sect. 6.4).
The high microturbulence velocity of the star HD 181321 is probably prompted by the strengthened convection and turbulence
in its upper photosphere, which is subjected to large non-thermal energy influxes from the
chromosphere. The UV radiation excess from the chromosphere of an active star can scape to
the photosphere and cause departures from LTE due to an ionisation imbalance. The induced
overionisation is commonly manifested by differences either in excitation and photometric
effective temperatures, or in ionisation and evolutionary surface gravities (see Porto de Mello et al. 2008; Ribas et al. 2010). For HD 181321, our determination of 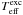 and
and
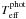 are in very good agreement with each
other. Therefore, only the difference in surface gravity and the large value of
microturbulence velocity are possible signs that an overionisation is taking place in the
photosphere of this active star. A full non-LTE analysis and a photospheric and
chromospheric modelling would probably settle the issue, but this goes beyond the scope
of this paper.
are in very good agreement with each
other. Therefore, only the difference in surface gravity and the large value of
microturbulence velocity are possible signs that an overionisation is taking place in the
photosphere of this active star. A full non-LTE analysis and a photospheric and
chromospheric modelling would probably settle the issue, but this goes beyond the scope
of this paper.
It is also very worthwhile to investigate the chemical abundances in stars that share similar values of age, metallicity, and Galactic orbit (Rm and e). These subgroup of stars are supposed to share the same physical conditions of the Galaxy at the time and galactocentric position of their birth. An example of this includes the stars HD 43834, HD 84117, HD 141004, and HD 146233, which also have ages, metallicities, and Galactic orbits close to the solar values (they were all classified as intermediate abundance stars in the tree clustering analysis, one in slight underabundance and the three others in slight overabundance with respect to the Sun). In spite of this, only HD 43834 and HD 141004 show solar abundances, within the uncertainties, for all (or almost all) elements. HD 84117 is deficient in Mn and enriched in Na and in elements of the s-process (Sr, Y, Zr, and Ba). HD 146233, proposed by Porto de Mello & da Silva (1997b) as the closest solar twin ever known at that time, is actually (as also proposed by these authors) enriched in some elements of the s-process (Sr and Ba) and possibly enriched in Sc, V, and Sm. Thus, possibly, the investigation of a larger sample of stars at a similar level of detail as done here could reveal that non-solar abundance ratios are present even for stars sharing the same place and time of birth. Whether this reflects intrinsic heterogeneities in their natal interstellar clouds (in principle a reasonable hypothesis since the elements reflecting non-solar ratios are related to different nucleosynthetic processes operating in different timescales) or else is evidence for considerable radial migration in the Galaxy is a question we plan to address in a subsequent work involving a larger sample.
Still concerning the relations involving the stellar groups from the clustering analysis and the kinematic and orbital parameters of our sample, we can see in Fig. 5 that the group of metal-poor and old stars seems to have larger velocities in the direction of the Galactic centre (| ULSR| > 40 km s-1) and larger eccentricities (e ≳ 0.2) than the other stars. The star HD 50806 appears to have a singular position in this figure (in particular, it has the most eccentric orbit among the sample stars), which is probably related to its membership in the transition population of thin-thick disc stars. The limitation of our sample does not allow to verify the results of Rocha-Pinto et al. (2006) that metal-poor and old stars show more orbital radial spread in the Galaxy.
6.2. Abundance trends as a function of [Fe/H]
Through the analysis of Fig. 8 we investigate possible trends in the abundance ratios as a function of the stellar metallicity. These trends are more clearly identified if the elements are grouped together, either based on their nucleosynthetic origin or because they share similar trends in the diagrams. For this reason, we show in the bottom panels of this figure the mean abundance ⟨ [X/Fe] ⟩ of a few groups of elements as a function of the metallicity (the same groups plotted in Fig. 7 and listed in Table 7). The stars are also identified according to the tree clustering analysis. We have fitted linear regressions on the diagrams in three ranges of metallicity: for stars poorer than the Sun, for stars of solar metallicity or richer, and for all the sample stars. We have then computed the cross-correlation coefficients in these three metallicity ranges and plotted the regressions of the more significant trends (only if |r| ≥ 0.5).
The overall trend of our abundance ratios as a function of the stellar metallicity normally follows what has been suggested in the literature concerning the nucleosynthetic origin of the elements and their abundance evolution in time (Chen et al. 2000; Reddy et al. 2003; Bensby et al. 2005; Chen et al. 2008; Neves et al. 2009). The light metals Ca, Sc, and Ti are predominantly produced by type II Supernovae (SN II) at the beginning of the enrichment history of the Galactic disc. On the other hand, iron and the iron-peak elements V, Cr, Co, and Ni are predominantly synthesised by type Ia Supernovae (SN Ia) in longer time scales. Therefore, it is expected that the abundance ratio of these light metals with respect to iron progressively decrease from metal-poor to metal-rich stars, whereas the abundance ratio of iron-peak elements with respect to iron, all produced at the same rate, remains constant and close to zero in the whole range of metallicity. Indeed, this is exactly what is observed in Fig. 8 for [Ca, Sc, Ti/Fe] and [V, Cr, Co, Ni/Fe], to within our stated abundance uncertainties.
The light metals Mg and Si may not only be produced by SN II considering that [Mg, Si/Fe] flattens out for metallicities higher than −0.1 dex. The same behaviour was found by Chen et al. (2000) and Neves et al. (2009), who suggested that SN Ia is possibly contributing. The star HD 50806 is clearly enriched in Mg (and in other elements as well) according to Fig. 8, probably reflecting its membership to the thin-thick disc transition.
The situation of Mn, Cu, and Zn is somewhat more complex. The hypothesis of production in SN Ia still stands, but this is probably not the unique source. Allen & Porto de Mello (2011), in their study of s-process enriched stars, suggested that SN Ia is the main source of production of manganese, in opposition to the conclusions of Feltzing et al. (2007), who suggested that this element is mainly produced by SN II. Our results in Fig. 8, which show an increasing trend of [Mn/Fe] as a function of [Fe/H] (see also the bottom panel of Fig. 6, in which there is a sequential crescent ordination of ⟨ [X/Fe] ⟩ from the metal-poor clustering group to the metal-rich one), seem to support the idea of an extra nucleosynthetic source for the Mn yields. Such an increasing trend is also usually attributed to a metallicity dependence in the production of Mn in both SN Ia and SN II. In this work, Mn and Cu were plotted together through the mean abundance ratio [Mn, Cu/Fe]. Both these elements have abundances that increase with metallicity, though for Cu this trend is not as significant as for Mn, and seems to happen only for higher metallicities, being constant and close to zero for [Fe/H] < 0. Cu and Zn, although being adjacent elements in the periodic table, stand in the transition between iron-peak and s-process elements, and their behaviour is in sharp contrast. A decreasing trend in [Zn/Fe] vs. [Fe/H] is seen for stars poorer than the Sun, in agreement with Fig. 1 of Allen & Porto de Mello (2011).
 |
Fig. 8 Abundance ratios as a function of the stellar metallicity for individual elements (top panels) and for nucleosynthetic groups (bottom panels). The ordinate axis has a different scale for [Ba/Fe] due to its larger abundances. The linear regressions (solid line), the 95% confidence intervals (hashed area), and the cross-correlation coefficients are also shown for |r| ≥ 0.5. The symbols follow the classification of Sect. 5 (see Fig. 6). |
 |
Fig. 9 Abundance ratios as a function of [Ba/Fe]. For the elements of the light s-process (Sr, Y, and Zr) the mean abundance ratios are plotted. The linear regressions (solid line), the 95% confidence intervals (hashed area), and the cross-correlation coefficients are also shown for |r| ≥ 0.5. The symbols follow the classification of Sect. 5 (see Fig. 6). |
The elements C and Na were not grouped together with other elements. C is synthesised in several different sites and behaves similarly to O and N, with [C/Fe] decreasing with increasing metallicity. This negative trend is mostly observed in the metal-poor regime ([Fe/H] < −0.3), hence not seen in Fig. 8 given the limited metallicity range of our programme stars. Nevertheless, our results agree very well with the recent C abundance determination performed by da Silva et al. (2011) for solar-like dwarfs. Na is probably produced, among other processes, in the core of massive stars and ejected by SN II into the interstellar medium. Here we found that [Na/Fe] is constant and nearly close to zero in the range of metal-poor stars, with a possible increasing trend for higher metallicities. Chen et al. (2000) suggested that maybe [Na/Fe] is close to zero for the whole metallicity range of disc stars. Neves et al. (2009), however, found that [Na/Fe] is close to zero for thin disc stars for [Fe/H] between −0.2 and +0.2, but above solar for other values of metallicity.
The [X/Fe] abundance ratios of elements of the s-process, mainly produced in TP-AGB of intermediate or low mass stars, and the r-process, produced in sites with high neutron density such as the final stages of massive stars (SN II, neutron stars), are supposed, respectively, to progressively increase and decrease from metal-poor stars to higher metallicities. These facts reflect the production of these elements in different time scales with respect to iron, the former products of long-lived AGB stars, the latter arising from short-lived massive stars which explode as supernovae. This is not clearly observed in the diagrams of Fig. 8 for Sm and the s-process elements because of the short metallicity range. An interesting result of the analysis of these diagrams are the properties involving some Ba-enriched stars, which we discuss in the next section.
6.3. Abundance trends as a function of [Ba/Fe]
A few stars in our sample are remarkably enriched in Ba by more than 3σ, especially HD 39587 and HD 147513. For this reason we also investigated the behaviour of the abundance ratios [X/Fe] or ⟨ [X/Fe] ⟩ as a function of [Ba/Fe] for some elements or groups of elements showing some kind of relation with the production of barium (see Fig. 9). Once more, we computed the cross-correlations coefficients and we plotted in the figure the regressions of the most significant trends (| r| ≥ 0.5).
Castro et al. (1999) proposed the existence of an anticorrelation between the abundances of Cu and the s-process elements. They found that [Cu/Fe] decreases with the increasing of [Ba/Fe], suggesting a relation between the destruction of Cu and the production of Ba (and other s-process elements). In the recent analysis of Ba-enriched stars of Allen & Porto de Mello (2011), the authors have not supported this scenario, arguing that Cu seems to be little (or not at all) affected by the s-process, even though they have acknowledged that some Ba-rich stars do present anticorrelated abundances of Cu and the s-process elements. Our results point to a statistically significant decrease in the abundances of Cu with increasing [Ba/Fe], in accordance with Castro et al. (1999).
Two other iron-peak elements, Mn and Zn, are also shown in Fig. 9 and no clear correlation is observed. This may indicate that Mn and Cu do not share the same nucleosynthetic origin. Indeed, Allen & Porto de Mello (2011) found that the synthesis of Cu receives a larger contribution from not so massive stars than Zn, a result roughly in line with those of Castro et al. (1999) and ours. Such results point towards the necessity of both more extensive observations of the abundances of Cu and Zn, and more protracted theoretical efforts, in order that a better understanding of the complex chemical history of these two elements may be achieved.
Castro et al. (1999) also proposed an anticorrelation in the abundances of C and Na with respect to [Ba/Fe]. Our results do not seem to support this anticorrelation, though our most Ba-rich stars, the Ursa Major group members HD 39587 and HD 147513, are markedly C-deficient. Porto de Mello & da Silva (1997a) attributed the [C/Fe] deficiency of a barium star to the 13C(α,n)16O reaction that occurred in the hot-bottom envelope of its companion during the TP-AGB phase. However, HD 39587 and HD 147513 are no longer regarded as true barium stars.
Figure 9 shows an evident expected correlation for the light s-process elements (Sr, Y, and Zr). Correlations involving Nd, another heavy element of the s-process may also exist, but its abundance determination has larger uncertainties. An anticorrelation between [Sm/Fe] and [Ba/Fe] also seems to exist. Sm is a good representative of the r-process elements, and despite the very large uncertainties in the determination of such elements, usually showing very few lines in the spectra of solar-type stars, an interpretation in which this anticorrelation is due to ever more efficient production of s-process elements in AGB stars, as compared to the production of the r-process in SN II, seems warranted.
6.4. Abundance trends as a function of age
One of the motivations of the present paper is to explore the abundance ratios of elements due to different nucleosynthetic processes and the stellar ages, taking advantage of the reasonably precise ages that can be attributed to our programme stars. Figure 11 shows the diagrams [X/Fe] and ⟨ [X/Fe] ⟩ as a function of the stellar age, and Fig. 12 explores the relation between the abundance ratios [X1/X2] of different elements and age. Similarly to Fig. 8, we have fitted linear regressions on the diagrams in three ranges of stellar age: for stars younger than the Sun (age <4.53 Gyr), for stars older than the Sun, and for all the sample stars. We have then computed the cross-correlation coefficients in these three ranges of stellar age and plotted the regressions of the more significant trends (only if |r| ≥ 0.5). In these figures there are positive, negative, or flat abundance trends in the three ranges of age. We notice, however, that the age of the Sun, used as a reference, was arbitrarily chosen. The exact value of the transition age when the abundance behaviour changes is not clear from these plots (it is a value between 4 and 6 Gyr).
 |
Fig. 10 Stellar metallicity as a function of age. The symbols follow the classification of Sect. 5 (see Fig. 6). |
In spite of the long recognition (though not undisputed) of the so-called age-metallicity relation (see Fig. 10), the individual abundances in Figs. 11 and those in 8 do not share exactly the same behaviour, leading us to suggest in the following that the age-metallicity relation may be a multidimensional concept. For this reason, we regrouped the elements according to their abundance behaviour with age (see the bottom panels of Fig. 11).
Carbon and sodium do not seem to present any important trends of [X/Fe] with age. The positive trends observed for Mg, Sc, and Ti (less clearly seen for Si and Ca) are simply the result of the Galactic chemical evolution. The production rate of these elements by SN II decrease with time since the formation of the Galactic disc (equivalently to increasing with age) compared to the increased production of Fe by the longer-lived SN Ia as we approach more recent epochs. Silicon perhaps shows no trend at all; Mg seems to have a more or less positive linear trend with increasing age; in their turn Ca, Sc, and Ti sport a more complex behaviour. The statistical significance of the behaviour of Ca is slight, and not much confidence should be placed in the apparent [Ca/Fe] decrease with time, followed by an increase towards more recent times. Taken at face value, this would appear to lend support to the suggestion that some fraction of the Ca synthesis might be due to SN Ia, in unison with their production of Fe. Sc and Ti seem to have a significant decrease with time with respect to Fe, but this decrease stops at a time close to the solar age and flattens thereafter towards present times.
Among the Fe-peak elements, no important trend is seen in the [X/Fe] relation with age for V, Cr, Co, and Zn; only a dubious one for Ni in the interval of young stars. Yet, again, Cu and Mn suggest more underlying complexity. Even though the statistical significance of the linear regressions is slight, the abundance ratios to Fe of both these elements seem first to increase towards the present epoch, and then decrease (a behaviour that is reinforced when these two elements are plotted together through the mean abundance ratio [Mn, Cu/Fe]). Recalling that Allen & Porto de Mello (2011) have found that Mn is mostly due to SN Ia, our result could imply that the relative yield of Mn to Fe in SN Ia decreases with time (and consequently the overall metallicity). The situation for Cu is less straightforward, as usual. Allen & Porto de Mello (2011) suggest that little of the synthesis of Mn, Cu, and Zn is owed to the main s-process, leaving the action of AGB stars an unlikely source of such a behaviour. These same authors assert that the action of the so-called weak s-process, sited at the He-burning core of massive stars, has a non negligible contribution to the synthesis of Mn, Cu, and Zn. One possible explanation for the decrease of the abundance ratios of [Mn/Fe] and [Cu/Fe] towards more recent times is a decreasing yield of the weak s-process in their synthesis, as contrasted to the production of Fe by SN Ia. Clearly, an understanding of the detailed chemical evolution of elements, in both the dimensions of metallicity and age, of the Fe-peak and its transition with the heavier elements deserves closer scrutiny, both observationally and theoretically.
 |
Fig. 11 Abundance ratios as a function of the stellar age for individual elements (top panels) and for nucleosynthetic groups (bottom panels). The vertical dashed line indicates the adopted solar age (4.53 Gyr). The linear regressions (solid line), the 95% confidence intervals (hashed area), and the cross-correlation coefficients are also shown for |r| ≥ 0.5. The symbols follow the classification of Sect. 5 (see Fig. 6). |
 |
Fig. 12 Abundance ratios as a function of the stellar age. The vertical dashed line indicates the adopted solar age (4.53 Gyr). The linear regressions (solid line), the 95% confidence intervals (hashed area), and the cross-correlation coefficients are also shown for |r| ≥ 0.5. The symbols follow the classification of Sect. 5 (see Fig. 6). |
Atomic line parameters of the elements used in the analysis.
We next turn to the [X/Fe]-age relation for the s-process elements. These present particular interest, since Castro et al. (1999) suggested, also using data from Edvardsson et al. (1993), that [Ba/H] has a steeper decrease with age than [Fe/H], and therefore that [Ba/Fe] increases towards modern times (see also Bensby et al. 2007). This fact might be interpreted, again, as a consequence of the larger yield of the s-process element synthesis by the long-lived AGB stars in relation to the not as-long-lived production of Fe by SN Ia. Do the other s-process elements show a behaviour similar to barium? Apparently this is so, but not in a straightforward way. The lighter s-process elements Sr and Y seem to have a linear trend of [X/Fe] with age (clearly seen for Sr), increasing towards present times, as expected. The [Zr/Fe], [Ce/Fe], and [Nd/Fe] ratio, however, appears flat in the old age regime, possibly increasing only for stars younger than the Sun. The [Ba/Fe] ratio behaves similarly but the increase towards younger ages is much sharper and more significant. At face value, these results point towards the evolution of the relative yields of such s-process elements with time (and metallicity) in AGB stars, apparently favouring the heavier species Ba and Nd over lighter ones. The simultaneous analysis of the [Cu/Fe] and [s-process/Fe] ratios, epitomised, for example, by the [Ba/Fe] relation with age, suggests an anticorrelation of Cu and Ba towards younger stars, as found by Castro et al. (1999), adding to the controversy surrounding the chemical evolution of copper.
Finally, a positive trend with increasing age is observed for [Sm/Fe] in stars younger than the Sun, again reflecting the smaller number of SN II than SN Ia in the present in comparison with the past (in this case the epoch of the Sun’s formation). Significant positive trends are also observed for Ni and Cu in the regime of younger stars.
Concerning the four groups yielded by the tree clustering analysis and their relation with age, we can only state that, as expected, the old stars in our sample are also metal-poor, whereas young stars tend to be metal-rich. Once more, the case of the star HD 50806 is evidenced. Although classified in the intermediate group of stars with slightly over-solar abundances (⟨ [X/H] ⟩ = +0.06 dex), it is situated close to the group of metal-poor stars (⟨ [X/H] ⟩ = −0.24 dex) in Fig. 11, which is maybe a consequence of its population membership.
The bottom panels of Fig. 11 shows the average of the [X/Fe] relations with age for selected groups of elements. Thus we see that grouping Sc and Ti reinforces the relation with age already shown by each element individually, and the same is seen for the grouping of Sr and Y. Similarly, averaging the [X/Fe] relations with age for Zr, Ba, and Nd produces a very steep increase towards present epochs, after a flat relation from the birth of the Galactic disc up to the solar age.
These results prompted us to investigate the specifics of the [X1/X2] ratios with age, where X1 and X2 designate elements other than Fe. In Fig. 12 we explore the time evolution of some elements that displayed a particular clear [X/Fe] relation with age. Thus, it is apparent that the [Ba/Mg] and [Ba/Zn] increase steeply towards present epochs, for stars younger than the Sun, reinforcing their individual and opposite behaviour in the [X/Fe]-age diagrams. Also, both [Sr/Mg] and [Y/Mg] increase linearly and significantly from the oldest to the youngest stars; the same is seen in the [Sr/Zn] and [Y/Zn] ratios. Investigating the [X1/X2] ratios of s-process to r-process elements, we found steep increases in the [Ba/Sm], [Sr/Sm], and [Y/Sm] ratios towards younger stars, but only for objects younger than the Sun. Significant age relations are, therefore, evidenced in the [X1/X2] ratios of diverse elements, representing a wide range of nucleosynthetic processes and tentatively allowing the proposition that the age-metallicity relation is a more complex constraint to Galactic chemo-dynamical models than hitherto recognised.
6.5. Abundance trends with condensation temperature
Our determination of multi-elemental abundances also provides the study of possible trends in the abundance ratios [X/Fe] as a function of the condensation temperature (TC) of each element. Values of 50% TC (the temperature when 50% of an element is in the condensed phase) for a solar-system composition gas were taken from Lodders (2003) and Lodders et al. (2009).
For a few stars in our sample we have found some correlations of [X/Fe]
with TC (even after corrections due to Galactic chemical
evolution effects were applied). However, no clear correlation seems to exist when
comparing the slopes for refractory elements (those with
TC ≳ 900 K) with several stellar
parameters (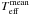 , [Fe/H],
log g, ξ, mass, and age). The one involving the
metallicity was proposed by Ramirez et al. (2010)
in the sense that higher-metallicity stars present more negative slopes. Our results agree
with their paper, but the number of metal-rich stars in our sample is too small to confirm
their conclusions.
, [Fe/H],
log g, ξ, mass, and age). The one involving the
metallicity was proposed by Ramirez et al. (2010)
in the sense that higher-metallicity stars present more negative slopes. Our results agree
with their paper, but the number of metal-rich stars in our sample is too small to confirm
their conclusions.
7. Conclusions
In this work we have performed a multi-elemental, differentially with respect to the Sun, spectroscopic analysis of a sample of 25 solar-type stars in the solar neighbourhood. We have derived their atmospheric parameters (from various nearly independent criteria and with low internal errors), masses, ages, kinematical and orbital parameters, and elemental abundances (derived with very low internal uncertainties) based on equivalent widths or spectral synthesis.
Despite small in size, our sample was carefully selected to undergo an homogeneous and detailed analysis based on spectra with high resolution and high S/N. We have: (i) checked the effective temperatures based on the excitation equilibrium of neutral iron lines against those from photometric calibrations and from the Hα wings profile; (ii) checked the surface gravities computed through the ionisation equilibrium between Fe i and Fe ii lines against those computed based on the evolutionary parameters; (iii) derived masses and ages from evolutionary tracks and isochrones computed considering the metallicity of each star; and (iv) applied a differential spectroscopic analysis relative to the Sun, hence minimising the systematic errors and yielding a mean uncertainty of 0.06 dex in the abundance ratios. We thus expect that our determinations have achieved a high level of precision and accuracy.
Oscillator strengths (log gf) for lines with hyperfine structure computed based on the Ganymede spectra observed in the first (Gany 1) and second (Gany 2) runs.
Elemental abundance relative to iron.
We have also applied a statistical study to our abundance results using the method of tree clustering analysis, through which we looked for groupings of stars that share similar abundances in the [X/H] space. Although our sample has a limited range in metallicity, it covers a broad range in age. The detailed abundance pattern was then investigated through correlations with kinematics, Galactic orbits, and stellar ages. Our conclusions are thus summarised:
-
1–
Four groups were identified, two having over-solarabundances (with averages +0.26 and+0.06 dex on [X/H]), and two withunder-solar abundance values (on average −0.06 and −0.24 dex). Possible non-solar abundance ratios, even for stars which share the same age, Galactic orbit, and metallicity as the Sun, are suggested. Whether these are due to heterogeneity in the stellar natal clouds, or by dynamical migration within the Galactic disc, should be investigated with larger samples. In particular, the results of Rocha-Pinto et al. (2006) that metal-poor and old stars show more orbital radial spread in the Galaxy could not be verified given the limitation of our sample.
-
2–
The presence of Ba-enriched stars in our sample prompted us to investigate in detail the relation of some elements with Ba. An anticorrelation between [Cu/Fe] and [Ba/Fe] was found, in line with similar claims in the literature. The [Sm/Fe] abundance ratios seem to be anticorrelated with [Ba/Fe], barely at the 95% confidence level. On the other hand, previous suggestions of [C/Fe] and [Na/Fe] anticorrelations with [Ba/Fe] could not be confirmed. Even though the possible connected chemical evolution of Mn, Cu, and Zn has been recently discussed in the literature, no significant trend of [Mn/Fe] and [Zn/Fe] with [Ba/Fe] is suggested.
-
3–
The consideration of the [X/Fe] ratios with age revealed much differing behaviour of the elements, suggesting that the age-metallicity relation has more underlying complexity than commonly recognised. The [Mg/Fe], [Sc/Fe], and [Ti/Fe] decrease towards younger ages. The [Cu/Fe] and [Mn/Fe] ratios initially increase towards younger stars up to the solar age, and then decrease towards the youngest objects, a result that may speak of differing yields in the SN Ia production of these elements, related to metallicity and age, as well as a possible influence of the evolution with time of the weak s-process yields, operating off of massive stars. The steepest relation with age was found for the [Ba/Fe] ratio, but only for ages younger than the solar one, and a similar but less evident behaviour is seen for Zr, Ce, and Nd. Other heavy s-process elements, however, such as Sr and Y, show a linearly increasing [X/Fe] towards younger ages, particularly clearer for Sr. [Sm/Fe] significantly decreases for stars younger than the Sun. Thus, the [Cu/Ba] ratio clearly decreases towards younger stars, and the same is seen at a significant level for [Sm/Ba].
-
4–
Considering the average of elements with similar behaviour with age considerably reinforces the aforementioned results, particularly for the [Sc,Ti/Fe], [Mn,Cu/Fe], [Sr,Y/Fe], and [Zr,Ba,Nd/Fe] relations.
-
5–
The consideration of element ratios not directly involving Fe shows some marked behaviour. Particularly, the [Ba/Mg], [Ba/Zn], [Ba/Sm], [Sr/Sm], and [Y/Sm] steeply increase towards younger ages for stars younger than the Sun. Also, the [Sr/Mg] and [Y/Mg] ratios linearly increase towards younger ages, and the same is seen for [Sr/Zn] and [Y/Zn].
-
6–
Possible correlations involving the abundances, the condensation temperatures of the different elements, and the presence of exoplanets in our programme stars were deeply investigated, but no significant correlation was found.
The detailed consideration of precise element abundances derived from high-quality atmospheric parameters and spectroscopic data, tied to masses, kinematics, and ages for solar-type stars, generally provides a wealth of interesting data, contributing towards a broader understanding of the evolution of the Galaxy in its chemical and dynamical aspects.
Acknowledgments
R.D.S. thanks the financial support from the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) in the form of a fellowship (PROAP/INPE). L.S.R. thanks the grants (100454/2004-6 and 309326/2009-5) received from the Brazilian Foundation CNPq, and also Luzia P. Rité and Charles Rité for their help in data reductions. G.F.P.M. acknowledges the financial support by CNPq (476909/2006-6 and 474972/2009-7) and FAPERJ (APQ1/26/170.687/2004) grants. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France, and of NASA’s Astrophysics Data System. We acknowledge many fruitful discussions with Verne V. Smith and Katia Cunha. We all thank the critical and important report from the referee Dr. Gustafsson, which has deeply improved this manuscript.
References
- Allen, D. M., & Porto de Mello, G. F. 2011, A&A, 525, 63 [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Batten, A. H., Fletcher, J. M., & MacCarthy, D. G. 1989, in Eighth Catalogue of the Spectroscopic Binary Systems, PDAO, 17, 1 [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyn, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Zenn, A. R., Oey, M. S., & Feltzing, S. 2007, ApJ, 663, L13 [CrossRef] [Google Scholar]
- Castro, S., Porto de Mello, G. F., & da Silva, L. 1999, MNRAS, 305, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y. Q., Nissen, P. E., Zhao, G., Zhang, H. W., & Benoni, T. 2000, A&AS, 141, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y. Q., Zhao, G., Izumiura, H., et al. 2008, AJ, 135, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L. 1975, AJ, 80, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., Barnes, J. V., Faure, B. Q., & Golson, J. C. 1966, AJ, 71, 709 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, R., Milone, A. C., & Reddy, B. E. 2011, A&A, 526, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dehnen, W., & Binney, J. J. 1998, MNRAS, 298, 387 [NASA ADS] [CrossRef] [Google Scholar]
- del Peloso, E. F., Cunha, K., da Silva, L., & Porto de Mello, G. F. 2005, A&A, 441, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-Cordovés, J., Claret, A., & Giménez, A. 1995, A&AS, 110, 329 [NASA ADS] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
- Everitt, B. S., Landau, S., Leese, M., & Stahl, D. 2001, in Cluster Analysis, 5th edn. (London: Wiley), 77 [Google Scholar]
- Fabregat, J., & Reglero, V. 1990, A&AS, 82, 531 [NASA ADS] [Google Scholar]
- Feltzing, S., Fohlman, M., & Bensby, T. 2007, A&A, 467, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferro, A. A., Parrao, L., Schuster, W., et al. 1990, A&AS, 83, 225 [NASA ADS] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 2004, Astron. Nachr., 325, 3 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements (Cambridge University Press) [Google Scholar]
- Gronbech, B., & Olsen, E. H. 1976, A&AS, 25, 213 [NASA ADS] [Google Scholar]
- Gronbech, B., & Olsen, E. H. 1977, A&AS, 27, 443 [NASA ADS] [Google Scholar]
- Guenther, D. B., & Demarque, P. 1997, ApJ, 484, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffleit, D., & Jaschek, C. 1982, in The Bright Star Catalogue, Yale University Observatory, New Haven [Google Scholar]
- Holberg, J. B., Oswalt, T. D., & Sion, E. M. 2002, ApJ, 571, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, D. R. H., & Soderblom, D. R. 1987, AJ, 93, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y.-C., Demarque, P., Yi, S. K., & Alexander, D. R. 2002, ApJS, 143, 499 [NASA ADS] [CrossRef] [Google Scholar]
- König, B., Fuhrmann, K., Neuhäuser, R., Charbonneau, D., & Jayawardhana, R. 2002, A&A, 394, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korotin, S., Mishenina, T., Gorbaneva, T., & Soubiran, C. 2011, MNRAS, 415, 2093 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N. E., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, BaltA, 9, 590 [Google Scholar]
- Kurucz, R. L. 1992, Rev. Mex. Astron. Astrofis., 23, 45 [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, in The Solar Flux Atlas from 296 nm to 1300 nm, National Solar Observatory [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, in Abundance of the Elements in the Solar System, Landolt Börnstein, New Series, Vol. VI/4B, Chap. 4.4, ed. J. E. Trümper (Berlin, Heidelberg, New York: Springer-Verlag), 560 [Google Scholar]
- López-Santiago, J., Montes, D., Gálvez-Ortiz, M. C., et al. 2010, A&A, 514, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., & Porto de Mello, G. F. 2005, A&A, 431, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- McWilliam, A. 1997, ARA&A, 35, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Meylan, T., Furenlid, I., Wiggs, M. S., & Kurucz, R. L. 1993, ApJS, 85, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Montes, D., López-Santiago, J., Gálvez, M. C., et al. 2001, MNRAS, 328, 45 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Moore, C.E., Minnaert, M., & Houtgast, J. 1966, in The Solar Spectrum 2935 Å to 8770 Å, Nat. Bur. Std., US Monograph 61 [Google Scholar]
- Neves, V., Santos, N. C., Sousa, S. G., Correia, A. C. M., & Israelian, G. 2009, A&A, 497, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olsen, E. H. 1977, A&AS, 29, 313 [NASA ADS] [Google Scholar]
- Olsen, E. H. 1983, A&AS, 54, 55 [NASA ADS] [Google Scholar]
- Olsen, E. H. 1993, A&AS, 102, 89 [NASA ADS] [Google Scholar]
- Olsen, E. H. 1994a, A&AS, 104, 429 [NASA ADS] [Google Scholar]
- Olsen, E. H. 1994b, A&AS, 106, 257 [NASA ADS] [Google Scholar]
- Olsen, E. H., & Perry, C. L. 1984, A&AS, 56, 229 [NASA ADS] [Google Scholar]
- Perry, C. L., Olsen, E. H., & Crawford, D. L. 1987, PASP, 99, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Porto de Mello, G. F., & da Silva, L. 1997a, ApJ, 476, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Porto de Mello, G. F., & da Silva, L. 1997b, ApJ, 482, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Porto de Mello, G. F., Lyra, W., & Keller, G. R. 2008, A&A, 488, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Asplund, M., Baumann, P., Meléndez, J., & Bensby, T. 2010, A&A, 521, 33 [Google Scholar]
- Reddy, B. E., Tomkin, J., Lambert, D. L., & Allen de Prieto, C. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Reglero, V., & Fabregat, J. 1991, A&AS, 90, 25 [NASA ADS] [Google Scholar]
- Ribas, I., Porto de Mello, G. F., Ferreira, L. D., et al. 2010, ApJ, 714, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Rocha-Pinto, H. J., Rangel, R. H. O., Porto de Mello, G. F., Bragança, G. A, & Maciel, W. J. 2006, A&A, 453, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, BaltA, 6, 244 [Google Scholar]
- Santos, N. C., Bouchy, F., Mayor, M., et al. 2004, A&A, 426, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuster, W. J., & Nissen, P. E. 1988, A&AS, 73, 225 [NASA ADS] [Google Scholar]
- Soderblom, D. R., & Mayor, M. 1993, AJ, 105, 226 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, M. 1967, Ann. Astrophys., 30, 211 [Google Scholar]
- Steffen, M. 1985, A&AS, 59, 403 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Torres, C. A. O., Quast, G. R., da Silva, L., et al. 2006, A&A, 460, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Twarog, B. A. 1980, ApJS, 44, 1 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data, Astrophys. Space Sci. Libr., 350 [Google Scholar]
- Warren, R. H., Jr., & Hoffleit, D. 1987, BAAS, 19, 733 [NASA ADS] [Google Scholar]
- Whiting, E. E., & Nicholls, R. W. 1974, ApJS, 27, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Carbon abundance ratios derived from the spectral synthesis of the two atomic lines (λ5052.2 and λ5380.3) and the two C2 band heads (λ5128 and λ5165) studied.
Groups of chemical elements and uncertainties in the mean abundance ratios ⟨ [X/Fe] ⟩ .
Oscillator strengths (log gf) for lines with hyperfine structure computed based on the Ganymede spectra observed in the first (Gany 1) and second (Gany 2) runs.
All Figures
 |
Fig. 1 Left panel: comparison of the EWs measured in this work in the Ganymede spectrum (second observation run) by Gaussian function fit to those measured by Meylan et al. (1993) in the Solar Flux Atlas by Voigt function fit; filled circles represent 145 lines of several elements; the linear regression (solid line) is the same expressed by Eq. (2). Right panel: comparison of the EWs listed in Table 8 of all lines in the Ganymede spectra in common to both runs after the conversions according to Eqs. (1) and (2); the coefficients of the linear regression (solid line) are shown. |
| In the text | |
 |
Fig. 2 Spectral synthesis of the C2 molecular band regions (λ5128 and λ5165) and of the C atomic lines (λ5052.2 and λ5380.3) for Ganymede of the second observation run (top panels) and for one metal-rich star of the first run, HD 160691 (bottom panels). The solid lines represent three models with different values of [C/Fe]: −0.05 (red), 0.0 (green), and +0.05 dex (blue). The differences between observed (dots) and computed spectra (o−c) are also shown in the bottom of each panel. |
| In the text | |
 |
Fig. 3 Comparisons of the three effective temperature indicators: the excitation vs. photometric (top panel), excitation vs. Hα (middle panel), and photometric vs. Hα (bottom panel) temperatures. The symbols represent the stellar groups defined in Sect. 5 (see Fig. 6). |
| In the text | |
 |
Fig. 4 Evolutionary tracks (magenta solid lines) and isochrones (blue dots and dashed lines) from Yonsei-Yale, calculated for different values of metallicity, showing how to derive the stellar masses and ages. The ages in Gyr are indicated alongside the evolutionary tracks, for which the masses are indicated in M⊙. The Sun’s position for Teff = 5777 K is also shown in the solar metallicity panel (top-left corner). |
| In the text | |
 |
Fig. 5 Galactic velocity components (left and middle panels) and orbital eccentricity as a function of the mean orbital distance from the Galactic centre (right panel) for the sample stars and the Sun. The symbols represent the stellar groups defined in Sect. 5. |
| In the text | |
 |
Fig. 6 Dendrogram (upper panel) and mean abundance ratios ⟨ [X/H] ⟩ (middle panel) and ⟨ [X/Fe] ⟩ (bottom panel) for the four stellar groups from the tree clustering analysis (Sect. 5). They are classified as metal-poor (▴), intermediate abundance (under solar △ or over solar °), or metal-rich (•) stars, and the same symbolism is adopted all over the paper. The dashed red line on the dendrogram represents a dissimilarity number of 0.9 dex. |
| In the text | |
 |
Fig. 7 Abundance ratios [X/Fe] for individual elements (top of each panel) and ⟨ [X/Fe] ⟩ for the nucleosynthetic groups (bottom of each panel). The uncertainties adopted are those listed in Tables 3 and 7. The symbols represent the stellar classification defined in Sect. 5 (see Fig. 6). |
| In the text | |
 |
Fig. 7 continued. |
| In the text | |
 |
Fig. 8 Abundance ratios as a function of the stellar metallicity for individual elements (top panels) and for nucleosynthetic groups (bottom panels). The ordinate axis has a different scale for [Ba/Fe] due to its larger abundances. The linear regressions (solid line), the 95% confidence intervals (hashed area), and the cross-correlation coefficients are also shown for |r| ≥ 0.5. The symbols follow the classification of Sect. 5 (see Fig. 6). |
| In the text | |
 |
Fig. 9 Abundance ratios as a function of [Ba/Fe]. For the elements of the light s-process (Sr, Y, and Zr) the mean abundance ratios are plotted. The linear regressions (solid line), the 95% confidence intervals (hashed area), and the cross-correlation coefficients are also shown for |r| ≥ 0.5. The symbols follow the classification of Sect. 5 (see Fig. 6). |
| In the text | |
 |
Fig. 10 Stellar metallicity as a function of age. The symbols follow the classification of Sect. 5 (see Fig. 6). |
| In the text | |
 |
Fig. 11 Abundance ratios as a function of the stellar age for individual elements (top panels) and for nucleosynthetic groups (bottom panels). The vertical dashed line indicates the adopted solar age (4.53 Gyr). The linear regressions (solid line), the 95% confidence intervals (hashed area), and the cross-correlation coefficients are also shown for |r| ≥ 0.5. The symbols follow the classification of Sect. 5 (see Fig. 6). |
| In the text | |
 |
Fig. 12 Abundance ratios as a function of the stellar age. The vertical dashed line indicates the adopted solar age (4.53 Gyr). The linear regressions (solid line), the 95% confidence intervals (hashed area), and the cross-correlation coefficients are also shown for |r| ≥ 0.5. The symbols follow the classification of Sect. 5 (see Fig. 6). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


