| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201218939 | |
| Published online | 20 April 2012 | |
Scaling laws for magnetic fields on the quiet Sun
1
Institute of Astronomy,
ETH Zurich,
8093
Zurich,
Switzerland
e-mail: stenflo@astro.phys.ethz.ch
2
Istituto Ricerche Solari Locarno, via Patocchi,
6605
Locarno Monti,
Switzerland
Received: 1 February 2012
Accepted: 13 March 2012
The Sun’s magnetic field is structured over a range of scales that span approximately seven orders of magnitudes, four of which lie beyond the resolving power of current telescopes. Here we have used a Hinode SOT/SP deep mode data set for the quiet-Sun disk center in combination with constraints from the Hanle effect to derive scaling laws that describe how the magnetic structuring varies from the resolved scales down to the magnetic diffusion limit, where the field ceases to be frozen-in. The focus of the analysis is a derivation of the magnetic energy spectrum, but we also discuss the scale dependence of the probability density function for the flux densities and the role of the cancellation function for the average unsigned flux density. Analysis of the Hinode data set with the line-ratio method reveals a collapsed flux population in the form of flux tubes with a size distribution that is peaked in the 10–100 km range. Magnetic energy is injected into this scale range by the instability mechanism of flux tube collapse, which is driven by the external gas pressure in the superadiabatic region at the top of the convection zone. This elevates the magnetic energy spectrum just beyond the telescope resolution limit. Flux tube decay feeds an inertial range that cascades down the scale spectrum to the magnetic diffusion limit, and which contains the tangled, “hidden” flux that is known to exist from observations of the Hanle effect. The observational constraints demand that the total magnetic energy in the hidden flux must be of the same order as the total energy in the kG flux tubes. Both the flux tubes and the hidden flux are found to be preferentially located in the intergranular lanes, which is to be expected since they are physically related.
Key words: Sun: atmosphere / magnetic fields / polarization / magnetohydrodynamics (MHD)
© ESO, 2012
1. Introduction
Different types of scaling laws have been used to explore how solar magnetic fields vary with scale size. Since the structuring is produced by turbulent convection and turbulent properties are usually described in terms of energy spectra, there have been a number of attempts to derive and analyse such spectra for magnetic fields observed in solar magnetograms (Nakagawa & Priest 1973; Nakagawa & Levine 1974; Knobloch 1981; Knobloch & Rosner 1981; Petrovay 2001; Abramenko et al. 2001; Abramenko & Yurchyshyn 2010b; Abramenko et al. 2011). The obtained spectra refer to the directly observed domain above the resolution cut-off of the data sets used. However, since the physical cut-off, the magnetic diffusion limit, where the magnetic field ceases to be frozen-in, is located at scales that are about four orders of magnitude smaller, the observationally resolved domain covers only the large-scale end of the spectrum. With the assumption that the fundamental dissipation of the magnetic field occurs as ohmic dissipation, the diffusion limit is the scale at which the magnetic Reynolds number becomes unity, or in other words, where the ohmic diffusion time scale becomes comparable to the dynamic time scale (cf. de Wijn et al. 2009).
Since the resolved magnetic fields appear to exhibit a high degree of self-similarity and scale invariance, they have been explored by fractal analysis (e.g. Lawrence et al. 1993, 1996; Cadavid et al. 1994; Janßen et al. 2003; Abramenko & Yurchyshyn 2010a). Another useful concept related to the multi-fractal nature of the field is the so-called cancellation function, introduced and applied by Pietarila Graham et al. (2009) in the analysis of quiet-Sun data from the Hinode SOT/SP instrument (Kosugi et al. 2007; Suematsu et al. 2008; Tsuneta et al. 2008), leading to the conclusion that at least 80% of the magnetic flux is invisible at the Hinode resolution due to cancellation of the contributions from the opposite magnetic polarities within the spatial resolution element. This confirms the long-standing (three decades old) conclusion from observations of the Hanle effect (Stenflo 1982, 1987; Trujillo Bueno et al. 2004) that the photosphere is seething with an ocean of tangled, “hidden” magnetic flux that is invisible to Zeeman-effect observations with the available angular resolution.
The statistical properties of the magnetic fields need to be described in terms of distribution functions, the most common of which is the probability density function (PDF) of the magnetic flux densities or of the field strengths. To avoid confusion we here want to reserve the term “field strength” for the resolved, unsmeared field, and use the term “flux density” for the field that has been smoothed by the spatial resolution window. As no quiet-Sun field structures are resolved with the Hinode resolution, the directly observed PDF, of the flux densities, is very different from the PDF for the field strengths, which can only be inferred by indirect methods. The flux density PDF for the quiet Sun, as observed with Hinode, is characterized by an extremely narrow core that is centered at zero field and can be approximated by a stretched exponential, and by extended wings that decline quadratically and extend out to the kG region (Stenflo 2010).
A powerful method to infer the magnetic structure at scales beyond the spatial resolution limit is the Stokes V line-ratio technique, which was introduced and used for the discovery four decades ago (Stenflo 1973) that a large fraction of the quiet-Sun magnetic flux is in the form of strong-field (kG) flux tubes with small filling factors (of order 1% in quiet regions). A theoretical explanation for this extreme intermittency was provided by the instability mechanism of flux tube collapse (Parker 1978; Spruit 1979; Spruit & Zweibel 1979; Unno & Ando 1979). Application of the line-ratio technique to Hinode SOT/SP data has allowed the two distinct flux populations, the collapsed and uncollapsed population, to be identified and statistically separated (Stenflo 2010). In a follow-up work (Stenflo 2011) the Hinode line-ratio data could be used to derive a histogram for the flux tube sizes (which is peaked in the 10–70 km range), and the collapsed population was found to be preferentially located in the intergranular lanes.
While it has been known since the early 1970s that much of the total quiet-Sun magnetic flux is in collapsed form and since the early 1980s that a large fraction of the flux must also be in hidden form (invisible in magnetograms), a comprehensive physical picture that connects these two apparently disjunct aspects of solar magnetism has been missing. The present work can be seen as an attempt to fill this gap.
Often the term “local dynamo” is used in discussions of small-scale magnetic structuring on the Sun. Here we avoid such terminology, since we find no evidence that the small-scale structuring that we will be discussing is produced by turbulent amplification of a weak seed field. Instead, as we will see, there is evidence that the very substantial amount of magnetic energy that exists on small scales (below a few km) is physically related to and fed from the magnetic energy at large scales, which is generated by the global dynamo. This implies that the rate of magnetic energy dissipation is faster than the rate of energy production by local dynamo action.
Our analysis of the magnetic scaling laws is based on the same Hinode SOT/SP data set for the quiet-Sun disk center that we used before (Stenflo 2010, 2011). This time the main focus is on the magnetic energy spectrum, its determination in the resolved domain, and its continuation throughout the unresolved domain down to the magnetic diffusion limit. In particular we explore the energy that is injected into the spectrum by the mechanism of flux tube collapse and try to identify the spectral location and the energy contents of the hidden magnetic flux that is responsible for the observed depolarization due to the Hanle effect. We further derive the PDF for the intrinsic field strengths that is needed to satisfy the joint Hanle and line-ratio constraints and discuss the nature and role of the cancellation function.
2. Energy spectra: concepts and definitions
The determination of the spectral energy density from solar observations of magnetic and velocity fields might seem to be a straightforward matter: compute the Fourier transform and square its absolute value to obtain the power spectrum. However, there are different ways in which the energy spectra can be defined, which sometimes leads to confusion, and the spectra are affected by noise and observational cut-offs. In addition there are technical issues like apodization and interpolation techniques.
2.1. Relations between the four versions of the energy spectra
In a 2D image the spatial x and y coordinates have their counterparts in the spectral domain in the wave numbers kx = 2π/Δx and ky = 2π/Δy, with total wave number 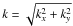 . We can distinguish between four versions of the spectral energy density: the 1D power spectra in the x and y directions, which after normalization (described below) we denote by Ex(kx) and Ey(ky), the 1D spectrum in k space, which we denote E1D(k), and the 2D spectrum E2D(kx,ky), which in the axially symmetric case can be written as E2D(k).
. We can distinguish between four versions of the spectral energy density: the 1D power spectra in the x and y directions, which after normalization (described below) we denote by Ex(kx) and Ey(ky), the 1D spectrum in k space, which we denote E1D(k), and the 2D spectrum E2D(kx,ky), which in the axially symmetric case can be written as E2D(k).
The normalization condition is 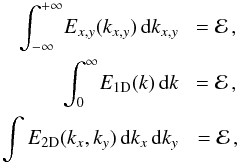 (1)where ℰ is the average energy density of the data set.
(1)where ℰ is the average energy density of the data set.
In SI units we have 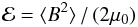 (2)for the magnetic field, where ⟨ B2 ⟩ is the spatial average of B2, and
(2)for the magnetic field, where ⟨ B2 ⟩ is the spatial average of B2, and 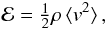 (3)where v is the velocity vector, and ρ is the mass density in the line-forming layer of the solar atmosphere, needed for the comparison between the magnetic and kinetic energy densities with respect to the issue of equipartition.
(3)where v is the velocity vector, and ρ is the mass density in the line-forming layer of the solar atmosphere, needed for the comparison between the magnetic and kinetic energy densities with respect to the issue of equipartition.
In the case of axial symmetry for E2D(kx,ky), which can safely be assumed for the disk center of the quiet Sun, the spectrum is independent of azimuthal angle, which means that 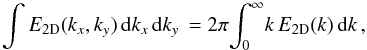 (4)from which follows that
(4)from which follows that 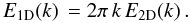 (5)In the axisymmetric case there is also a direct relation between Ex,y(kx,y) and E2D(k) via the Abel transform. If we for instance know Ey(ky), we obtain E2D(k) from the inverse Abel transform (introduced in solar physics for the analysis of solar granulation spectra by Uberoi 1955) through
(5)In the axisymmetric case there is also a direct relation between Ex,y(kx,y) and E2D(k) via the Abel transform. If we for instance know Ey(ky), we obtain E2D(k) from the inverse Abel transform (introduced in solar physics for the analysis of solar granulation spectra by Uberoi 1955) through 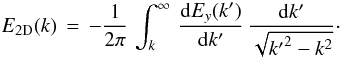 (6)Together with Eq. (5) we are then in a position to convert Ey(ky) into E1D(k).
(6)Together with Eq. (5) we are then in a position to convert Ey(ky) into E1D(k).
If Ey(ky) is given by a power law, then E1D(k) is also given by a power law with the same exponent. In contrast, the 2D spectrum E2D(k) does not obey the same power law.
We note that it is the version E1D(k) of the energy spectrum that is used in turbulence theory, for instance when the −5/3 power law is referred to in Kolmogorov (1941) theory.
2.2. Upper and lower cut-offs
The “true” 2D solar image is smeared by the effective resolution window (often called point spread function), determined by the size and quality of the telescope (and by atmospheric seeing in the case of ground-based instruments). This spatial smearing represents a convolution in the x-y plane, while in the kx-ky plane the power spectrum of the image gets multiplied by the 2D power spectrum of the resolution window, the modulation transfer function (MTF). The MTF is unity for small wave numbers k, but drops off steeply towards zero in the vicinity of the k that represents the resolution limit. This cut-off defines the upper boundary in k space of the observationally determined spectrum.
According to the sampling theorem, there have to be at least two pixels per resolution element (to avoid aliasing). If the pixel size is p, then the upper limit in k space is 2π/(2p), which approximately coincides with the resolution limit when one chooses two samples per resolution element.
There is a corresponding cut-off at low wave numbers, determined by the maximum size L of the field of view over which the energy spectrum is determined: 2π/L.
2.3. Field strengths and flux densities
The observed magnetic and velocity fields are not the “true” fields, but represent spatially smeared quantities due to the finite resolution of the instrument. To make this distinction explicit, we will mark the smeared (observed) quantities with a bar above the symbol. Thus the true velocity field along the line of sight (the z axis) is vz, while the corresponding observed quantity is 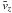 . Similarly, for the magnetic field we distinguish between Bz and
. Similarly, for the magnetic field we distinguish between Bz and 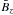 .
.
To avoid confusion, which has been abundant in previous literature, we employ the terminology introduced in Stenflo (2010), and never use the term “field strength” for 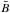 but the term “flux density” instead. We reserve the term “field strength” exclusively for B, the field seen with infinite resolution (a theoretical limit that is unreachable in practice). On the quiet Sun no flux elements are spatially resolved with the Hinode resolution. The quantities Bz and
but the term “flux density” instead. We reserve the term “field strength” exclusively for B, the field seen with infinite resolution (a theoretical limit that is unreachable in practice). On the quiet Sun no flux elements are spatially resolved with the Hinode resolution. The quantities Bz and 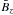 therefore differ profoundly, as we will see explicitly and quantitatively later when comparing the PDFs for the field strengths and the flux densities.
therefore differ profoundly, as we will see explicitly and quantitatively later when comparing the PDFs for the field strengths and the flux densities.
The set of equations given in Sect. 2.1 formally represent the unsmeared quantites. To obtain them in terms of the smeared quantities we place a bar above every physical quantity. If we denote the effective MTF of the telescope system by T(k), the relation between the apparent energy spectrum 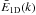 based on the smeared quantities, and the “intrinsic” energy spectrum E1D(k), becomes
based on the smeared quantities, and the “intrinsic” energy spectrum E1D(k), becomes 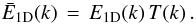 (7)
(7)
2.4. Apodization and interpolation
The Fourier integrals that are used for the determination of the spectrum extend to infinity, while the available field of view is finite. Mathematically the finite field of view can be described in terms of truncation of an ideally infinite image through multiplication by a window function that is unity within the field of view and zero outside. Due to this truncation the “true” Fourier spectrum gets convolved (or smeared) by a function that is the Fourier transform of the field-of-view window function.
As the Fourier transform of a rectangular window with sharp edges has large side lobes which could introduce unwanted spurious effects in the spectrum, one usually makes the sharp edges smooth by apodization. In the present work we apodize by tapering off the window function over the outer 1/3 of the field of view with a cosine bell function.
Since the k increment in the discrete, numerical representation of the energy spectrum becomes very course as we go to smaller wave numbers, it is desirable to make the representation and plotted curves smoother by interpolation. The standard way of doing this is not by direct interpolation in k space (which would not work well), but by extending the formal field of view with zeros, and then rescaling the resulting energy spectrum by dividing the spectrum with the fraction of the field of view that is occupied by real data (the “data filling factor”). In our case we have extended the length of our field of view by a factor of 6 to get a 6 times finer k grid.
2.5. Influence of noise and choice of data set
Since measurement noise can seriously distort the energy spectrum, it is of great importance to use data with the best possible signal-to-noise ratio, and in addition test the sensitivity of the data set to added artificial noise.
The best-quality magnetic-field data presently available in terms of well-defined high spatial resolution combined with low noise has been obtained with the Hinode satellite. There are two Hinode instruments that provide two types of magnetic-field data: the filter magnetograms in the Na i D1 line (FG data), and the spectrograph Stokes line profile data of the Fe i 6301.5 and 6302.5 Å lines (SOT/SP data). As the FG data are by far noisier than the SOT/SP data and in addition provide no information on the vector field or the filling factors, they are not suited for the present analysis.
Each exposure with the SOT/SP instrument provides 1D spatial information of the magnetic structuring along the spectrograph slit, here defined as the y direction (along the heliographic N-S direction). 2D images of the magnetic field distribution in the x-y plane can be built up by step-wise scanning in the x direction, but since the time it takes to cover a significant x range is generally much larger than the evolutionary time scale of the magnetic elements, the 2D images do not represent snapshots but mix spatial structuring with evolutionary effects. In addition, to cover a reasonable field of view in the x direction, the exposure time for each frame needs to be relatively short, with the consequence of more noise in these 2D magnetograms. Therefore they do not represent the best data set choice for a spectral analysis of quiet-Sun magnetic fields, for which the observable polarization signatures are very weak. The situation is different for active-region analysis, where the signals are strong.
Since low noise is so essential for quiet-Sun analysis, and since we need to avoid confusion between spatial structuring and evolutionary effects, the clearly best choice of data set is the SOT/SP deep mode recording with the slit at a fixed position at the quiet-Sun disk center. Our deep mode data set consists of a time series of 727 exposures, each with an integration time of 9.6 s, obtained on February 27, 2007. It is the identical data set that has already been subject to in-depth analysis by Lites et al. (2008) and Stenflo (2010, 2011). It provides high-quality magnetic-field data for the 1024 pixels of size 0.16 arcsec along the y direction.
The Stokes profile data for each pixel of this data set have been converted to vertical flux densities 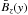 and total flux densities (the magnitude of the flux density vector)
and total flux densities (the magnitude of the flux density vector) 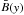 as described in Stenflo (2010), making use of the 6302/6301 line-ratio information to account for the non-linear effects on the pixel-averaged flux densities due to the subpixel flux tube structuring and line weakenings. Since the noise in the transverse field (after conversion from fractional polarization to G) is much larger (of order 25 times) than the noise in the longitudinal field, the determined total flux densities are much noisier than the vertical flux densities.
as described in Stenflo (2010), making use of the 6302/6301 line-ratio information to account for the non-linear effects on the pixel-averaged flux densities due to the subpixel flux tube structuring and line weakenings. Since the noise in the transverse field (after conversion from fractional polarization to G) is much larger (of order 25 times) than the noise in the longitudinal field, the determined total flux densities are much noisier than the vertical flux densities.
 |
Fig. 1 Magnetic energy spectra |
In Fig. 1 we show the computed 1D spectral energy density 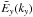 for the vertical flux densities, obtained by averaging the 727 power spectra along the slit (after apodization etc. as described in Sect. 2.4). The observational noise in the
for the vertical flux densities, obtained by averaging the 727 power spectra along the slit (after apodization etc. as described in Sect. 2.4). The observational noise in the 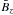 data is σobs = 1.4 G. To explore the effect of more noise, we have overplotted spectra for which random noise with a standard deviation of 1, 2, 4, 8, and 16 × σobs has been added to the
data is σobs = 1.4 G. To explore the effect of more noise, we have overplotted spectra for which random noise with a standard deviation of 1, 2, 4, 8, and 16 × σobs has been added to the 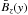 values. We see that adding only one σobs has almost no discernible effect on the spectrum, which confirms that the original spectrum is not significantly affected by noise. However, as more noise is added, the originally steep spectrum gets raised to become flatter (since the noise contribution is spectrally flat). As expected it is the largest wave numbers that are most affected by noise.
values. We see that adding only one σobs has almost no discernible effect on the spectrum, which confirms that the original spectrum is not significantly affected by noise. However, as more noise is added, the originally steep spectrum gets raised to become flatter (since the noise contribution is spectrally flat). As expected it is the largest wave numbers that are most affected by noise.
3. Equipartition between kinetic and magnetic energy
 |
Fig. 2 Magnetic energy spectra |
In Fig. 2 we compare (without added noise) the 1D spectra of the vertical and total flux densities. The two spectra are nearly indistinguishable except for the largest wave numbers, where the spectrum for the total flux densities flattens out. However, when comparing with the previous Fig. 1 we notice that the shape of this flattening is the same as obtained when random noise is added. Since we know that the noise level for the total flux densities is much larger than for the vertical flux densities, this behavior is expected.
There is therefore no evidence for a significant deviation between the spectra for the total and the vertical flux densities. This may seem surprising, because if for instance the field vectors would have an isotropic angular distribution, then the spectral density for the total flux density would be larger than that of the vertical flux density by a factor of 3 (due to the 3 spatial degrees of freedom). However, as was found in Stenflo (2010), the angular distribution of the field vectors is peaked around the vertical direction, except for the smallest flux densities, where the distribution becomes nearly isotropic (although the smallest flux densities are the ones that are most affected by noise). The contributions to the spectral energy density are proportional to  , which favors the contributions from the largest flux densities, which are the most vertical.
, which favors the contributions from the largest flux densities, which are the most vertical.
Therefore we will in the following take the energy spectrum for the vertical flux densities, being virtually noise free, to also represent the spectrum for the total flux densities. In the case of the velocity spectrum, however, the assumption of an isotropic angular distribution should be good (with some question marks for the lowest wave numbers or largest scales). Therefore we need to multiply the energy spectrum for the observed vertical velocities 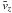 by 3, and in addition attach the factor
by 3, and in addition attach the factor 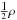 to obtain the kinetic energy spectrum that can be compared with the magnetic energy spectrum. The value of the mass density ρ does not come from observations, but must be chosen from a model atmosphere. The relevant choice for comparison with the magnetic energy density is the ρ that represents the height of formation of the Fe i lines on which the analysis is based.
to obtain the kinetic energy spectrum that can be compared with the magnetic energy spectrum. The value of the mass density ρ does not come from observations, but must be chosen from a model atmosphere. The relevant choice for comparison with the magnetic energy density is the ρ that represents the height of formation of the Fe i lines on which the analysis is based.
 |
Fig. 3 Comparison between the magnetic (solid) and kinetic (dotted) energy spectra |
For the comparison between the magnetic and kinetic energy spectra in Fig. 3 we have chosen ρ = 10-5 kg m-3 (or 10-8 g cm-3, the units normally used in model atmosphere tabulations), which is representative for the height of line formation (cf. Shchukina & Trujillo Bueno 2001). We find that for scales smaller than about 2 Mm the kinetic and magnetic energy spectra nearly coincide. This implies that there is equipartition between the magnetic and kinetic energies at scales in the range 0.3–2.0 Mm. Both spectra exhibit a steep slope that can be described by a power law with exponent −3.23 for scales smaller than about 1.2 Mm.
The equipartition between the magnetic and kinetic energies is of course independent of the type of 1D or 2D representation that we use for the spectral energy density, since the mathematical expressions that relate the different representations with each other are identical for the magnetic and velocity fields.
Note however that the equipartition that we see in Fig. 3 refers to the conditions in the upper photosphere, at a height of 400–450 km above the layer where the green continuum is formed. It does not at all imply that there is equipartition at other heights. On the contrary, since the density ρ decreases almost exponentially with height, while the magnetic and velocity fields vary much less, we expect the kinetic energy density to dominate at the bottom of the photosphere (and below) for the range of resolved scales that we are considering. At the level of continuum formation, for instance, the density is about 30 times the density in our line forming layer (cf. Vernazza et al. 1981).
4. Contribution of the flux tubes to the energy spectrum
In Stenflo (2010, 2011) it was shown how the line-ratio technique, when applied to the Hinode quiet-Sun data set that we are using here, reveals two distinct magnetic flux populations, representing collapsed (kG) and uncollapsed fields. The collapsed flux tube population was found to be the dominating contributor to the measured circular polarization signals that exceed 0.5%.
The line-ratio information also allowed us to find statistical relations between the vertical flux densities 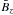 and the intrinsic field strengths of the flux tubes, and via the determined flux tube filling factors to obtain statistical estimates of the flux tube diameters df. The derived histograms for the flux tube sizes showed that most of the flux tubes exist in the 10–70 km size range, well beyond the Hinode resolution limit, but within reach of future telescope systems. It was also shown why this general size range can be expected from the theory of flux tube collapse.
and the intrinsic field strengths of the flux tubes, and via the determined flux tube filling factors to obtain statistical estimates of the flux tube diameters df. The derived histograms for the flux tube sizes showed that most of the flux tubes exist in the 10–70 km size range, well beyond the Hinode resolution limit, but within reach of future telescope systems. It was also shown why this general size range can be expected from the theory of flux tube collapse.
The existence of a collapsed flux population implies that there is a concentration of magnetic energy in the wave number range represented by the flux tubes. We therefore expect the spectral energy density to have a significant bump at these wave numbers. We will now try to model this spectral bump, based on the observationally determined histogram of flux tube sizes from Stenflo (2011).
 |
Fig. 4 Comparison between the 1D magnetic energy spectra |
The theoretical modeling of the flux tube spectral contributions is done in the k wave number domain, not in the ky domain that we used so far for the observationally determined spectra. As we will later combine the observationally and theoretically determined contributions, we need to convert the observational spectrum from ky to k space. We have done this with the help of Eqs. (5) and (6). The application of Eq. (6) is numerically tricky since it contains the derivative of the ky spectrum, which needs to be smoothed to avoid large noise fluctuations. The result of the conversion is shown as the solid line in Fig. 4, together with the original ky spectrum (dashed).
To model the flux tube contribution it is sufficient for our purposes to represent the magnetic field strength across a flux tube in the image plane with the following step function: 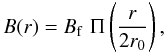 (8)where Bf is the intrinsic field strength of the flux tube, and the function Π(r/(2r0)) is unity for r ≤ r0 and zero otherwise. 2r0 is thus the diameter df of the flux tube.
(8)where Bf is the intrinsic field strength of the flux tube, and the function Π(r/(2r0)) is unity for r ≤ r0 and zero otherwise. 2r0 is thus the diameter df of the flux tube.
The power spectrum of B(r) is ![\begin{equation} \vert{\tilde B}(k,d_{\rm f})\vert^2 \,\sim\, [B_{\rm f}(d_{\rm f})]^2\,[J_1(k\,d_{\rm f}/2)]^2\,/\,k\,,\label{eq:bpower} \end{equation}](/articles/aa/full_html/2012/05/aa18939-12/aa18939-12-eq65.png) (9)where the constant of proportionality, which is the same for the whole flux tube population, will be determined later by normalization. J1 is the Bessel function of order 1. The integral of this expression over all k is proportional to
(9)where the constant of proportionality, which is the same for the whole flux tube population, will be determined later by normalization. J1 is the Bessel function of order 1. The integral of this expression over all k is proportional to 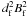 , as it must be to represent the energy contribution of a flux tube, since
, as it must be to represent the energy contribution of a flux tube, since 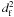 is proportional to the filling factor,
is proportional to the filling factor, 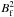 to the magnetic energy density of a flux tube. Note that the 2D power spectrum (E2D(k)) of the function Π would be the Airy function with k2 in the denominator, but as we are dealing with the 1D spectrum (E1D(k)), the denominator contains the unsquared k.
to the magnetic energy density of a flux tube. Note that the 2D power spectrum (E2D(k)) of the function Π would be the Airy function with k2 in the denominator, but as we are dealing with the 1D spectrum (E1D(k)), the denominator contains the unsquared k.
The power spectrum 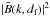 is thus proportional to the magnetic energy per unit wave number bin due to one flux tube of size df. If we have many flux tubes, we simply add their power spectra to obtain the combined contribution, since the spatial locations in the image plane of the various flux tubes can be assumed to be uncorrelated, without any systematic phase relations in the Fourier domain. Therefore the superposition in k space of the various flux tubes has no coherency but can be done incoherently.
is thus proportional to the magnetic energy per unit wave number bin due to one flux tube of size df. If we have many flux tubes, we simply add their power spectra to obtain the combined contribution, since the spatial locations in the image plane of the various flux tubes can be assumed to be uncorrelated, without any systematic phase relations in the Fourier domain. Therefore the superposition in k space of the various flux tubes has no coherency but can be done incoherently.
In Stenflo (2011) we determined the histogram hf(df) of the flux tube sizes df from the observational data. Since the determination depended significantly on the relative contribution of the collapsed flux population in the noise-dominated region with Stokes V polarization amplitudes less than 0.5%, two versions of the histogram were derived, based on two different assumptions for the contributions from the very small flux densities.
To obtain the combined contributions to the energy spectrum from all the flux tubes we need to multiply the power spectrum for a single flux tube with the distribution function hf and integrate over df. This integral can be written as the sum 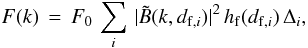 (10)where F0 is a normalization factor, and we sum over all the df bins, each having width Δi and representing flux tubes of size df,i. The normalization factor is determined by the requirement that
(10)where F0 is a normalization factor, and we sum over all the df bins, each having width Δi and representing flux tubes of size df,i. The normalization factor is determined by the requirement that 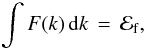 (11)where the average magnetic energy density contributed by the flux tubes, ℰf, has been extracted from the analysis of the data set in Stenflo (2011) and therefore represents an empirical constraint on the model. We use ℰf = 30.4 in SI units, which corresponds to an RMS field strength of 87 G. Note that while the flux tube field strengths Bf are of order kG, their filling factors are small, which together leads to an intermediate RMS value.
(11)where the average magnetic energy density contributed by the flux tubes, ℰf, has been extracted from the analysis of the data set in Stenflo (2011) and therefore represents an empirical constraint on the model. We use ℰf = 30.4 in SI units, which corresponds to an RMS field strength of 87 G. Note that while the flux tube field strengths Bf are of order kG, their filling factors are small, which together leads to an intermediate RMS value.
 |
Fig. 5 Modeled flux tube contributions to E1D(k) (dashed and dotted curves) based on two somewhat different versions of the flux tube distributions derived in Stenflo (2010). When the MTF of the Hinode telescope, T(k), is applied, the two curves get truncated near the Hinode resolution limit and become the dash-triple-dot and dash-dotted curves. The lower of the two solid curves is identical to the solid curve in Fig. 4. When this curve is divided by T(k) to compensate for the MTF quenching, the upper solid curve is obtained. |
The resulting, normalized F(k) spectra for the two different versions of the size histogram hf from Stenflo (2011) are shown as the dashed and dotted curves in Fig. 5, together with the observationally determined 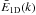 spectrum from Fig. 4 as the solid line.
spectrum from Fig. 4 as the solid line.
Due to the finite resolution of the observations, the F(k) spectra get truncated by the telescope function T(k), the Hinode MTF, as in Eq. (7). We let the MTF here be approximated by the Airy function ![\begin{equation} T(k)\,=4\,[\,J_1(0.5d_{\rm r}\,k)\,/\,(0.5d_{\rm r}\,k)\,]^2,\label{eq:tmtf} \end{equation}](/articles/aa/full_html/2012/05/aa18939-12/aa18939-12-eq84.png) (12)where the factor 4 makes T(k) amplitude normalized to unity for small wave numbers. In this representation, the spatial resolution is given by an averaging circular area of diameter dr. Since the lower limit for the resolution element must be two pixels, which with the present pixel size of 0.16 arcsec is 232 km (with 725 km per arcsec), we use the rounded value of dr = 250 km for the effective resolution when calculating T(k).
(12)where the factor 4 makes T(k) amplitude normalized to unity for small wave numbers. In this representation, the spatial resolution is given by an averaging circular area of diameter dr. Since the lower limit for the resolution element must be two pixels, which with the present pixel size of 0.16 arcsec is 232 km (with 725 km per arcsec), we use the rounded value of dr = 250 km for the effective resolution when calculating T(k).
After application of the MTF, the F(k) spectra get truncated into the dash-triple-dot and dash-dot curves in Fig. 5. These truncated spectra are in their descending branches quite similar to the observed spectrum 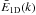 , indicating that the spectral shape in this range is largely determined by the MTF and not by the shape of the intrinsic spectrum.
, indicating that the spectral shape in this range is largely determined by the MTF and not by the shape of the intrinsic spectrum.
In principle one may retrieve the intrinsic spectrum E1D(k) through division of 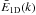 by T(k), although in practice this produces errors that escalate towards infinity where T(k) goes to zero near the cut-off. Still such a division may give an indication of the true shape of the spectrum. The result of this division is shown by the upper solid curve in Fig. 5. It demonstrates that the previously determined steep power law exponent of −3.23 in Fig. 3 is not representative of the intrinsic spectrum, which is much less steep.
by T(k), although in practice this produces errors that escalate towards infinity where T(k) goes to zero near the cut-off. Still such a division may give an indication of the true shape of the spectrum. The result of this division is shown by the upper solid curve in Fig. 5. It demonstrates that the previously determined steep power law exponent of −3.23 in Fig. 3 is not representative of the intrinsic spectrum, which is much less steep.
 |
Fig. 6 Comparison between the spectral shapes and power laws with exponent −5/3. The solid and dotted curves are identical to the corresponding curves in Fig. 5. |
When we instead compare the slopes of the corrected observational spectrum and of the flux tube F(k) spectra with power laws, we find that power laws with exponent −5/3 provide an optimum fit, as demonstrated in Fig. 6 (where we have simplified the plot by showing only one of the two versions of the F(k) spectrum). Kolmogorov (1941) theory explains in terms of purely dimensional arguments how a −5/3 power law is produced when the energy is injected at large scales and then cascades down the scale spectrum with a constant energy transfer rate per unit mass from smaller to larger wave numbers. The range of wave numbers between the scale at which the energy is fed in and the cut-off scale at the diffusion limit is called the inertial range, over which the −5/3 power law applies.
5. Intrinsic magnetic energy spectrum
In the solar case the inertial range that we see at resolved scales gets interrupted by the convective instability that causes the spontaneous collapse of magnetic flux into flux tubes. The collapse process is driven by the external gas pressure, which very effectively injects energy into the magnetic field at the scales that are populated by the flux tubes. This produces a significant bump or enhancement of the magnetic energy spectrum at these scales.
While the −5/3 power law seems to describe the descending branch of the flux tube spectrum F(k) over a substantial range, the dotted curve in Fig. 6 starts to drop off much faster near k = 0.001 m-1 (corresponding to a scale of 6 km). This cut-off is however an artefact of the circumstance that F(k) exclusively represents the flux tubes and ignores the smaller-scale fields beyond this range. The most likely scenario is that the magnetic energy that has been fed into the flux tubes by the collapse process later (as part of the flux tube decay process) cascades down the scale spectrum until the magnetic diffusion limit is reached. In the absence of other scale-dependent mechanisms between the flux tube and the diffusion scales, the most natural assumption is that, as in Kolmogorov theory, the rate of energy transfer from smaller to larger wave numbers stays constant. The resulting energy spectrum will then be a −5/3 power law also over this intertial range.
These considerations can now be used to construct an intrinsic magnetic energy spectrum that is independent of any telescope resolution and which covers all wave numbers, from the largest scales all the way down to the magnetic diffusion cut-off. For the small wave numbers the observed but MTF-corrected E1D(k) spectrum applies. When this spectrum encounters the flux tube spectrum near the Hinode resolution limit, the flux tube spectral contribution takes over. We then let the descending branch beyond the flux tube maximum be continued as a −5/3 power law all the way down to the diffusion cut-off.
 |
Fig. 7 Overview of our best estimate for the quiet-Sun magnetic energy spectrum E1D(k), down to the fundamental cut-off at the magnetic diffusion limit (located at a scale of 25 m), where the magnetic field ceases to be frozen-in and decouples from the plasma. The spectral bump due to the collapsed flux tubes just beyond the Hinode resolution limit is surrounded by inertial ranges with −5/3 power law behavior. While the flux tubes and the flux at larger scales are oriented preferentially in the vertical direction, the field below the flux tube scale range will have a much wider and randomized angular distribution. These small scales contain the “hidden” flux that was revealed by the Hanle effect three decades ago. |
The resulting magnetic spectrum is shown in Fig. 7. A smooth representation of the resolved part has been achieved by using an analytical −5/3 power law for the first inertial range, and letting the bump around wave numbers 10-7−10-8 be given the same shape as the bump described by the dotted curve in Fig. 6. For convenience, we let the quenching of the spectrum at the magnetic diffusion limit be described by a function of the same analytical form as the function T(k) of Eq. (12), but inserting for the “resolution” scale dr the value 25 m (rather than the 4 orders of magnitude larger value of 250 km for the Hinode resolution).
The magnetic diffusion limit is the spatial scale where the field line diffusion time scale becomes equal to the convective time scale, in other words, where the magnetic Reynolds number becomes unity. Below the diffusion limit the field lines cease to be frozen-in and decouple from the plasma. The scale where this happens was estimated in de Wijn et al. (2009) to be 15 m, based on Kolmogorov theory, the Spitzer conductivity for a temperature of 10 000 K, and observational constraints for the velocities. The 104 K value was used, because much of the magnetic structuring that we see throughout the photosphere is generated by the turbulence just below the photosphere. Even if the magnetic field decouples from the plasma earlier in the higher layers of the photosphere (like in the line-forming layers), structures generated lower down where the frozen-in condition still applies will be mapped by the field-line connectivity throughout the photosphere. The Spitzer conductivity may overestimate the actual conductivity, in which case the scale for the diffusion limit becomes larger. The estimate of 25 m that we here adopt for the diffusion limit should be subject to improvement in future work.
 |
Fig. 8 Conversion of the E1D(k) spectrum in Fig. 7 to a histogram that represents the relative amount of magnetic energy in bins of log d, where the scale size d is defined by d = 2π/k. The two bumps in the E1D(k) spectrum now become more pronounced, in particular since we use a linear vertical scale, and the −5/3 power laws get converted into d2/3 functions that govern the shapes of the left sides of the two peaks. |
The spectral energy density E1D(k), which represents the magnetic energy per unit wave number, can easily be converted into a spectral energy density 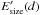 representing the energy per unit bin in log d, where d is the scale size, related to the wave number through d = 2π/k. As
representing the energy per unit bin in log d, where d is the scale size, related to the wave number through d = 2π/k. As 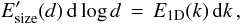 (13)we obtain
(13)we obtain 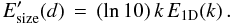 (14)This relation is used to convert the spectrum in Fig. 7 to the energy size distribution (with amplitude normalization) in Fig. 8.
(14)This relation is used to convert the spectrum in Fig. 7 to the energy size distribution (with amplitude normalization) in Fig. 8.
The two bumps in the E1D(k) spectrum appear much more pronouced in Fig. 8 since we now use a linear instead of logarithmic vertical scale. The k−5/3 power laws get converted into d2/3 power laws that determine the shapes of the left wings of the two peaks in Fig. 8. The collapsed flux tubes dominate the magnetic energy contribution over the approximate range 10–150 km. Note that the peak representing the flux tubes is shifted towards somewhat larger sizes than the histogram of flux tube sizes in Stenflo (2011), which was most prominent in the range 10–70 km. The reason for this is that the flux tube field strength Bf increases with size, and for the energy contributions in Fig. 8 the size distribution gets weighted with 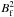 , which significantly enhances the contributions from the larger scales.
, which significantly enhances the contributions from the larger scales.
Since the power law behavior for the small scales (below about 10 km) implies that the field strength scales as B ~ d1/3 (as the magnetic energy scales with d2/3), the fields at a scale of for instance 80 m are about 5 times weaker than at the 10 km scale. Although this is a rather slow decline of field strength with decreasing scale size, it is significant and indicates that the main contribution to the observed Hanle depolarization caused by the “hidden” flux of tangled fields probably comes from fields with sizes of order 1 km. Much smaller sizes are less effective in producing the Hanle signature due to their weaker fields, while much larger sizes also contribute less, because they are dominated by the flux tubes, which are preferentially vertically oriented and for this reason do not contribute to the Hanle effect. We need to get down to scales where the angular distribution of the field vectors has become sufficiently wide, while the field has still retained enough strength. The Hanle effect and the tangled field will be explored more in the next section.
6. Probability density function for the vector field
While the energy spectra provide information on the sizes of the flux elements, weighted by the square of the field strength, there is no direct information on the distribution of field strengths or flux densities, for which we instead need the PDF. Although the PDF contains no direct information on the size distribution, it is strongly influenced by it and is in particular a very sensitive function of the telescope resolution cut-off.
There are two main effects of the finite resolution: (1) The contributions from subresolution elements, like flux tubes, get reduced because their filling factors are smaller than unity. (2) The topological mixing of opposite magnetic polarities leads to cancellation of the contributions to the circular polarization from the Zeeman effect, making such mixed-polarity flux invisible in magnetograms. In contrast to the Zeeman effect, such cancellation does not apply to the Hanle effect, since the depolarization effect does not change sign when the orientation of the field is reversed.
Due to the small-scale structuring, the quiet-Sun field that has been smoothed by the resolution element is very different from the unsmoothed field. To avoid confusion we therefore reserve the term “field strength” for the field as seen with infinite resolution (the intrinsic, resolution-independent field), while the corresponding term for the smoothed field is “flux density”. While the flux densities represent the observed quantities, the field strengths can only be inferred indirectly with the help of idealized models.
 |
Fig. 9 Comparison between the area-normalized probability distribution functions (PDF) for the field strengths (solid line) and the flux densities as observed with the Hinode resolution (dotted line for the vertical flux densities, dashed line for the total flux densities). The extended wings that decline quadratically are mainly due to the collapsed flux tubes. The large width of the Gaussian core region for the field strength PDF is required to satisfy the observational constraints from the Hanle effect. Due to cancellation of mixed polarities this Gaussian core contracts to become the narrow stretched exponential core for the flux density PDFs. |
The distinction between these two concepts is illustrated in Fig. 9, where we compare the PDFs for the observed flux densities of our Hinode quiet-Sun data set (dotted curve for the vertical flux densities, dashed curve for the total flux densities) with the inferred PDF for the intrinsic field strengths (solid curve). The procedure by which the properties of this field-strength PDF have been inferred and constrained by observations will be described next.
Let us however start by first considering the known properties of the PDF for the flux densities. As shown in Stenflo (2010), this PDF can be closely fitted by an analytical function that is represented by a stretched exponential in the extremely peaked core region, with the peak centered at zero flux density. The PDF has extended wings that decline quadratically with flux density. While the extended wings get their contributions from the largest (and strongest) flux tubes, the core region contains a mixture of contributions from the smallest flux tubes and from uncollapsed fields. “Hidden” flux for which the polarity contributions cancel within the resolution elements do not contribute anywhere at all to the PDF for the flux densities, although their existence is revealed by the Hanle effect (Stenflo 1982).
The cancellations do not much affect the outer wing regions of the PDF, since the low probability density there implies that the contributing larger flux tubes are relatively rare and therefore sparsely spaced with respect to each other. Instead, the resolution effect is mainly a filling-factor effect: the flux densities are smaller than the intrinsic field strengths in proportion to the filling factor. This leads to a contraction of the field-strength scale to generate a flux density scale, which approximately preserves the general shape of the PDF wings but compresses them to smaller field values. To retrieve the wing PDF for the intrinsic field strengths we need to divide the flux density values by the filling factor.
The determination of the wing region of the solid curve in Fig. 9 has been based on these considerations. The maximum flux density measured in our data set is 1145 G, while the line-ratio information implies that this is due to a flux tube with intrinsic field strength 1840 G and filling factor 62%. It is the largest filling factor found in this particular data set, but it is still relatively far from 100%. The value 1145 G represents the end point of the flux density PDFs in Fig. 9, and stretched in the horizontal direction by the factor 1/0.62 brings it to the solid curve and the value 1840 G. Other portions of the wing curve can be regarded as representing similar scalings.
The properties of the core region of the intrinsic PDF is governed by entirely different considerations, namely by the observational constraints from the Hanle effect. It was realized long ago (Stenflo 1982, 1987) that there could only be one consistent explanation for the observed deficit in the scattering polarization that is theoretically expected, namely depolarization by magnetic fields (Hanle effect) that are “hidden” in the sense that they do not show up in solar magnetograms due to spatial mixing of the magnetic polarities on scales much smaller than the telescope resolution. It was concluded that this hidden field needs to have a strength in the range 10–100 G to be consistent with the observations. The many papers since then on the theoretical development of the theory of polarized line formation with partial frequency redistribution in magnetized media together with breakthroughs in the observational techniques to record the Second Solar Spectrum (the linearly polarized spectrum that is formed by coherent scattering processes, and which is the playground for the Hanle effect) have confirmed the validity of these early insights and led to refined constraints on the hidden field.
The most detailed modeling so far of the Hanle effect produced by the hidden field (Trujillo Bueno et al. 2004) used 3D atmospheres generated by numerical simulations of magnetoconvection to model the scattering polarization that has been observed in the Sr i 4607 Å line and in molecular C2 lines. While the Sr line requires a 60 G field to fit the observations, a much weaker field of about 10 G is needed for the C2 lines. Trujillo Bueno et al. (2004) suggested that the explanation for this discrepancy by a factor of 6 lies in a correlation between the hidden magnetic flux and the solar granulation. The C2 lines are formed almost entirely in the interior of the granulation cells, where the hidden field is weaker, while the formation of the Sr line gets significant contributions from the intergranular lanes, where the hidden field is much stronger.
This explanation is supported by the finding in Stenflo (2011) that the collapsed flux population is preferentially located in the intergranular lanes, because the magnetic energy that has been injected into the magnetoturbulent spectrum by the flux collapse process cascades down the scale spectrum when the flux tubes dissolve (fraying by the interchange instability) and is thus directly fed into the inertial branch where the hidden flux resides. This physical connection between flux tubes and hidden flux implies that they should follow the same spatial distribution.
While the hidden flux is thus expected to be spatially structured, we will in the following restrict the discussion to the spatially averaged constraint represented by the 60 G value for the Sr line. Note however that the Hanle field strengths that we have quoted so far have all been based on an interpretational model, according to which the hidden flux consists of optically thin elements that have an isotropic angular distribution and a single field strength, i.e., a PDF in the form of a δ function. In contrast, the real Sun should be characterized by continuous PDFs, which get constrained by the observed net depolarization effect. The quantitative details will depend on the shape of the PDF.
As will be shown below, the extended PDF wings do not play any significant role for the observed Hanle depolarization effect. Instead nearly the entire effect must have its source in the PDF core region. The field-strength width of this core region must be about two orders of magnitude larger than the observed PDF core for the flux densities, which can be fitted with a stretched exponential that has a half width of only 1.2 G. No stretched exponential function can be used for the field-strength PDF if it is to satisfy the Hanle contraints.
It is natural to expect that the “hidden” fields in the inertial range below the flux tube scales would get randomized by the small-scale turbulence, as the scales are much smaller than the pressure scale height, which implies that the turbulence becomes nearly isotropic. This favors the development of a Gaussian field distribution. These considerations lead us to the choice of a Gaussian shape for the very wide PDF core region that represents the intrinsic field strengths.
The combination of a Gaussian core and quadratically declining extended wings is satisfied by a Voigt function H(a,b), where a is the damping parameter, and b = B/BD is the dimensionless field strength, normalized by the analog of a “Doppler” width BD. The function given as the solid line in Fig. 9 has a = 0.053 and BD = 170 G. We further assume that the PDF ends abruptly at 2000 G, since stronger fields can hardly be contained by the photospheric gas pressure, and larger structures like sunspots that have stronger fields are not representative of quiet solar regions. The one-sided truncated Voigt function in Fig. 9 has been normalized to unit area. It has a half width of 146 G. While the true solar PDF may have a shape that differs from a Voigt function, it must have a core with a similar large half width to satisfy the Sr i Hanle constraint, and have extended wings to satisfy the line-ratio constraints. Therefore the true general appearance of the PDF cannot differ that much from our chosen Voigt function.
 |
Fig. 10 PDF contributions to the mean Hanle depolarization of 0.45 observed in the Sr i 4607 Å line, assuming an isotropic angular distribution. The dashed curve represents the Hanle depolarization factor as a function of field strength. The value 0.45 is reached for 60 G, which would be the field strength of a single-valued PDF. The solid curve is the cumulative contribution to the Hanle depolarization from the PDF for all fields weaker than the given field strength B. The bulk of the contribution comes from the fields weaker than the PDF half width (146 G). |
The way in which the different parts of the PDF contribute to the observed Hanle depolarization is illustrated in Fig. 10, where the Hanle depolarization factor kH is plotted as a function of field strength B as the dashed curve. It starts from unity (implying no depolarization) for zero field, and decreases to asymptotically approach the saturation limit of 0.2 (implying 80% depolarization) as the field strength goes to infinity. The value of the saturation limit depends on the assumed angular distribution of the field vectors and is 0.2 for the isotropic case (Stenflo 1982, 1987). The observational constraint is a depolarization factor of 0.45. This value is reached by the dashed line for 60 G, the field strength of a δ function PDF that would satisfy the Hanle constraint.
Let us use P(B) to denote the area-normalized version of our Voigt function. The net Hanle depolarization factor is then obtained from integration over the product of P and kH. To illustrate how this integral builds up as we go from the inner to the outer parts of the PDF we have in Fig. 10 plotted as the solid curve the cumulative depolarization factor CH(B), defined as 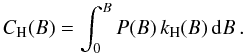 (15)In the limit of large B the solid line reaches the mean Hanle depolarization factor of 0.45, as required. We see that most of the contribution comes from the core region inside the core half width (146 G), while there is no significant contribution from the wings beyond about 250 G. This is another way of saying that the collapsed flux tubes are not relevant for the observed Hanle effect.
(15)In the limit of large B the solid line reaches the mean Hanle depolarization factor of 0.45, as required. We see that most of the contribution comes from the core region inside the core half width (146 G), while there is no significant contribution from the wings beyond about 250 G. This is another way of saying that the collapsed flux tubes are not relevant for the observed Hanle effect.
7. Energy and sizes of the hidden, tangled field
A long-standing question has been whether the stored magnetic energy of the tangled, hidden flux is significant for the energy balance of the solar atmosphere (cf. Trujillo Bueno et al. 2004). We know that the magnetic energy stored in kG-type flux tubes is comparable to the ambient kinetic energy, since it follows from the lateral pressure balance that the magnetic pressure is comparable to the ambient gas pressure (otherwise kG fields of narrow flux tubes could not be contained in the photosphere). In the following we will show that the energy in the hidden magnetic flux is comparable to the average energy that is due to the flux tubes. This implies that the hidden flux is as relevant to the energy balance of the solar atmosphere as the flux tubes are.
 |
Fig. 11 Relative contributions to the total magnetic energy from the different parts of the field strength PDF. While the solid line is the amplitude-normalized contribution function, the dashed line represents its integral from zero up to the given field strength (the cumulative contribution function), normalized to unity amplitude. We notice that the Gaussian PDF core is responsible for approximately 60% of the total energy, while the extended damping wings (due to the flux tubes) contribute the rest. The vertical dotted line marks the RMS ( |
We address this question here by illustrating in Fig. 11 the relative contributions to the total magnetic energy that come from the different parts of the PDF P(B) for the intrinsic field strengths B. For reference we mark the RMS value of the field (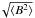 ) by the vertical dotted line. The solid curve that is labeled “contribution function” is P(B) B2, normalized to its maximum value. The peak around 200 G is produced by the Gaussian core of the PDF, while the PDF wing is responsible for the elevated ledge that stays constant until the PDF ends, since the multiplication of the quadratically declining P(B) with the quadratic function B2 makes a constant product.
) by the vertical dotted line. The solid curve that is labeled “contribution function” is P(B) B2, normalized to its maximum value. The peak around 200 G is produced by the Gaussian core of the PDF, while the PDF wing is responsible for the elevated ledge that stays constant until the PDF ends, since the multiplication of the quadratically declining P(B) with the quadratic function B2 makes a constant product.
To compare the relative contributions of the Gaussian core, which is the domain of the hidden flux, and the PDF wings, which is the domain of the collapsed flux tubes, we compute the cumulative contribution function CE(B), defined as 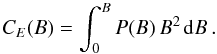 (16)CE(B), after having been normalized to its maximum value, is plotted as the dashed curve in Fig. 11. It is characterized by an initial steep rise, due to the Gaussian PDF core, followed by a shallower straight line region due to the PDF wing. The transition between these two regions occurs around a relative magnetic energy of 0.6. This implies that about 60% of the total magnetic energy comes from the hidden, tangled field, while the remaining part comes from the collapsed flux tubes. We can therefore conclude that the hidden magnetic flux is as relevant to the overall dynamics and energetics of the solar atmosphere as the flux tubes are.
(16)CE(B), after having been normalized to its maximum value, is plotted as the dashed curve in Fig. 11. It is characterized by an initial steep rise, due to the Gaussian PDF core, followed by a shallower straight line region due to the PDF wing. The transition between these two regions occurs around a relative magnetic energy of 0.6. This implies that about 60% of the total magnetic energy comes from the hidden, tangled field, while the remaining part comes from the collapsed flux tubes. We can therefore conclude that the hidden magnetic flux is as relevant to the overall dynamics and energetics of the solar atmosphere as the flux tubes are.
7.1. Role of the cancellation function
While the intrinsic PDF has an RMS field of 161 G, the average field (obtained from the integral of P(B) B) is 110 G. In contrast to the magnetic energy, the cumulative contribution function for the flux has its source almost exclusively from the Gaussian PDF core, because the contribution function for the flux does not have extended wings. Thus, while the magnetic energy is shared between the flux tubes and the hidden flux in approximately equal proportions, the contribution to the total flux is dominated by the hidden field.
The average field strength of 110 G is more than 5 times the average flux density of 20 G found for our Hinode data set (Stenflo 2011). This implies that about 80% of the total flux remains invisible at the Hinode resolution. The photosphere is a seething ocean of tangled fields, and an instrument like Hinode is able to see only the “tips of the icebergs”.
Pietarila Graham et al. (2009) used the cancellation function concept to estimate how much intrinsic magnetic flux remains invisible to Hinode due to cancellation of mixed polarities within the resolution element and also arrived at the conclusion that at least 80% of the total flux is missed by Hinode. The cancellation function represents the average unsigned flux density as a function of the spatial resolution, i.e., the size d of the smoothing window. Using the Hinode data set one can derive this function by artificially smoothing the data with running windows of various size. A power law d−χ is then found, characterized by the cancellation exponent χ. If χ can be considered independent of d, this power law may be extrapolated into the scale range below the resolution limit, to estimate what the average unsigned flux density would be if we could resolve these small scales.
Such extrapolation implicitly assumes that the field is scale invariant over the extrapolation range. However, this assumption now turns out not to be valid, since the instability process of flux collapse breaks the scale invariance and introduces, as we have seen, a preferred scale around 10–100 km, which is populated by the collapsed flux tubes.
The collapse process is the origin of the two observed, distinct populations: collapsed and uncollapsed flux. The two populations can be expected to contribute to very different cancellation functions. Since the flux tubes represent concentrated flux islands that are generally well separated from each other (since they are associated with small filling factors), there will be little mixing of opposite polarities from adjacent flux tubes within the resolution element. This implies a cancellation exponent χ that should be small, near zero. In contrast, the uncollapsed flux is expected to be rather randomized by the turbulent motions, leading to abundant mixing and a large cancellation exponent. For a completely random field, where the different spatial points are uncorrelated, χ would be unity (since the relative fluctuations scale with 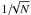 , where N is the number of magnetic elements within a smoothing window, and N is proportional to window area d2).
, where N is the number of magnetic elements within a smoothing window, and N is proportional to window area d2).
While the half width of our PDF P(B) for the intrinsic field strengths is 146 G, the half width of the PDF for the Hinode absolute flux densities is only 1.2 G. The PDF core region has therefore become contracted by a factor of about 120 when going from the intrinsic scales to the Hinode scale, due to flux cancellation within the smoothing window. If we would apply the maximum possible cancellation exponent of unity, treating the uncollapsed field as entirely random without any spatial correlations, then we would get down to a scale size for the “intrinsic magnetic elements” that is 120 times smaller than the Hinode resolution scale, i.e., 2 km. It may be interpreted as representing the largest possible size of the magnetic elements that are responsible for the broad Gaussian core of our PDF function P(B). 2 km is at the bottom of the flux tube size range and near the top of the inertial range where the hidden flux resides. Since the field strength B is expected to scale like d1/3 over this inertial range, the strongest fields will be located in the large-scale part of this range. It is the strongest fields with a broad angular distribution that contribute most to the observed Hanle depolarization signal.
There is no direct connection between the cancellation function and the scaling of the field strengths, since the cancellation function depends on the topological mixing of the positive and negative polarities. The cancellation function will not vary with scale size in monopolar regions, while the field strength scale variations do not depend on the polarity distributions. The field strength is expected to decrease as we go down in scale in the inertial range, while the cancellation function can only monotonically increase when the smoothing window is decreased.
The Hanle constraint depends on the intrinsic field strengths and angular distributions, but not on the polarity mixing. Therefore it is not the scaling of the cancellation function that is relevant for the Hanle constraint (as incorrectly assumed in Stenflo 2011), but the field strength scaling. While the angular distribution needs to be wide, since the Hanle effect is most sensitive to horizontal fields but insensitive to vertical fields, the polarities do not need to be mixed to generate Hanle depolarization. Wide angular distributions are possible also in monopolar regions.
8. Discussion
The magnetic energy spectrum extends over approximately 7 orders of magnitude (from the magnetic diffusion limit of order 25 m, to global scales of order 250 Mm), while current telescopes can only resolve 3 of these (for Hinode down to the resolution limit of about 250 km). Besides the resolution cut-off the observationally determined scale spectra in quiet solar regions are very sensitive to measurement noise, which has a flattening effect. Therefore we have chosen to work with the disk center quiet-Sun data set that provides the optimum combination of low noise and high spatial resolution, obtained with the Hinode SOT/SP instrument in deep integration mode.
We find approximate equipartition between the observationally determined kinetic and magnetic energy spectra over the scale range 0.3–1.2 Mm. This equipartition may be more accidental than it may first seem and be limited to the particular layer where the Fe i lines used for the Zeeman-effect analysis are formed, about 400 km above the continuum formation layer at the bottom of the photosphere. Since the height variation of the mass density is much steeper than the variation of the magnetic and velocity fields in the highly stratified solar atmosphere, equipartition at the 400 km level would imply dominance of the kinetic energy at the bottom of the photosphere, where magnetoconvection is more effective in producing magnetic structuring.
In idealized isotropic turbulence we may expect approximate scale invariance, and as a consequence have a cancellation function with a constant cancellation exponent that is associated with a scale-invariant fractal dimension. The solar atmosphere is however quite different with its pronounced stratification and large superadiabaticity at the top of the convection zone, conditions which lead to the instability of flux collapse. The circumstance that the collapse mechanism requires the collapsing flux regions to be optically thick in the horizontal direction (in the superadiabatic region, where the collapse is driven) implies that there is a preferred scale size (the photon mean free path in the superadiabatic layer), which breaks the scale invariance. The scale at which the invariance gets broken lies just beyond the resolution limit of current telescopes but within reach of the next generation of instruments.
The collapse is driven by the external gas pressure, which converts kinetic energy into magnetic energy in the form of the kG-type flux tubes, creating a bump in the energy spectrum around the 10–100 km scales. The energy injected into this bump is expected to cascade down the scale spectrum when the flux tubes decay via the interchange instability. As observationally confirmed, the flux tubes are on average nearly vertically oriented, both because they tend to be formed that way by adiabatic downdrafts, and because the powerful buoyancy forces will try to make the anchored field lines of the strong fields stand up. When the flux tubes dissolve into weaker fields, their field lines will begin to be tangled up by the turbulent motions. The resulting widening of the angular distribution of the field vectors will make these fields effective in depolarizing the scattering polarization and producing the observed Hanle-effect signature that is the evidence for the real existence of these “hidden” fields.
In this scenario the magnetic energy spectrum of the hidden flux is fed from the decay of the flux tubes, which implies that the flux tubes and the tangled, hidden flux are physically related. They should therefore statistically be spatially distributed in similar ways. It is known that the collapsed flux population is preferentially located in the intergranular lanes, for instance from high-resolution imaging of G-band bright points (e.g. Berger & Title 1996) as proxies for the concentrated magnetic flux, and recently from Stokes V line-ratio observations with Hinode (Stenflo 2011). It then follows that the hidden field must also be significantly stronger in the intergranular lanes than in the cell interiors. This provides an explanation for the finding of Trujillo Bueno et al. (2004) that the hidden field, when diagnosed with the Hanle effect in the molecular C2 lines, is about 6 times weaker than the field strength found when using the Sr i 4607 Å line. The C2 lines are formed almost exclusively in the cell interiors, where the hidden field is much weaker since it is fed by the flux tube field, while the Sr line can be assumed to represent the average atmosphere. As the Sr line thus gets contributions from both the cell interiors and the intergranular lanes, the hidden field would be found to be considerably stronger than suggested by our PDF for the intrinsic field strengths, if we could isolate the contributions from the intergranular lanes. This conclusion is observationally supported by Snik et al. (2010), who observed scattering polarization in the molecular CN band with high spatial resolution that allowed the intergranular lanes to be distinguished from the cell interiors. They found the polarization to be significantly more suppressed in the intergranular lanes, indicating that the hidden field is stronger there.
Our derived PDF for the intrinsic field strengths implies that there is comparable amounts of magnetic energy in the flux tubes and in the hidden field, which makes sense if the hidden field is fed from the decaying flux tubes. The processes that drive the flux tube formation and their dissolution take place much below the formation layer of the Fe lines that we have used to diagnose the field. As the second inertial range at scales below 10 km is much elevated because it has been fed by the decaying flux tubes, there may be a dominance of the magnetic over the kinetic energy densities in the line-forming layer at these scales. To be physically significant the comparison should however not be done for the line-forming layer, but rather for the lower layer that plays the main role for the structuring that is diagnosed higher up. The steep increase of the mass density with depth elevates the kinetic energy spectrum to levels sufficient to match the inferred small-scale magnetic energy spectrum.
9. Concluding remarks
The overall magnetic energy spectrum that we have illustrated in Fig. 7 is produced and sustained by convective turbulence in a highly stratified medium. The term “local dynamo” is often used to characterize the small-scale origin of the magnetic structuring. However, as the scale spectrum continuously connects the smallest with the largest scales over about 7 orders of magnitude, there is no clear separation of scales as would be implied by the terminology “local” vs. “global”. The only preferred scale that breaks the scale invariance seems to be the flux tube scale, which separates the “large” scales (above 100 km) from the “small” scales (below 10 km). However, the term “local dynamo” is usually not used to refer to this scale separation. Generally the term “global dynamo” is reserved for dynamo processes that have to do with the hemispheric left-right symmetry breaking in cyclonic turbulence that expresses itself in Joy’s law for the tilt of bipolar magnetic regions and in Hale’s polarity law. However, as shown in Stenflo & Kosovichev (2012), Joy’s law continues to be valid for small bipolar magnetic regions at least down to scales that are covered by the upper portion of the scale spectrum in our present analysis of Hinode data. Therefore the magnetoturbulent spectrum that we have been exploring here is relevant for the regeneration of the global solar magnetic field and for maintaining the 11-year cycle. Since it does not make physical sense here to distinguish between a “local” and a “global” dynamo, we have avoided the use of such dynamo terminology, and instead refer to the self-sustaining processes that maintain the magnetoconvective spectrum in the stratified Sun.
Most of the magnetic spectrum that we have derived resides at scales that lie beyond the resolution of current telescopes. Therefore it has been necessary to infer its shape from indirect
observational constraints, combined with general physical arguments. Since this procedure is based on model assumptions that may be questioned, our conclusions need to be validated by future observational tests. While the predicted bump in the magnetic energy spectrum lies at scales not yet covered by direct observations, these scales are already covered by numerical simulations of magnetoconvection. If the magnetic energy spectra produced by the simulations do not show a bump or elevation of the spectrum around the 10–100 km scale, then either the simulations do not include the needed physical ingredients and need to be overhauled, or our present data analysis and modeling has been faulty. Fortunately observational tests that can settle this issue are almost around the corner, since the critical scales lie just beyond the Hinode resolution limit, where we expect the energy spectrum to get elevated due to the flux collapse process. It will therefore not be long before this fundamental aspect of solar magnetism can be either verified or refuted.
Acknowledgments
I want to acknowledge the fruitful, in-depth discussions about related issues that took place at ISSI (International Space Science Institute) in Bern during a meeting with an ISSI International Team, November 21–25, 2011. The analysis has been based on observations done by the Hinode satellite. Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway).
References
- Abramenko, V., & Yurchyshyn, V. 2010a, ApJ, 722, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Abramenko, V., & Yurchyshyn, V. 2010b, ApJ, 720, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Abramenko, V., Yurchyshyn, V., Wang, H., & Goode, P. R. 2001, Sol. Phys., 201, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Abramenko, V. I., Yurchyshyn, V. B., & Goode, P. R. 2011 [arXiv:1112.2750] [Google Scholar]
- Berger, T. E., & Title, A. M. 1996, ApJ, 463, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Cadavid, A. C., Lawrence, J. K., Ruzmaikin, A. A., & Kayleng-Knight, A. 1994, ApJ, 429, 391 [NASA ADS] [CrossRef] [Google Scholar]
- de Wijn, A. G., Stenflo, J. O., Solanki, S. K., & Tsuneta, S. 2009, Space Sci. Rev., 144, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Janßen, K., Vögler, A., & Kneer, F. 2003, A&A, 409, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knobloch, E. 1981, ApJ, 248, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Knobloch, E., & Rosner, R. 1981, ApJ, 247, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, J. K., Ruzmaikin, A. A., & Cadavid, A. C. 1993, ApJ, 417, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, J. K., Cadavid, A. C., & Ruzmaikin, A. A. 1996, ApJ, 465, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Kubo, M., Socas-Navarro, H., et al. 2008, ApJ, 672, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., & Levine, R. H. 1974, ApJ, 190, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., & Priest, E. R. 1973, ApJ, 179, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1978, ApJ, 221, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovay, K. 2001, Space Sci. Rev., 95, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Pietari la Graham, J., Danilovic, S., & Schüssler, M. 2009, ApJ, 693, 1728 [Google Scholar]
- Shchukina, N., & Trujillo Bueno, J. 2001, ApJ, 550, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Snik, F., de Wijn, A. G., Ichimoto, K., et al. 2010, A&A, 519, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spruit, H. C. 1979, Sol. Phys., 61, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., & Zweibel, E. G. 1979, Sol. Phys., 62, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1973, Sol. Phys., 32, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1982, Sol. Phys., 80, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1987, Sol. Phys., 114, 1 [NASA ADS] [Google Scholar]
- Stenflo, J. O. 2010, A&A, 517, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O. 2011, A&A, 529, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O., & Kosovichev, A. G. 2012, ApJ, 745, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Suematsu, Y., Tsuneta, S., Ichimoto, K., et al. 2008, Sol. Phys., 249, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Uberoi, M. S. 1955, ApJ, 122, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., & Ando, H. 1979, Geophys. Astrophys. Fluid Dyn., 12, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Magnetic energy spectra |
| In the text | |
 |
Fig. 2 Magnetic energy spectra |
| In the text | |
 |
Fig. 3 Comparison between the magnetic (solid) and kinetic (dotted) energy spectra |
| In the text | |
 |
Fig. 4 Comparison between the 1D magnetic energy spectra |
| In the text | |
 |
Fig. 5 Modeled flux tube contributions to E1D(k) (dashed and dotted curves) based on two somewhat different versions of the flux tube distributions derived in Stenflo (2010). When the MTF of the Hinode telescope, T(k), is applied, the two curves get truncated near the Hinode resolution limit and become the dash-triple-dot and dash-dotted curves. The lower of the two solid curves is identical to the solid curve in Fig. 4. When this curve is divided by T(k) to compensate for the MTF quenching, the upper solid curve is obtained. |
| In the text | |
 |
Fig. 6 Comparison between the spectral shapes and power laws with exponent −5/3. The solid and dotted curves are identical to the corresponding curves in Fig. 5. |
| In the text | |
 |
Fig. 7 Overview of our best estimate for the quiet-Sun magnetic energy spectrum E1D(k), down to the fundamental cut-off at the magnetic diffusion limit (located at a scale of 25 m), where the magnetic field ceases to be frozen-in and decouples from the plasma. The spectral bump due to the collapsed flux tubes just beyond the Hinode resolution limit is surrounded by inertial ranges with −5/3 power law behavior. While the flux tubes and the flux at larger scales are oriented preferentially in the vertical direction, the field below the flux tube scale range will have a much wider and randomized angular distribution. These small scales contain the “hidden” flux that was revealed by the Hanle effect three decades ago. |
| In the text | |
 |
Fig. 8 Conversion of the E1D(k) spectrum in Fig. 7 to a histogram that represents the relative amount of magnetic energy in bins of log d, where the scale size d is defined by d = 2π/k. The two bumps in the E1D(k) spectrum now become more pronounced, in particular since we use a linear vertical scale, and the −5/3 power laws get converted into d2/3 functions that govern the shapes of the left sides of the two peaks. |
| In the text | |
 |
Fig. 9 Comparison between the area-normalized probability distribution functions (PDF) for the field strengths (solid line) and the flux densities as observed with the Hinode resolution (dotted line for the vertical flux densities, dashed line for the total flux densities). The extended wings that decline quadratically are mainly due to the collapsed flux tubes. The large width of the Gaussian core region for the field strength PDF is required to satisfy the observational constraints from the Hanle effect. Due to cancellation of mixed polarities this Gaussian core contracts to become the narrow stretched exponential core for the flux density PDFs. |
| In the text | |
 |
Fig. 10 PDF contributions to the mean Hanle depolarization of 0.45 observed in the Sr i 4607 Å line, assuming an isotropic angular distribution. The dashed curve represents the Hanle depolarization factor as a function of field strength. The value 0.45 is reached for 60 G, which would be the field strength of a single-valued PDF. The solid curve is the cumulative contribution to the Hanle depolarization from the PDF for all fields weaker than the given field strength B. The bulk of the contribution comes from the fields weaker than the PDF half width (146 G). |
| In the text | |
 |
Fig. 11 Relative contributions to the total magnetic energy from the different parts of the field strength PDF. While the solid line is the amplitude-normalized contribution function, the dashed line represents its integral from zero up to the given field strength (the cumulative contribution function), normalized to unity amplitude. We notice that the Gaussian PDF core is responsible for approximately 60% of the total energy, while the extended damping wings (due to the flux tubes) contribute the rest. The vertical dotted line marks the RMS ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


