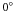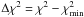| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201218818 | |
| Published online | 10 May 2012 | |
Near-infrared interferometric observation of the Herbig Ae star HD 144432 with VLTI/AMBER⋆
1 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: lchen@mpifr-bonn.mpg.de
2 Department of Astronomy, University of Michigan, 500 Church St., Ann Arbor, MI 48109-1090, USA
3 Laboratoire Lagrange, UMR7293, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300 Nice, France
4 INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
5 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
6 Inter-University Centre for Astronomy and Astrophysics (IUCAA), Post Bag 4, Ganeshkhind, 411007 Pune, India
Received: 13 January 2012
Accepted: 15 March 2012
Aims. We study the sub-AU-scale circumstellar environment of the Herbig Ae star HD 144432 with near-infrared VLTI/AMBER observations to investigate the structure of its inner dust disk.
Methods. The interferometric observations were carried out with the AMBER instrument in the H and K band. We interpret the measured H- and K-band visibilities, the near- and mid-infrared visibilities from the literature, and the spectral energy distribution (SED) of HD 144432 by using geometric ring models and ring-shaped temperature-gradient disk models with power-law temperature distributions.
Results. We derive a K-band ring-fit radius of 0.17 ± 0.01 AU and an H-band radius of 0.18 ± 0.01 AU (for a distance of 145 pc). This measured K-band radius of ~0.17 AU lies in the range between the dust sublimation radius of ~0.13 AU (predicted for a dust sublimation temperature of 1500 K and gray dust) and the prediction of models including backwarming (~0.27 AU). We find that an additional extended halo component is required in both the geometric and temperature-gradient modeling. In the best-fit temperature-gradient model, the disk consists of two components. The inner part of the disk is a thin ring with an inner radius of ~0.21 AU, a temperature of ~1600 K, and a ring thickness ~0.02 AU. The outer part extends from ~1 AU to ~10 AU with an inner temperature of ~400 K. We find that the disk is nearly face-on with an inclination angle of <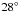 .
.
Conclusions. Our temperature-gradient modeling suggests that the near-infrared excess is dominated by emission from a narrow, bright rim located at the dust sublimation radius, while an extended halo component contributes ~6% to the total flux at 2 μm. The mid-infrared model emission has a two-component structure with ~20% of the flux originating from the inner ring and the rest from the outer parts. This two-component structure is indicative of a disk gap, which is possibly caused by the shadow of a puffed-up inner rim.
Key words: accretion, accretion disks / techniques: interferometric / protoplanetary disks / circumstellar matter / stars: pre-main sequence / stars: individual: HD 144432
© ESO, 2012
1. Introduction
HD 144432 (He3-1141) is an isolated Herbig Ae (HAE) star with spectral type A9/F0 (Thé et al. 1994; Sylvester et al. 1996) located at ~145 pc (Pérez et al. 2004; see also the discussion in Sect. 4). Since it is not closely associated with molecular cloud material (Malfait et al. 1998), its IR excess can be attributed to circumstellar (CS) material. By analyzing its spectral features, and considering its lack of photometric variability, Meeus et al. (1998) concluded that the central star of HD 144432 is directly seen, without CS material in the line of sight. Thus, they suggested that the CS material is confined to a face-on disk, instead of having a spherical geometry. HD 144432 belongs to the group II objects in the classification scheme by Meeus et al. (2001), i.e., it has a flat IR spectrum and a weaker mid-infrared (MIR) excess than the group I objects. A plausible explanation of a group II SED is that the dust disk is shadowed by its own puffed-up inner rim (Natta et al. 2001; Dullemond et al. 2001; Dullemond 2002; Dominik et al. 2003; Dullemond & Dominik 2004). The polycyclic-aromatic-hydrocarbon emission features in HD 144432 are weak (Acke & van den Ancker 2004; Keller et al. 2008), which supports the self-shadowed-disk interpretation.
Previous interferometric observations of HD 144432 in the H and K bands using IOTA and the Keck Interferometer (KI) were reported by Monnier et al. (2005, hereafter M05, 2006, hereafter M06), and Eisner et al. (2009). Spectrally dispersed interferometric K-band observations by Eisner et al. (2009) show that the size of the emission region increases with wavelength. Their modeling of the data suggests a dust disk with an inner radius of 0.25–0.3 AU (at 145 pc) and an inner temperature of 1000–1200 K, a gas disk between the star and the dust, and a Brγ line originating from a more compact region. In the MIR, Leinert et al. (2004) measured the half-light radius of the disk at 12.5 μm to 14 mas (~2 AU at 145 pc) using VLTI/MIDI. With Keck segment-tilting, Monnier et al. (2009) measured the Gaussian FWHM of HD 144432 to 39 ± 5 mas (5.6 ± 0.7 AU at 145 pc) at 10.7 μm.
Pérez et al. (2004) found that the object is a binary, with a K-type T Tauri star companion at a separation of 1.4′′, and estimated the age of the two stars to 1–3 Myr. Carmona et al. (2007) confirmed that the primary and the companion are physically associated, but estimated the age to 8 Myr.
In this paper, we present H- and K-band VLTI/AMBER observations of HD 144432. In Sect. 2, we summarize the observations and the data reduction. The modeling is presented in Sect. 3. We discuss the modeling results in Sect. 4 and present the summary and conclusion in Sect. 5.
2. Observation and data reduction
AMBER is the near-infrared (NIR) beam combiner instrument of the Very Large Telescope Interferometer (VLTI) and records spectrally dispersed three-beam interferograms, capable of measuring both visibilities and closure phases (CPs) (Petrov et al. 2007). HD 144432 was observed in the low spectral resolution mode (R = 35) in the H and K bands on 2009 Apr. 18 and 2010 Apr. 18 with VLTI/AMBER using the linear baseline configuration E0-G0-H0 and the triangle configuration D0-H0-G1, respectively (see Table 1). The visibilities and CPs are derived using the pixel-to-visibility-matrix (P2VM) algorithm of the data reduction package amdlib 3.0 1. In Fig. 1, we show the H- and K-band visibilities as a function of projected baseline length. The 1.4′′ binary companion has no influence on the visibility measurements of the primary star, since the field-of-view of the AMBER is only 0.25′′. The extracted CPs are shown in Fig. 2 and have wavelength-averaged values of 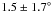 (2009),
(2009), 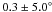 (2010a), and
(2010a), and 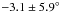 (2010b). In Fig. 3a (upper three rows), we present the derived wavelength-dependent AMBER visibilities of HD 144432 in the H and K bands. For data processing, we selected 30% of the frames with the highest fringe signal-to-noise ratio (Tatulli et al. 2007) of each target and calibrator data set. From the 2009 and 2010a data (see Table 1), we extracted both H- and K-band visibilities and CPs. From the 2010b data, only K-band visibilities and CPs were extracted owing to the low fringe signal-to-noise ratio of the H-band data. We used the method of OPD histogram equalization (Kreplin et al. 2012) to reduce the influence of the atmospheric optical path differences (OPDs) on the calibrated visibilities. In the calibration process, we used in both nights the calibrator star HD 142669 with an uniform disk diameter of dUD = 0.27 ± 0.05 mas2.
(2010b). In Fig. 3a (upper three rows), we present the derived wavelength-dependent AMBER visibilities of HD 144432 in the H and K bands. For data processing, we selected 30% of the frames with the highest fringe signal-to-noise ratio (Tatulli et al. 2007) of each target and calibrator data set. From the 2009 and 2010a data (see Table 1), we extracted both H- and K-band visibilities and CPs. From the 2010b data, only K-band visibilities and CPs were extracted owing to the low fringe signal-to-noise ratio of the H-band data. We used the method of OPD histogram equalization (Kreplin et al. 2012) to reduce the influence of the atmospheric optical path differences (OPDs) on the calibrated visibilities. In the calibration process, we used in both nights the calibrator star HD 142669 with an uniform disk diameter of dUD = 0.27 ± 0.05 mas2.
Observation log of our VLTI/AMBER observation of HD 144432.
3. Modeling
 |
Fig. 1 Band-averaged visibilities as a function of baseline length. The dots with errorbars are the observations (blue dots: our VLTI data; red and green dots: IOTA and KI data taken from Monnier et al. 2005, 2006; and Eisner et al. 2009). The lines are best-fit geometric models (inclination |
 |
Fig. 2 Observed HD 144432 closure phases as a function of wavelength. |
Best-fit parameters of our geometric modeling.
Best-fit parameters of the temperature-gradient models.
We attempt to build models that can reproduce both the data from our new observations and data sets available in literature, including the K-band observation with KI (M05, Eisner et al. 2009), the H-band observation with IOTA (M06), the MIR interferometry with VLTI/MIDI (Leinert et al. 2004), as well as the SED (Leinert et al. 2004). In the modeling process, we assume a distance of 145 pc (Pérez et al. 2004).
3.1. Geometric modeling
First, simple geometric models are employed to characterize the size of the disk. In order to be consistent with M05’s work, we used the uniform-brightness ring model, which has a ring thickness of 20% of the inner radius Rring. By fitting a Kurucz model (Kurucz 1992) to the stellar component of the dereddened SED (taken from Leinert et al. 2004) and measuring the flux excess in the H and K bands, we obtained the ring (disk) flux fractions fring = 0.54 for the H band and fring = 0.73 for the K band, respectively.
The wavelength-averaged H- and K-band visibilities were fitted with a ring model including the stellar contribution. The total visibility of the star-ring model can be described by 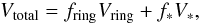 (1)where Vtotal is the measured visibility, f∗ = 1 − fring is the flux contribution from the central star, and V∗ is the stellar visibility. As the central star is unresolved (R∗ < 0.1 mas), we set V∗ = 1. The visibility Vring of an uniform ring is calculated following Eq. (8) in Eisner et al. (2004). The best-fit geometric star-ring models are presented in Fig. 1 and Table 2 (for a distance of 145 pc, Pérez et al. 2004). We derived ring-fit radii of Rring = 0.21 ± 0.01 AU for the K band and Rring = 0.20 ± 0.01 AU for the H band.
(1)where Vtotal is the measured visibility, f∗ = 1 − fring is the flux contribution from the central star, and V∗ is the stellar visibility. As the central star is unresolved (R∗ < 0.1 mas), we set V∗ = 1. The visibility Vring of an uniform ring is calculated following Eq. (8) in Eisner et al. (2004). The best-fit geometric star-ring models are presented in Fig. 1 and Table 2 (for a distance of 145 pc, Pérez et al. 2004). We derived ring-fit radii of Rring = 0.21 ± 0.01 AU for the K band and Rring = 0.20 ± 0.01 AU for the H band.
The high reduced chi-square errors 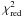 of the visibility fits (see last column in Table 2) indicate that even the best-fit star-ring models cannot reproduce the observational data well. M06 reported that for some Herbig Ae stars an additional overresolved halo component (i.e., a halo that is too large to be constrained by the short baselines) is required to permit us to fit the visibilities with simple geometric models. Therefore, we introduce a halo component into our model. We assume that the halo structure scatters the light from the central star. While fring remains the same parameter as above, f∗ is given by f∗ = 1 − fring − fhalo, where the halo flux ratio, fhalo, is an additional free parameter. The best-fit star-ring-halo model in the K band shows that 12 ± 2% of the flux is emitted by the halo, and that the ring has a ring-fit radius of Rring = 0.17 ± 0.01 AU. In the H band, the halo contributes 6 ± 2% to the total flux and the ring-fit radius is 0.18 ± 0.01 AU. With an additional halo component, the values of the
of the visibility fits (see last column in Table 2) indicate that even the best-fit star-ring models cannot reproduce the observational data well. M06 reported that for some Herbig Ae stars an additional overresolved halo component (i.e., a halo that is too large to be constrained by the short baselines) is required to permit us to fit the visibilities with simple geometric models. Therefore, we introduce a halo component into our model. We assume that the halo structure scatters the light from the central star. While fring remains the same parameter as above, f∗ is given by f∗ = 1 − fring − fhalo, where the halo flux ratio, fhalo, is an additional free parameter. The best-fit star-ring-halo model in the K band shows that 12 ± 2% of the flux is emitted by the halo, and that the ring has a ring-fit radius of Rring = 0.17 ± 0.01 AU. In the H band, the halo contributes 6 ± 2% to the total flux and the ring-fit radius is 0.18 ± 0.01 AU. With an additional halo component, the values of the 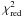 decrease by a factor of ~2.5 (see Table 2).
decrease by a factor of ~2.5 (see Table 2).
The measurements at different position angles allow us to investigate the inclination of the disk. Thus, we also employed inclined ring models with and without an extended halo. The fitting results are summarized in Table 2. The best-fit models suggest small inclination angles of ~30°, but the 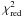 values do not show a significant decrease.
values do not show a significant decrease.
Finally, to roughly characterize the N-band size, we fitted the band-averaged visibility of 0.19 ± 0.1 with a thin-ring model and derived a ring radius of ~1.4 AU. We also studied a geometric two-ring model and derived a fit radius of 1.6 AU for the outer ring, by assuming an estimated N-band flux contribution of 15% from the inner model ring and an inner-ring radius of 0.18 AU, derived in the above star-ring-halo model (see Table 2).
 |
Fig. 3 Comparison of the best-fit two-component disk model (red lines; see Table 3) and best-fit one-component disk model (blue lines) with the observations of HD 144432. a) Near- and mid-infrared visibilities. The data sets 2004 IOTA, 2003 KI, 2007 KI, and 2003 MIDI mentioned in the panels are taken from Monnier et al. (2006), Monnier et al. (2005), Eisner et al. (2009), and Leinert et al. (2004), respectively. b) SED (from Leinert et al. 2004) and temperature-gradient models. The dashed lines denote the contributions from individual components in the best-fit two-component disk model. c) H-, K-, and N-band intensity distributions of the best-fit two-component disk model (Table 3). The second component of the disk, i.e., the more extended part, is visible only in the N band. The star and halo are not plotted. |
3.2. Temperature-gradient modeling with a one-component disk
Temperature-gradient models are employed to fit the NIR and MIR visibilities as well as the SED data simultaneously. We begin with a simple model including a star, an inclined one-component disk, and an extended overresolved halo. The star contributes to the flux F∗(λ) = A∗I∗(λ), where I∗(λ) is the intensity at the stellar surface and 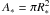 is the angular area of the star. The halo is assumed to be very extended, emitting a spectrum that is similar to the stellar spectrum. Thus, its flux is Fhalo(λ) = khaloF∗(λ). The disk is an optically thick ring with a power-law temperature distribution (Hillenbrand et al. 1992) T = Tin(r/rin) − q, rin ≤ r ≤ rout, with the inner and outer radius rin and rout of the disk, a disk temperature Tin at rin, and a power-law index q. Each part of the ring emits black body radiation at its local temperature. First, we fitted the SED in the UV/optical band (0.1–1 μm) with a Kurucz model (Kurucz 1992) to determine the stellar parameters that we should use in our subsequent modeling, i.e., temperature T∗ = 7180 K, surface gravity log g = 2.78, and metallicity log m = −0.415. The seven free parameters in the model are the inclination angle i, the position angle θD of the disk’s major axis, Tin, q, rin, the radial thickness Δr = rout − rin of the ring, and the flux fraction khalo.
is the angular area of the star. The halo is assumed to be very extended, emitting a spectrum that is similar to the stellar spectrum. Thus, its flux is Fhalo(λ) = khaloF∗(λ). The disk is an optically thick ring with a power-law temperature distribution (Hillenbrand et al. 1992) T = Tin(r/rin) − q, rin ≤ r ≤ rout, with the inner and outer radius rin and rout of the disk, a disk temperature Tin at rin, and a power-law index q. Each part of the ring emits black body radiation at its local temperature. First, we fitted the SED in the UV/optical band (0.1–1 μm) with a Kurucz model (Kurucz 1992) to determine the stellar parameters that we should use in our subsequent modeling, i.e., temperature T∗ = 7180 K, surface gravity log g = 2.78, and metallicity log m = −0.415. The seven free parameters in the model are the inclination angle i, the position angle θD of the disk’s major axis, Tin, q, rin, the radial thickness Δr = rout − rin of the ring, and the flux fraction khalo.
We tried to find the best-fit model by scanning the physically reasonable parameter range (calculation of approximately 6 × 107 models; details of the searching process is described in the Appendix A). Unfortunately, we did not find a model that can reproduce the data reasonably well. The best-fit model (see blue model lines in Fig. 3) deviates significantly from the data, and its 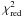 is 10.7. This deviation is indicative of a more sophisticated structure of the disk.
is 10.7. This deviation is indicative of a more sophisticated structure of the disk.
3.3. Temperature-gradient modeling with a two-component disk
Since the 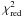 of the one-component disk model discussed above is very large, we introduced a slightly more complicated model in a second modeling step, in which the disk consists of two power-law components, with temperature T = T1,in(r/r1,in) − q1 for r1,in ≤ r ≤ r1,out and T = T2,in(r/r2,in) − q2 for r2,in ≤ r ≤ r2,out , respectively. We used the subscript 1 to denote the inner disk, and 2 for the outer disk. The assumptions for the star and halo remained unchanged. After computation of several 1010 models, we found the best-fit solution shown in Table 3 and Fig. 3 (with χ2 = 1.15; see Appendix A for the searching process).
of the one-component disk model discussed above is very large, we introduced a slightly more complicated model in a second modeling step, in which the disk consists of two power-law components, with temperature T = T1,in(r/r1,in) − q1 for r1,in ≤ r ≤ r1,out and T = T2,in(r/r2,in) − q2 for r2,in ≤ r ≤ r2,out , respectively. We used the subscript 1 to denote the inner disk, and 2 for the outer disk. The assumptions for the star and halo remained unchanged. After computation of several 1010 models, we found the best-fit solution shown in Table 3 and Fig. 3 (with χ2 = 1.15; see Appendix A for the searching process).
This best-fit model consists of the star, a halo with a brightness of 18% of the star, and a nearly face-on (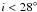 ) two-component disk. The inner part of the disk is a thin ring at r1,in ~ 0.21 AU, with a temperature T1,in ~ 1600 K, and a radial thickness Δr1 ~ 0.02 AU. The power-law index q1 was fixed to 0.5 (corresponding to a flared irradiated disk; Kenyon & Hartmann 1987), since q1 cannot be constrained because of the small radial thickness of the inner disk ring (see Appendix A.3). The outer part extends from ~1 AU to ~10 AU, with an inner temperature ~400 K. The contribution from the components to the total NIR flux (at 2 μm) are 60% from the inner disk, 33% from the central star, and 6% from the halo, and almost zero from the outer disk. The contribution from the components to the total MIR flux (at 10 μm) are 21% from the inner disk, 78% from the outer disk, and only 1% from the star and halo. In Fig. 3, we show the comparison of this best-fit model (
) two-component disk. The inner part of the disk is a thin ring at r1,in ~ 0.21 AU, with a temperature T1,in ~ 1600 K, and a radial thickness Δr1 ~ 0.02 AU. The power-law index q1 was fixed to 0.5 (corresponding to a flared irradiated disk; Kenyon & Hartmann 1987), since q1 cannot be constrained because of the small radial thickness of the inner disk ring (see Appendix A.3). The outer part extends from ~1 AU to ~10 AU, with an inner temperature ~400 K. The contribution from the components to the total NIR flux (at 2 μm) are 60% from the inner disk, 33% from the central star, and 6% from the halo, and almost zero from the outer disk. The contribution from the components to the total MIR flux (at 10 μm) are 21% from the inner disk, 78% from the outer disk, and only 1% from the star and halo. In Fig. 3, we show the comparison of this best-fit model (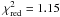 ) to our AMBER visibilities together with visibilites from IOTA, Keck, and MIDI measurements, as well as SED data from literature.
) to our AMBER visibilities together with visibilites from IOTA, Keck, and MIDI measurements, as well as SED data from literature.
A prominent feature of the model is the large gap between the inner and outer disk. The size of the NIR emitting region is confined to ~0.21 ± 0.01 AU by the NIR visibilities. The low visibilities in the MIR suggest a much larger size of ≳1 AU for the MIR emitting region. If a smooth temperature profile (and hence a continuous emission distribution) is assumed between the two distinct length scales, the NIR emitting region will be much broader than in our model, and would lead to a NIR flux much higher than the observation. Therefore, the gap in our model is strongly required when intepreting all data simultaneously.
4. Discussion
To compare the derived NIR sizes with the expected dust sublimation radius and other HAEBE stars, we plot HD 144432 in the size-luminosity diagram introduced by Monnier & Millan-Gabet (2002) using our K-band ring-fit radii (inclination 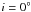 models, see Sect. 3.1 and Table 1) together with the luminosity L = 14.5 ± 4 L⊙ (M05). Figure 4 shows that the inner ring radius of 0.17 ± 0.01 AU (star-disk-halo model; adopting a distance of ~145 ± 20 pc, see below) is roughly consistent with the predicted dust-sublimation radius of 0.13 AU corresponding to a sublimation temperature of 1500 K and gray dust opacities. Furthermore, we compared the measured radius with the prediction of a model including backwarming and accretion luminosity (Millan-Gabet et al. 2007). This model suggests an inner disk radius of ~0.27 AU for a stellar luminosity of 14.5 L⊙ and an accretion luminosity of 1.0 L⊙ (Garcia Lopez et al. 2006; we scaled down the value according to the difference in assumed star parameters). Our measured inner-ring radius of ~0.17 AU lies in the range between these two model predictions of 0.13 AU and 0.27 AU.
models, see Sect. 3.1 and Table 1) together with the luminosity L = 14.5 ± 4 L⊙ (M05). Figure 4 shows that the inner ring radius of 0.17 ± 0.01 AU (star-disk-halo model; adopting a distance of ~145 ± 20 pc, see below) is roughly consistent with the predicted dust-sublimation radius of 0.13 AU corresponding to a sublimation temperature of 1500 K and gray dust opacities. Furthermore, we compared the measured radius with the prediction of a model including backwarming and accretion luminosity (Millan-Gabet et al. 2007). This model suggests an inner disk radius of ~0.27 AU for a stellar luminosity of 14.5 L⊙ and an accretion luminosity of 1.0 L⊙ (Garcia Lopez et al. 2006; we scaled down the value according to the difference in assumed star parameters). Our measured inner-ring radius of ~0.17 AU lies in the range between these two model predictions of 0.13 AU and 0.27 AU.
The error bars of the radii for HD 144432 in Fig. 4 represents only the uncertainties in the visibility measurements and do not include the uncertainty in the distance. Pérez et al. (2004) concluded that HD 144432 is likely a member of the star association Sco OB 2-2, with a distance of ~145 pc. However, in previous studies, distances in the range from 108 pc to 2.4 kpc were also reported (e.g., Pottasch & Parthasarathy 1988; Pérez et al. 2004). In this paper, we adopted the distance of 145 ± 20 pc (the error bar corresponds to the distance dispersion within Sco OB 2-2; see Preibisch et al. 2002). In spite of the distance uncertainty, it is possible to discuss the location of HD 144432 relative to the 1500 K line for the following reason. If the adopted distance is wrong by a certain factor, then this factor changes both the ring-fit radius and the luminosity in such a way that the location of the star moves parallel to the sublimation radius lines in the size-luminosity relation (Monnier & Millan-Gabet 2002).
Both our geometric and temperature-gradient modeling suggest the existence of a halo component, which contributes ~6–12% to the total NIR flux in the best-fit geometric model (in the best-fit temperature-gradient model ~6% at 2 μm). The size of the halo component cannot be measured precisely, but the visibilities suggest that it is ≳1 AU. Given its large distance to the central star, the halo emission is probably dominated by scattered stellar light (Akeson et al. 2005; M06). Plausible origins of the halo material include an infalling remnant envelope, dust entrained in the stellar wind/outflow (M06), or the flaring outer disk, which scatters the stellar light (Pinte et al. 2008).
Our temperature-gradient modeling suggests that the disk consists of two components with distinct length scales. The inner component is a thin ring at an inner radius of ~0.21 AU with a temperature of ~1600 K and a radial thickness ~0.02 AU. The outer part extends from ~1 AU to ~10 AU with an inner temperature of ~400 K. The disk is seen roughly face-on with an inclination angle of 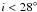 .
.
The small radial thickness of the inner ring-shaped disk is consistent with the puffed-up rim model (Natta et al. 2001; Dullemond et al. 2001; Dullemond 2002; Dominik et al. 2003; Dullemond & Dominik 2004). In such a model, the NIR emission is dominated by the puffed-up inner rim at the dust sublimation radius, and the region of the disk behind the rim is colder owing to shadowing effects, which can lead to a gap in the observed intensity distribution. A gap phenomenon was also reported for other Herbig stars (e.g., Benisty et al. 2010; Tatulli et al. 2011). While the NIR emission of the disk is dominated exclusively by the inner ring (presumably the puffed-up rim), the MIR emission has a bimodal distribution, with ~20% of the emission originating from the inner ring, and the rest from the outer parts. This spatial distribution of MIR emission is also consistent with the prediction of the rim model (van Boekel et al. 2005).
 |
Fig. 4 Size-luminosity diagram for HAeBe stars (Monnier & Millan-Gabet 2002). Blue dots: data taken from Monnier et al. (2005). Red square: HD 144432 (ring-fit K-band radius of the star-ring-halo uninclined model). Dark-green square: HD 144432 (ring-fit K-band radius of the star-ring uninclined model). The error bars of the radii for HD 144432 represent only the uncertainties in the visibilty measurements, and do not include the distance uncertainty. Lines: theoretical dust sublimation radius for gray dust and three different dust sublimation temperatures. Predictions of models including backwarming are discussed in Sect. 4. |
5. Summary and conclusions
We have presented VLTI/AMBER observations of the Herbig Ae star HD 144432 in the H and K bands. The following results were obtained.
The K- and H-band emitting regions have geometric ring-fit radii of 0.21 ± 0.01 AU and 0.20 ± 0.01 AU, respectively. When we introduced an additional halo component, we obtained the smaller disk ring-fit radii of 0.17 ± 0.01 AU (K band) and 0.18 ± 0.01 AU (H band). This measured K-band ring radius of ~0.17 AU lies in the range between the aforementioned dust sublimation radius of ~0.13 AU (size-luminosity relation in Fig.4; for sublimation temperature of 1500 K and gray dust), and the prediction of models including backwarming (~0.27 AU). Both our geometric and temperature-gradient modeling indicate the existence of an additional extended halo component. In the best-fit temperature-gradient model, the halo contributes ~6% at 2 μm.
Our best-fit temperature-gradient disk model can approximately reproduce both the NIR-MIR visibilities and the SED data (Fig. 3). The model consists of the central star, an extended halo, and a nearly face-on two-component disk. In the modeling procedure, we started with a very wide range for all model parameters, calculated several 1010 models corresponding to all combinations of the parameters, and finally obtained disk parameters that seem to be physically quite reasonable. The inner part of the disk is a thin ring at an inner radius of ~0.21 AU with a temperature of ~1600 K and a radial thickness ~0.02 AU. The outer part extends from ~1 AU to ~10 AU with an inner temperature of ~400 K. The NIR emission of the disk is dominated by the inner ring. The MIR emission has a bimodal distribution, with ~20% of the emission originating from the inner ring and the rest from the outer parts. The temperature-gradient modeling suggests an upper limit for the inclination angle of 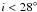 .
.
Available at: http://www.jmmc.fr/data_processing_amber.htm
Taken from the Catalogue of Stellar Diameters (CADARS) (Pasinetti Fracassini et al. 2001).
Acknowledgments
We thank the ESO VLTI team on Paranal for the excellent collaboration. The data presented here were reduced using the publicly available data-reduction software package amdlib kindly provided by the Jean-Marie Mariotti Center (http://www.jmmc.fr/datar_processing_amber.htm). This publication makes use of the SIMBAD database operated at CDS, Strasbourg, France. Finally, we thank the anonymous referee for his helpful comments.
References
- Acke, B., & van den Ancker, M. E. 2004, A&A, 426, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akeson, R. L., Walker, C. H., Wood, K., et al. 2005, ApJ, 622, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Benisty, M., Tatulli, E., Ménard, F., & Swain, M. R. 2010, A&A, 511, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carmona, A., van den Ancker, M. E., & Henning, T. 2007, A&A, 464, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dominik, C., Dullemond, C. P., Waters, L. B. F. M., & Walch, S. 2003, A&A, 398, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P. 2002, A&A, 395, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Lane, B. F., Hillenbrand, L. A., Akeson, R. L., & Sargent, A. I. 2004, ApJ, 613, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Graham, J. R., Akeson, R. L., & Najita, J. 2009, ApJ, 692, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia Lopez, R., Natta, A., Testi, L., & Habart, E. 2006, A&A, 459, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillenbrand, L. A., Strom, S. E., Vrba, F. J., & Keene, J. 1992, ApJ, 397, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, L. D., Sloan, G. C., Forrest, W. J., et al. 2008, ApJ, 684, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1987, ApJ, 323, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Kreplin, A., Kraus, S., Hofmann, K.-H., et al. 2012, A&A, 537, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1992, in The Stellar Populations of Galaxies, ed. B. Barbuy, & A. Renzini, IAU Symp., 149, 225 [Google Scholar]
- Leinert, C., van Boekel, R., Waters, L. B. F. M., et al. 2004, A&A, 423, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malfait, K., Bogaert, E., & Waelkens, C. 1998, A&A, 331, 211 [NASA ADS] [Google Scholar]
- Meeus, G., Waelkens, C., & Malfait, K. 1998, A&A, 329, 131 [NASA ADS] [Google Scholar]
- Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millan-Gabet, R., Malbet, F., Akeson, R., et al. 2007, Protostars and Planets V, 539 [Google Scholar]
- Monnier, J. D., & Millan-Gabet, R. 2002, ApJ, 579, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Millan-Gabet, R., Billmeier, R., et al. 2005, ApJ, 624, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Berger, J., Millan-Gabet, R., et al. 2006, ApJ, 647, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Tuthill, P. G., Ireland, M., et al. 2009, ApJ, 700, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Prusti, T., Neri, R., et al. 2001, A&A, 371, 186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasinetti Fracassini, L. E., Pastori, L., Covino, S., & Pozzi, A. 2001, A&A, 367, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez, M. R., van den Ancker, M. E., de Winter, D., & Bopp, B. W. 2004, A&A, 416, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Ménard, F., Berger, J. P., Benisty, M., & Malbet, F. 2008, ApJ, 673, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Pottasch, S. R., & Parthasarathy, M. 1988, A&A, 192, 182 [NASA ADS] [Google Scholar]
- Preibisch, T., Brown, A. G. A., Bridges, T., Guenther, E., & Zinnecker, H. 2002, AJ, 124, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Sylvester, R. J., Skinner, C. J., Barlow, M. J., & Mannings, V. 1996, MNRAS, 279, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tatulli, E., Benisty, M., Ménard, F., et al. 2011, A&A, 531, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thé, P. S., de Winter, D., & Perez, M. R. 1994, A&AS, 104, 315 [NASA ADS] [Google Scholar]
- van Boekel, R., Dullemond, C. P., & Dominik, C. 2005, A&A, 441, 563 [Google Scholar]
Appendix A: Searching for the best-fit models
A.1. General description of the searching method
We searched for the best-fit one-component and two-component models describing the visibility and SED data. We established a grid in the multi-dimensional parameter space, and evaluated the χ2 on each grid point to find the χ2-minimum. A large parameter range was first scanned to roughly locate the global minimum. In further processing, we then computed narrower grids around the global minimum to confine the parameters with higher precision. In each step, we computed the models for all combinations of all parameters.
We treated the parameter khalo in the following way. For each combination of all the other parameters, the modeled visibilities depend linearly on the halo fraction khalo/(1 + khalo), while the modeled fluxes are independent of khalo. Therefore, the best-fit value of khalo can be found with linear regression.
A.2. Searching for the best-fit one-component disk model
We searched for the best-fit one-component disk model within the wide parameter ranges listed in Table A.1. We divided the range of each parameter into 20 grid points and computed 206 ≈ 6 × 107 models for all combinations of all parameters. No model with reasonable fitting could be found.
A.3. Searching for the best-fit two-component disk model
When searching for the best-fit two-component disk model, we start from wide parameter ranges and gradually zoom in (see the ranges listed in Table A.1). The best-fit parameters are listed in Table 3. Owing to the small radial thickness of the inner ring, fits of equal quality (similar χ2 values) can be found for each q1 value (see the χ2 map in Fig. A.1). Therefore, we set q1 = 0.5 (corresponding to a flared irradiated disk; Kenyon & Hartmann 1987) in the last two search steps.
In each scanning step, we divided the range of each parameter into 10 grid points (except q1 in the last two steps) and computed the models for all combinations of all parameters. In total, we computed 4.2 × 1010 models.
 |
Fig. A.1 χ2 maps showing |
Scanned parameter space in the two-component disk temperature-gradient modeling. Upper part: one-component disk model. Lower part: two-component disk model.
All Tables
Scanned parameter space in the two-component disk temperature-gradient modeling. Upper part: one-component disk model. Lower part: two-component disk model.
All Figures
 |
Fig. 1 Band-averaged visibilities as a function of baseline length. The dots with errorbars are the observations (blue dots: our VLTI data; red and green dots: IOTA and KI data taken from Monnier et al. 2005, 2006; and Eisner et al. 2009). The lines are best-fit geometric models (inclination |
| In the text | |
 |
Fig. 2 Observed HD 144432 closure phases as a function of wavelength. |
| In the text | |
 |
Fig. 3 Comparison of the best-fit two-component disk model (red lines; see Table 3) and best-fit one-component disk model (blue lines) with the observations of HD 144432. a) Near- and mid-infrared visibilities. The data sets 2004 IOTA, 2003 KI, 2007 KI, and 2003 MIDI mentioned in the panels are taken from Monnier et al. (2006), Monnier et al. (2005), Eisner et al. (2009), and Leinert et al. (2004), respectively. b) SED (from Leinert et al. 2004) and temperature-gradient models. The dashed lines denote the contributions from individual components in the best-fit two-component disk model. c) H-, K-, and N-band intensity distributions of the best-fit two-component disk model (Table 3). The second component of the disk, i.e., the more extended part, is visible only in the N band. The star and halo are not plotted. |
| In the text | |
 |
Fig. 4 Size-luminosity diagram for HAeBe stars (Monnier & Millan-Gabet 2002). Blue dots: data taken from Monnier et al. (2005). Red square: HD 144432 (ring-fit K-band radius of the star-ring-halo uninclined model). Dark-green square: HD 144432 (ring-fit K-band radius of the star-ring uninclined model). The error bars of the radii for HD 144432 represent only the uncertainties in the visibilty measurements, and do not include the distance uncertainty. Lines: theoretical dust sublimation radius for gray dust and three different dust sublimation temperatures. Predictions of models including backwarming are discussed in Sect. 4. |
| In the text | |
 |
Fig. A.1 χ2 maps showing |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.