| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 9 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201218773 | |
| Published online | 16 May 2012 | |
NLTE determination of the calcium abundance and 3D corrections in extremely metal-poor stars⋆,⋆⋆
1 GEPI Observatoire de Paris, CNRS, Université Paris Diderot, 92195 Meudon Cedex, France
e-mail: monique.spite@obspm.fr
2 Department of Astronomy and Astronomical Observatory, Odessa National University, T.G. Shevchenko Park, 65014, Odessa ;
and Isaac Newton Institute of Chile, Odessa Branch, Ukraine
3 Zentrum für Astronomie der Universität Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
Received: 4 January 2012
Accepted: 19 March 2012
Context. Calcium is a key element for constraining the models of chemical enrichment of the Galaxy.
Aims. Extremely metal-poor stars contain the fossil records of the chemical composition of the early Galaxy and it is important to compare Ca abundance with abundances of other light elements, that are supposed to be synthesized in the same stellar evolution phases.
Methods. The NLTE profiles of the calcium lines were computed in a sample of 53 extremely metal-poor stars with a modified version of the program MULTI, which allows a very good description of the radiation field.
Results. With our new model atom we are able to reconcile the abundance of Ca deduced from the Ca I and Ca II lines in Procyon. This abundance is found to be solar. We find that ![$\overline{[Ca/Fe]}$](/articles/aa/full_html/2012/05/aa18773-12/aa18773-12-eq1.png) = 0.50±0.09 in the early Galaxy, a value slightly higher than the previous LTE estimations. The scatter of the ratios [X/Ca] is generally smaller than the scatter of the ratio [X/Mg] where X is a “light metal” (O, Na, Mg, Al, S, and K) with the exception of Al. These scatters cannot be explained by error of measurements, except for oxygen. Surprisingly, the scatter of [X/Fe] is always equal to, or even smaller than, the scatter around the mean value of [X/Ca]. We note that at low metallicity, the wavelength of the Ca I resonance line is shifted relative to the (weaker) subordinate lines, a signature of the effect of convection. The Ca abundance deduced from the Ca I resonance line (422.7 nm) is found to be systematically smaller at very low metallicity than the abundance deduced from the subordinate lines. Our computations of the effects of convection (3D effects) are not able to explain this difference. A fully consistent 3D NLTE model atmosphere and line formation scheme would be necessary to fully capture the physics of the stellar atmosphere.
= 0.50±0.09 in the early Galaxy, a value slightly higher than the previous LTE estimations. The scatter of the ratios [X/Ca] is generally smaller than the scatter of the ratio [X/Mg] where X is a “light metal” (O, Na, Mg, Al, S, and K) with the exception of Al. These scatters cannot be explained by error of measurements, except for oxygen. Surprisingly, the scatter of [X/Fe] is always equal to, or even smaller than, the scatter around the mean value of [X/Ca]. We note that at low metallicity, the wavelength of the Ca I resonance line is shifted relative to the (weaker) subordinate lines, a signature of the effect of convection. The Ca abundance deduced from the Ca I resonance line (422.7 nm) is found to be systematically smaller at very low metallicity than the abundance deduced from the subordinate lines. Our computations of the effects of convection (3D effects) are not able to explain this difference. A fully consistent 3D NLTE model atmosphere and line formation scheme would be necessary to fully capture the physics of the stellar atmosphere.
Key words: line: formation / line: profiles / stars: abundances / supernovae: general / Galaxy: evolution
Based on observations obtained with the ESO Very Large Telescope at Paranal Observatory, Chile (Large Programme “First Stars”, ID 165.N-0276(A); P.I.: R. Cayrel).
The NLTE corrections of the Ca lines are available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/541/A143
© ESO, 2012
1. Introduction
An homogeneous sample of 53 metal-poor stars, most of them extremely metal-poor (EMP stars with [Fe / H] < −2.9), has been observed by Cayrel et al. (2004), and Bonifacio et al. (2007, 2009). The aim of this paper is to determine the calcium abundance in these stars more precisely. These low mass stars have been formed at the very early phases of the Galaxy and the chemical composition of their atmosphere reflects the yields of the first massive type II supernovae which have a very short life-time. These supernovae produce more “α-elements” (O, Mg, Si, S, Ca) than “iron-peak” elements. In contrast, less massive type I supernovae, which have a much longer life-time and explode later, produce more iron-peak elements than α-elements. As a consequence in the atmosphere of the EMP stars formed at the beginning of the Galaxy a relative enhancement of the α-elements (compared to the Sun) is observed. The level of this overabundance is one of the fundamental parameters of the chemical evolution models of the Galaxy.
On the other hand, the relative production of the α-elements in a supernova depends on the mass of this supernova (e.g. Kobayashi et al. 2006): [Ca/Fe] tends to be lower for more massive supernovae. Therefore the level of [Ca/Fe] in the early Galaxy constrains the IMF in the early times.
Moreover, Cayrel et al. (2004) and Bonifacio et al. (2009) have shown that for [Fe / H] < −2.7 the abundances of the α-elements relative to iron ([Mg/Fe], [Si/Fe], [Ca/Fe], and [Ti/Fe]) are constant with a small scatter but that surprisingly the scatters of these elements relative to magnesium (another α-element) are larger. This larger scatter cannot be explained by a lower precision of the abundance of magnesium. Cayrel et al. (2004) and Bonifacio et al. (2009) computed the abundances under the LTE hypothesis. The non-LTE (NLTE) abundances of two α-elements Mg and S have been then computed in Andrievsky et al. (2010) and Spite et al. (2011). These papers confirm that the scatter of abundance ratios is generally larger when Mg replaces Fe as a reference element. It is then interesting to check wether the link between the abundance of Ca and the abundance of the other α-elements is closer.
In this paper we have carried out a NLTE analysis of the calcium abundance in the atmosphere of these EMP stars and have tried to estimate the influence of convection (3D computations).
For this new analysis we have used the resonance line of Ca I and about 15 subordinate lines. We have also used the line of the Ca II infrared triplet at 866.21 nm. Unfortunately, the two other lines of this triplet (at 849.81 and 854.21 nm) are outside the observed spectral range.
Program stars and their parameters.
2. Star sample and model parameters
The spectra of the stars investigated here have been presented in detail in Cayrel et al. (2004) and Bonifacio et al. (2007). The observations were performed with the high-resolution spectrograph UVES at ESO-VLT (Dekker et al. 2000). The resolving power of the spectrograph is R ≈ 45 000, with about five pixels per resolution element and the signal-to-noise ratio per pixel is typically about 150.
The fundamental parameters of the models (effective temperature Teff, logarithm of the gravity log g, and metallicity) have been derived by Cayrel et al. (2004) for the giants and Bonifacio et al. (2007) for the turnoff stars. Briefly, temperatures of the giants are deduced from the colors with the calibration of Alonso et al. (1999, 2001), and temperatures of the turnoff stars from the wings of the Hα line. Moreover we checked that these Hα temperatures agreed with the temperatures derived from the color V − K and the calibration of Alonso et al. (1996). The gravities are derived from the ionization equilibrium of iron (under the LTE approximation) and we note that they might be affected by NLTE effects. The parameters of the models are repeated in Table 1 for the reader’s convenience.
3. Determination of the calcium abundance
The NLTE profiles of the calcium lines were computed with a modified version of the code MULTI (Carlsson 1986; Korotin et al. 1999), which allows a very good description of the radiation field. This version includes opacities from ATLAS9 (Kurucz 1992), which modify the intensity distribution in the UV.
3.1. Atmospheric models
For these computations we used Kurucz models without overshooting (Castelli et al. 1997). These models have been shown to provide LTE abundances very similar (within 0.05 dex) to those of the MARCS models used by Cayrel et al. (2004) and Bonifacio et al. (2009). The solar model was taken from Castelli1 with a chromospheric contribution from the VAL-3C model of Vernazza et al. (1981) and the corresponding microturbulence distribution.
3.2. Atomic model
Our model atom of calcium is similar to the one used by Mashonkina et al. (2007) but it includes some more levels and more recent atomic data. Seventy levels of Ca I, thirty-eight levels of Ca II, and the ground state of Ca III were taken into account; in addition, more than 300 levels of Ca I and Ca II were included to keep the condition of the particle number conservation in LTE. The fine structure was taken into account for the levels 3d2D and 4p2P0 of Ca II.
The energy levels were taken from the NIST atomic spectra database (Sugar & Corliss 1985). The ionization cross-sections were taken from TOPBASE. The oscillator strengths of the Ca I and Ca II lines were taken from the most recent estimations: Wiese et al. (1969), Smith & Raggett (1981), Smith (1988), Theodosiou (1989), Morton (1991), Kurucz (1993), and from TOPBASE for the lines occuring between non-splitted levels. For the forbidden transitions, we used TOPBASE and Hirata & Horaguchi (1995).
We considered 351 transitions in detail; for 375 weak transitions the radiative rates were fixed. Collisional rates between the ground level and the ten lower levels of Ca I were taken from Samson & Berrington (2001). For Ca II, collisional rates were taken from Meléndez et al. (2007) instead of those of Burgess et al. (1995) used by Mashonkina et al. (2007) for the lower seven terms.
For the other transitions (without data) we used for allowed transitions, the Van Regemorter (1962) formula, and for the forbidden transitions the Allen (1973) formula.
Electron impact ionization cross-sections were calculated by applying the formula of Seaton (1962), with threshold photoionization cross-sections from the Opacity-Project data.
Collisions with hydrogen atoms were computed using the Steenbock & Holweger (1984) formula. The cross sections calculated with this formula were multiplied by a scaling factor SH: the “efficiency” of the hydrogenic collisions. This factor was constrained empirically by comparing the Ca abundance obtained from different lines in the Sun and in some reference stars (Procyon, HD 140283, HD 122563). The best agreement was obtained with SH = 0.1 which agrees well with Ivanova et al. (2002) and Mashonkina et al. (2007).
Parameters of the Ca lines used in the solar spectrum. γ1 = log γVW / NH for a temperature of 10 000 K.
 |
Fig. 1 Profiles of Ca I and Ca II lines in Procyon. The wavelengths are in Å. The small crosses represent the observed spectrum and the (red) line the computed profile. With our model atom, the observed and computed profiles of the Ca I and Ca II lines agree well. |
 |
Fig. 2 Profiles of Ca I and Ca II lines in HD 140283. The wavelengths are in Å. The symbols are the same as in Fig. 1. The observed spectrum and the synthetic profiles computed with log ϵ(Ca) = 4.12 agree well. |
3.3. Consistency check
To test the Ca atom model, we computed the profiles of the calcium lines in the Sun, in Procyon, and in two classical metal-poor stars HD 122563, and HD 140283. The synthetic spectra were computed following the procedure described in Korotin (2008): we calculated the departure coefficients factors “b” for the Ca lines with MULTI and then used these factors in the LTE synthetic spectrum code.
-
For the Sun we used the solar atmosphere model com-puted by Castelli with a chromospheric contributionfollowing Vernazza et al. (1981, seeSect. 3.1). A micro turbulence velocityξt = 1.0 km s-1 was adopted in the atmosphere. We computed the profile of 49 lines of Ca I and 17 lines of Ca II. The log gf value of the lines and the broadening parameter due to collisions with hydrogen atoms, log γVW / NH (for T = 10 000 K), are given in Table 2. We found log ϵ(Ca) = 6.31 ± 0.05 from the Ca I lines and log ϵ(Ca) = 6.30 ± 0.07 from the Ca II lines. These values agree well with the meteoritic calcium abundance log ϵ(Ca) = 6.31 ± 0.02 (Lodders et al. 2009) and the photospheric abundances derived by Asplund et al. (2009) for the solar atmosphere: log ϵ(Ca) = 6.34 ± 0.04 (a value that includes 3D effects). For most of the lines in Table 2, the broadening parameter log γVW / NH (for T = 10 000 K) due to collisions with hydrogen atoms, was taken from the precise calculations of Anstee & O’Mara (1995), Barklem & O’Mara (1997, 1998), and Barklem et al. (1998). For the other lines, this parameter was derived from the fit of the solar atlas (Kurucz et al. 1984). These values are, for the high excitation lines of Ca II, higher than the values obtained from the Unsöld or Kurucz approximation. However, they agree well with the values obtained by Ivanova et al. (2002), who note that the use of the Unsöld or Kurucz approximation often leads to an underestimation of the broadening parameter.
-
We retrieved the spectrum of Procyon from the UVES POP (Bagnulo et al. 2003). Procyon has a solar-like chemical composition, and its surface gravity, derived from Hipparcos measurements (Perryman et al. 1997), is log g = 3.96. We adopted a microturbulence ξt = 1.8 km s-1. For this star, Mashonkina et al. (2007) adopting Teff = 6510 K (Mashonkina et al. 2003) or Teff = 6590 K (Korn et al. 2003) found a subsolar abundance of Ca and a difference of about 0.2 dex between the NLTE calcium abundance derived from the Ca I and Ca II lines. With Teff = 6510 K and our model atom, we derive for Procyon a near solar calcium abundance and a much better agreement between Ca I and Ca II: log ϵ(Ca) = 6.25 ± 0.04 from Ca I lines and 6.27 ± 0.06 from Ca II lines (Fig. 1).
-
We also tested our model on two classical metal-poor stars: HD 122563 (a star from our sample of giants) and HD 140283. The spectrum of HD 140283 was retrieved from the ESO POP (Bagnulo et al. 2003). For HD 122563 we adopted the parameters given in Table 1, and for HD 140283 the parameters given by Hosford et al. (2009): Teff = 5750 K, log g = 3.4, ξt = 1.5 km s-1. The agreement is good. From the Ca I lines we obtain log ϵ(Ca) = 4.12 ± 0.04 and from the Ca II lines log ϵ(Ca) = 4.08 ± 0.05. In Fig. 2 we show the fit between the observed spectrum of HD 140283 and the synthetic profiles computed with log ϵ(Ca) = 4.12.
4. Calcium abundance in the EMP stars sample
4.1. Comparison between the different systems
In Fig. 3 we show the influence of the NLTE effects on the profile of some typical calcium lines measurable in extremely metal-poor stars. Evidently, in particular the wings of the lines of the Ca II infrared triplet are not sensitive to NLTE effects until the wings are strong enough.
 |
Fig. 3 Profiles of three Ca lines computed for a giant star with [Ca / H] ≈ − 2.5 with LTE (thin blue line) and NLTE (thick red line) hypotheses. The wavelengths are given in Å. a) The NLTE profile of the Ca I resonance line is narrower in the wings and deeper in the core. b) In a Ca I subordinate line, for the same abundance of calcium the equivalent width computed under the NLTE hypothesis is slightly smaller. c) The NLTE correction is important for the strong IR Ca II line (note that the scale in wavelength is different for this line), but the wings are not affected and a reliable calcium abundance can be deduced from these wings via LTE analysis. |
 |
Fig. 4 NLTE corrections for the Ca I resonance line at 422.67 nm and for a typical subordinate line of Ca I at 445.48 nm. |
In Fig. 4 the correction NLTE-LTE is given as a funtion of the temperature, the gravity, and the calcium abundance for the Ca I resonance line and a typical subordinate line of Ca I. The NLTE corrections for different temperatures, gravities, and abundances for all the Ca lines used in this analysis (Table 2) are available in electronic form2. The influence of the complex NLTE effects as a function of the stellar parameters and of the characteristics of the lines has been discussed by Mashonkina et al. (2007) and Merle et al. (2011).
In Table 1 we give for each star the mean abundance derived from the subordinate lines of Ca I (Col. 6), the number of lines used for the analysis (Col. 7), and the internal error (Col. 8). Column 9 lists the abundance deduced from the resonance line of Ca I, and Col. 10 the abundance computed from the infra-red Ca II line at 866.21 nm (only this line of the red Ca II triplet is in the wavelength range of our spectra). Columns 11 and 12 list [Ca/H] and [Ca/Fe] deduced from the subordinate lines of Ca I. For an easier comparison to the previous “First Stars” papers, the solar abundance of calcium was taken from Grevesse & Sauval (2000) as in Cayrel et al. (2004): log ϵ(Ca) ⊙ = 6.36. The oscillator strengths of the calcium lines measured in our metal-poor stars were updated (to be the same as in Sect. 3.2). As a consequence, for some lines (Table 2) they are slightly different from the log gf values used in Cayrel et al. (2004) and Bonifacio et al. (2009).
The abundance of Ca was deduced from the equivalent widths for the subordinate lines of Ca I. But for the resonance line, which is often strong and slightly blended with Fe I and CH lines, a fit of the profile was made. The Ca abundance was generally deduced from a fit of the wings (insensitive to NLTE effects) for the red Ca II lines. However, in the turnoff stars and in the most metal-poor giants, the wings almost disappear (when the equivalent widths are less than 400 mÅ) and in this case, equivalent widths were used.
 |
Fig. 5 Difference between [Ca/H] deduced from the subordinate lines of Ca I and [Ca/H] deduced from a) the infrared triplet of Ca II and b) the resonance line of Ca I. The filled circles represent the turnoff stars and the open symbols the giants. The error bar on [Ca/H], Δ Ca 866.21 and Δ Ca 422.67 is generally less than 0.1dex. It is indicated only when it exceeds 0.1 dex. a) The Ca abundance deduced from the line of the infrared triplet is, as a mean, 0.07 dex lower than the abundance derived from the subordinate lines of Ca I. b) For [Ca / H] ≈ − 2, the abundance deduced from the Ca I resonance line agrees quite well with the abundances deduced from subordinate lines, but a discrepancy appears and increases linearly when [Ca/H] decreases. It reaches about 0.4 dex for [Ca/H]= –3.5. |
In Fig. 5 we compare the abundances of calcium derived from these different systems. The abundance deduced from the line of the infrared triplet of Ca II at 862.21 nm is, as a mean, 0.07 dex lower than the abundance deduced from the subordinate lines of Ca I (Fig. 5a). This small difference is quite satisfactory since the abundance deduced from the Ca II lines depends on the surface gravity of the model, and this gravity can be affected by a systematic error since it has been derived from the ionization equilibrium of iron under the LTE hypothesis (see Cayrel et al. 2004).
In Fig. 5b, the calcium abundance derived from the subordinate lines of Ca I is compared to the abundance deduced from the Ca I resonance line at 422.67 nm. It is well known that in very metal-poor stars, under the LTE hypothesis, this resonance line leads to an underestimation of the calcium abundance: e.g. Magain (1988), Ryan et al. (1996). But it was expected that NLTE computations of the lines would remove this effect. For one typical metal-poor giant CS 22172-02 we show in Fig. 6 the observed spectrum and theoretical spectra computed with abundances log ϵ(Ca) = 2.52 (best fit), 2.8 and 3.1. The subordinate lines lead to a Ca abundance of 3.11; this value is well established: seven of the subordinate lines have an equivalent width stronger than 9 mÅ and the scatter in abundance is only 0.09 dex.
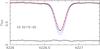 |
Fig. 6 Observed profile of the resonance line of Ca I (crosses) for one typical metal-poor giant compared to theoretical profiles computed with log ϵ(Ca) = 2.52 (thick red line), 2.8 and 3.1 (thin blue lines). The wavelengths are in Å. The (very small) difference between the observed spectrum and the profile computed with log ϵ(Ca) = 2.52 is shown at the bottom of the figure (dots, shifted by 0.1). For this star, the subordinate lines lead to log ϵ(Ca) = 3.11 (Table 1). |
A similar discrepancy has been observed, after NLTE computations, in several metal-poor stars by Mashonkina et al. (2007) and the authors suggested that the explanation could lie with the 1D atmospheric models adopted for the computations, since the Ca I resonance line is formed over a more extended range of atmospheric depths than the subordinate lines.
4.2. Influence of convection – 3D models
4.2.1. Shift of the calcium lines
The atmospheres of cool stars are not static. Velocity and intensity fluctuations caused by convection are observed in the Sun (Rutten et al. 2004) and in metal-poor stars. Ramírez et al. (2010) found that in HD 122563 (a star of our sample of giants) the cores of the Fe I lines are shifted relative to the mean radial velocity of the star, this shift increases with the equivalent width of the line. Weaker lines form in deeper layers, where the granulation velocities and intensity contrast are higher. We also observe this phenomenon for the calcium lines in all stars of our sample. The radial velocity of the stars were determined from a constant set of iron lines, and relative to this “zero point”, the radial velocity derived from the Ca I resonance line is about 0.4 km s-1 higher in the giants and 0.2 km s-1 higher in the dwarfs. In contrast, the radial velocity derived from the (weak) subordinate calcium lines is about 0.4 km s-1 lower in the giants and about 0.2 km s-1 lower in the dwarfs. (We were able to measure precisely the shift of the subordinate lines only on the “blue spectra” when these lines were larger than 20 mÅ.) At the resolution of our VLT/UVES spectra with R ≈ 45 000, the asymmetry of the lines cannot be reliably measured.
The shift of the Ca I resonance line does not clearly depend on [Ca/H], and therefore it does not seem that there is a clear correlation between the shift of the Ca lines and the discrepancy between the abundances deduced from the resonance or the subordinate lines.
4.2.2. Abundance correction
The largest abundance corrections caused by granulation effects occur at low metallicities. This is mainly because the difference between the 1D and 3D predictions for the mean temperature of the outer layers of metal-poor stars is very large (see e.g. González Hernández et al. 2010). We tried to investigate the change in abundances caused by thermal inhomogeneities and differences in formation depth (3D corrections hereafter) for the Ca I resonance line at 422.67 nm and for a typical subordinate line of Ca I at 445.48 nm.
-
For a representative turnoff star, we used a 3D-CO5BOLDmodel (Freytag et al. 2002, 2011) from the CIFISTgrid (see Ludwig et al. 2009) with parameters (Teff, log g,[Fe/H]): 6270 K/4.0/–3.0).
-
For the giants we used two models (4488 K/2.0/–3.0 and 5020 K/2.5/–3.0) from the CIFIST grid. They have both a gravity slightly higher than the ones in our sample of giants, but no closer 3D model is available at the moment.
From these computations we found that for [Fe/H] = –3, [Ca/H] = –2.6, the 3D correction for the subordinate lines of Ca I in turnoff and in giant stars is very small.
In giants, the 3D correction seems to be negligible also for the resonance line. But with the model of turnoff stars, we found for the resonance line a 3D correction of –0.44 dex, and therefore the 3D correction increases the discrepancy between the subordinate lines and the 422.67 resonance line.
To date, it is not well understood why the abundance of calcium deduced from the resonance line of Ca I is, at very low metallicity, lower than the abundance deduced from the subordinate lines. It would be interesting to repeat the 3D computations with more metal-poor models (not available today). A fully consistent 3D NLTE model atmosphere and line formation scheme is currently beyond our reach.
5. Results and discussion
 |
Fig. 7 [Ca/Fe] vs. [Fe/H] in our sample of EMP stars. Symbols as in Fig. 5. Turnoff and giant stars agrees quite well, [Ca/Fe] is constant in the range −4.3 < [Fe / H] < −2.5 and the mean value is equal to [Ca/Fe] = 0.5, a value slightly higher than the LTE value [Ca/Fe] = 0.35 (see Bonifacio et al. 2009). |
In this section we adopt the Ca abundance deduced from the subordinate lines of Ca I (Table 1, Cols. 11 and 12).
In Fig. 7 we present the new relation between [Ca/Fe] and [Fe/H]. The error bar plotted in for the subordinate lines the figure is the quadratic sum of the error due to the uncertainty of the model and the random error of the Ca abundance derived from the subordinate lines. The agreement between the turnoff and the giant stars is excellent, the ratio [Ca/Fe] is constant in the interval −4.5 < [Fe / H] < −2.5. The slope of the regression line is –0.05. The scatter of [Ca/Fe] is a little smaller when NLTE effects are taken into account: 0.09 from NLTE computations compared to 0.10 from LTE computation.
In Fig. 8 we present the behavior of the abundances of O, Na, Mg, Al, S and K relative to Ca. The computation of these abundances take into account the NLTE effects (Andrievsky et al. 2007, 2008, 2010; and Spite et al. 2011). Since the abundance of oxygen has been determined from the forbidden oxygen line at 630 nm (Cayrel et al. 2004), it is free of NLTE effects.
In Fig. 8, different symbols are used for mixed and unmixed giants. After Spite et al. (2005, 2006) we call “mixed giants”, those where, owing to mixing with deep layers, carbon has been partially transformed into nitrogen ([C / N] < −0.6), part of 12C has been transformed into 13C (12C / 13C < 10), and lithium is not detected (lithium has been severely depleted by this mixing). In the HR diagram, these “mixed giants” are located above the “bump”. It has been found (Andrievsky et al., 2007) that some mixed giants are enriched in sodium, this is visible in Fig. 8b. This Na-enhancement reflects a deep internal mixing (or an AGB status, or a contamination by AGB stars), but it does not reflect an anomaly of the chemical composition of the cloud that formed the star. Therefore the mixed stars cannot be used to determine the ratio [Na/Ca] in the early galactic matter.
 |
Fig. 8 Abundance ratios of O, Na, Mg, Al, S, and K relative to Ca in the early Galaxy. The abundances of all these elements were computed taking into account the NLTE effect. The black dots represent the turnoff stars, the open circles the giants (blue for the unmixed giants and red for the mixed giants). |
Mean value of the ratios [X/Fe], [X/Ca] and [X/Mg] in the interval − 3.6 < [Fe / H] < − 2.5 and scatter around the mean.
Since the abundance ratios of O, Na, Al, S, and K relative to Ca are fairly flat vs. [Fe/H] in the central part of the diagram, we can define a mean value in this central interval, say −3.6 < [Fe / H] < −2.5 as has been done with Mg in Andrievsky et al. (2010). The mean values of [X/Fe], [X/Mg] and [X/Ca] are given in Table 3 with the corresponding scatter. However, an anti-correlation seems to exist between [S/Ca] and [Fe/H] and also [S/Mg] and [Fe/H]: the Kendall τ coefficient is 98.9% for [S/Ca] and 99.1% for [S/Mg]. In these computations the weight of BD +17°3248 ([Fe/H] = –2.2) is important. This star is quite peculiar: according to For & Sneden (2010) it is a red horizontal branch star strongly enriched in heavy elements (Cowan et al. 2002). However, if this star is removed from the computations, the Kendall τ coefficient remains high: 97.6% for [S/Ca] and 97.9% for [S/Mg].
One turnoff star, BS 16023-046, and one unmixed giant CS 22956-50, have abnormally strong and broad sodium D lines. Their radial velocity (–7.5 km s-1 and –0.1 km s-1) is low, and the stellar lines are very probably blended with interstellar lines. These stars have not been plotted on Fig. 8b and were not taken into account in computing the mean value and the scatter of [Na/Fe], [Na/Mg] and [Na/Ca] in Table 3.
It is interesting to take advantage of the high quality of the data to compare in Table 3 the scatter around the mean value when Fe, Mg, or Ca are taken as reference elements. The scatter of [O/Fe], [O/Mg] or [O/Ca] is fairly large: about 0.2 dex but this can be explained by the scatter of the oxygen abundance due to the reduced number of oxygen lines and the difficulty of the measurements. For the other ratios the scatter lies between 0.09 and 0.15 dex and we consider that this difference of 0.06 dex is significant. The scatter is always significantly smaller when Ca is taken as the reference element, with two exceptions:
-
Oxygen: but in this case we have seen that the scatter is dominatedby the error on the measurement of the very weak oxygen line.
-
Aluminum: Al is better correlated with Mg than with Ca. But this correlation (opposite to the well known anti-correlation found in globular cluster stars) has at least one exception: CS 29516-024 is rather Al-poor but it is (relatively) Ca-rich and Mg-rich, and it does not seem possible to explain these differences by errors of measurements. A similar correlation between [Al/Fe] and [Mg/Fe] has been also suggested by Suda et al. (2011) even in a large but very inhomogeneous sample of metal-poor stars.
6. Concluding remarks
We determined the calcium abundance in a homogeneous sample of of 53 metal-poor stars (31 of them with [Fe / H] < − 2.9) taking into account departures from LTE. We have shown that the trend of the ratio [Ca/Fe] vs. [Fe/H], below [Fe/H] = –2.7 is almost flat and derived a new mean value of [Ca/Fe] in the early Galaxy: [Ca / Fe] = 0.5 ± 0.09.
Generally speaking, our NLTE calculations agree quite well with those of Mashonkina et al. (2007). However, Mashonkina et al. had found different Ca abundances from the Ca I and Ca II lines in Procyon. With our new model atom of calcium, we are able to reconcile the calcium abundance deduced from neutral and ionized calcium lines in Procyon. We derived log ϵ(Ca) = 6.25 ± 0.04 from Ca I lines and 6.27 ± 0.06 from Ca II lines (6.33 and 6.40 under the LTE hypothesis). Moreover, the calcium abundance is found to be solar, as expected.
In metal-poor stars (below [Ca/H] = –2.5), a discrepancy clearly appears between the Ca abundances deduced from either the resonance Ca I line, or the Ca I subordinate lines. A rough estimation of the effect of convection on the profile of these lines does not explain this discrepancy.
In the stars of our sample (giants and turnoff stars) the wavelengths of the calcium lines are shifted by convection as a function of the equivalent width of the lines as has been found for the iron lines by Ramírez et al. (2010) in HD 122563.
The scatter around the mean value of [Ca/Fe] is small but since the NLTE correction is about the same for all the subordinate lines used in this analysis, the scatter is almost the same as it was in the LTE analyses (Cayrel et al. 2004; Bonifacio et al. 2009).
The abundance of the light metals O, Na, Al, S, K is well correlated with the calcium abundance. The correlation is generally a little better than it is with the magnesium abundance (with exception of the tight aluminium/magnesium correlation). However, it is striking that in Table 3, even when NLTE is taken into account, the correlation of the light elements O, Na, Al, S, K with Ca or Mg (all supposed to be formed mainly by hydrostatic fusion of C, Ne or O), is never better than the correlation with iron, providing some support to supernovae models predicting nucleosynthesis of all these elements predominantly in explosive modes (e.g. Nomoto et al. 2006).
Acknowledgments
The authors thank the referee, who indicated new log gf values for the high excitation Ca II lines. This work has been supported in part by the “Programme National de Physique Stellaire” (CNRS). S.A. kindly thanks the Observatoire de Paris, the CNRS, and the laboratory GEPI for their hospitality and support during his stay in Meudon. He acknowledges the National Academy of Sciences of Ukraine and the franco-Ukrainian exchange program for its financial support under contract UKR CDIV N24008.
References
- Allen, C. W. 1973, Astrophys. Quant. (London: Athlone Press) [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1996, A&A, 313, 873 [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 2001, A&AS, 376, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S., Spite, M., Korotin, S., et al. 2007, A&A, 464, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2008, A&A, 481, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S., Spite, M., Korotin, S., et al. 2010, A&A, 509, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [NASA ADS] [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1997, MNRAS, 290, 102 [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1998, MNRAS, 300, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., O’Mara, B. J., & Ross, J. E. 1998, MNRAS, 296, 1057 [Google Scholar]
- Bonifacio, P., Molaro, P., Sivarani, T., et al. 2007, A&A, 462, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonifacio, P., Spite, M., Cayrel, R., et al. 2009, A&A, 501, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgess, A., Chidichimo, M. C., & Tully, J. A. 1995, A&A, 300, 627 [NASA ADS] [Google Scholar]
- Caffau, E., & Ludwig, H.-G. 2007, A&A, 467, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M. 1986, Uppsala Obs. Rep., 33 [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowan, J. J., Sneden, C., Burles, S., et al. 2002, ApJ, 572, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, Proc. SPIE, 4008, 534 [Google Scholar]
- For, B.-Q., & Sneden, C. 2010, AJ, 140, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Steffen, M., & Dorch, B. 2002, AN, 323, 213 [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2011, JCoPh, 231, 919 [Google Scholar]
- González Hernández, J. I., Bonifacio, P., Ludwig, H.-G., et al. 2010, A&A, 519, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 2000, Origin of the elements in the solar system, Implications of post-1957 Observations, ed. O. Manuel (Kluwer Academic/Plenum Publishers), 261 [Google Scholar]
- Hirata, R., & Horaguchi, T. 1995, Catalogue of Atomic Spectroscopic Lines (Strasbourg: CDS), 6, 69 [Google Scholar]
- Hosford, A., Ryan, S. G., Garcia Perez, A. E., Norris, J. E., & Olive, K. A. 2009, A&A, 493, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivanova, D. V., Sakhibullin, N. A., & Shimanskii, V. V. 2002, ARep, 46, 390 [Google Scholar]
- Kobayashi, Ch., Umeda, H., Nomoto, K., et al. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Korn, A., Shi, J., & Gehren, T. 2003, A&A, 407, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korotin, S. A. 2008, Odessa Astronomical Pub., 21, 42 [Google Scholar]
- Korotin, S. A., Andrievsky, S. M., & Luck, R. E. 1999, A&A, 351, 168 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1992, RMxAA, 23, 181 [Google Scholar]
- Kurucz, R. L. 1993, SAO, Cambridge, CDROM18 [Google Scholar]
- Kurucz, R. L., & Bell, B. 1995, SAO, Cambridge, CDROM23 [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, National Solar Observatory Atlas, Sunspot, New Mexico: National Solar Observatory [Google Scholar]
- Lodders, K., Plame, H., & Gail, H.-P. 2009, in Landolt-Börnstein, New Series, Vol. VI/4B, Chap. 4.4, ed. J. E. Trümper (Berlin Heifelberg New York: Springer-Verlag), 560 [Google Scholar]
- Ludwig, H.-G., Behara, N. T., Steffen, M., & Bonifacio, P. 2009, A&A, 502, L1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Magain, P. 1988, in The impact of Very High S/N spectroscopy on Stellar Physics, ed. G. Cayrel de Strobel, & M. Spite (Dordrecht, Kluwer), IAU Symp., 132, 485 [Google Scholar]
- Mashonkina, L., Gehren, T., Travaglio, C., & Borkova, T. 2003, A&A, 397, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Korn, A. J., & Przybilla, N. 2007, A&A, 461, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, M., Bautista, M. A., & Badnell, N. R. 2007, A&A, 469, 1203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merle, T., Thévenin, F., Pichon, B., & Bigot, L. 2011, MNRAS, 418, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, D. C. 1991, ApJS, 77,119 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Tominaga, N., Umeda, H., et al. 2006, Nucl. Phys. A, 777, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Ramírez, I., Collet, R., Lambert, D. L., Allen de Prieto, C., & Asplund, M. 2010, ApJ, 725, L223 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J., Hammerschlag, R. H., Bettonvil, F. C. M., Sütterlin, P., & de Wijn, A. G., 2004, A&A, 413, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryan, S. G., Norris, J. E., & Beers, T. C. 1996, ApJ, 471, 1996 [Google Scholar]
- Samson, A. M., & Berrington, K. A. 2001, ADNDT, 77, 87 [Google Scholar]
- Seaton, M. J. 1962, in Atomic and Molecular processes (New York: Academic Press) [Google Scholar]
- Smith, G. 1988, J. Phys. B, 21, 2827 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G., & Raggett, D. St. J. 1981, J. Phys. B, 14, 4015 [NASA ADS] [CrossRef] [Google Scholar]
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, M., Cayrel, R., Hill, V., et al. 2006, A&A, 455, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, M., Caffau, E., Andrievsky, S., et al. 2011, A&A, 528, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
- Suda, T., Yamada, S., Katsuta, Y., et al. 2011, MNRAS, 412, 843 [NASA ADS] [Google Scholar]
- Sugar, J., & Corliss, C. 1985, J. Phys. Chem. Ref. Data, 14 [Google Scholar]
- Theodosiou, C. E. 1989, Phys. Rev. A, 39, 4880 [NASA ADS] [CrossRef] [Google Scholar]
- Van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Wiese, W. L., & Martin, G. A. 1980, NSRDS-NBS 68, Part II [Google Scholar]
- Wiese, W. L., Smith, M. W., & Miles, B. M. 1969, NSRDS-NBS, 22, 2 [NASA ADS] [Google Scholar]
All Tables
Parameters of the Ca lines used in the solar spectrum. γ1 = log γVW / NH for a temperature of 10 000 K.
Mean value of the ratios [X/Fe], [X/Ca] and [X/Mg] in the interval − 3.6 < [Fe / H] < − 2.5 and scatter around the mean.
All Figures
 |
Fig. 1 Profiles of Ca I and Ca II lines in Procyon. The wavelengths are in Å. The small crosses represent the observed spectrum and the (red) line the computed profile. With our model atom, the observed and computed profiles of the Ca I and Ca II lines agree well. |
| In the text | |
 |
Fig. 2 Profiles of Ca I and Ca II lines in HD 140283. The wavelengths are in Å. The symbols are the same as in Fig. 1. The observed spectrum and the synthetic profiles computed with log ϵ(Ca) = 4.12 agree well. |
| In the text | |
 |
Fig. 3 Profiles of three Ca lines computed for a giant star with [Ca / H] ≈ − 2.5 with LTE (thin blue line) and NLTE (thick red line) hypotheses. The wavelengths are given in Å. a) The NLTE profile of the Ca I resonance line is narrower in the wings and deeper in the core. b) In a Ca I subordinate line, for the same abundance of calcium the equivalent width computed under the NLTE hypothesis is slightly smaller. c) The NLTE correction is important for the strong IR Ca II line (note that the scale in wavelength is different for this line), but the wings are not affected and a reliable calcium abundance can be deduced from these wings via LTE analysis. |
| In the text | |
 |
Fig. 4 NLTE corrections for the Ca I resonance line at 422.67 nm and for a typical subordinate line of Ca I at 445.48 nm. |
| In the text | |
 |
Fig. 5 Difference between [Ca/H] deduced from the subordinate lines of Ca I and [Ca/H] deduced from a) the infrared triplet of Ca II and b) the resonance line of Ca I. The filled circles represent the turnoff stars and the open symbols the giants. The error bar on [Ca/H], Δ Ca 866.21 and Δ Ca 422.67 is generally less than 0.1dex. It is indicated only when it exceeds 0.1 dex. a) The Ca abundance deduced from the line of the infrared triplet is, as a mean, 0.07 dex lower than the abundance derived from the subordinate lines of Ca I. b) For [Ca / H] ≈ − 2, the abundance deduced from the Ca I resonance line agrees quite well with the abundances deduced from subordinate lines, but a discrepancy appears and increases linearly when [Ca/H] decreases. It reaches about 0.4 dex for [Ca/H]= –3.5. |
| In the text | |
 |
Fig. 6 Observed profile of the resonance line of Ca I (crosses) for one typical metal-poor giant compared to theoretical profiles computed with log ϵ(Ca) = 2.52 (thick red line), 2.8 and 3.1 (thin blue lines). The wavelengths are in Å. The (very small) difference between the observed spectrum and the profile computed with log ϵ(Ca) = 2.52 is shown at the bottom of the figure (dots, shifted by 0.1). For this star, the subordinate lines lead to log ϵ(Ca) = 3.11 (Table 1). |
| In the text | |
 |
Fig. 7 [Ca/Fe] vs. [Fe/H] in our sample of EMP stars. Symbols as in Fig. 5. Turnoff and giant stars agrees quite well, [Ca/Fe] is constant in the range −4.3 < [Fe / H] < −2.5 and the mean value is equal to [Ca/Fe] = 0.5, a value slightly higher than the LTE value [Ca/Fe] = 0.35 (see Bonifacio et al. 2009). |
| In the text | |
 |
Fig. 8 Abundance ratios of O, Na, Mg, Al, S, and K relative to Ca in the early Galaxy. The abundances of all these elements were computed taking into account the NLTE effect. The black dots represent the turnoff stars, the open circles the giants (blue for the unmixed giants and red for the mixed giants). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


