| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201118498 | |
| Published online | 11 May 2012 | |
SN 2006oz: rise of a super-luminous supernova observed by the SDSS-II SN Survey
1 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, 2100 Copenhagen, Denmark
e-mail: giorgos@dark-cosmology.dk
2 Department of Astronomy, University of Texas at Austin, Austin, TX, USA
3 Las Cumbres Observatory Global Telescope Network, Goleta, CA 93117, USA
4 Department of Physics, University of California, Santa Barbara, Broida Hall, Santa Barbara, CA 93106-9530, USA
5 Instituto de Astrofísica de Andalucía (IAA-CSIC), Granada, Spain
6 Department of Optics and Quantum Electronics, University of Szeged, Szeged, Hungary
7 African Institute for Mathematical sciences, Muizenberg, Cape Town, South Africa
8 South African Astronomical Observatory, Cape Town, South Africa
9 Mathematics Department, University of Cape Town, Cape Town, South Africa
10 University of Pennsylvania, 209 South 33rd Street, PA 19104, USA
11 Department of Astronomy and Astrophysics, The University of Chicago, Chicago, IL 60637, USA
12 Kavli Institute for Cosmological Physics, The University of Chicago, Chicago, IL 60637, USA
13 Center for Particle Astrophysics, Fermi National Accelerator Laboratory, Batavia, IL 60510, USA
14 The Oskar Klein Centre, Stockholm University, Albanova University Centre, 10691 Stockholm, Sweden
15 Department of Physics, Stockholm University, Albanova University Centre, 10691 Stockholm, Sweden
16 Institute of Cosmology and Gravitation, Dennis Sciama Building, University of Portsmouth, Portsmouth, PO1 3FX, UK
17 Space Sciences Laboratory, University of California Berkeley, Berkeley, CA 94720, USA
18 E. O. Lawrence Berkeley National Lab, 1 Cyclotron Rd., Berkeley, CA 94720, USA
19 Institut de Física d’Altes Energies, Universitat Autonoma de Barcelona, 08193 Bellaterra (Barcelona), Spain
20 Department of Astronomy and Astrophysics, The Pennsylvania State University, University Park, PA 16802, USA
21 Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA
22 Astrophysics, Cosmology and Gravity Centre, Department of Mathematics and Applied Mathematics, University of Cape Town, 7700 Rondebosch, South Africa
23 Department of Astronomy, Stockholm University, Albanova University Centre, 10691 Stockholm, Sweden
24 Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
Received: 22 November 2011
Accepted: 29 February 2012
Context. A new class of super-luminous transients has recently been identified. These objects reach absolute luminosities of Mu < −21, lack hydrogen in their spectra, and are exclusively discovered by non-targeted surveys because they are associated with very faint galaxies.
Aims. We aim to contribute to a better understanding of these objects by studying SN 2006oz, a newly-recognized member of this class.
Methods. We present multi-color light curves of SN 2006oz from the SDSS-II SN Survey that cover its rise time, as well as an optical spectrum that shows that the explosion occurred at z ~ 0.376. We fitted black-body functions to estimate the temperature and radius evolution of the photosphere and used the parametrized code SYNOW to model the spectrum. We constructed a bolometric light curve and compared it with explosion models. In addition, we conducted a deep search for the host galaxy with the 10 m GTC telescope.
Results. The very early light curves show a dip in the g- and r-bands and a possible initial cooling phase in the u-band before rising to maximum light. The bolometric light curve shows a precursor plateau with a duration of 6–10 days in the rest-frame. A lower limit of Mu < − 21.5 can be placed on the absolute peak luminosity of the SN, while the rise time is constrained to be at least 29 days. During our observations, the emitting sphere doubled its radius to ~2 × 1015 cm, while the temperature remained hot at ~15 000 K. As for other similar SNe, the spectrum is best modeled with elements including O ii and Mg ii, while we tentatively suggest that Fe iii might be present. The host galaxy is detected in gri with 25.74 ± 0.19, 24.43 ± 0.06, and 24.14 ± 0.12, respectively. It is a faint dwarf galaxy with Mg = −16.9.
Conclusions. We suggest that the precursor plateau might be related to a recombination wave in a circumstellar medium (CSM) and discuss whether this is a common property of all similar explosions. The subsequent rise can be equally well described by input from a magnetar or by ejecta-CSM interaction, but the models are not well constrained owing to the lack of post-maximum observations, and CSM interaction has difficulties accounting for the precursor plateau self-consistently. Radioactive decay is less likely to be the mechanism that powers the luminosity. The host is a moderately young and star-forming, but not a starburst, galaxy.
Key words: supernovae: general / supernovae: individual: SN 2006oz / stars: massive
© ESO, 2012
1. Introduction
Historically, supernovae (SNe) have usually been discovered by monitoring bright, nearby galaxies. With a few exceptions, the supernovae discovered in this targeted way fit well within the traditional SN classification scheme (e.g. Filippenko 1997). During the last few years, however, rolling searches, such as the Texas SN Search (Quimby et al. 2005) and the Catalina Real-Time Transient Survey (Drake et al. 2009) have changed our view of stellar explosions. In particular, it has been shown that interesting transients were previously missed exactly because they occur in environments different from those probed by the traditional SN searches. Remarkably, these include the brightest SNe ever recorded (hereafter super-luminous supernovae, SLSNe) with luminosities exceeding those of SNe Ia by 10–100 times.
Many of these SLSNe are associated with SNe IIn and have high luminosities attributed (at least partly) to the interaction of the ejecta with a dense H-rich CSM (e.g. Ofek et al. 2007; Smith et al. 2007, 2008). SN 2005ap, in contrast, showed only weak evidence for hydrogen and yet reached an absolute magnitude of MR < −22.5 (Quimby et al. 2007). A seemingly unrelated object of peculiar nature was discovered by the Supernova Cosmology Project (SCP) with HST (Barbary et al. 2009). SCP06F6 had unprecedented spectra and light curves, but the lack of a robust redshift estimate left this study inconclusive with respect to its nature (see also Chatzopoulos et al. 2009; Gänsicke et al. 2009; Soker et al. 2010).
Significant progress was made when Quimby et al. (2011) showed that four objects detected by the Palomar Transient Factory (PTF; Rau et al. 2009; Law et al. 2009) could be grouped together with SN 2005ap and SCP06F6 to form a distinct class of H-poor SLSNe. The redshifts of these objects were identified by the detection of the Mg ii λ2800 doublet and SCP06F6 was shown to be at a much higher redshift (z = 1.189) than originally estimated. All objects had similar spectra, blue colors, and relatively symmetric light curves. Their typical absolute magnitude is M ~ −21.5 and their explosion mechanism remains a mystery. Possible suggestions include pulsational pair-instability (Woosley et al. 2007), the powering of the ejecta by a magnetar (Kasen & Bildsten 2010; Woosley 2010), or interaction with an CSM (Chevalier & Irwin 2011; Blinnikov & Sorokina 2010; Moriya & Tominaga 2012). A third class of SLSNe, also H-poor, but different from those in Quimby et al. (2011), might be represented by SN 2007bi, which has been proposed (Gal-Yam et al. 2009) to be a pair-instability event, although this explanation is not unique (Young et al. 2010; Moriya et al. 2010).
One of the objects studied by Quimby et al. (2011), SN 2010gx, was also extensively followed by Pastorello et al. (2010). By obtaining spectra at later phases, they managed to demonstrate that this SLSN transitioned to a SN Ic, showing that there is a possible link between these energetic explosions. Recently, two more SNe belonging to this intriguing class were discovered by Pan-STARRS1 at z ~ 0.90 (Chomiuk et al. 2011). These objects showed no signs of deceleration in their expansion velocities during observations obtained over a period of about three weeks around maximum light.
A common characteristic for H-poor SLSNe is that they are systematically found in faint galaxies. Indeed, to date, only three of these hosts have been detected; there are only upper limits on the others (typically MB > −18), suggesting that they are probably metal-poor (Neill et al. 2011). It has been speculated that low metallicity might be an indispensable ingredient to produce SLSNe.
One reason that our understanding of these objects is limited is that the available data are sparse and incomplete: observations are often obtained in 1 or 2 neighboring filters, and when multi-color light curves are available, they cover only part of the SN evolution. The study of SLSNe is a relatively new topic and any complementary dataset (especially covering the critical early phases) constitutes a valuable contribution to the field.
SN 2006oz was discovered by the SDSS-II SN Survey (Frieman et al. 2008) toward the end of the 2006 observing season at RA =  , Dec =
, Dec = 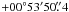 (J2000). Labeled internally as a “strange hostless transient”, it was initially classified (Stritzinger et al. 2006) as a possible SN Ib based on a spectrum obtained at the Nordic Optical Telescope (NOT). In the analysis by Östman et al. (2011), it was given a SN II designation, noting, however, that it matched less than five templates in SNID (Blondin & Tonry 2007). Today, we know that these misclassifications were due to the lack of suitable comparison spectra in the literature, and, here, we identify it as an H-poor SLSN, as defined by Quimby et al. (2011). Our observations and results are presented in the next section. Section 3 contains the discussion and Sect. 4 our concluding remarks.
(J2000). Labeled internally as a “strange hostless transient”, it was initially classified (Stritzinger et al. 2006) as a possible SN Ib based on a spectrum obtained at the Nordic Optical Telescope (NOT). In the analysis by Östman et al. (2011), it was given a SN II designation, noting, however, that it matched less than five templates in SNID (Blondin & Tonry 2007). Today, we know that these misclassifications were due to the lack of suitable comparison spectra in the literature, and, here, we identify it as an H-poor SLSN, as defined by Quimby et al. (2011). Our observations and results are presented in the next section. Section 3 contains the discussion and Sect. 4 our concluding remarks.
2. Observations and results
 |
Fig. 1 ugriz light curves of SN 2006oz obtained by the SDSS SN Survey, shifted as indicated for presentation purposes. Triangles denote 3σ upper limits. The lower panel focuses on the g-band evolution shown together with a cubic polynomial fit to the last 10 observations (solid line) extrapolated backward (dashed line). Clearly, the first points are strongly inconsistent with a smooth rise. The date of the NOT spectrum is also indicated. |
Photometric observations were carried out with the SDSS telescope at Apache Point Observatory (Gunn et al. 1998, 2006) in the SDSS ugriz filters (Fukugita et al. 1996). As for all SNe discovered by the SDSS SN survey, the identification was made according to Sako et al. (2008) and the photometry was performed in the way described in Holtzman et al. (2008), to which we refer the reader for more details. We just point out that these are “asinh” magnitudes, defined by Lupton et al. (1999) to be identical to the traditional astronomical magnitudes at higher signal-to-noise ratio, but which provide a well-behaved finite flux and error even in the low-flux regime. We have derived more traditional 3σ upper limits (see Table 3) for non-significant detections (error ≳ 0.5 mag), but used the asinh magnitudes for the construction of our bolometric light curve (Sect. 3.2).
The SDSS light curves are plotted in Fig. 1. As can be seen, our observations cover the rise of SN 2006oz, and end before or close to maximum light. Because of a six day gap in the observations, the explosion date is not very well constrained, but the g-band limit previous to our first detection suggests that the explosion occurred between MJD 54022 and 54028. Nevertheless, these ugriz light curves are very interesting: there are hints in our photometry that the SN initially faded in the u-band and re-brightened a few days later. This behavior has only been observed for a handful of stripped core-collapse SNe that were discovered at very early phases and is usually attributed to a phase of adiabatic cooling of the envelope following shock breakout (e.g. Richmond et al. 1994; Stritzinger et al. 2002). Our observations are only poorly constraining (because we are in the low-flux regime), but based on the error bars and upper limits we estimate that there is a probability of 78% that the SN faded between MJD 54028 and 54037 in the u-band. Additionally, a (significant) dip in the light curve is observed simultaneously in the g- and r-bands. Combining the ugr-bands there is strong evidence (>5σ) for a non-standard, non-increasing luminosity evolution of this SN during the first ten days of observations.
At MJD 54061.87, we obtained a spectrum of SN 2006oz at the NOT equipped with ALFOSC. The spectrum spans the wavelength range 3200–9100 Å with a resolution of 20 Å and was reduced in the manner described by Östman et al. (2011). The spectrum is displayed in Fig. 2 with a sample of comparison spectra from Quimby et al. (2011), obtained at comparable pre-maximum phases, to highlight their similarity. To obtain a redshift estimate, our spectrum was initially cross-correlated with the four objects presented in Quimby et al. (2011) by using SNID (Blondin & Tonry 2007). The constructed templates matched reasonably well, all within 0.365 < z < 0.397 with a mean z = 0.376 ± 0.014. It is possible, however, that there are intrinsic velocity differences between the features of SN 2006oz and the other SNe, which would influence our redshift estimate. We have searched in the wavelength window ~3500−4500 Å for any absorption lines, in particular Mg ii λλ2795, 2802 (Quimby et al. 2011) that would allow us to determine the redshift more accurately. At the low resolution of our spectrum the doublet will appear blended, making the search more complicated. The only candidate line that we were able to identify is at ~3856 Å. Although at low significance (~2.7σ), it appears consistently in all sets of extractions that we attempted and always with the same profile (Fig. 2; inset). Although this line is insufficient to derive a robust spectroscopic redshift (i.e. Mg ii at z = 0.377), it can be considered as supporting evidence for the redshift derived by cross-correlating the SN spectra.
 |
Fig. 2 Spectrum of SN 2006oz (red) obtained at the NOT. For comparison we show 3 spectra from Quimby et al. (2011) at similar pre-maximum phases. The colored spectra are smoothed versions (moving average of 5 pixels) of the original gray spectra. All spectra were plotted in their rest frame assuming z = 0.376 for SN 2006oz. The inset shows a zoom of the area around 2800 Å. At this redshift we identified the only probable line (although at low significance 2.7σ) consistent with the Mg ii doublet (which would appear blended at this resolution). |
Our best redshift estimate, used throughout the paper, is therefore z = 0.376. Assuming a cosmology with H0 = 71 km s-1 Mpc-1, Ωm = 0.27 and ΩΛ = 0.73, SN 2006oz reached an absolute (rest-frame) magnitude of Mu = −21.5 mag. This calculation contains the assumption that maximum light occurred in our last epoch of observations and is, therefore, only a lower limit to the peak luminosity of the SN. In addition, owing to the uncertainty in the cross-correlation redshift, one needs to assign a 0.1 mag systematic error in all quantities that depend on the distance to the SN. Similarly, we are able to place a strict constraint on the (rest-frame) rise time of >29 days. Rest-frame wavelengths and related quantities will suffer from an uncertainty of 1%.
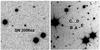 |
Fig. 3 Left: image of SN 2006oz obtained with the SDSS telescope (MJD 54061.17). Right: deep i image of the field, obtained almost 5 yr after the SN with GTC/OSIRIS. The SN is coincident with the position of galaxy A. However, within a radius of 7′′, there are four more objects, including one that appears extended, labeled B, C, D and E, respectively. Their photometry is reported in Table 1. Both images are 72′′ × 72′′. North is up and east is to the left. |
Host galaxy candidates for SN 2006oz.
On 26 August 2011, almost 5 yr after the SN, we obtained deep gri imaging of the field with OSIRIS on Gran Telescopio Canarias (GTC). The SN position is spatially coincident with a candidate host galaxy (object A; Fig. 3), but within a radius of 7′′ there are four more galaxies, including one that appears extended (object E). The photometry of these galaxies and their angular distances from the SN position are presented in Table 1. The error of these angular distances as determined from the rms of the IRAF1 task geomap was estimated to be 0.35′′. Because of its spatial proximity, we identify galaxy A as the host of SN 2006oz. Assuming z = 0.376, the SN occurred at a distance of 2.40 ± 1.36 kpc from the galaxy center, while the distance to the nearest other candidate would exceed 15 kpc. At this redshift, the host of SN 2006oz is intrinsically faint with a (rest-frame) absolute magnitude of Mg = −16.9. We note that the photometric redshift obtained for this galaxy (using the code Le Phare; Arnouts et al. 1999; Ilbert et al. 2006) is 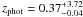 . Although not constraining, this value is consistent with what was obtained for the SN.
. Although not constraining, this value is consistent with what was obtained for the SN.
3. Discussion
3.1. Black-body fits
To estimate the photospheric temperature and radius of SN 2006oz, we fitted a black body (BB) function to the optical spectrum. As also pointed out by Chomiuk et al. (2011), these events miss some flux in the UV with respect to a BB, and therefore reliable BB fits can only be obtained by fitting data redward of rest-frame 3000 Å (i.e. the Rayleigh-Jeans tail). This was also the experience we gained by fitting the NOT spectrum. We achieved a reasonable fit with 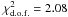 over 1309 data points, resulting in TBB = 15540 ± 430 K and RBB = (2.18 ± 0.08) × 1015 cm. It is also possible to fit the broad-band photometric data, although with higher uncertainties. We therefore performed a weighted fit of the griz data, excluding the u-band that corresponds to rest-frame 2574 Å. The fit results are shown in Table 2 and Fig. 4 and indicate that the emitting radius increased from ~1 to >2 × 1015 cm during the period of our observations. A linear increase describes the RBB evolution well with a weighted fit resulting in
over 1309 data points, resulting in TBB = 15540 ± 430 K and RBB = (2.18 ± 0.08) × 1015 cm. It is also possible to fit the broad-band photometric data, although with higher uncertainties. We therefore performed a weighted fit of the griz data, excluding the u-band that corresponds to rest-frame 2574 Å. The fit results are shown in Table 2 and Fig. 4 and indicate that the emitting radius increased from ~1 to >2 × 1015 cm during the period of our observations. A linear increase describes the RBB evolution well with a weighted fit resulting in  . In contrast, the temperature does not show any significant evolution: a linear fit results in a shallow slope, while fitting a constant temperature (~15 000 K) is also consistent with the observations (
. In contrast, the temperature does not show any significant evolution: a linear fit results in a shallow slope, while fitting a constant temperature (~15 000 K) is also consistent with the observations (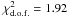 versus 1.27). However, during the first ten days the average temperature might have been lower (~12 400 K). The orders of magnitude obtained and the RBB evolution are consistent with what has been reported previously, although a cooling of the BB is usually observed (e.g. Quimby et al. 2011; Chomiuk et al. 2011). However, cooling is only observed conclusively at post-maximum phases, while, as discussed below, we are probing earlier stages of SLSN evolution with SN 2006oz.
versus 1.27). However, during the first ten days the average temperature might have been lower (~12 400 K). The orders of magnitude obtained and the RBB evolution are consistent with what has been reported previously, although a cooling of the BB is usually observed (e.g. Quimby et al. 2011; Chomiuk et al. 2011). However, cooling is only observed conclusively at post-maximum phases, while, as discussed below, we are probing earlier stages of SLSN evolution with SN 2006oz.
Black-body fits to SN 2006oz.
3.2. Bolometric and absolute light curves
To construct a (pseudo-) bolometric light curve of SN 2006oz we integrated the flux included within the limits of our simultaneous ugriz observations. To account for the epochs containing upper limits (in u and z) we used the asinh magnitudes provided by the SDSS photometry (Lupton et al. 1999; Holtzman et al. 2008), e.g. 2.6 ± 1.5 μJy for our u observation at MJD 54037. This is the most reliable assumption and the high uncertainties are propagated to the final bolometric light curve. A correction was applied only for foreground Galactic extinction (E(B − V) = 0.047; Schlegel et al. 1998) but not for any host galaxy extinction. The bolometric light curve is plotted in Fig. 5 (upper panel) together with that of PS1-10awh (z = 0.9084), which is the only other H-poor SLSN with a pre-maximum bolometric light curve (based on multi-filter observations) extending back to more than a week before maximum light. We constructed the bolometric light curve of PS1-10awh following the same procedure as for SN 2006oz based on the data of Chomiuk et al. (2011), but did not apply a bolometric correction for the red tail of the BB (this is why our light curve might appear a little different from theirs). Determining a bolometric correction is not trivial. The rest-frame wavelengths probed were ~2360−6980 Å (and ~2270–4720 Å for PS1-10awh; extending the integrations out to 0.5 × FWHM from the central wavelengths of the bracketing filters). Assuming the limiting case that these SLSNe can indeed be described by a BB, we can roughly estimate the bolometric correction by measuring the area below the BB curve covered by our observations. For the BB fit to the spectrum of SN 2006oz, the probed wavelength window captures 51% of the emitted flux, while another 43% is at bluer wavelengths and only 6% in the red tail. The corresponding percentages for PS1-10awh are 40%, 44%, and 16%, respectively. These rough numbers illustrate that the bolometric luminosities obtained could be subject to a correction of up to a factor of 2–2.5. This is the worst case, however, because the flux in the UV clearly deviates from a BB (see also Chomiuk et al. 2011).
 |
Fig. 4 Black-body fits to the SN 2006oz data. In the top panel, a fit to the NOT spectrum is shown. Only data redward of 3000 Å (rest-frame) are included in the fit. The middle and bottom panel show the radius and temperature evolution of SN 2006oz assuming it can be described by a black body. The filled circles are the results of fitting the griz photometry, while the spectrum fit is represented by a square symbol. The dashed lines show linear weighted fits to the data. |
 |
Fig. 5 Upper panel: bolometric light curve of SN 2006oz (circles) compared to PS1-10awh (solid line; data from Chomiuk et al. 2011), which has similar pre-maximum multi-color observations. To illustrate the uncertainty in tmax of SN 2006oz, its light curve was shifted horizontally with respect to the limiting case, where our last observation was assumed to be taken exactly at maximum light. Assuming the two events are similar, we obtain a reasonable match of the light curves by shifting tmax by −10 days (faded symbols). Middle and lower panels: the absolute pre-maximum light curves. The absolute luminosities at rest-frame ~4530 Å (observed r- and z-bands) and ~2560 Å (observed u- and g-bands) are compared, after correcting for cosmological expansion. As above, vivid and faded colors show the light curves of SN 2006oz shifted by 10 days. A few (non-constraining) upper limits were removed for presentation purposes. The early observations of SN 2006oz are below the detection limits of the PanSTARRS1 observations of PS1-10awh. |
In addition to the uncertainty of the total bolometric luminosity, there is also an uncertainty of the time of maximum. This is illustrated in Fig. 5 by applying a horizontal shift to the LC with respect to the limiting case for which we assume that our last observation was exactly at maximum light (vivid and faded colors). This experiment was made to show that it cannot be established whether SN 2006oz was a fainter event or whether we are probing earlier stages of its evolution (or a combination of both). Indeed, a reasonable match of the light curves can be obtained by shifting tmax by − 10 days (rest-frame, time-dilation corrected). It is certainly true that the very early data-points of SN 2006oz were below the sensitivity of the PanSTARRS1 observations of PS1-10awh at z ~ 0.9. This can also be seen in the lower panel of Fig. 5, which contains a comparison of absolute rest-frame light curves. In particular, the observed u and r-bands of SN 2006oz are compared to the g and z observations of PS1-10awh, which correspond to the same rest-frame wavelengths. This comparison shows that (despite the uncertainty in tmax) the SDSS observations of SN 2006oz reach deeper limits in an absolute level and provide a window to the early evolution of an SLSN.
The shape of this very early bolometric light curve is very interesting. The individual band observations discussed in the previous section were translated into a plateau-like phase in the bolometric light curve. This plateau has a minimum duration of six days and is followed by a dip, after which the luminosity begins to rise. Owing to the uncertainty in the time of explosion, the duration of this initial phase can be up to 14 days. Such a precursor plateau has not been observed before for an SLSN, so the reasonable question is whether it is intrinsic to all similar explosions or special to SN 2006oz. Its detection was possible by a combination of the SN redshift with multi-color observations including blue filters, a criterion not met by other H-poor SLSNe. The pre-maximum observations of the PTF SNe (Quimby et al. 2011) were mostly obtained in the R-band and do not extend to the rest-frame UV, while the PS1 observations of Chomiuk et al. (2011) are not as deep, due to the longer distances (Fig. 5). For SCP06F6 (Barbary et al. 2009), there might be hints for such a plateau in the z-band but the photometric errors are too large to allow any firm conclusion. It is therefore an intriguing possibility that this behavior is intrinsic to all events in this class. It is unlikely that this result will be changed because this bolometric light curve by construction misses some flux in the UV. Instead, the result will more probably be enhanced because the colors of SN 2006oz evolve from blue to red during this period, which reduces the fraction of missing flux with time. The nature of the plateau is discussed in more detail in Sect. 3.4.
3.3. The spectrum
The lack of clear hydrogen features is an important clue to the nature of this event and the others in its class (Quimby et al. 2011). It is difficult to avoid the conclusion that the object is hydrogen-deficient, although the possibility that some hydrogen is present, but difficult to detect, cannot be rejected. The lack of clear signatures of helium is a more ambiguous clue. The prominent lines of He i in the optical and NIR arise in transitions to the n = 2 level from higher levels. Ambient conditions in SN photospheres are typically insufficient to populate these upper levels, consequently they must be populated by non-thermal (Harkness et al. 1987; Lucy 1991) or non-LTE (Dessart et al. 2011) processes. Relevant ionization energies are H – 13.6 eV, He i – 24.6 eV, C i – 11.3 eV and O i – 13.6 eV. From the absence of obvious helium lines, it is then much less obvious that an absence of helium can be firmly deduced. In addition, the wavelength range of the SN 2006oz spectrum (and most similar events), does not cover the most prominent He lines, with the exception of λ5876, which is found in a noisy part of the spectrum. The question whether He might be expected requires additional investigation and better wavelength and temporal coverage.
We have applied the parametrized code SYNOW (Hatano et al. 1999; Branch et al. 2003) to model the spectrum of SN 2006oz. Although SYNOW is based on simplified physical assumptions, it is very useful for identifying spectral features that are strongly Doppler-broadened and sometimes heavily blended. Because SYNOW contains many adjustable parameters, we did not attempt an automated fitting via chi-squared minimization but instead looked for a reasonable agreement between the observed and the model spectra by eye, using the minimum number of different atoms/ions in the envelope. The photospheric expansion velocity and the temperature of the underlying blackbody radiation were initially set and kept fixed during the search for features. Adopting vphot = 12 000 km s-1 and TBB = 14 000 K resulted in a good fit to most spectral features. A power-law atmosphere, where the optical depth as a function of velocity varies as (v/vmax) − n with n = 7, has been assumed for all atoms/ions. Our tests showed that there are no significant differences between the line profiles obtained by using either power-law or exponential optical depth profiles for the spectral features of SN 2006oz. The maximum velocity of the envelope vmax was set to 40 000 km s-1, but this parameter is only weakly constrained by our spectrum.
 |
Fig. 6 SYNOW fit to the spectra of SN 2006oz and SCP06F6. The observed spectra were brought to the rest-frame by assuming z = 0.376 and z = 1.189, respectively, and their fluxes were scaled to match in the overlapping wavelength region. Two SYNOW models, with and without C ii, are overplotted. The inset shows a zoom in the spectrum of SN 2006oz around 3300 Å. The magenta line (inset only) shows a model without Fe iii that provides a worse fit in this region. The lower panel shows the contribution of the individual ions to the model spectra. The best-fitting model has τ(O ii) = 0.02, τ(Mg ii) = 0.05, τ(Si iii) = 0.5, τ(S iii) = 0.5 and τ(Fe iii) = 0.4. |
The observed spectrum and two model spectra, with and without C ii, are plotted together in Fig. 6. The figure also contains the spectrum of SCP06F6 (Barbary et al. 2009) to illustrate a possible extension of the spectrum to the (rest-frame) UV. The contributions of the individual ions to the model spectrum are also shown. The “W”-like feature around 4200 Å nicely matches the O ii feature that was also invoked by Quimby et al. (2011) to model other SLSNe. The strong feature around 2700 Å is probably due to Mg ii, although the spectrum is noisy in that region. Fe iii can explain the observed bump around 3180 Å (Fig. 6; inset), and none of the other ions considered here were able to model that feature. Si iii has a contribution around 3000 Å, but its presence was mostly motivated by the assumption that SN 2006oz is spectrally similar to other SLSNe. Indeed, the strongest Si iii feature matches the observed feature around 2420 Å in SCP06F6 and in other SLSNe (Quimby et al. 2011). We have also tried to include S iii in the model of SN 2006oz, but its spectral features are weak and easily obscured by the noise. We consider the presence of Si iii and S iii as a possibility, but they cannot be directly identified in SN 2006oz.
This model is consistent with the findings by Quimby et al. (2011) concerning the presence of O ii, Mg ii and Si iii (assuming there is indeed some similarity among the spectra of these extreme SNe). In addition, we suggest that Fe iii might also be present and it may also be a good candidate to model the sharp drop of the observed flux around 2000 Å in SCP06F6. We did not find the presence of C ii necessary to model SN 2006oz. This may be partially because the strongest feature that was explained with this ion by Quimby et al. (2011) is beyond the observed spectral range (rest-frame 2200 Å). On the other hand, Fig. 6 illustrates that C ii has strong contributions around 2800, 3800, and 4500 Å, but these features do not match the observed spectrum. There is some ambiguity between the presence of C ii and that of O ii plus Mg ii, but the latter ions better match the observed features than C ii alone. We also note that for C ii, unlike for all other ions for which Texc = TBB was assumed, we had to apply a lower excitation temperature (10 000 K), because hotter temperatures produced unacceptably strong features.
The chemical composition identified above (O ii, Mg ii, and maybe Fe iii, Si iii and S iii) is consistent with the “carbon-burned” SN atmosphere considered by Hatano et al. (1999). Although it is probably premature to conclude that SN 2006oz had such an atmosphere, it is interesting that together with the lack of H and He i and maybe C ii in the spectrum, all identified features belong to the ions that are expected to be the strongest at an excitation temperature of ~14 000 K in an atmosphere containing elements that underwent carbon-burning.
3.4. Models for the light curve
The bolometric light curve can be divided into two parts: the initial precursor plateau and the subsequent smooth monotonic rise. As discussed above, it is not clear if the maximum of the light curve was observed, a handicap in constraining models.
We note that precursor plateaus, some similar in shape to that of SN 2006oz, were found by Dessart et al. (2011) in their models of helium star explosions. In their models, the plateau is associated with the shock breakout, fireball-cooling phase, before the rise to the peak powered by radioactive decay. The plateau arises when the temperature decrease at the photosphere slows down, an effect associated with the recombination of ejecta layers to their neutral state (primarily He, but also CNO elements in the helium-rich progenitor models). The plateau brightness is determined by the amount of energy initially deposited by the shock and the size of the progenitor envelope. The bolometric light curves of Dessart et al. (2011) typically have a plateau that lasts about ten days and is about a factor of 20 to 30 dimmer than the subsequent peak.
The physics explored by the precursor plateaus of Dessart et al. (2011) may be relevant to SN 2006oz and its kin, but the plateau these authors find seems to be too dim to directly correspond to that observed in SN 2006oz. In SN 2006oz, this plateau is dimmer than the subsequent peak by about a factor of 8–10 in luminosity (depending on tmax; Fig. 5). Because the plateau is brighter than in the models of Dessart et al. (2011), the material must be distributed at larger radii. The structures in the models of Dessart et al. (2011) are originally in hydrostatic equilibrium as dictated by the systematics of stellar evolution. A substantially larger radius suggests that the plateau we observe in SN 2006oz does not arise in a stellar envelope, but in a circumstellar medium. Consequently, the only likely explanation that we have found for the plateau is that it might represent a recombination wave in a CSM that surrounds the progenitor star. A possible case of shock breakout from a H-rich dense CSM was discussed by Ofek et al. (2010). For SN 2006oz, unlike for SNe IIP, this plateau cannot be caused by recombination of H, which occurs at much lower temperatures (5000−6000 K). The derived temperature also makes a He recombination explanation unlikely, because most of the He atoms are singly ionized at T > 10 000 K, but double ionization starts above T > 15 000 K (Hatano et al. 1999). On the other hand, a recombination plateau could be consistent with the transition O iii to O ii (Hatano et al. 1999). This idea is also potentially consistent with the detection of O ii in the spectrum of H-poor SLSNe (Sect. 3.3). Interestingly, a precursor plateau was observed in the simulations of Blinnikov & Sorokina (2010) for SN Ia explosions in a C–O CSM, but, as the authors argue, it was an artifact of the arbitrary initial conditions. An early plateau is also present in the bolometric light curve of the 1987A-like SN 2006au (Taddia et al. 2012).
SDSS photometry of SN 2006oz (AB magnitudes).
 |
Fig. 7 Bolometric light curve of SN 2006oz shown along with models describing the rise to maximum (ignoring the precursor plateau). Models include the following power sources for the luminosity: radioactive decay (red, dashed), input from a magnetar (green, dot-dashed) and CSM interaction (blue, solid). Details concerning the model parameters are given in the text. |
The subsequent smooth rise of the light curve represents a more normal SN behavior and could be satisfied by a variety of processes, such as radioactive decay, input from a pulsar or magnetar, or luminosity from SN ejecta-CSM interaction. General semi-analytic models of these processes have been constructed by Chatzopoulos et al. (2012), and will be applied to a range of superluminous events in Chatzopoulos, Wheeler & Vinko (in prep.). Figure 7 shows a sample of models compared with the observed bolometric light curve of SN 2006oz, ignoring the precursor plateau. The models all peak at a time around the last observed data point, but the lack of a measured maximum (and subsequent decline) means the models are not well constrained. The models were not fitted in any formal sense, but constructed to be reasonable “by eye”. The ejecta masses derived may be somewhat underestimated as discussed by Chatzopoulos et al. (2012).
The red dashed curve shows a model driven by radioactive decay with MNi = 10.8 M⊙ and a diffusion time td = 36 days, determined by the time scale of the rise of the light curve. The SN ejecta mass, Mej = 14.4 M⊙, is derived from the diffusion time, td, assuming a velocity, v = 12 000 km s-1, and opacity κ = 0.05 cm2 g-1. The ejecta mass scales as κ-1 and consequently would be lower for higher opacity values. The fact that such a big fraction of Mej has been burned to 56Ni, unlike in most observed SN types, shows that a radioactive decay model has difficulties to account for the rise of SN 2006oz to maximum. Furthermore, the SN was not detected in the next observing season that started nine months later. By stacking the images from the first five weeks, we deduce a limit r > 24.2 (Table 3) implying a decay rate >2.03 mag 100-1 d-1. This is steeper than the radioactive decay of 56Co (0.98 mag 100-1 d-1), assuming complete γ-ray and positron trapping. The radioactive model for H-poor SLSNe has also been seriously challenged by the observations of Quimby et al. (2011), Pastorello et al. (2010), and Chomiuk et al. (2011). We stress, though, that an assumption involved in these calculations is that that 56Ni is centrally condensed (Arnett 1982). It is therefore possible that a configuration where 56Ni is substantially mixed into the outer envelope, thereby allowing γ-rays to escape freely, cannot be ruled out.
For the same velocity, opacity, and rise time, a magnetar model yields the same ejecta mass, 14.4 M⊙, as the radioactive decay model, but requires two more parameters, Ep and tp, where the decay model requires only one, MNi, to fit the rise and peak. The green dot-dashed curve shows a magnetar spin-down model with initial rotational energy Ep = 1.45 × 1051 erg and a characteristic spin-down time of tp = 13 days, giving an initial rotational period 3.7 ms and a magnetic field B = 2.24 × 1014 G.
The blue curve shows a model with SN ejecta and CSM interaction (including both forward and reverse shocks) for again the same velocity, opacity, rise time and ejecta mass as the previous models. This CSM model was adjusted to give both a reasonable fit to the rise time and a reasonable formal black-body temperature at maximum. The other parameters used are (see Chatzopoulos et al. 2012, for detailed definitions): Esn = 2.5 × 1051 erg, the density slope of the SN ejecta n = 12, the progenitor radius Rp = 2.5 × 1014 cm, the density slope of the CSM s = 0, the density scale at the base of the CSM ρcsm,1 = 5 × 10-13 g cm-3 (determined at Rp and equal to the constant density of the CSM shell), Mcsm = 6.5 M⊙, and MNi = 0.02 M⊙. The constant CSM photospheric radius of this model is Rph = 1.8 × 1015 cm, virtually the same as the radius of the shell itself, giving an optical depth of τcsm = 327. For these parameters and for Lbol = 1.3 × 1044 erg s-1 at peak, the formal black-body temperature at maximum light is TBB = 15 300 K. This model, with several free parameters, can also provide a decent fit to the data.
The uncertainty in the bolometric correction and tmax has, of course, an impact on the models discussed above, although this is not easy to quantify because of parameter degeneracies. It is, however, almost certain that constructing a viable radioactive model will become increasingly difficult as these uncertainties can only increase the necessary MNi (and the ratio MNi to Mej) to power the light curve. Our experience shows that it will still be possible to obtain viable magnetar or CSM models by modifying parameters such as Ep, tp, ρcsm and Mcsm. More constraining for these models would be the availability of post-maximum data and decay rate.
We have shown that a range of models can explain the smooth rise to maximum. Combining these models with the precursor plateau is less straightforward, as none of these models are presently able to numerically reproduce it. The possibility that the plateau is the result of a recombination wave in a (O-rich?) CSM, the only reasonable suggestion we have come up with, gives a rationale for considering that the same shell might be responsible for the rise. This picture is not perfectly self-consistent, however, because the first part requires the shock to have broken out of the CSM, while the second part requires the shock to still be interacting with it. It is therefore difficult to understand how the CSM was heated in the first place, i.e. before the ejecta-CSM interaction provides the rise to the peak. A possible answer could be by energy deposition to the CSM by the SN blast wave, although this possibility remains to be studied. Another alternative solution could be provided by a hybrid model with a CSM recombination accounting for the plateau and a magnetar for the rise to the peak. Additional observations of similar events, including more multi-color light curves from very early to very late phases, will be required to resolve this problem.
3.5. Host galaxy
The host of SN 2006oz is only the fourth out of nine similar H-poor SLSNe to have been identified (Neill et al. 2011; Chomiuk et al. 2011). Very little information is available on the hosts of these events, and many of them are detected in only one filter, so that a study of the properties of the host of SN 2006oz is warranted.
The colors g − r = 1.26 ± 0.20 and r − i = 0.26 ± 0.13 (after correcting for Galactic foreground extinction), suggest a significant break between the g and r filters. This can only be associated with the 4000 Å break, at a redshift consistent with the one we are examining. These colors are indeed consistent with an intermediate value Dn(4000) = 1.4 ± 0.1 for the 4000 Å break, indicative of relatively old stellar populations and, possibly, of a burst of star formation within the last 1–2 Gyr (e.g. Kauffmann et al. 2003; Gallazzi et al. 2005). In Fig. 8, the host galaxy colors (K-corrected to z = 0.1)2 are compared to a set of galaxies, selected3 from the main spectroscopic sample of SDSS DR4 (Adelman-McCarthy et al. 2006) to have 0.08 < z < 0.12, and to a set of dust-free model galaxies with different star-formation histories (Bruzual & Charlot 2003). Despite the high uncertainty, the galaxy position on this color-color diagram is more consistent with low-mass, star-forming galaxies and is far from the locus of elliptical, passive galaxies. It is not, however, a blue, starburst galaxy: by using the template of Kinney et al. (1996) and assuming the extinction law of Calzetti et al. (2000), it is not possible to reproduce these colors for any value of reddening.
 |
Fig. 8 Color–color diagram comparing the host of SN 2006oz (black cross) to SDSS galaxies (blue) and to a set of dust-free model galaxies (gray). The subsample of elliptical galaxies is shown in green. All data refer (or are K-corrected) to z = 0.1. |
To gain a more quantitative understanding of the nature of the host galaxy, its observer-frame colors were compared to those predicted by a Monte Carlo library of model spectra, redshifted to z = 0.376, based on Bruzual & Charlot (2003) population synthesis models spanning a wide range of star formation histories, metallicities, and dust attenuation (modeled as in Charlot & Fall 2000). In this way, we constructed probability density functions and derived the following estimates for the host properties: a stellar mass of log (M/M⊙) = 8.7 ± 0.23, a luminosity-weighted age of 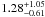 Gyr, and a SFR of
Gyr, and a SFR of 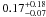 M⊙ yr-1. This results in a specific SFR of log (SFR/M ⋆ ) = −9.47 ± 0.39 yr-1, consistent with, but at the lower end of, the values reported by Neill et al. (2011) (although their uncertainties are high).
M⊙ yr-1. This results in a specific SFR of log (SFR/M ⋆ ) = −9.47 ± 0.39 yr-1, consistent with, but at the lower end of, the values reported by Neill et al. (2011) (although their uncertainties are high).
With an absolute luminosity of Mg = −16.9, this galaxy is probably metal-poor. By using the mass-metallicity relation of Tremonti et al. (2004), we obtain an indicative value of 12 + log (O/H) = 8.34 ± 0.16 for the oxygen abundance that corresponds to 0.45 Z⊙ (assuming the solar abundances of Asplund et al. 2009). A direct metallicity measurement exists only for the host of SN 2010gx (Stoll et al. 2011), indicating 0.47 Z⊙ (Kobulnicky & Kewley 2004; Asplund et al. 2009). These values are not particularly low, but the fact that all H-poor SLSNe have been found in faint galaxies suggests that metallicity might indeed play a role. The reason why this is interesting is that all viable models leading to H-poor SLSNe involve (one way or another) a very massive star that has suffered extensive mass loss. Since stellar winds are driven by metals (e.g. Vink & de Koter 2005; Puls et al. 2008) and are less efficient at low metallicity, it has been suggested that SLSN progenitors lose mass through episodic outbursts due to mechanisms that are not well understood, possibly involving pulsational pair instability (e.g. Woosley et al. 2007). On the other hand, a similar discussion has been going on about the preference of long GRBs, with optical afterglows, to be found in metal-poor galaxies, but it has been shown that this might be partly due to the fact that smaller galaxies have a higher SFR (Mannucci et al. 2010, 2011). It is therefore possible that the same bias exists for the SLSN hosts. The fundamental metallicity relation of Mannucci et al. (2011) for low-mass galaxies predicts 12 + log (O/H) = 8.39 for the host of SN 2006oz, i.e. again a value that is not very low.
4. Conclusions
We have studied SN 2006oz, an event belonging to the family of H-poor SLSNe identified by Quimby et al. (2011). The bolometric light curve shows a precursor plateau with a rest-frame duration of 6–10 days, while the bluest bands demonstrate a dip in the luminosity, before rising smoothly to maximum light. Our early observations are more sensitive than those of previous studies and it is therefore possible that this behavior might be common to more H-poor SLSN. If this is the case, it provides an important diagnostic for the nature of these events. We argued that the precursor plateau might be caused by a recombination wave in an H-deficient CSM. The subsequent rise in luminosity can be described by energy input from a magnetar or by ejecta-CSM interaction, but radioactive decay is less likely. Although the model parameters are not well constrained owing to the lack of post-maximum data, all models involve large ejected and CSM masses (if a CSM is required), pointing to a very massive progenitor.
Our deep observations with GTC have revealed the faint host galaxy of this event (Mg = −16.9). It is a moderately low-mass (log (M/M⊙) = 8.7), star-forming (0.17 M⊙ yr-1) galaxy with a luminosity-weighted age between 0.7 − 2.3 Gyr. It is not a blue, starburst galaxy and the metallicity, inferred indirectly, is not particularly low.
IRAF is distributed by the National Optical Astronomy Observatory: http://iraf.noao.edu/iraf/web/.
We used the MPA/JHU catalogs available at: http://www.mpa-garching.mpg.de/SDSS/
Acknowledgments
We are grateful to Thomas Krühler and Lars Mattson for discussions and help. G.L. especially thanks Stephen Smartt for the initial encouragement and for providing comments on the manuscript. G.L. is supported by the Carlsberg foundation. The Dark Cosmology Centre is funded by the Danish National Research Foundation. The research activity of J.G. and A.d.U.P. is supported by Spanish research grants AYA-2011-24780/ESP and AYA2009-14000-C03-01. J.V. received support from Hungarian OTKA Grant K76816. J.C.W. is supported in part by NSF AST-1109801. J.P.U.F. acknowledges support from the ERC-StG grant EGGS-278202. C.C.T. acknowledges partial funding by project AYA2010-21887-C04-01 “Estallidos” of the Spanish MEC and by FEDER. We acknowledge the use of the Weizmann Institute of Science Experimental Astrophysics Spectroscopy System. Based on observations made with the Gran Telescopio Canarias (GTC), installed in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, in the island of La Palma. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2006, ApJS, 162, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D. 1982, ApJ, 253, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barbary, K., Dawson, K. S., Tokita, K., et al. 2009, ApJ, 690, 1358 [NASA ADS] [CrossRef] [Google Scholar]
- Blinnikov, S. I., & Sorokina, E. I. 2010 [arXiv:1009.4353] [Google Scholar]
- Blondin, S., & Tonry, J. L. 2007, ApJ, 666, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Garnavich, P., Matheson, T., et al. 2003, AJ, 126, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Chatzopoulos, E., Wheeler, J. C., & Vinko, J. 2009, ApJ, 704, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Chatzopoulos, E., Wheeler, J. C., & Vinko, J. 2012, ApJ, 746, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Irwin, C. M. 2011, ApJ, 729, L6 [Google Scholar]
- Chomiuk, L., Chornock, R., Soderberg, A. M., et al. 2011, ApJ, 743, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Livne, E., et al. 2011, MNRAS, 414, 2985 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. J., Djorgovski, S. G., Mahabal, A., et al. 2009, ApJ, 696, 870 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Filippenko, A. V. 1997, ARA&A, 35, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Frieman, J. A., Bassett, B., Becker, A., et al. 2008, AJ, 135, 338 [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Gal-Yam, A., Mazzali, P., Ofek, E. O., et al. 2009, Nature, 462, 624 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Gänsicke, B. T., Levan, A. J., Marsh, T. R., & Wheatley, P. J. 2009, ApJ, 697, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Harkness, R. P., Wheeler, J. C., Margon, B., et al. 1987, ApJ, 317, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Hatano, K., Branch, D., Fisher, A., Millard, J., & Baron, E. 1999, ApJS, 121, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Holtzman, J. A., Marriner, J., Kessler, R., et al. 2008, AJ, 136, 2306 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasen, D., & Bildsten, L. 2010, ApJ, 717, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kinney, A. L., Calzetti, D., Bohlin, R. C., et al. 1996, ApJ, 467, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Kewley, L. J. 2004, ApJ, 617, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Law, N. M., Kulkarni, S. R., Dekany, R. G., et al. 2009, PASP, 121, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1991, ApJ, 383, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Lupton, R. H., Gunn, J. E., & Szalay, A. S. 1999, AJ, 118, 1406 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Salvaterra, R., & Campisi, M. A. 2011, MNRAS, 414, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T., Tominaga, N., Tanaka, M., Maeda, K., & Nomoto, K. 2010, ApJ, 717, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T. J., & Tominaga, N. 2012, ApJ, 747, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. D., Sullivan, M., Gal-Yam, A., et al. 2011, ApJ, 727, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Ofek, E. O., Cameron, P. B., Kasliwal, M. M., et al. 2007, ApJ, 659, L13 [CrossRef] [Google Scholar]
- Ofek, E. O., Rabinak, I., Neill, J. D., et al. 2010, ApJ, 724, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Östman, L., Nordin, J., Goobar, A., et al. 2011, A&A, 526, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pastorello, A., Smartt, S. J., Botticella, M. T., et al. 2010, ApJ, 724, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quimby, R. M., Castro, F., Gerardy, C. L., et al. 2005, in BAAS, 37, Am. Astron. Soc. Meet. Abstracts, 1431 [Google Scholar]
- Quimby, R. M., Aldering, G., Wheeler, J. C., et al. 2007, ApJ, 668, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Quimby, R. M., Kulkarni, S. R., Kasliwal, M. M., et al. 2011, Nature, 474, 487 [Google Scholar]
- Rau, A., Kulkarni, S. R., Law, N. M., et al. 2009, PASP, 121, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Richmond, M. W., Treffers, R. R., Filippenko, A. V., et al. 1994, AJ, 107, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Sako, M., Bassett, B., Becker, A., et al. 2008, AJ, 135, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Li, W., Foley, R. J., et al. 2007, ApJ, 666, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Chornock, R., Li, W., et al. 2008, ApJ, 686, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N., Frankowski, A., & Kashi, A. 2010, New A, 15, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Stoll, R., Prieto, J. L., Stanek, K. Z., et al. 2011, ApJ, 730, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Hamuy, M., Suntzeff, N. B., et al. 2002, AJ, 124, 2100 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Sollerman, J., Goobar, A., et al. 2006, Central Bureau Electronic Telegrams, 762, 3 [NASA ADS] [Google Scholar]
- Taddia, F., Stritzinger, M. D., Sollerman, J., et al. 2012, A&A, 537, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E. 2010, ApJ, 719, L204 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Blinnikov, S., & Heger, A. 2007, Nature, 450, 390 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Young, D. R., Smartt, S. J., Valenti, S., et al. 2010, A&A, 512, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 ugriz light curves of SN 2006oz obtained by the SDSS SN Survey, shifted as indicated for presentation purposes. Triangles denote 3σ upper limits. The lower panel focuses on the g-band evolution shown together with a cubic polynomial fit to the last 10 observations (solid line) extrapolated backward (dashed line). Clearly, the first points are strongly inconsistent with a smooth rise. The date of the NOT spectrum is also indicated. |
| In the text | |
 |
Fig. 2 Spectrum of SN 2006oz (red) obtained at the NOT. For comparison we show 3 spectra from Quimby et al. (2011) at similar pre-maximum phases. The colored spectra are smoothed versions (moving average of 5 pixels) of the original gray spectra. All spectra were plotted in their rest frame assuming z = 0.376 for SN 2006oz. The inset shows a zoom of the area around 2800 Å. At this redshift we identified the only probable line (although at low significance 2.7σ) consistent with the Mg ii doublet (which would appear blended at this resolution). |
| In the text | |
 |
Fig. 3 Left: image of SN 2006oz obtained with the SDSS telescope (MJD 54061.17). Right: deep i image of the field, obtained almost 5 yr after the SN with GTC/OSIRIS. The SN is coincident with the position of galaxy A. However, within a radius of 7′′, there are four more objects, including one that appears extended, labeled B, C, D and E, respectively. Their photometry is reported in Table 1. Both images are 72′′ × 72′′. North is up and east is to the left. |
| In the text | |
 |
Fig. 4 Black-body fits to the SN 2006oz data. In the top panel, a fit to the NOT spectrum is shown. Only data redward of 3000 Å (rest-frame) are included in the fit. The middle and bottom panel show the radius and temperature evolution of SN 2006oz assuming it can be described by a black body. The filled circles are the results of fitting the griz photometry, while the spectrum fit is represented by a square symbol. The dashed lines show linear weighted fits to the data. |
| In the text | |
 |
Fig. 5 Upper panel: bolometric light curve of SN 2006oz (circles) compared to PS1-10awh (solid line; data from Chomiuk et al. 2011), which has similar pre-maximum multi-color observations. To illustrate the uncertainty in tmax of SN 2006oz, its light curve was shifted horizontally with respect to the limiting case, where our last observation was assumed to be taken exactly at maximum light. Assuming the two events are similar, we obtain a reasonable match of the light curves by shifting tmax by −10 days (faded symbols). Middle and lower panels: the absolute pre-maximum light curves. The absolute luminosities at rest-frame ~4530 Å (observed r- and z-bands) and ~2560 Å (observed u- and g-bands) are compared, after correcting for cosmological expansion. As above, vivid and faded colors show the light curves of SN 2006oz shifted by 10 days. A few (non-constraining) upper limits were removed for presentation purposes. The early observations of SN 2006oz are below the detection limits of the PanSTARRS1 observations of PS1-10awh. |
| In the text | |
 |
Fig. 6 SYNOW fit to the spectra of SN 2006oz and SCP06F6. The observed spectra were brought to the rest-frame by assuming z = 0.376 and z = 1.189, respectively, and their fluxes were scaled to match in the overlapping wavelength region. Two SYNOW models, with and without C ii, are overplotted. The inset shows a zoom in the spectrum of SN 2006oz around 3300 Å. The magenta line (inset only) shows a model without Fe iii that provides a worse fit in this region. The lower panel shows the contribution of the individual ions to the model spectra. The best-fitting model has τ(O ii) = 0.02, τ(Mg ii) = 0.05, τ(Si iii) = 0.5, τ(S iii) = 0.5 and τ(Fe iii) = 0.4. |
| In the text | |
 |
Fig. 7 Bolometric light curve of SN 2006oz shown along with models describing the rise to maximum (ignoring the precursor plateau). Models include the following power sources for the luminosity: radioactive decay (red, dashed), input from a magnetar (green, dot-dashed) and CSM interaction (blue, solid). Details concerning the model parameters are given in the text. |
| In the text | |
 |
Fig. 8 Color–color diagram comparing the host of SN 2006oz (black cross) to SDSS galaxies (blue) and to a set of dust-free model galaxies (gray). The subsample of elliptical galaxies is shown in green. All data refer (or are K-corrected) to z = 0.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


