| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118002 | |
| Published online | 18 April 2012 | |
3D simulations of Betelgeuse’s bow shock⋆
1 Argelander Institut für Astronomie, Auf dem Hügel 71, Bonn 53121, Germany
2 South African Astronomical Observatory, PO Box 9, 7935 Observatory, South Africa
e-mail: shazrene@saao.ac.za
Received: 1 September 2011
Accepted: 14 January 2012
Betelgeuse, the bright, cool red supergiant in Orion, is moving supersonically relative to the local interstellar medium. The star emits a powerful stellar wind that collides with this medium, forming a cometary structure, a bow shock, pointing in the direction of motion. We present the first 3D hydrodynamic simulations of the formation and evolution of Betelgeuse’s bow shock. The models include realistic low-temperature cooling and cover a range of plausible interstellar medium densities of 0.3–1.9 cm-3 and stellar velocities of 28–73 km s-1. We show that the flow dynamics and morphology of the bow shock differ substantially because of the growth of Rayleigh-Taylor or Kelvin-Helmholtz instabilities. The former dominate the models with slow stellar velocities resulting in a clumpy bow shock substructure, whereas the latter produce a smoother, more layered substructure in the fast models. If the mass in the bow shock shell is low, as seems to be implied by the AKARI luminosities (~3 × 10-3 M⊙), then Betelgeuse’s bow shock is very young and is unlikely to have reached a steady state. The circular nature of the bow shock shell is consistent with this conclusion. Thus, our results suggest that Betelgeuse only entered the red supergiant phase recently.
Key words: hydrodynamics / instabilities / circumstellar matter / stars: winds, outflows / supergiants / ISM: structure
Movies are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Massive stars have a tremendous impact on their circumstellar environment. Betelgeuse (α Orionis, HD 39801, HIP 27989), the prototype red supergiant (RSG) and the brightest M supergiant in the sky (M1-M2 Ia-Iab), is no exception. Although Betelgeuse’s initial mass is uncertain, it is thought to be ≳ 10 M⊙ (see Table 1). Thus, the star is likely in the core helium-burning phase and is approaching its final stages of evolution – ultimately exploding as a core-collapse supernova and enriching the interstellar medium (ISM) with radiation, mechanical energy, mass, and heavy elements. Owing to its high luminosity, ~105 L⊙, and powerful stellar wind, Ṁwind ~ 3 × 10-6 M⊙ yr-1 (see Table 1), the star is already injecting copious amounts of mass and energy into the ISM.
For stationary stars, the wind-ISM interface is expected to be a spherical shell as shown, for example, by the analytic and hydrodynamic models of Weaver et al. (1977) and Garcia-Segura et al. (1996), respectively. Betelgeuse has an average radial (heliocentric) velocity of Vrad = + 20.7 ± 0.4 km s-1 away from the sun, and the tangential velocities are Vαcosδ = 23.7(D [pc]/200) km s-1 and Vδ = 9.1(D [pc]/200) km s-1 (Harper et al. 2008, and references therein). The distance D to Betelgeuse is not yet well established, the most recent estimate being 197 ± 45 pc (see Harper et al. 2008, for a detailed discussion). For this range of distances, Betelgeuse is moving supersonically relative to the local ISM, and the collision of its stellar wind with this medium has resulted in the formation of a cometary structure, a bow shock, pointing in the direction of motion (at a position angle of 69.0° east of north). Although it is the only known RSG runaway, theoretical models predict that up to 30% of RSGs can be runaway stars (Eldridge et al. 2011).
Early observations of the circumstellar medium around Betelgeuse suggested there is extended emission in the far-infrared (e.g. Stencel et al. 1988; Young et al. 1993b). However, because the star is so bright at these wavelengths, it was only in 1997 that the bow shock was imaged successfully using IRAS at 60 and 100 μm (Noriega-Crespo et al. 1997). More recently, Ueta et al. (2008) have imaged the bow shock with AKARI at higher spatial resolution in the 65, 90, 140, and 160 μm bands. The bow shock is a smooth, rather circular arc that has a thickness of ~1.5 arcmin and an inner radius of ~5 arcmin (see Fig. 1). Also detected by both IRAS and AKARI is a mysterious “bar” structure, of unknown origin, located just ahead of the bow shock arc.
Many of the observed properties of the bow shock can be derived in terms of parameters of the interacting flows, making this an invaluable probe of the physical conditions in both the stellar wind and the ISM. The characteristic size of the bow shock shell, known as the stand-off distance, RSO, is determined by the location where the ram pressures of the two “flows” are in equilibrium: 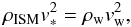 (1)where ρISM and ρw are the density of the ISM and stellar wind, respectively; v∗ is the velocity of the star with respect to the ISM, and vw is the stellar wind velocity. Assuming spherical mass loss from the star,
(1)where ρISM and ρw are the density of the ISM and stellar wind, respectively; v∗ is the velocity of the star with respect to the ISM, and vw is the stellar wind velocity. Assuming spherical mass loss from the star, 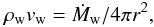 (2)and rearranging the resulting equation yields the well known solution:
(2)and rearranging the resulting equation yields the well known solution: 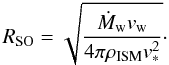 (3)Making the additional assumption of momentum conservation and assuming that the material mixes and cools instantaneously (so that the dense shell has negligible thickness, i.e. the thin-shell approximation), Wilkin (1996) derived an analytic expression for the shape of the bow shock:
(3)Making the additional assumption of momentum conservation and assuming that the material mixes and cools instantaneously (so that the dense shell has negligible thickness, i.e. the thin-shell approximation), Wilkin (1996) derived an analytic expression for the shape of the bow shock: 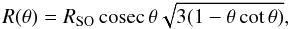 (4)where θ is the polar angle measured from the axis of symmetry.
(4)where θ is the polar angle measured from the axis of symmetry.
 |
Fig. 1 Bow shock and “bar” of Betelgeuse. Left. The 60 μm IRAS observation retrieved from the IRAS Galaxy Atlas (IGA) Image Server1 (for details about IGA, see Cao et al. 1997). Right. The high-resolution, composite AKARI image with 65 μm, 90 μm, and 140 μm emission in blue, green, and red, respectively (Ueta et al. 2008) [Credit: AKARI MLHES team]. |
Summary of Betelgeuse’s parameters.
Utilising the above analytic models and current estimates of Betelgeuse’s wind properties and distance (see Table 1), Ueta et al. (2008) derived a space velocity of 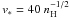 km s-1 with respect to the local ISM. Estimates of the ISM density, nH, range from 0.3 cm-3 for a flow emanating from the Orion Nebula Complex (ONC) (Frisch et al. 1990) to 1.5–1.9 cm-3 if the origin of the flow is the Orion OB 1 association (Ueta et al. 2008, 2009). Given this range of ISM densities, Betelgeuse’s space velocity with respect to the ambient medium is therefore likely to be between 73 km s-1 and 28 km s-1. If we assume strong shock conditions, the post-shock temperature corresponding to these stellar velocities, is at least 10 000 K. To date, the bow shock has only been detected in the far-infrared, where the bulk of the emission is probably caused by dust grains with an uncertain contribution from oxygen and carbon fine-structure lines.
km s-1 with respect to the local ISM. Estimates of the ISM density, nH, range from 0.3 cm-3 for a flow emanating from the Orion Nebula Complex (ONC) (Frisch et al. 1990) to 1.5–1.9 cm-3 if the origin of the flow is the Orion OB 1 association (Ueta et al. 2008, 2009). Given this range of ISM densities, Betelgeuse’s space velocity with respect to the ambient medium is therefore likely to be between 73 km s-1 and 28 km s-1. If we assume strong shock conditions, the post-shock temperature corresponding to these stellar velocities, is at least 10 000 K. To date, the bow shock has only been detected in the far-infrared, where the bulk of the emission is probably caused by dust grains with an uncertain contribution from oxygen and carbon fine-structure lines.
There are several multi-dimensional hydrodynamic models of wind-ISM interactions with relevant parameters for Betelgeuse. For example, Garcia-Segura et al. (1996) have investigated the interaction of the ISM with a wind ejected from a stationary star evolving from the main sequence to the RSG and then Wolf-Rayet (WR) phase. They found that the RSG wind had a significant effect on the subsequent WR phase. The same conclusion was reached by Brighenti & D’Ercole (1995) who studied the circumstellar medium (CSM) resulting from a moving star in 2D. As expected, in this case a bow shock arc was formed rather than a spherical shell. The implications of an RSG phase for the WR progenitors of gamma-ray bursts was also discussed in a similar investigation by van Marle et al. (2006). Wareing et al. (2007a) and Villaver et al. (2003) calculated a series of 3D and 2D hydrodynamic models, respectively, of the interaction of a stellar wind from an asymptotic giant branch (AGB) star with the ISM and the subsequent structure formed during the planetary nebula phase. Other models of the CSM around fast-moving AGB stars include 3D and axisymmetric models of Mira’s bow shock (Raga et al. 2008; Esquivel et al. 2010, respectively). More recently, van Marle et al. (2011) have modelled Betelgeuse’s bow shock with 2D high-resolution simulations that include a simple dust tracking scheme. They show that the flow for grains of various sizes differed and can have important consequences for interpreting infrared observations of bow shocks.
We build on the work above by including a realistic treatment of the thermal physics and chemistry in 3D models and consider a broader range of parameters. The numerical method and model parameters are described in Sect. 2. In Sect. 3, we present an adiabatic model that serves as a code test and a point of reference for the simulations that include radiative cooling. The flow characteristics, morphology, and shell properties of the latter are described in Sect. 4. Finally, the implications of this work, particularly with regard to Betelgeuse’s bow shock morphology, shell mass and age are discussed in Sect. 5.
2. Numerical method
2.1. Smoothed particle hydrodynamics
Smoothed particle hydrodynamics (SPH) is a Lagrangian method in which particles behave like discrete fluid elements. However, each of their fluid properties, e.g. density, temperature, or velocity, is the result of mutually overlapping summations and interpolations of the same properties of neighbouring particles. In this way, a continuous fluid is realised; i.e. physical fluid properties that vary smoothly over all points in space can be defined from interpolations on a finite number of particles.
SPH has been utilised to study a wide range of problems, not only in astrophysics, but also in other fields, e.g. engineering. Thus, the SPH equations are often adapted and optimised for a specific field or application. We briefly outline the particular SPH formulation implemented in the code, which serves as a basis for this work, GADGET-2 (Springel 2005; Springel et al. 2001), and refer the reader to detailed reviews of the method in Monaghan (1992), Rosswog (2009), and Springel (2010).
The momentum equation is derived based on an “entropy formulation” for SPH, which conserves entropy, energy, and momentum by construction (Springel & Hernquist 2002). In this formulation, a function of the entropy, A(s) = P/ργ, where γ is the ratio of specific heats, P the pressure, and ρ the density, is evolved instead of the internal energy, ϵ. To model shocks, viscosity terms that transform kinetic motion of the gas into internal energy are also included in the momentum equation. When the fluid is compressed, the viscosity acts as an excess pressure assigned to the particles in the equation of motion.
GADGET-2 also includes self-gravity and utilises a hierarchical Barnes and Hut oct-tree (Barnes & Hut 1986) algorithm to calculate the gravitational accelerations. The simulations carried out in this work are characterised by a broad dynamic range in densities. To obtain better and more efficient spatial and time resolution, particles have adaptive smoothing lengths and are evolved with individual and adaptive timesteps.
Summary of the parameters used for the different computed CSM evolution models.
2.2. Model setup
For numerical convenience, we choose a frame in which the star is stationary and located at the origin (x,y,z = 0, 0, 0) of a rectangular box. The ISM flows past the star in the direction of the x axis, interacting with the stellar wind as it does so. Two different flags are utilised to distinguish between ISM and wind particles.
2.2.1. The ISM
The ISM is assumed to be homogeneous. Although a cartesian grid of particles is the simplest approach to producing such a smooth medium, it also results in unwanted artefacts along preferred grid directions. To overcome this problem, we use a “glass tile”, where particles are randomly distributed in a periodic box and evolved with the sign of gravity reversed until an equilibrium configuration is reached (see Springel 2005, for details). The relaxed glass tile is then scaled and cropped to the required dimensions for the simulation.
We model a range of ISM densities, nH = 0.3, 1.0, 1.5, and 1.9 cm-3, with corresponding stellar velocities v∗ = 73, 40, 32, and 29 km -1, respectively (see Table 2). These number densities lie at the boundary between typical values expected for either a warm or cold neutral ISM, so we assume temperatures based on the phase diagram of the standard model of Wolfire et al. (1995, e.g. their Fig. 3d). The temperatures, TISM, are 8000, 1600, 1000, and 650 K, respectively. The mass of each particle is determined by the volume of the simulation domain, Vbox, the number of ISM particles, NISM, and the gas number density as follows: 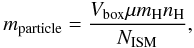 (5)where μ = 1.4 is the adopted mean molecular weight and mH the mass of atomic hydrogen. The chosen particle mass effectively determines the stellar wind resolution, i.e. the number of particles required to reproduce the observed mass-loss rate, as described in the section below.
(5)where μ = 1.4 is the adopted mean molecular weight and mH the mass of atomic hydrogen. The chosen particle mass effectively determines the stellar wind resolution, i.e. the number of particles required to reproduce the observed mass-loss rate, as described in the section below.
2.2.2. The stellar wind
Although the extended envelope of Betelgeuse is thought to be inhomogeneous and asymmetric close to the star, on much larger scales, and more importantly on the scales that we are interested in, the outflow is largely spherically symmetric (Smith et al. 2009). Furthermore, as discussed in Harper (2010), the mass-loss mechanism for M supergiant winds is not well understood. Given these uncertainties, we do not model the wind acceleration in detail, and instead assume that the wind is launched isotropically and with constant velocity.
The particle mass calculated above then determines the number of particles, Nwind, that are injected in an interval Δtwind to produce a constant mass-loss rate of 3.1 × 10-6 M⊙ yr-1. The wind particles are injected as spherical shells of typically a few hundred particles “cut” from the glass tiles described above. Each shell is randomly rotated in the x,y, and z directions. Although this reduces the smoothness of the outflow, it prevents the occurrence of numerical artefacts. The particles are injected at a radius, Rinner ~ 1015 cm, with a constant wind velocity, vw ~ 17 km s-1. The initial temperature of the particles is Twind ~ 1000 K, the temperature at Rinner derived from models of Betelgeuse’s circumstellar envelope, e.g. Glassgold & Huggins (1986) and Rodgers & Glassgold (1991).
2.2.3. Cooling
Radiative cooling plays an important role in determining the temperature structure and emission from the bow shock. Given the large uncertainties in the processes involved, we adopt the approach of Smith & Rosen (2003) rather than model the cooling in detail. Their cooling curve consists of analytic solutions and fits for various coolants based on detailed calculations described extensively in the appendices of Smith & Rosen (2003) and references therein, e.g. rotational and vibrational transitions of H2, CO and H2O, H2 dissociative cooling and reformation heating, gas-grain cooling/heating, and an atomic cooling function that includes non-equilibrium effects (see Table 3).
First the non-equilibrium molecular and atomic fractions of hydrogen are calculated according to the prescription of Suttner et al. (1997), and a limited equilibrium C and O chemistry is used to calculate the CO, OH, and H2O abundances (Smith & Rosen 2003). We adopt standard solar abundances of hydrogen and helium, and set the abundances of carbon and oxygen to χC ~ 2.5 × 10-4 and χO ~ 6.3 × 10-4, respectively (Lambert et al. 1984). We assume that the initial fraction of molecular to atomic hydrogen, f = nH2/nH, in the Betelgeuse outflow is small, f = 0.001 (on a scale where 0 is atomic and 0.5 is fully molecular). The hydrogen in the ISM is assumed to be atomic. The dust cooling function depends on the temperature of the grains, and we set this temperature to 40 K, the value derived by Ueta et al. (2008). The change in specific internal energy, ϵ, due to radiative cooling is then calculated semi-implicitly for each particle, i: ![\begin{equation} \epsilon^{(n+1)}_i = \epsilon^{(n)}_i + \frac{ \left(\Gamma - \Lambda\right) \left[\rho^{(n)}_i, \epsilon^{(n+1)}_i \right]}{\rho^{(n)}_i} \Delta t , \label{eq: cooling} \end{equation}](/articles/aa/full_html/2012/05/aa18002-11/aa18002-11-eq80.png) (6)where Λ and Γ are the volumetric cooling and heating rates in erg cm-3 s-1, respectively; Δt is the timestep; and n and n + 1 are the current and new timesteps, respectively (Springel et al. 2001). The change in specific internal energy is then converted to a change in the entropy of each particle.
(6)where Λ and Γ are the volumetric cooling and heating rates in erg cm-3 s-1, respectively; Δt is the timestep; and n and n + 1 are the current and new timesteps, respectively (Springel et al. 2001). The change in specific internal energy is then converted to a change in the entropy of each particle.
Summary of the combined cooling processes.
We do not include a treatment of dust formation and destruction, depletion of elements and molecules on to grains, the effects of magnetic or UV background radiation fields, density inhomogeneities in the stellar wind, and ISM. Collisional ionisation, likely important at high temperatures is not explicitly included; instead, hot gas, ≳104 K, cools primarily by atomic line emission (Sutherland & Dopita 1993) and thermal bremsstrahlung. Although these processes are likely to have an effect on the bow shock properties, both in terms of radiative transfer and cooling, the computational cost of their inclusion in 3D models is prohibitive.
In the following sections, we explore and discuss possible solutions for Betelgeuse’s bow shock with 3D numerical models (see Table 2). We simulate four basic models, A-D, with medium resolution, and with ISM number densities, nH = 0.3, 1.0, 1.5, and 1.9 cm-3, and stellar velocities v∗ = 73, 40, 32, and 29 km -1, respectively. Several lower resolution models are also calculated in order to study the long-term evolution of model D (model DL) and the effect of varying the assumed ISM temperature (models CL650, CL1600, CL8000) and the initial molecular hydrogen fraction (model CLf). Model AH has the same parameters as model A, but is computed with higher resolution. Finally, we have also computed an adiabatic model (model Bad), discussed in the next section, which provides a useful basis both for comparison to previous studies and to our models with radiative cooling (Sect. 4).
3. Numerical test: adiabatic model
We tested the numerical set-up with model Bad, a purely adiabatic model, i.e. no heat sources or sinks, and γ = 5/3. The simulation begins at the start of the red giant phase, with the star losing 3.1 × 10-6 M⊙ yr-1. Moving at ~32 km s-1, the star traverses a cold ISM with TISM = 100 K and density nH = 1.5 cm-3.
 |
Fig. 2 Position of the shock along the x axis (defined by the point with maximum temperature) as a function of time for the ISM (dashed line) and the stellar wind (dotted line). The black solid line demonstrates the trajectory for a vs = 10 km s-1 shock velocity. All velocities are measured with respect to the stationary frame of the star. |
The stellar wind collides with the ISM, and material accumulates at the contact discontinuity (the surface separating the two flows), where part of the kinetic energy of the gas is thermalised. The heated ISM and wind material expand outwards from either side of this surface, the former moves into the ISM and is called the forward shock, and the latter into the stellar wind and is known as the reverse shock. The expansion of these two regions is shown in Fig. 2. The position of the reverse shock (defined as the point of maximum temperature for the RSG wind particles along the x axis) changes slowly and reaches its average position, ~−0.25 pc, after 50 000 years. The forward shock (defined as the point of maximum temperature for the ISM particles along the x axis) expands at 10 km s-1 during that time, and then decelerates to a position of −0.48 pc. The bow shock reaches a steady state after 80 000 years, and has an average width of ~0.2 pc.
 |
Fig. 3 Adiabatic model, Bad, of the interaction of Betelgeuse’s dense stellar wind with the ISM after t ≈ 100 000 years. We plot cross-sectional profiles along the symmetry axis (the xy plane) for ρ, the gas density (top, left); T, the temperature (top, right); the velocity vector field plotted over |v|, the gas velocity (bottom, left); and the smoothing length, h (bottom, right). Approximately 1 × 107 ISM particles filled the simulation domain and ~6 × 105 particles were injected to produce the isotropic stellar wind. |
The density, temperature, and velocity in the bow shock are shown in the cross-section in Fig. 3. After 100 000 years, the maximum width of the tail is approximately 3 pc (Fig. 3, top right). The average temperature in the tail is approximately 4000 K; however, the cylindrical core of the tail is filled with much hotter, ~15 000 K, gas spanning ~0.8 pc in diameter. This hot gas is advected downstream from the forward shock, and flows towards the central part of the tail, filling the low-pressure void (beyond the RSG stellar wind) evacuated by the moving star (Fig. 3, bottom left).
 |
Fig. 4 Growth of the mass in the bow shock shell with time. The shell is defined as shocked regions with T > 2000 K and density above that in the ambient medium. The lines show the total shell mass (black), the contributions from the ISM (blue) and the RSG wind (red) for x < RSO or θ ≲ 115°, whereas the points represent the same parameters except for shell material with x < 0 or θ ≲ 90°. |
While the cometary tail is largely composed of ISM material at early times, both the RSG wind and ISM contribute similar amounts of mass to the bow shock head. Defining material in the bow shock shell as shocked regions with T > 2000 K and density above that in the ambient medium, we see in Fig. 4 that after ~40 000 years, the RSG wind contributes slightly more mass to the bow shock head (θ ≲ 90°, i.e. x < 0) than the ISM, and it takes ~90 000 years for this to occur for θ ≲ 115°, i.e. for x < RSO. The mass accumulates in the bow shock almost linearly after ~30 000 years and only reaches a steady state for θ ≲ 90° after ~80 000 years. An estimate for a typical shell mass can be obtained from 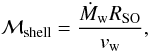 (7)which yields 0.05 M⊙. This expression assumes the mass is distributed over 4π sterad in a spherical shell and only takes the contribution from the stellar wind into account. Thus for θ ≲ 90°, the expected RSG shell mass would be 0.025 M⊙, i.e. half of ℳshell. With a significant contribution from the wings of the paraboloid (the shell radius is greater than RSO for all θ > 0°), the RSG shell mass obtained from the simulations is twice the theoretical value (red points in Fig. 4). Including the mass from the ISM, the total mass in the bow shock head after 100 000 years is ≈0.1 M⊙.
(7)which yields 0.05 M⊙. This expression assumes the mass is distributed over 4π sterad in a spherical shell and only takes the contribution from the stellar wind into account. Thus for θ ≲ 90°, the expected RSG shell mass would be 0.025 M⊙, i.e. half of ℳshell. With a significant contribution from the wings of the paraboloid (the shell radius is greater than RSO for all θ > 0°), the RSG shell mass obtained from the simulations is twice the theoretical value (red points in Fig. 4). Including the mass from the ISM, the total mass in the bow shock head after 100 000 years is ≈0.1 M⊙.
3.1. Numerical resolution and smoothing
The smoothing length, h, determines the scale on which the above fluid properties are smoothed, so it effectively defines the resolution of a simulation. In GADGET-2 the smoothing length of each particle is allowed to vary in both time and space, thus the full extent of SPH’s powerful Lagrangian adaptivity is achieved. As shown in Fig. 3 (bottom, right), the resolution in high-density regions (e.g. in the bow shock) is naturally increased with large particle numbers, hence smaller smoothing lengths (h ≲ 0.01 pc), and little computational time is wasted evolving voids, which can be described by fewer particles with longer smoothing lengths (h ~ 0.08 pc).
 |
Fig. 5 Particle density (top) and temperature (bottom) profiles for model Bad in a thin slice, −0.03 < z < 0.03 and −0.03 < y < 0.03, along the x axis. ISM and RSG particles are blue and red, respectively. |
Unfortunately, this smoothing process also means that the shock that results from the collision of the ISM and the stellar wind is broadened over a few particle smoothing lengths. To minimise this broadening, it is essential that simulations employ as large a number of particles as possible to achieve shorter smoothing lengths and thus sharper discontinuities. In this simulation, we model the ISM with ~107 particles and the stellar wind with ~105 particles, achieving a typical smoothing length of 0.03 pc or better in the regions of interest. More important, however, despite the shock broadening, the post-shock fluid properties are still described well; e.g. as expected from the Rankine-Hugoniot jump conditions, the density jump is a factor of 4 (Fig. 5, top). Assuming that all the kinetic energy in these winds is thermalised, we can derive an estimate for the expected temperature of the shocked gas, 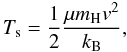 (8)where kB is the Boltzmann constant. For the parameters assumed here, this equation yields 19 000 K for the shocked stellar wind and 92 000 K for the shocked ISM temperature, so very similar to the results obtained in the simulation (Fig. 5, bottom).
(8)where kB is the Boltzmann constant. For the parameters assumed here, this equation yields 19 000 K for the shocked stellar wind and 92 000 K for the shocked ISM temperature, so very similar to the results obtained in the simulation (Fig. 5, bottom).
3.2. Development of instabilities
The shear produced by the relative motion of the shocked ISM and shocked stellar wind regions (as shown in the vector plot in Fig. 3, bottom left), excites Kelvin-Helmholtz (K-H) instabilities at the contact discontinuity. Utilising the prescriptions described by Brighenti & D’Ercole (1995, equations p. 55), we find that the K-H growth time scale is at least an order of magnitude smaller than the one required for the Rayleigh-Taylor (R-T) instability. Thus, it is the K-H rolls that are advected downstream, and the characteristic R-T “fingers” that appear in Brighenti & D’Ercole (1995, their Fig. 2, top panel) are absent from our simulation. The main reason for the different behaviour is that they utilise an order of magnitude higher mass-loss rate and a much slower wind velocity, both of which lead to a much stronger density contrast between the ISM and wind, which favours shorter growth scales for R-T instabilities.
The development of K-H instabilities in our model may be surprising. Previous studies, e.g. Agertz et al. (2007), have found that instabilities are suppressed in “standard” SPH, owing to difficulty estimating gradients in regions with strong density contrasts. Several methods have been proposed to address this issue. One approach is to include artificial conductivity, which acts as an additional pressure across the contact discontinuity, facilitating mixing between the two layers (Price 2008; Wadsley et al. 2008). However, at present the formulation is not consistent with including self-gravity and tends to be highly dissipative (Valcke et al. 2010). The other approach, which was the result of a detailed study by Valcke et al. (2010), is to minimise particle disorder, which prevents the “oily” problem (the development of an artificial gap between the fluids) and allows the gas to mix. They achieve this by using a higher order smoothing kernel to prevent particle clumping, but this kernel does not conserve energy as well as the cubic spline kernel. Given the caveats to the above solutions, we opted to use glass initial conditions instead, i.e. to start from a very smooth particle distribution with minimal particle disorder. Thus, strong K-H instabilities do develop, despite the factor of 10 in the density contrast.
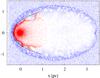 |
Fig. 6 Particles in the xy plane with the ISM in blue, and the stellar wind in red. The analytic solution (Eq. (4)) is shown in black. |
3.3. Comparison to analytic models
Although the contact discontinuity is distorted by the K-H instability, the overall shape of this surface is in fairly good agreement with the one predicted by the Wilkin (1996) solution (Eq. (1)) for small polar angles (θ), and the stand-off distance matches the position of the contact discontinuity well (see Fig. 6, top). In the thin-shell limit, the ISM and wind material are assumed to cool instantaneously and mix fully. In contrast, the forward and reverse shock of the adiabatic model have finite width, ~0.2 pc, and as expected, there is little mixing between these two layers of gas. Overall, the adiabatic model demonstrated that the set-up and code can achieve results that are consistent with both theoretical expectations and previous studies.
 |
Fig. 7 Density (top), temperature (middle), and total emissivity (bottom) cross-sections in the symmetry plane for models A-D (left to right) after 32 000 years. |
4. Models with cooling
The models that include radiative cooling exhibit a global structure that is similar to the structure of the adiabatic model. In Fig. 7, we show the density, temperature, and emissivity for models A-D. The four regions described above can easily be distinguished: the unshocked ISM and similarly unshocked, free-flowing stellar wind, separated by a layer of hot, shocked ISM (the forward shock) and shocked stellar wind (the reverse shock). Based on their flow characteristics and morphology, models A-D can be grouped into two classes: the “slow” models, A-C, with ISM densities ≳1 cm-3 and peculiar velocities ≲ 40 km s-1, and the “fast” model, D, with an ISM density of 0.3 cm-3 and a stellar velocity ~73 km s-1.
 |
Fig. 8 Particle density (top), temperature (middle), and velocity (bottom) profiles for models B (left) and D (right) in a thin slice, −0.02 < z < 0.02 and −0.02 < y < 0.02, along the x axis. In all plots, the ISM and RSG particles are blue and red, respectively. |
The fluid properties of the slow models show significant departures from the adiabatic case (Fig. 8); the most obvious being that the radiative cooling results in lower post-shock temperatures, e.g. Ts for model B is an order of magnitude lower than in model Bad for both the shocked ISM and RSG wind (Fig. 8, top middle). Furthermore, by reducing the thermal pressure of the gas, the strong cooling also enables further compression in the shock, resulting in greater post-shock densities (Fig. 8, top left) than in model Bad. Consequently, the time scale for the growth of R-T instabilities is reduced and, similar to the models of Brighenti & D’Ercole (1995, their Fig. 2.), R-T “fingers” develop faster than the K-H rolls that characterised the adiabatic case (see Sects. 3.2 and 4.1.1). Owing to the lower thermal pressure and mixing of the ISM and RSG gas, both the bow shock and the tail are narrower in the slow models; e.g., the model B width is approximately half that of model Bad.
The forward shock of the fast model shows similar characteristics to model Bad; the combination of a large stellar velocity through the ISM, and an initially hot and lower density ISM, means that the fast-moving gas does not have enough time to cool beyond its initial condition. The fast model achieves the same shocked ISM temperature, TISM, as the adiabatic case in which the star was moving approximately half as fast (Fig. 8, middle panel). Furthermore, this hot gas also flows along the bow shock and eventually settles in the core of the tail along the x axis, as it did in the adiabatic model. However, the shocked RSG wind temperature is approximately 1000 K, much lower than the adiabatic counterpart and similar to the value for the slow models.
The evolution of the forward and reverse shock positions for models B and DL, i.e. the position of maximum temperature along the symmetry axis, is shown in Fig. 9. Not only are the oscillations in the shock position less violent than the adiabatic case, an equilibrium shock position is attained more rapidly for the models with radiative cooling, after only 40 000 years. The strong cooling in both the forward and reverse shocks in the slow models results in the excitation of R-T type instabilities (see below), which causes the gas to mix, hence the small difference between the positions of the RSG and ISM components. In contrast, there is little mixing between the two layers in the fast model’s bow shock, the forward shock has significant width, thus the hottest gas extends much further into the impinging ISM flow.
 |
Fig. 10 Ratio of the cooling and dynamical time scales for models AH (left) and D (right). If the cooling time scale is much greater than the dynamical time scale, i.e. τΛ ≫ τdyn, the gas behaves adiabatically, and if τΛ ≪ τdyn, the gas is approximately isothermal. |
The typical cooling time scale in the bow shock for x < 0 is ~10 000 years, and is of the order of both the characteristic dynamical time scale for the shocked ISM, RSO/v∗, which is ~9400, 8300, 6800, 3700 years for models A-D, respectively, and the characteristic time scale for the shocked wind, RSO/vw, which is approximately 17 200 years. In Fig. 10 we compare the radiative cooling and characteristic dynamical time scales of the gas: 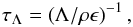 (9)and
(9)and 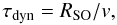 (10)respectively. For regions with τΛ ≪ τdyn, e.g. the bow shock arc where the gas is strongly decelerated, the gas cools strongly and behaves almost isothermally. The gas in the tail has a much longer cooling time scale, ~30 000 years (much greater than the cooling time scale for the shocked ISM) resulting in a largely adiabatic flow there.
(10)respectively. For regions with τΛ ≪ τdyn, e.g. the bow shock arc where the gas is strongly decelerated, the gas cools strongly and behaves almost isothermally. The gas in the tail has a much longer cooling time scale, ~30 000 years (much greater than the cooling time scale for the shocked ISM) resulting in a largely adiabatic flow there.
4.1. Bow shock morphology
The shape of the bow shock changes with time: it is initially circular and becomes increasingly “parabolic” until it reaches a steady state, at which point the global morphology is described by Eq. (4), the analytic Wilkin (1996) solution. The ratio of the shock position at angles θ = 0° and θ = 90°, rs(0°)/rs(90°), as a function of time, is shown in Fig. 11 (top). It takes several dynamical time scales for the bow shock to achieve the steady state value 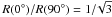 . The wind takes at least t = R(θ)/vw to reach the thin-shell position, ignoring the drag due to the moving environment, thus it takes ~16 000 years for θ = 0° (R(0°) = RSO), while for θ = 90° (
. The wind takes at least t = R(θ)/vw to reach the thin-shell position, ignoring the drag due to the moving environment, thus it takes ~16 000 years for θ = 0° (R(0°) = RSO), while for θ = 90° (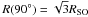 ) it takes ~28 000 years. In reality, the above time scales are longer. The drag is maximal for θ = 0°, so it takes about 30 000 years to reach RSO (e.g. Fig. 9), and coincidentally it takes about the same time to reach the solution position for θ = 90° since the distance traversed by the wind is greater, but the drag is reduced.
) it takes ~28 000 years. In reality, the above time scales are longer. The drag is maximal for θ = 0°, so it takes about 30 000 years to reach RSO (e.g. Fig. 9), and coincidentally it takes about the same time to reach the solution position for θ = 90° since the distance traversed by the wind is greater, but the drag is reduced.
It takes even longer for a steady state to be achieved for larger angles, θ > 90°. In Fig. 11 [bottom] we compare the thin-shell solution with model B at 43 000 years and at 73 000 years. Although the simulations coincide with the analytic solution in the latter, as expected, the agreement for large angles of θ at earlier times is not good, and the same effect is found for the fast model. The shape of the bow shock tail also changes with time, and younger systems show strong curvature in the bow shock tail. This is the case for both the slow and fast models; however, for the latter the curvature is quickly left far downstream due to the large space motion.
 |
Fig. 11 Top: ratio of R(0°)/R(90°) as a function of time for models B (magenta) and D (blue) compared to the analytic value in black. Bottom: hydrogen column density (on a logarithmic scale) for model B after 43 000 years (left) and 73 000 years (right). The analytic solution for the shape of the bow shock, given by Eq. (4), is shown in black 2. |
The inclination angle, the angle between the apex of the bow shock and the plane of the sky, also has a marked effect on the shape of the bow shock. In Fig. 12 we show the column densities for both the fast and slow models at different inclination angles. The bow shock becomes increasingly circular and the curvature in the tail also increases with larger inclination angles. At the same time, increasing the inclination angle reduces the density contrast between the peak at the apex of the bow shock and the rest of the cometary structure, making the detection and identification of highly inclined systems more difficult.
4.1.1. Substructure: instabilities
The bow shock is unstable for all models, however, the slow and fast models clearly exhibit very different bow shock substructure. The slow models show a thin, rather smooth outer shock and a contact discontinuity that is highly distorted (on a scale of ~0.1 pc) by prominent R-T “fingers” of the RSG wind (Figs. 8, 12, 13, B.2, and Appendix A). The protrusions are even more developed in the high-resolution model AH (Figs. 13, A.1). In the column density plots, the small-scale R-T instabilities result in a clumpy/knot-like structure that becomes one of the dominant features of the bow shock at large inclination angles (see Fig. 12).
In contrast, the bow shock in the fast model is much smoother overall, which results in a more layered/string-like appearance (Figs. 8, 12, 14, B.2, and Appendix A). As the bow shock becomes increasingly circular with larger i (Fig. 12), the instabilities in the slow and fast models appear more, and more distinct, with the fluctuations from the latter occurring at much larger wavelengths, ~0.2 pc. The vortex on the upper right of the bow shock is similar to those formed as a result of the K-H instability and dragged downstream in the adiabatic case. Indeed, K-H instabilities are likely to arise in the fast model due to the shear between the 73 km s-1 ISM and the 17 km s-1 RSG wind.
 |
Fig. 12 Hydrogen column density (on a logarithmic scale) at 76 000 years for models B (top) and DL (bottom) seen at inclination angles 0 ° (left) to 90 ° (right) in 30 ° intervals3. |
 |
Fig. 13 Projected emissivity (erg cm-2 s-1) in the symmetry plane for model AH for the various molecular, atomic and dust species. |
4.1.2. Emission maps
The strongest radiative emission for both the fast and slow models originates just ahead of the contact discontinuity, forming a bright ridge along that surface (Fig. 7, bottom). This overall emissivity is a sum of the contributions from 15 different coolants (see Appendix C for more details). While some species radiate from the entire bow shock surface, e.g. ΛH2O(r), others like ΛCO(r) are almost entirely confined to the reverse shock or forward shock. This has important consequences for the appearance of the bow shock shell as shown in Figs. 13 and 14. For example, the emission from the forward shock (hotter gas) results in a much smoother shell accentuated by small gentle “hill-like” ripples, e.g. Λatomic, whereas emission from the reverse shock (the shocked RSG wind) produces a layered, more “cloud-like” appearance, e.g. ΛH2O(H2). Several coolants, such as gas-grain, rotational transitions of CO and H2O, and the heating species produce a more “finger-like”, clumpy structure.
4.2. Luminosity of the bow shock
When the ISM and RSG winds collide, most of their kinetic energy is thermalised. An upper limit for total radiative luminosity in this case (assuming no other energy sources are present) is Ėtot ≈ Ėwind + ĖISM (Wilkin et al. 1997), where the kinetic luminosity of the RSG wind is 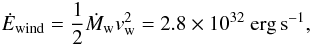 (11)and the ISM luminosity is
(11)and the ISM luminosity is 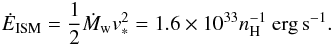 (12)In reality, only a fraction of the kinetic energy will be converted, therefore Ėtot is an upper limit for the radiative luminosity. ĖISM for the fast model is 5.3 × 1033 erg s-1, and is 1.1 × 1033 erg s-1 for the slow models assuming an average ISM density of nH = 1.5 cm-3. The combined mechanical luminosity Ėtot (Table 4) therefore does not exceed ~6 × 1033 erg s-1 for Betelgeuse’s parameters. This is a fairly robust upper limit because (a) for the most energetic case (model D) the wind kinetic luminosity is less than the ISM contribution; (b) uncertainties in the observed Betelgeuse mass-loss rate are towards lower values, e.g. Young et al. (1993a); and (c) the stellar velocity cannot be a factor of two greater since this scenario would produce a very bright forward shock at shorter wavelengths (cf. Mira and IRC 10216 – see Sect. 5).
(12)In reality, only a fraction of the kinetic energy will be converted, therefore Ėtot is an upper limit for the radiative luminosity. ĖISM for the fast model is 5.3 × 1033 erg s-1, and is 1.1 × 1033 erg s-1 for the slow models assuming an average ISM density of nH = 1.5 cm-3. The combined mechanical luminosity Ėtot (Table 4) therefore does not exceed ~6 × 1033 erg s-1 for Betelgeuse’s parameters. This is a fairly robust upper limit because (a) for the most energetic case (model D) the wind kinetic luminosity is less than the ISM contribution; (b) uncertainties in the observed Betelgeuse mass-loss rate are towards lower values, e.g. Young et al. (1993a); and (c) the stellar velocity cannot be a factor of two greater since this scenario would produce a very bright forward shock at shorter wavelengths (cf. Mira and IRC 10216 – see Sect. 5).
Bow shock luminosities in erg s-1.
We compare these theoretical values with estimates of the radiative luminosities from the simulations also given in Table 4. We used the following procedure to isolate only the contribution from the bow shock. For each model, a (1/r2) density profile was utilised to subtract the unshocked RSG wind, then only particles with both densities and temperatures greater than the ambient ISM were selected. We further restricted the integration to within θ ≲ 115° (x < RSO) the dominant emission region in the AKARI and IRAS images (the cut-off also serves to clearly delineate an emission region that can be directly compared with future high-resolution observations). The luminosities for the slow models do not differ significantly (the increasing stellar velocity largely compensates for the decreasing ISM density from model A to C), thus we only include the values for model B in Table 4. The total bow shock luminosity for the fast and slow models is approximately 16% and 29 % of the theoretical luminosity, respectively. Since Ėtot is the expected luminosity over 4π sterad and we only include emission from x < RSO, these values are a lower limit estimate for the fraction of kinetic energy that is thermalised. In Fig. 15, we show both the total radiative luminosities given in Table 4 and the individual ISM and RSG contributions of each species. Since the stellar wind properties are the same for all the models, it is not surprising that the luminosities produced by the RSG wind component are similar for both the fast and slow models. In contrast, the ISM contribution in the fast and slow models differs significantly: the higher density in the slow models leads to greater luminosities for all species except for the atomic lines, and the higher shock temperature in the fast model results in higher Latomic (Fig. 15, bottom).
We can estimate the luminosity in the IRAS and AKARI wavelength bands from the observed fluxes: 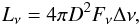 (13)where Δν is the instrument bandwidth at the given wavelength and Fν the flux measured in that wavelength band. This yields an underestimate of the bolometric luminosity. The AKARI flux is 10.7 Jy and 6.9 Jy at 65 μm and 90 μm, respectively (Ueta et al. 2008, private comm.), and the IRAS fluxes are significantly greater with 110 ± 20 Jy and 40 ± 10 Jy at 60 μm and 100 μm, respectively (Noriega-Crespo et al. 1997). The derived luminosities are given in Table 4 and show that, while the IRAS luminosities exceed the theoretical upper limit, the AKARI values are consistent given the uncertainties. Contamination by flux from the bar and Betelgeuse itself, which is very luminous in the infrared, may play a role and are likely to account for the difference between the AKARI and IRAS values. Higher resolution observations, together with a careful subtraction of the bar and central source, are essential for resolving this discrepancy.
(13)where Δν is the instrument bandwidth at the given wavelength and Fν the flux measured in that wavelength band. This yields an underestimate of the bolometric luminosity. The AKARI flux is 10.7 Jy and 6.9 Jy at 65 μm and 90 μm, respectively (Ueta et al. 2008, private comm.), and the IRAS fluxes are significantly greater with 110 ± 20 Jy and 40 ± 10 Jy at 60 μm and 100 μm, respectively (Noriega-Crespo et al. 1997). The derived luminosities are given in Table 4 and show that, while the IRAS luminosities exceed the theoretical upper limit, the AKARI values are consistent given the uncertainties. Contamination by flux from the bar and Betelgeuse itself, which is very luminous in the infrared, may play a role and are likely to account for the difference between the AKARI and IRAS values. Higher resolution observations, together with a careful subtraction of the bar and central source, are essential for resolving this discrepancy.
 |
Fig. 15 Models B and D radiative luminosity contributions for the various molecular and atomic species ordered on the x-axis as they are listed in Table 4. The total luminosity is shown in black (top), with the RSG and ISM components shown in red and blue (bottom), respectively. |
The most important coolants at low gas temperatures, ~300 K, are the gas-grain cooling, rotational modes of CO and H2O, and the rotational and vibrational transitions of H2. The dust, and C and O fine structure lines are often invoked to account for the infrared emission from bow shocks. It is possible that including non-LTE chemistry could change the abundance of OI, however it appears to contribute little to the far-infrared emission. In contrast, the dust and CI, CII fine structure lines appear to be the dominant far-infrared emitters in the bow shock shell, although it should be noted that the cooling rate of the latter is very uncertain (Smith & Rosen 2003, priv. comm.). The combined luminosity derived from the simulations due to grains, OI, CI, and CII is at least three orders of magnitude lower than inferred from the AKARI observations. A possible explanation is that there is an additional source of infrared flux, e.g. some of Betelgeuse’s radiation, or radiation produced by hot gas in the bow shock itself, is absorbed and reemitted by the gas and dust in the far-infrared.
5. Discussion
5.1. Comparison with previous studies
Our results are largely consistent with the previous hydrodynamic studies highlighted in Sect. 1. The slow models are similar to the 2D models of Brighenti & D’Ercole (1995) and van Marle et al. (2011) in their flow characteristics and their R-T substructure. However, the bow shocks in the 3D models of Wareing et al. (2007a) are generally smoother, and where instabilities are present, they occur on much larger scales than in our models. The difference is likely due to our including low-temperature cooling (below 10 000 K – the temperature they assume for the stellar wind) and may also be a resolution effect.
The smoother bow shock and the prominent vortex in the upper right of the fast model appear to be more consistent with the AKARI observations of Betelgeuse’s bow shock than the highly unstable bow shock in the slow models. However, with such high ISM shock temperatures (105 K), the bow shock should be visible at shorter wavelengths, e.g. in the UV. To our knowledge, no such emission has been detected for Betelgeuse. For Mira (o Ceti), an AGB star, 5 × 105 K gas was detected serendipitously with the GALEX UV satellite in both the bow shock and a 4 pc long tail (Martin et al. 2007). The star is estimated to be moving through a low density, nH ~ 0.03–0.8 cm-3, ISM at 130 km s-1 (Wareing et al. 2007b; Martin et al. 2007). The emission mechanism for this UV radiation is uncertain, but is thought to be the interaction of hot electrons (heated in the forward shock) with molecular hydrogen (Martin et al. 2007). The hot gas in the core of the tail for the fast model is certainly reminiscent of Mira’s narrow tail, and would provide a ready supply of electrons. Mira’s bow shock has also more recently been detected in the infrared with Herschel (Mayer et al. 2011). Another system with both UV and confirmed infrared emission from the bow shock is IRC 10216, an AGB star moving through the ISM at ~90 km s-1 (Sahai & Chronopoulos 2010; Ladjal et al. 2010).
High-resolution observations, e.g. with Herschel and SOFIA, should be able to distinguish between the fast and slow models based on the morphology of the bow shock and the presence/length scale of the instabilities.
 |
Fig. 16 Evolution of the bow shock shell mass for models B (left) and D (right). For both models, the RSG and ISM contributions are in red and blue, respectively, and their combined mass is plotted in black. The solid lines trace mass for x < RSO, while the points trace x < 0 gas. |
5.2. The age of Betelgeuse’s bow shock
5.2.1. Bow shock shell mass
By comparing the bow shock shell mass derived from the models with observational estimates, we can constrain the age of the bow shock shell. In Fig. 16 we show the evolution of the bow shock shell mass for models B (left) and D (right). Contributions from material in the bow shock were obtained using the same procedure as for the luminosity calculations described above, essentially only shocked particles in the bow shock head (i.e. with x < 0, points in Fig. 16) and x < RSO (solid lines in Fig. 16) were included. The former is useful for comparison with the theoretical estimates, while the latter is utilised when discussing the observations. The mass in the bow shock increases almost linearly at early times and only reaches an equilibrium state for the bow shock head after at least 60 000 years. The slow models take longer to achieve this steady state because the gas dragging material downstream has much lower velocity than in the fast models. Most of the mass in the bow shock shell is from the RSG wind, and as expected, its contribution does not differ significantly between the fast and slow models, except at later times when more wind material is able to accumulate at the bow shock due to mixing caused by R-T instabilities in the latter. As was the case for model Bad, the RSG shell mass for x < 0 is approximately ~0.05 M⊙, twice that of the theoretical estimate derived using 0.5 × ℳshell. Owing to the higher ISM density assumed, the ISM contribution in model B is larger (half as much as the RSG wind) than that in model D (only about a quarter), and as a result the total mass in the bow shock head, ≳ 0.08 M⊙, is also greater than in model D, ≳ 0.048 M⊙.
The mass in the bow shock based on the observed 60 μm flux is given by 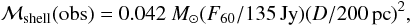 (14)(Noriega-Crespo et al. 1997). Again, assuming the Harper et al. (2008) distance of 197 pc, and the IRAS flux of 110 Jy in 7.5 arcmin yields a shell mass of 0.033 M⊙. (Noriega-Crespo et al. 1997 derived a shell mass of 0.14 M⊙, but assumed D = 400 pc for the distance to Betelgeuse.) The corresponding age of the bow shock is approximately 30 000 years (see Fig. 16, solid lines). However, as discussed in Sect. 4.2, this IRAS flux is most likely an overestimate, thus the age derived based on that value is an upper limit.
(14)(Noriega-Crespo et al. 1997). Again, assuming the Harper et al. (2008) distance of 197 pc, and the IRAS flux of 110 Jy in 7.5 arcmin yields a shell mass of 0.033 M⊙. (Noriega-Crespo et al. 1997 derived a shell mass of 0.14 M⊙, but assumed D = 400 pc for the distance to Betelgeuse.) The corresponding age of the bow shock is approximately 30 000 years (see Fig. 16, solid lines). However, as discussed in Sect. 4.2, this IRAS flux is most likely an overestimate, thus the age derived based on that value is an upper limit.
The shell mass from the AKARI fluxes is an order of magnitude lower (~0.0033 M⊙), which would imply an even younger bow shock age. If this is the case, however, the wind would not have sufficient time to expand to the stand-off distance. One possible solution is that the observed shell mass is underestimated due to uncertainties in the conversion from flux to mass (e.g. due to dust properties). In our models the shell takes ~20 000 years to reach the correct RSO (see Fig. 9), by which time the mass in the bow shock is approximately 0.02 M⊙. This is higher than the value obtained from AKARI observations, but may be consistent within the uncertainties and with the consensus estimates for Betelgeuse’s wind parameters. However, at this age none of our models are close to reaching a steady state.
Another possibility is that the shell is older; however, this requires extreme stellar wind properties. Utilising Eq. (7), we see that decreasing the mass-loss rate and increasing the wind velocity will both decrease the shell mass. However, the largest line widths observed in the wind are 40 km s-1 (Huggins et al. 1994, Fig. 1), thus the wind velocity, which is usually taken to be half of this linewidth, must be approximately 20 km s-1 or less. Thus, to decrease the shell mass from a steady state value of 0.05 M⊙ to 0.0033 M⊙ requires that we decrease the mass-loss rate by a factor of 15, i.e. Ṁ = 2 × 10-7 M⊙ yr-1, somewhat below the lowest estimate of Young et al. (1993a). The latter was derived from CO observations, which tends to underestimate the true mass-loss rate due to incomplete CO synthesis in Betelgeuse’s stellar wind (Noriega-Crespo et al. 1997). Although this lower mass-loss rate and a higher wind velocity cannot be excluded, they are outlying values in the range of observations so must be considered unlikely.
5.2.2. The shape of the bow shock
Based on these arguments, our results suggest that Betelgeuse’s bow shock is young and may not have reached a steady state yet. The circular nature and smoothness of bow shock can be naturally accounted for if this is the case, and need not be due solely to the inclination of the bow shock with respect to the plane of the sky; however, Betelgeuse’s tangential velocity, Vt = 25 km s-1, and radial velocity, Vrad = 20.7 km s-1 (assuming the distance to the star is 197 pc, see Sect. 1) yield an inclination angle of arctan(Vt/Vrad) ~ 50°. Given the uncertainty in the distance to the star, this inclination angle is consistent with the Ueta et al. (2008) value (56°) derived by fitting the shape of the observed arc with the analytic Wilkin (1996) solution, even though as discussed in Sect. 4.1, the latter is only valid if the bow shock has reached a steady state.
Utilising Betelgeuse’s radial and tangential motions, the stellar velocity is (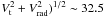 km s-1, the same as model B. Although the smooth appearance of the shell would seem to rule out the slow models, if the bow shock is young, the strong instabilities that characterise those simulations may not have had enough time to grow. We can estimate the age of the bow shock by comparing the observed shape with what is predicted by the simulations in Fig. 11 (top). From the AKARI observations, the ratio of R(0°)/R(90°) is approximately 0.7, which corresponds to an age of ≲ 30 000 years.
km s-1, the same as model B. Although the smooth appearance of the shell would seem to rule out the slow models, if the bow shock is young, the strong instabilities that characterise those simulations may not have had enough time to grow. We can estimate the age of the bow shock by comparing the observed shape with what is predicted by the simulations in Fig. 11 (top). From the AKARI observations, the ratio of R(0°)/R(90°) is approximately 0.7, which corresponds to an age of ≲ 30 000 years.
According to our simulations, if the bow shock is young, the bow shock tail should show strong curvature and should not be too distant from the head of the bow shock. Although the emission from such a tail is likely to be weak, deep, high-resolution observations may be able to detect it. Indeed, there appears to be faint emission extending from the bow shock head towards the tail in the AKARI observations, e.g. the structure located at (RA, Dec) offsets of ( − 2,9) arcmin in the WIDE-S image of Fig. 1 of Ueta et al. (2008). A curved tail has already been observed for the massive O9.5 supergiant α Camelopardalis (S. Mandel4) and likely for the O6 I(n)f runaway star λ Cep (Gvaramadze & Gualandris 2011). Although these are much hotter stars with faster stellar winds, the physical mechanism responsible for producing a curved tail is the same. In light of our simulations, such a feature implies either a very small space motion for the star relative to ambient ISM (unlikely given the strength of the bow shock emission) or that the bow shock is young. Thus, modelling the shape of the bow shock (head and tail, if present) is a promising avenue for constraining the age and the evolutionary stage of these systems.
5.2.3. Implications
Estimates for Betelgeuse’s age are highly uncertain, ranging from 8–13 million years depending on the stellar evolution model and distance assumed (Harper et al. 2008). The core helium-burning phase lasts about 10% of the total lifetime, thus τHe = 0.8−1.3 Myr. The star is expected to start and spend a significant fraction of this phase as an RSG. According to current stellar models, the star may or may not have undergone a so-called blue loop in the HR diagram, spending a fraction of core helium burning as a blue supergiant, before returning to the RSG stage at core helium exhaustion (Meynet & Maeder 2000; Heger & Langer 2000).
A young age of Betelgeuse’s bow shock might imply that the star has entered the RSG stage only recently. It may be interesting to relate this idea with the recent finding that the diameter of Betelgeuse at 11 μm has systematically decreased by about 15% over the past 15 years (Townes et al. 2009). While Ravi et al. (2010) and Ohnaka et al. (2011) debate whether this implies a real radius change, or rather a change in the density of certain layers in the envelope of the star, it is remarkable that the time scale of these changes is of the order of 100 years. This might imply that the envelope of Betelgeuse is not in thermal equilibrium, as might be the case when a star is entering the RSG stage.
On the other hand, the radius of a star entering the RSG phase for the first time after core hydrogen exhaustion only increases, with time scales for the radius change (R/Ṙ) down to about 1000 years. This is different, however, when the star enters the RSG stage after core helium exhaustion, because the igniting helium shell leads to an intermittent episode of shrinkage. Since the star might have lost a substantial fraction of its hydrogen-rich envelope by that time, its thermal time scale might also have decreased. Thus, while more observational and theoretical efforts are required to give this speculation more substance, a consistent picture might involve Betelgeuse recently having finished core helium burning and returning to the RSG stage from a previous blue supergiant excursion.
If Betelgeuse has only recently entered the RSG stage, it may not have had enough time to travel beyond its main sequence or blue supergiant wind bubble. Assuming a wind mass-loss rate of 10-7 M⊙ yr-1, and a wind velocity of ~103 km s-1, the stand-off distance for Betelgeuse’s main sequence or blue supergiant bow shock shell was around 1 pc. A RSG phase of a ~few × 10 000 years would bring the star close to the edge of such a bubble. This raises the possibility that the mysterious “bar” ahead of the bow shock could be a remnant of this earlier phase of evolution. A theoretical investigation of such a scenario is currently underway.
6. Conclusions
We presented the first 3D models of the interaction of Betelgeuse’s RSG wind with the ISM. We took dust, atomic-, molecular-, and metal-line cooling into account. The models cover a range of plausible ISM densities of 0.3–1.9 cm-3 and stellar velocities of 28–73 km s-1. We showed that the flow dynamics and morphology of the bow shocks in the models differed due to the growth of Rayleigh-Taylor or Kelvin-Helmholtz instabilities. The former dominate the slow models, resulting in a clumpy substructure, whereas the latter are characteristic of the fast model and produce a more layered substructure. In the fast model, gas is shocked to high temperatures. If gas as hot as this were to be detected at short wavelengths (e.g. UV), this would exclude the slow models as an explanation for Betelgeuse’s bow shock. High spatial and spectral resolution observations (e.g. Herschel, SOFIA and ALMA) particularly of the more dominant cooling/emitting species, e.g. rotational lines of H2O or CO, could also be used to further constrain the physical characteristics of the system. In addition, better determination of the molecular to atomic hydrogen fraction in the RSG wind, the abundances of various species, and temperature of the ISM would also reduce the number of free parameters in the model.
The large fluxes in the infrared compared to the theoretical limit for the bolometric luminosity suggest that the stellar flux and/or flux from hotter gas in the bow shock is reprocessed by the dust and reemitted in the far-infrared. We showed that, if the bow shock shell mass is low, as is suggested by the AKARI fluxes, then Betelgeuse’s bow shock is young. The smoothness and circular nature of the bow shock would be consistent with this conclusion. Furthermore, if the bow shock has not yet reached a steady state, we are less able to constrain the physical parameters of the system, e.g. the ram pressure of the ISM. This also raises the intriguing possibility that Betelgeuse has only recently become an RSG and that the mysterious “bar” ahead of the bow shock is a remnant of a wind shell created during an earlier phase of evolution.
Online material
Movie 1 Access here
Movie 2 Access here
See image on APOD at http://apod.nasa.gov/apod/ap061124.html
Acknowledgments
The authors are grateful to Vasilii Gvaramadze, Michael Smith, Toshiya Ueta, and the referee, Alejandro Esquivel, for many helpful and insightful comments and discussions. We thank the John von Neumann Institute for Computing for a grant for computing time on the JUROPA supercomputer at Juelich Supercomputing Centre and Lorne Nelson for computing time on the Centre de Calcul Scientifique de l’Université de Sherbrooke Usherbrooke. The rendered figures in this paper were made using a modified version of the SPLASH visualisation toolkit (Price 2007).
References
- Agertz, O., Moore, B., Stadel, J., et al. 2007, MNRAS, 380, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J., & Hut, P. 1986, Nature, 324, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Bernat, A. P., Hall, D. N. B., Hinkle, K. H., & Ridgway, S. T. 1979, ApJ, 233, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Brighenti, F., & D’Ercole, A. 1995, MNRAS, 277, 53 [NASA ADS] [Google Scholar]
- Cao, Y., Terebey, S., Prince, T. A., & Beichman, C. A. 1997, ApJS, 111, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Langer, N., & Tout, C. A. 2011, MNRAS, 414, 3501 [NASA ADS] [CrossRef] [Google Scholar]
- Esquivel, A., Raga, A. C., Cantó, J., et al. 2010, ApJ, 725, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C., Sembach, K., & York, D. G. 1990, ApJ, 364, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Segura, G., Langer, N., & Mac Low, M.-M. 1996, A&A, 316, 133 [NASA ADS] [Google Scholar]
- Glassgold, A. E., & Huggins, P. J. 1986, ApJ, 306, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Gvaramadze, V. V., & Gualandris, A. 2011, MNRAS, 410, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Harper, G. M. 2010, in Hot and Cool: Bridging Gaps in Massive Star Evolution, ed. C. Leitherer, P. Bennett, P. Morris, & J. van Loon, ASP Conf. Ser., 425, 152 [Google Scholar]
- Harper, G. M., Brown, A., & Guinan, E. F. 2008, AJ, 135, 1430 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., & Avrett, E. H. 1984, ApJ, 284, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Huggins, P. J., Bachiller, R., Cox, P., & Forveille, T. 1994, ApJ, 424, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Ladjal, D., Barlow, M. J., Groenewegen, M. A. T., et al. 2010, A&A, 518, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambert, D. L., Brown, J. A., Hinkle, K. H., & Johnson, H. R. 1984, ApJ, 284, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Seibert, M., Neill, J. D., et al. 2007, Nature, 448, 780 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mayer, A., Jorissen, A., Kerschbaum, F., et al. 2011, A&A, 531, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Monaghan, J. J. 1992, ARA&A, 30, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Neilson, H., Lester, J., & Haubois, X. 2011, in The Ninth Pacific Rim Conference on Stellar Astrophysics, ed. S. Qian, ASP Conf. Ser. [arXiv:1109.4562] [Google Scholar]
- Noriega-Crespo, A., van Buren, D., Cao, Y., & Dgani, R. 1997, AJ, 114, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Ohnaka, K., Weigelt, G., Millour, F., et al. 2011, A&A, 529, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price, D. J. 2007, PASA, 24, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J. 2008, J. Comp. Phys., 227, 10040 [Google Scholar]
- Raga, A. C., Cantó, J., De Colle, F., et al. 2008, ApJ, 680, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Ravi, V., Wishnow, E. H., Lockwood, S., & Townes, C. H. 2010 [arXiv:1012.0377] [Google Scholar]
- Rodgers, B., & Glassgold, A. E. 1991, ApJ, 382, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Rosswog, S. 2009, New A Rev., 53, 78 [Google Scholar]
- Sahai, R., & Chronopoulos, C. K. 2010, ApJ, 711, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. D., & Rosen, A. 2003, MNRAS, 339, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Hinkle, K. H., & Ryde, N. 2009, AJ, 137, 3558 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2010, ARA&A, 48, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New A, 6, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Stencel, R. E., Pesce, J. E., & Hagen Bauer, W. 1988, AJ, 95, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 2003, ApJS, 88, 253 [Google Scholar]
- Suttner, G., Smith, M. D., Yorke, H. W., & Zinnecker, H. 1997, A&A, 318, 595 [NASA ADS] [Google Scholar]
- Townes, C. H., Wishnow, E. H., Hale, D. D. S., & Walp, B. 2009, ApJ, 697, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Ueta, T., Izumiura, H., Yamamura, I., et al. 2008, PASJ, 60, 407 [Google Scholar]
- Ueta, T., Izumiura, H., Yamamura, I., et al. 2009, in ASP Conf. Ser. 418, ed. T. Onaka, G. J. White, T. Nakagawa, & I. Yamamura, 117 [Google Scholar]
- Valcke, S., de Rijcke, S., Rödiger, E., & Dejonghe, H. 2010, MNRAS, 408, 71 [Google Scholar]
- van Marle, A. J., Langer, N., Achterberg, A., & García-Segura, G. 2006, A&A, 460, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Marle, A. J., Meliani, Z., Keppens, R., & Decin, L. 2011, ApJ, 734, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Villaver, E., García-Segura, G., & Manchado, A. 2003, ApJ, 585, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Wadsley, J. W., Veeravalli, G., & Couchman, H. M. P. 2008, MNRAS, 387, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Wareing, C. J., Zijlstra, A. A., & O’Brien, T. J. 2007a, ApJ, 660, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Wareing, C. J., Zijlstra, A. A., O’Brien, T. J., & Seibert, M. 2007b, ApJ, 670, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkin, F. P. 1996, ApJ, 459, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkin, F. P., Canto, J., & Raga, A. C. 1997, in Herbig-Haro Flows and the Birth of Stars, ed. B. Reipurth, & C. Bertout, IAU Symp., 182, 343 [Google Scholar]
- Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [Google Scholar]
- Young, K., Phillips, T. G., & Knapp, G. R. 1993a, ApJ, 409, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Young, K., Phillips, T. G., & Knapp, G. R. 1993b, ApJS, 86, 517 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The effect of resolution
As discussed in Sect. 3.1, it is important to use a large number of particles to reduce shock broadening. High resolution is also necessary in order to resolve instabilities, particularly for the slow models. To test this, the slowest model (A) was rerun as model AH with an average six times higher mass resolution, and the results are compared in cross-section in Fig. A.1 [top]. A higher resolution version of model D was not computationally feasible, so a lower resolution version (model DL) was run instead with an average mass resolution that is two times lower, and the results are shown in the lower two panels of Fig. A.1. In both cases, as expected, the higher resolution model shows a smoother RSG wind and stronger instabilities developing in the bow shock. Model DL appears to have insufficient resolution to fully develop the instabilities seen in model D (e.g. the vortex in the upper right of the bow shock), whereas the difference between models A and AH is less dramatic because both models show the development of R-T instabilities. Despite these differences, the overall agreement between the larger scale fluid properties of the high and low resolution simulations is very good, and they do not differ by more than a few percent. Thus we conclude that our calculations are sufficiently numerically converged in terms of the quantities we are interested in measuring.
 |
Fig. A.1 Cross-sectional density profiles for models AH (top, left), A (top, right), D (bottom, left), and DL (bottom, right) in the symmetry plane. |
Appendix B: The effect of varying TISM and f
While the thermal pressure of the ISM is insignificant compared to its ram pressure in all models, it could affect the bow shock thermal and emission properties. The wind thermal pressure is insignificant owing to adiabatic expansion, but the hydrogen molecular fraction, f, entering the reverse shock may also affect the emissivity and cooling of shocked gas. The effects of the ISM temperature were tested by using three ISM temperatures for different runs of model C: TISM = 650 K for model CL650, 1600 K for model CL1600 and 8000 K for model CL8000. All models use a molecular fraction f = 0.001 (on a scale where 0 is atomic and 0.5 is fully molecular) for the wind boundary condition, so a comparison model CLf was run with f = 0.18. Cross-sections of the gas temperature and total emissivity for these four models are shown in Fig. B.1, and can be compared to the default model C in Fig. 7, although it should be noted that the logarithmic scales are different in the two figures. Higher ISM temperatures produce a smoother forward shock and result in a much fainter tail. The hotter gas that accumulates along the symmetry axis in the tail is also closer to the reverse shock, filling the void behind the RSG wind more efficiently. This is a relatively minor difference between the models, however, so the strongest impression we get from comparing the top three panels in Fig. B.1 is how similar they are in both the structure and emissivity of the bow shock.
 |
Fig. B.1 Temperature (left) and total emissivity (right) in the symmetry plane for models CL650 (top row), CL1600 (second row), CL8000 (third row), and CLf (bottom row). |
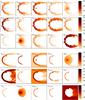 |
Fig. B.2 Cross-sectional profile of the emissivity (erg cm-3 s-1) for the various heating and cooling species in model AH (top three rows) and model D (bottom three rows). |
The molecular-to-atomic hydrogen fraction in the RSG wind increases as the wind cools and expands away from the star. The initial value depends on the temperature structure and chemistry near the stellar surface. We assumed a low value since Betelgeuse is thought to have a hot, ~8000 K chromosphere that would dissociate molecules (Hartmann & Avrett 1984). However, more recent studies suggest that the temperature in this region could be much lower at approximately 4 000 K (Harper 2010, and references therein), and thus f could be higher. This was tested in the f = 0.18 model CLf whose results are shown in the bottom panel of Fig. B.1. As expected, the cooling is much stronger for larger f, which leads to a more unstable bow shock – the apex of the bow shock has moved inwards in model CLf and its shape is far from a smooth curve for both the forward and reverse shock. The regular appearance and relative stability of the observed bow shock on similar scales (Ueta et al. 2008) suggests that the hydrogen is indeed mostly in atomic form.
Appendix C: Emission from the bow shock shell
 |
Fig. C.1 Snapshots of the movies for the model B (left) and D (right) simulations. First, the evolution of the gas column density is followed, then the final structure is rotated 360°, demonstrating the changing morphology of the bow shock with different inclination angles. |
The emissivities for each of the cooling and heating species included in the simulations are shown in cross-section in Fig. B.2 for models AH [top] and D [bottom]. These cross-sectional profiles show the location and morphology of the emitting regions for each species more clearly than the projections shown in Figs. 13 and 14. Here we also show results for each coolant individually. As expected, the processes that involve molecular hydrogen, e.g. ΛH2(r − v), tend to emit strongly from the gas in the reverse shock. The OI fine structure and CO rotational cooling are also more concentrated in the denser, cooler regions of the reverse shock. The other species tend to emit more evenly from the entire bow shock, with the atomic cooling greatest in the forward shock. In the slow models, the atomic cooling is largely absent from the cool, dense R-T “fingers”. In the fast model, several species that do emit from both the forward and reverse shocks tend to show a strong ridge of emission just ahead of the contact discontinuity, e.g. the grain, water, atomic, and carbon fine-structure cooling. The lower ISM density in the fast model results in much weaker emission from the bow shock tail than in the slow models, e.g. ΛH2O(H2) and ΛCO(H2).
All Tables
All Figures
 |
Fig. 1 Bow shock and “bar” of Betelgeuse. Left. The 60 μm IRAS observation retrieved from the IRAS Galaxy Atlas (IGA) Image Server1 (for details about IGA, see Cao et al. 1997). Right. The high-resolution, composite AKARI image with 65 μm, 90 μm, and 140 μm emission in blue, green, and red, respectively (Ueta et al. 2008) [Credit: AKARI MLHES team]. |
| In the text | |
 |
Fig. 2 Position of the shock along the x axis (defined by the point with maximum temperature) as a function of time for the ISM (dashed line) and the stellar wind (dotted line). The black solid line demonstrates the trajectory for a vs = 10 km s-1 shock velocity. All velocities are measured with respect to the stationary frame of the star. |
| In the text | |
 |
Fig. 3 Adiabatic model, Bad, of the interaction of Betelgeuse’s dense stellar wind with the ISM after t ≈ 100 000 years. We plot cross-sectional profiles along the symmetry axis (the xy plane) for ρ, the gas density (top, left); T, the temperature (top, right); the velocity vector field plotted over |v|, the gas velocity (bottom, left); and the smoothing length, h (bottom, right). Approximately 1 × 107 ISM particles filled the simulation domain and ~6 × 105 particles were injected to produce the isotropic stellar wind. |
| In the text | |
 |
Fig. 4 Growth of the mass in the bow shock shell with time. The shell is defined as shocked regions with T > 2000 K and density above that in the ambient medium. The lines show the total shell mass (black), the contributions from the ISM (blue) and the RSG wind (red) for x < RSO or θ ≲ 115°, whereas the points represent the same parameters except for shell material with x < 0 or θ ≲ 90°. |
| In the text | |
 |
Fig. 5 Particle density (top) and temperature (bottom) profiles for model Bad in a thin slice, −0.03 < z < 0.03 and −0.03 < y < 0.03, along the x axis. ISM and RSG particles are blue and red, respectively. |
| In the text | |
 |
Fig. 6 Particles in the xy plane with the ISM in blue, and the stellar wind in red. The analytic solution (Eq. (4)) is shown in black. |
| In the text | |
 |
Fig. 7 Density (top), temperature (middle), and total emissivity (bottom) cross-sections in the symmetry plane for models A-D (left to right) after 32 000 years. |
| In the text | |
 |
Fig. 8 Particle density (top), temperature (middle), and velocity (bottom) profiles for models B (left) and D (right) in a thin slice, −0.02 < z < 0.02 and −0.02 < y < 0.02, along the x axis. In all plots, the ISM and RSG particles are blue and red, respectively. |
| In the text | |
 |
Fig. 9 Same as Fig. 2 except for models B and DL. |
| In the text | |
 |
Fig. 10 Ratio of the cooling and dynamical time scales for models AH (left) and D (right). If the cooling time scale is much greater than the dynamical time scale, i.e. τΛ ≫ τdyn, the gas behaves adiabatically, and if τΛ ≪ τdyn, the gas is approximately isothermal. |
| In the text | |
 |
Fig. 11 Top: ratio of R(0°)/R(90°) as a function of time for models B (magenta) and D (blue) compared to the analytic value in black. Bottom: hydrogen column density (on a logarithmic scale) for model B after 43 000 years (left) and 73 000 years (right). The analytic solution for the shape of the bow shock, given by Eq. (4), is shown in black 2. |
| In the text | |
 |
Fig. 12 Hydrogen column density (on a logarithmic scale) at 76 000 years for models B (top) and DL (bottom) seen at inclination angles 0 ° (left) to 90 ° (right) in 30 ° intervals3. |
| In the text | |
 |
Fig. 13 Projected emissivity (erg cm-2 s-1) in the symmetry plane for model AH for the various molecular, atomic and dust species. |
| In the text | |
 |
Fig. 14 Same as Fig. 13 except for model D. |
| In the text | |
 |
Fig. 15 Models B and D radiative luminosity contributions for the various molecular and atomic species ordered on the x-axis as they are listed in Table 4. The total luminosity is shown in black (top), with the RSG and ISM components shown in red and blue (bottom), respectively. |
| In the text | |
 |
Fig. 16 Evolution of the bow shock shell mass for models B (left) and D (right). For both models, the RSG and ISM contributions are in red and blue, respectively, and their combined mass is plotted in black. The solid lines trace mass for x < RSO, while the points trace x < 0 gas. |
| In the text | |
 |
Fig. A.1 Cross-sectional density profiles for models AH (top, left), A (top, right), D (bottom, left), and DL (bottom, right) in the symmetry plane. |
| In the text | |
 |
Fig. B.1 Temperature (left) and total emissivity (right) in the symmetry plane for models CL650 (top row), CL1600 (second row), CL8000 (third row), and CLf (bottom row). |
| In the text | |
 |
Fig. B.2 Cross-sectional profile of the emissivity (erg cm-3 s-1) for the various heating and cooling species in model AH (top three rows) and model D (bottom three rows). |
| In the text | |
 |
Fig. C.1 Snapshots of the movies for the model B (left) and D (right) simulations. First, the evolution of the gas column density is followed, then the final structure is rotated 360°, demonstrating the changing morphology of the bow shock with different inclination angles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


