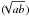| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201118283 | |
| Published online | 27 March 2012 | |
Dark matter distribution in the merging cluster Abell 2163⋆
1 Université de Toulouse, UPS-Observatoire Midi-Pyrénées, IRAP, Toulouse, France
2 CNRS, Institut de Recherche en Astrophysique et Planétologie, 14 avenue Edouard Belin, 31400 Toulouse, France
e-mail: gsoucail@irap.omp.eu
Received: 17 October 2011
Accepted: 24 January 2012
Context. The cluster Abell 2163 is a merging system of several subclusters with complex dynamics. It presents exceptional X-rays properties (high temperature and luminosity), suggesting that it is a very massive cluster. Recent 2D analysis of the gas distribution has revealed a complex and multiphase structure.
Aims. This paper presents a wide-field weak lensing study of the dark matter distribution in the cluster in order to provide an alternative vision of the merging status of the cluster. The 2D mass distribution was built and compared to the galaxies and gas distributions.
Methods. A Bayesian method, implemented in the Im2shape software, was used to fit the shape parameters of the faint background galaxies and to correct for PSF smearing. A careful color selection on the background galaxies was applied to retrieve the weak lensing signal. Shear signal was measured out to more than 2 Mpc (≃12′ from the center). The radial shear profile was fit with different parametric mass profiles. The 2D mass map was built from the shear distribution and used to identify the different mass components.
Results. The 2D mass map agrees with the galaxy distribution, while the total mass inferred from weak lensing shows a strong discrepancy to the X-ray deduced mass. Regardless of the method used, the virial mass M200 falls in the range 8 to 14 × 1014 h70-1 M๏ inside the virial radius (~2.0~h70-1 Mpc), a value that is two times less than the mass deduced from X-rays. The central mass clump appears bimodal in the dark matter distribution, with a mass ratio ~3:1 between the two components. The infalling clump A2163-B is detected in weak lensing as an independent entity. All these results are interpreted in the context of a multiple merger seen less than 1 Gyr after the main crossover.
Key words: galaxies: clusters: intracluster medium / gravitational lensing: weak / galaxies: clusters: general / galaxies: clusters: individual: Abell 2163
Based on observations obtained with MegaPrime/MegaCam, a joint project of Canada-France-Hawaii Telescope (CFHT) and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France and the University of Hawaii.
© ESO, 2012
1. Introduction
Clusters of galaxies are powerful probes for cosmology because they belong to the high-mass end of the halo mass function of collapsed structures (Voit 2005). The mass distribution within these structures is representative of the nonlinear development of the accretion processes during the cosmological evolution (Press & Schechter 1974; Frenk et al. 1990). But it is still a challenge to securely relate observational quantities like the X-ray luminosity and temperature, or the optical number counts and velocity dispersion, to constitutive properties such as the gravitational potential or the mass distribution (Reiprich & Böhringer 2002; Vikhlinin et al. 2009; Carlberg et al. 1996). Several internal processes also play major roles throughout cosmological times. They can distort the simple scaling relations between physical quantities initially set by the hierarchical clustering process of structures formation.
The rich cluster of galaxies Abell 2163 is an interesting cluster that displays several paradoxical properties. First, it is one of the richest Abell clusters, at a redshift z = 0.201, and among the most luminous ones in X-rays (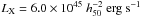 in the 2–10 keV band, Elbaz et al. 1995). Extensive analysis of the global properties of this exceptional cluster have soon been conducted after the initial detection of a very high X-ray temperature (TX = 14.6 ± 0.9 keV, measured with GINGA by Arnaud et al. 1992). They have rapidly pointed evidence of a nonisothermal gas distribution with a strong temperature drop in the outskirts (Markevitch et al. 1994; Markevitch 1996) and inhomogeneities of the gas temperature in the center (Markevitch & Vikhlinin 2001). More recently, Feretti et al. (2001) have detected a very extended and powerful radio halo, which they interpret as the tracer of a very hot nonthermal phase in the ICM. Moreover, areas with a flatter radio spectral index and higher energetic particles are found to be coincident with the most disturbed regions of the X-ray distribution (Feretti et al. 2004). Another component was identified as a secondary X-ray source in the map, spectroscopically confirmed to be much cooler than the main cluster (A2163-B). The strong temperature variations in the center displayed by Chandra imaging (Govoni et al. 2004) are also representative of ongoing merging processes; however, the X-ray properties in the external regions of the cluster are more regular, both in luminosity and temperature, and fall within the general category of massive clusters.
in the 2–10 keV band, Elbaz et al. 1995). Extensive analysis of the global properties of this exceptional cluster have soon been conducted after the initial detection of a very high X-ray temperature (TX = 14.6 ± 0.9 keV, measured with GINGA by Arnaud et al. 1992). They have rapidly pointed evidence of a nonisothermal gas distribution with a strong temperature drop in the outskirts (Markevitch et al. 1994; Markevitch 1996) and inhomogeneities of the gas temperature in the center (Markevitch & Vikhlinin 2001). More recently, Feretti et al. (2001) have detected a very extended and powerful radio halo, which they interpret as the tracer of a very hot nonthermal phase in the ICM. Moreover, areas with a flatter radio spectral index and higher energetic particles are found to be coincident with the most disturbed regions of the X-ray distribution (Feretti et al. 2004). Another component was identified as a secondary X-ray source in the map, spectroscopically confirmed to be much cooler than the main cluster (A2163-B). The strong temperature variations in the center displayed by Chandra imaging (Govoni et al. 2004) are also representative of ongoing merging processes; however, the X-ray properties in the external regions of the cluster are more regular, both in luminosity and temperature, and fall within the general category of massive clusters.
Recently, Maurogordato et al. (2008) have presented a very detailed optical analysis of this cluster that sheds new light on its merging status. Using both spectroscopy of a large sample of galaxy members and wide field multicolor imaging, they studied the galaxy distribution and confirm that the main cluster is dynamically separated from A2163-B, although they belong to the same complex. The galaxy density distribution of the main cluster A2163-A is strongly elongated in the EW direction and shows a bimodal distribution that depends on the luminosity range of the galaxies tracing the distribution. For the faintest ones, the distribution is split into two components, A1 and A2, for which the former is centered on the brightest cluster galaxy BCG1 while the latter is slightly shifted compared to the galaxy BCG2 (following the naming defined by Maurogordato et al. 2008). In addition, a strong velocity gradient in the main clump is related to the spatial galaxy distribution and is elongated in the NE/SW direction. All these properties point towards a post-merging phase where the main component has just undergone a recent merger along the elongation direction, nearly coplanar with the plane of the sky, while A2163-B is infalling onto A2163-A. Finally, a very detailed analysis of the complex X-ray emission, based on high-resolution imaging with Chandra, coupled with spectro-imaging with XMM-Newton, has brought new light on the complex gas distribution (Bourdin et al. 2011). The authors clearly identify a cold gas clump in the direction of A2 but not coincident with it. This clump may be seen crossing the main cluster’s hot-gas component, a scenario with features resembling those detected in the so-called “Bullet cluster” 1E 0657–56 (Markevitch et al. 2002).
To explore the physical state of the cluster and to better understand the relationship between the distributions of the galaxies, the hot ICM gas, and the dark matter, we propose in this paper to use the weak gravitational lensing effect, which is directly related to the dark matter content and its distribution. A2163 has already been observed in weak lensing by several groups but without strong and conclusive results. Squires et al. (1997) used a large and shallow image of the cluster and found a modest value for the velocity dispersion of about 700 km s-1 (adjusted with a singular isothermal potential), although the authors claim that the uncertainties are so great close to the center that they could accept higher values up to 1000 km s-1. With deeper data from the VLT but in a smaller field of view, Cypriano et al. (2004) measured σV = 1020 ± 150 km s-1. Again this is a low value compared to what could be expected from such a hot cluster and to what is measured dynamically from the galaxies. More recently, Radovich et al. (2008) have claimed that they solve this discrepancy with their new measure of the weak shear profile based on deep and wide field images of the cluster. However, their fit is not conclusive, so we decided to provide a new analysis of the weak lensing signal specifically dedicated to the spatial distribution of the dark matter, using the same CFHT/MegaCam data. We took special care in selecting the background galaxies and remove the cluster contamination close to the center as much as possible. Moreover, our goal is to compare the 2D mass map with the X-ray map in order to characterize the link between the dark matter and the baryonic mass better in this merging cluster. Similar approaches have led to the spectacular results in the “Bullet cluster” 1E0657–56 (Clowe et al. 2006) in which the separation between the collisional baryonic matter and the collisionless dark matter is obvious and allows accurate identification of the merging stage (Bradač et al. 2006). In parallel to this work, Okabe et al. (2011) used Subaru weak lensing data to provide a similar 2D analysis. Fortunately, their results are globally similar to ours, although some discrepancies remain, and these are investigated in the paper.
The paper is organized as follow: in Sect. 2 we describe the data and the weak lensing analysis, insisting on the process selecting the background galaxies. In Sect. 3, an analysis of the central arclets is proposed and some strong lensing properties are derived for the cluster center. Section 4 presents the 2D weak lensing reconstruction and the spatial distribution of the dark matter in the field of the cluster, while in Sect. 5 we discuss our mass estimates. Finally we present some conclusions in Sect. 6. Throughout the paper we use H0 = 70 km s-1 Mpc-1, ΩM = 0.3, ΩΛ = 0.7. At the redshift of the cluster (z = 0.2), 1″ corresponds to 3.3 kpc and 1′ to 200 kpc. Magnitudes are given in the AB system.
2. Image data and weak lensing analysis
2.1. Data reduction and photometry
Imaging data were obtained at the Canada-France-Hawaii Telescope with MegaCam, during the run 05AC12 (PI: H. Hoekstra) and were retrieved from the CFHT archives at CADC1. These data were already preprocessed by the CFHT Elixir pipeline (Magnier & Cuillandre 2004) and correspond to Master detrend images. Nineteen images of 600 s each were found: 15 in r′ and 4 in g′. The total integration time is 2.5 h in r′ and 40 min in g′.
Astrometric solutions for each CCD and then for each image were computed using SCAMP (Bertin 2006), a tool developed at Terapix2. Absolute coordinates of the stars detected in the field were selected from the USNO-B1 catalog. Internal accuracy for the calibration of the whole set of images reached 0.06′′, while the external accuracy was on the order of 0.27′′ or equivalently 1.5 pixels. All the images were combined and geometrically rescaled using SWARP, with a fixed pixel size of 0.186′′. Final images in g′ and r′ cover one square degree.
Photometric internal calibration is provided during the observing run and photometric zero points are measured and included in each image header. But some images were not taken in photometric conditions. They were post-calibrated with reference to other available data, cross-correlating our catalogs with those provided by Maurogordato et al. (2008): these were obtained with the ESO Wide Field Imager on the 2.2 m telescope and the Bessel R and V filters, under photometric conditions. In addition, they were corrected from the galaxy extinction, with an average value E(B − V) = 0.41. Therefore, the magnitude difference between both sets of data, taking the AB correction of the MegaCam filters into account, defines the correction to add to the magnitude zero points: − 0.08 mag in r′ and − 0.30 mag in g′. Both corrections include the galactic extinction correction and are estimated with an accuracy of 0.05 mag.
Photometric catalogs were built in both filters, using SExtractor (Bertin & Arnouts 1996). The r′ image, which is the deepest one, was the reference image for detection, and the g′ − r′ color index was computed inside the limiting isophote defined in the r′ image for each object. Completeness magnitudes were estimated from number counts to 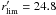 and
and 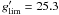 (Fig. 1). They are approximately 0.7 brighter than the 5σ limiting magnitudes computed inside an aperture with a diameter 1.45 times the full width at half maximum (FWHM) of the seeing disk, and defined in the MegaCam exposure time calculator (DIET3). This last magnitude is best suited to point-like objects, and that the 0.7 mag difference reflects that most of the faint objects are compact but extended ones. In the final images used in this paper, the measured average seeing is 0.75′′ in r′ and 0.67′′ in g′.
(Fig. 1). They are approximately 0.7 brighter than the 5σ limiting magnitudes computed inside an aperture with a diameter 1.45 times the full width at half maximum (FWHM) of the seeing disk, and defined in the MegaCam exposure time calculator (DIET3). This last magnitude is best suited to point-like objects, and that the 0.7 mag difference reflects that most of the faint objects are compact but extended ones. In the final images used in this paper, the measured average seeing is 0.75′′ in r′ and 0.67′′ in g′.
2.2. PSF correction and galaxy shape measurements
 |
Fig. 1 Galaxy number counts in the field of Abell 2163. The black dots correspond to r′ magnitudes. The diamonds are the r′ number counts in the CFHTLS deep field D1. In both fields, only galaxies with CLASS_STAR < 0.8 are kept. The excess at bright magnitudes in A2163 represents the cluster galaxies. The limiting magnitude is consistent with what is expected for compact objects measured at the 5σ level. |
Galaxies are first separated from stars with the help of the magnitude-peak surface-brightness diagram, which clearly identifies the stellar objects (Bardeau et al. 2005). Then for each galaxy, the local point spread function (PSF) is measured by averaging the shape parameters of the five closest stars. Intrinsic galaxy shape parameters are finally recovered using the Im2shape software developed by Bridle et al. (2001). This software performs an analytical deconvolution of the galaxy images, approximated by a single elliptical Gaussian, and returns the intrinsic shape parameters with their uncertainties, estimated by a Bayesian analysis of the image residuals. It has been successfully applied on a sample of clusters of galaxies by Bardeau et al. (2007), who developed a methodology for the shear analysis that we follow fairly closely. To test the validity of the analysis chain, we checked that the result of the deconvolution process applied to the stellar field itself shrinks the size of the deconvolved stars to less than 0.1′′, with a flat distribution of their orientation (Fig. 2). For the galaxies, the histogram extends to a larger size, up to several arcseconds. The whole pipeline was also applied on the simulated sheared images developed by the STEP consortium (Heymans et al. 2006). The results are presented in detail in Foex et al. (2012). In short, using simulated sheared images of faint galaxies, the average measured shear is compared to the true shear input in the simulations. This is done on a sequence of simulations with increasing shear value and several sets of realistic PSFs. The average difference bewteen the shears is fit with a linear function of the true shear. With our pipeline we systematically underestimate the true shear by 10%, but with no systematic offset in the measured shear. Consequently, we corrected the measures of the shear by applying a factor 1.1 to the value of average tangential ellipticity of the galaxies. This correction affects the total mass determination by ~15% upward.
2.3. Selection of background galaxies
 |
Fig. 2 Histogram of the average size |
An important step in building a photometric catalog of objects for weak lensing is to clean it from cluster and foreground contamination as much as possible. The cluster contamination is the major source of errors in the mass reconstruction for low redshift clusters: it is most prominent in the center so it distorts the shear profile and attenuates its central value, leading to an underestimation of the central mass density. In practice, we first selected the galaxies within a magnitude range large enough to have a high number of objects but limited in the bright end to remove a large fraction of cluster members. The lower limit of the magnitude cut was chosen as r′ = 22, a magnitude fainter than that of a 0.1 L⋆ galaxy at the cluster redshift. The upper limit was fixed to r′ = 25.5, i.e. 0.7 mag fainter than the completeness limit. This limit corresponds to the 5σ limiting magnitude of point sources estimated with DIET. We added a selection criterion based on the color index. This kind of selection by the galaxies color properties has already been tested in many studies (Kneib et al. 2003; Broadhurst et al. 2005; Limousin et al. 2007). It has proved to be quite powerful to remove galaxies with photometric properties compatible with cluster members. We built the color–magnitude diagram from the photometric catalog and identified the cluster red sequence (Fig. 3). The average color index of the bright ellipticals is g′ − r′ = 1.15 ± 0.05 mag, in good agreement with expected values from galaxy evolution codes (Bruzual & Charlot 2003). All galaxies located +0.15 and −0.20 from the red sequence line were stored in a catalog that we identify as the “cluster galaxy” catalog. Although it is not fully representative of the color diversity of cluster members, it includes early-type galaxies that dominate the density distribution of the galaxies. Moreover, a fraction of bluer ones is also included because the lower color limit is slightly widened. The galaxies outside this window and within the magnitude range [22.0−25.5] are stored for the weak lensing analysis. The resulting catalog contains 14 550 galaxies within a square area of side 37′ centered on the galaxy BCG1. This sample is expected to be substantially free of cluster contamination and is dominated by background sources. With this selection, the mean density of sources reduces from 18 to 12 galaxies/arcmin2 in the central area of the field, with a residual slight excess compared to the most external regions of the field (no more than 10%). Thus this corresponds to an efficient cleaning of the cluster contamination.
 |
Fig. 3 Color–magnitude plot of the galaxies in the field of Abell 2163, located within a 10′ radius from the central galaxy BCG1. The straight line corresponds to the cluster red sequence (RS), and the dashed lines define the window for selecting “cluster members”. Galaxies located less than 200′′ from the cluster center and within the selection window are plotted as large dots. |
The quantitative mass reconstruction based on the measure of the shear signal also requires an absolute scaling by the lensing factor ⟨ DLS/DOS ⟩ , which depends on the redshift distribution of lensed galaxies. In this ratio, DLS is the angular diameter distance between the lens and the source while DOS is between the source and the observer (Schneider et al. 1992). We do not have direct information on this redshift distribution in the present case, so we attempted to estimate it carefully. To do so, we built a photometric catalog considered as a reference catalog, using the T0004 release of the CFHTLS-Deep survey. Its main advantage is that the data have been collected with the same instrument and the same filter set. But they are much deeper than the present data (at least one magnitude deeper in g′ and r′) and multicolor observations in five filters allow the determination of accurate photometric redshifts. In practice we used the photometric redshifts that have been publicly available after the T0004 release. They were carefully calibrated and validated with spectroscopic samples (Coupon et al. 2009). We applied to this catalog the same selection criteria as we applied to the present catalog (magnitude cut 22 < r′ < 25.5 and color selection with g′ − r′ outside the red sequence window), and we only selected those objects having a photometric redshift 1σ error smaller than 0.15. We assumed that this sample is representative of the galaxy population on the line of sight of A2163. Looking at its redshift distribution, we measured a foreground contamination of 4%. Moreover, for all the galaxies with a photometric redshift zphot > zcluster + 0.15, we computed the average geometric factor for weak lensing (Fig. 4): 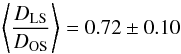 with an average redshift for the sources ⟨ zphot ⟩ = 1.1. Our weak lensing catalog includes objects fainter than the completeness limit (r′ ~ 24.8) so a significant fraction of the galaxies is probably missing in the range [25−25.5]. But we checked that it does not significantly affect the redshift distribution, and the average factor ⟨ DLS/DOS ⟩ is not changed by more than a few %.
with an average redshift for the sources ⟨ zphot ⟩ = 1.1. Our weak lensing catalog includes objects fainter than the completeness limit (r′ ~ 24.8) so a significant fraction of the galaxies is probably missing in the range [25−25.5]. But we checked that it does not significantly affect the redshift distribution, and the average factor ⟨ DLS/DOS ⟩ is not changed by more than a few %.
3. A 2D mass map
 |
Fig. 4 Photometric redshift distribution of the “reference catalog” built from the CFHTLS-D1 data. The photometric selection applied to the weak lensing catalog has been included (see text for details) as well as a photometric redshift cut with zzphot ≥ 0.35. |
 |
Fig. 5 MegaCam r′ image of the cluster Abell 2163, overlaid with the mass map reconstruction. The lowest contour corresponds to the 2σ level and the following ones are scaled with σ. The clump A2163-B is detected at the 3.5σ level. |
To map the 2D mass distribution, we use the LensEnt2 method, an entropy-regularized maximum-likelihood technique developed by Marshall et al. (2002). The mass map is built from the weak lensing catalog, using a smoothing scale characterized by the so-called intrinsic correlation function (ICF) of the model. A Gaussian ICF of 160′′ (~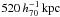 at the cluster redshift) is a good compromise between details and smoothness of the mass map, given the number density of sources in the background catalog. The final mass map is scaled in units of mass surface density (M⊙ pc-2) and can be used directly to estimate the masses of the different mass components. The code also generates an error map that allows the signal-to-noise ratio map to be built and the significance of the detected peaks to be quantified.
at the cluster redshift) is a good compromise between details and smoothness of the mass map, given the number density of sources in the background catalog. The final mass map is scaled in units of mass surface density (M⊙ pc-2) and can be used directly to estimate the masses of the different mass components. The code also generates an error map that allows the signal-to-noise ratio map to be built and the significance of the detected peaks to be quantified.
In the field of Abell 2163, the main peak is detected at more than 8σ and is centered close to the central galaxy BCG1. No strong lensing features or multiple images are identified around this galaxy, precluding any strong lensing model to explore the central mass distribution. However, a few single imaged arclets were reported around the BCG1 (Fort & Mellier 1994), confirming that a peak of dark matter coincides with the galaxy (Fig. 6).
The mass distribution is also significantly elongated towards the second brightest cluster member BCG2 (Fig. 5) with a second mass peak detected at ≃ 6σ. A detailed comparison between this mass map and the galaxy density obtained with the galaxies selected within the “red sequence” (Fig. 6 in Maurogordato et al. 2008) shows a striking concordance between the two distributions. Even the much less significant peaks in the mass distribution are coincident with other subclusters, namely the northern subcluster A2163-B, and other peripheral clumps C and D. The correlation between the dark matter distribution and the cluster galaxies density distribution clearly demonstrates that they both trace a noncollisional component in merging clusters. These maps are very different from the X-ray map (Govoni et al. 2004; Bourdin et al. 2011), which traces the gas distribution with the following characteristics: a single peaked distribution, with an E-W elongation and a peak center significantly off-center compared to BCG1. Maurogordato et al. (2008) propose in their paper a scenario in which we observe A2163 in a post-merger phase, less than 1 Gyr after the main collision. At this stage the gas morphology is expected to still be centrally concentrated, and elongated along the merger axis with a possible displacement of the gas relative to the main dark matter clump towards the secondary clump. This scenario remains fully compatible with the present observation of the dark matter distribution traced by weak lensing and is verified by numerical simulations of cluster mergers including both dark matter and intracluster gas physics (Roettiger et al. 1997). Moreover, it has been recently confirmed by the analysis of Bourdin et al. (2011), who show evidence of a cool gas “bullet” close to the cluster center that is clearly separated from its galaxy component and identified here as the second mass peak of the cluster.
As already mentioned, the northern secondary peak is also detected well in the mass map, at the 4σ level. It corresponds closely to the clump A2163-B identified by Maurogordato et al. (2008) as an infalling group with a separated velocity structure. However, there is some uncertainty in this mass distribution, which seems strongly elongated in this area. It is difficult to know whether this is related to an artifact in the mass reconstruction or to a realistic mass extension. The proximity of a bright star close to the mass clump (3′ north of the clump, see Fig. 5) reduces the available area where background galaxies can be used for shear measurements. Moreover, Dietrich et al. (2012) show that peak offsets in weak lensing maps can occur up to 1′ when the reconstruction is dominated by shape noise, i.e. the statistical noise due to the intrinsic ellipticity of the sources. This is indeed the case in this low S/N area of the mass map. The comparison with the galaxy density distribution (Fig. 5 in Maurogordato et al. 2008) also shows similarities in this elongated distribution, so regardless of the exact centering of the weak lensing mass clump, it is closely associated with the X-ray peak and the group A2163-B infalling on the main cluster. We therefore confirm that a significant amount of mass is associated with A2163-B. We propose to quantify better it in the next section.
4. Masses in Abell 2163
4.1. Weak lensing masses
 |
Fig. 6 Combined 3-color image of the center of the cluster Abell 2163 obtained with a combination of V, R and I images taken with FORS1 at the VLT in exceptional seeing conditions of 0.50′′. In this image, the identification of the most significant highly distorted features is reported. The central galaxy BCG1 is located at: α2000 = 16h15m49.0s; δ2000 = −06°08′42.8′′. |
 |
Fig. 7 Measured shear profile, averaged in sliding windows (circular annular rings of 110′′ each). Data with 100″ < r < 250″ or 375″ < r < 450″ have been removed from the fit because radial signal may be perturbed by the additional mass clumps A2 or B. The best fit with an SIS mass profile and an NFW one are plotted. The fit is limited to 700′′ around the cluster center because the signal is not significant enough at a greater distance. |
There are several ways to estimate the mass from the shear measurement of the background galaxies. The simplest one is to fit the shear profile directly by some analytical profiles, like the one expected from a singular isothermal sphere (SIS) or an NFW distribution (Navarro et al. 1997). These mass profiles correspond respectively to the density profiles 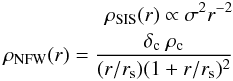 where ρc is the critical density at the cluster redshift. δc is related to the concentration parameter cvir by
where ρc is the critical density at the cluster redshift. δc is related to the concentration parameter cvir by 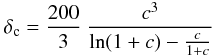 and the virial radius r200 is defined by r200 = cvirrs. The virial mass M200 is the mass enclosed inside the virial radius:
and the virial radius r200 is defined by r200 = cvirrs. The virial mass M200 is the mass enclosed inside the virial radius: 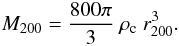 For all the fits, we assume spherical symmetry. However, we have shown in the previous section that subclustering is quite significant in the mass distribution, so we decided to remove from the fit the data points located inside two concentric circular annuli corresponding to A2163-A2 (100″ < r < 250″) and A2163-B (375″ < r < 450″). We also shifted the center of the lens 1.3′ west from BCG1 and fixed it between the two main mass peaks, to enclose the whole mass distribution better. In practice, this shift does not have a strong impact on the shear profile at large radius. The shear profile is shown in Fig. 7, with the result of the best fits by the two mass profiles. In both cases, we limited the extent of the fit to 700′′ because we consider that the signal is not reliable at a larger distance.
For all the fits, we assume spherical symmetry. However, we have shown in the previous section that subclustering is quite significant in the mass distribution, so we decided to remove from the fit the data points located inside two concentric circular annuli corresponding to A2163-A2 (100″ < r < 250″) and A2163-B (375″ < r < 450″). We also shifted the center of the lens 1.3′ west from BCG1 and fixed it between the two main mass peaks, to enclose the whole mass distribution better. In practice, this shift does not have a strong impact on the shear profile at large radius. The shear profile is shown in Fig. 7, with the result of the best fits by the two mass profiles. In both cases, we limited the extent of the fit to 700′′ because we consider that the signal is not reliable at a larger distance.
 |
Fig. 8 Distribution of the fitted parameters of the NFW profile in the M200 − cvir plane, scaled by their likelihood. The correlation between both parameters found from numerical simulations of dark matter halos is plotted as a dashed line. |
Instead of binning and averaging the shapes of the distorted galaxies in circular annuli, we also implemented a global approach. We used the McAdam software (Marshall et al. 2002; Marshall 2006), which is based on a Bayesian analysis of the shear distribution, approximated by a given parametric solution. The output of McAdam is a probability distribution of the fitted parameters, obtained using a maximum-likelihood estimator and an MCMC iterative minimization. McAdam works directly on the PSF-corrected faint galaxies catalog. It takes all the galaxies into account at their position with their shape parameters, without any ring averaging. Again the objects close to A2163-B are removed from the working sample, and the mass center is shifted 1.3′ west of BCG1, with the goal of estimating the global component of A2163-A.
Thanks to this global fit procedure, the shear field was fit with the SIS and NFW distributions, assuming spherical symmetry in both cases. A prior on the concentration parameter c is included (1.5 < c < 10), following the results of N-body simulations of cosmological structure formation at the galaxy cluster scale (Bullock et al. 2001; Hennawi et al. 2007). Fitting the shear profile with the SIS mass profile yields a velocity dispersion σshear or, equivalently, a value for the Einstein radius θE scaled by the ratio DLS/DOS averaged over all the sources. For the NFW mass profile, there is a well known degeneracy between M200, the mass enclosed within the virial radius r200, and the concentration parameter cvir (Fig. 8). But the average value of cvir resulting from our fit (cvir = 4.6 ± 1.6) is consistent with the values predicted by numerical simulations of dark matter halo properties (Bullock et al. 2001). The results of the different fits are presented in Table 1, and the integrated mass profiles are displayed in Fig. 9.
 |
Fig. 9 Integrated mass profiles obtained with the best-fit parameters of the SIS and NFW density profiles. The values of the projected mass directly measured on the 2D mass map and integrated up to the radii 1 Mpc and 2 Mpc (≃r200) are plotted for comparison. They correspond to projected masses inside cylinders so they overestimate the mass by ~ 25%. The total mass also includes the contribution of A2163-B with a mass of ~2 |
Best-fit values obtained from the fit of the SIS and NFW profiles.
The masses of the different mass clumps identified in the 2D mass map (Fig. 5) are also measured through direct integration of the mass distribution. No special shape is assumed and the mass is integrated in hand-defined contours or within given apertures. In a first attempt, we integrated the mass of the main clump in concentric annuli up to 300′′ (≃1 Mpc) and centered between the two mass peaks A1 and A2. This radius corresponds to the limit where A2163-B starts to be detected in the map, and it includes both mass peaks (A1 and A2). We find a projected mass of 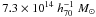 , which is the mass integrated within a cylinder of radius 1 Mpc. This projected mass exceeds the mass integrated inside a sphere of the same radius by approximately 25% for a standard NFW profile. In comparison, the projected mass deduced from the previously fitted values of the NFW profile and enclosed in a 1 Mpc radius is
, which is the mass integrated within a cylinder of radius 1 Mpc. This projected mass exceeds the mass integrated inside a sphere of the same radius by approximately 25% for a standard NFW profile. In comparison, the projected mass deduced from the previously fitted values of the NFW profile and enclosed in a 1 Mpc radius is 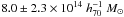 , consistent with the direct value. We also measured the total mass inside a cylinder defined by the “virial radius” r200 taken as 2.0 Mpc. This mass ~1
, consistent with the direct value. We also measured the total mass inside a cylinder defined by the “virial radius” r200 taken as 2.0 Mpc. This mass ~1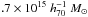 includes the contributions of the two mass clumps, A2163-A (A1 and A2) and A2163-B. It reduces to
includes the contributions of the two mass clumps, A2163-A (A1 and A2) and A2163-B. It reduces to 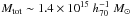 for the 3D mass inside a sphere of radius r200 centered between A1 and A2. This last value is considered as the total mass of the cluster within the virial radius (Table 1).
for the 3D mass inside a sphere of radius r200 centered between A1 and A2. This last value is considered as the total mass of the cluster within the virial radius (Table 1).
Going further in the mass measures from the 2D mass map, we also attempted to estimate separately the masses of each of the two mass subclumps that we have identified in A2163-A (A1 and A2). These are approximate measures because they are spatially limited and do not properly include the large-scale extension of the cluster. The measured masses are 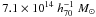 and
and 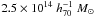 respectively, and their sum represents a major fraction of the total mass. Interestingly, we are able to measure a mass ratio ~3:1 between the 2 clumps, although this result must be taken with caution. This is not too different from the mass ratio 4:1 estimated by Bourdin et al. (2011) from interpretating of the merging scenario. Our ratio 3:1 also seems closer to the apparent ratio in the galaxy distribution and could be more representative of the total mass repartition.
respectively, and their sum represents a major fraction of the total mass. Interestingly, we are able to measure a mass ratio ~3:1 between the 2 clumps, although this result must be taken with caution. This is not too different from the mass ratio 4:1 estimated by Bourdin et al. (2011) from interpretating of the merging scenario. Our ratio 3:1 also seems closer to the apparent ratio in the galaxy distribution and could be more representative of the total mass repartition.
For the clump A2163-B, we integrated the mass within a hand-designed contour close to a circular annulus of 500 kpc, in order to avoid the contamination by the main cluster. This gives a mass of ~2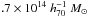 , so slightly higher than the mass estimated by Bourdin et al. (2011). However this is a rather uncertain measure, since the weak lensing signal and its distribution are not fully reliable.
, so slightly higher than the mass estimated by Bourdin et al. (2011). However this is a rather uncertain measure, since the weak lensing signal and its distribution are not fully reliable.
All these results are summarized in Table 1. It is interesting to note that the sum of the direct mass of the individual clumps (A1 + A2 + B) represents ~75% of the total mass. The remaining mass represents the large-scale extension of the distribution and possibly the additional clumps contribution. Moreover, although there are large uncertainties in the direct approach, the results are consistent with those derived from the fit with usual mass distributions.
4.2. Comparison with other lensing mass measurements
It has long been pointed that, regardless of the method used to determine the mass of A2163, the lensing estimates are much lower than the values expected for this very hot cluster. For example, Squires et al. (1997) fitted their data by an SIS profile with a velocity dispersion σSIS = 740 km s-1, and Cypriano et al. (2004) found σ = 1020 ± 150 km s-1. Both values are compatible with the present measure, even if they were obtained with fewer galaxies: 261 background galaxies for Cypriano et al. (2004) and 736 galaxies for Squires et al. (1997). We are more skeptical of the fitted values proposed by Radovich et al. (2008) derived from the same initial data as in the present work. With our selection process and the great care we took for the PSF correction, we ended with a higher galaxy density (12 instead of 8 galaxies/arcmin2), providing the largest sample of background sources used in the weak lensing mass determination in A2163 14550 galaxies within 0.38 square degree). Moreover, looking into details in the shear profile in Radovich et al. (2008), we note that their fit starts with data points located at a much larger radial distance than ours. From our study, removing data points below r < 200″ in the fit of the SIS profile increases the value of σ to 1100 km s-1, close to the value found by Radovich et al. (2008). The quality of the fit is very poor so we consider that the large-scale mass distribution in A2163 is too complex and shallow to be fitted by a single SIS profile. More recently, Okabe et al. (2011) have also performed a weak lensing analysis using Subaru imaging data. They confirm the bimodal structure of the mass in the central parts of the cluster, although the mass ratio between A1 and A2 is much higher (8:1 to 10:1), and the detection of the clump A2 is not as significant as in our own map. The 2D mass extractions from weak lensing reconstructions are still limited in their quantitative use and would strongly benefit from the higher source density of HST imaging (Becker & Kravtsov 2011). The total mass estimates obtained by Okabe et al. (2011) are also higher than the present ones, at least by 50% when they use a multicomponent analysis and by a factor 2 for a single mass profile reconstruction. But in the last case, their fit show high mass associated with a low value of the concentration parameter (c ~ 2.8). This combination of fitted parameters is probably representative of the mass-concentration degeneracy shown in Fig. 8.
In conclusion, there are still some discrepancies between different approaches used to infer quantitatively the total mass of this complex cluster, but the more recent results become more consistent with each other, provided similar criteria are taken into account to define a “total mass”. Absolute values for the mass still suffer from uncertainties in the large-scale structures’ contributions and are also highly dependent on the intrinsic noise owing to the limited number of background sources: Hoekstra et al. (2011) show that it can reach a 20% to 25% level for ground-based observations, whatever the methodology established to produce the results.
4.3. Galaxies, gas and dark matter distributions: consequences on the merger scenario
 |
Fig. 10 Multi-color image of the center of the cluster Abell 2163 with overlays of the dark matter distribution (green contours from the lensing map) and of the gas distribution (red contours for the Chandra X-rays image, courtesy Bourdin). The shift between the two mass clumps is 3′, while the distance between the X-ray maximum and the eastern clump A2163-A1 is 1.2′. The total size is 10′ × 10′. |
We focus in this section on a comparison between the masses derived from weak lensing, which trace the dark matter in the cluster, the masses derived from X-rays, and the spatial distribution of the galaxies. The X-ray temperature is very high (TX ~ 12 to 14 keV) regardless of the instruments used to measure it (Elbaz et al. 1995; Govoni et al. 2004). The temperature distribution shows strong variations in the central part of the cluster (Markevitch et al. 1996; Markevitch & Vikhlinin 2001) and a significant nonthermal component at high energy (Rephaeli et al. 2006). Extrapolating the mass under these conditions is a risky exercise and must be taken with caution because the cluster is obviously not in thermal equilibrium. To overcome this difficulty, Bourdin et al. (2011) have computed the YX parameter defined by Kravtsov et al. (2006). YX is considered as one of the best proxies for the total cluster mass. They used different calibrations of the scaling relation YX − M500 (Arnaud et al. 2010; Vikhlinin et al. 2009) to give a total mass estimate that does not rely explicitly on the hydrostatic equilibrium hypothesis. Regardless of the calibration used, they find a value M500 ≃ 1.8 to 2.0 × 1015 M⊙, i.e. this converts to a mass M200 within the virial radius 50% higher for a typical NFW mass profile, so this mass is two to three times higher than the lensing value. It is not clear why there is still such a significant discrepancy between the weak lensing mass estimates and the ones derived from X-ray proxies.
The spatial distributions of the three main components of the cluster are displayed in Fig. 10: the intracluster gas (Bourdin et al. 2011) and the dark matter (this paper) distributions are overlaid on the galaxy cluster image. As already observed in several other merging clusters, these distributions show evidence that the baryonic mass (the gas) does not follow the total mass (dominated by the dark matter). On the contrary, the galaxies distribution is spatially more coherent with the dark matter distribution A bi-dimensional Kolmogorov-Smirnov test (Fasano & Franceschini 1987) could be applied to get a more quantitative answer but his needs further adjustments in the galaxies selection, which are beyond the scope of this paper. Maurogordato et al. (2008) show morphological differences in the galaxy density distribution for different luminosity bins that require deeper insights to reconcile with the dark matter distribution. Nevertheless, in contrast to the intracluster gas, both galaxies and dark matter represent noncollisional mass components so we confirm that the total mass of the cluster is dominated by a collisionless form of dark matter. This is at least the fifth example of a cluster merger with such properties, after the initial work on the “Bullet cluster” 1E 0657–56 (Bradač et al. 2006) followed by similar trends observed in Abell 520 (Mahdavi et al. 2007) MACS J0025.4–1222 (Bradač et al. 2008) and Abell 2744 (Merten et al. 2011).
Abell 2163 is the cluster with the strongest discrepancy between X-rays and lensing masses. It is hard to reconcile both values, even when knowing the different limitations discussed above, and we still do not have a clear vision of the physical origin of the discrepancy. Because of the merging process, the gas distribution could be far from isothermal on large scales, and this might induce a strong uncertainty, which depends on the exact phase of the cluster merger (Poole et al. 2007). We suspect that all absolute mass determinations with X-ray proxies in a strong merger like A2163 must be taken with caution (Okabe et al. 2010), and the gas mass must be revisited in the framework of a colliding cluster. We also expect better lensing mass estimates using deep HST data. However, apart from a difference in the absolute mass scaling, the relative distributions of the three components are consistent with each other in a general scenario of a cluster major merger.
5. Conclusion
We have presented in this paper a detailed dark matter map of the cluster Abell 2163, using the weak lensing effect on background sources. We provide global masses, as well as the bi-dimensional mass distribution and mass estimates for each individual substructure identified in the map:
-
Thanks to a detailed mass reconstruction, we were able to sepa-rate the central mass clump into two components with a distribu-tion in agreement with the cluster galaxies density distribution(Maurogordato et al. 2008). Themass of the main clump is about
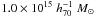 and is split in two clumps with amass ration ~3:1. It is consistent with previous weak lensing es-timates, but does not follow the expected correlations with theX-ray properties of the gas. Such a mass discrepancy is a strong ar-gument in favor of the merging scenario in the cluster. The secondmass clump A2163-A2 is shifted compared to the cold gas coredetected by Bourdin et al. (2011),and this shift can be due to the trailing of the gas compared to thenoncollisional dark matter during the crossing of the main clump.
and is split in two clumps with amass ration ~3:1. It is consistent with previous weak lensing es-timates, but does not follow the expected correlations with theX-ray properties of the gas. Such a mass discrepancy is a strong ar-gument in favor of the merging scenario in the cluster. The secondmass clump A2163-A2 is shifted compared to the cold gas coredetected by Bourdin et al. (2011),and this shift can be due to the trailing of the gas compared to thenoncollisional dark matter during the crossing of the main clump. -
We detect at more than 4σ the dark matter associated with the clump 2163-B, identified spectroscopically by Maurogordato et al. (2008). This clump has a mass value (≃2
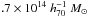 ) compatible with a small cluster. This is also coherent with the X-ray temperature on the order of 4 keV identified by Bourdin et al. (2011). As already suggested by Maurogordato et al. (2008), this clump has not yet undergone its main interaction with the central cluster and is still infalling towards the center.
) compatible with a small cluster. This is also coherent with the X-ray temperature on the order of 4 keV identified by Bourdin et al. (2011). As already suggested by Maurogordato et al. (2008), this clump has not yet undergone its main interaction with the central cluster and is still infalling towards the center. -
Concerning the total mass of the whole complex, our mass estimates do not exceed
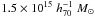 . This value is well below the expected mass given by the correlations with the X-ray properties of the cluster. We confirm that the scaling laws that use X-ray proxies to infer the mass of clusters must be taken with caution for structures that are far from the hydrostatic equilibrium.
. This value is well below the expected mass given by the correlations with the X-ray properties of the cluster. We confirm that the scaling laws that use X-ray proxies to infer the mass of clusters must be taken with caution for structures that are far from the hydrostatic equilibrium.
The results of our study are a new step forward in the process of building a coherent scenario for the multiple mergers in the cluster Abell 2163. This thorough analysis of the weak lensing mass reconstruction was possible thanks to the combination of both the spatial extent and the depth of the data. It confirms the bimodal structure of the matter distribution in the cluster center and the physical separation between the baryonic mass and the noncollisional mass components. Our results also show that there exists many similarities between the gas and dark matter distributions in Abell 2163 and in the “Bullet cluster” 1E0657–56. Both cases display a gas core spatially separated from its dark matter component, even if the mass ratio between the clumps, the 3D configuration of the merger and the age of the merger differ. But they offer different merging configurations that can feed the comparisons with numerical simulations (Poole et al. 2007). Moreover, Abell 2163 presents an additional complexity with the identification of several other mass clumps involved in the merger but at an earlier stage or in the premerging phase. In conclusion, Abell 2163 has long been considered as an exceptional cluster because of its high gas temperature. It is now more interesting to explore the richness and the complexity of the physical processes occurring within it.
Acknowledgments
I wish to thank Phil Marshall for his help in implementing the code Lensent2 and Monique Arnaud, Marceau Limousin, Sophie Maurogordato, Roser Pelló, Etienne Pointecouteau, and Gabriel Pratt for fruitful discussions. Hervé Bourdin kindly shared his X-ray data with us, and we benefited from his extensive knowledge. I also thank an anonymous referee for his careful reading of the paper and his pertinent questions. Finally I thank the Programme National de Cosmologie of the CNRS for financial support.
References
- Arnaud, M., Hughes, J. P., Forman, W., et al. 1992, ApJ, 390, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardeau, S., Kneib, J.-P., Czoske, O., et al. 2005, A&A, 434, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardeau, S., Soucail, G., Kneib, J.-P., et al. 2007, A&A, 470, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, M. R., & Kravtsov, A. V. 2011, ApJ, 740, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2006, in Astronomical Data Analysis Software and Systems XV, ed. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 112 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourdin, H., Arnaud, M., Mazzotta, P., et al. 2011, A&A, 527, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradač, M., Clowe, D., Gonzalez, A. H., et al. 2006, ApJ, 652, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Bradač, M., Allen, S. W., Treu, T., et al. 2008, ApJ, 687, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Bridle, S., Gull, S., Bardeau, S., & Kneib, J.-P. 2001, in Proceedings of the Yale Cosmology Workshop: The Shapes of Galaxies and their Dark Halos, ed. N. P. (World Scientific) [Google Scholar]
- Broadhurst, T., Takada, M., Umetsu, K., et al. 2005, ApJ, 619, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Carlberg, R. G., Yee, H. K. C., Ellingson, E., et al. 1996, ApJ, 462, 32 [Google Scholar]
- Clowe, D., Bradač, M., Gonzalez, A. H., et al. 2006, ApJ, 648, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Ilbert, O., Kilbinger, M., et al. 2009, A&A, 500, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cypriano, E. S., Sodré, L. J., Kneib, J.-P., & Campusano, L. E. 2004, ApJ, 613, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, J. P., Böhnert, A., Lombardi, M., Hilbert, S., & Hartlap, J. 2012, MNRAS, 419, 3547 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Arnaud, M., & Boehringer, H. 1995, A&A, 293, 337 [NASA ADS] [Google Scholar]
- Fasano, G., & Franceschini, A. 1987, MNRAS, 225, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Fusco-Femiano, R., Giovannini, G., & Govoni, F. 2001, A&A, 373, 106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feretti, L., Orrù, E., Brunetti, G., et al. 2004, A&A, 423, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foex, G., Soucail, G., Pointecouteau, E., et al. 2012, A&A, submitted [Google Scholar]
- Fort, B., & Mellier, Y. 1994, A&ARv, 5, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Frenk, C. S., White, S. D. M., Efstathiou, G., & Davis, M. 1990, ApJ, 351, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Govoni, F., Markevitch, M., Vikhlinin, A., et al. 2004, ApJ, 605, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Hennawi, J. F., Dalal, N., Bode, P., & Ostriker, J. P. 2007, ApJ, 654, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Van Waerbeke, L., Bacon, D., et al. 2006, MNRAS, 368, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Hartlap, J., Hilbert, S., & van Uitert, E. 2011, MNRAS, 412, 2095 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J.-P., Hudelot, P., Ellis, R. S., et al. 2003, ApJ, 598, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Richard, J., Jullo, E., et al. 2007, ApJ, 668, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Magnier, E. A., & Cuillandre, J.-C. 2004, PASP, 116, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., Balam, D. D., & Capak, P. L. 2007, ApJ, 668, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M. 1996, ApJ, 465, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., & Vikhlinin, A. 2001, ApJ, 563, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., Yamashita, K., Furuzawa, A., & Tawara, Y. 1994, ApJ, 436, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., Mushotzky, R., Inoue, H., et al. 1996, ApJ, 456, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., Gonzalez, A. H., David, L., et al. 2002, ApJ, 567, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, P. 2006, MNRAS, 372, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, P. J., Hobson, M. P., Gull, S. F., & Bridle, S. L. 2002, MNRAS, 335, 1037 [Google Scholar]
- Maurogordato, S., Cappi, A., Ferrari, C., et al. 2008, A&A, 481, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merten, J., Coe, D., Dupke, R., et al. 2011, MNRAS, 417, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., Zhang, Y., Finoguenov, A., et al. 2010, ApJ, 721, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., Bourdin, H., Mazzotta, P., & Maurogordato, S. 2011, ApJ, 741, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Poole, G. B., Babul, A., McCarthy, I. G., et al. 2007, MNRAS, 380, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Radovich, M., Puddu, E., Romano, A., Grado, A., & Getman, F. 2008, A&A, 487, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., Gruber, D., & Arieli, Y. 2006, ApJ, 649, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Roettiger, K., Loken, C., & Burns, J. O. 1997, ApJS, 109, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (XIV, 560) (Berlin Heidelberg New York: Springer-Verlag), Also Astronomy and Astrophysics Library [Google Scholar]
- Squires, G., Neumann, D. M., Kaiser, N., et al. 1997, ApJ, 482, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Galaxy number counts in the field of Abell 2163. The black dots correspond to r′ magnitudes. The diamonds are the r′ number counts in the CFHTLS deep field D1. In both fields, only galaxies with CLASS_STAR < 0.8 are kept. The excess at bright magnitudes in A2163 represents the cluster galaxies. The limiting magnitude is consistent with what is expected for compact objects measured at the 5σ level. |
| In the text | |
 |
Fig. 2 Histogram of the average size |
| In the text | |
 |
Fig. 3 Color–magnitude plot of the galaxies in the field of Abell 2163, located within a 10′ radius from the central galaxy BCG1. The straight line corresponds to the cluster red sequence (RS), and the dashed lines define the window for selecting “cluster members”. Galaxies located less than 200′′ from the cluster center and within the selection window are plotted as large dots. |
| In the text | |
 |
Fig. 4 Photometric redshift distribution of the “reference catalog” built from the CFHTLS-D1 data. The photometric selection applied to the weak lensing catalog has been included (see text for details) as well as a photometric redshift cut with zzphot ≥ 0.35. |
| In the text | |
 |
Fig. 5 MegaCam r′ image of the cluster Abell 2163, overlaid with the mass map reconstruction. The lowest contour corresponds to the 2σ level and the following ones are scaled with σ. The clump A2163-B is detected at the 3.5σ level. |
| In the text | |
 |
Fig. 6 Combined 3-color image of the center of the cluster Abell 2163 obtained with a combination of V, R and I images taken with FORS1 at the VLT in exceptional seeing conditions of 0.50′′. In this image, the identification of the most significant highly distorted features is reported. The central galaxy BCG1 is located at: α2000 = 16h15m49.0s; δ2000 = −06°08′42.8′′. |
| In the text | |
 |
Fig. 7 Measured shear profile, averaged in sliding windows (circular annular rings of 110′′ each). Data with 100″ < r < 250″ or 375″ < r < 450″ have been removed from the fit because radial signal may be perturbed by the additional mass clumps A2 or B. The best fit with an SIS mass profile and an NFW one are plotted. The fit is limited to 700′′ around the cluster center because the signal is not significant enough at a greater distance. |
| In the text | |
 |
Fig. 8 Distribution of the fitted parameters of the NFW profile in the M200 − cvir plane, scaled by their likelihood. The correlation between both parameters found from numerical simulations of dark matter halos is plotted as a dashed line. |
| In the text | |
 |
Fig. 9 Integrated mass profiles obtained with the best-fit parameters of the SIS and NFW density profiles. The values of the projected mass directly measured on the 2D mass map and integrated up to the radii 1 Mpc and 2 Mpc (≃r200) are plotted for comparison. They correspond to projected masses inside cylinders so they overestimate the mass by ~ 25%. The total mass also includes the contribution of A2163-B with a mass of ~2 |
| In the text | |
 |
Fig. 10 Multi-color image of the center of the cluster Abell 2163 with overlays of the dark matter distribution (green contours from the lensing map) and of the gas distribution (red contours for the Chandra X-rays image, courtesy Bourdin). The shift between the two mass clumps is 3′, while the distance between the X-ray maximum and the eastern clump A2163-A1 is 1.2′. The total size is 10′ × 10′. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.