| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201117687 | |
| Published online | 28 March 2012 | |
The accretion of Uranus and Neptune by collisions among planetary embryos in the vicinity of Jupiter and Saturn⋆
1 Astronomical Institute, Slovak Academy of Science, 05960 Tatranská Lomnica, Slovakia
e-mail: mjakubik@ta3.sk; ne@ta3.sk
2 Département Cassiopée, University of Nice – Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, Nice, France
3 Institute for Astronomy and Astrophysics, Academia Sinica, PO Box 23-141, Taipei 106, Taiwan
e-mail: morby@oca.eu; brasser_astro@yahoo.com
Received: 12 July 2011
Accepted: 9 February 2012
Context. Modeling the formation of the ice giants Uranus and Neptune has been a challenging problem in planetary science for a long time. Owing to gas-drag, collisional damping, and resonant shepherding, the planetary embryos repel the planetesimals from their reach and that is why they stop growing. This problem persists independently of whether the accretion took place at the current locations of the ice giants or closer to the Sun.
Aims. Instead of trying to push the runaway/oligarchic growth of planetary embryos up to 10−15 Earth masses, we envision the possibility that the planetesimal disk could generate a system of planetary embryos of only 1−3 Earth masses. Then we investigate whether these embryos could have collided with each other and grown enough to reach the masses of current Uranus and Neptune.
Methods. We performed several series of numerical simulations. The dynamics of a considered set of embryos is influenced by the presence of Jupiter and Saturn, assumed to be fully formed on non-migrating orbits in 2:3 resonance, and also by gravitational interactions with the gas disk.
Results. Our results point to two major problems. First, there is typically a large difference in mass between the first- and the second-most massive core formed and retained beyond Saturn. Second, in many simulations the final planetary system has more than two objects beyond Saturn. The growth of a major planet from a system of embryos requires strong damping of eccentricities and inclinations from the gas disk. But strong damping also enables embryos and cores to find a stable resonant configuration, so that systems with more than two surviving objects are found. In addition to these problems, it is necessary to assume that the surface density of the gas was several times higher than that of the minimum-mass solar nebula to achieve substantial accretion among embryos. However, this contradicts the common idea that Uranus and Neptune formed in a gas-starving disk, which is suggested by the relatively small amount of hydrogen and helium contained in the atmospheres of these planets.
Conclusions. Only one of our simulations serendipitously reproduced the structure of the outer solar system successfully. However, we point out that models of formation of Uranus and Neptune have non-trivial problems, which cannot be ignored and have to be addressed in future work.
Key words: planetary systems / planets and satellites: formation / planets and satellites: individual: Uranus / planets and satellites: individual: Neptune / protoplanetary disks
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The accretion of Uranus and Neptune has been a challenging problem in planetary science for a long time. Safronov (1969) was the first to point out that the accretion of these two planets from a planetesimal disk at their current locations would have taken an implausibly long time. This problem was confirmed by Levison & Stewart (2001) using modern numerical simulations. Goldreich et al. (2004a,b) claimed that the in-situ formation of Uranus and Neptune could have been possible in a planetesimal disk that was strongly dominated by collisional damping. This claim, however, is not correct because, as showed by Levison & Morbidelli (2007), planetary cores in a disk with strong collisional damping simply open up gaps in the planetesimal distribution around their own orbits and stop accreting.
There is now a consolidated view that the giant planets were closer to each other in the past (probably all within 12 AU from the Sun) and that they moved to their current orbits after their formation (Fernández & Ip 1984; Malhotra 1993, 1995; Hahn & Malhotra 1999; Thommes et al. 1999; Tsiganis et al. 2005; Morbidelli et al. 2007; Batygin & Brown 2010). Thus, it is no longer necessary to construct a model capable of explaining the formation of Uranus and Neptune at their current, remote locations.
Forming Uranus and Neptune within 12−15 AU from the Sun is in principle easier than forming them at 20−30 AU because the density of solid material was probably higher and the dynamical timescale (i.e. the orbital period) was shorter. However, forming 10 − 15 Earth mass (M⊕) cores from a planetesimal disk turns out to be difficult at any location. Indeed, Levison et al. (2010) showed that when planetary embryos achieve a mass of 1−3 M⊕, they tend to scatter the remaining planetesimals rather than accreting them. With the help of gas-drag, collisional damping and resonant shepherding, the embryos push the planetesimals out of their reach and thus they stop growing.
In this paper we explore another possible venue for the formation of Uranus and Neptune. Instead of trying to push the runaway/oligarchic growth of planetary embryos up to 10−15 M⊕, we envision the possibility that the planetesimal disk could generate a system of planetary embryos of only 1−3 M⊕; then we investigate with numerical simulations whether these embryos could have collided with each other because they converged at specific orbital radii where their radial migration in the gas-disk was stopped by the presence of Jupiter and Saturn. This growth mode by giant collisions would explain the large obliquities of Uranus and Neptune in a natural way.
More specifically, our scenario is based on the consideration that Jupiter and Saturn presumably got caught in their 2:3 mean motion resonance (MMR), which prevented them from migrating further toward the Sun. Instead, after being trapped in the 2:3 MMR, Jupiter and Saturn either migrated outward or stayed roughly at steady locations (Masset & Snellgrove 2001; Morbidelli & Crida 2007; Morbidelli et al. 2007; Pierens & Nelson 2008). To date, this is the only explanation we have for why our giant planets did not migrate permanently into the inner solar system.
The presence of Jupiter and Saturn on orbits not migrating toward the Sun would have acted as an obstacle against the inward type-I migration (Goldreich & Tremaine 1980) of the planetary embryos from the outer solar system. More precisely, any planetary embryo migrating toward the Sun would have been trapped sooner or later and halted in a MMR with Saturn. Then, the accumulation of embryos in these resonances could in principle have boosted their mutual accretion. This paper aims at investigating this possibility with numerical simulations.
We are aware of the new result according to which the real migration of planetary embryos is very different to the classical type-I migration envisioned in ideal, isothermal disks (Paardekooper & Mellema 2006; Baruteau & Masset 2008; Paardekooper & Papaloizou 2008; Kley & Crida 2008; Paardekooper et al. 2011). In particular, in disks with realistic cooling times, migration is expected to be outward in the inner part of the disk and inward in its outer part (Lyra et al. 2009). This generates a region in between the inner and the outer parts of the disk where type-I migration is basically inhibited. Planetary embryos are expected to be in/close to this no-migration zone, which seems to invalidate our assumption that embryos migrated toward the giant planets until they were caught in resonances.
However, Walsh et al. (2011) argued strongly because of the terrestrial planet system and the asteroid belt that Jupiter and Saturn migrated outward over a range of several AUs. What is important for our purposes is the relative motion of Jupiter/Saturn and the embryos. It does not really matter whether Jupiter/Saturn are on fixed orbits and the embryos tend to migrate toward the Sun, or the embryos do not migrate while Jupiter/Saturn move outward. Indeed, in both cases the embryos approach the giant planets until they are captured in MMRs, which may act like a privileged site for embryo clustering and mutual accretion. Therefore we assumed, in our simulations for simplicity that Jupiter/Saturn are on non-migrating resonant orbits while the embryos are affected by inward migration, with different migration speeds from one simulation to another. This migration speed can be interpreted as an actual inward migration speed of the embryos (most likely compared relative to the classical type-I migration speed in iso-thermal disks), or the outward migration speed of Jupiter/Saturn, or a combination of the two.
Two caveats related to our work need to be stated up-front. First, our study assumes that Jupiter and Saturn are fully formed, while the accretion of these planets is by itself an unsolved problem that we do not address here. This may sound strange. However, there is a consensus that Uranus and Neptune formed after Jupiter and Saturn, because they did not accrete nearly as much gas. This leads to two considerations: (a) Jupiter and Saturn existed already when Uranus and Neptune formed, so that the former should/may have influenced the accretion process of the latter and (b) whatever mechanism allowed the formation of Jupiter (obviously not the presence of a pre-existing giant planet!), it did not work for Uranus and Neptune, otherwise they would have formed nearly at the same time as Jupiter.
The second caveat is that because our model is based on migration of planets and embryos in a gas-disk, the study should be performed with hydro-dynamical simulations. These simulations, though, are too slow to treat the evolution of tens of bodies for a few millions of years, which is what we need to perform in this study. The paper by Morbidelli et al. (2008) is, to date, the only attempt to study the accretion of the cores of giant planets using hydro-dynamical simulations, and it shows all the limitations of this technique. Therefore, we use N-body simulations for this study, with artificial forces exerted onto the embryos to mimic the migration and tidal damping forces exerted from the disk. This approach also has its own limitations because it does not account for indirect mutual perturbations that the embryos may exert on each other through the modifications that they induce in the density distribution of the gas-disk.
The structure of this paper is as follows. In Sect. 2, we explain our simulation methods. In Sect. 3 we illustrate some basic ingredients of the dynamics of embryos and giant planets. In particular, we discuss the concept of resonance trapping with Saturn, resonant trapping in mutual embryo-embryo resonances, resonance loading, onset of a global dynamical instability and possible mutual accretion. Just for illustrative purposes, we do this by introducing one embryo at the time at a large distance from Saturn, even though this is NOT how we think the real evolution proceeded. Then, in Sect. 4 we move to more “realistic” simulations, where multiple 3 M⊕ embryos are introduced at the beginning of the simulation over the 10−35 AU range. We test the dependence of the results on the total amount of gas in the disk, the inward migration rate and the total number of embryos. Having realized that several embryos are lost through close encounters with Jupiter and Saturn, which either eject them to distant orbits or inject them into the inner solar system, we show in Sect. 5 how the coorbital corotation torque exerted at the edge of Saturn’s gap can act like a planet trap (Masset et al. 2006; Pierens & Nelson 2008) and prevent large mass losses. In Sect. 6 we discuss how the results depend on the initial mass of the embryos. In Sect. 7 we address the role of turbulence in the disk and Sect. 8 collects the conclusions and considerations that we derive from this study.
We anticipate that our study is not “successful” in the sense that our simulations do not typically lead to the formation of only two planets with masses close to those of Uranus and Neptune. However, it shows interesting dynamical mechanisms and intriguing consequences that will need to be addressed in detail in future studies, most likely using hydro-dynamical simulations.
Note on nomenclature: hereafter we call “embryos” the objects of 1–3 M⊕ that our simulations start with and “core” any object that is formed during the simulation by merging at least two embryos.
2. Simulation methods
For our simulations, we used the integration software Symba developed in Duncan et al. (1998), which we modified to take into account the planet-gas gravitational interactions.
The gas density profile that we considered was taken from the hydro-dynamical simulations of Morbidelli & Crida (2007), who accounted for Jupiter and Saturn in their mutual 2:3 resonance; it is shown in Fig. 1 (red curve). Notice the gap around the position of Jupiter at 5.2 AU and the “plateau” at the right-hand side of the gap, which is due to the presence of Saturn at ~7 AU. The figure also compares this density profile to those of three classical minimal mass solar nebulæ (MMSN). In the 10−35 AU range, the surface densities are comparable within an order of magnitude. In particular, our surface density falls in between the estimates from Weidenschilling (1977) and Hayashi (1981). Instead, inside of the orbit of Jupiter, the radial profile of our surface density is flat and significantly lower than those expected from the authors above. This is because the presence of Jupiter opens up a partial cavity inside its orbit by limiting the flow of gas from the outer part of the disk (see Crida et al. 2007). In Morbidelli & Crida (2007) the considered disk was narrow, with an outer boundary at 35 AU. Here, we extend its surface density profile beyond 35 AU assuming a r − 3/2 radial decay.
 |
Fig. 1 Gas surface densities according to different works. The red curve shows the result of the hydro-dynamical simulation by Morbidelli & Crida (2007), with Jupiter and Saturn in 2:3 resonance. This is the profile that we assumed in this paper, possibly scaled by a factor fd. The blue line is from Weidenschilling (1977) and is proportional to 1/r. The green line is from Hayashi (1981) and is proportional to 1/r3/2. The magenta curve reports the amount of gas required in the Pollack et al. (1996) model of giant planet accretion. |
The concept of MMSN was historically introduced assuming that giant planet formation was 100% efficient. In reality, there is growing evidence that much more mass is needed to grow the giant planets, even in the most optimistic scenarios (Thommes et al. 2003). Therefore, in our simulations we multiplied the assumed initial surface density profile by a factor fd, which will be specified from simulation to simulation. All simulations were run for 5 My and for simplicity we assumed that the gas density is constant over this simulated timescale. The role of the 5 My parameter will be discussed in Sect. 4. In our code, the surface density profile of the gas is used to compute the migration and damping forces acting on the embryos, namely the so-called “type-I torques”. The analytic formulae that we used are those reported in Cresswell & Nelson (2008); they depend on the local surface density of the disk and on the embryos’ eccentricities and inclinations. Because inward migration can be significantly slower in realistic disks with radiative transfer than in ideal, isothermal disks, we implemented the possibility of multiplying the forces acting on the embryo’s semi-major axes by a factor 1/fI, which will be specified below for each simulation.
However, in Sect. 5, we use a more sophisticated formula for the radial migration torque Γ, which accounts for the radial gradient of the surface density (Paardekooper et al. 2010; Lyra et al. 2010):
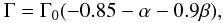 (1)where Γ0 = (M/h)2Σr4Ω2, M is the mass of the embryo relative to the Sun, h is the scale-height of the disk normalized by the semi-major axis, Σ stands for the local surface density, and Ω is the orbital frequency. In (1)
(1)where Γ0 = (M/h)2Σr4Ω2, M is the mass of the embryo relative to the Sun, h is the scale-height of the disk normalized by the semi-major axis, Σ stands for the local surface density, and Ω is the orbital frequency. In (1) 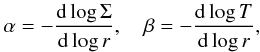 (2)where T is the local temperature of gas.
(2)where T is the local temperature of gas.
The radial migration torque in Cresswell & Nelson (2008), at zeroth order in eccentricity and inclination, corresponds to (1) for β = 1 and α = 0, i.e. it is valid for a flat disk with constant scale height. The inclusion of the α-dependence in (1) stops inward migration where α = −1.75, that is where there is a steep positive radial gradient of the surface density. With the surface density profile shown in Fig. 1, this happens at ~10 AU. This location acts like a planet trap (Masset et al. 2006): an embryo migrating inward from the outer disk, if not trapped in a MMR with Saturn, is ultimately trapped at this location.
In the simulations that mimic turbulent disks (see Sect. 7), we simply applied stochastic torques to the embryos following the recipe extensively described in Ogihara et al. (2007, see Sect. 2.2 of that paper). The only difference is that the total number of Fourier modes in the torque spectrum is not m = 50, as in Ogihara et al. (2007), but is m = 50/log 4 × log (rout/rin) which, given rout = 24 AU and rin = 8 AU in our case, results in m = 40. This functional form for m(rout,rin) is necessary to render the results independent of the simulated size of the disk. Indeed, if one were to use a fixed number of Fourier modes, the effect of turbulence would be stronger in a narrow disk than in an extended disk. With our recipe for the number of modes, the stochastic migration of planetesimals observed in the full MRI simulations of Nelson & Gressel (2010) is reproduced with a “turbulent strength” parameter γ (see Eq. (6) in Ogihara et al. 2007) equal to 3 × 10-3.
A final technical note concerns the treatment that we reserve for Jupiter and Saturn. The migration of these two planets is a two-planet type-II-like process (Masset & Snellgrove 2001; Morbidelli & Crida 2007), and therefore cannot be described with the type-I torques reported above. As stated in the introduction, we assumed that the disk parameters are such that Jupiter and Saturn do not migrate (see Morbidelli & Crida 2007, for the identification of the required conditions). Consequently, one could think that we should apply no fictitious forces to these planets. However, if we did so, the system would become unstable. Indeed, as soon as an embryo is trapped in a resonance with Saturn, it would push Saturn inward and in turn also Jupiter (because Jupiter and Saturn are locked in resonance). This would also increase the orbital eccentricities of the two major planets. This behavior is obviously artificial, because we do not consider the forces exerted by the gas onto Jupiter and Saturn, which would stabilize these planets against the perturbations from the much smaller embryo. To circumvent this problem, we applied damping forces to Jupiter and Saturn so that (de/dt)/e = (di/dt)/i = 10-5/y, together with a torque that tends to restore the initial semi-major axes of their orbits in 105 years. Tests show that, with this recipe, Jupiter and Saturn are stable under the effect of embryos piling up in resonances and pushing inward. Moreover, the eccentricities of Jupiter and Saturn attain finite but non-zero limit values. However, strong scattering events can remove Jupiter and Saturn from their 2:3 resonance (see Sect. 4).
3. Basic dynamical mechanisms in the migration of embryos and giant planets
To illustrate the interplay between migration, resonance trapping and mutual scattering, in this section we report on simple experiments, we introduced one embryo at the time into the system. The time-span between the introduction of two successive embryos is not fixed: we let the system relax to a stable configuration before introducing a new embryo into the simulation. Each embryo has initially 3 M ⊕ .
 |
Fig. 2 Simulations of the dynamical evolution of embryos in the disk outside of Saturn’s orbit. Top: a case with parameters fd = fI = 1. Bottom: a case with fd = fI = 2. The green and blue curves at ~ 5.4 and ~ 7.3 AU show the semi-major axis evolution of Jupiter and Saturn, respectively. The other curves of various colors illustrate the evolution of the semi-major axes of the embryos. See text for a description of the dynamical evolution and the accretion events. |
We started by assuming the nominal values of the parameters (fd = 1, fI = 1). The top panel of Fig. 2 shows the evolution. The first embryo is introduced at the beginning of the simulation at 15 AU. It migrates inward (cyan dotted curve) until it is trapped in resonance with Saturn (precisely the 1:2 MMR) at t ~ 150 000 y. Consequently, it stops migrating. Resonance trapping converts the force acting on the semi-major axis into an eccentricity excitation. Therefore, the eccentricity of the embryo grows to about 0.07 but then it stops (not shown in the figure). This happens because a balance is reached between the eccentricity excitation from the resonance and the direct damping from the disk. Thus, the three-planet system (Jupiter, Saturn and the embryo) reaches a stable, invariant configuration at about t = 200 000 y.
At t = 750 000 y we introduced a second embryo into the system, initially at 18 AU. This embryo also migrates inward (magenta dotted line). Because of the relatively high eccentricity of the cyan embryo, its outer MMRs are not stable enough to capture the incoming magenta embryo. Therefore the latter comes down to ~12 AU and starts to have close encounters with the cyan embryo. The system becomes unstable. The eccentricities and inclinations of the embryos become very high, up to 0.6 − 0.7 and 10 degrees, respectively. The cyan embryo has even close encounters with Saturn and Jupiter. Clearly, this phase of violent scattering is not very favorable for embryo-embryo accretion.
We then present another simulation, for which we increased the gas surface density by a factor of two (fd = 2), which has the effect of increasing both the eccentricity/inclination damping and the radial migration by the same factor. However, we also assumed fI = 2, so that the migration rate of the semi-major axis is the same as in the previous simulation. The result of this new simulation is illustrated in the bottom panel of Fig. 2. Evidently, the magenta embryo is now trapped in resonance with the cyan embryo (precisely, the 4:5 MMR). Consequently, it also stops migrating and a stable four-planet configuration is achieved. Given that the only difference with respect to the previous simulation is the eccentricity damping, this illustrates the crucial role of this parameter on the dynamics.
A third embryo (yellow) is introduced at t = 1.6 My. It also migrates until it stops, trapped in the 6:7 MMR with the cyan embryo. The fully resonant system is, again, stable.
A fourth embryo is then released at t = 2.3 My (orange). Now there are too many embryos to form a stable, resonant system. Accordingly, when the orange embryo comes in, resonance locking is broken. All embryos move inward and start to have encounters with each other. Because of the stronger damping from the disk, the eccentricities and inclinations do not become as high as in the previous experiment. Thus, the conditions are more favorable for mutual accretion. Indeed, at t = 2.64 My the yellow and cyan embryos accrete each other. Arbitrarily, we assumed that it is the yellow embryo that survives, with twice its original mass and the cyan embryo disappears. The system of embryos, however, is still too excited to be stable. It stabilizes only after the ejection of the magenta embryo at t = 2.9 My. The system consists now of two embryos, the yellow and the orange one, in their 6:7 MMR. The yellow embryo is in the 2:3 MMR with Saturn.
We proceeded with the experiment by introducing a new embryo (green) which, after a short phase of instability, ends in the 4:5 MMR with the orange embryo and forces the orange and yellow embryos to go to shorter heliocentric distances: the yellow embryo ends in the 5:7 MMR with Saturn. Given the high-order resonances involved, the system is close to instability.
Accordingly, the system becomes unstable when the next embryo (black) is introduced and moves inward. The new crisis is solved with the yellow embryo accreting the black one. At the end of the instability phase, the yellow embryo is back in the 2:3 MMR with Saturn and the three surviving embryos are in resonance with each other.
The final embryo is introduced at 5.5 My (black again). The new embryo generates a new phase of instability during which it first collides with the orange embryo, then the orange embryo also accretes the green one. Therefore, this simulation ends with two embryos, each with a mass of 9 M⊕, in a stable resonant configuration: the yellow embryo is in the 2:3 MMR with Saturn and in the 6:5 MMR with the orange one.
These experiments, as well as other similar ones that we do not present for brevity (with fd = fI = 3,5 and fd = 1, fI = 3), clearly show the importance of mutual resonances in the evolution of the embryos. For individual masses equal to 3 M⊕, embryos are easily trapped in these resonances if fI ≥ 2. If the embryos are smaller, fI needs to be larger, because the mutual resonant torques are weaker. A system of several embryos, all in resonance with each other, can be stable; if this is the case, the accretion is not possible. However, when the embryos are too numerous, resonances cannot continue to hold the embryos on orbits well separated from each other. The system eventually has to become unstable; collisions or ejections then occur. Finally, when the number of embryos is reduced, a new, stable resonant configuration is achieved again. This sequence of events (resonance loading, global dynamical instability, accretion or ejection) can repeat itself cyclically, as long as mass is added to the system. Eccentricity and inclination damping from the disk also play a pivotal role in the evolution of the system. If damping is weak, eccentricities and inclinations can become high and scattering dominates over accretion; eventually, the embryos encounter Jupiter or Saturn and are ejected from the system. If damping is strong, the most likely end-state of a dynamical instability is the mutual accretion of embryos, which leads to the growth of massive planets.
Of course, the experiments presented in this section are not realistic, because embryos are introduced one by one. The experiments are just intended to illustrate the basic dynamical mechanisms at play. In the next section, we present more realistic simulations, with all embryos simultaneously present from t = 0.
4. A first attempt to form Uranus and Neptune
We present a series of simulations with 14 embryos originally distributed in semi-major axis from 10 to 35 AU. The initial orbits have low eccentricities (e ~ 10-2) and inclinations (i ~ 10-2 rad) relative to the common invariable plane of the system. The initial mass of each embryo is assumed to be 3 M⊕ and the mutual orbital separation among embryos is 5 mutual Hill radii. We ran simulations with fd = 1, 3, and 6, which progressively increased the effects of eccentricity/inclination damping. Furthermore, we divided the speed of type-I migration by the factor fI = 1, 3, or 6. For each of these nine combinations of fd and fI, we performed ten simulations with embryos of different initial, randomly generated sets of position and velocity vectors (but which satisfy the above-mentioned distribution properties). Every simulation was run for 5 My, a typical lifetime for the disk, during which we kept the density of the gas constant (i.e. the values of fd and fI).
 |
Fig. 3 Evolution of the semi-major axes of the embryos in simulation No. 7 with fd = fI = 3. Each color represents a different embryo. The system stabilizes in ~1.2 My. The panel on the right shows the final masses of the embryos/cores, as a function of their semi-major axes. |
Figure 3 shows the evolution of the system for a simulation fd = fI = 3. The embryos migrate toward Jupiter and Saturn and frequently encounter each other, which makes the evolution very chaotic. Several of them also have close encounters with Jupiter and Saturn and are consequently scattered onto distant elliptic orbits or into the inner solar system. Through these scattering events and collisions, the number of embryos beyond Saturn eventually decreases to three in 1.5 My and the surviving bodies find a stable resonant configuration. The most massive object has grown to 9 M⊕, whereas the two others have preserved their initial mass (3 M⊕). The three embryos that were scattered into the inner solar system eventually accrete each other, forming a 9 Earth-mass object. Because the system remains “frozen” once a resonant stability is achieved, the lifetime of the gas-disk would not influence the results significantly. In the case illustrated in this figure, any lifetime longer than 1.5 My would produce the same final system. Instead, if the lifetime had been shorter than 1.5 My, the system would not have reached the final state, leaving many embryos on eccentric and chaotic orbits.
 |
Fig. 4 End-states (in 5 Myr) of the simulations starting with 14 embryos, each with 3 M⊕. The simulations are separated by horizontal dashed green lines. The surviving embryos/cores are shown with filled red dots, whose size is proportional to the objects mass. The scale is shown on the bottom panel. The red horizontal bar shows the perihelion-aphelion excursion of these objects on their eccentric orbits. The objects beyond 15 AU are plotted for simplicity at 15.5 AU, beyond the vertical solid green line. Jupiter and Saturn are shown as blue asterisks. The label above each panel reports the number N of embryos and the values of fI and fd adopted in the simulations. |
Figure 4 shows the end-states of the simulations for all combinations of fI = 1, 3, 6 and fd = 1, 3, 6. The number of bodies surviving beyond Saturn changes from one to three from one simulation to another. Similarly, the mass of the body in the inner solar system changes from 3 to 27 M⊕. Notice that Saturn is not always in the same position with regard to Jupiter, despite the forces that we applied to keep these planets in the 2:3 resonance. Indeed, in some cases Saturn moves out of the 2:3 resonance while scattering an embryo inward; then the forces drive it back toward Jupiter, but Saturn is caught in a resonance different from 2:3 (mostly 1:2 or 1:3). This evolution depends on the magnitude of the migration forces that we impose. We checked that if we increase the strength of the migration forces by an order of magnitude, Saturn returns to the 2:3 resonance in all simulations. Notice that the hydrodynamical simulations (Pierens & Nelson 2008) show that in the MMSN disk Saturn always reaches a 2:3 resonance with Jupiter.
 |
Fig. 5 Statistical analysis of the results of the simulations starting from 14 embryos. The x-axis of left plots reports the value of fI at fixed fd, given at the title of each plot. Similarly, the x-axis of right plots reports the value of fd at fixed fI. The dot, slightly displaced to the left, is the mean mass of the largest core surviving beyond Saturn, computed over the corresponding ten simulations. The thick vertical bar is the rms deviation of this quantity. The thin bar shows the excursion of the same quantity from minimum to maximum. The square, in the middle and related bars are the same, but for the second-largest core. The mass scale is reported left of the diagram. The cross, slightly displaced to the right, reports the mean number of embryos/cores surviving beyond Saturn, to be read against the scale on the right-hand side. Again, the thick bar is for the rms deviation and the thin bar for the minimum-maximum quantity. |
We now discuss the statistical dependence of the results on the values of fd and fI. Figure 5 shows the number of bodies surviving in the system and the masses of the first- and second-largest bodies beyond Saturn as a function of these parameters.
Clearly, there are no statistically significant trends of the considered quantities with respect to the investigated disk parameters. There is a significant trend, however, that is apparent from the panels in Fig. 4: the mass of the body formed in the inner solar system increases on average with fd and fI. If these parameters are small, several embryos are ejected from the system or can be found on distant orbits; instead, if fd and fI are larger, no bodies are ejected and most of the objects scattered by Jupiter and Saturn end up in the inner solar system. Notice that the injection of embryos inside the orbit of Jupiter (which happens in most simulations) is probably inconsistent with the current structure of the solar system, but might explain the structure of some extra-solar planetary systems, particularly those with a hot Neptune and a more distant giant planet like HD 215497. Similarly, the ejection of embryos to distant, long-period orbits might find one day an analog in the extra-solar planet catalogs.
Overall our results concerning the formation of the cores of Uranus and Neptune are disappointing. The best cases are simulation No. 4 with (fd, fI) = (1, 6) and No. 8 with (fd, fI) = (6, 6), both producing beyond Saturn two cores of 12 and 6 M⊕, together with one leftover embryo. Thus, in general, although the mass of the first core is close to the mass of Uranus, the mass of the second-biggest core is never large enough to correspond to Neptune.
One could think that our inability to produce two objects as massive as Uranus and Neptune is caused by an insufficient total mass in embryos in the initial disk beyond Saturn. To investigate if this is true, we performed another series of simulations with more embryos and, therefore, a higher initial total mass. Specifically, we considered 28 embryos distributed in the same range of heliocentric distances, from 10 to 35 AU. The initial mass of each embryo was assumed to be 3 M⊕, again. With this set-up, the orbital separation between embryos is on average smaller than 5 mutual Hill radii. This means that the embryos are on orbits that are closer to each other than predicted by the theory of runaway/oligarchic growth (Kokubo & Ida 1998). We nevertheless assumed these initial configurations to explore how the results change by doubling the total initial mass.
In the simulations with 28 embryos, the masses of the cores surviving beyond Saturn do not improve significantly, compared to the 14-embryo cases. (The final masses and orbital characteristics of the surviving objects in the 28-embryos simulations can be seen in Fig. A.1). The main effect of the doubled initial mass is in the mass of the cores formed in the inner solar system, the most massive of which reaches 57 M⊕ (simulation No. 8 for (fd, fI) = (6, 3)).
Statistically, no significant trend can be seen. (The statistical dependence for all combinations of fd and fI is shown in Fig. A.2). There are no significant differences from the results obtained with half the initial mass. The mass in excess in the new runs has ended up in the large cores in the inner solar system, but it does not contribute to form bigger cores beyond Saturn. The most massive core surviving beyond Saturn has 24 M⊕ (simulation No. 7 for (fd, fI) = (3, 6)) but there is no second core. The best system is that achieved in simulation No. 1 for (fd, fI) = (1, 6), with cores of 15 and 9 M⊕ beyond Saturn (together with three leftover embryos). These best-case results are better than those achieved starting from 14 embryos, but they still do not successfully reproduce the real case of Uranus and Neptune.
5. A “planet trap” at the edge of Saturn’s gap
In the previous section we have seen that a large part of the initial embryo population is lost due to migration into the Jupiter-Saturn region. Most of the embryos that come too close to the giant planets are eliminated because of collisions with Jupiter and Saturn, ejection to hyperbolic orbits or injection in the inner solar system.
This result arise because the migration torque that we implemented (from Cresswell & Nelson 2008, see Sect. 2) does not take into account the so-called coorbital corotation torque (Masset 2001). This torque would stop inward-migrating embryos at a “planet trap” just inward of the outer edge of the gap opened in the disk of gas by Jupiter and Saturn (Masset et al. 2006). The planet trap would prevent the embryos from coming too close to the giant planets. To test what effects this would have on planetary accretion and evolution, we performed simulations implementing a new formula from Paardekooper et al. (2010), which accounts for the co-orbital corotation torque, as explained in Sect. 2.
To reduce parameter-space we fixed fI = 1. This is legitimate, because in principle, there is no need to reduce the type-I migration speed because it automatically decreases to zero approaching ~10 AU. We made three series of ten simulations for fd = 1, 3, and 6. All started with a system of ten embryos of 3 M⊕, originally distributed from 11 to 34 AU, with orbital separation of 7 mutual Hill radii. (The end-states are illustrated in Fig. A.3). Figure 6 gives an example of the evolution taken from simulation No. 3 with fd = 3. It is instructive to compare this figure with Fig. 3 above. In this case we see much fewer embryos coming into the Jupiter-Saturn region and suffering scattering events. This is precisely the effect of the planet trap. As a consequence, 90 percent of the initial embryos mass is retained in the system beyond Saturn, whereas only 38 percent of the mass was retained in the case of Fig. 3. Notice also that the accretion process lasts for a shorter time (0.6 My against 1.2 My, respectively), because the system of embryos/cores remains less dynamically excited.
Nevertheless, we see from Fig. 6 that only one core grows massive (18 M⊕) and the rest of the mass (9 M⊕ in total) is split into three leftover embryos, which are on stable orbits in resonance with the massive core and with each other. Notice the presence of two embryos in co-orbital configuration at ~12 AU. This result is typical, as can be checked in Fig. A.3. This is very different from the case of the solar system, with two major planets of comparable masses beyond Saturn (Uranus and Neptune) and no leftover embryos.
Figure 7 shows the statistical analysis of our results as a function of the parameter fd. We see a trend, although only marginally significant: the mass of the largest core and the number of bodies surviving beyond Saturn increases with fd. However, the mass of the second-largest object is remarkably independent of fd and it is small in all cases. We interpret this result as follows: a higher value of fd increases the eccentricity damping on the embryos. With lower eccentricities, the embryos have a higher gravitational focusing factor (Greenzweig & Lissauer 1992) and therefore they can accrete each other more easily. However, because embryos tend to cluster at the location of the planet trap, basically only the innermost embryo, i.e. the one located the nearest to the trap, reaps the benefit of the situation.
Overall, these experiments show that the planet trap is very effective in reducing the loss of mass during the embryo’s evolution. Still, the final results do not agree well with the structure of the solar system. Indeed, only one major core grows and the rest of the mass remains stranded in too many embryos in stable resonant configuration. Consequently, although initially we have a total mass comparable to the combined mass of Uranus and Neptune, at the end only one massive planet is formed.
To test how these results would change with the total mass initially available in embryos, we ran a series of ten additional simulations starting with 15 embryos of 3 M⊕. The orbits of the embryos were initially separated by 5 mutual Hill radii and were distributed from 10 to 35 AU. For simplicity, we fixed fd = 3. No statistically significant trend with the initial total mass in the system appears (the end-states are reported in Fig. A.3) , so that the problems discussed above remain (too small mass of the second core and too many resonant leftovers). This implies that the additional mass is typically lost. Nevertheless, we obtained one simulation whose result is about perfect with regard to the solar system structure, with only two cores surviving beyond Saturn, each with a mass of 15 M⊕ (see Fig. 8).
 |
Fig. 8 Same as Fig. 3 but for the only simulation (No. 2) that successfully produces Uranus and Neptune. |
6. The initial mass of the embryos
All simulations presented up to this point started from a system of embryos of individual mass equal to 3 M⊕. In this section we study the influence of the individual mass of the embryos on the final results. Following the structure of the paper, we first present a series of simulations that do not account for the presence of a planet trap at the edge of Jupiter/Saturn’s gap, then we focus on the impact of the planet trap.
6.1. Without a planet trap
In this new series of simulations, we reduced the initial mass of embryos from 3 to 1.5 M⊕. However, we increased the number of embryos from 14 to 28, thus preserving the total mass of the system used in the first part of Sect. 4. The embryos are initially located in the 10−35-AU interval with respective orbital separations of 3.8 mutual Hill radii.
As in Sect. 4, we performed ten simulations for each combination of fI = 1, 3, 6 and fd = 1, 3, 6. We find much less growth than in the equivalent simulations of Sect. 4, starting with 3 M⊕. This is because the migration and damping forces are linear in the mass of the embryos and therefore are weaker in this case. Therefore, the embryos become more dynamically excited through their encounters and their collision probability decreases dramatically. Most of the simulations with fd = 1 and fI = 3, 6 did not reach a stable final configuration at 5 My and when many embryos are still on highly eccentric and mutually crossing orbits. We find the most significant growth in the runs with fd = 3 and fI = 6, but only one major core is produced, with a mean mass of 8 M⊕. The runs with fd = 6 and fI = 6 transfer most of the mass into the inner solar system. (The end-states of these simulations are summarized in Fig. A.4).
The statistical analysis of our results (Fig. A.5) reveals no correlation of the results with fd for any value of fI. However, we find some correlation between the mass of the largest core and the value of fI for each value of fd. Remember that without a planet trap, embryos are driven by migration to encounter the giant planets, unless they are trapped in resonance with Saturn. The larger fI is, the slower is the migration and therefore the easier it is for embryos to be stopped in resonance and (possibly) accrete with each other. This may explain the observed correlation.
6.2. With a planet trap
We performed a series of 10 simulations, starting from 30 embryos, each of 1 M⊕, thus preserving the total mass of the system used in the first part of Sect. 5. The embryos were initially distributed from 9 to 35 AU, with an orbital separation of 4.5 Hill radii. We fixed fI = 1 and fd = 3. The end-states are reported in Fig. A.3.
The results are significantly different from those of the runs starting from more massive individual embryos, reported in Sect. 5. On average, the mass of the largest core beyond Saturn decreases by a factor of 2 and that of the second-largest core decreases by a factor of 1.5. These decreases are statistically significant. The mean number of surviving cores/embryos is four, with simulations producing up to seven objects. Therefore the results are very far from the structure of the current solar system. More mass is lost in these simulations than in the corresponding simulations starting from more massive embryos. As said above, this is probably because the forces damping the eccentricities and inclinations of the embryos are weaker.
7. The effect of turbulence in the disk
The problems that we experienced in the previous sections because embryos and cores were protected by resonances from collisions suggests that some level of turbulence in the disk might promote accretion. Indeed, turbulence provides stochastic torques on the bodies, inducing a random walk of their semi-major axes (Nelson & Gressel 2010). If these torques are strong enough, the bodies may be dislodged from resonances, which in turn would allow them to have close encounters and collisions.
The problem is that one does not known a priori how strong the turbulence should be in the region of the disk where giant planets form. The strength of MRI turbulence depends on the level of ionization of the disk (Fleming et al. 2000), and it is possible that in the massive regions of the disk where giant planets form the ionization of the gas is very low because the radiation from the star(s) cannot penetrate down to the midplane (Gammie 1996). Several formation models argue, therefore, that the planets form in a “dead zone” where, in absence of ionization, there is no turbulence driven by the magneto-rotational instability. This justifies the assumption that we made up to this point that the disk is laminar.
For the sake of completeness, though, we test in this section how the results change if strong or weak turbulence is assumed in the disk. The experiments were conducted in the framework of the planet trap case, with ten embryos of 3 M⊕ (see Sect. 5). As in Sect. 6.1, we assumed fI = 1 and fd = 3. We performed three sets of ten simulations with three different values of the turbulent strength γ. We used γ = 3 × 10-4, 1 × 10-3 and 3 × 10-3. The latter corresponds to strong turbulence without dead-zone (Baruteau & Lin 2010). The end-states are, again, reported in Fig. A.3.
 |
Fig. 9 Same as Fig. 5 but for the series of simulations with different turbulence strength γ. The series for γ = 0 (no-turbulence) is that presented in Sect. 5. |
Figure 9 reports a statistical analysis of our results. There is a clear correlation as expected with the number of objects surviving beyond Saturn decreasing with increasing strength of the turbulence. The runs with γ = 3 × 10-3 typically leave only one object beyond Saturn. The mass of the second-largest core also decreases with increasing turbulence. Instead we do not see any statistical correlation between the mass of the largest core and the turbulence strength. This is a surprise, because we expected that with fewer embryos stranded in resonant isolation, the largest core would have grown more massive. In reality, though, it seems that more mass is lost as the turbulence increases so that the largest core does not benefit from the situation. The reason for this clearly is that resonant configurations are not stable if the turbulence is too strong. Figure 10 gives an illustration of this, showing the evolution of the system in simulation No. 6 with γ = 3 × 10-3. We can see a stochastic behavior of the semi-major axis of the cores, which eventually forces the last two cores to collide with each other. The surviving core in this simulation has a mass of 24 M⊕, which is the largest among all objects produced in our turbulence simulations. Typically, more objects interact with Jupiter and Saturn and are eventually lost.
We conclude from these tests that turbulence may be helpful to break the isolation of planets and to avoid the formation of a too crowded planetary system beyond Jupiter and Saturn. However, the formation of two massive cores, with no left-over embryos seems still to be a distant goal, because typically only one core is produced.
8. Conclusions and discussions
Simulating the formation of Uranus and Neptune through runaway/oligarchic growth from a disk of planetesimals is very difficult. The accretion rate is not high enough; moreover the accretion stalls when the major bodies achieve a few Earth masses (Safronov 1969; Levison & Stewart 2001; Levison & Morbidelli 2007).
We have explored a mechanism for the formation of Uranus and Neptune that is different from those explored before. We assumed that runaway/oligarchic growth from a planetesimal disk generated a system of embryos of 1 − 3 Earth masses, but not larger, in agreement with the results of Levison et al. (2010). Then, we followed the dynamical evolution of such a system of embryos, accounting for their interactions with each other, their interaction with a gas disk, and the presence of fully formed Jupiter and Saturn on resonant, non-migrating orbits. Because of computation speed, we did not perform the simulations with a hydro-dynamical code. Instead, we used an N-body code, and we applied fictitious forces to the embryos that mimic the orbital damping and migration torques that the disk exerts on the embryos. We used two prescriptions for the migration torque: one that ignores the co-orbital corotation torque and one that takes it into account. With the second prescription a “planet trap” (Masset et al. 2006) appears at about 10 AU, just inward of the outer edge of the gap opened by Jupiter and Saturn in the disk of gas.
Our results show that the idea works in principle. In many runs, particularly those accounting for a disk a few times more massive than the MMSN and those accounting for the presence of the planet trap, there is significant mass growth. In these cases, the major core beyond Saturn exceeds 10 Earth masses. These results highlight the importance of the planet trap and of the damping effect that the gas-disk has on the orbital eccentricities and the inclinations of planetary embryos.
Our simulations typically do not successfully reproduce the structure of the outer solar system. In the wide range of the end-states due to the stochasticity of the accretion process, only one simulation is successful, with two cores of 15 M⊕ produced and surviving beyond Saturn and no rogue embryos. In general, our results point to at least two major problems. The first is that there is typically a large difference in mass between the first- and second-most massive cores, particularly in the simulations showing the most spectacular mass growth. This is incompatible with Uranus and Neptune having comparable masses. The second problem appears mostly if we account for the planet trap, so that more material is kept beyond the orbit of Saturn. The problem is that the final planetary system typically has many more than two embryos/cores. Several original embryos, or partially grown cores, survive at the end on stable, resonant orbits. In several cases bodies are found in coorbital resonance with each other. This is in striking contrast with the outer solar system, where there are no intermediate-mass planets accompanying Uranus and Neptune. It might be possible that these additional planets have been removed during a late dynamical instability of the planetary system, but the likelihood of this process remains to be proven.
Accounting for some turbulence in the disk alleviates this last problem. However, when turbulence is strong enough to prevent the survival in resonance of many bodies, the typical result is the production of only one core.
In addition to the problems mentioned above, there is another intriguing aspect suggested by the results of our model. We have seen that to achieve substantial accretion among the embryos, it is necessary that the parameter fd is large, namely that the surface density of the gas is several times higher than that of the MMSN. However, this contrasts with the common idea that Uranus and Neptune formed in a gas-starving disk, which is suggested by the small amount of hydrogen and helium contained in the atmospheres of these planets compared to those of Jupiter and Saturn. How this conundrum may be solved is not clear to us.
In summary, our work does not bring solutions to the problem of the origin of Uranus and Neptune. However, we were able to point out non-trivial problems that cannot be ignored and have to be addressed in future work.
Online material
Appendix A: Additional figures
 |
Fig. A.1 End-states (in 5 Myr) of the simulations starting with 28 embryos, each with 3 M⊕. The simulations are separated by horizontal dashed green lines. The surviving embryos/cores are shown with filled red dots, whose size is proportional to the objects’ mass. The scale is shown in the bottom panel. The red horizontal bar shows the perihelion-aphelion excursion of these objects on their eccentric orbits. The objects beyond 15 AU are plotted for simplicity at 15.5 AU, beyond the vertical solid green line. Jupiter and Saturn are shown as blue asterisks. The label on top of each panel reports the number N of embryos and the values of fI and fd adopted in the simulations. (For the discussion – see Sect. 4.) |
 |
Fig. A.2 Statistical analysis of the results of the simulations starting from 28 embryos, each with 3 M⊕. The x-axis of left plots reports the value of fI at fixed fd, given at the title of each plot. Similarly, the x-axis of right plots reports the value of fd at fixed fI. The dot, slightly displaced to the left, is the mean mass of the largest core surviving beyond Saturn, computed over the corresponding ten simulations. The thick vertical bar is the rms deviation of this quantity. The thin bar shows the excursion of the same quantity from minimum to maximum. The square in the middle and related bars are the same, but for the second-largest core. The mass scale is reported left of the diagram. The cross, slightly displaced to the right, reports the mean number of embryos/cores surviving beyond Saturn, to be read against the scale on the right hand side. Again, the thick bar is for the rms deviation and the thin bar for the minimum-maximum quantity. (For the discussion – see Sect. 4.) |
 |
Fig. A.3 Same as Fig. A.1 but for the simulations in which the planet trap was considered. The plots a)–c) show the end-states starting with initial embryo-mass of 3 M⊕ when the turbulence is not taken into account, plots d)–f) are related to the cases with the turbulence characterized by γ = 3 × 10-4, 1 × 10-3, and 3 × 10-3, respectively. At the start, ten embryos are assumed in these simulations. Plot g) shows the end-states of simulations starting with a higher total mass (15 embryos of 3 M⊕) and plot h) does this for a larger number of initally less massive embryos (30 embryos of 1 M⊕). (For the discussion – see Sect. 5.) |
 |
Fig. A.4 Same as Fig. A.3 but with the initial mass of each embryo of 1.5 M ⊕ . (For the discussion – see Sect. 6.1.) |
 |
Fig. A.5 Same as Fig. A.2 but with the initial mass of each embryo of 1.5 M⊕. (For the discussion – see Sect. 6.1.) |
Acknowledgments
We thank the reviewer Eiichiro Kokubo for extremely useful comments, which have greatly improved this paper. This work was supported by France’s EGIDE and the Slovak Research and Development Agency, grant Ref. No. SK-FR-0004-09. R.B. thanks Germany’s Helmholz Alliance for funding through their “Planetary Evolution and Life” programme.
References
- Baruteau, C., & Lin, D. N. C. 2010, ApJ, 709, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., & Masset, F. 2008, ApJ, 678, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Brown, M. E. 2010, ApJ, 716, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2008, A&A, 482, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2007, A&A, 461, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, M. J., Levison, H. F., & Lee, M. H. 1998, AJ, 116, 2067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fernandez, J. A., & Ip, W.-H. 1984, Icarus, 58, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Fleming, T. P., Stone, J. M., & Hawley, J. F. 2000, ApJ, 530, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Goldreich, P., Lithwick, Y., & Sari, R. 2004a, ApJ, 614, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., Lithwick, Y., & Sari, R. 2004b, ARA&A, 42, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Greenzweig, Y., & Lissauer, J. J. 1992, Icarus, 100, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, J. M., & Malhotra, R. 1999, AJ, 117, 3041 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Progr. Theor. Phys. Suppl., 70, 35 [Google Scholar]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kokubo, E., & Ida, S. 1998, Icarus, 131, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., & Morbidelli, A. 2007, Icarus, 189, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., & Stewart, G. R. 2001, Icarus, 153, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Thommes, E., & Duncan, M. J. 2010, AJ, 139, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., Johansen, A., Zsom, A., Klahr, H., & Piskunov, N. 2009, A&A, 497, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., Paardekooper, S.-J., & Mac Low, M.-M. 2010, ApJ, 715, L68 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, R. 1993, Nature, 365, 819 [CrossRef] [Google Scholar]
- Malhotra, R. 1995, AJ, 110, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S. 2001, ApJ, 558, 453 [Google Scholar]
- Masset, F., & Snellgrove, M. 2001, MNRAS, 320, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., Morbidelli, A., Crida, A., & Ferreira, J. 2006, ApJ, 642, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Crida, A. 2007, Icarus, 191, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Tsiganis, K., Crida, A., Levison, H. F., & Gomes, R. 2007, AJ, 134, 1790 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Crida, A., Masset, F., & Nelson, R. P. 2008, A&A, 478, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, R. P., & Gressel, O. 2010, MNRAS, 409, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., Ida, S., & Morbidelli, A. 2007, Icarus, 188, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2006, A&A, 459, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Papaloizou, J. C. B. 2008, A&A, 485, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., Crida, A., & Kley, W. 2010, MNRAS, 401, 1950 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Pierens, A., & Nelson, R. P. 2008, A&A, 483, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Safronov, V. V. 1969, in Evolution of the Protoplanetary Cloud and Formation of the Earth and Planets (Moscow: Nauka) [Google Scholar]
- Terquem, C., & Papaloizou, J. C. B. 2002, MNRAS, 332, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 1999, Nature, 402, 635 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 2003, Icarus, 161, 431 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tsiganis, K., Gomes, R., Morbidelli, A., & Levison, H. F. 2005, Nature, 435, 459 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Weidenschilling, S. J. 1977, Ap&SS, 51, 153 [Google Scholar]
All Figures
 |
Fig. 1 Gas surface densities according to different works. The red curve shows the result of the hydro-dynamical simulation by Morbidelli & Crida (2007), with Jupiter and Saturn in 2:3 resonance. This is the profile that we assumed in this paper, possibly scaled by a factor fd. The blue line is from Weidenschilling (1977) and is proportional to 1/r. The green line is from Hayashi (1981) and is proportional to 1/r3/2. The magenta curve reports the amount of gas required in the Pollack et al. (1996) model of giant planet accretion. |
| In the text | |
 |
Fig. 2 Simulations of the dynamical evolution of embryos in the disk outside of Saturn’s orbit. Top: a case with parameters fd = fI = 1. Bottom: a case with fd = fI = 2. The green and blue curves at ~ 5.4 and ~ 7.3 AU show the semi-major axis evolution of Jupiter and Saturn, respectively. The other curves of various colors illustrate the evolution of the semi-major axes of the embryos. See text for a description of the dynamical evolution and the accretion events. |
| In the text | |
 |
Fig. 3 Evolution of the semi-major axes of the embryos in simulation No. 7 with fd = fI = 3. Each color represents a different embryo. The system stabilizes in ~1.2 My. The panel on the right shows the final masses of the embryos/cores, as a function of their semi-major axes. |
| In the text | |
 |
Fig. 4 End-states (in 5 Myr) of the simulations starting with 14 embryos, each with 3 M⊕. The simulations are separated by horizontal dashed green lines. The surviving embryos/cores are shown with filled red dots, whose size is proportional to the objects mass. The scale is shown on the bottom panel. The red horizontal bar shows the perihelion-aphelion excursion of these objects on their eccentric orbits. The objects beyond 15 AU are plotted for simplicity at 15.5 AU, beyond the vertical solid green line. Jupiter and Saturn are shown as blue asterisks. The label above each panel reports the number N of embryos and the values of fI and fd adopted in the simulations. |
| In the text | |
 |
Fig. 5 Statistical analysis of the results of the simulations starting from 14 embryos. The x-axis of left plots reports the value of fI at fixed fd, given at the title of each plot. Similarly, the x-axis of right plots reports the value of fd at fixed fI. The dot, slightly displaced to the left, is the mean mass of the largest core surviving beyond Saturn, computed over the corresponding ten simulations. The thick vertical bar is the rms deviation of this quantity. The thin bar shows the excursion of the same quantity from minimum to maximum. The square, in the middle and related bars are the same, but for the second-largest core. The mass scale is reported left of the diagram. The cross, slightly displaced to the right, reports the mean number of embryos/cores surviving beyond Saturn, to be read against the scale on the right-hand side. Again, the thick bar is for the rms deviation and the thin bar for the minimum-maximum quantity. |
| In the text | |
 |
Fig. 6 Same as Fig. 3 but for No. 3 with fd = 3, fI = 1 and accounting for the planet trap. |
| In the text | |
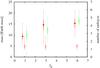 |
Fig. 7 Same as Fig. 5 but for the simulations with the planet trap. |
| In the text | |
 |
Fig. 8 Same as Fig. 3 but for the only simulation (No. 2) that successfully produces Uranus and Neptune. |
| In the text | |
 |
Fig. 9 Same as Fig. 5 but for the series of simulations with different turbulence strength γ. The series for γ = 0 (no-turbulence) is that presented in Sect. 5. |
| In the text | |
 |
Fig. 10 Same as Fig. 3 but for a simulation with strong turbulence (No. 6 with γ = 3 × 10-3). |
| In the text | |
 |
Fig. A.1 End-states (in 5 Myr) of the simulations starting with 28 embryos, each with 3 M⊕. The simulations are separated by horizontal dashed green lines. The surviving embryos/cores are shown with filled red dots, whose size is proportional to the objects’ mass. The scale is shown in the bottom panel. The red horizontal bar shows the perihelion-aphelion excursion of these objects on their eccentric orbits. The objects beyond 15 AU are plotted for simplicity at 15.5 AU, beyond the vertical solid green line. Jupiter and Saturn are shown as blue asterisks. The label on top of each panel reports the number N of embryos and the values of fI and fd adopted in the simulations. (For the discussion – see Sect. 4.) |
| In the text | |
 |
Fig. A.2 Statistical analysis of the results of the simulations starting from 28 embryos, each with 3 M⊕. The x-axis of left plots reports the value of fI at fixed fd, given at the title of each plot. Similarly, the x-axis of right plots reports the value of fd at fixed fI. The dot, slightly displaced to the left, is the mean mass of the largest core surviving beyond Saturn, computed over the corresponding ten simulations. The thick vertical bar is the rms deviation of this quantity. The thin bar shows the excursion of the same quantity from minimum to maximum. The square in the middle and related bars are the same, but for the second-largest core. The mass scale is reported left of the diagram. The cross, slightly displaced to the right, reports the mean number of embryos/cores surviving beyond Saturn, to be read against the scale on the right hand side. Again, the thick bar is for the rms deviation and the thin bar for the minimum-maximum quantity. (For the discussion – see Sect. 4.) |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1 but for the simulations in which the planet trap was considered. The plots a)–c) show the end-states starting with initial embryo-mass of 3 M⊕ when the turbulence is not taken into account, plots d)–f) are related to the cases with the turbulence characterized by γ = 3 × 10-4, 1 × 10-3, and 3 × 10-3, respectively. At the start, ten embryos are assumed in these simulations. Plot g) shows the end-states of simulations starting with a higher total mass (15 embryos of 3 M⊕) and plot h) does this for a larger number of initally less massive embryos (30 embryos of 1 M⊕). (For the discussion – see Sect. 5.) |
| In the text | |
 |
Fig. A.4 Same as Fig. A.3 but with the initial mass of each embryo of 1.5 M ⊕ . (For the discussion – see Sect. 6.1.) |
| In the text | |
 |
Fig. A.5 Same as Fig. A.2 but with the initial mass of each embryo of 1.5 M⊕. (For the discussion – see Sect. 6.1.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


