| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118493 | |
| Published online | 20 February 2012 | |
Shadows, gaps, and ring-like structures in protoplanetary disks
1 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching b. München, Germany
e-mail: rsiebenm@eso.org
2 Department of Physics and Astronomy, University of Kentucky, Lexington, KY 40506-0055, USA
Received: 21 November 2011
Accepted: 30 December 2011
We study the structure of passively heated disks around T Tauri and Herbig Ae stars, and present a vectorized Monte Carlo dust radiative transfer model of protoplanetary disks. The vectorization provides a speed up factor of ~100 when compared to a scalar version of the code. Disks are composed of either fluffy carbon and silicate grains of various sizes or dust of the diffuse ISM. The IR emission and the midplane temperature derived by the MC method differ from models where the radiative transfer is solved in slab geometry of small ring segments. In the MC treatment, dusty halos above the disks are considered. Halos lead to an enhanced IR emission and warmer midplane temperature than do pure disks. Under the assumption of hydrostatic equilibrium we find that the disk in the inner rim puffs up, followed by a shadowed region. The shadow reduces the temperature of the midplane and decreases the height of the extinction layer of the disk. It can be seen as a gap in the disk unless the surface is again exposed to direct stellar radiation. There the disk puffs up a second time, a third time, and so forth. Therefore several gaps and ring-like structures are present in the disk surface and appear in emission images. They result from shadows in the disks and are present without the need to postulate the existence of any companion or planet. As compared to Herbig Ae stars, such gaps and ring-like structures are more pronounced in regions of terrestrial planets around T Tauri stars.
Key words: radiative transfer / protoplanetary disks / dust, extinction
© ESO, 2012
1. Introduction
Low-mass stars are surrounded by gaseous dust disks; prominent examples are T Tauri and Herbig Ae/Be stars (Waters & Waelkens 1998). The existence of disks is derived from observations of the submillimeter continuum (Beckwith et al. 1990), the IR excess over the photospheric emission (Kenyon & Hartmann 1995), and direct imaging (McCaughrean & O’dell 1996). Protoplanetary disks with weak mid-IR and strong far-IR emission are called transitional disks (Najita et al. 2007; Furlan et al. 2009; Cieza et al. 2008). They are of interest because the missing mid-IR emission could be caused by grain growth or planet formation (Testi et al. 2003). Their optical extinction is flatter than the standard ISM extinction curve (Fitzpatrick & Massa 2007) and shows time variability (Schisano et al. 2009). This indicates that large grains or clumpy material orbits and partially obscures the star.
The evolution of the disk is followed theoretically by studying the time dependence of the surface density of gas and dust. Hydro-dynamical models of viscous protoplanetary disks including planets have been developed (Lubow et al. 1999; Ozernoy et al. 2000; Klahr & Bodenheimer 2003; Edgar & Quillen 2008; Tutukov & Fedorova 2006; Alexander & Armitage 2009). The models predict that the disk is cleared by an orbiting planet and that the surface density shows structures with holes and gaps, spiral arms, and rings. Such disk structures are inferred from fitting the spectral energy distribution (SED) by applying models considering pure disks (Calvet et al. 2002; Espaillat et al. 2010; Mulders et al. 2010) or disks with halos (Schegerer et al. 2008; Verhoeff et al. 2011).
Recently, several disks with rings have been observed (van Boekel et al. 2005; Fukagawa et al. 2006; Ratzka et al. 2007; Brown et al. 2007, 2008; Mayama et al. 2010; Thalmann et al. 2010; Olofsson et al. 2011). In the gaps, between the rings, companion candidates are detected (Huelamo et al. 2011; Kalas et al. 2008; Lagrange et al. 2010). Hydro-models account for the observed radial distribution of planets and lifetimes of the disks, which are a few Myr (Strom et al. 1989; Bertout et al. 2007). The strength of the disk-planet interactions are influenced by the gas pressure so that the structure of protoplanetary disks plays a key role in understanding the planet formation process.
There is a rich literature on radiative transfer models of protoplanetary disks (e.g. Wolf et al. 2003; Whitney et al. 2003; Pinte et al. 2006; Robitaille et al. 2006; Pinte et al. 2008). The structure of the disks is discussed by Nomura (2002), Walker et al. (2004), and Dullemond & Dominik (2004a), and self-shadowing ripples in the disks have already been mentioned by D’Alessio et al. (1999) and Dullemond (2000); for a recent review, see Dullemond & Monnier (2010). In this paper the thermal structure of disks is discussed by solving the hydrostatic and radiative balance equations. We are interested in deriving the structure and IR appearance of a starlight-heated, so-called passive disk. Dust models used in this paper are described in Sect. 2, and a vectorized 3D Monte Carlo (MC) radiative transfer code in Sect. 3. We compare results of the MC model against a method that samples the disk in small ring segments at radius r from the star and in which the radiative transfer of the segments is solved in a slab geometry (Sect. 4.3). The influence of different dust opacities on the SED of the disks is discussed in Sect. 4.4. We apply the models to T Tauri and Herbig Ae stars. The effect of a dust halo on the emission and temperature structure is presented (Sect. 4.5). The vertical temperature structure introduces variations of the height of the disk surface which causes shadows. They emerge as gaps and ring-like structures at distances from the star, which are thought to be the birthplaces of terrestrial planets (Sect. 5). Strikingly the structures are caused only by the coupling of the hydrostatic and radiative transfer equations without the need to postulate a planet.
2. Dust models
In protoplanetary disks the properties of dust are thought to evolve, and the mineralogy, composition, porosity and size distribution of the grains differs from that of the diffuse ISM. Thanks to an enhanced particle collision rate, fluffy grains are produced that grow in size over time (Natta et al. 2004; Acke et al. 2004; Natta et al. 2007; Lommen et al. 2007; Ricci et al. 2010). Disk particles settle towards the midplane under gravity, a process counteracted by grain fragmentation and disk turbulence (Mizuno et al. 1988; Weidenschilling et al. 1993; Sterzik et al. 1994; Dullemond & Dominik 2004b, 2005). It is found that grains of radius ≲ 10 μm settle towards the midplane, and depending on turbulent motions, will be blown up to the surface, where they remain for long time periods, and well coupled with the gas (Alexander & Armitage 2007; Charnoz et al. 2011).
Dust gets annealed in high-temperature regions of the disk, and crystalline structures are built. They are detected and the observed profiles of the 10 μm silicate band differ from that of the interstellar medium (Malfait et al. 1998; Bouwman et al. 2008; Schegerer et al. 2006; Kessler-Silacci et al. 2006; Furlan et al. 2011; Oliveira et al. 2010; Watson et al. 2009). About 4% to 7.5% of the dust mass of the solar system is in crystalline silicates whereas crystallization is ~2% in the diffuse ISM (Kemper et al. 2005). Ice coatings are built in frosty regions (Siebenmorgen & Gredel 1997; Pontoppidan et al. 2005; Visser et al. 2009). The location where water ice can exist is important for terrestrial planet formation (Ida & Lin 2008; Min et al. 2011). All of these processes are combined by mixing and transport mechanisms and are valid for the neutral part of the disks where grain charging can be ignored. Ionization becomes important in the disk surface; therefore, the true situation of the mineralogy in protoplanetary disks is a complicated matter with a rich chemical network and evolution mechanisms in place (Gail 2004).
The SED and the thermal structure of the disks depend on the applied dust model and for comparison we present results using dust opacities as derived for protoplanetary disks and the diffuse ISM. For the dust in the ISM, we use a power-law size distribution: n(a) ∝ a-3.5 with particle radii between a− ≤ a ≤ a+ of bare spherical particles of silicates (a− = 320 Å, a+ = 2600 Å) with optical constants by Draine (2003) and carbon (a− = 160 Å, a+ = 1300 Å), with optical constants by Zubko et al. (1996), and both with bulk density of 2.5 g/cm3. We use dust abundances (ppm) of 31 [Si]/[H] and 200 [C]/[H], which are in reasonable agreement with cosmic abundance constraints (Asplund et al. 2009). This gives a gas-to-dust mass ratio of 130. For protoplanetary dust we consider fluffy agglomerates of silicate and carbon as subparticles. Other parameters are as for the ISM dust except that grains grow to 100 times larger radii of a+ = 33 μm. As relative volume fraction of the composite grain we use 34% silicates, 16% carbon, and 50% vacuum, which translates to a relative mass fraction of 68% silicates and 32% aC. Absorption and scattering cross-sections and the scattering asymmetry factor is computed with Mie theory for the ISM grains, and we apply the Bruggeman rule for the fluffy composites. This gives a total mass extinction cross section for the large grains in the optical (0.55 μm) of 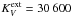 of the ISM dust and 4000 [cm2/g-dust] of the fluffy composites. The wavelength dependence
of the ISM dust and 4000 [cm2/g-dust] of the fluffy composites. The wavelength dependence 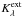 of both models is similar to those displayed in Krügel & Siebenmorgen (1994, Fig. 12).
of both models is similar to those displayed in Krügel & Siebenmorgen (1994, Fig. 12).
3. Vectorized MC radiative transfer
The radiative transfer problem is solved by a MC technique by following the flight path of many random photons. Basic ideas are given by Witt (1977), Lucy (1999), and Bjorkman & Wood (2001), and the original version of our code was developed by Krügel (2008). Our model space is a 3D Cartesian grid (x,y,z) that is partitioned into cubes and, where a finer grid is required, further divided into subcubes (cells). The star of luminosity L emits a total of N = nNν photon packages per second and in each of the Nν frequency bins n photon packages are emitted. Each package has a constant energy ε = L/N. A package entering a cell on its flight path may be absorbed there or scattered. The probability of such an interaction is given by the extinction optical depth along the path within the cell, Δτ, and occurs when Δτ ≥ −log (ξ) using unified random number ξ. The package is scattered if the dust albedo A > ξ′, using random number ξ′; otherwise, it is absorbed. When the package is scattered, it only changes direction determined in a probabilistic manner by the phase function. When it is absorbed, a new package of the same energy, but usually different frequency ν′ is emitted from the spot of absorption. The emission is isotropic. Each absorption event raises the energy of the cell by ε, and accordingly its temperature.
The computational speed of the code is increased considerably by calculating the flight paths of photons simultaneously. This type of vectorization is realized in two flavors using either conventional computer processing units (CPU) within FORTRAN 90 and OMP environment1 or graphics processing units (GPU) with NIVIDA cards and CUDA2 (Heymann, 2010). The speed-up scales almost linearly with the number of processing cores available. For parallelization particular attention needs to be paid to the random number generator, for which we choose the Mersene Twister algorithm (Matsumoto & Nishimura 1998).
Verification of the vectorized MC code against benchmarks (Ivezic et al. 1997; Pascucci et al. 2004) was done in an accompanying paper (Heymann & Siebenmorgen 2012). The code is also tested against the spheric symmetrical ray tracing code by Krügel (2008). The SED is computed by counting the photon packets leaving the cloud towards the observer using a large beam. The observed intensity can also be computed by following the radiative transfer of the line of sight from the observer or a pixel of the detector plane, through the model cloud using the MC computed dust temperatures and scattering events (Heymann 2010). The ray tracer is also vectorized and allows us to derive dust scattering and emission images with high signal to noise, which is not possible by photon counting procedures.
The number of interactions of photon packets with the dust increases exponentially with the optical depth of the cell. In cells of extreme high optical depth, τV ≲ 1000, the photon packages are trapped and interact with the dust over and over again before they have a chance to escape. In this way MC treatments are slowed down considerably. Unfortunately, this situation appears in cells close to the midplane of protoplanetary disks. A modified random walk (MRW) procedure for improving the computational efficiency of MC methods has been presented by Fleck & Canfield (1984). The MRW enlarges the mean free path length of packets by a diffusion approximation whenever necessary, and has been tested by Min et al. (2009) and Robitaille (2010). Let r be the distance of the interaction point to the nearest site wall of a cell. The MRW is considered in a cell when the photon package has a distance r ≥ γ/ρKR, where γ > 5 is a user specified constant, ρ the dust density, and KR the Rosseland mean extinction coefficient. The photon travel distance d is derived from 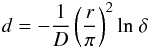 (1)with diffusion constant D = 1/3 ρKR and a pre-computed sample of δ given by
(1)with diffusion constant D = 1/3 ρKR and a pre-computed sample of δ given by 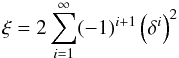 (2)with unified random number ξ. The number of absorption events within a cell is used to compute the dust temperature and, within r of the MRW, is estimated by nabs = d ρ KP, where KP is the Planck mean mass extinction coefficient of the dust. Ignorance of these acceleration methods has a tremendous effect on the run time requirements of a vectorized MC treatment. In our scheme the trajectory of photon packages through the model space is vectorized in so-called threads. Trajectories that hit the cells of high optical depth have many more interactions than others, most likely the majority of trajectories. This results in a rather unbalanced workload over all threads, so that the advantage of vectorization is lost. In such cases the run time increases by the number of CPU or GPU cores available, which in our case are 8 and 480, respectively. This factor of efficiency loss is on top of the speed up gain of 5–10 of the MRW procedure achieved in scalar MC treatments (Pinte et al. 2009).
(2)with unified random number ξ. The number of absorption events within a cell is used to compute the dust temperature and, within r of the MRW, is estimated by nabs = d ρ KP, where KP is the Planck mean mass extinction coefficient of the dust. Ignorance of these acceleration methods has a tremendous effect on the run time requirements of a vectorized MC treatment. In our scheme the trajectory of photon packages through the model space is vectorized in so-called threads. Trajectories that hit the cells of high optical depth have many more interactions than others, most likely the majority of trajectories. This results in a rather unbalanced workload over all threads, so that the advantage of vectorization is lost. In such cases the run time increases by the number of CPU or GPU cores available, which in our case are 8 and 480, respectively. This factor of efficiency loss is on top of the speed up gain of 5–10 of the MRW procedure achieved in scalar MC treatments (Pinte et al. 2009).
Parameters of the fiducial T Tauri and Herbig Ae disks.
4. Protoplanetary disk models
The time scale for disks to attain thermal equilibrium is set by the balance between heating and cooling. This time scale is much shorter than the evolution of the disk or the heating source. The number density of the gas, even in the upper layers of the disk, exceeds 105 cm-3, so that gas and dust are thermally coupled. Matter will spiral in the disk towards the star and dissipate gravitational energy. For a thin disk that extends to the stellar surface, an accretion luminosity of about a quarter of the stellar luminosity is converted in this way into heat. For classical T Tau stars, observed accretion rates are ~ 10−7... −9 M⊙/yr (Muzerolle et al. 1998). At early epochs when the accretion is strongest, dissipation dominates, but later heating by stellar radiation becomes more important. As fiducial model of the T Tau star, we take a mass of 1 M⊙, a luminosity of 2 L⊙, and a photospheric temperature of 4000 K. For comparison we treat a disk heated by a Herbig Ae star with 2.5 M⊙, 50 L⊙ and 104 K (van den Ancker et al. 1997).
From near-IR interferometry (Millan-Gabet et al. 2006) of T Tauri and Herbig Ae stars, it has been found that the inner disk scales with stellar luminosity 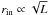 . Such a dependency is expected assuming that rin is set by evaporation of grains at temperatures of 1000 − 1500 K (Dullemond & Monnier 2010). For Herbig Be stars, larger deviations of the simple relation are measured at L > 103 L⊙. Spatially resolved spectroscopy, at milliarcsec resolution, allows detection of a hotter gaseous emission component closer to the star (Eisner et al. 2009; Najita et al. 2009; Pontoppidan et al. 2011). Evaporation temperatures of silicate and carbon particles are around 1500 K. The grains in the disk are assumed to be fluffy and to have been formed by coagulation of much smaller compact interstellar grains. The fluffy agglomerates are held together by weak van der Waals forces (binding energies ≳ 0.1 eV), and they are expected to fall apart into their refractory constituents when the temperature of the composite grain exceeds 1000 K. The constituent particles will then be hotter than the average porous grains because they are much smaller. We assume that the disk extends inwards up to the point where porous grains reach 1000 K, or equivalently small interstellar grains would be at about 1500 K.
. Such a dependency is expected assuming that rin is set by evaporation of grains at temperatures of 1000 − 1500 K (Dullemond & Monnier 2010). For Herbig Be stars, larger deviations of the simple relation are measured at L > 103 L⊙. Spatially resolved spectroscopy, at milliarcsec resolution, allows detection of a hotter gaseous emission component closer to the star (Eisner et al. 2009; Najita et al. 2009; Pontoppidan et al. 2011). Evaporation temperatures of silicate and carbon particles are around 1500 K. The grains in the disk are assumed to be fluffy and to have been formed by coagulation of much smaller compact interstellar grains. The fluffy agglomerates are held together by weak van der Waals forces (binding energies ≳ 0.1 eV), and they are expected to fall apart into their refractory constituents when the temperature of the composite grain exceeds 1000 K. The constituent particles will then be hotter than the average porous grains because they are much smaller. We assume that the disk extends inwards up to the point where porous grains reach 1000 K, or equivalently small interstellar grains would be at about 1500 K.
In star-forming regions dust is heated to about 30 K. At a large distance from the star grain heating by the ambient radiation field of nearby low or massive stars becomes important. We do not make additional assumptions on the outer radiation field and consider only the primary central heating source. Models are computed to an outer radius of rout = 22.5 AU for T Tau and 40 AU for Herbig Ae disks where the midplane temperature drops below 30 K.
Initially we assume that the disk is isothermal in z, and the density is given by 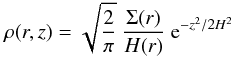 (3)with scale height H2 = kTmidr3/GM ∗ m, surface density Σ(r), molecular mass m = 2.3 mp and midplane temperature, Tmid, for which we use a power law as initial guess. The height of the disk is set to z0 = 4.5 H. In models with pure disks, the density ρhalo above z > z0 is 0 and constant when a halo is considered (Table 1). The surface density is adjusted to reach a given optical depth in the vertical direction τ ⊥ = Σ(r)KV, with visual extinction KV. We use τ ⊥ = τ1 AU (r/AU)γ with γ = −1 for r ≥ 1 AU and γ = 0.5 otherwise (Min et al. 2011). For the porous grain model with a + = 33 μm, we take a vertical optical depth from the surface to the midplane at 1 AU of τ ⊥ = 10 000. This choice holds computational time requirements of the MC code within reasonable limits. It translates to a surface density of Σ(1 AU) = 5 g-dust/cm2 or a gas surface density, which is half the value estimated for the minimum mass of the early solar nebulae (Hayashi 1981). Higher surface densities can be obtained considering larger or ice-coated grains because KV is reduced in such models (Krügel & Siebenmorgen 1994).
(3)with scale height H2 = kTmidr3/GM ∗ m, surface density Σ(r), molecular mass m = 2.3 mp and midplane temperature, Tmid, for which we use a power law as initial guess. The height of the disk is set to z0 = 4.5 H. In models with pure disks, the density ρhalo above z > z0 is 0 and constant when a halo is considered (Table 1). The surface density is adjusted to reach a given optical depth in the vertical direction τ ⊥ = Σ(r)KV, with visual extinction KV. We use τ ⊥ = τ1 AU (r/AU)γ with γ = −1 for r ≥ 1 AU and γ = 0.5 otherwise (Min et al. 2011). For the porous grain model with a + = 33 μm, we take a vertical optical depth from the surface to the midplane at 1 AU of τ ⊥ = 10 000. This choice holds computational time requirements of the MC code within reasonable limits. It translates to a surface density of Σ(1 AU) = 5 g-dust/cm2 or a gas surface density, which is half the value estimated for the minimum mass of the early solar nebulae (Hayashi 1981). Higher surface densities can be obtained considering larger or ice-coated grains because KV is reduced in such models (Krügel & Siebenmorgen 1994).
4.1. Disks with slab geometry
A solution of the radiative transfer of a hydrostatic and geometrically thin disk is developed by Krügel (2008, Sect. 11.3). The disk is symmetric with respect to the midplane at z = 0. The density structure is given in cylindrical coordinates ρ(r,z). Light from the star falls on the disk under a grazing angle αgr so that the star is visible from everywhere on the disk surface (Armitage 2007). Flat disks with a constant grazing angle of αgr = 2° and flared disks, similar to Chiang & Goldreich (1997), are considered with 3° ≤ αgr ∝ r2/7 ≤ 7°. The flat disk has a smaller grazing angle and intercepts less stellar radiation than the flared disk, and even more so at large distances from the star.
The disk is divided into small ring segments of width Δr at radius r from the star. For each ring the radiative transfer is solved under all inclination angles θ, for incoming I − and outgoing I + radiation, assuming a slab geometry. In the vertical direction the opacities are so high, e.g. τ⊥(1 AU) = 104, that each ring segment is split into a completely opaque midlayer and a much thinner top layer of optical thickness τtop. The midlayer is assumed to be isothermal at temperature Tmid and the top layer extends so far down that the temperature at its bottom approaches Tmid. For computing the SED it is sufficient to choose τtop ~ 20. The ray tracer is an iteration procedure and yields the temperature structure T(r,z) and the intensities of the upward I+ and downward I− directed radiation. By observing the disk at viewing angle θobs, the received flux is computed from the emission of the star, the intensity I+ at the disk surface at θ = θobs as well as by summing up contributions from all rings. The radiative transfer is solved for each ring segment at radius r separately. However, the propagation of the radiation in radial direction from one ring into the next is ignored. The procedure is often called the 1+1D disk model.
4.2. Disks with axial symmetry
In disks that are in hydrostatic equilibrium in a vertical direction, the gravitational force is balanced by the pressure gradient3: 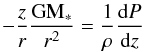 (4)with pressure P = ρkT(z)/m. For each height z and radius r2 = x2 + y2 from the star, the temperature T(r,z) is computed using the MC code of Sect. 3. The star is set at origin. Azimuthal dependencies in the disk structure are not considered, so that the problem can be solved in axial symmetry. It allows us to solve the radiative transfer in one octant of a cube and reduces the computational time by a factor 8 when compared to a full 3D treatment. For each height z ≥ 0 and radial distance at x ≥ 0 and y ≥ 0, we compute the azimuthal average of absorbed photon packets. This average is used to derive the dust temperature T(r,z), and with Eq. (4) a new estimate of the density structure of the disk ρ(r,z). Obviously there is an iterative scheme: starting with an initial guess of the midplane temperature and a first set up of the disk structure ρ(r,z) using Eq. (3), we compute the temperatures T(r,z) after a MC run. Once the temperatures are inserted into Eq. (4), we arrive at a new density structure ρ(r,z), which is used to update T(r,z) with a new MC run. Typically after less than a dozen iterations, the program converges to a stable disk configuration. The problem we are solving is intrinsically 2D, but our MC code is based on cubic cells that are 3D, therefore we label such computations 2D disk models hereafter.
(4)with pressure P = ρkT(z)/m. For each height z and radius r2 = x2 + y2 from the star, the temperature T(r,z) is computed using the MC code of Sect. 3. The star is set at origin. Azimuthal dependencies in the disk structure are not considered, so that the problem can be solved in axial symmetry. It allows us to solve the radiative transfer in one octant of a cube and reduces the computational time by a factor 8 when compared to a full 3D treatment. For each height z ≥ 0 and radial distance at x ≥ 0 and y ≥ 0, we compute the azimuthal average of absorbed photon packets. This average is used to derive the dust temperature T(r,z), and with Eq. (4) a new estimate of the density structure of the disk ρ(r,z). Obviously there is an iterative scheme: starting with an initial guess of the midplane temperature and a first set up of the disk structure ρ(r,z) using Eq. (3), we compute the temperatures T(r,z) after a MC run. Once the temperatures are inserted into Eq. (4), we arrive at a new density structure ρ(r,z), which is used to update T(r,z) with a new MC run. Typically after less than a dozen iterations, the program converges to a stable disk configuration. The problem we are solving is intrinsically 2D, but our MC code is based on cubic cells that are 3D, therefore we label such computations 2D disk models hereafter.
Particular attention has to be paid to a good set-up of the grid used in the MC code. In the positive (x,y,z) directions, we use a basic grid of (350, 350, 50) cubes. At locations where the radiation field varies strongly, cubes are sampled into subcubes. Large gradients of the radiation field are expected close to the surface, within the extinction layer or at the inner wall of the disk. Estimates of the height of the extinction layer z0 and its thickness ℓ ~ H/2 is given by Siebenmorgen & Krügel (2010).
 |
Fig. 1 Top: IR emission of a T Tau disk viewed at ~45°, which is either computed using the 1+1D model (label “1D”) in a flat (green full line), a flaring (dashed green line) disk configuration, or the 2D disk. Iterations 1 to 9 of Eq. (4) of the 2D disk are shown. Bottom: midplane temperatures of the 1+1D flat disk and the various iterations of the 2D disk. |
The extinction layer is sampled with cubes having τV ≳ 0.6. This is achieved by sampling cubes located close to the extinction layer in up to 20 subcubes. In total the disk has 107 cells, which provides a sampling with high spatial resolution. In each MC run a number of 108 photon packets are emitted from the star. The fairly high number of packets provide a high-energy resolution and is required to arrive at a stable estimate of the temperatures T(r,z), in particular near the midplane.
4.3. Comparison: 1+1D versus 2D
The SED and the midplane temperatures of a flat and flaring 1+1D disk are compared with those of a 2D disk model. As an example, we take a T Tauri star with parameters as specified in Table 1. For ease of comparison, the distribution of the dust column density Σ(r) is chosen to be identical in all three models. We take the one computed by the 2D disk as evaporation radius. The SED is compared in the upper panel of Fig. 1. In a 1+1D disk the heating is proportional to the grazing angle. Since flaring disks have a larger grazing angle than flat disks they show higher dust re-emission luminosities and appear warmer. The assumption of 1+1D disk models is that stellar photons impinge upon the disk at a given radius with constant grazing angle. Such a simple picture fails close to the dust evaporation zone. In early 1+1D models the inner disk region was treated as an optically thick vertical wall at constant temperature (Natta et al. 2001; Dullemond et al. 2001). Then the dependency of gas pressure on the dust evaporation temperature is included, resulting in a curved evaporation zone (Isella & Natta 2005; Kama et al. 2009). In the MC scheme the radiation transport in radial direction is included, which, because of the fairly difficult geometry, is otherwise not easy to implement in ray-tracing techniques as used in 1+1D disks. The SED of a 2D disk is very distinct with a much stronger mid-IR emission and overall flatter appearance. We also show in Fig. 1 the convergence of the SED and the midplane temperature of the MC model as computed during the first nine iterations of the density structure following Eq. (4). The midplane temperature distributions of the 1+1D disks are described well by a power law, whereas in the 2D disk striking up and downs with radius are derived. We extensively tested that the structure is not due to systematic effects that could be introduced by the noise caused by a pure photon statistics or inadequate sampling of the MC cells. Following Eq. (3) the midplane temperature is directly linked to the density, and one expects a hilly path, as derived in the lower panel of Fig. 1, to be reflected in the overall observed disk structure (Sect. 5).
 |
Fig. 2 IR emission of 2D disks viewed nearly face-on (~20°) computed by applying different dust opacities. |
4.4. SED dependency on dust opacities
A realistic description of dust in protoplanetary disks is an open and controversial issue, as are the applied dust absorption and scattering efficiencies. Because these parameters directly enter into the radiative transfer equation and the MC method, we wish to study their impact on the SED. As an example we take a T Tauri star with the parameters in Table 1. Three different dust models are distinguished: a) ISM like grains; b) fluffy grains with particle radii up to a+ = 0.3 μm; and c) fluffy grains with a+ = 33 μm. Other parameters remain as given in Sect. 2. The SEDs of the disks are compared using identical distributions of the column density Σ(r). Since the dust models have different visual extinction coefficients KV, the vertical optical depth at 1 AU of 104 for our standard dust (model c) needs to be increased by a factor 7.7 for ISM dust and by a factor 8.5 for fluffy grains with size distribution, as for ISM grains. SEDs of the 2D disks are displayed in Fig. 2, where one notices that:
-
i)
The flux in the far-IR peaks at longer wavelength when applying fluffy grains.
-
ii)
The silicate emission profile depends on grain porosity, particles size, and dust temperature (Voshchinikov & Henning 2008). In the band the cross section peaks at 9.5 μm for ISM dust and at 9.8 μm for the fluffy composites. The feature-to-continuum ratio of the extinction cross section in the 10 μm band, when averaged over the dust size distribution, is 25% higher for ISM than for fluffy grains of same size. Nevertheless, because of the detailed temperature structure, model b), which is made of fluffy grains with sizes typical of the ISM, shows the most striking silicate emission feature.
-
iii)
The disk with fluffy grains up to a+ = 0.3 μm have a similar submillimeter slope as the one with 100 times larger, a+ = 33 μm, particles (Fig. 2). This agrees with observations of protoplanetary disks where the silicate feature is not correlated with the millimeter slope of the SEDs (Lommen et al. 2010).
4.5. Disks plus halos
Protoplanetary disks are thought to be formed from their initial spheroidal configuration of the protostellar envelopes (Watson et al. 2007). It is speculated that there is some residual dust left or that it is replenished at high altitudes above the disk (Vinkovic et al. 2006). Dust in a halo decays through radiation pressure and gravity and may be replenished by dynamical processes, such as outflows and winds from the disk surface, or by planets in highly eccentric orbits (Krijt & Dominik 2011). Miroshnichenko et al. (1999) added the emission of an optical thin halo onto the SEDs computed for optically thick disks. They found that the halo dominates the IR emission and provides additional disk heating on top of the direct stellar radiation. The MC scheme allows a self-consistent treatment of the radiative transfer in a configuration of a disk plus halo. In the T Tauri disk models (Table 1) we add a halo so that the minimum dust density of Eqs. (3) and (4) in each cell of the MC grid exceeds ρ(r,z) ≥ ρhalo = 1.5 × 10-18 (g-dust/cm3). This gives an optical depth for the halo of τV ~ 0.4. The resulting SED of a disk plus halo is shown in Fig. 3. The SED appears warmer than the pure disk with ρhalo = 0. In the example, the disk plus halo model produces a factor ~3 stronger IR peak emission and less near-IR flux for wavelengths below 6 μm. The halo provides additional heating on top of the direct stellar light. Their midplane temperature becomes a factor ~2 warmer than derived in a disk without halo within 1–10 AU of the star.
 |
Fig. 3 IR emission of 2D disks viewed nearly edge-on (~20°) with (dashed) and without (full line) a dusty halo. The disks are either heated by a T Tauri star (top) or a Herbig Ae star (bottom). |
We repeat the exercise for the more luminous Herbig Ae stars with the parameters given in Table 1. With the same minimum dust density, ρhalo, the optical depth of the halo is τV ~ 0.6 as for the T Tauri star. The resulting SEDs are shown in Fig. 3. The halo dominates the IR emission for wavelengths ≲ 3 μm and produces warmer dust in the midplane than in pure disks. The midplane temperature of the Herbig Ae stars are displayed in Fig. 6. The midplane temperature in the pure disk shows a rapid decline in the inner 3–4 AU, followed by a 1/r0.6 dependency up to 12 AU and a strong decline farther out. The disk plus halo model is smoother and fit by Tmid ~ 1/r in the 2–15 AU region (Fig. 6).
 |
Fig. 4 Top: the relative height of the disk photosphere, zbot/r, as a function of radius of a disk heated by a T Tauri star without (full line) and with (dashed) halo. The scale height over radius, H/r, of a flat 1+1D disk (dashed) is shown for comparison. Gaps between ring structures are indicated. A shaded representation of zbot/r along the (x,y)-plane is displayed for a disk plus halo configuration (middle) and a pure disk (bottom). Color bars give the relative gray scale (%) in units of zbot/r. |
5. Ring structure of protoplanetary disks
We notice that the midplane temperature in 2D disks of T Tauri stars show a wavy structure in particular near the zone where terrestrial planets are supposed to form (Fig. 3). Here we investigate how this temperature behavior manifests itself in the appearance of the disk. First we study the height of the photosphere which we define as the height of the bottom of the extinction layer, zbot, where the vertical optical depth τ⊥(V) = 1. In Fig. 4 we show the height of the disk photosphere as a function of radius, expressed as a unitless ratio zbot/r. We do this for the T Tauri disk models with and without a halo using parameters of Table 1. For 1+1D disks the midplane temperature is a smooth function declining with radius, which can be approximated by a power law, and so is the scale height which smoothly increases with distance (Fig. 4). The geometrical thickness of the 1+1D disk increases with radius.
 |
Fig. 5 Mid-IR images of disks heated by a T Tauri star at distance of 50 pc and viewed at 30°. The image of a pure disk (top) and a disk plus halo is shown (middle). Color bars are in log (Jy/arcsec2). Bottom: corresponding surface brightness distribution measured as cut along δ through origin of the image. Gaps between emission rings are indicated. |
 |
Fig. 6 Top: the midplane temperature and relative height of the disk photosphere, zbot/r, as a function of radius of a 2D disk heated by a Herbig Ae star. Models are shown in a configuration of a pure disk (full line) and a disk plus halo (dashed). Power law fits (dotted) to the midplane temperature distribution are as labeled. Gaps between ring structures are indicated. Bottom: a shaded representation of zbot/r along the (x,y)-plane is shown for a pure disk model. Color bar gives relative gray scale (%) in units of zbot/r. |
 |
Fig. 7 Top: Mid-IR image of a disk heated by a Herbig Ae star at distance of 50 pc and viewed at 30°. Color bar is in log (Jy/arcsec2). Bottom: Mid-IR surface brightness distribution measured as a cut along δ through the origin of an emission image of a pure disk (full line) and that computed in a disk plus halo configuration (dashed). |
The 2D disk near the evaporation zone is puffed up, and then its thickness declines similar to the decrease in the midplane temperature. The temperature reduction is to be understand by shadowed region of the disk surface where light from the star is extincted and where grain heating becomes less efficient. The shadow is located close behind from the puffed-up inner rim. The disk becomes thicker with increasing distance, because the gravity decreases, so that there is a point where the shadow becomes less efficient, and the disk is exposed to direct stellar light. There again the disk is puffed up followed by a second shadow, which is located at about 1 AU in our example and a third one near 4 AU. Farther out ( ≲ 10 AU) the midplane temperature drops to below 30 K because the stellar heating of the passive disk is inefficient, and another distortion in the disk surface is not visible in most cases. The detailed structure of passively heated T Tauri disks are shown in Fig. 4 within the region of terrestrial planets. If one considers halos, then gaps and ring-like structures are dimmed and the disk appears thicker because their midplane temperature is warmer. The disk surface is visualized in a 3D representation by rotating the function zbot(r)/r along the midplane (Fig. 4). The innermost puffed-up rim, several gaps, and an overall wavy surface structure of the disk are visible. In Fig. 5 we display images and surface profiles for the mid-IR. At other wavelengths the emission structure is similar. In the image of the disk without halo there is a wide gap opening farther out and smaller gaps visible closer to the star. This structure is dimmed when a halo is considered.
Disks of the more luminous Herbig Ae stars have an evaporation zone farther out than around T Tauri stars. At these distances the gravitation is reduced and the disks become thicker than for T Tauri disks. The height of the Herbig Ae disks and a shadowed presentation is displayed in Fig. 6. When compared to T Tauri stars (Fig. 4), the ratio zbot(r)/r is indeed higher and has less structure. There is a pronounced puffed-up inner rim causing a far reaching shadow, so that a second one farther away than 30 AU is only envisaged. However, this far away the midplane temperature has dropped to below 30 K (Fig. 3) and other effects than stellar heating may dominate the disk structure. We display the mid-IR image and surface profile of the disk heated by a Herbig Ae star in Fig. 7. At least one striking gap and a ring in the disk are identified.
6. Conclusion
The infrared appearance of passive disks around low and medium mass stars has been discussed. Dust particles are made either of bare material or fluffy composites of silicate and carbon. Grain sizes range from 160 Å to 3000 Å as derived for the ISM and up to 33 μm assuming grain growth in the disks. The disks are heated by stellar light with luminosities between 2 L⊙ and 50 L⊙. The disks have an inner radius that is roughly determined by the dust evaporation temperature of the grain material. The surface density of the disks was set close to what is estimated for the minimum mass of the solar nebula. Disks are configured with or without halos. Two hydrostatic and geometrically thin disk scenarios were examined for which we assume that gas and dust are mixed and have the same temperature.
-
i)
In 1+1D the disks were divided in small ring segments in which the radiation transfer was solved. For each ring, a slab geometry was applied, and it was assumed that in deeper layers the disk is isothermal. The transport of radiation in the radial direction was ignored. From the surface of 1+1D disks, the star is always visible. A flat or flaring structure of the disk was considered. This type of disk is in widespread use in the literature.
-
ii)
In 2D disks the hydrostatic and radiative transfer equations were solved in an iterative scheme. For the latter an accurate MC method was presented that can be applied to arbitrary dust geometries. We used an adaptive 3D Cartesian grid where cubes are divided into subcubes whenever required, for example, close to the disk surface. The MC method is vectorized and the parallelization is realized to work on graphics cards or conventional processing units and provides a speed-up roughly proportional to the number of processor cores or parallel threads, available. On our conventional computer, the vectorized code is a factor 100 faster than the scalar version. In regions of very high optical depth, for example close to the midplane of the disk, photon packets may get trapped. In this case the algorithm is further accelerated by a modified random walk procedure. The 2D disks provide a more realistic description than the 1+1D disks: In the RT solution of the 1+1D disks it is assumed that the radial transport of radiation can be ignored and that layers with vertical optical of τtop ≲ 20 are isothermal. These assumptions break for example near the inner regions of the disk. On the other hand, in the 2D disks the radial transport of radiation is included and no assumptions are made that regions of the disks need to be isothermal. Therefore a self consistent treatment of the hydrostatic balance is only provided in the 2D disks. Our main findings are that:
-
1+1D disks have a smooth surface structure, and their midplane temperature is approximated by a power law well. They gravely underestimate the mid IR emission when compared to 2D disks.
-
Halos substantially increase the IR emission and the temperature of the midplane, which is smoother than obtained in disks without halos.
-
In 2D disks the midplane temperature shows up and downs with radius (Fig. 1). Such a hilly structure is also revealed in their surface structure.
-
Emission images of 2D disks display gaps and ring-like structures in particular in the region of terrestrial planets. Disk structures are caused by puffing up the disk surface and followed up by their shadows behind. The disk structure is dimmed when halos are considered. Rings and gaps are more pronounced in T Tauri stars than in Herbig Ae stars.
Acknowledgments
We are grateful to Endrik Krügel for discussions and helpful suggestions.
References
- Acke, B., van den Ancker, M. E., & Dullemond, C. P. 2004, A&A, 422, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armitage, P. J. 2007, Astrophysics of planet formation (Cambridge: University Press) [Google Scholar]
- Alexander, R. D., & Armitage, P. J. 2007, MNRAS, 375, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R. D., & Armitage, P. J. 2009, ApJ, 704, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Güsten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Bertout, C., Siess, L., & Cabrit, S. 2007, A&A, 473, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bjorkman, J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwman, J., Henning, Th., & Hillenbrand, L. A. 2008, ApJ, 683, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Dullemond, C. P., et al. 2007, ApJ, 664, 107 [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., et al. 2008, ApJ, 675, 1009 [Google Scholar]
- Calvet, N., D’Alessio, P., & Hartmann, L. 2002, ApJ, 568, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Charnoz, S., Fouchet, L., Aleon, J., & Moreira, M. 2011, ApJ, 737, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L. A., Swift, J. J., Mathews, G. S., & Williams, J. P. 2008, ApJ, 686, L115 [NASA ADS] [CrossRef] [Google Scholar]
- D’Alessio, P., Canto, J., Hartmann, L., et al. 1999, ApJ, 511, 896 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ApJ, 598, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P. 2000, A&A, 361, L17 [NASA ADS] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004a, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004b, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Monnier, J. D. 2010, ARA&A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Edgar, R. C., & Quillen, A. C. 2008, MNRAS, 387, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Graham, J. R., Akeson, R. L., & Najita, J. 2009, ApJ, 692, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., D’Alessio, P. D., Hernandez, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fleck, Jr. J. A., & Canfield, E. H. 1984, J. Comput. Phys., 54, 508 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukagawa, M., Tamura, M., Itoh, Y., et al. 2006, ApJ, 636, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Furlan, E., Watson, D. M., & McClure, M. K. 2009, ApJ, 703, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Furlan, E., Luhman, K. L., & Espaillat, C. 2011, ApJS, 195, 3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gail, H. P. 2004, A&A, 413, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayashi, C. 1981, PThPS, 70, 35 [Google Scholar]
- Heymann, F. 2010, Ph.D., University of Bochum [Google Scholar]
- Heymann, F., & Siebenmorgen, R. 2012, ApJ, submitted [Google Scholar]
- Huelamo, N., Lacour, S., Tuthill, P., et al. 2011, A&A, 528, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2008, ApJ, 685, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., & Natta, A. 2005, A&A, 438, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezic, Z., Groenewegen, M. A. T., Menshchikov, A., & Szczerba, R. 1997, MNRAS, 291, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kama, M., Min, M., & Dominik, C. 2009, A&A, 506, 1199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kemper, F., Vriend, W. J., & Tielens, A. G. G. M. 2005, ApJ, 633, 534 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler-Silacci, J., Augereau, J.-C., Dullemond, C., et al. 2006, ApJ, 639, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H. K., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Krijt, S., & Dominik, C. 2011, A&A, 531, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krügel, E. 2008, An introduction to the Physics of Interstellar Dust (IoP) [Google Scholar]
- Krügel, E., & Siebenmorgen, R. 1994, A&A, 288, 929 [NASA ADS] [Google Scholar]
- Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lommen, D., Wright, C. M., Maddison, S. T., et al. 2007, A&A, 462, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lommen, D., van Dishoeck, E. F., Wright, C. M., et al. 2010, A&A, 515, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lubow, S. H., Seibert, M., & Artymowicz, P. 1999, ApJ, 526, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1999, A&A, 344, 282 [NASA ADS] [Google Scholar]
- Malfait, K., Waelkens, C., & Waters, L. B. F. M. 1998, A&A, 332, 25 [Google Scholar]
- Matsumoto, M., & Nishimura, T. 1998, in Monte Carlo and Quasi-Monte Carlo Methods (Springer) [Google Scholar]
- Mayama, S., Tamura, M., Hanawa, T., et al. 2010, Science, 327, 306 [NASA ADS] [CrossRef] [Google Scholar]
- McCaughrean, M. J., & O’dell, C. R. 1996, AJ, 111, 1977 [NASA ADS] [CrossRef] [Google Scholar]
- Millan-Gabet, R., Monnier, J. D., Berger, J. P., et al. 2006, ApJ, 645, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Dullemond, C. P., de Koter, A., et al. 2009, A&A, 497, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Dullemond, C. P., Kama, M., & Dominik, C. 2011, Icarus, 212, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Miroshnichenko, A., Ivezic, Z., Vinkovic, D., & Elitzur, M. 1999, ApJ, 520, 115 [Google Scholar]
- Mizuno, H., Markiewicz, W. J., & Voelk, H. J. 1988, A&A, 195, 183 [NASA ADS] [Google Scholar]
- Mulders, G. D., Dominik, C., & Min, M. 2010, A&A, 512, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzerolle, J., Hartmann, L., & Calvet, N. 1998, AJ, 116, 2965 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., Strom, S. E., & Muzerolle, J. 2007, MNRAS, 378, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., Doppmann, G. W., Carr, J. S., et al. 2009, ApJ, 691, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Prusti, T., Neri, R., et al. 2001, A&A, 371, 186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natta, A., Testi, L., Neri, R., et al. 2004, A&A, 416, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natta, A., Testi, L., Calvet, N., et al. 2007, in Protostars and Planets V, ed B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 951, 767 [Google Scholar]
- Nomura, H. 2002, ApJ, 567, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Oliveira, I., Pontoppidan, K. M., Mern, B., et al. 2010, ApJ, 714, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, J., Benisty, M., Augereau, J.-C., et al. 2011, A&A, 528, A6 [Google Scholar]
- Ozernoy, L. M., Gorkavyi, N. N., Mather, J. C., & Taidakova, T. A. 2000, ApJ, 537, L151 [Google Scholar]
- Pascucci, I., Wolf, S., Steinacker, J., et al. 2004, A&A, 417, 793 [Google Scholar]
- Pinte, C., Menard, F., Duchene, G., & Bastien, P. 2006, A&A, 459, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Padgett, D. L., Menard, F., et al. 2008, A&A, 489, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Harries, T. J., Min, M., et al. 2009, A&A, 498, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontoppidan, K. M., Dullemond, C. P., van Dishoeck, E. F., et al. 2005, ApJ, 622, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Blake, G. A., & Smette, A. 2011, ApJ, 733, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Ratzka, Th., Leinert, C., Henning, T., et al. 2007, A&A, 471, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T. P. 2010, A&A, 520, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., et al. 2006, ApJS, 167, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Schegerer, A., Wolf, S., Voshchinnikov, N. V., et al. 2006, A&A, 456, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schegerer, A. A., Wolf, S., Ratzka, Th., & Leinert, Ch. 2008, A&A, 478, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schisano, E., Covino, E., Alcal, J. M., et al. 2009, A&A, 501, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siebenmorgen, R., & Gredel, R. 1997, ApJ, 485, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., & Krügel, E. 2010, A&A, 511, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sterzik, M. F., Durisen, R. H., Brandner, W., et al. 1994, Icarus, 111, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, K. M., Strom, S. E., Edwards, S., et al. 1989, AJ, 97, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Natta, A., Shepherd, D. S., & Wilner, D. J. 2003, A&A, 403, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thalmann, C., Grady, C. A., Goto, M., et al. 2010, ApJ, 718, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tutukov, A. V., & Fedorova, A. V. 2006, Astron. Reports, 50, 785 [Google Scholar]
- van Boekel, R., Dullemond, C. P., & Dominik, C. 2005, A&A, 441, 563 [Google Scholar]
- van den Ancker, M., The, P. S., & Tjin A Djie, H. R. E. 1997, A&A, 324, L33 [NASA ADS] [Google Scholar]
- Verhoeff, A. P., Min, M., Pantin, E., et al. 2011, A&A, 528, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vinkovic, D., Ivezic, Z., Jurkic, T., & Elitzur, M. 2006, ApJ, 636, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R., van Dishoeck, E. F., Doty, S. D., & Dullemond, C. P. 2009, A&A, 495, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voshchinikov, N. V., & Henning, T. 2008, A&A, 483, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, C., Wood, K., Lada, C. J., et al. 2004, MNRAS, 351, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Waters, L. B. F. M., & Waelkens, C. 1998, ARA&A, 36, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, D. M., Bohac, C. J., Hull, C., et al. 2007, Nature, 448, 1026 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Watson, D. M., Leisenring, J. M., Furlan, E., et al. 2009, ApJS, 180, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., & Cuzzi, J. N. 1993, Protostars and Planets III (A93-42937 17-90), 1031 [Google Scholar]
- Whitney, B. A., Wood, K., Bjorkman, J. E., & Cohen, M. 2003, ApJ, 598, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, A. N. 1977, ApJS, 35, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Padgett, D. L., & Stapelfeldt, K. R. 2003, ApJ, 588, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., et al. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top: IR emission of a T Tau disk viewed at ~45°, which is either computed using the 1+1D model (label “1D”) in a flat (green full line), a flaring (dashed green line) disk configuration, or the 2D disk. Iterations 1 to 9 of Eq. (4) of the 2D disk are shown. Bottom: midplane temperatures of the 1+1D flat disk and the various iterations of the 2D disk. |
| In the text | |
 |
Fig. 2 IR emission of 2D disks viewed nearly face-on (~20°) computed by applying different dust opacities. |
| In the text | |
 |
Fig. 3 IR emission of 2D disks viewed nearly edge-on (~20°) with (dashed) and without (full line) a dusty halo. The disks are either heated by a T Tauri star (top) or a Herbig Ae star (bottom). |
| In the text | |
 |
Fig. 4 Top: the relative height of the disk photosphere, zbot/r, as a function of radius of a disk heated by a T Tauri star without (full line) and with (dashed) halo. The scale height over radius, H/r, of a flat 1+1D disk (dashed) is shown for comparison. Gaps between ring structures are indicated. A shaded representation of zbot/r along the (x,y)-plane is displayed for a disk plus halo configuration (middle) and a pure disk (bottom). Color bars give the relative gray scale (%) in units of zbot/r. |
| In the text | |
 |
Fig. 5 Mid-IR images of disks heated by a T Tauri star at distance of 50 pc and viewed at 30°. The image of a pure disk (top) and a disk plus halo is shown (middle). Color bars are in log (Jy/arcsec2). Bottom: corresponding surface brightness distribution measured as cut along δ through origin of the image. Gaps between emission rings are indicated. |
| In the text | |
 |
Fig. 6 Top: the midplane temperature and relative height of the disk photosphere, zbot/r, as a function of radius of a 2D disk heated by a Herbig Ae star. Models are shown in a configuration of a pure disk (full line) and a disk plus halo (dashed). Power law fits (dotted) to the midplane temperature distribution are as labeled. Gaps between ring structures are indicated. Bottom: a shaded representation of zbot/r along the (x,y)-plane is shown for a pure disk model. Color bar gives relative gray scale (%) in units of zbot/r. |
| In the text | |
 |
Fig. 7 Top: Mid-IR image of a disk heated by a Herbig Ae star at distance of 50 pc and viewed at 30°. Color bar is in log (Jy/arcsec2). Bottom: Mid-IR surface brightness distribution measured as a cut along δ through the origin of an emission image of a pure disk (full line) and that computed in a disk plus halo configuration (dashed). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


