| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201118293 | |
| Published online | 23 February 2012 | |
A journey from the outskirts to the cores of groups
I. Color- and mass-segregation in 20K-zCOSMOS groups⋆
1 Universitá degli Studi dell’Insubria, via Valleggio 11, 22100 Como, Italy
e-mail: valentina.presotto@brera.inaf.it
2 INAF – Osservatorio Astronomico di Brera, via Brera, 28, 20159 Milano, Italy
3 INAF – IASF Milano, via Bassini 15, 20133 Milano, Italy
4 INAF – Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
5 Institute of Astronomy, ETH Zurich, 8093 Zürich, Switzerland
6 INAF – Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
7 UCO/Lick Observatory, Department of Astronomy and Astrophysics, University of California, Santa Cruz, CA 95064, USA
8 Max-Planck-Institut für extraterrestrische Physik, 84571 Garching b, 85748 Muenchen, Germany
9 IPMU, Institute for the Physics and Mathematics of the Universe, 5-1-5 Kashiwanoha, 277-8583 Kashiwa, Japan
10 MPA – Max Planck Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
11 Institut de Recherche en Astrophysique et Planétologie, CNRS, 14, avenue Edouard Belin, 31400 Toulouse, France
12 IRAP, Université de Toulouse, UPS-OMP, Toulouse, France
13 Laboratoire d’Astrophysique de Marseille, CNRS-Université d’Aix-Marseille, 38 rue Frederic Joliot Curie, 13388 Marseille, France
14 European Southern Observatory, Karl-Schwarzschild-Strasse 2, Garching b. Muenchen, 85748, Germany
15 Dipartimento di Astronomia, Università di Padova, vicolo Osservatorio 3, 35122 Padova, Italy
16 SUPA Institute for Astronomy, The University of Edinburgh, Royal Observatory, Edinburgh, EH9 3HJ, UK
17 University of Vienna, Department of Astronomy, Tuerkenschanzstrasse 17, 1180 Vienna, Austria
18 Instituto de Astrofisìca de Andalucìa, CSIC, Apartado de correos 3004, 18080 Granada, Spain
19 Instituto de Astrofsica de Canarias, Vía Lactea s/n, 38200 La Laguna, Tenerife, Spain
20 Dipartimento di Astronomia, Universitá di Bologna, via Ranzani 1, 40127 Bologna, Italy
21 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
22 Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre et Marie Curie, 98bis boulevard Arago, 75014 Paris, France
23 Institut d’Astrophysique Spatiale, Batiment 121, CNRS & Univ. Paris Sud XI, 91405 Orsay Cedex, France
24 INAF – IASF Bologna, via P. Gobetti 101, 40129 Bologna, Italy
Received: 18 October 2011
Accepted: 22 December 2011
Context. Studying theevolution of galaxies located within groups may have important implications for our understanding of the global evolution of the galaxy population as a whole. The fraction of galaxies bound in groups at z ~ 0 is as high as 60% and therefore any mechanism (among the many suggested) that could quench star formation when a galaxy enters group environment would be an important driver for galaxy evolution.
Aims. Using the group catalog obtained from zCOSMOS spectroscopic data and the complementary photometric data from the COSMOS survey, we explore segregation effects occurring in groups of galaxies at intermediate/high redshifts. Our aim is to reveal if, and how significantly, group environment affects the evolution of infalling galaxies.
Methods. We built two composite groups at intermediate (0.2 ≤ z ≤ 0.45) and high (0.45 < z ≤ 0.8) redshifts, and we divided the corresponding composite group galaxies into three samples according to their distance from the group center. The samples roughly correspond to galaxies located in a group’s inner core, intermediate, and infall region. We explored how galaxy stellar masses and colors – working in narrow bins of stellar masses – vary as a function of the galaxy distance from the group center.
Results. We found that the most massive galaxies in our sample (log (ℳgal/ℳ⊙) ≥ 10.6) do not display any strong group-centric dependence of the fractions of red/blue objects. For galaxies of lower masses (9.8 ≤ log (ℳgal/ℳ⊙) ≤ 10.6) there is a radial dependence in the changing mix of red and blue galaxies. This dependence is most evident in poor groups, whereas richer groups do not display any obvious trend of the blue fraction. Interestingly, mass segregation shows the opposite behavior: it is visible only in rich groups, while poorer groups have a a constant mix of galaxy stellar masses as a function of radius.
Conclusions. These findings can be explained in a simple scenario where color- and mass-segregation originate from different physical processes. While dynamical friction is the obvious cause for establishing mass segregation, both starvation and galaxy-galaxy collisions are plausible mechanisms to quench star formation in groups at a faster rate than in the field. In poorer groups the environmental effects are caught in action superimposed to secular galaxy evolution. Their member galaxies display increasing blue fractions when moving from the group center to more external regions, presumably reflecting the recent accretion history of these groups.
Key words: cosmology: observations / galaxies: groups: general / galaxies: evolution
© ESO, 2012
1. Introduction
The striking bi-modality of the color-magnitude and of the color-mass diagrams raises important questions about galaxy formation and evolution. What are the physical processes responsible for the sharp partition into blue cloud and red sequence galaxies? Does the environment play a key role in this process by boosting the transition into the red sequence region? What are the timescales for this transition? There is much evidence of correlations between galaxy properties and their environment, the oldest and best known being the morphology-density relation (see Oemler 1974; Dressler 1980, although the first mention of it dates back to Hubble). In general, blue, star-forming, disk-dominated galaxies are located preferentially in low-density regions, whereas red, inactive, elliptical galaxies favor high-density regions.
These two distinct galaxy evolutionary families can originate either from a priori differences set at galaxy formation epoch, the so-called nature scenario, or from environmentally driven processes taking place during the galaxy evolutionary history, the so-called nurture scenario.
The currently accepted ΛCDM model predicts the hierarchical growth of structures: as time proceeds, smaller structures merge to form progressively larger ones. This process implies that the fraction of galaxies located in groups progressively increases since z ~ 1.5, up to the Local Universe values, where most galaxies are found in groups (Huchra & Geller 1982; Eke et al. 2004; Berlind et al. 2006; Knobel et al. 2009). As a consequence, at least part of the observed decline of the global star-formation rate (SFR) from z ~ 1.5 until today (Lilly et al. 1996; Madau et al. 1998; Hopkins 2004) could be accelerated by environmentally driven phenomena.
In this context group environment plays a dominant role (Balogh et al. 2004; Wilman et al. 2005; Iovino et al. 2010; Peng et al. 2010), because only a small fraction of galaxies live in denser environments, such as cluster cores. There are observational indications that the color transition from blue to red galaxies proceeds faster in a group than in the coeval field population, an effect that becomes evident at redshifts lower than z ~ 1 and for galaxies of masses log (ℳgal/ℳ⊙) ≤ 10.6 (Iovino et al. 2010; Kovač et al. 2010; Bolzonella et al. 2010; Peng et al. 2010).
However, the physical phenomena responsible for accelerating the color transition from blue to red galaxies within groups are yet to be described. While the extreme local densities reached within cluster cores enable efficient ram pressure stripping of the galaxy cold gas on timescales of a few Myr (Gunn & Gott 1972; Abadi et al. 1999), within the groups different physical processes have been proposed. On one hand galaxy-group interactions like “strangulation”, starvation or halo gas stripping can remove warm and hot gas from a galaxy halo, efficiently cutting off the star formation gas supply (Larson et al. 1980; Cole et al. 2000; Balogh et al. 2000; Kawata & Mulchaey 2008). Alternatively, mergers/collisions and close tidal encounters among group member galaxies together with galaxy-galaxy harassment at the typical velocity dispersion of bound groups may also result in star-formation quenching (Moore et al. 1996). These physical processes do not require extreme local densities, and quench star formation in a more gradual and gentle way on timescales of several Gyr.
Among the observable effects of these processes are segregation phenomena, that is, not only differences between group – and field galaxy properties, but also radial trends of galaxy properties (e.g., colors, morphologies...) as a function of distance from the group/cluster center. These phenomena have already been extensively studied in galaxy clusters, where e.g., a strong radial dependence in the SFR is observed (Hashimoto & Oemler 1999; Balogh et al. 1999; Lewis et al. 2002; Balogh et al. 2004; Tanaka et al. 2004). The observed quenching of star-formation activity starts at large cluster-centric distances and low projected densities, in the so-called infalling regions, and even at large radii field star-formation values are not yet reached. This result suggests that galaxy transformation starts to occur in the infalling filaments, which consist of chains of groups in which field galaxies are affected by the group environment which changes their star-forming blue field-like properties into passive, red cluster-like galaxies. But even if groups seem to be the key environment to search for the nurture scenario, still the observational evidence for related segregation phenomena is quite scarce and holds mainly for the local Universe (Postman & Geller 1984; Mahdavi et al. 1999; Tran et al. 2001; Carlberg et al. 2001a,b; Girardi et al. 2003; Domínguez et al. 2002; Wilman et al. 2009; Bai et al. 2010; Ribeiro et al. 2010).
A complication to consider is the strong correlation between galaxy properties such as colors, morphologies and star formation, with galaxy stellar mass (Cowie et al. 1996; Gavazzi et al. 1996; Blanton et al. 2003; Kauffmann et al. 2003; Brinchmann et al. 2004; Baldry et al. 2004) and the additional correlation between the galaxy stellar mass itself and environment: galaxies in less dense environment tend to be less massive than those located in denser environment (Hogg et al. 2003; Kauffmann et al. 2004; Blanton et al. 2005; Scodeggio et al. 2009; Bolzonella et al. 2010). Thus any study performed on samples of galaxies containing a wide range of stellar masses cannot distinguish between true environmental effects and effects simply induced by the differing mass distributions of galaxies with environment. To isolate the true environmental effect, the analysis must be performed in narrow galaxy stellar mass bins. Much of the earlier work performed at intermediate/high z was based on incomplete and/or scarce samples of groups, where often the statistics was not high enough to perform such an accurate analysis in small mass bins.
In this paper we will study mass- and color segregation in groups over wide redshift and galaxy stellar mass ranges using the spectroscopic data from the recently completed zCOSMOS-Bright, a large survey reaching out to z ~ 1 with a fairly high and uniform sampling rate (Lilly et al. 2007), and its new group catalog (Knobel et al., in prep.). We will benefit also from the wide range of photometric data available for the COSMOS survey (Scoville et al. 2007; Ilbert et al. 2009; Oesch et al. 2010). Galaxy colors are the easiest parameter to measure among those that exhibit a distinctive bi-modality, and we selected rest-frame (U − B) color, bracketing the 4000 Å break, as a good indicator of the galaxy average star-formation histories over longer time-scales than emission line indicators such as e.g., [OII].
To shed light on how rapidly and significantly star formation is suppressed in groups and to overcome the low number statistics for individual systems (typically 7–8 members per group), we built stacked groups by co-adding spatial information from group member galaxies. This strategy enabled us to establish a statistically reliable sample and to reveal trends of galaxy properties as a function of the group-centric distance and of varying group richnesses.
The paper is organized as follows: in Sect. 2 we describe the data of our analysis, including the algorithm chosen to add the group member galaxies with photometric redshift. In Sect. 3 we illustrate the construction of the realistic mock catalogs with which we tested our algorithms. In Sect. 4 we explain how we stacked group member galaxies to build a composite group. In Sects. 5 and 6 we present our analysis and its results, which we discuss in Sect. 7. Our conclusions are summarized in Sect .8. A concordance cosmology is adopted throughout our paper, with h70 = H0/70 km s-1 Mpc-1, Ωm = 0.25 and ΩΛ = 0.75. All magnitudes are quoted in the AB system throughout.
2. Data
It is widely accepted in the literature that classical galaxy color/morphology trends in different environments are better investigated in bins of mass-volume-limited samples (Tasca et al. 2009; Iovino et al. 2010; Cucciati et al. 2010; Kovač et al. 2010; Xue et al. 2010; Cooper et al. 2010; Grützbauch et al. 2011). This strategy enables one to break the degeneracy caused by the relationships between galaxy stellar masses and environment and between galaxy stellar masses and colors/morphologies.
The recently completed zCOSMOS-bright survey with its high and uniform sampling rate offers unique opportunity to explore the presence/evolution of these trends over a wide range of cosmic time.
2.1. COSMOS and zCOSMOS surveys
The COSMOS survey is a large HST-ACS survey, with I-band exposures down to IAB = 28 on a field of 2 deg2 (Scoville et al. 2007). The COSMOS field has been the object of extensive multiwavelength ground- and space-based observations spanning the entire spectrum: X-ray, UV, optical/NIR, mid-infrared, mm/submillimeter and radio, providing fluxes measured over 30 bands (Hasinger et al. 2007; Taniguchi et al. 2007; Capak et al. 2007; Lilly et al. 2007; Sanders et al. 2007; Bertoldi et al. 2007; Schinnerer et al. 2007; Koekemoer et al. 2007; McCracken et al. 2010).
The zCOSMOS survey was planned to provide the crucial high-quality redshift information to the COSMOS field (Lilly et al. 2007). It benefitted of ~600 h of observations at VLT using the VIMOS spectrograph and it consists of two parts: zCOSMOS-bright, and zCOSMOS-deep. The zCOSMOS-deep targets ~10 000 galaxies within the central 1 deg2 of the COSMOS field, selected through color criteria to have 1.4 ≲ z ≲ 3.0. The zCOSMOS-bright is purely magnitude-limited and covers the whole area of 1.7 deg2 of the COSMOS field. It provides redshifts for ~20 000 galaxies down to IAB ≤ 22.5 as measured from the HST-ACS imaging. The success rate in redshift measurements is very high, 95% in the redshift range 0.5 < z < 0.8, and the velocity accuracy is ~100 km s-1 (Lilly et al. 2009). Each observed object has been assigned a flag according to the reliability of its measured redshift. Classes 3.x, 4.x redshifts, plus Classes 1.5, 2.4, 2.5, 9.3, and 9.5 are considered a secure set, with an overall reliability of 99% (see Lilly et al. 2009, for details).
Our work is based on the the zCOSMOS-bright survey final release: the so called 20K sample (simply 20K hereafter), totaling 16 623 galaxies with z ≤ 2 and secure redshifts according to the above flag classification (18 206 objects in total, irrespective of redshift and including stars).
Figure 1 shows the spatial distribution of the 20K galaxies. The red square corresponds to the region with the highest sampling rate, approximately ~62% of the parent galaxy catalog. Its boundaries are 149.55 ≤ RA ≤ 150.67 and 1.75 ≤ Dec ≤ 2.70. Within this region are 13 619 galaxies with secure redshift and z ≤ 1 (15 730 objects in total, irrespective of redshift and including stars) and their sky distribution is remarkably uniform.
 |
Fig. 1 RA-Dec distribution of the 16623 zCOSMOS-bright galaxies with secure redshift z ≤ 2 (the so-called 20K sample). The area within the red box (149.55 ≤ RA ≤ 150.67 and 1.75 ≤ Dec ≤ 2.70) has a nearly uniform sampling rate of ~62%. |
For objects brighter than IAB = 22.5 and without secure spectroscopic redshift, the wealth of ancillary photometric data provided by the COSMOS survey provides good quality photometric redshifts (Ilbert et al. 2009). Based on a comparison with the zCOSMOS spectroscopic redshifts, Ilbert et al. (2009) estimate an accuracy of σzphot = 0.007 × (1 + zs) for galaxies brighter than IAB = 22.5. Applying the ZEBRA code (Feldmann et al. 2006) to 30 bands, Oesch (in prep.) obtains a similar accuracy.
In our analysis we used photometric redshift values obtained by the ZEBRA code.
For all galaxies brighter than IAB = 22.5, absolute rest-frame magnitudes and stellar masses were obtained using standard multi-color spectral energy distribution (SED) fitting techniques, using the secure spectroscopic redshift, if available, or the photometric one. Rest-frame absolute magnitudes were obtained using the ZEBRA code (see Feldmann et al. 2006, for the details of the code), while stellar masses were obtained using the hyperzmass code (Pozzetti et al. 2010; Bolzonella et al. 2010). From the available stellar population synthesis libraries we adopted those of Bruzual & Charlot (2003), assuming a Chabrier initial mass function (Chabrier 2003).
2.2. The spectroscopic group catalog
The group catalog used in this paper is a subset of the 20K group catalog described in Knobel et al. (in prep., see also 2009, for an earlier version of the catalog). The 20K group catalog consists of 1496 groups with at least two spectroscopic member galaxies (188 with at least five spectroscopic members). Knobel et al. (in prep.) uses a “multi-pass procedure” to achieve an impressive quality in group reconstruction, as tested using realistic mock catalogs. This method, when combined with the standard friends-of-friends (FOF) algorithm, yields for the resulting group catalog values of completeness (i.e., fraction of real detected groups) and purity (i.e., fraction of non-spurious groups) that are extremely good and stable as a function of both redshift and number of members observed in the reconstructed groups. Typical values of these two quantities, for groups reconstructed with five or more spectroscopic observed members, are around ~80% at all redshifts and do not decrease substantially for groups with lower number of observed members. The interloper fraction, i.e., the fraction of field galaxies erroneously classed as group members, always remains below ~20% at all redshifts for groups reconstructed with more than five spectroscopic observed members, with only a slight increase for groups with lower number of observed members. Another point worth noticing is that the algorithm to detect groups treats each galaxy as a point in RA-Dec-redshift space, therefore avoiding any interloper/completeness dependence on galaxy properties such as colors or masses (see Knobel et al., in prep., for more details).
In this paper the analysis is restricted to groups with at least five spectroscopically observed members that are located within the high sampling rate box introduced in Fig. 1. From now on we will call this sample the spectroscopic group sample: it totals 178 groups and 1437 group member galaxies at z ≤ 1. Our choice enables us to work with groups that have best values for purity and interloper fraction, and to secure a reliable definition of group center and radius. These two parameters are crucial to build the composite group and for our algorithm which retrieves group members without spectroscopic redshift informationd (see later Sects. 2.4 and 4).
2.3. The spectroscopic field sample
To define the field galaxy sample, we started by selecting 20K galaxies located within the high sampling rate box and outside any of the reconstructed groups of Knobel et al. (in prep.). We therefore discarded from this sample galaxies located in pairs, triplets and quadruplets, i.e., members of the groups with fewer observed members are not considered in our science analysis.
To perform the fairest comparison between group and field samples, we took into account the possibility of spurious trend introduced by residual group contamination or by the different redshift ranges covered by the group/field galaxy samples. Galaxies lying in the closest proximity of groups could be contaminated by spectroscopic group members missed by the group-finding algorithm. In addition, the redshift distribution of the spectroscopic group catalog is far from being uniform, displaying prominent peaks, especially at low redshift where the 20K field of view limits the cosmic volume explored and we need to consider the appropriate coeval field population.
To take into account these two factors, we further more restricted the field sample to galaxies located within velocity distances 2000 ≤ |Δv| ≤ 5000 km s-1 from the spectroscopic group sample, – therefore following the same redshift ditribution of group member galaxies – and with radial projected distances R > 4 × Rfudge from any group of 20K group catalog, Rfudge being an estimate of the virial radius provided by Knobel et al. (in prep.) (see Sect. 4.2 for details). From now on we will call this set of galaxies the field sample, totalling 6556 galaxies at z ≤ 1.
We also introduced a complementary set of field galaxies that we call near-field galaxies. These are 20K galaxies within the high sampling rate box that do not belong to any of the reconstructed groups of Knobel et al. (in prep.), but with velocity distances |Δv| ≤ 2000 km s-1 and radial projected distances R ≤ 4 × Rfudge from at least one group of the spectroscopic group sample. The near-field sample so defined totals 1694 galaxies at z ≤ 1 and contains, by definition, galaxies located in the close proximity of the spectroscopic group sample. In Sect. 6.3 we will use this sample to check for possible environmental effects extending outside group radii, e.g., color differences of near-field galaxy population with respect to the general field sample.
 |
Fig. 2 Summary of the results obtained with our algorithm. Top left: completeness distribution (see text for definition) for the 20K mocks (black dot-dashed line) and for the 20K+photo-zs mock groups (red solid line). Top right: fraction of interlopers as a function of normalized group-centric distance for the 20K/20K+photo-zs mock groups (black stars and red triangles, respectively). Orange squares refer to the fraction of interlopers, |
2.4. Adding photo-zs: the spec+photo-z group catalog
For each group the number of available member galaxies down to IAB = 22.5 is limited by the incomplete sampling rate of 20K. To increase this number, we took advantage of the exquisite quality of the photometric redshifts available in the COSMOS field, see Sect. 2 to incorporate in our analysis photometric redshifts for galaxies brighter than IAB = 22.5 and without reliable spectroscopic data. A higher number of group member galaxies enables one to improve centering and richness estimates for each group, quantities crucial to properly center and rescale distinct groups to build a composite one (see e.g., Carlberg et al. 1997).
In Knobel et al. (in prep.) a probability approach was adopted to retrieve member galaxies brighter than IAB = 22.5 and that have no spectroscopic information. To each galaxy a probability, pin, of being part of a group was assigned, depending on its projected radial and velocity distance from the group center (we refer the reader to the paper by Knobel et al. (in prep.), for a more detailed description of the adopted method). The drawback of this approach is that each galaxy may have multiple associations to different groups.
To overcome this drawback, we developed a slightly different strategy, whose main advantage is that it assigns each galaxy only one spectroscopic group, thus avoiding multiple assignments of a galaxy to different groups, and the need to adopt an arbitrary probability cut-off to bypass this problem.
For a detailed description of our algorithm we refer the reader to Appendix A, while in Sect. 3 we will present extensive tests that we performed on mock catalogs to check the reliability of the final spec+photo-z group catalog.
Suffice is to say that we chose the selection function to identify putative photometric-redshift members in a way to not only keep the fraction of interlopers as low as possible, but also to avoid introducing any radial dependency of the interloper fraction. The last point is important because we will be looking for radial dependencies of galaxy properties.
As already mentioned in Sect. 2.2, we chose a conservative definition of the spectroscopic group sample, restricting ourselves to only 178 groups detected with at least five spectroscopic members within the high sampling rate box introduced in Fig. 1 box (149.55 ≤ RA ≤ 150.666 and 1.75 ≤ Dec ≤ 2.7). Within this area and up to z = 1.0 there are 13 619 galaxies with reliable spectroscopic redshift and 11 994 with an estimated photometric redshift.
Our algorithm adds another 684 member galaxies with photometric redshifts to the already existing 1437 spectroscopic group member galaxies, and from now on this is the group sample we will use. The final number of groups with more than 10(15) members after applying our algorithm is twice(three times) that in the spectroscopic group catalog, i.e., there are 78(41) groups instead of the original 39(14) groups. The number of groups with more than 20 members is six times the original one: 25 groups instead of the original four groups.
As a final point we notice that we repeated all analyses presented in this paper considering only galaxies from the spectroscopic group catalog and our results remained entirely unchanged, albeit at a lower significance.
3. The zCOSMOS mock catalogs
The use of realistic mock galaxy catalogs is important for assessing the reliability of the algorithm we adopted to produce the spec+photo-z group catalog and to validate the procedures we chose to define group centers and richnesses (see Sects. 2.4 and 4).
We took advantage of the 24 COSMOS mock light-cones provided by Kitzbichler & White (2007). These mock light-cones are based on the Millennium DM N-body simulations of Springel (2005) and use semianalytic recipes of Croton et al. (2006) as updated by De Lucia & Blaizot (2007) for populating the simulations volume with galaxies.
From each of these 24 light-cones we extracted three different types of mock catalogs:
-
1.
The 40K mock catalogs: 100% complete to IAB = 22.5. In these catalogs all galaxies brighter than IAB = 22.5 are spectroscopically observed with a 100% success rate. We added to each galaxy redshift an error of 100 km s-1 to account for the typical zCOSMOS spectroscopic redshift error as estimated from observations (see Lilly et al. 2009).
-
2.
The 20K mock catalogs: mimicking the 20K zCOSMOS spectroscopic sample. We applied the same observational strategy adopted to select the spectroscopic zCOSMOS targets: using the slit positioning algorithm SPOC on the 40K catalogs, see Bottini et al. (2005), and accounting for the spectroscopic redshift failures by including the same redshift success rate as the real data.
-
3.
The 20K+photo-zs mock catalogs: mimicking the data set we used in our analysis. The spectroscopic galaxies are those listed in the 20K mock catalogs, while a photometric redshift is provided for the remaining galaxies of the 40K mock catalogs. For the photometric redshift galaxy sample we reproduced the photometric redshift error σzphot = 0.007 × (1 + zs). We also took into account the presence of catastrophic failures in estimating photo-z, that is, the excess of galaxies with errors larger than Δphot-z = 3σzphot with respect to the simple Gaussian distribution. For the set of photometric redshift adopted in our analysis we were able to estimate a percentage of ~8% (by using the 20K subset flagged 4.x or 3.x and comparing their spectroscopic redshift to their photometric redshift). Group members with such high values of phot-z error cannot be retrieved by our algorithm and are a considerable source of incompleteness in group reconstruction. We chose a fairly conservative approach and also considered catastrophic errors of 10% in the 20K+photo-zs mock catalogs, by randomly permuting the photometric redshifts for 10% of the galaxies while keeping the galaxy RA-Dec fixed. coordinates.
We applied to the 20K mock catalogs the same group finding algorithm used for the 20K sample (see Knobel et al. 2009). We then selected groups with at least five spectroscopic members located within the high sampling rate box introduced in Fig. 1 and applied to the 20K+photo-zs mock catalogs the algorithm described in Sect. 2.4.
The COSMOS mock light-cones provide dark matter halos IDs that can easily be used to identify real groups and real group members, i.e., the set of galaxies located within the same dark matter halo in each mock catalog (see also Knobel et al. 2009). If we define completeness as the ratio of the reconstructed group members in the 20K/20K+photo-zs mock catalogs to the total number of real group members in the 40K mock catalogs, the improvement introduced by our algorithm is shown in the top left panel of Fig. 2. This panel shows the distribution of the completeness for all groups of the 20K mocks and for those obtained after applying our algorithm to the 20K+photo-zs mocks (black dot-dashed line and red-solid line, respectively). We were able to improve the median completeness from 67% of the 20K mock catalog up to 90% in the 20K+photo-zs mocks: the number of groups that are 100% complete is three times larger than using only the 20K mocks. As a consequence, the group richness, defined as the number of members brighter than an adopted rest-frame absolute magnitude cut-off, is also easier to recover in a reliable way. For more than half of the cases the richness as measured for reconstructed groups in the 20K+photo-zs mocks equals the same quantity as obtained from the 40K mock catalogs.
Our algorithm achieves this remarkable result while adding a negligible fraction of interloper members, i.e., galaxies that do not share the same dark matter halo in the 40K mock catalogs. For half of the groups we added less than 3% of new interlopers with respect to the total members in the 20K+photo-zs catalog, therefore attaining the same interlopers fraction as in the spectroscopic group catalog.
We also checked for any dependence of the interloper fraction on the normalized group-centric distance Rgal/Rfudge, Rfudge being an estimate of the virial radius provided by Knobel et al. (in prep., see Sect. 4.2 for details). For this test we divided each group into a central part and two concentric intermediate and external rings, as in Sect. 4.2, and adopted exactly the same mass and redshift limits adopted subsequently in our analysis, see Sect. 5.
In the top right panel of Fig. 2 we show the fraction of interlopers in each of these three regions for the 20K/20K+photo-zs mock groups (black stars and red triangles, respectively), as obtained using the low-z, mass-limited, mock group samples. Notice that the trend introduced by the group-finding algorithm in the 20K mock reconstructed groups is not modified by adding photo-zs members. In the same panel the orange squares display the fraction of interlopers in the 20K sample spectroscopic group catalog, estimated using the probabilities, pin,i, associated to each observed group spectroscopic member: 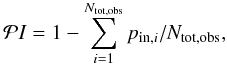 (1)as provided by Knobel et al. (in prep.). These values have been calibrated in Knobel et al. (in prep.) using simulations, and therefore by construction agree well with the interloper fraction estimated from 20K mock groups. In turn, because adding phot-z members does not alter the trends significantly, these values agree well with the interloper fraction for the 20K+photo-zs mock groups. The picture does not change when plotting the same quantities for the high-z, mass-limited, mock group samples, or when selecting subsets of groups according e.g., to their richness. Therefore we always used the
(1)as provided by Knobel et al. (in prep.). These values have been calibrated in Knobel et al. (in prep.) using simulations, and therefore by construction agree well with the interloper fraction estimated from 20K mock groups. In turn, because adding phot-z members does not alter the trends significantly, these values agree well with the interloper fraction for the 20K+photo-zs mock groups. The picture does not change when plotting the same quantities for the high-z, mass-limited, mock group samples, or when selecting subsets of groups according e.g., to their richness. Therefore we always used the 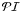 values obtained from spectroscopic group members to estimate the interlopers’ contamination as a function of the distance from the group center for our spec+photo-z group catalog, see Sect. 6.2.
values obtained from spectroscopic group members to estimate the interlopers’ contamination as a function of the distance from the group center for our spec+photo-z group catalog, see Sect. 6.2.
4. Building the stacked group
To explore galaxy properties as a function of the distance from the center of the group, we needed to build ensemble systems, because the scarcity of individual group members prevents a detailed analysis of each group. In this section we illustrate in detail the steps of building the so-called stacked-group: a composite group obtained by spatially co-adding all group member galaxies (simply SG from now on).
The two main ingredients to build a SG are precise re-centering and scaling of all available groups. It is therefore extremely important that each group center and richness is defined as reliably as possible, so that the trends we are searching for are not smoothed out. We will discuss precise definition of both quantities in this section. We remind the reader that from now on any number quoted, unless explicitly stated, includes both spectroscopic and photometric redshift group member galaxies, as obtained from the algorithm discussed in Sect. 2.4 and which we describe in more detail in Appendix A.
4.1. Group centering
A good group center definition is essential to our science analysis, because we will be searching for radial trends that can be easily erased by errors in group centering. After adding photo-zs, as discussed in the previous section, 50% of the groups in our sample possess more than nine members which makes group center definition more robust. However the simple methods of estimating group centers, such as the median of members coordinates, provide only rough estimates of the group center, especially for the numerically poorer groups. We therefore tried an alternative strategy, taking into account sky-projected group galaxy densities.
Using the 2D-Voronoi areas as proxy for density measurement, we defined the Voronoi-weighted center (VW center from now on) as 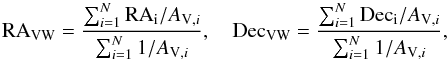 (2)where AV,i is the 2D-Voronoi area associated to the ith galaxy member, that is, the projected area containing all points closer to the ith galaxy than to any other member galaxy. We used galaxies located outside 3 × Rgr (where Rgr is the radius of the minumum circle containing all group members) and within 1 × σzphot to avoid divergence of 2D-Voronoi areas for galaxies located at the periphery of groups.
(2)where AV,i is the 2D-Voronoi area associated to the ith galaxy member, that is, the projected area containing all points closer to the ith galaxy than to any other member galaxy. We used galaxies located outside 3 × Rgr (where Rgr is the radius of the minumum circle containing all group members) and within 1 × σzphot to avoid divergence of 2D-Voronoi areas for galaxies located at the periphery of groups.
This way galaxies that are located in group denser regions will have a smaller AV,i and they will weigh more, while those that are in less dense regions will affect the center determination less. This method thus provides a center for the group, which is located by definition in the area of greatest galaxy over-density, and is not affected by the details of the spatial distribution of galaxies at the outskirt. For a similar approach see Diaz et al. (2005).
We used our set of mock catalogs to test the advantages of this center definition with respect to simpler ones, like the median of the member galaxies coordinates (median center from now on). We assumed the position of its central galaxy as fiducial center for each group, as provided by the mocks.
In the bottom left panel of Fig. 2 we show the median distance of the VW center (violet triangles) and that of the median center (cyan stars) for each of the three mock catalogs defined in Sect. 2.4. Error bars show the rms among mock catalogs extracted from the different 24 light-cones. We note that the VW center provides a better estimate of the center with respect to the median center on average. Furthermore, the VW centers, when applied to the groups whith photo-zs added using our algorithm, are nearly indistinguishable from those obtained when all members down to IAB = 22.5 possess spectroscopic redshift. The median value of the distance of the VW centers from the group central galaxy is 40 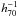 kpc for 20K+photo-zs mocks, with an improvement of nearly 40% in centering with respect to the 20K mocks.
kpc for 20K+photo-zs mocks, with an improvement of nearly 40% in centering with respect to the 20K mocks.
In the bottom right panel of Fig. 2 we show the distance histogram of the VW center to the central galaxy position for the 20K mocks as a black dot-dashed line and for the 20K+photoz mocks as a red solid line. The improvement in group centering obtained when adding photo-z members is quite obvious.
We therefore adopted the VW method to define the center of each group.
 |
Fig. 3 Left panel: redshift distribution of the zCOSMOS-bright galaxies (black). Red points represent group member galaxies with spectroscopic and photometric redshifts as obtained from our algorithm. The cyan solid line and the violet dashed line correspond to the two different magnitude cut-offs adopted to define the volume-limited samples of the low- and high-redshift bin respectively, see text for details. Central and right panel: (U − B) rest-frame color versus mass for the lowest and the highest redshift bin. The blue dashed line corresponds to the color-dependent ℳcut − off, while the red solid line corresponds to the fixed ℳcut − off for our mass volume-limited sample. The red dot-dashed lines highlight the mass ranges adopted in the mass-segregation analysis, see Sect. 6.5 for details. The cyan dotted line corresponds to the separation between red and blue galaxies (see text for its precise definition). |
4.2. Group rescaling
The procedure of stacking groups of different sizes and masses into an ensemble system requires rescaling of individual galaxy group-centric-distances. In studies of galaxy clusters, projected cluster-centric-distances R are generally rescaled with Rvir or R200, whose estimate is proportional to cluster velocity dispersion σv, that is, a proxy of cluster mass (Carlberg et al. 1997; Biviano et al. 2002; Katgert et al. 2004). However, the problem is not trivial when dealing with galaxy groups, where the uncertainties in the estimate of velocity dispersions, masses, size, and the group dynamical state in general are larger, because of the small number of group members.
In the literature there are different approaches in rescaling R for groups, using 1) the virial radius Rvir or R200, 2) an estimate of the rms of the position of member galaxies RH, and 3) sometimes radial distances are not rescaled at all (see Girardi et al. 2003, for a detailed review).
Our groups span a wide range of sizes, and therefore a rescaling of physical distances seemed unavoidable. We decided to use Rfudge as the scaling factor, provided by Knobel et al. (in prep.). This fudge quantity, as many other ones correlating with the observed group richness, was estimated and calibrated using our realistic mock catalogs. In brief, given an observed group at redshift z with richness 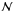 , defined as the number of members brighter than an adopted rest-frame absolute magnitude cut-off, its Rfudge corresponds to the mean Rvir among all reconstructed mock groups wjth the same
, defined as the number of members brighter than an adopted rest-frame absolute magnitude cut-off, its Rfudge corresponds to the mean Rvir among all reconstructed mock groups wjth the same 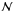 and redshift (see Knobel et al. (in prep.), for more details on how this quantity is calculated). The quantity Rfudge correlates with Mhalo fudge, an estimate of the mass of the group well, which additionally shows its relevance for our analysis (see Knobel et al. 2009 (in prep.), for more details on how both these quantities are estimated).
and redshift (see Knobel et al. (in prep.), for more details on how this quantity is calculated). The quantity Rfudge correlates with Mhalo fudge, an estimate of the mass of the group well, which additionally shows its relevance for our analysis (see Knobel et al. 2009 (in prep.), for more details on how both these quantities are estimated).
Because our goal is to distinguish property of galaxies located in regions with different physical properties rescaling by Rfudge, a quantity related to Rvir, suits our needs well. Indeed, the virial radius is a scaling factor for many timescales of different processes such as the crossing time, the relaxation time or the merging time (Boselli & Gavazzi 2006; Weinmann et al. 2006). All galaxies that are inside the virial radius are experiencing the group potential effects either for the first time or many times. In contrast, those galaxies that are outside the virial radius are a mixed population of both in-falling galaxies and galaxies that once passed through the virial radius but now are in the outskirts, the so-called back-splash population (Gill et al. 2005).
Before stacking groups, we therefore rescaled each member galaxy distance to the VW center, Rgal, with the corresponding Rfudge of its group. Below we will use only scaled distances, ℛ, unless otherwise specified.
We add a final caveat: when discussing our results, we should take into account projection effects. We observed the 2-D projection of a 3-D distribution of member galaxies. Assuming a spherical distribution, this implies that e.g., the inner observed region includes galaxies located in the outer group shells that are located along the line of sight of the group central part. Hence a fraction of galaxies observed, in projection, in the inner region actually belongs to the outskirts. These projection effects will tend to smooth the radial trends we are looking for, so that any observed trend is a lower limit for the real trend present in 3-D. Vice versa in the external regions of groups the contamination by field galaxies, on average bluer and less massive than group galaxies, will tend to introduce spurious segregation trends, and we need to account for them carefully.
5. Analysis
5.1. Selecting mass volume-limited samples
We focused our analysis on two redshift bins: 0.2 ≤ z ≤ 0.45 and 0.45 < z ≤ 0.8, where we defined the classical volume-limited samples taking into account the luminosity evolution of individual galaxies. Following Zucca et al. (2009), we adopted a linear evolution with redshift: 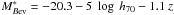 to parametrize the evolution of
to parametrize the evolution of 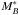 of the luminosity function. The corresponding evolving cut-off magnitudes are
of the luminosity function. The corresponding evolving cut-off magnitudes are 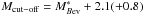 for the low(high) redshift bin. For 0.2 ≤ z ≤ 0.45 the volume-limited sample consists of 829 out of 1128 total galaxies, belonging to 79 groups. For 0.45 < z ≤ 0.8 it consists of 510 out of 660 total galaxies, belonging to 64 groups (see Table 1). The total volume-limited field sample consists of 1869(2893) galaxies, while the near-field volume limited sample consists of 683(612) galaxies for the low(high) redshift bin. In the left panel of Fig. 3 we show the
for the low(high) redshift bin. For 0.2 ≤ z ≤ 0.45 the volume-limited sample consists of 829 out of 1128 total galaxies, belonging to 79 groups. For 0.45 < z ≤ 0.8 it consists of 510 out of 660 total galaxies, belonging to 64 groups (see Table 1). The total volume-limited field sample consists of 1869(2893) galaxies, while the near-field volume limited sample consists of 683(612) galaxies for the low(high) redshift bin. In the left panel of Fig. 3 we show the 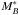 versus redshift distribution of the total galaxy sample (black points) and that of both spectroscopic and photometric redshift group member galaxies (red points). The cyan solid line and the violet dashed line correspond to the magnitude cut-offs defining the low- and high-redshift volume-limited samples. In the following, the group richness
versus redshift distribution of the total galaxy sample (black points) and that of both spectroscopic and photometric redshift group member galaxies (red points). The cyan solid line and the violet dashed line correspond to the magnitude cut-offs defining the low- and high-redshift volume-limited samples. In the following, the group richness 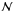 for each group is defined as the number of (phot+spec-z) member galaxies surviving to the more conservative absolute rest-frame magnitude cut-off:
for each group is defined as the number of (phot+spec-z) member galaxies surviving to the more conservative absolute rest-frame magnitude cut-off: 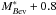 , unless explicitely stated. This quantity correlates, albeit with a large scatter, with the mass of the halo where the group resides and therefore is a good proxy for it (see Knobel et al. 2009).
, unless explicitely stated. This quantity correlates, albeit with a large scatter, with the mass of the halo where the group resides and therefore is a good proxy for it (see Knobel et al. 2009).
Number of volume-limited and mass-volume-limited (spec+phot-z) group member galaxies.
The flux-limited target definition of zCOSMOS-bright, IAB ≤ 22.5, translates into a B-band rest-frame selection at z ~ 0.8. Therefore the 20K galaxy sample, when rest-frame B-band selection is adopted, is free from significant color-dependent incompleteness in (U − B) rest-frame colors up to z ~ 1. However the (U − B) rest-frame color completeness in the B-band rest frame selection does not imply completeness in mass selection: the B-band rest-frame selection is biased toward blue, low-mass galaxies, while missing the corresponding red, equally low-mass ones. Environmental trends observed in samples selected using rest-frame B-band magnitudes could therefore be simply the results of this incompleteness coupled with different galaxy mass distributions in different environments (Bolzonella et al. 2010).
To separate true environmental effects from mass-driven ones, we used in our analysis mass volume-limited samples, that is, samples complete down to a fixed galaxy mass cut-off. To obtain them, we followed the same approach as in Iovino et al. (2010). In brief, we first calculated the limiting stellar mass for each galaxy in the 20K sample, i.e., the stellar mass it would have at its spectroscopic redshift, if its apparent magnitude were equal to the limiting magnitude of our survey: log (ℳlim(zgal)) = log (ℳgal) + 0.4 (IAB − 22.5). We then used these estimated limiting masses to define, in bins of (U − B) rest-frame colors for each redshift bin, the mass ℳcut − off below which 85% of galaxies of that color lie. We fitted ℳcut − off to obtain a color-dependent mass limit cut-off. The value of ℳcut − off for the reddest galaxies in each redshift bin is the one that we used as the limiting mass for that bin.
In the central and right panel of Fig. 3 we show the (U − B) rest-frame color versus the stellar mass for the lowest and highest redshift bin respectively. The blue dashed line shows the color-dependent ℳcut − off, while the red solid line shows the value chosen to define mass-limited samples: log (ℳgal/ℳ⊙) ≥ ℳcut−off = 9.8 and log (ℳgal/ℳ⊙) ≥ ℳcut − off = 10.56 for the lowest and highest redshift bins.
 |
Fig. 4 Comparison of the general properties of groups in the 0.2 ≤ z ≤ 0.45 (black dot-dashed line) and 0.45 < z ≤ 0.8 (red solid line) redshift bin. From left to right we compare Rfudge (the estimate of the virial radius), log ℳfudge (the estimate of the mass of the group), both fudge quantities are calibrated with the mocks as defined in Knobel et al. (2009), and |
To define the mass-dependent color cut separating the blue and red galaxies, we performed a robust fit of the red sequence as a function of the galaxy stellar mass in the high-z bin, where a large number of observed galaxies displays a prominent and well defined red sequence. The color cut was then obtain by shifting the fitting line by 2·rmsred, where rmsred ~ 0.08 is the dispersion of the red galaxies along the red sequence. We adopted the same color cut for the low-z bin. Numerically, the stellar mass dependent color cut is 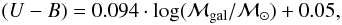 (3)and it is shown by the cyan dotted lines in Fig. 3.
(3)and it is shown by the cyan dotted lines in Fig. 3.
We tested that our results do not change if we apply a constant color cut, (U − B) = 1, to separate red and blue galaxies, a simpler definition that corresponds equally well to the dip of the bimodal distribution.
For the lowest redshift bin the final group mass-complete sample contains 571 galaxies, while for the highest redshift bin it contains 265 galaxies. The mass-complete field samples consist of 743(728) galaxies for the lowest(highest) redshift bin, while the near-field samples consist of 293(211) galaxies for the lowest(highest) redshift bin.
5.2. Low-z and high-z stacked-groups
For each of the two redshift bins defined in the previous section, 0.2 ≤ z ≤ 0.45 and 0.45 < z ≤ 0.8, we proceeded to build the corresponding SG. Notice that while for centering purposes we used all spec-z and phot-z galaxies available in our group catalog, irrespective of their mass and B-band rest-frame luminosity, for our analysis we will use only galaxies within the mass volume-limited samples as defined in Table 1.
Before moving to a detailed study of the group member galaxies properties, it is interesting to compare the general properties of groups in low- and high-redshift bins, to highlight any redshift-dependent trend in the group sample we used in our science analysis.
In Fig. 4 we compare from left to right Rfudge – the virial radius estimate (Knobel et al., in prep.), Mfudge – the mass of the group calibrated with the mocks as in Knobel et al. (2009), and the group richness, 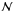 , as defined in Sect. 5.1, for low- (black dot-dashed line) and high- (red solid line) redshift galaxy groups. The KS test always rejects with more than 99.99% confidence the hypothesis that properties of low and high redshift groups are drawn from the same distribution. In the low-redshift bin on the mean we deal with smaller, less massive and poorer groups than those in the highest- redshift bin. This is not an unexpected result given that zCOSMOS is a flux-limited survey and therefore the observed population of both galaxies and groups varies with increasing redshift. As a consequence, the group detection works only on progressively brighter/more massive galaxies moving to higher redshifts. We shall need to take into account these differences when discussing our results. We define a subset of richer groups for the low-redshift bin using richness
, as defined in Sect. 5.1, for low- (black dot-dashed line) and high- (red solid line) redshift galaxy groups. The KS test always rejects with more than 99.99% confidence the hypothesis that properties of low and high redshift groups are drawn from the same distribution. In the low-redshift bin on the mean we deal with smaller, less massive and poorer groups than those in the highest- redshift bin. This is not an unexpected result given that zCOSMOS is a flux-limited survey and therefore the observed population of both galaxies and groups varies with increasing redshift. As a consequence, the group detection works only on progressively brighter/more massive galaxies moving to higher redshifts. We shall need to take into account these differences when discussing our results. We define a subset of richer groups for the low-redshift bin using richness 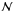 , defined for this bin as the number of member galaxies surviving the evolving magnitude cut-off:
, defined for this bin as the number of member galaxies surviving the evolving magnitude cut-off: 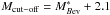 (see left panel of Fig. 3). We adopted a separation of
(see left panel of Fig. 3). We adopted a separation of 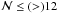 to distinguish between poor(rich) groups, a value roughly corresponding to Mfudge ≤ (>)13.3, so that rich low-z groups are virtually indistinguishable in mass distribution from the high-redshift sample. Indeed, while a KS test comparing the distributions of Mfudge of poor and rich groups defined this way rejects the hypothesis that they are drawn from the same distribution with more than 99.99% confidence, the KS test comparing distributions of Mfudge of rich low-z groups and of high-z groups does not reveal any significant difference between the two.
to distinguish between poor(rich) groups, a value roughly corresponding to Mfudge ≤ (>)13.3, so that rich low-z groups are virtually indistinguishable in mass distribution from the high-redshift sample. Indeed, while a KS test comparing the distributions of Mfudge of poor and rich groups defined this way rejects the hypothesis that they are drawn from the same distribution with more than 99.99% confidence, the KS test comparing distributions of Mfudge of rich low-z groups and of high-z groups does not reveal any significant difference between the two.
Radial range explored in the three SG regions.
To explore how galaxy population properties change as a function of group-centric distance, we first sorted SG galaxies into increasing scaled distances from SG center and then divided their distribution into three equipopulated bins corresponding to inner, intermediate, and peripheral SG regions.
In Table 2 we list the exact radial ranges of each of these three regions, all values are normalized to Rfudge. The corresponding three median distances are ℛ ~ 0.15, ℛ ~ 0.4 and ℛ ~ 0.85, respectively, therefore these regions can be considered as the group inner core, intermediate, and more external/in-fall region.
Given that the median Rfudge is ~500 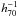 kpc in both redshift bins, the inner region extends typically up to ~150
kpc in both redshift bins, the inner region extends typically up to ~150 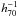 kpc. Because the VW center is on the average only ~40
kpc. Because the VW center is on the average only ~40 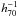 kpc away from the group fiducial center (see Sect. 4.1), our error in centering is negligible with respect to the median inner region size, and should not have a significant impact when exploring the group-centric dependence of galaxy properties.
kpc away from the group fiducial center (see Sect. 4.1), our error in centering is negligible with respect to the median inner region size, and should not have a significant impact when exploring the group-centric dependence of galaxy properties.
 |
Fig. 5 Sky distribution of the galaxies belonging to the low-z (left) and high-z (right) composite group. RA-Dec positions are expressed in terms of the rescaled distances ℛ. Points are colored according to the (U − B) colors of the galaxies, while point dimensions are scaled according to the masses of the galaxies. As a reference we draw dashed circles corresponding to the different central/intermediate/external region limits in each composite group. |
The sky distribution of galaxies belonging to the low-z (left) and high-z (right) composite group is shown in Fig. 5. Points are coded according to the (U − B) colors of the galaxies, while point dimensions are scaled according to galaxy masses. As a reference we draw dashed circles corresponding to the division between the different regions in each composite group. We note that the overall shape of the composite group has a well-defined peak corresponding to the center, while the projected density decreases as we move from the center to the outskirts. A visual inspection of the galaxy sky distribution already shows rough differences in masses and colors depending on the area we explore. In the next section we proceed to extensively analyze these trends and their dependence on intrinsic galaxy/group properties, properly accounting for possible field contamination effects.
6. Results
We will start our analysis by exploring how galaxy colors are affected by group environment, irrespective of galaxy position within the group (see Sect. 6.1). We will then move to investigate the presence of color segregation within the group environment (Sect. 6.2), and if the effect of the group environment extends to scales somewhat larger than those of the group size itself (see Sect. 6.3). Thanks to the high statistic of the 20K we will also be able to investigate if and how observed trends depend on group richness and on galaxy stellar mass (see Sect. 6.4). Finally we will search for evidence of mass segregation inside groups and how it might depend on group richness and affect observed mass trends (see Sect. 6.5).
 |
Fig. 6 Top panels: cumulative galaxy stellar mass distribution of the mass-complete group and field samples in red and cyan colors. Bottom panels: Fblue at fixed galaxy mass in groups (red circles) and field (cyan stars). Left panels always refer to the low-redshift bin, while right panels refer to the high redshift one. We used galaxy mass bins 0.4 dex wide. |
6.1. Fblue and galaxy stellar masses in groups vs. field
The cumulative galaxy stellar mass distributions of the mass-complete group and field samples are shown in the top panels of Fig. 6, red solid and cyan dot-dashed lines, respectively, the left(right) panels refer to the low(high) redshift bin. The KS test rejects the hypothesis that group and field galaxy mass distributions are drawn from the same population with more than 99.99% confidence for both redshift bins. Group environment hosts preferentially more massive galaxies than the field one, confirming well-known literature results (Iovino et al. 2010; Kovač et al. 2010; Bolzonella et al. 2010).
As a consequence, to explore the presence of color trends as a function of environment, we need to separate the joint effect of mass and environment and to perform the analysis in narrow mass bins of galaxy stellar mass. We adopted a galaxy stellar mass bin of 0.4 dex, which is approximately twice our error in estimating galaxy stellar masses (Pozzetti et al. 2010). Bottom panels of Fig. 6 show Fblue at fixed galaxy stellar mass in groups (red circles) and field (cyan stars), while Table 3 lists in detail the Fblue values and their errors. Both at high and low redshift, the blue fraction increases when moving toward less massive galaxies. Fblue is always higher in the field than in the group, a difference that decreases moving to more massive galaxies. The most massive galaxies (log (ℳgal/ℳ⊙) > 11.0) do not show any significant Fblue evolution with redshift within the error bars. For the galaxies with 10.6 ≤ log (ℳgal/ℳ⊙) ≤ 11.0, Fblue decreases for both group and field environment when moving from high to low redshift.
Notice that on average, groups in the low-z bin are poorer than those in the high-z bin. As we will show below, see Sect. 6.4, Fblue depends on the group richness, Fblue being lower in richer groups. As a consequence, the decrease of Fblue across the explored redshift range for the sample of group galaxies should be even more pronounced.
Observed blue fractions in groups and field for different galaxy stellar mass bins.
At fixed galaxy stellar mass, the migration to the red sequence happens earlier in the groups and later in the field, suggesting the presence of physical mechanisms able to remove gas that causes the earlier quenching of galaxies in groups. We remind the reader that any contamination of the group sample by field galaxies and vice versa, for which we are not applying any correction, will only render the observed trends less prominent. The real, corrected, trends therefore would be even more pronounced. This result excellently agrees with our previous zCOSMOS results on groups (Iovino et al. 2010; Bolzonella et al. 2010; Peng et al. 2010).
The questions we will address in the following sections are: do the group member galaxies all share the same Fblue value irrespective of their position within the group? Do the galaxies located in the central region of groups share the same mass distribution as the galaxies located in the group outskirts? Ideally, the first question is better addressed in narrow bins of galaxy stellar mass to avoid the mass-color degeneracy. However, even with such a dataset as the 20K, we are still limited by small number statistics, when splitting our sample according to distances from group center and therefore we will start our analysis working in cumulative mass ranges in the next section.
 |
Fig. 7 SG blue fraction as a function of the group-centric distance. Left/(right) panels refer to the low/(high) redshift bin and mass limits are ℳcut − off = 9.8/(ℳcut − off = 10.56). Open circles refer to observed Fblue while filled ones to corrected Fblue, i.e., taking into account interloper contamination (see text for details). The points refer to the three regions: inner core, intermediate, and more external/infall region. Corrected blue fractions values are displayed at the median distance of each region, while observed blue fractions are offset for clarity. As a reference we plot the fraction of the blue field galaxies (cyan star) and the mean corrected blue fraction in groups (big red circle). |
6.2. Color segregation: Fblue as a function of the group-centric distance
To explore the color segregation, we measured 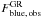 , the observed fraction of blue group member galaxies, in each of the three SG regions defined in Sect. 5.2. We used the formula
, the observed fraction of blue group member galaxies, in each of the three SG regions defined in Sect. 5.2. We used the formula 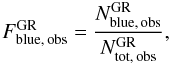 (4)where the index GR refers to group galaxies. However, to establish the reliability of any observed changing mix of galaxy colors at different radial distances from the group center, it is essential to properly account for the presence of field galaxy contaminants and their (changing) relative contribution at differente distances from the group center, because the field population has a higher Fblue than the group. We thus need to estimate the corrected group fraction of blue galaxies,
(4)where the index GR refers to group galaxies. However, to establish the reliability of any observed changing mix of galaxy colors at different radial distances from the group center, it is essential to properly account for the presence of field galaxy contaminants and their (changing) relative contribution at differente distances from the group center, because the field population has a higher Fblue than the group. We thus need to estimate the corrected group fraction of blue galaxies, 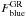 :
: 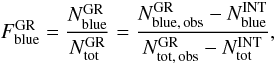 (5)that is, the corrected ratio of the blue member galaxies to the total number of member galaxies, after excluding the percentage of interlopers – indicated by the index INT – entering in the observed list of group members because of group detection algorithm failures.
(5)that is, the corrected ratio of the blue member galaxies to the total number of member galaxies, after excluding the percentage of interlopers – indicated by the index INT – entering in the observed list of group members because of group detection algorithm failures.
If 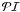 is the estimated percentage of interlopers defined in Sect. 4, we can obtain
is the estimated percentage of interlopers defined in Sect. 4, we can obtain 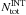 for each group region by
for each group region by 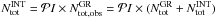 . The value of
. The value of 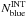 can simply be estimated as
can simply be estimated as 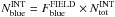 , where
, where 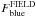 is the known blue fraction of the field galaxies. This way we take into account the radial trend of interloper contamination and have all ingredients to retrieve the corrected values of
is the known blue fraction of the field galaxies. This way we take into account the radial trend of interloper contamination and have all ingredients to retrieve the corrected values of 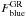 from Eq. (5).
from Eq. (5).
In Fig. 7 the left/(right) panel shows the blue fraction as a function of the group-centric distance in the SG for the low/(high) redshift bin in the mass-complete sample down to ℳcut−off = 9.8/(ℳcut − off = 10.56). Uncorrected and corrected blue fraction values are indicated with open and filled circles, respectively. Corrected blue fractions are displayed at the median normalized ℛ distance of galaxies in each region, while uncorrected blue fractions are slightly offset for clarity. As a reference we plot the fraction of blue field galaxies (cyan stars) and of the whole group (big red filled circle, corrected values only). Error bars are estimated using the approximate analytical formulas for a binomial distribution provided by Gehrels (1986). In Table 4 we list the values of observed and corrected Fblue for each region and sample considered.
Blue fractions in groups, observed and corrected for field contamination.
In the low-redshift bin, the observed 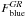 rises as the distance from the group center increases (left panel of Fig. 7). Though becoming less prominent, this color segregation holds even when correcting for interlopers contamination. Considering the field point, we can see a trend of increasing Fblue moving from the inner core of groups to their outskirts and farther away to the field.
rises as the distance from the group center increases (left panel of Fig. 7). Though becoming less prominent, this color segregation holds even when correcting for interlopers contamination. Considering the field point, we can see a trend of increasing Fblue moving from the inner core of groups to their outskirts and farther away to the field.
The difference between 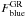 in the inner core and that in the outskirts is 1.7σ1st − 3nd, where σ1st − 3nd is the sum in quadrature of σ1st and σ3rd, the error of the fraction of blue galaxies in the inner core and outskirts. The difference between
in the inner core and that in the outskirts is 1.7σ1st − 3nd, where σ1st − 3nd is the sum in quadrature of σ1st and σ3rd, the error of the fraction of blue galaxies in the inner core and outskirts. The difference between 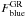 in the outskirts and
in the outskirts and 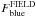 is 7σ3nd − field. Entering the group potential well has a considerable influence in changing galaxy colors, but the most relevant difference is between
is 7σ3nd − field. Entering the group potential well has a considerable influence in changing galaxy colors, but the most relevant difference is between 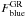 in the inner core and
in the inner core and 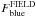 : 11σ1st − field.
: 11σ1st − field.
Moving to the highest redshift bin, we do not detect any significant color radial trend within the SG, while we still detect a significant difference with respect to the field galaxy population (right panel of Fig. 7). The group blue fraction is at a constant value of 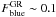 , a value 3.9σ lower than the corresponding blue fraction in the field sample. The values of Fblue for group and field are significantly lower in this redshift bin than those obtained in the low redshift bin discussed previously. In order to understand this result, we need to remember that we applied a higher galaxy stellar mass cut-off in the high-redshift bin: log (ℳgal) ≥ 10.56, thus we are observing galaxies more massive than in the low redshift bin, which is the obvious cause for the general lowering of the values of Fblue for the field and the group population. Another factor to consider is that we are observing groups that are on average more massive than their low-redshift counterparts (see Fig. 4).
, a value 3.9σ lower than the corresponding blue fraction in the field sample. The values of Fblue for group and field are significantly lower in this redshift bin than those obtained in the low redshift bin discussed previously. In order to understand this result, we need to remember that we applied a higher galaxy stellar mass cut-off in the high-redshift bin: log (ℳgal) ≥ 10.56, thus we are observing galaxies more massive than in the low redshift bin, which is the obvious cause for the general lowering of the values of Fblue for the field and the group population. Another factor to consider is that we are observing groups that are on average more massive than their low-redshift counterparts (see Fig. 4).
Before moving to investigate in detail how our findings depend on group richness and galaxy stellar masses in Sect. 6.4, we will explore in the next section whether the observed differences between group and field stop at group boundaries, or if there is a continuous trend of increasing Fblue in the closest proximity of groups.
 |
Fig. 8 Fblue of near-field galaxies (violet empty stars) as a function of increasing projected radial distances from groups in the low-redshift bin: ℛ ≤ 2.0, ℛ ≤ 3.0 and ℛ ≤ 4.0. Violet filled stars show Fblue of near field after excluding near-field galaxies with projected radial distances ℛ ≤ 2.0. The filled square shows Fblue for the first near-field annulus, after correcting for the 15% spectroscopic galaxy-group incompleteness, see text for details. Observed Fblue values are displayed at the median distance of each near-field region, while corrected ones are slightly offset for clarity. As a reference we display the Fblue of the field with a cyan star. |
6.3. Near-field vs. global field: is there a large-scale F trend?
trend?
The physical scale, in terms of density or projected distances, over which environment begins to set up the well known correlations with galaxy SFRs, colors, and morphologies is a question that is still open (Kauffmann et al. 2004; Balogh et al. 2004; Blanton et al. 2006). We explored the possible presence of large-scale trends of 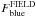 , with the aim of detecting e.g., colors redder than those of field sample for the galaxy population located in the closest proximity of our groups. As discussed in Sect. 2.3, we defined a sample of field galaxies ideally not affected by group environment, and a sample of so-called near-field galaxies, i.e., galaxies located in the closest proximity of groups.
, with the aim of detecting e.g., colors redder than those of field sample for the galaxy population located in the closest proximity of our groups. As discussed in Sect. 2.3, we defined a sample of field galaxies ideally not affected by group environment, and a sample of so-called near-field galaxies, i.e., galaxies located in the closest proximity of groups.
In the low-redshift bin, where the sample size enables us to perform this analysis, we split the near-field into subsets of three nested rings of increasing projected radial distances from the SG center that were defined as follows: ℛ ≤ 2.0, ℛ ≤ 3.0 and ℛ ≤ 4.0, and measured Fblue for each of them. These values are plotted in Fig. 8 with empty stars, and display a regular increase moving away from the group center, progressively nearing the value obtained for the field sample. However, this apparent continuous trend, extending beyond group size, disappears when excluding field galaxies with projected radial distances ℛ ≤ 2.0 (filled stars) from each of the points shown in Fig. 8, suggesting that the trend in question is caused by contamination from missed group members, predominantly located in the nearest neighborhood of groups.
The same result can be obtained correcting the values of the first near-field ring with a procedure similar to that used for group galaxies. The galaxy success rate of the group-finding algorithm turns into a spectroscopic incompleteness on galaxy-group basis of 15%, as estimated in Knobel et al. (2009). Correcting for this percentage of contamination by group galaxies is enough to raise the observed value of 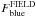 in the first near-field annulus to that of the field, as shown by the filled square in Fig. 8.
in the first near-field annulus to that of the field, as shown by the filled square in Fig. 8.
This analysis confirms that the physical scale on which the environment plays its role coincides with the group physical scales, in agreement with Kauffmann et al. (2004), Blanton et al. (2006), and Wilman et al. (2010). It therefore suggests that there is no transition region from field to group domain and field galaxies start to be affected by the group environment when they enter it.
Interstingly, it also implies that the values we estimated for the incompleteness of our group catalog is realistic, because it produces, once the corresponding correction is applied, values of Fblue for the first near-field annulus that agree well with field values.
 |
Fig. 9 Corrected blue fraction as a function of the group-centric distance in the low-z poor groups (left) and rich groups (right). We define poor(rich) groups as those with number of member galaxies ≤ ( > )12 after applying the evolving magnitude cut off |
6.4. Color segregation: a closer look at galaxy mass and group richness dependencies
In Sect. 6.2 we have shown that low- and high-z group galaxies display different radial color trends. However, we also noticed two important differences: the galaxy stellar mass cut-off adopted (log (ℳgal/ℳ⊙) ≥ 9.8 to be compared to log (ℳgal/ℳ⊙) ≥ 10.56), and the different range in group richness spanned in these two redshift bins. It is therefore interesting to investigate how the observed radial trends of Fblue depend on these two quantities. We split the low-z group sample according to richness 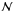 defined as the number of member galaxies surviving after applying the evolving magnitude cut-off
defined as the number of member galaxies surviving after applying the evolving magnitude cut-off 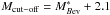 , adopting a separation of
, adopting a separation of 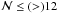 to distinguish between poor(rich) groups. We then split the total galaxy sample for each of the two rich and poor SG into two bins of galaxy stellar mass: galaxies with stellar masses 9.8 ≤ log (ℳcut − off) ≤ 10.56 and log (ℳcut − off) ≥ 10.56.
to distinguish between poor(rich) groups. We then split the total galaxy sample for each of the two rich and poor SG into two bins of galaxy stellar mass: galaxies with stellar masses 9.8 ≤ log (ℳcut − off) ≤ 10.56 and log (ℳcut − off) ≥ 10.56.
In Fig. 9 we show how Fblue varies for the subsamples defined this way (from now on we display only corrected values). Poor(rich) groups are on the left(right) panel and triangles refer to lower stellar mass bin, squares to higher stellar mass bin, and filled circles to the total mass volume-limited sample. As a reference and with the same symbols for each stellar mass bin, we plot the values of Fblue for field galaxies and those for the total poor and rich group galaxies sample considered.
The value of Fblue increases moving from higher to lower galaxy stellar masses for each environment considered (see also Sect. 6.1). However, there is another trend superimposed to this one: at fixed stellar mass the mean Fblue is higher in poor groups than in rich ones, confirming previous tentative results (see Margoniner et al. 2001; Gerke et al. 2007; Iovino et al. 2010, and references therein).
Figure 9 shows for radial trends that bluer galaxies are preferentially located in the group outskirts only for poor groups. No such trend is observed for richer groups. For poor groups, galaxies with lower stellar mass show a continuous trend of increasing Fblue, whereas Fblue for most massive galaxies increases only in the outermost group region. Rich groups do not show any obvious radial trend.
Thus poor groups display higher Fblue values for their member galaxies than richer groups and stronger radial trends at fixed galaxy stellar mass than richer groups. The observed galaxy color radial trends become more evident moving from richer to poorer groups and moving from higher to lower galaxy stellar masses.
We can therefore better explain the observed differences between low- and the high-z groups trends discussed in Sect. 6.2 as caused by the different cut-off in galaxy stellar masses and to the different group richness ranges observed in the two different redshift bins.
It is somewhat expected that at high-z the massive groups we explore do not display any radial trend for the massive galaxies shown in plot Fig. 7.
We will now proceed to explore if the differences observed in radial trends between poor groups and rich groups relate to the possible presence of galaxy stellar mass segregation within groups, a factor that could be important in creating and/or enhancing observed color trends.
 |
Fig. 10 Cumulative radial distribution of the galaxies belonging to each mass bin for both the lowest (left) and highest (right) redshift bin. We show the most massive galaxies with an orange solid line and the less massive galaxies with a green dotted line. As a reference we draw the limits of the first and second regions with a dot-dashed black line. |
 |
Fig. 11 Cumulative radial distribution of the galaxies belonging to each mass bin for poor (left) and rich (right) groups in the lowest redshift bin. We show the most massive galaxies with an orange solid line and the less massive galaxies with a green dotted line. As a reference we draw the limits of the first and second regions with a dot-dashed black line. |
6.5. Mass segregation
The goal of this section is to check for the presence of mass segregation within our group sample, to clarify if any of galaxy colors radial trends we observed are simply the reflection of the galaxy colors and stellar mass correlation coupled with varying galaxy stellar mass functions moving from central to peripheral group regions.
We split the mass-complete galaxy sample into two stellar mass bins: at low redshift the stellar mass limits chosen are 9.8 ≤ log (ℳgal/ℳ⊙) ≤ 10.56 and log (ℳgal/ℳ⊙) > 10.56, with a total of 320(251) galaxies in the lowest(highest) mass bin. At high redshift the stellar mass limits chosen are 10.56 ≤ log (ℳgal/ℳ⊙) ≤ 10.9 and log (ℳgal/ℳ⊙) > 10.9; in this case there are 132(133) galaxies in the lowest(highest) mass bin. In the left(right) panel of Fig. 10 we show the cumulative radial distribution of the galaxies belonging to these bins for the low(high) redshift SGs. The dotted line always refers to the lowest stellar mass bin, while the solid line refers to the highest stellar mass bin. As a reference a dot-dashed black line indicates the boundaries of the different group regions defined in Sect. 5.2. In both redshift bins the most massive galaxies preferentially populate the innermost regions, while the less massive galaxies prefer the outer ones. A KS test confirms the existence of a mass segregation for the low(high) redshift bin with confidence higher than 98.6%(99.99%).
KS test probabilities that the mass distribution of the galaxies in each group region and that of the field sample of galaxies are drawn from the same distribution.
We here also explored the group richness dependency of the mass segregation by repeating the same radial analysis but dividing the low-z bin groups into poor and rich subsamples (see Sect. 6.2 for definitions). The cumulative radial distributions of galaxies are plotted in Fig. 11 for poor groups in the left panel, and for rich groups in the right panel. In both panels dotted lines refer to galaxies with 9.8 ≤ log (ℳgal/ℳ⊙) ≤ 10.56, while the solid lines denote galaxies at log (ℳgal/ℳ⊙) > 10.56. For poor groups there is no significant mass segregation because the KS test results are consistent with the hypothesis that the radial distribution of galaxies from the two mass bins are drawn from the same distribution. Vice versa, galaxies located in rich groups display a significant mass segregation, with most massive galaxies being closer to the SG center than the less massive ones. In this case the KS test rejects the hypothesis that the radial distribution of galaxies from the two mass bins are drawn from the same distribution with more than 99.3% confidence.
We performed a KS test comparing the galaxy stellar mass distribution in different SG regions and field galaxies. For low-z rich and high-z groups there is no significant difference between field galaxies and the outermost SG region, while the inner/intermediate regions display a significant difference with respect to the field, in agreement with their observed galaxy stellar mass segregation. For low-z, poor groups the galaxy stellar mass distribution is only marginally different from that of field galaxies (a ~ 2.5σ result), and this outcome holds irrespective of group-centric distance, in agreement with the absence of galaxy stellar mass segregation in these groups. In Table 5 we detail all numerical results of the various KS tests.
One could argue that the mass segregation we are detecting within rich low-z groups and high-z groups increases through interloper contamination. On average, interlopers would preferentially populate group peripheral regions, where we actually observe a galaxy stellar mass distribution that resembles more that of field galaxies, thus producing the observed stellar galaxy mass distribution radial trends. We used a Monte Carlo technique to establish the robustness of our results with respect to this effect. For each of the two SGs – rich low-z and high-z – we depleted the mass-complete sample of its galaxy members by the estimated interloper fraction in each group region. We used galaxy colors to select the most probable interlopers, so that the galaxies removed had a value of Fblue equal to that estimated for field galaxies (see Sect. 6.1). We performed this exercise 1000 times, keeping constant the total number of galaxies (i.e., randomly counting some of the surviving galaxies twice). Each time we estimated the KS test probability that the radial distribution of less and most massive member galaxies were drawn from the same radial distribution.
For rich low-z groups the KS test confirms a mass segregation with a median confidence level of 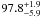 . For high-z groups, the KS test confirms a mass segregation with a median confidence level of
. For high-z groups, the KS test confirms a mass segregation with a median confidence level of 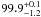 . In both cases the quoted errors correspond to the lowest and highest quartiles of the KS test probability distribution. We can conclude that at high-z the signal for a genuine and significant radial stellar mass segregation for group galaxies is strong and reliable, while at low-z the observed mass segregation for rich group galaxies is somewhat enhanced by interloper contamination, but, albeit at lower significance, an indication of its existence is still present.
. In both cases the quoted errors correspond to the lowest and highest quartiles of the KS test probability distribution. We can conclude that at high-z the signal for a genuine and significant radial stellar mass segregation for group galaxies is strong and reliable, while at low-z the observed mass segregation for rich group galaxies is somewhat enhanced by interloper contamination, but, albeit at lower significance, an indication of its existence is still present.
The main result of this section is therefore that low-z poor groups do not show significant mass segregation; whereas low-z rich groups and high-z groups, whose group mass ranges are somewhat similar, display a significant mass segregation in the galaxy stellar mass ranges explored.
Because low-z poor groups are those that show a significant color segregation, which is undetected in low-z rich groups and high-z groups (see Sect. 6.4), we conclude that the changing mix of color and masses are unrelated phenomena, possibly originating from different physical mechanisms. In the next section we will discuss a possible interpretation.
7. Migration from blue to red: the effects of group environment
Our analysis has confirmed that stellar mass is an important parameter in the discussion of environmental influence on galaxy properties and their evolution.
In Sect. 6.1 we have shown that for massive galaxies, log (ℳgal/ℳ⊙) ≥ 11.0, the value of Fblue does not change moving from field to group galaxies: most massive galaxies are red and dead irrespective of the environment they live in, a well-known result both at low redshift (see e.g., Hansen et al. 2009; Bamford et al. 2009; Kimm et al. 2009, and references therein) and at intermediate/high redshift (see e.g., Iovino et al. 2010; Kovač et al. 2010; Peng et al. 2010; McGee et al. 2011, and references therein).
Below this mass threshold we observe a gradual “opening up” of the difference between group and field values, so that lower values of Fblue are reached earlier in groups than in the field (see Fig. 6), confirming results previously obtained using the zCOSMOS 10K sample (see e.g., Iovino et al. 2010; Kovač et al. 2010; Bolzonella et al. 2010, and references therein) and recent results from the COSMOS survey (George et al. 2011).
In addition to these trends, our analysis has shown that moving to masses below log (ℳgal/ℳ⊙) = 11.0 some subtler differences emerge when observing trends within groups, both as a function of galaxy stellar mass and as a function of group richness. In the following discussion we concentrate on the lower redshift bin of our sample (0.2 < z < 0.45), where we were able to study in detail the joined effect of galaxy stellar mass and group richness on galaxy colors. The conclusions we will infer are easy to translate into the higher redshift bin, where (see Sects. 5.2 and 6.4) we can explore only higher group richnesses and higher galaxy stellar mass ranges.
For galaxies in the mass range log (ℳgal/ℳ⊙) > 10.56 we do not observe any strong radial trend within groups in the mix of red and blue galaxies (except possibly for poorer groups of our sample, where the Fblue value in the outermost region increases) while we observe a clear difference with respect to Fblue for field galaxies.
For galaxies in the lower mass range 9.8 ≤ log (ℳgal/ℳ⊙ < 10.56), we observe a significant radial dependence of the mix of red and blue galaxies in poorer groups: red galaxies are preferentially found in the group center. In contrast the trend disappears for the richer group, suggesting that galaxies situated in richer groups (i.e., presumably located in more massive dark matter halos) reach a redder color at earlier redshifts for each fixed galaxy stellar mass.
This picture reflects what is found in the local Universe: most massive galaxies do not show a significant color radial trend within groups, while less massive galaxies are responsible for the progressive blueing of the group member galaxies at intermediate and long group-centric distances. Furthermore, these trends are stronger in poorer environments (see e.g., Bamford et al. 2009).
Opposite to this differentiation in terms of a color segregation is the result shown in Fig. 11, implying that a significant mass segregation is already set up in rich groups, whereas poor groups display a constant mix of galaxy stellar masses irrespective of the radial distance from group center.
Do these differences provide the means to better understand how the group environment influences the migration of galaxies from the blue cloud to the red sequence, and to derive estimates for the timescales involved in this process?
In other words, does the observed difference in the radial color segregation between richer and poorer groups imply the presence of a different efficiency in the two environments of the mechanisms that cause the transition of a galaxy from the blue cloud to the red sequence? Or could this difference just be caused by a different time-scale for the evolution of structures of different mass (different overdensity), such that richer groups formed earlier than poorer ones, so that within them there simply has been more time for environmental effects to act upon group member galaxies?
The observed difference in mass segregation trends provides an important element for us to try and answer this question. It is well known that mass segregation occurs when the exchange of energy among group member galaxies has led most massive galaxies to set in the core of the group while the lighter galaxies, moving at higher velocities, preferentially reside in the outer regions. The setting/absence of mass segregation in a group therefore is a rough indication of the time lapse since group formation, and because we do not dectect any significant mass segregation in poor groups, these systems are probably formed later than the richer ones.
This in turn may suggest that the absence of a color radial gradient in richer groups at all masses we explored it is the result of the longer time-scale of these systems, that is, of the longer time available for the group environment to influence its member galaxies.
In contrast poorer groups have not yet been able to set mass segregation, because they are possibly still in the process of forming and accreting field galaxies. Their radial distribution in galaxy stellar masses does therefore not show any strong segregation yet. The radial color trends we observe are somewhat reminescent of the still recent accretion history of these groups and suggest that peripheral galaxies have been accreted more recently than those located near the group center.
Interestingly, however, even the galaxies located at the outskirts show redder colors than field galaxies of similar masses. In addition, the simple exercise we performed in Sect. 6.3 shows that there is no continuous trend in color segregation moving from the outskirts of groups toward the nearest field: the physical scale on which the environment plays its role coincides with the group physical scales, and the processes that affect galaxy colors starts to operate as soon as galaxies enter the group environment. This result confirms that group environment influences galaxy colors on short time-scales, in agreement with what is suggested by the strong bimodality in color distribution itself: any quenching process that would last more than 1.5–2 Gyr would erase the observed bimodality of galaxy colors by overpopulating green valley (Balogh et al. 2009; McCarthy et al. 2008; Font et al. 2008).
Our analysis therefore implies that galaxy color transformation and mass segregation originate from different physical processes, whose time-scales, of a few Gyr, are only slightly different, so that whenever mass segregation is observed, color segregation has already been wiped out and viceversa. Furthermore, it suggests that up to a fixed galaxy stellar mass limit, galaxies have already been residing for a longer time within richer groups compared to poorer groups, while for each considered group richness the galaxies of lower masses are presumably those that have entered the group environment more recently (see Fig. 9). The physical processes causing the color trends observed in our data could be both starvation and/or galaxy-galaxy collisions/interactions, because both operate on a similar time-scale. Starvation operates exclusively on the hot-gas reservoir, i.e., there are no indications that it results in structural transformation (Weinmann et al. 2009).
On the other hand, galaxy-galaxy interactions can change morphology, boost specific SFR (sSFR) and quench galaxies, and galaxy-pair fractions are highly environmentally dependent, because denser environments show more pairs (Kampczyk et al. 2011). An analysis including galaxy morphologies and spectral features could help to understand which the most likely process between the two is, because galaxy-galaxy collisions cause morphological transformations while starvation produces the so called “strangled” red-spiral population, and we plan to present it in a forthcoming paper.
Our high-z results satisfactorily fit within the above picture presented for low-z groups. McGee et al. (2009) show that at a fixed mass of group/cluster considered, the accretion history of member galaxies is remarkably similar and independent of redshift.
Given that the ℳfudge distributions of rich low-z groups and high-z groups do not differ significantly, we would expect a similar behavior in terms of both color- and mass-segregation.
A KS test shows that the stellar mass distribution of galaxies more massive than log (ℳgal/ℳ⊙) > 10.56 does not differ significantly for low-z rich groups and high-z groups and in both cases they do not show any color radial trend. Finally, both rich low-z groups and high-z groups show evidence of mass segregation, confirming that the high-z groups we observed in zCOSMOS do not deviate from the simple picture we proposed.
8. Conclusions
Taking advantage of the new 20K zCOSMOS spectroscopic data, its excellent group catalog and the wide photometric coverage of the COSMOS survey, we built two composite groups at intermediate (0.2 ≤ z ≤ 0.45) and high (0.45 < z ≤ 0.8) redshifts. We studied in detail how galaxy stellar masses and colors vary as a function of the distance from the group center. The analysis was performed using mass-complete samples to separate the obvious galaxy stellar mass/color dependencies.
Our main results are:
- (i)
In the lowest redshift bin explored, the blue fraction of most massive galaxies, i.e., log (ℳgal/ℳ⊙) ≥ 10.56, does not display strong group-centric dependence, despite displaying a clear lower blue fraction in groups than in the field. This result holds irrespective of group richness, except possibly for poorer groups of our sample, where it is driven exclusively by the Fblue value in the outermost region, however. In contrast, there is a radial dependence in the changing mix of red and blue galaxies for galaxies of lower masses, i.e., 9.8 ≤ log (ℳgal/ℳ⊙) < 10.56, with red galaxies being found preferentially in the group center. This trend is stronger for poorer groups, while it disappears for richer groups.
- (ii)
In the highest redshift bin, where only higher galaxy stellar masses and richer groups are available within the zCOSMOS survey, the blue fraction of observed galaxies at log (ℳgal/ℳ⊙) ≥ 10.56 does not display strong group-centric dependence, although it displays a lower blue fraction in groups than in the field.
- (iii)
The global Fblue for group galaxies shows a clear dependence on group richness: rich group galaxies are redder than poor group galaxies on average.
- (iv)
Mass segregation shows the opposite behavior with respect to galaxy color trends: it is visible only in rich groups, while poorer groups have a constant mix of galaxy stellar masses as a function of group-centric distances. Therefore the observed color trends cannot be simply explained as caused by different stellar mass distributions in different group regions.
- (v)
The physical length-scale on which the environment plays its role coincides with the group physical scales.
The parallel absence(presence) of color segregation in rich(poor) groups indicates that nurture effects are still in action in poorer structures, whereas richer systems have already exhausted their effects, so that all galaxies are uniformly red irrespective of their position within the group (at least down to the galaxy stellar masses we explored). The corresponding presence(absence) in rich(poor) groups of mass segregation suggests that richer systems have been in place for long enough so that more massive galaxies have sunk to the group center, something that has yet to happen for the poorer groups, which still keep a memory of their more recent growth history.
Both observations suggest a simple scenario where color- and mass-segregation originates from different physical processes with similar time-scales, so that whenever mass segregation is observed, color segregation has been already wiped out and viceversa.
Lower mass galaxies in poorer groups are the witnesses of environmental effects in action superimposed to secular galaxy evolution: these galaxies still display gradually bluer colors moving from group center to more external regions as a consequence of the still recent accretion history of these groups. Starvation and galaxy-galaxy interactions could both be the reason for a mechanism that quenches star formation in groups at a faster rate than in the field.
Future work will include a detailed analysis of galaxy morphologies and composite spectra to investigate the scenario we presented in this paper in greater detail.
Acknowledgments
We are grateful to De Lucia, G., Girardi, M. and Andreon, S. for useful discussions and comments. V.P. acknowledges support from INAF-OAB Ph.D. Grant.
References
- Abadi, M. G., Moore, B., & Bower, R. G. 1999, MNRAS, 308, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, L., Rasmussen, J., Mulchaey, J. S., et al. 2010, ApJ, 713, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Glazebrook, K., Brinkmann, J., et al. 2004, ApJ, 600, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Morris, S. L., Yee, H. K. C., Carlberg, R. G., & Ellingson, E. 1999, ApJ, 527, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Navarro, J. F., & Morris, S. L. 2000, ApJ, 540, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M., Eke, V., Miller, C., et al. 2004, MNRAS, 348, 1355 [Google Scholar]
- Balogh, M. L., McGee, S. L., Wilman, D., et al. 2009, MNRAS, 398, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Bamford, S. P., Nichol, R. C., Baldry, I. K., et al. 2009, MNRAS, 393, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., Frieman, J., Weinberg, D. H., et al. 2006, ApJS, 167, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., Carilli, C., Aravena, M., et al. 2007, ApJS, 172, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., Katgert, P., Thomas, T., & Adami, C. 2002, A&A, 387, 8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanton, M. R., Hogg, D. W., Bahcall, N. A., et al. 2003, ApJ, 594, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Eisenstein, D., Hogg, D. W., Schlegel, D. J., & Brinkmann, J. 2005, ApJ, 629, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Eisenstein, D., Hogg, D. W., & Zehavi, I. 2006, ApJ, 645, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Kovač, K., Pozzetti, L., et al. 2010, A&A, 524, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., & Gavazzi, G. 2006, PASP, 118, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Bottini, D., Garilli, B., Maccagni, D., et al. 2005, PASP, 117, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G., Yee, H. K. C., & Ellingson, E. 1997, ApJ, 478, 462 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlberg, R. G., Yee, H. K. C., Morris, S. L., et al. 2001a, ApJ, 563, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G., Yee, H. K. C., Morris, S. L., et al. 2001b, ApJ, 552, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Lacey, C. G., Baugh, C. M., & Frenk, C. S. 2000, MNRAS, 319, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Coil, A. L., Gerke, B. F., et al. 2010, MNRAS, 409, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Iovino, A., Kovač, K., et al. 2010, A&A, 524, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Diaz, E., Zandivarez, A., Merchan, M. E., & Muriel, H. 2005, ApJ, 629, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, M. J., Zandivarez, A. A., Martínez, H. J., et al. 2002, MNRAS, 335, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Baugh, C. M., Cole, S., et al. 2004, MNRAS, 348, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmann, R., Carollo, C. M., Porciani, C., et al. 2006, MNRAS, 372, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Font, A. S., Bower, R. G., McCarthy, I. G., et al. 2008, MNRAS, 389, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Pierini, D., & Boselli, A. 1996, A&A, 312, 397 [NASA ADS] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- George, M. R., Leauthaud, A., Bundy, K., et al. 2011, ApJ, 742, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Gerke, B. F., Newman, J. A., Faber, S. M., et al. 2007, MNRAS, 376, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, S. P. D., Knebe, A., & Gibson, B. K. 2005, MNRAS, 356, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Rigoni, E., Mardirossian, F., & Mezzetti, M. 2003, A&A, 406, 403 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Grützbauch, R., Conselice, C. J., Varela, J., et al. 2011, MNRAS, 411, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Gott, III, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, S. M., Sheldon, E. S., Wechsler, R. H., & Koester, B. P. 2009, ApJ, 699, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, Y., & Oemler, Jr., A. 1999, ApJ, 510, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., Cappelluti, N., Brunner, H., et al. 2007, ApJS, 172, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Blanton, M. R., Eisenstein, D. J., et al. 2003, ApJ, 585, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M. 2004, ApJ, 615, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., & Geller, M. J. 1982, ApJ, 257, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Iovino, A., Cucciati, O., Scodeggio, M., et al. 2010, A&A, 509, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kampczyk, P., Lilly, S. J., de Ravel, L., et al. 2011, ApJ, submitted [arXiv:1112.4842] [Google Scholar]
- Katgert, P., Biviano, A., & Mazure, A. 2004, ApJ, 600, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 54 [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kawata, D., & Mulchaey, J. S. 2008, ApJ, 672, L103 [Google Scholar]
- Kimm, T., Somerville, R. S., Yi, S. K., et al. 2009, MNRAS, 394, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzbichler, M. G., & White, S. D. M. 2007, MNRAS, 376, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2009, ApJ, 697, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Lilly, S. J., Knobel, C., et al. 2010, ApJ, 718, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., Tinsley, B. M., & Caldwell, C. N. 1980, ApJ, 237, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, I., Balogh, M., De Propris, R., et al. 2002, MNRAS, 334, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fevre, O., Hammer, F., & Crampton, D. 1996, ApJ, 460, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., LeFèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Madau, P., Pozzetti, L., & Dickinson, M. 1998, ApJ, 498, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Mahdavi, A., Geller, M. J., Böhringer, H., Kurtz, M. J., & Ramella, M. 1999, ApJ, 518, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Margoniner, V. E., de Carvalho, R. R., Gal, R. R., & Djorgovski, S. G. 2001, ApJ, 548, L143 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Frenk, C. S., Font, A. S., et al. 2008, MNRAS, 383, 593 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Capak, P., Salvato, M., et al. 2010, ApJ, 708, 202 [NASA ADS] [CrossRef] [Google Scholar]
- McGee, S. L., Balogh, M. L., Bower, R. G., Font, A. S., & McCarthy, I. G. 2009, MNRAS, 400, 937 [NASA ADS] [CrossRef] [Google Scholar]
- McGee, S. L., Balogh, M. L., Wilman, D. J., et al. 2011, MNRAS, 413, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Oemler, Jr., A. 1974, ApJ, 194, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Oesch, P. A., Carollo, C. M., Feldmann, R., et al. 2010, ApJ, 714, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Postman, M., & Geller, M. J. 1984, ApJ, 281, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribeiro, A. L. B., Lopes, P. A. A., & Trevisan, M. 2010, MNRAS, 409, L124 [NASA ADS] [Google Scholar]
- Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
- Schinnerer, E., Smolčić, V., Carilli, C. L., et al. 2007, ApJS, 172, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Vergani, D., Cucciati, O., et al. 2009, A&A, 501, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Goto, T., Okamura, S., Shimasaku, K., & Brinkmann, J. 2004, AJ, 128, 2677 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, Y., Scoville, N., Murayama, T., et al. 2007, ApJS, 172, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Tasca, L. A. M., Kneib, J., Iovino, A., et al. 2009, A&A, 503, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tran, K., Simard, L., Zabludoff, A. I., & Mulchaey, J. S. 2001, ApJ, 549, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Weinmann, S. M., van den Bosch, F. C., Yang, X., & Mo, H. J. 2006, MNRAS, 366, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Weinmann, S. M., Kauffmann, G., van den Bosch, F. C., et al. 2009, MNRAS, 394, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, D. J., Balogh, M. L., Bower, R. G., et al. 2005, MNRAS, 358, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, D. J., Oemler, A., Mulchaey, J. S., et al. 2009, ApJ, 692, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, D. J., Zibetti, S., & Budavári, T. 2010, MNRAS, 406, 1701 [NASA ADS] [Google Scholar]
- Xue, Y. Q., Brandt, W. N., Luo, B., et al. 2010, ApJ, 720, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Bardelli, S., Bolzonella, M., et al. 2009, A&A, 508, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: The algorithm to add photo-zs
In this appendix we present the details of the algorithm we adopted to add photometric candidate group members to the spectroscopic ones, thus recovering group members that were not observed spectroscopically because of the incomplete sampling of 20K.
Given a group with N observed spectroscopic members, we define its center on the sky: RAgr and Decgr center and its redshift position, zgroup, using the mean of the coordinates of its member galaxies (as in Knobel et al., in prep.).
We then define Rgr as the minimum radius of the circle centered on (RAgr, Decgr) containing all spectroscopic confirmed members.
For each galaxy with apparent magnitude IAB ≤ 22.5 and photometric redshift zgal we define
-
Rgal, the projected radial distance of the galaxy to the center of the group on the sky;
-
x = Rgal/Rgr, the projected radial distance normalized to group size;
-
Δz = |zgal − zgroup|, the distance in redshift space to the position in redshift of the group;
-
y = Δz/σzphot(IAB), the distance in redshift space normalized to σzphot(IAB), the photometric redshift accuracy computed at the galaxy magnitude IAB.
To accept/reject a photo-z galaxy as group member we tested different selection functions F(x,y), depending on the galaxy normalized radial and redshift distances from group center and all satisfying the simple empirical criterion that the accepted normalized distance in redshift space for a galaxy to be accepted as group member decreases at larger normalized radial distances.
Since one of our main goals is to recover the real richness of the groups, we excluded selection functions that were too conservative or too sharp in their radial dependence, producing a negligible increase of interlopers to the group at the expense of a small gain in terms of recovered real members.
After many trials we adopted a simple linear profile to associate acceptable normalized distances in redshift space to radial distances from group center on the sky. The formula we chose is y = 2 − x, and x = 1 is the maximum distance to which the search was extended. This way the selection function linearly decreases the acceptable distance in redshift space as we go away from the center up to Rgr.
For each group, we applied this selection function to all galaxies with photometric redshifts and IAB ≤ 22.5 located within a cylinder of ± 2 × σzphot depth and within a region of inner radius Ri and an outer radius Ri + 0.2 × Rgr, increasing Ri iteratively in steps of 0.2 × Rgr from zero to Rgr − 0.2 × Rgr.
We note that the 95% of the missing real members are always confined within ± 2 × σzphot(IAB), while the interlopers are spread over the entire range ± 4 × σzphot(IAB). This is the reason why we constrained the maximum redshift depth to ± 2 × σzphot(IAB). Furthermore, in the inner regions the number of real missing members is always higher than that of interlopers, while the ratio is reversed as we go far away from the center.
At the end of each run of the algorithm a new catalog of 20K+photo-z member galaxies is produced. If there was any multiple assignment for a single photo-z we used a check function, Fcheck, to univocally assign it to a group. The check function uses both the phot-z information and the more reliable spatial information. It is defined as Fcheck(x,y) = x2 × y, so that the photo-z is assigned to the group with the minimum Fcheck(x,y). Tests on simulations show that this check function is able to recover the real membership for 74% of photo-z with multiple assignments to different groups.
Once the new catalog of group member galaxies is created, we determine the new RAgr and Decgr centers, this time defined using Eq. (2), while leaving zgroup unchanged, and the new Rgr for each group using both spectroscopic and newly added photometric members.
The whole algorithm then runs iteratively: the jth iteration uses the center and radius of the (j − 1)th iteration to search for photo-z member galaxies. We define the center-shift as the distance between the jth center and the (j − 1)th one. After two iterations the center shift is less than 5% of 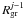 for 90% of the groups, meaning that the centering for these groups has converged. The third iteration is enough for the centering to converge also for the remaining 10% of the groups.
for 90% of the groups, meaning that the centering for these groups has converged. The third iteration is enough for the centering to converge also for the remaining 10% of the groups.
Once applied to our data, our algorithm adds a total of 684 member galaxies with photometric redshifts to the already existing 1437 spectroscopic groups member galaxies.
Reassuringly, the ratio of the number of spectroscopic redshift members to the total number of members, i.e., including member galaxies with photometric redshift only, agrees well with the value ~62% of the median sampling rate within the central area, once we take into account our completeness of ~90%, as tested from simulations (see Sect. 3).
If we had used the complete group catalog (spec+phot-z) as provided in Knobel et al. (in prep.), adding as photometric redshift members to each group only the galaxies with an association probability ≥0.5 (to easily reject multiple associations and select only the most reliable phot-z members), we would have obtained a set of phot-z member galaxies overlapping by ~70% with our photometric member galaxies. These common galaxies are assigned to the same group in ~95% of the cases, while the group centers and richnesses are not noticebly modified, differences in centering being in agreement with our typical centering error (see Sect. 4.1).
All Tables
Number of volume-limited and mass-volume-limited (spec+phot-z) group member galaxies.
Observed blue fractions in groups and field for different galaxy stellar mass bins.
KS test probabilities that the mass distribution of the galaxies in each group region and that of the field sample of galaxies are drawn from the same distribution.
All Figures
 |
Fig. 1 RA-Dec distribution of the 16623 zCOSMOS-bright galaxies with secure redshift z ≤ 2 (the so-called 20K sample). The area within the red box (149.55 ≤ RA ≤ 150.67 and 1.75 ≤ Dec ≤ 2.70) has a nearly uniform sampling rate of ~62%. |
| In the text | |
 |
Fig. 2 Summary of the results obtained with our algorithm. Top left: completeness distribution (see text for definition) for the 20K mocks (black dot-dashed line) and for the 20K+photo-zs mock groups (red solid line). Top right: fraction of interlopers as a function of normalized group-centric distance for the 20K/20K+photo-zs mock groups (black stars and red triangles, respectively). Orange squares refer to the fraction of interlopers, |
| In the text | |
 |
Fig. 3 Left panel: redshift distribution of the zCOSMOS-bright galaxies (black). Red points represent group member galaxies with spectroscopic and photometric redshifts as obtained from our algorithm. The cyan solid line and the violet dashed line correspond to the two different magnitude cut-offs adopted to define the volume-limited samples of the low- and high-redshift bin respectively, see text for details. Central and right panel: (U − B) rest-frame color versus mass for the lowest and the highest redshift bin. The blue dashed line corresponds to the color-dependent ℳcut − off, while the red solid line corresponds to the fixed ℳcut − off for our mass volume-limited sample. The red dot-dashed lines highlight the mass ranges adopted in the mass-segregation analysis, see Sect. 6.5 for details. The cyan dotted line corresponds to the separation between red and blue galaxies (see text for its precise definition). |
| In the text | |
 |
Fig. 4 Comparison of the general properties of groups in the 0.2 ≤ z ≤ 0.45 (black dot-dashed line) and 0.45 < z ≤ 0.8 (red solid line) redshift bin. From left to right we compare Rfudge (the estimate of the virial radius), log ℳfudge (the estimate of the mass of the group), both fudge quantities are calibrated with the mocks as defined in Knobel et al. (2009), and |
| In the text | |
 |
Fig. 5 Sky distribution of the galaxies belonging to the low-z (left) and high-z (right) composite group. RA-Dec positions are expressed in terms of the rescaled distances ℛ. Points are colored according to the (U − B) colors of the galaxies, while point dimensions are scaled according to the masses of the galaxies. As a reference we draw dashed circles corresponding to the different central/intermediate/external region limits in each composite group. |
| In the text | |
 |
Fig. 6 Top panels: cumulative galaxy stellar mass distribution of the mass-complete group and field samples in red and cyan colors. Bottom panels: Fblue at fixed galaxy mass in groups (red circles) and field (cyan stars). Left panels always refer to the low-redshift bin, while right panels refer to the high redshift one. We used galaxy mass bins 0.4 dex wide. |
| In the text | |
 |
Fig. 7 SG blue fraction as a function of the group-centric distance. Left/(right) panels refer to the low/(high) redshift bin and mass limits are ℳcut − off = 9.8/(ℳcut − off = 10.56). Open circles refer to observed Fblue while filled ones to corrected Fblue, i.e., taking into account interloper contamination (see text for details). The points refer to the three regions: inner core, intermediate, and more external/infall region. Corrected blue fractions values are displayed at the median distance of each region, while observed blue fractions are offset for clarity. As a reference we plot the fraction of the blue field galaxies (cyan star) and the mean corrected blue fraction in groups (big red circle). |
| In the text | |
 |
Fig. 8 Fblue of near-field galaxies (violet empty stars) as a function of increasing projected radial distances from groups in the low-redshift bin: ℛ ≤ 2.0, ℛ ≤ 3.0 and ℛ ≤ 4.0. Violet filled stars show Fblue of near field after excluding near-field galaxies with projected radial distances ℛ ≤ 2.0. The filled square shows Fblue for the first near-field annulus, after correcting for the 15% spectroscopic galaxy-group incompleteness, see text for details. Observed Fblue values are displayed at the median distance of each near-field region, while corrected ones are slightly offset for clarity. As a reference we display the Fblue of the field with a cyan star. |
| In the text | |
 |
Fig. 9 Corrected blue fraction as a function of the group-centric distance in the low-z poor groups (left) and rich groups (right). We define poor(rich) groups as those with number of member galaxies ≤ ( > )12 after applying the evolving magnitude cut off |
| In the text | |
 |
Fig. 10 Cumulative radial distribution of the galaxies belonging to each mass bin for both the lowest (left) and highest (right) redshift bin. We show the most massive galaxies with an orange solid line and the less massive galaxies with a green dotted line. As a reference we draw the limits of the first and second regions with a dot-dashed black line. |
| In the text | |
 |
Fig. 11 Cumulative radial distribution of the galaxies belonging to each mass bin for poor (left) and rich (right) groups in the lowest redshift bin. We show the most massive galaxies with an orange solid line and the less massive galaxies with a green dotted line. As a reference we draw the limits of the first and second regions with a dot-dashed black line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


