| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 22 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201118098 | |
| Published online | 14 February 2012 | |
Magnetic field measurements and their uncertainties: the FORS1 legacy⋆
1 Armagh Observatory, College Hill, Armagh BT61 9DG, Northern Ireland, UK
e-mail: sba@arm.ac.uk
2 Physics & Astronomy Department, The University of Western Ontario, London, N6A 3K7 Ontario, Canada
e-mail: jlandstr@uwo.ca
3 Department of Physics and Astronomy, Open University, Walton Hall, Milton Keynes MK7 6AA, UK
e-mail: l.fossati@open.ac.uk
4 Department of Physics and Astronomy, Uppsala University, 75120 Uppsala, Sweden
e-mail: Oleg.Kochukhov@fysast.uu.se
Received: 15 September 2011
Accepted: 24 November 2011
Context. During the last decade, the FORS1 instrument of the ESO Very Large Telescope has been extensively used to study stellar magnetism. A number of interesting discoveries of magnetic fields in several classes of stars have been announced, many of which obtained at a ~3σ level; some of the discoveries are confirmed by measurements obtained with other instruments, some are not.
Aims. We investigate the reasons for the discrepancies between the results obtained with FORS1 and those obtained with other instruments.
Methods. Using the ESO FORS pipeline, we have developed a semi-automatic procedure for magnetic field determination. We have applied this procedure to the full content of circular spectropolarimetric measurements of the FORS1 archive (except for most of the observations obtained in multi-object spectropolarimetric mode). We have devised and applied a number of consistency checks to our field determinations, and we have compared our results to those previously published in the literature.
Results. We find that for high signal-to-noise ratio measurements, photon noise does not account for the full error bars. We discuss how field measurements depend on the specific algorithm adopted for data reduction, and we show that very small instrument flexures, negligible in most of the instrument applications, may be responsible for some spurious field detections in the null profiles. Finally, we find that we are unable to reproduce some results previously published in the literature. Consequently, we do not confirm some important discoveries of magnetic fields obtained with FORS1 and reported in previous publications.
Conclusions. Our revised field measurements show that there is no contradiction between the results obtained with the low-resolution spectropolarimeter FORS1 and those obtained with high-resolution spectropolarimeters. FORS1 is an instrument capable of performing reliable magnetic field measurements, provided that the various sources of uncertainties are properly taken into account.
Key words: polarization / techniques: polarimetric / stars: magnetic field
Table 5 is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
During a full decade of operations, the FORS1 instrument of the ESO Very Large Telescope has collected a large number of magnetic field measurements in various kinds of stars. Together with the ESPaDOnS instrument of the Canada-France-Hawaii Telescope, and with the MuSiCoS and NARVAL instruments of the 2 m Telescope Bernard Lyot of the Pic-du-Midi Observatory, FORS1 has been one of the workhorse instruments for the observational studies of stellar magnetism.
Several important detections obtained with FORS1 have led to the conclusion that magnetic fields are quite common in a variety of stars across the Hertzsprung-Russell diagram, including for instance central stars of planetary nebulae (Jordan et al. 2005), hot subdwarfs (O’Toole et al. 2005), β Cephei and slowly pulsating B stars (Hubrig et al. 2009a), B stars with emission lines (Hubrig et al. 2009b), and normal O-type stars (Hubrig et al. 2008b).
In practice, a close inspection to the published results shows a number of problems:
-
i)
Inconsistencies between field measurements obtained with FORS1 and field measurements obtained with other instruments. For instance, Hubrig et al. (2004a) reported the discovery of a magnetic field in the Herbig Ae/Be star HD 139614, while repeated ESPaDOnS measurements failed to confirm the magnetic nature of that star (Wade et al. 2005). Similarly, Silvester et al. (2009) failed to confirm the presence of a magnetic field in several of the β Cep and SPB stars observed by Hubrig et al. (2006a) and Hubrig et al. (2009a).
-
ii)
Inconsistencies between the analysis of the same FORS dataset performed by different authors. For instance, McSwain (2008) observed the normal B stars NGC 3766 MG 111 and NGC 3766 MG 176, and the Be star NGC 3766 MG 200, and reported no field detection. Using the same data, Hubrig et al. (2009b) reported new field detections for all three stars.
-
iii)
Inconsistencies between the analysis of the same FORS dataset performed by the same authors but at different epochs. For instance, Wade et al. (2005) reported a possible detection in the young Ap star HD 72106A, which was not confirmed by the later analysis of the same data performed by the same group (Wade et al. 2007a). Note that the magnetic nature of that star was established with data independently obtained with ESPaDOnS (see Folsom et al. 2008).
-
iv)
Inconsistencies between field measurements obtained from different subsets of an observing series of frames. Magnetic field measurements are often obtained by combining a number of pairs of frames obtained at two different position angles of the retarder waveplate. This redundancy is mainly motivated by the need to reach a very high signal-to-noise ratio. In some rare cases, a magnetic field may be firmly detected in a pair of frames, but not in the remaining pairs. This is for instance the case of the measurements of HD 139614 reported by Hubrig et al. (2004a), where the magnetic field is detected only in a subset of frames, and in a couple of H Balmer lines.
-
v)
Finally, there are some global inconsistencies of the full FORS dataset, revealed for instance by the high incidence of field detection in the null profiles; this kind of problem was not previously reported in the literature, and will be discussed in Sect. 4.1.
The release of the FORS pipeline for spectropolarimetric data (Izzo et al. 2010, 2011) gave us the opportunity to develop an accurate and efficient reduction method. The FORS pipeline is a software tool specifically designed for that instrument, which makes it easier to handle some characteristics that are specific to the data obtained with FORS1. Furthermore, the FORS pipeline allows a high degree of automatization in the data reduction process. Complemented with a suite of software tools for data pre-processing (for frame classification and quality check) and data post-processing (for the computation of the magnetic field), we were able to build up a nearly automatic tool for data analysis which allowed us to treat the entire FORS archive data in a homogeneous way. Using our tool suite, the difference in terms of effort required to perform the analysis of a single series of observations compared to performing the analysis of the entire archive of FORS1 data consists mainly in the amount of the necessary disk space and CPU time.
Compared to the reduction of raw data coming from individual observing runs, the mass-production of reduced spectra offers the possibility to perform a quality check of the final products on a very large scale. The aim of this paper is to present: (1) a preliminary discussion of the methods, (2) the results of our quality checks, and (3) to caution the reader about the lack of robustness of some of the results previously published in the literature. A deeper analysis and a comprehensive and homogeneous catalogue of FORS1 magnetic field measurements will be published in a forthcoming paper.
2. Instrument and instrument settings
FORS1 (Appenzeller et al. 1998) is a multi-purpose instrument capable of doing imaging and low-resolution spectroscopy in the optical, equipped with polarimetric optics. It was attached at the Cassegrain focus of one of the 8 m units of the ESO Very Large Telescope (VLT) of the Paranal Observatory from the beginning of operations in 1999 until instrument decommissioning in March 2009. The FORS1 polarimetric optics were subsequently moved to the twin instrument FORS2.
Two detectors have been used in the FORS1 instrument: a 2k × 2k Tektronix CCD (TK2048) (pixel size 24 μm × 24 μm), and a mosaic composed of two 2k × 4k E2V CCDs (pixel size of 15 μm × 15 μm). TK2048 was used from the beginning of operations to March 2007 (P65 to P78), E2V from April 2007 to the decommissioning of the instrument in March 2009 (P79 to P82). For more details about the two detectors, see Szeifert et al. (2007).
Summary of the characteristic of the grisms+CCD setting most commonly employed for magnetic field measurements.
Most of the observing programmes used the so-called “fast-mode”. In this mode the target is just one star in the centre of the instrument field of view. A small number of observing programmes used the multi-object mode, which allows the simultaneous recording of the polarized spectra for up to nine different stars within a ~7′ × 7′ field of view (see e.g. Bagnulo et al. 2006). In multi-object mode, the FORS pipeline is not yet robust enough to correctly associate the parallel and the perpendicular beams of the same target, especially when the observations are performed with the grism 600 B. The reason is due to the presence of a number of ghost images (probably coming from the Longitudinal Atmospheric Dispersion Corrector), which are interpreted by the pipeline as stellar spectra. The solution to this problem would be to force the pipeline to extract only user selected spectra, an option that has not been implemented yet. Therefore we did not re-reduce the large majority of the observations performed in multi-object mode.
Most of the observations were performed with grism 600 B, some with grism 1200 B, and a small number with grism 1200 g and 600 R (see Table 1). In most of the cases, the slit width was set to 0.4′′ or 0.5′′, for a typical spectral resolution of about 1600–2300 (with grism 600 B or 600 R) or 3000–3400 (with grism 1200 g or 1200B).
3. Data reduction
In the following, we will adopt the same formalism used in Bagnulo et al. (2009); f∥ and f⊥ are the fluxes in the parallel and in the perpendicular beam of the polarisation analyser, respectively, PV = V/I is the circular polarization normalised to the intensity, and NV is the null profile, a quantity that was introduced by Donati et al. (1997), and that is representative of the noise of PV.
We always obtained the PV profiles from a series of one or more pairs of exposures. Each pair of exposures is composed of two frames obtained with the retarder waveplate at position angles separated by 90°. For most of the observing series, it was also possible to calculate the null profile. For those cases in which the number of pairs of exposures N was odd and ≥ 3, the null profile was obtained omitting the last pair of exposures. Obviously, with just one pair of exposure, the null profile could not be calculated.
The extracted fluxes were combined to obtain the PV and NV profiles using the formulas of the difference methods given in Eqs. (A2) and (A7) of Bagnulo et al. (2009), which for convenience we reproduce below: ![\begin{equation} \begin{array}{rcl} \pv &=& {1 \over 2 N} \sum\limits_{j=1}^N \left[ \left(\frac{\fo - \fe}{\fo + \fe}\right)_{\alpha_j} - \left(\frac{\fo - \fe}{\fo + \fe}\right)_{\alpha_j + \dalphao}\right] \\[2mm] \nv &=& {1 \over 2 N} \sum\limits_{j=1}^N (-1)^{(j-1)}\left[ \left(\frac{\fo - \fe}{\fo + \fe}\right)_{\alpha_j} - \left(\frac{\fo - \fe}{\fo + \fe}\right)_{\alpha_j + \dalphao}\right] ,\\ \end{array} \label{Eq_V_and_N} \end{equation}](/articles/aa/full_html/2012/02/aa18098-11/aa18098-11-eq21.png) (1)where ΔA = 90° and αj belongs to the set { − 45°, 135° } 1. However, in this work we adopt an important modification as described below.
(1)where ΔA = 90° and αj belongs to the set { − 45°, 135° } 1. However, in this work we adopt an important modification as described below.
3.1. Rectifying Stokes profiles
In some cases we found the PV profile clearly offset from zero, even when no circular polarization of the continuum is expected. This happened for instance in Herbig Ae/Be stars observed by Wade et al. (2007a), and in several other cases in the course of the present work.
A possible explanation is cross-talk from linear to circular polarization, as discussed by Bagnulo et al. (2009). Cross-talk may be a problem only if the observed source is linearly polarised, and is especially significant for spectra acquired with a slitlet close to the edge of the instrument field of view (as in some observations obtained in multi-object mode). However, we often found slight but noticeable offsets also in FORS data for stars that are not linearly polarised, and that were observed in the centre of the field of view. These offsets may be explained if the ratio between the transmission functions in the perpendicular beam h⊥, and the transmission function in the parallel beam, h∥, is not constant as the retarder waveplate is set to the different position angles.
Inspection of the null profile may help to discriminate between the two cases. If PV is offset from zero due to cross-talk from linear polarization (or in fact because the source is intrinsically circularly polarized in the continuum), the null profile will still be oscillating about zero, while an offset introduced by a non constant ratio h⊥/h∥ will still appear (somewhat scaled down) in the null profile. This can be seen analytically as follows. We first recall that within the framework of the difference method, the ratio h = h⊥/h∥ is developed to first order: 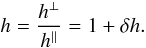 (2)We then assume that the term δh that appears in Eqs. (34) of Bagnulo et al. (2009) depends on the position angle α0 of the retarder waveplate, and we repeat the computations that lead to their Eqs. (37). We obtain
(2)We then assume that the term δh that appears in Eqs. (34) of Bagnulo et al. (2009) depends on the position angle α0 of the retarder waveplate, and we repeat the computations that lead to their Eqs. (37). We obtain ![\begin{equation} \begin{array}{rcl} \pvr &=& {1 \over 2 N} \sum\limits_{j=1}^N \left[ \left(\frac{\fo - \fe}{\fo + \fe}\right)_{\alpha_j} - \left(\frac{\fo - \fe}{\fo + \fe}\right)_{\alpha_j + \dalphao} - a_j\right] b_j^{-1} \\[2mm] \nvr &=& {1 \over 2 N} \sum\limits_{j=1}^N (-1)^{(j-1)}\left[ \left(\frac{\fo - \fe}{\fo + \fe}\right)_{\alpha_j} - \left(\frac{\fo - \fe}{\fo + \fe}\right)_{\alpha_j + \dalphao} - a_j\right] b_j^{-1} ,\\ \end{array} \label{Eq_Rectified} \end{equation}](/articles/aa/full_html/2012/02/aa18098-11/aa18098-11-eq33.png) (3)where
(3)where ![\begin{eqnarray} a_j &=& \frac{2 \left[\dhh(\alpha_j + \dalphao) - \dhh(\alpha_j)\right]} {4 + 2 \left[\dhh(\alpha_j) + \dhh(\alpha_j + \dalphao)\right] + \dhh(\alpha_j)\, \dhh(\alpha_j + \dalphao)}\notag\\ b_j &=& \frac{4 + 2 \left[\dhh(\alpha_j) + \dhh(\alpha_j + \dalphao)\right]} {4 + 2 \left[\dhh(\alpha_j) + \dhh(\alpha_j + \dalphao)\right] + \dhh(\alpha_j)\, \dhh(\alpha_j + \dalphao)} \label{Eq_ak_bk} \end{eqnarray}](/articles/aa/full_html/2012/02/aa18098-11/aa18098-11-eq34.png) (4)and where we have introduced the new symbols
(4)and where we have introduced the new symbols 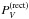 and
and 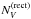 to denote the PV and NV profiles rectified.
to denote the PV and NV profiles rectified.
Equation (3) shows that if δh(αj) δh(αj + ΔA) ≪ 1, then bj ≃ 1, and 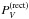 and
and 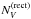 can be simply obtained by subtracting from the PV and NV profiles obtained from Eqs. (1) two smooth curves that interpolate the continuum of those profiles. These smooth curves may be obtained fitting a polynomial to PV and to NV, or using a Fourier filter. Following this simple method, PV and NV are rectified independently, and NV loses part of its diagnostic content, because it is forced to oscillate about zero in a way that is totally independent of PV. An alternative method consists of estimating the transmission functions δh by smoothing the ratios between fluxes on the parallel and perpendicular beams, then obtaining the explicit expressions for the individual aj and bj coefficient, and finally using Eqs. (3) to compute the
can be simply obtained by subtracting from the PV and NV profiles obtained from Eqs. (1) two smooth curves that interpolate the continuum of those profiles. These smooth curves may be obtained fitting a polynomial to PV and to NV, or using a Fourier filter. Following this simple method, PV and NV are rectified independently, and NV loses part of its diagnostic content, because it is forced to oscillate about zero in a way that is totally independent of PV. An alternative method consists of estimating the transmission functions δh by smoothing the ratios between fluxes on the parallel and perpendicular beams, then obtaining the explicit expressions for the individual aj and bj coefficient, and finally using Eqs. (3) to compute the 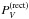 and
and 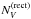 profiles in a consistent way. In practice, we found that the two alternative methods lead always to very similar results.
profiles in a consistent way. In practice, we found that the two alternative methods lead always to very similar results.
3.2. Clipping with the null profile
Both PV and NV profiles show occasional spikes which occur in the same wavelength bin. Most of these spikes are probably produced by cosmic ray hits, and, if not removed, may lead to spurious detections of magnetic fields, or at least decrease the precision of its determination. A possible remedy is to exploit the null profiles to clip the PV profiles by discarding from the computation of the ⟨ Bz ⟩ values those points for which the (rectified) NV value depart from zero by more than k σ, where k is a constant typically ~3. The clipping may be applied to the individual deviating points, or may also remove the adjacent points.
3.3. Magnetic fields determinations
FORS longitudinal magnetic field measurements are obtained using the relationship 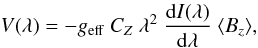 (5)where V(λ) and I(λ) are the Stokes V and I profiles of a spectral line, geff is the effective Landé factor, and
(5)where V(λ) and I(λ) are the Stokes V and I profiles of a spectral line, geff is the effective Landé factor, and 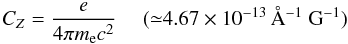 (6)where e is the electron charge, me the electron mass, and c the speed of light.
(6)where e is the electron charge, me the electron mass, and c the speed of light.
Bagnulo et al. (2002) proposed to use a least-squares technique to derive the longitudinal field via Eq. (5), by minimising the expression 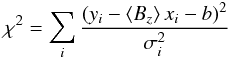 (7)where, for each spectral point i, yi = PV(λi),
(7)where, for each spectral point i, yi = PV(λi), 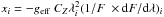 , Fi is the flux measured in the spectral bin at λi, and b is a constant introduced to account for possible spurious residual polarization in the continuum. Note that the spurious polarization is assumed constant in wavelength, which may not be true if we adopt PV from Eqs. (1), but it is a realistic assumption if we use
, Fi is the flux measured in the spectral bin at λi, and b is a constant introduced to account for possible spurious residual polarization in the continuum. Note that the spurious polarization is assumed constant in wavelength, which may not be true if we adopt PV from Eqs. (1), but it is a realistic assumption if we use  of Eq. (3), for which we must retrieve b = 0 within its error bar.
of Eq. (3), for which we must retrieve b = 0 within its error bar.
Equation (5) is subject to several important limitations. (i) It is valid only in the limit of fields weak enough that Zeeman splitting is small compared to the local spectral line width, typically with a ≲ 1 kG strength in the case of optical metal spectral lines, or ≲ 10 kG for Balmer lines. (ii) It applies to isolated, unblended lines. (iii) The value of geff varies by a significant amount from line to line; the use of an average value means that for many lines, the actual circular polarization will vary from the average one by up to 25%. The impact of these limitations was discussed by Bagnulo et al. (2002); they are not important if one is simply interested in field detection, or to asses the magnitude of the longitudinanal field, but they should be kept in mind whenever FORS measurements are used for modelling purposes.
 |
Fig. 1 The polarised spectrum of HD 94660 observed on 2007-03-22 with grism 600B. The top panel shows the normalised derivative of the observed flux, and the panel immediately below shows the observed flux F (black solid line, in arbitrary units, and not corrected for the instrument response), the PV profile (red solid line centred about 0), and the null profile (blue solid line, offset by –0.75% for display purpose). The null profile is expected to be centred about zero and scattered according to a Gaussian with σ given by the PV error bars. The PV error bars are represented with light blue bars centred about –0.75%. The slope of the interpolating lines in the bottom panels gives the mean longitudinal field from PV (left bottom panel) and from the null profile (right bottom panel) both calculated using the H Balmer lines only. The corresponding ⟨ Bz ⟩ and ⟨ Nz ⟩ values are − 1885 ± 90 G and − 192 ± 62 G, respectively. |
 |
Fig. 2 Results obtained from the analysis of the H Balmer lines (top panels), of the metal lines (mid panels), and of the full spectrum (bottom panels) for three stars, using standard error theory and Montecarlo simulations. The (red) thick solid lines are Gaussian curves centred about the various field values and with σ given by Eq. (11). The blue lines show the distributions obtained with Monte Carlo simulations as explained in the text. Note that HD 94660 has a large field, HD 96441 has no detected field, and HD 171184 has a weak but probably real field. |
When we derive ⟨ Bz ⟩ by minimizing the χ2 of Eq. (7), we make the implicit assumption 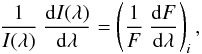 (8)which is justified provided that
(8)which is justified provided that 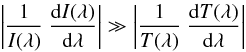 (9)where T(λ) is a function that accounts for the stellar continuum, the transmission functions of the interstellar medium, of the Earth atmosphere, of the telescope, and of the instrument. The validity of this approximation can be empirically evaluated case by case by verifying that the impact of the continuum rectification to the normalised derivative of Stokes I is negligible. Practically, a quick check can be performed even without continuum normalization. Since the function T(λ) is much smoother than I(λ), the contributions due to the terms [1/I(λ) × dI(λ)/dλ] and [1/T(λ) × dT(λ)/dλ] to the quantity [1/F × dF/dλ] i can be visually disentangled simply by plotting the function [1/F × dF/dλ] i versus λ over a zero line. The top panel of Fig. 1 shows that the broad contribution due to T(λ) is totally negligible compared to the fine structure due to I(λ), and that [1/F × dF/dλ] i practically oscillates about zero. For hot stars observed with grism 1200 B, T(λ) is very steep, and [1/T(λ) × dT(λ)/dλ] may depart from zero more significantly than what displayed in Fig. 1, yet the impact of the continuum normalisation on the ⟨ Bz ⟩ determination is still within the error bars due to photon-noise.
(9)where T(λ) is a function that accounts for the stellar continuum, the transmission functions of the interstellar medium, of the Earth atmosphere, of the telescope, and of the instrument. The validity of this approximation can be empirically evaluated case by case by verifying that the impact of the continuum rectification to the normalised derivative of Stokes I is negligible. Practically, a quick check can be performed even without continuum normalization. Since the function T(λ) is much smoother than I(λ), the contributions due to the terms [1/I(λ) × dI(λ)/dλ] and [1/T(λ) × dT(λ)/dλ] to the quantity [1/F × dF/dλ] i can be visually disentangled simply by plotting the function [1/F × dF/dλ] i versus λ over a zero line. The top panel of Fig. 1 shows that the broad contribution due to T(λ) is totally negligible compared to the fine structure due to I(λ), and that [1/F × dF/dλ] i practically oscillates about zero. For hot stars observed with grism 1200 B, T(λ) is very steep, and [1/T(λ) × dT(λ)/dλ] may depart from zero more significantly than what displayed in Fig. 1, yet the impact of the continuum normalisation on the ⟨ Bz ⟩ determination is still within the error bars due to photon-noise.
Finally, we note that for quality check purpose, it is useful to measure the mean longitudinal field by using the null profiles instead of the PV profiles. This null field value ⟨ Nz ⟩ should be found consistent with zero within its error bars.
Figure 1 illustrates the technique discussed in this section, showing the results obtained for the FORS observations of the well known magnetic star HD 94660.
3.4. Error bars
Bagnulo et al. (2002) have obtained the error bar of the longitudinal magnetic field from the inverse of the χ2 matrix. This way, the “internal” error bar s ⟨ Bz ⟩ was obtained by propagating the errors σi of the PV profiles onto the analytical expression of ⟨ Bz ⟩ that is obtained by minimising the χ2 expression of Eq. (7):
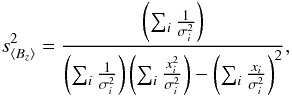 (10)where ∑ i is a sum extended to all i spectral bins used in Eq. (7). An analogous expression holds for the error on the null field ⟨ Nz ⟩ , s ⟨ Nz ⟩ , which turns to be numerically identical to s ⟨ Bz ⟩ , since
(10)where ∑ i is a sum extended to all i spectral bins used in Eq. (7). An analogous expression holds for the error on the null field ⟨ Nz ⟩ , s ⟨ Nz ⟩ , which turns to be numerically identical to s ⟨ Bz ⟩ , since 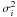 are identical for the PV and NV profiles.
are identical for the PV and NV profiles.
Since there are numerous indications that the error bars of FORS1 field measurements are underestimated, in this work we introduce an “external” error bar σ ⟨ Bz ⟩ that takes into account the actual scattering about the interpolating line, i.e.: 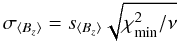 (11)where
(11)where 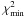 is the minimum value of the χ2 of Eq. (7) and ν is the number of degrees of freedom of the system, i.e., the number of spectral points minus two. Strictly speaking, the use of Eq. (11) is not theoretically justified. It is equivalent to the hypothesis that Eq. (5) is correct, but that the errors σi on PV are all underestimated by a constant value
is the minimum value of the χ2 of Eq. (7) and ν is the number of degrees of freedom of the system, i.e., the number of spectral points minus two. Strictly speaking, the use of Eq. (11) is not theoretically justified. It is equivalent to the hypothesis that Eq. (5) is correct, but that the errors σi on PV are all underestimated by a constant value 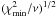 .
.
The reality is that, as discussed above, Eq. (5) is not rigorously valid, especially for strong fields. Departures from the behaviour predicted by Eq. (5) mean that points in the regression (as shown in the lower panels of Fig. 1) will deviate from the interpolating line by more than the amount predicted by photon statistics, and the reduced χ2 values will be >1. For stars with weak or no magnetic field, or if the field is computed from the null profiles, the scatter in the positions of individual points around the regression line is dominated by noise rather than by the approximations implicit in Eq. (5). In this case the reduced χ2 is expected to be very close to 1, and the “internal” and “external” errors tend to be quite similar. The advantage of systematically using Eq. (11) is to automatically take into account a few cases where even if the field is weak or non-existent, the reduced χ2 is >1.
To check the validity of our error estimates we have performed some Monte Carlo simulations. All pixel values of the raw frames of an observing series were scattered, using a random number generator, according to a Gaussian distribution with σ given by the square root of their electron counts. This altered dataset was reduced, and an estimate of the ⟨ Bz ⟩ and ⟨ Nz ⟩ values was obtained. The same procedure was repeated 5000 times to obtain a distribution for both ⟨ Bz ⟩ and ⟨ Nz ⟩ values. Then, the centres of these distributions ⟨ Bz ⟩ MC and ⟨ Nz ⟩ MC, and their standard deviations σ ⟨ Bz ⟩ MC and σ ⟨ Nz ⟩ MC were compared to the ⟨ Bz ⟩ , ⟨ Nz ⟩ , σ ⟨ Bz ⟩ , σ ⟨ Nz ⟩ , s ⟨ Bz ⟩ (=s ⟨ Nz ⟩ ) values obtained from the observing series not altered by the Monte Carlo simulation. Results for three observing series are shown in Fig. 2. For the (large) ⟨ Bz ⟩ values of HD 94660 we found σ ⟨ Bz ⟩ > s ⟨ Bz ⟩ and σ ⟨ Bz ⟩ > σ ⟨ Bz ⟩ MC; for all the remaining cases the error bars coming from the three methods are similar.
3.5. Additional details about data reduction
In this section we briefly discuss some issues related to data reduction which influence the estimates of the mean longitudinal magnetic field and their uncertainties, i.e., i) flat-field correction; ii) the algorithm for spectrum extraction; ii) spectral rebinning; iv) rectification of the PV and NV profiles; and v) the choice of the Landé factor and of the spectral region used to determine the magnetic field.
This (non-exhaustive) list gives an idea of the multiple choices that are either implicitly or expliciting taken during the process of data reduction. The following discussion helps to understand how much the final results may depend on the actual algorithm adopted for data reduction.
-
i)
While flat-fielding is not needed to measure Stokes profiles (see, e.g., Bagnulo et al. 2009), pixel-to-pixel variation may have an impact on the evaluation of the xi term of Eq. (7), as pointed out by Rivinius et al. (2010). However, in most of the cases, the signal-to-noise ratio of the combined flat field frames is not much higher than that of the science frames. Furthermore, calibration frames show internal reflections (especially in the bluest regions), but with different patterns than seen in science frames. In some cases, it is clear that internal reflections observed in the flat-field affect the ⟨ Bz ⟩ determination, e.g., the difference between cases (a) and (b) of Table 2 described later in this section is entirely due to spurious features of the master screen flat. In summary, it is not possible to conclude that flat-fielding correction improves the longitudinal field determination, at least with the CCDs that were used in FORS1. We found however that the difference between magnetic field values obtained with and without flat-fielding corrections were generally well within photon-noise error bars.
-
ii)
The FORS pipeline (Izzo et al. 2011) offers two different options for spectral extraction: optimal extraction (Horne 1986), and aperture extraction. Using the former method, each pixel in the spectra extraction is weighted according to the fraction of the flux which is expected assuming a model of the spatial profile across the dispersion. The method substantially increases the signal-to-noise ratio when the noise is dominated by background, and automatically accounts for cosmic-rays, but may be less suitable than “average extraction” when the noise is determined mainly by Poisson statistics. We found that in general, the polarized spectra obtained with optimal extraction have numerous spurious spikes; an example is shown in Fig. 3 with the detail of the polarized spectrum of HD 94660 reduced with average extraction (blue thick lines) and with optimal extraction (red thin lines). This suggests that the aperture extraction should be preferred to optimal extraction. Note that FORS pipeline assumes a certain default aperture which may not be the optimal one for all cases. For our data re-reduction we generally adopted a 12 pixel aperture, using a larger one for a few cases of very bad seeing.

Fig. 3 PV and NV profiles of HD 94660 obtained with average extraction (red thick lines) an optimal extraction (blue thin lines). The null profiles are offset by −1% for display purpose, and overplotted to the statistical error bars of the PV and NV profiles.
Table 2Longitudinal magnetic fields of three stars obtained with different algorithms.
-
iii)
Generally, the wavelength bin size of the calibrated spectra is set equal to the dispersion (measured as Å per pixel) pertaining to each given instrument setting, but there is no obvious reason why one should not experiment with an interpolation over a more refined wavelength grid, or with a rebinning to a larger bin size to increase the signal-to-noise ratio of each point. Surprisingly, the final ⟨ Bz ⟩ value depends on the adopted choice of the bin size, in a way that deserves further investigation.
-
iv)
The choice whether to use Balmer lines only or the full spectrum, and the choice for the Landé factor that best represents the average Zeeman pattern of the spectral lines may be different from work to work, and therefore lead to different numerical values for ⟨ Bz ⟩ . However, since these choices affect both the field value and its error bar in the same way, they will not change a detection into a non-detection nor vice-versa. For more details on how field results change when Eq. (7) is applied to Balmer lines only, or only to He+metal lines, or to the full spectrum, see, e.g., Bagnulo et al. (2002) and Bagnulo et al. (2006).
-
v)
In some cases, using the rectified profiles of Eq. (3) instead of the non-rectified PV profiles of Eq. (1) leads to significant changes in the field values, and may even turn a field detection into a non-detection, but in most of the cases, field changes are within the error bars.
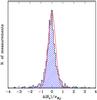 |
Fig. 4 The distribution of the difference between ⟨Bz⟩ values obtained with two slightly different algorithms for data reduction, normalised to the error bars, and compared to a Gaussian with identical area, centred about zero, and with σ = 0.33. |
While it is certainly possible to argue that certain algorithms for data reduction lead to more robust results than other methods, some alternative choices may be equally reasonable. The fact that there are alternative and reasonable choices during the process of data reduction adds a contribution to the error bar of the mean longitudinal field. This contribution is difficult to quantify in general, but it is a non-negligible fraction of the error bar from photon noise.
The results discussed in the remainder of this paper are based on a full reduction of the entire FORS1 “fast mode” data archive, making the following choices: no flat-fielding is implemented, spectra are extracted with average extraction using a 12 pixel radius aperture, and rebinned at the dispersion value; the PV profiles are rectified using a 150 pixel wide Fourier filter, clipped with k = 3 (including also the two bins that are adjacent to the deviant one) as explained in Sect. 3.2; the field is calculated from the full spectrum, although the first 3% and the last 3% of spectral points are ignored, setting the Landé factor = 1 in proximity of the H Balmer lines, and 1.25 everywhere else. This method is referred to as method (a) in Table 2. The choices made are relatively conservative ones, tend to alter the actual data as little as possible, and attempt to describe the uncertainties realistically.
We note that no rectification is implemented in the FORS pipeline, since it would bring the aim of the software to a high-level of data manipulation which is in fact outside of the scope of a common user tool. Therefore, rather than using the final products of the pipeline, we have always extracted the individual beams and treated them individually according to the algorithm described above.
 |
Fig. 5 LSD profiles for HD 94660 observed with grism 600 B (left panel) and 1200 B (right panel). Red solid line: Stokes V/Ic; blue dotted line: N/Ic; black solid line Stokes I/Ic. V/Ic and N/Ic are offset to +1 % for display purpose. |
3.6. Alternative techniques for field measurements
Traditionally, two main techniques are used in the literature to measure the mean longitudinal magnetic field. Measurements can be obtained from low resolution spectropolarimetric data using the least-square technique used in this paper, or (more commonly) from high-resolution spectropolarimetric data treated with the Least-Square Deconvolution (LSD) technique. In the latter case, the mean longitudinal field is obtained from the measurement of the first-order moment of LSD Stokes V about the line centre, and of the equivalent width of LSD Stokes I – both profiles normalised to the continuum intensity (Donati et al. 1997; Kochukhov et al. 2010).
One may experiment with variations of these two techniques. Equation (5) could be applied to high-resolution spectra, or to their corresponding LSD profiles. LSD profiles themselves may be obtained even from low-resolution data, allowing one to measure ⟨ Bz ⟩ either with Eq. (5), or with the moment technique. In practice, none of these alternative methods has been adopted so far, and it still has to be demonstrated that one can extract fully meaningful LSD profiles from low-resolution spectra. While discussing alternative techniques for ⟨ Bz ⟩ measurements is beyond the scope of this paper, we report on our LSD experiments with three stars that were all observed with both grisms 600 B and 1200 B: HD 358 (a non-magnetic star), HD 201601, and HD 94660 (both magnetic). Using the moment technique, no field was detected in the LSD profiles of HD 358, while the fields measured in HD 201601 and HD 94660 were found to be ~25% smaller (in absolute value) and more dependent on the adopted grism, than those obtained with the technique of Sect. 3.3. In all three cases, we found no field detection in the null profiles, although for HD 94660 observed with grism 1200 B, the null field value was =2.4σ (while with the least-square technique, the null field was consistent with 0 within 1.6σ). We performed numerical simulations, which confirmed that the ⟨ Bz ⟩ values obtained with the moment technique applied to LSD profiles tend to underestimate the actual field strength, at least for ≳ 1 kG field (see also Kochukhov et al. 2010). Photon-noise error bars obtained with the two different methods were found similar among themselves, but for the field obtained from LSD profiles we found an additional large uncertainty due to the continuum normalisation: the ⟨ Bz ⟩ values measured with the moment technique applied to the LSD profiles would change by more than 1σ if spectra were normalised according to different but still reasonable criteria. (We note that normalisation criteria of single order spectra are somewhat more arbitrary than in case of echelle spectra.)
In spite of these drawbacks, we note that in fast rotating stars, LSD V profiles may potentially reveal the signature of a magnetic field even when its average longitudinal component is zero. Therefore, applying LSD techniques to FORS data may be still of some interest. Figure 5 shows the LSD profiles of HD 94660, observed with grisms 600 B and 1200 B.
4. Quality checks of the field measurements
Inspection of the FORS1 archive data shows that between 2000 and 2009 about 1000 h of telescope time were dedicated to acquiring stellar circular spectropolarimetric data for magnetic field measurements. Almost 600 h of telescope time were granted in service mode, and 42 nights were granted in visitor mode.
Figure 6 gives a qualitative technical overview of the nature of the observations, i.e., the distributions of the spectral resolution, of the total exposure time per observing series, of the peak signal-to-noise ratio per Å, and the signal-to-noise ratio integrated over all pixel bins used for the field determination (when using the full spectrum). The former two histograms demonstrate that the FORS instrument was often used for very bright objects, pushing the spectral resolution close to the limit fixed by sampling, and with substantial slit losses. This suggests that some FORS1 users would have instead benefitted from high-resolution spectropolarimetric facilities at smaller telescopes. The latter two histograms show that most of the observations were obtained with a ultra-high signal-to-noise ratio, hence FORS field measurements are generally close to the highest possible precision obtainable with a reasonable use of the telescope time. The actual precision of the FORS field measurement is the subject of this section.
The discussion of Sect. 3.5 shows that using different reduction procedures to infer magnetic field strengths may lead to significantly different results, in terms of both the mean longitudinal field ⟨ Bz ⟩ and its associated uncertainty σ ⟨ Bz ⟩ obtained from any specific observation. In this section we fix the data reduction algorithm, and explore how the deduced fields and uncertainties still lead to a number of inconsistencies. This discussion has two goals: (1) to use what we know about some of the stars observed to try to learn more about the characteristics of the FORS1 measurements, and (2) to examine the reliability of various results, particularly announced discoveries of new magnetic stars, based on FORS1 measurements.
 |
Fig. 6 Some characteristics of the FORS spectropolarimetric observations retrieved in the archive. |
4.1. Internal tests
In principle, calibration and testing of the measurements from any spectropolarimeter should rely on calibration observations made on a set of stars whose magnetic fields are well characterised by previous work, particularly including some which are known to be non-magnetic at the level of precision expected for the instrument. Unfortunately, such calibration measurements were not systematically obtained during the working life of FORS1. Therefore we have searched the catalogue of measurements for observations of stars with well known magnetic characteristics to test the actual precision that has been achieved with the FORS1 observations.
4.1.1. Repeated observations of well-known magnetic stars
A dispersion test that has been very useful in determining how realistic the measurement uncertainties are of other instruments such as the MuSiCoS spectropolarimeter (e.g., Wade et al. 2000) is to examine the measurements of ⟨ Bz ⟩ as a function of the star’s rotation phase around the mean variation. Thus, for example, 17 measures of ⟨ Bz ⟩ of β CrB with MuSiCoS with uncertainties of 20 to 30 G were fully consistent with the mean curve at signal to noise ratios of up to 30:1. This kind of instrument monitoring was not performed with the FORS1 instrument, and we suggest it should be implemented in the FORS2 calibration plan. A somewhat useful test was performed by some users who repeatedly observed the magnetic star HD 94660. The star’s rotation period is not known, but is probably longer than two years. The star’s longitudinal field appears nearly (but not perfectly) constant and about − 2 kG, thus spectropolarimetric observations of HD 94660 allow one to assess if the polarimetric optics are at least approximately aligned.
4.1.2. Repeated observations of non-magnetic stars
One particular test that should be carried out frequently as part of routine calibration of any spectropolarimeter used for magnetic measurements is the observation of stars known to be non-magnetic, or at least to be non-magnetic to within rather small uncertainties (a few G or tens of G). Such measurements are a particularly powerful test of the uncertainties computed for individual observations, since the actual field value expected (zero) is known with high precision. An example of such a test was the monitoring of δ Eri by Donati et al. (1997) with the SEMPOL instrument at the Anglo-Australian Telescope (AAT). No main sequence stars known with high precision to be non-magnetic have been deliberately observed with FORS1. However, some of the peculiar A stars of the HgMn type, and in particular α And = HD 358, have been repeatedly observed, probably because they were suspected to be magnetic. Numerous investigations of magnetism in such stars (e.g. Borra & Landstreet 1980; Glagolevskij et al. 1985; Shorlin et al. 2002; Aurière et al. 2010; Makaganiuk et al. 2011) have found no convincing evidence for fields in this class of stars with uncertainties often in the range of a few G up to a few tens of G. Furthermore, α And has been specifically investigated with the MuSiCoS (13 observations, typical σ ~ 30–60 G) and ESPaDOnS (5 observations, typical σ ~ 6–19 G) spectropolarimeters without any significant detection of a non-zero longitudinal field or of any Stokes V signature indicative of a non-zero field (Wade et al. 2006).
⟨ Bz ⟩ measurements of α And = HD 358.
The field of α And has been measured eight times with FORS1. The first six observations have been published (Hubrig et al. 2006b). Table 3 lists the published ⟨ Bz ⟩ measurements and the ⟨ Bz ⟩ values of the same observations resulting from our reduction.
We note several interesting features of the data in this table. First, our new reduction invariably gives somewhat larger measurement uncertainties than the published data. Secondly, the published data report three field detections at the level of 3σ or higher; our new reduction finds only a single detection at the 3σ level, and it is not one of the three initially reported 3σ measurements. Furthermore, the null field ⟨ Nz ⟩ (i.e., the magnetic field calculated using the null profiles instead of the PV profiles) is also detected once at about the 3σ level. Thus, our new results, independently of any external evidence, make the detection of a longitudinal field in this star from FORS1 data very uncertain. The quite substantial differences between the field values published previously and those we have measured are probably not due to errors of reduction, but to the sensitivity of the results to the specific reduction method used to obtain the ⟨ Bz ⟩ value.
If we now assume that the more precise measurements reported by Wade et al. (2006) establish that no longitudinal field is present in α And at the level of 20 or 30 G, so that effectively we assume that α And is a null standard, we may regard the results of Table 3 as providing useful information about the behaviour of the ⟨ Bz ⟩ values and associated uncertainties obtained from FORS1 measurements. In particular, both ⟨ Bz ⟩ and ⟨ Nz ⟩ values scatter from zero by more than is expected from the standard deviation of their individual measurements. Our results suggests that even the “external” error of Eq. (11), which is still “internal” to a single measurement, leads to occasional underestimates of the actual ⟨ Bz ⟩ error bars.
4.1.3. Time series
A further test of the stability of measured field values, and of the associated uncertainties, can be obtained by studying the statistical properties of a long series of magnetic observations of the same star taken during a single night. One example is the study by Hubrig et al. (2004b), who observed six known cool magnetic rapidly oscillating Ap stars (roAp stars). These observations had a cadence of the order of one frame per minute, and were typically continued for one to a few hours over ten or twenty pulsation cycles. The observations were intended to search for possible periodic variations in the magnetic field ⟨ Bz ⟩ at known pulsation periods. According to the published result of this study, no short-period field variations were reliably detected. If we make the assumption that during the short time interval in which each star was observed, the field was in fact constant, we can compare the standard deviation of the values of ⟨ Bz ⟩ i about their mean value 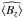 with the computed uncertainties σ ⟨ Bz ⟩ (i). If this standard deviation (the “external error”) is similar to the published values of σ ⟨ Bz ⟩ (i) (“internal errors”), then the comparision supports the correctness of the internal errors. Excess standard deviation indicates problems with deduced values of σ ⟨ Bz ⟩ .
with the computed uncertainties σ ⟨ Bz ⟩ (i). If this standard deviation (the “external error”) is similar to the published values of σ ⟨ Bz ⟩ (i) (“internal errors”), then the comparision supports the correctness of the internal errors. Excess standard deviation indicates problems with deduced values of σ ⟨ Bz ⟩ .
This comparison was carried out by the team who did the observations (see Table 9 in Hubrig et al. 2004b). Of the six stars reported, only two had external errors close to the internal ones. The other four stars all showed excess scatter, up to an extreme external error of more than three times the internal errors for HD 201601. One interpretation of this excess, of course, would be that these roAp stars were actually displaying pulsational field variations, but in only one case could a frequency be identified that is similar to one of the known pulsation frequencies of the roAp star, and a second observing run on this star (HD 101065) revealed no signal at that frequency (Hubrig et al. 2004b). Furthermore, HD 101065 is one of the two stars observed for which external and internal errors are very similar in magnitude; none of the stars with a significant discrepancy between internal and external errors showed significant variations at known pulsation periods. Thus it seems far more likely that the difference between internal and external errors reveals something about FORS1 and/or the reduction methods used for spectropolarimetric observations.
We have repeated the dispersion analysis for these stars, using our new reductions2. However, rather than using ⟨ Bz ⟩ , for this kind of analysis we have preferred to use the mean longitudinal field ⟨ Nz ⟩ from the null profiles. The reason is that Eq. (5) is strictly valid only in the weak-field regime, and for non blended spectral lines. These conditions are not met in the observed roAp stars, hence it is more likely that the null field ⟨ Nz ⟩ has a more linear response to the photon noise than the magnetic field ⟨ Bz ⟩ . We have proceeded in the following way. From all M frames of a given observing series we have selected 4 × n frames, where n is the integer part of M/4, and calculated n ⟨ Nz ⟩ (i) ± σ ⟨ Nz ⟩ (i) values. Then we have calculated: the weighted mean of the ⟨ Nz ⟩ (i) value 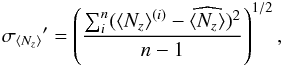 (12)the average “internal” standard deviation
(12)the average “internal” standard deviation 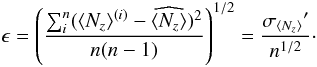 (13)the “external” standard deviation
(13)the “external” standard deviation 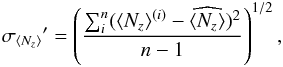 (14)and error of the mean
(14)and error of the mean 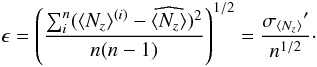 (15)We have also combined all 4n frames and obtained a ⟨ Bz ⟩ [n] ± σ ⟨ Bz ⟩ [n] value for each star.
(15)We have also combined all 4n frames and obtained a ⟨ Bz ⟩ [n] ± σ ⟨ Bz ⟩ [n] value for each star.
 |
Fig. 7 Histogram of the ⟨ Nz ⟩ values calculated from Balmer lines, and normalised to the error bars σ ⟨ Nz ⟩ . The red solid lines show the Gaussian with σ = 1, and the blue solid line a Gaussian with σ = 1.365, both with the same areas as the observed distribution. The vertical lines mark the limits at − 3 and 3. |
Null field values and their error bars for six roAp stars.
Table 4 reports these quantities for each observed star. While there is good agreement between the 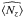 and ⟨ Nz ⟩ [n] values, in all cases but one we found
and ⟨ Nz ⟩ [n] values, in all cases but one we found 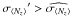 and, consistently, ϵ > σ ⟨ Nz ⟩ [n] . Our data sets appear to reveal excess noise over what would be expected from the internal uncertainties. Excess noise arises irregularly: it increases the standard deviation by a factor varying from 1 to about 2, qualitatively suggesting that the standard errors of measurement of ⟨ Bz ⟩ from internal dispersions within each measurement are underestimates of the true uncertainties.
and, consistently, ϵ > σ ⟨ Nz ⟩ [n] . Our data sets appear to reveal excess noise over what would be expected from the internal uncertainties. Excess noise arises irregularly: it increases the standard deviation by a factor varying from 1 to about 2, qualitatively suggesting that the standard errors of measurement of ⟨ Bz ⟩ from internal dispersions within each measurement are underestimates of the true uncertainties.
4.1.4. The distribution of the magnetic field from the null profiles
A final internal test is to compute the distribution over the entire FORS1 sample of field measurements of the null field values normalized by their error bars.
The null profiles should represent measurements of zero fields, as the combinations of different waveplate settings used are chosen so that the real polarisation signal cancels out, to the precision of the measurements. If the field values measured from the null profiles have a distribution determined by photon noise only, this distribution should closely resemble to a Gaussian distribution with σ = 1. Figure 7 shows that there is a significant excess of ⟨ Nz ⟩ /σ ⟨ Nz ⟩ points outside of the interval [−3,3] . The standard deviation of the ⟨ Nz ⟩ /σ ⟨ Nz ⟩ is 1.37, 1.20, 1.36 for the Balmer lines, metal lines, and the full spectrum, respectively.
4.2. Possible explanations for the internal inconsistencies
The results obtained for non magnetic stars, and the analysis of the time series and of the distribution of the null profiles, suggest that error bars, even when calculated with Eq. (11) – which are generally higher than those obtained with Eq. (10) – are underestimated. Our conclusion is that Poisson noise is not the only source of uncertainty of the field measurements. We have already seen that an additional source of uncertainty is introduced by the choice of the algorithm for data reduction, but the results of Sects. 4.1.3 and 4.1.4 were obtained consistently using the same algorithm. Therefore we suggest that some physical, probably instrumental, limit is hit, especially when measurements are obtained with ultra-high signal-to-noise ratio.
Possible reasons that could contribute to explaining this phenomenon are:
-
i)
Undetected problems with the raw data, such as saturated frames, or various kinds of errors in the organisation of the scientific frames and their calibrations, which range from the awkward mixing up of frames of different stars, to more difficult to detect hardware failures which could be responsible for an erroneous recording of the position angle of the retarder waveplate in the fits-headers (these problems are known to have occurred at some time in the FORS1 data).
-
ii)
Change of the line profiles during the observations for reasons intrinsically due to the source (e.g., stellar pulsations).
-
iii)
Changes of the radial velocity of the target occurring during the observing series.
-
iv)
Small instrument flexures occurring due to instrument motion during the observing series.
-
v)
For series of very short exposures in good seeing, changes in the mean position of the star in the slit from one exposure to the next, with corresponding changes in the mean wavelengths associated with each pixel. We note that many observations were obtained with exposure time of 0.25 s per frame.
 |
Fig. 8 The distribution of the differences between the null field values measured after flexure simulation and their original values, normalised to the error bars, compared to a Gaussian curve centred about zero and with σ = 0.2. Null field values were calculated from the H Balmer lines. |
In the case of FORS1 and FORS2, instrument flexures are kept at a minimum. However, we must note that ultra-high precision polarimetric measurements can be performed only with an extremely stable instrument, and it is for that reason that the ESPaDOnS and NARVAL instruments are sitting in thermally and mechanically isolated benches. The question is what level of stability the Cassegrain mounted FORS instruments can guarantee, and how possible instrument flexures would impact the ⟨ Bz ⟩ and ⟨ Nz ⟩ measurements. This does not have a simple answer. Numerical simulations on a single spectral line show that a drift in wavelength equal in both beams (e.g., due to a star’s radial velocity change) has a much stronger impact on the null profiles than on the Stokes profiles. A wavelength offset that acts differentially on the two beams, and that depends on the position of the retarder waveplate, has a larger impact on the Stokes profiles than on the null profiles3. We note also that instrument flexures affect not only the Stokes and the null profiles, but also the normalised derivative of the flux (which is calculated as explained in Sect. 4.2 of Bagnulo et al. 2002), and, finally, that the impact of all these effects on ⟨ Bz ⟩ and ⟨ Nz ⟩ values depends also on line profile and blending.
In an attempt to roughly evaluate the potential consequences of instrument flexures, we have performed the following test. In the data reduction process, we have numerically simulated a drift in wavelength continuously and homogeneously acting between the first and the last exposure. The total amplitude of the drift (i.e., calculated between the last exposure and the first exposure), was equal to a quarter of the spectral bin. Then we have computed the difference Δ ⟨ Nz ⟩ between the ⟨ Nz ⟩ value so obtained, and the value obtained without introducing any offset. We have repeated this simulation for all FORS archive datasets, and calculated the distribution of the ratio Δ ⟨ Nz ⟩ /σ ⟨ Nz ⟩ . Figure 8 displays the results obtained from H Balmer lines. This histogram shows that even a nearly negligible offset during the observations may produce changes in the ⟨ Nz ⟩ determinations comparable to the error bars. For the narrower metal lines, the consequences of flexures are more pronounced, and the ⟨ Nz ⟩ offsets being twice larger than when calculated from H Balmer lines. Qualitatively similar results was retrieved for the ⟨ Bz ⟩ values. However, we should note that for a certain dataset, a given simulated drift does not necessarily produce an offset with identical magnitude for both the ⟨ Bz ⟩ and ⟨ Nz ⟩ values. This suggests that, at least for small flexures, the warning coming from the ⟨ Nz ⟩ detections has a statistical relevance. For individual cases, a detection in ⟨ Nz ⟩ does not necessarily invalidate a ⟨ Bz ⟩ detection in the same dataset. Vice versa, a ⟨ Bz ⟩ detection may be spurious even if there is no detection in the null profile.
According to the FORS instrument manual, in imaging mode the instrument is stable within 0.2 pixel during 1 h exposure. However, Fig. 2.4 of that manual shows that flexures as large as a quarter of a pixel are not uncommon if the instrument rotator rotates by 10–20°. Furthermore, the instrument manual refers to a situation in imaging mode; the additional optical elements introduced in spectro-polarimetric mode (PMOS mask, slit mask, Wollaston prism, retarder waveplate, grism, and possibly a filter) certainly cannot improve the instrument stability. While we conclude that instrument flexures may explain at least in part why FORS field measurement uncertainties seem to be underestimated, we must also point out that we were unable to find a correlation between ⟨ Nz ⟩ /σ ⟨ Nz ⟩ values and the airmass.
5. The incidence of magnetic fields in various classes of stars
Our conclusion that the error bars computed from photon statistics underestimate by at least 30–40% the real uncertainties of field measurements has significant implications for the body of data obtained from FORS1, in particular for those measurements which have been used to announce new discoveries of a magnetic field at a relatively low significance level. Because of problems that spurious discovery announcements can cause, in the rest of this paper we concentrate on those stars in which a magnetic field was detected with FORS1 at ≲ 6σ level, and present a detailed comparison of our new results with previously announced discoveries of magnetic fields. A homogeneous and comprehensive catalogue of all FORS1 measurements will be published in a forthcoming paper.
The results of our comparison are summarised in Table 5. The stars are grouped into families of various kinds, identified by bold-face titles such as “HgMn stars”, “Be stars”, etc. The first two columns in this table list the star name, and the mean MJD of the observation as computed for the frames used in our data reductions (a blank in one of these two columns means that the line refers to a second published value of the same data as appears immediately above). The third and fourth columns give the value of ⟨ Bz ⟩ and its uncertainty as published, and a code denoting the reference where the field measurement was published. The fifth column reports the ⟨ Bz ⟩ value and its uncertainty obtained from our adopted reduction process. The sixth column includes a code character describing our conclusion on whether a field is detected in the star: D means that the star is definitely magnetic; P means that a field is possibly present, but that the currently available measurements do not provide firm evidence for that; N means that none of the measurements shows evidence of the presence of a magnetic field. Note that a few of the entries in Table 5 have MJD values that differ from those published, mostly by 0.5 day. Our values are computed directly and uniformly from the data in the fits headers of the observations, and should replace the published values where these differ.
Note that Table 5 does not include the “marginal” fields detections in Ap and Bp stars – most of which are reported by Hubrig et al. (2004b), Bagnulo et al. (2006), Hubrig et al. (2006b) and Kochukhov & Bagnulo (2006). It is already clearly demonstrated that magnetic fields are detected in essentially every Ap star if high enough precision is reached (Aurière et al. 2007). Therefore, the reliability of the detection of weak fields reported in these papers will not greatly change what we know about the occurrence of magnetic Ap and Bp stars. Accordingly, we postpone a discussion of these data to our forthcoming paper.
The uncertainty of our field measurements of Table 5 is calculated with Eq. (11), which is still an underestimate of the real error bar. Unfortunately, the source of errors that are not due to photon noise cannot be estimated for the individual cases. Although one may be strongly tempted to multiply all error estimates by a factor ~1.5, the correct way to proceed is to remember that 3σ level is not a safe detection threshold. For that reason, the discussion presented in this section will also rely on checking whether a field detection has been repeatedly confirmed with numerous FORS1 measurements, and on corroborating or conflicting field measurements made with other spectropolarimeters.
We found that several important FORS1 discoveries announced in the past are simply not confirmed by our new data reduction, even without taking into account a possible underestimate of our error bar. In many cases, in contrast to the originally published result, the absolute value of our new field measurement does not exceed three times its associated σ ⟨ Bz ⟩ value estimated with Eq. (11). We have two possible general explanations for this finding. The first one is based on the general considerations of Sect. 3.5 that different data reduction methods lead to slightly different results. Also, in some cases we have removed some frames (e.g., because of saturation), or used a slightly different frame selection than used for the original publication. In an attempt to keep this aspect under control, we have compiled a very large catalogue that includes, for each observation, all ⟨ Bz ⟩ values obtained with several different data reduction methods (e.g., without rectifying Stokes profiles, or using optimal extraction instead of average extraction). In the following discussion we will explicitly comment on those cases in which one or more methods for data reduction alternative to the one used to compile Table 5 would lead to a qualitatively different result. These cases are comparatively rare. A second explanation of the discrepancies between our results and those published in the literature is that our error bars are generally larger than those obtained in previous works. In the following we comment in detail on our new results.
5.1. Am, HgMn and PGa stars
The HgMn peculiar late B stars have already been mentioned in Sect. 4.1.2, where we concluded that the overwhelming bulk of evidence is against the presence of fields having ⟨ Bz ⟩ values of more than a couple of tens of G. Table 5 contains six measures claimed as field detections of four such stars by Hubrig et al. (2006b). The new reductions have increased the standard errors of all the measurements by factors of 1.3 or more, in two cases by much more. None of the measurements now shows a field at the 3σ level, and three of the five measures that were reported to be over 100 G and detected at even 4σ or more are now only some tens of G, and at roughly the 1σ level. In contrast, two of the large values are still relatively large, but are no longer significant at the 3σ level, and may represent the occasional spurious large field values that appear in a few percent of FORS1 field measurements.
We conclude that the FORS1 data do not alter the general non-detection of magnetic fields in HgMn stars. There is still no significant evidence of fields in such stars.
The PGa stars are considered to be the extension of the HgMn phenomenon to higher effective temperatures. A survey of several such stars some years ago (Borra et al. 1983) revealed no fields, with uncertainties of hundreds of G. The large FORS1 survey reported by Hubrig et al. (2006b) included two PGa stars observed with much smaller uncertainties. One of these stars, HD 19400, was reported to have a field. Our re-reduction of these data show no significant field, and we consider this detection to be spurious.
The Am (metallic-line) stars are considered to be analogues of the HgMn stars at lower Teff. There have been only a few observations of such stars with FORS1, and no claims of field detections based on these observations have been made.
5.2. Classical Be stars
By classical Be stars we mean those B stars which show evidence (at least some of the time) of centrifugally supported, slowly evolving, fairly massive disks. For many years some theoreticians have argued that magnetic fields may play an important role in the creation and/or maintenance of the circumstellar disks. However, there have not been very many serious searches for magnetic fields in such stars. A search by Barker et al. (1985) with uncertainties in the range of 50–250 G did not reveal any fields.
On the basis of data from the MuSiCoS spectropolarimeter, Henrichs et al. (2000), Neiner et al. (2001) and Donati et al. (2001) have reported the detection of a weak field in HD 205021 = β Cep, a double system composed of a Be star and a pulsating star – the latter being the proto-type of β Cep pulsating stars. Schnerr et al. (2006) have shown that the primary star of the β Cep system is the pulsating and magnetic star, while the Be star is a non-magnetic companion that can be separated with speckle interferometry. Thus the detected field is not connected with the Be phenomenon. Neiner et al. (2003a) reported a magnetic field in the classical Be star ω Ori, but it is not clear that the data provide a convincing case for the presence of a field. Silvester et al. (2009) have observed the two classical Be stars HD 148184 and HD 181615 several times each with ESPaDOnS, with uncertainties of order 100 G and 10 G respectively, but found neither significantly non-zero values of ⟨ Bz ⟩ , nor signficant polarisation signatures. Thus from the limited data available from instruments other than FORS1, there is no strong evidence for magnetic fields in any classical Be star.
The largest recent surveys for fields in classical Be stars have been carried out using FORS1 by Hubrig et al. (2007b) and Hubrig et al. (2009b) (summarised by Yudin et al. 2011), both searching for magnetism in field Be stars, and by McSwain (2008), who studied normal, chemically peculiar, and emission-line B stars in the young open cluster NGC 3766. Between them, these surveys have included more than 40 Be and possible Be stars, of which 10 stars were reported to have weak but significant magnetic fields. The reports by Hubrig et al. (2007b) and Hubrig et al. (2009b) suggest that weak (~100 G) fields may be ubiquitous in Be stars, a result that would have important consequences for modelling the Be phenomenon.
Note that there is some doubt as whether all of the stars in these surveys are Be stars. For example, NGC 3766 MG 94, 111, and 176 are listed as a He strong star, normal star, and normal star by McSwain (2008), but as B stars with emission lines in Table 2 of Hubrig et al. (2009b). In Table 5 we followed the classication by McSwain (2008). Furthermore, there are differences among these publications as to which stars show field detections; McSwain (2008) did not find a significant field in the normal B stars NGC 3766 MG 111 or NGC 3766 MG 176, nor in the Be star NGC 3766 MG 200, all of which are reported, using the same data, as new detections by Hubrig et al. (2009b).
When we compare the new reductions of these observations with the published ones, we see that only one of the reported ⟨ Bz ⟩ values that differ from zero by more than 3σ are still significantly non-zero. In part this is because most (but not all) of the measurement uncertainties resulting from our re-reductions are larger than those originally reported, and in part because most of the new ⟨ Bz ⟩ values are also smaller (in absolute value) than originally reported. The only remaining apparently significant detection is in HD 181615; however, the photon-noise error of the measurement that still shows field detection in our reduction is certainly very small, and the presence of a field of the claimed size is clearly contradicted by the three negative observations of Silvester et al. (2009).
There is a huge discrepancy between the uncertainty of the published field detections for HD 148184 and our uncertainties in Table 5. These spectra are heavily polluted with emission lines, and we were unable to reproduce the very tiny field uncertainties published by Hubrig et al. (2007b). However, we must note that the quality of our reduced data corresponding to the second detection is particularly poor, probably due to image quality. We note that the published detections are contradicted by four negative observations of Silvester et al. (2009) with uncertainties mostly of about 70 G.
Our reductions using the ESO pipeline give apparently significant field detections for an observation of HD 56014 and two observations of HD 209409, in which the original observers did not find report any significant fields (for that reason, the corresponding entries are not included in Table 5). We also obtained a 15σ detection (!) in HD 224686, in which the original observers measured ⟨ Bz ⟩ = 74 ± 24 G. All these data were obtained in the same two nights, MJD = 54 432 and 54 433. We are very sceptical of our reductions, since they all show a significant signal in the bluest Balmer lines both in the PV and in the NV profiles, which we believe the symptom of a not yet understood problem with calibrations or with our data reduction. In Table 5, for HD 224686, instead of our field estimate, we left an empty space.
Our global conclusion is that most if not all of the detections reported in Be stars by Hubrig et al. (2007b) and Hubrig et al. (2009b), as well as the marginal detection reported by McSwain (2008), are probably spurious, and that magnetic fields much above 100 G rarely if ever occur in classical Be stars.
5.3. Herbig AeBe stars
The Herbig AeBe stars are pre-main sequence stars which are in the final stages of contraction, and which are destined to become main sequence A- or B-type stars. These stars are identified by their locations in regions of current or very recent star formation, by the presence of optical emission lines (especially Hα) produced by circumstellar or accreting material, and by the presence of an infrared excess due to cool circumstellar material not yet accreted onto the star. The stars themselves have spectral types A or B.
The first discovery of a field in a Herbig Ae star, HD 104237, was reported by Donati et al. (1997) from observations at the AAT with an experimental spectropolarimeter. The star was observed again with SEMPOL at the AAT by Alecian (priv. comm.) who confirms the magnetic detection previously reported by Donati et al. (1997).
Based on FORS1 observations, the discovery of a magnetic field in the Herbig Ae star HD 139614 was reported by Hubrig et al. (2004a), who measured ⟨ Bz ⟩ = −450 ± 93 G. Wade et al. (2005) re-analysed the FORS1 dataset acquired by Hubrig et al. (2004a), and obtained the more marginal result ⟨ Bz ⟩ = −150 ± 50 G. Wade et al. (2005) reported also that ESPaDOnS data did not show any presence of a magnetic field. A second detection in HD 139614 ( ⟨ Bz ⟩ = −116 ± 34 G) was claimed by Hubrig et al. (2006c), who also confirmed their previous measurement of −450 G. Later, Hubrig et al. (2007a) revised both FORS1 observations, and reported ⟨ Bz ⟩ − 112 ± 36 G and ⟨ Bz ⟩ = −93 ± 14 G, for the first and the second measurement, respectively. A magnetic field was not detected in a third FORS1 measurement reported by Hubrig et al. (2009c). Our re-reduction of all three observations clearly shows that no field is detected in any of these three measurements. This star has also been observed three times using the high-resolution spectropolarimeter ESPaDOnS (Wade et al. 2005, 2007b; Alecian et al. 2011). ESPaDOnS data, with ⟨ Bz ⟩ uncertainties of about 12 G, show no trace of magnetic field, and demonstrate quite definitely that no field anywhere near the level originally reported is detected in this star. Our conclusion is that the reported discovery of a magnetic field in HD 139614 is spurious.
The results of a survey with FORS1 of about 50 Herbig AeBe stars were briefly described by Wade et al. (2005). The same paper also reported first results from the use of the new ESPaDOnS spectropolarimeter at the CFHT to search for fields in Herbig AeBe stars. From the FORS1 survey, magnetic fields were reported in two stars: HD 72106A (a very young main sequence star whose companion, HD 72106B, is a Herbig star), and HD 101412. Although the uncertainties of the measurements of these two stars have increased in our re-reduction of these data, both fields are apparently still detected. Since detections are only at a significance level between 3 and 4σ, FORS1 data by themselves do not strongly establish the presence of magnetic fields. In fact, Wade et al. (2007a) revisited their FORS1 measurement of HD 72106A, finding that their data could not support a field detection. The field of HD 72106A was confirmed by the ESPaDOnS component of this survey (Wade et al. 2005), and the star has subsequently been studied in detail by Folsom et al. (2008). The presence of a field in HD 101412 has been fully confirmed by Alecian et al. (2008a,b, 2009a) with SEMPOL observations, and by Hubrig et al. (2009c) with further FORS1 field measurements at a level ≳ 6σ (therefore these measurements do not appear in Table 5). The field of HD 101412 has been studied in more detail by Hubrig et al. (2011a).
In the survey reported by Wade et al. (2005), the star V380 Ori was observed with FORS1 without a significant detection. However, the same paper reports a clear detection of this star (on a different date) with ESPaDOnS. The magnetic field has been detected at more than the 3σ level a number of times, and was studied in detail by Alecian et al. (2009b).
Further surveys of Herbig AeBe stars using FORS1 were described by Hubrig et al. (2006c) and Hubrig et al. (2007a). Altogether, these papers reported the discovery of a magnetic field in three Herbig stars: HD 31648, HD 144432, and HD 144668. The observations of HD 31648, presented as a new field discovery by Hubrig et al. (2006c), were re-reduced by Hubrig et al. (2007a), who reported a final ⟨ Bz ⟩ measurement below the 3σ significance. For HD 144432, both papers reported a similar field value, but the uncertainty published by Hubrig et al. (2007a) was a factor of almost 2.5 smaller than estimated by Hubrig et al. (2006c). Two measurements of HD 144668 published by Hubrig et al. (2006c) are marginally significant, but do not exceed 3σ. Hubrig et al. (2007a) revised both measurements, and found for this star a new field detection with a 4σ significance. We also note that a survey by Hubrig et al. (2009c), that we will review later in more detail, reports for HD 144668 a second, marginally significant detection. Our re-reduction of all these observations brings the field measurement of HD 31648 by Hubrig et al. (2006c), and the field measurement of HD 144668 by Hubrig et al. (2007a) to zero within errors. Our re-reduction confirms the field detection by Hubrig et al. (2006c, 2007a) in HD 144432 at almost 5σ level, as well as the ~3σ detection from the observations of HD 144668 obtained by Hubrig et al. (2009c). These same three stars were also observed with FORS1 (with similar uncertainties to those of Hubrig et al. 2006c) by Wade et al. (2007a), who did not detect any significant fields. In addition, magnetic field measurements of HD 31648, HD 144432, and HD 144668 have been obtained with ESPaDOnS by Alecian et al. (2011). These new measurements have error bars between 40 G and 145 G, and do not show any strong indication of the presence of fields (although one field measurement for each star reaches 2σ). Thus, it appears that the reported detections of HD 144668 and HD 144432 might possibly be real, but these detections are quite uncertain, and need substantial new evidence to be convincing.
The FORS1 survey briefly described by Wade et al. (2005) was analysed in more detail by Wade et al. (2007a). Altogether, 68 field measurements of 50 stars were carried out. The data were re-reduced by the authors, who concluded that HD 101412 and BF Ori probably host magnetic fields, while HD 36112 and CPD − 53 295 might be magnetic, but that these marginal detections would require confirmation. After our new reduction, magnetic fields are still detected in HD 101412 and CPD − 53 295 at a slightly more than 3σ confidence, while the measurements of HD 36112 and BF Ori no longer show field detection. As discussed above, the detection of HD 101412 was later fully confirmed. A second measurement of CPD − 53 295 (published by Hubrig et al. 2009c) was reported as field detection but does not appear significant in our re-reduction of the data. The only further data available for HD 36112 or BF Ori are two observations with ESPaDOnS or NARVAL for each of the stars, which show no hint of fields (Alecian et al. 2011). We conclude that a field might be present in CPD − 53 295, but this result would certainly need further confirmation. The marginal field detections of HD 36112 and BF Ori reported by Wade et al. (2007a) are probably spurious.
The most recent FORS1 survey of Herbig stars is due to Hubrig et al. (2009c). Nine field detections at more than the 3σ level are reported, including two field detections in HD 101412 and one in HD 190073, two stars previously known to be magnetic Herbig AeBe stars. New field discoveries are claimed for six stars (on the basis of one measurement each), although one of these new magnetic stars is CPD − 53 295, which was already reported to be possibly magnetic by Wade et al. (2007a). Four of these six detections, including the measurement of CPD − 53 295, disappear in our re-reduction, while two of them remain signficant. As discussed above, a 3σ detection of a field in HD 144668, might be real but requires confirmation. The detection at the 5–6σ level of a field in HD 150193 is even stronger after our re-reduction than originally published. However, a single ESPaDOnS observation (with an uncertainty of about 120 G) detects no field (Alecian et al. 2011).
Finally, we note that our new reduction of the datasets obtained by Wade et al. (2007a) yields two field detections in the star HD 97048 (which were not found in the original reductions), at just slightly over the 3σ level. Hubrig et al. (2009c) also has one detection at about the 4σ level, which by constrast is not retrieved in our new reduction. It is possible that this star has a weak field of a few hundred G, but we do not consider the evidence for this to be very strong.
In summary, FORS1 observations have successfully been used to discover the field of one Herbig star, HD 101412, and of the binary companion of another Herbig star, HD 72660A (Wade et al. 2005). FORS1 observations have shown that fields are possibly present, but certainly not yet definitely established, in HD 97048 and HD 144668 (Hubrig et al. 2006c), HD 144332 (Hubrig et al. 2006c, 2007a), CPD −53 295 (Wade et al. 2007a; Hubrig et al. 2009c), and HD 150193 (Hubrig et al. 2009c). All other published FORS1 field discoveries of Herbig AeBe stars appear to be spurious. Detectable magnetic fields appear to occur in only a few percent of all Herbig AeBe stars observed with FORS1. This result is consistent with the 7% found by Alecian et al. (2011) from the comparable size ESPaDOnS survey.
5.4. β Cephei pulsators and slowly pulsating B stars
The β Cep pulsators are early B stars, with spectral types mostly earlier than B3, and masses in the range of about 10 to 20 M⊙, that pulsate in at least one radial p mode with periods in the range of 0.1 to 0.5 d. The slowly pulsating B stars (SPBs) are stars that are B2 or later, have slightly lower masses than β Cep stars, and show non-radial g mode pulsations with periods of order 1 d. It appears that these pulsations are excited by the kappa mechanism operating in a deep region of high iron opacity.
A field was discovered in the prototype β Cep star, β Cep = HD 205021 itself (Henrichs et al. 2000; Neiner et al. 2001; Donati et al. 2001). The field of this star appears to be very securely detected (see Sect. 5.2).
A magnetic field was reported in the β Cep star V2052 Oph = HD 163472 by Neiner et al. (2003b), again based on MuSiCoS observations. The measurements presented appear to support the claimed discovery, but are very close to the limit of detection. The reality of this field is now clearly confirmed by NARVAL observations (Neiner et al. 2012).
Neiner et al. (2003c) reported the presence of a magnetic field in the SPB star ζ Cas = HD 3360 (still based on MuSiCoS data). Although these observations appear consistent with the presence of a field, they do not support fully convincing evidence for it. However, the presence of a magnetic field in ζ Cas is definitely confirmed by further (unpublished) observations with MuSiCoS and NARVAL (Neiner, priv. comm.).
Major surveys of both β Cep and SPB pulsators have been carried out by Hubrig et al. (2006a) and Hubrig et al. (2009a). Nearly 70 stars were observed for magnetic fields using the FORS1 spectropolarimeter (19 known and suspected β Cep stars, 50 known and suspected SPBs). In this survey, fields were reported to have been detected in five β Cep stars and 26 SPB stars. If these results were confirmed, they would be quite important; such high incidence of detected fields would strongly suggest that magnetism is intrinsically connected with the pulsation phenomenon in early B-type stars, as it is in the cool rapidly oscillating Ap (roAp) stars.
Hubrig et al. (2006a) and Hubrig et al. (2009a) have reported discovery of a field in the β Cep star ξ1 CMa = HD 46328, based on altogether 13 detections at approximately the 6 or 7σ level. The field always appears to be close to + 350 G. These detections are further supported by a single field detection by Silvester et al. (2009) using ESPaDOnS at about the 30σ level, by two ESPaDOnS field measurements reported by Shultz et al. (2012), and by further ESPaDOnS observations not yet published in detail (Fourtune-Ravard et al. 2011). The re-reductions of the FORS1 data (not shown in Table 5 because the measurements exceed the 6σ upper limit for inclusion) also confirm the presence of a field. This discovery appears very robust, and clearly indicates the capability of FORS1 to detect rather modest magnetic fields in B-type stars.
The reported field detections in β Cep stars in Table 5 have mostly become insignificant in the new reductions. In particular, the six reported detections of a field in HD 16582 all have decreased below the 3σ significance limit, although one measurement not originally claimed as detection by Hubrig et al. (2009a), on MJD = 54 343.259, has risen to the apparently significant value of −104 ± 19 G. A single ESPaDOnS field measurement detects no trace of a field with ⟨ Bz ⟩ uncertainty of 10 G (Silvester et al. 2009). While it is still possible that a field might be present in HD 16582, this must certainly be regarded at present as – at best – extremely uncertain. Only two published field detections, one each for HD 74575 and HD 136504, are still significant at the 3σ level, and each of these measurements is only barely significant. Three field measurements with ESPaDOnS of HD 74575 show no trace of a field at the 6 G level (Shultz et al. 2012); we regard these measurements as clear evidence that no field has been detected in this star. On the other hand, a field is definitely detected by Shultz et al. (2012) in two out of two measurements of HD 136504 (=ϵ Lupi); these measurements clearly confirm the field discovered by Hubrig et al. (2009a). All the remaining reported detections in β Cep stars appear to be the result essentially of underestimated measurement uncertainties; currently there is no significant evidence for fields based on these measurements.
Of the more than 40 field detections reported in SPB stars by Hubrig et al. (2006a) and Hubrig et al. (2009a), all but five have decreased to non-detections in the new reductions.
For HD 28114, the re-reduced field strength is considerably larger than the published value (and of the opposite sign), but significant at the 4σ level. Field detection is obtained only on the higher order Balmer lines, which suggests that our detection is spurious. A single ESPaDOnS observation finds no trace of a field at the 30 G level (Silvester et al. 2009); it is presently not at all clear that a field has been detected in HD 28114.
For HD 74195, the published detection is no longer significant, but a field detection on MJD = 54 143.072, contradicted by the non-significant published field value, is now found at slightly more than 3σ significance, so that a field might possibly be present.
In the new reductions, HD 53921 still has one significant field detection, although with the opposite sign to the published value; the other two published detections are no longer significant. The star is a visual binary with 1.4′′ separation; in less than optimal seeing conditions the two components cannot be easily disentangled (e.g., on MJD = 53 630.401 and 53 631.408 the two spectra were not distinguishable). Note that a field has also been detected in this star in two HARPSpol measurements recently obtained by one of us (Kochukhov), so the detection of a field in this star appears to be secure.
The new reductions of HD 152511 still have two apparently very significant detections (but we note that for reasons probably related to bad image quality, our reductions of data obtained on MJD = 54 609 lead to poor results).
For 16 Peg = HD 208057, the new reductions confirm the original detection published by Hubrig et al. (2006a), and also indicate a significant detection of − 195 ± 60 G at slightly over the 3σ significance level for the other measurement of this star (for which the original published field was not a detection). Note that a field has also been marginally detected by Silvester et al. (2009) in a single ESPaDOnS measurement of HD 208057; the reality of this field has also been much more extensively confirmed by Henrichs et al. (2009).
In ≲ 1% of the observations, the FORS pipeline failed to reduce the scientific frames. The dataset of HD 161783 obtained on MJD = 53 520.308 is one of these rare cases, and our entry in Table 5 is an empty space.
We finally note that the field measurement of HD 215573 obtained on MJD = 53 193.321 and published by Hubrig et al. (2006a) is obtained from frames that seem to have reached saturation, even though the ADU count is just around 50 000. We found that the CCD gain was set such that the electron level would reach the full well capacity before ADC saturation. Accordingly, we have discarded this dataset, and left an empty space in the entry of Table 5. The same problem affects many observations of programme ID 073.D-0466, dedicated to the observations of SPB and Bp stars.
Based on the re-reductions of the FORS1 data, as well as other published material, we conclude that the securely detected fields at present among the β Cep pulsators are those of β Cep, V2052 Oph, ξ1 CMa, and HD 136504 (=ϵ Lupi). Securely detected fields occur in the SPB stars ζ Cas = HD 3360, HD 53921, and 16 Peg = HD 208057. The β Cep star HD 16582, and the SPB stars HD 74195 and HD 152511 may possibly have weak fields, but these apparent detections still need to be firmly confirmed or rejected. The great majority of field discoveries announced by Hubrig et al. (2006a) and Hubrig et al. (2009a) are spurious. Based on this conclusion, it appears that, as in other kinds of upper main sequence stars, magnetic fields are relatively rare. Grunhut & Wade (2011) estimate that fields are present in 16% of pulsating B stars, only marginally more than the incidence of magnetic fields among A stars. More importantly, there is currently no significant case for considering that the pulsation properties of these B pulsators are intrinsically connected to the presence of weak magnetic fields.
5.5. δ Scuti pulsating late A-type stars
Delta Scuti stars are late A- or early F-type stars, on or near the main sequence, that pulsate by the kappa mechanism with periods of a few hours. The pulsations are a mixture of radial and non-radial modes.
Although δ Sct stars occur in stars of the same mass and evolution state as cool magnetic Ap stars, there are no confirmed magnetic Ap stars that show δ Sct pulsations. From photometry with Kepler mission, several possible magnetic Ap δ Sct stars have been reported, although the spectral classification of these stars is still quite uncertain. One definite case of a field in a pulsation γ Dor star has been discovered (Balona et al. 2011). On the other hand, there does not appear to have been any substantial survey of known δ Sct stars for magnetic fields, although occasionally surveys of bright A- and F-type stars have included one or two δ Sct stars such as Altair and β Cas (Landstreet 1982; Monin et al. 2002). No field detections have emerged from these observations, although it would be interesting to carry out a larger survey of δ Sct stars.
Using FORS1, Kurtz et al. (2008) have observed the δ Sct star HD 21190, for which an Ap classification was proposed (Koen et al. 2001), and have reported an apparently significant field of ⟨ Bz ⟩ = 47 ± 13 G, although they comment that this detection requires confirmation. Our re-reduction of this measurement increases the uncertainty only a little, but the result is that there is no significant detection. We regard this detection as spurious. We also need to add that a few Ap classifications of known δ Scuti stars are inconclusive, since none was supported by a detailed spectroscopic study. A quick inspection of archival UVES spectra allows us to conclude in particular that HD 21190 is not an Ap star.
5.6. Non-peculiar B-type main sequence and giant stars
Magnetic fields have begun to be detected in B-type stars that do not show the obvious chemical peculiarities that signal magnetic Bp or He-peculiar stars. The stars β Cep, ζ Cas, and ξ1 CMa have been discussed above in the context of pulsating B stars. Fields have also been reported in τ Sco = HD 149438 (Donati et al. 2006b), HD 36982 = Par 1772 and NU Ori = HD 37061 (Petit et al. 2008).
FORS1 surveys including such stars have been reported by Hubrig et al. (2006b), McSwain (2008), Hubrig et al. (2009a) and Hubrig et al. (2009b). As noted in Table 5, detections of fields have been reported in several stars. In our new reductions, the only remaining measurement that shows a significant field is one of two observations of HD 52089, whose field appears to be significant at about the 5σ level. McSwain (2008) reported a marginal detection in NGC 3766 MG 45, apparently contradicted by our estimate of Table 5 obtained from the full spectrum. However, from H Balmer lines, we measure ⟨ Bz ⟩ = −258 ± 77 G. In conclusion, a field might be present both these stars, but would certainly require confirmation. The other reported detections resulting from these surveys are probably spurious.
In addition, Hubrig et al. (2008a) report a number of magnetic field measurements of the B0Vp star θ Car = HD 93030, the brightest star in the open cluster IC 2602. Five of these measurements are significant at ≳3σ level, as listed in Table 5, although Hubrig et al. (2008a) do not conclude that the star is magnetic. Because the 26 measurements were all obtained within about 80 min, in our re-reduction of the field measurements we have combined all measurements into a single average value. The average measurement does not show any signficant field, and we conclude that FORS data do not reveal presence of a magnetic field.
5.7. O-type stars
O-type stars are relatively difficult targets for magnetic field measurements, because they have few strong spectral lines, high projected rotational velocities (~100 km s-1), and often fairly strong emission filling in some of the photospheric absorption lines. The first detections came when a field was detected in θ1 Ori C, the brightest star in the Trapezium, by Donati et al. (2002), and in the Of?p star HD 191612 by Donati et al. (2006a), using high-resolution spectropolarimetery.
A field of order 100 G has been reported in the O9.7 supergiant ζ Ori A = HD 37742 (Bouret et al. 2008), but the field detection is near the limit of detectability and needs confirmation.
Hubrig et al. (2008b) carried out the first large survey of O-type stars with FORS1, and reported field measurements of 13 O stars (including one star previously reported by Hubrig et al. 2007b). Field discoveries were claimed for five of these stars, as listed in Table 5. When reduced with our tools, only one of these stars still shows a significant magnetic field, the O6.5f?p star HD 148937. The field of this star has more recently been detected in three more observations with FORS2 by Hubrig et al. (2011b). Furthermore, the field has been confirmed by Wade et al. (2012) from observations obtained by the MiMeS project. This discovery is clearly real, but it appears that the field of this star, always about −250 G, is close to the limit for reliable field detection by FORS1 in such stars.
The other O-type stars for which fields are reported by Hubrig et al. (2008b) appear to be spurious detections.
Hubrig et al. (2011c) have reported the detection of a magnetic field at just over the 3σ level in the runaway O-type star ζ Oph = HD 149757. Our re-reduced measurement of this star no longer shows a significant field. This detection is probably spurious.
5.8. X-ray binary star systems
Under this heading, we consider two different types of possibly magnetic stars: nearby A-type stars identified with X-ray sources in the ROSAT catalogue, and the brilliant and distant X-ray source Cyg X-1.
A-type stars are not expected to emit detectable levels of X-ray flux. They are not hot enough to have the strong radiatively driven winds whose instabilities or collision regions are strong X-ray generators, and the A-type stars do not have the deep convection zones that lead to stellar activity and essentially universal coronal X-ray emission. However, about 15% of A-type stars are associated with detected X-ray sources. Some of these X-ray sources are low-mass, active companions, but it is not clear that in all cases this is an adequate explanation.
Schröder et al. (2008) have carried out an extensive survey with FORS1 for magnetic fields in X-ray emitting A-type stars in which the companion hypothesis seems doubtful. This survey has led to three reported discoveries of fields in A-type stars, as listed in Table 5. In the cases of HD 147084 and HD 159312, the new reductions show no significant field, and these detections are probably spurious. The other detection is in HD 148898, which is known to be a magnetic Ap star. Although no field has previously been convincingly detected in this star (Borra & Landstreet 1980), it is expected (Aurière et al. 2007) to have a weak magnetic field. The field reported by Schröder et al. (2008) is still present at almost the 3σ level in our new reductions, and may be correctly detected by this observation.
The system Cyg X-1 = HD 226868 is a binary composed of a black hole orbiting with an O9.7Iab supergiant, which is losing mass onto the black hole. FORS1 has been used to search for the presence of a magnetic field in the optical primary star of this system by Karitskaya et al. (2009, 2010). They report 13 field measurements spread over 1.5 months. Three of their measurements show apparently significant detections. In our new reductions, two of these three measurements are still significant at about 5σ level. Two other measurements, not showing a 3σ detection in the original reductions, reveal a ≳ 3 sigma field detection in our new reductions. The field apparently detected in this star is very near the reliable detection limit for FORS1. We also note that due to the target declination, all observations were obtained with the telescope at a large zenith distance (~60°), and that in the course of the 1.1 h long observations, the instrument was rotating by ~20°. Should flexures play a role in the magnetic field determinations obtained with FORS, they certainly have an impact on these observations. Finally, we must remark that we measure an unusually high fraction of circular polarization in the continuum (about − 0.4% at 3600 Å, linearly changing to about − 0.3% at 5200 Å). While this signal is possibly real, it could potentially be due to cross-talk from linear polarization (see Sect. 7.4 of Bagnulo et al. 2009). It is clear that further observations of Cyg X-1, both in linear and circular polarization, would be of considerable interest.
5.9. Hot subdwarfs
Detections of kG magnetic fields in two sdO stars, Feige 66 = BD +25° 2534, and BD +75° 325, were reported by Elkin (1996).
Magnetic fields were measured using FORS1 in six hot subdwarfs by O’Toole et al. (2005), and significant detections were claimed for all six stars, as listed in Table 5. Four of these stars are B subdwarfs, probably stars that are essentially in the horizontal branch stage of evolution but have somehow lost virtually all their hydrogen envelopes. The other two, CD −31 4800 and LSE 153, are O subdwarfs, probably stars on their way from being central stars of planetary nebulae to being white dwarfs.
In our new reductions, the uncertainties of the ⟨ Bz ⟩ measurements are slightly reduced compared to the values originally published, but no detections at even the 2σ level are found. This survey provides no significant evidence for the presence of magnetic fields in such stars at the level of 1 kG. Furthermore, new ESPaDOnS measurements of HD 76431, one of the sdB stars reported to host a kG field by O’Toole et al. (2005), find no indication of any field above a level of order 100 G (Petit et al. 2011). Petit et al. (2011) have also shown that the FORS1 field measurement of HD 76431 does not support any significant field detection. Finally, they also report no detection in Feige 66, for which Elkin (1996) claimed detection of a kG field.
Valyavin et al. (2006) have carried out a search for weak (kG) magnetic fields in a number of white dwarfs, and the sdO star WD 1036+433, using the spectropolarimeter on the Russian 6-m telescope of the Special Astrophysical Observatory. Of the three observations of this subdwarf, one reveals a field of 9.6 ± 2.6 kG, at the 3.7σ level, which is suggestive of the presence of a field, but not yet conclusive.
At present there is at most marginal evidence for fields of a few kG in subdwarfs, and it appears that most of the reported detections are spurious. However, the total sample studied is very small. This is a category of star that would clearly benefit from a larger survey with FORS.
5.10. Central stars of planetary nebulae
Jordan et al. (2005) carried out six field measurements of four central stars of planetary nebulae (CSPN), and concluded that at least two of these stars have highly significant fields in the kG range. This result supports the idea that such fields have an important shaping effect on the the planetary nebulae themselves. It also suggests that important loss of magnetic flux must occur between this evolution state and that of white dwarf, since white dwarfs with as much magnetic flux as that inferred for the CSPN are relatively rare. These results were called into question recently by Leone et al. (2011), who obtained one new measurement of each of the CSPNs NGC 1360 and LSS 1362, detecting no significant field in either star, and who re-reduced the older data of Jordan et al. (2005), also finding no significant fields.
Our new reductions are completely consistent with the re-reductions carried out by Leone et al. (2011). None of the original field measurements by Jordan et al. (2005) reveals a significant field. As remarked by Leone et al. (2011), there is now no significant evidence for coherent magnetic fields in the central stars of planetary nebulae, and the current best upper limits on ⟨ Bz ⟩ are at roughly the 1 to 2 kG level.
5.11. (Weak-field) magnetic white dwarfs
It has been known for 40 years that strong magnetic fields occur in a small fraction of white dwarf stars. The fields can be as large as ~300 MG, and as small as tens of kG. In recent years, there has been considerable interest in establishing how the low field end of the distribution of field strengths found in the sample of magnetic white dwarfs behaves: do most or all white dwarfs have weak (a few kG) fields, or are weak fields as rare as the stronger fields are, occurring in only a few percent of white dwarfs?
A first effort to answer this question was made by Schmidt & Smith (1995), who surveyed nearly 170 DA white dwarfs (i.e. white dwarfs with strong Balmer line spectra) using the Zeeman effect in the H lines. Schmidt & Smith (1995) found two white dwarfs with fields of order 102 kG. More recently, a smaller survey was carried out by Fabrika et al. (2003) and Valyavin et al. (2006), using the Russian 6-m telescope, which has reported several field detections. The fields detected range in size from a few kG to a few tens of kG.
FORS1 has made a substantial contribution to this search. Aznar Cuadrado et al. (2004) detected kG fields in three white dwarfs. Jordan et al. (2007) have continued the survey, and identified three more stars that they consider probably weakly magnetic (although no single field measurement reached the 3σ level of significance). Our re-reduced data for the three magnetic white dwarfs reported by Aznar Cuadrado et al. (2004) still show field values that consistently differ from zero by between 3.3 and 6.2σ. Although none of these measurements is completely outside of the range of spurious detections, the fact that significant fields are detected in two measurements each of WD 0446-789 and WD 2359-434, and that the single measurement of WD 1105-048 is significant at the 5.3σ level, suggests that all three field detections may well be correct. However, confirming observations are required. In contrast, the (less significant) field measurements reported by Jordan et al. (2007) all have diminished to an insignificant level in the new reductions. At present there is no strong evidence for fields in any of these stars.
Note that the sign of the field values has been reversed to conform to the convention used in magnetic main sequence stars.
Since the fields apparently detected with FORS1 are among the very smallest fields known in white dwarfs, it is clear that the instrument is a very powerful tool for this kind of work, and that further observations would be of considerable value.
6. Conclusions
We have investigated the robustness of magnetic field detections obtained with the FORS1 instrument of the ESO VLT. To carry out our study, we have developed a semi-automatic data reduction procedure and applied it to the entire FORS1 archive of circular spectropolarimetric data.
We have performed sophisticated Monte Carlo simulations (based on the repetition of the entire data reduction process after altering the original raw frames to simulate photon noise), and concluded that our estimate of the field error bar correctly accounts for the photon noise.
We have performed all our field measurements adopting several different and reasonable data reduction algorithms, and concluded that the taking certain (somewhat arbitrary) choices during the process of data reduction contributes to the budget of the measurement error in a significant way.
We have determined the magnetic field from the null profiles, and studied its distribution. Our conclusion is that photon-noise is not the only source of uncertainties. Among the possible causes of non-Poisson noise, we find that small instrument flexures, negligible in most of the other instrument applications, set a lower limit to the accuracy of the field measurements, and may be responsible for some of the field detections in the null profiles.
Overall, non-statistical noise cannot be characterised in detail, but as a rough guide we estimate that actual error bars may be some 50% higher than estimated from photon-noise, especially for high signal-to-noise ratio measurements.
We have performed a detailed comparison with the results previously published in the literature. Even without considering the impact of non-photon noise, we are unable to confirm many of the previously published new discoveries that were obtained at a 3 to 6σ level, and we have discussed how the incidence of the magnetic field in various classes of stars should be revised. The fact that our analysis of FORS1 data does not allow us to confirm many of the recent discoveries, leads us to conclude that there is no contradiction between the results obtained with FORS1 and those obtained with high-resolution spectropolarimeters.
FORS is a low resolution spectropolarimeter perfectly suitable for the detection of magnetic fields with ≳ 300 G strength. Fields weaker than about 100 G are probably out of its reach. In general, we argue that any field detection reported at a less than 5–6σ level should be corroborated by repeated observations, and, if possible, cross-checked with other instruments. While it cannot reach the same accuracy of a high-resolution instrument sitting in a thermally and mechanically isolated bench (like ESPaDOnS and HARPSpol), FORS remains an invaluable instrument for the detection of magnetic fields in faint and/or rapidly rotating stars.
Online material
List of published “marginal” field detections.
One particular feature of the newly reduced data is the change in sign of the data for HD 83368 compared to the earlier publication by Hubrig et al. (2004b). This point has been carefully investigated, and we believe that the signs in Hubrig et al. (2004b) are incorrect for all the data for this star, and should be changed to positive signs.
This case is illustrated in Bagnulo et al. (2009), who also claimed that the null profiles obtained with the difference method are more sensitive to differential wavelength offsets than the null profiles obtained with the ratio method. In fact, we found that this claim is wrong. Both ways to calculate the null profiles are equivalent, and in the cases (c) and (d) presented in their Fig. 6, both null profiles obtained with the ratio and the different methods are zero.
Acknowledgments
This work is based on data obtained from the ESO Science Archive Facility, under the following programmes: 069.D-0210, 070.D-0259, 071.D-0308, 270.D-5023, 072.C-0447, 072.D-0089, 072.D-0290, 072.D-0377, 272.C-5063, 073.D-0356, 073.D-0466, 073.D-0464, 074.C-0442, 074.C-0463, 075.D-0295, 075.D-0432, 075.D-0507, 077.D-0406, 077.D-0556, 078.D-0140, 278.D-5056, 079.D-0241, 079.D-0549, 080.D-0383, 081.C-0410, 381.D-0138. J.D.L. has been supported by the Natural Sciences and Engineering Research Council of Canada. We thank E. Alecian and C. Neiner, for many useful discussions and suggestions, and the referee, P. Petit, for his constructive comments. S.B. would like to dedicate his contribution to this paper to the memory of Carlo Izzo, dearest friend, and precious collaborator. We acknowledge the crucial importance for this paper provided by his work at ESO, and by numerous useful discussions. Carlo Izzo also kindly provided us with some of the scripts used for data organisation.
References
- Alecian, E., Catala, C., Wade, G. A., et al. 2008a, MNRAS, 385, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Alecian, E., Wade, G. A., Catala, C., et al. 2008b, Contr. Astron. Obs. Skalnaté Pleso, 38, 235 [Google Scholar]
- Alecian, E., Catala, C., Wade, G. A., et al. 2009a, in Stellar Magnetism, ed. C. Neiner, & J.-P. Zahn, EAS Publ. Ser., 39, 121 [Google Scholar]
- Alecian, E., Wade, G. A., Catala, C., et al. 2009b, MNRAS, 400, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Alecian, E., Wade, G. A., Catala, C., et al. 2011, MNRAS, submitted [Google Scholar]
- Appenzeller, I. 1967, PASP, 79, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I., Fricke, K., Furtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Aurière, M., Wade, G. A., Silvester, J. A., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aurière, M., Wade, G. A., Lignières, F., et al. 2010, A&A, 523, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aznar Cuadrado, R., Jordan, S., Napiwotzki, R., et al. 2004, A&A, 423, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Szeifert, T., Wade, G. A., Landstreet, J. D., & Mathys, G. 2002, A&A, 389, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landstreet, J. D., Mason, E., et al. 2006, A&A, 450, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landolfi, M., Landstreet, J. D., et al. 2009, PASP, 121, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A., Cunha, M. S., Kurtz, D. W., et al. 2011, MNRAS, 410, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, P. K., Landstreet, J. D., Marlborough, J. M., & Thompson, I. B. 1985, ApJ, 288, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Borra, E. F., & Landstreet, J. D. 1980, ApJS, 42, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Borra, E. F., Landstreet, J. D., & Thompson, I. 1983, ApJS, 53, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Bouret, J.-C., Donati, J.-F., Martins, F., et al. 2008, MNRAS, 389, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Wade, G. A., Babel, J., et al. 2001, MNRAS, 326, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Babel, J., Harries, T. J., et al. 2002, MNRAS, 333, 55 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Howarth, I. D., Bouret, J.-C., et al. 2006a, MNRAS, 365, 6 [Google Scholar]
- Donati, J.-F., Howarth, I. D., Jardine, M. M., et al. 2006b, MNRAS, 370, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Elkin, V. G. 1996, A&A, 312, L5 [NASA ADS] [Google Scholar]
- Fabrika, S., Valyavin, G. G., & Burlakova, T. E. 2003, AstL, 29, 737 [Google Scholar]
- Folsom, C. P., Wade, G. A., Kochukhov, O., et al. 2008, MNRAS, 391, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Fourtune-Ravard, C., Wade, G. A., Marcolino, W., et al. 2011, in Active OB stars: structure, evolution, mass loss, and critical limits, Proc. International Astronomical Union (Cambridge: CUP), IAU Symp., 272, 180 [Google Scholar]
- Glagolevskij, Yu. V., Romanyuk, I. I., Bychkov, V. D., & Najdenov, I. D. 1985, Sov. Astr. Lett. 11, 45 [NASA ADS] [Google Scholar]
- Grunhut, J. H., & Wade, G. A. 2011 [arXiv:1109.6384v1] [Google Scholar]
- Henrichs, H., de Jong, J. A., Donati, J.-F., et al. 2000, in The Be Phenomenon in Early-Type Stars, ed. M. A. Smith, H. F. Henrichs, & J. Fabregat, ASP Conf. Ser., 214, 324 [Google Scholar]
- Henrichs, H. F., Neiner, C., Schnerr, R. S., et al. 2009, in Cosmic magnetic fields: from planets to stars and galaxies (Cambridge: CUP), Proc. IAU Symp., 259, 393 [NASA ADS] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Schöller, M., & Yudin, R. V. 2004a, A&A, 428, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Kurtz, D. W., Bagnulo, S., et al. 2004b, A&A, 415, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Briquet, M., Schöller, M., et al. 2006a, MNRAS, 369, 61 [Google Scholar]
- Hubrig, S., North, P., Schöller, M., & Mathys, G. 2006b, AN, 327, 289 [Google Scholar]
- Hubrig, S., Yudin, R. V., Schöller, M., & Pogodin, M. A. 2006c, A&A, 446, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Pogodin, M. A., Yudin, R. V., Schöller, M., & Schnerr, R. S. 2007a, A&A, 463, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Yudin, R. V., Pogodin, M., Schöller, M., & Peters, G. J. 2007b, AN, 328, 1133 [Google Scholar]
- Hubrig, S., Briquet, M., Morel, T., et al. 2008a, A&A, 488, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Schöller, M., Schnerr, R. S., et al. 2008b, A&A, 490, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Briquet, M., De Cat, P., et al. 2009a, AN, 330, 317 [Google Scholar]
- Hubrig, S., Schöller, M., Savanov, I., et al. 2009b, AN, 330, 708 [Google Scholar]
- Hubrig, S., Stelzer, B., Schöller, M., et al. 2009c, A&A, 502, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Mikulášek, Z., González, J. F., et al. 2011a A&A, 525, L4 [Google Scholar]
- Hubrig, S., Schöller, M., Kharchenko, N. V., et al. 2011b, A&A, 528, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Oskinova, L. M., & Schöller, M. 2011c, AN, 332, 147 [Google Scholar]
- Izzo, C., de Bilbao, L., Larsen, J., et al. 2010, SPIE, 7737, 773729 [Google Scholar]
- Izzo, C., de Bilbao, L., & Larsen, J. M. 2011, FORS Pipeline User Manual, Issue 4.1, VLT-MAN-ESO_19500-4106 [Google Scholar]
- Jordan, S., Werner, K., & O’Toole, S. J. 2005, A&A, 432, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jordan, S., Aznar Cuadrado, R., Napiwotzki, R., Schmid, H. M., & Solanki, S. K. 2007, A&A, 462, 1097 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karitskaya, E. A., Bochkarev, N. G., Hubrig, S., et al. 2009 [arXiv:0908.2719] [Google Scholar]
- Karitskaya, E. A., Bochkarev, N. G., Hubrig, S., et al. 2010, Inf. Bull. Var. Stars, 5950 [Google Scholar]
- Kochukhov, O., & Bagnulo, S. 2006, A&A, 450, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kochukhov, O., Makaganiuk, V., & Piskunov, N. 2010, A&A, 524, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koen, C., Kurtz, D. W., Gray, R. O., et al. 2001, MNRAS, 326, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D.W., Hubrig, S., González, J. F., van Wyk, F., & Martinez, P. 2008, MNRAS, 386, 1750 [NASA ADS] [CrossRef] [Google Scholar]
- Landstreet, J. D. 1982, ApJ, 258, 659 [Google Scholar]
- Leone, F., Martínez González, M. J., Corradi, R. L. M., Privitera, G., & Mason Sainz, R. 2011, ApJ, 731, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Makaganiuk, V., Kochukhov, O., Piskunov, N., et al. 2011, A&A, 529, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McSwain, M. V. 2008, ApJ, 686, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Monin, D. N., Fabrika, S. N., & Valyavin, G. G. 2002, A&A, 396, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, T., Hubrig, S., & Briquet, M. 2008, A&A, 481, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neiner, C., Henrichs, H., & Hubert, A.-M. 2001, in Magnetic Fields Across the Hertzsprung-Russell Diagram, ed. G. Mathys, S. K. Solanki, & D. T. Wickramasinghe, ASP Conf. Ser., 248, 419 [Google Scholar]
- Neiner, C., Hubert, A.-M., Frémat, Y., et al. 2003a, A&A, 409, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neiner, C., Henrichs, H., Floquet, M., et al. 2003b, A&A, 411, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neiner, C., Geers, V. C., Henrichs, H., et al. 2003c, A&A, 406, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neiner, C., Alecian, E., Briquet, M., et al. 2012, A&A, 537, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Toole, S. J., Jordan, S., Friedrich, S., & Heber, U. 2005, A&A, 437, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, V., Wade, G. A., Drissen, L., Montmerle, T., & Alecian, E. 2008, MNRAS, 387, L23 [NASA ADS] [Google Scholar]
- Petit, P., Van Grootel, V., Bagnulo, S., et al. 2011 [arXiv:1110.5227v2] [Google Scholar]
- Rivinius, Th., Szeifert, Th., Barrera, L., et al. 2010, MNRAS, 405, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, G. D., & Smith, P. S. 1995, ApJ, 448, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Schnerr, R. S., Henrichs, H. F., Oudmaijer, R. D., & Telting, J. H. 2006, A&A, 459, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schröder, C., Hubrig, S., & Schmitt, J. H. M. M. 2008, A&A, 484, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shorlin, S. L. S., Wade, G. A., Donati, J.-F., et al. 2002, A&A, 392, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shultz, M., Wade, G. A., Grunhut, J., et al. 2012, ApJ, in press [Google Scholar]
- Silvester, J., Neiner, C., Henrichs, H. F., et al. 2009, MNRAS, 398, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Szeifert, Th., Reiss, R., Baksai, P., et al. 2007, The Messenger, 128, 9 [NASA ADS] [Google Scholar]
- Valyavin, G., Bagnulo, S., Fabrika, S., et al. 2006, ApJ, 648, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Valyavin, G., Wade, G. A., Bagnulo, S., et al. 2008, ApJ, 683, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Donati, J.-F., Landstreet, J. D., & Shorlin, S. L. S. 2000, MNRAS, 313, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Drouin, D., Bagnulo, S., et al. 2005, A&A, 442, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Aurière, M., Bagnulo, S., et al. 2006, A&A, 451, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Bagnulo, S., Drouin, D., Landstreet, J. D., & Monin, D. 2007a, MNRAS, 376, 1145 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wade, G. A., Alecian, E., Catala, C., et al. 2007b, Contr. Astr. Obs. Skalnaté Pleso, 38, 251 [NASA ADS] [Google Scholar]
- Wade, G. A., Grunhut, J., Gräfener, G., et al. 2012, MNRAS, 419, 2459 [NASA ADS] [CrossRef] [Google Scholar]
- Yudin, R. V., Hubrig, S., Pogodin, M. A., & Schoeller, M. 2011, in Active OB stars: structure, evolution, mass loss, and critical limits, Proc. International Astronomical Union (Cambridge: CUP), IAU Symp., 272, 222 [NASA ADS] [Google Scholar]
All Tables
Summary of the characteristic of the grisms+CCD setting most commonly employed for magnetic field measurements.
All Figures
 |
Fig. 1 The polarised spectrum of HD 94660 observed on 2007-03-22 with grism 600B. The top panel shows the normalised derivative of the observed flux, and the panel immediately below shows the observed flux F (black solid line, in arbitrary units, and not corrected for the instrument response), the PV profile (red solid line centred about 0), and the null profile (blue solid line, offset by –0.75% for display purpose). The null profile is expected to be centred about zero and scattered according to a Gaussian with σ given by the PV error bars. The PV error bars are represented with light blue bars centred about –0.75%. The slope of the interpolating lines in the bottom panels gives the mean longitudinal field from PV (left bottom panel) and from the null profile (right bottom panel) both calculated using the H Balmer lines only. The corresponding ⟨ Bz ⟩ and ⟨ Nz ⟩ values are − 1885 ± 90 G and − 192 ± 62 G, respectively. |
| In the text | |
 |
Fig. 2 Results obtained from the analysis of the H Balmer lines (top panels), of the metal lines (mid panels), and of the full spectrum (bottom panels) for three stars, using standard error theory and Montecarlo simulations. The (red) thick solid lines are Gaussian curves centred about the various field values and with σ given by Eq. (11). The blue lines show the distributions obtained with Monte Carlo simulations as explained in the text. Note that HD 94660 has a large field, HD 96441 has no detected field, and HD 171184 has a weak but probably real field. |
| In the text | |
 |
Fig. 3 PV and NV profiles of HD 94660 obtained with average extraction (red thick lines) an optimal extraction (blue thin lines). The null profiles are offset by −1% for display purpose, and overplotted to the statistical error bars of the PV and NV profiles. |
| In the text | |
 |
Fig. 4 The distribution of the difference between ⟨Bz⟩ values obtained with two slightly different algorithms for data reduction, normalised to the error bars, and compared to a Gaussian with identical area, centred about zero, and with σ = 0.33. |
| In the text | |
 |
Fig. 5 LSD profiles for HD 94660 observed with grism 600 B (left panel) and 1200 B (right panel). Red solid line: Stokes V/Ic; blue dotted line: N/Ic; black solid line Stokes I/Ic. V/Ic and N/Ic are offset to +1 % for display purpose. |
| In the text | |
 |
Fig. 6 Some characteristics of the FORS spectropolarimetric observations retrieved in the archive. |
| In the text | |
 |
Fig. 7 Histogram of the ⟨ Nz ⟩ values calculated from Balmer lines, and normalised to the error bars σ ⟨ Nz ⟩ . The red solid lines show the Gaussian with σ = 1, and the blue solid line a Gaussian with σ = 1.365, both with the same areas as the observed distribution. The vertical lines mark the limits at − 3 and 3. |
| In the text | |
 |
Fig. 8 The distribution of the differences between the null field values measured after flexure simulation and their original values, normalised to the error bars, compared to a Gaussian curve centred about zero and with σ = 0.2. Null field values were calculated from the H Balmer lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


