| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117922 | |
| Published online | 09 January 2012 | |
Properties and nature of Be stars
29. Orbital and long-term spectral variations of γ Cassiopeiae⋆,⋆⋆,⋆⋆⋆
1
Astronomical Institute of the Charles University, Faculty of
Mathematics and Physics, V
Holešovičkách 2, 180
00
Praha 8,
Czech Republic
e-mail: janicka.ari@seznam.cz
2
Astronomical Institute of the Academy of Sciences,
251 65
Ondřejov, Czech
Republic
3
Department of Physics and Astronomy, University of North Carolina
at Greensboro, Greensboro, NC
27402,
USA
4
Physics & Astronomy Department, University of
Victoria, PO Box 3055 STN
CSC, Victoria,
BC, V8W 3P6, Canada
5
Association des Utilisateurs de Détecteurs Électroniques (AUDE),
28 rue du Pic du Midi, 31130
Quint-Fonsegrives,
France
Received: 20 August 2011
Accepted: 12 October 2011
A detailed analysis of more than 800 electronic high-resolution spectra of gamma Cas, which were obtained during a time interval of over 6000 days (16.84 yr) at several observatories, documents the smooth variations in the density and/or extent of its circumstellar envelope. We found a clear anticorrelation between the peak intensity and FWHM of the Hα emission, which seems to agree with recent models of such emission lines. The main result of this study is a confirmation of the binary nature of the object, determination of a reliable linear ephemeris 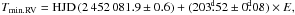 and a rather definitive set of orbital elements. We clearly demonstrated that the orbit is circular within the limits of accuracy of our measurements and has a semi-amplitude of radial-velocity curve of 4.30 ± 0.09 km s-1. No trace of the low-mass secondary was found. The time distribution of our spectra does not allow a reliable investigation of rapid spectral variations, which are undoubtedly present in the spectra. We postpone this investigation for a future study, based on series of dedicated whole-night spectral observations.
and a rather definitive set of orbital elements. We clearly demonstrated that the orbit is circular within the limits of accuracy of our measurements and has a semi-amplitude of radial-velocity curve of 4.30 ± 0.09 km s-1. No trace of the low-mass secondary was found. The time distribution of our spectra does not allow a reliable investigation of rapid spectral variations, which are undoubtedly present in the spectra. We postpone this investigation for a future study, based on series of dedicated whole-night spectral observations.
Key words: binaries: spectroscopic / stars: early-type / stars: emission-line, Be
Based on new spectral and photometric observations from the Castanet-Tolosan, Dominion Astrophysical, Haute Provence, Hvar, Ondřejov, and Ritter Observatories.
Tables 2 and 3 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/537/A59
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The well-known Be star of spectral type B0IVe γ Cassiopeiæ (27 Cas, HR 264, HD 5394, HIP 4427, MWC 9, ADS 782A), is one of the first two Be stars ever discovered (see Secchi 1866) and a member of a visual multiple system. It exhibits spectral and brightness variations on several timescales. It underwent two major shell phases in 1935–36 and 1939–40. Afterwards, it appeared briefly as a normal B star. Emission strength of the Balmer lines and the brightness of the star in the visual region had been rising slowly during the rest of the 20th century. The observational history of the star has been summarized in detail by Harmanec (2002).
In 1976, γ Cas was identified as an X-ray source. This discovery started a long debate over whether the source of X-rays is the star itself or whether γ Cas is an X-ray binary with a mass accreting compact binary companion. In an effort to prove the duplicity of γ Cas, Cowley et al. (1976) measured radial velocities (RVs hereafter) on a rich collection of photographic spectra obtained in the years 1941–1967. They were unable to find any RV changes exceeding 20 km s-1 or to detect any coherent periods between 2 5 and 4000
5 and 4000 0. Jarad (1987) measured RVs on 81 medium-dispersion (30 Å mm-1) photographic spectra using the cross-correlation technique. They concluded that the RVs vary with a short period of 1
0. Jarad (1987) measured RVs on 81 medium-dispersion (30 Å mm-1) photographic spectra using the cross-correlation technique. They concluded that the RVs vary with a short period of 1 16885, a semi-amplitude of 27.7 km s-1, and a well-defined phase curve. Combining their RVs with those measured by Cowley et al. (1976), they found a period of 0
16885, a semi-amplitude of 27.7 km s-1, and a well-defined phase curve. Combining their RVs with those measured by Cowley et al. (1976), they found a period of 0 705163 with a semi-amplitude of only 8.6 km s-1. They preferred the shorter period, which they interpreted as either a rotational or pulsation period of the star. Robinson & Smith (2000) published a detailed study of the X-ray flux of γ Cas. They found that the X-ray flux varied with a period P = 1
705163 with a semi-amplitude of only 8.6 km s-1. They preferred the shorter period, which they interpreted as either a rotational or pulsation period of the star. Robinson & Smith (2000) published a detailed study of the X-ray flux of γ Cas. They found that the X-ray flux varied with a period P = 1 12277, which they tentatively interpreted as the rotational period of γ Cas. They used this finding as one of the arguments against the binary scenario for the X-ray flux. More recently, Smith et al. (2006) have reported a coherent periodicity of 1
12277, which they tentatively interpreted as the rotational period of γ Cas. They used this finding as one of the arguments against the binary scenario for the X-ray flux. More recently, Smith et al. (2006) have reported a coherent periodicity of 1 21581 ± 0
21581 ± 0 00004 from the 1998–2006 optical photometry, prewhitened for variations on longer time scales. The latter authors pointed out that the initial period estimate of 1
00004 from the 1998–2006 optical photometry, prewhitened for variations on longer time scales. The latter authors pointed out that the initial period estimate of 1 12277 was probably an alias of the correct period near 1
12277 was probably an alias of the correct period near 1 21581.
21581.
Harmanec et al. (2000) measured RVs of the steep Hα emission wings in a series of 295 Ondřejov Reticon spectra spanning nearly 2500 days from 1993 to 2000. After removing the long-term RV changes, they discovered periodic RV variations with a period P = 203 59 ± 0
59 ± 0 29, semi-amplitude K1 = 4.68 km s-1, and eccentricity e = 0.26, which they interpreted as the binary motion around a common centre of gravity with a low-mass companion. They demonstrate that the published RVs from the photographic spectra can also be reconciled with the 203
29, semi-amplitude K1 = 4.68 km s-1, and eccentricity e = 0.26, which they interpreted as the binary motion around a common centre of gravity with a low-mass companion. They demonstrate that the published RVs from the photographic spectra can also be reconciled with the 203 59 period and discuss the possible properties of the system. Their result was confirmed by Miroshnichenko et al. (2002), who also measured the RVs of the Hα emission wings in a series of 130 electronic echelle spectra, secured with the 1 m reflector of the Ritter Observatory between 1993 and 2002. These two studies differ in the technique of RV measurements. While Harmanec et al. (2000) measured the RVs manually, sliding the direct and reversed continuum-normalized line profiles within a range of intensities on the computer screen until the best match was obtained, Miroshnichenko et al. (2002) also matched the original and reversed profiles, but used an automatic procedure. They arrived at a period of 205
59 period and discuss the possible properties of the system. Their result was confirmed by Miroshnichenko et al. (2002), who also measured the RVs of the Hα emission wings in a series of 130 electronic echelle spectra, secured with the 1 m reflector of the Ritter Observatory between 1993 and 2002. These two studies differ in the technique of RV measurements. While Harmanec et al. (2000) measured the RVs manually, sliding the direct and reversed continuum-normalized line profiles within a range of intensities on the computer screen until the best match was obtained, Miroshnichenko et al. (2002) also matched the original and reversed profiles, but used an automatic procedure. They arrived at a period of 205 50 ± 0
50 ± 0 38, semi-amplitude of 3.80 ± 0.12 km s-1, and a circular orbit. They discuss several possible reasons why their results differ significantly from those of Harmanec et al. (2000). Miroshnichenko et al. (2002) also document the cyclic long-term spectral variations of γ Cas over a time interval from 1973 to 2002.
38, semi-amplitude of 3.80 ± 0.12 km s-1, and a circular orbit. They discuss several possible reasons why their results differ significantly from those of Harmanec et al. (2000). Miroshnichenko et al. (2002) also document the cyclic long-term spectral variations of γ Cas over a time interval from 1973 to 2002.
To shed more light on the differences between these two RVs studies, to obtain truly reliable orbital elements of γ Cas, and to exclude possible 1 d aliases of the 204 d period, we combined our efforts and analysed the two sets of spectra, complemented by more recent observations from Ondřejov and additional spectra from the Dominion Astrophysical (DAO), Haute Provence (OHP) and Castanet-Tolosan Observatories. The RVs in all these spectra were measured by both measuring techniques – alternatively used by Harmanec et al. (2000) and Miroshnichenko et al. (2002) – and analysed in several different ways. Here we present the results of our investigation. We also studied the long-term and rapid spectral variations of γ Cas in our data.
2. Spectral variations
We have collected and analysed series of electronic spectra from five observatories. They cover the time interval from 1993 to 2010. The journal of the observations is in Table 1, where the wavelength range, time interval covered, the number of spectra, and the spectral lines are given. For more details on the individual datasets, readers are referred to Appendix A.
Journal of spectral observations.
We focused our study on the lines in the Hα region, which are available for all spectra, although several echelle spectra cover almost the whole visible region of the electromagnetic spectrum. In particular, we studied the following spectral lines: Hα, He i 6678 Å, Si II 6347 Å, and Si II 6371 Å. No dramatic changes were found in these line profiles. The He i 6678 Å and Si ii lines exhibit double-peaked emissions with the well-known V / R variations (changes in the relative strength of the shorter wavelength, “violet”, to the longer wavelength, “red”, peak) on the timescale of several years. Over the whole time interval covered by our spectra, the Hα line was observed as a strong, basically single-peaked emission, having a peak intensity between 3.5 and 5.0 in the units of the continuum level. Its V / R variations manifest themselves as a relative shift in the emission peak with respect to the centre of the emission profile. Several shallow absorptions can be noted in the Hα line in some of the studied spectra, but most of them are the telluric water vapour lines. Ocassionally, some weak shallow absorptions of probably stellar origin were seen, but they disappeared in less than several tens of days, and we found no regularity in their appearance and disappearance. The He i 6678 Å line consists of a double-peaked emission filling a large part of the rotationally broadened photospheric (or pseudophotospheric) absorption. The whole line is very weak and can only be measured reliably on the spectra with high S / N. The emission peaks rise only a few percent above the continuum level. Nevertheless, the time variations are seen most prominently in this line. The red peak of the He i 6678 Å emission disappeared almost completely at certain times. It is hard to say whether these variations represent only real long-term changes or whether they are partly caused by line blending. The Si II 6347 Å and Si II 6371 Å double emission lines are even weaker than the He i 6678 Å line, and their peak intensity never exceeds 5% of the continuum level. The more recent evolution of the Hα line profile is shown in Fig. 1. All line profiles shown were obtained after RJD = 52225 and were not included in the study by Harmanec et al. (2000). A similar sequences of the He i 6678 Å, Si II 6347 Å, and Si II 6371 Å line profiles are shown in Fig. 2. All displayed spectra are from Ondřejov, to compare the data with the same resolution. There are, however, the huge differences in the flux scale between Hα, He i 6678 Å, Si II 6347 Å, and Si II 6371 Å lines.
 |
Fig. 1 Recent evolution of the Hα line profile. Mid-exposure times of the displayed spectra are in RJD = HJD–2 400 000. |
 |
Fig. 2 Recent evolution of the He i 6678 Å (left), Si II 6347 Å, and Si II 6371 Å (right) line profiles. Mid-exposure times of the displayed spectra are in RJD = HJD–2 400 000. The vertical axis is in the units of the continuum flux. |
We fitted the Hα line profiles with a Gaussian profile to obtain their peak intensity (Ip hereafter) and full width at half maximum (FWHM). This procedure naturally returns a value of Ip, which is slightly less than the very maximum of the emission profile, which is affected by both the V / R variations and blending with the neighbouring telluric lines. We do believe, however, that the fitted Gaussian provides an objective measure of the gradual changes in the emission-line strength. We omitted the saturated Hα line profiles, of course. One example of a Gaussian fit is in Fig. 3 to show where the FWHM and Ip were measured.
 |
Fig. 3 An example of the Gaussian fit to an Hα line profile, which also shows the derived quantities Ip and FWHM. Dashed line: the observed Hα profile; solid line: the Gaussian fit to it; dotted line: the continuum level. |
Figure 4 shows the time variations of the FWHM and Ip. An interesting finding is that the secular variations of these two quantities are anticorrelated with each other. The apparently increased scatter of both dependencies between RJDs ≈ 50 000 and 52 000 is caused solely by the lower resolution in intensity of the Ondřejov Reticon spectra taken prior RJD = 52 0001.
 |
Fig. 4 The secular time variations of Ip (upper panel) and FWHM (bottom panel) of the Hα line. The time on abscissa is in RJD = HJD-2 400 000. The open symbols denote measurements from the Ondřejov Reticon detector, capable of distinguishing only 4000 intensity steps, which is why these measurements deviate systematically from the rest. See the text for details. |
3. RV changes
3.1. Long-term and periodic RV changes and the new orbital solutions
Similar to Harmanec et al. (2000) and Miroshnichenko et al. (2002), we measured the steep wings of the Hα emission in all unsaturated profiles. The reasons the emission wings should provide a good estimate of the true orbital motion of the Be primary around the common centre of gravity with the secondary were recently summarized in detail by Ruždjak et al. (2009). To them, we can add that Poeckert & Marlborough (1978) modelled the Hα emission of γ Cas, and their model showed that the Hα emission wings originate in regions that are much closer to the star than the radiation that is forming the upper part of the line.
Moreover, we also attempted to measure the RVs of other available spectral lines (He i 6678 Å, Si II 6347 Å and Si II 6371 Å) to see if they undergo similar time changes. We primarily measured also the outer emission wings of these lines, but for the He i 6678 Å line it was possible to obtain a relatively accurate RV of the central absorption core. The RVs measured on the emission wings of the Si II 6347 Å and Si II 6371 Å lines were averaged.
Two methods of RV measurement were used as follows.
-
1.
Manual measurements were carriedout in the program SPEFO, written byDr. J. Horn and more recentlyimproved by Dr. P. Škodaand Mr. J. Krpata(see Horn et al. 1996; Škoda 1996).The user can slide the direct and reversed line profile on the com-puter screen until a perfect match of the selected parts of theprofiles is achieved. The advantage of this, admittedly a bit te-dious procedure, is that the user actually sees all measured lineprofiles and can avoid any flaws and blends with the telluric orweak stellar lines. It is invaluable for measurements of weakspectral lines, where any automatic method can be easily fooledby the noise. The same measuring technique has also been usedby Harmanec et al. (2000). Oneof us, JN, also re-measured all Reticon spectra used in theirstudy. Plots of the old vs. newmeasurements are available as Fig. A.4 inAppendix A. Considering the good agreementof both measurements, we used the mean value of the originaland new RV measurements for each studied feature. All lines(whenever available) were measured with this technique.
-
2.
Automatic measurements were obtained with a program written by AM, which also shifts the direct and reversed line-profile images for a selected range of relative intensities in the continuum units to find a minimum difference between them. The advantages of this method are that it is fast and impersonal. A potential danger is that it can be fooled by flaws and blends in some particular cases. Only the Hα emission wings were measured with this method.
We denote the RVs measured by the first method as manual and those measured by the second method as automatic to distinguish them in following sections. In Fig. 5 the automatic Hα emission RVs are plotted vs. the manually measured ones to see whether there is any systematic difference between the two methods. We fitted the data with a linear relation and somewhat surprisingly the slope was found to be 0.968 ± 0.009; i.e., the automatic method finds a slightly narrower total range of RV variations than the manual one. All individual RV measurements on the steep wings of the Hα emission are published in detail in Table 2 for the manual, and in Table 3 for the automatic measurements2.
The Hα emission RVs measured manually and automatically are plotted vs. time in Fig. 6. Additional time plots for other measured features can be found in Appendix A. Figure 6 shows that γ Cas exhibits long-term RV variations over several years, which seem to correlate with those of the peak intensity of the emission. To be able to search for periodic RV changes on a shorter timescale, one has first to remove the long-term ones. To check how robust the result is or how much it depends on the specific way of secular-changes removal, we applied three different approaches to this goal.
 |
Fig. 5 Comparison of the automatically measured Hα emission-wing RVs (ordinate = y) with those measured manually (abscissa = x). The dashed line is a fitted linear function y = 0.968 x. |
The first was to use the program HEC13 written by PH, which is based on the smoothing technique developed by Vondrák (1969, 1977) and which uses some subroutines kindly provided by Dr. Vondrák3. The level of smoothing is controlled by a smoothing parameter ϵ (the lower the value of ϵ, the higher the smoothing), and the smoothing routine can operate either through individual data points or through suitably chosen normal points, which are the weighted mean values of the observed quantity (RV in our case) over the chosen constant time intervals. In both cases, the O−C residua are provided for all individual observations. In these particular cases the following specifications for smoothing were used: ϵ = 5 × 10-16 and 200 d normals for the Hα emission-wing RVs measured by both methods, and ϵ = 1 × 10-16 and 200 d normals for the RVs measured on the He i 6678 Å absorption core. These particular choices of ϵ make the smoothing function follow only the secular RV variations. The solid lines in the three panels of Fig. 6 show the estimated long-term changes, which were then substracted from the original RVs. These prewhitened RVs were than searched for periodicity from 3000 0 down to 0
0 down to 0 5 with the program HEC27 (also written by PH), based on the PDM technique developed by Stellingwerf (1978). The θ-statistics periodograms for the manually and automatically measured Hα emission RVs are plotted in Figs. 7 and 8, respectively. The upper panels in both plots show the range of periods from 3000
5 with the program HEC27 (also written by PH), based on the PDM technique developed by Stellingwerf (1978). The θ-statistics periodograms for the manually and automatically measured Hα emission RVs are plotted in Figs. 7 and 8, respectively. The upper panels in both plots show the range of periods from 3000 0 down to 50
0 down to 50 0, while the periods from 2
0, while the periods from 2 0 down to 0
0 down to 0 5 are shown in the lower panels. The periodograms are flat, with θ close to a value of 1 for all periods between 2 and 50 d, which is why we do not show these parts of the periodograms in the figures. One can see that the combination of RVs from several observatories, which are different from each other in their local times, safely excluded the one-day aliases.
5 are shown in the lower panels. The periodograms are flat, with θ close to a value of 1 for all periods between 2 and 50 d, which is why we do not show these parts of the periodograms in the figures. One can see that the combination of RVs from several observatories, which are different from each other in their local times, safely excluded the one-day aliases.
 |
Fig. 6 Plots of RVs vs. RJD = HJD-2 400 000: Top panel: manually measured Hα emission-wing RVs. Bottom panel: automatically measured Hα emission-wing RVs. The solid lines in all panels represent the long-term RV change as derived with the program HEC13. The squares in both panels denote the local “systemic” velocities calculated with the program SPEL for individual data subsets. The dashed line represents Hermite-polynomial fit computed with program HEC36. See the text for details. |
 |
Fig. 7 Stellingwerf’s θ statistics for the manually measured RVs of the Hα emission wings plotted vs. frequency f. Upper panel: periods from 3000 |
 |
Fig. 8 Stellingwerf’s θ statistics for the automatically measured RVs of the Hα emission wings plotted vs. frequency f. Upper panel: periods from 3000 |
The deepest minimum in both periodograms at a frequency f ≈ 0.004910 d-1 corresponds to a period of P ≈ 203
 0. The two shallower peaks at lower frequencies in Figs. 7 and 8 correspond to the integer multiples of the 203 d period. The 203 d period was also detected in the measured RVs of other spectral lines, though with a larger scatter in the RV curves. These additional results are presented in Appendix A.
0. The two shallower peaks at lower frequencies in Figs. 7 and 8 correspond to the integer multiples of the 203 d period. The 203 d period was also detected in the measured RVs of other spectral lines, though with a larger scatter in the RV curves. These additional results are presented in Appendix A.
Since no obvious signs of the secondary companion are seen in the spectrum, we adopted γ Cas as a single-line spectroscopic binary. We derived a number of orbital solutions for the Hα emission RVs, prewhitened for the long-term changes with HEC13. We used the program SPEL (written by Dr. J. Horn and never published) for this purpose. The program has already been used in several previous studies, e.g., Harmanec (1983, 1984), Koubský et al. (1985), Štefl et al. (1990), and Horn et al. (1992, 1994).
Our first goal was to decide whether the orbital eccentricity found by Harmanec et al. (2000) is real or whether the orbit is actually circular as concluded by Miroshnichenko et al. (2002). In Table 4 the eccentric-orbit solutions for the manually and automatically measured Hα emission-wing RVs are compared. Lucy & Sweeney (1971) have pointed out that observational uncertainties may cause the estimated eccentricity to be biased when the eccentricity is low. The probability that the true eccentricity is zero can be calculated, and this is given in the column “L-S test”. If this probability is greater than 0.05 we accept the hypothesis that the true eccentricity is zero at a 5% confidence level.
To shed more light on the problem, we split both manually and automatically measured RVs into a number of data subsets, each of them covering a time interval not longer than three consecutive orbital periods and containing enough observations to define the orbital RV curve. We used the original, not the prewhitened RVs. The phase diagrams for a period P = 203 52 for all selected data subsets are shown in Fig. 9. We derived the elliptical-orbit solutions for them, again testing the reality of the non-zero orbital eccentricity after Lucy & Sweeney (1971). To always find the solution with the smallest rms error, we started the trial solutions for each subset with initial values of ω for four possible orientations of the orbit, namely 45°, 135°, 225°, and 315°.
52 for all selected data subsets are shown in Fig. 9. We derived the elliptical-orbit solutions for them, again testing the reality of the non-zero orbital eccentricity after Lucy & Sweeney (1971). To always find the solution with the smallest rms error, we started the trial solutions for each subset with initial values of ω for four possible orientations of the orbit, namely 45°, 135°, 225°, and 315°.
The corresponding orbital elements for the selected subsets, together with the Lucy-Sweeney test, are summarized in Table 5 for manually measured RVs and in Table 6 for automatically measured RVs. The results show very convincingly that the true orbit must be circular (or has a very low eccentricity, which is beyond the accuracy limit of our data). Although the L–S test detected a definite eccentricity for several subsets, the individual values of the longitude of periastron are basically accidental, and that is probably the strongest argument for the eccentric-orbit solutions not being trusted.
Eccentric-orbit solutions based on the Hα emission-wing RVs measured manually and automatically and prewhitened for the long-term changes with the program HEC13.
The eccentric-orbit solutions for the subsets of automatically measured Hα emission-wing RVs.
 |
Fig. 9 Phase diagrams for subsets of Hα emission-wing RVs measured manually. The ordinates of all plots are RVs in km s-1 and the individual subsets vertical axis is in RV and the different ranges reflect the fact that the original, not prewhitened RVs are used. Trial orbital solutions for these subsets are in Tables 5 and 6. |
Adopting the circular orbit from now on, we attempted to remove the long-term RV variations with a different approach. Using the manually measured Hα emission-wing RVs, we treated each data subset spanning no more than three orbital periods (last four subsets) and two orbital periods (remaining subsets) as data coming from separate spectrographs, allowing SPEL to derive individual “systemic velocities” for each subset. This way, the orbital solution was again free of the long-term changes but they were removed in discrete velocity steps. The corresponding orbital solution is in Table 7, and individual velocity levels (γ’s) are shown in the top panel of Fig. 6 and listed in Table A.2. At first sight, this way of removing the long-term changes might seem less accurate, but it leads to smaller rms error for the solution than the removal via HEC13. There are two reasons for that:
-
1.
The HEC13 program computes normal points from RV subsetscovering constant time intervals, while for γ velocities the length of subsets was chosen more suitably to our data distribution in time.
-
2.
The HEC13 program computes the normal points as weighted means, but the γ velocities computed with the SPEL program are elements of the Keplerian orbital model.
For completeness, a solution for an eccentric orbit was also derived but the L-S test gave the probability of 0.18, reassuring us that the eccentricity is spurious. Also for this method of the long-term removal the rms error of the orbital solution is better for the manually than for the automatically measured RVs.
Orbital elements obtained using RVs measured manually (3) and automatically (4) on the Hα line, with the removal of the long-term changes using different γ velocities for individual data subsets.
We tested yet another method of removing the long-term variations. It can only be used when one has a RV curve uniformly enough covered by observations. The RVs are averaged over chosen time intervals, and the Hermite polynomials are fitted through these averaged (normal) points. We used the program HEC23 to compute the normal points and program HEC36 to fit them4. We tentatively averaged the RVs over a 300 d and a 400 d interval. New orbital solutions were derived using RVs prewhitened this way. The rms error of the resulting solution was approximately the same as the rms error of the solution for RVs prewhitened HEC13. We decided to use this approach in another way. We used the systemic velocities derived with SPEL as normal points and fitted them with the Hermite polynomials using HEC36. The RJDs of RVs in a subset were averaged and the mean RJD was used as the epoch of the γ velocity. The same approach to computing epochs of normal points is also used in the program HEC13. This way we effectively removed one of the disadvantages of the previous method since HEC36 connects the normal points with a smooth curve, thus removing the discontinuous shifts introduced with the second method. The Hermite-polynomial fit is shown in the first two panels of Fig. 6. The O−C residua were again used to derive circular-orbit solutions with SPEL. These are presented in Table 8. As expected, the improvement in the resulting rms errors with the second method is relatively small.
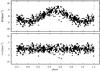 |
Fig. 10 Top panel: the net orbital RV curve corresponding to the circular-orbit solution (5) of Table 8. Bottom panel: the O−C residua from the orbital solution. Both plots have the same velocity scale, and the epoch of RVmin is used as a reference epoch. The short abcissa in the right upper corner of the top panel denotes the rms of 1 observation for the Keplerian fit No. 5. |
Orbital elements obtained using the Hα RVs measured manually (5) and automatically (6) and removing the long-term RV variations via a Hermite-polynomial fit through the locally derived γ velocities.
The net orbital RV curves and the corresponding O−C residua from the orbital solutions are shown in Fig. 10 for the manual and in Fig. 11 for the automatically measured Hα RVs. The rms errors per one observation of the Keplerian fit No. 5 based on manually measured RVs (No. 6 in the case of automatic measurements) are shown as short abscissae in the upper right corners of both figures. The RVs prewhitened for the long-term changes, on which these best solutions 5 and 6 are based, are also presented in Tables 2 and 3.
 |
Fig. 11 Top panel: the net orbital RV curve corresponding to the circular-orbit solution (6) of Table 8. Bottom panel: the O−C residua from the orbital solution. Both plots have the same velocity scale, and the epoch of RVmin is used as a reference epoch. The short abcissa in the right upper corner of the top panel denotes the rms of 1 observation for the Keplerian fit No. 6. |
We did several preliminary tests of the possible rapid variations of γ Cas. Although the results clearly demonstrated their presence, the quantitative results were inconclusive so we decided to postpone analysis of rapid spectral changes for a future study, based on dedicated series of whole-night spectral observations.
4. Interpretation of results
4.1. Spectral variations
We have confirmed the continuing presence of long-term variations in the Hα emission profile using the Gaussian fit and RV measurements. The former procedure gives more objective results than a direct measurement of the peak height and the full width of the line at half maximum (FWHM), because the observed height of the highest peak of a very strong emission line partly reflects the long-term V / R changes, while the measured FWHM can be affected by the presence of several telluric water vapour-lines of variable strength. Figure 4 shows that the Ip and FWHM of the Hα emission are anti-correlated over the interval covered by our observations and seem to also show some variability on shorter time scales. We carried out period searches for both these quantities prewhitened for the long-term changes, but no significant periodicities were detected, and trial plots of prewhitened data did not show any evidence of variations connected with the orbital period.
It is probable that the observed long-term changes reflect some variations in the density and/or the extent of the circumstellar disk around the Be primary. Using optical interferometry, Quirrenbach et al. (1997) and Tycner et al. (2006) were able to resolve the envelope around the primary component of γ Cas and estimate that its inclination must be higher than 46° and 55°, respectively. Adopting a reasonable assumption that the rotational axis of the disk is roughly perpendicular to the binary orbit, we can conclude that the binary system is also seen under an orbital inclination higher than some 45°. We then suggest the following possible interpretation of the observed changes.
It is very probable that the envelope around the Be primary is rotationally supported and that its linear rotational velocity decreases with the axial distance from the star. Regardless of the process causing secular variations of the disk, one can assume that the increase in the height of the emission peak reflects the presence of more emission power at lower rotational velocities, thus implying either an increase in the density of the outer parts of the disk and/or an increase in the geometrical extent of the disk. This must naturally decrease the observed FWHM of the emission as observed. This qualitative scenario seems to be supported by the line-profile calculations published by Silaj et al. (2010).
4.2. Orbital motion
As mentioned in Sect. 1, one of the principal motivations of this study was to resolve the differences in the orbital solutions obtained by Harmanec et al. (2000) and by Miroshnichenko et al. (2002) and to arrive at a more definitive set of the orbital elements. We were able to combine both independent datasets and complement them with more recent spectra. In Sect. 3 we carried out a number of various tests, analysing separately the RVs measured by a manual and an automatic technique. We also tested the effect of the different ways of data prewhitening on the resulting elements. Special attention was payed to the test of whether the orbit is actually circular or has a significant eccentricity.
The principal results are the following.
-
1.
The binary orbit of γ Cas is circular, at least withinthe limits of the accuracy of our data, as concluded byMiroshnichenko et al. (2002).
-
2.
The resulting value of the orbital period is now well constrained by the data at hand, and it is robust with respect to different ways of analysis. From all experiments, we were finding values between 203
 0 and 203
0 and 203 6, close to the value already found by Harmanec et al. (2000). An inspection of all trial solutions shows that the solutions based on manually measured RVs have rms errors that are systematically lower for ≈ 15% in comparison to the solutions for the automatically measured Hα emission-wing RVs. We therefore conclude that solution 5 of Table 8 is the best we can offer and suggest the following linear ephemeris for the epoch of RV minimum to be used in the future studies of this binary:
6, close to the value already found by Harmanec et al. (2000). An inspection of all trial solutions shows that the solutions based on manually measured RVs have rms errors that are systematically lower for ≈ 15% in comparison to the solutions for the automatically measured Hα emission-wing RVs. We therefore conclude that solution 5 of Table 8 is the best we can offer and suggest the following linear ephemeris for the epoch of RV minimum to be used in the future studies of this binary: 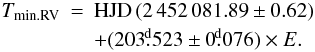 (1)
(1) -
3.
The semiamplitude of the orbital motion is close to 4 km s-1 for all solutions. The recommended value from solution 5 is K1 = 4.297 ± 0.090 km s-1, implying the mass function f(M) = 0.00168 M⊙. For comparison, Harmanec et al. (2000) and Miroshnichenko et al. (2002) obtained semiamplitudes of 4.68 ± 0.25 km s-1 and 3.80 ± 0.12 km s-1, respectively. If we adopt the inclination value i = 45° and the primary star mass M1 = 13 M⊙ suggested by Harmanec et al. (2000), we can estimate the secondary star mass M2 = 0.98 M⊙. If the system is at a post mass-transfer phase, then the secondary might be a hot helium star that could be directly detectable in the UV region of the electromagnetic spectrum.
Note: After our paper was accepted for publication, we had the privilege to read a preliminary version of another study of
γ Cas kindly communicated to us by Dr. Myron A. Smith and his coauthors. They analysed in particular a smaller and partly independent set of RVs to obtain their own orbital solution. Their results are compatible with our final solution within the respective error bars.
Online material
Appendix A: Details of spectroscopic observations and their analyses
A.1. Observational equipment
Here we provide more details on the spectra used in this study (see Table 1) and their reduction:
-
1.
Ondřejov spectra: All 439 spectra were obtained in the coudéfocus of the 2.0 m reflector and have a lineardispersion 17.2 Å.mm-1 and a 2–pixel resolution R ~ 12 600 (~11–12 km s-1 per pixel). The first 318 spectra were taken with a Reticon 1872RF detector. Complete reductions of these spectrograms were carried out by Mr. Josef Havelka, Mr. Pavol Habuda and by PH in the program SPEFO. The remaining spectra were secured with an SITe–5800 × 2000 CCD detector. Their initial reductions (bias substraction, flatfielding, extraction of 1D image and wavelength calibration) were done by MŠ with the IRAF program.
-
2.
DAO spectra: all 136 spectra were obtained in the coudé focus of the 1.22 m Dominion Observatory reflector by SY, who carried out initial reductions (bias substraction, flatfielding, extraction of 1D image). The wavelength calibration of the spectra was carried out by JN in SPEFO. The spectra were obtained with the 32121H spectrograph with the IS32R image slicer. The detectors were UBC–1 4096 × 200 CCD for the data prior to May 2005 and SITe–4 4096 × 2048 CCD for the data after May 2005. The spectra have a linear dispersion of 10 Å.mm-1 and 2–pixel resolution R ~ 21 700 (s~7 km s-1 per pixel).
-
3.
OHP spectra: Public ELODIE archive5 of the Haute Provence Observatory (Moultaka et al. 2004) contains 35 echelle spectra obtained at the 1.93 m telescope. They have resolution R ~ 42 000. Initial reductions (bias substraction, flatfielding, extraction of 1D image, and wavelength calibration) was carried out at the OHP. We only extracted and studied the red parts of the spectra.
-
4.
Ritter spectra: All 204 spectra were obtained with a fiber-fed echelle spectrograph at the 1 m telescope of the Ritter Observatory of the University of Toledo. We obtained spectra in form of ASCII table covering only region close to Hα spectra line. The resolution of the spectra is R ~ 26 000. Initial reductions of spectra (bias substraction, flatfielding, extraction of 1D image and wavelength calibration) were carried out at the Ritter Observatory with the IRAF program.
-
5.
Castanet Tolosan and OHP spectra: We downloaded these spectra from the Be Star Spectra database6. All of them were obtained by CB with several different spectrographs7. Only spectra with a resolution comparable to spectra obtained at the rest of observatories were used in the study. Initial reductions (bias substraction, flatfielding, extraction of 1D image, and wavelength calibration) were carried out by CB.
For all individual spectrograms, the zero point of the heliocentric wavelength scale was corrected via the RV measurements of selected unblended telluric lines in SPEFO (see Horn et al. 1996, for details).
Orbital elements obtained using RVs measured on the emission wings of He i 6678 Å line, absorption core of the He i 6678 Å line, and emission wings of the Si II 6347 Å and Si II 6371 Å lines. RJD = HJD–2 400 000.
A.2. Additional RV measurements
We measured RVs on emission wings and absorption core of He i 6678 Å and emission wings of Si II 6347 Å and Si II 6371 Å lines. The program SPEFO was used to the task. The precision of these RV measurements is quite low, since the relative flux in the lines is only several percent greater than in surrounding continuum (see Fig. 2). One could be easily misled during measurements, because measured lines are deformed with continuum fluctuations, and they blend with telluric lines. Despite these complications RVs measured on these lines exhibit long-term variations very similar to the variations that can be seen in Fig. 6. RVs measured on emission wings of He i 6678 Å line, absorption core of He i 6678 Å line, and emission wings of Si II 6347 Å and Si II 6371 Å lines are shown in Fig. A.1.
 |
Fig. A.1 A time plot of the RVs measured manually in SPEFO. Top panel: the emission wings of the He i 6678 Å line, middle panel: the absorption core of the He i 6678 Å line, bottom panel: the emission wings of Si II 6347 Å and Si II 6371 Å lines. The HEC13 model of the long-term variations is shown by a solid line in each panel. |
The long-term variations were removed with the program HEC13, using the 200 d normals and ϵ = 5 × 10-16. The model of long-term variations derived by HEC13 is shown in Fig. A.1. The residua were searched for periodicity using the HEC27 program. A period near 200 d was detected in all cases, although with a lower significance than the Hα emission RV (see Figs. 7 and 8). The θ statistics periodograms for trial periods from 3000 0 down to 50
0 down to 50 0 are shown in Fig. A.2, where the period P = 203
0 are shown in Fig. A.2, where the period P = 203 0 is denoted. The θ mininum for this period is not the dominant one only in the case of RV measured on the silicon lines. It is probably due to their low precision and/or incomplete removal of the long-term changes via HEC13.
0 is denoted. The θ mininum for this period is not the dominant one only in the case of RV measured on the silicon lines. It is probably due to their low precision and/or incomplete removal of the long-term changes via HEC13.
 |
Fig. A.2 The θ statistics periodograms. Top panel: the emission wings of He i 6678 Å line, middle panel: the absorption core of He i 6678 Å line, bottom panel: the emission wings of Si II 6347 Å and Si II 6371 Å lines. The period P = 203 |
The circular-orbit solutions were computed for all prewhitened RVs, keeping the orbital period fixed at the value P = 203 52. The corresponding orbital elements are in Table A.1.
52. The corresponding orbital elements are in Table A.1.
Data smoothing with different γ velocities derived with the SPEL program was tested as well. It led to none or a slight (lower than 5%) improvement in rms for the Keplerian fit.
In passing, we wish to mention that the Gaussian fits of the Hα line also provided individual RVs of this line. Not surprisingly, a Keplerian fit of these RVs resulted in a semiamplitude lower than was obtained for the directly measured RVs and for some 40% greater rms than that for our preferred solution 5.
 |
Fig. A.3 Phase diagrams of RVs prewithened with HEC13. Top panel: the emission wings of the He i 6678 Å line, middle panel: the absorption core of the He i 6678 Å line, bottom panel: the emission wings of the Si II 6347 Å and Si II 6371 Å lines. The period P = 203 |
A.3. Comparison
PH and JN measured RVs independently on spectra obtained with Reticon detector at Ondřejov observatory. Comparison of their results is shown in Fig. A.4. Dependency was fitted with linear function y = a.x. The resulting parameters are emission wings of Hα line a = 1.024 ± 0.006, emission wings of He i 6678 Å line a = 1.038 ± 0.024, absorption core of He i 6678 Å line a = 1.022 ± 0.008. Differences between the measurements of both authors are quite high for He i 6678 Å line emission wings measurements. It is probably because wings of the line are affected by the background noise and because the red peak of the He i 6678 Å line is very low at some point in the V / R cycle.
 |
Fig. A.4 RVs measured by JN plotted vs. RVs measured by PH on spectra obtained at Ondřejov Observatory with Reticon detector. Top panel: emission wings of Hα line, middle panel: emission wings of He i 6678 Å line, bottom panel: absorption core of He i 6678 Å line. |
Although the original Reticon detector and the currently used CCD detector were attached to the same camera of the coudé spectrograph and have the same spectral resolution, the control electronics of the Reticon detector allowed distinguishing only 4000 steps in intensity, while the CCD detector recognizes 60 000 intensity steps. This leads to a systematic difference for strong emission lines.
The program HEC13 with brief instructions how to use it is available to interested users at http://astro.troja.mff.cuni.cz/ftp/hec/HEC13
Both programs, written by PH, and the instructions how to use them, are available at http://astro.troja.mff.cuni.cz/ftp/hec/HEC36
For detailed information on the spectrographs used, see the CB homepage at http://astrosurf.com/buil/
Acknowledgments
We gratefully acknowledge the use of spectrograms of γ Cas from the public archives of the Elodie spectrograph of the Haute Provence Observatory. Our thanks are also due to Drs. P. Chadima, M. Dovčiak, P. Hadrava, J. Kubát, P. Mayer, P. Škoda, S. Štefl, M. Wolf, and P. Zasche, who obtained some of the spectra used in this study. Constructive criticism and a careful proofreading of the original version by an anonymous referee helped to improve the paper and are gratefully acknowledged. We thank Dr. M. A. Smith and his collaborators for allowing us to see a preliminary version of their new complex study of γ Cas before it was submitted for publication and for useful comments. This research was supported by the grants 205/06/0304, 205/08/H005, and P209/10/0715 of the Czech Science Foundation, from the Research Programme MSM0021620860 Physical study of objects and processes in the solar system and in astrophysics of the Ministry of Education of the Czech Republic, and from the research project AV0Z10030501 of the Academy of Sciences of the Czech Republic. The research of J.N. was supported from the grant SVV-263301 of the Charles University of Prague, while P.K. was supported from the ESA PECS grant 98058. We acknowledge the use of the electronic database from the CDS Strasbourg, and the electronic bibliography maintained by the NASA/ADS system.
References
- Cowley, A. P., Rogers, L., & Hutchings, J. B. 1976, PASP, 88, 911 [Google Scholar]
- Harmanec, P. 1983, Bull. Astr. Inst. Czechosl., 34, 324 [NASA ADS] [Google Scholar]
- Harmanec, P. 1984, Bull. Astr. Inst. Czechosl., 35, 164 [Google Scholar]
- Harmanec, P. 2002, in Exotic Stars as Challenges to Evolution, ed. C. A. Tout, & W. van Hamme (San Francisco, USA: ASP), ASP Conf. Ser., 279, 221 [Google Scholar]
- Harmanec, P., Habuda, P., Štefl, S., et al. 2000, A&A, 364, L85 [NASA ADS] [Google Scholar]
- Horn, J., Hubert, A. M., Hubert, H., Koubský, P., & Bailloux, N. 1992, A&A, 259, L5 [NASA ADS] [Google Scholar]
- Horn, J., Koubský, P., Hadrava, P., et al. 1994, A&AS, 105, 119 [NASA ADS] [Google Scholar]
- Horn, J., Kubát, J., Harmanec, P., et al. 1996, A&A, 309, 521 [NASA ADS] [Google Scholar]
- Jarad, M. M. 1987, J. Space Astron. Res., 4, 87 [NASA ADS] [Google Scholar]
- Koubský, P., Horn, J., Harmanec, P., et al. 1985, Inf. Bull. Variable Stars, 2778, 1 [NASA ADS] [Google Scholar]
- Lucy, L. B., & Sweeney, M. A. 1971, AJ, 76, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Miroshnichenko, A. S., Bjorkman, K. S., & Krugov, V. D. 2002, PASP, 114, 1226 [NASA ADS] [CrossRef] [Google Scholar]
- Moultaka, J., Ilovaisky, S. A., Prugniel, P., & Soubiran, C. 2004, PASP, 116, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Poeckert, R., & Marlborough, J. M. 1978, ApJ, 220, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Quirrenbach, A., Bjorkman, K. S., Bjorkman, J. E., et al. 1997, ApJ, 479, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, R. D., & Smith, M. A. 2000, ApJ, 540, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Ruždjak, D., Božić, H., Harmanec, P., et al. 2009, A&A, 506, 1319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Secchi, A. 1866, Astron. Nachr., 68, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Silaj, J., Jones, C. E., Tycner, C., Sigut, T. A. A., & Smith, A. D. 2010, ApJS, 187, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Škoda, P. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 187 [Google Scholar]
- Smith, M. A., Henry, G. W., & Vishniac, E. 2006, ApJ, 647, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Štefl, S., Harmanec, P., Horn, J., et al. 1990, Bull. astr. Inst. Czechosl., 41, 29 [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Tycner, C., Gilbreath, G. C., Zavala, R. T., et al. 2006, AJ, 131, 2710 [NASA ADS] [CrossRef] [Google Scholar]
- Vondrák, J. 1969, Bull. Astr. Inst. Czechosl., 20, 349 [Google Scholar]
- Vondrák, J. 1977, Bull. Astr. Inst. Czechosl., 28, 84 [Google Scholar]
All Tables
Eccentric-orbit solutions based on the Hα emission-wing RVs measured manually and automatically and prewhitened for the long-term changes with the program HEC13.
The eccentric-orbit solutions for the subsets of automatically measured Hα emission-wing RVs.
Orbital elements obtained using RVs measured manually (3) and automatically (4) on the Hα line, with the removal of the long-term changes using different γ velocities for individual data subsets.
Orbital elements obtained using the Hα RVs measured manually (5) and automatically (6) and removing the long-term RV variations via a Hermite-polynomial fit through the locally derived γ velocities.
Orbital elements obtained using RVs measured on the emission wings of He i 6678 Å line, absorption core of the He i 6678 Å line, and emission wings of the Si II 6347 Å and Si II 6371 Å lines. RJD = HJD–2 400 000.
All Figures
 |
Fig. 1 Recent evolution of the Hα line profile. Mid-exposure times of the displayed spectra are in RJD = HJD–2 400 000. |
| In the text | |
 |
Fig. 2 Recent evolution of the He i 6678 Å (left), Si II 6347 Å, and Si II 6371 Å (right) line profiles. Mid-exposure times of the displayed spectra are in RJD = HJD–2 400 000. The vertical axis is in the units of the continuum flux. |
| In the text | |
 |
Fig. 3 An example of the Gaussian fit to an Hα line profile, which also shows the derived quantities Ip and FWHM. Dashed line: the observed Hα profile; solid line: the Gaussian fit to it; dotted line: the continuum level. |
| In the text | |
 |
Fig. 4 The secular time variations of Ip (upper panel) and FWHM (bottom panel) of the Hα line. The time on abscissa is in RJD = HJD-2 400 000. The open symbols denote measurements from the Ondřejov Reticon detector, capable of distinguishing only 4000 intensity steps, which is why these measurements deviate systematically from the rest. See the text for details. |
| In the text | |
 |
Fig. 5 Comparison of the automatically measured Hα emission-wing RVs (ordinate = y) with those measured manually (abscissa = x). The dashed line is a fitted linear function y = 0.968 x. |
| In the text | |
 |
Fig. 6 Plots of RVs vs. RJD = HJD-2 400 000: Top panel: manually measured Hα emission-wing RVs. Bottom panel: automatically measured Hα emission-wing RVs. The solid lines in all panels represent the long-term RV change as derived with the program HEC13. The squares in both panels denote the local “systemic” velocities calculated with the program SPEL for individual data subsets. The dashed line represents Hermite-polynomial fit computed with program HEC36. See the text for details. |
| In the text | |
 |
Fig. 7 Stellingwerf’s θ statistics for the manually measured RVs of the Hα emission wings plotted vs. frequency f. Upper panel: periods from 3000 |
| In the text | |
 |
Fig. 8 Stellingwerf’s θ statistics for the automatically measured RVs of the Hα emission wings plotted vs. frequency f. Upper panel: periods from 3000 |
| In the text | |
 |
Fig. 9 Phase diagrams for subsets of Hα emission-wing RVs measured manually. The ordinates of all plots are RVs in km s-1 and the individual subsets vertical axis is in RV and the different ranges reflect the fact that the original, not prewhitened RVs are used. Trial orbital solutions for these subsets are in Tables 5 and 6. |
| In the text | |
 |
Fig. 10 Top panel: the net orbital RV curve corresponding to the circular-orbit solution (5) of Table 8. Bottom panel: the O−C residua from the orbital solution. Both plots have the same velocity scale, and the epoch of RVmin is used as a reference epoch. The short abcissa in the right upper corner of the top panel denotes the rms of 1 observation for the Keplerian fit No. 5. |
| In the text | |
 |
Fig. 11 Top panel: the net orbital RV curve corresponding to the circular-orbit solution (6) of Table 8. Bottom panel: the O−C residua from the orbital solution. Both plots have the same velocity scale, and the epoch of RVmin is used as a reference epoch. The short abcissa in the right upper corner of the top panel denotes the rms of 1 observation for the Keplerian fit No. 6. |
| In the text | |
 |
Fig. A.1 A time plot of the RVs measured manually in SPEFO. Top panel: the emission wings of the He i 6678 Å line, middle panel: the absorption core of the He i 6678 Å line, bottom panel: the emission wings of Si II 6347 Å and Si II 6371 Å lines. The HEC13 model of the long-term variations is shown by a solid line in each panel. |
| In the text | |
 |
Fig. A.2 The θ statistics periodograms. Top panel: the emission wings of He i 6678 Å line, middle panel: the absorption core of He i 6678 Å line, bottom panel: the emission wings of Si II 6347 Å and Si II 6371 Å lines. The period P = 203 |
| In the text | |
 |
Fig. A.3 Phase diagrams of RVs prewithened with HEC13. Top panel: the emission wings of the He i 6678 Å line, middle panel: the absorption core of the He i 6678 Å line, bottom panel: the emission wings of the Si II 6347 Å and Si II 6371 Å lines. The period P = 203 |
| In the text | |
 |
Fig. A.4 RVs measured by JN plotted vs. RVs measured by PH on spectra obtained at Ondřejov Observatory with Reticon detector. Top panel: emission wings of Hα line, middle panel: emission wings of He i 6678 Å line, bottom panel: absorption core of He i 6678 Å line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


